Synthesis of Reversible Circuits with Reduced Nearest-Neighbor Cost Using Kronecker Functional Decision Diagrams

Abstract

Motivated by the importance of fault tolerance in quantum computing, there has been renewed interest in quantum circuits that are realized with Clifford+T gates. Quantum computers that are based on ion-trap technology, superconducting, and quantum dots need to fulfill certain nearest-neighbor (NN) constraints. Fault-tolerant implementations of quantum circuits also require restricted interactions among neighboring quantum bits. The insertion of SWAP-gates is often deployed to make quantum circuits nearest-neighbor (NN) compliant. As quantum operations are prone to various errors, it is important to reduce the nearest-neighbor cost (NNC) which is a marker to the number of SWAP-gates needed to make a quantum circuit NN-compliant. Such an optimization problem arises while synthesizing reversible circuits using the Kronecker functional decision diagram (KFDD). In this work, we propose a method based on KFDD that reduces NNC during synthesis. Considering the Clifford+T quantum mapping for NOT, CNOT, and Toffoli (NCT) gates, and mixed-polarity Peres (MPP) gates, NNC metrics are defined for reversible circuits. Governed by NNC metrics, the nodes are then ranked for reducing NNC in resulting reversible circuits. Furthermore, local transformations are applied on node functions while mapping a node to a cascade of reversible gates. Experimental results on several benchmark functions reveal that the proposed synthesis technique reduces NNC in many cases while slightly impacting the number of qubits, T-depth, and T-count. Compared to prior methods based on functional decision diagrams or binary decision diagrams, the proposed synthesis technique reduces quantum cost for NCV-realizations (i.e., with NOT, CNOT, V, and V$^\dagger$ gates) in most of the cases.

1 Introduction

With the shrinking of transistor size according to Moore’s law, the ongoing miniaturization of integrated circuits will reach soon its limits [2, 5, 28]. Shrinking transistor sizes has become one of the major barriers in the development of circuits to provide an exponential increase of computing power [5, 28]. As a new computation paradigm, quantum computing, which performs computation using properties of quantum mechanics and processes information in terms of quantum bits (or, for short, qubits) instead of just classical bits, provides a promising alternative to further satisfy the needs for more computational power [2, 5, 16]. It has been shown that a quantum computer could efficiently solve certain problems (e.g., database search, integer factorization, graph problems) which have no efficient solution on a classical computer [2, 5, 16, 18, 26].

In recent years, the physical realizations of quantum computers have received significant attention [4]. Companies, such as IBM, Intel, Google, and Microsoft had started developments toward the realization of actual quantum computers for practical purposes [4]. Moreover, IBM, Intel, and Google have all announced their quantum devices with around 50-70 qubits [12]. Motivated by this, the synthesis of quantum circuits has become an active research area [2, 4, 5, 9, 12, 18]. As quantum logic synthesis is a complex and challenging problem, Boolean functions, which constitute a major component in many quantum algorithms (e.g., the Oracle function in the Deutsch Algorithm or Grover’s database search as well as the modular exponentiation in Shor’s factorization algorithm), are usually treated separately using a two-step approach [2, 17, 18, 26]. First, a reversible circuit is designed for the desired Boolean function using established reversible gate libraries [23, 29]. Then, the resulting reversible circuit is mapped into a functionally equivalent quantum circuit by decomposing reversible gates into elementary quantum gates [4, 17, 18]. Accordingly, how to efficiently realize reversible circuits has received significant interest [4, 29].

There have been several functional and structural synthesis methods for reversible circuits proposed [29]. Such as transformation based synthesis methods [15], the positive-polarity Reed-Muller expansion based synthesis method [8], the one-pass synthesis method using a quantum multiple-valued decision diagram to represent the function matrix for improving the limited scalability of functional synthesis methods [29], exclusive-sum-of-products expansion based synthesis methods [7], as well as hierarchical synthesis methods including lookup-table networks based [21] or decision diagrams (DD) based synthesis methods [1, 3, 23, 24]. Although functional methods outperform others in terms of the cost of the synthesized circuits, they are limited to small functions [1, 29]. Consequently, structural or hierarchical synthesis methods which can offer satisfactory scalability have gained more attractions.

DD-based methods are intended for the synthesis of functions with a large number of variables [23, 24]. Compared to other structural methods, although DD-based methods incurs a large number of ancilla qubits, they can achieve low quantum cost, and thus can reduce the cost that makes the quantum realizations fault tolerant [14, 21]. Furthermore, for reducing the number of qubits required for the reversible circuits generated from DDs, techniques including using Davio decompositions [22], applying local transformations on the function represented by a node [3], as well as sorting the ordering of nodes to be mapped by using dependency matrices to express dependencies between nodes [23] or by using genetic algorithm [1] had been proposed.

The decoherence of quantum states while quantum systems interact with environment will result in error and consequent failure of computation, as a result, quantum circuits need to be fault-tolerant in a practical implementation [14, 16]. Because the gates can be implemented in a fault-tolerant way, and the fault-tolerant implementations of the gates are known for most technologies that are considered promising for large-scale quantum computing, there has been renewed interest in using Clifford+T library to realize quantum circuits [2, 21, 29]. Quantum computers that are based on ion-trap technology, superconducting, and quantum dots need to fulfill certain physical constraints [4, 5, 26, 27]. Fault-tolerant implementations of quantum circuits also require restricted interactions among neighboring quantum bits [4, 14]. While realizing a given quantum functionality to a given quantum architecture, in order to achieve high fidelity, the so-called nearest-neighbor (NN) constraints imposed by lattice models, which require that quantum operations can be performed only between adjacent qubits [5, 26, 27], or the coupling constraints imposed by IBM quantum architectures, which are also called CNOT-constraints and allow quantum operations applied only between certain pairs of qubits on the coupling graph [4], must be complied with.

Usually, to realize reversible circuits to a quantum architecture, gate decomposition is first performed to decompose reversible gates in the circuit into quantum gates from a particular gate library, and then, qubit placement or qubit mapping is conducted to convert the resulting quantum circuits to satisfy the NN-constraints or coupling constraints at the quantum circuit level [4, 5, 9, 10, 12, 19, 27]. However, by combining gate decomposition and qubit mapping, NN-constraints or coupling constraints can also be addressed at the reversible logic level by defining proper cost metrics for the nearest-neighbor cost (NNC) [11, 26], designing nearest-neighbor templates [19], or computing the optimal combination of SWAPs and templates [17].

Different from the binary decision diagram (BDD) or the functional decision diagram (FDD) which are built by carrying out only Shannon decompositions or Davio decompositions over the variables of a function, the Kronecker FDD (KFDD) is built by applying Shannon and Davio decompositions over the variables. The KFDD as a generalization of the BDD and the FDD always will be more compact than the two [6]. Hence, the reversible circuits synthesized using the KFDD are potentially better than which synthesized using the BDD or the FDD. While synthesizing reversible circuits using the KFDD, although how to reduce the quantum cost and the number of qubits has been extensively researched, the restricted interactions between quibts are rarely considered.

In this work, we focus on the NN-constraints. By using gates from the Clifford+T library which are also supported by IBM quantum architectures [4] to realize reversible circuits, we attempt to handle the NN-constraints at the reversible logic level while synthesizing reversible circuits from the KFDD using NOT, CNOT, Toffoli and mixed-polarity Peres (MPP) gates. A common way to make a quantum circuit nearest-neighbor (NN) compliant is to apply SWAP-gates for quantum gates over non-adjacent qubits [5, 10, 19]. The insertion of SWAP-gates increases the total number of quantum gates, and thus affects the operational reliability of quantum circuits [4, 9]. Therefore, it is necessary to keep the NNC, which is a marker to the number of SWAP-gates needed to make a quantum circuit NN-compliant, as low as possible.

The main contributions of this work are listed as follows.

• 1) The NN-constraints are handled at the reversible logic level while synthesizing reversible circuits using the KFDD. It is an attempt to combine reversible logic synthesis, gate decomposition, and qubit mapping in one synthesis flow.

• 2) The Clifford+T quantum mappings of different MPP gates are presented.

• 3) NNC metrics for the reversible logic level are defined by considering the Clifford+T quantum mapping for the Toffoli and MPP gates.

• 4) Strategies guided by NNC metrics are presented to rank the ordering of nodes to be mapped for reducing the NNC while synthesizing reversible circuits using the KFDD.

The rest of this paper is structured as follows: Section 2 first briefly introduces reversible and quantum circuits, and then presents the Clifford+T quantum mappings of MPP gates and the NNC metrics defined for the NOT, CNOT, Toffoli, and MPP gates. Section 3 describes the KFDD and dependency matrices. In Sect. 4, the mapping of nodes by node dependency and by using local transformations are first introduced to keep the paper self-contained, and then, the synthesis of reversible circuits using the KFDD by combining the dependency matrix and local transformations is described, at last, the proposed synthesis method is detailed. Finally, the obtained experimental results are summarized in Sect. 5 while the paper is concluded in Sect. 6.

2 Reversible and Quantum Circuits

A reversible gate realizes a reversible function. A reversible circuit is a cascade of reversible gates without fanout or feedback [28].

In this work, graphic forms are adopted to illustrate a reversible gate or circuit, also a quantum gate or circuit. In the graphic form of a gate or circuit, the horizontal lines are called circuit lines, or, for short, lines. The symbols located on the left of a line indicate the input of the line. Whereas the symbols located on the right of a line indicate the output of the line.

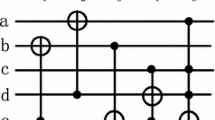
Figure 1 presents the graphic illustrations of the NOT, CNOT and Toffoli gates which compose the NCT library [2]. The symbol ‘$\oplus$’ in Fig. 1 represents the exclusive-or operation.

Fig. 1

NCT gate library: (a) NOT gate, (b) CNOT gate, (c) Toffoli gate

For evaluating the quality of reversible circuits, the number of lines (or, for short, #lines) and quantum cost which depends on the quantum gate library used while realizing reversible circuits are often taken into account. A frequently used quantum gate library is the NCV library which is composed of the NOT, CNOT, V, and V$^\dagger$ gates [2]. Because the gates can be implemented in a fault-tolerant way and are supported by IBM quantum architectures, there has been renewed interest in using Clifford+T library to realize quantum circuits [2, 4, 21, 29].

When the NCV library is used, the quantum cost of a circuit is usually measured by NCV-cost. The NCV-cost of a reversible gate is equal to the number of elementary quantum operations required to implement its functionality [13]. Both the NOT gate and the CNOT gate have an NCV-cost of 1 [2]. The NCV-cost of the Toffoli gate is 5 [2]. For a reversible circuit, the NCV-cost is the cumulative NCV-cost sum of the reversible gates in the circuit.

When the Clifford+T library is used, the quantum cost of a circuit is often measured by T-count and also by T-depth [2, 21, 29]. This is due to the high cost of fault tolerant implementations of the T gate, exceeding the cost of Clifford group gates (CNOT, H, S gates) by as much as a factor of a hundred or more [18]. The T-count of a circuit is the total number of T and T$^\dagger$ gates in the circuit. Whereas the T-depth of a circuit is the number of T or T$^\dagger$ gates that have to be processed sequentially [2]. In addition, since quantum operations are prone to various errors, the number of quantum gates (or, for short, #QG) in the circuit is also an important cost metric for evaluating a quantum circuit [4, 9].

Figure 2 graphically illustrates the mixed-polarity Peres (MPP) gates. Using MPP gates to synthesize reversible circuits helps reduce the quantum cost [3]. The NCV-cost of MPP gates are all 4 [3]. In the graphic forms of NCT or MPP gates as presented in Fig. 1 or Fig. 2, the lines on which symbols ‘$\bullet$’, ‘$\circ$’, ‘$\blacktriangle$’, ‘$\vartriangle$’, or ‘$\square$’ are located are considered as control lines. They take A or B as the input. The line on which the symbol ‘$\oplus$’ is located is the target line. It takes C as the input.

Fig. 2

MPP gate library: (a) Peres gate, (b) Peres gate with the first control negated, (c) inverse Peres gate, (d) or-Peres gate

According to the Clifford+T quantum mappings of Toffoli gates with different polarities [2], by using equivalence and permutation, the Clifford+T quantum mappings of different MPP gates can be derived. Figure 3 presents the Clifford+T quantum mappings of different MPP gates. To keep the paper self-contained, Fig. 3(e) presents the Clifford+T quantum mapping of the Toffoli gate [2]. As can be seen from Fig. 3, the T-count and the T-depth of the Toffoli and MPP gates are 7 and 3, respectively. The #QG of the Peres gate, Peres gate with the first control negated, and inverse Peres gate are all 15. Whereas, the #QG of the or-Peres gate and Toffoli gate are both 16.

Fig. 3

Clifford+T quantum mappings of different MPP gates and the Toffoli gate: (a) Peres gate, (b) Peres gate with the first control negated, (c) inverse Peres gate, (d) or-Peres gate, (e) Toffoli gate

For making a quantum circuit NN-compliant, a common way is to apply SWAP-gates for two-qubit quantum gates over non-adjacent qubits [5, 10, 19]. Accordingly, for evaluating the effort to convert a quantum gate or quantum circuit to be NN-compliant, the NNC metrics for a quantum gate or quantum circuit which are defined as the number of SWAP-gates applied are proposed [10, 11]. The NNC of a quantum gate can directly be determined by considering the distance between the control line and the target line [11, 19]. Obviously, single-qubit quantum gates (e.g., the NOT, T, or H gates) have an NNC of 0.

By considering NCV quantum mapping for multiple-control Toffoli gates, Kole et al. [11] proposed NNC metrics for the reversible logic level. In this work, by considering the Clifford+T quantum mapping for NCT and MPP gates, the NNC metrics for NCT and MPP gates for the reversible logic level are defined.

Assuming a numerical encoding of the circuit lines from the topmost line to the undermost line. For the CNOT, Toffoli, or MPP gates presented in Fig. 1 or Fig. 2, and the Clifford+T quantum mappings of the Toffoli gate and different MPP gates presented in Fig. 3, suppose that the lines taking A, B, or C as the input are numerically encoded by $L_A$, $L_B$, and $L_C$, respectively. In the following, those lines are called line $L_A$, line $L_B$, and line $L_C$, respectively.

In this work, NCT and MPP gates are used to synthesize reversible circuits from the KFDD. That is, the reversible circuits are composed of NOT, CNOT, Toffoli, and MPP gates. To realize a reversible circuit using gates from the Clifford+T library, a NOT or CNOT gate in the reversible circuit is directly mapped to a NOT or CNOT gate, without the need to be decomposed. Whereas, the Toffoli and MPP gates in the reversible circuit need to be mapped or decomposed into the quantum gate cascades as shown in Fig. 3. If the Clifford+T quantum mappings presented in Fig. 3 are considered as templates, the mapping or decomposition of a Toffoli or an MPP gate is to substitute the reversible gate by the corresponding template. Single-qubit quantum gates have an NNC of 0. Thus, for making the resulting quantum circuits NN-compliant, only whether those CNOT gates are NN-compliant needs to be considered.

It is usually assumed that two SWAP-gates are required in order to decrease the distance between the control and the target line of a two-qubit gate by one (one SWAP-gate for moving the control and the target line together, another to restore the original order) [11, 19]. Considering the first CNOT gate presented in Fig. 3(a) as an example. When the CNOT gate is not NN-compliant (i.e., $|L_A-L_B|>1$), firstly, $|L_A-L_B|-1$ SWAP-gates are inserted in front of the CNOT gate for moving the control and the target line of the CNOT gate being next to each other, and then, $|L_A-L_B|-1$ SWAP-gates are inserted behind the CNOT gate for restoring the original order of lines.

Example 1

Figure 4 presents a trivial circuit with 4 lines and a CNOT gate which takes line $L_A$ as the control line and line $L_B$ as the target line, as well as the transformed circuit which satisfies the NN-constraints. Assuming that $L_A=1$ and $L_B=4$.

Known that $|L_A-L_B|=3$. Then for converting the CNOT gate presented in Fig. 4(a) to be NN-compliant, 2 SWAP-gates are successively inserted in front of the CNOT gate to make the control and the target line of the CNOT gate adjacent. After the CNOT operation has been performed, 2 SWAP-gates are successively inserted behind the CNOT gate to restore the original order of lines. Consequently, $2(|L_A-L_B|-1)=4$ SWAP-gates are inserted in the circuit, the transformed circuit presented in Fig. 4(b) is resulted.

Fig. 4

SWAP insertion: (a) the original circuit, (b) the transformed circuit

As can be seen from Fig. 3(a), the Clifford+T quantum mapping of a Peres gate has 6 CNOT gates. To convert those CNOT gates to be NN-compliant, $4(|L_A-L_B|-1)$, $4(|L_A-L_C|-1)$, and $4(|L_B-L_C|-1)$ SWAP-gates are required for the two CNOT gates applied between line $L_A$ and line $L_B$, the two CNOT gates applied between line $L_C$ and line $L_A$, and the two CNOT gates applied between line $L_B$ and line $L_C$, respectively. Consequently, to convert the Clifford+T quantum mapping of a Peres gate as shown in Fig. 3(a) to be NN-compliant, a total of $4(|L_A-L_B|-1)+4(|L_B-L_C|-1)+4(|L_A-L_C|-1)$ SWAP-gates are needed. In a similar way, the number of SWAP-gates needed to make the Clifford+T quantum mappings of a Toffoli gate, a Peres gate with the first control negated, an inverse Peres gate, or an or-Peres gate as shown in Fig. 3 to be NN-compliant can be derived.

In conclusion, by the CNOT gate presented in Fig. 1(b) as well as the Clifford+T quantum mappings presented in Fig. 3, the NNC of the CNOT, Toffoli, and MPP gates can be evaluated using the equations as follows.

$$\begin{aligned} {\left\{ \begin{array}{ll} {\begin{matrix} NNC(CNOT)&{}=2(|L_A-L_C|-1)\\ NNC(TOF)&{}=4(|L_A-L_C|-1)\\ &{}+4(|L_B-L_C|-1)\\ &{}+6(|L_A-L_B|-1)\\ NNC(MPP)&{}=4(|L_A-L_C|-1)\\ &{}+4(|L_B-L_C|-1)\\ &{}+4(|L_A-L_B|-1) \end{matrix}} \end{array}\right. } \end{aligned}$$

(1)

By using the above equations, the NNC of a circuit can be evaluated at the reversible logic level. The T-count, #QG, or NNC of a reversible circuit is the cumulative sum of the T-count, #QG, or NNC of the reversible gates in the circuit, respectively. Similarly, the T-depth of a reversible circuit is estimated as the cumulative sum of the T-depth of the reversible gates in the circuit.

The insertion of SWAP-gates affects the operational reliability of quantum circuits [9]. Thus, it is important to reduce the NNC which is a marker to the number of SWAP-gates needed to make a quantum circuit NN-compliant. By using the NNC metrics in Eq. (1), the NNC can be reduced (i.e., the NN-constraints can be handled) at the reversible logic level while synthesizing a reversible circuit. Therefore, it is possible to combine reversible logic synthesis, gate decomposition, and qubit mapping in one synthesis flow.

At the quantum circuit level, a SWAP-gate is usually realized using 3 CNOT gates [12] as shown in Fig. 5. Therefore, known the NNC of a circuit, the number of quantum gates needed to convert the quantum circuit to be NN-compliant is 3 times of the NNC.

Fig. 5

Quantum realization of the SWAP-gate

3 KFDD and Dependency Matrices

3.1 KFDD

Let $f:B^n\rightarrow {B}$ be a totally defined Boolean function and $X=\{x_1,x_2,\cdots ,x_n\}$ be the corresponding set of primary variables. The function f can be decomposed over the primary variable set X using the following well-known decomposition types [20].

$$\begin{aligned} {\left\{ \begin{array}{ll} f=\bar{x}_i{f_{\bar{x}_i}}\oplus {x}_i{f_{x_i}}\qquad &{}{Shannon}\\ f={f_{\bar{x}_i}}\oplus {x}_i({f_{\bar{x}_i}}\oplus {f_{x_i}})\qquad &{}{Positive\,{Davio}}\\ f={f_{{x}_i}}\oplus \bar{x}_i({f_{\bar{x}_i}}\oplus {f_{x_i}})\qquad &{}{Negative\,{Davio}} \end{array}\right. } \end{aligned}$$

(2)

where $f_{\bar{x}_i}$ and $f_{x_i}$ denote the cofactors of f with respect to ${x_{i}}=0$ and ${x_{i}}=1$ respectively, $\oplus$ is the exclusive-OR operation.

Definition 1

A KFDD for the function f is a rooted DAG $G=(V,E)$ with node set V and edge set E.

A KFDD for the function f is built by carrying out Shannon decomposition, positive or negative Davio decompositions as shown in Eq. (2) over X, with one type of decomposition per primary variable. An inner node in the KFDD is labeled with one of the primary variables and has exactly two successors, the low and the high successors. The terminal nodes of a KFDD indicate constant 0 or 1 and have no successors. The primary variable that labels an inner node $v_i\in {V}$ is denoted as $var(v_i)$ ($var(v_i)\in {X}$). The level at which node $v_i$ is positioned in the KFDD is denoted as $lev(v_i)$ ($lev(v_i)\ge {1}$). The root of the KFDD is positioned at the top level, the terminal 0 or 1 nodes are positioned at the $(n+1)$-th level. If node $v_j\in {V}$ is one of the descendants of node $v_i$ (i.e., $v_i$ is a paraent node of $v_j$), $lev(v_j)>lev(v_i)$. Since variable $x_j\in {X}$ labels all of the nodes positioned at one level in the KFDD, the level at which $x_j$ is positioned in the KFDD is denoted as $lev(x_j)$.

In this work, the conventions for a KFDD presented in [6] are complied with. Only the edge from node $v_i$ to its high successor (i.e., this edge takes node $v_i$ and its high successor as the tail and the head, respectively) can be a complemented edge, and only the terminal 1 node is used in a KFDD. The terminal 0 node is represented by a terminal 1 node pointed to by a complemented edge.

Suppose the low and high successors of node $v_i$ are nodes $v_j$ and $v_k$, respectively. Then the following definitions are presented.

Definition 2

The function represented by node $v_i$, which is denoted by $f_{v_i}$, can be derived by the following equations depending on the decomposition type of the variable $x_l=var(v_i)$.

$$\begin{aligned} {\left\{ \begin{array}{ll} f_{v_i}=\bar{x}_l{f_{v_j}}\oplus {x}_l{f_{v_k}}\qquad &{}{Shannon}\\ f_{v_i}={f_{v_j}}\oplus {x}_l{f_{v_k}}\qquad &{}{Positive\,{Davio}}\\ f_{v_i}={f_{v_j}}\oplus \bar{x}_l{f_{v_k}}\qquad &{}{Negative\,{Davio}} \end{array}\right. } \end{aligned}$$

where $f_{v_j}$ and $f_{v_k}$ are the functions represented by nodes $v_j$ and $v_k$, respectively. If the edge from node $v_i$ to node $v_k$ is a complemented edge, the function $f_{v_k}$ in above equations is complemented.

Definition 3

For an inner node $v_i$, if the function $f_{v_i}$ can be expressed as $f_{v_i}=var(v_i)\oplus {g}$ or $f_{v_i}=\overline{var(v_i)}\oplus {g}$, where the function g is independent of variable $var(v_i)$, then $v_i$ is called a linear node.

Fig. 6 presents sub-graphs for linear nodes in the KFDD. Note that in Fig. 6, a dashed (solid) edge having node $v_i$ as a tail means an edge from node $v_i$ to the low (high) successor of $v_i$. A white dot on a solid edge means that the edge is a complemented edge.

Fig. 6

Sub-graphs for linear nodes. The decomposition type of variable $var(v_i)$ is a: (a) Davio decomposition, (b) Shannon decomposition

As shown in Fig. 6, if $v_i$ is a linear node, by Definition 2 and Definition 3, it is known that its high successor (node $v_k$) must be the terminal 1 node and the edge from node $v_i$ to the terminal 1 node must not be a complemented edge when the decomposition type of variable $var(v_i)$ is a Davio decomposition, or there is $v_j=v_k$ and the edge from node $v_i$ to node $v_k$ must be a complemented edge when the decomposition type of variable $var(v_i)$ is a Shannon decomposition.

Variable nodes defined in the following are special kinds of linear nodes.

Definition 4

For a linear node $v_i$, if ${v_j}$ is the terminal 1 node, $v_i$ is called a variable node, due to the fact that $f_{v_i}=var(v_i)$ or $f_{v_i}=\overline{var(v_i)}$.

FDDs are special kinds of the KFDD [6]. An FDD for the function f is built by carrying out positive or negative Davio decompositions as shown in Eq. (2) over X, with one type of decomposition per primary variable.

3.2 Dependency Between Nodes and Dependency Matrices

Due to the sharing of nodes in FDDs or KFDDs, while mapping a node to a cascade of reversible gates (or, for simplicity, a reversible gate cascade or reversible cascade), an ancilla line is generally added to the circuit to store the result of the node function. In order to reduce the number of circuit lines required for the resulting circuits by reusing ancilla lines, Stojković et al. [23] proposed dependency between nodes in FDDs for ranking the ordering of nodes to be mapped and dependency matrices for expressing the dependency between nodes. In this work, dependency between nodes and dependency matrices are generalized to KFDDs.

For inner nodes $v_i$, $v_j$, and $v_k$ in a KFDD, suppose that node $v_k$ is a successor of both node $v_i$ and node $v_j$. Then the definitions of dependency between nodes are presented in the following.

Definition 5

Nodes $v_i$ and $v_j$ are strongly dependent on node $v_k$.

Definition 6

When the decomposition type of variable $var(v_i)$ is a Davio decomposition and node $v_k$ is the low successor of node $v_i$, or the decomposition type of variable $var(v_i)$ is a Shannon decomposition and $v_i$ is a linear node. If the decomposition type of variable $var(v_j)$ is a Davio decomposition and node $v_k$ is the high successor of $v_j$, or the decomposition type of variable $var(v_j)$ is a Shannon decomposition and $v_j$ is not a linear node, then node $v_i$ is weakly dependent on node $v_j$.

Fig. 7

Sub-graphs in which node $v_i$ weakly depends on node $v_j$: (a) the decomposition types of $var(v_i)$ and $var(v_j)$ are both Davio decompositions, (b) the decomposition types of $var(v_i)$ and $var(v_j)$ are Davio and Shannon decompositions, respectively, and node $v_j$ is not a linear node, (c) the decomposition types of $var(v_i)$ and $var(v_j)$ are Shannon and Davio decompositions, respectively, (d) the decomposition types of $var(v_i)$ and $var(v_j)$ are both Shannon decompositions and node $v_j$ is not a linear node

Figure  7 presents sub-graphs in which node $v_i$ weakly depends on node $v_j$. According to Definitions 5 and 6, if node $v_i$ strongly or weakly depends on node $v_j$, it is called that node $v_i$ depends on node $v_j$. Otherwise, it is called that node $v_i$ does not depend on node $v_j$, or node $v_i$ is independent of node $v_j$.

Suppose there are w inner nodes in a KFDD which constitute a set $V=\{v_i|1\le {i}\le {w}\}$. Then for using a dependency matrix to express the dependency between those w nodes, V is mapped onto the set $J=\{j|1\le {j}\le {w}\}$. In other words, every node in V is encoded by one and only one integer in the set J and every integer in the set J corresponds to one and only one node in V. Suppose that node $v_i$ is encoded by $j\in {J}$ which is also the row index or column index of the dependency matrix. Then in the dependency matrix, the j-th row and the j-th column are both correlated to node $v_i$. The j-th row indicates that node $v_i$ strongly or weakly depends on which nodes. Whereas the j-th column indicates which nodes weakly or strongly depend on node $v_i$. In the following, in the context of dependency matrices, node j or Node(j) is referred to as the node which is encoded by the integer $j\in {J}$. For a KFDD, suppose that $w_l$ is the number of nodes positioned at level l in the KFDD and w is the number of inner nodes in the KFDD. Then based on Definitions 5 and 6, the dependency matrix [23] is generalized to express the dependency between nodes in the KFDD as follows.

Definition 7

The level dependency matrix (LDM) with respect to the l-th level in the KFDD is a ${w_l}\times {w_l}$ matrix, whose element $d_{ij}$ is set to 1 when node i weakly depends on node j, or set to 0 when node i is independent of node j.

Definition 8

The diagram dependency matrix (DDM) for the KFDD is a ${w}\times {w}$ matrix, whose element $d_{ij}$ is set to 2 when node i strongly depends on node j, set to 1 when node i weakly depends on node j, or set to 0 when node i is independent of node j.

In a dependency matrix, if all of the elements of the i-th row have an value of 0, the row is called a zero row. The i-th row being a zero row implies that the mapping conditions for node i are satisfied. That is, node i can be mapped to a cascade of reversible gates.

4 Synthesis of Reversible Circuits With Reduced NNC Using the KFDD

4.1 Mapping Nodes By Node Dependency

For inner nodes $v_i$ and $v_j$ in a KFDD, when node $v_i$ strongly depends on node $v_j$, node $v_i$ has to be mapped after node $v_j$ [23]. Strong dependency between nodes assures the functional equivalence of the resulting reversible circuit to the original function by applying strong constraint on the ordering of nodes to be mapped. When node $v_i$ weakly depends on node $v_j$, node $v_i$ is preferred to be mapped after node $v_j$ [23]. Weak dependency aims at reusing ancilla lines by applying weak constraint on the ordering of nodes to be mapped.

Example 2 presented in the following is used to demonstrate the mapping of nodes by node dependency. Note that, if a node has been mapped into a reversible cascade, it is called a mapped node. Otherwise, it is called a node not mapped.

Example 2

Figure  8 presents a sub-graph for nodes $v_1$ and $v_2$ which is extracted from a KFDD and reversible cascades mapped for nodes $v_1$ and $v_2$ by using different ordering of nodes to be mapped. Following the conventions presented in Sect. 2, in Fig. 8(b) and (c), the symbols located on the left of a line indicate the input of the line, whereas the symbols located on the right of a line indicate the output of the line. In addition, the reversible cascade indicated by symbol ‘$v_i$’ ($1\le {i}\le {2}$) is the mapping result for node $v_i$. For the sake of the simplicity of description, suppose that $L_{v_3}$, $L_{v_4}$, and $L_{v_5}$ indicate the numerical encoding of the lines taking $f_{v_3}$, $f_{v_4}$, and $f_{v_5}$ as the input, respectively. Then the lines taking $f_{v_3}$, $f_{v_4}$, and $f_{v_5}$ as the input are called line $L_{v_3}$, line $L_{v_4}$, and line $L_{v_5}$, respectively.

The sub graph presented in Fig. 8(a) consists of 5 nodes which are all inner nodes in the complete KFDD. Assuming that $var(v_1)=var(v_2)=x_1$, and the decomposition type of $x_1$ is a positive Davio decomposition. Moreover, in the complete KFDD, there is not any other node which takes node $v_5$ as a successor excepting node $v_2$, and there is not any other node which takes node $v_4$ as a successor excepting nodes $v_1$ and $v_2$.

Known by Definitions 5 and 6, node $v_1$ strongly depends on nodes $v_3$ and $v_4$, node $v_2$ strongly depends on nodes $v_4$ and $v_5$, and node $v_1$ weakly depends on node $v_2$. According to Definition 2, there are $f_{v_1}=f_{v_4}\oplus {x_1}{f_{v_3}}$ and $f_{v_2}=f_{v_5}\oplus {x_1}{f_{v_4}}$.

Node $v_1$ strongly depends on nodes $v_3$ and $v_4$. Thus, nodes $v_3$ and $v_4$ should be mapped before node $v_1$. Similarly, nodes $v_4$ and $v_5$ should be mapped before node $v_2$. Here, we focus on the effect of mapping nodes by weak dependency. That is, we focus on the ordering of nodes $v_1$ and $v_2$ to be mapped.

Assuming that nodes $v_3$, $v_4$, and $v_5$ have been mapped into reversible cascades (which are not presented in Fig. 8(b) and (c)), and lines $L_{v_3}$, $L_{v_4}$, and $L_{v_5}$ have been used to store the results of the functions $f_{v_3}$, $f_{v_4}$, and $f_{v_5}$, respectively. Next, the impact of the ordering of nodes $v_1$ and $v_2$ to be mapped on the number of required lines is demonstrated.

If node $v_1$ is mapped before node $v_2$, by the expressions of the functions $f_{v_1}$ and $f_{v_2}$, the reversible cascade as shown in Fig. 8(b) is constructed. When mapping node $v_1$, because node $v_4$ has another parent node not mapped (i.e., node $v_2$), line $L_{v_4}$ can not be reused to store the result of $f_{v_1}$. An ancilla line with the initial value of 0 needs to be first added to the circuit, and then, the function $h_1={x_1}{f_{v_3}}\oplus {0}$ is synthesized to a Peres gate and a CNOT gate as shown in Fig. 8(b). The CNOT gate (the first CNOT gate presented in Fig. 8(b)) is used to recover the value on line $L_{v_3}$, becuase there may be other nodes not mapped in the complete KFDD which take $v_3$ as a successor in addition to node $v_1$. After that, the function $f_{v_1}=f_{v_4}\oplus {h_1}$ is synthesized to a CNOT gate (the second CNOT gate presented in Fig. 8(b)) and the added ancilla line is used to store the result of function $f_{v_1}$ as shown in Fig. 8(b). Node $v_4$ has two parent nodes (i.e., the nodes $v_1$ and $v_2$) in the complete KFDD, but node $v_1$ is a mapped node when mapping node $v_2$. Hence, while mapping node $v_2$, there is not any other node not mapped which takes node $v_4$ as a successor excepting node $v_2$. Meanwhile, there is not any other node in the complete KFDD which takes node $v_5$ as a successor excepting node $v_2$. Consequently, the function $f_{v_2}={x_1}{f_{v_4}}\oplus {f_{v_5}}$ is synthesized to a Peres gate by reusing line $L_{v_5}$ to store the result of function $f_{v_2}$. Note that, the output of line $L_{v_4}$ becomes a garbage output indicated by the symbol ‘$\mathrm {g}$’. The reversible cascade presented in Fig. 8(b) is composed of 2 Peres gates, 2 CNOT gates, and 5 lines.

However, since node $v_1$ weakly depends on node $v_2$, node $v_1$ is preferred to be mapped after node $v_2$. Therefore, by weak dependency, node $v_2$ is first mapped, and then node $v_1$. While mapping node $v_2$, because there is not any other node in the complete KFDD which takes node $v_5$ as a successor excepting node $v_2$, the function $f_{v_2}={x_1}{f_{v_4}}\oplus {f_{v_5}}$ is synthesized to a Peres gate and a CNOT gate by reusing line $L_{v_5}$ to store the result of function $f_{v_2}$. Node $v_4$ has two parent nodes (i.e., the nodes $v_1$ and $v_2$) in the complete KFDD, but node $v_2$ is a mapped node when mapping node $v_1$. Hence, while mapping node $v_1$, there is not any other node not mapped in the complete KFDD which takes $v_4$ as a successor excepting node $v_1$. As a result, $f_{v_1}={x_1}{f_{v_3}}\oplus {f_{v_4}}$ is synthesized to a Peres gate and a CNOT gate by reusing line $L_{v_4}$ to store the result of function $f_{v_1}$. The reversible cascade as shown in Fig. 8(c) is constructed. This reversible cascade is composed of 2 Peres gates, 2 CNOT gates, and 4 lines.

As can be seen from above, mapping nodes by weak dependency, excepting that line $L_{v_5}$ is reused to store the result of function $f_{v_2}$ while mapping node $v_2$, line $L_{v_4}$ is also reused to store the result of function $f_{v_1}$ while mapping node $v_1$, no extra ancilla lines need to be added to the circuit. As a result, the number of required lines is reduced.

Fig. 8

Sub-graph for nodes $v_1$ and $v_2$ as well as the constructed reversible cascades by using different ordering of nodes $v_1$ and $v_2$ to be mapped: (a) the sub graph for nodes $v_1$ and $v_2$, (b) node $v_1$ is mapped before node $v_2$, (c) node $v_2$ is mapped before node $v_1$

4.2 Mapping Nodes By Applying Local Transformations

While mapping a node, Bu and Wang [3] had detailed that which type of local transformations can be applied on the node function and the conditions to be satisfied for applying the local transformations, as well as the reversible cascades constructed for the node by applying different local transformations on the node function in their paper. More details about local transformations are referred to Ref. [3]. However, to keep the paper self-contained, Example 3 presented in the following is used to demonstrate the construction of a reversible cascade by applying local transformations on the node function while mapping a node.

Example 3

Figure  9 presents the sub-graph for node $v_1$ and the reversible cascades mapped for $v_1$. Suppose that $var(v_1)=x_1$ and the decomposition type of $x_1$ is a Shannon decomposition. In addition, nodes $v_2$ and $v_3$ are both inner nodes in the complete KFDD, and have been mapped into reversible cascades (which are not presented in Fig. 9) by using lines taking $f_{v_2}$ and $f_{v_3}$ as the input to store the results of function $f_{v_2}$ and function $f_{v_3}$, respectively, as shown in Fig. 9(b)-(f).

Known from Definition 2, $f_{v_1}={\bar{x}_1}f_{v_2}\oplus {{x_1}f_{v_3}}$, which is the original form of the expression of function $f_{v_1}$. When mapping node $v_1$ by this expression of function $f_{v_1}$, an ancilla line with the initial value of 0 is first appended to the circuit. And then, the functions $h_1={x_1}f_{v_3}\oplus {0}$ and $f_{v_1}={\bar{x}_1}f_{v_2}\oplus {h_1}$ are successively synthesized to reversible gates as shown in Fig. 9(b). The function $h_1$ is realized using a Toffoli gate. Whereas, the function $f_{v_1}={\bar{x}_1}f_{v_2}\oplus {h_1}$ is realized using a Peres gate with the first control negated and a CNOT gate. Note that, the CNOT gate is used to recover the value on the line taking $f_{v_2}$ as the input. The #lines, T-depth, T-count, and #QG of the reversible cascade presented in Fig. 9(b) are 4, 6, 14, and 32, respectively.

However, by applying local transformations on function $f_{v_1}$, the expression $f_{v_1}={x_1}(f_{v_2}\oplus {f_{v_3}})\oplus {f_{v_2}}$ can be derived. Node $v_1$ can be mapped into different reversible cascades by further applying local transformations on function $f_{v_1}$ as the four cases described in the following.

• (i) Case I. When nodes $v_2$ and $v_3$ both have other parent nodes not mapped in the complete KFDD in addition to node $v_1$, by successively synthesizing the functions $h_2=f_{v_2}\oplus {f_{v_3}}$, $h_3={x_1}{h_2}\oplus {0}$, $f_{v_1}=f_{v_2}\oplus {h_3}$, and $f_{v_3}={f_{v_2}}\oplus {h_2}$, the reversible cascade as shown in Fig. 9(c) is constructed. An ancilla line with the initial value of 0 is added to the circuit when synthesizing the function $h_3$ and is used to store the result of function $f_{v_1}$ when synthesizing $f_{v_1}=f_{v_2}\oplus {h_3}$. The #lines, T-depth, T-count, and #QG of the reversible cascade presented in Fig. 9(c) are 4, 3, 7, and 19, respectively.

• (ii) Case II. When node $v_2$ has other parent nodes not mapped in the complete KFDD in addition to node $v_1$, but node $v_3$ does not have any other parent node not mapped excepting node $v_1$, node $v_1$ can be mapped in a similar way as the above case. However, while mapping node $v_1$ in this case, node $v_3$ does not have any other parent node not mapped excepting node $v_1$. Hence, a Peres gate instead of a Toffoli gate is used to realize the function $h_3$, and the last function $f_{v_3}={f_{v_2}}\oplus {h_2}$, which is used to recover the value on the line taking $f_{v_3}$ as the input, does not need to be realized. As a result, the output of the line taking $f_{v_3}$ as the input becomes a garbage output indicated by the symbol ‘$\mathrm {g}$’. The constructed reversible cascade is presented in Fig. 9(d). The #lines, T-depth, T-count, and #QG of this reversible cascade are 4, 3, 7, and 17, respectively.

• (iii) Case III. When node $v_3$ has other parent nodes not mapped in the complete KFDD in addition to node $v_1$, but node $v_2$ does not have any other parent node not mapped excepting node $v_1$, by successively synthesizing the functions $h_4=f_{v_2}\oplus {0}$, $h_2=f_{v_3}\oplus {f_{v_2}}$, and $f_{v_1}={x_1}{h_2}\oplus {h_4}$, the reversible cascade as shown in Fig. 9(e) is constructed. An ancilla line with the initial value of 0 is appended to the circuit when synthesizing the function $h_4$ and is used to store the result of function $f_{v_1}$ when synthesizing $f_{v_1}={x_1}{h_2}\oplus {h_4}$. Moreover, the output of the line taking $f_{v_2}$ as the input becomes a garbage output indicated by the symbol ‘$\mathrm {g}$’. The #lines, T-depth, T-count, and #QG of the reversible cascade presented in Fig. 9(e) are 4, 3, 7, and 17, respectively.

• (iv) Case IV. When neither of nodes $v_2$ and $v_3$ have any other parent node not mapped in the complete KFDD excepting node $v_1$, by successively synthesizing the functions $h_2=f_{v_2}\oplus {f_{v_3}}$ and $f_{v_1}={x_1}{h_2}\oplus {f_{v_2}}$, the reversible cascade as shown in Fig. 9(f) is constructed. Note that, when synthesizing the function $f_{v_1}={x_1}{h_2}\oplus {f_{v_2}}$, the line taking $f_{v_2}$ as the input is reused to store the result of function $f_{v_1}$. Hence, no ancilla line is added for mapping node $v_1$ in this case. Moreover, the output of the line taking $f_{v_3}$ as the input becomes a garbage output indicated by the symbol ‘$\mathrm {g}$’. The #lines, T-depth, T-count, and #QG of the reversible cascade presented in Fig. 9(f) are 3, 3, 7, and 16, respectively.

Known from Example 3 in the above and the descriptions of local transformations presented in Ref. [3], when synthesizing reversible circuits using the KFDD by mapping a node into a reversible cascade, applying local transformations on the node function helps reduce the quantum cost of the resulting circuit, even helps reduce the number of required lines by reusing ancilla lines. Nevertheless, due to the sharing of a node in the KFDD (i.e., a node may have more than one parent node in the KFDD), there are different types of local transformations which can be applied on the node function. In fact, while mapping a node, the type of local transformations applied on the node function depends on the ordering of the node to be mapped [3].

Fig. 9

Sub-graph for node $v_1$ and reversible cascades mapped for $v_1$: (a) the sub graph for node $v_1$, (b) reversible cascade constructed by using the original form of the expression of function $f_{v_1}$, (c) Case I, (d) Case II, (e) Case III, (f) Case IV

4.3 Reversible Circuit Synthesis By Combining the Dependency Matrix and Local Transformations

Performing local transformations on the node function when mapping a node into a reversible cascade helps reduce the quantum cost, even the number of lines of reversible circuits synthesized using the KFDD [3]. On the other hand, the ordering of nodes in a KFDD to be mapped influences the number of lines, T-count, T-depth, and NNC of the circuit synthesized using the KFDD. Consequently, combining the dependency matrix and local transformations for synthesizing reversible circuits using the KFDD helps improve the quality of the resulting circuits.

For a node $v_i$, there are different types of local transformations which can be applied on function $f_{v_i}$ [3]. Nevertheless, the type of local transformations applied on function $f_{v_i}$ can be determined only after the ordering of node $v_i$ to be mapped has been determined [3]. Consequently, in this work, the dependency matrix and local transformations are combined in a two-step way. Firstly, the ordering of nodes to be mapped is ranked by using dependency matrices. And then, local transformations are applied on the node function while mapping a node into a reversible cascade [3]. However, dependency matrices only apply constraint on the ordering of nodes to be mapped which have dependencies between each other. The ordering of nodes to be mapped which do not depend on each other also influences the quality of the resulting circuit.

Fig. 10

The KFDD and reversible circuit for an exemplar function: (a) the KFDD, (b) the reversible circuit

Fig. 11

Other reversible circuits synthesized for the exemplar function by using different ordering of nodes to be mapped: (a) $(v_1, v_2, v_4, v_3, v_5, v_{7}, v_{6})$, (b) $(v_1, v_2, v_4, v_3, v_7, v_{5}, v_{6})$

Example 4

Figure  10 presents a KFDD for an exemplar function with 3 inputs and 3 outputs as well as the circuit synthesized by using the DDM for that KFDD. Whereas, Fig. 11 presents two other reversible circuits synthesized from the KFDD presented in Fig. 10(a).

In the KFDD presented in Fig. 10(a), the variable labeling those nodes positioned at one level is placed on the left. The decomposition types of variables $x_1$, $x_3$, and $x_2$ are positive Davio decomposition, Shannon decomposition, and negative Davio decomposition, respectively.

According to the KFDD presented in Fig. 10(a) as well as the definitions of dependency between nodes and diagram dependency matrix, the DDM for the KFDD is created as follows.

By the above DDM, according to ‘$Algorithm\ 3$’ in Ref. [23], the ordering of nodes to be mapped is determined as $($ $v_1$ $,$ $v_2$ $,$ $v_5$ $,$ $v_4$ $,$ $v_3$ $,$ $v_{7}$ $,$ $v_{6}$ $)$, the reversible circuit presented in Fig. 10(b) is generated by applying local transformations on the node function while mapping a node into a reversible gate cascade [3]. The number of lines, T-count, T-depth, and NNC of that circuit is 6, 35, 15, and 92, respectively. Note that the symbols ‘1’ or ‘0’ located on the left of a circuit line imply that the initial value of the circuit line is 1 or 0. The symbol ‘$\mathrm {g}$’ located on the right of a circuit line indicates that the output of the circuit line is a garbage output [2]. The reversible gate cascade indicated by symbol ‘$v_i$’ is the mapping result for node $v_i$.

On the other hand, according to the definitions of weak dependency between nodes and level dependency matrix, the LDMs for the KFDD presented in Fig. 10(a) are created as follows.

By the above LDMs, according to ‘$Algorithm\ 2$’ in Ref. [23], the ordering of nodes to be mapped is determined as $(v_1, v_2, v_4, v_3, v_5, v_{7}, v_{6})$, the reversible circuit presented in Fig. 11(a) is resulted by applying local transformations on the node function while mapping a node into a reversible gate cascade [3]. The number of lines, T-count, T-depth, and NNC of the circuit is 6, 35, 15, and 64, respectively. Compared to the circuit presented in Fig. 10(b), the NNC of the circuit presented in Fig. 11(a) is reduced by 28.

Nodes $v_5$, $v_6$, and $v_7$ positioned at level $lev(x_1)$ in the KFDD presented in Fig. 10(a) do not depend on each other. When mapping nodes in a BFS manner, in other words, level by level from the bottom to the top level, the ordering of the nodes $v_5$, $v_6$, and $v_7$ to be mapped does not impact the functionality of the resulting circuit, but may influence the quality of the resulting circuit. If those three nodes are mapped in order of $(v_{7}, v_{5}, v_6)$, a reversible circuit with the NNC of 56 as shown in Fig. 11(b) can be obtained. Compared to the circuit presented in Fig. 11(a), the NNC is further reduced by 8.

Note that, the symbols $L_{x_2}$, $L_{x_3}$, $L_{v_2}$, $L_{v_4}$, $L_{x_1}$, and $L_{v_7}$ presented in Fig. 11(b) indicate the numerical encoding of the circuit lines from the topmost line to the undermost line (e.g., $L_{x_2}$ indicates the numerical encoding of the line taking $x_2$ as the input). They will be used in Example 5 presented in Sect. 4.4.2 to describe the construction of the circuit presented in Fig. 11(b).

4.4 Synthesis of Reversible Circuits With Reduced NNC

From Example 4 presented in Sect. 4.3, it can be seen that the ordering of nodes in a KFDD to be mapped influences the NNC of the resulting circuit. Since NN-constraints require the control and the target line of a reversible gate to be adjacent, it is necessary to reduce the distance between the control and the target line of a reversible gate for reducing the NNC of reversible circuits.

Ranking the ordering of nodes to be mapped for reducing the NNC is a combinational optimization problem. Many discrete optimization algorithms (e.g., integer programming, genetic algorithm, etc.) can be used to solve this problem. However, in this work, a method by using strategies guided by NNC metrics is proposed for solving this problem. In the following, the strategies for ranking the ordering of nodes to be mapped are first elaborated. And then, the reversible circuit synthesis method is presented.

4.4.1 Strategies for Ranking the Ordering of Nodes to Be Mapped

For an inner node $v_i$, suppose that $var(v_i)=x_l$, and the low and high successors of node $v_i$ are inner nodes $v_j$ and $v_k$, respectively. Although local transformations will be applied on function $f_{v_i}$ while mapping node $v_i$ into a reversible cascade. However, as mentioned in Sect. 4.2, due to the sharing of node $v_i$ in the KFDD, the type of local transformations applied on function $f_{v_i}$ can not be determined before the ordering of node $v_i$ to be mapped has been determined. Consequently, in order to be able to provide directive rules for ranking the ordering of nodes to be mapped, the reversible cascades mapped for node $v_i$ by using the original form of the expression of function $f_{v_i}$ are discussed in the following.

Figure  12 presents the reversible cascades mapped for node $v_i$ by using the original form of the expression of function $f_{v_i}$ when the decomposition type of variable $x_l$ is a Shannon or positive Davio decomposition. When the decomposition type of variable $x_l$ is a negative Davio decomposition, the reversible cascade mapped for node $v_i$ is similar to the reversible cascade presented in Fig. 12(b).

Fig. 12

Reversible gate cascades mapped for node $v_i$ labeled with variable $x_l$. The decomposition type of variable $x_l$ is a: (a) Shannon decomposition, (b) positive Davio decomposition

For the sake of description, assuming that symbols $L_{v_i}$, $L_{v_j}$, $L_{v_k}$, and $L_{x_l}$ indicate the numerical encoding of the lines presented in Fig. 12 which take 0, $f_{v_j}$, $f_{v_k}$, and $x_l$ as the input, respectively. In the following, those lines are called line $L_{v_i}$, line $L_{v_j}$, line $L_{v_k}$, and line $L_{x_l}$, respectively.

Lines $L_{v_j}$, $L_{v_k}$, and $L_{v_i}$ are used to store the results of functions $f_{v_j}$, $f_{v_k}$, and $f_{v_i}$, and paired with nodes $v_j$, $v_k$, and $v_i$, respectively. Line $L_{x_l}$ is used to trace the value of variable $x_l$ before it is reused to store the result of a node function. Since nodes $v_j$ and $v_k$ are mapped before node $v_i$, and line $L_{x_l}$ is added to the circuit while the first node positioned at level $lev(x_l)$ in the KFDD is mapped. There are $L_{v_i}>L_{v_j}$, $L_{v_i}>L_{v_k}$, $L_{x_l}>L_{v_j}$, $L_{x_l} > L_{v_k}$, and $L_{v_i}>L_{x_l}$.

Let $NNC(v_i)$ indicate the NNC of the reversible cascade mapped for node $v_i$. For simplicity, $NNC(v_i)$ is also referred to as the NNC for node $v_i$. By Eq. (1) and Fig. 12(a), the following approximate equations can be derived if the decomposition type of variable $x_l$ is a Shannon decomposition.

$$\begin{aligned} NNC(v_i)=& NNC(TOF)+NNC(MPP) \nonumber \\&+NNC(CNOT) \nonumber \\=& 6(L_{x_l}-L_{v_k}-1)+4(L_{v_i}-L_{x_l}-1) \nonumber \\&+4(L_{v_i}-L_{v_k}-1)+6(L_{x_l}-L_{v_j}-1) \nonumber \\&+4(L_{v_i}-L_{x_l}-1)+4(L_{v_i}-L_{v_j}-1) \nonumber \\&\varpropto 4{L_{x_l}}+16{L_{v_i}}-10(L_{v_j}+L_{v_k}) \nonumber \\&\varpropto 2{L_{x_l}}+8{L_{v_i}}-5(L_{v_j}+L_{v_k}) \nonumber \\=& 2({L_{x_l}}-{L_{v_i}})+5({L_{v_i}}-L_{v_j}) \nonumber \\&+5(L_{v_i}-L_{v_k}) \end{aligned}$$

(3)

When the decomposition type of variable $x_l$ is a Davio decomposition, there is $f_{v_i}=f_{v_j}\oplus {{\tilde{x}_l}{f_{v_k}}}$, where $\tilde{x}_l\in \{x_l, \bar{x}_l\}$. Then by Eq. (1) and Fig. 12(b), the following approximate equations can be derived.

$$\begin{aligned} NNC(v_i)=& NNC(TOF)+NNC(CNOT) \nonumber \\=& 6(L_{x_l}-L_{v_k}-1)+4(L_{v_i}-L_{x_l}-1) \nonumber \\&+4(L_{v_i}-L_{v_k}-1)+2(L_{v_i}-L_{v_j}-1) \nonumber \\ \varpropto& 2{L_{x_l}}+10{L_{v_i}}-2(L_{v_j}+5{L_{v_k}}) \nonumber \\ \varpropto& {L_{x_l}}+5{L_{v_i}}-(L_{v_j}+5{L_{v_k}}) \nonumber \\ =& {L_{x_l}} + 5({L_{v_i}}-{L_{v_k}}) - L_{v_j} \end{aligned}$$

(4)

Guided by the NNC metrics as shown in Eqs. (3) and (4), the strategies for ranking the ordering of nodes to be mapped are described in the following.

Above all, as can be seen from Fig. 12 and Eqs. (3) and (4), for reducing the NNC of the reversible cascade mapped for node $v_i$, line $L_{v_i}$ should be near to lines $L_{v_j}$ and $L_{v_k}$. Because $lev(v_j)=lev(v_k)$ and $lev(v_i)=lev(v_j)-1$ in many cases, mapping nodes level by level in a BFS manner helps reduce the NNC compared to mapping nodes in a DFS manner. Consequently, it is better to use LDM rather than DDM to rank the ordering of nodes to be mapped.

Secondly, the weak dependency between nodes positioned at level $lev(x_l)$ in the KFDD is common when the decomposition type of variable $x_l$ is a Davio decomposition. The ordering of those nodes to be mapped is determined by using LDM [23].

However, when the decomposition type of variable $x_l$ is a Shannon decomposition, only a linear node is weakly dependent on other nodes positioned at level $lev(x_l)$ which are not linear nodes. In other words, most of those nodes positioned at level $lev(x_l)$ do not depend on each other according to the definitions of dependency presented in Sect. 3.2, the ordering of those nodes to be mapped can not be determined by using LDM. Accordingly, for reducing the NNC of the resulting circuit, when the decomposition type of variable $x_l$ is a Shannon decomposition, the ordering of nodes positioned at level $lev(x_l)$ to be mapped should be cautiously considered. For ranking the ordering of those nodes to be mapped, a look-ahead strategy is adopted. That is, the impact of the ordering of nodes positioned at level $lev(x_l)$ to be mapped on the NNC for nodes positioned at level $lev(x_l)-1$ is considered. Suppose that variable $x_t$ is positioned at level $lev(x_l)-1$ in the KFDD. Then the look-ahead strategy is as follows.

• (i) When the decomposition type of variable $x_t$ is a Davio decomposition, known from Eq. (4), the weight of $L_{v_k}$ with respect to the NNC for nodes positioned at level $lev(x_t)$ in the KFDD is larger than that of $L_{v_j}$. That is, the larger the value of $L_{v_i}-L_{v_k}$ is, the NNC of the reversible cascades mapped for nodes positioned at level $lev(x_t)$ in the KFDD is also larger. For reducing the NNC, at first, every node $v_i$ positioned at level $lev(x_l)$ is assigned a weight which is indicated by $wt_{v_i}$ and computed as the number of nodes that take $v_i$ as the high successor. And then, nodes positioned at level $lev(x_l)$ are sorted by the value of $wt_{v_i}$ in ascending order. Doing that helps reduce the value of the component $5({L_{v_i}}-{L_{v_k}})$ in Eq. (4), and thus the NNC.

• (ii) When the decomposition type of variable $x_t$ is a Shannon decomposition, known from Eq. (3), the weight of $L_{v_k}$ with respect to the NNC for nodes positioned at level $lev(x_t)$ in the KFDD is the same as that of $L_{v_j}$. As a result, the ordering of nodes positioned at level $lev(x_l)$ is left unchanged.

Once more, while mapping nodes positioned at level $lev(x_l)$ by using $LDM(lev(x_l))$, there may be more than one row in $LDM(lev(x_l))$ being zero row. In other words, the mapping conditions for more than one node are satisfied. The ordering of those nodes to be mapped also influences the NNC of the resulting circuit. In that case, one of those nodes is selected to be first mapped by using the best mapping node selecting strategy described as follows. Suppose the nodes whose mapping conditions are satisfied constitute a set denoted by S.

• (i) When the decomposition type of variable $x_l$ is a Shannon decomposition, from Eq. (3), it is known that the weight of $L_{v_k}$ with respect to the NNC is the same as that of $L_{v_j}$. To reduce the NNC, for a node $v_i\in {S}$ with the non-terminal low successor $v_j$ and the non-terminal high successor $v_k$, the number of nodes that take node $v_j$ or node $v_k$ as a successor and are positioned at level $lev(x_l)$ is first counted and indicated by ${ws}_{v_i}$. Then the node for which the value of ${ws}_{v_i}$ is the largest is selected from the set S as the node to be first mapped. The reason for doing that is to reduce the component $5({L_{v_i}}-L_{v_j})$ and the component $5(L_{v_i}-L_{v_k})$ in Eq. (3).

• (ii) When the decomposition type of variable $x_l$ is a Davio decomposition, by Eq. (4), it is known that the weight of $L_{v_k}$ with respect to the NNC is larger than that of $L_{v_j}$. Suppose the index of the first zero row in $LDM(lev(x_l))$ is r, the low successor of node r is node $v_j$, and nodes in the set S which take node $v_j$ as the low successor constitute a set indicated by N. If there is not any other node not mapped which takes node $v_j$ as the low successor excepting nodes in N, then the node $v_i\in {N}$ with the high successor $v_k$ for which the paired line $L_{v_k}$ has the largest numerical value is greedily selected from the set N as the node to be first mapped. Otherwise, node r is selected as the node to be first mapped.

Lastly, for nodes positioned at level $lev(x_l)$ which take node $v_j$ as the low successor when the decomposition type of variable $x_l$ is a Davio decomposition, or for linear nodes positioned at level $lev(x_l)$ which take node $v_j$ as a successor when the decomposition type of variable $x_l$ is a Shannon decomposition, the last node to be mapped can reuse line $L_{v_j}$ to store the result of the function represented by this node [3, 23]. For reducing the NNC as well as the number of required lines, if there is a variable node positioned at level $lev(x_l)$, the variable node is selected as the last node to be mapped for using line $L_{x_l}$ to store the result of the function represented by it. Otherwise, the last linear node in the set of nodes that are positioned at level $lev(x_l)$ is selected as the last node to be mapped.

Note that, always selecting a linear node (e.g., linear node $v_i$ which takes node $v_j$ as the low successor) as the last node to be mapped may help reduce the the number of CNOT gates in some cases [3]. However, doing that will increase the NNC. Because node $v_i$ can be mapped only after all the other nodes positioned at level $lev(x_l)$ have been mapped, the distance between line $L_{v_j}$ and line $L_{x_l}$ will be increased.

4.4.2 The Proposed Synthesis Method

Following the strategies described in Sect. 4.4.1, the KFDD based method of synthesizing reversible circuits with reduced NNC is presented as Algorithm 1 in the following.

In Step 7 of Algorithm 1, ‘DT’ implies decomposition type, ‘SD’ and ‘DD’ indicate Shannon and Davio decomposition, respectively. In Step 8, the implication of $wt_{vi}$ has been described in Sect. 4.4.1. In Step 11, in a level dependency matrix LDM(l), if there is a row which does not have an element with the value of $-1$, ‘HasValidRow(LDM(l))’ returns true, otherwise it returns false. In Step 12, ‘GetAllZeroRows’ returns the indices of the zero rows in LDM(l) which constitute a set R. In Step 14, ‘GetMaxColumn’ returns the index of the column in LDM(l) which does not have an element with the value of $-1$ and has a maximal number of non-zero elements [23]. In Step 18, the mapping technique by performing local transformations on node functions and by using NCT and MPP gates proposed in Ref. [3] is used. In Step 19, the elements of the j-th column in LDM(l) take the value 0 [23]. In Step 20, the value of the element $d_{jj}$ in LDM(l) is set to $-1$ [23]. In Step 22, the strategy proposed in Ref. [3] is used.

Subsequently, the KFDD presented in Fig. 10(a) is considered as a running example for demonstrating Algorithm 1. Remember that, the symbols $L_{x_2}$, $L_{x_3}$, $L_{v_2}$, $L_{v_4}$, $L_{x_1}$, and $L_{v_7}$ presented in Fig. 11(b) indicate the numerical encoding of the circuit lines from the topmost line to the undermost line.

Example 5

The nodes of the KFDD presented in Fig. 10(a) are partitioned into 3 levels. As can be seen from Fig. 10(a), $lev(x_2)=3$, $lev(x_3)=2$, and $lev(x_1)=1$. From level 3 to level 1, the nodes will be mapped into reversible cascades for generating a reversible circuit.

• 1) Map nodes positioned at level 3. The decomposition type of $x_2$ is a negative Davio decomposition. Node $v_1$ is positioned at level 3. That is, $V=\{v_1\}$. A line encoded by $L_{x_2}=1$ (the topmost horizontal line in the circuit presented in 11(b) which takes $x_2$ as the input) is added to the circuit in Step 4. Because node $v_1$ is a variable node, it is selected as the last node to be mapped in Step 5. That is, $u=v_1$. Because $V=V\backslash \{u\}=\varnothing$, the algorithm goes to Step 22. Since $f_{v_1}=x_2$, there is no need to add any gate in this round.

• 2) Map nodes positioned at level 2. The decomposition type of $x_3$ is a Shannon decomposition. Nodes $v_2$, $v_3$, and $v_4$ are positioned at level 2. That is, $V=\{v_2, v_3, v_4\}$. A line encoded by $L_{x_3}=2$ (the second horizontal line in the circuit presented in Fig. 11(b) which takes $x_3$ as the input) is added to the circuit in Step 4. Since $f_{v_3}=x_3\oplus {f_{v_1}}$, node $v_3$ is a linear node. Because node ${v_3}$ is the only linear or variable node positioned at level 2, it is selected as the last node to be mapped in Step 5. That is, $u=v_3$. After that, $V=\{v_2, v_4\}$. Because $DT(x_3)=SD$ and $DT(x_1)=DD$, nodes in V are sorted by the value of $wt_{v_i}$ in ascending order in Step 8. Since $wt_{v_2}=0$ and $wt_{v_4}=2$, $V=\{v_2, v_4\}$ is resulted. In Step 10, the LDM for level 2 is created as follows

  

  In Step 12, there are $R=\{1, 2\}$, $Node(1)=v_2$, and $Node(2)=v_4$. Node $v_2$ has the non-terminal high successor $v_1$. Whereas node $v_4$ has the non-terminal low successor $v_1$. Because there are two nodes (i.e., nodes $v_2$ and $v_4$) in the set V which take node $v_1$ as a successor, $ws_{v_2}=2$ and $ws_{v_4}=2$. Consequently, $v_2$ is selected as Node(j) in Step 16 by using the best mapping node selecting strategy. In Step 18, known that $f_{v_2}=1\oplus {{x_3}{\bar{f}_{v_1}}}$, an ancilla line encoded by $L_{v_2}=3$ (the third horizontal line in the circuit presented in Fig. 11(b)) which has the initial value of 1 is first added to the circuit, and then node $v_2$ is mapped into the reversible cascade indicated by the symbol ‘$v_2$’ as shown in Fig. 11(b). The reversible cascade is composed of an inverse Peres gate and a CNOT gate. The inverse Peres gate realizes function $f_{v_2}$. The CNOT gate is used to recover the value on line $L_{x_2}$, because node $v_1$ has two parent nodes not mapped (i.e., nodes $v_3$ and $v_4$). Thereafter, LDM(2) becomes

  

  The algorithm goes to Step 11. Because $R=\{2\}$ and $f_{v_4}={\bar{x}_3}{f_{v_1}}$, an ancilla line encoded by $L_{v_4}=4$ (the fourth horizontal line in the circuit presented in Fig. 11(b)) which has the initial value of 0 is first added to the circuit, and then node $v_4$ is mapped into the reversible cascade indicated by the symbol ‘$v_4$’ as shown in Fig. 11(b). The reversible cascade is composed of a Peres gate with the first control negated and a CNOT gate. The Peres gate with the first control negated realizes function $f_{v_4}$. The CNOT gate is used to recover the value on line $L_{x_2}$, because node $v_1$ has one parent node not mapped (i.e., node $v_3$). In Step 22, known that $f_{v_3}=x_3\oplus {f_{v_1}}$, node $v_3$ is mapped into a CNOT gate using line $L_{x_3}$ as the target line which is indicated by the symbol ‘$v_3$’ as shown in Fig. 11(b).

• 3) Map nodes positioned at level 1. The decomposition type of $x_1$ is a positive Davio decomposition. Node $v_5$, $v_7$, and $v_6$ are positioned at level 1. That is, $V=\{v_5, v_7, v_6\}$. A line encoded by $L_{x_1}=5$ (the fifth horizontal line in the circuit presented in Fig. 11(b) which takes $x_1$ as the input) is added to the circuit in Step 4. Known from Fig. 10(a), there is not a linear or variable node in V. Furthermore, the decomposition type of $x_1$ is a positive Davio decomposition. Subsequently, the algorithm goes to Step 10, the LDM for level 1 is created as follows

  

  In Step 12, there are $R=\{1, 2, 3\}$, $Node(1)=v_5$, $Node(2)=v_7$, and $Node(3)=v_6$. The index of the first zero row in LDM(1) is 1. As can be seen from Fig. 10(a), nodes $v_5$ and $v_7$ share the low successor $v_2$. That is, $N=\{v_5, v_7\}$. The high successors of nodes $v_5$ and $v_7$ are nodes $v_1$ and $v_4$, respectively. In addition, there is not any other node not mapped which takes $v_2$ as the low successor excepting nodes in N, and there is $L_{v_4} > L_{v_1}$ where $L_{v_1}=L_{x_2}$. Thus, by the best mapping node selecting strategy, node $v_7$ is greedily selected as the node to be first mapped in Step 16. In Step 18, known that $f_{v_7}=f_{v_2}\oplus {x_1}{\bar{f}_{v_4}}$, an ancilla line encoded by $L_{v_7}=6$ (the sixth horizontal line in the circuit presented in Fig. 11(b)) which has the initial value of 0 is first added to the circuit, and then node $v_7$ is mapped into the reversible cascade indicated by the symbol ‘$v_7$’ as shown in Fig. 11(b). The reversible cascade is composed of an inverse Peres gate and two CNOT gates. The inverse Peres gate realizes the function $h_1={x_1}{\bar{f}_{v_4}}\oplus {0}$. The first CNOT gate is used to recover the value on line $L_{v_4}$. The second CNOT gate realizes the function $f_{v_7}=f_{v_2}\oplus {h_1}$. Thereafter, LDM(1) becomes

  

  Subsequently, according to the functions $f_{v_5}={x_1}{f_{v_1}}\oplus {f_{v_2}}$ and $f_{v_6}={x_1}{f_{v_4}}\oplus {f_{v_3}}$, nodes $v_5$ and $v_6$ are both mapped into a Peres gate indicated by the symbol ‘$v_5$’ and the symbol ‘$v_6$’ as shown in Fig. 11(b), respectively. Because neither of nodes $v_2$ and $v_3$ have parent nodes not mapped, line $L_{v_2}$ and line $L_{x_3}$ are reused to store the results of functions $f_{v_5}$ and $f_{v_6}$, respectively. In addition, since neither of nodes $v_1$ and $v_4$ have parent nodes not mapped, the values on line $L_{x_2}$ and line $L_{v_4}$ do not need to be recovered, and the outputs of line $L_{x_2}$ and line $L_{v_4}$ become garbage outputs indicated by the symbol ‘$\mathrm {g}$’.

• 4) Add a NOT gate for every root node of G which has an incoming complemented edge. Since all the nodes in the KFDD presented in Fig. 10(a) have been mapped into reversible cascades, the algorithm goes to Step 24. The KFDD presented in Fig. 10(a) has 3 root nodes which are nodes $v_5$, $v_6$, and $v_7$. As can be seen from Fig. 10(a), nodes $v_5$ and $v_6$ both have incoming complemented edges. Consequently, two NOT gates are added on lines $L_{v_2}$ and $L_{x_3}$, respectively. Thereafter, the circuit is generated completely, the algorithm terminates.

According to the circuit presented in Fig. 11(b), by Eq. (1), the NNC of the reversible gate cascade mapped for every node can be computed as follows.

$NNC(v_1)=0$, $NNC(v_2)=4$, $NNC(v_4)=12$, $NNC(v_3)=0$, $NNC(v_7)=8$, $NNC(v_5)=20$, and $NNC(v_6)=12$.

The NNC of the circuit presented in Fig. 11(b) is 56 which is the cumulative sum of the NNC of the reversible gate cascades in the circuit. In addition, the circuit is composed of 5 MPP gates, 5 CNOT gates, and 2 NOT gates. Consequently, the T-count of the circuit is $5\times 7=35$, which is the cumulative sum of the T-count of the 5 MPP gates. Whereas the T-depth of the circuit is estimated as $5\times 3=15$, which is the cumulative sum of the T-depth of the 5 MPP gates. Since the MPP gates all consist of 15 quantum gates excepting the or-Peres gate, the number of quantum gates of the circuit presented in Fig. 11(b) before SWAP insertion is $\#\mathrm {QG}=5\times 15+5+2=82$. Let #QG_A indicate the number of quantum gates of a circuit after SWAP insertion. Then there is $\#\mathrm {QG\_A}=\#\mathrm {QG}+3\times \mathrm {NNC}=82+3\times {56}=250$ for the circuit presented in Fig. 11(b).

Table 1 The costs of the circuits presented in Fig. 10(b) and Fig. 11

The costs of the circuits presented Fig. 10(b) and Fig. 11 are summarized in Table 1. As can be seen from Table 1, the circuit as shown in Fig. 11(b) which is achieved with Algorithm 1 has lower NNC and lower $\#\mathrm {QG\_A}$ compared to two other circuits as shown in Fig. 10(b) and Fig. 11(a).

5 Experimental Evaluations

Algorithm 1 has been implemented in C++ on the top of Revkit [30]. With regard to the KFDD data structure, the PUMA package [6] has been used. The experimental evaluations have been carried out on an Intel Core i7-10700 Processor with 32 GB of main memory running Ubuntu 16.04 64bit OS.

5.1 Evaluating the Effect of the Proposed Method On NNC

For reducing the NNC, the proposed synthesis method uses strategies governed by NNC metrics to rank the ordering of nodes in the KFDD to be mapped. In order to evaluate the effect of the proposed method on the NNC of the synthesized reversible circuits, two other algorithms named by FDD+DDM and KFDD+DDM have been designed. FDD+DDM synthesizes a reversible circuit from an FDD and uses the DDM to rank the ordering of nodes in the FDD to be mapped as described in Ref. [23]. Similarly, KFDD+DDM synthesizes a reversible circuit from a KFDD and also uses the DDM to rank the ordering of nodes in the KFDD to be mapped as described in Ref. [23]. While mapping a node into a reversible cascade, algorithms FDD+DDM and KFDD+DDM both apply local transformations on node functions [3] and both use the NCT and MPP gates to generate reversible cascades. Similarly to Algorithm 1, the KFDDs used by KFDD+DDM are generated by using the PUMA package and sifting techniques [6]. As FDDs are special kinds of the KFDD, the FDDs used by FDD+DDM are also generated by using the PUMA package and sifting techniques [6].

Algorithms FDD+DDM, KFDD+DDM, and Algorithm 1 have been used to synthesize reversible circuits for 31 functions available in the RevLib benchmark suite [25] which were also used by Stojković et al. [23] to evaluate their FDD-based synthesis method or used by Abdalhaq et al. [1] to evaluate their BDD-based synthesis method. In the following, Table 2 presents the results with respect to #lines, #QG, NNC, #QG_A, and #nodes. Table 3 presents the percentage reduction (improvement) in those results achieved by comparing KFDD+DDM to FDD+DDM and by comparing Algorithm 1 to KFDD+DDM. In Table 2, the column indicated by ‘#in/#out’ gives the number of inputs and outputs of the functions. Note that #nodes indicates the number of nodes in the FDD or KFDD, #QG indicates the number of Clifford+T quantum gates before SWAP insertion, and #QG_A indicates the number of Clifford+T quantum gates after SWAP insertion. Because a SWAP-gate is commonly realized using 3 CNOT gates, there is $\mathrm {\#QG\_A=\#QG+3\times {NNC}}$. In addition, Fig. 13 illustrates the improvement results of those functions presented in Table 2 for which KFDD+DDM achieves results different from FDD+DDM. Figure  14 illustrates the improvement results of those functions presented in Table 2 for which Algorithm 1 achieves results different from KFDD+DDM.

Table 2 The results wrt. #lines, #QG, NNC, #QG_A, and #nodes

Table 3 Improvement (%) results of KFDD+DDM and Algorithm 1

As can be seen from Tables 2 and 3, KFDD+DDM can achieve #lines, #QG, NNC, and #QG_A not inferior to FDD+DDM for all of the functions excepting function $mini\text{- }alu\_84$ and function $mod5adder\_66$. Compared to FDD+DDM, KFDD+DDM increases the NNC, #QG, and #QG_A while not increasing the number of lines for function $mini\text{- }alu\_84$. Whereas for function $mod5adder\_66$, KFDD+DDM only slightly increases the NNC and #QG_A. Note that, compared to FDD+DDM, there are 7 cases where KFDD+DDM reduces #lines, #QG, NNC, and #QG_A. As can be obviously observed from Table 3 and Fig. 13, this is because the KFDD is more compact than the FDD. In other words, for a given function, the KFDD has the number of nodes (#nodes) less than the FDD. For function $mini\text{- }alu\_84$, although the number of nodes of the FDD is the same as that of the KFDD, the KFDD is not same as the FDD. For that function, synthesizing a reversible circuit using the KFDD instead of the FDD significantly increases the NNC and #QG_A. For the functions presented in Tables 2 and 3, compared to FDD+DDM, the average reductions achieved by KFDD+DDM in #lines, #QG, NNC, and #QG_A are $3.62\%$, $5.31\%$, $7.44\%$, and $7.59\%$, respectively. As can be seen, while synthesizing reversible circuits by mapping a node into a reversible cascade, using the KFDD instead of the FDD helps reduce the NNC, also the number of lines, the number of Clifford+T gates before and after SWAP insertion.

Algorithm 1 and KFDD+DDM both synthesize a reversible circuit from a KFDD and the KFDDs used by them are both generated by using the PUMA package and sifting techniques [6]. That is, for a given function, Algorithm 1 and KFDD+DDM synthesize reversible circuits from the same KFDD. Subsequently, Algorithm 1 is compared to KFDD+DDM.

As can be seen from Tables 2 and 3, out of the 31 functions, there are 15 cases where Algorithm 1 outperforms KFDD+DDM on NNC as well as #QG_A, and 9 cases where Algorithm 1 achieves the NNC and #QG_A both same as KFDD+DDM. In the other 7 cases, compared to algorithm KFDD+DDM, although Algorithm 1 increases both the NNC and #QG_A, the NNC and #QG_A are increased by no more than $11\%$ and $10\%$, respectively. Whereas, compared to KFDD+DDM, Algorithm 1 reduces the NNC and #QG_A by up to $65.26\%$ and $65.07\%$ (function $pdc\_191$), respectively. Moreover, there are 12 cases where Algorithm 1 reduce both the NNC and #QG_A by no less than $11\%$. On the other hand, Algorithm 1 achieves the same #QG as KFDD+DDM in 18 cases. In the other 13 cases, Algorithm 1 slightly increases (by no more than $0.69\%$) or decreases (by no more than $1.96\%$) the #QG compared to KFDD+DDM. Consequently, it can be concluded that, compared to KFDD+DDM, the reduction in the number of Clifford+T gates after SWAP insertion which is achieved by Algorithm 1 is mainly contributed to the reduction in NNC. Compared to KFDD+DDM, the average reductions achieved by Algorithm 1 in NNC and #QG_A are $13.47\%$ and $12.86\%$, respectively.

In addition, as can be seen from Table 3 and Fig. 14, compared to KFDD+DDM, there are 9 cases where Algorithm 1 increases the number of lines (#lines). Increasing the number of lines may help reduce the NNC and #QG_A. In the 15 cases where Algorithm 1 reduces both the NNC and #QG_A, there are 7 cases where Algorithm 1 increases the number of lines. However, it is worth noting that there are 6 cases where Algorithm 1 achieves the same #lines as KFDD+DDM, and 2 cases where Algorithm 1 even reduces the number of lines. For the functions presented in Table 2, compared to KFDD+DDM, the average reduction achieved by Algorithm 1 in the number of lines is $0.13\%$.

Fig. 13

Improvement results of KFDD+DDM wrt. FDD+DDM

Fig. 14

Improvement results of Algorithm 1 wrt. KFDD+DDM

Table 4 presents the T-count and the T-depth of the reversible circuits obtained with algorithms FDD+DDM, KFDD+DDM, and Algorithm 1. In Table 4, the columns indicated by ‘Imp_1’ show the percentage reduction in T-depth or T-count achieved by comparing KFDD+DDM to FDD+DDM. Whereas the columns indicated by ‘Imp_2’ give the percentage reduction in T-depth or T-count achieved by comparing Algorithm 1 to KFDD+DDM. It can be observed from Table 4 that, compared to FDD+DDM, there are 7 cases where algorithm KFDD+DDM reduces both the T-depth and the T-count. For the other 24 cases, KFDD+DDM achieves the T-depth and the T-count both same as FDD+DDM. Compared to FDD+DDM, the average reductions achieved by KFDD+DDM in T-depth and T-count are both $5.50\%$. As can be seen, while synthesizing reversible circuits by mapping a node into a reversible cascade, using KFDDs is also better than using FDDs in terms of the T-depth and T-count.

On the other hand, since KFDD+DDM and Algorithm 1 both synthesize a reversible circuit from a KFDD, the resulting T-depth or T-count of the two algorithms are quite close to each other.

Table 4 The results wrt. T-depth and T-count

It can be concluded from above analyses that, the strategies presented for ranking the ordering of nodes to be mapped for reducing NNC which are used by the proposed synthesis method is effective. While synthesizing reversible circuits using the KFDD, the proposed method helps reduce the NNC as well as the number of Clifford+T gates after SWAP insertion and has a slight impact on the resulting #lines, T-depth, T-count, and the number of Clifford+T gates before SWAP insertion.

5.2 Comparison to Prior Synthesis Methods Based On FDD or BDD

Stojković et al. [23] used FDDs to synthesize reversible circuits. Whereas, Abdalhaq et al. [1] used BDDs to synthesize reversible circuits. They did not consider the reduction of the NNC in their works. However, for the completeness of this work and due to the fact that BDDs and FDDs are both special kinds of the KFDD, we compare the proposed synthesis method to their methods in this section.

Stojković et al. [23] and Abdalhaq et al. [1] both used the NCV-cost to measure the quantum cost of reversible circuits. In other words, they considered the NCV quantum realizations for reversible circuits. In the following, Algorithm 1 is compared to their methods by using the NCV-cost metric. The results are listed in Tables 5 and 6.

In Tables 5 or 6, OFPFDD+LDM indicates the algorithm in Ref. [23] which synthesizes circuits from the optimal fixed-polarity FDDs by using LDMs. Whereas OFPFDD+DDM indicates the algorithm in Ref. [23] which synthesizes circuits from the optimal fixed-polarity FDDs by using DDMs. BDD+GA indicates the algorithm in Ref. [1] which synthesizes circuits from BDDs by using a genetic algorithm to search the optimal BDDs. The columns indicated by ‘runtime’ list the runtime in CPU seconds of those algorithms. Table 6 shows the percentage reduction (improvement) in #lines and NCV-cost achieved by comparing Algorithm 1 to OFPFDD+DDM or BDD+GA.

Table 5 Comparison with the results of FDD based and BDD based methods

Table 6 Improvement (%) results of Algorithm 1 wrt. OFPFDD+DDM and BDD+GA

As can be observed from Table 5, the results of OFPFDD+LDM and OFPFDD+DDM are quite close to each other. This is because the two algorithms both synthesize reversible circuits from the optimal fixed-polarity FDDs. Consequently, Algorithm 1 is only compared to OFPFDD+DDM and BDD+GA in the following.

As can be seen from Tables 5 and 6, there are 14 cases where Algorithm 1 achieves results not inferior to OFPFDD+DDM in terms of #lines and NCV-cost. Compared to OFPFDD+DDM [23], there are only 2 cases (functions $ham7\_29$ and $hwb6\_14$) where Algorithm 1 only increases the number of lines, and 4 cases (functions $plus127mod8192\_78$, $plus63mod4096\_79$, $rd53\_68$, and $rd73\_69$) where Algorithm 1 only increases the NCV-cost. Furthermore, Algorithm 1 reduces the number of lines and the NCV-cost by up to $78.35\%$ and $86.59\%$ (function $cycle10\_2\_61$), respectively. The average reductions achieved by Algorithm 1 in the number of lines and NCV-cost are $5.67\%$ and $14.07\%$, respectively.

On the other hand, compared to BDD+GA [1], there are only 3 cases (functions $alu\_9$, $apex2\_101$, and $hwb9\_65$) where Algorithm 1 only increases the number of lines. In the other 27 cases, Algorithm 1 outperforms BDD+GA in terms of #lines and NCV-cost. Furthermore, Algorithm 1 reduces the number of lines and the NCV-cost by up to $66.90\%$ and $78.41\%$ (function $apex5\_104$), respectively. The average reductions achieved by Algorithm 1 in the number of lines and NCV-cost are $22.39\%$ and $40.33\%$, respectively.

With regard to the runtime of the algorithms, Stojković et al. [23] did not report the runtime of their algorithms. It can be observed from Table 5 that, the time efficiency of Algorithm 1 is better than BDD+GA.

As can be seen from the above analyses, while using NCV library to realize reversible circuits, using KFDDs to generate reversible circuits is also better than using FDDs or BDDs.

6 Conclusion

While synthesizing reversible circuits using the KFDD, although how to reduce the quantum cost and the number of qubits has been extensively researched, the restricted interactions between qubits are rarely considered. In this work, focusing on the NN-constraints, an attempt to combine reversible logic synthesis, gate decomposition, and qubit mapping in one synthesis flow is conducted. Based on the Clifford+T gate library, by defining NNC metrics for the NCT and MPP gates for the reversible logic level, we address the reduction of the NNC of reversible circuits synthesized from the KFDD. The ordering of nodes to be mapped influences the quality of reversible circuits synthesized from the KFDD. Thus, for reducing the NNC of the resulting reversible circuits, the ordering of nodes to be mapped is ranked by applying strategies guided by NNC metrics. For further improving the quality of the resulting circuits, local transformations are applied on node functions while mapping a node to a cascade of reversible gates.

In the Clifford+T quantum mappings of NCT and MPP gates, two SWAP-gates are applied in order to decrease the distance between the control and the target line of each CNOT gate by one. One SWAP-gate is used for moving the control and the target line together, another is used to restore the original order of lines [11, 19]. As a result, the NNC metrics defined for the NCT and MPP gates and the NNC evaluation of the reversible circuits are pessimistic. On the other hand, it is usually considered that the NN-constraints imposed by lattice models are less restricted than the coupling constraints imposed by IBM quantum architectures. Combining reversible logic synthesis, gate decomposition, and qubit mapping in a more general synthesis flow for handling the coupling constraints at the reversible logic level by defining more exact NNC metrics and designing more exact strategies is future work.