1 Introduction

A pressure sensor is one of the most utilized sensing devices in industries ranging from the biomedical, nuclear power plant, oil and gas, automobile and avionic applications [1,2,3,4,5]. The microelectromechanical system (MEMS) plays an essential role in the fabrication of microsensors with high sensitivity as compared to its conventional counterpart [1]. Generally, a pressure sensor consists of thin microstructures (cantilever and diaphragm) as a primary sensing element, a secondary sensing element, which is based on the transduction mechanism (i.e., piezoresistors for piezoresistive technique and parallel plates or comb drive for capacitive technique), and a reference cavity to decide the type of pressure measurement (i.e., absolute, atmospheric or differential pressure). The geometrical optimization of the thin diaphragm is an important task that forced the overall sensitivity of the pressure sensor. Various researchers have worked on the design optimization of MEMS technology-based pressure sensors using different geometry [6,7,8,9,10]. Complete analytical modeling for the circular diaphragm of freely supported is presented by S. K. Jindal et al. 2015 using SolidWorks® [6]. Their another work has demonstrated the analytical modeling and simulation for freely supported and rigidly clamped square diaphragm [7]. The quantitative simulation studies for temperature-induced effects and impact of material used in pressure sensors are presented by Vinod Belwanshi et al. [8, 10] using FEA simulation tool. To decide the sensitivity of pressure sensor and the effect of piezoresistors placement on top of the diaphragm, the simulation model and fabrication of polysilicon-based piezoresistive pressure sensors are presented by Kumar et al. [11, 12] using CoventorWare®. In addition, the design optimization of novel geometry-based piezoresistive pressure sensor was carried out by Chueng Li et al. 2018 using Comsol Multiphysics® and followed by the fabrication [13]. Ansys® is also adopted for design optimization of piezoresistive pressure sensors for design optimization presented by Bhat [14]. The availabilities of such FEM tools are prime requirements for design optimization and estimation of sensitivity for pressure sensor. The analytical calculation of the sensitivity is presented based on maximum stresses at the point of piezoresistors. However, piezoresistors experience the average stresses, and hence, it may led to deviation in prediction of piezoresistive pressure sensor sensitivity. The average stress-based sensitivity calculation using analytical modeling was not much explored so far. In the current scenario of research and development, a design of the sensors is to be re-investigated based on the specific application requirements. The use of such design tools becomes a primary requirement for optimization of parameters to estimate the performance of pressure sensor before fabrication. Hence, the cost and time for trial fabrications and performance investigations are reduced. However, cost of such tools is high as well as their availabilities are more complicated. Therefore, in the current research work, analytical calculation of sensitivity was carried out using the average stresses experienced by piezoresistors. A mathematical model is established for the mechanical response of thin plate and electrical response of the piezoresistive pressure sensor using readily available Microsoft office excel. The effect of the average stress on the sensitivity of the MEMS piezoresistive pressure sensor is studied and presented in terms of the sensitivity change. The paper is divided as follows: Sect. 2 introduces the theory and mathematical model of piezoresistive pressure sensor, Sect. 3 deals with methodology and material used, Sect. 4 describes the results and discussions, and Sect. 5 outlines the summary and conclusion.

2 An analytical model for piezoresistive pressure sensor

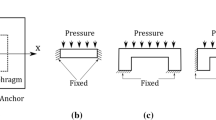
A piezoresistive pressure sensor consists of a thin plate and the piezoresistors in a Wheatstone bridge configuration. The basic working principle of piezoresistive pressure sensor is based on the deflection and induced stresses under externally applied pressure. In other words, when external pressure is applied to the top of diaphragm, the diaphragm is deflected and stresses are induced in the thin diaphragm (Fig. 1). The induced stresses are responsible for the change in the resistance of piezoresistors and hence change in the output voltage of the Wheatstone bridge configuration. The working principle of piezoresistive pressure is explained using the flow diagram, and the schematic of a pressure sensor is depicted in Fig. 1a, b, respectively. A cleaned silicon (100) wafers are used to fabricate the MEMS piezoresistive pressure sensor. The thermal grown SiO2 layer is fabricated and patterned for gridlines, alignment marks and backside opening. The backside openings are used to fabricate a diaphragm using wet or dry etching. Further, the boron-doped piezoresistors are fabricated using diffusion and implantation, or deposited on top of the thin diaphragm. Thereafter, metallization is performed to connect the piezoresistors in a Wheatstone bridge configuration. A passivation layer of SiO2 is deposited as a safeguard to the piezoresistors and metal lines from outer environments. Further, a glass wafer is bonded with a processed wafer consisting of the pressure sensors chips. Finally, the LASER dicing is performed to separate the pressure sensor chips and can be packaged in a stainless steel housing [15, 16].

Fig. 1
figure 1

a Working of pressure sensor using flow diagram, b schematic of piezoresistive pressure sensor

Full size image

2.1 Mechanical response using thin plate theory

The governing differential equation for deflection of thin plate with small deflection is given as [17,18,19],

$$\frac{{\partial^{4} w}}{{\partial x^{4} }} + \frac{{\partial^{4} w}}{{\partial x^{2} \partial y^{2} }} + \frac{{\partial^{4} w}}{{\partial y^{4} }} = \frac{P}{D}$$
(1)

A schematic used for the analytical model is presented in Fig. 2. The various solutions are proposed for a governing equation (Eq. 1) of the thin plate. One of the standard solutions is suggested by the Grashof [20], for the calculation of thin rectangular plate deflection with \(2b\) length and \(2a\) width, which can be given as:

$$w = \frac{P}{24D}\frac{{\left( {a^{2} - x^{2} } \right)^{2} \left( {b^{2} - y^{2} } \right)^{2} }}{{a^{4} + b^{4} }}$$
(2)
$$D = \frac{{Eh^{3} }}{{12\left( {1 - \upsilon^{2} } \right)}}$$
(3)

where \(P\) is applied pressure, \(D\) is bending rigidity of thin plate, \(h\) is the thickness of a plate, \(E\) is Young’s modulus of the plate material, \(\upsilon\) is Poisson’s ratio, \(2b\) is length, \(2a\) is the width of thin plate and \(w\) is the deflection of a plate.

Fig. 2
figure 2

Schematic of thin plate diaphragm, a top view of rectangular thin plate diaphragm, b side view of rectangular thin plate diaphragm, c top view of wet etched silicon rectangular thin plate diaphragm, d side view of wet etched silicon rectangular thin plate diaphragm

Full size image

Displacement of a thin diaphragm plate is responsible for bending moment. The bending moments (Mx and My) are accountable for induced stress on the thin plate under the applied load. The bending moment is calculated as [19],

$$M_{x} = - D\left( {\frac{{\partial^{2} w}}{{\partial x^{2} }} + \upsilon \frac{{\partial^{2} w}}{{\partial y^{2} }}} \right)\;{\text{and}}\;M_{y} = - D\left( {\upsilon \frac{{\partial^{2} w}}{{\partial x^{2} }} + \frac{{\partial^{2} w}}{{\partial y^{2} }}} \right)$$
(4)

Differentiating Eq. 2 with respect to \(x\) and \(y\), respectively:

$$\begin{aligned} \frac{{\partial^{2} w}}{{\partial x^{2} }} & = - \frac{{Pa^{2} b^{4} }}{{6D\left( {a^{4} + b^{4} } \right)}}\left( {1 - 3\left( {\frac{x}{a}} \right)^{2} } \right)\left( {1 - \left( {\frac{y}{b}} \right)^{2} } \right)^{2} \;{\text{and}} \\ \frac{{\partial^{2} w}}{{\partial y^{2} }} & = - \frac{{Pa^{4} b^{2} }}{{6D\left( {a^{4} + b^{4} } \right)}}\left( {1 - \left( {\frac{x}{a}} \right)^{2} } \right)^{2} \left( {1 - 3\left( {\frac{y}{b}} \right)^{2} } \right) \\ \end{aligned}$$

Putting the value of \(\frac{{\partial^{2} w}}{{\partial x^{2} }}\) and \(\frac{{\partial^{2} w}}{{\partial y^{2} }}\) in Eq. 4:

$$M_{x} = \frac{{Pa^{2} b^{4} }}{{6\left( {a^{4} + b^{4} } \right)}}\left[ {\left( {1 - 3\left( {\frac{x}{a}} \right)^{2} } \right)\left( {1 - \left( {\frac{y}{b}} \right)^{2} } \right) + \upsilon \left( {\frac{a}{b}} \right)^{2} \left( {1 - \left( {\frac{x}{a}} \right)^{2} } \right)^{2} \left( {1 - 3\left( {\frac{y}{b}} \right)^{2} } \right)} \right]$$
(5)

Similarly,

$$M_{y} = \frac{{Pa^{2} b^{4} }}{{6\left( {a^{4} + b^{4} } \right)}}\left[ {\upsilon \left( {1 - 3\left( {\frac{x}{a}} \right)^{2} } \right)\left( {1 - \left( {\frac{y}{b}} \right)^{2} } \right)^{2} + \left( {\frac{a}{b}} \right)^{2} \left( {1 - \left( {\frac{x}{a}} \right)^{2} } \right)^{2} \left( {1 - 3\left( {\frac{y}{b}} \right)^{2} } \right)} \right]$$
(6)

The moment equation is used to calculate the stresses on the thin plate as:

$$\sigma_{x} = \frac{{6M_{x} }}{{h^{2} }}\;{\text{and}}\;\sigma_{y} = \frac{{6M_{y} }}{{h^{2} }}$$
(7)

Stress on the thin plate is calculated by putting the value of \(M_{x}\) and \(M_{y}\) in Eq. 7:

$$\sigma_{x} = \frac{{Pb^{4} }}{{\left( {a^{4} + b^{4} } \right)}}\left( {\frac{a}{h}} \right)^{2} \left[ {\left( {1 - 3\left( {\frac{x}{a}} \right)^{2} } \right)\left( {1 - \left( {\frac{y}{b}} \right)^{2} } \right)^{2} + \upsilon \left( {\frac{a}{b}} \right)^{2} \left( {1 - \left( {\frac{x}{a}} \right)^{2} } \right)^{2} \left( {1 - 3\left( {\frac{y}{b}} \right)^{2} } \right)} \right]$$
(8)

Similarly,

$$\sigma_{y} = \frac{{Pb^{4} }}{{\left( {a^{4} + b^{4} } \right)}}\left( {\frac{a}{h}} \right)^{2} \left[ {\upsilon \left( {1 - 3\left( {\frac{x}{a}} \right)^{2} } \right)\left( {1 - \left( {\frac{y}{b}} \right)^{2} } \right)^{2} + \left( {\frac{a}{b}} \right)^{2} \left( {1 - \left( {\frac{x}{a}} \right)^{2} } \right)^{2} \left( {1 - 3\left( {\frac{y}{b}} \right)^{2} } \right)} \right]$$
(9)

The simplified schematic of the rectangular plate is presented in Fig. 2a, b that explains how the stress in the direction of X (\(\sigma_{x}\)) and Y (\(\sigma_{y}\)) is induced, respectively. Also, the schematic of MEMS technology-based pressure sensor is depicted in Fig. 2c, d.

Maximum displacement magnitude is obtained at the center (\(x = 0\), \(y = 0\)) of the clamped edge thin plate. However, maximum stress is induced at the center edge of the clamped thin plate: \(x = 0\), \(y = \pm b\) and \(x = \pm a\), \(y = 0\). The contour plots are presented in “Results and discussions” section. The calculation of maximum deflection and maximum induced stresses are presented in the following subsection.

2.1.1 Case I: Calculation of maximum displacement magnitude

The boundary conditions are applied as \(x = 0\) and \(y = 0\), i.e., center of the thin plate (Fig. 2a) to get maximum displacement at the center of the thin diaphragm using Eq. 2.

$$w_{\hbox{max} } = \frac{P}{24D}\frac{{a^{4} b^{4} }}{{a^{4} + b^{4} }}\;{\text{or}}\;\frac{{w_{\hbox{max} } }}{h} = \frac{{\left( {1 - \upsilon^{2} } \right)P}}{2E}\frac{1}{{\left( {\frac{a}{b}} \right)^{4} + 1}}\left( {\frac{a}{h}} \right)^{4}$$
(10)

where \(b = {\raise0.7ex\hbox{${length}$} \!\mathord{\left/ {\vphantom {{length} 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}\) and \(a = {\raise0.7ex\hbox{${width}$} \!\mathord{\left/ {\vphantom {{width} 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}\) \(D\) is bending rigidity of thin plate defined in Eq. 3.

2.1.2 Case 2: Calculation of maximum stress

The center of the edge has the maximum induced stress at \(x = 0\), \(y = \pm b\) and \(x = \pm a\), \(y = 0\) The contour profiles of the induced stresses on top of the thin diaphragm are presented in “Results and discussions” section.

  1. (a)

    Induced stress at \(x = 0\), \(y = \pm b\)

$$\sigma_{x} |_{x = 0,y = \pm b} = \frac{{ - 2\upsilon \left( {\frac{a}{b}} \right)^{2} Pb^{4} }}{{\left( {a^{4} + b^{4} } \right)}}\left( {\frac{a}{h}} \right)^{2} \;{\text{or}}\;\sigma_{x} |_{x = 0,y = \pm b} = \frac{{ - 2\upsilon \left( {\frac{a}{b}} \right)^{2} P}}{{\left( {\left( {\frac{a}{b}} \right)^{4} + 1} \right)}}\left( {\frac{a}{h}} \right)^{2}$$
(11)

Similarly,

$$\sigma_{y} |_{x = 0,y = \pm b} = \frac{{2\left( {\frac{a}{b}} \right)^{2} Pb^{4} }}{{\left( {a^{4} + b^{4} } \right)}}\left( {\frac{a}{h}} \right)^{2} \;{\text{or}}\;\sigma_{y} |_{x = 0,y = \pm b} = \frac{{2\left( {\frac{a}{b}} \right)^{2} P}}{{\left( {\left( {\frac{a}{b}} \right)^{4} + 1} \right)}}\left( {\frac{a}{h}} \right)^{2}$$
(12)
  1. (b)

    Induced stress at \(x = \pm a\), \(y = 0\).

$$\sigma_{x} |_{x = \pm a,y = 0} = \frac{{ - 2Pb^{4} }}{{\left( {a^{4} + b^{4} } \right)}}\left( {\frac{a}{h}} \right)^{2} \;{\text{or}}\;\sigma_{x} |_{x = \pm a,y = 0} = \frac{ - 2P}{{\left( {\left( {\frac{a}{b}} \right)^{4} + 1} \right)}}\left( {\frac{a}{h}} \right)^{2}$$
(13)

Similarly,

$$\sigma_{y} |_{x = \pm a,y = 0} = \frac{{ - 2\upsilon Pb^{4} }}{{\left( {a^{4} + b^{4} } \right)}}\left( {\frac{a}{h}} \right)^{2} \;{\text{or}}\;\sigma_{y} |_{x = \pm a,y = 0} = \frac{ - 2\upsilon P}{{\left( {\left( {\frac{a}{b}} \right)^{4} + 1} \right)}}\left( {\frac{a}{h}} \right)^{2}$$
(14)

The parameters \(\frac{a}{h}\) and \(\frac{a}{b}\) are taken for further analysis of the thin diaphragm plate under different loads and analyzed the variation in \(\frac{{w_{\hbox{max} } }}{h}\), \(\sigma_{x}\) and \(\sigma_{y}\) which is presented in “Results and discussions” sections.

2.2 Electrical response using the theory of piezoresistivity

2.2.1 Change in resistance of piezoresistors using maximum stress

The thin diaphragm is used for the pressure sensor as a stress-magnifying element under the applied load. Induced stress is responsible for the change in resistance of diffused/implanted/deposited piezoresistors. The above stress equations are used for further analysis of the pressure sensor response. The output voltage is a function of the piezoresistive coefficient of the piezoresistors and induced stress. Since piezoresistors are embedded in the diaphragm, they are influenced by the same induced stresses. Change in the resistance due to induced stress is given by:

$$\left( {\frac{\Delta R}{R}} \right)_{l} = \pi_{l} \sigma_{l} + \pi_{t} \sigma_{t} \;{\text{and}}\;\left( {\frac{\Delta R}{R}} \right)_{t} = \pi_{l} \sigma_{t} + \pi_{t} \sigma_{l}$$
(15)

where \(\left( {\frac{\Delta R}{R}} \right)_{l}\) and \(\left( {\frac{\Delta R}{R}} \right)_{t}\) are a change in the resistance in the longitudinal direction and transverse direction, respectively. The \(\pi_{l}\) and \(\pi_{t}\) are longitudinal and transverse piezoresistive coefficients of piezoresistor, respectively. The \(\sigma_{l}\) and \(\sigma_{t}\) are longitudinal and transverse induce stresses, respectively. \(\sigma_{l} = \sigma_{x}\) and \(\sigma_{t} = \sigma_{y}\) are longitudinal and transverse stresses for resistor perpendicular to diaphragm edge, respectively. \(\sigma_{l} = \sigma_{y}\) and \(\sigma_{t} = \sigma_{x}\) are longitudinal and transverse stresses for resistor parallel to diaphragm edge, respectively.

The piezoresistors design is rectangular; hence, they experience the stresses from a rectangular region of the diaphragm shown in Fig. 2. However, average stresses experienced by piezoresistors on rectangular region are calculated for further analysis.

2.2.2 Change in resistance of piezoresistors using average stress

Since the stresses experienced by the piezoresistors are not point stresses, they experience the average stresses from the rectangular region. Therefore, the average stress on piezoresistor \(R_{p}\) with a dimension of \(l_{p} \times w_{p}\) is calculated by:

  1. (a)

    Average stresses for longitudinal resistors

    $$\sigma_{x} ,avg = \frac{1}{{A_{p} }}\int\limits_{{x - l_{p} }}^{x} {\int\limits_{{\frac{{ - w_{p} }}{2}}}^{{\frac{{w_{p} }}{2}}} {\sigma_{x} dxdy} } \;{\text{and}}\;\sigma_{y} ,avg = \frac{1}{{A_{p} }}\int\limits_{{x - l_{p} }}^{x} {\int\limits_{{\frac{{ - w_{p} }}{2}}}^{{\frac{{w_{p} }}{2}}} {\sigma_{y} dxdy} }$$
    (16)
  2. (b)

    Similarly, average stresses for transverse resistors,

    $$\sigma_{y} ,avg = \frac{1}{{A_{p} }}\int\limits_{{\frac{{ - w_{p} }}{2}}}^{{\frac{{w_{p} }}{2}}} {\int\limits_{{y - l_{p} }}^{y} {\sigma_{y} dxdy} } \;{\text{and}}\;\sigma_{y} ,avg = \frac{1}{{A_{p} }}\int\limits_{{\frac{{ - w_{p} }}{2}}}^{{\frac{{w_{p} }}{2}}} {\int\limits_{{y - l_{p} }}^{y} {\sigma_{y} dxdy} }$$
    (17)

    where \(A_{p} = l_{p} \times w_{p}\) is an area of rectangular piezoresistor with \(l_{p}\) and \(w_{p}\) are length and width, respectively.

The average stresses are calculated by putting the value of \(\sigma_{x}\) and \(\sigma_{y}\) in Eq. 17.

Hence, for longitudinal resistors:

$$\sigma_{x,avg} = \frac{1}{{A_{p} }}C\int\limits_{{x - l_{p} }}^{x} {\int\limits_{{\frac{{w_{p} }}{2}}}^{{\frac{{w_{p} }}{2}}} {\left[ {A + \upsilon B} \right]dxdy} } \;{\text{and}}\;\sigma_{y,avg} = \frac{1}{{A_{p} }}C\int\limits_{{x - l_{p} }}^{x} {\int\limits_{{\frac{{w_{p} }}{2}}}^{{\frac{{w_{p} }}{2}}} {\left[ {\upsilon A + B} \right]dxdy} }$$
(18)

for transverse resistors

$$\sigma_{x,avg} = C\frac{1}{{A_{p} }}\int\limits_{{\frac{{w_{p} }}{2}}}^{{\frac{{w_{p} }}{2}}} {\int\limits_{{y - l_{p} }}^{y} {\left[ {A + \upsilon B} \right]dxdy} } \;{\text{and}}\;\sigma_{y,avg} = C\frac{1}{{A_{p} }}\int\limits_{{\frac{{w_{p} }}{2}}}^{{\frac{{w_{p} }}{2}}} {\int\limits_{{y - l_{p} }}^{y} {\left[ {\upsilon A + B} \right]dxdy} }$$
(19)

where \(C = \frac{{Pb^{4} }}{{\left( {a^{4} + b^{4} } \right)}}\left( {\frac{a}{h}} \right)^{2}\), \(A = \left( {1 - 3\left( {\frac{x}{a}} \right)^{2} } \right)\left( {1 - \left( {\frac{y}{b}} \right)^{2} } \right)^{2}\) and \(B = \left( {\frac{a}{b}} \right)^{2} \left( {1 - \left( {\frac{x}{a}} \right)^{2} } \right)^{2} \left( {1 - 3\left( {\frac{y}{b}} \right)^{2} } \right)\).

Hence, change in the resistance is described as:

$$\left( {\frac{\Delta R}{R}} \right)_{l} = \pi_{l} \sigma_{l,avg} + \pi_{t} \sigma_{t,avg} \;{\text{and}}\;\left( {\frac{\Delta R}{R}} \right)_{t} = \pi_{l} \sigma_{t,avg} + \pi_{t} \sigma_{l,avg}$$
(20)

where \(\sigma_{l,avg} = \sigma_{x,avg}\) and \(\sigma_{t,avg} = \sigma_{y,avg}\) for resistor perpendicular to diaphragm edge (longitudinal stress), and \(\sigma_{l,avg} = \sigma_{y,avg}\) and \(\sigma_{t,avg} = \sigma_{x,avg}\) for resistor parallel to diaphragm edge (transverse stress). Schematic of the diaphragm with piezoresistors are shown in Fig. 2c. Piezoresistors are connected in full Wheatstone bridge configuration that leads to the output voltage response. The output voltage is calibrated in terms of the standard pressure. The output response of the Wheatstone bridge configuration is given by (Fig. 3):

$$V_{out} = 0.5\left( {\left( {\frac{\Delta R}{R}} \right)_{l} - \left( {\frac{\Delta R}{R}} \right)_{t} } \right)V_{in}$$
(21)
$$V_{out} = 0.5\left( {\left( {\frac{\Delta R}{R}} \right)_{l} - \left( {\frac{\Delta R}{R}} \right)_{t} } \right)V_{in}$$
(21)

The sensitivity of the pressure sensor is described as:

$$S = \frac{{V_{out} }}{{V_{in} }}\frac{1}{P}$$
(22)
$$V_{out} = 0.5\left( {\left( {\frac{\Delta R}{R}} \right)_{l} - \left( {\frac{\Delta R}{R}} \right)_{t} } \right)V_{in}$$
(21)

The sensitivity of the pressure sensor is described as:

$$S = \frac{{V_{out} }}{{V_{in} }}\frac{1}{P}$$
(22)
Fig. 3
figure 3

Wheatstone bridge configuration to get an output voltage

Full size image

2.2.3 Selection of piezoresistor parameters

Generally, a rectangular shape of the piezoresistors is used. The resistance of piezoresistors is a function of geometrical dimensions, i.e., length, width, thickness and dopant concentration. These parameters play an important role to calculate the overall sensitivity of the piezoresistive pressure sensor. However, sensitivity is mainly influenced by the piezoresistive coefficients which depend on dopant concentration. As dopant concentration of piezoresistor is increasing, the piezoresistive coefficient is decreasing which led to the decrease in the sensitivity of the piezoresistive pressure sensor. Mathematically, the resistance of piezoresistor can be defined as,

$$R = f(l,w,t,p)$$
(23)
$$R = \rho \frac{l}{w \times t}$$
(24)
$$R = \frac{1}{{p \times q \times \mu_{p} }}\frac{l}{w \times t}$$
(25)

where \(R\) is the resistance of piezoresistors, \(\rho\) is resistivity, \(p\) is boron concentration of p-type piezoresistor, \(\mu_{p}\) is mobility of carriers, and \(l,w\) and \(t\) are geometrical parameters, i.e., length, width and thickness, respectively.

3 Methodology and material used

The analytical approach was used for modeling the thin diaphragm for the calculation of sensitivity for piezoresistive pressure sensor. The mechanical response of thin diaphragm, i.e., deflection and induced stress are defined using the thin plate theory. Further, maximum induced stresses are identified and average stresses are calculated based on the geometry of the piezoresistors on top of the thin diaphragm. The output voltage was calculated using the piezoresistive coefficient and average stresses experienced by piezoresistors. The results are presented in the next section.

Moreover, the material of thin diaphragm and piezoresistors plays an important role in fabrication using MEMS technology and for the sensitivity. The silicon as a thin diaphragm and p-type silicon for piezoresistors are selected in this study. The corresponding material properties of silicon are presented in Table 1.

Table 1 Material properties used for the analytical study
Full size table

4 Results and discussions

The deflection and induced stress profiles are analyzed for the calculation of mechanical sensitivity (i.e., stresses per applied pressure or deflection per applied pressure) of the thin diaphragm. The induced stresses and piezoresistive coefficients of piezoresistors are governing parameters to estimate the overall sensitivity of the piezoresistive pressure sensor. The results of the analytical model are presented in the current section.

4.1 Deflection of a thin diaphragm

In order to understand the deflection profile of thin diaphragm, a contour plot is depicted in Fig. 4. It describes that the maximum deflection is observed at the center of the diaphragm. The deflection sensitivity of 0.014 µm/MPa was recorded for the thin diaphragm with geometry of 1000 µm × 1000 µm × 200 µm. The deflection is increasing with an increase in applied pressure. The deflection sensitivity is calculated and compared with a model available in the literature. The comparison of deflection sensitivities was done between the current model and Gong and Lee model [21]. The deviation in the deflection profile is observed to be 3% as shown in Fig. 5 (using Eq. 10).

Fig. 4
figure 4

Deflection contour of a thin plate under applied pressure of 40 MPa, diaphragm size 1000 µm × 1000 µm × 200 µm

Full size image
Fig. 5
figure 5

Normalized deflection by diaphragm thickness versus applied pressure and comparison with Gong and Lee model [21]

Full size image

In Case I, the variation in deflection of the thin plate with varying a/h ratios is calculated for \(a/b = 1\), i.e., for square thin plate (where a and b are half of width and length of the diaphragm) and presented in Fig. 6 (a). As the a/h ratio is increasing, the deflection of the thin plate is also increasing as shown in Fig. 6b. The normalized deflection sensitivity \(S_{nd}\)(\(w_{\hbox{max} } /h/MPa\)) is obtained using the power curve fitting as \(S_{nd} = A(a/h)^{B}\), where \(A = 2.0 \times 10^{ - 6}\) = and \(B = 3.9991 \cong 4\) at \(a/b = 1\). As shown in Fig. 6a, b, there is a very strong dependency of \(a/h\) ratio on the deflection of the thin diaphragm. The variations in \(w_{\hbox{max} } /h\) and \(w_{\hbox{max} } /h/MPa\) are plotted in the logarithmic scale for more clarity as shown in Fig. 6a, b, respectively. The maximum possible deflection can be calculated for any possible \(a/h\) ratio for design optimization for \(a/b = 1\) using this analysis presented.

Fig. 6
figure 6

a Normalized deflection by diaphragm thickness versus applied pressure with varying a/h ratios and a/b = 1, b relation between normalized deflection sensitivity, \(S_{nd}\)(Wmax/h/MPa) versus a/h ratio with a/b = 1

Full size image

Moreover, in Case II, the effect of \(a/b\) ratio is investigated for thin plate deflection with \(a/h = 2.5\) shown in Fig. 7a. It can be seen that there is a dependency of \(a/b\) ratio with the thin plate deflection; as \(a/b\) ratio approached unity the deflection of a thin plate gets decreased as shown in Fig. 7b for \(a/h = 2.5\). The normalized deflection sensitivity in this case shows the linear relation with \(a/b\) ratio shown in Fig. 7b. It is also inferred that as \(a/b\) ratio approaches unity, it becomes square diaphragm, whereas beyond the unity it acts as a rectangular diaphragm.

Fig. 7
figure 7

a Normalized deflection by diaphragm thickness vs applied pressure for varying a/b ratios at a/h = 2.5, b Normalize deflection sensitivity as a function of a/b at a/h = 2.5

Full size image

4.2 Induced stresses in a thin diaphragm

Under the applied pressure and with a boundary condition of all four edges fixed, the stresses are induced on the thin diaphragm edges. Induced stress is proportional to the applied pressure and it is dependent on the geometrical parameters and material (i.e., silicon) of the thin diaphragm. Under the assumption of thin plate theory, z directional stress is assumed to be negligible as compared to the other two stress components, i.e., stress X and stress Y. The contour plots of induced stresses on thin diaphragms are presented in Figs. 8 and 9 for stress X and Y, respectively. It is observed that maximum stresses are induced at center of edge and the center of diaphragm. It is also inferred that stress components in the center are equal for the x and y directions; however, at the edge the stresses components are differed by the large amount shown in Fig. 10a, b (from Eqs. 8–9).

Fig. 8
figure 8

Stress XX contour plot for diaphragm size 1000 µm × 1000 µm × 200 µm, pressure − 40 MPa

Full size image
Fig. 9
figure 9

Stress YY contour plot for diaphragm size-1000 µm × 1000 µm × 200 µm, pressure − 40 MPa

Full size image
Fig. 10
figure 10

a Stress components along the edge of the thin diaphragm, b stress components along the center of the thin diaphragm, size-1000 µm × 1000 µm × 200 µm, pressure - 40 MPa

Full size image

Based on the above analysis, it is being confirmed that resultant stress is higher in the center of the diaphragm edge. Therefore, the placement of piezoresistors at this place is the best choice in order to get higher sensitivity. Therefore, the analysis of stress components versus applied pressure at the center of edge is carried out. The induced directional stress components are calculated under the varying applied pressures from 0 to 40 MPa because the design is targeted for high-pressure applications. It is found that there is a linear increase in induced stress with an increase in the applied pressure. The stress sensitivities for the stress components, i.e., stress X and stress Y, are obtained as 6.25 and 1.68 MPa/MPa, respectively, shown in Fig. 11. It is seen that stress component, i.e., stress X, is higher as compared to stress component Y. The calculations are carried out using Eqs. 11 to 14 discussed in the earlier section.

Fig. 11
figure 11

Stress XX versus applied pressure for diaphragm size-1000 µm × 1000 µm × 200 µm, pressure - 40 MPa

Full size image

Further, the variation of stresses with varying a/h ratios with a/b = 1 is carried out under varying applied pressures shown in Fig. 12a. It is observed that as a/h ratio is increasing the stress sensitivity is also increasing. Stress sensitivities for components stress X and stress Y are calculated as under varying a/h ratios as shown in Fig. 12b.

Fig. 12
figure 12

a Stress profiles with varying a/h ratios for a/b = 1 versus applied pressure, b variation in stress sensitivity versus a/h ratio for a/b = 1

Full size image

4.3 Calculation of average stresses

The average stresses experienced by the piezoresistors are calculated based on the geometry of the piezoresistors on top of the thin diaphragm. The average stresses are smaller than the maximum stresses used for the calculation of pressure response. It is observed that average stresses are comparatively less by 28.62% and 36.46% for stresses in the direction of X and Y, respectively, shown in Fig. 13. However, the differences between stress X and stress Y are remained identical, and hence, there is no significant effect in the calculation of pressure sensor sensitivity.

Fig. 13
figure 13

Stress X and stress Y versus applied pressure for diaphragm size-1000 µm × 1000 µm × 200 µm, pressure − 40 MPa

Full size image

4.4 Output voltage of piezoresistive pressure sensor

Based on the maximum stresses and average stresses, the response of the pressure sensor is calculated and plotted in Fig. 14. It is observed that 3% change in the response of pressure sensor is under calculation based on the average and maximum induced stresses. As the piezoresistors experienced resultant stresses, i.e., difference between stress X and stress Y, there is a large difference between maximum and average stresses; however, resultant stresses, i.e., difference between stress X and stress Y, remain nearly equal. Therefore, a very small deviation is obtained in the output voltage of piezoresistive pressure sensor as shown in Fig. 14.

Fig. 14
figure 14

Pressure response calculation based on maximum and average induced stresses on top of thin diaphragm, diaphragm size 1000 µm × 1000 µm × 200 µm

Full size image

5 Conclusion

In this article, an analytical model is presented to calculate the sensitivity of piezoresistive pressure sensor. The deflection and induced stresses are calculated and analyzed the variation in parameters of \(a/h\), \(a/b\). The deflection profile was compared with the model available in the literature with 3% deviation. Moreover, the calculation of the sensitivity using the analytical model is proposed based on the average stresses and obtained the ~ 3% change with calculations based on maximum stresses. Such a small deviation is occurred due to nearly identical resultant stresses (i.e., difference between stress X and stress Y) in case of average and maximum induced stress calculation method. However, the calculation shows 11% and 27% decrease in average stresses with maximum stresses for stresses X and Y, respectively. This article helps to estimate the sensitivity of piezoresistive pressure sensor analytically before going for fabrication and further characterization.