Introduction

An accurate and reliable computational prediction of binding affinities of small molecules binding to larger molecules, such as proteins, remains a major objective of computer simulations for molecular design [1]. In order to assess state-of-the-art tools for computational predictions of thermodynamic properties of binding the Statistical Assessment of the Modeling of Proteins and Ligands (SAMPL) challenge was formulated almost 10 years ago [2–4]. The goal of SAMPL5, as in previous years, was to compare different computational approaches in blinded challenges for different properties. This report is concerned with host-guest standard binding free energies, as predicted by our group.

Host-guest systems can be regarded as a toy model for protein ligand systems and represent a good play ground for testing the accuracy of thermodynamic property predictions. Various computational methods are available to compute free energies of binding of the host-guest systems [5–8]. Previous SAMPL challenges have featured potential energy functions ranging from quantum chemical [9–11] to molecular mechanical approaches [12, 13]. Molecular dynamics (MD) or Monte Carlo (MC) simulations are frequently carried out to estimate the ensemble averages that yield standard free energies of binding. These methodologies still face three major problems: the sampling problem [14], the translation of host-guest systems into force field terms [15] and the presence of finite size effects [16]. Different approximations lead to various ways of estimating free energies of binding from molecular simulations trajectories, e.g. free energy perturbations (FEP) [17], finite difference thermodynamic integration (FDTI) [18], or end-states only variants such as MM-PBSA [19].

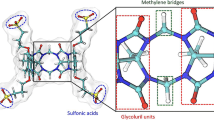
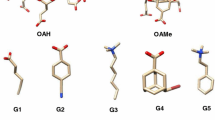
In this study a trajectory based alchemical free energy approach was used to predict standard free energies of binding for 22 host-guest complexes. The dataset consists of 16 guests that bind to three different molecules: two octa-acid hosts (OAH and OAMe), and a cucurbituril clip (CBC) as shown in Fig. 1. The octa-acid systems are basket shaped. OAH [20] has four flexible propionate side chains bearing two rotatable single bonds each, while, OAMe contains four methyl groups, which alter the shape and depth of the hydrophobic cavity. CBC [21, 22] is a more flexible host, which has shown a high binding affinity for ferrocene, adamantane and bicyclooctane guests [23]. The aim of this paper is to illustrate the accuracy and agreement with experiments that can be reached by means of standard free energy of binding calculations using a molecular mechanics approach with the general Amber forcefield (GAFF) [24]. In recent studies by Mirshra et al. and Aldeghi et al. [25, 26] the GAFF force field has not systematically been the most accurate forcefield, but it remains an attractive choice due to the ease of parameter generation, especially given the limited time available in SAMPL between datasets release and deadline for predictions submissions. The performance of three different variants of a double annihilation methodology for binding free energy predictions is critically assessed, as well as overall standing with respect to other SAMPL5 submissions.

Fig. 1
figure 1

a Octa-acid systems OAH and OAMe and their respective six guests, plus SAMPL4 guest O1. b Cucurbituril clip CBC and its ten guests

Full size image

Theory and methods

Several approaches have been proposed to compute standard free energies of binding from molecular simulations.

Computing free energies of binding: models A, B, and C

One way of estimating a free energy of binding \({\varDelta }G_{\mathrm {bind}}\) from MD simulations is by means of a double annihilation technique proposed originally by Jorgensen et al. [27] and discussed extensively by Gilson et al. [28]. The free energy of binding \({\varDelta }G_{\mathrm {bind}}\) is given by:

$$\begin{aligned} {\varDelta }G_{\mathrm {bind}} = -k_BT\ln \frac{Z_{\mathrm {HG,solv}}Z_{\mathrm {solv}}}{Z_{\mathrm {G,solv}}Z_{\mathrm {H,solv}}}, \end{aligned}$$
(1)

where \(k_{\mathrm {B}}\) is the Boltzmann constant, T the temperature, \(Z_{\mathrm {HG,solv}}\), \(Z_{\mathrm {G,solv}}\), \(Z_{\mathrm {H,solv}}\) and \(Z_{\mathrm {solv}}\) are the configuration integrals for host-guest complex, the guest, the host and the solvent molecules respectively. Figure 2 depicts how the double annihilation approach may be used to evaluate \({\varDelta }G_{\mathrm {bind}}\) by means of thermodynamic cycles. First the guest’s partial charges are turned off both in water and in the host-guest-complex phase (discharging step), giving the discharging free energy change \({\varDelta }G_{\mathrm {elec}}^{\mathrm {solv}}\) and \({\varDelta }G_{\mathrm {elec}}^{\mathrm {host}}\) respectively. Secondly, the guest is fully decoupled from the solvent or host, switching off the van der Waals terms (vanishing step), \({\varDelta }G_{\mathrm {vdW}}^{\mathrm {solv}}\) and \({\varDelta }G_{\mathrm {vdW}}^{\mathrm {host}}\). The discharging and vanishing steps are usually performed with a series of intermediate simulations that depend on a coupling parameter \(\lambda \in [0,1]\). In the double annihilation method the term \({\varDelta }G_{\mathrm {rest}}\) shown in Fig. 2 is zero (see details below). Closure of the thermodynamic cycle in Fig. 2 shows that in the double annihilation technique the free energy of binding \({\varDelta }G_{\mathrm {bind}}\) is given as [29]:

$$\begin{aligned} {\varDelta }G_{\mathrm {bind}}= \left( {\varDelta }G_{\mathrm {elec}}^{\mathrm {solv}} + {\varDelta }G_{\mathrm {vdW}}^{\mathrm {solv}}\right) -\left( {\varDelta }G_{\mathrm {elec}}^{\mathrm {host}} + {\varDelta }G_{\mathrm {vdW}}^{\mathrm {host}}\right) . \end{aligned}$$
(2)
Fig. 2
figure 2

Thermodynamic cycle for free energy of binding calculation. First, a fully interacting ligand is simulated in a water phase (top left), then charges and Lennard Jones terms are switched off sequentially, resulting in a fully non-interacting ligand in water (bottom left). The same transformation is performed in the complex, going from a fully interacting ligand (top right) to a dummy ligand (bottom right). The middle step (middle two panels) is concerned with the evaluation of a free energy change associated with the introduction of a host-guest restraining potential in the complex simulations. This term is neglected in model A and model B, and numerically evaluated with respect to standard state conditions in model C. Consequently model A and model B yield a free energy of binding \({\varDelta }G_{\mathrm {bind}}\), whereas model C yields a standard free energy of binding \({\varDelta }G_{\mathrm {bind}}^{\mathrm {0}}\)

Full size image

Free energies of binding computed according to Eq. (2), will be referred to as model A. In the actual MD simulation an empirical distance-restraint term is added to the potential energy function. This is done to prevent the non-interacting guest from drifting out of the host cavity. A flat-bottom restraining potential is used between one atom of the guest, chosen to be the one closest to the centre of mass, and four equivalent carbon atoms of the host. The restraint potential for atom j of the guest is based on work presented in Ref. [5] and takes the following form:

$$\begin{aligned} U^{\mathrm {restr}}(d_{j1},...,d_{jN_{host}}) =\sum _{i=1}^{N_{\mathrm {host}}} {\left\{ \begin{array}{ll} 0 &{} \quad \mathrm {if}\; | d_{ji} - R_{ji} | \le D_{ji} \\ \kappa _{ij}\left( | d_{ji} - R_{ji} | - D_{ji} \right) ^2 &{}\quad \mathrm {ji}\; | d_{ji}- R_{ji} | > D_{ji} \end{array}\right. }, \end{aligned}$$
(3)

where \(U^{\mathrm {restr}}(d_{j1},...,d_{jN_{host}})\) is the potential energy of the restraint as a function of the distance between a guest atom j  and a set of host atoms i, \(d_{ji}=|| \mathbf {r}_{i}-\mathbf {r}_{j} ||\) where \(||\circ ||\) denotes a 2-norm, \(D_{ji}\) is the restraint deviation tolerance, \(R_{ji}\) the reference distance between host and guest atom, \(\kappa _{ji}\) the restraint force constant, and \(N_{\mathrm {host}}\) the number of host atoms that contribute to the restraint.

Model A neglects, among other things, the contribution of long range dispersions, since a cutoff for the Lennard Jones interaction was set to 12 Å to speed up simulations (see protocols). Following work from Shirts et al. [30], it is possible to introduce a long range dispersion correction term to the free energy of binding as a post processing step of the simulation trajectories. This leads to a corrected free energy of binding \({\varDelta }G_{\mathrm {bind,LJRC}}\) given by:

$$\begin{aligned} {\varDelta }G_{\mathrm {bind,LJLRC}}= & {} \left( {\varDelta }G^{\mathrm {solv}}_{\mathrm {elec}} + {\varDelta }G^{\mathrm {solv}}_{\mathrm {vdW}}\right) \nonumber \\&\quad -\,\left( {\varDelta }G^{\mathrm {host}}_{\mathrm {elec}}+{\varDelta }G^{\mathrm {host}}_{\mathrm {vdW}}\right) \nonumber \\&\quad +\,\left( {\varDelta }G^{\mathrm {host}}_{\mathrm {LJLRC}}-{\varDelta }G^{\mathrm {solv}}_{\mathrm {LJLRC}}\right) . \end{aligned}$$
(4)

Equation (4) gives the free energy of binding for model B, where the Lennard Jones dispersion correction \({\varDelta }G^{\mathrm {X}}_{\mathrm {LJLRC}}\) can be computed making use of the Zwanzig relation [31] in the following way:

$$\begin{aligned} {\varDelta }G^{\mathrm {X}}_{\mathrm {LJLRC}}=k_BT\ln \langle \exp [-\beta (U_{\mathrm {LJ,long}}(\mathbf {r})-U_{\mathrm {LJ,sim}}(\mathbf {r})]\rangle _{\mathrm {X}}+U_{\mathrm {LJ,ana}}, \end{aligned}$$
(5)

where X = host or solv, \(U_{\mathrm {LJ,long}}\) is the Lennard Jones energy computed with an increased long range cutoff and \(U_{\mathrm {LJ,ana}}(\mathbf {r})\) is an analytical correction from the increased range long cutoff to infinity. The long range correction \(U_{\mathrm {LJ,long}}\) is estimated in a post processing step of the ‘vanishing’ trajectories generated at \(\lambda =0\) and \(\lambda =1\), by extending the domain of the typical Lennard Jones cutoff radius in the simulation from 12 Å to cover almost the entire box instead. To define this long cutoff, the minimum box length in all directions in the input coordinates is calculated, and the new cutoff radius is set to \(r_{c,\mathrm {long}}=0.95 \min (L_x,L_y,L_z)/2\) to allow for some fluctuations in box size. This allows an averaging over the whole trajectory of the additional contribution of the long range potential \(U_{\mathrm {LJ,long}}\), with respect to the simulated Lennard Jones term \(U_{\mathrm {LJ,sim}}\). This correction, however, does not account for an infinitely large box size giving rise to an analytical correction over an infinite domain, which is given by the additive constant given below:

$$\begin{aligned} U_{\mathrm {LJ,ana}} = 8\pi \rho \sum _i^{N_{\mathrm {sol}}}\sum _{j}^{N_{\mathrm {solv}}}\left[ \frac{\epsilon _{ij}\sigma _{ij}^{12}}{9r_{\mathrm {c}}^9} - \frac{\epsilon _{ij}\sigma _{ij}^6}{3r_{\mathrm {c}}^3}\right] , \end{aligned}$$
(6)

where \(\rho\) is the solvent density in mol Å−3, \(N_{\mathrm {sol}}\) is the total number of atoms in the guest, \(N_{\mathrm {solv}}\) the number of solvent molecules, \(\epsilon _{ij}\) is the Lennard Jones well depth, expressed in kcal mol−1, and \(\sigma _{ij}\) is the Lennard Jones distance, in Å, calculated with the Lorentz–Berthelot combining rule [32]. Lennard Jones parameters for the solvent are those of the oxygen atom of the TIP3P water model [33]. It is implicitly assumed that the radial distribution function g(r) = 1 for distance greater than \(r_{\mathrm {c}}\). Both model A and model B lack a well defined reference state in their definition of the free energy change upon binding of the guest molecules. Therefore a third model is proposed to enable a standard state definition. For this purpose the standard state correction is subtracted from the free energy of binding given by Eq. (4). The standard free energy of binding is given by:

$$\begin{aligned} {\varDelta }G^{\circ }_{\mathrm {bind}}= & {} \left( {\varDelta }G^{\mathrm {solv}}_{\mathrm {elec}} + {\varDelta }G^{\mathrm {solv}}_{\mathrm {vdW}}\right) \nonumber \\&\quad -\,\left( {\varDelta }G^{\mathrm {host}}_{\mathrm {elec}}+{\varDelta }G^{\mathrm {host}}_{\mathrm {vdW}}\right) \nonumber \\&\quad +\,\left( {\varDelta }G^{\mathrm {host}}_{\mathrm {LJLRC}}-{\varDelta }G^{\mathrm {solv}}_{\mathrm {LJLRC}}\right) + {\varDelta }G^{\circ }_{\mathrm {restr}}, \end{aligned}$$
(7)

where \({\varDelta }G^{\circ }_{\mathrm {restr}}\) accounts for the introduced flat-bottom restraint. Considering the cycle in Fig. 2, the restraint free energy change can be computed as:

$$\begin{aligned} {\varDelta }G_{\rm {restr}}^{\circ } = -k_{\rm {B}}T\ln \left( \frac{Z_{{{\rm H}\circ \circ{\rm G}^{\rm{ideal}}}, {\rm solv}}}{Z_{\rm H,solv} Z_{\rm {G,gas}}} \right) , \end{aligned}$$
(8)

where \(Z_{{{\rm H}\circ \circ {\rm G}^{\rm{ideal}}}, {\hbox{solv}}}\) is the configuration integral for the restrained decoupled guest bound to the host, \(Z_{\mathrm {H, solv}}\) is the configuration integral for the solvated host and \(Z_{\mathrm {G,gas}}\) is the configuration integral for the guest in an ideal thermodynamic state (i.e. no non-bonded interactions). Assuming that the restraint potential is decoupled from the solvent and host degrees of freedom, Eq. (8) simplifies to:

$$\begin{aligned} {\varDelta }G_{\rm restr}^{\circ } = -k_{\rm B}T\ln \left( \frac{Z_{{\circ \circ {\rm G}^{\rm{ideal}}} , {\hbox{solv}}}}{Z_{{\rm G},{\rm gas}}}\right) , \end{aligned}$$
(9)

where \(Z_{{\circ \circ {\rm G}^{\rm{ideal}}} , {\hbox{solv}}}\) is the configuration integral for the decoupled guest. Because the guest has no intermolecular interactions in both thermodynamic states defined in Eq. (9), and because the restraint does not hinder rotational motions, internal and rotational contributions to the configuration integrals cancel out and the only term left is the translational contribution to the configuration integral. For \(Z_{\mathrm {G,gas}}\) a standard volume of measurement \(V^{\circ }\) is used, with the 1 M dilute solute convention corresponding to \(V^{\circ }\) = 1660 \({\AA}^3\,\hbox {mol}^{-1}\). Therefore Eq. (9) simplifies further to:

$$\begin{aligned} {\varDelta }G_{\mathrm {restr}}^{\circ } = -k_{\mathrm {B}}T\ln \left( \frac{V^{\mathrm {restr}}}{V^{\circ }}\right) , \end{aligned}$$
(10)

where the restraint volume \(V^{\mathrm {restr}}\) is given by:

$$\begin{aligned} V^{\mathrm {restr}} = \int _{-\infty }^{+\infty }\int _{-\infty }^{+\infty }\int _{-\infty }^{+\infty }dx_{j}\,dy_{j}\,dz_{j} \exp (-\beta U^{restr}(d_{j1},\ldots ,d_{jN_{host}})). \end{aligned}$$
(11)

\(V^{\mathrm {restr}}\) can be calculated by numerically integrating Eq. (11). The following procedure was used. First, the coordinates of the host-guest complex in the generated trajectory at \(\lambda =1\) of the vanishing step was aligned to the first frame of the trajectory. Then, the average coordinate of each of the four host atoms used for the restraint was computed. Next, a grid spacing and an integration domain needed to be defined. The grid spacing was set to 0.1 Å and the integration domain was defined by the rectangular cuboid that is given by the minimum/maximum coordinates of the four defined host atoms with an additional buffer around the bounding domain of ±5 Å. Numerical integration was then performed via the multidimensional trapezoidal rule.

Host-guest simulation set-up

Host-guest input files were used as provided by the challenge organizers. For the simulations of the solvated guests, guest force field parameters and coordinates were extracted from the provided topologies and the guests were solvated in a rectangular box of TIP3P water molecules [33], with a minimum distance between the solute and the box of 12 Å, using the software tleap. Ions were added to neutralize the overall charge of the box. The system was energy minimized with 100 steps of the steepest decent algorithm. The following equilibration protocol was used: Solute molecules were position restrained with a force constant of 10 kcal mol−1 Å−2, while the water was allowed to equilibrate in an NVT ensemble for 200 ps at 298 K, followed by an NPT equilibration for a further 200 ps and a pressure of 1 atm using the Amber module Sander [34]. Lastly, 2 ns of NPT simulation was run with Sire/OpenMM6.3 (SOMD) software (revision 2015.0.0) [35, 36], to reach a final density of about 1 \(\mathrm {g/cm}^3\) using a timestep of 1 fs. The final coordinate files were retrieved with CPPTRAJ [37]. The same protocol for preparation and equilibration was used for the host-guest complex.

Additionally, the reference system OAH-O1, taken from the SAMPL4 challenge [38], was set-up from scratch. Guest O1 was obtained from the modification of compound G6 using Maestro (v.10.1.012, rel 2015-1, Schrödinger) [39] and further parametrized using AM1-BCC charges [40] using Antechamber 14 [34]. Complex and water phase systems were created with tleap, according to the above protocol, using the same binding mode as the one provided for G6.

Alchemical free energy production simulations

For the discharging steps nine equidistant \(\lambda\) windows were selected for the host-guest complex and the guest in water phases. For the vanishing step 12 and 18 equidistant windows were used for octa-acid guests and CBC guests respectively. The reasoning behind these different choices was that the CBC guests were larger, therefore a denser number of \(\lambda\) windows was deemed necessary in order to guarantee good overlap of the potential energy distributions of neighbouring \(\lambda\) windows, which is essential for free energy estimation via multistate Bennett’s acceptance ratio (MBAR) [41]. All simulations were run for 8 ns. A velocity-Verlet integrator was used with a time step of 4 fs using a hydrogen mass repartitioning (HMR) scheme [42]. All bonds were constrained. All simulations were performed in an NPT ensemble and temperature control was achieved with an Andersen Thermostat with a coupling constant of 10 ps\(^{-1}\) [43]. Pressure was maintained by a Monte Carlo barostat that attempted isotropic box edge scaling every 100 fs. Periodic boundary conditions were imposed with a 12 Å atom-based cutoff distance for the non-bonded interactions, using a Barker Watts reaction field with dielectric constant of 78.3 [44]. In the host-guest complex the guest molecules were restrained according to Eq. (3). The parameters were R ji  = 5 Å, D ji  = 2 Å and \(\kappa _{{ji}} = 10\;{\text{kcal}}\;{\text{mol}}^{{ - 1}}{\AA}^{{ - 2}}\).

Estimation of free energy changes for models A, B, and C

Individual free energy contributions from the discharging and vanishing steps were estimated by using MBAR [41]. To estimate the accuracy and consistency of the computed binding free energy from Eq. (2), each simulation was repeated twice using different initial assignments of velocities drawn from the Maxwell–Boltzmann distribution. Final binding free energies are reported as the average of both runs and statistical uncertainties were calculated according:

$$\begin{aligned} {\mathrm {err}}({\varDelta }G) = \frac{\sigma }{\sqrt{n}}, \end{aligned}$$
(12)

where \(\sigma\) is the standard deviation of both runs and n=2 unless otherwise mentioned.

The computed binding free energies with each model are then compared to experimental values considering two different measures: the determination coefficient \(R^2\) and mean unsigned error (MUE). To gain insight into the distribution of the two different measures a bootstrapping scheme is used in which each computed free energy point is considered to parameterize a normal distribution with its mean given by the computed free energy and \(\sigma\) the associated computed error. Ten thousand samples are then drawn from the artificial normal distributions for each data point and correlated with the experimental values, giving rise to a distribution of \(R^2\) and MUE. The resulting distributions are typically not symmetric around the mean and uncertainties in the dataset metrics are reported with a 95 % confidence interval. All simulation input files and post processing scripts needed for reproducing the results, as well results files, can be found in a github repository https://github.com/michellab/Sire-SAMPL5.

Experimental data

Experimental data for the host-guest complexes of the octa-acids were obtained by a mixture of NMR and ITC measurements. CBC host-guest complexes standard free energy of binding were obtained using UV, visible, and florescent spectroscopic measurements. All data was measured in the laboratory of Bruce Gibb (Tulane University), with detailed description of the two octacid hosts found in [20, 45]. Details on the experimental procedures and error analysis of the experimental data will be described elsewhere [46]. A summary of the experimental data used for the analysis in this work, as provided by the organizers, can be found in Table 1.

Results

Host-guest binding free energy predictions

To test the precision and accuracy of the protocols implementing the three models A, B, and C the free energy of binding of guest O1 to host OAH (used in SAMPL4) was retrospectively predicted. Figure 3 compares the results with experimental data [38]. Both models A,B yield a similar free energy of binding \({\varDelta }G_{bind} = -6.1 \pm 0.5\,\hbox {kcal}\,\hbox {mol}^{-1}\). This is because the long-range corrections for Lennard Jones interactions implemented in model B produce a negligible correction term of \(0.03\;{\text{kcal}}\;{\text{mol}}^{{ - 1}}\). By contrast, the addition of a standard state correction in model C leads to a standard free energy of binding of \({\varDelta }G^{\circ }_{bind}=-4.4 \pm 0.5\,\hbox {kcal}\,\hbox {mol}^{-1}\) which is in good agreement with the experimental data of \({\varDelta }G^{\circ }_{\mathrm {bind}} =-3.7\pm 0.1\,\hbox {kcal}\,\hbox {mol}^{-1}\) [38].

Next, blinded predictions were performed for each SAMPL5 host-guest. Figure 4 contrasts the predictive power of the different models against the experimental data that was released after submission of the predictions. Figure 4a, shows the results for model A, b for model B and c for model C respectively. Results for each host-guest system are also reported in Table 1. Taking the full dataset into account, all three models yield a similar \(\hbox {R}^2\) value of ca. \(0.65\,<\,0.70\,<\,0.75\). Models A, B have a similar MUE of ca. \(4.3<4.5<4.7\,\hbox {kcal}\,\hbox {mol}^{-1}\), whereas model C is statistically more accurate, with a MUE of ca. \(3.2<3.4<3.6\,\hbox {kcal}\,\hbox {mol}^{-1}\). The accuracy of the predictions for the three different hosts was also considered individually and summarised in Table 1. As judged by the MUE measures, the models perform better across the octa-acid systems than for CBC. In particular, model C gives the best predictions compared to A and B for octa-acid systems, with a MUE of \(1.7<2.1<2.4\,\hbox {kcal}\,\hbox {mol}^{-1}\) and \(1.4<1.7<2.0\,\hbox {kcal}\,\hbox {mol}^{-1}\) for OAH and OAMe respectively. \(R^2\) is on average slightly higher for both octa-acid hosts (\(R^2 \,0.77\,<\,0.87\,<\,0.93\), model C for OAH and \(R^2 \,0.52\,<\,0.74\,<\,0.93\), model C for OAMe) than CBC (\(R^2\,0.70\,<\,0.76\,<\,0.82\)) for models A, B and C, but the trend is not strong given statistical uncertainties.

Fig. 3
figure 3

Comparison of the computed binding free energy \({\varDelta }G_{\mathrm {bind}}\) according to models A, B and the computed standard binding free energy \({\varDelta }G_{\mathrm {bind}}^{\circ }\) according to model C with respect to experimental data for the SAMPL4 OAH-O1 complex

Full size image
Fig. 4
figure 4

a Comparison of the binding free energy \({\varDelta }G_{\mathrm {bind}}\) to experiments according to model A and model B in b and standard binding free energy of \({\varDelta }G_{\mathrm {bind}}^{\circ }\) according to model C with respect to experimental results in c for all host-guest systems. The red line indicates ideal correlation between experiments and computed results and the yellow shaded region gives a binding free energy error bound of 1 \(\hbox {kcal}\cdot \hbox {mol}^{-1}\). OAH systems are colored in blue, OAMe in green and CBC in red. Error bars denote ± Eq. of (12)

Full size image
Fig. 5
figure 5

Comparison between standard binding free energies computed with model C (blue) and with the attach-pull-release method (red) for OAH in (a) and OAMe in (b)

Full size image

Next, attention was focussed on the guests for which predictions showed the largest discrepancy with respect to experimental data. For instance, the standard free energy of binding of guest G5 in complex with both OAH and OAMe is overestimated by \(-3.6\,\hbox {and}\,-2.8\,\hbox {kcal}\,\hbox {mol}^{-1}\) respectively. Guest G4 is also significantly stabilised in complex with OAH. G4 is arguably the most hydrophobic guest in the series studied and evidence from our accompanying distribution coefficient article suggest that the GAFF force field appear to favor the transfer of hydrophobic solutes into hydrophobic environments [47]. Since G5 is the largest outlier in both octa-acid hosts, the validity of its simulated binding mode was evaluated. For this purpose, G5 in the host-guest complexes was rotated by approximately 180\(^\circ\) about its centre of mass such that the amine group pointed towards the bottom of the host cavities, and calculations were repeated using these new coordinates after solvent equilibration. Binding free energy predictions from model C obtained for this alternative binding mode were poor (\({\varDelta }G^{\circ }_{bind}= +1.8\pm 0.1\,\hbox {and}\,+16.7\pm 0.1\,\hbox {kcal}\,\hbox {mol}^{-1}\) for OAH and OAMe respectively), suggesting that the original binding mode is more likely.

For the CBC host, the best MUE is about \(4.8\,<\,5.1\,<\,5.4\hbox {kcal}\,\hbox {mol}^{-1}\) for model C, with no significant difference over model A and B. This is surprising since the determination coefficient \(R^20.69\,<\,0.76\,<\,0.82\) is quite reasonable. In particular, model C performs better than A and B, but large errors are present for a series of guests. Guests G2 and G3 are predicted to bind substantially worse than observed in experiments. The main difference with other guests in this dataset is that these two molecules are made up of linear flexible alkyl chains, and contain several (presumably) positively charged ammonium groups. By contrast, G4–G7, G9 and G10 are predicted to bind significantly better than experimentally observed. These compounds present a variety of net charges, but are all made up of conjugated aromatic rings. Additionally, empirical pKA estimations [48] suggest that G5, G6, G9 and G10 could adopt multiple protonation states at the pH where binding constants were measured. Hence, it is unclear whether the discrepancies are due to forcefield errors or finite-size effects.

As a separate issue, the reproducibility of standard free energies of binding was evaluated by comparing the results from model C with those reported by the Gilson lab (UCSD) for the octa-acid hosts [49]. The same input files were used, but the free energy calculations were performed with the pmemd.cuda program from AMBER 14 [50], and a different potential of mean force based ’attach-pull-release’ (APR) methodology [51]. Figure 5 shows that a good agreement is observed between both OAH (Fig. 5a) and OAMe (Fig. 5b) hosts, with a mean unsigned differences of about 0.4 \(\hbox {kcal}\,\hbox {mol}^{-1}\) in the former case and 0.6 \(\hbox {kcal}\,\hbox {mol}^{-1}\) for the latter. At first glance this level of variability seems reasonable given the typical statistical uncertainties of each methodology. Nonetheless closer inspection indicates that OAH-G5, OAMe-G5 and OAMe-G4 show significant discrepancies. Since the model C standard free energies of binding were only estimated from two repeats a concern was that the error estimates were not reliable. To test this two additional repeats were performed for these systems. The standard free energies of binding obtained from four repeats of model C are: \({\varDelta }G^{\circ }_{bind}\) (SOMD, OAH-G5) = −6.9±0.1, \({\varDelta }G^{\circ }_{bind}\) (SOMD, OAMe-G4) \(=\,-3.4\pm 0.2, {\varDelta }G^{\circ }_{bind}\)(SOMD, OAMe-G5) \(=\,-6.5\pm 0.3\, \hbox {kcal}\,\hbox {mol}^{-1}\) respectively. The results were statistically identical to those obtained from two repeats (Table 1) for OAMe-G4 and OAMe-G5, but not OAH-G5. Personal discussions with the Gilson lab prompted additional APR calculations which produced revised values for \({\varDelta }G^{\circ }_{bind}\)(APR, OAMe-G4)\(\,=\,-4.3\pm 0.3\, \hbox {kcal}\,\hbox {mol}^{-1}\), and \({\varDelta }G^{\circ }_{bind}\) (APR, OAH-G5)\(\,=\,-4.5\pm 0.5\, \hbox {kcal}\,\hbox {mol}^{-1}\). However, discrepancies remain and further work is needed to establish the protocol variations that introduced this variability in the computed standard free energies of binding.

Conclusions

The present alchemical free energy calculation protocols proved reasonably reproducible (Table 1). This was unexpected given the size of the guests that was deemed large for an absolute binding free energy calculation, suggesting that longer per-\(\lambda\) simulation time than what was used here would be necessary. Factors that may have contributed to this outcome include the relative rigidity of some of the guests, the rapid relaxation of the hosts upon guest decoupling, the symmetry of the hosts, and the use of distance restraints to limit translational motions of the decoupled guests. Encouragingly, the results were also reasonably predictive, at least when judged by correlation with experiment (\(\hbox {R}^2 0.65\,<\, 0.70 \,<\, 0.75\) for model C). Indeed, the SAMPL5 submissions for models A,B,C were among the top-performing protocols of this entire competition with respect to this metric. Nevertheless, systematic errors are present and the same models do not fare as well when ranked according to a mean unsigned error metric. Model B yields results that are identical to model A since the long range correction for missing dispersion interactions is essentially negligible. This was unexpected given previous reports were this term was found to be a significant contribution to standard free energies of binding [30]. For the systems considered here it seems that the simulation cutoffs used were sufficient to include most of the guest-host dispersion interactions. Satisfactorily, addition of a standard state correction term in model C systematically improves agreement with experimental data. In addition the computed standard free energies of binding for model C agree well with those produced independently by members of the Gilson lab (UCSD) using a different code and methodology. However, it is not currently understood why a few compounds show more significant deviations between the double decoupling and APR methodologies and this should receive further attention. It is well known that the computation of free energies of solvation of charged solutes via molecular simulations is typically affected by significant finite-size effects [52–55]. Given the broad range of net charges in the guests considered here, it is perhaps surprising that encouraging R 2 values were obtained. For the host-guest binding energies reported here errors due to finite-size electrostatics is mitigated since partial error compensation occur between the simulations of the solvated guest and the host-guest complex. However, it seems reasonable to anticipate that the significant MUE values could be decreased with the use of suitable schemes to reduce or eliminate finite-size errors.Footnote 1 Other areas where further improvement could be sought for this dataset include the explicit consideration of multiple tautomeric forms of the guests, as well as a more systematic evaluation of alternative potential energy functions.

Table 1 Binding free energy, in \(\hbox {kcal}\,\hbox {mol}^{-1}\), determination coefficient \(\hbox {R}^2\), mean unsigned error (MUE), in \(\hbox {kcal}\,\hbox {mol}^{-1}\), model A, B and C
Full size table