Abstract
I present a formalization in Isabelle/HOL of the resolution calculus for first-order logic with formal soundness and completeness proofs. To prove the calculus sound, I use the substitution lemma, and to prove it complete, I use Herbrand interpretations and semantic trees. The correspondence between unsatisfiable sets of clauses and finite semantic trees is formalized in Herbrand’s theorem. I discuss the difficulties that I had formalizing proofs of the lifting lemma found in the literature, and I formalize a correct proof. The completeness proof is by induction on the size of a finite semantic tree. Throughout the paper I emphasize details that are often glossed over in paper proofs. I give a thorough overview of formalizations of first-order logic found in the literature. The formalization of resolution is part of the IsaFoL project, which is an effort to formalize logics in Isabelle/HOL.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
The resolution calculus plays an important role in automatic theorem proving for first-order logic as many of the most efficient automatic theorem provers, e.g. E [69], SPASS [74], and Vampire [57], are based on superposition, an extension of resolution. Studying the resolution calculus is furthermore an integral part of many university courses on logic in computer science. The resolution calculus was introduced by Robinson in his ground-breaking paper [60] which also introduced most general unifiers (MGUs).
The resolution calculus reasons about first-order literals, i.e. atoms and their negations. Since the literals are first-order, they may contain full first-order terms. Literals are collected in clauses, i.e. disjunctions of literals. The calculus is refutationally complete, which means that if a set of clauses is unsatisfiable, then the resolution calculus can derive a contradiction (the empty clause) from it. One can also use the calculus to prove any valid sentence by first negating it, then transforming it to an equisatisfiable set of clauses, and lastly refuting this set with the resolution calculus. Resolution is a calculus for first-order logic, but it does not have any machinery to handle equality or any other theories.
There are several techniques for proving the completeness of resolution calculi. In this work I use the one of semantic trees, which was introduced by Robinson [61]. Semantic trees are binary trees that represent interpretations. I mostly follow textbooks by Ben-Ari [4], Chang and Lee [19], and Leitsch [43]. The idea of Chang and Lee’s completeness proof is that a semantic tree is cut smaller and smaller, and for each cut, a derivation is done towards the empty clause. I also formalize Herbrand’s theorem, which cuts the tree down to finite size. I prove a stronger version of the usual refutational completeness theorem by weakening its assumption to require unsatisfiability in only a single countably infinite universe instead of in all universes. The usual theorem follows directly from this, which is proven, e.g. by Chang and Lee as Theorem 4.2. I discuss why this usual theorem is not formalized.
The formalization is included in the IsaFoL project [33] and the Archive of Formal Proofs [65] where it is available for download. The IsaFoL project formalizes several logics in Isabelle/HOL [47]. IsaFoL is part of a larger effort of research in this area. This also includes formalizations of ground resolution, which is propositional by nature. The formalization in this paper stands out from these by formalizing resolution for first-order logic. The theory needed to do this is very different from that of ground resolution since first-order logic involves a richer syntax and semantics. To the best of my knowledge, I present the first formalized completeness proof of the resolution calculus for first-order logic.
Harrison [28] formalized Herbrand’s theorem, also known as uniformity, in a model theoretic formulation. It says that if a purely existential formula is valid, then some disjunction of instances of the body is propositionally valid. In automatic theorem proving, the theorem is viewed in a different, equivalent way: A set of clauses is unsatisfiable only if some finite set of ground, i.e. variable free, instances of its clauses is as well. This can be used to build a first-order refutation prover from a propositional SAT solver. Such a prover enumerates ground instances, which it tries to refute with the SAT solver. I formalize a third equivalent view stating exactly what the completeness proof needs: If a set of clauses is unsatisfiable, then there is a finite semantic tree whose branches falsify the set. This bridges first-order unsatisfiability with decisions made in a semantic tree.
Understanding proofs of logical systems can be challenging since one must keep separate the parts of the proofs that are about the syntactic level, and the parts that are about the semantic level. It can be tempting to mix intuition about syntax and semantics. Fortunately, a formalization makes the distinction very clear, and ideally this can aid in understanding the proofs.
This paper extends my previous paper [64] which I presented at ITP 2016. It is extended with more thorough explanations and now contains illustrative examples of structured Isar proofs. Furthermore, the discussion of the tools used in the formalization has been expanded, and the related-works section now contains a much more thorough overview of the formalizations of first-order logic found in the literature. Additionally, the formalization now contains three new versions of the soundness theorem and two new illustrative versions of the completeness theorem, which are explained.
2 Overview
This section introduces the terminology of clausal first-order logic and the resolution rule. It gives a brief explanation of semantic trees and gives the big picture of the proofs of Herbrand’s theorem, the lifting lemma, and completeness.
A literal l is either an atom or its negation. The \( sign \) of an atom is \( True \), while that of its negation is \( False \). The complement \(p^{\mathrm {c}}\) of an atom p is \(\lnot p\), and the complement \((\lnot p)^{\mathrm {c}}\) of its negation is p. The complement \(L^{\mathrm {C}}\) of a set of literals L is \(\{l^{\mathrm {c}}\;|\;l\in L\}\). The set of variables in a set of literals L is \( vars_{\mathrm {ls}}\; L \). A clause is a set of literals representing the universal closure of the disjunction of the literals in the clause. The empty clause represents a contradiction since it is an empty disjunction. A clause with an empty set of variables is called ground. A substitution \(\sigma \) is a function from variables to terms, and is applied to a clause C by applying it to all variables in C. The result is written  and is called an instance of C. We can likewise apply a substitution to a single literal
and is called an instance of C. We can likewise apply a substitution to a single literal  . The composition \(\sigma _1 \cdot \sigma _2\) of two substitutions is the substitution that maps any variable x to
. The composition \(\sigma _1 \cdot \sigma _2\) of two substitutions is the substitution that maps any variable x to  . A unifier \(\sigma \) for a set of literals L is a substitution such that applying it to L makes all the literals therein equal. A most general unifier (MGU) for a set of literals L is a unifier \(\sigma \) for L such that any other unifier for L can be expressed as \(\sigma \cdot \tau \) for some substitution \(\tau \).
. A unifier \(\sigma \) for a set of literals L is a substitution such that applying it to L makes all the literals therein equal. A most general unifier (MGU) for a set of literals L is a unifier \(\sigma \) for L such that any other unifier for L can be expressed as \(\sigma \cdot \tau \) for some substitution \(\tau \).
We will consider the following formulation of the resolution rule:

The conclusion of the rule is called a resolvent of \({C_1}\) and \({C_2}\). \({L_1}\) and \({L_2}\) are called clashing sets of literals. Additionally, the calculus allows us to apply variable renaming to clauses before we apply the resolution rule. Renaming variables in two clauses \({C_1}\) and \({C_2}\) such that \( vars_{\mathrm {ls}}\; {C_1}\cap vars_{\mathrm {ls}}\; {C_2}= \{\} \) is called standardizing apart. Notice that \({L_1}\) and \({L_2}\) are sets of literals. Some other resolution calculi instead let \({L_1}\) and \({L_2}\) be single literals. These calculi then have an additional rule called factoring, which allows unification of subsets of clauses. The completeness of the above rule implies the completeness of resolution on single literals with factoring, as explained by e.g. Fitting [25], but I have not formalized this result. The idea is that the above rule can be simulated by applications of resolution on single literals and factoring.
I now give an overview of the completeness proof. The completeness proof is very much inspired by that of Chang and Lee [19], while the proof of the lifting lemma is inspired by that of Leitsch [43].
Semantic trees are defined from an enumeration of Herbrand, i.e. ground, atoms. A semantic tree is essentially a binary decision tree in which the decision of going left in a node on level i corresponds to mapping the ith atom of the enumeration to \( True \), and in which going right corresponds to mapping it to \( False \). See Fig. 1. Therefore, a finite path in a semantic tree can be seen as a partial interpretation. This differs from the usual interpretations in first-order logic in two ways. Firstly, it does not consist of a function denotation and a predicate denotation, but instead assigns \( True \) and \( False \) to ground atoms directly. Secondly, it is finite, which means that some ground literals are assigned neither \( True \) nor \( False \). A partial interpretation is said to falsify a ground clause if it, to all literals in the clause, assigns the opposite of their signs. A branch is a path from the root of a tree to one of its leaves. An internal path is a path from the root of a tree to some node that is not a leaf. A closed path is a path whose corresponding partial interpretation falsifies some ground instance of a clause in the set of clauses. A closed semantic tree for a set of clauses is a tree that has two properties: Firstly, each of its branches is closed. Secondly, the internal paths in the tree are not closed. The second property expresses minimality of the first property, because it ensures that no proper subtree of a closed semantic tree can have the first property.
Note that Chang and Lee’s notion of semantic trees is more general than mine since it allows each decision to assign truth values to several atoms. This generality is not needed in the completeness proof, and therefore I prefer a simpler definition in order to ease formalization.
Herbrand’s theorem is proven in the following formulation: If a set of clauses is unsatisfiable, then there is a finite and closed semantic tree for that set. I prove it in its contrapositive formulation and therefore assume that all finite semantic trees of a set of clauses have an open (non-closed) branch. By obtaining longer and longer branches of larger and larger finite semantic trees, we can, using König’s lemma, obtain an infinite path, all of whose prefixes are open branches of finite semantic trees. Thus these branches satisfy, that is, do not falsify, the set of clauses. We can then prove that this infinite path, when seen as an Herbrand interpretation, also satisfies the set of clauses, and this concludes the proof. Converting the infinite path to a full interpretation can be seen as the step that goes from syntax to semantics.
The lifting lemma lifts resolution derivation steps done on the ground level up to the first-order world. The lemma considers two instances, \({C_1'}\) and \({C_2'}\), of two first-order clauses, \({C_1}\) and \({C_2}\). It states that if \({C_1'}\) and \({C_2'}\) can be resolved to a clause \(C'\) then also \({C_1}\) and \({C_2}\) can be resolved to a clause C. And not only that, it can even be done in such a way that \(C'\) is an instance of this C. See Fig. 2. To prove the theorem, we look at the clashing sets of literals \({L_1'}\subseteq {C_1'}\) and \({L_2'}\subseteq {C_2'}\). We partition \({C_1'}\) in \({L_1'}\) and the rest, \(R_1' = {C_1'}- {L_1'}\). Then we lift this up to \({C_1}\) by partitioning it in \({L_1}\), the part that instantiates to \({L_1'}\), and the rest \(R_1\), which instantiates to \(R_1'\). We do the same for \({C_2}\). Since \({L_1'}\) and \({L_2'}^{\mathrm {C}}\) can be unified, so can \({L_1}\) and \({L_2}^{\mathrm {C}}\), and therefore they have an MGU. Thus \({C_1}\) and \({C_2}\) can be resolved to a resolvent C. With some bookkeeping of the substitutions and unifiers, we can also show that C has the ground resolvent \(C'\) as an instance.
Lastly, completeness itself is proven. It states that the empty clause can be derived from any unsatisfiable set of clauses. We start by obtaining a finite closed semantic tree for the set of clauses. Then we cut off two sibling leaves. The branches ending in these leaves agree on all atoms except for the one, a, in their leaves. Additionally they falsify a ground clause each, but, by minimality of closed trees, their prefixes do not. Therefore, setting a to \( True \) in a sibling, must have falsified a clause, and thus the literal \( \lnot a \) must be in a clause. Likewise, setting a to \( False \) in a sibling, must have falsified a clause, and thus the literal \( a \) must be in a clause. These clauses can be resolved. We lift this up to the first-order world by the lifting lemma and resolve the first-order clauses. Repeating this procedure, we obtain a derivation that ends when we have cut the tree down to the root. Only the empty clause can be falsified here, so we have a derivation of the empty clause.
3 Isabelle
This section explains the logic of Isabelle/HOL and the Isar language [75] for writing structured proofs. Isar is illustrated with some simple examples.
Isabelle is a generic proof assistant that implements several logics, and Isabelle/HOL is its implementation of a higher-order logic (HOL). HOL can be seen as a combination of typed functional programming and logic. This gives, among other things, access to the usual logical operators and quantifiers such as \(\longrightarrow \), \(\wedge \), \(\vee \), \(\lnot \), \(\forall \) and \(\exists \). The long arrow (\(\Longrightarrow \)) is Isabelle’s meta-implication, which for the purpose of this paper can be thought of as a normal implication (\(\longrightarrow \)), and likewise the big wedge (\(\bigwedge \)) can be thought of as universal quantification (\(\forall \)).
In Isabelle’s Isar language one can write structured proofs that both humans can read and Isabelle/HOL can check. I present a subset here, which is large enough for the reader to understand this paper. Let us consider a template Isar proof:

Here L is the theorem’s name, \(A_1, \ldots , A_n\) are optional assumptions of the theorem, \(a_1, \ldots , a_n\) are optional names of the assumption, and B is the theorem’s conclusion. If there are no assumptions the keyword \(\mathbf {shows}\) may be omitted. R instructs Isabelle on how to start the proof. For instance, if nothing is written, it applies a well-suited rule, and if a dash (−) is written, then no rule is applied. \(C_1, \ldots , C_m\) is a list of statements, similar to the sentences of a paper proof, which is to prove the theorem. Let us look at three kinds of statements. First, we have the \(\mathbf {have}\) goal:

Here S is a proposition which is proven by proof method M. Proof method M could be one of Isabelle/HOL’s proof methods that implement automatic theorem provers. s is an optional name of S. \(F_1\) and \(F_2\) are lists of names of facts that M is allowed to use. They could be names of previously proven theorems, assumptions or of a proposition of one of the preceding statements. Both \(\mathbf {from}\; F_1\) and \(\mathbf {using}\; F_2\) can be omitted. Additionally \(\mathbf {from}\; F_1\) can be replaced with \(\mathbf {then}\), which refers to the fact that was most recently established, i.e. the proposition in the previous statement.
Second, we have the \(\mathbf {obtain}\) goal:

Here t is a new constant that is introduced in the proof. S is a proposition that characterizes t. It is named s. \(F_1\) and \(F_2\) are lists of facts that the proof method M is instructed to use to prove the existence of t.
Third, we have the \(\mathbf {show}\) goal:

This is similar to the \(\mathbf {have}\) goal except that it requires S to be one of the propositions that R instructs us to prove. Sometimes S will be \( ?thesis \), which refers to B. When we have shown all statements required by R we can end the proof with \(\mathbf {qed}\).
Let us look at a variation of a simple proof of Cantor’s theorem from an introduction to Isabelle/HOL by Nipkow and Klein [46] that illustrates the language. The theorem states that a function from a set to its powerset cannot be surjective. Here the set is formalized as a type \('a\) and its powerset as the type \('a\; set\).

A list of statements can also form a calculation. In the example below the horizontal ellipses (\(\ldots \)) are part of the concrete Isabelle syntax while the vertical ellipsis

indicates that some intermediate steps were omitted.

This list of statements proves \(S_0=S_n\) by proving \(S_0 = S_1 = S_2 =\cdots =S_n\) where the first equality \(S_0 = S_1\) is proven by the first \(\mathbf {have}\) goal and each subsequent equality \(S_i = S_{i+1}\) is proven by the \(\mathbf {also\;have}\) goal with name \(s_i\).
For example we can prove a simple lemma about the identity function:

Isar allows many more kinds of constructions of proofs, for instance nesting proofs, combining proof methods and more.
4 Clausal First-Order Logic
This section explains the formalization of the syntax and semantics of first-order clausal logic.
First, a signature is fixed where variable symbols, function symbols, and predicate symbols are represented by the type \( string \). The type \( string \) consists of strings over a finite alphabet, and is thus a countably infinite type.

Similar to, e.g. Berghofer’s formalization of first-order logic [5], the predicate and function symbols do not have fixed arities.
A first-order term is either a variable consisting of a variable symbol or it is a function application consisting of a function symbol and a list of subterms:

A literal is either positive or negative, and it contains a predicate symbol (a string) and a list of terms. The datatype is parametrized with the type of terms \('t\) since it will both represent first-order literals (\( fterm \; literal \)) and Herbrand literals. A clause is a set of literals.


Ground \( fterm\; literal \)s are formalized using a predicate \( ground_{\mathrm {l}} \) which holds for l if it contains no variables. Ground \( fterm\; clause \)s are similarly formalized using a predicate \( ground_{\mathrm {ls}} \).
A semantics of terms and literals is also formalized. A variable denotation, \( var\text {-}denot \), maps variable symbols to values of the domain. The universe is represented by the type variable \('u\).

Interpretations consist of denotations of functions and predicates. A function denotation maps function symbols and lists of values to values:

Likewise, a predicate denotation maps predicate symbols and lists of values to the two boolean values:

The semantics of a term is defined by the recursive function  :
:

Here, \( map \; (eval_{\mathrm {t}}\; E\; F) \; [e_1,\dots ,e_n] = [eval_{\mathrm {t}}\; E\; F \; e_1,\dots ,eval_{\mathrm {t}}\; E\; F \; e_n] \), and from now on \( map\; (eval_{\mathrm {t}}\; E\; F) \; ts \) is abbreviated as \( eval_{\mathrm {ts}}\; E \; F \; ts \).
If an expression evaluates to \( True \) in an interpretation, we say that it is satisfied by the interpretation. If it evaluates to \( False \), we say that it is falsified. The semantics of literals is a function \( eval_{\mathrm {l}} \) that evaluates literals:

The semantics is extended to clauses:

It is important that the ranges of all the environments that \( eval_{\mathrm {c}} \) quantifies over are actually subsets of the considered universe. The type system of Isabelle/HOL ensures this, as we can inspect that the type of E indeed is \( 'u\;var\text {-}denot \). Had I instead chosen to represent the universe as a set, I would have to pass it as an argument to \( eval_{\mathrm {c}} \) and have a predicate ensure that all the environments considered did not go outside this universe. Likewise, I would also have to make a decision of what to do if the range of F was not a subset of the universe.
A set of clauses \( Cs \) is satisfied, written \( eval_{\mathrm {cs}}\; F \; G \; Cs \), if all its clauses are satisfied:

The semantics can be illustrated with the universe \( nat \) of natural numbers, a function denotation that maps \( add \), \( mul \), \( one \), and \( zero \) to their usual meanings, a predicate denotation that maps \( less \), \( greater \), and \( equals \) to their usual meanings, as well as a variable denotation that maps \( x \) to 26 and y to 5:

It is also illustrative to evaluate the literal \( equals(add(mul(y,y),one),x) \) with the above denotations:

5 Substitutions and Unifiers
This section formalizes substitutions, unifiers, MGUs, and the unification theorem, which states the existence of MGUs.
A substitution is a function from variable symbols into terms:

This is very different from Chang and Lee where they are represented by finite sets [19]. The advantage of functions is that they make it much easier to apply and compose substitutions. If \(C'\) is an instance of C we write \( instance\text {-}of_{\mathrm {ls}}\; C' \; C \). The composition of two substitutions, \(\sigma _1\) and \(\sigma _2\), is also defined, and written \(\sigma _1 \cdot \sigma _2\). We also define unifiers and MGUs of literals (and similarly of terms):


One important theorem is the unification theorem, which states that if a finite set of literals has a unifier, then it also has an MGU. This is usually proven by defining a unification algorithm and proving it correct. This has been formalized several times. An early formalization is by Paulson [48] in LCF of an algorithm by Manna and Waldinger [44]. Coen [21] used this as basis for a formalization of the algorithm in Isabelle, and his formalization was improved first by Slind [72] and later Krauss [38]. Their formalization [20] is now part of the Isabelle distribution. There, terms are formalized as binary tree structures and substitutions as association lists. Sternagel and Thiemann [73] formalize in the IsaFoR project [34] an algorithm presented by Baader and Nipkow [2]. They formalize terms, unifiers and MGUs in a similar way to me. Therefore it is relatively easy to obtain the unification theorem by proving my terms, unifiers, and MGUs equivalent to the ones in IsaFoR.

For the purpose of formalizing the resolution calculus the choice of unification algorithm is irrelevant since we only need one to prove the existence of MGUs. If one wants to formalize a resolution prover the choice is important especially with respect to runtime. The two presented algorithms seem to be efficient in practice, but have an exponential worst-case runtime. Ruiz-Reina, Martín-Mateos, and Hidalgo [62], however, formalize, in ACL2, an algorithm by Corbin and Bidoit [22] as presented by Baader and Nipkow [2], which has a quadratic worst-case runtime. Some automatic theorem provers, e.g. SPASS, use the technique of term indexing to compute MGUs – see, e.g. Sekar, Ramakrishnan, and Voronkov’s chapter on the topic [55]. I do not know of any formalization of this technique in a proof assistant.
6 The Resolution Calculus
This section formalizes the resolution calculus and its soundness proof. It also formalizes steps and derivations in the resolution calculus.
First, resolvents are formalized, i.e. the conclusions of the resolution rule:

In Sect. 2 we saw that the resolution rule had three side-conditions. The rule is additionally restricted to require that \({L_1}\) and \({L_2}\) are non-empty. When these side-conditions are fulfilled, the rule is applicable.

A step in the resolution calculus either inserts a resolvent of two clauses in a set of clauses, or it inserts a variable renaming of one of the clauses. Two clauses are variable renamings of each other if they can be instantiated to each other. Alternatively, we could say that we apply a substitution which is a bijection between the variables in the clause and another set of variables.

A step in the resolution calculus is formalized as an inductive predicate named \( resolution\text {-}step \). In Isabelle/HOL this is done by specifying a number of rules characterizing the predicate. Specifically there are two rules. One \(\mathsf {resolution\text {-}rule}\) allows us to apply the resolution rule, and the other \(\mathsf {standardize\text {-}apart}\) allows us to rename clauses such that we can standardize them apart.

Derivation steps are extended to derivations by taking the reflexive transitive closure of \( resolution\text {-}step \), which is given by \( rtranclp \):

The soundness proofs in the three books were not immediately ready to be formalized. The proof by Ben-Ari uses Herbrand interpretations, but this machinery is actually not necessary to prove soundness and does not seem to give a simpler proof. Chang and Lee prove soundness for first-order logic by referring to the soundness proof for the propositional case, but they do not make it clear how variables should be handled. Leitsch’s soundness proof refers to the substitution principle, but neither states nor proves it. It can be found elsewhere, e.g. in the textbook by Ebbinghaus, Flum, and Thomas [24] in the form of the substitution lemma. The formalized soundness proof also uses the substitution lemma.
I prove the resolution rule sound by combining three simpler rules:
-
1.
A substitution rule that allows us to infer instances.
-
2.
A special, simpler, resolution rule.
-
3.
A superset rule that allows us to infer supersets.
Rule 1, the substitution rule, states that we can do substitution:

Informally this seems obvious. C is satisfied and is a first-order clause, i.e. it represents a universal quantification.  then instantiates its variables, which are bound and universally quantified, and must therefore also be satisfied. Formally, however, this is not precise enough since C being satisfied is a statement about variable denotations, i.e. a semantic form of instantiation, while a substitution is a syntactic form of instantiation. This problem is overcome by the substitution principle. The needed insight is that given a function denotation and a variable denotation, any substitution can be converted to a variable denotation by evaluating the terms of its domain. In the formalization this is done using Isabelle/HOL’s function composition operator which is written as \(\circ \) in infix notation.
then instantiates its variables, which are bound and universally quantified, and must therefore also be satisfied. Formally, however, this is not precise enough since C being satisfied is a statement about variable denotations, i.e. a semantic form of instantiation, while a substitution is a syntactic form of instantiation. This problem is overcome by the substitution principle. The needed insight is that given a function denotation and a variable denotation, any substitution can be converted to a variable denotation by evaluating the terms of its domain. In the formalization this is done using Isabelle/HOL’s function composition operator which is written as \(\circ \) in infix notation.

The substitution lemma then states that applying a substitution to a literal is semantically the same as instead turning the substitution into a variable denotation:

Let us now look at the soundness proof of substitution. The proof is written in Isar and uses \( evalsub \) and the substitution lemma:

Notice that I am \(\mathbf {unfolding}\) the definition of \( eval_{\mathrm {c}} \) before the \(\mathbf {proof}\) begins. The definition says that \( eval_{\mathrm {c}} \) is a universal quantification over the variable denotations. Therefore Isabelle now requires us to \(\mathbf {fix}\) an arbitrary variable denotation and find a satisfied literal in \(C \cdot \sigma \). By the assumption C has such a literal for any variable denotation \(E'\) and in particular for \(\sigma \) transformed to a variable denotation \( evalsub\; E\; F\; \sigma \). The substitution lemma allows the substitution to be applied instead of transformed and this concludes the proof.
Rule 2, the special substitution rule, is a special, ground-like, version of the resolution rule. The rule is special since it is only allowed to remove two literals \(l_1\) and \(l_2\) instead of two sets of literals and because it requires \(l_1\) and \(l_2^c\) to be equal instead of unifiable:

Rule 3, the superset rule, states that from a clause follows any superset of the clause:

The proofs of all three rules are made as short structured Isar proofs.
These four sound rules are combined to give the resolution rule, which must consequently be sound. We are of course allowed to use the assumptions of the resolution rule, so we know that when \(\sigma \) is applied to \({L_1}\) and \({L_2}\), they turn into a complementary pair of literals, which we denote  and
and  . This justifies the bookkeeping inference below. It also means that we can apply the special resolution rule. The bottom-most rule application uses the superset rule.
. This justifies the bookkeeping inference below. It also means that we can apply the special resolution rule. The bottom-most rule application uses the superset rule.

All this reasoning is made as structured Isar proofs. The soundness theorem is stated as follows:

From this it follows that resolution steps are sound:

And then it follows that resolution derivations are sound:

The soundness theorem is also formalized in the refutational style:

To summarize, I have defined a function \( resolution \) giving the conclusion of the resolution rule, as well as a predicate \( applicable \) which formalizes its side conditions. I have combined these to form the predicates \( resolution\text {-}step \) and \( resolution\text {-}derivation \) which formalize when a set of clauses follows from another, respectively by a step or derivation of the resolution calculus. The resolution rule and its steps and derivations were proven sound.
7 Herbrand Interpretations and Semantic Trees
Now that soundness is proven, it is time to take the first steps towards proving completeness. Therefore this section formalizes Herbrand interpretations and semantic trees. It also formalizes Herbrand’s theorem and emphasizes how an infinite path in a semantic tree is transformed to an interpretation.
Herbrand interpretations are a special kind of interpretation characterized by two properties. The first is that their universe is the set of all Herbrand terms. I chose that universes should be represented by types and this is of course also the case for the universe of Herbrand terms. Therefore, a new type \( hterm \) is introduced which is similar to \( fterm \), but does not have a constructor for variables:

This is the same datatype as in Berghofer’s formalization of natural deduction [5]. Had I chosen to represent the universes by sets like Ridge and Margetson [59], then I could instead have represented the Herbrand universe by the set of ground \( fterm \)s.
Two functions called \( fterm\text {-}of \text {-}hterm \) and \( hterm\text {-}of \text {-}fterm \) are introduced that convert between \( hterm \)s and ground \( fterm \)s. Note that some authors require the terms in the Herbrand universe to be built from the function symbols in a considered set of clauses. I choose to use all function symbols because it allows the Herbrand universe to be represented by the above datatype.
The second characteristic property is that the function denotation of an Herbrand interpretation is \( HFun \), and thus, evaluating a ground term under such an interpretation corresponds to replacing all applications of \( Fun \) with \( HFun \), that is, the ground term is interpreted as itself.
As we saw in Sect. 2, an enumeration of Herbrand atoms is needed, such that we can construct our semantic trees. Therefore, the type of atoms is defined:

Again the symbols are not restricted to those occurring in a considered set of clauses. Isabelle/HOL provides the proof method \( countable\text {-}datatype \) that can automatically prove that a given datatype, in our case \( hterm \), is countable. Since also the predicate symbols are countable, then so must \( hterm \; atom \) be. Furthermore, it is easy to prove that there are infinitely many \( hterm\;atom \)s. Using these facts and Hilbert’s choice operator, I specify a bijection \( hatom\text {-}of\text {-}nat \) between the natural numbers and the \( hterm \;atom \)s. Its inverse is called \( nat\text {-}of\text {-}hatom \). Additionally, the functions \( nat\text {-}of\text {-}fatom \) and \( fatom\text {-}of\text {-}nat \) enumerate the ground \( fterm \) atoms in the same order. A function \(\textit{get}\text {-}\textit{atom}\) returns the atom corresponding to a literal. The enumeration will be used to define which levels of the semantic trees correspond to which atoms.
7.1 Semantic Trees
In paper-proofs semantic trees are often labeled with the atoms that their nodes set to \( True \) or \( False \). In this formalization the trees are unlabeled, because for a given level, the corresponding atom can always be calculated using the enumeration:

The formalization contains a quite substantial, approximately 700-lines, theory on these unlabeled binary trees, paths within them, and their branches. The details are not particularly interesting, but a theory of binary trees is necessary.
In the formalization, \( bool\; list \)s represent both paths in trees and partial interpretations, denoted by the type \( partial\text {-}pred\text {-}denot \). E.g. if we consider the path \( [True,True,False] \), then it is the path from the root of a semantic tree that goes first left, then left again, and lastly right. On the other hand, it is also the partial interpretation that considers \( hatom\text {-}of\text {-}nat \; 0 \) to be \( True \), \( hatom\text {-}of\text {-}nat \; 1 \) to be \( True \) and \( hatom\text {-}of\text {-}nat \; 2 \) to be \( False \). Our formalization illustrates the correspondence between partial interpretations and paths clearly by identifying their types. Therefore, synonym \( dir \) is introduced for \( bool \) as well as the abbreviations \( Left \) for \( True \) and \( Right \) for \( False \).
The above datatype cannot represent infinite trees. Thus, infinite trees are modeled as sets of paths with a wellformedness property:

Alternatively I could have used Isabelle’s codatatype package [8, 10], since codatatypes can represent infinite-depth trees in a very natural way.
Infinite paths are modeled as functions from natural numbers into finite paths. Applying the function to number i gives us the prefix of length i. From here on such functions are called infinite paths, and their characteristic property is

It must be made formal, what it means for a partial interpretation, i.e. a path, to falsify an expression. A partial interpretation G falsifies, written \( falsifies_{\mathrm {l}}\; G \;l \), a ground literal l, if the opposite of its sign occurs on index \( nat\text {-}of\text {-}fatom \; (get\text {-}atom\; l) \) of the interpretation. The exclamation mark (!) is Isabelle/HOL’s \( nth \) operator, i.e. \(G\; !\; i\) gives the ith element of G.

A ground clause C is falsified, written \( falsifies_{\mathrm {g}}\; G \;C \), if all its literals are falsified. A first-order clause C is falsified, written \( falsifies_{\mathrm {c}}\; G \;C \), if it has a falsified ground instance. A partial interpretation satisfies an expression if the partial interpretation does not falsify it. A set \(\textit{Cs}\) of first-order clauses is falsified by a partial interpretation if it falsifies some clause in \(\textit{Cs}\). A set \(\textit{Cs}\) of first-order clauses is falsified by a tree if each of the tree’s branches falsifies some clause in \(\textit{Cs}\). Lastly, a semantic tree T is closed, written \( closed\text {-}tree \; T\; Cs \), for a set of clauses \( Cs \) if it is a tree that falsifies \( Cs \), but whose internal paths do not. Notice that a closed tree is minimal with respect to having falsifying branches, since any proper subtree has a branch that does not falsify anything in the set.
7.2 Herbrand’s Theorem
The formalization of Herbrand’s theorem is mostly straightforward and is done as an Isar proof that follows the sketch from Sect. 2. The challenging part is to take an infinite path, all of whose prefixes satisfy a set of clauses \( Cs \) and then prove that its translation to an interpretation also satisfies \( Cs \). Chang and Lee [19] do not elaborate much on this, but it takes up a large part of the formalization and illustrates the interplay of syntax and semantics.
The first step is to define how to transform the infinite path to an Herbrand interpretation. The function denotation has to be \( HFun \), and the infinite path needs to be converted to a predicate denotation. This can be done as follows:

Because of currying, P and \( ts \) can be thought of as the predicate symbol and list of values that we wish to evaluate in our semantics. It is done by collecting them to an Herbrand atom, and finding its index. Thereafter a prefix of our infinite path is found that is long enough to have decided whether the atom is considered \( True \) or \( False \).
I now prove that if the prefixes collected in the infinite path f satisfy a set of clauses \( Cs \), then so does its extension to a full predicate denotation \( extend \; f \).
Since I want to prove that the clauses in \( Cs \) are satisfied, I fix one C and prove that it has the same property:

There are four ways in which clauses can be satisfied:
-
1.
A first-order clause can be satisfied by a partial interpretation.
-
2.
A ground clause can be satisfied by a partial interpretation.
-
3.
A ground clause can be satisfied by an Herbrand interpretation.
-
4.
A first-order clause can be satisfied by an Herbrand interpretation.
The four ways are illustrated as the nodes in Fig. 3. The \( extend\text {-}infpath \) lemma relates 1 and 4 using lemmas that relate 1 to 2 to 3 to 4. The four ways seem similar, but they are in fact very different. For instance, a ground clause being satisfied is very different from a first-order clause being satisfied, since there are no ground instances or variables to worry about. Likewise, a ground clause being satisfied by a partial interpretation is clearly different from being satisfied by an Herbrand interpretation, since the two types are vastly different: A partial interpretation is a \( bool\; list \) while an Herbrand interpretation consists of a \( fun\text {-}sym \; \Rightarrow hterm\; list \Rightarrow hterm \) and a \( pred\text {-}sym \; \Rightarrow hterm\; list \Rightarrow bool \).
1 and 2 are related: If a first-order clause is satisfied by all prefixes of an infinite path, then so is any, in particular ground, instance. This follows from the definition of being satisfied by a partial interpretation.
2 and 3 are related: If a ground clause is satisfied by all prefixes of an infinite path f, then it is also satisfied by \( extend \; f \). This follows almost directly from the definition of \( extend \).
3 and 4 are related: Ideally one would prove that if a ground clause is satisfied by an Herbrand interpretation, then so is a first-order clause of which it is an instance. That is, however, too general. Fortunately, there is a similarity that ties first-order clauses and ground clauses together. Consider a variable denotation in the Herbrand universe, i.e. of type \( var\text {-}sym \Rightarrow hterm \). There is a function that converts its domain to \( fterm \)s, and thus turns it in to a substitution:

This is the machinery necessary to state the needed lemma: If the ground clause  is satisfied by an Herbrand interpretation under E, then so is the first-order clause C. The reason is simply that any variable in C is replaced by some ground term in the domain of \( sub\text {-}of\text {-}denot\;E \). This term evaluates to the same as the Herbrand term that it is interpreted as in E.
is satisfied by an Herbrand interpretation under E, then so is the first-order clause C. The reason is simply that any variable in C is replaced by some ground term in the domain of \( sub\text {-}of\text {-}denot\;E \). This term evaluates to the same as the Herbrand term that it is interpreted as in E.
The final step is to chain 1, 2, 3, and 4 together to relate 1 and 4. The steps are shown as the arrows in Fig. 3.
-
1.
Assume that C is satisfied by all prefixes of f.
-
2.
Then the ground instance
 is satisfied by all f’s prefixes.
is satisfied by all f’s prefixes. -
3.
Then the ground instance
 is satisfied by \( extend\; f \) under E in particular.
is satisfied by \( extend\; f \) under E in particular. -
4.
Then C is satisfied by \( extend\; f \) under E.
With this, Herbrand’s theorem is formalized:

The proof, as said, follows the sketch from Sect. 2.
8 Completeness
The completeness proof combines Herbrand’s theorem, the lifting lemma, and reasoning about semantic trees and derivations. The purpose of this section is to take a look at the most challenging parts of the formalization of the proof. These are the lifting lemma, standardizing clauses apart, and some finer details of reasoning about branches in semantic trees. Furthermore, the section illustrates the derivation of the empty clause and shows a number of formal completeness theorems.
8.1 Lifting Lemma
Let us first take a look at the formalization of the lifting lemma. More precisely I will explain a flaw in proofs from the literature and present the formalization of a correct proof.
Let us look at the flawed proofs. The formalization of the resolution rule removes literals from clauses before it applies the MGU. This is similar to several presentations from the literature including those of Robinson [60] and Leitsch [43]. Another approach, which the formalization used in an earlier version, is to apply the MGU before the literals are removed:

This is exactly the rule used by Ben-Ari [4]. Chang and Lee [19] use a similar approach with more possibilities for factoring. However, I was not able to formalize their proofs of the lifting lemma because they had some flaws. The flaws are described in my master’s thesis [63]. The most critical flaw is that the proofs seem to use that \(B \subseteq A\) implies  , which does not hold in general. Leitsch [42, Proposition 4.1] noticed flaws in Chang and Lee’s proof already, and presented a counter-example to it.
, which does not hold in general. Leitsch [42, Proposition 4.1] noticed flaws in Chang and Lee’s proof already, and presented a counter-example to it.
Let us now look at a formalization of a correct proof. With the current approach the lifting lemma is straightforward to formalize as an Isar proof following the proof by Leitsch [43]. The Isar proof is presented below. It consists of four parts. First we obtain the subsets \(L_1\) and \(L_2\) of \(C_1\) and \(C_2\) that we want to resolve upon. Next we obtain substitutions \(\tau \) and \(\varphi \) as illustrated in Fig. 4. This is where we use the \( unification \) theorem to obtain \(\tau \). We can then construct the desired resolvent, and show that resolution is applicable.
To illustrate the correspondence between informal proofs and Isar proofs I present the whole Isar proof below, interleaved with an informal proof that expands on the sketch from Sect. 2. The reader should notice the similarities between formal and informal proof, but is not expected to understand all details of the formal proof. Notice also that we do not need to assume groundness of \({C_1'}\) and \({C_2'}\).
The substitutions of the lifting lemma. An arrow from L to \(L'\) labeled with \(\eta \) indicates that  . Full arrows are relations we know. The dashed ones are established in the proof of the lemma by noticing that \(\eta \cdot \sigma \) is a unifier of \(L_1\) and \(L_2^C\), which means we can obtain the MGU \(\tau \) and by the definition of MGUs also \(\varphi \)
. Full arrows are relations we know. The dashed ones are established in the proof of the lemma by noticing that \(\eta \cdot \sigma \) is a unifier of \(L_1\) and \(L_2^C\), which means we can obtain the MGU \(\tau \) and by the definition of MGUs also \(\varphi \)
Lemma
Assume we have two finite clauses \({C_1}\) and \({C_2}\) that share no variables. Assume also that \({C_1'}\) is an instance of \({C_1}\) and that \({C_2'}\) is an instance of \({C_2}\). Furthermore, assume that the resolution rule is applicable to \({C_1'}\) and \({C_2'}\) on clashing sets of literals \({L_1'}\) and \({L_2'}\) with MGU \(\sigma \). Then there exist sets of literals \({L_1}\) and \({L_2}\) and substitution \(\tau \) such that the resolution rule is applicable to \({C_1}\) and \({C_2}\) on clashing sets of literals \({L_1}\) and \({L_2}\) with MGU \(\tau \) and that their conclusion has the conclusion from \({C_1'}\) and \({C_2'}\) as an instance.

proof–
– First we obtain the subsets to resolve upon:
Look at the clashing sets of literals \({L_1'}\) and \({L_2'}\). We partition \({C_1'}\) in \({L_1'}\) and the rest, \({R_1'}= {C_1'}- {L_1'}\). Likewise, we partition \({C_2'}\) in \({L_2'}\) and the rest, \({R_2'}= {C_2'}- {L_2'}\). Since \({C_1'}\) is an instance of \({C_1}\) there must be a substitution \(\gamma \) such that  . Likewise there must be a \(\mu \) such that
. Likewise there must be a \(\mu \) such that  . Since the \({C_1}\) and \({C_2}\) share no variables, we can replace this with a single substitution \(\eta \). We now partition \({C_1}\) in a part, \({L_1}\), that \(\eta \) instantiates to \({L_1'}\) and a rest \({C_1}- {L_1}\) that \(\eta \) instantiates to \({R_1'}\). We call the rest \({R_1}\). Likewise we obtain an \({L_2}\) which \(\eta \) instantiates to \({L_2'}\) and an \({R_2}\) that \(\eta \) instantiates to \({R_2'}\).
. Since the \({C_1}\) and \({C_2}\) share no variables, we can replace this with a single substitution \(\eta \). We now partition \({C_1}\) in a part, \({L_1}\), that \(\eta \) instantiates to \({L_1'}\) and a rest \({C_1}- {L_1}\) that \(\eta \) instantiates to \({R_1'}\). We call the rest \({R_1}\). Likewise we obtain an \({L_2}\) which \(\eta \) instantiates to \({L_2'}\) and an \({R_2}\) that \(\eta \) instantiates to \({R_2'}\).

– Then we obtain their MGU:
We assumed that resolution is applicable on clashing sets of literals \({L_1'}\) and \({L_2'}\) with MGU \(\sigma \). Therefore \(\sigma \) is an MGU of \({L_1'}\cup {L_2'}^{\mathrm {C}}\) which is the same as it being an MGU of  which again is the same as it being an MGU of
which again is the same as it being an MGU of  . Thus \(\sigma \) is a unifier of
. Thus \(\sigma \) is a unifier of  , and therefore \(\eta \cdot \sigma \) is a unifier of \({L_1}\cup {L_2}^{\mathrm {C}}\). By the unification theorem there must also be an MGU \(\tau \) of \({L_1}\cup {L_2}^{\mathrm {C}}\), and by the definition of it being an MGU there must also be a substitution \(\varphi \) such that \(\tau \cdot \varphi = \eta \cdot \sigma \).
, and therefore \(\eta \cdot \sigma \) is a unifier of \({L_1}\cup {L_2}^{\mathrm {C}}\). By the unification theorem there must also be an MGU \(\tau \) of \({L_1}\cup {L_2}^{\mathrm {C}}\), and by the definition of it being an MGU there must also be a substitution \(\varphi \) such that \(\tau \cdot \varphi = \eta \cdot \sigma \).

– We show that we have the desired conclusion:
Define C as  , i.e. the resolvent of \({C_1}\) and \({C_2}\) on clashing sets of literals \({L_1}\) and \({L_2}\) with MGU \(\tau \). Let us see what \(\varphi \) instantiates it to:
, i.e. the resolvent of \({C_1}\) and \({C_2}\) on clashing sets of literals \({L_1}\) and \({L_2}\) with MGU \(\tau \). Let us see what \(\varphi \) instantiates it to:
-
 – by the definitions of C, \({R_1}\), and \({R_2}\).
– by the definitions of C, \({R_1}\), and \({R_2}\). -
 – since these two composed substitutions were equal.
– since these two composed substitutions were equal. -

-
 – by the definitions of \({R_1'}\) and \({R_2'}\).
– by the definitions of \({R_1'}\) and \({R_2'}\).
In conclusion  , i.e. the conclusion from \({C_1}\) and \({C_2}\) has the one from \({C_1'}\) and \({C_2'}\) as an instance.
, i.e. the conclusion from \({C_1}\) and \({C_2}\) has the one from \({C_1'}\) and \({C_2'}\) as an instance.

– We show that the resolution rule is applicable:
We know that the resolution rule was applicable on \({C_1'}\) and \({C_2'}\) with clashing sets of literals \({L_1'}\) and \({L_2'}\). Therefore these sets must be non-empty. Since they are instances of \({C_1'}\), \({C_2'}\), \({L_1'}\), and \({L_2'}\), these must also be non-empty. We have already established all other conditions of resolution being applicable.
This concludes the proof.

8.2 The Formal Completeness Proof
Like Herbrand’s theorem, I formalize completeness as an Isar proof following Chang and Lee [19]. This time, however, the proof is much longer than its informal counterpart. The paper proof is about 30 lines, while the formal proof is approximately 150 lines. There are several reasons for this:
-
1.
Clauses have to be explicitly standardized apart.
-
2.
The clauses falsified by branches ending in two sibling leaves must be resolved and the sibling leaves must be cut off.
-
3.
Even more of the tree must be cut off to minimize it.
-
4.
The derivation-steps must be tied together.
We need to prove that the cut tree is closed. Furthermore, cutting the tree requires very precise reasoning about the numbers of the ground atoms. In the following subsection I tackle 1, 2 and 4 which are particularly interesting.
Let us now look at the completeness proof from a high level to choose an appropriate induction principle. The completeness proof consists of two steps. First Herbrand’s theorem is applied to obtain a finite tree. Next the finite tree is cut smaller and a derivation step is made. Then the process is repeated on the smaller tree. To prove that this works, I formalize the process using induction on the size of the tree. The formalization uses the induction rule \( measure\_induct\_rule \) instantiated with the size of a tree. This gives the following induction principle:

Here, the induction hypothesis holds for any tree of a smaller size, and this is needed since several nodes are cut off in each step.
In order for the completeness theorem to fit with the above induction principle, it is first formulated in an appropriate way, assuming the existence of a closed semantic tree. I show this formulation along with a sketch of the inductive Isar proof:

An alternative approach would have been to use an induction on the subtree relationship.
8.3 Standardizing Apart
In each step the resolved clauses must be standardized apart. Two functions can do this:


They take clauses \({C_1}\) and \({C_2}\) and create the clauses \( std_\mathrm {1}\; {C_1} \) and \( std_\mathrm {2}\; {C_2} \) which have added respectively 1 and 2 to the beginning of all variables. The most important property is that the clauses actually have distinct variables after the functions are applied. We need this such that we can apply the resolution rule, and so we can use the lifting lemma.

I prove that the functions actually rename the variables. This was a prerequisite for the standardize apart rule of the calculus.

In the completeness proof I need that \(C_1\) and \(std_\mathrm {1}\;C_1\) are falsified by the same partial interpretations:

8.4 Resolving Falsified Clauses
Let us now look at how to formalize the removal of two sibling leaves, and why the clauses that their branches falsified can be resolved. In each step, the completeness proof removes two sibling leaves. The branches, \( {B_1}=B\;@\;[True] \) and \( {B_2}=B\;@\;[False] \), ending in these sibling leaves falsified a first-order clause each, \({C_1}\) and \({C_2}\). By the definition of falsification of first-order clauses, \({B_1}\) and \({B_2}\) falsified ground instances \({C_1'}\) and \({C_2'}\) of \({C_1}\) and \({C_2}\) respectively. These ground clauses are then resolved, and the resolvent is falsified by B. This is then lifted to the first-order level using the lifting lemma. See the situation in Fig. 5.
Thus, on the ground level, two properties must be established:
-
1.
The two ground clauses \({C_1'}\) and \({C_2'}\) falsified by \({B_1}\) and \({B_2}\) can be resolved.
-
2.
Their ground resolvent \(C'\) is falsified by B. This ensures that the tree is closed when we cut off \({B_1}\) and \({B_2}\) and minimize it.
Let us prove 1 first. This is done by proving that \({C_1'}\) contains the negative literal \( l=Neg\;a \) of number \( length\; B \) in the enumeration, and that \({C_2'}\) contains its complement. Here, the case for \({C_1'}\) is presented. \({C_1'}\) is falsified by \({B_1}\), but not B, because the closed semantic tree is minimal. Thus, it must be the decision of going left that was necessary to falsify \({C_1'}\). Going left falsified the negative literal l with number \( length\; B \) in the enumeration, and hence it must be in \({C_1'}\).
Let us prove 2 next. To prove it we must show that the ground resolvent \(C' = ({C_1'}- \{l\})\; \cup \; ({C_2'}- \{l^{\mathrm {c}}\})\) is falsified by B. We do it by proving that the literals in both \({C_1'}- \{l\}\) and \({C_2'}- \{l^{\mathrm {c}}\}\) are falsified. The case for \({C_1'}- \{l\}\) is presented here. The overall idea is that l is falsified by \({B_1}\), but not by B. The decision of going left falsified l, and then all of \({C_1'}\) was falsified. Therefore, the other literals must have been falsified before we made the decision, in other words, they must have been falsified already by B.
To formalize this we must prove that all the literals in \({C_1'}-\{l\}\) are indeed falsified by B. We do it by a lemma showing that any other literal \( lo \in {C_1'} \) than l is falsified by B. Its proof first shows that \( lo \) has another number than l has, i.e. other than \( length\; B \). It seems obvious since \( lo \ne l \), but we also need to ensure that \( lo \ne l^{\mathrm {c}} \). We do this by proving another lemma, which says that a clause only can be falsified by a partial interpretation if it does not contain two complementary literals. Then we show that \( lo \) has a number smaller than \( length \; (B\;@\;[True]) \), since \( lo \) is falsified by \( B\;@\;[True] \). This concludes the proof.
I abstract from \( True \) to d such that the lemma also will work for the path \( B\;@\;[False] \) that goes left:

8.5 The Derivation
At the end of the proof the derivations are tied together:

The dots represent the derivation we obtain from the induction hypothesis. It is done using the definitions of \( resolution\text {-}step \) and \( resolution\text {-}deriv \). From \( herbrand \) and \( completeness' \) follows the completeness theorem:

8.6 Further Completeness Theorems
Let us now look at the strength of the above completeness proof and consider several other variants.
Notice that the above completeness theorem is actually stronger than the usual one. Usually, the assumption would consider all interpretations of all universes. Here, however, the assumption is weakened to consider only all interpretations of the Herbrand universe.
It could be illustrative to also formalize the usual formulation, but unfortunately, because of my choice of representing universes by types this is not possible. The reason is that although all statements in HOL are implicitly universally quantified over all types at the top, we are not allowed to do type quantification explicitly inside HOL formulas.
I instead prove some other instructive formulations of the theorem. For the completeness proof it was central that we considered the Herbrand universe, but for the theorem it is actually not important. The Herbrand universe can be replaced by any countably infinite universe. To prove this we fix an arbitrary uncountably infinite universe and obtain a bijection between it and the Herbrand terms. Three functions are defined that can apply the bijection to respectively variable denotations, function denotations, and predicate denotations:

Proving some appropriate lemmas about these functions I arrive at the following completeness theorem:

In particular, I use it to replace the Herbrand universe with the universe of the natural numbers:

9 Discussion
Since this paper is a case study in formalizing mathematics, it is worthwhile considering which tools were helpful in this regard. This section discusses each of these tools. The section also gives an idea of how much work went in to making the formalization. It discusses the consequences of the choice of representing universes as types. Lastly, it discusses the applicability of the formalization to implemented automated theorem provers.
Integrated Development Environments (IDEs) help their users do software development. Isabelle includes the Isabelle/jEdit Prover IDE, which has many useful features for navigating, reading, and writing proof documents. For instance it reveals type information of constants when the user hovers the mouse cursor over them. The user can click on any constant or type to jump to its definition and with another click she can jump back again. These features were especially advantageous when the theory grew larger. This is not only useful when writing proofs but also when reading them. In a formalization, every word is formally tied to its definition, so if at some point I forget the meaning of some expression the definitions are available by the click of a button. In my opinion this corroborates the claim that formal companions to paper proofs are highly useful.
The structured proof language Isar was beneficial because it allows formal proofs to be written as sequences of claims that follow from the previous claims. This clearly mirrors mathematical paper proof, which is what I am formalizing. Furthermore, it makes the proofs easy to read, and this is important when a formalization is to help in the understanding of a theory.
Isabelle/HOL includes several generic proof methods or tactics that can discharge proof goals. Writing a proof in Isabelle/HOL is a process of stating the formula you think holds and showing this from the previous statements with the right proof method. The simp and auto methods do rewriting and more while, e.g. blast and metis are first-order automatic theorem provers. Knowing which one to use in a given situation is a matter of knowledge of how the prover works, of experience, and of trial and error.
The Sledgehammer tool [6] finds proofs by picking important facts from the theory and then employing top-of-the-line automatic theorem provers and satisfiability modulo theory solvers. It often helps proving claims that we know are true, but where finding the necessary facts from the theory and libraries as well as choosing and instructing a proof method would be tedious.
It is also worthwhile considering how much work went into the formalization. The whole development is about 3300 lines of code. A preliminary version of the theory was developed during 5 months as part of my master’s thesis [63] including formalizations of clausal logic, its semantics, unifiers, a resolution calculus, its soundness, Herbrand interpretations, semantic trees and Herbrand’s theorem. I developed the rest of the theory during the first 5 months of my PhD studies concurrently with my other duties. The completeness theorems in Sect. 8.6 were formalized with little work while writing this extended paper. The lifting lemma was the greatest challenge because of the flaws in Chang and Lee’s proof. As soon as I looked at the proof by Leitsch, it was straightforward to finish.
In Sect. 4, I chose to represent universes as sets. The advantage of this was that I did not need additional predicates to restrict the ranges of variable and function denotations to stay within the fixed universe, since this was captured in the types. This is rather convenient, since then the proofs are not cluttered with reasoning about these predicates. On the other hand, in Sect. 7, I needed to introduce a type for the Herbrand universe, where it could otherwise have been captured directly as the set of ground terms. In Sect. 8, we also saw that a consequence was that we could not express completeness in its usual formulation, but had to go with a stronger formulation. To sum up, by formalizing universes as types rather than sets, I gained convenience, but lost some expressibility.
Finally, it is worthwhile considering the applicability of the formalization to implementations of automated theorem provers such as E, SPASS, and Vampire. Such automatic theorem provers consist of a calculus and a function to construct proofs in the calculus. The present formalization is purely of a calculus. Furthermore, the mentioned provers use the superposition calculus, which is an extension of resolution to first-order logic with equality. Resolution and superposition coincide for first-order logic without equality. The rules of superposition have several side conditions which only serve to rule out unnecessary inferences while the resolution rule I formalize has no such side conditions.
10 Related Work
The literature describes several formalizations of logic. This section takes a look at formalizations of both intuitionistic and classical first-order logic. Furthermore, it looks at two results that go beyond first-order logic. Lastly, it gives an overview of the IsaFoL project, which is an effort to bring together researchers of formalizations of logic.
10.1 Formalizations of Proof Systems for First-Order Logic
The completeness of first-order logic is a landmark of logic and thus formalizing this theorem is interesting in itself. Natural deduction calculi and sequent calculi are very suited for this purpose because of their simplicity.
Persson [54] formalized, in ALF, intuitionistic first-order logic. He formalized an intuitionistic natural deduction system and an intuitionistic sequent calculus. The semantics are defined using topology, which is a generalization of the semantics for classical first-order logic. He formalized both natural deduction, sequent calculi, and an axiomatic system. He proved the natural deduction systems and the sequent calculus sound, and proved the natural deduction with named variables complete. Ilik [31] also formalized, in Coq, natural deduction for intuitionistic first-order logic. He proved it complete with respect to a Kripke semantics. He also studied properties of intuitionistic logic extended with delimited control operators known from programming languages.
Harrison [28] formalized, in HOL Light, model theoretic results about classical first-order logic, including the compactness theorem, the Löwenheim-Skolem theorem, and Herbrand’s theorem.
Moreover, there are several formalized completeness proofs for classical first-order natural deduction. Berghofer [5] formalized natural deduction, in Isabelle/HOL, and proved it sound and complete. He also proved the Löwenheim-Skolem theorem. Raffalli [56] proved, in Phox, natural deduction complete for first-order logic. His semantics is that of minimal models. These are similar to the sets of formulas true in the usual semantics, but behave differently with respect to negation. The completeness statement is equivalent to the one with respect to the usual semantics, but this is not formalized. Ilik [31] formalized, essentially, the same result in Coq, although less abstractly.
Other authors formalized completeness proofs for classical first-order sequent calculi. Margetson and Ridge [45] formalized, in Isabelle/HOL, a sequent calculus. Their syntax is that of formulas on negation normal form without first-order functions. They proved the calculus sound and complete with respect to a semantics on this syntax. Braselmann and Koepke [14, 15] proved, in Mizar, a sequent calculus for first-order logic sound and complete. Schlöder and Koepke [68] proved it complete even for uncountable languages. Ilik [31] also proved a sequent calculus complete with respect to a Kripke-style semantics that he, Lee, and Herbelin [32] introduced for classical first-order logic.
Many completeness proofs follow similar recipes. Blanchette, Popescu, and Traytel [9, 12] formalized one such recipe, in Isabelle/HOL, as an abstract completeness proof for first-order logic that is independent of syntax and proof system. An interesting aspect of the proof is that it uses codatatypes to define and reason about infinite derivation trees. Their abstract completeness theorem states that if a proof system has a number of fairness properties, then it is complete in the following abstract sense: Any formula can either be proved or there exists some infinite path in a fair derivation tree of the formula. This means that the user of their formalization has three things to do in order to get a concrete completeness proof. First she needs to define a syntax, second she needs to define a fair proof system and third, she has to interpret the infinite paths as countermodels. The authors performed this step for a sequent calculus for first-order logic with equality and sorts. My formalization does not follow this recipe, opting instead for formalizing semantic trees. Blanchette, Popescu, and Traytel [11, 12] also formalized abstract soundness results and used them to prove a certain kind of infinite proofs correct.
Breitner and Lohner [17] defined natural deduction in an abstract way that is independent of syntax and the concrete rules of the system. They then used the abstract completeness proof by Blanchette, Popescu, and Traytel to prove it complete in the abstract sense. They also defined a novel graph representation of proofs, which is also independent of syntax and rules. They proved that any natural deduction system and the corresponding graph representation can prove the same theorems. Thus the graph representation is as sound and complete as the corresponding natural deduction system. They concretely instantiated it with a propositional logic with only conjunction and implication as well as a first-order logic with only universal quantification and implication. Breitner [16] used their graph representation to implement a tool for teaching logic.
For automatic theorem provers, it is not only important that the calculus is complete, but also that it can be implemented as a program. Ridge and Margetson [58, 59] verified a prover based on their formalized sequent calculus. Since their calculus does not contain full first-order terms, it means that they do not need any machinery such as MGUs to handle them. They also implement the prover as an OCaml program.
In his master’s thesis, Gebhard [26] formalized several ground resolution calculi in the \(\mathrm \Omega \) MEGA proof assistant. A version of this development is available online in The Theorem Prover Museum [37]. Gebhard proved completeness using induction on the excess literal number. The excess literal number is the number of occurrences of literals in a set of clauses minus the number of clauses. The technique was introduced by Anderson and Bledsoe [1] who used it to prove a linear format for resolution complete. Arguably, semantic trees are a more pedagogical construction since they so naturally express interpretations, and therefore I prefer them. Furthermore, Goubault-Larrecq and Jouannaud [27] showed that semantic trees can actually be used to prove many of the refinements of resolution complete – including linear resolution. Another difference from my formalization is that Gebhard uses proof planning. Proof plans were introduced by Bundy [18] as formal specifications of LCF-style tactics, which are functions that can replace a goal in a proof with zero or more new subgoals. I instead made structured proofs in the declarative Isar language, which allowed me to write humanly readable proofs that can be checked by the Isabelle/HOL proof assistant.
Concurrent with this Isabelle/HOL formalization of resolution, an important step in formalizing automatic theorem provers for first-order logic was taken. Peltier proved propositional resolution [52] and a variant of the superposition calculus for first-order logic [53] sound and complete. The superposition calculus can be seen as a highly efficient generalization of resolution for first-order logic to first-order logic with equality. Therefore his formalization is representative of the state of the art in formalizing the theory of automatic theorem proving.
10.2 Beyond Completeness of First-Order Logic
There are also results that go beyond completeness of first-order logic. An early such result is Shankar’s formalization [70, 71], in Nqthm, of Gödel’s first incompleteness theorem. Raffalli [56] proved, in Phox, parts of the second incompleteness theorem. His proof is very abstract and thus relies on strong assumptions about codings of formulas. He does not provide an explicit coding and thus does not prove these assumptions. Paulson [49,50,51] did not take any shortcuts and managed to formalize the entirety of both Gödel’s incompleteness theorems with a concrete coding of formulas based on hereditarily finite set theory.
Harrison [29] proved the soundness and consistency of HOL Light. He did this in two ways. First, he added an extra axiom to HOL Light that assumes the existence of a very large cardinal, and with this he was able to prove the unaltered HOL Light sound and consistent. Secondly, in unaltered HOL Light he proved the soundness and consistency of HOL Light altered by removing its axiom of infinity. Kumar, Arthan, Myreen, and Owens [39] extended Harrison’s result by proving, in HOL4, soundness and consistency of HOL Light with definitions. Their approach is a bit different from Harrison’s. Instead of adding an axiom describing a large cardinal to HOL4, their soundness proof assumes a specification of set theory. Additionally, they synthesize a verified implementation of the inference rules of their definition of HOL Light. A similar result is Davis and Myreen’s soundness proof [23], in HOL4, of the Milawa theorem prover.
10.3 IsaFoL
This formalization is part of IsaFoL [33], the Isabelle Formalization of Logic, which is a project that brings together researchers of logic from many institutions. In the project we aim to develop libraries of lemmas and methods for formalizing research on logic. In addition to this formalization of logic, several other results have emerged from the project.
This paper is an example of IsaFoL catching up with classical unformalized results in Isabelle/HOL. Likewise, Jensen, Villadsen, and I [35, 36] formalized an axiomatic system that forms the kernel of a proof assistant for first-order logic with equality by Harrison [30]. In addition to the advantages of having a formal companion to Harrison’s chapter on the proof assistant, the formalization also enabled us to build a certified prover based on the calculus. Other efforts in this direction are the work due to Blanchette, Traytel, Waldmann, and me [66] on a formalization of a resolution prover for first-order logic, as well as the formalizations of many ground calculi including SAT solvers and propositional resolution due to Blanchette, Fleury, and Weidenbach [7].
Additionally we develop new results in conjunction with formalizing them. Several term-orders have been formalized by Becker, Blanchette, Waldmann, and Wand [3] as well as Blanchette, Waldmann, and Wand [13]. These could serve as a basis for a higher-order superposition calculus. Villadsen and I [67] formalized a propositional paraconsistent logic with infinitely many truth values. Lammich wrote and verified a program that checks the certificates of satisfiability and unsatisfiability that SAT solvers can generate [40, 41].
11 Conclusion
This paper describes a formalization of the resolution calculus for first-order logic as well as its soundness and completeness. This includes formalizations of the substitution lemma, Herbrand’s theorem, and the lifting lemma. As far as I know, this is the first formalized soundness and completeness proof of the resolution calculus for first-order logic.
The paper emphasizes how the formalization illustrates details glossed over in the paper proofs. Such details are necessary in a formalization. For instance it shows the jump from satisfiability by an infinite path in a semantic tree to satisfiability by an interpretation. It likewise illustrates how and when to standardize clauses apart in the completeness proof, and the lemmas necessary to allow this. Furthermore, the formalization combines theory from different sources. The proofs of Herbrand’s theorem and completeness are based mainly on those by Chang and Lee [19], while the proof of the lifting lemma is based on that by Leitsch [43]. The existence proof of MGUs for unifiable clauses comes from IsaFoR [34].
The formalization is part of the IsaFoL project [33] on formalizing logics. When the project was started in 2015, we hoped it would attract other researchers to join and formalize their results by using and extending the library. It seems that we have had success with this since the number of authors in the project has more than tripled since then.
Proof assistants take advantage of automatic theorem provers by using them to prove subgoals. This formalization is a step towards mutual benefit between the two areas of research. Formalizations in proof assistants can help automatic theorem provers by contributing a highly rigorous understanding of their meta-theory.
References
Anderson, R., Bledsoe, W.W.: A linear format for resolution with merging and a new technique for establishing completeness. J. ACM 17(3), 525–534 (1970)
Baader, F., Nipkow, T.: Term Rewriting and All That. Cambridge University Press, Cambridge (1998)
Becker, H., Blanchette, J.C., Waldmann, U., Wand, D.: Formalization of Knuth–Bendix orders for lambda-free higher-order terms. Archive of Formal Proofs (2016). http://isa-afp.org/entries/Lambda_Free_KBOs.shtml, Formal proof development
Ben-Ari, M.: Mathematical Logic for Computer Science, 3rd edn. Springer, New York (2012)
Berghofer, S.: First-order logic according to Fitting. Archive of Formal Proofs (2007). http://isa-afp.org/entries/FOL-Fitting.shtml, Formal proof development
Blanchette, J.C., Böhme, S., Paulson, L.C.: Extending Sledgehammer with SMT solvers. J. Autom. Reason. 51(1), 109–128 (2013)
Blanchette, J.C., Fleury, M., Weidenbach, C.: A verified SAT solver framework with learn, forget, restart, and incrementality. In: Olivetti, N., Tiwari, A. (eds.) IJCAR 2016, LNCS, vol. 9706, pp. 25–44. Springer, New York (2016)
Blanchette, J.C., Hölzl, J., Lochbihler, A., Panny, L., Popescu, A., Traytel, D.: Truly modular (co)datatypes for Isabelle/HOL. In: Klein, G., Gamboa, R. (eds.) ITP 2014, LNCS, vol. 8558, pp. 93–110. Springer, New York (2014)
Blanchette, J.C., Popescu, A., Traytel, D.: Abstract completeness. Archive of Formal Proofs (2014). http://isa-afp.org/entries/Abstract_Completeness.shtml, Formal proof development
Blanchette, J.C., Popescu, A., Traytel, D.: Foundational extensible corecursion: a proof assistant perspective. In: Fisher, K., Reppy, J. (eds.) ICFP’15, pp. 192–204. ACM (2015)
Blanchette, J.C., Popescu, A., Traytel, D.: Abstract soundness. Archive of Formal Proofs (2017). http://isa-afp.org/entries/Abstract_Soundness.shtml, Formal proof development
Blanchette, J.C., Popescu, A., Traytel, D.: Soundness and completeness proofs by coinductive methods. J. Autom. Reason. 58(1), 149–179 (2017)
Blanchette, J.C., Waldmann, U., Wand, D.: Formalization of recursive path orders for lambda-free higher-order terms. Archive of Formal Proofs (2016). http://isa-afp.org/entries/Lambda_Free_RPOs.shtml, Formal proof development
Braselmann, P., Koepke, P.: Gödel completeness theorem. Formaliz. Math. 13(1), 49–53 (2005)
Braselmann, P., Koepke, P.: A sequent calculus for first-order logic. Formaliz. Math. 13(1), 33–39 (2005)
Breitner, J.: Visual theorem proving with the Incredible Proof Machine. In: Blanchette, J.C., Merz, S. (eds.) ITP 2016, LNCS, vol. 9807, pp. 123–139. Springer, New York (2016)
Breitner, J., Lohner, D.: The meta theory of the Incredible Proof Machine. Archive of Formal Proofs (2016). http://isa-afp.org/entries/Incredible_Proof_Machine.shtml, Formal proof development
Bundy, A.: The use of explicit plans to guide inductive proofs. In: Lusk, E., Overbeek, R. (eds.) CADE-9, LNCS, vol. 310, pp. 111–120. Springer, New York (1988)
Chang, C.L., Lee, R.C.T.: Symbolic Logic and Mechanical Theorem Proving, 1st edn. Academic Press, Cambridge (1973)
Coen, M., Slind, K., Krauss, A.: Theory unification. Isabelle. http://isabelle.in.tum.de/library/HOL/HOL-ex/Unification.html. Accessed 13 Dec 2017
Coen, M.D.: Interactive program derivation. Ph.D. thesis, University of Cambridge (1992). http://www.cl.cam.ac.uk/techreports/UCAM-CL-TR-272.html
Corbin, J., Bidoit, M.: A rehabilitation of Robinson’s unification algorithm. In: IFIP Congress, pp. 909–914 (1983)
Davis, J., Myreen, M.O.: The reflective Milawa theorem prover is sound (down to the machine code that runs it). J. Autom. Reason. (2015)
Ebbinghaus, H., Flum, J., Thomas, W.: Mathematical Logic, 2nd edn. Springer, New York (1994)
Fitting, M.: First-Order Logic and Automated Theorem Proving, 2nd edn. Springer, New York (1996). Second Edition
Gebhard, H.: Beweisplanung für die Beweise der Vollständigkeit verschiedener Resolutionskalküle in \(\rm \Omega \it \) MEGA. Master’s thesis, Saarland University (1999)
Goubault-Larrecq, J., Jouannaud, J.P.: The blossom of finite semantic trees. In: Voronkov, A., Weidenbach, C. (eds.) Programming Logics: Essays in Memory of Harald Ganzinger, LNCS, pp. 90–122. Springer, New York (2013)
Harrison, J.: Formalizing basic first order model theory. In: Grundy, J., Newey, M. (eds.) TPHOL’s 1998, LNCS, vol. 1497, pp. 153–170. Springer, New York (1998)
Harrison, J.: Towards self-verification of HOL Light. In: Furbach, U., Shankar, N. (eds.) IJCAR 2006, LNCS, vol. 4130, pp. 177–191. Springer, New York (2006)
Harrison, J.: Handbook of Practical Logic and Automated Reasoning. Cambridge University Press, Cambridge (2009)
Ilik, D.: Constructive completeness proofs and delimited control. Ph.D. thesis, École Polytechnique (2010). https://tel.archives-ouvertes.fr/tel-00529021/document
Ilik, D., Lee, G., Herbelin, H.: Kripke models for classical logic. Ann. Pure Appl. Log. 161(11), 1367–1378 (2010)
IsaFoL authors: IsaFoL: Isabelle Formalization of Logic. https://bitbucket.org/isafol/isafol. Accessed 13 Dec 2017
IsaFoR developers: An Isabelle/HOL formalization of rewriting for certified termination analysis. http://cl-informatik.uibk.ac.at/software/ceta/. Accessed 13 Dec 2017
Jensen, A.B., Schlichtkrull, A., Villadsen, J.: Verification of an LCF-style first-order prover with equality. In: Isabelle Workshop 2016 Associated with ITP 2016 (2016)
Jensen, A.B., Schlichtkrull, A., Villadsen, J.: First-order logic according to Harrison. Archive of Formal Proofs (2017). http://isa-afp.org/entries/FOL_Harrison.shtml, Formal proof development
Kohlhase, M.: Theorem prover museum – OMEGA theories – folders: propositional-logic, resolution, proof-theory, prop-res. https://github.com/theoremprover-museum/OMEGA/tree/master/theories. Accessed 13 Dec 2017
Krauss, A.: Partial and nested recursive function definitions in higher-order logic. J. Autom. Reason. 44(4), 303–336 (2010)
Kumar, R., Arthan, R., Myreen, M.O., Owens, S.: Self-formalisation of higher-order logic: semantics, soundness, and a verified implementation. J. Autom. Reason. 56(3), 221–259 (2016)
Lammich, P.: Efficient verified (UN)SAT certificate checking. In: de Moura, L. (ed.) CADE-26, LNCS, vol. 10395, pp. 237–254. Springer, New York (2017)
Lammich, P.: The GRAT tool chain. In: Gaspers, S., Walsh, T. (eds.) SAT 2017, LNCS, vol. 10491, pp. 457–463. Springer, New York (2017)
Leitsch, A.: On different concepts of resolution. Math. Log. Q. 35(1), 71–77 (1989)
Leitsch, A.: The Resolution Calculus. Springer, New York (1997)
Manna, Z., Waldinger, R.: Deductive synthesis of the unification algorithm. Sci. Comput. Program. 1(1), 5–48 (1981)
Margetson, J., Ridge, T.: Completeness theorem. Archive of Formal Proofs (2004). http://isa-afp.org/entries/Completeness.shtml, Formal proof development
Nipkow, T., Klein, G.: Concrete Semantics: With Isabelle/HOL. Springer, New York (2014)
Nipkow, T., Paulson, L.C., Wenzel, M.: Isabelle/HOL—A Proof Assistant for Higher-Order Logic. Springer, New York (2002)
Paulson, L.C.: Verifying the unification algorithm in LCF. Sci. Comput. Program. 5(2), 143–169 (1985)
Paulson, L.C.: Gödel’s incompleteness theorems. Archive of Formal Proofs (2013). http://isa-afp.org/entries/Incompleteness.shtml, Formal proof development
Paulson, L.C.: A machine-assisted proof of Gödel’s incompleteness theorems for the theory of hereditarily finite sets. Rev. Symb. Log. 7(03), 484–498 (2014)
Paulson, L.C.: A mechanised proof of Gödel’s incompleteness theorems using Nominal Isabelle. J. Autom. Reason. 55(1), 1–37 (2015)
Peltier, N.: Propositional resolution and prime implicates generation. Archive of Formal Proofs (2016). http://isa-afp.org/entries/PropResPI.shtml, Formal proof development
Peltier, N.: A variant of the superposition calculus. Archive of Formal Proofs (2016). http://isa-afp.org/entries/SuperCalc.shtml, Formal proof development
Persson, H.: Constructive completeness of intuitionistic predicate logic. Ph.D. thesis, Chalmers University of Technology (1996). http://web.archive.org/web/19970715002824/http://www.cs.chalmers.se/~henrikp/Lic/
Sekar, R., Ramakrishnan, I.V., Voronkov, A.: Term indexing. In: Handbook of Automated Reasoning, vol. 2, pp. 1853–1964 (2001)
Raffalli, C.: Krivine’s abstract completeness proof for classical predicate logic. https://github.com/craff/phox/blob/master/examples/complete.phx (2005, possibly earlier). Accessed 13 Dec 2017
Riazanov, A., Voronkov, A.: Vampire. In: Ganzinger, H. (ed.) CADE-16, LNCS, vol. 1632, pp. 292–296. Springer, New York (1999)
Ridge, T.: A mechanically verified, efficient, sound and complete theorem prover for first order logic. Archive of Formal Proofs (2004). http://isa-afp.org/entries/Verified-Prover.shtml, Formal proof development
Ridge, T., Margetson, J.: A mechanically verified, sound and complete theorem prover for first order logic. In: Hurd, J., Melham, T. (eds.) TPHOL’s 2005, LNCS, vol. 3603, pp. 294–309. Springer, New York (2005)
Robinson, J.A.: A machine-oriented logic based on the resolution principle. J. ACM 12(1), 23–41 (1965)
Robinson, J.A.: The generalized resolution principle. Mach. Intell. 3, 77–93 (1968)
Ruiz-Reina, J.L., Martín-Mateos, F.J., Alonso, J.A., Hidalgo, M.J.: Formal correctness of a quadratic unification algorithm. J. Autom. Reason. 37(1), 67–92 (2006)
Schlichtkrull, A.: Formalization of resolution calculus in Isabelle. Master’s thesis, Technical University of Denmark (2015). https://people.compute.dtu.dk/andschl/Thesis.pdf
Schlichtkrull, A.: Formalization of the resolution calculus for first-order logic. In: Blanchette, J.C., Merz, S. (eds.) ITP 2016, LNCS, vol. 9807, pp. 341–357. Springer, New York (2016)
Schlichtkrull, A.: The resolution calculus for first-order logic. Archive of Formal Proofs (2016). http://isa-afp.org/entries/Resolution_FOL.shtml, Formal proof development
Schlichtkrull, A., Blanchette, J.C., Traytel, D., Waldmann, U.: Formalization of Bachmair and Ganzinger’s simple ordered resolution prover. https://bitbucket.org/isafol/isafol/src/master/Ordered_Resolution_Prover/. Accessed 13 Dec 2017
Schlichtkrull, A., Villadsen, J.: Paraconsistency. Archive of Formal Proofs (2016). http://isa-afp.org/entries/Paraconsistency.shtml, Formal proof development
Schlöder, J.J., Koepke, P.: The Gödel completeness theorem for uncountable languages. Formaliz. Math. 20(3), 199–203 (2012)
Schulz, S.: System description: E 1.8. In: McMillan, K., Middeldorp, A., Voronkov, A. (eds.) LPAR-19, LNCS, vol. 8312, pp. 735–743. Springer, New York (2013)
Shankar, N.: Proof-checking metamathematics. Ph.D. thesis, University of Texas (1986)
Shankar, N.: Metamathematics, Machines, and Gödel’s Proof. Cambridge University Press, Cambridge (1994)
Slind, K.: Reasoning about terminating functional programs. Ph.D. thesis, Technical University of Munich (1999). https://mediatum.ub.tum.de/?id=601660
Sternagel, C., Thiemann, R.: Formalizing Knuth-Bendix orders and Knuth-Bendix completion. In: F. van Raamsdonk (ed.) RTA ’13, LIPIcs, vol. 21, pp. 287–302. Schloss Dagstuhl–Leibniz-Zentrum für Informatik (2013)
Weidenbach, C., Dimova, D., Fietzke, A., Kumar, R., Suda, M., Wischnewski, P.: SPASS version 3.5. In: Schmidt, R.A. (ed.) CADE-22, LNCS, vol. 5663, pp. 140–145. Springer, New York (2009)
Wenzel, M.: Isar—a generic interpretative approach to readable formal proof documents. In: Bertot, Y., Dowek, G., Théry, L., Hirschowitz, A., Paulin, C. (eds.) TPHOL’s 1999, LNCS, vol. 1690, pp. 167–183. Springer, New York (1999)
Acknowledgements
I would like to thank Jørgen Villadsen, Jasmin Christian Blanchette, and Dmitriy Traytel who supervised me in making the formalization. I would also like to thank Jørgen, Jasmin, John Bruntse Larsen, Andreas Halkjær From, and the anonymous referees for their valuable feedback on the paper.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Schlichtkrull, A. Formalization of the Resolution Calculus for First-Order Logic. J Autom Reasoning 61, 455–484 (2018). https://doi.org/10.1007/s10817-017-9447-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10817-017-9447-z



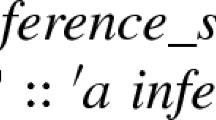



 is satisfied by all f’s prefixes.
is satisfied by all f’s prefixes. is satisfied by
is satisfied by 

 – by the definitions of C,
– by the definitions of C,  – since these two composed substitutions were equal.
– since these two composed substitutions were equal.
 – by the definitions of
– by the definitions of 