Formalization of the Resolution Calculus for First-Order Logic

Abstract

A formalization in Isabelle/HOL of the resolution calculus for first-order logic is presented. Its soundness and completeness are formally proven using the substitution lemma, semantic trees, Herbrand’s theorem, and the lifting lemma. In contrast to previous formalizations of resolution, it considers first-order logic with full first-order terms, instead of the propositional case.

1 Introduction

The resolution calculus plays an important role in automatic theorem proving for first-order logic as many of the most efficient automatic theorem provers, e.g. E [23], SPASS [25], and Vampire [18], are based on resolution and an extension called superposition. Studying the resolution calculus is furthermore an integral part of many university courses on logic in computer science. The resolution calculus was introduced by Robinson in his groundbreaking paper which also introduced most general unifiers (MGUs) [20].

The calculus reasons about first-order literals, i.e. atoms and their negations. Since the literals are first-order, they may contain full first-order terms. Literals are collected in clauses, i.e. disjunctions of literals. The calculus is refutationally complete, which means that if a set of clauses is unsatisfiable, then the resolution calculus can derive a contradiction (the empty clause) from it. One can also use the calculus to prove any valid formula by first negating it, then transforming it to an equisatisfiable set of clauses, and lastly refuting this set with the resolution calculus. Resolution is a calculus for first-order logic, but it does not have any machinery to handle equality or any other theories.

We mostly follow textbooks by Ben-Ari [1], Chang and Lee [8], and Leitsch [15]. The idea of Chang and Lee’s completeness proof is to consider semantic trees, which are binary trees that represent interpretations. Such a tree is cut smaller and smaller, and for each cut, a derivation is done towards the empty clause. The theorem that cuts the tree down to finite size is Herbrand’s theorem, which we also formalize. We prove the completeness theorem for Herbrand universes only, but e.g. Chang and Lee’s Theorem 4.2 states that this is sufficient to prove it complete for any universe. That theorem is, however, not formalized.

The formalization is included in the IsaFoL project [3], which formalizes several logical calculi in Isabelle/HOL. IsaFoL is part of a larger effort to formally prove theorems about logics and logical calculi. This also includes formalizations of ground resolution, which is propositional by nature. The formalization in this paper stands out from these by formalizing resolution for first-order logic. The theory needed to do this is very different from that of ground resolution since first-order logic involves a richer syntax and semantics. To the best of my knowledge, I present the first formalized completeness proof of the resolution calculus for first-order logic.

Harrison formalizes Herbrand’s theorem in a model theoretic formulation [10]. It says that if a purely existential formula is valid, then some disjunction of instances of the body is propositionally valid. In automatic theorem proving, the theorem is viewed in a different, equivalent way: A finite set of clauses is unsatisfiable if some finite set of ground, i.e. variable free, instances of its clauses is as well. This is what SAT solvers take advantage of when refuting first-order formulas. Essentially, they enumerate ground instances and try to refute them. We formalize a third equivalent view stating exactly what the completeness proof needs: If a set of clauses is unsatisfiable, then it has a finite closed semantic tree. This bridges first-order unsatisfiability with decisions made in a semantic tree.

Since this paper is a case study in formalizing mathematics, it is also worthwhile to consider which tools were helpful in this regard:

• The Isabelle/jEdit Prover IDE has many useful features to navigate proof documents. This was advantageous when the theory grew larger.

• The structured proof language Isar was beneficial because it allows formal proofs to be written as sequences of claims that follow from the previous claims. This clearly mirrors mathematical paper proof, which is what we are formalizing. Furthermore, it makes the proofs easy to read, and this is important when a formalization is to help in the understanding of a theory.

• The proof methods of Isabelle such as auto, blast, and metis were effective in discharging proof goals.

• The Sledgehammer tool finds proofs by picking important facts from the theory and then employing top-of-the-line automatic theorem provers and satisfiability modulo solvers. It often helps proving claims that we know are true, but where finding the necessary facts from the theory and libraries as well as choosing and instructing a proof method would be tedious.

Understanding proofs of logical systems can be challenging since one must keep separate which parts of the proofs are about the syntactic level, and which are about the semantic level. It can be tempting to mix intuition about semantics and syntax. Fortunately, a formalization makes the distinction very clear, and hopefully this can aid in understanding the proofs.

2 Overview

A literal l is either an atom or its negation. The $sign$ of an atom is $True$, while that of its negation is $False$. The complement $p^{\mathrm {c}}$ of an atom p is $\lnot p$, and the complement $(\lnot p)^{\mathrm {c}}$ of its negation is p. The complement $L^{\mathrm {C}}$ of a set of literals L is $\{l^{\mathrm {c}}\;|\;l\in L\}$. The set of variables in a clause is $vars_{\mathrm {ls}}\; C$. A clause with an empty set of variables is called ground. A clause is a set of literals representing the universal quantification of the disjunction of the literals in the clause. The empty clause represents a contradiction since it is an empty disjunction. A substitution $\sigma$ is a function from variables to terms, and is applied to a clause C by applying it to all variables in C. The result is written and is called an instance of C. We can likewise apply a substitution to a single literal: .

We will consider the following formulation of the resolution calculus:

The conclusion of the rule is called a resolvent of $C_\mathrm {1}$ and $C_\mathrm {2}$. $L_\mathrm {1}$ and $L_\mathrm {2}$ are called clashing sets of literals. Additionally, the calculus allows us to apply variable renaming to clauses before we apply the resolution rule. Renaming variables in two clauses $C_\mathrm {1}$ and $C_\mathrm {2}$ such that $vars_{\mathrm {ls}}\; C_\mathrm {1}\cap vars_{\mathrm {ls}}\; C_\mathrm {2}= \{\}$ is called standardizing apart. Notice that $L_\mathrm {1}$ and $L_\mathrm {2}$ are sets of literals. Some other resolution calculi instead let $L_\mathrm {1}$ and $L_\mathrm {2}$ be single literals. These calculi then have an additional rule called factoring, which allows unification of subsets of clauses.

The completeness proof we consider is very much inspired by that of Chang and Lee [8], and the proof of the lifting lemma by that of Leitsch [15].

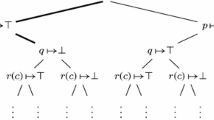
Semantic trees are defined from an enumeration of Herbrand, i.e. ground, atoms. A semantic tree is essentially a binary decision tree in which the decision of going left in a node on level i corresponds to mapping the ith atom of the enumeration to $True$, and in which going right corresponds to mapping it to $False$. See Fig. 1. Therefore, a finite path in a semantic tree can be seen as a partial interpretation. This differs from the usual interpretations in first-order logic in two ways. Firstly, it does not consist of a function denotation and a predicate denotation, but instead assigns $True$ and $False$ to ground atoms directly. Secondly, it is finite, which means that some ground literals are assigned neither $True$ nor $False$. A partial interpretation is said to falsify a ground clause if it, to all literals in the clause, assigns the opposite of their signs. A branch is a path from the root of a tree to one of its leaves. A closed branch is a branch whose corresponding partial interpretation falsifies some ground instance of a clause in the set of clauses. A closed semantic tree for a set of clauses is a minimal tree in which all branches are closed.

Fig. 1.

Semantic tree with partial interpretation $[p \mapsto True, q \mapsto False ]$

Herbrand’s theorem is proven in the following formulation: If a set of clauses is unsatisfiable, then there is a finite and closed semantic tree for that set. We prove it in its contrapositive formulation and therefore assume that all finite semantic trees of a set of clauses have an open (non-closed) branch. Obtaining longer and longer branches of larger and larger finite semantic trees, we can, using König’s lemma, obtain an infinite path all of whose prefixes are open branches of finite semantic trees. Thus these branches satisfy, that is, do not falsify, the set of clauses. We can then prove that this infinite path, when seen as an Herbrand interpretation, also satisfies the set of clauses, and this concludes the proof. Converting the infinite path to a full interpretation can be seen as the step that goes from syntax to semantics.

The lifting lemma lifts resolution derivation steps done on the ground level up to the first-order world. The lemma considers two instances, $C_\mathrm {1}'$ and $C_\mathrm {2}'$, of two first-order clauses, $C_\mathrm {1}$ and $C_\mathrm {2}$. It states that if $C_\mathrm {1}'$ and $C_\mathrm {2}'$ can be resolved to a clause $C'$ then also $C_\mathrm {1}$ and $C_\mathrm {2}$ can be resolved to a clause C. And not only that, but it can even be done in such a way that $C'$ is an instance of this C. See Fig. 2. To prove the theorem we look at the clashing sets of literals $L_\mathrm {1}' \subseteq C_\mathrm {1}'$ and $L_\mathrm {2}' \subseteq C_\mathrm {2}'$. We partition $C_\mathrm {1}'$ in $L_\mathrm {1}'$ and the rest, $R_1' = C_\mathrm {1}' - L_\mathrm {1}'$. Then we lift this up to $C_\mathrm {1}$ by partitioning it in $L_\mathrm {1}$, the part that instantiates to $L_\mathrm {1}'$, and the rest $R_1$ which instantiates to $R_1'$. We do the same for $C_\mathrm {2}$. Since $L_\mathrm {1}'$ and $L_\mathrm {2}'^{\mathrm {C}}$ can be unified, so can $L_\mathrm {1}$ and $L_\mathrm {2}^{\mathrm {C}}$, and therefore they have an MGU. Thus $C_\mathrm {1}$ and $C_\mathrm {2}$ can be resolved to a resolvent C. With some bookkeeping of the substitutions and unifiers, we can also show that C has the ground resolvent $C'$ as an instance.

Fig. 2.

The lifting lemma. An arrow from C to $C'$ indicates that $C'$ is an instance of C. The bars are derivations. Full bars or arrows are relations we know, and the stippled ones are established by the lemma.

Lastly, completeness itself is proven. It states that the empty clause can be derived from any unsatisfiable set of clauses. We start by obtaining a finite closed semantic tree for the set of clauses. Then we cut off two sibling leaves. The branches ending in these leaves falsify a ground clause each, and these clauses can be resolved. We lift this up to the first-order world by the lifting lemma and resolve the first-order clauses. Repeating this procedure, we obtain a derivation which ends when we have cut the tree down to the root. Only the empty clause can be falsified here, and so we have a derivation of the empty clause.

3 Clausal First-Order Logic

We briefly explain the formalization of first-order clausal logic. A first-order term is either a variable consisting of a variable symbol (a string) or it is a function application consisting of a function symbol (a string) and a list of subterms:

A literal is either positive or negative, and it contains a predicate symbol (a string) and a list of terms. The datatype is parametrized with the type of terms $'t$ since it will both represent first-order literals ($fterm \; literal$) and Herbrand literals. A clause is a set of literals.

We formalize the ground $fterm\; literal$s using a predicate $ground_{\mathrm {l}}$ which holds for l if it contains no variables. Likewise, we formalize ground $fterm\; clause$s using a predicate $ground_{\mathrm {ls}}$.

A substitution is a function from variable symbols into terms:

$\mathbf {type\text {-}synonym} \; substitution = var\text {-}sym \Rightarrow fterm$

This is very different from Chang and Lee where they are represented by finite sets [8]. The advantage of functions is that they make it much easier to apply and compose substitutions. If $C'$ is an instance of C we write $instance\text {-}of_{\mathrm {ls}}$. The composition of two substitutions, $\sigma _1$ and $\sigma _2$, is also defined, and written $\sigma _1 \cdot \sigma _2$. We also define unifiers and most-general unifiers of literals (and similarly of terms):

One important theorem is that if a finite set of literals has a unifier, then it also has an MGU. This theorem is formalized in the IsaFoR project [24] by means of a unification algorithm, and we obtain it by proving the literals, unifiers, and MGUs of IsaFoR equivalent to ours.

We also formalize a semantics of terms and literals. A variable denotation, $var\text {-}denot$, maps variable symbols to values of the domain. The domain is represented by the type variable $'u$:

Interpretations consist of denotations of functions and predicates. A function denotation maps function symbols and lists of values to values:

Likewise, a predicate denotation maps predicate symbols and lists of values to the two boolean values:

Similar to other formalizations of first-order logic, the predicate and function symbols do not have fixed arities. The semantics of a term is then defined by the recursive function $eval_{\mathrm {t}}$.

Here, $map \; (eval_{\mathrm {t}}\; E\; F) \; [e_1,\dots ,e_n] = [eval_{\mathrm {t}}\; E\; F \; e_1,\dots ,eval_{\mathrm {t}}\; E\; F \; e_n]$, and from now on we abbreviate $map\; (eval_{\mathrm {t}}\; E\; F) \; ts$ as $eval_{\mathrm {ts}}\; E \; F \; ts$.

If an expression evaluates to $True$ in an interpretation, we say that it is satisfied by the interpretation. If it evaluates to $False$, we say that it is falsified. The semantics of literals is a function $eval_{\mathrm {l}}$ that evaluates literals.

We extend the semantics to clauses.

A set of clauses $Cs$ is satisfied, written $eval_{\mathrm {cs}}\; F \; G \; Cs$, if all its clauses are satisfied.

4 The Resolution Calculus

We first formalize resolvents, i.e. the conclusion of the resolution rule.

In Sect. 2 we saw that the resolution rule had three side-conditions. We additionally restrict the rule to require that $L_\mathrm {1}$ and $L_\mathrm {2}$ are non-empty. When these side-conditions are fulfilled, the rule is applicable.

A step in the resolution calculus either inserts a resolvent of two clauses in a set of clauses, or it inserts a variable renaming of one of the clauses. Two clauses are variable renamings of each other if they can be instantiated to each other. Alternatively we could say that we apply a substitution which is a bijection between the variables in the clause and another set of variables.

The rule for variable renaming allows us to standardize clauses apart.

Derivation steps are extended to derivations by taking the reflexive transitive closure of $resolution\text {-}step$, which is given by $rtranclp$.

We will prove the resolution rule sound by combining several simpler rules. The first we need looks as follows:

It is not entirely trivial to prove, but the needed insight is that given a function denotation and a variable denotation, any substitution can be converted to a variable denotation by evaluating the terms of its domain. We do this using function composition $\circ$:

We can then prove the substitution lemma:

Next, we prove a special version of the resolution rule sound. The rule is special since it is only allowed to remove two literals instead of two sets of literals:

Lastly, we prove that from a clause follows any superset of the clause:

$$\begin{aligned} \frac{C_\mathrm {1}}{C_\mathrm {1}\cup C_\mathrm {2}} \end{aligned}$$

The proofs of all four rules are made as short structured Isar-proofs.

These four sound rules are combined to give the resolution rule, which must consequently be sound. We are of course allowed to use the assumptions of the resolution rule, so we know that when $\sigma$ is applied to $L_\mathrm {1}$ and $L_\mathrm {2}$, they turn in to a complementary pair of literals, which we denote and . This justifies the book keeping inference below. It also means that we can apply the special resolution rule. The bottommost rule application uses the superset rule.

All this reasoning is made as a structured Isar-proofs.

5 Herbrand Interpretations

Herbrand interpretations are a special kind of interpretations, which are characterized by two properties. The first is that their universe is the set of Herbrand terms. Since we chose that the universe should be a type, we need to represent the universe of Herbrand terms by a type. We do it by introducing a new type $hterm$ which is similar to $fterm$, but does not have a constructor for variables.

This is the same datatype as in Berghofer’s formalization of natural deduction [2]. Had we chosen to represent the universes by sets like Ridge and Margetson [19], then we could have represented the Herbrand universe by the set of ground $fterm$s. Unfortunately, we would then need wellformedness predicates for variable and function denotations. We introduce functions $fterm\text {-}of \text {-}hterm$ and $hterm\text {-}of \text {-}fterm$, converting between $hterm$s and ground $fterm$s.

The second characteristic property is that the function denotation of an Herbrand interpretation is $HFun$, and thus, evaluating a ground term under such an interpretation corresponds to replacing all applications of $Fun$ with $HFun$, that is, the ground term is interpreted as itself.

As we saw in Sect. 2, we need an enumeration of Herbrand atoms, such that we can construct our semantic trees. So we define the type of atoms:

Isabelle/HOL provides the proof method $countable\text {-}datatype$ that can automatically prove that a given datatype, in our case $hterm$, is countable. Since also the predicate symbols are countable, then so must $hterm \; atom$ be. Furthermore, it is easy to prove that there are infinitely many $hterm\;atom$s. Using these facts and Hilbert’s choice operator, we specify a bijection $hatom\text {-}from\text {-}nat$ between the natural numbers and the $hterm \;atom$s. We call its inverse $nat\text {-}from\text {-}hatom$. Additionally, we write functions, $nat\text {-}from\text {-}fatom$ and $fatom\text {-}from\text {-}nat$, enumerating the ground $fterm$ atoms in the same order. We also introduce a function $get\text {-}atom$ which returns the atom corresponding to a literal.

5.1 Semantic Trees

We need to formalize semantic trees. In paper-proofs the trees are often labeled with the atoms which we add to or remove from our partial interpretations. In this formalization the trees are unlabeled, because for a given level we can always calculate the corresponding atom.

Our formalization contains a quite substantial, approximately 700 lines, theory on these unlabeled binary trees, paths within them, and their branches. The details are not particularly interesting, but a theory of binary trees is necessary because we, in contrast to paper proofs, cannot rely on intuition about trees.

In our formalization, $bool\; list$s represent both paths in trees and partial interpretations, denoted by the type $partial\text {-}pred\text {-}denot$. E.g., if we consider the path $[True,True,False]$, then it is the path from the root of a semantic tree that goes first left, then left again, and lastly right. On the other hand, it is also the partial interpretation which considers $hatom\text {-}from\text {-}nat \; 0$ to be $True$, $hatom\text {-}from\text {-}nat \; 1$ to be $True$ and $hatom\text {-}from\text {-}nat \; 2$ to be $False$. Our formalization illustrates the correspondence between partial interpretations and paths clearly by identifying their types.

Infinite trees and paths can not be represented by datatypes. We, thus, model possibly infinite trees as sets of paths with a wellformedness property:

Similarly, we model infinite paths as functions from natural numbers into finite paths. Applying the function to number i gives us the prefix of length i. We call such functions infinite paths, and their characteristic property is:

We must make formal, what it means for a partial interpretation to falsify an expression. A partial interpretation G falsifies, written $falsifies_{\mathrm {l}}\; G \;l$, a ground literal l, if the opposite of its sign occurs on index $nat\text {-}from\text {-}fatom \; (get\text {-}atom\; l)$ of the interpretation.

A ground clause C is falsified, written $falsifies_{\mathrm {g}}\; G \;C$, if all its literals are falsified. A first-order clause C is falsified, written $falsifies_{\mathrm {c}}\; G \;C$, if it has a falsified ground instance. A partial interpretation satisfies an expression if it does not falsify it. Lastly, a semantic tree T is closed, written $closed\text {-}tree \; T\; Cs$, for a set of clauses Cs if it is a minimal tree that falsifies all the clauses in Cs.

5.2 Herbrand’s Theorem

The formalization of Herbrand’s theorem is mostly straightforward and is done as an Isar-proof that follows the sketch from Sect. 2. The challenging part is to take an infinite path, all of whose prefixes satisfy a set of clauses $Cs$ and then prove that its conversion to an interpretation also satisfies $Cs$. Chang and Lee [8] do not elaborate much on this, but it takes up a large part of the formalization and illustrates the interplay of syntax and semantics.

First we must define how to convert the infinite path to an Herbrand interpretation. We know that the function denotation must be $HFun$, so we just need to convert the infinite path to a predicate denotation. We do it as follows:

We use currying, so P and $ts$ can be thought of as the predicate symbol and list of values which we wish to evaluate in our semantics. We do it by collecting them to an Herbrand atom, and finding its index. Then we look up a prefix of our infinite path that is long enough to have decided whether the atom is considered $True$ or $False$.

We now prove that if the prefixes collected in the infinite path f satisfy a set of clauses $Cs$ then so does its extension to a full predicate denotation $extend \; f$.

Since we want to prove that the clauses in $Cs$ are satisfied, we fix one C and prove that it has the same property.

We will consider four ways in which clauses can be satisfied:

• 1. A first-order clause can be satisfied by a partial interpretation.

• 2. A ground clause can be satisfied by a partial interpretation.

• 3. A ground clause can be satisfied by an interpretation.

• 4. A first-order clause can be satisfied by an interpretation.

The $extend\text {-}infpath$ lemma relates 1 and 4, and does so by using lemmas that relate 1 to 2 to 3 to 4. The four ways seem similar, but they are in fact very different. That a ground clause is satisfied is very different from a first-order clause being satisfied since we do not need to worry about any ground instances or variables. Likewise, a ground clause being satisfied by a partial interpretation is clearly different from being satisfied by an interpretation since the two types are vastly different: a partial interpretation is a $bool\; list$ while an interpretation consists of a $fun\text {-}sym \; \Rightarrow hterm\; list \Rightarrow hterm$ and a $pred\text {-}sym \; \Rightarrow hterm\; list \Rightarrow bool$.

We relate 1 and 2: If a first-order clause is satisfied by all prefixes of an infinite path, then so is any, in particular ground, instance. This follows from the definition of being satisfied by a partial interpretation.

We relate 2 and 3: If a ground clause is satisfied by all prefixes of an infinite path f, then it is also satisfied by $extend \; f$. This follows almost directly from the definition of $extend$.

We relate 3 and 4: Ideally we would prove that if a ground clause is satisfied by an Herbrand interpretation, then so is a first-order clause of which it is an instance. That is, however, too general. Fortunately, we notice a similarity that ties first-order clauses and ground clauses together by considering a variable denotation in the Herbrand universe, i.e. of type $var\text {-}sym \Rightarrow hterm$. We can create a function that converts its domain to $fterm$s, and thus get a substitution.

Now we have the machinery to state the needed lemma: If the ground clause is satisfied by an Herbrand interpretation under E, then so is the first-order clause C. The reason is simply that if we look at a variable in C, then it is replaced by a ground term in $sub\text {-}of\text {-}denot\;E$. This term evaluates to the same as the Herbrand term that it is interpreted as in E.

The final step is to chain 1, 2, 3, and 4 together to relate 1 and 4.

• 1. Assume that C is satisfied by all prefixes of f.

• 2. Then the ground instance is satisfied by all f’s prefixes.

• 3. Then the ground instance is satisfied by $extend\; f$ under E in particular.

• 4. Then C is satisfied by $extend\; f$ under E.

With this, we can formalize Herbrand’s theorem:

6 Completeness

The completeness proof combines Herbrand’s theorem, the lifting lemma, and reasoning about semantic trees and derivations. We will take a look at the most challenging parts of the formalization of the proof.

6.1 Lifting Lemma

Our formalization of the resolution rule removes literals from clauses before it applies the MGU. This is similar to several presentations from the literature [15, 20]. Another approach, which our formalization used in an earlier version, is to apply the MGU before the literals are removed:

This is exactly the rule used by Ben-Ari [1]. Chang and Lee use a similar approach [8]. However, we were not able to formalize their proofs of the lifting lemma because they had some flaws. The flaws are described in my MSc thesis [21]. The most critical flaw is that the proofs seem to use that , which does not hold in general. Leitsch [14, Proposition 4.1] noticed flaws in Chang and Lee’s proof already, and presented a counter-example to it.

With our current approach, however, the lifting lemma is straightforward to formalize as an Isar-proof using the proof by Leitsch [15]. The lemma uses the $unification$ lemma from Sect. 3 to obtain MGUs.

6.2 The Formal Completeness Proof

Like Herbrand’s theorem, we formalize completeness as an Isar-proof following Chang and Lee [8]. This time, however, the proof is much longer than its informal counterpart. The paper proof is about 30 lines while the formal proof is approximately 150 lines. There are several reasons for this:

• We explicitly have to standardize our clauses apart.

• We need to reason very precisely about the numbers of the ground atoms.

• We need to cut the tree twice.

  • First to remove two leaves.

  • Next to minimize it.

• In both cases we must prove that all branches are closed.

• We must tie our derivation-steps together.

Our completeness proof consists of two steps. First we apply Herbrand’s theorem to obtain a finite tree. Next we take a finite tree and cut it smaller while making a derivation. Then we repeat the process on that tree. To prove that this works, we formalize the process using induction on the size of the tree. Our formalization uses the induction rule $measure\_induct\_rule$ instantiated with the size of a tree. This gives us the following induction principle.

Here, the induction hypothesis holds for any tree of a smaller size, and we need this since we will cut off several nodes in each step.

6.3 Standardizing Apart

In each step we need to make sure that the clauses we resolve are standardized apart. We create functions to do this.

They take clauses $C_\mathrm {1}$ and $C_\mathrm {2}$ and create the clauses $std_\mathrm {1}\; C_\mathrm {1}$ and $std_\mathrm {2}\; C_\mathrm {2}$ which have added respectively 1 and 2 to the beginning of all variables. The most important property is that the clauses actually have distinct variables after we apply it. We need this such that we can apply the resolution rule, and so we can use the lifting lemma.

We also need to prove that it actually renames the variables. This was a prerequisite for the standardize apart rule of the calculus.

In the completeness proof $C_\mathrm {1}$ is falsified by $B_\mathrm {1}$, but not by B. The same holds for $std_\mathrm {1}\; C_\mathrm {1}$ since it is falsified by the same partial interpretations as $C_\mathrm {1}$.

6.4 Branches and Ground Clauses

In each step, the completeness proof removes two sibling leaves and resolves the clauses, $C_\mathrm {1}$ and $C_\mathrm {2}$, that were falsified by the branches, $B_\mathrm {1}=B\;@\;[True]$ and $B_\mathrm {2}=B\;@\;[False]$, ending in the leaves. The resolvent is falsified by B. This is first proven on the ground level and then lifted to the first-order level using the lifting lemma. Thus, on the ground level we must prove two properties.

• 1. The two ground clauses $C_\mathrm {1}'$ and $C_\mathrm {2}'$ falsified by $B_\mathrm {1}$ and $B_\mathrm {2}$ can be resolved.

• 2. Their ground resolvent $C'$ is falsified by B.

We prove 1 first. We do it by proving that $C_\mathrm {1}'$ contains the negative literal of number $length\; B$ and that $C_\mathrm {2}'$ contains its complement. Here, the case for $C_\mathrm {1}'$ is presented. $C_\mathrm {1}'$ is falsified by $B_\mathrm {1}$, but not B, since the closed semantic tree is minimal. Thus, it must be the decision of going left that was necessary to falsify $C_\mathrm {1}'$. Going left falsified the negative literal l with number $length\; B$ in the enumeration, and hence it must be in $C_\mathrm {1}'$.

We prove 2 next. To prove it we must show that the ground resolvent $C' = (C_\mathrm {1}' - \{l\})\; \cup \; (C_\mathrm {2}' - \{l^{\mathrm {c}}\})$ is falsified by B. We do it by proving that the literals in both $C_\mathrm {1}' - \{l\}$ and $C_\mathrm {2}' - \{l^{\mathrm {c}}\}$ are falsified. The case for $C_\mathrm {1}' - \{l\}$ is presented here. The overall idea is that l is falsified by $B_\mathrm {1}$, but not by B. The decision of going left falsified l, and then all of $C_\mathrm {1}'$ was falsified. Therefore, the other literals must have been falsified before we made the decision, in other words, they must have been falsified already by B.

To formalize this we must prove that all the literals in $C_\mathrm {1}'-\{l\}$ are indeed falsified by B. We do it by a lemma showing that any other literal $lo \in C_\mathrm {1}'$ than l is falsified by B. Its proof first shows that lo has another number than l has, i.e. other than $length\; B$. It seems obvious since $lo \ne l$, but we also need to ensure that $lo \ne l^{\mathrm {c}}$. We do this by proving another lemma which says that a clause only can be falsified by a partial interpretation if it does not contain two complementary literals. Then we show that $lo$ has a number smaller than $length \; B\;@\;[True]$, since $lo$ is falsified by $B\;@\;[True]$. This concludes the proof. We abstracts from $True$ to d such that the lemma also works for $B\;@\;[False]$.

6.5 The Derivation

At the end of the proof we must tie the derivations together:

The dots represent the derivation we obtain from the induction hypothesis. It is done using the definitions of $resolution\text {-}step$ and $resolution\text {-}deriv$. The completeness lemma is formalized as follows:

7 Related Work

The literature contains several formalizations of first-order logic. Harrison proves model theoretic results about first-order logic, including the compactness theorem, the Löwenheim-Skolem theorem, and Herbrand’s theorem [10]. There are also formalizations of the completeness of several logical calculi for first-order logic. Margetson and Ridge [16] prove, in Isabelle/HOL, a sequent calculus sound and complete, and they formalize a verified prover based on the calculus [19]. Braselmann and Koepke prove, in Mizar, a sequent calculus sound and complete [6, 7]. Schlöder and Koepke prove it complete even for uncountable languages [22]. Berghofer proves, in Isabelle/HOL, a natural deduction calculus sound and complete [2]. Illik formalizes constructive versions of completeness proofs for classical logic and full intuitionistic predicate logic [12]. Blanchette, Popescu, and Traytel formalize, in Isabelle/HOL, an abstract completeness proof that is independent of any specific proof system and syntax for first-order logic [5]. Other important formalizations of logic are Paulson’s formalization of Gödel’s incompleteness theorems [17], and Harrison’s soundness proof of HOL Light [11] which is extended upon by Kumar, Arthan, Myreen and Owens [13].

There are also formalizations of sound and complete propositional resolution calculi. Blanchette and Traytel formalize, in Isabelle/HOL, propositional resolution [4]. Fleury formalizes, in Isabelle/HOL, many ground calculi including SAT solvers and propositional resolution [9].

8 Conclusion

This paper describes a formalization of the resolution calculus for first-order logic as well as its soundness and completeness. This includes formalizations of the substitution lemma, Herbrand’s theorem, and the lifting lemma. As far as I know, this is the first formalized soundness and completeness proof of the resolution calculus for first-order logic.

The paper emphasizes how the formalization illustrates details glanced over in the paper proofs, which are necessary in a formalization. For instance it shows the jump from satisfiability by an infinite path in a semantic tree to satisfiability by an interpretation. It likewise illustrates how and when to standardize clauses apart in the completeness proof, and the lemmas necessary to allow this. Furthermore, the formalization combines theory from different sources. The proofs of Herbrand’s theorem and completeness are based mainly on those by Chang and Lee [8], while the proof of the lifting lemma is based on that by Leitsch [15]. The existence proof of MGUs for unifiable clauses comes from IsaFoR [24].

Proof assistants take advantage of automatic theorem provers by using them to dispense of subgoals. This formalization could be a step towards mutual benefit between the two. Perhaps formalizations in proof assistants can help automatic theorem provers by contributing a highly rigorous understanding of their meta-theory.