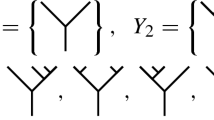Typed angularly decorated planar rooted trees and generalized Rota–Baxter algebras

Abstract

We introduce a generalization of parametrized Rota–Baxter algebras, named $\Omega$-Rota–Baxter algebra, which includes family and matching Rota–Baxter algebras. We study the structure needed on the set $\Omega$ of parameters in order to obtain that free $\Omega$-Rota–Baxter algebras are described in terms of typed and angularly decorated planar rooted trees: we obtain the notion of $\lambda$-extended diassociative semigroup, which includes sets (for matching Rota–Baxter algebras) and semigroups (for family Rota–Baxter algebras), and many other examples. We also describe free commutative $\Omega$-Rota–Baxter algebras generated by a commutative algebra A in terms of typed words.

1 Introduction

A Rota–Baxter algebra is an associative algebra A with a linear endomorphism $P:A\longrightarrow A$, such that for any $a,b\in A$,

$$\begin{aligned}P(a)P(b)=P(aP(b))+P(P(a)b)+\lambda P(ab),\end{aligned}$$

where $\lambda$ is a scalar called the weight of the Rota–Baxter operator P. Firstly introduced by Baxter [1] in a context of probability theory and popularized by Rota [8, 9, 10], they now appear in numerous fields of mathematics and physics, see for example [3] for examples and more details.

The first appearance of family Rota–Baxter algebras seems to be in [2], in the context of Renormalization in Quantum Field Theories. This terminology, due to Li Guo [6], refers to an associative algebra A with a family of linear endomorphism $P_{\alpha }:A\longrightarrow A$ indexed by the elements of a semigroup $(\Omega ,*)$, such that for any $a,b\in A$, for any $\alpha ,\beta \in \Omega$,

$$\begin{aligned} P_{\alpha }(a)P_{\beta }(b)=P_{\alpha *\beta }(P_{\alpha }(a)b+aP_{\beta }(b)+\lambda ab). \end{aligned}$$

This notion of matching Rota–Baxter algebra is introduced in [11]. This time, the Rota–Baxter operators are indexed by the elements of a set $\Omega$ with no structure, and the weights are given by a family of scalars $(\lambda _{\alpha })_{\alpha \in \Omega }$. For any $a,b\in A$, for any $\alpha ,\beta \in \Omega$,

$$\begin{aligned} P_{\alpha }(a)P_{\beta }(b)=P_{\beta }(P_{\alpha }(a)b)+P_{\alpha }(aP_{\beta }(b))+\lambda _{\beta } P_{\alpha }(ab). \end{aligned}$$

These notions have been extended to other types of algebras (Lie, pre-Lie, dendriform$\ldots$), see for example [11, 12, 13, 14].

Our aim here is a generalization of both family and matching Rota–Baxter algebras, in the spirit of what is made in [5] for dendriform algebras. We here consider that the set of parameters $\Omega$ is given five operations $\leftarrow , \rightarrow , \lhd , \rhd$ and $\cdot$, and a family of scalars $\lambda =(\lambda _{\alpha ,\beta })_{\alpha ,\beta \in \Omega }$. An $\Omega$-Rota–Baxter algebra of weight $\lambda$ is an associative algebra A with a family of linear endomorphisms indexed by $\Omega$ such that for any $a,b\in A$, for any $\alpha ,\beta \in \Omega$,

$$\begin{aligned} P_{\alpha }(a)P_{\beta }(b)=P_{\alpha \rightarrow \beta }(P_{\alpha \rhd \beta }(a)b)+P_{\alpha \leftarrow \beta }(a P_{\alpha \lhd \beta }(b))+ \lambda _{\alpha , \beta } P_{\alpha \cdot \beta } (ab). \end{aligned}$$

Taking

$$\begin{aligned} \alpha \rightarrow \beta =\alpha \leftarrow \beta =\alpha \cdot \beta =\alpha *\beta ,\quad \alpha \rhd \beta =\alpha ,\quad \alpha \lhd \beta =\beta , \end{aligned}$$

and $\lambda _{\alpha ,\beta }$ being constant, we recover in this way family Rota–Baxter algebras. Taking

$$\begin{aligned} \alpha \rightarrow \beta =\beta ,\alpha \leftarrow \beta =\alpha ,\alpha \cdot \beta =\alpha ,\quad \alpha \rhd \beta =\alpha ,\quad \alpha \lhd \beta =\beta , \end{aligned}$$

and $\lambda _{\alpha ,\beta }$ depending only on $\beta$, w recover matching Rota–Baxter algebras.

For any set $\Omega$ with five operations and any family of scalars $\lambda$, we define an operad and a category of $\Omega$-Rota–Baxter algebras (Definition 2.8). This is far too general, and we impose the extra constraint that the combinatorics of Rota–Baxter algebras is somehow preserved. To be more precise, as free Rota–Baxter algebras are based on planar rooted trees [14], we impose that free $\Omega$-Rota–Baxter algebras own a description in terms of angularly decorated (by the set of generators) and typed (by $\Omega$) planar rooted trees, that is to say in terms of planar rooted trees with angles decorated by the generators and internal edges decorated by elements of $\Omega$, with an inductive description of the associative product and the Rota–Baxter operators being given by the grafting on a new root, the created internal edge begin of the required type. We show in Theorem 2.14 that this imposes strong constraints on $\Omega$: we obtain that this combinatorial description holds if, and only if $\Omega$ is a $\lambda$-$\mathrm {ETS}$, as defined in Definition 2.3. In particular, $(\Omega ,\leftarrow ,\rightarrow )$ has to be a diassociative semigroup: for any $\alpha ,\beta ,\gamma \in \Omega$,

$$\begin{aligned} (\alpha \leftarrow \beta ) \leftarrow \gamma =&\ \alpha \leftarrow (\beta \leftarrow \gamma )= \alpha \leftarrow (\beta \rightarrow \gamma ),\\ (\alpha \rightarrow \beta ) \leftarrow \gamma =&\ \alpha \rightarrow (\beta \leftarrow \gamma ),\\ (\alpha \rightarrow \beta ) \rightarrow \gamma =&\ (\alpha \leftarrow \beta ) \rightarrow \gamma =\alpha \rightarrow (\beta \rightarrow \gamma ). \end{aligned}$$

This notion firstly appeared in Loday’s work [7] under the name of (associative) dimonoid; the free dimonoid is also constructed in Loday’s article. Moreover, $(\Omega ,\leftarrow ,\rightarrow ,\lhd ,\rhd )$ is an extended semigroup (see Definition 2.2 below), a notion used in [5] for parametrization of dendriform algebras. Particular examples of $\lambda$-$\mathrm {ETS}$ attached to a set give matching Rota–Baxter algebras (see Example 2.4-(b), with $\psi _\cdot (\alpha \otimes \beta )=\lambda \alpha$) and particular examples of $\lambda$-$\mathrm {ETS}$ attached to a semigroup gives family Rota–Baxter algebras (see Example 2.4-(c)). In the case of weight 0, we obtain the generalization of the result [3] establishing that any Rota–Baxter of weight 0 is a dendriform algebra, see Proposition 2.11. Moreover, generalizing the construction of free commutative Rota–Baxter algebras, we obtain that free commutative $\Omega$-Rota–Baxter algebras can be described in terms of $\Omega$-typed words (Proposition 2.18 and Theorem 2.20).

This paper is organised as follows. The first section introduces the definitions of EDS, $\lambda$-$\mathrm {ETS}$, $\mathrm {ETS}$ and of $\Omega$-Rota–Baxter algebras. The main result on free Rota–Baxter algebras and $\lambda$-$\mathrm {ETS}$ is then proved (Theorem 2.14), with a description of free $\Omega$-Rota–Baxter algebras in terms of trees. The last subsection deals with commutative $\Omega$-Rota–Baxter algebras and their description in terms of typed words (Theorem 2.20). The second section gives more examples of $\lambda$-$\mathrm {ETS}$ and $\mathrm {ETS}$, and in particular a classification of these objects of cardinality 2.

Notation. Throughout this paper, k is a unitary commutative ring which will be the base ring of all modules, algebras, as well as linear maps.

2 $\Omega$-Rota–Baxter algebras

2.1 Definitions

We first recall the definition of diassociative semigroups and extended diassociative semigroups of [5], where these objects were used for parametrized versions of dendriform algebras.

Definition 2.1

[5, 7] A diassociative semigroup is a family $(\Omega , \leftarrow , \rightarrow )$, where $\Omega$ is a set and $\leftarrow , \rightarrow : \Omega \times \Omega \rightarrow \Omega$ are maps such that

$$\begin{aligned} (\alpha \leftarrow \beta ) \leftarrow \gamma =&\ \alpha \leftarrow (\beta \leftarrow \gamma )= \alpha \leftarrow (\beta \rightarrow \gamma ),\\ (\alpha \rightarrow \beta ) \leftarrow \gamma =&\ \alpha \rightarrow (\beta \leftarrow \gamma ),\\ (\alpha \rightarrow \beta ) \rightarrow \gamma =&\ (\alpha \leftarrow \beta ) \rightarrow \gamma =\alpha \rightarrow (\beta \rightarrow \gamma ), \end{aligned}$$

for all $\alpha , \beta , \gamma \in \Omega .$

Definition 2.2

[5, Definition 2] An extended diassociative semigroup (abbr. EDS) is a family $(\Omega , \leftarrow , \rightarrow , \lhd ,\rhd )$, where $\Omega$ is a set and $\leftarrow ,\rightarrow , \lhd ,\rhd : \Omega \times \Omega \rightarrow \Omega$ such that $(\Omega , \leftarrow , \rightarrow )$ is a diassociative semigroup and

$$\begin{aligned} \alpha \rhd (\beta \leftarrow \gamma )=&\ \alpha \rhd \beta , \end{aligned}$$

(1)

$$\begin{aligned} (\alpha \rightarrow \beta ) \lhd \gamma =&\ \beta \lhd \gamma , \end{aligned}$$

(2)

$$\begin{aligned} (\alpha \lhd \beta ) \leftarrow ((\alpha \leftarrow \beta ) \lhd \gamma )=&\ \alpha \lhd (\beta \leftarrow \gamma ), \end{aligned}$$

(3)

$$\begin{aligned} (\alpha \lhd \beta ) \lhd ((\alpha \leftarrow \beta ) \lhd \gamma )=&\ \beta \lhd \gamma ,\end{aligned}$$

(4)

$$\begin{aligned} (\alpha \lhd \beta ) \rightarrow ((\alpha \leftarrow \beta ) \lhd \gamma )=&\ \alpha \lhd (\beta \rightarrow \gamma ),\end{aligned}$$

(5)

$$\begin{aligned} (\alpha \lhd \beta ) \rhd ((\alpha \leftarrow \beta ) \lhd \gamma )=&\ \beta \rhd \gamma ,\end{aligned}$$

(6)

$$\begin{aligned} (\alpha \rhd (\beta \rightarrow \gamma )) \leftarrow (\beta \rhd \gamma )=&\ (\alpha \leftarrow \beta ) \rhd \gamma ,\end{aligned}$$

(7)

$$\begin{aligned} (\alpha \rhd (\beta \rightarrow \gamma )) \lhd (\beta \rhd \gamma )=&\ \alpha \lhd \beta ,\end{aligned}$$

(8)

$$\begin{aligned} (\alpha \rhd (\beta \rightarrow \gamma )) \rightarrow (\beta \rhd \gamma )=&\ (\alpha \rightarrow \beta ) \rhd \gamma ,\end{aligned}$$

(9)

$$\begin{aligned} (\alpha \rhd (\beta \rightarrow \gamma )) \rhd (\beta \rhd \gamma )=&\ \alpha \rhd \beta , \end{aligned}$$

(10)

for all $\alpha ,\beta , \gamma \in \Omega$.

We shall use here the notion of $\lambda$-extended triassociative semigroup, where a family of scalars plays the role of weights.

Definition 2.3

An $\lambda$ -extended triassociative semigroup (abbr. $\lambda$-$\mathrm {ETS}$) is a family $(\Omega , \leftarrow , \rightarrow , \lhd ,\rhd , \cdot , *, \lambda )$, where $(\Omega , \leftarrow , \rightarrow , \lhd , \rhd )$ is an EDS and $\lambda =(\lambda _{\alpha ,\beta })_{\alpha ,\beta \in \Omega }$ is a family of elements in $\mathbf{k}$ indexed by $\Omega ^2$ such that

$$\begin{aligned} \lambda _{\alpha \rightarrow \beta , \gamma }=&\ \lambda _{\beta , \gamma }\end{aligned}$$

(11)

$$\begin{aligned} \lambda _{\alpha \lhd \beta , (\alpha \leftarrow \beta ) \lhd \gamma }=&\ \lambda _{\beta , \gamma }\end{aligned}$$

(12)

$$\begin{aligned} \lambda _{\alpha \leftarrow \beta , \gamma }=&\ \lambda _{\alpha , \beta \rightarrow \gamma }\end{aligned}$$

(13)

$$\begin{aligned} \lambda _{\alpha \rhd (\beta \rightarrow \gamma ),\beta \rhd \gamma }=&\ \lambda _{\alpha , \beta }\end{aligned}$$

(14)

$$\begin{aligned} \lambda _{\alpha ,\beta }=&\ \lambda _{\alpha ,\beta \leftarrow \gamma }\end{aligned}$$

(15)

$$\begin{aligned} \lambda _{\alpha ,\beta } \lambda _{\alpha \cdot \beta , \gamma }=&\ \lambda _{\beta ,\gamma } \lambda _{\alpha , \beta \cdot \gamma } \end{aligned}$$

(16)

and, for all $\alpha , \beta , \gamma \in \Omega$:

• (a) If $\lambda _{\alpha \rightarrow \beta , \gamma }= \lambda _{\beta , \gamma }\ne 0$, then

  $$\begin{aligned} \alpha \rhd \beta =&\ \alpha \rhd (\beta \cdot \gamma ),\end{aligned}$$

  (17)
  $$\begin{aligned} (\alpha \rightarrow \beta ) \cdot \gamma =&\ \alpha \rightarrow (\beta \cdot \gamma ). \end{aligned}$$

  (18)

• (b) If $\lambda _{\alpha \lhd \beta , (\alpha \leftarrow \beta ) \lhd \gamma }= \lambda _{\beta , \gamma }\ne 0$, then

  $$\begin{aligned} (\alpha \lhd \beta ) \cdot ((\alpha \leftarrow \beta ) \lhd \gamma )=&\ \alpha \lhd (\beta \cdot \gamma ),\end{aligned}$$

  (19)
  $$\begin{aligned} (\alpha \leftarrow \beta ) \leftarrow \gamma =&\ \alpha \leftarrow (\beta \cdot \gamma ). \end{aligned}$$

  (20)

• (c) If $\lambda _{\alpha \rhd (\beta \rightarrow \gamma ),\beta \rhd \gamma }= \lambda _{\alpha , \beta }\ne 0$, then

  $$\begin{aligned} \alpha \rightarrow (\beta \rightarrow \gamma )=&\ (\alpha \cdot \beta ) \rightarrow \gamma ,\end{aligned}$$

  (21)
  $$\begin{aligned} (\alpha \rhd (\beta \rightarrow \gamma )) \cdot (\beta \rhd \gamma )=&\ (\alpha \cdot \beta ) \rhd \gamma . \end{aligned}$$

  (22)

• (d) If $\lambda _{\alpha \leftarrow \beta , \gamma }=\ \lambda _{\alpha , \beta \rightarrow \gamma }\ne 0$, then

  $$\begin{aligned} (\alpha \leftarrow \beta ) \cdot \gamma =&\ \alpha \cdot (\beta \rightarrow \gamma ),\end{aligned}$$

  (23)
  $$\begin{aligned} \alpha \lhd \beta =&\ \beta \rhd \gamma . \end{aligned}$$

  (24)

• (e) If $\lambda _{\alpha , \beta }= \lambda _{\alpha , \beta \leftarrow \gamma }\ne 0$, then

  $$\begin{aligned} (\alpha \cdot \beta ) \lhd \gamma =&\ \beta \lhd \gamma ,\end{aligned}$$

  (25)
  $$\begin{aligned} (\alpha \cdot \beta ) \leftarrow \gamma =&\ \alpha \cdot (\beta \leftarrow \gamma ). \end{aligned}$$

  (26)

• (f) If $\lambda _{\alpha , \beta } \lambda _{\alpha \cdot \beta , \gamma } = \lambda _{\beta , \gamma } \lambda _{\alpha , \beta \cdot \gamma }\ne 0$, then

  $$\begin{aligned} (\alpha \cdot \beta ) \cdot \gamma =&\ \alpha \cdot (\beta \cdot \gamma ). \end{aligned}$$

  (27)

Example 2.4

• (a) Let $(\Omega ,\leftarrow ,\rightarrow ,\lhd ,\rhd )$ be an EDS. If we put $\lambda _{\alpha ,\beta }=0$ for any $\alpha ,\beta \in \Omega$, then for any product $\cdot$, $(\Omega ,\leftarrow ,\rightarrow ,\lhd ,\rhd ,\cdot ,\lambda )$ is a $\lambda$-$\mathrm {ETS}$.

• (b) If for any $\alpha ,\beta \in \Omega$,

  $$\begin{aligned}\alpha \leftarrow \beta =\beta \rightarrow \alpha =\beta \lhd \alpha =\alpha \rhd \beta =\alpha ,\end{aligned}$$

  then $(\Omega ,\leftarrow ,\rightarrow ,\lhd ,\rhd ,\cdot ,\lambda )$ is a $\lambda$-$\mathrm {ETS}$ if, and only if, the following map defines an associative product:

  $$\begin{aligned}\psi _\cdot :\left\{ \begin{array}{rcl} \mathbf {k}\Omega \otimes \mathbf {k}\Omega &{}\longrightarrow &{}\mathbf {k}\Omega \\ \alpha \otimes \beta &{}\longrightarrow &{}\lambda _{\alpha ,\beta } \alpha \cdot \beta . \end{array}\right. \end{aligned}$$

  Indeed, for any $\alpha$, $\beta$, $\gamma \in \Omega$,

  $$\begin{aligned} \psi _\cdot \circ (\psi _\cdot \otimes \mathrm {id})(\alpha \otimes \beta \otimes \gamma )&=\lambda _{\alpha ,\beta }\lambda _{\alpha \cdot \beta ,\gamma }(\alpha \cdot \beta )\cdot \gamma ,\\ \psi _\cdot \circ (\mathrm {id}\otimes \psi _\cdot )(\alpha \otimes \beta \otimes \gamma )&=\lambda _{\beta ,\gamma }\lambda _{\alpha , \beta \cdot \gamma }\alpha \cdot (\beta \cdot \gamma ), \end{aligned}$$

  which gives the missing condition (27).

• (c) Let $(\Omega ,\star )$ be a semigroup and $\lambda \in \mathbf {k}$. We put, for any $\alpha ,\beta \in \Omega$:

  $$\begin{aligned} \alpha \leftarrow \beta&=\alpha \star \beta ,&\alpha \lhd \beta&=\beta ,\\ \alpha \rightarrow \beta&=\alpha \star \beta ,&\alpha \rhd \beta&=\alpha ,\\ \lambda _{\alpha ,\beta }&=\lambda ,&\alpha \cdot \beta&=\alpha \star \beta . \end{aligned}$$

  Then $(\Omega ,\leftarrow ,\rightarrow ,\lhd ,\rhd ,\cdot ,\lambda )$ is a $\lambda$-$\mathrm {ETS}$.

• (d) Let $(\Omega ,\star )$ be an abelian group and let $\lambda \in \mathbf {k}$. For any $\alpha ,\beta \in \Omega$, we put:

  $$\begin{aligned} \alpha \leftarrow \beta&=\alpha ,&\alpha \rightarrow \beta&,\beta ,\\ \alpha \lhd \beta&=\alpha \star \beta ^{\star -1},&\alpha \rhd \beta&=\alpha ^{\star -1}\star \beta ,\\ \lambda _{\alpha ,\beta }&=\lambda ,&\alpha \cdot \beta&=\alpha . \end{aligned}$$

  Then $(\Omega ,\leftarrow ,\rightarrow ,\lhd ,\rhd ,\cdot ,\lambda )$ is a $\lambda$-$\mathrm {ETS}$.

• (e) Let $\Omega =(\Omega ,\leftarrow ,\rightarrow ,\lhd ,\rhd ,\cdot ,\lambda )$ be a $\lambda$-$\mathrm {ETS}$. For any $\alpha ,\beta \in \Omega$, we put

  $$\begin{aligned} \alpha \leftarrow ^{op}\beta&=\beta \rightarrow \alpha ,&\alpha \lhd ^{op}\alpha&=\beta \rhd \alpha ,\\ \alpha \rightarrow ^{op}\beta&=\beta \leftarrow \alpha ,&\alpha \rhd ^{op}\alpha&=\beta \lhd \alpha ,\\ \alpha \cdot ^{op}\beta&=\beta \cdot \alpha ,&\lambda ^{op}_{\alpha ,\beta }&=\lambda _{\beta ,\alpha }. \end{aligned}$$

  Then $(\Omega ,\leftarrow ^{op},\rightarrow ^{op},\lhd ^{op},\rhd ^{op},\cdot ^{op},\lambda ^{op})$ is also a $\lambda$-$\mathrm {ETS}$, called the opposite of $\Omega$ and denoted by $\Omega ^{op}$. We shall say that $\Omega$ is commutative if it is equal to its opposite.

Definition 2.5

A extended triassociative semigroup (abbr. $\mathrm {ETS}$) is a family $(\Omega , \leftarrow , \rightarrow , \lhd ,\rhd , \cdot , *)$, where $(\Omega , \leftarrow , \rightarrow , \lhd , \rhd )$ is an EDS and

$$\begin{aligned} (\alpha \rightarrow \beta ) *\gamma =&\ \beta *\gamma ,\nonumber \\ {}\alpha \rhd \beta =&\ \alpha \rhd (\beta \cdot \gamma ),\nonumber \\ {}(\alpha \rightarrow \beta ) \cdot \gamma =&\ \alpha \rightarrow (\beta \cdot \gamma ), \end{aligned}$$

(28)

$$\begin{aligned} (\alpha \lhd \beta ) *((\alpha \leftarrow \beta ) \lhd \gamma )=&\ \beta *\gamma ,\nonumber \\ {}(\alpha \lhd \beta ) \cdot ((\alpha \leftarrow \beta ) \lhd \gamma )=&\ \alpha \lhd (\beta \cdot \gamma ),\nonumber \\ {}(\alpha \leftarrow \beta ) \leftarrow \gamma =&\ \alpha \leftarrow (\beta \cdot \gamma ),\end{aligned}$$

(29)

$$\begin{aligned} (\alpha \rhd (\beta \rightarrow \gamma ))*(\beta \rhd \gamma )=&\ \alpha *\beta ,\nonumber \\ {}\alpha \rightarrow (\beta \rightarrow \gamma )=&\ (\alpha \cdot \beta ) \rightarrow \gamma ,\nonumber \\ {}(\alpha \rhd (\beta \rightarrow \gamma )) \cdot (\beta \rhd \gamma )=&\ (\alpha \cdot \beta ) \rhd \gamma , \end{aligned}$$

(30)

$$\begin{aligned} (\alpha \leftarrow \beta )*\gamma =&\ \alpha *(\beta \rightarrow \gamma ),\nonumber \\ {}(\alpha \leftarrow \beta ) \cdot \gamma =&\ \alpha \cdot (\beta \rightarrow \gamma ),\nonumber \\ {}\alpha \lhd \beta =&\ \beta \rhd \gamma , \end{aligned}$$

(31)

$$\begin{aligned} \alpha *\beta =&\ \alpha *(\beta \leftarrow \gamma ),\nonumber \\ {}(\alpha \cdot \beta ) \lhd \gamma =&\ \beta \lhd \gamma ,\nonumber \\ {}(\alpha \cdot \beta ) \leftarrow \gamma =&\ \alpha \cdot (\beta \leftarrow \gamma ), \end{aligned}$$

(32)

$$\begin{aligned} \alpha *\beta =&\ \alpha *(\beta \cdot \gamma ), \end{aligned}$$

(33)

$$\begin{aligned} (\alpha \cdot \beta ) *\gamma =&\ \beta *\gamma ,\nonumber \\ {}(\alpha \cdot \beta ) \cdot \gamma =&\ \alpha \cdot (\beta \cdot \gamma ). \end{aligned}$$

(34)

Example 2.6

• (a) Let $(\Omega ,*,\cdot )$ be a set with two products such that for any $\alpha ,\beta ,\gamma \in \Omega$:

  $$\begin{aligned} \alpha *\beta =&\ \alpha *(\beta \cdot \gamma ),\end{aligned}$$

  (35)
  $$\begin{aligned} (\alpha \cdot \beta ) *\gamma =&\ \beta *\gamma ,\end{aligned}$$

  (36)
  $$\begin{aligned} (\alpha \cdot \beta ) \cdot \gamma =&\ \alpha \cdot (\beta \cdot \gamma ). \end{aligned}$$

  (37)

  We put, for any $\alpha ,\beta \in \Omega$:

  $$\begin{aligned} \alpha \leftarrow \beta&=\alpha ,&\alpha \lhd \beta&=\beta ,\\ \alpha \rightarrow \beta&=\alpha ,&\alpha \rhd \beta&=\beta . \end{aligned}$$

  Then $(\Omega , \leftarrow , \rightarrow , \lhd ,\rhd , \cdot , *)$ is an $\mathrm {ETS}$.

• (b) Let $(\Omega , \leftarrow , \rightarrow , \lhd ,\rhd , \cdot , *)$ be an $\mathrm {ETS}$. For any $\alpha ,\beta \in \Omega$, we put

  $$\begin{aligned} \alpha \leftarrow ^{op}\beta&=\beta \rightarrow \alpha ,&\alpha \lhd ^{op}\alpha&=\beta \rhd \alpha ,\\ \alpha \rightarrow ^{op}\beta&=\beta \leftarrow \alpha ,&\alpha \rhd ^{op}\alpha&=\beta \lhd \alpha ,\\ \alpha *^{op}\beta&=\beta *\alpha ,&\alpha \cdot ^{op}\beta&=\beta \cdot \alpha . \end{aligned}$$

  Then $(\Omega ,\leftarrow ^{op},\rightarrow ^{op},\lhd ^{op},\rhd ^{op},*^{op},\cdot ^{op})$ is also an $\mathrm {ETS}$, called the opposite of $\Omega$. We shall say that $\Omega$ is commutative if it is equal to its opposite.

Actually, each $\mathrm {ETS}$ induces a $\lambda$-$\mathrm {ETS}$, as the following result indicates:

Proposition 2.7

Let $(\Omega , \leftarrow , \rightarrow , \lhd ,\rhd , \cdot , *)$ be an $\mathrm {ETS}$ and let $(\mu _{\alpha })_{\alpha \in \Omega }$ be a family of scalars. For any $\alpha ,\beta \in \Omega$, we put:

$$\begin{aligned}\lambda _{\alpha ,\beta }=\mu _{\alpha *\beta }.\end{aligned}$$

Then $(\Omega , \leftarrow , \rightarrow , \lhd ,\rhd , \cdot , \lambda )$ is a $\lambda$-$\mathrm {ETS}$.

Proof

Conditions (a)-(f) of Definition 2.3 are obviously satisfied by (17)-(27). (11) is (28), (12) is (29), (13) is (31), (14) is (30), (15) is (32), and (16) comes from (33) and (34). $\square$

We now propose the concept of $\Omega$-Rota–Baxter algebras as follows:

Definition 2.8

Let $\Omega$ be a set with five products $\leftarrow , \rightarrow , \lhd , \rhd , \cdot$ and $\lambda =(\lambda _{\alpha ,\beta })_{\alpha ,\beta \in \Omega }$ be a family of elements in $\mathbf{k}$ indexed by $\Omega ^2$. An $\Omega$-Rota–Baxter algebra of weight $\lambda$ is a family $(A, (P_{\omega })_{\omega \in \Omega })$ where A is an associative algebra and $P_{\omega }: A \otimes A \rightarrow A$ is a linear map for each $\omega \in \Omega$, such that

$$\begin{aligned} P_{\alpha }(a)P_{\beta }(b)=P_{\alpha \rightarrow \beta }(P_{\alpha \rhd \beta }(a)b)+P_{\alpha \leftarrow \beta }(a P_{\alpha \lhd \beta }(b))+ \lambda _{\alpha , \beta } P_{\alpha \cdot \beta } (ab), \end{aligned}$$

for all $a, b \in A$ and $\alpha , \beta \in \Omega$. If, further, A is commutative, then $(A, (P_{\omega })_{\omega \in \Omega })$ is a commutative $\Omega$-Rota–Baxter algebra.

Taking all elements of $\lambda$ equal to 0, we get the concept of $\Omega$-Rota–Baxter algebras of weight 0:

Definition 2.9

Let $\Omega$ be a set with four products $\leftarrow , \rightarrow , \lhd , \rhd$. An $\Omega$-Rota–Baxter algebra of weight 0 is a family $(A, (P_{\omega })_{\omega \in \Omega })$ where A is an associative algebra and $P_{\omega }: A \otimes A \rightarrow A$ is a linear map for each $\omega \in \Omega$, such that

$$\begin{aligned} P_{\alpha }(a)P_{\beta }(b)=P_{\alpha \rightarrow \beta }(P_{\alpha \rhd \beta }(a)b)+P_{\alpha \leftarrow \beta }(a P_{\alpha \lhd \beta }(b)), \end{aligned}$$

for all $a, b \in A$ and $\alpha , \beta \in \Omega$.

Example 2.10

• (a) If $(\Omega , \star )$ is a semigroup, we recover the definition of Rota–Baxter family algebras [6, 13] by defining

  $$\begin{aligned} \alpha \leftarrow \beta&= \alpha \rightarrow \beta =\alpha \cdot \beta = \alpha \star \beta ,&\alpha \rhd \beta&=\alpha ,&\alpha \lhd \beta&=\beta , \end{aligned}$$

  and requiring all elements of $\lambda$ to be equal. Note that this is the $\lambda$-$\mathrm {ETS}$ of Example 2.4 (c).

• (b) For a set $\Omega$, define

  $$\begin{aligned} \alpha \rightarrow \beta&=\alpha \lhd \beta =\beta ,&\alpha \rhd \beta&=\alpha \leftarrow \beta =\alpha \cdot \beta =\alpha , \end{aligned}$$

  and $\lambda _{\alpha ,\beta }=\lambda _{\alpha }$, for a family $(\lambda _{\alpha })_{\alpha \in \Omega }$ of elements of $\mathbf{k}$. Then we get the concept of matching Rota–Baxter algebra  [12], up to the change of the product of A into its opposite.

As we know, Rota–Baxter algebras of weight 0 induce dendriform algebras [3]. Similarly, we can show that each $\Omega$-Rota–Baxter algebra of weight 0 has a structure of an $\Omega$-dendriform algebra [5, definition 11]:

Proposition 2.11

Let $\Omega$ be a set with four products $\leftarrow , \rightarrow , \lhd , \rhd$ and $(A, (P_{\omega })_{\omega \in \Omega })$ an $\Omega$-Rota–Baxter algebra of weight 0. Then $(A, (\prec _{\omega })_{\omega \in \Omega }, (\succ _{\omega })_{\omega \in \Omega })$ is an $\Omega$-dendriform algebra, where

$$\begin{aligned} a \prec _{\omega } b&{:}{=}aP_{\omega }(b),&a \succ _{\omega } b&{:}{=}P_{\omega }(a)b, \end{aligned}$$

for all $a, b \in A$ and $\omega \in \Omega$.

Proof

For $a,b,c \in A$ and $\alpha , \beta \in \Omega$,

$$\begin{aligned} (a \prec _{\alpha } b) \prec _{\beta } c&= \big (aP_{\alpha }(b)\big )P_{\beta }(c)\\&=a\big (P_{\alpha }(b)P_{\beta }(c)\big )=a\big (P_{\alpha \rightarrow \beta } (P_{\alpha \rhd \beta }(b)c)+ P_{\alpha \leftarrow \beta } (b P_{\alpha \lhd \beta }(c))\big )\\&=\ aP_{\alpha \rightarrow \beta }(P_{\alpha \rhd \beta }(b)c)+ aP_{\alpha \leftarrow \beta } (b P_{\alpha \lhd \beta }(c))\\&=a \prec _{\alpha \rightarrow \beta } (b \succ _{\alpha \rhd \beta } c)\\&\quad + a\prec _{\alpha \leftarrow \beta } (b \prec _{\alpha \lhd \beta } c),a\succ _{\alpha }(b \prec _{\beta } c)=\\&\quad P_{\alpha }(a)\big (bP_{\beta }(c)\big )\\&=\big (P_{\alpha }(a)b\big )P_{\beta }(c)=(a \succ _{\alpha } b) \prec _{\beta } c,\\&\quad a \succ _{\alpha } (b \succ _{\beta } c)=\ P_{\alpha }(a) \big (P_{\beta }(b)c \big )=\big (P_{\alpha }(a)P_{\beta }(b)\big )c\\&=\big (P_{\alpha \rightarrow \beta } (P_{\alpha \rhd \beta }(a)b)\\&\quad + P_{\alpha \leftarrow \beta } (a P_{\alpha \lhd \beta }(b)) \big )c=\ P_{\alpha \rightarrow \beta } (P_{\alpha \rhd \beta }(a)b)c+P_{\alpha \leftarrow \beta } (a P_{\alpha \lhd \beta }(b)c\\&=(a \succ _{\alpha \rhd \beta } b) \succ _{\alpha \rightarrow \beta } c+(a \prec _{\alpha \lhd \beta } b) \succ _{\alpha \leftarrow \beta } c. \end{aligned}$$

$\square$

2.2 $\Omega$-Rota–Baxter algebras on typed angularly decorated planar rooted trees

First, let us recall some notations on planar rooted trees (see  [14] for more details). For a planar rooted tree T, we shall consider the root and the leaves of T as edges rather than vertices. Denote by IE(T) the set of internal edges of T, i.e. edges which are neither leaves nor the root and denote by V(T) the set of vertices of T. For each vertex v yields a (possibly empty) set of angles A(v), an angle being a pair $(e, e')$ of adjacent incoming edges for v. Let $\displaystyle A(T)=\bigsqcup _{v \in V(T)}A(v)$ be the set of angles of T. Then:

Definition 2.12

[14, Definition 2.2] Let X and $\Omega$ be two sets. An X-angularly decorated $\Omega$ -typed (abbr. typed angularly decorated) planar rooted tree is a triple $T = (T, \mathrm {dec}, \mathrm {type})$, where T is a planar rooted tree, $\mathrm {dec}: A(T) \rightarrow X$ and $\mathrm {type}: IE(T) \rightarrow \Omega$ are maps.

For $n\ge 0$, let ${\mathcal {T}}_n(X,\,\Omega )$ denote the set of X-angularly decorated $\Omega$-typed planar rooted trees with $n+1$ leaves and at least one internal vertex such that internal edges are decorated by elements of $\Omega$. We put

$$\begin{aligned} {\mathcal {T}}(X,\,\Omega )&{:}{=} \bigsqcup _{n\ge 0}{\mathcal {T}}_n(X,\,\Omega )&\text { and }&\mathbf{k}{\mathcal {T}}(X,\,\Omega )&{:}{=}\bigoplus _{n\ge 0}\mathbf{k}{\mathcal {T}}_n(X,\,\Omega ). \end{aligned}$$

For example,

Graphically, an element $T\in \mathcal {T}(X,\,\Omega )$ is of the form:

$\alpha _i$ does not exist for $1 \le i \le n+1$.

For each $\omega \in \Omega$, there is a grafting operator $B^{+}_{\omega }: \mathbf{k}{\mathcal {T}}(X,\,\Omega )\rightarrow \mathbf{k}{\mathcal {T}}(X,\,\Omega )$ which add a new root to a tree and an new internal edge typed by $\omega$ between the new root and the root of the tree.

For example,

The depth $\mathrm {dep}{(T)}$ of a rooted tree T is the maximal length of linear chains from the root to the leaves of the tree. For example,

We also consider the trivial tree $\vert$ and put by convention $\mathrm {dep}(\vert ) {:}{=}0$. For each typed angularly decorated planar rooted tree T, define the number of branches of T to be ${\mathrm {bra}}(T)=0$ if $T=\vert$. Otherwise, $\mathrm {dep}(T)\ge 1$ and T is of the form

where $T_j\in {\mathcal {T}}(X,\,\Omega )\sqcup \{\vert \}, j=1,\ldots , n+1$. We define ${\mathrm {bra}}(T){:}{=}n+1$. For example,

Let X be a set, $(\Omega ,\leftarrow , \rightarrow , \lhd , \rhd , \cdot )$ be a set with five products, and $\lambda =(\lambda _{\alpha ,\beta })_{(\alpha ,\beta ) \in \Omega ^2}$ be a family of elements in $\mathbf{k}$ indexed by $\Omega ^2$. By analogy with the construction of free Rota–Baxter algebras, we define a product $\diamond$ on $\mathbf{k}{\mathcal {T}}(X,\,\Omega )$ as follows. For $T,T'\in {\mathcal {T}}(X,\,\Omega )$, we define $T\diamond T'$ by induction on $\mathrm {dep}(T)+\mathrm {dep}(T')\ge 2$. For the initial step $\mathrm {dep}(T)+\mathrm {dep}(T')=2$, we have $\mathrm {dep}(T)=\mathrm {dep}(T')=1$ and $T, T'$ are of the form

Define

(38)

For the induction step $\mathrm {dep}(T)+\mathrm {dep}(T')\ge 3$, the trees T and $T'$ are of the form

There are four cases to consider.

Case 1: $T_{m+1}=|=T'_1$. Define

(39)

Case 2: $T_{m+1}\ne |=T'_1$. Define

(40)

Case 3: $T_{m+1}=|\ne T'_1$. Define

(41)

Case 4: $T_{m+1}\ne |\ne T'_1$. Define

(42)

Here the first $\diamond$ is defined by Case 3, the second, third and fourth $\diamond$ are defined by induction and the last $\diamond$ is defined by Case 2. This inductively define the multiplication $\diamond$ on ${\mathcal {T}}(X,\,\Omega )$. We then extend $\diamond$ by linearity to $\mathbf{k}{\mathcal {T}}(X,\,\Omega )$. We then have the following result:

Lemma 2.13

Let $(\Omega , \leftarrow , \rightarrow , \lhd , \rhd , \cdot , \lambda )$ be a $\lambda$-$\mathrm {ETS}$. Then $(\mathbf{k}{\mathcal {T}}(X,\,\Omega ), \diamond )$ is an associative algebra with identity .

Proof

By the construction of $\diamond$, $\mathbf{k}{\mathcal {T}}(X,\,\Omega )$ is closed under $\diamond$ and is the identity of $\diamond$.

Now we show the associativity of $\diamond$, i.e.

$$\begin{aligned} (T_1 \diamond T_2) \diamond T_3=T_1 \diamond (T_2 \diamond T_3), \end{aligned}$$

(43)

for all $T_1,T_2,T_3 \in {\mathcal {T}}(X,\,\Omega )$ We prove Eq. (43) by induction on the sum of depths $p{:}{=}\mathrm {dep}(T_1)+\mathrm {dep}(T_2)+\mathrm {dep}(T_3)$. If $p=3$, then $\mathrm {dep}(T_1)=\mathrm {dep}(T_2)=\mathrm {dep}(T_3)=1$ and $T_1, T_2, T_3$ are of the form

Then $(T_1 \diamond T_2) \diamond T_3=T_1 \diamond (T_2 \diamond T_3)$ by a direct calculation.

For the induction step $p \ge 4$, we use induction on the sum of branches $q{:}{=}{\mathrm {bra}}(T_1)+{\mathrm {bra}}(T_2)+{\mathrm {bra}}(T_3)$. If $q=3$ and one of $T_1,T_2, T_3$ has depth 1, then this tree must be of the form and the associativity of $\diamond$ follows directly. Assume

$$\begin{aligned} T_1&=B^{+}_{\alpha }(T'_1),\, T_2=B^{+}_{\beta }(T'_2), \, T_3=B^{+}_{\gamma }(T'_3) \,\, \text { for some} \alpha ,\beta , \gamma \in \Omega \text {and} T'_1,T'_2,T'_3 \\&\in {\mathcal {T}}(X,\,\Omega ), \end{aligned}$$

then

$$\begin{aligned}&\ (T_1 \diamond T_2) \diamond T_3=\big (B^{+}_{\alpha }(T'_1) \diamond B^{+}_{\beta }(T'_2) \big ) \diamond B^{+}_{\gamma }(T'_3)\\&\quad =\ B^{+}_{\alpha \rightarrow \beta }(B^{+}_{\alpha \rhd \beta }(T'_1) \diamond T'_2) \diamond B^{+}_{\gamma }(T'_3) \\&\qquad +B^{+}_{\alpha \leftarrow \beta }(T'_1 \diamond B^{+}_{\alpha \lhd \beta }(T'_2)) \diamond B^{+}_{\gamma } (T'_3)\\&\qquad + \lambda _{\alpha , \beta } B^{+}_{\alpha \cdot \beta }(T'_1 \diamond T'_2) \diamond B^{+}_{\gamma }(T'_3) \\&\quad =\ B^{+}_{(\alpha \rightarrow \beta ) \rightarrow \gamma } \big (B^{+}_{(\alpha \rightarrow \beta ) \rhd \gamma }(B^{+}_{\alpha \rhd \beta }(T'_1) \diamond T'_2) \diamond T'_3 \big )\\&\qquad +B^{+}_{(\alpha \rightarrow \beta ) \leftarrow \gamma } \big ((B^{+}_{\alpha \rhd \beta }(T'_1) \diamond T'_2) \diamond B^{+}_{(\alpha \rightarrow \beta )\lhd \gamma }(T'_3) \big )\\&\qquad +\lambda _{\alpha \rightarrow \beta , \gamma } B^{+}_{(\alpha \rightarrow \beta ) \cdot \gamma } \big ((B^{+}_{\alpha \rhd \beta }(T'_1) \diamond T'_2) \diamond T'_3 \big )\\&\qquad +B^{+}_{(\alpha \leftarrow \beta ) \rightarrow \gamma } \big (B^{+}_{(\alpha \leftarrow \beta ) \rhd \gamma }(T'_1 \diamond B^{+}_{\alpha \lhd \beta }(T'_2)) \diamond T'_3 \big )\\&\qquad +B^{+}_{(\alpha \leftarrow \beta ) \leftarrow \gamma } \big ((T'_1 \diamond B^{+}_{\alpha \lhd \beta }(T'_2)) \diamond B^{+}_{(\alpha \leftarrow \beta ) \lhd \gamma }(T'_3) \big )\\&\qquad + \lambda _{\alpha \leftarrow \beta , \gamma } B^{+}_{(\alpha \leftarrow \beta ) \cdot \gamma } \big ((T'_1 \diamond B^{+}_{\alpha \lhd \beta }(T'_2)) \diamond T'_3 \big ) \\&\qquad +\lambda _{\alpha , \beta } B^{+}_{(\alpha \cdot \beta ) \rightarrow \gamma } \big (B^{+}_{(\alpha \cdot \beta ) \rhd \gamma }(T'_1 \diamond T'_2) \diamond T'_3 \big )\\&\qquad + \lambda _{\alpha , \beta } B^{+}_{(\alpha \cdot \beta ) \leftarrow \gamma } \big ((T'_1 \diamond T'_2) \diamond B^{+}_{(\alpha \cdot \beta ) \lhd \gamma }(T'_3) \big )\\&\qquad +\lambda _{\alpha , \beta } \lambda _{\alpha \cdot \beta , \gamma }B^{+}_{(\alpha \cdot \beta ) \cdot \gamma } \big ((T'_1 \diamond T'_2) \diamond T'_3 \big )\\&\quad =\ B^{+}_{(\alpha \rightarrow \beta ) \rightarrow \gamma } \big (B^{+}_{(\alpha \rightarrow \beta ) \rhd \gamma }(B^{+}_{\alpha \rhd \beta }(T'_1) \diamond T'_2) \diamond T'_3 \big )\\&\qquad +B^{+}_{(\alpha \rightarrow \beta ) \leftarrow \gamma } \big ((B^{+}_{\alpha \rhd \beta }(T'_1) \diamond T'_2) \diamond B^{+}_{(\alpha \rightarrow \beta )\lhd \gamma }(T'_3) \big )\\&\qquad +\lambda _{\alpha \rightarrow \beta , \gamma } B^{+}_{(\alpha \rightarrow \beta ) \cdot \gamma } \big ((B^{+}_{\alpha \rhd \beta }(T'_1) \diamond T'_2) \diamond T'_3 \big ) \\&\qquad +B^{+}_{(\alpha \leftarrow \beta ) \rightarrow \gamma } \big (B^{+}_{(\alpha \leftarrow \beta ) \rhd \gamma }(T'_1 \diamond B^{+}_{\alpha \lhd \beta }(T'_2)) \diamond T'_3 \big )\\&\qquad +B^{+}_{(\alpha \leftarrow \beta ) \leftarrow \gamma } \big (T'_1 \diamond (B^{+}_{\alpha \lhd \beta }(T'_2) \diamond B^{+}_{(\alpha \leftarrow \beta ) \lhd \gamma }(T'_3)) \big )\\&\qquad + \lambda _{\alpha \leftarrow \beta , \gamma } B^{+}_{(\alpha \leftarrow \beta ) \cdot \gamma } \big ((T'_1 \diamond B^{+}_{\alpha \lhd \beta }(T'_2)) \diamond T'_3 \big ) \\&\qquad +\lambda _{\alpha , \beta } B^{+}_{(\alpha \cdot \beta ) \rightarrow \gamma } \big (B^{+}_{(\alpha \cdot \beta ) \rhd \gamma }(T'_1 \diamond T'_2) \diamond T'_3 \big )\\&\qquad + \lambda _{\alpha , \beta } B^{+}_{(\alpha \cdot \beta ) \leftarrow \gamma } \big ((T'_1 \diamond T'_2) \diamond B^{+}_{(\alpha \cdot \beta ) \lhd \gamma }(T'_3) \big )\\&\qquad +\lambda _{\alpha , \beta } \lambda _{\alpha \cdot \beta , \gamma }B^{+}_{(\alpha \cdot \beta ) \cdot \gamma } \big ((T'_1 \diamond T'_2) \diamond T'_3 \big )\,\, {\text {(by the induction hypothesis)}} \end{aligned}$$

$$\begin{aligned}&\quad =\ B^{+}_{(\alpha \rightarrow \beta ) \rightarrow \gamma } \big (B^{+}_{(\alpha \rightarrow \beta )\rhd \gamma } (B^{+}_{\alpha \rhd \gamma }(T'_1) \diamond T'_2) \diamond T'_3 \big )\\&\qquad +B^{+}_{(\alpha \rightarrow \beta ) \leftarrow \gamma } \big ((B^{+}_{\alpha \rhd \beta } (T'_1) \diamond T'_2) \diamond B^{+}_{(\alpha \rightarrow \beta ) \lhd \gamma }(T'_3) \big )\\&\qquad +\lambda _{\alpha \rightarrow \beta , \gamma } B^{+}_{(\alpha \rightarrow \beta ) \cdot \gamma } \big ((B^{+}_{\alpha \rhd \beta }(T'_1) \diamond T'_2) \diamond T'_3 \big ) \\&\qquad +B^{+}_{(\alpha \leftarrow \beta ) \rightarrow \gamma } \big (B^{+}_{(\alpha \leftarrow \beta ) \rhd \gamma }(T'_1 \diamond B^{+}_{\alpha \lhd \beta }(T'_2)) \diamond T'_3 \big )\\&\qquad +B^{+}_{(\alpha \leftarrow \beta ) \leftarrow \gamma } \big (T'_1 \diamond B^{+}_{(\alpha \lhd \beta ) \rightarrow ((\alpha \leftarrow \beta ) \lhd \gamma )}( B^{+}_{(\alpha \lhd \beta ) \rhd ((\alpha \leftarrow \beta ) \lhd \gamma )} (T'_2) \diamond T'_3) \big )\\&\qquad +B^{+}_{(\alpha \leftarrow \beta ) \leftarrow \gamma }(T'_1 \diamond B^{+}_{(\alpha \lhd \beta ) \leftarrow ((\alpha \leftarrow \beta )\lhd \gamma )} (T'_2 \diamond B^{+}_{(\alpha \lhd \beta ) \lhd ((\alpha \leftarrow \beta ) \lhd \gamma )}(T'_3)))\\&\qquad +\lambda _{\alpha \lhd \beta , (\alpha \leftarrow \beta ) \lhd \gamma } B^{+}_{(\alpha \leftarrow \beta ) \leftarrow \gamma } \big (T'_1 \diamond B^{+}_{(\alpha \lhd \beta ) \cdot ((\alpha \leftarrow \beta ) \lhd \gamma )} (T'_2 \diamond T'_3) \big )\\&\qquad + \lambda _{\alpha \leftarrow \beta , \gamma } B^{+}_{(\alpha \leftarrow \beta ) \cdot \gamma } \big ((T'_1 \diamond B^{+}_{\alpha \lhd \beta }(T'_2)) \diamond T'_3 \big ) \\&\qquad +\lambda _{\alpha , \beta } B^{+}_{(\alpha \cdot \beta ) \rightarrow \gamma } \big (B^{+}_{(\alpha \cdot \beta ) \rhd \gamma }(T'_1 \diamond T'_2) \diamond T'_3 \big )\\&\qquad +\lambda _{\alpha , \beta } B^{+}_{(\alpha \cdot \beta ) \leftarrow \gamma } \big ((T'_1 \diamond T'_2) \diamond B^{+}_{(\alpha \cdot \beta ) \lhd \gamma }(T'_3) \big )\\&\qquad +\lambda _{\alpha , \beta } \lambda _{\alpha \cdot \beta , \gamma }B^{+}_{(\alpha \cdot \beta ) \cdot \gamma } \big ((T'_1 \diamond T'_2) \diamond T'_3 \big ), \end{aligned}$$

and

$$\begin{aligned}&\ T_1 \diamond (T_2 \diamond T_3)=B^{+}_{\alpha }(T'_1) \diamond \big (B^{+}_{\beta }(T'_2) \diamond B^{+}_{\gamma }(T'_3) \big )\\&\quad =\ B^{+}_{\alpha }(T'_1) \diamond B^{+}_{\beta \rightarrow \gamma }(B^{+}_{\beta \rhd \gamma }(T'_2) \diamond T'_3)+ B^{+}_{\alpha }(T'_1) \diamond B^{+}_{\beta \leftarrow \gamma }(T'_2 \diamond B^{+}_{\beta \lhd \gamma } (T'_3))\\&\qquad + \lambda _{\beta , \gamma } B^{+}_{\alpha }(T'_1) \diamond B^{+}_{\beta \cdot \gamma } (T'_2 \diamond T'_3)\\&\quad =\ B^{+}_{\alpha \rightarrow (\beta \rightarrow \gamma )} \big (B^{+}_{\alpha \rhd (\beta \rightarrow \gamma )}(T'_1) \diamond (B^{+}_{\beta \rhd \gamma }(T'_2) \diamond T'_3) \big )\\&\qquad +B^{+}_{\alpha \leftarrow (\beta \rightarrow \gamma )} \big (T'_1 \diamond B^{+}_{\alpha \lhd (\beta \rightarrow \gamma )}(B^{+}_{\beta \rhd \gamma }(T'_2) \diamond T'_3) \big )\\&\qquad +\lambda _{\alpha , \beta \rightarrow \gamma } B^{+}_{\alpha \cdot (\beta \rightarrow \gamma )} \big (T'_1 \diamond (B^{+}_{\beta \rhd \gamma }(T'_2) \diamond T'_3) \big )\\&\qquad +B^{+}_{\alpha \rightarrow (\beta \leftarrow \gamma )}\big (B^{+}_{\alpha \rhd (\beta \leftarrow \gamma )} (T'_1) \diamond (T'_2 \diamond B^{+}_{\beta \lhd \gamma }(T'_3)) \big )\\&\qquad +B^{+}_{\alpha \leftarrow (\beta \leftarrow \gamma )} \big (T'_1 \diamond B^{+}_{\alpha \lhd (\beta \leftarrow \gamma )}(T'_2 \diamond B^{+}_{\beta \lhd \gamma }(T'_3)) \big )\\&\qquad + \lambda _{\alpha , \beta \leftarrow \gamma } B^{+}_{\alpha \cdot (\beta \leftarrow \gamma )} \big (T'_1 \diamond (T'_2 \diamond B^{+}_{\beta \lhd \gamma } (T'_3)) \big )\\&\qquad +\lambda _{\beta , \gamma } B^{+}_{\alpha \rightarrow (\beta \cdot \gamma )} \big (B^{+}_{\alpha \rhd (\beta \cdot \gamma )}(T'_1) \diamond (T'_2 \diamond T'_3) \big )\\&\qquad + \lambda _{\beta , \gamma } B^{+}_{\alpha \leftarrow (\beta \cdot \gamma )} \big (T'_1 \diamond B^{+}_{\alpha \leftarrow (\beta \cdot \gamma )}(T'_2 \diamond T'_3) \big )\\&\qquad +\lambda _{\beta , \gamma } \lambda _{\alpha , \beta \cdot \gamma } B^{+}_{\alpha \cdot (\beta \cdot \gamma )} \big (T'_1 \diamond (T'_2 \diamond T'_3) \big )\\&\quad =\ B^{+}_{\alpha \rightarrow (\beta \rightarrow \gamma )} \big ((B^{+}_{\alpha \rhd (\beta \rightarrow \gamma )}(T'_1) \diamond B^{+}_{\beta \rhd \gamma }(T'_2)) \diamond T'_3 \big )\\&\qquad +B^{+}_{\alpha \leftarrow (\beta \rightarrow \gamma )} \big (T'_1 \diamond B^{+}_{\alpha \lhd (\beta \rightarrow \gamma )}(B^{+}_{\beta \rhd \gamma }(T'_2) \diamond T'_3) \big )\\&\qquad +\lambda _{\alpha , \beta \rightarrow \gamma } B^{+}_{\alpha \cdot (\beta \rightarrow \gamma )} \big (T'_1 \diamond (B^{+}_{\beta \rhd \gamma }(T'_2) \diamond T'_3) \big )\\&\qquad +B^{+}_{\alpha \rightarrow (\beta \leftarrow \gamma )}\big (B^{+}_{\alpha \rhd (\beta \leftarrow \gamma )} (T'_1) \diamond (T'_2 \diamond B^{+}_{\beta \lhd \gamma }(T'_3)) \big )\\&\qquad +B^{+}_{\alpha \leftarrow (\beta \leftarrow \gamma )} \big (T'_1 \diamond B^{+}_{\alpha \lhd (\beta \leftarrow \gamma )}(T'_2 \diamond B^{+}_{\beta \lhd \gamma }(T'_3)) \big )\\&\qquad + \lambda _{\alpha , \beta \leftarrow \gamma } B^{+}_{\alpha \cdot (\beta \leftarrow \gamma )} \big (T'_1 \diamond (T'_2 \diamond B^{+}_{\beta \lhd \gamma } (T'_3)) \big )\\&\qquad +\lambda _{\beta , \gamma } B^{+}_{\alpha \rightarrow (\beta \cdot \gamma )} \big (B^{+}_{\alpha \rhd (\beta \cdot \gamma )}(T'_1) \diamond (T'_2 \diamond T'_3) \big )\\&\qquad + \lambda _{\beta , \gamma } B^{+}_{\alpha \leftarrow (\beta \cdot \gamma )} \big (T'_1 \diamond B^{+}_{\alpha \leftarrow (\beta \cdot \gamma )}(T'_2 \diamond T'_3) \big )\\&\qquad +\lambda _{\beta , \gamma } \lambda _{\alpha , \beta \cdot \gamma } B^{+}_{\alpha \cdot (\beta \cdot \gamma )} \big (T'_1 \diamond (T'_2 \diamond T'_3) \big )\quad \quad {\text {(by the induction hypothesis)}} \end{aligned}$$

$$\begin{aligned}&\quad =\ B^{+}_{\alpha \rightarrow (\beta \rightarrow \gamma )} \big ( B^{+}_{(\alpha \rhd (\beta \rightarrow \gamma )) \rightarrow (\beta \rhd \gamma )}(B^{+}_{(\alpha \rhd (\beta \rightarrow \gamma )) \rhd (\beta \rhd \gamma )}(T'_1) \diamond T'_2) \diamond T'_3 \big )\\&\qquad +B^{+}_{\alpha \rightarrow (\beta \rightarrow \gamma )} \big (B^{+}_{\alpha \rhd (\beta \rightarrow \gamma ) \leftarrow (\beta \rhd \gamma )}(T'_1 \diamond B^{+}_{(\alpha \rhd (\beta \rightarrow \gamma ) \lhd (\beta \rhd \gamma ))}(T'_2)) \diamond T'_3 \big )\\&\qquad + \lambda _{\alpha \rhd (\beta \rightarrow \gamma ),\beta \rhd \gamma } B^{+}_{\alpha \rightarrow (\beta \rightarrow \gamma )} (B^{+}_{(\alpha \rhd (\beta \rightarrow \gamma )) \cdot (\beta \rhd \gamma )} (T'_1 \diamond T'_2) \diamond T'_3)\\&\qquad +B^{+}_{\alpha \leftarrow (\beta \rightarrow \gamma )} \big (T'_1 \diamond B^{+}_{\alpha \lhd (\beta \rightarrow \gamma )}(B^{+}_{\beta \rhd \gamma }(T'_2) \diamond T'_3) \big )\\&\qquad +\lambda _{\alpha , \beta \rightarrow \gamma } B^{+}_{\alpha \cdot (\beta \rightarrow \gamma )} \big (T'_1 \diamond (B^{+}_{\beta \rhd \gamma }(T'_2) \diamond T'_3) \big )\\&\qquad +B^{+}_{\alpha \rightarrow (\beta \leftarrow \gamma )}\big (B^{+}_{\alpha \rhd (\beta \leftarrow \gamma )} (T'_1) \diamond (T'_2 \diamond B^{+}_{\beta \lhd \gamma }(T'_3)) \big )\\&\qquad +B^{+}_{\alpha \leftarrow (\beta \leftarrow \gamma )} \big (T'_1 \diamond B^{+}_{\alpha \lhd (\beta \leftarrow \gamma )}(T'_2 \diamond B^{+}_{\beta \lhd \gamma }(T'_3)) \big )\\&\qquad + \lambda _{\alpha , \beta \leftarrow \gamma } B^{+}_{\alpha \cdot (\beta \leftarrow \gamma )} \big (T'_1 \diamond (T'_2 \diamond B^{+}_{\beta \lhd \gamma } (T'_3)) \big )\\&\qquad +\lambda _{\beta , \gamma } B^{+}_{\alpha \rightarrow (\beta \cdot \gamma )} \big (B^{+}_{\alpha \rhd (\beta \cdot \gamma )}(T'_1) \diamond (T'_2 \diamond T'_3) \big )\\&\qquad + \lambda _{\beta , \gamma } B^{+}_{\alpha \leftarrow (\beta \cdot \gamma )} \big (T'_1 \diamond B^{+}_{\alpha \leftarrow (\beta \cdot \gamma )}(T'_2 \diamond T'_3) \big )\\&\qquad +\lambda _{\beta , \gamma } \lambda _{\alpha , \beta \cdot \gamma } B^{+}_{\alpha \cdot (\beta \cdot \gamma )} \big (T'_1 \diamond (T'_2 \diamond T'_3) \big ). \end{aligned}$$

By the induction hypothesis and $(\Omega , \leftarrow , \rightarrow , \lhd , \rhd ,\cdot , \lambda )$ being a $\lambda$-$\mathrm {ETS}$, we get

$$\begin{aligned} (T_1 \diamond T_2) \diamond T_3= T_1 \diamond (T_2 \diamond T_3). \end{aligned}$$

If $q >3$, then at least one of $T_1,T_2, T_3$ have branches greater than or equal to 2. If ${\mathrm {bra}}(T_1) \ge 2$, then there exist $T'_1, T''_1$ of the form

such that $T_1=T'_1 \diamond T''_1$. Hence

$$\begin{aligned}&\ (T_1 \diamond T_2) \diamond T_3=((T'_1 \diamond T''_1) \diamond T_2) \diamond T_3\\ =&\ (T'_1 \diamond (T''_1 \diamond T_2)) \diamond T_3&\text {(by the induction hypothesis)}\\ =&\ T'_1 \diamond ((T''_1 \diamond T_2) \diamond T_3)&\text {(by the form of} T'_1 \text {and the definition of} \diamond )\\ =&\ T'_1 \diamond (T''_1 \diamond (T_2 \diamond T_3))&\text {(by the induction hypothesis)}\\ =&\ T'_1 \diamond T''_1 \diamond (T_2 \diamond T_3)&\text {(by the form of} T'_1 \text {and the definition of} \diamond )\\ =&\ T_1 \diamond (T_2 \diamond T_3). \end{aligned}$$

If ${\mathrm {bra}}(T_2) \ge 2$ or ${\mathrm {bra}}(T_3) \ge 2$, the associativity can be proved similarly. $\square$

Let be the natural inclusion. Then

Theorem 2.14

Let $\Omega$ be a set with five products $\leftarrow , \rightarrow , \lhd , \rhd , \cdot$ and $\lambda$ a family of elements in ${\mathbf{k}}$ indexed by $\Omega ^2$. Then the following conditions are equivalent:

• (a) $(\mathbf{k}{\mathcal {T}}(X,\,\Omega ), \diamond , (B^{+}_{\omega })_{\omega \in \Omega })$ together with the map i is the free $\Omega$-Rota–Baxter algebra generated by X.

• (b) $(\mathbf{k}{\mathcal {T}}(X,\,\Omega ), \diamond , (B^{+}_{\omega })_{\omega \in \Omega })$ is an $\Omega$-Rota–Baxter algebra.

• (c) $(\Omega , \leftarrow , \rightarrow , \lhd , \rhd ,\cdot ,\lambda )$ is a $\lambda$-$\mathrm {ETS}$.

Proof

(a) $\Longrightarrow$ (b) It is obvious. (b) $\Longrightarrow$ (c) For $\alpha , \beta , \gamma \in \Omega$ and , we have

and

By Lemma 2.13 and identifying the types of the planar rooted trees, we get that $(\Omega , \leftarrow , \rightarrow , \lhd$, $\rhd , \cdot , \lambda )$ is a $\lambda$-$\mathrm {ETS}$.

(c) $\Longrightarrow$ (a) By Lemma 2.13 and the definition of $\diamond$, $(\mathbf{k}{\mathcal {T}}(X,\,\Omega ), \diamond , (B^{+}_{\omega })_{\omega \in \Omega })$ is an $\Omega$-Rota–Baxter algebra. Now we show the freeness of $\mathbf{k}{\mathcal {T}}(X,\,\Omega )$.

Let $(R, \cdot , (P_{\omega })_{\omega \in \Omega })$ be an $\Omega$-Rota–Baxter algebra of weight $\lambda _{\Omega }$ and $f : X \rightarrow R$ a set map. We extend f to an $\Omega$-Rota–Baxter algebra morphism $\overline{f}: \mathbf{k}{\mathcal {T}}(X,\,\Omega )\rightarrow R$ such that $\overline{f} \circ i=f$.

For $T \in {\mathcal {T}}(X,\,\Omega )$, we define $\overline{f}(T)$ by induction on $\mathrm {dep}(T)$. If $\mathrm {dep}(T)=1$, then T is of the form

Define

$$\begin{aligned} \overline{f}(T){:}{=}f(x_1) \cdot f(x_2) \cdots f(x_m). \end{aligned}$$

For the induction step of $\mathrm {dep}(T) \ge 2$, we define $\overline{f}(T)$ by induction on the branches of T. If ${\mathrm {bra}}(T)=1$, then T is of the form

Define

$$\begin{aligned}\overline{f}(T){:}{=}P_{\omega } \left( P_{\alpha _1} \big (\overline{f}(T_1) \big ) \cdot f(x_1) \cdot P_{\alpha _2} \big (\overline{f}(T_2) \big ) \cdots P_{\alpha _m} \big ( \overline{f}(T_m) \big ) \cdot f(x_m) \cdot P_{\alpha } \big (\overline{f} (T_{m+1}) \big ) \right) .\end{aligned}$$

If ${\mathrm {bra}}(T)>1$, then T is of the form

Define

$$\begin{aligned}\overline{f}(T){:}{=}P_{\alpha _1} \big ( \overline{f}(T_1) \big ) \cdot f(x_1) \cdot P_{\alpha _2} \big (\overline{f}(T_2) \big ) \cdots P_{\alpha _m} \big ( \overline{f}(T_m) \big ) \cdot f(x_m) \cdot P_{\alpha } \big (\overline{f} (T_{m+1}) \big ).\end{aligned}$$

By construction of $\overline{f}$, $\overline{f} \circ i=f$ and $P_{\omega } \overline{f}=\overline{f} B^{+}_{\omega }$ for all $\omega \in \Omega$. Next we show that $\overline{f}$ is an algebra homomorphism, i.e.

$$\begin{aligned} \overline{f}(T \diamond T')=\overline{f}(T) \cdot \overline{f}(T') \,\, \text { for all} T,T' \in {\mathcal {T}}(X,\,\Omega ). \end{aligned}$$

(44)

We prove Eq. (44) by induction on $\mathrm {dep}(T)+\mathrm {dep}(T')$. If $\mathrm {dep}(T)+\mathrm {dep}(T')=2$, then $\mathrm {dep}(T)=\mathrm {dep}(T')=1$ and

and

$$\begin{aligned}&\overline{f}(T \diamond T')= f(x_1) \cdots f(x_m) \cdot f(y_1) \cdots f(y_n)=(f(x_1) \cdots f(x_m)) \cdot (f(y_1) \cdots \\&f(y_n))=\overline{f}(T) \diamond \overline{f}(T'). \end{aligned}$$

For the induction step of $\mathrm {dep}(T)+\mathrm {dep}(T') \ge 3$. If $T \diamond T'$ belongs to the first three cases, then $\overline{f}(T \diamond T')=\overline{f}(T) \cdot \overline{f}(T')$ by the definition of $\diamond$ and the construction of $\overline{f}$. So we only need to consider the fourth case. Then

Moreover, by the construction of $\overline{f}$, it is the unique way to extend f as an $\Omega$-Rota–Baxter algebra morphism. Hence $(\mathbf{k}{\mathcal {T}}(X,\,\Omega ), \diamond , (B^{+}_{\omega })_{\omega \in \Omega })$ together with the map i is the free $\Omega$-Rota–Baxter algebra generated by X. $\square$

Remark 2.15

• (a) In Definition 2.8, $\Omega$ is required to be a set with five products $\leftarrow , \rightarrow , \lhd , \rhd , \cdot$ and $\lambda$ is required to be a family of elements in ${\mathbf{k}}$ indexed by $\Omega ^2$. This defines a category of $\Omega$-Rota–Baxter algebras for any such $\Omega$. Generally, free $\Omega$-Rota–Baxter algebras are not based on $\Omega$-angularly decorated planar trees. However, by Theorem 2.14, the condition of a free $\Omega$-Rota–Baxter algebra based on the combinatorics of $\Omega$-angularly decorated planar trees, similar to the one of (classical) Rota–Baxter algebras, is equivalent to $(\Omega , \leftarrow , \rightarrow , \lhd , \rhd ,\cdot ,\lambda )$ being a $\lambda$-$\mathrm {ETS}$.

• (b) As a particular case, we recover the description of free family Rota–Baxter algebras of [14]. An alternative description of free Rota–Baxter algebras (with rooted forests) is done in [4].

Taking all elements in $\lambda$ to be 0, we get the following result:

Corollary 2.16

Let $\Omega$ be a set with four products $\leftarrow , \rightarrow , \lhd , \rhd$. Then the following conditions are equivalent:

• (a) $(\mathbf{k}{\mathcal {T}}(X,\,\Omega ), \diamond , (B^{+}_{\omega })_{\omega \in \Omega })$ together with the map i is the free $\Omega$-Rota–Baxter algebra of weight 0 generated by X.

• (b) $(\mathbf{k}{\mathcal {T}}(X,\,\Omega ), \diamond , (B^{+}_{\omega })_{\omega \in \Omega })$ is an $\Omega$-Rota–Baxter algebra of weight 0.

• (c) $(\Omega , \leftarrow , \rightarrow , \lhd , \rhd )$ is an EDS.

2.3 Commutative $\Omega$-Rota–Baxter algebras on typed words

Let $\Omega$ be a set and V a vector space. Recall from [5] that the space of $\Omega$-typed words in V is

$$\begin{aligned} \mathrm {Sh}^+_{\Omega }(V)=\bigoplus _{n \ge 1} (\mathbf{k}\Omega )^{\otimes (n-1)} \otimes V^{\otimes n}. \end{aligned}$$

For the ease of statement, we redefine the space of $\Omega$-typed words in V as

$$\begin{aligned} \mathrm {Sh}^+_{\Omega }(V)=\bigoplus _{n \ge 0} \underbrace{V \otimes (\mathbf{k}\Omega ) \otimes \cdots \otimes (\mathbf{k}\Omega ) \otimes V}_{(n+1)'s V \text {and} n's (\mathbf{k}\Omega )} \end{aligned}$$

and write each pure tensor $\mathbf {v}=v_0 \otimes \omega _1 \otimes \cdots \otimes \omega _n \otimes v_n \in \Omega$ under the form

$$\begin{aligned} \mathbf {v}=v_0 \otimes _{\omega _1} v_1 \otimes _{\omega _2} \cdots \otimes _{\omega _n} v_n, \end{aligned}$$

where $n \ge 0$, $\omega _1, \cdots , \omega _n \in \Omega$ and $v_0, \cdots , v_n \in V$ with the convention $\mathbf {v}=v_0$ if $n=0$. We call $\mathbf {v}$ an $\Omega$ -typed word in V and define its length $\ell (\mathbf {v}){:}{=}n+1$.

Let A be an algebra with identity $1_A$, $(\Omega ,\leftarrow , \rightarrow , \lhd , \rhd , \cdot )$ be a set with five products and $\lambda =(\lambda _{\alpha ,\beta })_{(\alpha ,\beta )\in \Omega ^2}$ be a family of elements in ${\mathbf{k}}$ indexed by $\Omega ^2$. For any pure tensors $\mathbf {a}=a_0 \otimes _{\alpha _1} \mathbf {a}', \mathbf {b}=b_0 \otimes _{\beta _1} \mathbf {b}' \in \mathrm {Sh}^+_{\Omega }(A)$ with $\ell (\mathbf {a})=m$ and $\ell (\mathbf {b})=n$, define $\mathbf {a} \diamond \mathbf {b}$ inductively as follows:

$$\begin{aligned} \mathbf {a} \diamond \mathbf {b}{:}{=} \left\{ \begin{array}{l} \ a_0b_0, \text {if m=n=0}, \\ \ a_0b_0 \otimes _{\alpha _1} \mathbf {a}', \text {if m>0, n=0},\\ \ a_0b_0 \otimes _{\beta _1} \mathbf {b}', \text {if m=0, n>0},\\ \ a_0b_0 \otimes _{\alpha _1 \rightarrow \beta _1} \big ((1_A \otimes _{\alpha _1 \rhd \beta _1} \mathbf {a}') \diamond \mathbf {b}' \big ) + a_0b_0 \otimes _{\alpha \leftarrow \beta _1} \big (\mathbf {a}' \diamond (1_A \otimes _{\alpha _1 \lhd \beta _1} \mathbf {b}') \big ) \\ + \lambda _{\alpha _1 , \beta _1} a_0b_0 \otimes _{\alpha _1 \cdot \beta _1}(\mathbf {a}' \diamond \mathbf {b}'), \text {if m>0, n>0}.\\ \end{array} \right. \end{aligned}$$

(45)

Extending bilinearly, we construct a product $\diamond$ on $\mathrm {Sh}^+_{\Omega }(A)$.

Lemma 2.17

Let A be an algebra with identity $1_A$, $\Omega$ a set with five products $\leftarrow , \rightarrow , \lhd , \rhd , \cdot$ and $\lambda$ a family of elements in ${\mathbf{k}}$ indexed by $\Omega ^2$. If $(\Omega , \leftarrow , \rightarrow , \lhd , \rhd , \cdot ,\lambda )$ is a $\lambda$-ESD, then $(\mathrm {Sh}^+_{\Omega }(A), \diamond )$ is an associative algebra with identity $1_A$.

Proof

By Eq. (45), $\mathrm {Sh}^+_{\Omega }(A)$ is closed under $\diamond$ and $1_A$ is the identity of $\diamond$.

For pure tensors $\mathbf {a},\mathbf {b},\mathbf {c} \in \mathrm {Sh}^+_{\Omega }(A)$, we prove

$$\begin{aligned} (\mathbf {a} \diamond \mathbf {b}) \diamond \mathbf {c}=\mathbf {a} \diamond (\mathbf {b} \diamond \mathbf {c}) \end{aligned}$$

(46)

by induction on $\ell (\mathbf {a})+\ell (\mathbf {b})+\ell (\mathbf {c})$. If $\ell (\mathbf {a})+\ell (\mathbf {b})+\ell (\mathbf {c})=3$, then $\ell (\mathbf {a})=\ell (\mathbf {b})=\ell (\mathbf {c})=1$ and $\mathbf {a}=a_0, \mathbf {b}=b_0, \mathbf {c}=c_0$. Hence

$$\begin{aligned} (\mathbf {a} \diamond \mathbf {b}) \diamond \mathbf {c}=a_0b_0c_0=\mathbf {a} \diamond (\mathbf {b} \diamond \mathbf {c}). \end{aligned}$$

Suppose Eq. (46) holds for $\ell (\mathbf {a})+\ell (\mathbf {b})+\ell (\mathbf {c})\le p$, where $p \ge 3$ is a fixed integer. Consider the case of $\ell (\mathbf {a})+\ell (\mathbf {b})+\ell (\mathbf {c})=p+1$. If one of $\ell (\mathbf {a}), \ell (\mathbf {b}), \ell (\mathbf {c})$ is equal to 1, then Eq. (46) holds by direct calculation. Hence we assume $\ell (\mathbf {a})>1, \ell (\mathbf {b})>1, \ell (\mathbf {c})>1$ and

$$\begin{aligned} \mathbf {a}=a_0 \otimes _{\alpha _1} \mathbf {a}', \,\, \mathbf {b}=b_0 \otimes _{\beta _1} \mathbf {b}', \,\, \mathbf {c}=c_0 \otimes _{\gamma _1} \mathbf {c}'. \end{aligned}$$

Then

$$\begin{aligned}&\ (\mathbf {a} \diamond \mathbf {b}) \diamond \mathbf {c}\\ =&\ (a_0b_0)c_0 \otimes _{(\alpha _1 \rightarrow \beta _1) \rightarrow \gamma _1}\big ((1_A \otimes _{(\alpha _1 \rightarrow \beta _1) \rhd \gamma _1} ((1_A \otimes _{\alpha _1 \otimes \rhd \beta _1} \mathbf {a}') \diamond \mathbf {b}')) \diamond \mathbf {c}' \big )\\&\ +(a_0b_0)c_0 \otimes _{(\alpha _1 \rightarrow \beta _1) \leftarrow \gamma _1} \big ( ((1_A \otimes _{\alpha _1 \rhd \beta _1} \mathbf {a}') \diamond \mathbf {b}') \diamond (1_A \otimes _{(\alpha _1 \rightarrow \beta _1) \lhd \gamma _1} \mathbf {c}') \big )\\&\ +\lambda _{(\alpha _1 \rightarrow \beta _1), \gamma _1} (a_0b_0)c_0\otimes _{(\alpha _1 \rightarrow \beta _1) \cdot \gamma _1}\big (((1_A \otimes _{\alpha _1 \rhd \beta _1} \mathbf {a}') \diamond \mathbf {b}') \diamond \mathbf {c}'\big )\\&\ +(a_0b_0)c_0 \otimes _{(\alpha _1 \leftarrow \beta _1) \rightarrow \gamma _1} \\&\big ((1_A \otimes _{(\alpha _1 \leftarrow \beta _1) \rhd \gamma _1} (\mathbf {a}' \diamond (1_A \otimes _{\alpha _1 \lhd \beta _1} \mathbf {b}'))) \diamond \mathbf {c}' \big )\\&\ +(a_0b_0)c_0 \otimes _{(\alpha _1 \leftarrow \beta _1) \leftarrow \gamma _1} \\&\big (\mathbf {a}' \diamond (1_A \otimes _{(\alpha _1 \lhd \beta _1) \rightarrow ((\alpha _1 \leftarrow \beta _1) \lhd \gamma _1)} ((1_A \otimes _{(\alpha _1 \lhd \beta _1) \rhd ((\alpha _1 \leftarrow \beta _1) \lhd \gamma _1)} \mathbf {b}') \diamond \mathbf {c}') )\big )\\&\ +(a_0b_0)c_0 \otimes _{(\alpha _1 \leftarrow \beta _1) \leftarrow \gamma _1} \\&\big (\mathbf {a}' \diamond (1_A \otimes _{(\alpha _1 \lhd \beta _1) \leftarrow ((\alpha _1 \leftarrow \beta _1)\lhd \gamma _1)}(\mathbf {b}' \diamond (1_A \otimes _{(\alpha _1 \lhd \beta _1) \lhd ((\alpha _1 \leftarrow \beta _1) \lhd \gamma _1)} \mathbf {c}'))) \big )\\&\ +\lambda _{(\alpha _1 \lhd \beta _1) , ((\alpha _1 \leftarrow \beta _1) \lhd \gamma _1)} (a_0b_0)c_0 \otimes _{(\alpha _1 \leftarrow \beta _1)\leftarrow \gamma _1} \big (\mathbf {a}' \diamond (1_A \otimes _{(\alpha _1 \lhd \beta _1) \cdot ((\alpha _1 \leftarrow \beta _1) \lhd \gamma _1)}(\mathbf {b}' \diamond \mathbf {c}')) \big )\\&\ +\lambda _{(\alpha _1 \leftarrow \beta _1), \gamma _1} (a_0b_0)c_0 \otimes _{(\alpha _1 \leftarrow \beta _1) \cdot \gamma _1} \big ((\mathbf {a}' \diamond (1_A \otimes _{\alpha _1 \lhd \beta _1} \mathbf {b}'))\diamond \mathbf {c}' \big )\\&\ +\lambda _{\alpha _1 , \beta _1} (a_0b_0)c_0 \otimes _{(\alpha _1 \cdot \beta _1) \rightarrow \gamma _1} \big ((1_A \otimes _{(\alpha _1 \cdot \beta _1)\rhd \gamma _1} (\mathbf {a}' \diamond \mathbf {b}'))\diamond \mathbf {c}' \big )\\&\ +\lambda _{\alpha _1 , \beta _1} (a_0b_0)c_0 \otimes _{(\alpha _1 \cdot \beta _1)\leftarrow \gamma _1}\big ((\mathbf {a}' \diamond \mathbf {b}') \diamond (1_A \otimes _{(\alpha _1 \cdot \beta _1)\lhd \gamma _1} \mathbf {c}') \big )\\&\ +\lambda _{\alpha _1 , \beta _1}\lambda _{(\alpha _1 \cdot \beta _1) , \gamma _1} (a_0b_0)c_0 \otimes _{(\alpha _1 \cdot \beta _1) \cdot \gamma _1} \big ((\mathbf {a}' \diamond \mathbf {b}') \diamond \mathbf {c}' \big ) \end{aligned}$$

and

$$\begin{aligned}&\ \mathbf {a} \diamond (\mathbf {b} \diamond \mathbf {c})\\ =&\ a_0(b_0c_0) \otimes _{\alpha _1 \rightarrow (\beta _1 \rightarrow \gamma _1)}\\&\big ((1_A \otimes _{(\alpha _1 \rhd (\beta _1 \rightarrow \gamma _1)) \rightarrow (\beta _1 \rhd \gamma _1)}((1_A \otimes _{(\alpha _1 \rhd (\beta _1 \rightarrow \gamma _1)) \rhd (\beta _1 \rhd \gamma _1)} \mathbf {a}') \diamond \mathbf {b}'))\diamond \mathbf {c}' \big )\\&\ +a_0(b_0c_0) \otimes _{\alpha _1 \rightarrow (\beta _1 \rightarrow \gamma _1)} \\&\big ((1_A \otimes _{(\alpha _1 \rhd (\beta _1 \rightarrow \gamma _1))\leftarrow (\beta _1 \rhd \gamma _1)}(\mathbf {a}' \diamond (1_A \otimes _{(\alpha _1 \rhd (\beta _1 \rightarrow \gamma _1)) \lhd (\beta _1 \rhd \gamma _1)} \mathbf {b}'))) \diamond \mathbf {c}' \big )\\&\ +\lambda _{(\alpha _1 \rhd (\beta _1 \rightarrow \gamma _1)) , (\beta _1 \rhd \gamma _1)} a_0(b_0c_0) \otimes _{\alpha _1 \rightarrow (\beta _1 \rightarrow \gamma _1)} \big ((1_A \otimes _{(\alpha _1 \rhd (\beta _1 \rightarrow \gamma _1)) \cdot (\beta _1 \rhd \gamma _1)} (\mathbf {a}' \diamond \mathbf {b}'))\diamond \mathbf {c}' \big )\\&\ +a_0(b_0c_0)\otimes _{\alpha _1 \leftarrow (\beta _1 \rightarrow \gamma _1)} \big (\mathbf {a}' \diamond (1_A \otimes _{\alpha _1 \lhd (\beta _1 \rightarrow \gamma _1)} ((1_A \otimes _{\beta _1 \rhd \gamma _1} \mathbf {b}') \diamond \mathbf {c}')) \big )\\&\ +\lambda _{\alpha _1 , (\beta _1 \rightarrow \gamma _1)} a_0(b_0c_0) \otimes _{\alpha _1 \cdot (\beta _1 \rightarrow \gamma _1)} \big (\mathbf {a}' \diamond ((1_A \otimes _{\beta _1 \rhd \gamma _1} \mathbf {b}') \diamond \mathbf {c}') \big )\\&\ +a_0(b_0c_0) \otimes _{\alpha _1 \rightarrow (\beta _1 \leftarrow \gamma _1)} \big ((1_A \otimes _{\alpha _1 \rhd (\beta _1 \leftarrow \gamma _1)} \mathbf {a}') \diamond (\mathbf {b}' \diamond (1_A \otimes _{\beta _1 \lhd \gamma _1} \mathbf {c}')) \big )\\&\ +a_0(b_0c_0) \otimes _{\alpha _1 \leftarrow (\beta _1 \leftarrow \gamma _1)} \big (\mathbf {a}' \diamond (1_A \otimes _{\alpha _1 \lhd (\beta _1 \leftarrow \gamma _1)}(\mathbf {b}' \diamond (1_A \otimes _{\beta _1 \lhd \gamma _1} \mathbf {c}'))) \big )\\&\ +\lambda _{\alpha _1 , (\beta _1 \leftarrow \gamma _1)} a_0(b_0c_0) \otimes _{\alpha _1 \cdot (\beta _1 \leftarrow \gamma _1)} \big (\mathbf {a}' \diamond (\mathbf {b}' \diamond (1_A \otimes _{\beta _1 \lhd \gamma _1} \mathbf {c}')) \big )\\&\ +\lambda _{\beta _1 , \gamma _1} a_0(b_0c_0) \otimes _{\alpha _1 \rightarrow (\beta _1 \cdot \gamma _1)} \big ((1_A \otimes _{\alpha _1 \rhd (\beta _1 \cdot \gamma _1)} \mathbf {a}') \diamond (\mathbf {b}' \diamond \mathbf {c}') \big )\\&\ +\lambda _{\beta _1 , \gamma _1} a_0(b_0c_0) \otimes _{\alpha _1 \leftarrow (\beta _1 \cdot \gamma _1)} \big (\mathbf {a}' \diamond (1_A \otimes _{\alpha _1 \lhd (\beta _1 \cdot \gamma _1)} (\mathbf {b}' \diamond \mathbf {c}')) \big )\\&\ +\lambda _{\beta _1 , \gamma _1} \lambda _{\alpha _1 , (\beta _1 \cdot \gamma _1)} a_0(b_0c_0) \otimes _{\alpha _1 \cdot (\beta _1 \cdot \gamma _1)} \big (\mathbf {a}'\diamond (\mathbf {b}' \diamond \mathbf {c}') \big ). \end{aligned}$$

By induction hypothesis and $(\Omega ,\leftarrow , \rightarrow ,\lhd , \rhd , \cdot ,\lambda )$ being a $\lambda$-$\mathrm {ETS}$, $(\mathbf {a} \diamond \mathbf {b}) \diamond \mathbf {c}=\mathbf {a} \diamond (\mathbf {b} \diamond \mathbf {c})$. Hence $(\mathrm {Sh}^+_{\Omega }(A), \diamond )$ is an associative algebra with identity $1_A$. $\square$

For each $\omega \in \Omega$, define a linear map $P_{\omega }: \mathrm {Sh}^+_{\Omega }(A) \rightarrow \mathrm {Sh}^+_{\Omega }(A), \mathbf {a} \mapsto 1_A \otimes _{\omega } \mathbf {a}$. If further A is a commutative algebra and $(\Omega , \leftarrow , \rightarrow , \lhd , \rhd , \cdot ,\lambda )$ is a commutative $\lambda$-$\mathrm {ETS}$, we get the following result:

Proposition 2.18

If A is a commutative algebra with identity $1_A$ and $(\Omega , \leftarrow , \rightarrow , \lhd , \rhd , \cdot ,\lambda )$ is a commutative $\lambda$-$\mathrm {ETS}$, then $(\mathrm {Sh}^+_{\Omega }(A), \diamond ,(P_{\omega })_{\omega \in \Omega })$ is the free commutative $\Omega$-Rota–Baxter algebra generated by A.

Proof

For $\mathbf {a}, \mathbf {b} \in \mathrm {Sh}^+_{\Omega }(A)$ and $\alpha , \beta \in \Omega$,

$$\begin{aligned}&\ P_{\alpha }(\mathbf {a}) \diamond P_{\beta } (\mathbf {b})=(1_A \otimes _{\alpha } \mathbf {a}) \diamond (1_A \otimes _{\beta } \mathbf {b})\\ =&\ 1_A \otimes _{\alpha \rightarrow \beta } \big ((1 \otimes _{\alpha \rhd \beta } \mathbf {a}) \diamond \mathbf {b} \big )+ 1 \otimes _{\alpha \leftarrow \beta } \big (\mathbf {a} \diamond (1_A \otimes _{\alpha \lhd \beta } \mathbf {b}) \big )\\&\ +\lambda _{\alpha , \beta } 1_A \otimes _{\alpha \cdot \beta }(\mathbf {a} \diamond \mathbf {b})\\ =&\ P_{\alpha \rightarrow \beta } (P_{\alpha \rhd \beta }(\mathbf {a}) \diamond \mathbf {b})+ P_{\alpha \leftarrow \beta } (\mathbf {a} \diamond P_{\alpha \lhd \beta }(\mathbf {b}))+ \lambda _{\alpha , \beta } P_{\alpha \cdot \beta } (\mathbf {a} \diamond \mathbf {b}), \end{aligned}$$

hence $\mathrm {Sh}_{\Omega }(A)$ is an $\Omega$-Rota–Baxter algebra. Next we show

$$\begin{aligned} \mathbf {a} \diamond \mathbf {b}=\mathbf {b} \diamond \mathbf {a} \end{aligned}$$

(47)

by induction on $\ell (\mathbf {a})+ \ell (\mathbf {b})$. If $\ell (\mathbf {a})+ \ell (\mathbf {b})=2$, then $\ell (\mathbf {a})=\ell (\mathbf {b})=1$ and

$$\begin{aligned} \mathbf {a} \diamond \mathbf {b}=a_0 \diamond b_0=a_0b_0=b_0a_0=b_0 \diamond a_0=\mathbf {b} \diamond \mathbf {a}. \end{aligned}$$

Suppose Eq. (47) holds for $\ell (\mathbf {a})+ \ell (\mathbf {b})< p$, where $p \ge 2$ is a fixed integer. We consider the case of $\ell (\mathbf {a})+\ell (\mathbf {b})=p+1$. If one of $\ell (\mathbf {a}), \ell (\mathbf {b})$ is equal to 1, then Eq. (47) holds directly. We assume that $\mathbf {a}=a_0 \otimes _{\alpha _1} \mathbf {a}', \mathbf {b}=b_0 \otimes _{\beta _1} \mathbf {b}'$, then

$$\begin{aligned}&\mathbf {a} \diamond \mathbf {b}=(a_0 \otimes _{\alpha _1} \mathbf {a}') \diamond (b_0 \otimes _{\beta _1} \mathbf {b}')\\&\quad =\ a_0b_0 \otimes _{\alpha _1 \rightarrow \beta _1} \big ( (1_A \otimes _{\alpha _1 \rhd \beta _1} \mathbf {a}') \diamond \mathbf {b}' \big )+ a_0b_0 \otimes _{\alpha _1 \leftarrow \beta _1} \big (\mathbf {a}' \diamond (1_A \otimes _{\alpha _1 \lhd \beta _1} \mathbf {b}') \big )\\&\qquad + \lambda _{\alpha _1 , \beta _1} a_0b_0 \otimes _{\alpha _1 \cdot \beta _1} (\mathbf {a}' \diamond \mathbf {b}')\\&\quad =\ b_0a_0 \otimes _{\alpha _1 \rightarrow \beta _1} \big ( (1_A \otimes _{\alpha _1 \rhd \beta _1} \mathbf {a}') \diamond \mathbf {b}' \big )\\&\qquad + b_0a_0 \otimes _{\alpha _1 \leftarrow \beta _1} \big (\mathbf {a}' \diamond (1_A \otimes _{\alpha _1 \lhd \beta _1} \mathbf {b}') \big )+ \lambda _{\alpha _1 , \beta _1} b_0a_0 \otimes _{\alpha _1 \cdot \beta _1} (\mathbf {a}' \diamond \mathbf {b}')\\&\ \text {(by} A \text {being a commutative algebra)}\\&\quad =\ b_0a_0 \otimes _{\alpha _1 \rightarrow \beta _1} \big ( \mathbf {b}' \diamond (1_A \otimes _{\alpha _1 \rhd \beta _1} \mathbf {a}') \big )\\&\qquad + b_0a_0 \otimes _{\alpha _1 \leftarrow \beta _1} \big ((1_A \otimes _{\alpha _1 \lhd \beta _1} \mathbf {b}')\diamond \mathbf {a}' \big )+ \lambda _{\alpha _1 , \beta _1} b_0a_0 \otimes _{\alpha _1 \cdot \beta _1} ( \mathbf {b}' \diamond \mathbf {a}')\\&\ \text {(by the induction hypothesis)}\\&\quad =\ b_0a_0 \otimes _{\beta _1 \leftarrow \alpha _1} \big ( \mathbf {b}' \diamond (1_A \otimes _{\beta _1 \lhd \alpha _1} \mathbf {a}') \big )\\&\qquad + b_0a_0 \otimes _{\beta _1 \rightarrow \alpha _1} \big ((1_A \otimes _{\beta _1 \rhd \alpha _1} \mathbf {b}')\diamond \mathbf {a}' \big )+ \lambda _{\beta _1 , \alpha _1} b_0a_0 \otimes _{\beta _1 \cdot \alpha _1} ( \mathbf {b}' \diamond \mathbf {a}')\\&\ \text {(by} \Omega \text {being commutative)}\\&\quad =\ (b_0 \otimes _{\beta _1} \mathbf {b}') \diamond (a_0 \otimes _{\alpha _1} \mathbf {a}')=\mathbf {b} \otimes \mathbf {a}. \end{aligned}$$

Hence $(\mathrm {Sh}^+_{\Omega }(A), \diamond )$ is a commutative algebra.

Let $(R,\cdot ,(P_{\omega })_{\omega \in \Omega })$ be a commutative $\Omega$-Rota–Baxter algebra and $f : A \rightarrow R$ a commutative algebra homomorphism. We extend f to an $\Omega$-Rota–Baxter algebra morphism $\overline{f}: \mathrm {Sh}^+_{\Omega }(A) \rightarrow R$ as follows: for $\mathbf {a} \in \mathrm {Sh}^+_{\Omega }(A)$, we define $\overline{f}(a)$ by induction on $\ell (\mathbf {a})$. If $\ell (\mathbf {a})=1$, then define $\overline{f}(\mathbf {a})=f(\mathbf {a})$. Suppose $\overline{f}(\mathbf {a})$ has been defined for all $\mathbf {a}$ with $\ell (\mathbf {a}) \le p$, where $p \ge 1$ is a fixed integer. Consider the case of $\ell (\mathbf {a})=p+1$. We suppose that $\mathbf {a}=a_0 \otimes _{\alpha _1} \mathbf {a}'$, and we then put:

$$\begin{aligned} \overline{f}(\mathbf {a}) {:}{=} f(a_0) \cdot P_{\alpha _1}(\overline{f}(\mathbf {a}')). \end{aligned}$$

We can get that it is the unique way to extend f as an $\Omega$-Rota–Baxter algebra morphism. Hence $(\mathrm {Sh}^+_{\Omega }(A), \diamond )$ is the free commutative $\Omega$-Rota–Baxter algebra generated by A. $\square$

Let us assume that A is unitary. We denote its unit by $1_A$. For each $\omega \in \Omega$, define a linear map $P_{\omega }: \mathrm {Sh}_{\Omega }(A) \rightarrow \mathrm {Sh}_{\Omega }(A), \mathbf {a} \mapsto 1_A \otimes _{\omega } \mathbf {a}$.

Proposition 2.19

If A is a unitary commutative algebra and $(\Omega , \leftarrow , \rightarrow , \lhd , \rhd , \cdot ,\lambda )$ is a commutative $\lambda$-$\mathrm {ETS}$, then $(\mathrm {Sh}_{\Omega }(A), \diamond ,(P_{\omega })_{\omega \in \Omega })$ is a commutative $\Omega$-Rota–Baxter algebra.

Proof

For $\mathbf {a}, \mathbf {b} \in \mathrm {Sh}_{\Omega }(A)$ and $\alpha , \beta \in \Omega$,

$$\begin{aligned}&\ P_{\alpha }(\mathbf {a}) \diamond P_{\beta } (\mathbf {b})=(1_A \otimes _{\alpha } \mathbf {a}) \diamond (1_A \otimes _{\beta } \mathbf {b})\\ =&\ 1_A \otimes _{\alpha \rightarrow \beta } \big ((1_A \otimes _{\alpha \rhd \beta } \mathbf {a}) \diamond \mathbf {b} \big )+ 1_A \otimes _{\alpha \leftarrow \beta } \big (\mathbf {a} \diamond (1_A \otimes _{\alpha \lhd \beta } \mathbf {b}) \big )\\&\ +\lambda _{\alpha , \beta } 1_A \otimes _{\alpha \cdot \beta }(\mathbf {a} \diamond \mathbf {b})\\ =&\ P_{\alpha \rightarrow \beta } (P_{\alpha \rhd \beta }(\mathbf {a}) \diamond \mathbf {b})+ P_{\alpha \leftarrow \beta } (\mathbf {a} \diamond P_{\alpha \lhd \beta }(\mathbf {b}))+ \lambda _{\alpha , \beta } P_{\alpha \cdot \beta } (\mathbf {a} \diamond \mathbf {b}), \end{aligned}$$

hence $\mathrm {Sh}_{\Omega }(A)$ is an $\Omega$-Rota–Baxter algebra. Next we show

$$\begin{aligned} \mathbf {a} \diamond \mathbf {b}=\mathbf {b} \diamond \mathbf {a} \end{aligned}$$

(48)

by induction on $\ell (\mathbf {a})+ \ell (\mathbf {b})$. If $\ell (\mathbf {a})+ \ell (\mathbf {b})=2$, then $\ell (\mathbf {a})=\ell (\mathbf {b})=1$ and

$$\begin{aligned} \mathbf {a} \diamond \mathbf {b}=a_0 \diamond b_0=a_0b_0=b_0a_0=b_0 \diamond a_0=\mathbf {b} \diamond \mathbf {a}. \end{aligned}$$

Suppose Eq. (48) holds for $\ell (\mathbf {a})+ \ell (\mathbf {b})< p$, where $p \ge 2$ is a fixed integer. We consider the case of $\ell (\mathbf {a})+\ell (\mathbf {b})=p+1$. If one of $\ell (\mathbf {a}), \ell (\mathbf {b})$ is equal to 1, then Eq. (48) holds directly. So assume $\mathbf {a}=a_0 \otimes _{\alpha _1} \mathbf {a}', \mathbf {b}=b_0 \otimes _{\beta _1} \mathbf {b}'$, then

$$\begin{aligned}&\ \mathbf {a} \diamond \mathbf {b}=(a_0 \otimes _{\alpha _1} \mathbf {a}') \diamond (b_0 \otimes _{\beta _1} \mathbf {b}')\\ =&\ a_0b_0 \otimes _{\alpha _1 \rightarrow \beta _1} \big ( (1_A \otimes _{\alpha _1 \rhd \beta _1} \mathbf {a}') \diamond \mathbf {b}' \big )\\&+ a_0b_0 \otimes _{\alpha _1 \leftarrow \beta _1} \big (\mathbf {a}' \diamond (1_A \otimes _{\alpha _1 \lhd \beta _1} \mathbf {b}') \big )+ \lambda _{\alpha _1 , \beta _1} a_0b_0 \otimes _{\alpha _1 \cdot \beta _1} (\mathbf {a}' \diamond \mathbf {b}')\\ =&\ b_0a_0 \otimes _{\alpha _1 \rightarrow \beta _1} \big ( (1_A \otimes _{\alpha _1 \rhd \beta _1} \mathbf {a}') \diamond \mathbf {b}' \big )\\&+ b_0a_0 \otimes _{\alpha _1 \leftarrow \beta _1} \big (\mathbf {a}' \diamond (1_A \otimes _{\alpha _1 \lhd \beta _1} \mathbf {b}') \big )+ \lambda _{\alpha _1 , \beta _1} b_0a_0 \otimes _{\alpha _1 \cdot \beta _1} (\mathbf {a}' \diamond \mathbf {b}')\\&\ \text {(by} A \text {being a commutative algebra)}\\ =&\ b_0a_0 \otimes _{\alpha _1 \rightarrow \beta _1} \big ( \mathbf {b}' \diamond (1_A \otimes _{\alpha _1 \rhd \beta _1} \mathbf {a}') \big )\\&+ b_0a_0 \otimes _{\alpha _1 \leftarrow \beta _1} \big ((1_A \otimes _{\alpha _1 \lhd \beta _1} \mathbf {b}')\diamond \mathbf {a}' \big )+ \lambda _{\alpha _1 , \beta _1} b_0a_0 \otimes _{\alpha _1 \cdot \beta _1} ( \mathbf {b}' \diamond \mathbf {a}')\\&\ \text {(by the induction hypothesis)}\\ =&\ b_0a_0 \otimes _{\beta _1 \leftarrow \alpha _1} \big ( \mathbf {b}' \diamond (1_A \otimes _{\beta _1 \lhd \alpha _1} \mathbf {a}') \big )\\&+ b_0a_0 \otimes _{\beta _1 \rightarrow \alpha _1} \big ((1_A \otimes _{\beta _1 \rhd \alpha _1} \mathbf {b}')\diamond \mathbf {a}' \big )+ \lambda _{\beta _1 , \alpha _1} b_0a_0 \otimes _{\beta _1 \cdot \alpha _1} ( \mathbf {b}' \diamond \mathbf {a}')\\&\ \text {(by} \Omega \text {being commutative)}\\ =&\ (b_0 \otimes _{\beta _1} \mathbf {b}') \diamond (a_0 \otimes _{\alpha _1} \mathbf {a}')=\mathbf {b} \otimes \mathbf {a}. \end{aligned}$$

Hence $(\mathrm {Sh}_{\Omega }(A), \diamond )$ is a commutative algebra. $\square$

Let A be a commutative algebra. We put $uA=\mathbf {k}\oplus A$ and give it a product defined by

$$\begin{aligned}(\lambda +a)(\mu +b)=\lambda \mu +(\lambda b+\mu a+ab).\end{aligned}$$

Then uA is a commutative unitary algebra and its unit $1_A$ is the unit 1 of $\mathbf {k}$.

Theorem 2.20

We put

$$\begin{aligned}\mathrm {Sh}_{\Omega }'(A)=A\oplus \bigoplus _{n \ge 2} \underbrace{uA\otimes (\mathbf{k}\Omega ) \otimes \cdots \otimes (\mathbf{k}\Omega ) \otimes uA}_{n's V \text {and} (n-1)'s (\mathbf{k}\Omega )}.\end{aligned}$$

Then $\mathrm {Sh}_{\Omega }'(A)$ is the free commutative $\Omega$-Rota–Baxter algebra generated by the algebra A.

Proof

Let $(R,\cdot ,(P_{\omega })_{\omega \in \Omega })$ be a commutative $\Omega$-Rota–Baxter algebra and $f : A \rightarrow R$ a (nonunitary) algebra homomorphism. We extend f, first from uA to R as a unitary algebra morphism by sending $1_{uA}$ to $1_R$, then as an $\Omega$-Rota–Baxter algebra morphism $\overline{f}: \mathrm {Sh}_{\Omega }'(A) \rightarrow R$ as follows: for $\mathbf {a} \in \mathrm {Sh}_{\Omega }(A)$, we define $\overline{f}(a)$ by induction on $\ell (\mathbf {a})$. If $\ell (\mathbf {a})=1$, then define $\overline{f}(\mathbf {a})=f(\mathbf {a})$. Suppose $\overline{f}(\mathbf {a})$ has been defined for all $\mathbf {a}$ with $\ell (\mathbf {a}) \le p$, where $p \ge 1$ is a fixed integer. Consider the case of $\ell (\mathbf {a})=p+1$. Suppose $\mathbf {a}=a_0 \otimes _{\alpha _1} \mathbf {a}'$, then define

$$\begin{aligned} \overline{f}(\mathbf {a}) {:}{=} f(a_0) \cdot P_{\alpha _1}(\overline{f}(\mathbf {a}')). \end{aligned}$$

For any $\mathbf {a}\in \mathrm {Sh}_{\Omega }'(A)$ and for any $\alpha \in \Omega$:

$$\begin{aligned}\overline{f}\circ P_\alpha (\mathbf {a}) =\overline{f}(1_A\otimes _\alpha \mathbf {a}) =1_B\cdot P_\alpha (\overline{f}(\mathbf {a}))=P_\alpha \circ \overline{f}(\mathbf {a}).\end{aligned}$$

Let us prove that this is an algebra morphism. Let $\mathbf {a},\mathbf {b}\in \mathrm {Sh}_{\Omega }'(A)$, let us prove that $\overline{f}(\mathbf {a}\diamond \mathbf {b})=\overline{f}(\mathbf {a})\overline{f}(\mathbf {b})$ by induction on $n=\ell (\mathbf {a})+\ell (\mathbf {b})$. If $\ell (\mathbf {a})=\ell (\mathbf {b})=1$, then

$$\begin{aligned}\overline{f}(\mathbf {a}\diamond \mathbf {b})=\overline{f}(a_0b_0)=f(a_0b_0) =f(a_0)\cdot f(b_0)=\overline{f}(\mathbf {a})\cdot \overline{f}(\mathbf {b}).\end{aligned}$$

If $\ell (\overline{a})=1$ and $\ell (\overline{b})>1$, then

$$\begin{aligned} \overline{f}(\mathbf {a}\diamond \mathbf {b})&=\overline{f}(a_0b_0\otimes _{\alpha _1}\mathbf {a}')\\&=f(a_0b_0)\cdot P_{\alpha _1}\circ \overline{f}(\mathbf {a}')\\&=f(a_0)\cdot f(b_0)\cdot P_{\alpha _1}\circ \overline{f}(\mathbf {a}')\\&=\overline{f}(\mathbf {a})\cdot \overline{f}(\mathbf {b}). \end{aligned}$$

This is similar if $\ell (\overline{a})>1$ and $\ell (\overline{b})=1$. If $\ell (\overline{a})>1$ and $\ell (\overline{b})>1$, then

$$\begin{aligned} \overline{f}(\mathbf {a}\diamond \mathbf {b})&= \overline{f}(\ a_0b_0 \otimes _{\alpha _1 \rightarrow \beta _1} ((1 \otimes _{\alpha _1 \rhd \beta _1} \mathbf {a}') \diamond \mathbf {b}' )) +\overline{f}(a_0b_0 \otimes _{\alpha \leftarrow \beta _1} (\mathbf {a}' \diamond (1 \otimes _{\alpha _1 \lhd \beta _1} \mathbf {b}') )) \\&\quad +\overline{f}(\lambda _{\alpha _1 , \beta _1} a_0b_0 \otimes _{\alpha _1 \cdot \beta _1}(\mathbf {a}' \diamond \mathbf {b}'))\\&=f(\ a_0b_0)\cdot P_{\alpha _1 \rightarrow \beta _1}\circ \overline{f}((1 \otimes _{\alpha _1 \rhd \beta _1} \mathbf {a}') \diamond \mathbf {b}' )\\&\quad +f(a_0b_0)\cdot P_{\alpha \leftarrow \beta _1}\circ \overline{f}(\mathbf {a}' \diamond (1 \otimes _{\alpha _1 \lhd \beta _1} \mathbf {b}') )) \\&\quad +\lambda _{\alpha _1 , \beta _1} f(a_0b_0)\cdot P_{\alpha _1 \cdot \beta _1}\circ \overline{f}(\mathbf {a}' \diamond \mathbf {b}')\\&=f(a_0)\cdot f(b_0)\cdot \overline{f}( P_{\alpha _1 \rightarrow \beta _1}(P_{\alpha _1 \rhd \beta _1}( \mathbf {a}')\diamond \mathbf {b}' )) \\&+f(a_0)\cdot f(b_0)\cdot \overline{f}( P_{\alpha \leftarrow \beta _1}(\mathbf {a}' \diamond P_{\alpha _1 \lhd \beta _1}(\mathbf {b}')))\\&\quad +\lambda _{\alpha _1 , \beta _1}f(a_0)\cdot f(b_0)\cdot \overline{f}(P_{\alpha _1 \cdot \beta _1} (\mathbf {a}' \diamond \mathbf {b}'))\\&=f(a_0)\cdot f(b_0)\cdot \overline{f}(P_{\alpha _1}(\mathbf {a}')P_{\beta _1}(\mathbf {b}'))\\&=f(a_0)\cdot f(b_0)\cdot \overline{f}(P_{\alpha _1}(\mathbf {a}'))\cdot \overline{f}(P_{\beta _1}(\mathbf {b}')) \text {(by the induction hypothesis)}\\&=f(a_0)\cdot f(b_0)\cdot P_{\alpha _1}\circ \overline{f}(\mathbf {a}')\cdot P_{\beta _1}\circ \overline{f}(\mathbf {b}')\\&=f(a_0)\cdot P_{\alpha _1}\circ \overline{f}(\mathbf {a}')\cdot f(b_0)\cdot P_{\beta _1}\circ \overline{f}(\mathbf {b}') \text {(as} B \text {is commutative)}\\&=\overline{f}(\mathbf {a})\cdot \overline{f}(\mathbf {b}). \end{aligned}$$

We get that it is the unique way to extend f as an $\Omega$-Rota–Baxter algebra morphism. Hence $\mathrm {Sh}_{\Omega }'(A)$ is the free commutative $\Omega$-Rota–Baxter algebra generated by A. $\square$

3 More results on $\lambda$-$\mathrm {ETS}$ and $\mathrm {ETS}$

3.1 Description in terms of linear and bilinear maps

As in Lemma 5 of [5], we obtain:

Lemma 3.1

Let $(\Omega ,\leftarrow ,\rightarrow ,\lhd ,\rhd ,\cdot )$ be a set with five operations and $\lambda =(\lambda _{\alpha ,\beta })_{\alpha ,\beta \in \Omega }$ be a family of elements in $\mathbf{k}$ indexed by $\Omega ^2$ . We denote by $\mathbf {k}\Omega$ the vector space generated by $\Omega$. We put:

$$\begin{aligned} \varphi _\leftarrow&:\left\{ \begin{array}{rcl} \mathbf {k}\Omega ^{\otimes 2}&{}\longrightarrow &{}\mathbf {k}\Omega ^{\otimes 2}\\ \alpha \otimes \beta &{}\longrightarrow &{}\alpha \leftarrow \beta \otimes \alpha \lhd \beta , \end{array}\right. \\ \varphi _\rightarrow&:\left\{ \begin{array}{rcl} \mathbf {k}\Omega ^{\otimes 2}&{}\longrightarrow &{}\mathbf {k}\Omega ^{\otimes 2}\\ \alpha \otimes \beta &{}\longrightarrow &{}\alpha \rightarrow \beta \otimes \alpha \rhd \beta , \end{array}\right. \\ \psi _\cdot&:\left\{ \begin{array}{rcl} \mathbf {k}\Omega ^{\otimes 2}&{}\longrightarrow &{}\mathbf {k}\Omega \\ \alpha \otimes \beta &{}\longrightarrow &{}\lambda _{\alpha , \beta } \alpha \cdot \beta . \end{array}\right. \end{aligned}$$

Then $(\Omega ,\leftarrow ,\rightarrow ,\lhd ,\rhd ,\cdot ,\lambda )$ is a $\lambda$-$\mathrm {ETS}$ if, and only if:

$$\begin{aligned}&(\tau \otimes \mathrm {id})\circ (\mathrm {id}\otimes \varphi _\leftarrow )\circ (\tau \otimes \mathrm {id})\circ (\varphi _\rightarrow \otimes \mathrm {id}) = (\varphi _\rightarrow \otimes \mathrm {id})\circ (\mathrm {id}\otimes \varphi _\leftarrow ), \end{aligned}$$

(49)

$$\begin{aligned}&(\mathrm {id}\otimes \varphi _\leftarrow )\circ (\tau \otimes \mathrm {id})\circ (\mathrm {id}\otimes \varphi _\leftarrow )\otimes (\tau \otimes \mathrm {id})\circ (\varphi _\leftarrow \otimes \mathrm {id})=(\varphi _\leftarrow \otimes \mathrm {id})\circ (\mathrm {id}\otimes \varphi _\leftarrow ), \end{aligned}$$

(50)

$$\begin{aligned}&(\mathrm {id}\otimes \varphi _\rightarrow )\circ (\tau \otimes \mathrm {id})\circ (\mathrm {id}\otimes \varphi _\leftarrow ) \circ (\tau \otimes \mathrm {id})\circ (\varphi _\leftarrow \otimes \mathrm {id})=(\varphi _\leftarrow \otimes \mathrm {id})\circ (\mathrm {id}\otimes \varphi _\rightarrow ), \end{aligned}$$

(51)

$$\begin{aligned}&(\mathrm {id}\otimes \varphi _\leftarrow )\circ (\varphi _\rightarrow \otimes \mathrm {id})\circ (\mathrm {id}\otimes \varphi _\rightarrow ) =(\varphi _\rightarrow \otimes \mathrm {id})\circ (\mathrm {id}\otimes \tau )\circ (\varphi _\leftarrow \otimes \mathrm {id}), \end{aligned}$$

(52)

$$\begin{aligned}&(\mathrm {id}\otimes \varphi _\rightarrow )\circ (\varphi _\rightarrow \otimes \mathrm {id})\circ (\mathrm {id}\otimes \varphi _\rightarrow ) =(\varphi _\rightarrow \otimes \mathrm {id})\circ (\mathrm {id}\otimes \tau )\circ (\varphi _\rightarrow \otimes \mathrm {id}), \end{aligned}$$

(53)

$$\begin{aligned}&\varphi _\rightarrow \circ (\mathrm {id}\otimes \psi _\cdot ) =(\psi _\cdot \otimes \mathrm {id})\circ (\mathrm {id}\otimes \tau )\circ (\varphi _\rightarrow \otimes \mathrm {id}), \end{aligned}$$

(54)

$$\begin{aligned}&(\psi _\cdot \otimes \mathrm {id})\circ (\mathrm {id}\otimes \tau )\circ (\mathrm {id}\otimes \varphi _\leftarrow )\circ (\tau \otimes \mathrm {id}) \circ (\varphi _\leftarrow \otimes \mathrm {id})=\tau \circ \varphi _\leftarrow \circ (\mathrm {id}\otimes \psi _\cdot ), \end{aligned}$$

(55)

$$\begin{aligned}&(\mathrm {id}\otimes \psi _\cdot )\circ (\varphi _\rightarrow \otimes \mathrm {id})\circ (\mathrm {id}\otimes \varphi _\rightarrow ) =\varphi _\rightarrow \circ (\psi _\cdot \otimes \mathrm {id}), \end{aligned}$$

(56)

$$\begin{aligned}&(\psi _\cdot \otimes \mathrm {id})\circ (\mathrm {id}\otimes \tau )\circ (\varphi _\leftarrow \otimes \mathrm {id})=(\psi _\cdot \otimes \mathrm {id}) \circ (\mathrm {id}\otimes \varphi _\rightarrow ), \end{aligned}$$

(57)

$$\begin{aligned}&(\psi _\cdot \otimes \mathrm {id})\circ (\mathrm {id}\otimes \varphi _\leftarrow )=\varphi _\leftarrow \circ (\psi _\cdot \otimes \mathrm {id}), \end{aligned}$$

(58)

$$\begin{aligned}&\psi _\cdot \circ (\psi _\cdot \otimes \mathrm {id})=\psi _\cdot \circ (\mathrm {id}\otimes \psi _\cdot ). \end{aligned}$$

(59)

In particular, $\psi _\cdot$ is an associative product.

Proof

By Lemma 5 in [5], Eqs. (49)-(53) are equivalent to $(\Omega , \leftarrow , \rightarrow , \lhd ,\rhd )$ being an EDS. Moreover, direct computations prove that Eq. (54) is equivalent to Eq. (11) and condition (a); Eq. (55) is equivalent to Eq. (12) and condition (b); Eq. (56) is equivalent to Eq. (13) and condition (c); Eq. (57) is equivalent to Eq. (14) and condition (d); Eq. (58) is equivalent to Eq. (15) and condition (e); Eq. (59) is equivalent to Eq. (16) and condition (f) in Definition 2.3. $\square$

Similarly, we obtain for $\mathrm {ETS}$:

Lemma 3.2

Let $(\Omega ,\leftarrow ,\rightarrow ,\lhd ,\rhd ,*,\cdot )$ be a set with six operations. We put:

$$\begin{aligned} \varphi _\leftarrow&:\left\{ \begin{array}{rcl} \Omega ^{ 2}&{}\longrightarrow &{} \Omega ^{ 2}\\ (\alpha , \beta ) &{}\longrightarrow &{} (\alpha \leftarrow \beta , \alpha \lhd \beta ), \end{array}\right. \\ \varphi _\rightarrow&:\left\{ \begin{array}{rcl} \Omega ^{2}&{}\longrightarrow &{} \Omega ^{2}\\ (\alpha , \beta )&{}\longrightarrow &{} ( \alpha \rightarrow \beta , \alpha \rhd \beta ), \end{array}\right. \\ \varphi _*&:\left\{ \begin{array}{rcl} \Omega ^{ 2}&{}\longrightarrow &{} \Omega ^{ 2}\\ (\alpha , \beta ) &{}\longrightarrow &{} (\alpha \cdot \beta , \alpha *\beta ). \end{array}\right. \end{aligned}$$

Then $(\Omega ,\leftarrow ,\rightarrow ,\lhd ,\rhd ,*,\cdot )$ is an $\mathrm {ETS}$ if, and only if, (34)-(38) of [5] are satisfied and:

$$\begin{aligned} (\varphi _\rightarrow \otimes \mathrm {id})\circ (\mathrm {id}\otimes \varphi _*)= (\tau \otimes \mathrm {id})\circ (\mathrm {id}\otimes \varphi _*)\circ (\tau \otimes \mathrm {id})\circ (\varphi _\rightarrow \otimes \mathrm {id}), \end{aligned}$$

(60)

$$\begin{aligned} (\varphi _\leftarrow \otimes \mathrm {id})\circ (\mathrm {id}\otimes \varphi _*)=(\mathrm {id}\otimes \varphi _*)\circ (\tau \otimes \mathrm {id})\circ (\mathrm {id}\otimes \varphi _\leftarrow )\circ (\tau \otimes \mathrm {id}) \circ (\varphi _\leftarrow \otimes \mathrm {id}), \end{aligned}$$

(61)

$$\begin{aligned} (\mathrm {id}\otimes \varphi _*)\circ (\varphi _\rightarrow \otimes \mathrm {id})\circ (\mathrm {id}\otimes \varphi _\rightarrow ) =(\varphi _\rightarrow \otimes \mathrm {id})\circ (\mathrm {id}\otimes \tau )\circ (\mathrm {id}\otimes \varphi _*), \end{aligned}$$

(62)

$$\begin{aligned} (\mathrm {id}\otimes \varphi _*)\circ (\tau \otimes \mathrm {id})\circ (\varphi _\leftarrow \otimes \mathrm {id}) =(\mathrm {id}\otimes \varphi _*)\circ (\tau \otimes \mathrm {id})\circ (\mathrm {id}\otimes \tau )\circ (\mathrm {id}\otimes \varphi _\rightarrow ), \end{aligned}$$

(63)

$$\begin{aligned} (\varphi _*\otimes \mathrm {id})\circ (\mathrm {id}\otimes \varphi _\leftarrow )=(\tau \otimes \mathrm {id})\circ (\mathrm {id}\otimes \varphi _\leftarrow )\circ (\tau \otimes \mathrm {id})\circ (\varphi _*\otimes \mathrm {id}), \end{aligned}$$

(64)

$$\begin{aligned} (\varphi _*\otimes \mathrm {id})\circ (\mathrm {id}\otimes \tau )\circ (\varphi _*\otimes \mathrm {id}) =(\mathrm {id}\otimes \tau )\circ (\varphi _*\otimes \mathrm {id})\circ (\mathrm {id}\otimes \varphi _*). \end{aligned}$$

(65)

Proof

By Lemma 5 in [5], Eqs. (34)-(38) are equivalent to $(\Omega , \leftarrow , \rightarrow , \lhd ,\rhd )$ being an EDS. Moreover, direct computations prove that Eq. (60) is equivalent to Eqs. (17),(18) and (28); Eq. (61) is equivalent to Eqs. (19), (20) and (29); Eq. (62) is equivalent to Eqs. (21), (22) and (30); Eq. (63) is equivalent to Eqs. (23), (24) and (31); Eq. (64) is equivalent to Eqs. (25), (26) and (32); Eq. (65) is equivalent to Eqs. (27), (33) and (34). $\square$

3.2 A description of all $\lambda$-$\mathrm {ETS}$ of cardinality two

The following table gives all $\lambda$-$\mathrm {ETS}$. We slightly generalize our definition, by accepting more general maps $\varphi _\cdot :\mathbf {k}\Omega ^{\otimes 2}\longrightarrow \mathbf {k}\Omega$. The underlying set is $\{a,b\}$ and all the products are given by a $2\times 2$ table. Here, $\lambda ,\mu$ are elements of the base field $\mathbf {k}$.

Type	$\leftarrow$	$\rightarrow$	$\triangleleft$	$\triangleright$	$\varphi _{*}$	Name
A	$\begin{pmatrix} a&{}a\\ a&{}a \end{pmatrix}$	$\begin{pmatrix} a&{}a\\ a&{}a \end{pmatrix}$	$\begin{pmatrix} a&{}a\\ a&{}a \end{pmatrix}$	$\begin{pmatrix} a&{}a\\ a&{}a \end{pmatrix}$	$\begin{pmatrix} (\lambda +\mu )a&{}(\lambda +\mu )a\\ (\lambda +\mu )a&{}\lambda a+\mu b \end{pmatrix}$	$A_1(\lambda ,\mu )$
			$\begin{pmatrix} a&{}b\\ a&{}b \end{pmatrix}$	$\begin{pmatrix} a&{}a\\ b&{}b \end{pmatrix}$	$\begin{pmatrix} (\lambda +\mu )a&{}(\lambda +\mu )a\\ (\lambda +\mu )a&{}\lambda a+\mu b \end{pmatrix}$	$A_2(\lambda ,\mu )$
B	$\begin{pmatrix} a&{}a\\ a&{}a \end{pmatrix}$	$\begin{pmatrix} a&{}b\\ a&{}b \end{pmatrix}$	$\begin{pmatrix} a&{}a\\ a&{}a \end{pmatrix}$	$\begin{pmatrix} a&{}a\\ a&{}a \end{pmatrix}$	$\begin{pmatrix} \lambda a&{}\lambda a\\ \lambda a&{}\lambda a \end{pmatrix}$,  $\begin{pmatrix} \lambda a&{}\lambda b\\ \lambda a&{}\lambda b \end{pmatrix}$	$B_1'(\lambda ),\,B_1''(\lambda )$
			$\begin{pmatrix} a&{}b\\ a&{}b \end{pmatrix}$	$\begin{pmatrix} a&{}a\\ b&{}b \end{pmatrix}$		$B_2'(\lambda ),\,B_2''(\lambda )$
C	$\begin{pmatrix} a&{}a\\ a&{}b \end{pmatrix}$	$\begin{pmatrix} a&{}a\\ a&{}b \end{pmatrix}$	$\begin{pmatrix} a&{}a\\ a&{}a \end{pmatrix}$	$\begin{pmatrix} a&{}a\\ a&{}a \end{pmatrix}$	$\begin{pmatrix} \lambda a&{}\lambda a\\ \lambda a&{}\lambda b \end{pmatrix}$	$C_1(\lambda )$
			$\begin{pmatrix} a&{}b\\ a&{}b \end{pmatrix}$	$\begin{pmatrix} a&{}a\\ b&{}b \end{pmatrix}$		$C_3(\lambda )$
			$\begin{pmatrix} b&{}b\\ b&{}b \end{pmatrix}$	$\begin{pmatrix} b&{}b\\ b&{}b \end{pmatrix}$		$C_5(\lambda )$
			$\begin{pmatrix} a&{}a\\ a&{}a \end{pmatrix}$	$\begin{pmatrix} b&{}b\\ b&{}b \end{pmatrix}$	$\begin{pmatrix} 0&{}0\\ 0&{}0 \end{pmatrix}$	$C_2$
			$\begin{pmatrix} b&{}b\\ b&{}b \end{pmatrix}$	$\begin{pmatrix} a&{}a\\ a&{}a \end{pmatrix}$		$C_4$

Type	$\leftarrow$	$\rightarrow$	$\triangleleft$	$\triangleright$	$\varphi _{*}$	Name
D	$\begin{pmatrix} a&{}a\\ b&{}b \end{pmatrix}$	$\begin{pmatrix} a&{}a\\ a&{}a \end{pmatrix}$	$\begin{pmatrix} a&{}a\\ a&{}a \end{pmatrix}$	$\begin{pmatrix} a&{}a\\ a&{}a \end{pmatrix}$	$\begin{pmatrix} \lambda a&{}\lambda a\\ \lambda a&{}\lambda a \end{pmatrix}$,  $\begin{pmatrix} \lambda a&{}\lambda a\\ \lambda b&{}\lambda b \end{pmatrix}$	$D_1'(\lambda ),\,D_1''(\lambda )$
			$\begin{pmatrix} a&{}b\\ a&{}b \end{pmatrix}$	$\begin{pmatrix} a&{}a\\ b&{}b \end{pmatrix}$		$D_2'(\lambda ),\,D_2''(\lambda )$
E	$\begin{pmatrix} a&{}a\\ b&{}b \end{pmatrix}$	$\begin{pmatrix} a&{}a\\ b&{}b \end{pmatrix}$	$\begin{pmatrix} a&{}a\\ a&{}a \end{pmatrix}$	$\begin{pmatrix} a&{}a\\ a&{}a \end{pmatrix}$	$\begin{pmatrix} \lambda a&{}\lambda a\\ \lambda b&{}\lambda b \end{pmatrix}$	$E_1(\lambda )$
			$\begin{pmatrix} a&{}b\\ a&{}b \end{pmatrix}$	$\begin{pmatrix} a&{}a\\ b&{}b \end{pmatrix}$		$E_3(\lambda )$
			$\begin{pmatrix} a&{}a\\ a&{}a \end{pmatrix}$	$\begin{pmatrix} b&{}b\\ b&{}b \end{pmatrix}$	$\begin{pmatrix} 0&{}0\\ 0&{}0 \end{pmatrix}$	$E_2$
F	$\begin{pmatrix} a&{}a\\ b&{}b \end{pmatrix}$	$\begin{pmatrix} a&{}b\\ a&{}b \end{pmatrix}$	$\begin{pmatrix} a&{}a\\ a&{}a \end{pmatrix}$	$\begin{pmatrix} a&{}a\\ a&{}a \end{pmatrix}$	$\begin{pmatrix} (\lambda +\mu ) a&{}(\lambda +\mu )a\\ (\lambda +\mu )a&{}\lambda a+\mu b \end{pmatrix}$,  $\begin{pmatrix} (\lambda +\mu )a&{}(\lambda +\mu )b\\ (\lambda +\mu )b&{}\lambda a+\mu b \end{pmatrix}$,	$F'_1(\lambda ,\mu ),\,F_1''(\lambda ,\mu )$
					$\begin{pmatrix} \lambda a&{}\lambda b\\ \lambda a&{}\lambda b \end{pmatrix}$,  $\begin{pmatrix} \lambda a&{}\lambda a\\ \lambda b&{}\lambda b \end{pmatrix}$	$F_1'(\lambda ),\,F_1''(\lambda )$
			$\begin{pmatrix} a&{}b\\ a&{}b \end{pmatrix}$	$\begin{pmatrix} a&{}a\\ b&{}b \end{pmatrix}$	any associative product $*$	$F_3(*)$
			$\begin{pmatrix} a&{}b\\ b&{}a \end{pmatrix}$	$\begin{pmatrix} a&{}b\\ b&{}a \end{pmatrix}$	$\begin{pmatrix} \lambda a&{}0\\ 0&{}\lambda b \end{pmatrix}$	$F_4(\lambda )$
			$\begin{pmatrix} a&{}a\\ a&{}a \end{pmatrix}$	$\begin{pmatrix} b&{}b\\ b&{}b \end{pmatrix}$	$\begin{pmatrix} 0&{}0\\ 0&{}0 \end{pmatrix}$	$F_2$
			$\begin{pmatrix} a&{}b\\ b&{}a \end{pmatrix}$	$\begin{pmatrix} b&{}a\\ a&{}b \end{pmatrix}$		$F_5$
G	$\begin{pmatrix} a&{}b\\ a&{}b \end{pmatrix}$	$\begin{pmatrix} a&{}b\\ a&{}b \end{pmatrix}$	$\begin{pmatrix} a&{}a\\ a&{}a \end{pmatrix}$	$\begin{pmatrix} a&{}a\\ a&{}a \end{pmatrix}$	$\begin{pmatrix} \lambda a&{}\lambda b\\ \lambda a&{}\lambda b \end{pmatrix}$	$G_1(\lambda )$
			$\begin{pmatrix} a&{}b\\ a&{}b \end{pmatrix}$	$\begin{pmatrix} a&{}a\\ b&{}b \end{pmatrix}$		$G_3(\lambda )$
			$\begin{pmatrix} a&{}a\\ a&{}a \end{pmatrix}$	$\begin{pmatrix} b&{}b\\ b&{}b \end{pmatrix}$	$\begin{pmatrix} 0&{}0\\ 0&{}0 \end{pmatrix}$	$G_2$
H	$\begin{pmatrix} a&{}b\\ b&{}a \end{pmatrix}$	$\begin{pmatrix} a&{}b\\ b&{}a \end{pmatrix}$	$\begin{pmatrix} a&{}a\\ a&{}a \end{pmatrix}$	$\begin{pmatrix} a&{}a\\ a&{}a \end{pmatrix}$	$\begin{pmatrix} \lambda a&{}\lambda b\\ \lambda b&{}\lambda a \end{pmatrix}$	$H_1(\lambda )$
			$\begin{pmatrix} a&{}b\\ a&{}b \end{pmatrix}$	$\begin{pmatrix} a&{}a\\ b&{}b \end{pmatrix}$		$H_2(\lambda )$

The commutative $\lambda$-$\mathrm {ETS}$ are the ones of type A and H, $C_1(\lambda )$, $C_3(\lambda )$, $C_5(\lambda )$, $F'_1(\lambda ,\mu )$, $F_1''(\lambda ,\mu )$ and $F_4(\lambda )$. The opposite of $B_1'(\lambda )$, $B_1''(\lambda )$, $B_2'(\lambda )$ and $B_2''(\lambda )$ are respectively $D_1'(\lambda )$, $D_1''(\lambda )$, $D_2'(\lambda )$ and $D_2''(\lambda )$. The opposite of $C_2$ is $C_4$. The opposite of $E_1(\lambda )$, $E_2$ and $E_3(\lambda )$ are respectively $G_1(\lambda )$, $G_2$ and $G_3(\lambda )$. The opposite of $F'_1(\lambda )$ is $F''_1(\lambda )$. The $\lambda$-$\mathrm {ETS}$ $F_2$ and $F_5$ are not commutative but are isomorphic to their opposite in a non-trivial way. Finally, if $*$ is an associative product, the opposite of $F_3(*)$ is $F_3(*^{op})$.

3.3 A description of all $\mathrm {ETS}$ of cardinality two

The following table gives all the $\mathrm {ETS}$ of cardinality 2.

Type	$\leftarrow$	$\rightarrow$	$\triangleleft$	$\triangleright$	$*$	$\cdot$
$A_1$	$\begin{pmatrix} a&{}a\\ a&{}a \end{pmatrix}$	$\begin{pmatrix} a&{}a\\ a&{}a \end{pmatrix}$	$\begin{pmatrix} a&{}a\\ a&{}a \end{pmatrix}$	$\begin{pmatrix} a&{}a\\ a&{}a \end{pmatrix}$	$\begin{pmatrix} a&{}a\\ a&{}a \end{pmatrix}$,  $\begin{pmatrix} b&{}b\\ b&{}b \end{pmatrix}$	$\begin{pmatrix} a&{}a\\ a&{}a \end{pmatrix}$,  $\begin{pmatrix} a&{}a\\ a&{}b \end{pmatrix}$
$A_2$			$\begin{pmatrix} a&{}b\\ a&{}b \end{pmatrix}$	$\begin{pmatrix} a&{}a\\ b&{}b \end{pmatrix}$
$B_1$	$\begin{pmatrix} a&{}a\\ a&{}a \end{pmatrix}$	$\begin{pmatrix} a&{}b\\ a&{}b \end{pmatrix}$	$\begin{pmatrix} a&{}a\\ a&{}a \end{pmatrix}$	$\begin{pmatrix} a&{}a\\ a&{}a \end{pmatrix}$	$\begin{pmatrix} a&{}a\\ a&{}a \end{pmatrix}$,  $\begin{pmatrix} b&{}b\\ b&{}b \end{pmatrix}$	$\begin{pmatrix} a&{}a\\ a&{}a \end{pmatrix}$,  $\begin{pmatrix} a&{}b\\ a&{}b \end{pmatrix}$
$B_2$			$\begin{pmatrix} a&{}b\\ a&{}b \end{pmatrix}$	$\begin{pmatrix} a&{}a\\ b&{}b \end{pmatrix}$
$C_1$	$\begin{pmatrix} a&{}a\\ a&{}b \end{pmatrix}$	$\begin{pmatrix} a&{}a\\ a&{}b \end{pmatrix}$	$\begin{pmatrix} a&{}a\\ a&{}a \end{pmatrix}$	$\begin{pmatrix} a&{}a\\ a&{}a \end{pmatrix}$	$\begin{pmatrix} a&{}a\\ a&{}a \end{pmatrix}$,  $\begin{pmatrix} b&{}b\\ b&{}b \end{pmatrix}$	$\begin{pmatrix} a&{}a\\ a&{}b \end{pmatrix}$
$C_3$			$\begin{pmatrix} a&{}b\\ a&{}b \end{pmatrix}$	$\begin{pmatrix} a&{}a\\ b&{}b \end{pmatrix}$
$C_5$			$\begin{pmatrix} b&{}b\\ b&{}b \end{pmatrix}$	$\begin{pmatrix} b&{}b\\ b&{}b \end{pmatrix}$
$D_{1}$	$\begin{pmatrix} a&{}a\\ b&{}b \end{pmatrix}$	$\begin{pmatrix} a&{}a\\ a&{}a \end{pmatrix}$	$\begin{pmatrix} a&{}a\\ a&{}a \end{pmatrix}$	$\begin{pmatrix} a&{}a\\ a&{}a \end{pmatrix}$	$\begin{pmatrix} a&{}a\\ a&{}a \end{pmatrix}$,  $\begin{pmatrix} b&{}b\\ b&{}b \end{pmatrix}$	$\begin{pmatrix} a&{}a\\ a&{}a \end{pmatrix}$,  $\begin{pmatrix} a&{}a\\ b&{}b \end{pmatrix}$
$D_2$			$\begin{pmatrix} a&{}b\\ a&{}b \end{pmatrix}$	$\begin{pmatrix} a&{}a\\ b&{}b \end{pmatrix}$
$E_1$	$\begin{pmatrix} a&{}a\\ b&{}b \end{pmatrix}$	$\begin{pmatrix} a&{}a\\ b&{}b \end{pmatrix}$	$\begin{pmatrix} a&{}a\\ a&{}a \end{pmatrix}$	$\begin{pmatrix} a&{}a\\ a&{}a \end{pmatrix}$	$\begin{pmatrix} a&{}a\\ a&{}a \end{pmatrix}$,  $\begin{pmatrix} b&{}b\\ b&{}b \end{pmatrix}$	$\begin{pmatrix} a&{}a\\ b&{}b \end{pmatrix}$
$E_{3}$			$\begin{pmatrix} a&{}b\\ a&{}b \end{pmatrix}$	$\begin{pmatrix} a&{}a\\ b&{}b \end{pmatrix}$	$\begin{pmatrix} a&{}a\\ a&{}a \end{pmatrix}$
$F_{1}$	$\begin{pmatrix} a&{}a\\ b&{}b \end{pmatrix}$	$\begin{pmatrix} a&{}b\\ a&{}b \end{pmatrix}$	$\begin{pmatrix} a&{}a\\ a&{}a \end{pmatrix}$	$\begin{pmatrix} a&{}a\\ a&{}a \end{pmatrix}$	$\begin{pmatrix} a&{}a\\ a&{}a \end{pmatrix}$,  $\begin{pmatrix} b&{}b\\ b&{}b \end{pmatrix}$	$\begin{pmatrix} a&{}a\\ a&{}a \end{pmatrix}$,  $\begin{pmatrix} a&{}a\\ a&{}b \end{pmatrix}$,  $\begin{pmatrix} a&{}a\\ b&{}b \end{pmatrix}$,
						$\begin{pmatrix} a&{}b\\ a&{}b \end{pmatrix}$,  $\begin{pmatrix} a&{}b\\ b&{}a \end{pmatrix}$,  $\begin{pmatrix} a&{}b\\ b&{}b \end{pmatrix}$
$F_{3}$			$\begin{pmatrix} a&{}b\\ a&{}b \end{pmatrix}$	$\begin{pmatrix} a&{}a\\ b&{}b \end{pmatrix}$	$\begin{pmatrix} a&{}a\\ a&{}a \end{pmatrix}$	$\begin{pmatrix} a&{}a\\ a&{}a \end{pmatrix}$,  $\begin{pmatrix} a&{}a\\ a&{}b \end{pmatrix}$,  $\begin{pmatrix} a&{}a\\ b&{}b \end{pmatrix}$,
						$\begin{pmatrix} a&{}b\\ a&{}b \end{pmatrix}$,  $\begin{pmatrix} a&{}b\\ b&{}a \end{pmatrix}$,  $\begin{pmatrix} a&{}b\\ b&{}b \end{pmatrix}$,
						$\begin{pmatrix} b&{}a\\ a&{}b \end{pmatrix}$,  $\begin{pmatrix} b&{}b\\ b&{}b \end{pmatrix}$
					$\begin{pmatrix} a&{}a\\ b&{}b \end{pmatrix}$,  $\begin{pmatrix} b&{}b\\ a&{}a \end{pmatrix}$	$\begin{pmatrix} a&{}b\\ a&{}b \end{pmatrix}$
					$\begin{pmatrix} a&{}b\\ a&{}b \end{pmatrix}$,  $\begin{pmatrix} b&{}a\\ b&{}a \end{pmatrix}$	$\begin{pmatrix} a&{}a\\ b&{}b \end{pmatrix}$
$G_{1}$	$\begin{pmatrix} a&{}b\\ a&{}b \end{pmatrix}$	$\begin{pmatrix} a&{}b\\ a&{}b \end{pmatrix}$	$\begin{pmatrix} a&{}a\\ a&{}a \end{pmatrix}$	$\begin{pmatrix} a&{}a\\ a&{}a \end{pmatrix}$	$\begin{pmatrix} a&{}a\\ a&{}a \end{pmatrix}$,  $\begin{pmatrix} b&{}b\\ b&{}b \end{pmatrix}$	$\begin{pmatrix} a&{}b\\ a&{}b \end{pmatrix}$
$G_{3}$			$\begin{pmatrix} a&{}b\\ a&{}b \end{pmatrix}$	$\begin{pmatrix} a&{}a\\ b&{}b \end{pmatrix}$	$\begin{pmatrix} a&{}a\\ a&{}a \end{pmatrix}$	$\begin{pmatrix} a&{}b\\ a&{}b \end{pmatrix}$
$H_{1}$	$\begin{pmatrix} a&{}b\\ b&{}a \end{pmatrix}$	$\begin{pmatrix} a&{}b\\ b&{}a \end{pmatrix}$	$\begin{pmatrix} a&{}a\\ a&{}a \end{pmatrix}$	$\begin{pmatrix} a&{}a\\ a&{}a \end{pmatrix}$	$\begin{pmatrix} a&{}a\\ a&{}a \end{pmatrix}$,  $\begin{pmatrix} b&{}b\\ b&{}b \end{pmatrix}$	$\begin{pmatrix} a&{}a\\ a&{}b \end{pmatrix}$
$H_{2}$			$\begin{pmatrix} a&{}b\\ a&{}b \end{pmatrix}$	$\begin{pmatrix} a&{}a\\ b&{}b \end{pmatrix}$