Abstract
By means of a new notion of subforests of an angularly decorated rooted forest, we give a combinatorial construction of a coproduct on the free Rota–Baxter algebra on angularly decorated rooted forests. We show that this coproduct equips the Rota–Baxter algebra with a bialgebra structure and further a Hopf algebra structure.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The study of rooted trees is important in combinatorics and has broad applications. Many algebraic structures have been equipped on rooted trees, which give intuitive meaning to these abstract structures. Well-known examples of Hopf algebras on rooted trees include those of Connes–Kreimer, Loday–Ronco, Foissy–Holtkamp and Grassman–Larson [8, 13, 14, 16, 22, 25].
A major advantage of applying combinatorial objects and methods in algebra, especially in Hopf algebra, is that the algebraic operations can be described intuitively and explicitly. A prime example is the Connes–Kreimer Hopf algebra of rooted trees, as a baby model of the Hopf algebra of Feynman graphs arising from their study on renormalization of quantum field theory [23, 24, 28]. Even though the coproduct has a recursive formula by a cocycle condition, the coproduct is made clear and useful by its explicit formula first in terms of admissible cuts and then in terms of subtrees and subforests. The recent work of Gao and Zhang [32] on explicit construction of the coproduct in Loday–Ronco Hopf algebra of planar rooted trees is a similar contribution.
We are interested in the combinatorial construction of a Hopf algebra structures on free Rota–Baxter algebras by rooted trees.
The study of Rota–Baxter algebras was originated from the work of G.Baxter [5] on fluctuation theory in probability in 1960. It was studied by well-known mathematicians such as Atkinson, Cartier and Rota [3, 7, 30] in the 1960–1970s. Their study has experienced a quite remarkable renascence in the recent decades with many applications in mathematics and physics [1, 4, 10, 17, 18, 26, 27, 29, 31], most notably the work of Connes and Kreimer on renormalization of quantum field theory [8, 9, 12]. See [19] for further details and references.
As in the case of any algebraic structures, the understanding of free Rota–Baxter algebras is fundamental in the study of Rota–Baxter algebras and their applications. In the commutative case, the first construction of free commutative Rota–Baxter algebras by Rota [30] led him to the close relationship between Spitzer’s identity and Waring formula for symmetric functions. In the second construction of free commutative Rota–Baxter algebra [7], Cartier introduced a notion (later called a stuffle) that became instrumental in the study of multiple zeta values [6] many years later. In the third construction [17], the authors gave a generalization of the shuffle product, which turned out to be equivalent to the well-known quasi-shuffle product [21] and shuffles. In the non-commutative case, free Rota–Baxter algebras have been constructed by various combinatorial objects, including bracketed words, leaf decorated forests and angularly decorated forests [2, 10, 20]. As in the commutative case, the different constructions of free Rota–Baxter algebras give different angles to study free Rota–Baxter algebras, even though they are naturally isomorphic. More recently, a Hopf algebra structure has been given to free Rota–Baxter algebras on leaf decorated forests [31]. The construction of free Rota–Baxter algebra is from a selected set of leaf decorated forests. The coproduct is obtained by first defining a coproduct on the whole space of leaf decorated forests and then taking the quotient to the space for the free Rota–Baxter algebra. As such, the coproduct cannot be explicitly computed, since it is not clear how to obtain the coproduct of any given leaf decorated forest in the free Rota–Baxter algebra without taking quotients or going through a recursion.
In light of the importance of explicit constructions of the Connes–Kreimer and Loday–Ronco Hopf algebras mentioned above, for further study of the Hopf algebra on free Rota–Baxter algebras and for its applications, it is desirable to describe the coproduct directly on the rooted trees without the ambiguity of taking a quotient or the indirectness of going through a recursion.
This is the purpose of this paper. We will work with free Rota–Baxter algebras on angularly decorated planar rooted trees, following the construction in [10, 19]. The advantage of this construction is that the underlying module is spanned by all planar rooted trees with angular decorations, in contrast to the construction by leaf decorated forests in [31] where a selected class of forests are used as representatives of the Hopf algebra on all leaf decorated planar rooted forests modulo the Rota–Baxter relation. We then introduce a coproduct on the angularly decorated planar rooted forests by suitably defining cuts and subforests, leading to a connected Hopf algebra structure on the free Rota–Baxter algebra.
The layout of the paper is as follows: In Sect. 2, we first recall the notions of angularly decorated rooted forests and their use in constructing free Rota–Baxter algebras. We then construct in Sect. 3 a coproduct on free unitary Rota–Baxter algebra of angularly decorated rooted forests using a suitable notion of subforests, in analogy to the construction of the Connes–Kreimer coproduct on rooted trees. This coproduct is shown to be compatible with the multiplication on the free Rota–Baxter algebra, leading to a bialgebra structure on these forests. Finally, the resulting bialgebra is shown in Sect. 4 to be coaugmented, cofiltered and connected and hence can be enriched to a Hopf algebra.
2 Rota–Baxter algebras and angularly decorated forests
In this section, we recall the construction of the free Rota–Baxter algebra on angularly decorated forests.
2.1 Angularly decorated forests
We first recall the notion of Rota–Baxter algebras [5, 19].
Definition 2.1
Let \(\lambda \) be a given element of commutative ring \(\mathbf{k}\). A Rota–Baxter algebra of weight \(\lambda \) is a pair (R, P) consisting of a \(\mathbf{k}\)-algebra R and a linear operator \(P:R\rightarrow R\) that satisfies the Rota–Baxter equation
We give some basic examples of Rota–Baxter algebras and refer the reader to [19] for more details.
Example 2.1
(Integration) Let R be the \({{\mathbb {R}}}\)-algebra of continuous functions on \({{\mathbb {R}}}\). Define \(P:R\rightarrow R\) by the integration
Then, P is a Rota–Baxter operator of weight 0.
Example 2.2
(Scalar product) Let R be a k-algebra. For any given \(\lambda \in \mathbf{k}\), the operator
is a Rota–Baxter operator of weight \(\lambda \).
Example 2.3
(Laurent series) Let \(R={\mathbb {C}}[t^{-1},t]]\) be the algebra of Laurent series with coefficients in \({\mathbb {C}}\), consisting of series \(\sum \limits _{n\ge N} a_n t^n\) where N is any integer. Then, the projection to the pole part:
is a Rota–Baxter operator of weight \(-1\). Here the sum on the right is understood to be zero if \(N\ge 0\). This operator plays an essential role in the study of renormalization of quantum field theory [8].
In order to construct free Rota–Baxter algebras, we next recall the notions of planar rooted trees and planar rooted forests. Then, we introduce angularly decorated rooted forests, which will be our basic tools used in this paper.
A rooted tree is a connected and simply connected set of vertices and oriented edges such that there is precisely one distinguished vertex, called the root, with no incoming edge. A planar rooted tree is a plane rooted tree with a fixed embedding into the plane. The following list shows the first few of them.

Let \({{\mathcal {T}}}\) denote the set of planar rooted trees and \({{\mathcal {F}}}\) the set of planar forests, which can be identified with \(S({{\mathcal {T}}})\), the free semigroup generated by \({{\mathcal {T}}}\) in which the product is denoted by \(\bigsqcup \) or simply suppressed if there is no danger of confusion. Then, a planar rooted forest can be naturally expressed as an element of \(S({{\mathcal {T}}})\), of the form \(T_1\bigsqcup T_2\cdots \bigsqcup T_n\) consisting of trees \(T_1,\cdots , T_n.\) Here \(\bigsqcup \) means putting two trees next to each other and will often be suppressed. Here some examples of planar rooted forests.

Obviously the multiplication \(\bigsqcup \) satisfies the associativity.
We use \(\lfloor T_1\bigsqcup T_2\cdots \bigsqcup T_n \rfloor \) to denote the tree obtained from the forest \(T_1\bigsqcup T_2\cdots \bigsqcup T_n\) by adding a new root and an edge from the new root to each of the trees \(T_1, \cdots , T_n\). In combinatorial terms, this is called the grafting of \(T_1\bigsqcup T_2\cdots \bigsqcup T_n\) and is denoted by \(B^+(T_1, \cdots ,T_n).\) So the operator \(B^+\) is called the grafting operator. For example,

For a rooted tree T, define the depth \(\mathrm{dep}(T)\) of T to be the maximal length of the paths from the root to the leaves of the tree. For a forest \(F=T_1\bigsqcup T_2\cdots \bigsqcup T_\ell \) with rooted trees \(T_1,T_2\cdots ,T_\ell \), we define the depth \(\mathrm{dep}(F)\) of F to be the maximum of the depths of the trees \(T_1,\cdots ,T_k\). We also define \(\ell \) to be the length of the forest F. So \(\ell (F)\) is the number of tree factors in F. For example,

We now recall the construction of angularly decorated rooted trees. See [11, 19] for further details.
Definition 2.2
Let X be a set.
-
(a)
An angularly decorated rooted tree is a planar rooted tree in which each angle (between two adjacent leafs) is decorated by an element of X.
-
(b)
An angularly decorated rooted forest is a planar rooted forest with each angle decorated by an element of X. Let \({{\mathcal {F}}}_X^a\) denote the set of angularly decorated rooted forests with decoration set X.
Note that the space between two rooted trees is taken as an angle. For example,

are angularly decorated trees, while

are angularly decorated forests.
From the definition of angularly decorated rooted forests, we add decorations to the angles of \({{\mathcal {F}}}=S({{\mathcal {T}}})\) to obtain angularly decorated forests. Intuitively, we use elements from X to replace \(\bigsqcup .\) So an angularly decorated rooted forest is of the form
consisting of angularly decorated rooted trees \(T_1,\cdots ,T_\ell \). The length and depth of an angularly decorated forest are defined to be the same as the underlying decorated forest. We note that the notion of length is different from the notion of breadth that we will introduced later.
2.2 Rota–Baxter algebras by angularly decorated trees
With notations in Sect. 2.1, we let \(\mathbf{k}{{\mathcal {F}}}_X^a\) denote the free \(\mathbf{k}\)-module with basis \({{\mathcal {F}}}_X^a\). We will equip \(\mathbf{k}{{\mathcal {F}}}_X^a\) with a Rota–Baxter algebra structure. In order to do this, we define a multiplication \(\diamond _a\) on \(\mathbf{k}{{\mathcal {F}}}_X^a\).
For this purpose, we define
and then extend by bilinearity to a multiplication
The multiplication
is defined recursively utilizing a grading structure on \({{\mathcal {F}}}_X^a\) together with the grafting operator
The grading is given by the disjoint union (note the different meaning from the concatenation of trees)
where \({{\mathcal {F}}}_{X,n}^a\) is the set of angularly decorated forests of depth n. Then, we have the linear grading
We will see later that the multiplication \(\diamond _a\) gives \(\mathbf{k}\,{{\mathcal {F}}}_X^a\) a filtered algebra, not a graded algebra. So we have to be careful.
To be precise, the recursive definition of
means that we can apply induction on \(n\ge 0\) to define
for all \(i, j\ge 0\) with \(i+j=n\). Once this is achieved, then \(\diamond _a\) is well defined as the direct sum of \(\diamond _a{}_{,n}, n\ge 0\), because of the disjoint union
First let \(n=0\). Then \(i+j=n\) implies \(i=j=0\). Note that
with the convention that \(\bullet x_1 \bullet \cdots \bullet x_k \bullet =\bullet \) when \(k=0\). Then, it is valid to define
by
For a given \(k\ge 0\), assume that \(\diamond _a{}_{,m}, 0\le m\le k\), have been defined, and we define \(\diamond _a{}_{,k+1}\). Then \(k+1\) is greater than or equal to 1.
Let \(T\in {{\mathcal {F}}}_{X,i}^a,\) \(T'\in {{\mathcal {F}}}_{X,j}^a\) with \(i+j=k+1\ge 1.\) We consider two cases.
(a) Suppose the length \(\ell (T)=\ell (T')=1\), that is, T and \(T'\) are both angularly decorated rooted trees. Then, T can be one and only one of the forms \(\bullet \) or \(B^+({\overline{T}})\), and \(T'\) can be one and only one of the forms \(\bullet \) or \(B^+({\overline{T}}')\). Thus, there are four cases and we define
Everything is clear except the last case. There, we note that \(\mathrm{dep}(B^+({\overline{T}}))=\mathrm{dep}({\overline{T}})+1\) and \(\mathrm{dep}(B^+({\overline{T}}'))=\mathrm{dep}({\overline{T}}')+1\). So for the three terms in the last case, we have
Therefore, \(T\diamond _a{}_{\!\!\!,k} {\overline{T}}'\), \({\overline{T}}\diamond _a{}_{\!\!\!,k} T'\) and \({\overline{T}}\diamond _a{}_{\!\!\!,k-1} {\overline{T}}'\) are all well defined by the induction hypothesis. Thus, the expression \(T\diamond _a{}_{\!\!\!,k+1} T'\) is well defined.
(b) Suppose \(\ell (T)=m\ge 2\) or \(\ell (T')=n\ge 2\). Then \(T=T_1 x_1\ldots x_{m-1} T_m\) and \(T'=T_1'y_1\ldots y_{n-1} T_n'\) with \(T_1,\cdots ,T_m,\text { }T_1',\cdots ,T_n'\in {{\mathcal {F}}}_X^a\), \(x_1,\ldots ,x_{m-1},y_1,\ldots , y_{n-1}\in X\). Then, we define:
with \(T_m\diamond _aT_1'\) defined in Case (a). Note that \(T_m\diamond _aT_1'\) is a sum of angularly decorated trees by Case (a). So the above equation gives a well-defined sum of angularly decorated forests.
This completes the recursive definition of \(\diamond _a\) on \({{\mathcal {F}}}_X^a\). Finally, as noted above, we expand the binary operation \(\diamond _a\) and \(B^+\) to \(\mathbf{k}{{\mathcal {F}}}_X^a\) by bilinearity. Note that the multiplication \(\diamond _a\) is not commutative. For example, for  \(T_2:=\bullet x\bullet \), we have
\(T_2:=\bullet x\bullet \), we have

Theorem 2.3
-
(a)
The triple \((\mathbf{k}{{\mathcal {F}}}_X^a,\diamond _a,B^+)\) is a non-commutative unitary Rota–Baxter algebra of weight \(\lambda \) with unit \(\bullet \).
-
(b)
Let \(i_{x}:X\rightarrow \mathbf{k}{{\mathcal {F}}}_X^a,\text { }x\rightarrow \bullet x \bullet \) be the set map. The triple \((\mathbf{k}{{\mathcal {F}}}_X^a,\diamond _a,B^+,i_x)\) is a free non-commutative unitary Rota–Baxter algebra on a set X characterized by the following universal property: for any non-commutative unitary Rota–Baxter algebra \((R,\diamond _R,P)\) and any set map \(f:X \rightarrow R\), there is a unique Rota–Baxter algebra homomorphism \(\bar{f}:\mathbf{k}{{\mathcal {F}}}_X^a\rightarrow R\) such that \(\bar{f}\circ i_x=f.\)
3 Bialgebra structure on the free Rota–Baxter algebra
In [31], the free Rota–Baxter algebra on leaf decorated rooted forests was equipped with a bialgebra and Hopf algebra structure. Through the isomorphism between the free Rota–Baxter algebra in [31] and the free Rota–Baxter algebra on angularly decorated rooted forests in this paper, the bialgebra and Hopf algebra structures on the former free Rota–Baxter algebra can be transported to the latter one. However, in either case, the coproduct is defined by a recursion via a cocycle condition. Even though there is a combinatorial description of the coproduct on leaf decorated rooted forests, like in the work of Connes and Kreimer [8], this combinatorial description does not carry over to the quotient, which gives the free Rota–Baxter algebra on leaf decorated rooted trees. Thus, such a definition of coproduct is not explicit and does not reveal possible relationship with the combinatorial properties of rooted forests.
In this section, we use a combinatorial procedure to define a coproduct on the free Rota–Baxter algebra on angularly decorated rooted forests. This procedure is given in terms of substructures of angularly decorated rooted forest, in analogue to the substructures of leaf decorated rooted forests in the coproduct of Connes and Kreimer.
3.1 Construction of the coproduct
First we define the counit
by sending \(\bullet \) to \(1_\mathbf{k}\) and 0 otherwise. Also, we denote \(m:\mathbf{k}{{\mathcal {F}}}_X^a\otimes \mathbf{k}{{\mathcal {F}}}_X^a\rightarrow \mathbf{k}{{\mathcal {F}}}_X^a\) for the product \(\diamond _a\) defined in the last section and \(u:\mathbf{k}\rightarrow \mathbf{k}{{\mathcal {F}}}_X^a, 1_k\mapsto \bullet \) for the unit.
Now we give a combinatorial definition of a coproduct on angularly decorated rooted forests \(\mathbf{k}{{\mathcal {F}}}_X^a\).
Our construction is motivated by the coproduct of rooted trees and forests of Connes and Kreimer [8], defined by subforests. So we briefly recall their definition.
Let T be a rooted tree or forest. Recall that a subtree \(T'\) of a tree T, denoted \(T'\preceq T\), is a vertex of T together with its descendants and the edges connecting these vertices. A subtree is called non-trivial if it is not the one vertex tree \(\bullet \). More generally, a subforest \(F'\) of a forest \(F=T_1\cdots T_k\), denoted \(F'\preceq F\), is \(F'=T_1'\cdots T_k'\) where \(T_i'\preceq T_i, 1\le i\le k\). Equivalently, a subforest \(F'\) of F is a subset of vertices of F together with the edges connecting them, so that if a vertex is in F, then all descendants of the vertex are in F.
In this language, the Connes–Kreimer coproduct of rooted forests is defined by:
where \(F/F'\) is the forest obtained when the vertices of F and edges (both internal and external) connecting to these vertices are removed from F.
Now let F be an angularly decorated forest, with the decomposition
as in Eq. (2). A vertex of F is called a non-leaf vertex if it is not a leaf. A subtree T of F, denoted \(T\preceq F\), is a subset of vertices of T together with the edges connecting them, so that if a vertex is in F, then all descendants of the vertex are in F. The only vertex of \(\bullet \) is regarded as a leaf.
Definition 3.1
Let F be an angularly decorated forest. Let \(\iota \) be a symbol not in X.
-
(a)
A real subtree of F is a non-leaf subtree of F as defined above for rooted trees together with all its angular decorations.
-
(b)
A letter subtree is a set (in fact a vector) of decorations of a real subtree without the underlying subtree.
-
(c)
A virtual subtree is either a real subtrees or a letter subtrees.
-
(d)
A (angularly decorated) virtual subforest H of an angularly decorated forest F, denoted \(H\preceq F\), consists of a sequence \(H_1,\cdots , H_n\) of mutually disjoint virtual subtrees of F in the order that they appear in F.
-
(e)
The closure of a virtual subforest \(H=H_1\cdots H_n\) of F, denoted \(\mathrm {cl}(H)\), is the angularly decorated forest obtained from expanding H as follows.
-
(i)
If \(H_1\) (resp. \(H_n\)) is a letter subtree, then replace \(H_1\) (resp. \(H_n\)) by \(\bullet H_1\) (resp. \(H_n \bullet \));
-
(ii)
If \(H_i\) and \(H_{i+1}\) are both letter subtrees, then replace \(H_iH_{i+1}\) by \(H_i \bullet H_{i+1}\)
-
(iii)
If \(H_i\) and \(H_{i+1}\) are both real subtrees, then replace \(H_iH_{i+1}\) by \(H_i \iota H_{i+1}\).
The role of the symbol \(\iota \) is to represent the operation \(\diamond _a\) without executing it, that is, without multiplying out \(H_i\diamond _aH_{i+1}\), in order to keep and show the combinatorial structure. This closure is called the angularly decorated forest generated by H .
-
(i)
-
(f)
For a virtual subforest \(H=H_1\cdots H_n\) of F, the quotient forest F/H is obtained from F by carrying out the following procedure for each \(H_i, 1\le i\le n\):
-
(i)
if \(H_i\) is a real subtree, then take it out of F as for the usual rooted forests;
-
(ii)
if \(H_i=\{x\}\) is a letter subtree, then replace x by \(\iota \) at the angle that x decorates.
-
(i)
In both cases, the role of \(\iota \) is the multiplication \(\diamond _a\). See the examples below.
Example 3.1
-
(a)
For the angularly decorated tree
 , the real subtrees are the trivial tree \(\bullet \) and
, the real subtrees are the trivial tree \(\bullet \) and  , the only letter subtree is x. Thus, the virtual subforests are
, the only letter subtree is x. Thus, the virtual subforests are  . Their closures are
. Their closures are  (6)
(6)The corresponding quotients are

-
(b)
For the angularly decorated tree
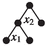 , the real subtrees are
, the real subtrees are  , the letter subtrees are \(x_1, x_2\). Thus, the virtual subforests, their closures and quotients are:
, the letter subtrees are \(x_1, x_2\). Thus, the virtual subforests, their closures and quotients are: Virtual subforests
\(\bullet \)
\(x_1\)

\(x_2\)
\(x_1 x_2\)


Closures
\(\bullet \)
\(\bullet x_1\bullet \)

\(\bullet x_2\bullet \)
\(\bullet x_1\bullet x_2\bullet \)
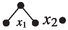
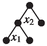
Quotients



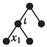


\({\bullet }\)
Definition 3.2
For \(F\in \mathbf{k}{{\mathcal {F}}}_X^a\), with notations above, we define the angular coproduct of F by
where the sum is taken over virtual subforests.
If \(\iota \) appears in the right-hand side, then replace \(\iota \) by \(\diamond _a\).
Example 3.2
For the angularly decorated trees in Example 3.1, we have

For another example, we compute

Next we give another description of the angular coproduct in compatible with the decomposition of F in (2):
for \(x_1,\cdots x_{k-1}\in X,\) \(T_1,\cdots T_k\in {{\mathcal {F}}}_X^a.\) Then, a virtual subforest of F is of the form, called a factorwise virtual subforest
where \(T_i'\) is a virtual subforest of \(T_i, 1\le i\le k,\) and \(x_i'\) is either \(x_i\) or \(\iota , 1\le i\le k\). Then, the quotient forest \(F/F'\) is:
where \(T_i/T_i'\) is the quotient tree and \(x_i/x_i'\) is \(\iota \) or \(x_i\) depending on \(x_i'\) being \(x_i\) or \(\iota \). It is called as factorwise quotient forest.
Then, we have the following alternative definition of \(\Delta _a\). For \(F\in {{\mathcal {F}}}_X^a\) with the decomposition \(F=T_1 x_1 T_2 x_2 \cdots x_{k-1} T_k\) where \(T_1,\) \(\cdots ,\) \(T_k\in {{\mathcal {F}}}_X^a,\) and \(x_1,\) \(\cdots ,\) \(x_{k-1}\in X.\) Then, with the notions above, we have
This description is particularly convenient when there are multiple tree factors in a forest, as shown in the following example.
Example 3.3
Consider the angularly decorated forest  . The following table gives the virtual subforests, their closures and the virtual subforests given factor by factor. We first note that
. The following table gives the virtual subforests, their closures and the virtual subforests given factor by factor. We first note that  has three virtual subforests, \(\bullet \) has one and \(x_2'\) has two choices: \(x_2'=\iota , x_2\). Thus altogether, there are six virtual subforests of F. Their corresponding closures, factorwise subforests, factorwise quotients are listed in the following table.
has three virtual subforests, \(\bullet \) has one and \(x_2'\) has two choices: \(x_2'=\iota , x_2\). Thus altogether, there are six virtual subforests of F. Their corresponding closures, factorwise subforests, factorwise quotients are listed in the following table.
Virtual subforests | \(\bullet \) | \(x_1\) |
| \(x_2\) | \(x_1 x_2\) |
|
Closures | \(\bullet \) | \(\bullet x_1\bullet \) |
| \(\bullet x_2\bullet \) | \(\bullet x_1\bullet x_2\bullet \) |
|
Factorwise virtual subforests | \(\bullet \iota \bullet \iota \bullet \) | \(\bullet x_1\bullet \iota \bullet \) |
| \(\bullet \iota \bullet x_2\bullet \) | \(\bullet x_1\bullet x_2\bullet \) |
|
Factorwise quotient |
|
| \(\bullet \iota \bullet x_2 \bullet \) |
|
| \(\bullet \iota \bullet \iota \bullet \) |
Reduced quotient |
|
| \( \bullet x_2 \bullet \) |
|
| \(\bullet \) |
Thus, we have the coproduct

3.2 The bialgebra structure
Theorem 3.3
Let \(\Delta _a:\mathbf{k}{{\mathcal {F}}}_X^a\rightarrow \mathbf{k}{{\mathcal {F}}}_X^a\otimes \mathbf{k}{{\mathcal {F}}}_X^a\) be the angular coproduct defined in Eq. (7) or (8). Then, \(\Delta _a\) satisfies the following properties.
-
(a)
\(\Delta _a(\bullet )=\bullet \otimes \bullet ;\)
-
(b)
\(\Delta _a(\bullet x\bullet )=\bullet x\bullet \otimes \bullet +\bullet \otimes \bullet x\bullet ,\) \(x\in X\);
-
(c)
\(\Delta _a(B^+(F))=B^+(F)\otimes \bullet +(\mathrm{id}\otimes B^+)(\Delta _a(F))\) for all \(F\in {{\mathcal {F}}}_X^a\);
-
(d)
\(\Delta _a(F_1\diamond _aF_2)=\Delta _a(F_1)\diamond _a\Delta _a(F_2)\) for \(F_1,\) \(F_2\in {{\mathcal {F}}}_X^a\).
Proof
By the definition of \(\Delta _a\), it is direct that Items (a) and (b) hold.
(c) We verify
by the same argument for the cocycle property of the Connes–Kreimer coproduct for rooted trees and here made possible by the combinatorial description of the angular coproduct. Consider the coproduct
If \(G\preceq B^+(F)\) contains the root of \(B^+(F)\), then \(G=B^+(F)\) and the corresponding term in the sum is \(B^+(F)\otimes \bullet \). If \(G\preceq B^+(F)\) does not contain the root of \(B^+(F)\), then by the definition of angular subforests, we have \(G\preceq F\). Further, the corresponding quotient forest is obtained from the grafting of F/G. Therefore, the corresponding term in the sum is \(G \otimes B^+(F/G)\). In summary, we obtain
as needed.
(d). We prove the desired multiplicativity by induction on the sum \(\mathrm{dep}(F_1)+\mathrm{dep}(F_2)\) of depths of \(F_1\) and \(F_2\) in \({{\mathcal {F}}}_X^a\).
First when \(\mathrm{dep}(F_1)+\mathrm{dep}(F_2)=0\), then \(F_1=\bullet x_1\bullet \cdots \bullet x_m\) and \(F_2=\bullet x_{m+1}\bullet \cdots \bullet x_{m+n}\) for some \(m, n\ge 1\). For a set \(I=\{i_1<\cdots <i_r\}\) of positive integers, we use the notation \(\bullet x_I \bullet : =\bullet x_{i_1}\bullet \cdots \bullet x_{i_r}\bullet \). Also denote \([m]=\{1, \cdots , m\}\) and \([m+1,m+n]:=\{m+1, \cdots , m+n\}\). With these notations, we obtain
Therefore,
Next assume that for \(k\ge 0\), Item (c) holds whenever \(\mathrm{dep}(F_1)+\mathrm{dep}(F_2)\le k\). Consider \(F_1, F_2\in {{\mathcal {F}}}_X^a\) with \(\mathrm{dep}(F_1)+\mathrm{dep}(F_2)=k+1\). We first consider the case when the breadths of \(F_1\) and \(F_2\) are one. In this case, if further one of \(F_1\) or \(F_2\) has depth zero and so is of the form \(\bullet x\bullet \), then by the definition of \(\diamond _a\) in Eqs. (3) and (4), we have \(F_1\diamond _aF_2 = \bullet x F_2\) or \(F_1\diamond _aF_2= F_1 x \bullet \). Then, it is direct to check that Item (c) holds. In the remaining case, when \(F_1\) and \(F_2\) both have positive depths, then \(F_1=B^+(\overline{F_1})\) and \(F_2=B^+(\overline{F_2})\). Denote
so that \(F_1\diamond _aF_2=B^+(\overline{F_1} \star \overline{F_2})\). Then, by the cocycle condition and the induction hypothesis, we have
It is a general fact that if P is a Rota–Baxter operator on an algebra R, then \(\mathrm{id}\otimes P\) is a Rota–Baxter algebra on the tensor product algebra \(R\otimes R\). Thus combining the third, fifth and sixth terms of the above equation gives \((\mathrm{id}\otimes B^+)(\Delta _a(\overline{F_1})) \diamond _a(\mathrm{id}\otimes B^+)(\Delta _a(\overline{F_2}))\). Thus, from the above equation we obtain
On the other hand, we have
Since
we find that
Finally when \(F_1\) and \(F_2\) have breadths \(r\ge 1\) and \(s\ge 1\), respectively, with standard decompositions
Then noting that \(\Delta _a\) is defined to be compatible with the standard decomposition (see the alternative description) and that the standard decomposition of \(F_1\diamond _aF_2\) is
Thus applying the previous case, we obtain
This completes the proof of Item (d). \(\square \)
Now we verify the other conditions for \(\mathbf{k}{{\mathcal {F}}}_X^a\) to be a bialgebra.
Theorem 3.4
The quintuple \((\mathbf{k}{{\mathcal {F}}}_X^a,m,u,\Delta _a,\epsilon _a)\) is a bialgebra.
Proof
By Theorem 3.3, the natural algebraic isomorphism between \((\mathbf{k}{{\mathcal {F}}}_X^a,m,u)\) and the free Rota–Baxter algebra on X in [31] preserves the coproducts. Then, since the coproduct in [31] is compatible with the product and gives rise to a bialgebra, the same holds for the quintuple \((\mathbf{k}{{\mathcal {F}}}_X^a,m,u,\Delta _a,\epsilon _a)\). \(\square \)
4 The Hopf algebra structure
We end the paper by showing that the bialgebra of angularly decorated forests obtained in the last section is a Hopf algebra.
Definition 4.1
A coaugmented coalgebra is a quadruple \((C, \triangle , \epsilon ,u)\) where \((C,\triangle ,\epsilon )\) is a coalgebra and \(u:k\rightarrow C\) is a linear map, called the coaugmentation, such that \(\epsilon \circ u= \mathrm{id}_k.\)
In Sect. 3, we have defined \(\epsilon _a:\mathbf{k}{{\mathcal {F}}}_X^a\rightarrow \mathbf{k}\) and \(u:\mathbf{k}\rightarrow \mathbf{k}{{\mathcal {F}}}_X^a\), so that
In other words, we have shown that \((\mathbf{k}{{\mathcal {F}}}_X^a,\Delta _a,\epsilon _a)\) is a coaugmented coalgebra.
Definition 4.2
([15]) A bialgebra \((H,m,u,\Delta ,\epsilon )\) is called cofiltered if there are \(\mathbf{k}-\)submodules \(H^n\), \(n\ge 0\), such that
-
(a)
\(H^n\subseteq H^{n+1}\) for all \(n\ge 0\);
-
(c)
\(H=\cup _{n\ge 0}^\infty H^n\) for all \(n\ge 0\);
-
(c)
\(\Delta (H^n)\subseteq \sum _{p+q=n} H^p\otimes H^q,\) \(n\ge 0\);
-
(d)
\(H^n=\mathrm{im}u\oplus (H^n\cap \ker \epsilon ),\) where \(p,q\ge 0\). H is called connected (cofiltered) if in addition \(H^0=\mathrm{im}u\).
Definition 4.3
Let \(\deg (F)\) denote the number of vertices of \(F\in {{\mathcal {F}}}_X^a.\)
Then we have \(\deg (F_1\diamond _aF_2)=\deg (F_1)+\deg (F_2)-1.\)
Now we prove
Proposition 4.4
With the above notations, \(\mathbf{k}{{\mathcal {F}}}_X^a\) is a connected, cofiltered coaugmented coalgebra.
Proof
First we define
And we denote \(H^n:=\mathbf{k}{{\mathfrak {a}}}^n.\) Then, we have \(H^0= \mathbf{k}=\mathrm{im}u\) and \(\mathbf{k}{{\mathcal {F}}}_X^a=\cup _{n\ge 0}^\infty H^n\), so (b) is clear.
(a) Obviously, for \(F\in H^n,\text { }\deg (F)\le n+1,\)
So, \(F\in H^{n+1},\) that is, \(H^n\subseteq H^{n+1}.\)
(c) When \(n=0,\) \(F=\bullet \in H^0,\)
Assume that for \(n=k\ge 0,\text { }\Delta _a(H^k)\subseteq \sum _{p+q=k} H^p\otimes H^q\). Then, we consider the case of \(n=k+1\). Let \(F\in H^n\). We consider two cases.
Case 1. If \(\mathrm{bre}(F)=1\), then we have \(F=B^+(\overline{F})\text { and }\deg (\overline{F})=k+1.\) Also, we have
so we have \((\mathrm{id}\otimes B^+ )\circ \Delta _a(\overline{F})\in \sum _{p+q+1=k+1}H^p\otimes H^{q+1}\) and \(F\otimes \bullet \in H^{k+1}\otimes H^0\). Then,
Case 2. If \(\mathrm{bre}(F)\ge 2,\) we have \(F=F_1\diamond _aF_2,\text { and }\deg (F)=\deg (F_1)+\deg (F_2)-1=k+2\), so we have
This completes the induction.
(d) Since \(\epsilon _a\circ u=\mathrm{id}_\mathbf{k}\), \(u\circ \epsilon _a\) is idempotent. Further u is injective and \(\epsilon _a\) is surjective. Thus,
In summary, we have proved that \((\mathbf{k}{{\mathcal {F}}}_X^a,\Delta _a,\epsilon _a)\) is a connected coaugmented cofiltered coalgebra. \(\square \)
Lemma 4.5
[15] Let \((H,m,u,\Delta _a,\varepsilon )\) be a bialgebra such that \( (H,\Delta _a,\varepsilon ,u)\) is a connected coaugmented cofiltered coalgebra. Then H is a Hopf algebra and the antipode S is given by
where \({\bar{\Delta }}(x):=\Delta (x)-1_H\otimes x- x\otimes 1_H\in \ker \varepsilon \otimes \ker \varepsilon .\)
Here are examples of the antipodes for some angularly decorated forests.

Combining Proposition 4.4 and Lemma 4.5, we obtain
Theorem 4.6
\((\mathbf{k}{{\mathcal {F}}}_X^a,\diamond _a, u, \Delta _a,\epsilon _a,S)\) is a Hopf algebra.
Data availability
The data that support the findings of this study can be found in journal publications and the arxiv.
References
Aguiar, M.: On the associative analog of Lie bialgebras. J. Algebra 244, 492–532 (2001)
Aguiar, M., Moreira, W.: Combinatorics of the free Baxter algebra. Electron. J. Combin. 13, #R17 (2006)
Atkinson, F.V.: Some aspects of Baxter’s functional equation. J. Math. Anal. Appl. 7, 1–30 (1963)
Bai, C., Bellier, O., Guo, L., Ni, X.: Spliting of operations, Manin products and Rota–Baxter operators. Int. Math. Res. Not. IMRN 2013, 485–524 (2013)
Baxter, G.: An analytic problem whose solution follows from a simple algebraic identity. Pacific J. Math. 10, 731–742 (1960)
Borwein, J., Bradley, D., Broadhurst, D., Lisoněk, P.: Special values of multiple polylogarithms. Trans. Amer. Math. Soc. 353, 907–941 (2001)
Cartier, P.: On the structure of free Baxter algebras. Adv. Math. 9, 253–265 (1972)
Connes, A., Kreimer, D.: Hopf algebras, renormalization and non-commutative geometry. Comm. Math. Phys. 199, 203–242 (1998)
Connes, A., Kreimer, D.: Renormalization in quantum field theory and the Riemann–Hilbert problem. I. The Hopf algebra structure of graphs and the main theorem. Comm. Math. Phys. 210, 249–273 (2000)
Ebrahimi-Fard, K., Guo, L.: Rota–Baxter algebras and dendriform algebras. J. Pure Appl. Algebra 212, 320–339 (2008)
Ebrahimi-Fard, K., Guo, L.: Free Rota–Baxter algebras and rooted trees. J. Algebra Appl. 7, 167–194 (2008)
Ebrahimi-Fard, K., Guo, L., Kreimer, D.: Spitzer’s identity and the algebraic Birkhoff decomposition in pQFT. J. Phys. A 37(45), 11037–11052 (2004)
Foissy, L.: Les algèbres de Hopf des arbres enracinés décorés, I. Bull. Sci. Math. 126, 193–239 (2002)
Foissy, L.: Les algèbres de Hopf des arbres enracinés décorés, II. Bull. Sci. Math. 126, 249–288 (2002)
Gao, X., Guo, L.: A note on connected cofiltered coalgebras, conilpotent coalgebras and Hopf algebras. Southeast Asian Bull. Math. 43, 313–321 (2019)
Grossman, R., Larson, R.: Hopf-algebraic structure of families of trees. J. Algebra 126, 184–21 (1989)
Guo, L., Keigher, W.: Baxter algebras and shuffle products. Adv. Math. 150, 117–149 (2000)
Guo, L., Keigher, W.: On differential Rota–Baxter algebras. J. Pure Appl. Algebra 212, 522–540 (2008)
Guo, L.: An Introduction to Rota–Baxter Algebra. International Press (2012)
Guo, L.: Operated semigroups, Motzkin paths and rooted trees. J. Algebraic Combin. 29, 35–62 (2009)
Hoffman, M.: Quasi-shuffle products. J. Algebraic Combin. 11, 49–68 (2000)
Holtkamp, R.: Comparison of Hopf algebras on trees. Arch. Math. (Basel) 80, 338–368 (2003)
Kreimer, D.: On the Hopf algebra structure of perturbative quantum field theories. Adv. Theor. Math. Phys. 2, 303–334 (1998)
Kreimer, D.: On overlapping divergences. Comm. Math. Phys. 204, 669–689 (1999)
Loday, J.-L., Ronco, M.: Hopf algebra of the planar binary trees. Adv. Math. 139, 293–309 (1998)
Ma, T., Liu, L.: Rota–Baxter coalgebras and Rota–Baxter bialgebras. Linear Multilinear Algebra 64(5), 968–979 (2016)
Makhlouf, A., Yau, D.: Rota–Baxter Hom–Lie-admissible algebras. Comm. Algebra 42, 1231–1257 (2014)
Manchon, D.: Hopf algebras, from basics to applications to renormalization. Comptes-rendus des Rencontres mathematiques de Glanon (2001)
Pei, J., Bai, C., Guo, L.: Splitting of operads and Rota–Baxter operators on operads. Appl. Categ. Structures 25, 505–538 (2017)
Rota, G.C.: Baxter algebras and combinatorial identities I, II. Bull. Amer. Math. Soc. 75(325–329), 330–334 (1969)
Zhang, T.J., Gao, X., Guo, L.: Hopf algebras, cocycles and Rota–Baxter algebras. J. Math. Phys. 57, 101701 (2016)
Zhang, Y., Gao, X.: Hopf algebras of planar binary trees: an operated algebra approach. J. Algebraic Combin. 51, 567–588 (2020)
Acknowledgements
This work was supported by the National Natural Science Foundation of China (Grant No. 11771190). The authors thank the referees for helpful suggestions.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Zhang, X., Xu, A. & Guo, L. Hopf algebra structure on free Rota–Baxter algebras by angularly decorated rooted trees. J Algebr Comb 55, 1331–1349 (2022). https://doi.org/10.1007/s10801-021-01098-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10801-021-01098-8




 , the real subtrees are the trivial tree
, the real subtrees are the trivial tree  , the only letter subtree is x. Thus, the virtual subforests are
, the only letter subtree is x. Thus, the virtual subforests are  . Their closures are
. Their closures are 

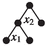 , the real subtrees are
, the real subtrees are  , the letter subtrees are
, the letter subtrees are