1 Introduction

A vast variety of scientific phenomena can be modeled, examined, and explained with the use of nonlinear partial differential equations (NLPDEs). A lively area of research that is essential for comprehending the applications of nonlinear partial differential equations (NLPDEs) in practical settings is the investigation of exact solutions to these equations [1,2,3,4]. The role of non-linearity in waves is extremely essential generally over nonlinear sciences; advancing the study of exact solutions to PDEs has been top priority in recent years. Therefore, the finding of accurate analytical solutions for NLPDEs remains one of the foremost topics of popular interest. The majority of previous studies have focused on creating novel approaches to existing techniques in order to generate fresh, exact analytical frameworks that may specify challenging and intricate physical implementations. The majority of research has seemed to be based on direct methods to determine exact analytical solutions for NLPDEs in the last few years, regardless of whether this is due to the development of symbolic computational programs that help us to perform laborious and complex calculations on computer systems. Moreover, a number of potent, effective, and credible techniques have been developed to find analytical solutions for travelling waves, such as exp-function technique [5, 6], there are multiple techniques to observe the voltage in transmission line problems [7], the sine-cosine approach [8, 9], the Lie symmetry analysis scheme [10, 11], the sine-Gordon expansion technique [12, 13], tanh approach [14, 15], the modified Kudryashov method [16,17,18], the extended hyperbolic function approach [19, 20], and many others [21,22,23,24,25]. Zhao et al. studied lump chain solutions of the \((2+1)\)-dimensional Bogoyavlenskii-Kadomtsev-Petviashvili (BKP) equation [26]. Recently, Zhao and He investigated an integrable \((2+1)\)-dimensional generalized KdV equation using Hirota’s bilinear method [27]. Recent developments in the field of soliton dynamics extend across several scientific fields and technology domains. In the field of optics, scientists are working to improve modulation strategies for soliton-based communication networks to increase data speeds and improve signal integrity [28, 29]. Furthermore, the study of solitons in plasma physics has significance for comprehending the dynamics of magnetized plasma and space weather [30]. Experiments in the field of Bose-Einstein condensates (BECs) are providing important insights into soliton behavior and explain phenomena such as quantum turbulence and superfluidity [31, 32].

In this research, lump soliton (LS), rogue waves (RWs), breather waves (BWs), Ma-breather, and Kuznetsov-Ma-breather solutions of generalized reaction Duffing model (gRDM) are found by using distinct types of ansatz transformations. The innovative aspect of the research is the utilization of tailored ansatz transformations for the generalized reaction Duffing model. A deeper investigation of the behaviors and dynamics of the system is made possible by these customized transformations, which allow the study to examine particular wave phenomena that are exclusive to this model. The transformations employed in the article for studying nonlinear waves in the generalized reaction Duffing model present several challenges and areas for improvement when compared to the methods discussed in the reference. One significant challenge is the complexity of the ansatz transformations used in the paper, which can require complex computations and careful parameter selection. Lump waves (LWs) have been observed in many domains as superior nonlinear wave occurrences. LWs are considered to be a particular type of soliton that propagate with more energy than regular solitons. As a result, LWs have the potential to be disastrous in some systems, such as the financial and oceanic domains. Finding and anticipating LWs in real-world applications is crucial. In a variety of disciplines, including as solid-state physics, quantum mechanics, and electromagnetic, the lump soliton solutions are useful for the mathematical description of wave phenomena. These solutions appear as localized energy concentrations in the wave, and are solutions to specific NLEEs. They shed light on the stability of plasma in fusion experiments as well as the structure of plasma waves. In order to more fully comprehend extreme wave events and their effects on the ecosystem, the RWs are investigated. Early warning mechanisms and maritime operations readiness are aided by this modeling. Designing coastal infrastructure, such as wind turbines and oil rigs, to withstand the impact of rogue waves requires an understanding of these waves. The investigation of breathers advances knowledge of nonlinear wave dynamics in general. They provide information about the behavior of waves in the presence of nonlinear influences. They are fundamental to the theory of soliton, which is applied in domains such as water waves and optical fibers. The behavior of some materials, especially those having nonlinear features, can be modeled and studied using the BWs in material science. There is a wide variety of NLPDEs that are specifically designed to explain various physical phenomena. There are two forms of freak waves in nonlinear media, the Ma-breathers and the Kuznetsov-Ma (KM) breathers [33, 34]. The Ma-breather is a localized, explicit periodic solution. For instance, Ma-breathers are present in the generalized Boussinesq equation. KM breather, also known as KM soliton, was discovered for the first time in the 1970. KM breather, often referred to as “temporal periodic breather” [35], is localized in space and periodic in temporal variable. It does not exhibit a traveling wave. In this manuscript, some ansatz transformations will be applied to obtain the multiple soliton such as, rogue waves, lump soliton, breather waves, Ma-breather, and Kuznetsov-Ma-breather solutions of the generalized reaction Duffing model (gRDM) of the form

$$\begin{aligned} {w_{tt}} + a{w_{xx}} + bw + c{w^2} + d{w^3} = 0, \end{aligned}$$
(1)

where a, b, c, and d are all constants. The wave profile is represented by w, and the spatial and temporal coordinates are depicted by the independent variables x and t. The behavior of specific dynamic systems can be described mathematically by the generalized reaction-Duffing model, which is utilized in nonlinear dynamics and employed in physics, engineering, and biology. Researchers are interested in this model because it can display a broad range of complicated behaviors, and it is a generalization of several well-known physics equations. The Duffing equation has its origins in the work of German mathematician and engineer Georg Duffing, who developed the idea of the Duffing oscillator in the early 20th century. The motion of a damped driven oscillator is described by the second-order nonlinear differential equation known as the Duffing oscillator. Based on the basic Duffing equation, the generalized reaction Duffing model has additional nonlinear features and reaction-diffusion components. A more thorough investigation of nonlinear dynamics and wave propagation in physical systems is made possible by this expansion. The gRDM has been studied by researchers to find novel periodic solutions, shock waves, solitary waves, and other intriguing characteristics. The analysis of this model has shed light on the interactions between solitary waves, the dynamics of nonlinear systems, and the impact of various coefficients on wave propagation. The rest of the paper is organized as follows: In Section 2, the lump soliton solution will be obtained. In Section 3, rogue waves solution will be obtained. In Section 4, the breather waves solution will be studied. In Section 5, types of breather waves will be provided. In Section 6, we will discuss our results. The conclusion will be provided in Section 7.

2 Lump Soliton Solution

In this section, we will find the lump soliton solutions of proposed model. Among the several exact solutions, lump solutions are a type of rational function solution to nonlinear partial differential equations (NLPDEs) that are localized in all directions in the space. The lump soliton solution can be found by applying the following transformation:

$$\begin{aligned} w = 2{(\ln f)_{xx}}. \end{aligned}$$
(2)

The lump soliton solution of (1) can be found using (2), which will yield the bilinear form of the equation.

$$\begin{aligned} - 2b{f^4}f_x^2 - 12{f^2}f_t^2f_x^2 + 4{f^3}{f_{tt}}f_x^2 - 12a{f^2}f_x^4 + 4c{f^2}f_x^4 - 8df_x^6 + 16{f^3}{f_t}{f_x}{f_{xt}} - 4{f^4}f_{xt}^2 - 4{f^4}{f_x}{f_{xtt}}\\ + 2b{f^5}{f_{xx}} + 4{f^3}f_t^2{f_{xx}} - 2{f^4}{f_{tt}}{f_{xx}} + 24a{f^3}f_x^2{f_{xx}} - 8c{f^3}f_x^2{f_{xx}} + 24dff_x^4{f_{xx}} - 6a{f^4}f_{xx}^2 + 4c{f^4}f_{xx}^2 - \\ 24d{f^2}f_x^2f_{xx}^2 + 8d{f^3}f_{xx}^3 - 4{f^4}{f_t}{f_{xxt}} + 2{f^5}{f_{xxtt}} - 8a{f^4}{f_x}{f_{xxx}} + 2a{f^5}{f_{xxxx}}. \end{aligned}$$
(3)

Now, using the function \({\zeta _1}\), \({\zeta _2}\) and f given as [36]:

$$\begin{aligned} {\left\{ \begin{array}{ll} f = \zeta _1^2 + \zeta _2^2 + {a_7},\\ {\zeta _1} = {a_1}x + {a_2}t + {a_3},\\ {\zeta _2} = {a_4}x + {a_5}t + {a_6}. \end{array}\right. } \end{aligned}$$
(4)

where \(1 \le {a_i} \le 7\), are the real parameters to be found. After replacing f into (3), we are able to derive the subsequent sets of parameters by eliminating the coefficients of x and t.

When \({a_1}={a_6}=0\), we obtain the following solutions:

$$ {a_2} = {a_2}, {a_3} = \frac{2}{3}\sqrt{\frac{{15a - 2c + \sqrt{225{a^2} - 60ac - 18bd + 4{c^2}} }}{b}}, {a_4} = {a_4}, {a_5}=0, $$
$$ {a_7}= - \frac{{10}}{9}\frac{{15a - 2c + \sqrt{225{a^2} - 60ac - 18bd + 4{c^2}} }}{b}a_4^2. $$

By using the above values in (2), we get

$$\begin{aligned} w = 2\frac{{(\zeta _1^2 + \zeta _2^2 + {a_7})(2a_4^2) - {{(2a_4^2x)}^2}}}{{{{(\zeta _1^2 + \zeta _2^2 + {a_7})}^2}}}, \end{aligned}$$
(5)

where

$$ {\zeta _1} = \frac{2}{3}{a_4}\sqrt{\frac{{15a - 2c + \sqrt{225{a^2} - 60ac + 4{c^2} - 18bd} }}{b}} + {a_2}t, {\zeta _2} = {a_4}x, 225{a^2} - 60ac - 18bd + 4{c^2} > 0. $$

Here, a few graphical representations of the above solution are examined.

3 Rogue Waves Solution

Rogue waves, sometimes referred to as freak, monster, or killer waves, are unusually huge, erratic, and abruptly arising surface waves that pose a serious risk to ships, including large ones. They are frequently nearly undetectable in deep waters and are brought on by the displacement of water as a result of other occurrences, such as earthquakes. Due to their unpredictable nature and powerful impact, they might appear suddenly. The following transformation will be used for rogue wave solution:

$$\begin{aligned} {\left\{ \begin{array}{ll} f(x,t) = \zeta _1^2 + \zeta _2^2 + {m_1}\cosh (\alpha (x,t)) + a_7,\\ {\zeta _1} = {a_1}x + {a_2}t + {a_3},\\ {\zeta _2} = {a_4}x + {a_5}t + {a_6},\\ \alpha (x,t) = {b_1}x + {b_2}t, \end{array}\right. } \end{aligned}$$
(6)

where \(1 \le {a_i} \le 7\), \({b_1}\), \({b_2}\), and \({m_1}\) are real parameters to be determined. Inserting (6) into (3) will provide the specific equations that yield parameter values.

When \({a_1}= {b_2}={a_6}=0\), we obtain the following solutions:

$$ {a_2} ={a_2}, {a_3} ={a_3}, {a_4} = \sqrt{\frac{3}{{4c - 21a}}}, {a_5}={a_5}, {a_7}={a_7}, {b_1} = \sqrt{ - \frac{b}{a}}, {m_1}={m_1}. $$

By substituting the above values in (2), yields

$$\begin{aligned} w = 2\frac{{\Omega {\kappa _1} - {\kappa _2}}}{{{\Omega ^2}}}, \end{aligned}$$
(7)

where

$$ f(x,t)= \Omega = \zeta _1^2 + \zeta _2^2 + {m_1}\cosh (\alpha (x,t)) + a_7, $$
$$ {\kappa _1} = \frac{{6{a_5}^2}}{{4c-21a}} - \frac{{b{m_1}\cosh \left( {{b_2}t + \sqrt{ - \frac{b}{a}} x} \right) }}{a}, $$
$$ {\kappa _2} \!=\! {\left( {2\sqrt{3} {a_5}\sqrt{ \frac{1}{{4c-21a}}} \left( {{a_5}t \!+\! \sqrt{3} {a_5}\sqrt{ \frac{1}{{4c-21a}}} x} \right) +\! \sqrt{ - \frac{b}{a}} {m_1}\sinh \left( {{b_2}t +\! \sqrt{ - \frac{b}{a}} x} \right) } \right) ^2}, {\zeta _1} ={a_3} + {a_2}t, $$
$$ {\zeta _2} ={a_5}t + \sqrt{3} {a_5}\sqrt{ \frac{1}{{4c-21a}}} x, \alpha (x,t)= \sqrt{ - \frac{b}{a}} x, 4c - 21a > 0, ab<0. $$

Here, a few graphical representations of the above solution are examined.

4 Breather Waves Solution

This section will provide the breather wave (BW) solution for (1). Breathers are nonlinear waves characterized by localized, oscillating energy concentrations. Breathers are solitonic structures. A breather soliton can be found in several natural scientific subfields, including solid-state physics, chemistry, plasma physics, fluid dynamics, nonlinear optics, and molecular biology. The following transformation will be applied for breather wave solutions:

$$\begin{aligned} {\left\{ \begin{array}{ll} f(x,t) = {m_1}{e^{q{\zeta _1}(x,t)}} + {e^{ - q{\zeta _1}(x,t)}} + {m_2}\cos ({q_1}{\zeta _2}(x,t)) + {a_6},\\ {\zeta _1} = {a_1}x + {a_2}t + {a_3},\\ \zeta _2= a_4x+a_5t, \end{array}\right. } \end{aligned}$$
(8)

where \(m_1, m_2, \) and \(a_i\) are real parameters to be determined. By inserting (8) into (3), some equations that yield coefficient values are found.

When \({a_2}= {a_6}=0\), the subsequent solutions are obtained:

$$ {a_1} = \frac{{\sqrt{ - \frac{1}{4}\frac{{ - \frac{1}{5}\frac{{ - 6ac + 5bd + 2\sqrt{ - 60{a^2}bd + 9{a^2}{c^2}} }}{d}}}{a} + b} }}{q}, {a_3}= {a_3}, {a_4} = \frac{{\sqrt{ - \frac{1}{4}\frac{{ - \frac{1}{5}\frac{{ - 6ac + 5bd + 2\sqrt{ - 60{a^2}bd + 9{a^2}{c^2}} }}{d}}}{a} - b} }}{{{q_1}}}, $$
$$ {a_5}=\frac{{\sqrt{\frac{{ - 6ac + 5bd + 2\sqrt{ - 60{a^2}bd + 9{a^2}{c^2}} }}{d}} }}{{\sqrt{5} {q_1}}}, {m_1}=0, {m_2}={m_2}. $$

By inserting the above values in (2), we get

$$\begin{aligned} w = 2\frac{{\Omega {\kappa _1} - {\kappa _2}}}{{{\Omega ^2}}}, \end{aligned}$$
(9)

where

$$ \Omega = f(x,t) = {m_1}{e^{q{\zeta _1}(x,t)}} + {e^{ - q{\zeta _1}(x,t)}} + {m_2}\cos ({q_1}{\zeta _2}(x,t)) + {a_6}, $$
$$ {\kappa _1} = \left( {b + \lambda } \right) {\mathrm{{e}}^{ - q\left( {{a_3} + \frac{{\sqrt{b + \lambda } x}}{q}} \right) }} - \left( { - b + \lambda } \right) {m_2}\cos \left( {{q_1}\left( {\frac{{\sqrt{\frac{{ - 6ac + 5bd + 2\sqrt{9{a^2}{c^2} - 60{a^2}bd} }}{d}} t}}{{\sqrt{5} {q_1}}} + \frac{{\sqrt{ - b + \lambda } x}}{{{q_1}}}} \right) } \right) , $$
$$ {\kappa _2} = {\left( { - \sqrt{b + \lambda } {\mathrm{{e}}^{ - q\left( {{a_3} + \frac{{\sqrt{b + \lambda } x}}{q}} \right) }} - \sqrt{ - b + \lambda } {m_2}\sin \left( {{q_1}\left( {\frac{{\sqrt{\frac{{ - 6ac + 5bd + 2\sqrt{9{a^2}{c^2} - 60{a^2}bd} }}{d}} t}}{{\sqrt{5} {q_1}}} + \frac{{\sqrt{ - b + \lambda } x}}{{{q_1}}}} \right) } \right) } \right) ^2}, $$
$$ \lambda = \frac{{ - 6ac + 5bd + 2\sqrt{9{a^2}{c^2} - 60{a^2}bd} }}{{20ad}}, - 60{a^2}bd + 9{a^2}{c^2}>0. $$

Here, a few graphical representations of the above solution are examined.

5 Types of Breather

In this section Ma-Breathers and Kuznetsov-Ma-Breathers solutions for (1) are discussed.

5.1 Ma-breather

The Ma-breather is a localized, explicit periodic solution. For instance, Ma-breathers are present in the generalized Boussinesq equation. The following transformation will be used for Ma-Breather:

$$\begin{aligned} f(x,t) = {\mathrm{{e}}^{ - \mathrm{{i}}\left( {{p_1}x} \right) }}{\mathrm{{e}}^{{k_1}t + {k_2}}} + {m_1}{\mathrm{{e}}^{2\left( {{k_1}t + {k_2}} \right) }} + {\mathrm{{e}}^{\mathrm{{i}}\left( {{p_1}x} \right) }} + {a_1}, \end{aligned}$$
(10)

where \({a_1}\), \({p_1}\), \({k_1}\), \({k_2}\), and \({m_1}\) are real parameters. By inserting (10) into (3), some equations are obtained to determine coefficient values. The subsequent solutions are then derived:

$$ {a_1} = {a_1}, b = - \frac{{38}}{{69}}dp_1^4 - \frac{{15}}{{23}}ap_1^2 + \frac{{50}}{{69}}cp_1^2, {k_1} = \sqrt{\frac{8}{{69}}dp_1^2 + \frac{8}{{23}}a + \frac{4}{{69}}c}, $$
$$ {m_1} = \frac{{2( - 14dp_1^2 + 27a - 30c)}}{{(28dp_1^2 + 15a - 9c)a_1^3}}, {p_1} = {p_1}, {k_2} = {k_2}. $$

By substituting the above values in (2), we get

$$\begin{aligned} w = 2\frac{{\Omega {\kappa _1} - {\kappa _2}}}{{{\Omega ^2}}}, \end{aligned}$$
(11)

where

$$\begin{aligned} \Omega= & f(x,t)= {\mathrm{{e}}^{ - \mathrm{{i}}\left( {{p_1}x} \right) }}{\mathrm{{e}}^{{k_1}t + {k_2}}} + {m_1}{\mathrm{{e}}^{2\left( {{k_1}t + {k_2}} \right) }} + {\mathrm{{e}}^{\mathrm{{i}}\left( {{p_1}x} \right) }} + {a_1}, \\ {\kappa _1}= & - {\mathrm{{e}}^{\mathrm{{i}}{p_1}x}}p_1^2 - {\mathrm{{e}}^{{k_2} + {p_1}\sqrt{\frac{{8a}}{{23}} + \frac{{4c}}{{69}} + \frac{{8dp_1^2}}{{69}}} t - \mathrm{{i}}{p_1}x}}p_1^2, \\ {\kappa _2}= & {\left( {\mathrm{{i}}{\mathrm{{e}}^{\mathrm{{i}}{p_1}x}}{p_1} - \mathrm{{i}}{\mathrm{{e}}^{{k_2} + {p_1}\sqrt{\frac{{8a}}{{23}} + \frac{{4c}}{{69}} + \frac{{8dp_1^2}}{{69}}} t - \mathrm{{i}}{p_1}x}}{p_1}} \right) ^2}, \frac{8}{{69}}dp_1^2 + \frac{8}{{23}}a + \frac{4}{{69}}c. \end{aligned}$$

Here, a few graphical representations of the above solution are examined.

5.2 Kuznetsov-Ma-breather

The Kuznetsov-Ma breather is an explicit time-periodic solution. For instance, Kuznetsov-Ma breathers are present in the fully integrable Ablowitz-Ladik (AL) model. The following transformation will be used for Kuznetsov-Ma-Breather:

$$\begin{aligned} f(x,t) = {\mathrm{{e}}^{ - {p_1}\left( {x - {b_1}t} \right) }} + {a_1}\cos \left( {p\left( {x + {b_1}t} \right) } \right) + {a_2}\cos \left( {p\left( {x - {b_1}t} \right) } \right) , \end{aligned}$$
(12)

where \({a_1}\), \({p_1}\), p, \({a_2}\), and \({b_1}\) are real parameters. Certain equations that yield coefficient values can be acquired by inserting (12) into (3). The subsequent solutions are obtained:

$$ {a_1}={a_1}, {a_2}=0, p = \frac{{\sqrt{b} }}{2}, b>0, {p_1} = \frac{{\sqrt{ - b} }}{2}, {b_1} = - 6\sqrt{ - b}, b<0. $$

By substituting the above values in (2), we get

$$\begin{aligned} w = 2\frac{{\Omega {\kappa _1} - {\kappa _2}}}{{{\Omega ^2}}}, \end{aligned}$$
(13)

where

$$ \Omega = f(x,t)= {\mathrm{{e}}^{ - {p_1}\left( {x - {b_1}t} \right) }} + {a_1}\cos \left( {p\left( {x + {b_1}t} \right) } \right) + {a_2}\cos \left( {p\left( {x - {b_1}t} \right) } \right) , $$
$$ {\kappa _1} = - \frac{1}{4}b{\mathrm{{e}}^{ - \frac{1}{2}\sqrt{ - b} \left( {6\sqrt{ - b} t + x} \right) }} - \frac{1}{4}{a_1}b\cos \left( {\frac{1}{2}\sqrt{b} \left( { - 6\sqrt{ - b} t + x} \right) } \right) , $$
$$ {\kappa _2} = {\left( { - \frac{1}{2}\sqrt{ - b} {\mathrm{{e}}^{ - \frac{1}{2}\sqrt{ - b} \left( {6\sqrt{ - b} t + x} \right) }} - \frac{1}{2}{a_1}\sqrt{b} \sin \left( {\frac{1}{2}\sqrt{b} \left( { - 6\sqrt{ - b} t + x} \right) } \right) } \right) ^2}. $$

Here, a few graphical representations of the above solution are examined.

6 Result and Discussion

Fig. 1
figure 1

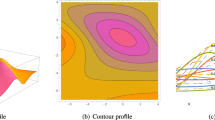
The visual depiction of w(x, t) for (5) is given. (a) 3D profile (b) contour profile (c) 2D profile, when \({a_4} = - 0.5\), \({a_2} = 0.5\), \(a = -0.5\), \(b = 0.5\), \(c = 0.5\), \(d=5\)

Full size image
Fig. 2
figure 2

The visual depiction of w(x, t) for (5) is given. (a) 3D profile (b) contour profile (c) 2D profile, when \({a_4} = 0.5\), \({a_2} = -0.5\), \(a = 0.7\), \(b = 5.5\), \(c = -0.5\), \(d=20.5\)

Full size image
Fig. 3
figure 3

The visual depiction of w(x, t) for (5) is given. (a) 3D profile (b) contour profile (c) 2D profile, when \({a_4} = 0.5\), \({a_2} = 0.5\), \(a = -0.7\), \(b = -0.5\), \(c = 6.5\), \(d=10.5\)

Full size image
Fig. 4
figure 4

The visual depiction of w(x, t) for (7) is given. (a) 3D profile (b) contour profile (c) 2D profile, when \({a_5}=0.9\), \( {a_7}=-0.5\), \( {m_1}=5.25\), \( {b_2}=-0.7\), \(c = -2.5\), \(a = -0.05\), \(a_2 = -1.5\), \(a_3 = 5.5\), \(b=0.3\)

Full size image
Fig. 5
figure 5

The visual depiction of w(x, t) for (7) is given. (a) 3D profile (b) contour profile (c) 2D profile, when \({a_5}=-0.9\), \( {a_7}=0.5\), \( {m_1}=3.25\), \( {b_2}=-0.7\), \(c = -2.5\), \(a = -0.05\), \(a_2 = 1.5\), \(a_3 = -1.5\), \(b=0.3\)

Full size image
Fig. 6
figure 6

The visual depiction of w(x, t) for (7) is given. (a) 3D profile (b) contour profile (c) 2D profile, when \({a_5}=-0.9\), \( {a_7}=0.5\), \( {m_1}=5.25\), \( {b_2}=0.7\), \(c = -0.5\), \(a = -0.05\), \(a_2 = -1.5\), \(a_3 = -5.5\), \(b=0.5\)

Full size image

The generalized reaction Duffing model has been extensively studied.The functional variable approach was developed by Attaf et al. [37, 38] to provide analytical solutions for an extensive variety of linear and nonlinear wave equations.Numerous authors improved this technique [39, 40].Aminikhah et al. studied gRDM to acquire the exact solutions using functional variable approach [41].Tian and Gao [42] studied gRDM to obtain soliton solutions by using generalized hyperbolic-function approach.In this research, we studied generalized reaction Duffing model for lump soliton, rogue waves, breather waves, Ma-breather, and Kuznetsov-Ma-breather by using some distinct ansatz transformations.In the generalized reaction Duffing model, the derived results provide significant insights into the behavior of nonlinear waves.

The found solutions, including breather waves, rogue waves, and lump solitons, have real-world applications in a variety of disciplines, including material science, quantum mechanics, solid-state physics, and electromagnetic studies. These solutions can be used to represent nonlinear wave dynamics and describe localized energy concentrations in waves. In Figs. 1, 2, and 3, the lump soliton solutions of w are obtained. Figure 1(a) depicts 3D profile of w that illustrates bright face of lump solution. Figure 2(a) depicts 3D profile of w that illustrates two bright faces of lump solution. Figure 3(a) depicts 3D profile of w that illustrates one dark and one bright face of solution. In Fig. 1(b) depicts contour profile of w. Figure 1(c) depicts 2D profile of w. Figures 2 and 3 also describe the same properties of w.

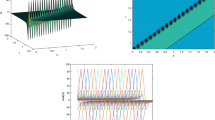
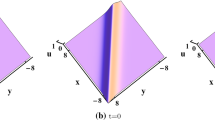
In Fig. 4, (a) depicts the appearance of some non-periodic waves, Fig. 5(a) depicts the appearance of a large, bright lump wave. Fig. 6 (a) shows bright and dark faces of rogue wave solution. In Figs. 4, 5 and 6(b) depicts contour profile and (c) depicts 2D profile of w. In Figs. 7, 8, 9, 10, 11 and 12(a) shows several bright and dark solitons as well as a periodic wave, (b) depicts contour profile and (c) depicts 2D profile of w. In Fig. 13, (a) depicts 3D profile of w which describes 2 bright faces of solution. Figure 13(b) depicts contour profile and (c) depicts 2D profile of w. In Fig. 14, (a) depicts 3D profile of w which also describes 2 bright faces of solution. Figure 14(b) depicts contour profile and (c) depicts 2D profile of w. In Fig. 15, (a) depicts 3D profile of w which describes 2 bright and one dark faces of solution. Figure 15(b) depicts contour profile and (c) depicts 2D profile of w.

Fig. 7
figure 7

The visual depiction of w(x, t) for (9) is given. (a) 3D profile (b) contour profile (c) 2D profile, when \(q=0.5\), \(b = -0.09\), \({m_2} =-0.5\), \({q_1} = -1.5\), \(a_3 = -0.5\), \(a = 0.5\), \(c = -0.5\), \(d = 10\)

Full size image
Fig. 8
figure 8

The visual depiction of w(x, t) for (9) is given. (a) 3D profile (b) contour profile (c) 2D profile, when \(q=0.05\), \(b = -0.1\), \({m_2} =0.05\), \({q_1} = 1.5\), \(a_3 = 0.5\), \(a = -0.5\), \(c = 0.5\), \(d = 10\)

Full size image
Fig. 9
figure 9

The visual depiction of w(x, t) for (9) is given. (a) 3D profile (b) contour profile (c) 2D profile, when \(q=0.5\), \(b = -0.09\), \({m_2} =0.05\), \({q_1} = -0.5\), \(a_3 = 0.5\), \(a = -0.5\), \(c = 0.5\), \(d = 10\)

Full size image
Fig. 10
figure 10

The visual depiction of w(x, t) for (11) is given. (a) 3D profile (b) contour profile (c) 2D profile, when \({p_1}=0.7\), \({k_2}=1.5\), \(a=4\), \(c=0.5\), \(d=10\), \({a_1}=1\)

Full size image
Fig. 11
figure 11

The visual depiction of w(x, t) for (11) is given. (a) 3D profile (b) contour profile (c) 2D profile, when \({p_1}=-0.5\), \({k_2}=-0.5\), \(a=-4\), \(c=-0.5\), \(d=10\), \({a_1}=1\)

Full size image
Fig. 12
figure 12

The visual depiction of w(x, t) for (11) is given.(a) 3D profile (b) contour profile (c) 2D profile, when \({p_1}=0.5\), \({k_2}=0.5\), \(a=-4\), \(c=0.5\), \(d=10\), \({a_1}=1\)

Full size image
Fig. 13
figure 13

The visual depiction of w(x, t) for (13) is given. (a) 3D profile (b) contour profile (c) 2D profile, when \(b=0.5\), \({a_1}=-10.5\)

Full size image
Fig. 14
figure 14

The visual depiction of w(x, t) for (13) is given. (a) 3D profile (b) contour profile (c) 2D profile, when \(b=0.7\), \({a_1}=15.5\)

Full size image
Fig. 15
figure 15

The visual depiction of w(x, t) for (13) is given. (a) 3D profile (b) contour profile (c) 2D profile, when \(b=0.5\), \({a_1}=-2.5\)

Full size image

7 Conclusions

In this paper, we applied some ansatz transformations to the generalized reaction Duffing model in order to derive the innovative soliton solutions such as lump soliton, rogue waves, breather waves, Ma-breather and Kuznetsov-Ma-breather. In non linear evaluation equations, the lump soliton is a form of solitary wave solution. Rogue wave represents for rare and exceptionally large solutions to non linear waves equations in mathematics. These waves have attracted a lot of attention because of their severe and erratic in nature. By customizing the ansatz transformations to the characteristics of this specific dynamical system, the research uncovers the complex nonlinear behaviors and dynamics that may not be easily observable using standard methods. By selecting appropriate parameter values, specific findings are displayed in 2D, 3D, and contour profiles to illustrate the physical behavior of solutions. Finally, in the results and discussion section, we present the geometry of our solutions.