The Influence of Counter Rotating Terms on the Entanglement Dynamics of Two Dipole-Coupled Qutrits Interacting with a Two-Mode Field: Intensity-Dependent Coupling Approach

Abstract

In this paper we propose a scheme containing two qutrits (Λ-type three-level atoms) that interact with a two-mode quantized field using the Rabi model (i.e., without considering the rotating wave approximation (RWA)), where the dipole-dipole (D-D) interaction between the two atoms is also taken into account. At first, we transform the corresponding Rabi model Hamiltonian to the generalized Jaynes-Cummings model (JCM) i.e., with intensity-dependent atom-field coupling, via an approximate method. Afterwards, by solving the time-dependent Schrödinger equation and thus achieving the state vector of the system at arbitrary time, we readily arrive at the density matrix of the system. In this way, by attainment of the reduced density matrices for different constituents of the system, we are able to evaluate their entanglement between various system components via the calculation of linear entropy. By an overview of the numerical results, regular and irregular oscillations, collapse-revival (CR) phenomena, low and high, quasi-stable or even stable amount of entanglement can be observed. Also, the death and then sudden birth of entanglement are available in some cases. Among the above-mentioned consequences, stability and quasi-stability of entanglement (under the influence of both aforesaid effects, CRTs and D-D interaction) is practically remarkable due to its various usefulness in quantum information processing schemes.

1 Introduction

Quantum entanglement [1] has been considered as one of the most important non-classical aspects of quantum physics. This phenomenon is now of particular importance in the field of quantum information science and technology [2]. As a few of its applications, one may refer to the quantum computing [3], quantum teleportation [4,5,6], entanglement swapping [7,8,9,10], quantum dense coding [11,12,13], quantum key distribution [14, 15] and cryptography [16, 17].

The standard Jaynes-Cummings model (JCM), as one of the simplest model for describing and generation of entanglement, contains the interaction between a two-level atom with a single-mode quantized field [18]. As some of the advantages of this model, one may refer to its simplicity for generalization to more complicated atoms and fields, as well as its ability to predict collapse-revival (CR) patterns in atomic population inversion and other quantities, the results of which are largely consistent with experimental realizations. It is noticeable that, this model is accompanied with the rotating wave approximation (RWA), i.e., the counter rotating terms (CRTs) in this model are neglected [19] and thus, it is one of the solvable models in quantum optics field [18, 20]. In this line, Tavis-Cummings model is a generalization of JCM in which the two-level atom is replaced by two or more two- or multi-level atoms and the field may be replaced by multi-mode quantized field [21]. As a few of such schemes one may refer to: systems including two two- and three-level atoms interacting with a two-mode quantized field [22, 23], two qubits each of which interacts with a single-mode field in two separate cavities [24], a moving three-level atom that interacts with a two-mode quantized field [25], two three-level atoms that interact with a two-mode field [26] as well as other more or less similar atom-field interacting models in the literature [27,28,29,30,31,32,33]. Note that, CRTs describe virtual transitions between atomic and field states, i.e., unstable energy terms; so that they are usually ignored in atom-field interactions (especially in weak coupling regimes) wherein the RWA is valid [19]. However, such terms cannot be ignored in strong atom-field couplings. To take into account CRTs (virtual photons), while complicates computations, but can create new features such as the spontaneous release of virtual photons [34, 35] and non-classical photon statistics [36, 37]. These terms can also influence on Zeno and anti-Zeno effects [38, 39] and the CR dynamics [40].

In addition, as we implicitly mentioned in above, models describing atom-field interacting quantum systems, even the simplest of them, i.e., the standard JCM, may be solved analytically only in the RWA (if the CRTs are neglected) [18, 20]; in fact the existence of CRTs creates serious problems in arriving at analytical solution of the time-dependent Schrödinger equation. Therefore, a lot of researches has been performed in order to remove such limitations, which are mainly based on numerical solution.

The dynamics of a micro-maser based on the interaction of light and matter in the absence of RWA has been studied in [41]. The Rabi model, in the presence of gravity has been discussed [42]. This model using the coherent state generalization technique has been reviewed in [43]. The Rabi model under non-resonant conditions has been examined in [44], where it is shown that the RWA is not satisfactory even under complete resonant conditions for strong coupling coefficients. The authors in [45] discussed the effect of anti-bunching of the field in a system of interaction between a two-level atom and a single-mode quantized field without RWA. Also, the effect of CRTs on the population inversion and squeezed field in a system consisting of the interaction between a two-level atom with a single-mode quantized field has been recently studied in [46]. The effect of virtual photon processes (CRTs) on quantum entropy and entanglement while a two-level atom interact with a single-mode radiation field has been evaluated in [47]. The statistics of photon and the total energy of a system containing of a two-level atom interacting with a single-mode quantized field in the absence of RWA have been evaluated using the coherent state propagator [48]. Also, the eigen-energy spectrum as well as a formalism for exact analytical form of the eigen-functions and eigen-values of the Rabi model have been discussed in [49, 50]. Entanglement dynamics of two independent atoms without RWA has been discussed [51]. The effective Hamiltonian for two-photon processes in the system of a three-level atom interacting with a single-mode quantized radiation field beyond the RWA has been obtained and studied using the perturbation method [52].

However, recently many attempts have been made to solve the problem analytically or approximately analytically while CRTs are taken into account; among them we may refer to [53,54,55] wherein the perturbation method has been utilized. In detail, recently an appropriate analytical method, based on perturbation theory has been proposed for a two-level atom which interacts with a single-mode field beyond the RWA [53, 54]. Following this method, a system of interaction between a Λ-type three-level atom with a single-mode quantized field has been investigated by one of us [55]. In the above-mentioned two models, either for two- or three-level atoms, it is shown that taking into account the CRTs is equivalent to considering the intensity-dependent (nonlinear) atom-field interaction with some particular nonlinearity function in the dynamical Hamiltonian, i.e., we concern with a Hamiltonian with RWA, however, with the price of appearing a specific intensity-dependent atom-field coupling (recall that atom-field intensity-dependent coupling first introduced by Buck and Sukumar in [56, 57]). In this respect and in direct relation to our present work, more recently, one of us extended the latter-mentioned models to the interaction between various configurations of three-level atoms with a quantized two-mode radiation field [58], wherein we encountered with intensity-dependent Hamiltonians with some particular intermixed intensity-dependent couplings; by this we mean that while in the first steps of outlining the model we assumed that each mode of the field interacts individually with only one of the transition lines of the considered three-level atoms separately, in the resultant effective Hamiltonians, in each of the interacting transition lines, both mode operators of the field are appeared in the corresponding nonlinearity functions. In addition, noticing that the D-D interaction possesses particular importance in atoms with enough strong dipole moment values such as Rydberg atoms (see [59,60,61,62] for their usefulness), using the approach in [53, 54] we recently discussed the influence of D-D interaction on the entanglement and population inversion in the system of two qubits interacting with a two-mode quantized field beyond the RWA [63].

Fig. 1

The scheme of the interaction between two Λ-type three-level atoms and a two-mode field in the presence of both D-D interaction and CRTs

We end our introductory discussion with mentioning that, numerous advantages for three-level systems relative to two-level systems can be enumerated in quantum information processing [64]. Quantum cryptography using three-dimensional systems are more secure than two-dimensional systems in eavesdropping, so that they play an important role in optimization or preventing eavesdropping [65]. Also, three-level systems have more evident quantum nonlocality compared with two-level systems [66]. The importance and aforesaid advantages motivated us to study three-level atomic systems here. Therefore, summing up the above-mentioned facts, in this paper we have considered a system of two three-level atoms interacting with a two-mode quantum field in an optical cavity by taking into account CRTs as well as D-D interaction, and then examined the influence of the two mentioned effects on the entanglement dynamics of different components of the system (Fig. 1).

The contents of this paper are arranged in this order: In Section 2 by proposing a scheme containing two qutrits interacting with a two-mode cavity field, we introduce an effective Hamiltonian using an approximate method based on perturbation theory, while the CRTs are also taken into account. In the continuation, we solve the associated time-dependent Schrödinger equation in order to achieve the state vector of the system and also the reduced density matrices of the various components of the system. Then, the dynamics of entanglement associated with different parts of the system in the presence and absence of the D-D interaction as well as the CRTs is examined in Section 3. Finally, we give a summary and a brief of concluding remarks in Section 4.

2 The Model Hamiltonian and its Solution

As mentioned in the previous section, in the strong atom-field coupling regimes, the RWA is inoperative and the CRTs can no longer be ignored. So in this section by inspiring from the introduced method in Refs. [53,54,55] and specially [58], we are going to consider a system of two identical Λ-type qutrits interacting with a two-mode quantized field in an optical cavity while CRTs are also taken into account. At first, the Hamiltonian of this system in the dipole approximation can be written as follows,

$$ \begin{array}{@{}rcl@{}} \hat{H} = \hat{H}_{free} + \hat{H}_{RWA} + \hat{H}_{CRT}. \end{array} $$

(1)

Here, the free Hamiltonians of atoms and field, atom-field interaction and CRTs are defined as follows respectively,

$$ \begin{array}{@{}rcl@{}} \hat{H}_{free}={\nu_{1}}\hat{a}^{\dag} \hat{a} + {\nu_{2}}\hat{b}^{\dag} \hat{b} + \sum\limits_{j} {{E_{j}}{\hat{\sigma }_{jj}}},\quad j = a,b,c,\acute{a},\acute{b},\acute{c}, \end{array} $$

(2)

$$ \begin{array}{@{}rcl@{}} {\hat{H}_{RWA}}&=&{g_{1}}\left( \hat{a}\hat{\sigma}_{ab}^{+} + {\hat{a}^{\dag} }\hat{\sigma}_{ab}^{-} \right) + {g_{2}}\left( \hat{b}\hat{\sigma}_{ac}^{+} + {\hat{b}^{\dag} }\hat{\sigma}_{ac}^{-} \right)\\ &+&\acute{g}_{1}\left( \hat{a}\hat{\sigma}_{\acute{a}\acute{b}}^{+} + {\hat{a}^{\dag} }\hat{\sigma}_{\acute{a}\acute{b}}^{-} \right) +\acute{g}_{2}\left( \hat{b}\hat{\sigma}_{\acute{a}\acute{c}}^{+} + {\hat{b}^{\dag} }\hat{\sigma}_{\acute{a}\acute{c}}^{-} \right), \end{array} $$

(3)

$$ \begin{array}{@{}rcl@{}} {\hat{H}_{CRT}}&=&{g_{1}}\left( {{\hat{a}^{\dag} }\hat{\sigma}_{ab}^{+} + \hat a\hat{\sigma}_{ab}^{-} } \right) + {g_{2}}\left( {{\hat{b}^{\dag} }\hat{\sigma}_{ac}^{+} +\hat b\hat{\sigma}_{ac}^{-} } \right)\\ &+&\acute{g}_{1}\left( {{\hat{a}^{\dag} }\hat{\sigma}_{\acute{a}\acute{b}}^{+} +\hat a\hat{\sigma}_{\acute{a}\acute{b}}^{-} } \right) + \acute{g}_{2}\left( {{\hat{b}^{\dag} }\hat{\sigma}_{\acute{a}\acute{c}}^{+} + \hat b\hat{\sigma}_{\acute{a}\acute{c}}^{-} } \right), \end{array} $$

(4)

where ν_i (i = 1,2) are the frequencies of each mode of the field within the cavity, and $\hat {a}$ ($\hat {b}$) and $\hat {a}^{\dag }$ ($\hat {b}^{\dag }$) are bosonic annihilation and creation operators related to each of the corresponding field modes, respectively. Also, $\hat {\sigma }^{+}_{ij}=|i\rangle \langle j|$ ($\hat {\sigma }^{-}_{ij}=|j\rangle \langle i|$) is atomic raising (lowering) operator. In addition, the parameters g₁, $\acute {g}_{1}$ (g₂, $\acute {g}_{2}$) are atom-field coupling coefficients associated with the left (right) allowed transition lines of atoms 1, 2. Notice that |a〉, |b〉, |c〉, $|\acute {a}\rangle$, $|\acute {b}\rangle$ and $|\acute {c}\rangle$ are the atomic levels of each qutrit with energies E_a, E_b, E_c, $E_{\acute {a}}$, $E_{\acute {b}}$ and $E_{\acute {c}}$, respectively. Also, the transition from level |b〉($|\acute {b}\rangle$) to |c〉($|\acute {c}\rangle$) and vice versa is prohibited in the electric-dipole approximation and thus, only the transitions $|a\rangle (|\acute {a}\rangle )\rightleftarrows |b\rangle (|\acute {b}\rangle )$ (left lines) and $|a\rangle (|\acute {a}\rangle )\rightleftarrows |c\rangle (|\acute {c}\rangle )$ (right lines) are allowed.

It is not necessary to state that considering the time-dependent Schrödinger equation based on the above Hamitonian does not have an analytical solution. Indeed, due to the presence of CRTs, the coupled differential equations of the probability amplitudes of the state vector of the system can no longer be solved analytically. Moreover, many attempts have been made to solve the related equations analytically [53,54,55, 58]. In this line, a relatively accurate analytical method based on perturbation theory for a system of interaction between a three-level atom with a two-mode quantized field has been recently presented in [58] by one of us. Following the introduced approach, we finally obtain the effective Hamiltonian for each atom in our above-desired system as:

$$ \begin{array}{@{}rcl@{}} {{\hat{H}}_{eff}}&=&{\hat{H}_{free}}+\hat{H}^{(ID)}_{RWA}+{\varepsilon_{1}}{g_{1}}\left[ {\left( {{\hat{n}_{a}} + \frac{1}{2}} \right)\hat{\sigma}_{z}^{ab} + \frac{{{\hat{\sigma }_{cc}}}}{2} - \frac{1}{2}} \right]\\ &+&{\varepsilon_{2}}{g_{2}}\left[ {\left( {{\hat{n}_{b}} + \frac{1}{2}} \right)\hat{\sigma}_{z}^{ac} + \frac{{{\hat{\sigma }_{bb}}}}{2} - \frac{1}{2}} \right]+{\varepsilon_{3}}{\acute{g}_{1}}\left[ {\left( {{\hat{n}_{a}} + \frac{1}{2}} \right)\hat{\sigma}_{z}^{\acute{a}\acute{b}} + \frac{{{\hat{\sigma }_{\acute{c}\acute{c}}}}}{2} - \frac{1}{2}} \right]\\ &+&{\varepsilon_{4}}{\acute{g}_{2}}\left[ {\left( {{\hat{n}_{b}} + \frac{1}{2}} \right)\hat{\sigma}_{z}^{\acute{a}\acute{c}} + \frac{{{\hat{\sigma }_{\acute{b}\acute{b}}}}}{2} - \frac{1}{2}} \right], \end{array} $$

(5)

where $\hat {\sigma }_{z}^{ij} = {\hat {\sigma }_{ii}} - {\hat {\sigma }_{jj}}$, ${\hat {\sigma }_{ij}} = \left | i \right \rangle \left \langle j \right |$, and $\hat {n}_{a}=\hat {a}^{\dag }\hat {a}$, $\hat {n}_{b}=\hat {b}^{\dag }\hat {b}$.

Furthermore, the first two terms of above Hamiltonian can be distinctly rewritten as:

$$ \begin{array}{@{}rcl@{}} {\hat{H}_{free}}&=&\sum\limits_{j = 1}^{2} {{\nu_{j}}{\mathbb{N}_{j}}} + \frac{{2{{\Delta}_{ab}} - {{\Delta}_{ac}}}}{3}\hat{\sigma}_{z}^{ab}+ \frac{{2{{\Delta}_{ac}} - {{\Delta}_{ab}}}}{3}\hat{\sigma}_{z}^{ac}\\ & +& \frac{{2{{\Delta}_{\acute{a}\acute{b}}} - {{\Delta}_{\acute{a}\acute{c}}}}}{3}\hat{\sigma}_{z}^{\acute{a}\acute{b}}+ \frac{{2{{\Delta}_{\acute{a}\acute{c}}} - {{\Delta}_{\acute{a}\acute{b}}}}}{3}\hat{\sigma}_{z}^{\acute{a}\acute{c}} + \frac{1}{3}\sum\limits_{i = 1}^{2} {{E_{i}}{\hat{I}_{i}}}, \end{array} $$

(6)

$$ \begin{array}{@{}rcl@{}} \hat{H}^{(ID)}_{RWA}&=&{g_{1}}\left[ {{f_{1}}({\hat{n}_{a}},{\hat{n}_{b}}) {\hat{a}^{\dag} }\hat{\sigma}_{ab}^{-} + \hat{\sigma}_{ab}^{+} \hat a {f_{1}}({\hat{n}_{a}},{\hat{n}_{b}})} \right]\\ &+& {g_{2}}\left[ {{f_{2}}({\hat{n}_{a}},{\hat{n}_{b}}) {\hat{b}^{\dag} }\hat{\sigma}_{ac}^{-} + \hat{\sigma}_{ac}^{+} \hat b {f_{2}}({\hat{n}_{a}},{\hat{n}_{b}})} \right]\\ &+& {\acute{g}_{1}}\left[ {{f_{3}}({\hat{n}_{a}},{\hat{n}_{b}}) {\hat{a}^{\dag} }\hat{\sigma}_{\acute{a}\acute{b}}^{-} + \hat{\sigma}_{\acute{a}\acute{b}}^{+} \hat a {f_{3}}({\hat{ n}_{a}},{\hat{n}_{b}})} \right]\\ &+& {\acute{g}_{2}}\left[ {{f_{4}}({\hat{n}_{a}},{\hat{n}_{b}}) {\hat{b}^{\dag} }\hat{\sigma}_{a\acute{}\acute{c}}^{-} + \hat{\sigma}_{\acute{a}\acute{c}}^{+} \hat b {f_{4}}({\hat{ n}_{a}},{\hat{n}_{b}})} \right]. \end{array} $$

(7)

Various parameters in the above relations are defined as below:

$$ \begin{array}{@{}rcl@{}} {\mathbb{N}_{1}}&=&{\hat{n}_{a}} + \frac{\hat{\sigma_{z}^{ab}}}{3} + \frac{\hat{\sigma}_{z}^{\acute{a}\acute{b}}}{3},\qquad {\mathbb{N}_{2}} = {\hat{n}_{b}} + \frac{\hat{\sigma_{z}^{ac}}}{3} + \frac{\hat{\sigma}_{z}^{\acute{a}\acute{c}}}{3},\\ {\Delta}_{ab}&=&{E_{a}} - {E_{b}} - {\nu_{1}},\qquad{{\Delta}_{ac}} = {E_{a}} - {E_{c}} - {\nu_{2}},\\ {{\Delta}_{\acute{a}\acute{b}}}&=&{E_{\acute{a}}} - {E_{\acute{b}}} - {\nu_{1}},\qquad{{\Delta}_{\acute{a}\acute{c}}} = {E_{\acute{a}}} - {E_{\acute{c}}} - {\nu_{2}},\\ \varepsilon_{1}&=&\frac{g_{1}}{{E_{a}} - {E_{b}} + {\nu_{1}}},\qquad \varepsilon_{2}=\frac{g_{2}}{{E_{a}} - {E_{c}} + {\nu_{2}}},\\ \varepsilon_{3}&=&\frac{\acute{g}_{1}}{{E_{\acute{a}}} - {E_{\acute{b}}} + {\nu_{1}}},\qquad \varepsilon_{4}=\frac{\acute{g}_{2}}{{E_{\acute{a}}} - {E_{\acute{c}}} + {\nu_{2}}},\\ {\hat{I}_{1}}&=&{\hat{\sigma }_{aa}} + {\hat{\sigma }_{bb}} + {\hat{\sigma }_{cc}},\qquad{E_{1}} = {E_{a}} + {E_{b}} + {E_{c}},\\ {\hat{I}_{2}}&=&{\hat{\sigma }_{\acute{a}\acute{a}}} + {\hat{\sigma }_{\acute{b}\acute{b}}} + {\hat{\sigma }_{\acute{c}\acute{c}}},\qquad{E_{2}} = {E_{\acute{a}}} + {E_{\acute{b}}} + {E_{\acute{c}}}. \end{array} $$

(8)

And in particular, the four nonlinearity functions in (7) are defined by the following statements,

$$ \begin{array}{@{}rcl@{}} {f_{1}}({\hat{n}_{a}},{\hat{n}_{b}})&=&1 - {\varepsilon_{1}^{2}}{\hat{n}_{a}} - \frac{{{\varepsilon_{2}^{2}}}}{2}{\hat{n}_{b}},\quad{f_{2}}({\hat{n}_{a}},{\hat{n}_{b}}) = 1 - {\varepsilon_{2}^{2}}{\hat{n}_{b}} - \frac{{{\varepsilon_{1}^{2}}}}{2}{\hat{n}_{a}},\\ {f_{3}}({\hat{n}_{a}},{\hat{n}_{b}})&=&1 - {\varepsilon_{3}^{2}}{\hat{n}_{a}} - \frac{{{\varepsilon_{4}^{2}}}}{2}{\hat{n}_{b}},\quad{f_{4}}({\hat{n}_{a}},{\hat{n}_{b}}) = 1 - {\varepsilon_{4}^{2}}{\hat{n}_{b}} - \frac{{{\varepsilon_{3}^{2}}}}{2}{\hat{n}_{a}}. \end{array} $$

(9)

As is observed, comparing with the initial Hamiltonian (1), in the effective Hamiltonian introduced in (5) several intensity-dependent (nonlinear) functions are appeared as $f_{i}(\hat {n}_{a},\hat {n}_{b}),\quad i=1,2,3,4$. An interesting feature of this approach is that: usually the intensity-dependent functions which are found in the literature [56, 57, 67] are only dependent on one of the field modes even in the two-mode fields and with arbitrary functions, usually chosen as $\sqrt {\hat {n}}$ [68,69,70,71,72] $\frac {1}{\sqrt {\hat {n}}}$ [30, 73, 74] and etc. In other words, these functions are chosen quite arbitrarily, so that there is no real relation between the considered functions and the details of atom-field interaction in the systems under study. However, in our interacting model, even though only one mode, say, mode 1, interacts with one of the transition lines in the qutrit, the nonlinearity function associated with each line admixes the two number operators $\hat {n}_{a}$, $\hat {n}_{b}$ associated with the two field modes, i.e., we have $f_{i}(\hat {n}_{a},\hat {n}_{b})$ and not $f_{i}(\hat {n}_{a})$, $f_{i}(\hat {n}_{b})$ or even $f_{i}(\hat {n}_{a})f_{i}(\hat {n}_{b})$, in addition to the fact that the form functions of the intensity-dependent function are explicitly obtained.

To consider the D-D interaction in the desired system, the Hamiltonian responsible to this type of interaction may be added to the effective Hamiltonian (5). To do this task, we write the Hamiltonian associated with D-D interaction between the two qutrits as,

$$ \begin{array}{@{}rcl@{}} \hat{H}_{D-D}=\lambda_{1}\hat{\sigma}^{+}_{ab}\hat{\sigma}^{-}_{\acute{a}\acute{b}}+\lambda_{2}\hat{\sigma}^{+}_{ab}\hat{\sigma}^{-}_{\acute{a}\acute{c}}+\lambda_{3}\hat{\sigma}^{+}_{ac}\hat{\sigma}^{-}_{\acute{a}\acute{b}}+\lambda_{4}\hat{\sigma}^{+}_{ac}\hat{\sigma}^{-}_{\acute{a}\acute{c}}+H. c., \end{array} $$

(10)

where λ_i (i = 1,2,3,4) is the coefficients dependent on the strength of D-D interaction terms. Finally, the new effective Hamiltonian for our system can be written as follows:

$$ \begin{array}{@{}rcl@{}} {{\hat{\mathcal{H}}}_{eff}}&=&\hat{H}_{free}+\hat{H}_{RWA}^{(ID)}+\hat{H}_{D-D}+{\varepsilon_{1}}{g_{1}}\left[ {\left( {{\hat{n}_{a}} + \frac{1}{2}} \right)\hat{\sigma}_{z}^{ab} + \frac{{{\hat{\sigma }_{cc}}}}{2} - \frac{1}{2}} \right]\\ &&+{\varepsilon_{2}}{g_{2}}\left[ {\left( {{\hat{n}_{b}} + \frac{1}{2}} \right)\hat{\sigma}_{z}^{ac} + \frac{{{\hat{\sigma }_{bb}}}}{2} - \frac{1}{2}} \right]+{\varepsilon_{3}}{\acute{g}_{1}}\left[ {\left( {{\hat{n}_{a}} + \frac{1}{2}} \right)\hat{\sigma}_{z}^{\acute{a}\acute{b}} + \frac{{{\hat{\sigma }_{\acute{c}\acute{c}}}}}{2} - \frac{1}{2}} \right]\\ &&+{\varepsilon_{4}}{\acute{g}_{2}}\left[ {\left( {{\hat{n}_{b}} + \frac{1}{2}} \right)\hat{\sigma}_{z}^{\acute{a}\acute{c}} + \frac{{{\hat{\sigma }_{\acute{b}\acute{b}}}}}{2} - \frac{1}{2}} \right]. \end{array} $$

(11)

Now, which we arrived at a solvable Hamiltonian, in order to investigate any physical property, say the entanglement dynamics, we should first solve the time-dependent Schrödinger equation ${{\hat {{\mathscr{H}}}}_{eff}}|\psi (t)\rangle =i \frac {\partial }{\partial t}|\psi (t)\rangle$ using the Hamiltonian in (11). Assuming the initial state of the system in the form of a superposition of the atomic ground and excited states, and supposing the field modes to be initially in their vacuum state, we have the normalized atom-field state as below,

$$ \begin{array}{@{}rcl@{}} |\psi(0)\rangle=\left( \sin^{2} \alpha|a, \acute{a}\rangle+\sin \alpha \cos \alpha |b, \acute{b}\rangle+\cos \alpha |c, \acute{c}\rangle\right)\bigotimes|0, 0\rangle. \end{array} $$

(12)

A typical initial condition has been used in Refs. [24, 26, 63]. Also note that, if one chooses the parameter α such that ${\sin \limits } \alpha =0$, or ${\cos \limits } \alpha =0$ then we have no atomic superposition, no coherence and in this case no (initial) entanglement. Consequently, usually the parameter α has been named as coherence parameter. Accordingly, in this case the general state of the desired system at any time t can be prescribed as:

$$ \begin{array}{@{}rcl@{}} |\psi(t)\rangle&=&y_{1}(t)|a, \acute{a}, 0, 0\rangle+y_{2}(t)|b, \acute{a}, 1, 0\rangle+y_{3}(t)|b, \acute{a}, 0, 1\rangle+y_{4}(t)|c, \acute{a}, 1, 0\rangle\\ &+&y_{5}(t)|c, \acute{a}, 0, 1\rangle+y_{6}(t)|a, \acute{b}, 1, 0\rangle+y_{7}(t)|a, \acute{b}, 0, 1\rangle+y_{8}(t)|a, \acute{c}, 1, 0\rangle\\ &+&y_{9}(t)|a, \acute{c}, 0, 1\rangle+y_{10}(t)|b, \acute{b}, 1, 1\rangle+y_{11}(t)|c, \acute{c}, 1, 1\rangle+y_{12}(t)|b, \acute{c}, 1, 1\rangle\\ &+&y_{13}(t)|c, \acute{b}, 1, 1\rangle+y_{14}(t)|b, \acute{c}, 2, 0\rangle+y_{15}(t)|b, \acute{c}, 0, 2\rangle+y_{16}(t)|c, \acute{c}, 0, 2\rangle\\ &+&y_{17}(t)|b, \acute{b}, 2, 0\rangle+y_{18}(t)|c, \acute{b}, 2, 0\rangle+y_{19}(t)|c, \acute{b}, 0, 2\rangle+y_{20}(t)|b, \acute{b}, 0, 0\rangle\\ &+&y_{21}(t)|c, \acute{c}, 0, 0\rangle. \end{array} $$

(13)

We should mention that the obtained intermixed intensity-dependent Hamiltonian in (11) results in working in the Hilbert space with the used bases in (13). The state bases is closed in the considered space, unlike the original Rabi model in (1) for which no closed bases is accessible, the fact that makes the latter model unsolvable. Although at first we supposed that the first mode interacts with the left transition $|a\rangle \rightleftarrows |b\rangle$ corresponding to the field mode ν₁ and the second mode with the right transition $|a\rangle \rightleftarrows |c\rangle$ with the field frequency ν₂, distinctly (and the same for the second atom), however, our used approach led to an intermixed intensity-dependent coupling (please see (7) and also Ref. [58]). This observation, breaks down our latter-mentioned restriction. Considering this realization, all considered bases in (13) can be justifiable. Meanwhile, in order to obtain the corresponding coefficients y₁(τ),y₂(τ),⋯ ,y₂₁(τ); by definition of the rescaled time $\uptau =\frac {2 g_{1}t}{\pi }$ and solving the Schrödinger equation, we will arrive at 21 coupled differential equations (see Appendix A). Via solving these equations, we found the explicit form of the general atom-field quantum state of the system (|ψ(τ)〉), however, the explicit solutions cannot be provided here due to their length. In the continuation, the density matrix of the system under consideration can be easily described as $\hat {\rho }(\uptau )=|\psi (\uptau )\rangle \langle \psi (\uptau )|$. Then, via taking the trace over the “atom 2+field 1+field 2” and “field 1+field 2”, one can achieve the reduced density matrices of “atom 1” and “atom 1+atom 2”, respectively,

$$ \begin{array}{@{}rcl@{}} \hat{\rho}_{A_{1}}(\uptau)=Tr_{A_{2},F_{1},F_{2}}[\hat{\rho}(\uptau)]=\left( \begin{array}{ccc} r_{11} & 0 & 0 \\ 0 & r_{22} & r_{23} \\ 0 & r^{\ast}_{23} & r_{33} \end{array} \right), \end{array} $$

(14)

and

$$ \begin{array}{@{}rcl@{}} \hat{\rho}_{A_{1}A_{2}}(\uptau)=Tr_{F_{1},F_{2}}[\hat{\rho}(\uptau)]=\left( \begin{array}{ccccccccc} z_{11} & 0 & 0 & 0 & 0 & z_{16} & z_{17} & 0 & 0 \\ 0 & z_{22} & z_{23} & z_{24} & z_{25} & 0 & 0 & 0 & 0 \\ 0 & z^{\ast}_{23} & z_{33} & z_{34} & z_{35} & 0 & 0 & 0 & 0 \\ 0 & z^{\ast}_{24} & z^{\ast}_{34} & z_{44} & z_{45} & 0 & 0 & 0 & 0 \\ 0 & z^{\ast}_{25} & z^{\ast}_{35} & z^{\ast}_{45} & z_{55} & 0 & 0 & 0 & 0 \\ z^{\ast}_{16} & 0 & 0 & 0 & 0 & z_{66} & z_{67} & z_{68} & z_{69} \\ z^{\ast}_{17} & 0 & 0 & 0 & 0 & z^{\ast}_{67} & z_{77} & z_{78} & z_{79} \\ 0 & 0 & 0 & 0 & 0 & z^{\ast}_{68} & z^{\ast}_{78} & z_{88} & z_{89} \\ 0 & 0 & 0 & 0 & 0 & z^{\ast}_{69} & z^{\ast}_{79} & z^{\ast}_{89} & z_{99} \end{array} \right), \end{array} $$

(15)

where the nonzero elements of above matrices are presented in Appendix A. Our goal in this study is to investigate the effect of D-D interaction and virtual photons (CRTs) on the entanglement dynamics of different components of the system. Therefore, we will pay our attention to the linear entropy as a criterion to examine this quantity using the above reduced matrices.

3 Entanglement Evaluation Using the Linear Entropy

Investigating the amount of entanglement between subsystems associated with different pure systems from the general system is one of the most important issues in the field of quantum technologies. There are various appropriate criteria for examining this quantity in systems consisting of two qubits such as concurrence [75, 76] and negativity [77, 78]. Since we are now dealing with a system of three-level atoms, the linear entropy is considered as a suitable criterion for examining the entanglement degree of different constituents of the system. In a compound system consisting of two subsystems A and B, linear entropy is described as follows [79],

$$ \begin{array}{@{}rcl@{}} S_{A(B)}(t)= 1-Tr[\hat{\rho}^{2}_{A(B)}(t)], \end{array} $$

(16)

where subscripts A and B belong to subsystems of the quantum system after taking trace from another one ($\hat {\rho }_{A(B)}(t)=Tr_{B(A)}[\hat {\rho }(t)]$). In general, the range of the linear entropy (as a parameter to evaluate the degree of purity of each system) for systems with dimensions m × n, assuming that d = min(m,n), changes from zero (for a pure state) to $\frac {d-1}{d}$ (for a state with maximum entanglement) [80,81,82].

This quantity for “atom 1” of our system is obtained as $S_{A_{1}}(\uptau )=1-r^{2}_{11}-r^{2}_{22}-r^{2}_{33}-2|r_{23}|^{2}$ using (14). Without loss of generality, throughout the following plots all perturbation parameters are taken equal (except for Fig. 9), i.e., 𝜖₁ = ..... = 𝜖₄ = 𝜖. Also whenever we write in the figure captions that λ is equal to a number, by this we mean that we assumed all coefficients of the D-D interactions are equal, i.e., λ₁ = λ₂ = λ₃ = λ₄ = λ. It should be noted that in all plotted figures in the continuation of the paper four different conditions including,

• (a) without D-D interaction and CRTs,

• (b) without D-D interaction and with CRTs,

• (c) with D-D interaction and without CRTs,

• (d) with D-D interaction and CRTs,

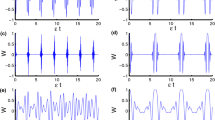
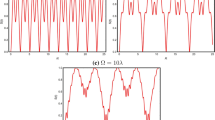
are considered. Figures 2, 3, 4, 5 and 6 are plotted in the continuation for $S_{A_{1}}(\uptau )$, i.e., the linear entropy of “atom 1 ” versus rescaled time τ for different values of the atomic coherence angles α = π/2, α = π/4 and α = π/6, which describes the amount of entanglement of “atom 1 ” with the other components of the system. Note that we used the scaled (dimensionless) time and all involved parameters like $\acute {g}_{1}, g_{2}, \acute {g}_{2}, \nu _{1}, \nu _{2},...$ are considered relative to g₁. As is expected, the numerical results shown by these plots refer to the fact that there is no initial entanglement for α = π/2 in all cases in Figs. 2-6. In the event that for α = π/4 and α = π/6, the entanglement is well visible at the beginning of the interaction (the linear entropy for α = π/4 (α = π/6) is about 0.625 (0.4)). In more detail, regarding Fig. 2, the degree of entanglement never reaches zero for different atomic coherences α with the passage of time unless at a few moments of time in Figs. 2a and b. In addition, quasi-stable value (even though not high) of entanglement may be achieved for α = π/6. Looking at Fig. 2, we find that the typical CR phenomena is accessible for all values of α unless the case α = π/6. But, by comparing the subspecies of this figure, it can be seen that the number, as well as the pattern of CRs increase in the presence of D-D interaction and CRTs, generally. In Fig. 3, typical CR phenomenon is visible only for α = π/2 in all subspecies (a)-(d) with some changes in their patterns. Also, the quasi-stability of entanglement (ignoring the small fluctuations) in this figure can be achieved for α = π/4 and α = π/6. Taking a look on the results of Fig. 4 shows that typical CR phenomenon occurs only in the absence of D-D interaction, therefore, it seems that D-D interaction destroys the CR phenomenon and thus the entanglement experiences irregular fluctuations. Also, for α = π/2, in the absence of both mentioned effects (CRTs and D-D interaction), the degree of entanglement tends to zero after some finite intervals of time. Also, in the absence of D-D interaction, the entanglement has reached a relatively good stability in case of α = π/6 (see subspecies 4c and d). Figure 5, indicates that the entanglement experiences only irregular fluctuations in various atomic coherence angles α. Of course, regardless of the small-amplitude of fluctuations in case of α = π/6, we achieved the relative stability for entanglement in this figure. The results obtained from Fig. 6 show that, in the absence of D-D interaction but in the presence or absence of CRTs, the transparent patterns of CR phenomenon is well accessible for α = π/2; also, the quantum state of the system is located in a completely stable state for α = π/4 and α = π/6. In the event that in the presence of D-D interaction, we can only see regular fluctuations with small amplitude (for α = π/4,π/6) and irregular fluctuations (for α = π/2). It should be noted that in this figure for α = π/2, the death and then birth of entanglement happen in all given plots, irrespective of the presence or absence of D-D interaction and CRTs.

Fig. 2

The linear entropy of “atom 1” for different values of atomic coherent angle α versus rescaled time τ with ν₁/g₁ = 1.2, ν₂/g₁ = 1.1, Δ_ab/g₁ = 0.3, Δ_ac/g₁ = 0.27, ${\Delta }_{\acute {a}\acute {b}}/g_{1}=0.25$, ${\Delta }_{\acute {a}\acute {c}}/g_{1}=0.38$, g₂/g₁ = 1.3, $\acute {g}_{1}/g_{1}=1.2$ and $\acute {g}_{2}/g_{1}=1.15$: a ε = 0, λ = 0; b ε = 0.1, λ = 0; c ε = 0, λ₁/g₁ = 1, λ₂/g₁ = 1.1, λ₃/g₁ = 0.8, λ₄/g₁ = 0.6 and d ε = 0.1, λ₁/g₁ = 1, λ₂/g₁ = 1.1, λ₃/g₁ = 0.8, λ₄/g₁ = 0.6

Fig. 3

The linear entropy of “atom 1” for different values of atomic coherent angle α versus rescaled time τ with ν₁/g₁ = 1.75, ν₂/g₁ = 2.25, Δ_ab/g₁ = 4, Δ_ac/g₁ = 3.5, ${\Delta }_{\acute {a}\acute {b}}/g_{1}=3.7$, ${\Delta }_{\acute {a}\acute {c}}/g_{1}=4.3$, g₂/g₁ = 0.8, $\acute {g}_{1}/g_{1}=1.1$ and $\acute {g}_{2}/g_{1}=0.65$: a ε = 0, λ = 0; b ε = 0.1, λ = 0; c ε = 0, λ₁/g₁ = 2.75, λ₂/g₁ = 4, λ₃/g₁ = 4.3, λ₄/g₁ = 3.25 and d ε = 0.1, λ₁/g₁ = 2.75, λ₂/g₁ = 4, λ₃/g₁ = 4.3, λ₄/g₁ = 3.25

Fig. 4

The linear entropy of “atom 1” for different values of atomic coherent angle α versus rescaled time τ with ν₁/g₁ = 5, ν₂/g₁ = 4, Δ_ab/g₁ = 3, Δ_ac/g₁ = 2.75, ${\Delta }_{\acute {a}\acute {b}}/g_{1}=4$, ${\Delta }_{\acute {a}\acute {c}}/g_{1}=3.5$, g₂/g₁ = 2, $\acute {g}_{1}/g_{1}=1.7$ and $\acute {g}_{2}/g_{1}=2.25$: a ε = 0, λ = 0; b ε = 0.1, λ = 0; c ε = 0, λ₁/g₁ = 3.75, λ₂/g₁ = 2.25, λ₃/g₁ = 5, λ₄/g₁ = 2.75 and d ε = 0.1, λ₁/g₁ = 3.75, λ₂/g₁ = 2.25, λ₃/g₁ = 5, λ₄/g₁ = 2.75

Fig. 5

The linear entropy of “atom 1” for different values of atomic coherent angle α versus rescaled time τ with ν₁/g₁ = 3, ν₂/g₁ = 2, Δ_ab/g₁ = 1.4, Δ_ac/g₁ = 1.7, ${\Delta }_{\acute {a}\acute {b}}/g_{1}=1.4$, ${\Delta }_{\acute {a}\acute {c}}/g_{1}=1.7$, g₂/g₁ = 1.2, $\acute {g}_{1}/g_{1}=1$ and $\acute {g}_{2}/g_{1}=1.2$: a ε = 0, λ = 0; b ε = 0.1, λ = 0; c ε = 0, λ/g₁ = 2 and d ε = 0.1, λ/g₁ = 2

Fig. 6

The linear entropy of “atom 1” for different values of atomic coherent angle α versus rescaled time τ with ν₁/g₁ = 10, ν₂/g₁ = 15, Δ_ab/g₁ = 9, Δ_ac/g₁ = 13, ${\Delta }_{\acute {a}\acute {b}}/g_{1}=10$, ${\Delta }_{\acute {a}\acute {c}}/g_{1}=15$, g₂/g₁ = 0.9, $\acute {g}_{1}/g_{1}=1.15$ and $\acute {g}_{2}/g_{1}=0.95$: a ε = 0, λ = 0; b ε = 0.1, λ = 0; c ε = 0, λ₁/g₁ = 5, λ₂/g₁ = 7.5, λ₃/g₁ = 6.3, λ₄/g₁ = 9 and d ε = 0.1, λ₁/g₁ = 5, λ₂/g₁ = 7.5, λ₃/g₁ = 6.3, λ₄/g₁ = 9

The next goal in this study is to calculate the linear entropy of atoms 1, 2; $S_{A_{1}A_{2}}(\uptau )=1-Tr[\hat {\rho }^{2}_{A_{1}A_{2}}(\uptau )]$ by using of (15), in order to investigate the degree of entanglement of the two atoms with two field modes (see Figs. 7, 8, 9 and 10). Given that the atomic states and the vacuum field in the initial separable states of the system (|ψ(0)〉), result in the fact that there exists no entanglement at τ = 0. In addition, in these figures, we can see the death and then birth of entanglement during the time for α = π/6 (except in Fig. 7). Also, in none of these Figs. 7-10 stability or even nearly stable entanglement can be achieved. Moreover, the highest (lowest) value of entanglement generally corresponds to α = π/2 (α = π/6). The latter overall conclusion can never be extracted from the Figs. 2-6. In more detail, in Fig. 7, the entanglement shows irregular oscillations in all cases. In Fig. 8, in the presence and absence of CRTs as well as in the absence of D-D interaction, typical CR patterns are available for all atomic coherence angles α. But, this is not the case in the presence of both effects together or only in the presence of D-D interaction. At a glance, Figs. 9 and 10 are generally similar, wherein the entanglement experiences different irregular fluctuations for all considered atomic coherence angles α. In addition, in Fig. 10, in the absence of both D-D interaction and CRTs (for α = π/6) as well as in the presence of only CRTs (for α = π/4,π/6), the entanglement experiences fluctuations with small amplitude about zero (see subspecies 10a and b).

Fig. 7

The linear entropy of “atom 1+atom 2” for different values of atomic coherent angle α versus rescaled time τ with ν₁/g₁ = 0.7, ν₂/g₁ = 0.5, Δ_ab/g₁ = 0.2, Δ_ac/g₁ = 0.3, ${\Delta }_{\acute {a}\acute {b}}/g_{1}=0.15$, ${\Delta }_{\acute {a}\acute {c}}/g_{1}=0.25$, g₂/g₁ = 0.5, $\acute {g}_{1}/g_{1}=0.3$ and $\acute {g}_{2}/g_{1}=0.7$: a ε = 0, λ = 0; b ε = 0.1, λ = 0; c ε = 0, λ₁/g₁ = 0.4, λ₂/g₁ = 0.7, λ₃/g₁ = 0.6, λ₄/g₁ = 0.45 and d ε = 0.1, λ₁/g₁ = 0.4, λ₂/g₁ = 0.7, λ₃/g₁ = 0.6, λ₄/g₁ = 0.45

Fig. 8

The linear entropy of “atom 1+atom 2” for different values of atomic coherent angle α versus rescaled time τ with ν₁/g₁ = 5, ν₂/g₁ = 7, Δ_ab/g₁ = 4, Δ_ac/g₁ = 6, ${\Delta }_{\acute {a}\acute {b}}/g_{1}=3.5$, ${\Delta }_{\acute {a}\acute {c}}/g_{1}=5$, g₂/g₁ = 1.5, $\acute {g}_{1}/g_{1}=2$ and $\acute {g}_{2}/g_{1}=1.75$: a ε = 0, λ = 0; b ε = 0.1, λ = 0; c ε = 0, λ₁/g₁ = 3, λ₂/g₁ = 2, λ₃/g₁ = 2.25, λ₄/g₁ = 2.75 and d ε = 0.1, λ₁/g₁ = 3, λ₂/g₁ = 2, λ₃/g₁ = 2.25, λ₄/g₁ = 2.75

Fig. 9

The linear entropy of “atom 1+atom 2” for different values of atomic coherent angle α versus rescaled time τ with ν₁/g₁ = 0.1, ν₂/g₁ = 0.15, Δ_ab/g₁ = 0.2, Δ_ac/g₁ = 0.17, ${\Delta }_{\acute {a}\acute {b}}/g_{1}=0.25$, ${\Delta }_{\acute {a}\acute {c}}/g_{1}=0.31$, g₂/g₁ = 0.7, $\acute {g}_{1}/g_{1}=0.57$ and $\acute {g}_{2}/g_{1}=0.66$: a ε = 0, λ = 0; b ε₁ = ε₂ = 0.05, ε₃ = ε₄ = 0.1, λ = 0; c ε = 0, λ₁/g₁ = 0.3, λ₂/g₁ = 0.35, λ₃/g₁ = 0.16, λ₄/g₁ = 0.23 and d ε₁ = ε₂ = 0.05, ε₃ = ε₄ = 0.1, λ₁/g₁ = 0.3, λ₂/g₁ = 0.35, λ₃/g₁ = 0.16, λ₄/g₁ = 0.23

Fig. 10

The linear entropy of “atom 1+atom 2” for different values of atomic coherent angle α versus rescaled time τ with ν₁/g₁ = 10, ν₂/g₁ = 15, Δ_ab/g₁ = 9, Δ_ac/g₁ = 13, ${\Delta }_{\acute {a}\acute {b}}/g_{1}=10$, ${\Delta }_{\acute {a}\acute {c}}/g_{1}=15$, g₂/g₁ = 3, $\acute {g}_{1}/g_{1}=2.5$ and $\acute {g}_{2}/g_{1}=3.25$: a ε = 0, λ = 0; b ε = 0.1, λ = 0; c ε = 0, λ₁/g₁ = 5, λ₂/g₁ = 7.5, λ₃/g₁ = 6.3, λ₄/g₁ = 9 and d ε = 0.1, λ₁/g₁ = 5, λ₂/g₁ = 7.5, λ₃/g₁ = 6.3, λ₄/g₁ = 9

4 Summary and Conclusions

In summary, we introduced a system containing the interaction between two qutrits with a two-mode quantized field in the presence of D-D interaction between the atoms, while CRTs are also taken into account, particularly. It is well-known that these terms cannot be ignored in the strong atom-field coupling regimes. We should mention that while a lot of papers deal with atom-field interaction by JCM or Tavis-Cummings model, as we found there exist only very few articles in this field that pay attention to interaction between two three-level atoms and a two-mode field, even without CRTs [23, 26]. Anyway, to reach the goal of the paper, by solving the time-dependent Schrödinger equation, we obtained the corresponding density matrix in order to evaluate the entanglement (via the calculation of linear entropy) of different components of the considered system. Keeping in mind that Rabi model is guaranteed under the condition of strong atom-field coupling, it can be seen that the Figs. 2, 3, 4, 5, 8 and 10 are drawn under conditions of ultra-strong, Figs. 7 and 9 using deep-strong and Fig. 6 under strong coupling (our mentioned classification is based on Ref. [83, 84]). Generally, there exists more or less entanglement in different parts of the system which can be tuned by choosing appropriate parameters in the system. In particular, the most favorable observations of the results are accessibly of the stability or at least quasi-stability of the entanglement, and also death and then sudden birth of entanglement which both can be appeared by tuning the parameters involve in the model interaction. As a marginal result, one may refer to the CR phenomenon in the entanglement dynamics of entanglement available in some cases. In particular, the effect of CRTs can be seen in the change of the CR patterns, for instance, as may be seen in some cases the number of CRs or typical CRs have been changed in the considered time interval in the presented plots. This fact clearly shows that at each moment of time the degree of entanglement is changed in the absence and presence of CRTs. In fact, since the main goal of this paper is the investigation of the influences of CRTs on the entanglement properties, we end this conclusion section with mentioning that, at first glance on the plots a and b in all figures it may seem that there is no critical difference between the presented plots (and so CRTs do not effectively change the entropy). However, an exact inspection on the details of our numerical results show that at some moments of time, a significant difference of the calculated linear entropy between the presence and absence of CRTs can be observed, which asserts that such terms are not generally ignorable in the atom-field interacting systems.

Appendices

Appendix A

In this appendix we present the coupled differential equations obtained from solving the time-dependent Schrödinger equation which are as follow,

$$ \begin{array}{@{}rcl@{}} \frac{2i g_{1}}{\pi}\dot{y}_{1}(\uptau)&=&\frac{2}{3}(\nu_{1}+\nu_{2})y_{1}(\uptau)+\frac{1}{3}({\Delta}_{ab}+{\Delta}_{ac}+{\Delta}_{\acute{a}\acute{b}}+{\Delta}_{\acute{a}\acute{c}})y_{1}(\uptau)+g_{1}(1-{\varepsilon^{2}_{1}})y_{2}(\uptau)\\ &&+g_{2}(1-{\varepsilon^{2}_{2}})y_{5}(\uptau)+\acute{g}_{1}(1-{\varepsilon^{2}_{3}})y_{6}(\uptau)+\acute{g}_{2}(1-{\varepsilon^{2}_{4}})y_{9}(\uptau),\\ \frac{2i g_{1}}{\pi}\dot{y}_{2}(\uptau)&=&(\nu_{1}+\frac{1}{3}\nu_{2})y_{2}(\uptau)+\frac{1}{3}({\Delta}_{ac}-2{\Delta}_{ab}+{\Delta}_{\acute{a}\acute{b}}+{\Delta}_{\acute{a}\acute{c}})y_{2}(\uptau)-(2\varepsilon_{1}g_{1}-\varepsilon_{3}\acute{g}_{1})y_{2}(\uptau)\\ &&+g_{1}(1-{\varepsilon^{2}_{1}})y_{1}(\uptau)+\sqrt{2}\acute{g}_{1}(1-2{\varepsilon^{2}_{3}})y_{17}(\uptau)+\acute{g}_{2}(1-{\varepsilon^{2}_{4}}-\frac{{\varepsilon^{2}_{3}}}{2})y_{12}(\uptau)+\lambda_{1}y_{6}(\uptau)+\lambda_{2}y_{8}(\uptau),\\ \frac{2i g_{1}}{\pi}\dot{y}_{3}(\uptau)&=&\frac{4}{3}\nu_{2}y_{3}(\uptau)+\frac{1}{3}({\Delta}_{ac}-2{\Delta}_{ab}+{\Delta}_{\acute{a}\acute{b}}+{\Delta}_{\acute{a}\acute{c}})y_{3}(\uptau)-(\varepsilon_{1}g_{1}-\varepsilon_{4}\acute{g}_{2})y_{3}(\uptau)\\ &&+\sqrt{2}\acute{g}_{2}(1-2{\varepsilon^{2}_{4}})y_{15}(\uptau)+\acute{g}_{1}(1-{\varepsilon^{2}_{3}}-\frac{{\varepsilon^{2}_{4}}}{2})y_{10}(\uptau)+\lambda_{1}y_{7}(\uptau)+\lambda_{2}y_{9}(\uptau),\\ \frac{2i g_{1}}{\pi}\dot{y}_{4}(\uptau)&=&\frac{4}{3}\nu_{1}y_{4}(\uptau)+\frac{1}{3}({\Delta}_{ab}-2{\Delta}_{ac}+{\Delta}_{\acute{a}\acute{b}}+{\Delta}_{\acute{a}\acute{c}})y_{4}(\uptau)-(\varepsilon_{2}g_{2}-\varepsilon_{3}\acute{g}_{1})y_{4}(\uptau)\\ &&+\sqrt{2}\acute{g}_{1}(1-2{\varepsilon^{2}_{3}})y_{18}(\uptau)+\acute{g}_{2}(1-{\varepsilon^{2}_{4}}-\frac{{\varepsilon^{2}_{3}}}{2})y_{11}(\uptau)+\lambda_{3}y_{6}(\uptau)+\lambda_{4}y_{8}(\uptau),\\ \frac{2i g_{1}}{\pi}\dot{y}_{5}(\uptau)&=&(\nu_{2}+\frac{1}{3}\nu_{1})y_{5}(\uptau)+\frac{1}{3}({\Delta}_{ab}-2{\Delta}_{ac}+{\Delta}_{\acute{a}\acute{b}}+{\Delta}_{\acute{a}\acute{c}})y_{5}(\uptau)-(2\varepsilon_{2}g_{2}-\varepsilon_{4}\acute{g}_{2})y_{5}(\uptau)\\ &&+g_{2}(1-{\varepsilon^{2}_{2}})y_{1}(\uptau)+\sqrt{2}\acute{g}_{2}(1-2{\varepsilon^{2}_{4}})y_{16}(\uptau)+\acute{g}_{1}(1-{\varepsilon^{2}_{3}}-\frac{{\varepsilon^{2}_{4}}}{2})y_{13}(\uptau)+\lambda_{3}y_{7}(\uptau)+\lambda_{4}y_{9}(\uptau),\\ \frac{2i g_{1}}{\pi}\dot{y}_{6}(\uptau)&=&(\nu_{1}+\frac{1}{3}\nu_{2})y_{6}(\uptau)+\frac{1}{3}({\Delta}_{ab}+{\Delta}_{ac}-2{\Delta}_{\acute{a}\acute{b}}+{\Delta}_{\acute{a}\acute{c}})y_{6}(\uptau)+(\varepsilon_{1}g_{1}-2\varepsilon_{3}\acute{g}_{1})y_{6}(\uptau)\\ &&+\acute{g}_{1}(1-{\varepsilon^{2}_{3}})y_{1}(\uptau)+\sqrt{2}g_{1}(1-2{\varepsilon^{2}_{1}})y_{17}(\uptau)+g_{2}(1-{\varepsilon^{2}_{2}}-\frac{{\varepsilon^{2}_{1}}}{2})y_{13}(\uptau)+\lambda_{1}y_{2}(\uptau)+\lambda_{3}y_{4}(\uptau),\\ \frac{2i g_{1}}{\pi}\dot{y}_{7}(\uptau)&=&\frac{4}{3}\nu_{2}y_{7}(\uptau)+\frac{1}{3}({\Delta}_{ab}+{\Delta}_{ac}-2{\Delta}_{\acute{a}\acute{b}}+{\Delta}_{\acute{a}\acute{c}})y_{7}(\uptau)+(\varepsilon_{2}g_{2}-\varepsilon_{3}\acute{g}_{1})y_{7}(\uptau)\\ &&+\sqrt{2}g_{2}(1-2{\varepsilon^{2}_{2}})y_{19}(\uptau)+g_{1}(1-{\varepsilon^{2}_{1}}-\frac{{\varepsilon^{2}_{2}}}{2})y_{10}(\uptau)+\lambda_{1}y_{3}(\uptau)+\lambda_{3}y_{5}(\uptau), \end{array} $$

$$ \begin{array}{@{}rcl@{}} \frac{2i g_{1}}{\pi}\dot{y}_{8}(\uptau)&=&\frac{4}{3}\nu_{1}y_{8}(\uptau)+\frac{1}{3}({\Delta}_{ab}+{\Delta}_{ac}+{\Delta}_{\acute{a}\acute{b}}-2{\Delta}_{\acute{a}\acute{c}})y_{8}(\uptau)+(\varepsilon_{1}g_{1}-\varepsilon_{4}\acute{g}_{2})y_{8}(\uptau)\\ &&+\sqrt{2}g_{1}(1-2{\varepsilon^{2}_{1}})y_{14}(\uptau)+g_{2}(1-{\varepsilon^{2}_{2}}-\frac{{\varepsilon^{2}_{1}}}{2})y_{11}(\uptau)+\lambda_{2}y_{2}(\uptau)+\lambda_{4}y_{4}(\uptau),\\ \frac{2i g_{1}}{\pi}\dot{y}_{9}(\uptau)&=&(\nu_{2}+\frac{1}{3}\nu_{1})y_{9}(\uptau)+\frac{1}{3}({\Delta}_{ab}+{\Delta}_{ac}+{\Delta}_{\acute{a}\acute{b}}-2{\Delta}_{\acute{a}\acute{c}})y_{9}(\uptau)+(\varepsilon_{2}g_{2}-2\varepsilon_{4}\acute{g}_{2})y_{9}(\uptau)\\ &&+\acute{g}_{2}(1-{\varepsilon^{2}_{4}})y_{1}(\uptau)+\sqrt{2}g_{2}(1-2{\varepsilon^{2}_{2}})y_{16}(\uptau)+g_{1}(1-{\varepsilon^{2}_{1}}-\frac{{\varepsilon^{2}_{2}}}{2})y_{12}(\uptau)+\lambda_{2}y_{3}(\uptau)+\lambda_{4}y_{5}(\uptau),\\ \frac{2i g_{1}}{\pi}\dot{y}_{10}(\uptau)&=&(\nu_{2}+\frac{1}{3}\nu_{1})y_{10}(\uptau)+\frac{1}{3}({\Delta}_{ac}-2{\Delta}_{ab}-2{\Delta}_{\acute{a}\acute{b}}+{\Delta}_{\acute{a}\acute{c}})y_{10}(\uptau)-2(\varepsilon_{1}g_{1}+\varepsilon_{3}\acute{g}_{1})y_{10}(\uptau)\\ &&+g_{1}(1-{\varepsilon^{2}_{1}}-\frac{{\varepsilon^{2}_{2}}}{2})y_{7}(\uptau)+\acute{g}_{1}(1-{\varepsilon^{2}_{3}}-\frac{{\varepsilon^{2}_{4}}}{2})y_{3}(\uptau),\\ \frac{2i g_{1}}{\pi}\dot{y}_{11}(\uptau)&=&(\nu_{1}+\frac{1}{3}\nu_{2})y_{11}(\uptau)+\frac{1}{3}({\Delta}_{ab}-2{\Delta}_{ac}+{\Delta}_{\acute{a}\acute{b}}-2{\Delta}_{\acute{a}\acute{c}})y_{11}(\uptau)-2(\varepsilon_{2}g_{2}+\varepsilon_{4}\acute{g}_{2})y_{11}(\uptau)\\ &&+g_{2}(1-{\varepsilon^{2}_{2}}-\frac{{\varepsilon^{2}_{1}}}{2})y_{8}(\uptau)+\acute{g}_{2}(1-{\varepsilon^{2}_{4}}-\frac{{\varepsilon^{2}_{3}}}{2})y_{4}(\uptau),\\ \frac{2i g_{1}}{\pi}\dot{y}_{12}(\uptau)&=&\frac{2}{3}(\nu_{1}+\nu_{2})y_{12}(\uptau)+\frac{1}{3}({\Delta}_{ac}-2{\Delta}_{ab}+{\Delta}_{\acute{a}\acute{b}}-2{\Delta}_{\acute{a}\acute{c}})y_{12}(\uptau)-2(\varepsilon_{1}g_{1}+\varepsilon_{4}\acute{g}_{2})y_{12}(\uptau)\\ &&+g_{1}(1-{\varepsilon^{2}_{1}}-\frac{{\varepsilon^{2}_{2}}}{2})y_{9}(\uptau)+\acute{g}_{2}(1-{\varepsilon^{2}_{4}}-\frac{{\varepsilon^{2}_{3}}}{2})y_{2}(\uptau),\\ \frac{2i g_{1}}{\pi}\dot{y}_{13}(\uptau)&=&\frac{2}{3}(\nu_{1}+\nu_{2})y_{13}(\uptau)+\frac{1}{3}({\Delta}_{ab}-2{\Delta}_{ac}-2{\Delta}_{\acute{a}\acute{b}}+{\Delta}_{\acute{a}\acute{c}})y_{13}(\uptau)-2(\varepsilon_{2}g_{2}+\varepsilon_{3}\acute{g}_{1})y_{13}(\uptau)\\ &&+g_{2}(1-{\varepsilon^{2}_{2}}-\frac{{\varepsilon^{2}_{1}}}{2})y_{6}(\uptau)+\acute{g}_{1}(1-{\varepsilon^{2}_{3}}-\frac{{\varepsilon^{2}_{4}}}{2})y_{5}(\uptau),\\ \frac{2i g_{1}}{\pi}\dot{y}_{14}(\uptau)&=&(\frac{5}{3}\nu_{1}-\frac{1}{3}\nu_{2})y_{14}(\uptau)+\frac{1}{3}({\Delta}_{ac}-2{\Delta}_{ab}+{\Delta}_{\acute{a}\acute{b}}-2{\Delta}_{\acute{a}\acute{c}})y_{14}(\uptau)-(3\varepsilon_{1}g_{1}+\varepsilon_{4}\acute{g}_{2})y_{14}(\uptau)\\ &&+\sqrt{2}g_{1}(1-2{\varepsilon^{2}_{1}})y_{8}(\uptau),\\ \frac{2i g_{1}}{\pi}\dot{y}_{15}(\uptau)&=&(\frac{5}{3}\nu_{2}-\frac{1}{3}\nu_{1})y_{15}(\uptau)+\frac{1}{3}({\Delta}_{ac}-2{\Delta}_{ab}+{\Delta}_{\acute{a}\acute{b}}-2{\Delta}_{\acute{a}\acute{c}})y_{15}(\uptau)-(\varepsilon_{1}g_{1}+3\varepsilon_{4}\acute{g}_{2})y_{15}(\uptau)\\ &&+\sqrt{2}\acute{g}_{2}(1-2{\varepsilon^{2}_{4}})y_{3}(\uptau),\\ \frac{2i g_{1}}{\pi}\dot{y}_{16}(\uptau)&=&\frac{4}{3}\nu_{2}y_{16}(\uptau)+\frac{1}{3}({\Delta}_{ab}-2{\Delta}_{ac}+{\Delta}_{\acute{a}\acute{b}}-2{\Delta}_{\acute{a}\acute{c}})y_{16}(\uptau)-3(\varepsilon_{2}g_{2}+\varepsilon_{4}\acute{g}_{2})y_{16}(\uptau)\\ &&+\sqrt{2}\acute{g}_{2}(1-2{\varepsilon^{2}_{4}})y_{5}(\uptau)+\sqrt{2}g_{2}(1-2{\varepsilon^{2}_{2}})y_{9}(\uptau),\\ \frac{2i g_{1}}{\pi}\dot{y}_{17}(\uptau)&=&\frac{4}{3}\nu_{1}y_{17}(\uptau)+\frac{1}{3}({\Delta}_{ac}-2{\Delta}_{ab}-2{\Delta}_{\acute{a}\acute{b}}+{\Delta}_{\acute{a}\acute{c}})y_{17}(\uptau)-3(\varepsilon_{1}g_{1}+\varepsilon_{3}\acute{g}_{1})y_{17}(\uptau)\\ &&+\sqrt{2}\acute{g}_{1}(1-2{\varepsilon^{2}_{3}})y_{2}(\uptau)+\sqrt{2}g_{1}(1-2{\varepsilon^{2}_{1}})y_{6}(\uptau),\\ \frac{2i g_{1}}{\pi}\dot{y}_{18}(\uptau)&=&(\frac{5}{3}\nu_{1}-\frac{1}{3}\nu_{2})y_{18}(\uptau)+\frac{1}{3}({\Delta}_{ab}-2{\Delta}_{ac}-2{\Delta}_{\acute{a}\acute{b}}+{\Delta}_{\acute{a}\acute{c}})y_{18}(\uptau)-(\varepsilon_{2}g_{2}+3\varepsilon_{3}\acute{g}_{1})y_{18}(\uptau)\\ &&+\sqrt{2}\acute{g}_{1}(1-2{\varepsilon^{2}_{3}})y_{4}(\uptau),\\ \frac{2i g_{1}}{\pi}\dot{y}_{19}(\uptau)&=&(\frac{5}{3}\nu_{2}-\frac{1}{3}\nu_{1})y_{19}(\uptau)+\frac{1}{3}({\Delta}_{ab}-2{\Delta}_{ac}-2{\Delta}_{\acute{a}\acute{b}}+{\Delta}_{\acute{a}\acute{c}})y_{19}(\uptau)-(3\varepsilon_{2}g_{2}+\varepsilon_{3}\acute{g}_{1})y_{19}(\uptau)\\ &&+\sqrt{2}g_{2}(1-2{\varepsilon^{2}_{2}})y_{7}(\uptau),\\ \frac{2i g_{1}}{\pi}\dot{y}_{20}(\uptau)&=&-\frac{2}{3}\nu_{1}y_{20}(\uptau)+\frac{1}{3}({\Delta}_{ac}-2{\Delta}_{ab}-2{\Delta}_{\acute{a}\acute{b}}+{\Delta}_{\acute{a}\acute{c}})y_{20}(\uptau)-(\varepsilon_{1}g_{1}+\varepsilon_{3}\acute{g}_{1})y_{20}(\uptau),\\ \frac{2i g_{1}}{\pi}\dot{y}_{21}(\uptau)&=&-\frac{2}{3}\nu_{2}y_{21}(\uptau)+\frac{1}{3}({\Delta}_{ab}-2{\Delta}_{ac}+{\Delta}_{\acute{a}\acute{b}}-2{\Delta}_{\acute{a}\acute{c}})y_{21}(\uptau)-(\varepsilon_{2}g_{2}+\varepsilon_{4}\acute{g}_{2})y_{21}(\uptau). \end{array} $$

Appendix B

The nonzero matrix elements of (14) are defined as follow,

$$ \begin{array}{@{}rcl@{}} r_{11}&=&|y_{1}(\uptau)|^{2}+|y_{6}(\uptau)|^{2}+|y_{7}(\uptau)|^{2}+|y_{8}(\uptau)|^{2}+|y_{9}(\uptau)|^{2},\\ r_{22}&=&|y_{2}(\uptau)|^{2}+|y_{3}(\uptau)|^{2}+|y_{10}(\uptau)|^{2}+|y_{12}(\uptau)|^{2}+|y_{14}(\uptau)|^{2}+|y_{15}(\uptau)|^{2}\\ &&+|y_{17}(\uptau)|^{2}+|y_{20}(\uptau)|^{2},\\ r_{33}&=&|y_{4}(\uptau)|^{2}+|y_{5}(\uptau)|^{2}+|y_{11}(\uptau)|^{2}+|y_{13}(\uptau)|^{2}+|y_{16}(\uptau)|^{2}+|y_{18}(\uptau)|^{2}\\ &&+|y_{19}(\uptau)|^{2}+|y_{21}(\uptau)|^{2},\\ r_{23}&=&y_{2}(\uptau)y^{\ast}_{4}(\uptau)+y_{3}(\uptau)y^{\ast}_{5}(\uptau)+y_{10}(\uptau)y^{\ast}_{13}(\uptau)+y_{12}(\uptau)y^{\ast}_{11}(\uptau)\\ &&+y_{15}(\uptau)y^{\ast}_{16}(\uptau)+y_{17}(\uptau)y^{\ast}_{18}(\uptau). \end{array} $$

Also, the nonzero matrix elements of (15) are defined as follow,

$$ \begin{array}{@{}rcl@{}} z_{11}&=&|y_{1}(\uptau)|^{2},z_{22}=|y_{2}(\uptau)|^{2}+|y_{3}(\uptau)|^{2},z_{33}=|y_{4}(\uptau)|^{2}+|y_{5}(\uptau)|^{2},\\ z_{44}&=&|y_{6}(\uptau)|^{2}+|y_{7}(\uptau)|^{2},z_{66}=|y_{10}(\uptau)|^{2}+|y_{17}(\uptau)|^{2}+|y_{20}(\uptau)|^{2},\\ z_{55}&=&|y_{8}(\uptau)|^{2}+|y_{9}(\uptau)|^{2},z_{77}=|y_{11}(\uptau)|^{2}+|y_{16}(\uptau)|^{2}+|y_{21}(\uptau)|^{2},\\ z_{88}&=&|y_{12}(\uptau)|^{2}+|y_{14}(\uptau)|^{2}+|y_{15}(\uptau)|^{2},z_{99}=|y_{13}(\uptau)|^{2}+|y_{18}(\uptau)|^{2}+|y_{19}(\uptau)|^{2},\\ z_{23}&=&y_{2}(\uptau)y^{\ast}_{4}(\uptau)+y_{3}(\uptau)y^{\ast}_{5}(\uptau),z_{25}=y_{2}(\uptau)y^{\ast}_{8}(\uptau)+y_{3}(\uptau)y^{\ast}_{9}(\uptau),z_{17}=y_{1}(\uptau)y^{\ast}_{21}(\uptau),\\ z_{24}&=&y_{2}(\uptau)y^{\ast}_{6}(\uptau)+y_{3}(\uptau)y^{\ast}_{7}(\uptau),z_{16}=y_{1}(\uptau)y^{\ast}_{20}(\uptau),z_{34}=y_{4}(\uptau)y^{\ast}_{6}(\uptau)+y_{5}(\uptau)y^{\ast}_{7}(\uptau),\\ z_{35}&=&y_{4}(\uptau)y^{\ast}_{8}(\uptau)+y_{5}(\uptau)y^{\ast}_{9}(\uptau),z_{45}=y_{6}(\uptau)y^{\ast}_{8}(\uptau)+y_{7}(\uptau)y^{\ast}_{9}(\uptau),\\ z_{67}&=&y_{10}(\uptau)y^{\ast}_{11}(\uptau)+y_{20}(\uptau)y^{\ast}_{21}(\uptau), z_{68}=y_{10}(\uptau)y^{\ast}_{12}(\uptau)+y_{17}(\uptau)y^{\ast}_{14}(\uptau),\\ z_{78}&=&y_{11}(\uptau)y^{\ast}_{12}(\uptau)+y_{16}(\uptau)y^{\ast}_{15}(\uptau), z_{69}=y_{10}(\uptau)y^{\ast}_{13}(\uptau)+y_{17}(\uptau)y^{\ast}_{18}(\uptau),\\ z_{79}&=&y_{11}(\uptau)y^{\ast}_{13}(\uptau)+y_{16}(\uptau)y^{\ast}_{19}(\uptau), z_{89}=y_{12}(\uptau)y^{\ast}_{13}(\uptau)+y_{14}(\uptau)y^{\ast}_{18}(\uptau)+y_{15}(t)y^{\ast}_{19}(\uptau). \end{array} $$