Approximate conditional teleportation of a $\varLambda$-type three-level atomic state based on cavity QED method beyond Bell-state measurement

Abstract

Inspiring from the scheme proposed in (Zheng in Phys Rev A 69:064,302 2004), our aim is to teleport an unknown qubit atomic state using the cavity QED method without using the explicit Bell-state measurement, and so the additional atom is not required. Two identical $\varLambda$-type three-level atoms are interacted separately and subsequently with a two-mode quantized cavity field where each mode is expressed with a single-photon field state. The interaction between atoms and field is well described via the Jaynes–Cummings model. It is then shown that how if the atomic detection results a particular state of atom 1, an unknown state can be appropriately teleported from atom 1 to atom 2. This teleportation procedure successfully leads to the high fidelity F (success probability $P_g$) in between $69\%\lesssim F\lesssim 100\%$ ($0.14\lesssim P_g\lesssim 0.56$). At last, we illustrated that our scheme considerably improves similar previous proposals.

1 Introduction

Entanglement is one of the most wonderful characteristics of quantum mechanics which plays a crucial role in quantum information theory [1, 2]. This notion has various practical applications such as quantum teleportation [3,4,5,6] and quantum cryptography [7, 8]. Teleportation process first suggested by Benett et al. [9] consists of the transmission of an unknown state from one system (sender) to a remote system (receiver) via a quantum channel using local operations and classical communication. The initial unknown state at the sender (Alice) is destroyed after the occurrence of quantum teleportation. This phenomenon has been experimentally demonstrated using optical systems (for instance see [10, 11]). Cavity quantum electrodynamics (QED) method provides a convenient approach which can demonstrate the quantum information processing in general, and quantum teleportation in particular. This is due to the fact that, by using cavity QED method one is able to prepare and hereinafter desirably control the interaction between atoms and photons.

In this paper, we intend to perform our teleportation scheme using the proposal in [12] based on the cavity QED method. In more detail, we utilize two identical $\varLambda$-type three-level atoms which are initially prepared in some appropriate states. Then, these two atoms are interacted separately and subsequently with a two-mode quantized field, where the initial field state is such that each mode possesses a single photon. With the help of extended Jaynes–Cummings model, the atom-field interaction may be appropriately described. We show that how by detecting special state of atom 1, one can teleport an unknown state of atom 1 to atom 2. The used scheme has enough high efficiency. By this, we mean that the minimum of fidelity is achieved about 69%, and this value may reach its complete possible value nearly 100% by appropriately tuning the evolved parameters. This range of fidelity is satisfactorily acceptable in this field of research. Also, the success probability of about 0.56 may be obtained, which is also a considerable value in this content. Briefly, as will be illustrated in detail in the continuation of the paper, by our scheme, the success probability and the necessary interaction time are considerably improved in comparison with the previous literature (see for instance [13] and the realizations that this Ref. emphasizes on them).

2 Quantum teleportation model

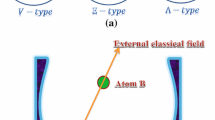
Many unconditional schemes [14, 15] have been proposed for quantum teleportation purposes; however, none of them have been realized experimentally (since these schemes require Bell-state measurement [16,17,18]). Moreover, further schemes without Bell-state measurement have also been proposed for atomic state teleportation [12, 19,20,21]. In this regard, Zheng has suggested a scheme to teleport an unknown atomic state of a two-level atom, approximately and conditionally without Bell-state measurement [12]. Following this proposal, in this paper we present an alternative scheme for approximate conditional teleportation of an unknown atomic state of a $\varLambda$-type three-level atom by using the generalized Jaynes–Cummings model. Our three-level atoms shown in Fig. 1 consist of two allowed transitions, $\vert {e}\leftrightarrow \vert {f}\rangle$ and $\vert {e}\rangle \leftrightarrow \vert {g}\rangle$ each interacts with a distinct mode of the field. The two-photon resonance condition is assumed; otherwise, the individual modes are allowed to be detuned by an arbitrary amount from the intermediate atomic level. In our scheme, we do not use the Bell-state measurement explicitly and hence additional atom is not necessary. Therefore, we have only two atoms that interact with a two-mode cavity field. The state of atom 1 is teleported, and atom 2 receives the teleported state. At first, the atom 2 and then atom 1 interact with the same cavity field modes. Finally, with a (suitable) measurement on the atom 1, the state of atom 2 converts to the initial state of atom 1.

Fig. 1

The energy level diagram of a three-level atom in the $\varLambda$-configuration which interacts with the two-mode quantized radiation field with detuning $\Delta$.

In detail, the interaction Hamiltonian in the Jaynes-Cummings model in the rotating wave approximation is given by [22]:

$$\begin{aligned} \begin{aligned} H_\mathrm{eff}=\hbar \Delta \vert {e}\rangle \langle {e}\vert +\hbar \left[ g_a(a^{\dagger }\vert {f}\rangle \langle {e}\vert +\vert {e}\rangle \langle {f}\vert a)+g_b(b^{\dagger }\vert {g}\rangle \langle {e}\vert +\vert {e}\rangle \langle {g}\vert b)\right] , \end{aligned} \end{aligned}$$

(1)

where $\vert {e}\rangle \langle {e}\vert$, $\vert {f(e)}\rangle \langle {e(f)}\vert$ and $\vert {g(e)}\rangle \langle {e(g)}\vert$ are atomic operators and $\Delta =\omega _e-\omega _g-\Omega _b=\omega _e-\omega _f-\Omega _a$ is the detuning parameter where $\Omega _a$ and $\Omega _b$ are the cavity field frequencies and $\omega _e$, $\omega _f$ and $\omega _g$ are the frequencies associated with the atomic levels $\vert {e}\rangle$, $\vert {f}\rangle$ and $\vert {g}\rangle$, respectively. Also, $a (a^{\dagger })$ and $b (b^{\dagger })$ are the annihilation (creation) operators of the respective field modes and the constants $g_a$ and $g_b$ denote the atom-field coupling strengths. In general, the atom-field state vector that appropriately describes such a system may be given as:

$$\begin{aligned} \begin{aligned} \vert {\psi (t)}\rangle =\sum _{n_a,n_b}[&C_f(n_a,n_b,t)\vert {f,n_a,n_b}\rangle +C_e(n_a-1,n_b,t)\vert {e,n_a-1,n_b}\rangle \\ +\,&C_g(n_a-1,n_b+1,t)\vert {g,n_a-1,n_b+1}\rangle ]. \end{aligned} \end{aligned}$$

(2)

Now, the coefficients $C_{i=f,e,g}(n'_a,n'_b,t)$ should be calculated in a general manner. For this purpose, the following initial conditions have been considered: $C_f(n_a,n_b,0)= C_f C_{n_a,n_b}, C_e(n_a-1,n_b,0)= C_e C_{n_a-1,n_b}, C_g(n_a-1,n_b+1,0)= C_g C_{n_a-1,n_b+1},$ where $C_{n'_a,n'_b}$ determines the amplitude of arbitrary initial field state and $C_f$, $C_e$ and $C_g$ specify the atomic amplitudes of the initial normalized atomic state. In this way, we considered the atom-field system to be decoupled at the initial time $t=0$. Defining $\delta ={\Delta \over 2}$, the coefficients $C_{i=f,e,g}(n'_a,n'_b,t)$ can be calculated from the time-dependent Schrödinger equation $i\hbar \vert {\dot{\psi }(t)}\rangle = H_\mathrm{eff}\vert {\psi (t)}\rangle$ by taking in to account the previously determined initial conditions. This procedure led us to the following results:

$$\begin{aligned} C_f(n_a,n_b,t)&=-i{\Omega _{n_a-1}\over \tilde{\Omega }_{n_a-1,n_b}}\sin (\tilde{\Omega }_{n_a-1,n_b}t)e^{-i\delta t}C_eC_{n_a-1,n_b} \nonumber \\&\quad +\, C_fC_{n_a,n_b} \left[ {\Omega _{n_b}^2\over \Omega _{n_a-1,n_b}^2} +{\Omega _{n_a-1}^2\over \Omega _{n_a-1,n_b}^2}e^{-i\delta t} \left( \cos (\tilde{\Omega }_{n_a-1,n_b}t)\right. \right. \nonumber \\&\quad \left. \left. +\, i{\delta \over \tilde{\Omega }_{n_a-1,n_b}}\sin (\tilde{\Omega }_{n_a-1,n_b}t)\right) \right] \nonumber \\&\quad +\, C_gC_{n_a-1,n_b+1}\left[ -{\Omega _{n_b}\Omega _{n_a-1}\over \Omega _{n_a-1,n_b}^2}+{\Omega _{n_a-1}\Omega _{n_b}\over \Omega _{n_a-1,n_b}^2}e^{-i\delta t}\left( \cos (\tilde{\Omega }_{n_a-1,n_b}t)\right. \right. \nonumber \\&\quad \left. \left. +\, i{\delta \over \tilde{\Omega }_{n_a-1,n_b}}\sin (\tilde{\Omega }_{n_a-1,n_b}t)\right) \right] , \end{aligned}$$

(3)

$$\begin{aligned} C_e(n_a-1, n_b, t)= & {} \left[ \cos (\tilde{\Omega }_{n_a-1,n_b}t)-i{\delta \over \tilde{\Omega }_{n_a-1,n_b}}\sin (\tilde{\Omega }_{n_a-1,n_b}t)\right] e^{-i\delta t}C_eC_{n_a-1,n_b}\nonumber \\&-\,i{\Omega _{n_a-1}\over \Omega _{n_a-1,n_b}}\sin (\tilde{\Omega }_{n_a-1,n_b}t)e^{-i\delta t}C_fC_{n_a,n_b} \nonumber \\&-\,i{\Omega _{n_b}\over \Omega _{n_a-1,n_b}}\sin (\tilde{\Omega }_{n_a-1,n_b}t)e^{-i\delta t}C_gC_{n_a-1,n_b+1}, \end{aligned}$$

(4)

$$\begin{aligned} \begin{aligned} C_g(n_a-1, n_b+1, t)=&-i{\Omega _{n_b}\over \tilde{\Omega }_{n_a-1,n_b}}\sin (\tilde{\Omega }_{n_a-1,n_b}t)e^{-i\delta t}C_eC_{n_a-1,n_b}\\&+C_fC_{n_a,n_b} \left[ -{\Omega _{n_b}\Omega _{n_a-1}\over \Omega _{n_a-1,n_b}^2}+{\Omega _{n_a-1}\Omega _{n_b}\over \Omega _{n_a-1,n_b}^2}e^{-i\delta t} \right. \\&\left. \times \left( \cos (\tilde{\Omega }_{n_a-1,n_b}t)+\,i{\delta \over \tilde{\Omega }_{n_a-1,n_b}}\sin (\tilde{\Omega }_{n_a-1,n_b}t)\right) \right] \\&+C_gC_{n_a-1,n_b+1} \left[ {\Omega _{n_a-1}^2\over \Omega _{n_a-1,n_b}^2}+{\Omega _{n_b}^2\over \Omega _{n_a-1,n_b}^2}e^{-i\delta t}\right. \\&\left. \times \left( \cos (\tilde{\Omega }_{n_a-1,n_b}t) +\,i{\delta \over \tilde{\Omega }_{n_a-1,n_b}}\sin (\tilde{\Omega }_{n_a-1,n_b}t)\right) \right] . \end{aligned} \end{aligned}$$

(5)

In the above relations, the Rabi frequencies have been defined as:

$$\begin{aligned}&\Omega _{n_{a(b)}}=g_{a(b)}\sqrt{n_{a(b)}+1},\nonumber \\&\Omega _{n_a-1,n_b}=\sqrt{\Omega _{n_a-1}^2+\Omega _{n_b}^2},\nonumber \\&\tilde{\Omega }_{n_a-1,n_b}=\sqrt{\Omega _{n_a-1,n_b}^2+\delta ^2}. \end{aligned}$$

(6)

Now, all requirements are prepared to perform our designed teleportation process. To achieve the goal of the paper, we assume that the atom 1 is initially in the unknown state $\vert {\varphi }\rangle _\mathrm{in}=\alpha \vert {f}\rangle _1+\beta \vert {g}\rangle _1$ (where the coefficients $\alpha$ and $\beta$ satisfy the normalization condition ${\arrowvert \alpha \arrowvert }^2+{\arrowvert \beta \arrowvert }^2=1$). We intend to teleport the quantum state $\vert {\varphi }\rangle _\mathrm{in}$ from atom 1 to atom 2. To do such a task, at first, the atom 2, which is initially prepared in the state $\vert {f}\rangle _2$, interacts with the two-mode cavity field (modes a and b), where each mode is expressed with a one-photon state, $\vert {1,1}\rangle$, for an appropriate time $t_1$. We have indeed modeled the two-mode initial field (single photon in each mode) as a cavity initialized with one photon in each of the two modes of the cavity (see for instance [23, 24] and references therein). Therefore, a “quantum channel” is created which may be given by:

$$\begin{aligned} \begin{aligned} \vert {\phi (t_1)}\rangle&=C_f(1,1,t_1)\vert {f,1,1}\rangle +C_e(0,1,t_1)\vert {e,0,1}\rangle +C_g(0,2,t_1)\vert {g,0,2}\rangle . \end{aligned} \end{aligned}$$

(7)

Consequently, the whole system state reads as:

$$\begin{aligned} \begin{aligned} \vert {\Psi }\rangle&= \alpha \left[ C_f(1,1,t_1)\vert {f,f,1,1}\rangle +\, C_e(0,1,t_1)\vert {f,e,0,1}\rangle \right. \\&\quad \left. +\, C_g(0,2,t_1)\vert {f,g,0,2}\rangle \right] \\&\quad + \beta \left[ C_f(1,1,t_1)\vert {g,f,1,1}\rangle +\, C_e(0,1,t_1)\vert {g,e,0,1}\rangle \right. \\&\quad \left. +\,C_g(0,2,t_1)\vert {g,g,0,2}\rangle \right] , \end{aligned} \end{aligned}$$

(8)

where the coefficients in (7), (8) can be readily determined from the relations in (3)–(5). In the next step, while the atom 2 is sent to the receiver (Bob), the atom 1 is sent to interact with the cavity field for an appropriate time $t_2$. In calculating the state vector of atom-field system, it should be noticed that the coefficients $C_{i=f,e,g}(n'_a,n'_b,t)$ are dependent on the initial conditions of atom and field. In the first step, the initial state of atom 2 was $\vert {f}\rangle _2$ (the initial state of cavity was $\vert {1,1}\rangle$). However, in the next step, the initial states of atom and field are changed, atom 1 which is in the initial state $\vert {\varphi }\rangle _\mathrm{in}$, interacts with the cavity whose state is $\vert {1,1}\rangle$, $\vert {0,1}\rangle$, or $\vert {0,2}\rangle$. Each of these states may be determined from the external (final) state of atom 2. The state vector results from the interaction between atom 1 (in the state $\vert {\varphi }\rangle _\mathrm{in}$) and the cavity (in the states $\vert {1,1}\rangle$, $\vert {0,1}\rangle$, or $\vert {0,2}\rangle$) are obtained by Eq. (2), and the coefficients of this state can be calculated from Eqs. (3)–(5). This state vector together with the final state of atom 2 describes the whole state of the system as:

$$\begin{aligned}&\vert {\Phi }\rangle =\alpha C_f(1,1,t_1)\left[ C_f(1,1,t_2)\vert {f,f,1,1}\rangle +\, C_e(0,1,t_2)\vert {e,f,0,1}\rangle \right. \nonumber \\&\quad \qquad \left. +\, C_g(0,2,t_2)\vert {g,f,0,2}\rangle \right] + \alpha C_g(0,2,t_1)C_f(0,2,t_2)\vert {f,g,0,2}\rangle \nonumber \\&\quad \qquad +\, \alpha C_e(0,1,t_1)C_f(0,1,t_2)\vert {f,e,0,1}\rangle \nonumber \\&\quad \qquad +\,\beta C_f(1,1,t_1)\left[ C_g(1,1,t_2)\vert {g,f,1,1}\rangle +\, C_e(1,0,t_2 )\vert {e,f,1,0}\rangle \right. \nonumber \\&\quad \qquad \left. +\, C_f(2,0,t_2)\vert {f,f,2,0}\rangle \right] \nonumber \\&\quad \qquad +\, \beta C_e(0,1,t_1)\left[ C_g(0,1,t_2)\vert {g,e,0,1}\rangle +\,C_e(0,0,t_2 )\vert {e,e,0,0}\rangle \right. \nonumber \\&\quad \qquad \left. +\,C_f(1,0,t_2)\vert {f,e,1,0}\rangle \right] \nonumber \\&\quad \qquad +\, \beta C_g(0,2,t_1)\left[ C_g(0,2,t_2)\vert {g,g,0,2}\rangle +\,C_e(0,1,t_2 )\vert {e,g,0,1}\rangle \right. \nonumber \\&\quad \qquad \left. +\, C_f(1,1,t_2)\vert {f,g,1,1}\rangle \right] . \end{aligned}$$

(9)

Now, if the transmitter (Alice) detects the atom 1 in the state $\vert {g}\rangle$, then the state of the reduced subsystem composed of atom 2 and cavity field results in:

$$\begin{aligned} \begin{aligned} \vert {\phi }\rangle _{2,C}&=N\left[ \xi \vert {f,0,2}\rangle +\lambda \vert {f,1,1}\rangle +\eta \vert {e,0,1}\rangle +\gamma \vert {g,0,2}\rangle \right] , \end{aligned} \end{aligned}$$

(10)

where the parameter N is a normalized coefficient which may be easily determined when $\xi =\alpha C_f(1,1,t_1)C_g(0,2,t_2), \lambda =\beta C_f(1,1,t_1)C_g(1,1,t_2), \eta =\beta C_e(0,1,t_1)C_g(0,1,t_2), \gamma =\beta C_g(0,2,t_1)C_g(0,2,t_2).$ If the atom which is in the initial state $\vert {f}\rangle$ enters the cavity, it was shown that the dynamics of the mentioned three-level atomic system becomes particularly simple in the large one-photon detuning limit [22]. In this Ref., by defining small parameter $\varepsilon _{n_a-1,n_b}={\Omega _{n_a-1,n_b}\over \Delta }<<1$, the authors showed that after performing the interaction of atom with the cavity field, the occupation probability of the atomic level $\vert {e}\rangle _2$ becomes considerably small and so may be eliminated, adiabatically. Accordingly, the coefficient $C_e(0,1,t_1)$ becomes small and the atom 2 approximately collapses to the state $\vert {\varphi }\rangle _2=\alpha \vert {f}\rangle _2+\beta \vert {g}\rangle _2$, which is exactly like the initial state of atom 1. As a result, the state of atom 1 is properly teleported to atom 2. The probability of measuring the state $\vert {g}_1\rangle$ (success probability) may be readily calculated as:

$$\begin{aligned} P_g={\vert \xi \vert }^2+{\vert \lambda \vert }^2+{\vert \eta \vert }^2+{\vert \gamma \vert }^2=N^{-2}. \end{aligned}$$

(11)

Also, the fidelity of the teleported state ($\vert {\phi }\rangle _{2,C}$), relative to the initial state $\vert {\varphi }\rangle _\mathrm{in}$, is given by:

$$\begin{aligned} \begin{aligned} F&=\vert \langle {\phi _{2,C}\vert {\varphi }\rangle _\mathrm{in}}\vert ^2\\&=N^2 \left[ {\vert \alpha \xi \vert }^2+{\vert \alpha \lambda \vert }^2+{\vert \beta \gamma |}^2+\alpha ^*\beta \xi \gamma ^*+\beta ^*\alpha \gamma \xi ^*\right] . \end{aligned} \end{aligned}$$

(12)

It should be emphasized that the times $t_1$ and $t_2$ in the relations $P_g$ and F should be chosen such that they optimize the fidelity of the teleported state ($\vert {\phi }\rangle _{2,C}$).

3 Results and discussion

At first, it should be noticed that in all numerical results which are followed in this section (as well as in Fig. 2), we used $g_a=g_b=g=16$ MHz and $\delta =10g$ (see Refs. [22, 25]). This value of atom-field coupling is of the order of which a Rydberg atom in the interaction with a quantized field can acquire. Indeed, this is accessible by adjusting appropriate energy levels n of the Rydberg atom as well as the applied electric field amplitude [26]. Recall that the probability of induced transitions between adjacent levels in Rydberg atoms scales as $n^4$, where n denotes the principle quantum number. Therefore, by choosing the energy levels as $n \simeq 100$, less or even greater than 100 [27], the value of g can be adjusted on demand. Accordingly, the Rydberg atoms and the related atomic techniques together with the superconducting Niobium cavity which provides very high quality cavities constitute an appropriate framework in our proposed model, especially to achieve the considered values of $g=16$ MHz. In this respect, we would like to emphasize that as we examined our calculations with different g’s while preserving its order, the results are not so sensitive to its value. In Fig. 2, we display the maximum fidelity of the teleported atomic state (while we considered the optimized values of $t_1$ and $t_2$) versus the unknown coefficient of the teleported state $\alpha$. This figure shows that distribution of the fidelity is between about 69 and 100%. We now select the interaction times associated with the minimum value of fidelity (about 69%), where this result corresponds in particular to the special times $t_1=1.7\mu$s and $t_2=2.0\mu$s.

Fig. 2

The maximum fidelity of the teleported atomic state by optimization of the time values of $t_1$ and $t_2$ versus $\alpha$ ($\alpha$ is one of the unknown coefficients of the teleported atomic state), $g_a=g_b=g=16$ MHz and $\delta =10g$.

Fig. 3

Success probability versus coefficient $\alpha$ for two particular interaction times $t_1=1.7\mu$s, $t_2=2.0~\mu$s, other parameters are as in Fig. 2.

Fig. 4

Fidelity of the teleported atomic state with the parameters as in Fig. 3.

Figure 3 displays success probability, $P_g$, versus the coefficient $\alpha$ using the latter extracted interaction times. This figure shows that the rate of Alice’s success in detecting $\vert {g}\rangle _1$ after the interaction of atom 1 with the cavity field. As is seen, the values of success probability are constrained to $0.14 \lesssim P_g \lesssim 0.56$, which are satisfactorily values in this particular field of research [12, 13, 25, 28].

In Fig. 4, the fidelity of the teleported atomic state is plotted versus $\vert \alpha \vert ^2$ (the probability of finding the initial unknown atomic state in $\vert f\rangle$) also for the above two interaction times $t_1=1.7 \mu$s and $t_2=2.0\mu$s that are extracted from the minimum fidelity in Fig. 2. The fidelity begins from 0.72 at zero value of $\vert \alpha \vert ^2$, decreases a little at the intermediate values of $\vert \alpha \vert ^2$ to 0.69, and then eventually increases and finally reaches its maximum possible value 1. It is worthwhile to notice that the minima of the plots 2 and 4 coincides at the value 0.69, as is expected. To make more clear the procedure, we imply that in plotting Fig. 4 we have used the interaction times corresponding to the minimum fidelity. Therefore, it can be concluded that, using other possible values of interaction times may even lead to more favorite values of fidelity with minima greater than 0.69 and so closer to its maximum value 1.

4 Summary and conclusion

Summing up, we presented a scheme for the teleportation of an unknown state of a three-level atomic state, based on the cavity QED method. In our scheme, we have not used the Bell-state measurement explicitly due to the hardness of the implementation of latter method [29, 30]; this is indeed one of the significant benefits of our used proposal. In the scheme, two three-level atoms in $\varLambda$-type interact separately and subsequently with the two-mode cavity field. The state we want to teleport belongs to atom 1. To achieve the purpose, we perform our implementation such that, at first atom 2 and then atom 1 interact with the cavity field. Next, only with an appropriate measurement on atom 1, the state of atom 2 properly transfers to the atom 1. With the scheme, the fidelity of the state of atom 2 to the initial state of atom 1 is always more than $69\%$ and can reach to even 1, which are satisfactory values in the contents which concern the teleportation. In the continuation, by obtaining the times from the optimization of fidelity, success probability by Alice is evaluated versus $\alpha$ [with the minimum (maximum) at 0.14 (0.56)]. It should be pointed out that the mentioned success probabilities are satisfactory values comparing with the literature concern with this subject. Then, the fidelity of the state of atom 2 to the initial state of atom 1 is evaluated. It is seen that when $|\alpha |^2$ (or the probability of finding $\vert {f}\rangle$) increases, the fidelity increases to unit value. We now give a comparison of our results with the reported results in the literature [12, 13, 25, 28] (see Table 1). As may clearly be seen, there is not a significant difference among the results of the latter four Refs. However, the main distinguishable advantage of our presentation relative to the these Refs. lies in the fact that the success probability of our teleportation process becomes more than twice of those of the those Refs. This is while the complete fidelity in all mentioned cases (and ours, too) is achievable. We end this section with giving a brief discussion on the experimental feasibility of the present scheme. Taking a look on Table 1, which is prepared by considering the experimental information indicated within [13], and comparing all the above related works with our scheme clearly show that our proposal improves all previous schemes, by making the success probability more than twice of the previous works in the literature and the required interaction time much shorter than the most appropriate ones.

It ought to be mentioned that while the teleportation schemes in [12, 13, 25, 28] required the initial vacuum field state, our presented scheme is based on using the single-photon state as the initial field state. In this relation, two points should be addressed. At first, it is noneducable that the designated initial state for the purpose of teleportation is part of the scheme, and secondly the generation of single-photon state is not as straightforward as the vacuum state. Returning to these points, the benefits of our proposal may likely be questioned. Briefly, a question that may naturally be arisen about the possibility of generation of single-photon state. Fortunately, it seems that the recent and present researches have been successfully overcome such problem and better single-photon sources are expected in near future (for an extended theoretical treatment on the subject, see the special issue “Focus on Single Photons on Demand” in [31] as well as the published papers therein and for the related experimental demonstrations see [32,33,34,35,36]).

Table 1 The comparison of our results with the previously reported