Multi-Party Quantum Secret Sharing Protocol Based on GHZ States Entanglement Swapping

Abstract

In this paper, a multi-party quantum secret sharing protocol based on GHZ states entanglement swapping and measurement is proposed. Firstly, we define the “characteristic”, then, using the property that multiple groups of GHZ states swapping any particles to keep the characteristics unchanged, a relationship between the characteristics of measurement results, initial state characteristics and Pauli operator characteristics is given, and the protocol is completed by utilizing this equation. In this scheme, the quantum resources involved are only the n GHZ state particles distributed by Trent transmitted in the quantum channel to the participants, and the other classical bit resources are distributed in advance or generated by the participants themselves, which improves the security of resource transmission. Furthermore, all participants only need to make GHZ measurements and contribute their own sub-secrets, and can recover the shared secret through a simple XOR formula. It is proud that the efficiency of the whole scheme (i.e. 1/3n) has also reached the ideal situation.

1 Introduction

As a branch of cryptography, Shamir [1] and Blakley [2] first proposed the classical secret sharing (CSS) scheme in 1979. CSS is an important technology to ensure the security and availability of confidential information. It has a typical application: the company manager has a secret, and he doesn’t want any employees to know his secret completely. Therefore, he divided his secret into many parts and let each employee know only one part. Only with the cooperation of all the staff can his secret be completely restored. The security of CSS depends on the complexity of large prime decomposition, and its research has become mature [3]. However, all CSS schemes assume of computational complexity, that is, security is conditional.

With the development of quantum computers, especially the emergence of quantum algorithms [4], the security of classical cryptography is facing severe challenges. Since Bennett and brassard [5] first introduced quantum cryptography in 1984, classical secret sharing was soon combined with quantum mechanics, and quantum secret sharing (QSS) was born. In 1999, Hillery et al. [6] proposed quantum secret sharing protocol for the first time. As one of the earliest famous branches of quantum cryptography, this protocol has attracted extensive attention. In the scheme, quantum states are used as the coding carrier of secret information, so that all parties share a common secret, which can be restored only by the cooperation of all parties. From the perspective of the types of shared secrets, QSS schemes can be divided into two categories: shared quantum information [7] and shared classical information [8]. The former is mainly realized by quantum operations such as quantum entanglement swapping and quantum teleportation. The latter can show various characteristics in scheme design. The security of these two protocols has been proved in theory. In 2003, Guo et al. [9] proposed a non-entangled QSS protocol, which essentially encodes qubits directly. In 2004, Xiao et al. [10] extended the QSS scheme of Hillery et al. [6] to multiple parties and used the optimal measurement method to improve the efficiency. In 2005, Yan et al. [11] proved that A (t, m) - (s, n) threshold QSS protocol is effective in the absence of channel based on Greenberger-Horne-Zeilinger (GHZ) state.

Semi-quantum secret sharing (SQSS) is also an important research point, which is more in line with the actual application. In 2010, Li et al. [12] proposed SQSS protocol based on two GHZ-like states. In 2012, Wang et al. [13] proposed a SQSS scheme based on two particle entangled states. In 2013, Li et al. [14] proposed a SQSS protocol using the state of tensor product of two particles. In the same year, to improve the efficiency of key generation, Yang and Hwang [15] desynchronized the measurement of the classical party. In 2015, Qin and Dai [16] constructed a proactive QSS scheme. In the same year, Xie et al. [17] proposed a SQSS protocol in which a quantum party can share specific messages with two classical parties. However, Yin and Fu [18] pointed out in 2016 that the SQSS protocol of Xie et al. [17] would suffer intercept-resend attacks from dishonest parties, and put forward corresponding improvement protocols. In 2017, Gao et al. [19] found that Yin and Fu [18] analyzed the intercept-resend attack of dishonest parties incorrectly, and the protocol does not meet the semi-quantum conditions, so they made improvements accordingly. Later, Ye and Ye [20] proposed two circular SQSS protocols based on single particle. The first protocol requires the classical party to have measurement capability, and the second protocol does not.

Up to now, QSS protocol has made great progress, and QSS protocols designed from various angles emerge in endlessly. In 2018, Qin and Tso [21] proposed an efficient QSS scheme based on special multi-dimensional GHZ state. In 2019, Kang et al. [22] proposed a continuous variable QSS scheme by using the Chinese Remainder Theorem. In 2020, Liu et al. [23] proposed a QSS scheme with verifiable function. In the same year, Lai et al. [24] proposed a high-capacity (2,3) threshold QSS scheme based on asymmetric Quantum lossy channel. Subsequently, Sutradhar and Om [25] proposed an effective QSS scheme without trusted participants.

Based on the theorem that the entanglement swapping characteristics of GHZ state particles are invariant, an anonymously verifiable multi-party quantum secret sharing scheme is proposed, in which the shared secret is classical information. The protocol conforms to the basic principle of secret sharing. Any participant less than n cannot recover the secret alone. All participants must cooperate and take their share before they can get the secret. Moreover, the proposed scheme also meets the high standard of efficiency and security requirements, and can complete the purpose of the experiment with less quantum resources.

The rest of the work is arranged as follows: Section 2 gives some preliminary preparations, mainly several theorems quoted and deduced. Section 3 describes in detail the specific process of how to share classical information with the help of quantum methods. Sections 4 provides the security analysis of the protocol and sections 5 analyzes the efficiency. Finally, a summary is given in section 6.

2 Preliminaries

2.1 GHZ State and Pauli Operation

There are eight three-particle entangled GHZ states, written as follows:

$$ {\displaystyle \begin{array}{c}\mid {\varPsi}_{000}\left\rangle =\frac{1}{\sqrt{2}}\left(|100\Big\rangle +|011\Big\rangle \right),\kern1em \mid {\varPsi}_{001}\right\rangle =\frac{1}{\sqrt{2}}\left(|100\Big\rangle -|011\Big\rangle \right)\\ {}\mid {\varPsi}_{010}\left\rangle =\frac{1}{\sqrt{2}}\left(|111\Big\rangle +|000\Big\rangle \right),\kern1em \mid {\varPsi}_{011}\right\rangle =\frac{1}{\sqrt{2}}\left(|111\Big\rangle -|000\Big\rangle \right)\\ {}\mid {\varPsi}_{100}\left\rangle =\frac{1}{\sqrt{2}}\left(|101\Big\rangle +|010\Big\rangle \right),\kern0.75em \mid {\varPsi}_{101}\right\rangle =\frac{1}{\sqrt{2}}\left(|101\Big\rangle -|010\Big\rangle \right)\\ {}\mid {\varPsi}_{110}\left\rangle =\frac{1}{\sqrt{2}}\left(|110\Big\rangle +|001\Big\rangle \right),\kern0.75em \mid {\varPsi}_{111}\right\rangle =\frac{1}{\sqrt{2}}\left(|110\Big\rangle -|001\Big\rangle \right)\end{array}} $$

Furthermore, any GHZ state |Ψ_ijk〉 can be rewritten as the following general formula:

$$ \left|{\Psi}_{ijk}\right\rangle =\frac{1}{\sqrt{2}}\left(\left|1 jt\right\rangle +{\left(-1\right)}^k\left|0\overline{j}\overline{t}\right\rangle \right) $$

where i, j, k, t ∈ (0, 1), t = i ⊕ j and $\overline{j}=j\oplus 1$, $\overline{t}=t\oplus 1$ (i.e., a bar over a bit value indicates its logical negation). In this paper, ⊕ represents XOR operation, and the classical bit string ijk is regarded as the characteristic of GHZ state |Ψ_ijk〉.

Next, we introduce four basic Pauli operators, as follows:

$$ {\displaystyle \begin{array}{c}{U}_{000}=I=\left|0\right\rangle \left\langle 0\right|+\left|1\right\rangle \left\langle 1\right|,{U}_{001}={\sigma}_z=\left|0\right\rangle \left\langle 0\right|-\left|1\right\rangle \left\langle 1\right|\\ {}{U}_{110}={\sigma}_x=\left|0\right\rangle \left\langle 1\right|+\left|1\right\rangle \left\langle 0\right|,{U}_{111}=i{\sigma}_y=\left|0\right\rangle \left\langle 1\right|-\left|1\right\rangle \left\langle 0\right|\end{array}} $$

Similarly, the subscript k₁k₂k₃ is regarded as the characteristic of the Pauli operator ${U}_{k_1{k}_2{k}_3}$, where k₁, k₂, k₃ ∈ (0, 1).

Here, the state change of |0〉 or |1〉 after being operated by each Pauli operator is given:

$$ {\displaystyle \begin{array}{c}I\left|0\right\rangle =\left|0\right\rangle, I\left|1\right\rangle =\left|1\right\rangle {\sigma}_z\left|0\right\rangle =\left|0\right\rangle, {\sigma}_z\left|1\right\rangle =-\left|1\right\rangle \\ {}{\sigma}_x\left|0\right\rangle =\left|1\right\rangle, I\left|1\right\rangle =\left|0\right\rangle {\sigma}_y\left|0\right\rangle =-\left|1\right\rangle, {\sigma}_z\left|1\right\rangle =\left|0\right\rangle \end{array}} $$

2.2 Entanglement Swapping Theorem

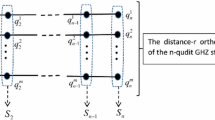
Theorem 1. [26] For n GHZ states {(1, 2, 3), (4, 5, 6), …, (3n-2, 3n-1, 3n)}, after entanglement swapping as Fig. 1, the possible measurement results and the initial states always meet the following equation:

$$ {M}_{1,2,3n}\oplus {M}_{4,5,3}\oplus \dots \oplus {M}_{3n-2,3n-1,3n-3}={B}_{1,2,3}\oplus {B}_{4,5,6}\oplus \dots \oplus {B}_{3n-2,3n-1,3n} $$

(1)

where B_ijk and M_rst denote the characteristics of the initial states of the particles i, j and k, and the possible measurement results of the particles r, s and t, respectively. This formula applies when only one set of particles is exchanged.

Fig. 1

Entanglement swapping of a group of particles in n GHZ states

Theorem 2. [26] For n GHZ states {(1, 2, 3), (4, 5, 6), …, (3n-2, 3n-1, 3n)}, after entanglement swapping as Fig. 2, the possible measurement results and the initial states always meet the following equation:

$$ {M}_{1,3n-1,3n}\oplus {M}_{4,2,3}\oplus \dots \oplus {M}_{3n-2,3n-4,3n-3}={B}_{1,2,3}\oplus {B}_{4,5,6}\oplus \dots \oplus {B}_{3n-2,3n-1,3n} $$

(2)

where B_ijk and M_rst denote the characteristics of the initial states of the particles i, j and k, and the possible measurement results of the particles r, s and t, respectively. This formula applies when two sets of particles are exchanged.

Fig. 2

Entanglement swapping of two groups of particles in n GHZ states

Theorem 3. If we perform any Pauli operator ${U}_{k_1{k}_2{k}_3}$ on any particle in any GHZ state |Ψ_ijk〉₁₂₃, the characteristic ${B}_{123}^{\prime }$ of transformed particles 1, 2 and 3 always satisfies the following equation:

$$ {B}_{123}^{\prime }={k}_1{k}_2{k}_3\oplus {B}_{123} $$

(3)

Proof. Suppose we apply any Pauli operator ${U}_{k_1{k}_2{k}_3}$ to the first particle of GHZ state |Ψ_ijk〉₁₂₃, we will get,

$$ {U}_{k_1{k}_2{k}_3}{\left|{\Psi}_{ijk}\right\rangle}_{123}={U}_{k_1{k}_2{k}_3}\frac{1}{\sqrt{2}}{\left(\left|1 jt\right\rangle +{\left(-1\right)}^k\left|0\overline{j}\overline{t}\right\rangle \right)}_{123} $$

When k₁ = k₂ = 0, there will be:

$$ {\displaystyle \begin{array}{c}{U}_{k_1{k}_2{k}_3}{\left|{\Psi}_{ij k}\right\rangle}_{123}=\frac{1}{\sqrt{2}}{\left({\left(-1\right)}^{k_3}\left|1 jt\right\rangle +{\left(-1\right)}^k\left|0\overline{j}\overline{t}\right\rangle \right)}_{123}\\ {}=\frac{1}{\sqrt{2}}{\left({\left(-1\right)}^{k_3}\left(\left|1 jt\right\rangle +{\left(-1\right)}^{k\oplus {k}_3}\left|0\overline{j}\overline{t}\right\rangle \right)\right)}_{123}={\left(-1\right)}^{k_3}{\left|{\Psi}_{ij\left(k\oplus {k}_3\right)}\right\rangle}_{123}\end{array}} $$

So ${B}_{123}^{\prime }= ij\left(k\oplus {k}_3\right)={k}_1{k}_2{k}_3\oplus ijk$, that is, ${B}_{123}^{\prime }={k}_1{k}_2{k}_3\oplus {B}_{123}$.When k₁ = k₂ = 1, there will be:

$$ {\displaystyle \begin{array}{c}{U}_{k_1{k}_2{k}_3}{\left|{\Psi}_{ijk}\right\rangle}_{123}=\frac{1}{\sqrt{2}}{\left(\left|0 jt\right\rangle +{\left(-1\right)}^k{\left(-1\right)}^{k_3}\left|1\overline{j}\overline{t}\right\rangle \right)}_{123}\\ {}=\frac{1}{\sqrt{2}}{\left(\left|0 jt\right\rangle +{\left(-1\right)}^{k\oplus {k}_3}\left|1\overline{j}\overline{t}\right\rangle \right)}_{123}={\left|{\Psi}_{\overline{i}\overline{j}\left(k\oplus {k}_3\right)}\right\rangle}_{123}\end{array}} $$

So ${B}_{123}^{\prime }=\overline{i}\overline{j}\left(k\oplus {k}_3\right)=\left(i\oplus 1\right)\left(j\oplus 1\right)\left(k\oplus {k}_3\right)={k}_1{k}_2{k}_3\oplus ijk$, that is, ${B}_{123}^{\prime }={k}_1{k}_2{k}_3\oplus {B}_{123}$.

After verification, the result of applying any Pauli operator ${U}_{k_1{k}_2{k}_3}$ to the second or third particle is the same as the above conclusion, which will not be repeated here. Therefore, we can conclude that no matter which Pauli operator is executed on which particle, it satisfies Eq. (3).

Theorem 4. For n GHZ states {(1, 2, 3), (4, 5, 6), …, (3n-2, 3n-1, 3n)}, If we perform Pauli operator ${U}_{k_{3i-2}{k}_{3i-1}{k}_{3i}}$ on any particle of the i-th GHZ state (3i,3i + 1,3i + 2) or (3i-2,3i-1,3i), the measurement results after entanglement swapping (as shown in Fig. 3) have the following relationship with the initial state:

$$ {\oplus}_{i=1}^n{M}_{3i,3i+1,3i+2}={\oplus}_{i=1}^n{M}_{3i-1,3i,3i+1}=\left\{{\oplus}_{i=1}^n{B}_{3i-2,3i-1,3i}\right\}\oplus \left\{{\oplus}_{i=1}^n{k}_{3i-2}{k}_{3i-1}{k}_{3i}\right\} $$

(4)

Where M_{3i, 3i + 1, 3i + 2} and M_{3i − 1, 3i, 3i + 1} represents the characteristics of particles (3i,3i + 1,3i + 2) and (3i-1,3i,3i + 1) measurement results, respectively, B_{3i − 2, 3i − 1, 3i} is the characteristics of the initial state particle (3i-2,3i-1,3i), and k_3i − 2k_3i − 1k_3i denotes the characteristics of Pauli operator ${U}_{k_{3i-2}{k}_{3i-1}{k}_{3i}}$.

Fig. 3

Entanglement swapping of n GHZ state particles after applying n Pauli operators

Proof. From Theorems 1 and 2, we can get,

$$ {\displaystyle \begin{array}{c}{M}_{1,2,3n}\oplus {M}_{4,5,3}\oplus \dots \oplus {M}_{3n-2,3n-1,3n-3}\\ {}={M}_{1,3n-1,3n}\oplus {M}_{4,2,3}\oplus \dots \oplus {M}_{3n-2,3n-4,3n-3}\\ {}={B}_{1,2,3}^{\prime}\oplus {B}_{4,5,6}^{\prime}\oplus \dots \oplus {B}_{3n-2,3n-1,3n}^{\prime}\end{array}} $$

In addition, by Theorem 3, there are the following equations,

$$ {B}_{3i-2,3i-1,3i}^{\prime }={k}_{3i-2}{k}_{3i-1}{k}_{3i}\oplus {B}_{3i-2,3i-1,3i} $$

Therefore, ${\oplus}_{i=1}^n{M}_{3i,3i+1,3i+2}={\oplus}_{i=1}^n{M}_{3i-1,3i,3i+1}=\left\{{\oplus}_{i=1}^n{B}_{3i-2,3i-1,3i}\right\}\oplus \left\{{\oplus}_{i=1}^n{k}_{3i-2}{k}_{3i-1}{k}_{3i}\right\}$ is established.

The black solid line represents the entanglement between the initial three particles, and both GM and red dotted box represent GHZ measurement.

3 The Proposed Protocol

Suppose Trent has a secret S to be shared among n participants: p₁, p₂, …, p_n. For convenience, we only consider the case where the shared secret is 3-bit. In addition, we assume that Trent verified the identity of the participant p_i for i = 1, 2, …, n in advance and distributed a 3-bit subkey K_i face-to-face for each authenticated p_i. Then, Trent computed the XOR result of all subkeys, that is, $K={\oplus}_{i=1}^n{K}_i$.

Next, we will introduce the protocol in detail.

• Step 1. Trent prepared n GHZ states, in which each GHZ state was randomly in one of eight states, and then disrupted the particles of all GHZ states. Currently, there are 3n particles in disorder. Next, for i = 1, 2, …, n, Trent randomly selects three particles and sends them to p_i through the quantum channel. That is, each participant has three particles in the disordered n GHZ states at random.

• Step 2. Each participant p_i (i = 1, 2, …, n) randomly prepares a 3-bit sub-secret S_i as its private secret and computes Q_i = S_i ⊕ K_i. It should be noted here that when the first two bits of Q_i are different, p_i needs to replace them with the same two bits, i.e. 00 or 11. Furthermore, p_i applies the Pauli operator ${U}_{Q_i}$ on any one of the three received particles, and then performs GHZ measurement on the three particles.

• Step 3. All participants p₁, p₂, …, p_n publish their measurement results ${M}_{p_1},{M}_{p_2},\dots, {M}_{p_n}$, where ${M}_{p_i}$ represents the characteristics of the measurement results of participant p_i.

• Step 4. We specify $M={\oplus}_{i=1}^n{M}_{p_i}$, $B={\oplus}_{i=1}^n{B}_i$, where B_i denotes the characteristics of the i-th initial GHZ state after the Pauli operator is executed. Next, Trent computes T = M ⊕ B ⊕ S ⊕ K and declares the value of T.

• Step 5. When n participants p₁, p₂, …, p_n need to obtain Trent’s secret S, first, all of them need to contribute their private secret S_i. Through Theorem 4, we can infer that the characteristics of n GHZ measurement results, the characteristics of the initial GHZ state after the application of n Pauli operator and the characteristics of n Pauli operator meet the following relations:

• $$ \left\{{\oplus}_{i=1}^n{M}_{p_i}\right\}=\left\{{\oplus}_{i=1}^n{B}_i\right\}\oplus \left\{{\oplus}_{i=1}^n{Q}_i\right\} $$

Consequently, we can get the shared secret S:

$$ {\displaystyle \begin{array}{c}S=T\oplus M\oplus B\oplus K=T\oplus \left\{{\oplus}_{i=1}^n{Q}_i\right\}\oplus K\\ {}=T\oplus \left\{{\oplus}_{i=1}^n\left({S}_i\oplus {K}_i\right)\right\}\oplus K=T\oplus \left\{{\oplus}_{i=1}^n{S}_i\right\}\end{array}} $$

(5)

Example. Suppose there are three users: p₁, p₂ and p₃. Each user has three particles distributed by Trent, as shown in Fig. 4, p₁, p₂ and p₃ hold particles (1, 4, 9), (3, 7, 6) and (2, 5, 8), respectively. The Pauli operators ${U}_{Q_1}$, ${U}_{Q_2}$ and ${U}_{Q_3}$ of the three users are applied to particles 4, 7 and 2 respectively.

Fig. 4

Distribute three GHZ state particles to three participants

The black solid line represents the entanglement between the initial three particles, and the red dotted box denotes the GHZ measurement.

From Theorem 3, we can obtain the following equations:

$$ {B}_{123}^{\prime }={Q}_3\oplus {B}_{123}=\left({S}_3\oplus {K}_3\right)\oplus {B}_{123} $$

$$ {B}_{456}^{\prime }={Q}_1\oplus {B}_{456}=\left({S}_1\oplus {K}_1\right)\oplus {B}_{456} $$

$$ {B}_{789}^{\prime }={Q}_2\oplus {B}_{789}=\left({S}_2\oplus {K}_2\right)\oplus {B}_{789} $$

Besides, by Theorems 1 and 2, we can get,

$$ {\displaystyle \begin{array}{c}{M}_{p_1}\oplus {M}_{p_2}\oplus {M}_{p_3}={B}_{456}^{\prime}\oplus {B}_{789}^{\prime}\oplus {B}_{123}^{\prime}\\ {}=\left\{\left({S}_1\oplus {K}_1\right)\oplus {B}_{456}\right\}\oplus \left\{\left({S}_2\oplus {K}_2\right)\oplus {B}_{789}\right\}\oplus \left\{\left({S}_3\oplus {K}_3\right)\oplus {B}_{123}\right\}\\ {}=\left\{{S}_1\oplus {S}_2\oplus {S}_3\right\}\oplus \left\{{K}_1\oplus {K}_2\oplus {K}_3\right\}\oplus \left\{{B}_{123}\oplus {B}_{456}\oplus {B}_{789}\right\}\\ {}=\left\{{\oplus}_{i=1}^3{S}_i\right\}\oplus \left\{{\oplus}_{i=1}^3{K}_i\right\}\oplus \left\{{\oplus}_i^3{B}_{3i-2,3i-1,3i}\right\}\end{array}} $$

(6)

From Eq. (6), we get,

$$ {\displaystyle \begin{array}{c}\left\{{\oplus}_{i=1}^3{S}_i\right\}\oplus T=\left\{{\oplus}_{i=1}^3{S}_i\right\}\oplus S\oplus K\oplus M\oplus B\\ {}=\left\{{\oplus}_{i=1}^3{S}_i\right\}\oplus S\oplus K\oplus \left\{{\oplus}_{i=1}^3{S}_i\right\}\oplus \left\{{\oplus}_{i=1}^3{K}_i\right\}=S\end{array}} $$

As can be seen, only authenticated participants with a subkey (i.e. K_i) can recover the secret through Eq. (5). But the protocol needs to ensure that the subkey is not disclosed, that is, it can realize anonymous authentication through different K_i of each participant.

4 Security Analysis

This section analyzes the security of the proposed protocol. We discuss two aspects: external attacks and participant attacks. For external attack, we mainly consider interception-measure attack and entangle-measure attack. The following is a detailed analysis.

4.1 External Attack

• (1) Intercept-Measure Attack

Firstly, the external attacker can perform intercept-measure attacks. We assume that the external attacker Eve can intercept three particles assigned to any participant, then he directly measures the three particles in GHZ basis, and finally sends them back to the participant. If the attacker Eve successfully implements this attack, he will obtain the measurement state of the three particles distributed to the participant p_i. Furthermore, since the characteristic ${M}_{p_i}$ of the measurement results of the participants is public, Eve can easily infer Q_i. However, Q_i = S_i ⊕ K_i, where S_i is randomly selected by the user p_i, and K_i is p_i‘s absolutely secure private key. Therefore, even though Eve can obtain Q_i, he still cannot obtain any relevant information about S_i or K_i. That is, Eve cannot get any private information about K and $\left\{{\oplus}_{i=1}^n{S}_i\right\}$. Without relevant information about K and $\left\{{\oplus}_{i=1}^n{S}_i\right\}$, it is obvious that Eve cannot know the secret S shared by Trent to the participants, because T = S ⊕ K ⊕ M ⊕ B and $S=\left\{{\oplus}_{i=1}^n{S}_i\right\}\oplus T$. Therefore, this attack is completely infeasible for the proposed quantum secret sharing protocol.

• (2) Entangle-Measure Attack

External attackers can also perform more complex attacks, namely entangle-measure attacks. Suppose that the external attacker Eve intercepts the particles assigned to the participants and prepares ancillary particles for each intercepted particle. Eve first entangles the ancillary particles with the intercepted particles through the local unitary operator, and finally extracts some useful information by measuring the ancillary particles. For example, as shown in Fig. 5, the attacker Eve intercepts six particles 1, 2, 3, 4, 5, 6 transmitted through the quantum channel, where (1, 2, 3) and (4, 5, 6) are two pairs of entangled GHZ state particles, and executes CNOT gate operators for particle pairs (1,a₁), (2,a₂), (3,a₃), (4,a₄), (5,a₅) and (6,a₆), where a₁, a₂, a₃, a₄, a₅ and a₆ are six ancillary particles prepared by Eve for the target particles. Finally, Eve sends the intercepted particles back to the corresponding participants. Here, for simplicity, we omit the Pauli operators and assume that the corresponding participants directly perform GHZ-basis measurements on particles (1,2,6) and (3,4,5), respectively. Without losing generality, we assume that the initial states of GHZ state particles (1, 2, 3) and (4, 5, 6) are ${\left|{\Psi}_{000}\right\rangle}_{123}=\frac{1}{\sqrt{2}}{\left(\left|100\right\rangle +\left|011\right\rangle \right)}_{123}$, ${\left|{\Psi}_{010}\right\rangle}_{456}=\frac{1}{\sqrt{2}}{\left(\left|111\right\rangle +\left|000\right\rangle \right)}_{456}$, and the initial states of all ancillary particles are |0〉.

Fig. 5

The entangle-measure attack

Next, we start to execute the CNOT gate operators, and then we can get:

$$ {\displaystyle \begin{array}{c} CNOT\left[1,{a}_1\right] CNOT\left[2,{a}_2\right] CNOT\left[3,{a}_3\right]\left(|{\varPsi}_{000}\Big\rangle {}_{123}\otimes |0\Big\rangle {}_{a_1}\otimes |0\Big\rangle {}_{a_2}\otimes |0\Big\rangle {}_{a_3}\right)\\ {}= CNOT\left[1,{a}_1\right] CNOT\left[2,{a}_2\right] CNOT\left[3,{a}_3\right]\left(\frac{1}{\sqrt{2}}{\left(|100\Big\rangle +|011\Big\rangle \right)}_{123}\otimes |0\Big\rangle {}_{a_1}\otimes |0\Big\rangle {}_{a_2}\otimes |0\Big\rangle {}_{a_3}\right)\\ {}\begin{array}{c}=\frac{1}{\sqrt{2}}{\left(|100100\Big\rangle +|011011\Big\rangle \right)}_{123{a}_1{a}_2{a}_3}\\ {} CNOT\left[4,{a}_4\right] CNOT\left[5,{a}_5\right] CNOT\left[6,{a}_6\right]\left(|{\varPsi}_{010}\Big\rangle {}_{456}\otimes |0\Big\rangle {}_{a_4}\otimes |0\Big\rangle {}_{a_5}\otimes |0\Big\rangle {}_{a_6}\right)\\ {}\begin{array}{c}= CNOT\left[4,{a}_4\right] CNOT\left[5,{a}_5\right] CNOT\left[6,{a}_6\right]\left(\frac{1}{\sqrt{2}}{\left(|111\Big\rangle +|000\Big\rangle \right)}_{456}\otimes |0\Big\rangle {}_{a_4}\otimes |0\Big\rangle {}_{a_5}\otimes |0\Big\rangle {}_{a_6}\right)\\ {}=\frac{1}{\sqrt{2}}{\left(|111111\Big\rangle +|000000\Big\rangle \right)}_{456{a}_4{a}_5{a}_6}\end{array}\end{array}\end{array}} $$

Due to the randomness of the measurement, if the measurement results of particles (1, 2, 6) and (3, 4, 5) are ${\left|{\Psi}_{100}\right\rangle}_{126}=\frac{1}{\sqrt{2}}{\left(\left|101\right\rangle +\left|010\right\rangle \right)}_{126}$ and ${\left|{\Psi}_{110}\right\rangle}_{345}=\frac{1}{\sqrt{2}}{\left(\left|110\right\rangle +\left|001\right\rangle \right)}_{345}$, the following results will be obtained:

$$ {\displaystyle \begin{array}{c}\Big\langle {\varPsi}_{100}{\left|{}_{123}\otimes \Big\langle {\varPsi}_{110}\right|}_{345}\otimes \frac{1}{\sqrt{2}}{\left(|100100\Big\rangle +|011011\Big\rangle \right)}_{123{a}_1{a}_2{a}_3}\otimes \frac{1}{\sqrt{2}}{\left(|111111\Big\rangle +|000000\Big\rangle \right)}_{456{a}_4{a}_5{a}_6}\\ {}=\frac{1}{\sqrt{2}}\left(\right\langle 101\mid +\left\langle 010\mid \right){}_{126}\otimes \frac{1}{\sqrt{2}}\left(\right\langle 110\mid +\left\langle 001\mid \right){}_{345}\otimes \frac{1}{\sqrt{2}}{\left(|100100\Big\rangle +|011011\Big\rangle \right)}_{123{a}_1{a}_2{a}_3}\\ {}\otimes \frac{1}{\sqrt{2}}{\left(|111111\Big\rangle +|000000\Big\rangle \right)}_{456{a}_4{a}_5{a}_6}=\frac{1}{4}{\left(|100111\Big\rangle +|011000\Big\rangle \right)}_{a_1{a}_2{a}_3{a}_4{a}_5{a}_6}\end{array}} $$

Obviously, the state of possible measurement results of ancillary particles (1, 2, 6) and (3, 4, 5) are $\left\{{\left|{\Psi}_{100}\right\rangle}_{a_1{a}_2{a}_6},{\left|{\Psi}_{000}\right\rangle}_{a_3{a}_4{a}_5}\right\}$ or $\left\{{\left|{\Psi}_{101}\right\rangle}_{a_1{a}_2{a}_6},{\left|{\Psi}_{001}\right\rangle}_{a_3{a}_4{a}_5}\right\}$. This means that the attacker Eve can infer the XOR result of the measurement results of n participants, i.e. ${\oplus}_{i=1}^n{M}_{p_i}$, by measuring ancillary particles on the GHZ basis. However, ${\oplus}_{i=1}^n{M}_{p_i}$ is originally public, so Eve does not obtain substantive information. In fact, he still can’t get K and ${\oplus}_{i=1}^n{S}_i$, so he never learns about the shared secret S. According to the above, our quantum secret sharing protocol can resist the entangle-measure attack.

The black solid line represents the entanglement relationship, and the red dotted box denotes GHZ measurement.

4.2 Participant Attack

We assume that there are any dishonest participants with n-1 or less than n-1 who want to recover secret S through illegal conspiracy. However, all quantum resources used and all subkeys distributed are privately generated by Trent, and each sub-secret S_i is randomly selected by each participant. Obviously, any dishonest participant with n-1 or less than n-1 cannot obtain the values of K and ${\oplus}_{i=1}^n{S}_i$, that is, they cannot obtain secret S by collusion. Therefore, our protocol can resist participant attack.

4.3 Others

In addition, the initial subkey K_i distributed by Trent in advance can ensure the authenticity of GHZ state particles distributed by Trent, because only Trent knows the value of K (i.e. ${\oplus}_{i=1}^n{K}_i$). Of course, Trent can also assign a group of particles to each participant instead of three particles, so that Trent and participants can select some particles to jointly check the security of quantum channels [27]. Moreover, we can also use decoy photon detection technology [28] to check eavesdropping on quantum channels. Besides, participants can privately exchange particles before executing Pauli operators, to avoid distributing known GHZ states to designated participants. Consequently, the attacker Eve (even Trent) cannot infer the private operator executed by the participant only from its public measurement results.

Our QSS protocol has the following advantages:

• (1) Particles are randomly distributed, and each participant does not know whose particles are entangled with the particles he holds.

• (2) Anonymous authentication can be provided.

• (3) All subkeys K_i and sub-secrets S_i do not need to be transmitted through any classical or quantum channel.

• (4) The operator performed by each participant is completely independent of its sub-secret or subkey. That is, no attacker or eavesdropper can obtain any private information about single subkey or single sub-secret.

• (5) The attacker cannot obtain any private information about K and ${\oplus}_{i=1}^n{S}_i$, and he has no information about the shared secret S. Hence, the proposed secret sharing protocol is unconditionally secure.

5 Efficiency Analysis

Now let us discuss the efficiency of our protocol. According to [29], some efficiency factors can be defined as the following formula, which can be used to obtain the efficiency of quantum communication protocols.

$$ \eta =\frac{b_s}{q_t+{b}_t} $$

Where b_s is the bit length of the shared secret, and q_t is the total number of quantum resources utilized, and b_t represents the number of classical bits used in the protocol. In this scheme, the length of secret S to be shared by Trent is 3-bit, so b_s is 3; The quantum resources utilized in the protocol are only n GHZ state particles distributed by Trent at the beginning, so q_t is 3n; Before the start of the protocol, Trent distributed a 3-bit subkey K_i to each participant, after the start of the protocol, each participant randomly generated a 3-bit sub-secret S_i, so b_t is 6n. It can be concluded that the efficiency of our protocol is $\eta =\frac{b_s}{q_t+{b}_t}=\frac{1}{3n}$.

In Table 1, we also show comparisons with several similar typical protocols in many aspects.

Table 1 Comparison among related protocols

6 Conclusion

Firstly, we quote the theorem that the entanglement swapping characteristics of GHZ state are invariant. Through the existing theorems, we deduce two new theorems: one is the relationship between the characteristics of initial GHZ state, the characteristics of initial state after executing Pauli operator and the characteristics of Pauli operator; The other is the relationship among the characteristics after swapping measurement, initial state characteristics and Pauli operator characteristics. By the transformation relationship between equations and the nature of XOR operation, all honest participants obtain the final shared secret. This scheme has many advantages, such as particle randomness, anonymous authentication, unconditional security and so on. The security analysis and efficiency analysis show that it cannot only resist most attacks and ensure that the shared secret is not leaked, but also has ideal efficiency. Therefore, under the existing quantum technology conditions, our multi-party quantum secret sharing protocol is completely feasible. In the future, we will combine our derived formulas with machine learning, such as quantum neural structure search, quantum intelligent program synthesis and other fields.