Abstract
An efficient quantum secret sharing scheme based on multi-dimensional GHZ state is proposed. The dealer performs the special unitary operation on the special n-dimensional n-particle GHZ state to encode the secret, and uses the distinguishability of two nonorthogonal basis to protect the secret, but the participants can get the secret through measuring the state in either basis. So every particle can be used to bring secret information, and the utilization ratio of the particles is much higher than the BB84 protocol. Besides, the multi-dimensional particle can bring more information than the traditional 2-dimensional particle. Compared to the existing schemes based on the BB84 protocol, our scheme will be more efficient in practice.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
It is well known that quantum coherence and interference lead to many interesting phenomena in quantum and nonlinear optics (Asadpour et al. 2013; Asadpour and Soleimani 2014; Asadpour and Hamedi 2013). Recently, many studies have been done to investigate quantum coherence and interference phenomena (Wu and Deng 2004; Wu 2005; Zhang et al. 2013; Li et al. 2013; Asadpour et al. 2013; Prataviera et al. 2013 Asadpour and Soleimani 2014). We can use these phenomena to transfer information with the minimum of corruption. Now quantum coherence and interference have been regarded as important topics of quantum information theory, and their technologies have greatly encouraged the improvements of quantum communication and quantum cryptography.
“Quantum secret sharing” (QSS) is an important branch of quantum cryptography. Hillery et al. (1999) proposed the first QSS scheme in 1999. QSS can be seen as the extension of Shamir’s secret sharing (Shamir 1979) into the quantum area. In QSS, the secret (classical information or quantum state) is split, distributed and reconstructed through the quantum operations, and its security is based on the quantum theory such as the uncertainty principle and the no-cloning theorem. So QSS will have perfect security against the quantum computer.
Since Hillery et al. (1999) proposed the first scheme, QSS has attracted lots of interests, and many other schemes have been proposed (Cleve et al. 1999; Tyc and Sanders 2002; Yang et al. 2012; Li et al. 2011; Gao 2013; Lau and Weedbrook 2013; Shi et al. 2013; Tseng et al. 2012; Chen et al. 2014, 2017; Sarvepalli and Klappenecker 2009; Gao et al. 2010; Liu et al. 2012, 2014; Hsu et al. 2013; Dehkordi and Fattahi 2013; Wang et al. 2013, 2017; Cao and Ma 2017; Matsumoto 2017; Kogias et al. 2017; Qin and Dai 2017). For example, Cleve et al. (1999) and Tyc and Sanders (2002) realized the (t, n) threshold of QSS, in which any t out of n participants can recover the initial quantum state. Cleve’s scheme is based on the quantum error-correcting codes. They encode the single quantum state into an entanglement state and distribute to the participants. Then the participants separate the shared quantum state from the entanglement state through performing the linear transformation. Tyc’s scheme is based on the continuous-variable state, in which the dealer and the participants also use the linear mapping to distribute and recover the quantum state. Some schemes studied the security of QSS. For example, Yang et al. (2012) proposed the verifiable QSS, in which the participants can check the validity of the recovered secret. Li et al. (2011) proposed a QSS scheme without the trusted party, and the participants can distribute the secret themselves. Gao (2013) used the special check procedure to design a secure QSS scheme which can resist the collective eavesdropping. Some other schemes used the novel methods to design the special QSS. For example, Lau et al. (2013) used the continuous-variable cluster states to design a QSS scheme which can share both the classical information and the quantum state. Shi et al. (2013) used the Chinese Remainder Theorem to improve the framework of QSS. Tseng et al. (2012) designed a QSS scheme by using the quantum search algorithm. Chen et al. (2014) used the two-party Cascade protocol to propose an error-correcting QSS scheme.
Although QSS has gotten a rapid development in recent years, it is still a frontier area, and many related technologies are immature in practice. The generation, storage, transmission and measurement of the quantum state will still exhaust much resource. So how to use less quantum state to share more information is a very valuable topic. In this paper, we will use the special unitary operation and special n-dimensional n-particle GHZ state to propose an efficient QSS scheme. In our scheme, the special unitary operations are performed on the n-dimensional n-particle GHZ states to encode the secret. The secret can be recovered through measuring the states in two nonorthogonal basis, that is, we use the distinguishability of two nonorthogonal basis to prevent the eavesdropper from stealing secret, but the secret can be recovered through measuring the state in either basis. So every particle can be used to bring the secret information, and the utilization ratio of the particles is much higher than the BB84 protocol. Besides, the n-dimensional particle can bring more information than the traditional 2-dimensional particle. Therefore, our protocol will be more efficient in practice.
The rest of this paper is organized as follows. In Sect. 2, some correlative preliminaries are introduced. Section 3 explicates the design method of the proposed scheme. In Sect. 4, an example is given to explain the proposed protocol. Section 5 proves the correctness. Section 6 analyzes the security. Section 7 describes the efficiency. Section 8 compares our scheme with an existing scheme. Finally, in Sect. 9, the conclusion of this paper is given.
2 Preliminaries
2.1 n-dimensional GHZ state
In n-dimensional Hilbert space, an m-particle GHZ state can be described as
2.2 Two nonorthogonal basis: Z-basis and X-basis
In n-dimensional Hilbert space, we define two nonorthogonal basis: Z-basis and X-basis.
2.3 Unitary operation
For an n-dimensional particle \( |\,j\rangle ,\;j \in \{ 0,1, \ldots ,n - 1\} \), we define the unitary operation \( U_{a,b} \) performed on \( |\,j\rangle \) as
3 The proposed scheme
If we assume there are n participants, then our scheme will use the special n-dimensional n-particle GHZ states to share the secret. We assume the dealer is Alice, the n participants are {Bob1, Bob2,…,Bob n }, and the secret is \( S = s_{1} s_{2} \ldots s_{t} \), where \( s_{1} ,s_{2} , \ldots ,s_{t} \in \{ 0,1, \ldots ,n - 1\} \). Alice uses the following operations to share \( S \) among {Bob1, Bob2,…,Bob n }.
-
1.
Alice generates t GHZ states, and each one is n-dimensional and n-particle. We assume they are \( \varPsi_{l} = \frac{1}{\sqrt n }\sum\limits_{j = 0}^{n - 1} {|\,j\rangle^{ \otimes n} } ,\;l = 1,2, \ldots ,t \).
-
2.
Alice divides the sub-secret \( s_{l} \;(l = 1,2, \ldots ,t) \) into n parts randomly, that is, \( s_{l} = s_{l1} + s_{l2} + \cdots + s_{ln} \), where \( s_{l1} ,s_{l2} , \ldots ,s_{\ln } \in \{ 0,1, \ldots ,n - 1\} \) and “+” means the add modulo n. Then she performs the special unitary operation \( U_{{s_{lm} ,s_{lm} }} \) on the m-th particle of \( \varPsi_{l} \), \( m = 1,2, \ldots ,n \).
-
3.
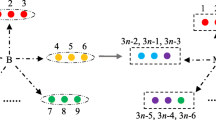
Alice uses all the first particles of the t GHZ states to compose the sequence P1, and uses all the second particles to compose the sequence P2,…, until uses all the n-th particles to compose the sequence P n . Then Alice sends the sequence P1 to the participant Bob1, sends the sequence P2 to the participant Bob2,…, until Bob n .
-
4.
After confirming that all the participants have received their particles, Alice asks the participants to measure each of their particles with Z-basis or X-basis randomly. But for the particles in the same position of the sequence, the participants must use the same basis. For example, Alice asks every participant to measure the first particle in his sequence with X-basis, measure the second particle in his sequence with Z-basis,…The measurement result will be denoted as \( j \) if the particle is \( |\,j\rangle \) in Z-basis or \( |\overline{j} \rangle \) in X-basis.
-
5.
The participants obtain their shares according to the measurements. For example, if the measurement results of Bob1 are \( r_{11} ,r_{12} , \ldots ,r_{1t} \), then his share will be \( R_{1} = r_{11} r_{12} \ldots r_{1t} \). The other participants are similar. Then Alice asks the participants to publish a subset of their shares to check the security. If the subset is not correct, Alice will think that the particles have been eavesdropped, and she asks the participants to discard their shares and start the above process again. Otherwise, she asks the participants to store their shares, and the distribution is over.
-
6.
In the recovery, the participants {Bob1, Bob2,…,Bob n } can get the shared secret through computing \( S = R_{1} + R_{2} + \cdots + R_{n} \), where “+” means the bitwise add modulo n.
4 Example
We give an example to explain our protocol more clearly. Assume Alice wants to share the secret among three participants {Bob1, Bob2, Bob3}, and the secret is \( S = s_{1} s_{2} = 12 \). Then Alice needs to generate two special 3-dimensional 3-particle GHZ states. We assume they are \( \varPsi_{1} = \frac{1}{\sqrt 3 }(|000\rangle + |111\rangle + |222\rangle ),\;\varPsi_{2} = \frac{1}{\sqrt 3 }(|000\rangle + |111\rangle + |222\rangle ) \).
Alice randomly divides the sub-secrets \( s_{1} \) and \( s_{2} \) into three parts, and we assume the divisions are \( s_{1} = s_{11} + s_{12} + s_{13} = 2 + 1 + 1,\;s_{2} = s_{21} + s_{22} + s_{23} = 1 + 0 + 1 \). Then Alice performs the special unitary operation \( U_{2,2} \) on the first particle of \( \varPsi_{1} \), \( U_{1,1} \) on the second particle of \( \varPsi_{1} \), \( U_{1,1} \) on the third particle of \( \varPsi_{1} \); \( U_{1,1} \) on the first particle of \( \varPsi_{2} \), \( U_{0,0} \) on the second particle of \( \varPsi_{2} \), and \( U_{1,1} \) on the third particle of \( \varPsi_{2} \). After these unitary operations, \( \varPsi_{1} \) and \( \varPsi_{2} \) become
Alice uses the first particles of \( \varPsi_{1} \) and \( \varPsi_{2} \) to compose the sequence P1, uses the second particles of \( \varPsi_{1} \) and \( \varPsi_{2} \) to compose the sequence P2, and uses the third particles of \( \varPsi_{1} \) and \( \varPsi_{2} \) to compose the sequence P3. Then Alice sends P1 to Bob1, sends P2 to Bob2, and sends P3 to Bob3. After confirming that all the participants have received their particles, Alice asks the participants to measure their particles in Z-basis or X-basis. But the particles in the same position of the sequence must be in the same basis. For example, Alice asks all the participants to measure the first particles in the sequences with X-basis, measure the second particles in the sequences with Z-basis. The measurement result is denoted as \( j \) if the particle is \( |\,j\rangle \) in Z-basis or \( |\overline{j} \rangle \) in X-basis.
If the first particles in the sequences are measured in Z-basis, that is, \( \varPsi_{1} \) is measured in Z-basis. We know that \( \varPsi_{1} = \frac{1}{\sqrt 3 }(|211\rangle + \omega |022\rangle + \omega^{2} |100\rangle ) \), so the measurement result will be “211”, “022” or “100”. We can see that \( 2 + 1 + 1 = 0 + 2 + 2 = 1 + 0 + 0 = 1 = r_{11} + r_{21} + r_{31} = s_{1} \). Similarly, if the second particles in the sequences are measured in Z-basis, that is, \( \varPsi_{2} \) is measured in Z-basis. We know that \( \varPsi_{2} = \frac{1}{\sqrt 3 }(|101\rangle + \omega^{2} |212\rangle + \omega |020\rangle ) \), so the measurement result will be “101”, “212” or “020”. We can see that \( 1 + 0 + 1 = 2 + 1 + 2 = 0 + 2 + 0 = 2 = r_{12} + r_{22} + r_{32} = s_{2} \).
If \( \varPsi_{1} \) and \( \varPsi_{2} \) are measured in X-basis, then \( \varPsi_{1} \) and \( \varPsi_{2} \) can be rewritten as
We can see that the measurement results will still satisfy \( r_{11} + r_{21} + r_{31} = s_{1} \) and \( r_{12} + r_{22} + r_{32} = s_{2} \).
Therefore, {Bob1, Bob2, Bob3} can get the shared secret through computing \( S = R_{1} + R_{2} + R_{3} = r_{11} r_{12} + r_{21} r_{22} + r_{31} r_{32} = 12 \).
Z-basis and X-basis are two nonorthogonal basis. Their distinguishability can protect the secret information in the states. But the participants can get the same result through measuring the states in either Z-basis or X-basis. So every particle in the states can be used to bring the secret information. This is the main merit of our scheme.
5 Correctness
The GHZ state Alice prepared is \( \varPsi_{l} = \frac{1}{\sqrt n }\sum\limits_{j = 0}^{n - 1} {|\,j\rangle^{ \otimes n} } ,\;l \in \{ 1,2, \ldots ,t\} \). After being performed the special unitary operation \( U_{{s_{lm} ,s_{lm} }} \) (step (2) of Sect. 3), the state will become
5.1 \( \varPsi_{l} \) are measured in Z-basis
If the particles of \( \varPsi_{l} \) are measured in Z-basis, the measurement results will be \( j + s_{lm} ,\;j \in \{ 0,1, \ldots ,n - 1\} ,\;m = 1,2, \ldots ,n \). So the measurement results will satisfy \( \sum\limits_{m = 1}^{n} {(j + s_{lm} )} = \sum\limits_{m = 1}^{n} {s_{lm} = s_{l} } \), that is, the participants can get the sub-secret \( s_{l} \) through measuring \( \varPsi_{l} \) in Z-basis.
5.2 \( \varPsi_{l} \) are measured in X -basis
We know that \( |\,j\rangle = \frac{1}{\sqrt n }\sum\limits_{k = 0}^{n - 1} {\omega^{ - kj} |\overline{k} \rangle } ,\;j \in \{ 0,1, \ldots ,n - 1\} \), so in X-basis, \( \varPsi_{l} \) can be written as
If we assume the measurement results of \( \varPsi_{l} \) in X-basis are \( r_{1} ,r_{2} , \ldots ,r_{n} \), then \( \varPsi_{l} \) can be written as
If \( r_{1} + r_{2} + \cdots + r_{n} = s_{l} \), then
We know \( \omega^{n} = 1 \), so
If \( r_{1} + r_{2} + \cdots + r_{n} \ne s_{l} \), then
We know \( \omega = e^{{\frac{2\pi i}{n}}} \), so \( \omega^{{n\;[s_{l} - (r_{1} + r_{2} + \cdots + r_{n} )]}} = 1 \). Then \( \varPsi_{l} = 0 \).
In summary, when \( \varPsi_{l} \) is measured in X-basis, it can be written as follows.
We can see that the measurement results in X-basis will satisfy \( r_{1} + r_{2} + \cdots + r_{n} = s_{l} \), so the participants can get the sub-secret \( s_{l} \) through measuring \( \varPsi_{l} \) in X-basis.
6 Security
6.1 Confidentiality
After being performed the special unitary operation \( U_{{s_{lm} ,s_{lm} }} \) (step (2) of Sect. 3), the state \( \varPsi_{l} \) will become
We can see that each particle of \( \varPsi_{l} \) can be in any state from \( \{ 0,1, \ldots ,n - 1\} \) whether \( \varPsi_{l} \) is in Z-basis or in X-basis. Any participant cannot get the quantum states of others from his own measurement result. After n − 1 particles of \( \varPsi_{l} \) have been measured, the reduced density matrix of the last particle is
where R is the summation modulo n of the n − 1 measurement results. We can see that, without knowing the sub-secret \( s_{l} \), the n − 1 participants cannot get the quantum state of the n-th participant. So the share of each participant is confidential, and our scheme can meet the security of reconstruction.
6.2 Security for eavesdropping
In our scheme, each GHZ state may be measured in Z-basis or X-basis randomly. The eavesdropper cannot know which basis will be selected in advance. If he eavesdrops on the particles, then he may bring some errors into the particles, and be detected when the participants publish the subset of their shares to check the security. For example, if the eavesdropper measures \( \varPsi_{l} \) in Z-basis, but the participants measure \( \varPsi_{l} \) in X-basis, then the participants will get the correct results with the probability \( \frac{n - 1}{n} \). Therefore, for one GHZ state, the error rate comes from eavesdropping is \( \frac{n - 1}{2n} \) (the eavesdropper will select the wrong basis with the probability 50%). For \( l \) GHZ states, the eavesdropper will be detected with the probability \( 1 - \left( {\frac{n + 1}{2n}} \right)^{l} \). When \( l \) is large enough, the probability will converge to 1.
7 Efficiency
In our protocol, we use the special n-dimensional n-particle GHZ state to distribute the secret. After being performed the special unitary operation, the GHZ state can be measured in two nonorthogonal basis to recover the secret. So every particle in our protocol can be used to bring the secret information. The utilization ratio of the particles is much higher than the BB84 protocol (in which only about half of the particles can be used to bring the secret information).
Besides, the secret information is encoded through the n-dimensional particle in our protocol. So the information one particle can bring is \( \log_{2}^{n} \), which is much larger than the traditional 2-dimensional particle.
8 Comparisons
In Qin and Dai (2017), a dynamic QSS scheme is proposed by using the property of multi-dimensional GHZ state. In this scheme, the dealer generates the GHZ state in Z-basis, and the participants measure the GHZ state in X-basis to get their shares. The main property used in this scheme is that, if the Z-basis multi-dimensional GHZ state is measured in X-basis, then the sum of the measurement results is zero, that is, if the state \( \varPsi = \frac{1}{\sqrt d }\sum\limits_{j = 0}^{d - 1} {|\,j\rangle^{ \otimes n} } \) is measured in X-basis and the measurement results are denoted as \( r_{1} ,r_{2} , \ldots ,r_{n} \), then \( r_{1} + r_{2} + \cdots + r_{n} = 0 \). Qin and Dai (2017) uses this property to add or delete participants to realize the dynamic QSS.
Our scheme is different from the scheme in Qin and Dai (2017) although our scheme is still based on the multi-dimensional GHZ state. We use the special unitary operation and the special n-dimensional n-particle GHZ state to design efficient QSS, that is, we find if the special unitary operation \( U_{a,a} \) is performed on the special state \( \varPsi = \frac{1}{\sqrt n }\sum\limits_{j = 0}^{n - 1} {|\,j\rangle^{ \otimes n} } \), then this state can be measured in Z-basis or X-basis to recover the secret. So we can use the distinguishability of two nonorthogonal basis to protect secret, but the secret can be recovered in either basis. Then every particle can be used to bring the secret information, and the utilization ratio of the particles can be increased. We can see that the main method and the application scenario in our scheme are both different from Qin and Dai (2017).
9 Conclusion
So far, we have used the special multi-dimensional GHZ state to propose an efficient QSS scheme. In our scheme, the secret can be encoded through performing the special unitary operation on the special n-dimensional n-particle GHZ state. The secret is protected by the distinguishability of two nonorthogonal basis, but the participants can get the secret through measuring the states in either basis. The main merit of our scheme is that, every particle can be used to bring the secret information. Compared to the schemes based on the BB84 protocol, our scheme is more efficient.
References
Asadpour, S.H., Hamedi, H.R.: Giant Kerr nonlinearity in an n-doped semiconductor quantum well. Opt. Quant. Electron. 45, 11–20 (2013)
Asadpour, S.H., Soleimani, H.R.: Phase control of optical bistability based biexciton coherence in a quantum dot nanostructure. Phys. B 440, 124–129 (2014a)
Asadpour, S.H., Soleimani, H.R.: Phase control of optical bistability based biexciton coherence in a quantum dot nanostructure. Phys. B 440, 124–129 (2014b)
Asadpour, S.H., Hamedi, H.R., Soleimani, H.R.: Optical bistability and multistability in an open ladder-type atomic system. J. Mod. Opt. 60, 659–665 (2013a)
Asadpour, S.H., Jaberi, M., Soleimani, H.R.: Phase control of optical bistability and multistability via spin coherence in a quantum well waveguide. J. Opt. Soc. Am. B 30, 1815–1820 (2013b)
Cao, H., Ma, W.P.: (t, n) threshold quantum state sharing scheme based on linear equations and unitary operation. IEEE Photon. J. 9, 1–7 (2017)
Chen, R.K., Zhang, Y.Y., Shi, J.H., et al.: A multiparty error-correcting method for quantum secret sharing. Quantum Inf. Process. 13, 21–31 (2014)
Chen, X.B., Dou, Z., Xu, G., et al.: A kind of university quantum secret sharing protocol. Sci. Rep. 7, 39845 (2017). https://doi.org/10.1038/srep39845
Cleve, R., Gottesman, D., Lo, H.K.: How to share a quantum secret. Phys. Rev. Lett. 83, 648–651 (1999)
Dehkordi, M.H., Fattahi, E.: Threshold quantum secret sharing between multiparty and multiparty using Greenberger–Horne–Zeilinger state. Quantum Inf. Process. 12, 1299–1306 (2013)
Gao, G.: Secure multiparty quantum secret sharing with the collective eavesdropping-check character. Quantum Inf. Process. 12, 55–68 (2013)
Gao, F., Qin, S.J., Wen, Q.Y., et al.: Cryptanalysis of multiparty controlled quantum secure direct communication using Greenberger–Horne–Zeilinger state. Opt. Commun. 382, 192–195 (2010)
Hillery, M., Buzek, V., Berthiaume, A.: Quantum secret sharing. Phys. Rev. A 59, 1829–1834 (1999)
Hsu, J.L., Chong, S.K., Hwang, T., et al.: Dynamic quantum secret sharing. Quantum Inf. Process. 12, 331–344 (2013)
Kogias, I., Xiang, Y., He, Q.Y., et al.: Unconditional security of entanglement-based continuous-variable quantum secret sharing. Phys. Rev. A 95, 012315 (2017). https://doi.org/10.1103/PhysRevA.95.012315
Lau, H.K., Weedbrook, C.: Quantum secret sharing with continuous-variable cluster states. Phys. Rev. A 88, 042313 (2013). https://doi.org/10.1103/PhysRevA.88.042313
Li, Q., Long, D.Y., Chan, W.H., et al.: Sharing a quantum secret without a trusted party. Quantum Inf. Process. 10, 97–106 (2011)
Li, J.H., Yu, R., Yang, X.: Phase-controlled absorption-gain properties and optical switching in nanodiamond nitrogen-vacancy center. Appl. Phys. B 111, 65–73 (2013a)
Li, J.H., Yu, R., Wu, Y.: Propagation of magnetically controllable lasers and magneto-optic dual switching using nitrogen-vacancy centers in diamond. J. Appl. Phys. 113, 103104 (2013b). https://doi.org/10.1063/1.4795275
Liu, L.L., Tsai, C.W., Hwang, T.: Quantum secret sharing using symmetric W state. Int. J. Theor. Phys. 51, 2291–2306 (2012)
Liu, F., Qin, S.J., Wen, Q.Y.: A quantum secret-sharing protocol with fairness. Phys. Scr. 89, 075104 (2014)
Matsumoto, R.: Quantum optimal multiple assignment scheme for realizing general access structure of secret sharing. IEICE Trans. Fund. Electron. 100, 726–728 (2017)
Prataviera, G.A., Yoshida, A.C., Mizrahi, S.S.: Mean-field optical bistability of two-level atoms in structured reservoirs. Phys. Rev. A 87, 043831 (2013). https://doi.org/10.1103/PhysRevA.87.043831
Qin, H.W., Dai, Y.W.: Dynamic quantum secret sharing by using d-dimensional GHZ state. Quantum Inf. Process. 16, 1–13 (2017)
Sarvepalli, P.K., Klappenecker, A.: Sharing classical secrets with Calderbank-Shor-Steane codes. Phys. Rev. A 80, 022321 (2009). https://doi.org/10.1103/PhysRevA.80.022321
Shamir, A.: How to share a secret. Commun. ACM 22, 612–613 (1979)
Shi, R.H., Lv, G.L., Wang, Y., et al.: On quantum secret sharing via Chinese remainder theorem with the non-maximally entanglement state analysis. Int. J. Theor. Phys. 52, 539–548 (2013)
Tseng, H.Y., Tsai, C.W., Hwang, T., et al.: Quantum secret sharing based on quantum search algorithm. Int. J. Theor. Phys. 51, 3101–3108 (2012)
Tyc, T., Sanders, B.C.: How to share a continuous-variable quantum secret by optical interferometry. Phys. Rev. A 65, 042310 (2002). https://doi.org/10.1103/PhysRevA.65.042310
Wang, H.B., Huang, Y.G., Fang, X., et al.: High-capacity three-party quantum secret sharing with single photons in both the polarization and the spatial-mode degrees of freedom. Int. J. Theor. Phys. 52, 1043–1051 (2013)
Wang, J.T., Xu, G., Chen, X.B., et al.: Local distinguishability of Dicke states in quantum secret sharing. Phys. Lett. A 381, 998–1002 (2017)
Wu, Y.: Two-color ultraslow optical solitons via four-wave mixing in cold-atom media. Phys. Rev. A 71, 053820 (2005). https://doi.org/10.1103/PhysRevA.71.053820
Wu, Y., Deng, L.: Ultraslow bright and dark optical solitons in a cold three-state medium. Opt. Lett. 29, 2064–2066 (2004)
Yang, Y.G., Jia, X., Wang, H.Y., et al.: Verifiable quantum (k, n)-threshold secret sharing. Quantum Inf. Process. 11, 1619–1625 (2012)
Zhang, D., Yu, R., Li, J.H., Ding, C.L., Yang, X.X.: Laser-polarization-dependent and magnetically controlled optical bistability in diamond nitrogen-vacancy centers. Phys. Lett. A 377, 2621–2627 (2013)
Acknowledgements
This study is supported by Natural Science Foundation of China (Grant No. 61602247) and Natural Science Foundation of Jiangsu Province (Grant No. BK20160840).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Qin, H., Tso, R. Efficient quantum secret sharing based on special multi-dimensional GHZ state. Opt Quant Electron 50, 167 (2018). https://doi.org/10.1007/s11082-018-1435-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11082-018-1435-y