1 Introduction

It is known that entanglement is a fundamental feature of the quantum mechanics, and it plays an important role for many kinds of applications, such as quantum information [1], superdense coding [2], quantum teleportation and telecloning [3]. As one of the simplest quantum systems, the Heisenberg spin chain is a natural candidate in the solid state systems for the realization of quantum entanglement compared with other physics systems [4]. Recently, an interesting type of quantum entanglement, i.e., thermal entanglement has been extensively studied due to its advantages over other kinds of entanglement.

In a recent paper, the entanglement and intrinsic decoherence in the two-qubit Heisenberg XXX model with Dzyaloshinski-Moriya(DM) anisotropic antisymmetric interaction under a inhomogeneous magnetic field was investigated by Qin Meng [5]. His team also considered the thermal entanglement in a two-qubit XY chain with the DM interaction [6]. And the thermal entanglement of a two-qubit XXZ chain in the DM anisotropic antisymmetric interaction with a homogeneous magnetic field was studied [7], while the thermal entanglement in the mixed three-spin XXZ Heisenberg model on a triangular cell with nonuniform magnetic fields was researched [8]. Also, Xu Lin discussed the quantum correlations and thermal entanglement in a two-qubit Heisenberg XXZ model with external magnetic fields [9]. What’s more, the thermal entanglement in a two-qubit Heisenberg XXZ model with DM anisotropic antisymmetric interaction in a inhomogeneous magnetic field was discussed [10]. However, the thermal entanglement in a two-qubit Ising model with DM anisotropic antisymmetric interaction is rarely considered [11, 12]. In view of the above results, in this paper we are going to study the thermal entanglement of a two-qubit Ising spin chain with the DM anisotropic antisymmetric interaction under a nonuniform magnetic field.

The article is organized as follows. In Section 2, we introduce the model under consideration. In Section 3, the influences of various factors on the thermal entanglement are discussed. In Section 4, a summary is given.

2 The Model

Consider a Ising spin chain of two qubits in the presence of the DM anisotropic antisymmetric interaction with a nonuniform external magnetic field. The Hamiltonian of the system is given by

$$ H=J{\sigma_{1}^{x}}{\sigma_{2}^{x}}+\frac{1}{2}[(B+h){\sigma_{1}^{z}}+(B-h){\sigma_{2}^{z}}+D({\sigma_{1}^{x}}{\sigma_{2}^{y}}-{\sigma_{1}^{y}}{\sigma_{2}^{x}})]. $$
(1)

where \({\sigma _{i}^{x}}\), \({\sigma _{i}^{y}}\) and \({\sigma _{i}^{z}}\) are Pauli operators. J is the real coupling constant and D is the DM vector coupling. The DM anisotropic antisymmetric interaction arises from spin-orbit coupling [13, 14]. The positive J corresponds to the antiferromagnetic case, and the negative J refers to the ferromagnetic case. B is the uniform magnetic field. h ≥ 0 is restricted, and the magnetic fields on the two spins have been parameterized that h controls the degree of inhomogeneity.

In the standard basis{|00〉,|01〉,|10〉,|11〉}, the Hamiltonian can be expressed as

$$ H=\left( \begin{array}{cccc} B & 0 & 0 & J \\ 0 & h & J+iD & 0 \\ 0 & J-iD & -h & 0 \\ J & 0 & 0 & -B \end{array} \right) $$
(2)

A straightforward calculation gives the eigenstates:

$$ \begin{array}{@{}rcl@{}} &|\varphi_{1}\rangle&=\frac{1}{a_{+}}\left[\frac{B+\delta}{J}|00\rangle+|11\rangle\right],\\ &|\varphi_{2}\rangle&=\frac{1}{a_{-}}\left[\frac{B-\delta}{J}|00\rangle+|11\rangle\right],\\ &|\varphi_{3}\rangle&=\frac{1}{b_{+}}\left[\frac{i(h+u)}{D+iJ}|01\rangle+|10\rangle\right],\\ &|\varphi_{4}\rangle&=\frac{1}{b_{-}}\left[\frac{i(h-u)}{D+iJ})|01\rangle+|10\rangle\right]. \end{array} $$
(3)

where \(\delta =\sqrt {J^{2}+B^{2}}, u=\sqrt {J^{2}+h^{2}+D^{2}}, a_{\pm }^{2}=\frac {2\delta ^{2}\pm 2B\delta }{J}, b_{\pm }^{2}=\frac {2u^{2}\pm 2hu}{J^{2}+D^{2}}\).

With corresponding eigenvalues

$$ \begin{array}{@{}rcl@{}} &E_{1,2}&=\pm\delta,\\ &E_{3,4}&=\pm u. \end{array} $$
(4)

The state of a spin chain with the above Hamiltonian H at a thermal equilibrium can be described by a density matrix

$$ \begin{array}{@{}rcl@{}} \rho(T)=\exp(-\beta H)/Z \end{array} $$
(5)

where β = 1/(kT), k is the Boltzmann constant, which is henceforth taken as 1, and T is the temperature, H is the system Hamiltonian and \(Z=\text {tr}[\exp (-\beta H)]\) is the partition function. As ρ(T) represents a thermal state, the entanglement in the thermal state is called thermal entanglement [15].

In the standard basis{|00〉,|01〉,|10〉,|11〉},

$$ \begin{array}{@{}rcl@{}} \rho(T)&=&\frac{1}{Z}\exp(-\beta H)\\ &=&\frac{1}{Z}\sum\limits_{k=1}^{4}\exp(-\beta E_{k})|\varphi_{k}\rangle\langle\varphi_{k}|\\ &=&\frac{1}{Z}\left( \begin{array}{cccc} m & 0 & 0 & r \\ 0 & p & y^{*} & 0 \\ 0 & y & q & 0 \\ r & 0 & 0 & n \end{array} \right) \end{array} $$
(6)

where

$$ \begin{array}{@{}rcl@{}} &m&=e^{-\beta\delta}\frac{1}{a_{+}^{2}}\left( \frac{B+\delta}{J}\right)^{2}+e^{\beta\delta}\frac{1}{a_{-}^{2}}\left( \frac{B-\delta}{J}\right)^{2},\\ &r&=e^{-\beta\delta}\frac{1}{a_{+}^{2}}\frac{B+\delta}{J}+e^{\beta\delta}\frac{1}{a_{-}^{2}}\frac{B-\delta}{J},\\ &p&=e^{-\beta u}\frac{1}{b_{+}^{2}}\frac{(h+u)^{2}}{D^{2}+J^{2}}+e^{\beta u}\frac{1}{b_{-}^{2}}\frac{(h-u)^{2}}{D^{2}+J^{2}},\\ &q&=e^{-\beta u}\frac{1}{b_{+}^{2}}+e^{\beta u}\frac{1}{b_{-}^{2}},\\ &y&=e^{-\beta u}\frac{1}{b_{+}^{2}}\frac{h+u}{J+iD}+e^{\beta u}\frac{1}{b_{-}^{2}}\frac{h-u}{J+iD},\\ &n&=e^{-\beta\delta}\frac{1}{a_{+}^{2}}+e^{\beta\delta}\frac{1}{a_{-}^{2}},\\ &Z&=2\cosh(\beta\delta)+2\cosh(\beta u). \end{array} $$
(7)

3 Thermal Entanglement

Before computer the thermal entanglement, we review a measure of entanglement. Concurrence [16] is one of the most prevalently used entanglement monotones for two qubits. Let ρ12 be the joint density matrix of the system consisting of qubits 1 and 2, which may be pure or mixed. The concurrence corresponding ρ12 is defined as

$$ C_{12}=\max\lbrace\lambda_{1}-\lambda_{2}-\lambda_{3}-\lambda_{4}, 0\rbrace, $$
(8)

where λ1, λ2, λ3 and λ4 are the square roots of the four eigenvalues of \(\varrho _{12}=\rho _{12}(\sigma ^{y}\otimes \sigma ^{y})\rho _{12}^{*}(\sigma ^{y}\otimes \sigma ^{y})\) in descending order, with the asterisk denoting the complex conjugation. The value of C ranges from 0 for completely disentangled states to 1 for maximally entangled states.

So the thermal entanglement of the above density matrix can be measured by the concurrence C which has been defined as

$$ C=\frac{2}{Z}\max\lbrace|y|-\sqrt{mn}, |r|-\sqrt{pq}, 0\rbrace. $$
(9)

Figure 1 gives the plots of C as a function of B and T for different D, for the coupling constant J is set to be 1. From Fig. 1, it is clear that the concurrence C is symmetrical with B = 0. In general, the C decreases with the increasing value of |B|, and the C increases with the increasing value of D. It is also observed that under the influence of the increasing T, the C decreases gently. That is to say, the |B| and T have negative effects while the D has a positive effect on the C. In detail, the increasing D not only raises the maximum value of C but also expands the range of the |B| and T where exists thermal entanglement simultaneously. In other words, the threshold value |Bt| as well as Tt above which the thermal entanglement vanishes increases with the increasing D. Moreover, for a definite D, the threshold value |Bt| is also increased with the increasing T. So we can adjust the values of D, B and T to control the region of thermal entanglement we want. It is found that this conclusion accords with the conclusion of Huang in Refs. [10].

Fig. 1
figure 1

The thermal entanglement measured by the concurrence C as a function of the uniform magnetic field B and the temperature T for different DM coupling constant D. The coupling constant J = 1 and the nonuniform magnetic field h = 0. a D = 1; b D = 2; c D = 3; d D = 4

Full size image

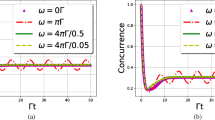
It must be noted that, the influence of h on C is different from them. Figure 2 shows the plots of the C versus h, T for different D. From Fig. 2, it is obvious that, for a definite D, when the T is small, as the h increases, the C decreases monotonically. When the T is bigger than a critical value Tc, as the h increases, the C develops to a maximum value and then drops much slowly. In other words, before and after Tc, the effect of h on C is different. What’s more, when the h is raised, the key temperature Tk at which the C reaches the maximum value increases, while the maximum value of C becomes smaller. Through comparison between Fig. 2a, b, c and d, it is found that, the larger the value of D is, the the bigger the value of Tc is. So we always can adjust the value of T and h to get the maximal thermal entanglement C for different D.

Fig. 2
figure 2

The thermal entanglement measured by the concurrence C as a function of the nonuniform magnetic field h and the temperature T for different DM coupling constant D. The coupling constant J = 1 and the uniform magnetic field B = 0. a D = 1; b D = 2; c D = 3; d D = 4

Full size image

4 Conclusion

In this paper, we have studied the thermal entanglement in the two-qubit Ising spin chain in the presence of the Dzyaloshinski-Moriya anisotropic antisymmetric interaction in a nonuniform magnetic field. During the discussions, some conclusions are obtained. The external magnetic field |B| has a negative effect on the value of C, and the h has the double influence on C. The D can not only develop the value of C but also heighten the values of the |Bt| and the Tt above which the thermal entanglement vanishes. When the T is bigger than a critical value Tc, the increasing h can develop the C to a maximum value and then drop it much slowly. Though the increasing h makes the maximum value of C smaller, it increases the key temperature Tk at which the C reaches the maximum value. The increasing T makes the C smaller, but it makes the |Bt| bigger. In brief, we can adjust the values of B, h, D and T to control the thermal entanglement, which is useful for the quantum teleportation and other applications.