Controlled Remote State Preparation of an Eight-Qubit Entangled State

Abstract

In this paper, we propose a controlled remote state preparation scheme for a known eight-qubit entangled state. In this scheme, the sender, controller, and receiver share a six-qubit cluster state. The sender first performs a two-qubit state measurement, and the controller performs a corresponding two-qubit system measurement based on the sender’s measurement result. After receiving the measurement results from the sender and controller, the receiver can reconstruct this initial eight-qubit entangled state by using an appropriate unitary operation. This unitary operation depends on the different measurements of the sender and controller.

FormalPara PACS numbers

03.67.Hk03.65.Ud42.50.Dv

1 Introduction

Quantum entangled states have important applications in quantum communication and quantum computing [1], and are important carriers for transmitting quantum information and verifying quantum theory. Transmission of quantum information requires the preparation of quantum states of different bits, and the preparation of these quantum states requires the use of quantum entangled states [2,3,4,5]. At present, different entangled states can be used to prepare quantum states with different bits [6,7,8]. Recently, some controlled remote state preparation (CRSP) schemes have been proposed using different entangled states [9,10,11,12]. Some of multi-qubit CRSP schemes are discussed in the following.

Ma et al. proposed a novel scheme for asymmetric bidirectional CRSP of an arbitrary four-qubit cluster-type state and a single-qubit state by using a ten-qubit entangled state as the quantum channel [13]. Binayak et al. introduced a CRSP protocol for a known four-qubit entangled state by using a six-qubit cluster state [14]. Ma et al. devised a CRSP scheme for an arbitrary four-qubit χ-state by using the pre-sharing partially entangled channel [15]. Nie et al. proposed a scheme for the CRSP of an arbitrary six-qubit cluster-type state with two sets of five-qubit GHZ states [16]. Ding and Jiang proposed a CRSP scheme for an arbitrary seven-qubit cluster-type state by using several GHZ entangled states [17].

In this paper, we propose a CRSP scheme for an eight-qubit entangled state. The three parties in the scheme share a six-qubit cluster state, and only the sender and controller know the information to prepare the eight-qubit entangled state. The receiver can reconstruct this quantum state with the help of the controller by performing a proper unitary operation. In order to reconstruct this quantum state, it is necessary to know the measurement results of the sender and the controller. Different measurement results require different unitary operations.

2 CRSP of an Eight-Qubit Entangled State

Suppose there are three parties, the sender Alice, the controller Bob, and the receiver Charlie. The intended eight-qubit entangled state to be prepared is of the form

$$ \left|\phi \right\rangle ={a}_0{e}^{ib_0}\left|00000000\right\rangle +{a}_1{e}^{ib_1}\left|000011111\right\rangle +{a}_2{e}^{ib_2}\left|11110000\right\rangle +{a}_3{e}^{ib_3}\left|11111111\right\rangle, $$

(1)

where a_i(i = 0, 1, 2, 3) and b_j(j = 0, 1, 2, 3) are real numbers. In our scheme, Alice, Bob and Charlie share a six-qubit cluster state, which is given by

$$ \left|\psi \right\rangle =\frac{1}{2}{\left(\left|000000\right\rangle +\left|000111\right\rangle +\left|111000\right\rangle -\left|111111\right\rangle \right)}_{123456}, $$

(2)

where qubits 1, 4 belong to Alice, qubits 2, 5 belong to Bob, qubits 3, 6 belong to Charlie, respectively. To help Charlie remotely prepare the eight-qubit entangled state, the four steps are described in the following.

• Step 1 Alice performs a two-qubit measurement on her own qubits 1 and 4 in the basis consisting of four mutually orthogonal vectors |φⁱ〉₁₄(i = 0, 1, 2, 3) given by

$$ {\left|{\varphi}^0\right\rangle}_{14}={\left({a}_0\left|00\right\rangle +{a}_1\left|01\right\rangle +{a}_2\left|10\right\rangle -{a}_3\left|11\right\rangle \right)}_{14}, $$

(3)

$$ {\left|{\varphi}^1\right\rangle}_{14}={\left({a}_1\left|00\right\rangle -{a}_0\left|01\right\rangle +{a}_3\left|10\right\rangle +{a}_2\left|11\right\rangle \right)}_{14}, $$

(4)

$$ {\left|{\varphi}^2\right\rangle}_{14}={\left({a}_2\left|00\right\rangle -{a}_3\left|01\right\rangle -{a}_0\left|10\right\rangle -{a}_1\left|11\right\rangle \right)}_{14}, $$

(5)

$$ {\left|{\varphi}^3\right\rangle}_{14}={\left({a}_3\left|00\right\rangle +{a}_2\left|01\right\rangle -{a}_1\left|10\right\rangle +{a}_0\left|11\right\rangle \right)}_{14}. $$

(6)

Then, the Eq. (2) can be rewritten as

$$ \left|\mathrm{K}\right\rangle =\frac{1}{2}\sum \limits_{k=0}^3{\left|{\varphi}^k\right\rangle}_{14}{\left|{\xi}^k\right\rangle}_{2356}, $$

(7)

where

$$ {\left|{\xi}^0\right\rangle}_{2356}={\left({a}_0\left|0000\right\rangle +{a}_1\left|0011\right\rangle +{a}_2\left|1100\right\rangle +{a}_3\left|1111\right\rangle \right)}_{2356}, $$

(8)

$$ {\left|{\xi}^1\right\rangle}_{2356}={\left({a}_1\left|0000\right\rangle -{a}_0\left|0011\right\rangle +{a}_3\left|1100\right\rangle -{a}_2\left|1111\right\rangle \right)}_{2356}, $$

(9)

$$ {\left|{\xi}^2\right\rangle}_{2356}={\left({a}_2\left|0000\right\rangle -{a}_3\left|0011\right\rangle -{a}_0\left|1100\right\rangle +{a}_1\left|1111\right\rangle \right)}_{2356}, $$

(10)

$$ {\left|{\xi}^3\right\rangle}_{2356}={\left({a}_3\left|0000\right\rangle +{a}_2\left|0011\right\rangle -{a}_1\left|1100\right\rangle -{a}_0\left|1111\right\rangle \right)}_{2356}. $$

(11)

After the two-qubit measurement, Alice sends the measurement result to Bob and Charlie by using a classical channel.

• Step 2 Using k and the complex number b_j(j = 0, 1, 2, 3), Bob performs a two-qubit measurement on her own qubits 2 and 5 in the basis consisting of four mutually orthogonal vectors |ζ^m〉₁₄(m = 0, 1, 2, 3) given by

$$ \left(\begin{array}{c}\left|{\zeta}^0\right\rangle \\ {}\left|{\zeta}^1\right\rangle \\ {}\left|{\zeta}^2\right\rangle \\ {}\left|{\zeta}^3\right\rangle \end{array}\right)={\Pi}^{(k)}\left(\begin{array}{c}\left|00\right\rangle \\ {}\left|01\right\rangle \\ {}\left|10\right\rangle \\ {}\left|11\right\rangle \end{array}\right), $$

(12)

where

$$ {\varPi}^{(0)}=\frac{1}{2}\left(\begin{array}{cccc}{e}^{-i{b}_0}& {e}^{-i{b}_1}& {e}^{-i{b}_2}& {e}^{-i{b}_3}\\ {}{e}^{-i{b}_0}& -{e}^{-i{b}_1}& {e}^{-i{b}_2}& -{e}^{-i{b}_3}\\ {}{e}^{-i{b}_0}& -{e}^{-i{b}_1}& -{e}^{-i{b}_2}& {e}^{-i{b}_3}\\ {}{e}^{-i{b}_0}& {e}^{-i{b}_1}& -{e}^{-i{b}_2}& -{e}^{-i{b}_3}\end{array}\right), $$

(13)

$$ {\varPi}^{(1)}=\frac{1}{2}\left(\begin{array}{cccc}{e}^{-i{b}_1}& {e}^{-i{b}_0}& {e}^{-i{b}_3}& {e}^{-i{b}_2}\\ {}{e}^{-i{b}_1}& -{e}^{-i{b}_0}& {e}^{-i{b}_3}& -{e}^{-i{b}_2}\\ {}{e}^{-i{b}_1}& -{e}^{-i{b}_0}& -{e}^{-i{b}_3}& {e}^{-i{b}_2}\\ {}{e}^{-i{b}_1}& {e}^{-i{b}_0}& -{e}^{-i{b}_3}& -{e}^{-i{b}_2}\end{array}\right), $$

(14)

$$ {\varPi}^{(2)}=\frac{1}{2}\left(\begin{array}{cccc}{e}^{-i{b}_2}& {e}^{-i{b}_3}& {e}^{-i{b}_0}& {e}^{-i{b}_1}\\ {}{e}^{-i{b}_2}& -{e}^{-i{b}_3}& {e}^{-i{b}_0}& -{e}^{-i{b}_1}\\ {}{e}^{-i{b}_2}& -{e}^{-i{b}_3}& -{e}^{-i{b}_0}& {e}^{-i{b}_1}\\ {}{e}^{-i{b}_2}& {e}^{-i{b}_3}& -{e}^{-i{b}_0}& -{e}^{-i{b}_1}\end{array}\right), $$

(15)

$$ {\varPi}^{(3)}=\frac{1}{2}\left(\begin{array}{cccc}{e}^{-i{b}_3}& {e}^{-i{b}_2}& {e}^{-i{b}_1}& {e}^{-i{b}_0}\\ {}{e}^{-i{b}_3}& -{e}^{-i{b}_2}& {e}^{-i{b}_1}& -{e}^{-i{b}_0}\\ {}{e}^{-i{b}_3}& -{e}^{-i{b}_2}& -{e}^{-i{b}_1}& {e}^{-i{b}_0}\\ {}{e}^{-i{b}_3}& {e}^{-i{b}_2}& -{e}^{-i{b}_1}& -{e}^{-i{b}_0}\end{array}\right). $$

(16)

In terms of these measurement bases, |ξ^k〉₂₃₅₆ can be rewritten as

$$ {\left|{\xi}^k\right\rangle}_{2356}=\sum \limits_{m=0}^3{\left|{\zeta}^m\right\rangle}_{25}{\left|{\eta}^{km}\right\rangle}_{36}, $$

(17)

where |η^km〉₃₆ is the final states of qubits 3 and 6. Bob performs the two-qubit measurement on qubits 2 and 5, and then sends the measurement result to Charlie.

• Step 3 According to the measurement results k and m, Charlie applies unitary operators U^km (shown in Table 1) to transfer |η^mk〉₃₆ to the below state,

Table 1 The unitary operation of qubits 3 and 6

$$ {\left|\mathrm{M}\right\rangle}_{36}={\left({a}_0{e}^{ib_0}\left|00\right\rangle +{a}_1{e}^{ib_1}\left|01\right\rangle +{a}_2{e}^{ib_2}\left|10\right\rangle +{a}_3{e}^{ib_3}\left|11\right\rangle \right)}_{36}. $$

(18)

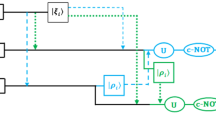
• Step 4 To complete the CRSP protocol, Charlie makes two controlled NOT operations on the qubits 3 and 6 as initial qubits and with six ancillary qubits |000〉_ABC and |000〉_DEFas the target qubits. Finally, Charlie recovers the original eight-qubit entangled state described in (1), that is,

$$ {\displaystyle \begin{array}{c}{\left|\phi \right\rangle}_{3 ABC6 DEF}=\left({a}_0{e}^{ib_0}\left|00000000\right\rangle +{a}_1{e}^{ib_1}\left|000011111\right\rangle \right.\\ {}{\left.+{a}_2{e}^{ib_2}\left|11110000\right\rangle +{a}_3{e}^{ib_3}\left|11111111\right\rangle \right)}_{3 ABC6 DEF}.\end{array}} $$

(19)

That is the end of the CRSP protocol, and the success probability of this protocol is 100%.

3 Conclusion

In summary, we present a CRSP protocol for an eight-qubit entangled state by using a six-qubit cluster state, where the sender and controller each have information on the prepared quantum state. The sender measures his own particles based on the information she has. The controller constructs the measurement basis vector according to the measurement result of the sender. The receiver can reconstruct the original quantum state after performing a corresponding unitary transformation on their own particles according to their measurement results. Our protocol is extensible and has potential applications for building quantum networks.