Abstract
We propose an optimal protocol for remotely preparing a four-qubit entangled state. In this protocol, a sender and two potential receivers share a ten-qubit entangled state. The sender performs a two-qubit state measurement based on the information of the quantum state that needs to be prepared. According to the measurement results of the sender, any potential receiver can obtain the quantum state that the sender needs to prepare by using the corresponding unitary transformation.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
In a quantum network [1], users need to communicate with each other by transmitting quantum states. Currently, there are two different methods for transmitting quantum states, one is the quantum teleportation [2] and the other is the remote state preparation (RSP) [3]. In the quantum teleportation scheme, the sender directly prepares the quantum state to be transmitted, and by sharing a quantum entangled state with the receiver, the information of this quantum state is sent to the receiver after performing a Bell-state measurement. However, in the RSP scheme, the sender performs a quantum state measurement based on the information of the quantum state to be transmitted, and the receiver can obtain the quantum state after performing the corresponding unitary transformation. Therefore, the latter scheme is more efficient in the task of transmitting quantum states. Due to the advantages of the RSP scheme, different kinds of quantum states have been prepared, such as a single-qubit state [4,5,6,7], two-qubit state [8,9,10,11,12], three-qubit state [13,14,15,16], and four-qubit state [17,18,19,20].
In this paper, we propose a scheme for remote preparation of a four-qubit entangled state by using a ten-qubit entangled state. Compared with the previous schemes of preparing four-qubit state [17,18,19,20], any potential receiver in our scheme can obtain the quantum state transmitted by the sender based on the measurement results of the sender.
2 RSP of a Four-qubit Entangled State
In our scheme, there are three parties namely one sender Alice and two potential receiver Bob and Charlie. The sender Alice wants to remotely prepare a known four-qubit entangled state to any potential receiver Bob or Charlie. The four-qubit entangled state is written as
where \(\alpha,\beta,\delta,\gamma\) are all real number and \(\alpha^{2}+\beta^{2}+\delta^{2}+\gamma^{2}=1\). Here Alice knows all the information about the above four-qubit entangled state completely but neither Bob nor Charlie knows the information about the quantum state which the sender wants to prepare at the receiver’s end. In our scheme, Alice, Bob and Charlie share a ten-qubit entangled state, which is given by
where the qubits (1, 6) belong to Alice, the qubits (2, 3, 7, 8) and (4, 5, 9, 10) belong to the receivers Bob and Charlie, respectively. The above quantum state (2) can be rewritten as
where \({\left| {{\eta ^i}} \right\rangle _{16}}\left( {i=1,2,3,4} \right)\) are given by
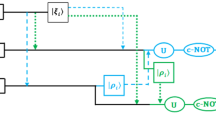
Alice first makes a two-qubit joint measurement on her own qubits (1, 6) in the basis given in Eqs. (4)–(7). The two-qubit orthogonal basis (4)–(7) is determined by the quantum state of the Eq. (1). Now Alice has two options, that is, she can remotely prepare the quantum state of Eq. (1) to Bob or Charlie. Here we assume that Alice want to remotely prepare the quantum state of Eq. (1) to Charlie. Then Alice tells the receivers the measurement result over a classical channel. To accomplish this RSP, Bob performs a measurement on his four qubits (2, 3, 7, 8) in the basis consisting of four mutually orthogonal vectors \({\left| {{\xi ^j}} \right\rangle _{2378}}\left( {j=1,2,3,4} \right)\) given by
After the measurement, Bob sends the measurement result to Charlie. Based on the measurement results from Alice and Bob, Charlie performs an appropriate unitary operation to convert each of the collapsed state into the state of qubits (4, 5, 9, 10) given by
That is the end of the scheme. The appropriate unitary operation of Charlie depends on the measurement results of both Alice and Bob. The unitary operation is obtained in the following four cases.
2.1 Case-I
If Alice’s measurement result is \({\left| {{\eta ^1}} \right\rangle _{16}}\), then the state of the qubits of Bob and Charlie collapse into the state
With the four-qubit orthogonal basis (8)–(11), the above entangled state can be rewritten as
Bob’s measurement result is \({\left| {{\xi ^1}} \right\rangle _{2378}}\), \({\left| {{\xi ^2}} \right\rangle _{2378}}\), \({\left| {{\xi ^3}} \right\rangle _{2378}}\) or \({\left| {{\xi ^4}} \right\rangle _{2378}}\), Charlie can carry out the local unitary operation \(I_{4}^{{}} \otimes I_{9}^{{}}\), \(\sigma _{4}^{z} \otimes \sigma _{9}^{z}\), \(\sigma _{4}^{z} \otimes I_{9}^{{}}\) or \(I_{4}^{{}} \otimes \sigma _{9}^{z}\) on his qubits 4 and 9 and then the original four-qubit state of Eq. (1) can be reconstructed.
2.2 Case-II
If Alice’s measurement result is \({\left| {{\eta ^2}} \right\rangle _{16}}\), then the state of the qubits of Bob and Charlie collapse into the state
With the four-qubit orthogonal basis (8)–(11), the above entangled state can be rewritten as
Bob’s measurement result is \({\left| {{\xi ^1}} \right\rangle _{2378}}\), \({\left| {{\xi ^2}} \right\rangle _{2378}}\), \({\left| {{\xi ^3}} \right\rangle _{2378}}\) or \({\left| {{\xi ^4}} \right\rangle _{2378}}\), Charlie can carry out the local unitary operation \(\sigma _{4}^{z} \otimes \sigma _{9}^{x}\sigma _{9}^{z} \otimes \sigma _{{10}}^{x}\), \(I_{4}^{{}} \otimes \sigma _{9}^{x} \otimes \sigma _{{10}}^{x}\), \(I_{4}^{{}} \otimes \sigma _{9}^{x}\sigma _{9}^{z} \otimes \sigma _{{10}}^{x}\) or \(\sigma _{4}^{z} \otimes \sigma _{9}^{x} \otimes \sigma _{{10}}^{x}\) on his qubits 4, 9 and 10 and then the original four-qubit state of Eq. (1) can be reconstructed.
2.3 Case-III
If Alice’s measurement result is \({\left| {{\eta ^3}} \right\rangle _{16}}\), then the state of the qubits of Bob and Charlie collapse into the state
With the four-qubit orthogonal basis (8)–(11), the above entangled state can be rewritten as
Bob’s measurement result is \({\left| {{\xi ^1}} \right\rangle _{2378}}\), \({\left| {{\xi ^2}} \right\rangle _{2378}}\), \({\left| {{\xi ^3}} \right\rangle _{2378}}\) or \({\left| {{\xi ^4}} \right\rangle _{2378}}\), Charlie can carry out the local unitary operation \(\sigma _{4}^{x}\sigma _{4}^{z} \otimes \sigma _{5}^{x} \otimes I_{9}^{{}}\), \(\sigma _{4}^{x} \otimes \sigma _{5}^{x} \otimes \sigma _{9}^{z}\), \(\sigma _{4}^{x} \otimes \sigma _{5}^{x} \otimes I_{9}^{{}}\) or \(\sigma _{4}^{x}\sigma _{4}^{z} \otimes \sigma _{5}^{x} \otimes \sigma _{9}^{z}\) on his qubits 4, 5 and 9 and then the original four-qubit state of Eq. (1) can be reconstructed.
2.4 Case-IV
If Alice’s measurement result is \({\left| {{\eta ^4}} \right\rangle _{16}}\), then the state of the qubits of Bob and Charlie collapse into the state
With the four-qubit orthogonal basis (8)–(11), the above entangled state can be rewritten as
Bob’s measurement result is \({\left| {{\xi ^1}} \right\rangle _{2378}}\), \({\left| {{\xi ^2}} \right\rangle _{2378}}\), \({\left| {{\xi ^3}} \right\rangle _{2378}}\) or \({\left| {{\xi ^4}} \right\rangle _{2378}}\), Charlie can carry out the local unitary operation \(\sigma _{4}^{x} \otimes \sigma _{5}^{x} \otimes \sigma _{9}^{x}\sigma _{9}^{z} \otimes \sigma _{{10}}^{x}\), \(\sigma _{4}^{x}\sigma _{4}^{z} \otimes \sigma _{5}^{x} \otimes \sigma _{9}^{x} \otimes \sigma _{{10}}^{x}\), \(\sigma _{4}^{x}\sigma _{4}^{z} \otimes \sigma _{5}^{x} \otimes \sigma _{9}^{x}\sigma _{9}^{z} \otimes \sigma _{{10}}^{x}\) or \(\sigma _{4}^{x} \otimes \sigma _{5}^{x} \otimes \sigma _{9}^{x} \otimes \sigma _{{10}}^{x}\) on his qubits 4, 5, 9 and 10 and then the original four-qubit state of Eq. (1) can be reconstructed.
The other option, that is, if Alice want to remotely prepare the quantum state of Eq. (1) to Bob, then Charlie must measure his own qubits using the four-qubit orthogonal basis (8)–(11). According to the measurement results of Alice and Charlie, Bob can obtain the original four-qubit entangled state of Eq. (1) by using a corresponding unitary transformation.
3 Conclusion
In summary, we present a new approach to implement RSP of a four-qubit entangled state. In our RSP scheme, the measurement basis used is experimentally achievable. In addition, the RSP scheme is bidirectional, that is, any receiver can obtain the original four-qubit entangled state. Such a scheme has guiding significance in the construction of future quantum networks.
References
Li, Y.H., Huang, Y.W., Xiang, T., Nie, Y.Y., Sang, M.H., Yuan, L.Q., Chen, X.F.: Multiuser time-energy entanglement swapping based on dense wavelength division multiplexed and sum-frequency generation. Phys. Rev. Lett. 123(25), 250505 (2019)
Yoshida, B., Yao, N.Y.: Disentangling scrambling and decoherence via quantum teleportation. Phys. Rev. X 9(1), 011006 (2019)
Pogorzalek, S., Fedorov, K.G., Xu, M., Parra-Rodriguez, A., Sanz, M., Fischer, M., Xie, E., Inomata, K., Nakamura, Y., Solano, E., Marx, A., Deppe, F., Gross, R.: Secure quantum remote state preparation of squeezed microwave states. Nat. Commun. 10(1), 1–6 (2019)
Barreiro, J.T., Wei, T.C., Kwiat, P.G.: Remote preparation of single-photon “hybrid” entangled and vector-polarization states. Phys. Rev. Lett. 105(3), 030407 (2010)
Wang, C., Zeng, Z., Li, X.H.: Controlled remote state preparation via partially entangled quantum channel. Quantum Inf. Process. 14(3), 1077–1089 (2015)
Peng, J.Y., Bai, M.Q., Mo, Z.W.: Bidirectional controlled joint remote state preparation. Quantum Inf. Process. 14(11), 4263–4278 (2015)
Li, Y.H., Wang, Z.S., Zhou, H.Q., Luo, H.M., Sang, M.H., Nie, Y.Y.: Noise effects and perfect controlled remote state preparation. Int. J. Theor. Phys. 58(4), 1172–1194 (2019)
Sang, M.H., Yu, S.D.: Controlled joint remote state preparation of an arbitrary equatorial two-qubit state. Int. J. Theor. Phys. 58(9), 2910–2913 (2019)
Sang, M.H., Nie, L.P.: Controlled remote state preparation of an arbitrary two-qubit state via a six-qubit cluster state. Int. J. Theor. Phys. 56(7), 2345–2349 (2017)
Choudhury, B.S., Dhara, A.: Joint remote state preparation for two-qubit equatorial states. Quantum Inf. Process. 14(1), 373–379 (2015)
Guan, X.W., Chen, X.B., Wang, L.C., Yang, Y.X.: Joint remote preparation of an arbitrary two-qubit state in noisy environments. Int. J. Theor. Phys. 53(7), 2236–2245 (2014)
Li, Y.H., Qiao, Y., Sang, M.H., Nie, Y.Y.: Bidirectional controlled remote state preparation of an arbitrary two-qubit state. Int. J. Theor. Phys. 58(7), 2228–2234 (2019)
Wang, D., Liu, Y., Zhang, Z.: Remote preparation of a class of three-qubit states. Opt. Commun. 281(4), 871–875 (2008)
Sang, Z.W.: Deterministic joint remote state preparation of an arbitrary equatorial three-qubit state. Int. J. Theor. Phys. 58(4), 1157–1160 (2019)
Choudhury, B.S., Samanta, S.: Remote preparation of some three particle entangled states under divided information. Int. J. Theor. Phys. 58(1), 83–91 (2019)
Chen, X.B., Sun, Y.R., Xu, G., Jia, H.Y., Qu, Z.G., Yang, Y.X.: Controlled bidirectional remote preparation of three-qubit state. Quantum Inf. Process. 16(10), 244 (2017)
Nie, Y.Y., Sang, M.H., Nie, L.P.: Controlled remote state preparation of an arbitrary four-qubit entangled cluster-type state using seven-qubit cluster state. Int. J. Theor. Phys. 56(6), 1883–1187 (2017)
Xue, Y., Shi, L., Da, X.Y., Zhou, K.H., Ma, L.H., Wei, J.H., Yu, L.Q., Hu, H.: Remote preparation of four-qubit states via two-qubit maximally entangled states. Quantum Inf. Process. 18(4), 103 (2019)
Du, Z.L., Li, X.L.: Deterministic joint remote state preparation of four-qubit cluster type with tripartite involvement. Quantum Inf. Process. 19(1), 39 (2020)
Zha, X.W., Wang, M.R., Jiang, R.X.: Two forms schemes of deterministic remote state preparation for four-qubit cluster-type state. Int. J. Theor. Phys. 59(3), 960–973 (2020)
Acknowledgements
This work is supported by the Research Foundation of the Education Department of Jiangxi Province (No. GJJ190889).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Sang, Zw. Optimal Remote Preparation of a Four-qubit Entangled State Via a Ten-qubit Entangled State. Int J Theor Phys 59, 2480–2485 (2020). https://doi.org/10.1007/s10773-020-04515-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10773-020-04515-z