1 Introduction

Realistic quantum systems are important for their fundamental concepts and up-to-date technological applications. Such physical systems are open and their unavoidable correlations with surrounding environments are of statistical nature. [1,2,3,4]. Nowadays, many researchers have focused on the investigation of open quantum systems in the fields of quantum optics [5], quantum information [6, 7] and more recently in quantum biophysics [8] to investigate and interpret their non-unitary behaviors. The composite open quantum systems are essential tools for quantum information and computation tasks. In quantum information theory entanglement plays a key role for many different applications, for instance in quantum cryptography [9], teleportation schemes or quantum computation [10]. Keeping and maintenance of entanglement in open quantum systems as long as possible require to protect it against different environmental influences. Therefore, representation and investigation of different dissipative models of open quantum systems help us to develop our understanding about plausible phenomena occurring in such interacting systems. Engineering and control of dynamical evolution of qubits in the presence of environmental noises and manipulation inaccuracies is one of the challenges for realizing quantum information processing [1]. Since the dynamics of composite open quantum systems strongly depends on the noises produced by the surrounding environment, therefore the most important aspects of the environment is whether it can be described either as memoryless (Markovian) or as with memory (non-Markovian). The Markovian or non-Markovian behavior of environment, with respect to a given system, can be characterized by comparing its typical correlation time and the system relaxation time [11,12,13].

For two-qubit systems interacting with Markovian environments, some kinds of correlations may undergo early-stage disappearance (ESD) or sudden death. Indeed, they completely disappear at a finite time in spite of exponential decaying manner of single-qubit coherence [11]. In the other hand, two-qubit systems subjected to non-Markovian environments may present phenomena such as revivals and trapping of correlations meaning that such systems may overcome ESD process. The study of dynamics of correlations under non-Markovian noise is of fundamental interest for quantum information purposes [14,15,16,17,18,19,20]. One of the most useful and applicable approach for the study of open two-qubit system is the master equations correspond to the density operator of the system under consideration. The master equations describe both memoryless Markovian dynamics and non-Markovian evolutions [21, 22]. The master equations are usually used for microscopical modeling of the interaction of the system under study and its environment via the tracing out the environment variables in some exact or perturbative treatment [21, 23]. The master equation approach has been frequently utilized in dissipative qubit systems. In this line, the authors in [24] have shown that stationary entanglement can be achieved by environment-induced chain links into dissipative qubit systems. Furthermore, the static behavior of entanglement power in two-qubit system interacting with a glocal environment has been studied in [25].

The keystone of the present paper is the model proposed in [26] wherein the authors have considered two qubits, while each of them interacts with an independent (local) environment. Here, we aim to consider their model to survey the influence of a common (global) environments on the decoherence effects on a two-qubit system. Indeed, we motivated to find out whether one can maintain (or at least restore) the quantum entanglement in dissipative two-qubit systems for a long time in the case of global environment (since in Ref. [26] the entanglement decay has been reported). We show that, the preservation of entanglement can be adjusted by controlling the parameters involved in the model such as thermal excitation number as well as the initial state of two-qubit system. As we will observe in the continuation of the paper, an outstanding effect of global environment on the dynamics of two-qubit system is the restoring effect (revival phenomenon) of entanglement which has not been reported in [26] in the case of local environment. Indeed, our results describe that the system under study can be conditionally found in both Markovian and non-Markovian regimes. In this regard, as is observed, the revival of entanglement can be appeared in some special conditions (non-Markovian regime) while in some other cases the permanent death of entanglement occurs due to Markovian behavior of environment.

This paper is organized as follows. In the next section, we introduce the master equation of a two-qubit system under the influence of global environment. The entanglement dynamics of the system under study is investigated by considering different initial conditions in Section 3 and finally the last section is allocated to our conclusions and remarks.

2 Master Equation of Two-Qubit System Under the Influence of Global Environment

We consider a two-qubit system undergoing a global dissipative dynamics described by the following dissipator [25]:

$$ \begin{array}{@{}rcl@{}} \dot\rho(t)&=&\mathcal{L} \rho(t) \\ &=&\gamma\bar{n}[2 (\sigma_{1}+\sigma_{2}) \rho (\sigma_{1}+\sigma_{2})^{\dag} - (\sigma_{1}+\sigma_{2})^{\dag} (\sigma_{1}+\sigma_{2})\rho -\rho (\sigma_{1}+\sigma_{2})^{\dag} (\sigma_{1}+\sigma_{2})]\\ &&+ \gamma(\bar{n} + 1) [2(\sigma_{1} + \sigma_{2})^{\dag} \rho (\sigma_{1} + \sigma_{2})- (\sigma_{1} + \sigma_{2}) (\sigma_{1} + \sigma_{2})^{\dag}\rho -\rho (\sigma_{1} + \sigma_{2}) (\sigma_{1} + \sigma_{2})^{\dag}],\\ \end{array} $$
(1)

where σ1, σ2 are the lowering operator of qubit 1 and 2, respectively, and \(\bar {n}\) is the mean number of thermal excitations corresponds to the global environment and γ is the common dissipation parameter which indicates the presence of global environment.

Figure 1 shows the schematic of the two-qubit interaction in the presence of a common environment.

Fig. 1
figure 1

Schematic of two-qubit system undergoes dissipative dynamics via interaction with environment. The coefficients of local and global dissipations are respectively introduced by Γ and γ in such systems. Here, we focus on the effect of global environment

Full size image

To study the dynamics we can formally expand the density operator in the basis {|1〉 := |e〉|e〉;|2〉 := |e〉|g〉;|3〉 := |g〉|e〉;|4〉 := |g〉|g〉}. So, we have

$$ \rho(t) = \sum\limits_{j,k=1}^{4} \rho_{j,k}(t) |j\rangle\langle k|, $$
(2)

where ρj,k(t) are unknown time-dependent coefficients. Upon inserting (2) into (1), the dynamics will be described by a set of linear differential equations for the unknown coefficients ρj,k(t). The sixteen coupled differential equations can be compactly expressed via the following relation:

$$ \dot{\mathbf v}(t) = M{\mathbf v}(t), $$
(3)

where

$$ {\mathbf v}(t) = \left( \rho_{11}(t), \rho_{12}(t), {\ldots} , \rho_{43}(t), \rho_{44}(t)\right)^{\top}, $$

with M as a 16 × 16 matrix with constant elements. After some lengthy calculations, the matrix M can be obtained as below:

$$ M=\gamma \left[\begin{array}{ll} M_{11}& M_{12} \\ M_{21} & M_{22} \end{array}\right], $$
(4)

where

$$ M_{11}= \left[\begin{array}{llllllll} -4\bar {n}-4 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & -4\bar {n}-3 & -\bar {n}-1 & 0 & 0 & 0 & 0 & 2\bar {n}\\ 0 & -2\bar {n}-1 & -4\bar {n}-3 & 0 & 0 & 0 & 0 & 2\bar {n}\\ 0 & 0 & 0 & -4\bar {n}-2 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & -4\bar {n}-3 & 0 & 0 & 0\\ 2\bar {n}+2 & 0 & 0 & 0 & 0 & -4\bar {n}-2 & -2\bar {n}-1 & 0\\ 2\bar {n}+2 & 0 & 0 & 0 & 0 & -2\bar {n}-1 & -4\bar {n}-2 & 0\\ 0 & 2\bar {n}+2 & 2\bar {n}+2 & 0 & 0 & 0 & 0 & -4\bar {n}-1 \end{array}\right] $$
$$ M_{12}= \left[\begin{array}{llllllll} 0 & 2\bar {n} & 2\bar {n} & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 2\bar {n} & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 2\bar {n} & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ -2\bar {n}-1 & 0 & 0 & 0 & 0 & 2\bar {n} & 2\bar {n} & 0\\ 0 & -2\bar {n}-1 & 0 & 0 & 0 & 0 & 0 & 2\bar {n}\\ 0 & 0 & -2\bar {n}-1 & 0 & 0 & 0 & 0 & 2\bar {n}\\ 0 & 0 & 0 & -2\bar {n}-1 & 0 & 0 & 0 & 0 \end{array}\right] $$
$$ M_{21}= \left[\begin{array}{llllllll} 0 & 0 & 0 & 0 & -2\bar {n}-1 & 0 & 0 & 0\\ 2\bar {n}+2 & 0 & 0 & 0 & 0 & -2\bar {n}-1 & 0 & 0\\ 2\bar {n}+2 & 0 & 0 & 0 & 0 & 0 & -2\bar {n}-1 & 0\\ 0 & 2\bar {n}+2 & 2\bar {n}+2 & 0 & 0 & 0 & 0 & -2\bar {n}-1\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 2\bar {n}+2 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 2\bar {n}+2 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 2\bar {n}+2 & 2\bar {n}+2 & 0 \end{array}\right] $$
$$ M_{22}= \left[\begin{array}{llllllll} -4\bar {n}-3 & 0 & 0 & 0 & 0 & 2\bar {n} & 2\bar {n} & 0\\ 0 & -4\bar {n}-2 & -2\bar {n}-1 & 0 & 0 & 0 & 0 & 2\bar {n}\\ 0 & -2\bar {n}-1 & -4\bar {n}-2 & 0 & 0 & 0 & 0 & 2\bar {n}\\ 0 & 0 & 0 & -4\bar {n}-1 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & -4\bar {n}-2 & 0 & 0 & 0\\ 2\bar {n}+2 & 0 & 0 & 0 & 0 & -4\bar {n}-1 & -4\bar {n}-1 & 0\\ 2\bar {n}+2 & 0 & 0 & 0 & 0 & -2\bar {n}-1 & -2\bar {n}-1 & 0\\ 0 & 2\bar {n}+2 & 2\bar {n}+2 & 0 & 0 & 0 & 0 & -4\bar {n} \end{array}\right] $$

In fact, the matrix M, which plays the role of Lindblad operator in matrix representation, can be found from the comparison of (1) and (3).

3 Concurrence of the Two-Qubit System for Different Initial States

For a mixed state represented by the density operator ρ, one can perform a spin-flip operation as below [27]:

$$ \begin{array}{@{}rcl@{}} \tilde{\rho}=({\sigma_{y}^{1}} \otimes {\sigma_{y}^{2}}) \rho^{*} ({\sigma_{y}^{1}} \otimes {\sigma_{y}^{2}}), \end{array} $$
(5)

where ρ∗ is the complex conjugate of the density matrix ρ and σy is the Pauli matrix. Now, if one defines \(R:=\rho \cdot \tilde {\rho }\) and uses the square roots of the eigenvalues of the matrix R denoted by \(\mathcal {G}_{i}\), then the concurrence of the mixed state ρ can be obtained as below:

$$ \begin{array}{@{}rcl@{}} C(\rho)=\max(0,\mathcal{G}_{1}-\mathcal{G}_{2}-\mathcal{G}_{3}-\mathcal{G}_{4}), \end{array} $$
(6)

where \(\mathcal {G}_{i}>0\) and also \(\mathcal {G}_{1}\) is the largest of them. Now we want to investigate the entanglement dynamics of system by considering different initial states of the two qubits. For this purpose, we initially consider entangled two-qubit state within the class of X-state:

$$ \rho_{X} (0)= \left[\begin{array}{llll} \rho_{11} & 0 & 0 & \rho_{14}\\ 0 & \rho_{22} & \rho_{23} & 0\\ 0 & \rho_{32} & \rho_{33} & 0\\ \rho_{41} & 0 & 0 & \rho_{44} \end{array}\right], $$
(7)

Therefore, the matrix R has the following explicit form:

$$ R_{X}= \left[\begin{array}{llll} \rho_{14}\rho_{41}+\rho_{11} \rho_{44} & 0 & 0 & 2\rho_{11}\rho_{44}\\ 0 & \rho_{23}\rho_{32}+\rho_{22}\rho_{33} & 2\rho_{22}\rho_{23} & 0\\ 0 & 2\rho_{32}\rho_{33} & \rho_{23}\rho_{32}+\rho_{22}\rho_{33} & 0\\ 2\rho_{44}\rho_{41} & 0 & 0 & \rho_{14}\rho_{41}+\rho_{11}\rho_{44} \end{array}\right], $$
(8)

where its eigenvalues are as below:

$$ \begin{array}{@{}rcl@{}} E_{1(2)}&=&(\sqrt{\rho_{22}\rho_{33}} \pm \sqrt{\rho_{23}\rho_{32}})^{2},\\ E_{3(4)}&=&(\sqrt{\rho_{11}\rho_{44}} \pm \sqrt{\rho_{14}\rho_{41}})^{2}. \end{array} $$
(9)

The X states may be found in a wide variety of physical situations like in the Ising and the XY models [30, 31]. Now, we proceed to obtain the solution of (3) with different initial conditions and then investigate the dynamics of entanglement. In this line, we consider tunable Werner states [28], maximally entangled mixed states (MEMS) [29] and a typical X state as the initial states of system. These two well-known families of mixed states which are important in quantum information. Werner states can be defined as a mixture of the maximally mixed state and a Bell state where their density matrix can be written as:

$$ \rho_{W} = \left[\begin{array}{llll} \mathcal{A} & 0 & 0 & 0\\ 0 & \mathcal{B} & \mathcal{C} & 0\\ 0 & \mathcal{C} & \mathcal{B} & 0\\ 0 & 0 & 0 & \mathcal{D} \end{array}\right], $$
(10)

where \(\mathcal {A}+2{\mathcal{B}}+\mathcal {D}=1\).

3.1 First Initial State

As the first case, let us consider the following initial state:

$$ \rho_{1} (0)= \left[\begin{array}{llll} A & 0 & 0 & 0\\ 0 & \frac{1-A}{2} & \frac{1-A}{2} & 0\\ 0 & \frac{1-A}{2} & \frac{1-A}{2} & 0\\ 0 & 0 & 0 & 0 \end{array}\right], $$
(11)

which is indeed a mixed state constitutes from the maximally entangled state \((|{e,g}\rangle +|{g,e}\rangle )/\sqrt {2}\) and a double excited state |e,e〉 respectively with weights 1-A and A (0 ≤ A < 1). So, the initial state of two-qubit system can be changed by varying the parameter A. So, in general, the dynamics of the system can be tuned by choosing different values of parameter A, various initial atomic states.

Considering vacuum reservoir (\(\bar {n}=0\)), the solution of (3) with initial state (11) can be obtained as follows:

$$ \rho_{1} (t)= \left[\begin{array}{llll} \rho_{11}(t) & 0 & 0 & 0\\ 0 & \rho_{22}(t) & \rho_{23}(t) & 0\\ 0 & \rho_{32}(t) & \rho_{33}(t) & 0\\ 0 & 0 & 0 & \rho_{44}(t) \end{array}\right], $$
(12)

where

$$ \begin{array}{@{}rcl@{}} \rho_{11}(t)&=& Ae^{-4\gamma t},\\ \rho_{22}(t)&=& \frac{1}{2} (4At-A+1)e^{-4\gamma t}, \qquad \rho_{33}(t)=\rho_{23}(t)=\rho_{32}(t) \\ \rho_{44}(t)&=&-(4At+1)e^{-4\gamma t}+1. \end{array} $$
(13)

In this case, the corresponding eigenvalues of matrix (12) can be obtained as:

$$ E_{1}=0, \quad E_{2}=(4At-A+1)e^{-4\gamma t}, \quad E_{3}=Ae^{-4\gamma t}, \quad E_{4}=1-(4At+A)e^{-4\gamma t}. $$
(14)

On the other hand, in the presence of thermal reservoir (\(\bar {n}\neq 0\)) the analytical solution of (3) is a very complicated expression. For instance, for a thermal reservoir with mean number of excitation as \(\bar {n}=1\), the corresponding eigenvalues of matrix R can be calculated as follow:

$$ \begin{array}{@{}rcl@{}} E_{1}\!&=&\!0, \\ E_{2}\!&=&\!-\frac{1}{14}[(7A-1+2\sqrt{2})e^{8\sqrt{2}\gamma t}-7A-4\sqrt{2}e^{4(3+\sqrt{2})\gamma t}+1+2\sqrt{2}]e^{-4(3+\sqrt{2})\gamma t},\\ E_{3}\!&=&\!-\frac{\sqrt{2}}{14}[(7A-1+2\sqrt{2})e^{8\sqrt{2} \gamma t}-7A-4\sqrt{2}e^{4(3+\sqrt{2})\gamma t}+1+2\sqrt{2}]e^{-4(3+\sqrt{2})\gamma t}, \\ E_{4}\!&=&\!-\frac{1}{14}\frac{[(-7A + 1 - 2\sqrt{2})e^{8\sqrt{2} \gamma t} - 4(1 + \sqrt{2})e^{4(3+\sqrt{2})\gamma t} + (21 + 14\sqrt{2})A - 11 - 8\sqrt{2}]e^{-4(3+\sqrt{2})\gamma t}}{1+\sqrt{2}}.\\ \end{array} $$
(15)

The analytical expression of concurrence can then be written in terms of Ei as follows:

$$ \begin{array}{@{}rcl@{}} C_{1}=\max(0,\sqrt{E_{2}}-\sqrt{E_{3}}-\sqrt{E_{4}}) \end{array} $$
(16)

The time evolution of concurrence for different values of parameter A, i.e. various initial states, is plotted in Fig. 2. As is clear, the amount of entanglement reduces due to the interaction of system with its surrounding environment. Also, the entanglement dies in the presence of both vacuum (\(\bar {n}=0\)) and thermal (\(\bar {n}=1\)) reservoirs. The death time of entanglement can be manipulated by tuning the parameters involved in the model. In particular, the entanglement wipes out sooner by increasing the parameter A in the presence of vacuum (Fig. 2c) and thermal (Fig. 2d) environments. Also, the thermal excitations degrades the maintenance of entanglement. Therefore, one can deduce that the system possesses a Markovian behaviour in the considered cases (all plots in Fig. 2 show death of entanglement which indicate the memoryless regime).

Fig. 2
figure 2

The time evolution of entanglement with initial state (11) in the presence of vacuum and thermal reservoirs. Clearly, death time of entanglement decreases by increasing both thermal excitation and parameter A

Full size image

3.2 Second Initial State

As the second case, we consider the following initial state for the two-qubit system:

$$ \rho_{2} (0)= \left[\begin{array}{llll} \frac{A}{4}+\frac{2-A}{2} & 0 & 0 & \frac{A}{4}\\ 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0\\ \frac{A}{4} & 0 & 0 & \frac{A}{4} \end{array}\right]. $$
(17)

This state consists of the maximally entangled Bell state \((|{e,e}\rangle +|{g,g}\rangle )/\sqrt {2}\) and double excited state |e,e〉.

The solution of (3) with \(\bar {n}=0\) considering (17) can be obtained as below:

$$ \rho_{2} (t)= \left[\begin{array}{llll} \rho_{11}(t) & 0 & 0 & \rho_{14}(t)\\ 0 & \rho_{22}(t) & \rho_{23}(t) & 0\\ 0 & \rho_{32}(t) & \rho_{33}(t) & 0\\ \rho_{41}(t) & 0 & 0 & \rho_{44}(t) \end{array}\right], $$
(18)

where

$$ \begin{array}{@{}rcl@{}} \rho_{11}(t)&=&-\frac{1}{4} (A-4)e^{-4\gamma t}, \rho_{14}(t)=\frac{A}{4}e^{-4\gamma t}, \\ \rho_{22}(t)&=&-\frac{1}{2} (A-4)\gamma te^{-4\gamma t}, \\ \rho_{23}(t)&=&\rho_{32}(t)=\rho_{33}(t)=\rho_{22}(t),\\ \rho_{44}(t)&=&\left( At+\frac{1}{4}A-4\gamma t-1\right)e^{-4\gamma t}+1. \end{array} $$
(19)

Equation (18) is a X-type density matrix. The eigenvalues of matrix R are as follow:

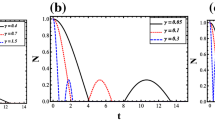
$$ \begin{array}{@{}rcl@{}} E_{1}&=&0 \\ E_{2}&=&(4-A)\gamma te^{-4\gamma t}\\ E_{3}&=&=\frac{1}{2}+\frac{1}{2}(A-2)te^{-4\gamma t} \\ &&+ \frac{1}{4}[(4A^{2}\gamma^{2} t^{2} - 32A\gamma^{2}t^{2} + 64\gamma^{2}t^{2} + 4A^{2}\gamma t + A^{2} - 32A\gamma t - 8A+64\gamma t + 16)e^{-8\gamma t} \\ &&+ (8A\gamma t-32\gamma t+A^{2}+4A-16)e^{-4\gamma t}+4]^{1/2}, \\ E_{4}&=&\frac{1}{2}+\frac{1}{2}(A-2)\gamma te^{-4\gamma t}\\ &&- \frac{1}{4}[(4A^{2}\gamma^{2} t^{2} - 32A\gamma^{2}t^{2} + 64\gamma^{2}t^{2} + 4A^{2}\gamma t + A^{2} - 32A\gamma t - 8A + 64\gamma t+16)e^{-8\gamma t} \\ &&+ (8A\gamma t-32\gamma t+A^{2}+4A-16)e^{-4\gamma t}+4]^{1/2}. \end{array} $$
(20)

Figure 3 clearly shows that after beginning the interaction, the entanglement decreases very rapidly and tends to zero at some moments of time. Also, there is a time interval without entanglement. After this time interval of entanglement death, the revival of entanglement takes place and the amount of concurrence tends to its maximum values. Figure 3b shows the sudden death and then revival of entanglement for three different values of A = 0.1,1.0,2.0, respectively. Recovering the entanglement implies that the system is in the non-Markovian regime and the memory effects of the environment restore the concurrence. In this case, the entanglement is stored in the reservoir and then transfered into the system. Therefore, we can conclude that the system and its surrounding reservoir are in a correlated state. It is worth noticing that the time interval of sudden death of entanglement can be tunned by justifying the parameter A. The time of sudden death decreases by increasing parameter A. Since the eigenvalues of matrix R for \(\bar {n}=1\) are very complicated and more lengthy than the case of \(\bar {n}=0\), therefore we only present the numerical result of concurrence in Fig. 4. In this case, only the sudden death of entanglement occurs in the dynamics of system and there is no revival of entanglement. Also, as is clear from Fig. 4a the time of sudden death depends on the amount of parameter A. Figure 4b shows the time evolution of concurrence for A = 0.5.

Fig. 3
figure 3

The time evolution of concurrence with initial state (17) for different values of parameter A. The sudden death and revival of entanglement can be manipulated by adjusting parameter A. In this case, the revival of entanglement indicates the non-Markovianity of the interaction model

Full size image
Fig. 4
figure 4

The time variation of concurrence for the two-qubit system with initial state (17). In this case, the memoryless effect corresponding to Markovian regime leads to disappearing of entanglement

Full size image

3.3 Third Initial State

Now, we choose the following initial state:

$$ \rho_3 (0)= \left[\begin{array}{llll} \frac{A}{3} & 0 & 0 & 0\\ 0 & \frac{1}{3} & \frac{1}{3} & 0\\ 0 & \frac{1}{3} & \frac{1}{3} & 0\\ 0 & 0 & 0 & \frac{1-A}{3}\\ \end{array}\right]. $$
(21)

This state consists of both double excitation (|e,e〉) and the ground state (|g,g〉) components in addition to a maximally entangled state as \((|{e,g}\rangle +|{g,e}\rangle )/\sqrt {2}\). The solution of (3) with \(\bar {n}=0\) can be obtained as,

$$ \rho_3 (t)= \left[\begin{array}{llll} \rho_{11}(t) & 0 & 0 & 0\\ 0 & \rho_{22}(t) & \rho_{23}(t) & 0\\ 0 & \rho_{32}(t) & \rho_{33}(t) & 0\\ 0 & 0 & 0 & \rho_{44}(t)\\ \end{array}\right], $$
(22)

where

$$ \begin{array}{@{}rcl@{}} \rho_{11}(t)&=&\frac{1}{3} Ae^{-4\gamma t},\\ \rho_{22}(t)&=&\frac{1}{3} (2A\gamma t+1)e^{-4\gamma t}, \\ \rho_{23}(t)&=&\rho_{32}(t)=\rho_{33}(t)=\rho_{22}(t),\\ \rho_{44}(t)&=&-\frac{1}{3}(4A\gamma t+A+2)e^{-4\gamma t}+1. \end{array} $$
(23)

The eigenvalues of matrix R with this initial state for \(\bar {n}=0\) can be obtained as:

$$ \begin{array}{@{}rcl@{}} E_1&=&0 \\ E_2&=&\frac{A}{3}e^{-4\gamma t}\\ E_3&=&\frac{2}{3}(2At+1)e^{-4\gamma t}, \\ E_4&=&-\frac{1}{3}(4At+A+2)e^{-4\gamma t}+1. \end{array} $$
(24)

and for \(\bar {n}=1\) as follow,

$$ \begin{array}{@{}rcl@{}} E_1\!&=&\!0 \\ E_2\!&=&\!-\frac{1}{42}\frac{[-2\sqrt{2} - 1 + (8\sqrt{2} - 11 + 7A)e^{8\sqrt{2}\gamma t} + 21A - 14\sqrt{2}A + (12 - 6\sqrt{2})e^{4(3+\sqrt{2})\gamma t}]e^{-4(3+\sqrt{2})\gamma t}}{\sqrt{2}-2},\\ E_3\!&=&\!-\frac{1}{42}\frac{[(7A-11 + 8\sqrt{2})e^{8\sqrt{2}\gamma t} + (24 - 24\sqrt{2})e^{4(3+\sqrt{2})\gamma t} - 21A + 14\sqrt{2}A + 2\sqrt{2} + 1]e^{-4(3+\sqrt{2})\gamma t}}{\sqrt{2}-1}, \!\\ E_4\!&=&\!\frac{\sqrt{2}}{84}[(7A-11-8\sqrt{2})e^{8\sqrt{2}\gamma t}+12e^{4(3+\sqrt{2}\gamma t}-7A+11+8\sqrt{2}]e^{-4(3+\sqrt{2})\gamma t}. \end{array} $$
(25)

Figure 5 shows the concurrence of two-qubit system with initial state (21). In this case the initial value of concurrence is smaller than the other cases. Also, the moment of time at which the sudden death of entanglement occurs is sooner than the previous discussed cases in this paper. In addition one can observe a symmetric behavior of concurrence with respect to A = 0.5 (the maximal values of concurrence take place at A = 0 and A = 1, while for A = 0.5 the concurrence tends to zero).

Fig. 5
figure 5

The time evolution of the concurrence when the system is initially in the state (21). In both plots, the entanglement wipes out, indicating the Markovian regime

Full size image

Figure 6 depicts the time evolution of concurrence when the system is initially in the maximally entangled state \((|{e,g}\rangle +|{g,e}\rangle )/\sqrt {2}\) for different thermal excitations. The solid line is the concurrence for vacuum reservoir (\(\bar {n}=0\)), the dashed and dotted lines are for thermal reservoir wit \(\bar {n}=0.5\) and \(\bar {n}=1\), respectively. As can be seen, by increasing the thermal excitation (\(\bar {n}\)) the time at which sudden death of entanglement occurs decreases. In conclusion, the two-qubit system reaches sooner to its separable state by increasing the mean number of photons (excitations) in the thermal reservoir.

Fig. 6
figure 6

Time evolution of concurrence of the two-qubit system for different thermal excitations with initial state \((|{e,g}\rangle +|{g,e}\rangle )/\sqrt {2}\) for A = 1. Solid line is for vacuum reservoir (\(\bar {n}=0\)), dashed and dotted lines are for \(\bar {n}=0.5\) and \(\bar {n}=1\), respectively

Full size image

4 Conclusion

In this paper we considered an open quantum system consists of two qubits under the influence of a common environment. Here, we focused on the dissipator part of master equation to investigate the time evolution of concurrence as a suitable measure of entanglement. Considering different initial conditions, we computed the analytical expressions for concurrence and then investigated its time evolution, numerically. Our results showed that the given system behaves in both Markovian and non-Markovian regimes. In the Markovian regime, concurrence permanently deceases and cannot recover again, till the entanglement tends to small values and eventually vanishes. In this case, the system reaches a separable quantum state by passing of time. In fact, the environment forgets the past interactions with the system due to the dispersion of correlations into the many environmental degrees of freedom. In addition, the non-Markovian manner can be observed in the dynamical evolution of our two-qubit system. In this situation, the entanglement is lost (or transfered) to the reservoir, however, it can be restored by the memory effects. Our results imply that two-qubit systems in non-Markovian regime may play a crucial role in recovering or restoring entanglement in a quantum dynamical system. Therefore, generally the state of system can be governed by tunning the parameters involved in the proposed model in such a way that the system and its surrounding reservoir can be found in a correlated or separable state.