1 Introduction

The important ingredient for quantum computation and information processing is the presence of coherent superpositions. A single isolated two-level system can be prepared in a coherent superposition of |0〉 and |1〉 states, and the manipulation of such states leads to new possibilities for storage and processing of information [1]. In contrast to the ideal isolated case, the interactions of real quantum systems with their environment lead to the loss of these coherent superpositions, in other words, decoherence. However, the more realistic case would be the manipulation of many qubits. Coherent superposition of such states leads to the concept of entanglement, which forms a precious resource for quantum computation and information. The fragility of entanglement is due to the coupling between a quantum system and its environment; such a coupling leads to decoherence, the process by which information is degraded [2,3]. In fact, decoherence is one of the main obstacles for the preparation, observation, and implementation of multiqubit entangled states. The intensive work on quantum information and computing in recent years has tremendously increased the interest in exploring and controlling decoherence effects [4–11]. In this work, we address the problem where each of the two qubits is dissipatively coupled to a local bosonic bath; in quantum optical sense it would mean that both the two-level systems are subject to spontaneous emission and would imply that there exist a relaxation between the excited state and the ground state. Dissipation can assist the generation of entanglement [12–14] that can be used for various quantum information processing. For example, Verstraete et al [10] have shown that dissipation can be used as a resource for universal quantum computation without any coherent dynamics needed to implement it. Contrary to other methods, entanglement generation by dissipation does not require the preparation of a system in a particular input state and exists, in principle, for an arbitrarily long time. These features make dissipative methods inherently stable against weak random perturbations, with the dissipative dynamics stabilizing the entanglement.

The effects on a system due to environment can be classified into the process with memory (non-Markovian) and without memory (Markovian) effects [15–20]. In Markovian processes, the environment acts as a sink for the system information; the system of interest loses information into the environment and this lost information plays no role in the dynamics of the system. However, due to memory effects in case of non-Markovian dynamics, the information lost by the system during the interaction with the environment will return back to the system at a later time. This makes the non-Markovian dynamics complicated. Understanding the nature of non-Markovian dynamics is naturally a very important topic for quantum information science, where the aim is to control a quantum system for use in technological applications [21–24]. In general, three time-scales in an open system exist to characterize non-Markovian dynamics: (i) the time-scale of the system, (ii) the time-scale of the bath given by the bandwidth of bath spectral density and (iii) the mutual time-scale arising from the coupling between the system and the bath. It is usually believed that non-Markovian effects strongly rely on the relations among these different time-scales [25–27].

In this paper, we derive a quantum master equation for interacting qubits with local dissipation. The equation is derived by utilizing the completeness of the eigenbasis of the Hamiltonian representing the interacting qubits. The time evolution of the density matrix turns out to be the sum of the time evolution corresponding to individual qubits with no cross terms. Next, we solve this master equation for X-type states with the assumption that individual bath has the same properties. The main content of this paper will however remain the same as for other kind of states and by assuming different bath correlation functions for each bath. Different bath correlation functions can give rise to different time-scales in the dynamics and are treated separately. Next, we identify different regimes of dynamics (Markovian and non-Markovian) and show that under non-Markovian regimes of the dynamics, there exists finite entanglement in an initially unentangled state. This entanglement decays in the same way as the pure state entanglement and we find that the decay rate of entanglement is strongly modified by the non-Markovian behaviour.

The rest of the paper is organized as follows: In §2, we introduce the model Hamiltonian and derive the quantum master equation. In related works done earlier [15–19], non-interacting qubits have been considered. These qubits are then coupled to a common bath. However, in this paper, we consider qubits interacting through isotropic Heisenberg interaction which is a general kind of interaction in condensed matter physics. In §3, we solve the quantum master equation in the eigenbasis of the system Hamiltonian for a general class of initial quantum states under the assumption that the bath correlation function decays in the same way. In §4 we give the decay of entanglement of certain X-type state. Finally, we conclude in §5 with the remarks of wider context of our results.

2 Master equation for local dissipation

In this section, we shall first derive master equation for the reduced density matrix of the system which govern the dynamics of the system. We consider two qubits represented by spin-\(\frac {1}{2}\) particles or two-level atoms coupled to each other via isotropic Heisenberg interaction. The qubits are subject to local dissipation through a coupling with a bosonic bath. The Hamiltonian of the two-qubit system is

$$\begin{array}{@{}rcl@{}} H_{\mathrm{s}} = J \vec{\sigma}_{1} \cdot \vec{\sigma}_{2} = J[\sigma_{1}^{+}\sigma_{2}^{-} + \sigma_{1}^{-}\sigma_{2}^{+} + {\sigma_{1}^{z}}{\sigma_{2}^{z}}], \end{array} $$
(1)

where \(\sigma _{i}^{\pm } \hspace *{-.1pt}=\hspace *{-.1pt} ({{\sigma _{i}^{x}} \hspace *{-.1pt}\pm \hspace *{-.1pt} i{\sigma _{i}^{y}}})/{2}\) and J represents the energy scale of the system. The Hamiltonian H s can be diagonalized exactly, i.e., H s|ψ i 〉 = 𝜖 i |ψ i 〉, where |ψ i 〉’s are the eigenstates of the Hamiltonian H s with the eigenenergies 𝜖 i and are given as follows (with notation \(|0\rangle =|{}\uparrow \rangle \) and \(|1\rangle =|{}\downarrow \rangle \)):

$$\begin{array}{@{}rcl@{}} &&\epsilon_{1}= J; \quad\psi_{1} = |00\rangle \\ &&\epsilon_{2}= 0; \quad\psi_{2} = \frac{1}{\sqrt{2}}[|01\rangle + |01\rangle] \\ &&\epsilon_{3}= -2J;\quad\psi_{3} = \frac{1}{\sqrt{2}}[|01\rangle - |01\rangle] \\ &&\epsilon_{4}= J; \quad\psi_{4} = |11\rangle. \end{array} $$

We write the total Hamiltonian (system + bath)

$$\begin{array}{@{}rcl@{}} H=H_{\mathrm{s}} + H_{\mathrm{B}} + H_{\mathrm{I}}, \end{array} $$
(2)

where H B, the Hamiltonian for the bath is represented by

$$\begin{array}{@{}rcl@{}} H_{\mathrm{B}} = \sum\limits_{i=1}^{2} \sum\limits_{k} \omega_{k} b_{i k}^{\dagger} b_{i k}, \end{array} $$
(3)

and the dissipative interaction of the system with bath is represented by the Hamiltonian

$$\begin{array}{@{}rcl@{}} H_{\mathrm{I}} &=& \sum\limits_{i=1}^{2} {\sigma_{i}^{x}} \sum\limits_{k}[g_{i k} b_{i k} +g_{i k}^{\star} b_{i k}^{\dagger} ] \\ &=& \sum\limits_{i=1}^{2} {\sigma_{i}^{x}} (B_{i} + B_{i}^{\dagger}), \end{array} $$
(4)

where \(B_{i} = {\sum }_{k} g_{i k} b_{i k}\). Let \(\tilde {O}(t)= {\mathrm {e}}^{i H_{\mathrm {o}} t} O {\mathrm {e}}^{-i H_{\mathrm {o}} t}\) represents an operator defined in interaction picture with respect to the system and the bath (H o = H s + H B). We can therefore write H I in the interaction picture, under rotating wave approximation as

$$\begin{array}{@{}rcl@{}} \tilde{H}_{\mathrm{I}}(t)=\sum\limits_{i=1}^{2} [\tilde{\sigma}_{i}^{+}(t) \tilde{B}_{i}(t) + \tilde{\sigma}_{i}^{-}(t) \tilde{B}_{i}^{\dagger}(t)]. \end{array} $$
(5)

The time evolution of the system operators can be evaluated using the eigenbasis of the system Hamiltonian H s as

$$\begin{array}{@{}rcl@{}} \sigma_{1}^{+}(\tau)\! &=&\! \sum\limits_{i,j=1}^{4} \!\!\! P_{ij} \langle \psi_{i}| \sigma_{1}^{+}\! \otimes\! I_{2}| \psi_{j} \rangle \exp[i (\epsilon_{i}-\epsilon_{j})\tau], \end{array} $$
(6)
$$\begin{array}{@{}rcl@{}} \sigma_{2}^{+}(\tau)\! &=&\! \sum\limits_{i,j=1}^{4} \!\!\! P_{ij} \langle \psi_{i}| I_{1}\! \otimes\! \sigma_{2}^{+} | \psi_{j} \rangle \exp[i (\epsilon_{i}-\epsilon_{j})\tau], \end{array} $$
(7)

where P ij = |ψ i 〉〈ψ j | is the projection operator, P ij P jk = P ik and \({\sum }_{i}P_{ii}=I\). In interaction picture, the time evolution of the total density matrix (the system and the bath), ρ T(t ), is given by the von Neuman–Liouville equation as

$$\begin{array}{@{}rcl@{}} \frac{{\mathrm{d}} \tilde{\rho}_{\mathrm{T}}(t)}{{\mathrm{d}}t} = -i[\tilde{H}_{\mathrm{I}}(t), \tilde{\rho}_{\mathrm{T}}(t)]. \end{array} $$
(8)

Here we have used \(\hbar =1\). We can formally integrate eq. (8) and write its solution as

$$\begin{array}{@{}rcl@{}} \tilde{\rho}_{\mathrm{T}}(t)= \tilde{\rho}_{\mathrm{T}}(0)- i {{\int}_{0}^{t}}\!\! {\mathrm{d}}s [\tilde{H}_{\mathrm{I}}(s), \tilde{\rho}_{\mathrm{T}}(s)]. \end{array} $$
(9)

Subsituting this solution back into the commutator of eq. (8), we get upto second order, the following equation:

$$\begin{array}{@{}rcl@{}} \frac{{\mathrm{d}}\tilde{\rho}_{{\mathrm{T}}}(t)}{{\mathrm{d}}t} =&-&i[ \tilde{H}_{{\mathrm{I}}}\left( t\right),\tilde{\rho}_{\mathrm{T}}\left( 0\right) ] \\ &-&{\int\nolimits_{0}^{t}}\mathrm{d}s[ \tilde{H} _{{\mathrm{I}}}\left( t\right),[ \tilde{H}_{{\mathrm{I}}}\left( s\right),\tilde{ \rho}_{{\mathrm{T}}}\left( s \right) ] ]. \end{array} $$
(10)

The solution of this equation depends on the initial conditions of the total density operator. We consider an initially uncorrelated situation, i.e., ρ T(0) = ρ s(0)⊗ρ B, where ρ s and ρ B are respectively the density operators for the system and the bath. Tracing out the degrees of freedom of the bath and assuming that \(\text {tr}_{\mathrm {B}}[\tilde {H}_{\mathrm {I}}(t) \rho _{\mathrm {B}}]=0\), we get the following time non-local master equation for the reduced density matrix:

$$\begin{array}{@{}rcl@{}} \frac{{\mathrm{d}} \tilde{\rho}_{\mathrm{s}}(t)}{{\mathrm{d}}t}=- {{\int}_{0}^{t}} \!\!\! {\mathrm{d}}s ~{\text{tr}}_{\mathrm{B}} [ \tilde{H}_{\mathrm{I}}(t), [ \tilde{H}_{\mathrm{I}} (s), \tilde{\rho}_{\mathrm{T}}(s) ] ]. \end{array} $$
(11)

The bath degree of freedom is infinite so that the influence of the system on the bath is small in the weak system–bath coupling case. As a consequence, we write the total density operator \( \tilde {\rho }_{\mathrm {T}}(s)= \tilde {\rho }_{\mathrm {s}}(s)\hspace *{-1.5pt}\otimes \hspace *{-1.5pt}\rho _{\mathrm {B}} + \mathcal {O}(\tilde {H_{\mathrm {I}}})\) within the second-order perturbation of the system–bath coupling [15,28–32]. The replacement of total density matrix \(\tilde {\rho }_{\mathrm {T}}(s)\) with an uncorrelated state \(\tilde {\rho }_{\mathrm {s}}(s)\hspace *{-2pt}\otimes \hspace *{-2pt}\rho _{\mathrm {B}} \) is called the Born approximation. Therefore, under Born approximation, we write

$$\begin{array}{@{}rcl@{}} \frac{{\mathrm{d}} \tilde{\rho}_{\mathrm{s}}(t)}{{\mathrm{d}}t}=- {{\int}_{0}^{t}}\!\!\! {\mathrm{d}}s ~{\text{tr}}_{\mathrm{B}} [ \tilde{H}_{\mathrm{I}}(t), [ \tilde{H}_{\mathrm{I}} (s), \tilde{\rho}_{\mathrm{s}}(s)\otimes\rho_{\mathrm{B}} ] ]. \end{array} $$
(12)

This equation is in the form of delayed integro-differential equation and is therefore a time non-local master equation. Replacing \(\tilde {\rho }_{\mathrm {s}}(s)\) with \(\tilde {\rho }_{\mathrm {s}}(t)\) in this equation [15,29,30], we get the time-local master equation:

$$\begin{array}{@{}rcl@{}} \frac{{\mathrm{d}} \tilde{\rho}_{\mathrm{s}}(t)}{{\mathrm{d}}t}=- {{\int}_{0}^{t}}\!\!\! {\mathrm{d}}s ~{\text{tr}}_{\mathrm{B}} [ \tilde{H}_{\mathrm{I}}(t), [ \tilde{H}_{\mathrm{I}} (s), \tilde{\rho}_{\mathrm{s}}(t)\otimes\rho_{\mathrm{B}} ] ]. \end{array} $$
(13)

Assume that the bath is in the vacuum state initially, i.e., ρ B = |0〉〈0|; using the form of \(\tilde {H}_{\mathrm {I}}(t)\), we arrive at the following equation:

$$\begin{array}{@{}rcl@{}} \frac{{\mathrm{d}} \tilde{\rho}_{\mathrm{s}}(t)}{{\mathrm{d}}t} = \mathcal{L}_{1}[\tilde{\rho}_{\mathrm{s}}(t)] + \mathcal{L}_{2}[\tilde{\rho}_{\mathrm{s}}(t)]. \end{array} $$
(14)

This forms a non-trivial result. The master equations contain sums of \(\mathcal {L}_{i}\) for each qubit and no cross terms with different \(\mathcal {L}_{i}\)’s. This result is the same as that for the non-interacting qubits. Here, we have (i = 1,2)

$$\begin{array}{@{}rcl@{}} \mathcal{L}_{i}(\tilde{\rho}_{\mathrm{s}}(t))\! &=&\! {{\int}_{0}^{t}} \!\!\! {\mathrm{d}}s \{{\Phi}_{i}(t-s)[\tilde{\sigma}_{i}^{-} (s) \tilde{\rho}_{\mathrm{s}}(t),\tilde{\sigma}_{i}^{+} (t) ] \\ &&~~~~~~+ {\Phi}_{i}^{\dagger}(t\! -\! s) [\tilde{\sigma}_{i}^{-} (t), \tilde{\rho}_{\mathrm{s}}(t) \tilde{\sigma}_{i}^{+} (s)] \} \end{array} $$
(15)

and the bath correlation function is defined as

$$\begin{array}{@{}rcl@{}} {\Phi}_{i}(t-s)&=& \langle B_{i}(t-s) B_{i}^{\dagger}\rangle_{0}\\ &=&\sum\limits_{k} |g_{i k}|^{2} \exp[-i\omega_{k} (t-s)]. \end{array} $$
(16)

Next, we revert back to the Schrödinger picture with a change in variable τ = t−s, and we write

$$\begin{array}{@{}rcl@{}} \frac{{\mathrm{d}} \rho_{\mathrm{s}}(t)}{{\mathrm{d}}t} &=& -i [H_{\mathrm{s}}, \rho_{\mathrm{s}}(t)] \\ &&+ \sum\limits_{i=1}^{2} {{\int}_{0}^{t}} {\mathrm{d}}\tau [{\Phi}_{i}(\tau)[\sigma_{i}^{-} (-\tau) \rho_{\mathrm{s}}(t),\sigma_{i}^{+} ] \\ &&~~~~~~~~~~~~~~+ {\Phi}_{i}^{\dagger}({\kern-.5pt}\tau{\kern-.5pt}) [\sigma_{i}^{-}{\kern-.5pt},{\kern-.5pt} \rho_{\mathrm{s}}{\kern-.5pt}({\kern-.5pt}t{\kern-.5pt}) \sigma_{i}^{+}{\kern-.5pt}(-\tau){\kern-.5pt}]{\kern-.5pt} ]{\kern-.5pt}. \end{array} $$
(17)

This represents the quantum master equation in the Schrödinger picture. The solution of the above master equation depends on the type of initial states. In the next section, we find its solution for general X-type initial states.

3 Solution of master equation

In order to obtain the dynamics of entanglement of our two-qubit system, we assume that the qubits are initially prepared in an X state [33]:

$$ \rho_{\mathrm{s}}(0)= \left[ \begin{array}{cccc} u(0) & 0 & 0 & w(0) \\ 0 & x_{1}(0) & y(0) & 0 \\ 0 & y^{\star}(0) & x_{2}(0) & 0 \\ w^{\star}(0) & 0 & 0 & v(0) \end{array} \right], $$
(18)

where we have used the standard basis {|00〉,|01〉,\(|10\rangle ,{\kern -.5pt} |11\rangle \}\). As the normalization and positivity of ρ s(0), i.e., tr (ρ s(0))=1 and ρ s(0)>0, the matrix elements u, x 1, x 2, v are non-negative parameters with u + x 1 + x 2 + v = 1, \(\sqrt {uv}\ge |w|\) and \(\sqrt {x_{1} x_{2}}\ge |y|\). We can use more general forms of density matrix with all elements non-zero and this makes the master equation intractable analytically. Next, we express the X state ρ s(0) in the eigenbasis of H s as

$$\begin{array}{@{}rcl@{}} \rho_{\mathrm{s}}(0)\! & =&\! a(0) |\psi_{1} \rangle \langle \psi_{1}|\! +\! b(0) |\psi_{2}\rangle \langle \psi_{2}| + e(0) |\psi_{3}\rangle \langle \psi_{3}|\\ &&\! + ~d{\kern-.5pt}({\kern-.5pt}0{\kern-.5pt}){\kern-.5pt} |{\kern-.5pt}\psi_{4}\rangle\! \langle{\kern-.5pt} \psi_{4}{\kern-.5pt}|\! +\! c({\kern-.5pt}0{\kern-.5pt}) |\psi_{1}\rangle\! \langle \psi_{4}| + c^{\star}(0) |\psi_{4}\rangle\! \langle \psi_{1}| \\ &&\! +~ h(0) |\psi_{2}\rangle \langle \psi_{3}| + h^{\star}(0) |\psi_{3}\rangle \langle \psi_{2}|, \end{array} $$
(19)

where various parameters of the density operator in the eigenbasis of H s are related to the parameters in the standard basis in the following way: a(0) = u(0), \( b(0) =\frac {1}{2}[x_{1}(0) + x_{2}(0) + y(0) + y^{\star }(0)] \), \( e(0) = \frac {1}{2}[x_{1}(0) + x_{2}(0) - y(0) - y^{\star }(0)] \), \(h(0) = \frac {1}{2}[x_{1}(0) - x_{2}(0) - y(0) + y^{\star }(0)] \), d(0) = v(0), c(0) = w(0). Next, we see that the form of the density matrix is invariant during the time evolution generated by the quantum master equation. Therefore, we can define the density matrix at time t as

$$\begin{array}{@{}rcl@{}} \rho_{\mathrm{s}}(t)\! & =&\! a(t) |\psi_{1} \rangle \langle \psi_{1}| + b(t) |\psi_{2}\rangle \langle \psi_{2}| + e(t) |\psi_{3}\rangle \langle \psi_{3}| \\ &&\! + ~d(t) |\psi_{4}\rangle \langle \psi_{4}|\! +\! c(t) |\psi_{1}\rangle \langle \psi_{4}|\! +\! c^{\star}(t) |\psi_{4}\rangle \langle \psi_{1}| \\ &&\! +~ h(t) |\psi_{2}\rangle \langle \psi_{3}| + h^{\star}(t) |\psi_{3}\rangle \langle \psi_{2}|. \end{array} $$
(20)

In order to find the time evolution equations of the various parameters involved in eq. (20), we assume that the bath correlation functions have the same form

$$\begin{array}{@{}rcl@{}} {\Phi}_{i}(s) =\frac{{\Gamma}_{i} \lambda}{2} {\mathrm{e}}^{-\lambda |s|}, \end{array} $$
(21)

where λ is the spectral width of the bath and Γ i is related to the microscopic system–bath coupling constant. It defines the relaxation time-scale τ R over which the state of the system: \(\tau _{\mathrm {R}} \sim {\Gamma }_{i}^{-1}\). It can be shown to be related to the Markovian decay rate ΓM in Markovian limit of flat spectrum. This form of correlation function corresponds to the Lorentzian spectral density of the bath [15]. Assuming that Γ1 = Γ2≡ΓM for simplicity, we substitute ρ s(t) as in eq. (20) in the quantum master equation (17) and obtain the time dependence of the parameters as

$$\begin{array}{@{}rcl@{}} a(t) &=& a(0) {\mathrm{e}}^{-{\Gamma}(t)}, \end{array} $$
(22)
$$\begin{array}{@{}rcl@{}} d(t) &= & d(0) + {{\int}_{0}^{t}}\!\!\!{\mathrm{d}}z [\eta(z) b(z) + {\Sigma}(z) e(z)], \end{array} $$
(23)
$$\begin{array}{@{}rcl@{}} c(t) &=& c(0) {\mathrm{e}}^{-iS_{1} t-{\Gamma}(t)}, \end{array} $$
(24)
$$\begin{array}{@{}rcl@{}} h(t) &=& h(0) {\mathrm{e}}^{-iS_{2} t - {\Gamma}(t)}, \end{array} $$
(25)
$$\begin{array}{@{}rcl@{}} \frac{{\mathrm{d}} b(t)}{{\mathrm{d}}t} + \eta(t) b(t)& =& \eta(t) a(t), \end{array} $$
(26)
$$\begin{array}{@{}rcl@{}} \frac{{\mathrm{d}} e(t)}{{\mathrm{d}}t} + {\Sigma}(t) e(t) &= &{\Sigma}(t) a(t), \end{array} $$
(27)

where

$$\begin{array}{@{}rcl@{}} &&{\kern-.6pc}{\Gamma}(t) = {\Gamma}_{+}(t) + {\Gamma}_{-}(t);\quad{\Gamma}_{+}(t)=\frac{1}{2} {{\int}_{0}^{t}} \!{\mathrm{d}}z~{\Sigma}(z) ;\\ &&{\kern-.6pc}{\Gamma}_{-}(t)=\frac{1}{2} {{\int}_{0}^{t}} \!{\mathrm{d}}z~\eta(z) ;\quad S_{1}(t)= S_{+}(t) + S_{-}(t);\\ &&{\kern-.6pc}S_{2}(t) = 2Jt+S_{1}(t) \end{array} $$

and the explicit forms of these functions are given in Appendix A.

4 Decay of entanglement

In this section, we study entanglement of a two-qubit system by means of concurrence [34]. For a density matrix ρ, concurrence is defined as

$$\mathcal{C}= \max \{0,\sqrt{r_{1}}-\sqrt{r_{2}}-\sqrt{r_{3}}-\sqrt{r_{4}}\}, $$

where r 1, r 2, r 3 and r 4 are the eigenvalues of matrix R in the descending order. Matrix R is defined as \(R\hspace *{-2pt}=\hspace *{-2.5pt}\rho ({\sigma ^{y}_{1}} \hspace *{-2pt}\otimes \hspace *{-2pt}{\sigma ^{y}_{2}}) \rho ^{\star } ({\sigma ^{y}_{1}}\hspace *{-2pt}\otimes \hspace *{-2pt}{\sigma ^{y}_{2}}) \) and ρ ⋆ represents complex conjugation of ρ in the standard basis. For X state in the standard basis, we write concurrence as [33]

$$\begin{array}{@{}rcl@{}} \mathcal{C}{\kern-.6pt}({}t{}) \!= \! 2~{\kern-.5pt}\max\{{\kern-.6pt}0{\kern-.6pt},{\kern-.6pt} |{\kern-.6pt}w{\kern-.6pt}({}t{}){}|\! - \! \sqrt{{}x_{1}{}({\kern-.6pt}t{\kern-.6pt}){\kern-.6pt} x_{2}{\kern-.5pt}({\kern-.6pt}t{\kern-.6pt}){}},{} |{\kern-.6pt}y{\kern-.6pt}({\kern-.6pt}t{\kern-.6pt}){}|\! - \!\sqrt{{}u{}({\kern-.6pt}t{\kern-.6pt}){} v{\kern-.6pt}({\kern-.6pt}t{\kern-.6pt}){\kern-.6pt}}\},\\ \end{array} $$
(28)

where we have

$$\begin{array}{@{}rcl@{}} && u(t)=a(t),~ w(t) = c(t),\\ && x_{1}(t) = \frac{1}{2}[b(t) + h(t) + h^{\star}(t) + e(t)],\\ && x_{2}(t) = \frac{1}{2}[b(t) - h(t) - h^{\star}(t) + e(t)],\\ && y(t) = \frac{1}{2}[b(t) - h(t) + h^{\star}(t) - e(t)],\\ && y^{\star}(t) = \frac{1}{2}[b(t) + h(t) - h^{\star}(t) - e(t)],~ v(t)= d(t). \end{array} $$

Next, we use these results to investigate the decay of entanglement in some specific cases. First, we consider the decay of the pure entangled state \(|{\Psi }\rangle = \cos \frac {\theta }{2} |01\rangle + \sin \frac {\theta }{2}|10\rangle \). This state has initial entanglement \(\mathcal {C}(0)=\sin \theta \) and at time t we write with the help of the above results

$$\begin{array}{@{}rcl@{}} \mathcal{C}(t) = 2~ \max\{0, |y(t)|\} \end{array} $$
(29)

or

$$\begin{array}{@{}rcl@{}} C{\kern-.5pt}({\kern-.5pt}t{\kern-.7pt})\! =\! 2{\kern-.5pt}|{\kern-.5pt}y({\kern-.7pt}t{\kern-.7pt}){\kern-.5pt}|\! =\! \frac{1\! +\! \mathcal{C}{\kern-.5pt}({\kern-.7pt}0{\kern-.7pt})}{2} {\mathrm{e}}^{-{\Gamma}_{-}({\kern-.5pt}t{\kern-.5pt})}\! -\! \frac{1{\kern-.5pt}\! -\! \mathcal{C}{\kern-.5pt}({\kern-.5pt}0{\kern-.5pt})}{2} {\mathrm{e}}^{-{\Gamma}_{+}(t)}. \end{array} $$
(30)

This forms an important result. It shows that even though initially we have an unentangled state \(\mathcal {C}(0)=0\), we still have entanglement at later time t. This can be attributed to the dissipative interaction between the system and the bath. Let us suppose 𝜃 = π, which corresponds to |10〉 state; the effect of dissipative interaction (\(H_{\mathrm {I}}(t)|10\rangle = B_{1}^{\dagger }(t)|11\rangle + B_{2}(t)|00\rangle \)) results in an entangled state.

Next, we analyse the Markovian and non-Markovian regimes of the dynamics and for that we define the following parameters: τ = ΓM t , Q = J / λ , R = λ / ΓM. Therefore, using this parametrization, we have

$$\begin{array}{@{}rcl@{}} \!\!{\Gamma}_{+}({\kern-.5pt}t{\kern-.5pt})\! &=&\! \frac{\tau}{2[1\! +\! 9Q^{2}]}\! -\! \frac{[{\kern-.5pt}1\! -\! 9Q^{2}{\kern-.5pt}]{\kern-.5pt}[1\! -\! {\mathrm{e}}^{-R\tau}{\kern-.5pt} \cos(3QR\tau{\kern-.5pt}){\kern-.5pt}]}{2R[1+9Q^{2}]^{2}} \\ && -\frac{3Q}{R[1+9Q^{2}]^{2}}{\mathrm{e}}^{-R\tau}\sin(3QR\tau) \end{array} $$
(31)
$$\begin{array}{@{}rcl@{}} {\Gamma}_{-}({\kern-.5pt}t{\kern-.5pt})\! &=&\! \frac{\tau}{2[1 + Q^{2}]} - \frac{[1 - Q^{2}][1-{\mathrm{e}}^{-R\tau} \cos(QR\tau)]}{2R[1+Q^{2}]^{2}} \\ && -\frac{Q}{R[1+Q^{2}]^{2}}{\mathrm{e}}^{-R\tau}\sin(QR\tau). \end{array} $$
(32)

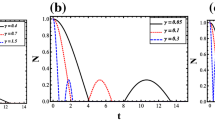
In order to understand how the Markovian limit is obtained from the above expressions, we plot in figures 1a–1b, \(\mathcal {C}(\tau )\) for 𝜃 = π/2, with respect to dimensionless parameter τ for R = 100 and R = 1 at different values of Q. We observe that the Markovian curve is recovered for R ≫ 1 with Q = 0. We can understand this behaviour of \(\mathcal {C}(t)\) by looking at the different parameters involved. The typical time-scale over which the system of two qubits changes is τ s∼1/J and the time-scale over which the bath changes is τ B∼1/λ, while relaxation time-scale for each qubit would be given by τ R∼1/ΓM. It means R ≫1 implies τ B≪τ R and Q<1 implies τ R<τ s. Thus, physically R≫1 and Q<1 would imply that the system evolves over a large time compared to very fast bath dynamics. Therefore, Markovian regime corresponds to R≫1 and Q<1 and we have

$$\begin{array}{@{}rcl@{}} {\Gamma}_{+}(t) = {\Gamma}_{-}(t)= \frac{\tau}{2} \end{array} $$
(33)

and therefore we get the standard Markovian limit:

$$\begin{array}{@{}rcl@{}} \mathcal{C}(t)=\mathcal{C}(0) {\mathrm{e}}^{-\frac{1}{2}{\Gamma}_{\mathrm{M}} t}. \end{array} $$
(34)

We observe that under the Markovian limit, an initially unentangled state remains unentangled always. In situations where the spectral width λ of the bath is narrower than the energy scale J involved for the system, Q≫1. This would mean τ R≪τ s. In figure 1b, for R = 1, we observe that as Q increases from 0, there is larger deviation from the Markovian dynamics of the concurrence \(\mathcal {C}(t)\). The general trend is similar for all values of R as can be seen on comparison to figure 1a. These observations suggest that Markovian regime is in fact opposite to the regime R<1 and Q≫1, which we call as non-Markovian regime. This larger deviation can be attributed to first terms of Γ−(t) and Γ+(t) containing Q 2 in the denominator. Q 2≫1 suggest defining another time scale

$$\begin{array}{@{}rcl@{}} \tau^{\prime} = \frac{{\Gamma}_{\mathrm{M}} }{Q^{2}} t. \end{array} $$
(35)

The decay of entanglement defined by \(\mathcal {C}(t)\) at various values of Q for non-Markovian regime R<1 in terms of rescaled time \(\tau ^{\prime } = \tau /Q^{2}\) is shown in figures 1c–1d. We see that for large Q, the concurrence \(\mathcal {C}(\tau ^{\prime })\) coincides with exponential decay in units of the rescaled time. Next, we see that before reaching the limiting behaviour of exponential decay in rescaled time (35), we observe some oscillatory behaviour (figures 1c–1d). The deviation from an exponential decay can be attributed to the memory effects developed in the two-qubit system. This occurs clearly due to the second terms in Γ−(t) and Γ+(t). For Q≫1, we may approximate this as

$$\begin{array}{@{}rcl@{}} {\Gamma}_{-}(\tau^{\prime}) & \approx & \frac{1}{2}\left[ \tau^{\prime} + \frac{1- {\mathrm{e}}^{-R Q^{2} \tau^{\prime} }\cos (R Q^{3} \tau^{\prime})}{R Q^{2}}\right], \end{array} $$
(36)
$$\begin{array}{@{}rcl@{}} {\Gamma}_{+}(\tau^{\prime}) &\! \approx\! & \frac{1}{18}\! \left[ \tau^{\prime}\! +\! \frac{1- {\mathrm{e}}^{-R Q^{2} \tau^{\prime} }\cos (3R Q^{3} \tau^{\prime})}{R Q^{2}}\!\right]. \end{array} $$
(37)
Figure 1
figure 1

Decay of entanglement as measured by concurrence C(t) with time at different values of the parameters Q and R. Here, we have used 𝜃 = π/2. Plots for different Q values at (a) R = 100, (b) R = 1, (c) R = 0.01 and (d) R = 0.001. Plots (a) and (b) are in units of Markovian decay rate ΓM, i.e., τ = ΓM t, while plots (c) and (d) are in units of rescaled decay rate ΓM/Q 2, i.e., \(\tau ^{\prime }=({{\Gamma }_{\mathrm {M}}}/{Q^{2}}) t \).

Full size image

In order for the oscillatory term to be visible, we require the exponential decay term in (36)–(37) to be not too fast giving RQ 2<1, but simultaneously the oscillation frequency should be faster than the overall decay envelope RQ 3 > RQ 2 > 1. The strongest oscillations therefore occur when RQ 2∼1, which agree with the numerical plots in figures 1c–1d. The deviation from an exponential decay can be attributed to the memory effects developed initially, typical of non-Markovian behaviour. The criteria for the strongest oscillatory behaviour are satisfied when all the characteristic time-scales are approximately the same, i.e., τ R∼τ s∼τ B.

5 Conclusions

In conclusion, we have derived a quantum master equation for a system of two interacting qubits under the influence of local dissipation. Using the assumption that the correlation functions have the same form for each of the bath, the solution of the master equation is found for the general X-type state. The time dependence of concurrence, a measure of entanglement, is studied for a pure entangled state \(|{\Psi }\rangle = \cos \frac {\theta }{2} |01\rangle + \sin \frac {\theta }{2}|10\rangle \) (a special case of X-type state) under both Markovian and non-Markovian regimes of the dynamics. It is found that for finite time evolution, an unentangled state can go to an entangled state in contrast to the Markovian case, where the unentangled state remains unentangled always. By identifying the parameter space, we have found that our results reduce to standard Markovian decay rate which in general is not a physically relevant regime [20]. In the physically relevant regime with narrower spectral width as compared to J, the decay rate is better approximated by Γ(t)=ΓM/Q 2, which is the standard Markovian decay rate divided by Q 2, which can be quite large in practice.

Next, we compare our work with several other works that studied non-Markovian dynamics of entanglement. Taking the example of ref. [17], the authors derive the non-Markovian decay of the entanglement for the pure state \(|{\Psi }\rangle = \cos \frac {\theta }{2} |01\rangle + \sin \frac {\theta }{2}|10\rangle \). The time dependence of concurrence is given by

$$\begin{array}{@{}rcl@{}} \mathcal{C}(t)= \max \{0, C(0) G(t)\}, \end{array} $$
(38)

where

$$\begin{array}{@{}rcl@{}} G(t)=\mathrm{e}^{-\lambda t/2}\left[ \cosh\left( \frac{\lambda t}{2}\delta\right)+ \frac{1}{\delta}\sinh\left( \frac{\lambda t }{2}\delta\right) \right] \end{array} $$
(39)

and \(\delta = \sqrt {1- (2 {\Gamma }_{\mathrm {M}}/\lambda })\) and ΓM is the Markovian decay rate. Our result (eq. (30)) is more general than this result. The results in these works [16–19] do not tell about the amount of entanglement and its decay that would be present in an entangled state generated from dissipation. To more clearly see the behaviour, let us examine this in two limiting cases.

Weak coupling limit

ΓM≪λ: This regime corresponds to a weak coupling regime or a very broad coupling to many frequency modes, which gives Markovian behaviour. Here, δ≈1−(ΓM/λ) and the decay function G(t) gives purely exponential behaviour. To first order the decay function may be approximated as

$$\begin{array}{@{}rcl@{}} G(t) \approx {\mathrm{e}}^{-{\Gamma}_{\mathrm{M}} t/2} \end{array} $$
(40)

which is nothing but standard Markovian spontaneous decay.

Strong coupling limit

ΓM≫λ: The reverse regime is when the linewidth of the bath is extremely narrow, which gives rise to strongly non-Markovian behaviour. Here we may approximate \(\delta =i\sqrt {2 {\Gamma }_{\mathrm {M}}/\lambda }\) and

$$\begin{array}{@{}rcl@{}} G(t) &=& {\mathrm{e}}^{-\lambda t /2}\left[ \cos \left( \sqrt{\frac{{\Gamma}_{\mathrm{M}} \lambda}{2}} t \right)\right.\\ && \left. + \sqrt{\frac{\lambda}{2 {\Gamma}_{\mathrm{M}}}} \sin \left( \sqrt{\frac{{\Gamma}_{\mathrm{M}} \lambda}{2}} t \right) \right], \end{array} $$
(41)

which corresponds to damped oscillations at frequency \(\sqrt {\lambda {\Gamma }_{\mathrm {M}}/2}\) and a decay envelope with rate λ. Thus, we see that in both the cases the previous results do not yield the scaling factor Q 2 as derived in eq. (35).

The current result would be important for applications where spontaneous emission is a serious drawback of using excited states, such as for quantum information processors, quantum simulators and quantum metrological applications.