1 Introduction

Uncertainty principle, which bounds our ability to predict measurement outcomes for a couple of incompatible observables with an arbitrarily small uncertainty, is viewed as one of the most remarkable characteristics in the region of quantum mechanics and intrinsically illuminates the discrepancy between classical and quantum mechanics [1, 2]. Later, Kennard and Robertson generalized this principle to the so-called standard deviation [3, 4]. Several authors [5,6,7] have demonstrated several tighter uncertainty relations based on the variances’ sum, in which the lower bounds are showing their significance in quantum physics with respect to any pair of incompatible observables. However, the aforementioned deviation is not always optimal when evaluating the magnitude of the uncertainty, since the bounds for the deviation are state dependent, which would give rise to a trivial result if the commutator related to the observables has zero expectation value. Whereafter, Deutsch [8] put forward a new and progressive type of uncertainty relation in terms of information entropy, entropic uncertainty relations (EURs), and subsequently these EURs were simplified by Refs. [9] and [10] into

$$\begin{aligned} H({\hat{P}})+H({{\hat{R}}})\ge \mathrm{log}_2{\frac{1}{c}}, \end{aligned}$$
(1)

here the Shannon entropy \(H(\epsilon )=-\sum _\epsilon p_\epsilon \mathrm{log}p_\epsilon \) with \(p_\epsilon =\langle \varphi _\epsilon |\hat{\rho }|\varphi _\epsilon \rangle \), \(\mathrm{log}_2\frac{1}{c}\) describes the incompatibility of the two observables \({\hat{P}}\) and \({\hat{R}}\) while \(c=\mathrm{max}\{|\langle \varphi _{\hat{P}}| \varphi _{\hat{R}}\rangle |^2\}\); here, \(|\varphi _{\hat{P}}\rangle \) and \(|\varphi _{\hat{R}}\rangle \) denote the corresponding eigenstates of \({\hat{P}}\) and \({\hat{R}}\). Compared with the standard deviation, the EUR’s bound completely is irrelevant to the system’s state \(\hat{\rho }\), which does not occur in the standard deviation [11, 12].

Furthermore, some authors had proved that the measurement uncertainty can be reduced in the presence of quantum entanglement (memory) [13,14,15,16] with a new Heisenberg expression

$$\begin{aligned} S({\hat{P}}|B)+S({{\hat{R}}}|B)\ge S(A|B)+ \mathrm{log}_2 {\frac{1}{c}}, \end{aligned}$$
(2)

which canonically is deemed as quantum-memory-assisted entropic uncertainty relations (QMA-EUR). Within the above, the conditional entropy \(S({X}|B)=S({\hat{\rho }}_{{X}B})-S({\hat{\rho }}_B)\) with \({X}\in (\hat{P},\hat{R})\), \(S(\hat{\rho })=-\mathrm{Tr}(\hat{\rho }\mathrm{log}\hat{\rho })\), and \({\hat{\rho }}_{{{X}}B}=\sum _x\left( |\phi _x\rangle \langle \phi _x|\otimes {{\varvec{I}}}\right) {\hat{\rho }}_{AB} \left( |\phi _x\rangle \langle \phi _x|\otimes {{\varvec{I}}}\right) \) is the post-measurement state with the eigenstate \(|\phi _x\rangle \) of observable X and \(\varvec{I}\) being the identical operator. To better understand the physics behind this new relation, Berta et al. [14] ingeniously introduced so-called uncertainty game. To be specific, the game scenario may be depicted as follows: To start with, there are two legitimate players (say, Alice and Bob). Bob in priori prepares a wanted entanglement of qubits A to be measured and B as quantum memory and then transmits A to Alice, who will make the measurement of either \(\hat{P}\) or \(\hat{R}\) and later inform Bob of the measured selection with classical information. By the received information, Bob is capable of predicting Alice’s result with a minimal uncertainty. Specifically, the above expression for von Neumann entropy given in Eq. (2) directly shows that the bipartite entanglement can effectively reduce the lower bound as \(S(A|B)<0\) and consequently is capable of minimizing the measurement uncertainty. Additionally, this relation naturally reduces to Deutsch’s outcome if A and B remain disentangled [8].

Besides, the QMA-EUR had received a great deal of attention because of its amazing applications in quantum entanglement witnessing [14,15,16,17], quantum metrology [18], quantum cryptography [19, 20], quantum randomness [21, 22], and quantum key distribution [23, 24]. Contemporaneously, the inequality has been generalized to the several different forms through the Rényi entropy [25,26,27]. Moreover, there also have existed some other situationally specific optimized results [28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44]. Indeed, any systems are essentially open and inevitably interact with their surrounding environment, which induces decoherence or dissipation phenomena [45,46,47,48]. Therefore, to clarify how various environments influence the uncertainty for measurement is a basic requirement during measurement estimation. Indeed, some studies expend effort toward exploiting the effects of various forms of real environmental noises on the dynamics of QMA-EUR [49,50,51,52,53,54,55,56,57,58]. In light of with and without memory effect, environments can be typically classified into Markovian ones and non-Markovian ones. Until now, there existed several investigations on dynamics of the entropic uncertainty in the non-Markovian regimes [30, 49, 59, 60]. Different from the previous, our work will focus on revealing the evolution characteristic of the measurement uncertainty within a canonical scenario that any two qubits independently suffer from non-Markovian reservoirs.

Fig. 1
figure 1

(Color online) Schematic of the two-atom system where each independently couples with its own reservoirs \(E_A\) and \(E_B\), \(J(\omega )\), respectively. Each reservoir is characterized by a Lorentz spectral distribution, \(J(\omega )\)

Full size image

2 Physical model, analytical solution, and non-Markovianity

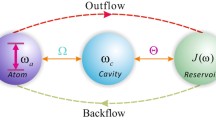
Before exploring non-Markovian effects on the entropic uncertainty, let us briefly describe the model considered here with a toy system comprised of two atoms acting as qubits, where each atom interacts independently with its local environment, as illustrated in Fig. 1. For the purpose of this work, we will consider a single qubit-reservoir Hamiltonian with \(\hbar =1\) written as [61, 62]

$$\begin{aligned} \mathcal{H}=\omega _0\hat{\sigma }^+\hat{\sigma }^-+\sum _k\omega _k\hat{b}_k^{\dag }\hat{b}_k+\sum _k(g_k\hat{\sigma }^+\hat{b}_k+g_k^{*}\hat{\sigma }^-\hat{b}_k^{\dag }), \end{aligned}$$
(3)

with the qubits’ transition frequency \(\omega _0\), the k-th field mode frequency \(\omega _k\) in the reservoir, the system’s raising (lowering) operator \(\hat{\sigma }^+=|e\rangle \langle g|\) (\(\hat{\sigma }^-=|g\rangle \langle e|\)), \(\hat{b}_k\) (\(\hat{b}_k^{\dag }\)) denoting the creation (annihilation) operator of the reservoir’s k-th mode, and the coupling strength \(g_k\). In the zero-temperature approximation, the given Hamiltonian \(\mathcal{H}\) stands as a specific open system which possesses an analytical solution. Within such a quantum system, the qubits’ dynamics can be expressed as the density matrix [63]

$$\begin{aligned} \hat{\rho }^{\alpha }(t)=\left( \begin{array}{cc} \rho _{ee}^{\alpha }(0){\xi _t} &{} \rho _{eg}^{\alpha }(0)\sqrt{{\xi _t}}\\ \rho _{ge}^{\alpha }(0)\sqrt{{\xi _t}} &{} 1-\rho _{gg}^{\alpha }(0){{\xi _t}} \\ \end{array} \right) \end{aligned}$$
(4)

for qubit \(\alpha \), where \({\xi _t}\) complies with the differential equation

$$\begin{aligned} \dot{\xi }_t=-\int _0^tdt_1f(t-t_1)\xi (t_1) . \end{aligned}$$
(5)

\(f(t-t_1)\) is referred to the correlation function, which is highly relevant to the reservoir’s spectral density \(J(\omega )\) through

$$\begin{aligned} f(t-t_1)=-\int J(\omega ){ e}^{i(\omega _0-\omega )(t-t_1)}d\omega . \end{aligned}$$
(6)

Thereby, \({\xi }_t\) mainly depends on the spectral density \(J(\omega )\). Since the Hamiltonian given by Eq. (3) describes a canonical model where an atom in a cavity undergoes energetic decay, by considering a single excitation in the observed system, one here can obtain the exact dynamics of the system. \(J(\omega )\) adopts the spectral distribution as to an external driven field inside a deficient cavity providing \(\omega _0\); such a system would result from the combination of the reservoir spectrum and the system–reservoir coupling through \(\delta _0\) (called as a coupling constant of system and reservoir) and given a Lorentz form [61]

$$\begin{aligned} J(\omega )=\frac{1}{2\pi }\frac{\delta _0\Gamma ^2}{(\omega -\omega _0)^2+\Gamma ^2} . \end{aligned}$$
(7)

\(\Gamma \) represents the spectral width for the coupling, which is quantified by the correlation time \(\tau _\mathrm{r}\) of the reservoir in terms of \(\tau _\mathrm{r}=1/\Gamma \). Additionally, the parameter \(\delta _0\) relates to the decay of the atomic excitation in the Markovian limit of flat spectrum and is correlated with the relaxation time \(\tau _q\) by \(\tau _q=1/\delta _0\), which is the time over which the state of the qubit system evolves. In the weak-coupling regime (with \(\delta _0<\Gamma /2\)), \(\tau _q> \tau _\mathrm{r}\) and \({\xi _t}\) will substantially become a Markovian exponential decay mediated by \(\delta _0\). By contrast, \(\tau _q\le \tau _\mathrm{r}\) in the regime of strong-coupling regime (with \(\delta _0>\Gamma /2\)) and then the system is responsible for a non-Markovian evolution. In our consideration, we will focus on the strong-coupling regime to reveal the non-Markovian environmental effects on the uncertainty. Within this regime, the function \({\xi _t}\) can be written as [64]

$$\begin{aligned} \xi _t=e^{-\Gamma t}\left[ \mathrm{cos}\left( \frac{\lambda t}{2}\right) +\frac{\Gamma }{\lambda }\mathrm{sin}\left( \frac{\lambda t}{2}\right) \right] ^2, \end{aligned}$$
(8)

where \(\lambda =\sqrt{2\delta _0\Gamma -\Gamma ^2}\). \({\xi _t}\) presents oscillations in its description of the damping process for the atomic excitation generated by the coherent processes of the system–reservoir. Note that \({\xi _t}\equiv 0\) in the limit of \(t_\kappa =2[\kappa \pi -\mathrm{arctan}(\lambda /\Gamma )]/\lambda \) \(\iff \kappa \in Z\). In the standard basis vectors \(\{|ee\rangle ,|eg\rangle ,|ge\rangle ,|gg\rangle \}\), one thus can derive the system’s density matrix with elements of [64]

$$\begin{aligned} \rho _{11}(t)&={\xi _t}^2\rho _{11}(0),\ \ \rho _{22}(t)={\xi _t}\rho _{22}(0)+{\xi _t}(1-{\xi _t})\rho _{11}(0), \nonumber \\ \rho _{33}(t)&={\xi _t}\rho _{33}(0)+{\xi _t}(1-{\xi _t})\rho _{11}(0), \nonumber \\ \rho _{44}(t)&=1-[\rho _{11}(t)+\rho _{22}(t)+\rho _{33}(t)],\nonumber \\ \rho _{12}(t)&={\xi _t}^{3/2}\rho _{12}(0), \ \ \rho _{13}(t)={\xi _t}^{3/2}\rho _{13}(0),\nonumber \\ \rho _{14}(t)&={\xi _t}\rho _{14}(0), \ \ \rho _{23}(t)={\xi _t}\rho _{23}(0), \nonumber \\ \rho _{24}(t)&=\sqrt{{\xi _t}}[\rho _{24}(0)+(1-{\xi _t})\rho _{13}(0)], \nonumber \\ \rho _{34}(t)&=\sqrt{{\xi _t}}[\rho _{34}(0)+(1-{\xi _t})\rho _{12}(0)], \end{aligned}$$
(9)

and \(\rho _{ij}(t)=\rho _{ji}^{*}(t)\), where \(\hat{\rho }(t)\) is Hermite.

A working approach of measuring Markovianity with respect to a given system is to utilize the trace distance (TD), which is considered as a metric determined by performing the trace norm on the set of quantum states. The TD with respect to any pair of states \(\hat{\rho }_1\) and \(\hat{\rho }_2\) can be expressed by [65]

$$\begin{aligned} \mathcal{D}(\hat{\rho }_1(t),\hat{\rho }_2(t)) = \frac{1}{2} \parallel \hat{\rho }_1(t)-\hat{\rho }_2(t) \parallel _\mathrm{Tr}, \end{aligned}$$
(10)

where \(\parallel {\chi } \parallel _\mathrm{Tr}=\mathrm{Tr}(\sqrt{{\chi }^{\dag } \chi })\). The \(\mathcal{D}\) stands for a canonical metric within the density-matrix space with \(0\le \mathcal{D}\le 1\). Consequently, the TD may be explained by a measurement for two quantum states’ distinguishability. Notably, there exists a distinctive characteristic of the TD, which is contractility to this metric

$$\begin{aligned} \mathcal{D}(\Psi _{\hat{\rho }_1(t)},\Psi _{\hat{\rho }_2(t)})\le \mathcal{D}({\hat{\rho }_1(t)},{\hat{\rho }_2(t)}) \end{aligned}$$
(11)

for all absolutely positive and trace-preserving maps \(\Psi \). On the contrary, non-trace-preserving quantum operations ever enable us to raise the states’ distinguishability.

An increase of \(\mathcal{D}\) between pairs of states associated with a system is understood as the information backflow into the system, characteristic of non-Markovian regimes. Otherwise, a reduction (or invariant value) of \(\mathcal{D}\) means information is outflowing into the environment from the system in an unidirectional manner, characteristic of Markovian regimes. Then, the corresponding non-Markovianity can be measured by the BLP formula [66]

$$\begin{aligned} \mathcal{N}={\mathop {{\mathrm{max}}}\limits _{\hat{\rho }_1(0),\hat{\rho }_2(0)}}\int _{\sigma >0} dt\ \sigma (t,\hat{\rho }_1(0),\hat{\rho }_2(0)), \end{aligned}$$
(12)

with the changing rate \(\sigma (t,\hat{\rho }_1(0),\hat{\rho }_2(0))=\frac{d}{dt}\mathcal{D}(\hat{\rho }_1(t),\hat{\rho }_2(t))\) related to the TD as expressed by Equation (10).

3 Non-Markovian effects on the measurement uncertainty via entropy

In the uncertainty game mentioned before, Bob transmits A, which in prior is entangled with B, to Alice. Alice makes a measurement by one of the two incompatible observables \(\hat{P}\) and \(\hat{R}\) and subsequently tells Bob her measuring selection for \(\hat{P}\) or \(\hat{R}\) through the classical information; Bob can obtain the minimal uncertainty regarding Alice’s measured outcome based on the information. To explore the non-Markovian effects on the game of interest, we herein take into account a generic bipartite system, initially sharing an any two-qubit state with Bloch representation,

$$\begin{aligned} {\hat{\rho }}_{AB}=\frac{1}{4}\left( {\varvec{I}}^A\otimes {\varvec{I}}^B+{{\varvec{r}}}\cdot {{{\varvec{\sigma }}}}^A\otimes {\varvec{I}}^B+ {\varvec{I}}^A\otimes {{\varvec{s}}}\cdot {{{\varvec{\sigma }}}}^B+\sum _{k=1}^3c_{k}{{\sigma }}_k^A\otimes {{\sigma }}_k^B\right) , \end{aligned}$$
(13)

where \(\varvec{r}\) and \(\varvec{s}\) denote Bloch vectors, \(\{{\sigma }_k\}_{k=1}^3\) corresponds to the standard Pauli operators, and the correlation matrix \(c_{k}=\mathrm{Tr}_{AB}({\hat{\rho }}_{AB}{\sigma }_k^A\otimes {\sigma }_k^B)\) with \(0\le |c_{k}|\le 1\). In particular, \(\varvec{r}=\varvec{s}=\varvec{0}\), \(\hat{\rho }_{AB}\) reduces to a two-qubit Bell-diagonal state. In the following, suppose that the Bloch vectors are z-directional, we have \(\varvec{r}=(0,0,r)\) and \(\varvec{s}=(0,0,s)\) with \(r=\mathrm{Tr}_{AB}(\hat{{\rho }}_{AB}{\sigma }_z^A\otimes {\varvec{I}}^B)\) and \(s=\mathrm{Tr}_{AB}(\hat{\rho }_{AB}{\varvec{I}}^A\otimes {\sigma }_z^B)\). Incidentally, we can also transform them to be x- or y-directional by means of an proper local unitary transformation without loss of its diagonal property of the correlation term.

To uncover the dynamical traits of the uncertainty with regard to a pair of incompatible measurements under two separate bosonic reservoirs while considering memory effect, we resort to using \({\sigma }_x\) and \({\sigma }_z\) as the incompatible measurements. Derived from the entropies in Equation (2), the post-measurement states are given by

$$\begin{aligned} {\hat{\rho }}_{\sigma _xB}=&\frac{(1+s)}{4}{\xi _t}(|00\rangle \langle 00|+|10\rangle \langle 10|)+\frac{ (2-{\xi _t}-s{\xi _t})}{4}(|01\rangle \langle 01|+|11\rangle \langle 11|)\nonumber \\&+\frac{c_1{\xi _t} }{4}(|01\rangle \langle 10|+|10\rangle \langle 01|+|00\rangle \langle 11|+|11\rangle \langle 00|),\nonumber \\ {\hat{\rho }}_{\sigma _zB}=&\frac{1+{{c_3}}+r+s}{4}{{\xi _t}}^2|00\rangle \langle 00|+\frac{2+2r-{\xi _t}(1+{{c_3}}+r+s)}{4}{{\xi _t}}(|10\rangle \langle 10|+|01\rangle \langle 01|)\nonumber \\&+ \frac{4-2{\xi _t}(2+r+s)+{\xi _t}^2(1+{{c_3}}+r+s)}{4}|11\rangle \langle 11|, \end{aligned}$$
(14)

respectively, and by calculating the corresponding eigenvalues, the von Neumann entropies can be written as

$$\begin{aligned} S({\hat{\rho }}_{\sigma _xB})&= S_\mathrm{bin}\left( \frac{1-\sqrt{\Delta }}{2}\right) +1, \nonumber \\ S({\hat{\rho }}_{\sigma _zB})&= -(\eta \mathrm{log}_2\eta +2\vartheta \mathrm{log}_2\vartheta +\nu \mathrm{log}_2\nu ), \end{aligned}$$
(15)

where \(S_\mathrm{bin}(x)=-x\mathrm{log}_2x-(1-x)\mathrm{log}_2(1-x)\) is defined as a binary entropy, \(\Delta =1-2{\xi _t}+{\xi _t}^2+{c_1}^2{\xi _t}^2-2\xi _ts + 2 {\xi _t}^2 s + {\xi _t}^2 s^2\), \(\eta =({1+{{c_3}}+r+s}){{\xi _t}}^2/4\), \(\vartheta =[{2+2r-{\xi _t}(1+{{c_3}}+r+s)}]{{\xi _t}}/4\), and \(\nu =1-\eta -2\vartheta \).

On account of \({{\hat{\rho }}}_{B}=\mathrm{Tr}_A({{\hat{\rho }}}_{AB})\), the entropy of the quantum memory is easily given as \(S({{\hat{\rho }}}_{B})=S_\mathrm{bin}(({1+r}){\xi _t}/2)\). Speaking to the measurement for the observables \(\sigma _x\) and \(\sigma _z\), we obtain a form for the left-hand side (LHS) of the inequality (2), analytically described by

$$\begin{aligned} {U}=S_\mathrm{bin}\left( \frac{1-\sqrt{\Delta }}{2}\right) -(\eta \mathrm{log}_2\eta +2\vartheta \mathrm{log}_2\vartheta +\nu \mathrm{log}_2\nu )-2S_\mathrm{bin}(({1+r}){\xi _t}/2)+1. \end{aligned}$$
(16)
Fig. 2
figure 2

(Color online) Dynamics of entropic uncertainty, lower bound, QD and the trace distance of the bipartite system versus timescale, \(\delta _0t\), when the initial state is prepared in a maximal entangled state with \(r=s=0\) and \((c_{1},c_{2},{{c_{3}}})= (1,-1,1).\) LHS: the entropic uncertainty expressed by Eq. (2); RHS: right-hand side of Equation (2); QD: the quantum discord of AB; \(\mathcal{D}(\rho _1(t),\rho _2(t))\): trace distance of the system independently interacting with a structured reservoir possessing Lorentz spectrum, \(J(\omega )\). In the strong-coupling regime, \(\delta _0/\Gamma =100\) is set for subgraphs (a) and (d), and \(\delta _0/\Gamma =10\) for subgraphs (b) and (e); In the weak-coupling regime, \(\delta _0/\Gamma =0.2\) is set for subgraphs (c) and (f)

Full size image

Now, let us examine the non-Markovian effect on the uncertainty in detail. When a maximally entangled state is taken as the initial state with \(r=s=0\) and \((c_1,c_2,{{c_3}})= (1,-1,1)\), we here draw the dynamical uncertainty with respect to the evolution time, t, for different ratios of the coupling strengths \(\delta _0/\Gamma \) in Fig. 2. Following Fig. 2, one can see that in the strong-coupling regime (with \(\delta _0/\Gamma >0.5\)), as shown in Fig. 2a, b, d, e, the initial variation in the uncertainty behaves periodically with time and diminishes to a fixed value. This can be interpreted as the characteristic non-Markovianity of the information will lead to information being able to not only outflowing but also backflowing as strong coupling induces the fluctuations in the trace distance of the qubit system. These fluctuations result in the characteristic resonance in the system’s evolution as well as the uncertainty.

In the weak-coupling regime (with \(\delta _0/\Gamma <0.5\)), shown in Fig. 2c, f, the uncertainty would first rise and then reduce with time, saturating into a fixed value in the limit of long time. In addition, let us impose an effective method to map system’s evolution, i.e., quantum correlation, which can be measured by so-called quantum discord (QD) [67,68,69]

$$\begin{aligned} \mathcal{Q}(\hat{\rho }_{AB})=\mathcal{I}(A:B)-\mathcal{C}(A:B). \end{aligned}$$
(17)

For a bipartite system AB, the total correlation \(\mathcal{I}(A:B)=S({\hat{\rho }}_{A})+S(\hat{\rho }_{B})-S(\hat{\rho }_{AB})\) and the classical correlation \(\mathcal{C}(A:B)=S({\hat{\rho }}_A)-\mathrm{min}_{\Pi _i^B}S({\hat{\rho }}_{AB}{|{\Pi _i^B}})\). Where \(\Pi _i^B\) is denoted by all possible POVM on qubit B, \(S({\hat{\rho }}_{AB}{|{\Pi _i^B}})=\sum _iq_iS({\hat{\rho }}_i^A)\) represents the conditional von Neumann entropy of A. The density operator is \({\hat{\rho }}_i^A=\mathrm{Tr}_B(\Pi _i^B{\hat{\rho }}_{AB}\Pi _{i}^B)/{q_i}\) with the probability \(q_i=\mathrm{Tr}_{AB}({\hat{\rho }}_{AB}\Pi _i^B)\). The quantum correlation (i.e., QD) and trace distance of the bipartite system monotonically reduce with the increasing time. With these results in mind, we can ascertain that the measurement uncertainty via entropy is not completely dependent upon the system’s quantum correlation, \(\mathcal{Q}(\hat{\rho }_{AB})\), which can been derived analytically to be:

$$\begin{aligned} {Q}(\hat{\rho }_{AB})={S_\mathrm{bin}}({{\rho } _{22}} + {{\rho } _{44}}) + \sum \nolimits _{i = 1}^4 {\lambda _i} {\log _2}\lambda _i + \mathrm{min}\{\mathcal{F}_1, \mathcal{F}_2\}, \end{aligned}$$
(18)

for an arbitrary state of X-structure density matrix \({\hat{\rho } _{AB}}\), with

$$\begin{aligned} {\mathcal{F}_1}&= {S_\mathrm{bin}}(\Delta ), \end{aligned}$$
(19)
$$\begin{aligned} {\mathcal{F}_2}&= - \sum \nolimits _i {{{\rho } _{ii}}} {\log _2}{{\rho } _{ii}} - {S_\mathrm{bin}}({{\rho } _{11}} + {{\rho } _{33}}), \end{aligned}$$
(20)

where \(\Delta = \frac{1}{2} {{\left\{ {1 + \sqrt{{{\left[ {1 - 2( {\rho _{33}}+{\rho _{44}})} \right] }^2} + 4{{\left( {\left| {{\rho _{14}}} \right| + \left| {{\rho _{23}}} \right| } \right) }^2}} } \right\} }}\), \({{\rho } _{ij}}\) stands for the elements of the \({\hat{\rho } _{AB}}\)’s density matrix and \({\lambda _i}\) denotes the four eigenstates of \({\hat{\rho } _{AB}}\).

Fig. 3
figure 3

(Color online) Non-Markovianity (of the composite system independently interacting with a bosonic structured reservoir possessing a Lorentz spectral distribution) as a function of \(\delta _0/\Gamma \). Note that the line is broken at \(\delta _0/\Gamma =0.5\), which is a singular point

Full size image

To clearly display the evolution of an atomic system interacting with reservoirs with memory, we may utilize an optimal pair of quantum states \(\hat{\rho }_1(0)=|++\rangle \langle ++|\) and \(\hat{\rho }_2(0)=|--\rangle \langle --|\) as two initial states with \(|\pm \rangle =\frac{1}{\sqrt{2}}(|e\rangle \pm |g\rangle )\), as having been verified in previous works [70]. After some algebra, the trace distance of the any bipartite system can be derived as

$$\begin{aligned} \mathcal{D}(\hat{\rho }_1(t),\hat{\rho }_2(t))=\sqrt{{\xi _t}(2-2{\xi _t}+{\xi _t}^2)}. \end{aligned}$$
(21)

To be explicit, \(\mathcal{D}(\hat{\rho }_1(t),\hat{\rho }_2(t))\) versus \(\delta _0t\) has been provided in Fig. 2(e-f) for different coupling regimes. Obviously, in the strong-coupling regime, \(\mathcal{D}(\hat{\rho }_1(t),\hat{\rho }_2(t))\) shows a resonant properties, implying information exchange between the system to be measured and the environment is bidirectional rather than mono-directional (non-Markovian). Moreover, it is directly shown that the larger value of \(\delta _0/\Gamma \) (non-Markovianity) induces period-increasing resonance of the uncertainty. By contrast, \(\mathcal{D}(\hat{\rho }_1(t),\hat{\rho }_2(t))\) is monotonically reduced which leads to a one-way information flow from system to environment (Markovian). For the sake of quantifying the non-Markovianity of the observed system, we draw \(\mathcal N\) with respect to \(\delta _0/\Gamma \) in Fig. 3. From the figure, it shows that for the weak-coupling regime with \(0\le \delta _0/\Gamma <0.5\), \(\mathcal N\) is equal to zero; this displays that the trace distance never increases during the evolution of the system and consequently the evolution of the system is Markovian. With respect to the strong-coupling regime with \(\delta _0/\Gamma >0.5\), the evolution implies that \(\mathcal{D}\) is characterized by the resonant variation in the course of the evolution and thereby the evolution is non-Markovian. Additionally, a larger \(\mathcal N\) can induce a larger-amplitude and longer-period oscillations in the uncertainty, as shown in Fig. 2.

Let us proceed by investigating the lower bound given by relation (2). For any two Pauli observables, the complementarity c will be 1/2 always. Moreover, the eigenvalues of the generic state in (13) are derived as

$$\begin{aligned} \Lambda _{\pm }&=\frac{{\xi _t}}{4}(\phi \pm \sqrt{\psi }), \end{aligned}$$
(22)
$$\begin{aligned} \Xi _{\pm }&=(\varphi \pm \sqrt{\chi })/4, \end{aligned}$$
(23)

where \(\phi ={2-{{\xi _t}}-{{c_3}}}+(s+r)(1-{\xi _t})\), \(\psi ={{(c_1+c_2})^2+(r-s)^2}\), \(\varphi =2 - 2 {{\xi _t}} + {{\xi _t}}^2 +{{c_3}}{{\xi _t}}^2-{\xi _t}(1-{\xi _t})(r+s)\) and \(\chi =4(1-{{\xi _t}})^2+({c_1}-{c_2})^2{{\xi _t}}^2-4 {\xi _t} r + 4 {\xi _t}^2 r + {\xi _t}^2 r^2 - 4 {\xi _t} s + 4 p^2 s + 2 {\xi _t}^2 r s + {\xi _t}^2 s^2\). Thus, one can get the RHS of the uncertainty relation which is analytically expressed as

$$\begin{aligned} {U}_b=1-\sum \limits _{\upsilon , \epsilon =\pm }\left( \Lambda _{\upsilon }\mathrm{log}_2\Lambda _{\upsilon }+\Xi _{\epsilon }\mathrm{log}_2\Xi _{\epsilon }\right) -S_\mathrm{bin}(({1+r}){\xi _t}/2). \end{aligned}$$
(24)

As plotted in Fig. 2, \(\mathrm{LHS}=\mathrm{RHS}\) holds and the uncertainty will be minimal at \(t=0\), implying Bob is capable of precisely capturing Alice’s measurement outcome in this limitation. While \(\mathrm{LHS}>\mathrm{RHS}\) is satisfied and the uncertainty will increase \(\forall \) t, \(t>0\), which weakens Bob’s ability to predict the measurement outcome to some degree. It is deserving of noting that the uncertainty and the bound will saturate toward a fixed nonzero value in the limitation of \(t\rightarrow \infty \).

Remarkably, we argue that the uncertainty is capable of being well applied as an entanglement witness. As we know, one of the criteria for witnessing entanglement is the condition \(S(A|B)<0\) is held; notably, this is a sufficient but not necessary condition for entanglement witness. In this regard, we can infer that A and B are entangled affirmatively when \({U}_b\le 1\) within this model. In this sense, the lower bound can be effectively applied as an entanglement witness. If \({U}_b\le 1\) is satisfied, we can conclude that bipartite entanglement is emerging.

Fig. 4
figure 4

(Color online) Uncertainty with respect to \(\Gamma /\delta _0\) for different values of \(\delta _0t\) when the initial state is chosen to \(r=s=0\) and \((c_1,c_2,{c_3})=(1,-1,1)\). In graph (a), \(\delta _0t=1\); in graph (b), \(\delta _0t=10\). For the two graphs, \(\Gamma /\delta _0=2\) is the critical point (singular point) in both Markovian and non-Markovian regimes

Full size image

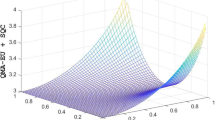
Now we continue to examine the effect of the different ratio \(\Gamma /\delta _0\) on the measurement uncertainty. It has been shown that the uncertainty as a function of \(\Gamma /\delta _0\) is drawn in Fig. 4 for different \(\delta _0t\). For a fixed value of \(\delta _0t\), the QD monotonically decreases with the growth of \(\Gamma /\delta _0\). The uncertainty will experience diverse dynamical performance with different \(\delta _0t\). The uncertainty will increase with the increasing ratio \(\Gamma /\delta _0\) for small \(\delta _0t\); otherwise, the uncertainty will initially increase and then decrease with increasing \(\Gamma /\delta _0\) in the case of relatively large \(\delta _0t\), as shown in Fig. 4. We note that when t is fixed, a small value of reservoir correlation time, \(\tau _\mathrm{r}\), can induce the larger amount of the measurement uncertainty of interest, and vice versa. This is not surprising as a smaller \(\tau _\mathrm{r}\) can induce Markovianity in the observed system, resulting in faster one-way information outflow into the environment.

4 Physical interpretations on the dynamical properties of the uncertainty

Empirically, the dynamical evolution of the uncertainty stems from the quantum correlation of the system to be observed. However, as stated before, we obtain an interesting result that the lower bound of the uncertainty is not completely determined by the degree of quantum correlation of the composite system. To explicitly explain this, let us render a reliable proof to our statements and reveal the quantum nature of the phenomenon with respect to the dynamics of the uncertainty.

4.1 The origin of the lower bound

To explain the dynamical behavior of the uncertainty within the current scenario, we combine Eqs. (2) and (17); one can easily obtain a relation between the QD and the lower bound

$$\begin{aligned} {U_b}=\mathcal{S}_\mathrm{ce}-\mathcal{Q}({\rho }_{AB})+\mathrm{log}_2\frac{1}{c}, \end{aligned}$$
(25)

with \(\mathcal{S}_\mathrm{ce}\equiv \mathrm{min}_{\Pi _i^B}[S({\hat{\rho }}_{AB}|{{\Pi _i^B}})]\). We can differentiate both sides of the above equation with respect to time, t, and obtain

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}t}{U_b}\equiv \frac{\mathrm{d}}{\mathrm{d}t}{\mathcal{S}_\mathrm{ce}}-\frac{\mathrm{d}}{\mathrm{d}t}\mathcal{Q}({\rho }_{AB}), \end{aligned}$$
(26)

due to \(\mathrm{log}_2\frac{1}{c}\) being a constant, which straightforwardly indicates that the lower bound is inherently anti-correlated with the quantum discord \(\mathcal{Q}({\rho }_{AB})\) and meanwhile correlated with the conditional von Neumann entropy \(\mathcal{S}_\mathrm{ce}\) of A to be observed. As a result, we can infer that the rate of change of \({U_b}\) is not only determined by the variation in QD, but also by the variation in the entropy \(\mathcal{S}_\mathrm{ce}\). With these in mind, we can conclude that \(\mathcal{Q}({\rho }_{AB})\) and \(\mathcal{S}_\mathrm{ce}\) act as competing factors in determining the magnitude of the bound. Therefore, we argue that the uncertainty should be not entirely synchronous with quantum correlation of the observed system.

Fig. 5
figure 5

(Color online) Dynamics of the uncertainty bound, the mutual information and the entropy of A under Markovian and non-Markovian regimes. Graph a: \(\Gamma /\delta _0=5\) and graph b \(\Gamma /\delta _0=0.01\) when the initial state is prepared in \(r=s=0\) and \((c_1,c_2,{c_3})=(1,-1,1)\). The blue line represents the bound \(U_b\), the red line represents the mutual information \(\mathcal{I}(A:B)\), and the magenta line represents the entropy of the subsystem A

Full size image

Another explanation can be given according to mutual information. The bound can be expressed as \(U_b=S(\hat{\rho }_A)-\mathcal{I}(A:B)+\mathrm{log}_2\frac{1}{c}\), which can lead to a differential equation

$$\begin{aligned} \frac{d}{dt}{U_b}\equiv \frac{d}{dt}{{S}({\hat{\rho }_A}})-\frac{d}{dt}\mathcal{I}(A:B). \end{aligned}$$
(27)

From the above equation, one can infer that the variation rate of \(U_b\) is correlated with von Neumann entropy \({{S}({\hat{\rho }_A}})\) of A to be measured, while anti-correlated with the mutual information \(\mathcal{I}(A:B)\). For clearness, we draw the dynamics of uncertainty bound, the mutual information, and the entropy of the subsystem A in Fig. 5. As to the maximally entangled initial state employed, in the weak-coupling (Markovian) regimes, the mutual information will decrease from the maximum 2 and saturate into the minimum 0 as the evolution time goes, while the entropy of A will decrease from the maximum 1 and saturate into the minimum 0, as shown in Fig. 5a. This reflects that the A and B will become disentangled in a long time limit under such Markovian regimes. And the measurement uncertainty will increase and saturate into a fixed value. On the other hand, in the strong-coupling (non-Markovian) regimes, the mutual information will firstly decrease from the maximum 2 and then vibrate up to the minimum 0 as the time goes, and the entropy of A exhibits the same variation trend as \(\mathcal{I}(A:B)\), which shows the dynamic of the mutual information is synchronous with that of A’s entropy as displayed in Fig. 5b. And the measurement uncertainty will increase and then vibrate up to a fixed value. Specially, there exists another case which is that how the uncertainty will evolve if the A is isolated and free from any noises. To answer this question, we can resort to Eq. (27) and \(\frac{\mathrm{d}}{\mathrm{d}t}{{S}({\hat{\rho }_A}})=0\). Based on this equation, one can easily get that the mutual information of the system is responsible for the dynamic of the lower bound, and explicitly the lower bound is completely anti-correlated with the mutual information in the situation of qubit A being isolated from any noises.

4.2 The relation between the measurement uncertainty and Bell non-locality

In this subsection, let us examine the relation between the entropic uncertainty and the quantum non-locality. It has been found the entropic uncertainty is oppositely associated with the quantum non-locality of the system. Firstly, let us briefly review the Bell-CHSH inequality [71, 72], which can be canonically written as

$$\begin{aligned} \mathcal{B}_\mathrm{CHSH}={\varvec{a}}\cdot {\varvec{\sigma }}\otimes ({\varvec{b}}+{\varvec{b}^{\prime }})\cdot {\varvec{\sigma }}+{\varvec{a}^{\prime }}\cdot {\varvec{\sigma }}\otimes ({\varvec{b}}-{\varvec{b}^{\prime }})\cdot {\varvec{\sigma }}, \end{aligned}$$
(28)

with the unit vectors \({\varvec{a}}\), \({\varvec{a}^{\prime }}\), \({\varvec{b}}\), \({\varvec{b}^{\prime }}\) in the three dimensions, and \({\varvec{\sigma }}=(\sigma _x,\sigma _y,\sigma _z)\) being the standard Pauli matrices. For a bipartite system with the density matrix \(\hat{\rho }\), its CHSH inequality can be expressed as

$$\begin{aligned} \mathcal{B}=|\langle \mathcal{B}_\mathrm{CHSH}\rangle |=|\mathrm{Tr}(\hat{\rho }\mathcal{B}_\mathrm{CHSH})|\le 2. \end{aligned}$$
(29)

Derived from the results in Ref. [73,74,75], the maximal quantum CHSH inequality of an arbitrary two-qubit X-structure state can be simplified as \(\mathcal{B}=2\sqrt{\mathrm{max}_{i<j}(\Lambda _{i}^2+\Lambda _j^2)}\) with \(i,j=1,2,3\), where

$$\begin{aligned} \Lambda _1=2(|\rho _{14}+\rho _{23}|), \ \ \Lambda _2=2(|\rho _{14}-\rho _{23}|),\ \ \Lambda _3=\rho _{11}-\rho _{22}-\rho _{33}+\rho _{44}. \end{aligned}$$
(30)

The lower bound of the measurement uncertainty and the Bell non-locality versus the time t are drawn in Fig. 6. In Markovian regimes, it is shown that the lower bound firstly increases from a small value and then decreases into a fixed value, with the growing time. In shape comparison with former, the Bell non-locality has the opposite evolutionary trend, as shown in Fig. 6a. Notably, the Bell non-locality exists the maximal violation \(\mathcal{B}=2\sqrt{2}>2\). With respect to non-Markovian regimes, the dynamic of the Bell non-locality shows a resonant character and is frozen to a value less than 2 with the growing time, and we can see that the dynamic of the lower bound is fully anti-correlated with that of \(\mathcal{B}\). By the above analysis, we thus argue that the lower bound is essentially anti-correlated with the Bell non-locality of the system to be probed. Incidentally, there exist the similar freezing behaviors for quantum discord and coherence in the current scenario [76, 77]. For simplicity, we here do not illustrate them in detail.

Fig. 6
figure 6

(Color online) The uncertainty and the non-locality \(\mathcal B\) of the system as a function of t in units of \(\delta _0\) with the different coupling ratio \(\Gamma /\delta _0\) when the initial state is prepared in \(r=s=0\) and \((c_1,c_2,{c_3})=(1,-1,1)\). In graph (a), the blue lines: \(\Gamma /\delta _0=10\), and the red lines: \(\Gamma /\delta _0=1\); in graph (b), \(\delta _0t=10\)

Full size image

5 Conclusions and remarks

Herein we have examined the dynamics of the measurement uncertainty for bipartite separately coupled with two structured bosonic reservoirs. Explicitly, we study the non-Markovian effects on the entropic uncertainty for measuring two incompatible observables. It has been verified that stronger non-Markovianity can lead to both larger-amplitude and longer-period oscillations in the dynamics of QMA-EUR, resulting from a slower pace variation in the trace distant \(\mathcal{D}\). This may be understood as the information undergoing bidirectional flow between the qubits and the multi-degree-of-freedom reservoirs in the long time limit. While, in the Markovian regime (with \(\delta _0/\Gamma <0.5\)), the uncertainty will first increase and then gradually decrease to a fixed value with increasing time accompanied by a monotonic decrease in \(\mathcal{D}\) and in \(\mathcal{Q}(\hat{\rho }_{AB})\). Notably, we deduce that the dynamical behavior of the lower bound is not fully determined by quantum correlation of the system, but by the conditional entropy \(\mathcal{S}_\mathrm{ce}\); this implies there exists a competition between \(\mathcal{Q}(\hat{\rho }_{AB})\) and \(\mathcal{S}_\mathrm{ce}\) determining the magnitude of \(U_b\). Moreover, the uncertainty bound has been proved which is alternatively affected by both the mutual information \(\mathcal{I}(A:B)\) of the system and the entropy of the reduced subsystem A to be measured. At last, we reveal the entropic uncertainty of interest is possibly oppositely correlated with the Bell non-locality \(\mathcal B\) of the system. Thus, we believe that our explorations may provide some insight into the dynamical characteristic of the measurement uncertainty via entropy in non-Markovian regimes and shed light on quantum multi-component incompatible measurements in realistic environments.