1 Introduction

In the process of scaling feature size of complementary metal oxide semiconductor (CMOS) devices, several fatal flaws, i.e. short-channel effects and leakage power dissipation, compel researchers to investigate alternative technologies for complementing conventional CMOS-based integrated circuits technique [1, 2]. The probable technologies, i.e. carbon nanotube (CNT), single electron transistor (SET) and quantum-dot cellular automata (QCA), have been put forward to seek out a promising one [3,4,5]. Among them, QCA provide a hopeful computing paradigm and information transmission pattern in the nanoscale regime [6]. The ultra-high integration, extremely low power consumption and high processing speed make QCA more promising in applications [6]. To achieve the steady operation of a system at ambient working temperature, nanomagnetic logic and molecular QCA may be hopeful in physical implementations [7, 8]. Recently, silicon atom dangling bonds were successfully realized to implement logic gates on a H-Si (100)-2 × 1 surface [9,10,11].

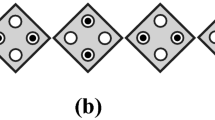
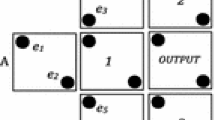
The binary information in QCA is represented by the positions of electrons confined in a cell as shown in Fig. 1a, either binary 1 or binary 0. The data transmission between cells is purely performed by the Coulomb interaction, thus it just avoids the leakage current occurred in conventional circuits [5]. The typical semiconductor-based cell model is defined as 18 nm width and height, 2 nm spacing between two nearest cells in QCADesigner [12]. As illustrated in Fig. 1b, the three-input majority voter (M3) is a basic logic component in QCA. The logic function for a M3 with inputs A, B, and C is F = M3(A, B, C) = AB + AC + BC, which tends to produce the majority of three inputs to get a lowest electrostatic energy level. The NAND-NOR-Inverter (NNI) is a composite logic gate, which needs a set of gates to realize its function. Its layout in QCA technique is very simple as shown in Fig. 1c. The logic function is expressed as \( F= NNI\left(A,\overline{B},\overline{C}\right)=A\overline{B}+A\overline{C}+\overline{B}\overline{C} \), where input signals B and C are inverted to output. Another frequently used voter is a five-input majority voter (M5), as shown in Fig. 1d, whose logic function is F = M5(A, B, C, D, E) = ABC + ABD+ ABE + ACD + ACE + ADE + BCD + BCE + BDE + CDE [13]. A M5 can further reduce the complexity of complex QCA circuits by properly replacing M3 s. In addition, if two cells are diagonally placed to each other, they will take opposite polarizations because of the Coulomb interaction between them. With this diagonal configuration, an inverter for realizing NOT operation is then realized in QCA.

Fig. 1
figure 1

QCA basics (a) QCA cells (b) three-input majority voter (c) five-input majority voter

Full size image

To control the direction of signals propagating between cells and ensure a circuit to remain in instantaneous ground state, the quasi-adiabatic switching mechanism was introduced and it results in four clock zones [5]. Each zone is composed of four phases: switch, hold, release, and relax, as shown in Fig. 2. Taking the clock0 as an example, the inter-dot barrier will gradually increase during the switch phase from t = 0 to t = π/2 and then peaks in the hold phase. During the hold phase, the cells in clock1 are polarized by cells in clock0. After the hold phase, the tunnel barrier continually decreases in the release phase in clock0, while the cells in clock1 keep polarized. When the inter-dot barrier reaches the minimum value, the cells completely lose their polarizations and do not have any influence on neighboring cells while getting ready for the next cycle at t = 2π. Data will be propagated from the hold phase in clock0 to the next one in clock1, then to clock2 and finally to clock3 as the arrow lines denoted. To distinguish the cells in each clock zone, four colors (green, purple, teal and white) are used to indicate them as in the right side in Fig. 2. These cells in various colors will be sequentially polarized. One clock period in a QCA circuit is a clock cycle from clock0, clock1, clock2 to clock3.

Fig. 2
figure 2

QCA four-phase clock mechanism

Full size image

With the majority voters, inverters and four-phase clock, one can implement any complex circuit in QCA. Several simple Boolean logic functions were also realized by using the intercellular Coulomb interaction [14, 15]. Although this method can get an efficient circuit in terms of area and delay, it is immature and time consuming; the cells in the circuit cannot be fully saturated and thus are unstable [16]. The approach to map AND and OR gates to majority voters is straightforward, thus it is costly and inefficient. Logic synthesis methodologies using the M3 s and inverters were put forward to design QCA circuits with less logic gates so that logic gate-based design method is the mainstream in QCA at present [17,18,19,20,21,22]. Meanwhile, basic logic arithmetic and memory circuits were realized as well [23,24,25,26]. Further, the XOR occupies an important position in digital logic circuits and communications, which has been deeply studied in existing works [27,28,29,30,31,32,33,34,35]. An important thing in circuit design is to handle the complex crossovers. Researchers tried to minimize the number of wire crossings for simplifying QCA circuits [36,37,38]. Several above XORs include a crossover, while others exclude it. These XOR schemes will be comprehensively analyzed in Section 2 Related work to show their merits and limitations.

In this paper, to get an efficient XOR with respect to reliability, cell count, circuit area, latency, QCA cost and dissipated energy, we propose a coplanar scheme using NAND-NOR-Inverter (NNI) and five-input majority voter (M5). The main contributions of this paper are as follows:

  1. 1)

    We analyze existing gate-based XORs and parity generators to show their advantages and limitations in detail.

  2. 2)

    We then propose a coplanar XOR consisting of NNI and M5 to get an efficient layout for the first time.

  3. 3)

    The multi-bit parity generators are proposed by using the proposed XOR to show its merits.

  4. 4)

    We perform a detailed analysis regarding validity, reliability, performances, power dissipation, complexity and QCA cost for the proposed circuits.

The rest of this paper is organized as follows: Section 2 describes the existing XORs and parity generators to show their limitations and advantages. Section 3 proposes a coplanar XOR and the proposed multi-bit parity generators. Section 4 shows the analysis results for the proposed circuits. Finally, Section 5 concludes this paper.

2 Related Work

Due to the critical role of an XOR in logic circuit design, it has attracted much attention in QCA. The existing gate-based XORs in [27,28,29,30,31,32,33,34,35] are classified as five categories as listed in Table 1. The third column gives the gate-based logic expression for each type of XORs. The fourth column shows the schematic for each XOR according to its corresponding gate-based logic expression. We utilize four items to evaluate their advantages and limitations in fifth and sixth columns respectively as follows:

  1. 1)

    Gate count: the total number of M3 s, M5 s, NNIs and inverters in a circuit. The complexity of a circuit increases with an increasing number of gates.

  2. 2)

    Clock delay: the number of clock cycles in a circuit. The processing speed increases for a QCA system with less clock delay.

  3. 3)

    Structure: either coplanar layout or multilayer layout with crossovers. The QCA cost increases for a QCA system with multilayer crossovers.

  4. 4)

    I/O accessibility: the accessibility to input and output pins. The cascade is readily to be achieved for circuits with I/O accessibility.

Table 1 Existing gate-based XORs
Full size table

As listed in Table 1, a coplanar layout in Ref. [27] gets rid of unstable crossovers to realize the I/O accessibility, while it is costly due to the 5 logic gates and 1 clock cycle. The XORs designed by using this scheme in QCA have a high complexity and low processing speed. The XOR scheme in Refs. [28, 29] introduces a crossover and consists of 5 operational gates. The QCA cost dramatically increases, leading to an inefficient XOR implementation in QCA. In Ref. [30], a M5 is employed to perform a coplanar XOR, which clearly demonstrates that the M5 can effectively reduce the complexity of an XOR. This scheme also has 4 logic gates. Another deformation scheme in Refs. [31,32,33,34] was proposed to simplify the XOR by reducing one inverter. Further, a coplanar XOR using 4 NNI gates was achieved in Ref. [35], while it consumes 4 logic gates and 1 clock cycle. With above analyses, we can conclude that the XOR scheme in [31,32,33,34] should be the best one among them, by means of the aforementioned criteria.

Accordingly, various gate-based XORs were implemented in QCA by using aforementioned schemes, as shown in Fig. 3. The design in Ref. [27] utilizes four M3 s to implement a coplanar XOR. This gate consumes 1.5 clock cycles for completing computation. The designs in Refs. [28, 29] realize a coplanar XOR by employing coplanar crossovers with rotated cells or placing input cells inside a circuit, respectively. The implementation in Ref. [29] is difficult to cascade XORs for constructing complex systems. With a M3, M5 and two inverters, a coplanar XOR is realized in small area and clock delay. The schemes in Fig. 3e, f, g and h are based on one M3, M5 and inverter. The design in Ref. [31] has a clock-based coplanar crossover, occupies 1.25 clock cycles and large area. By embedding the inverter to either the M3 or M5, one can get efficient XORs in Refs. [32,33,34]. These implementations not only get small area and complexity, but also make the information processing speed fast. In addition, two designs in Refs. [33, 34] in QCA are almost the same except the positions of output cells. The last design in Ref. [35] consists of four NNI gates, whose delay is 1.0 clock cycle. The performance figures for these XORs will be quantified in Section 4 Simulation results to compare with the proposed XOR.

Fig. 3
figure 3

Existing gate-based XORs (a) in [27] (b) in [28] (c) in [29] (d) in [30] (e) in [31] (f) in [32] (g) in [33] (h) in [34] (i) in [35]

Full size image

In digital communications, parity bits are utilized to detect errors in coded messages. The basic element of a parity generator is an XOR, thus multi-bit parity generators are usually illustrated to verify the performances of designed XORs. The generators can be implemented by hierarchically connecting XORs. Fig. 4 shows the 4-bit parity generators in Refs. [30,31,32,33,34,35]. Except the design using two XORs in Ref. [31], others are regularly composed of three XORs. The design in Ref. [31] also uses the clock-based crossovers to get full I/O accessibility to connect XORs; other schemes are implemented without crossovers due to the I/O accessibility of the utilized XORs. Moreover, we can see that the least clock delay for 4-bit parity generators is 1.25 clock cycles. Again, the performance figures for these generators will be shown in Section 4 Simulation results.

Fig. 4
figure 4

Existing parity generators (a) in [30] (b) in [31] (c) in [32] (d) in [33] (e) in [34] (f) in [35]

Full size image

3 Proposed XOR and Parity Generators

3.1 XOR

As mentioned above, the main method for circuit design in QCA at present is connecting logic components to implement complex systems. A NNI and M5 are used to design an efficient coplanar XOR as shown in Fig. 5a, where A and B are input ports; F is output. The logic function of a NNI is \( NNI\left(A,B,C\right)=\overline{A}\overline{B}+\overline{A}C+\overline{B}C \), which implicitly realizes the NOT operation in ports A and B. By fixing the value of input C in binary 1, we have \( NNI\left(A,B,1\right)=\overline{A}+\overline{B} \), which is usually realized by a majority voter and an inverter. Thus, one NNI gate fulfils the NAND operation of inputs A and B. The logic expression for the proposed XOR is \( F=M5\left(A,B, NNI\left(A,B,1\right), NNI\left(A,B,1\right),0\right)=\overline{A}B+A\overline{B} \). The implementation for the proposed XOR in QCA is shown in Fig. 5b. In this circuit, each clock zone has at least two cells to keep all cells fully polarized. The proposed coplanar XOR has 27 cells, occupies 0.0196 μm2 and 0.75 clock cycles. Note that the area of a circuit in QCA technique is computed by using the area of a smallest rectangle the circuit occupied in this paper. The truth table of the XOR verifies its correctness as shown in Table 2. It is worth pointing out that input and output cells of the proposed XOR are not surrounded by other cells so that the I/O accessibility is realized and one can readily design complex systems by cascading the proposed XORs.

Fig. 5
figure 5

The proposed coplanar XOR (a) schematic (b) implementation in QCA

Full size image
Table 2 Truth table of the proposed coplanar XOR
Full size table

3.2 Parity Generators

As aforementioned, the multi-bit parity generators can be constructed by hierarchically connecting XORs. Fig. 6a demonstrates the design method for a 4-bit parity generator that consists of three XORs. Due to the full I/O accessibility of the proposed XOR, it is able to connect any number of XORs in this means. Fig. 6b shows the implementation in QCA for a 4-bit parity generator, which has only 84 cells, consumes 1.25 clock cycles and occupies 0.0840 μm2. Table 3 lists the truth table for the proposed generator, which indicates the input vectors and corresponding output signals. The generator generates 0 for even number of 1 s in inputs and produces 1 for odd number of 1 s. It is clear that the generator can complete its intended functions. To show the expansibility of the circuit design approach, we also design 8-bit, 16-bit and 32-bit parity generators. The 32-bit parity generator is realized by serially connecting 31 XORs, as shown in Fig. 7. As illustrated in these figures, the presented designs provide regular structures, full I/O accessibility, perfect expansibility, and efficient area and clock delay.

Fig. 6
figure 6

The proposed 4-bit parity generator using the proposed XOR (a) schematic (b) implementation in QCA

Full size image
Table 3 Truth table of the proposed 4-bit parity generator
Full size table
Fig. 7
figure 7

The proposed 32-bit parity generator using the proposed XOR

Full size image

4 Simulation Results

4.1 Coplanar XORs

First, we consider the reliability of the proposed coplanar XOR scheme and its counterparts in Table 1, by using probabilistic transfer matrix that provides a method for computing the reliability of a combinational circuit [39]. Fig. 8 shows the calculation results, where the device probability of failure means the probability of each component to be faulty; the XOR probability of failure denotes the possibility of generating error outputs. It is clear that the proposed XOR has smallest probability of failure so that the XOR has highest stability among these schemes. Specifically, the designs consisting of the M3 gates in Refs. [27,28,29] get larger probability of failure than others as increasing the device probability of failure. The NNI-based XOR in Ref. [35] has almost the same stability as the schemes composed of the M3 and M5 in Refs. [30,31,32,33,34].

Fig. 8
figure 8

XOR probability of failure versus device probability of failure

Full size image

For validating our method to design XOR using NNI and M5, Tables 4 and 5 list the performance figures and power dissipation for M3 and NNI gates, respectively. The dissipated power is simulated by using QCAPro [40], where average energy dissipation is the sum of average leakage energy dissipation and average switching energy dissipation. It is clear that although the physical features of them are similar, the dissipated power of the NNI gate is much less than that of the M3 gate, at various tunneling energy and at 2 K operating temperature.

The bistable approximation simulation engine in QCADesigner 2.0.3 is used to verify the functions of the proposed circuits [12]. The simulation parameters are listed in Table 6. Due to the Coulomb interaction between two cells dramatically decays with the increasing distance between them, 41 nm for the radius of effect is usually sufficient for a simulation. Other parameters are set as default in the software. Fig. 9 is the simulation results for the proposed XOR. The first pair of input/output values is labelled, which directly verifies the correctness of this gate. In addition, we can see that the output signals of this gate are delayed by 0.75 clock cycles; each signal can achieve a stable waveform.

Table 4 Performance figures of M3 and NNI gates
Full size table
Fig. 9
figure 9

Simulation results for the proposed XOR

Full size image
Table 5 Upper bound of power dissipation for M3 and NNI at 2.0 K
Full size table
Table 6 Bistable approximation simulation engine parameters
Full size table
Table 7 Performance figures of XORs
Full size table
Table 8 Upper bound of power dissipation for XORs at 2.0 K
Full size table
Table 9 Performance figures of parity generators
Full size table
Table 10 Upper bound of power dissipation for 4-bit parity generators at 2.0 K
Full size table

We then begin to qualify the proposed XOR in QCA and its counterparts. Table 7 lists their performance figures. The new XOR has the least cell count as the design in Ref. [34] and least clock delay as the designs in Refs. [30, 32, 34]. In addition, the occupied area of the proposed XOR is reduced by 9.26% compared with the state-of-the-art design in Ref. [30]. Moreover, the new XOR not only gets rid of complex crossovers but also has full I/O accessibility.

Table 8 gives the upper bound of dissipated energy for these XORs. Although the designs in Refs. [30, 34] slightly outperform the proposed XOR at low tunneling energy in terms of average energy dissipation, the performance of our circuit will surpass them with the increasing tunneling energy. Moreover, the new XOR is superior to others in respect to power dissipation. Figure 10 shows the power dissipation map for the proposed XOR gate at 0.5Ek tunneling energy level and 2.0 K temperature, which shows the cell that dissipates more energy than others because the darker the cell is, the more energy it dissipates.

Fig. 10
figure 10

Power dissipation map for the proposed XOR gate at 0.5Ek tunneling energy level and 2.0 K temperature

Full size image

Further, the complexity of a system is expressed as

$$ \mathrm{C} omplexity=M+I+C $$
(1)

where M, I and C are the number of M3 s, inverters, crossovers [41]. It is used to calculate the number of operational gates in a system. In this paper, we extend this equation by taking account of the NNI and M5 gates because they also realize simple logical operations like a M3. This metric does not account for the information processing speed of a system, so that QCA cost was introduced by including clock delay. The QCA cost function is also employed to evaluate these circuits, which is represented as

$$ Cost=\left({M}^x+I+{C}^y\right)\times {L}^z $$
(2)

where M, I, C and L are the number of M3 s, inverters, crossovers, and clock delay of a circuit; x, y, and z are the exponential weightings for these parameters, respectively [41]. In this paper, we assume x = y = z = 1, thus QCA cost is equal to the product of complexity and clock delay. Figures 11 and 12 illustrate the complexity and QCA cost for the proposed XOR and aforementioned existing XORs, resepctively. It is clear that the proposed one has the least complexity and cost among all circuits. For example, the complexity and QCA cost of proposed XOR is reduced by 33.33% and 33.33% compared with the best one in Ref. [34], respectively. With above analyses, one can briefly conclude that the proposed XOR is more efficient than previous designs with respect to cell count, area, clock delay, power dissipation, complexity and QCA cost.

Fig. 11
figure 11

Complexity for XORs

Full size image
Fig. 12
figure 12

QCA Cost = (M + I + C) × L for XORs

Full size image

4.2 Parity Generators

Figure 13 provides the simulation results for the proposed 4-bit parity generator. Again, the generator generates 0 for even number of 1 s and produces 1 for odd number of 1 s. These results authenticate the validity of this circuit. The first pair of input and output signals is marked by dotted lines. This result also shows that the proposed 4-bit parity generator consumes 1.25 clock cycles to complete signal transmission. Additionally, each output signal can achieve a stable waveform in this figure.

Fig. 13
figure 13

Simulation results for the proposed 4-bit parity generator

Full size image

Table 9 lists the comparisons for the proposed multi-bit parity generators and their counterparts. Although the number of cells of designs in Ref. [34] is slightly less than that of our circuits for 16-bit and 32-bit generators, the proposed generators are superior to others with respect to cell count. Most importantly, the new parity generators save large occupied area compared with all counterparts. For example, the areas of the proposed 4-bit and 32-bit generators is reduced by 12.50% and 39.47% compared with the state-of-the-art designs in Ref. [34]. Moreover, the proposed circuits hold a minimum clock delay. In addition, the designs in Ref. [31] employ the clock-based crossovers to realize coplanar structures, while other circuits exclude the crossovers. Again, the new coplanar parity generators have full I/O accessibility because of the I/O accessibility of the proposed XOR.

Table 10 shows the power dissipation for the 4-bit parity generators at different tunneling energy, at 2.0 K temperature. We can see that the parity generator in Ref. [30] has a slightly smaller power consumption than our proposed scheme at 0.5Ek for average energy dissipation. With the increasing tunneling energy, the proposed circuit will be superior to the design. For example, the average energy dissipation of the proposed 4-bit generator is reduced by 1.36% at 1.5Ek compared with the scheme in Ref. [30]. Further, the proposed design outperforms others in terms of the average energy dissipation at various tunneling energy. Figure 14 shows the power dissipation map for the proposed 4-bit parity generator at 0.5Ek tunneling energy level and 2.0 K temperature.

Fig. 14
figure 14

Power dissipation map for the proposed 4-bit parity generator at 0.5Ek tunneling energy level and 2.0 K temperature

Full size image

Figures 15 and 16 display the complexity and QCA cost for the proposed and existing multi-bit parity generators in Refs. [30,31,32,33,34,35], respectively. It is clear that the proposed parity generators rank first among them regarding the complexity and cost. Specifically, as for the 32-bit generators, the complexity of the proposed generators is reduced by 71.05%, 37.32%, 61.40%, 63.33%, 33.33%, and 72.50%; the cost of the generators is reduced by 50.00%, 3.13%, 33.33%, 33.33%, 33.33%, and 50.00% compared with these counterparts, respectively.

Fig. 15
figure 15

Complexity for parity generators

Full size image
Fig. 16
figure 16

QCA Cost = (M + I + C) × L for parity generators

Full size image

5 Conclusion

To solve the deficiencies of conventional integrated circuits, quantum-dot cellular automata (QCA) provide a prospective design paradigm. The XOR occupies an important position in digital logic circuits and communctions. To get an efficient XOR gate, this paper proposes a coplanar scheme using a NAND-NOR-Inverter (NNI) and five-input majority voter (M5) for the first time. Reliability analysis by using probabilistic transfer matrix reveals that the proposed XOR scheme has higher stability than previous ones. The proposed XOR is also implemented in QCA regime, whose correctness is verified by using simulation results on QCADesigner. Its performance figures show that the proposed XOR utilizes less overhead in terms of area and QCA cost than the state-of-the-art design. Most importantly, the proposed XOR excludes the complex crossovers and keeps full accessibility to its input and output pins, so that it has a scalable structure. To demonstrate its scalability, multi-bit parity generators including 4-bit, 8-bit, 16-bit and 32-bit generators are also designed by hierarchically connecting the XORs. The analysis results account for their improvements with respect to occupied area and cost.