Three-Party Quantum Key Agreement Protocol with Seven-Qubit Entangled States

Abstract

A new three-party quantum key agreement protocol based on seven-qubit states is proposed. In this protocol, each participant adopts different encryption methods to transmit a secret key of the same length. Subsequently, the participants utilize joint measurement to gain the ultimate shared secret key. No participant can determine the ultimate shared key by himself/herself. In addition, the proposed three-party quantum key agreement protocol could resist several well-known attacks. Compared with typical quantum key agreement protocols, our proposed three-party quantum key agreement protocol is more efficient.

1 Introduction

As a significant branch of quantum cryptography, quantum key agreement (QKA) can build secure key between or among participants and even can maintain the fairness of the participants’ contribution to the shared secret key.

Zhou et al. proposed the first weak quantum key agreement protocol based on quantum teleportation without considering the fairness [1]. In the same year, a two-party quantum key agreement protocol with the maximally entangled states [2] was proposed, however, Hwang and Tsai et al. hold that this protocol has security issues, because an eavesdropper can obtain the entire final shared secret key by executing CNOT attack and intercept-resend attack without being detected. Meanwhile, they proposed a new quantum key agreement protocol [3, 4] to withstand the resistance attack. Chong et al. [5] presented a quantum key agreement protocol based on BB84 which makes the best use of unitary operations and delayed measurement [6]. Shi et al. successfully extended the two-party QKA protocol into a multi-party QKA protocol [7]. However, Liu et al. pointed out that it was insecure and unfair since dishonest participants could determine the final shared secret key by themselves and proposed a QKA protocol [8] that only utilized single photons for encryption to resist the participant attack. Sun improved Liu et al.’s protocol by adding unitary operations. Huang et al. [9] conducted a detailed analysis on Sun’s protocol and came up with a method to resist the attacks at the cost of qubit efficiency. Shukla et al. [10] put forward a multi-party quantum key agreement (MQKA) protocol with Bell states, which was a protocol in travelling mode [11]. Unfortunately, an eavesdropper can flip qubit of the final shared secret key of Shukla’s protocol without introducing any error [12]. Huang et al. improved the travelling mode of MQKA protocol [13]. In recent years, researchers have shifted their focus on the multi-qubit states. Sun et al. put forward an MQKA protocol based on genuinely maximally entangled six-qubit states [14]. Four-qubit cluster states were also utilized in quantum key agreement protocol [15,16,17]. In addition, multi-qubit states can be generated by combining multiple states [18,19,20,21,22,23]. Thus, how to make full use of the characteristics of multi-qubit states is of great significance for quantum communication.

Based on seven-qubit entangled states, a three-party quantum key agreement protocol is devised. Each participant adopts different encryption methods and utilizes the characteristics of the seven-qubit entangled states to generate six-bit shared secret keys. In Section 2, the related quantum gates and the seven-qubit entangled states will be introduced. Section 3 will offer a detailed description of the proposed three-party QKA protocol. In Section 4, the security analysis will be given. Comparisons among previous QKA protocols and our proposed QKA protocol will be provided in Section 5. Finally, a brief conclusion will be drawn in Section 6.

2 Quantum Gate and Qubit

In this section, several unitary operations, Controlled NOT gate, Bell states and seven-qubit entangled states are introduced.

2.1 Quantum Gate

Quantum information processing is a series of unitary evolutions of the quantum states encoded. Quantum logic gate refers to the most fundamental unitary operations of qubits. The basic one-qubit gates are as follows:

$$I=\left( {\begin{array}{l} 1\text{ } 0 \\ 0\text{ } 1 \end{array}} \right),\!\! \quad X=\left( {\begin{array}{l} 0\text{ } 1 \\ \text{1 } 0 \end{array}} \right),\!\! \quad Z=\left( {\begin{array}{l} 1\text{ } 0 \\ 0-1 \end{array}} \right), \!\!\quad Y=\left( {\begin{array}{l} \text{ } 0\text{ } 1 \\ -1\text{ } 0 \end{array}} \right),\!\! \quad H=\frac{1}{\sqrt 2} \left( {\begin{array}{c} 1\text{ } 1 \\ 1-1 \end{array}} \right). $$

(1)

As for the controlled NOT (CNOT) gate, the first qubit is called the control bit, while the second quantum bit is called the target bit. The unitary operation of the CNOT gate is:

$$ \text{CNOT}=\left( {{\begin{array}{*{20}c} I \hfill & {{\mathbf{0}}} \hfill \\ {{\mathbf{0}}} \hfill & X \hfill \end{array}} } \right) $$

(2)

Bell states are four specific maximally entangled quantum states of two qubits. Four Bell states can be expressed as:

$$ \vert \phi^{\pm} \rangle =\frac{1}{\sqrt 2} (\vert 00\rangle \pm \vert 11\rangle ) $$

(3)

$$ \vert \psi^{\pm} \rangle =\frac{1}{\sqrt 2} (\vert 01\rangle \pm \vert 10\rangle ) $$

(4)

Suppose four local unitary operations are respectively denoted by U₀₀, U₀₁, U₁₀ and U₁₁ such as U₀₀ ≡ I, U₀₁ ≡ X, U₁₀ ≡ Y Z, U₁₁ ≡ H, where the subscripts are the encoded bits associated with their operations. Furthermore, two sets of orthogonal bases are Z-basis and X-basis. |0〉 and |1〉 form the Z-basis, while |+〉 and |−〉 form the X-basis, where $\vert \pm \rangle \text {=}\textstyle {1 \over {\sqrt 2} }(\vert 0\rangle \pm \vert 1\rangle )$.

2.2 Seven-Qubit Entangled State

Zha et al. presented a seven-qubit entangled state |ψ〉_1234567 [24], which is a maximally multipartite entangled state [25]. This state is more highly entangled than the previously discovered states [26]. The seven-qubit entangled state whose marginal density matrices for subsystems of one and two qubits are wholly mixed and most but not all of the marginal density matrices of three qubits are completely mixed.

$$\begin{array}{@{}rcl@{}} \vert \psi \rangle_{1234567} &=&\frac{1}{4\sqrt 2} [(\vert \mathbf{0}\rangle +\vert \mathbf{3}\rangle +\vert \mathbf{13}\rangle +\vert \mathbf{14}\rangle)\\ &&+\left( {\vert \mathbf{17}\rangle -\vert \mathbf{18}\rangle +\vert \mathbf{28}\rangle -\vert \mathbf{31}\rangle}\right)\\ &&-(\vert \mathbf{37}\rangle +\vert \mathbf{38}\rangle -\vert \mathbf{40}\rangle -\vert \mathbf{43}\rangle )\\ &&+(\vert \mathbf{52}\rangle -\vert \mathbf{55}\rangle -\vert \mathbf{57}\rangle +\vert \mathbf{58}\rangle )\\ &&-(\vert \mathbf{68}\rangle +\vert \mathbf{71}\rangle -\vert \mathbf{73}\rangle -\vert \mathbf{74}\rangle )\\ &&+(\vert \mathbf{85}\rangle -\vert \mathbf{86}\rangle -\vert \mathbf{88}\rangle +\vert \mathbf{91}\rangle )\\ &&+(\vert \mathbf{97}\rangle +\vert \mathbf{98}\rangle +\vert \mathbf{108}\rangle +\vert \mathbf{111}\rangle )\\ &&+(\vert \mathbf{112}\rangle -\vert \mathbf{115}\rangle +\vert \mathbf{125}\rangle -\vert \mathbf{126}\rangle)]_{1234567} \end{array} $$

(5)

where the bold numbers represent the decimal system, for example, |0〉 denotes |0000000〉. By factoring (5), the new expression of maximally entangled seven-qubit state is as follows.

$$\begin{array}{@{}rcl@{}} \vert \psi \rangle_{1234567} &=&\frac{1}{4}[(\vert 00\rangle \vert \phi^{+}\rangle +\vert 11\rangle \vert \psi^{+}\rangle )_{1267} \vert \mathbf{{0}}\rangle_{345} -(\vert 10\rangle \vert \phi^{+}\rangle +\vert 01\rangle \vert \psi^{+}\rangle )_{1267} \vert \mathbf{1}\rangle_{345} \\ &&+(\vert 01\rangle \vert \phi^{+}\rangle +\vert 10\rangle \vert \psi^{+}\rangle )_{1267} \vert \mathbf{2}\rangle_{345} +(\vert 11\rangle \vert \phi^{+}\rangle +\vert 00\rangle \vert \psi^{+}\rangle )_{1267} \vert \mathbf{3}\rangle_{345} \\ &&+(\vert 11\rangle \vert \phi^{-}\rangle +\vert 00\rangle \vert \psi^{-}\rangle )_{1267} \vert \mathbf{4}\rangle_{345} +(\vert 01\rangle \vert \phi^{-}\rangle +\vert 10\rangle \vert \psi^{-}\rangle )_{1267} \vert \mathbf{5}\rangle_{345} \\ &&-(\vert 10\rangle \vert \phi^{-}\rangle +\vert 01\rangle \vert \psi^{-}\rangle )_{1267} \vert \mathbf{6}\rangle_{345} +\!(\vert 00\rangle \vert \phi^{-}\rangle +\vert 11\rangle \vert \psi^{-}\rangle )_{1267} \vert \mathbf{7}\rangle_{345} ] \end{array} $$

(6)

3 Three-Party QKA Protocol

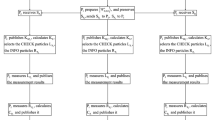
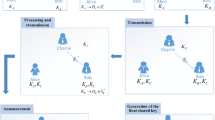
The three-party quantum key agreement protocol with seven-qubit entangled states is shown in Fig. 1, where there are three participants in the considered protocol, i.e., Alice, Bob and Charlie. They plan to share secret key K via quantum channel, and adopt different encryption methods to transmit a secret key. For example, Alice uses the method of introducing a new sequence related to secret key, Bob utilizes the CNOT operation method, while Charlie employs the four unitary operations. The detailed process of the three-party QKA protocol is described as follows.

• Step. 1  The participants randomly generate 2n-bit strings as secret keys, $K_{A} =\{{K_{A}^{i}} \vert i = 1,2,\mathellipsis ,n\}$, $K_{B} =\{{K_{B}^{i}} \vert i = 1,2,\mathellipsis ,n\}$ and $K_{C} =\{{K_{C}^{i}} \vert i = 1,2,\mathellipsis ,n\}$, respectively. Every participant negotiates that the encoding rule is I : 00, X : 01, Y Z : 10, H : 11, and represents the Bell states correspondingly, i.e., |ϕ⁺〉 : 00, |ϕ⁻〉 : 01, |ψ⁺〉 : 10, |ψ⁻〉 : 11.

• Step. 2  Alice prepares n seven-qubit entangled states and divides all the particles into seven ordered sequences S_j(j = 1,2,…,7). Then, Alice randomly selects decoy states in one of the four states |0〉,|1〉,|+〉 and |−〉 and randomly inserts them into S₁, S₂, S₄ and S₅, respectively. Alice sends the mixed sequences $S_{1}^{\prime }$ and $S_{2}^{\prime }$ ($S_{4}^{\prime }$ and $S_{5}^{\prime } )$ to Bob (Charlie).

• Step. 3  After confirming that Bob and Charlie have received the sequences, eavesdropping check should be executed. Alice announces the positions of the decoy states and their corresponding measurement bases {|0〉,|1〉} or {|+〉,|−〉}. Afterward, Bob and Charlie measure the decoy states with correct bases and tell Alice the measurement results. Alice compares the measurement results of Bob and Charlie with the initial decoy states and computes the error rate among the measurement results. If the error rate exceeds the predetermined value associated with the channel state information, all participants will abandon this round of communication and restart after a random time. Otherwise, they will proceed to the next step.

• Step. 4  Bob and Charlie remove the inserted decoy states. Moreover, Bob performs the Z-basis measurement on every state in S₁ and S₂. Similarly, Charlie performs Z-basis measurement on every state in S₄ and S₅. In addition, Bob and Charlie compare the measurement results of S₁ with that of S₄ to see whether the measurement results are same. In the end, Alice announces the measurement results of S₃ and that of Bell states denoted by $M_{A} =\{{M_{A}^{i}} \vert i = 1,2,\mathellipsis ,n\}$, where ${M_{A}^{i}}$ is the corresponding code of Alice’s i-th states in S₆ and S₇. The characteristics of the highly entangled seven-qubit states can be used to obtain the initial states. For example, assume that Bob’s measurement result of S₁ and S₂ is |00〉, if the comparison result between Bob’s and Charlie’s is same, then the measurement result of S₄ and S₅ is |00〉. Otherwise, the result is |11〉. After Alice announces the measurement result of S₃, Bob and Charlie can obtain the initial states of the seven-qubit entangled states in terms of |00〉₁₂|000〉₃₄₅ or |00〉₁₂|100〉₃₄₅.

• Step. 5  According to $K_{B} =\{{K_{B}^{i}} \vert i = 1,2,\mathellipsis ,n\}$, Bob performs the CNOT operations on every state in S₁ and S₂. K_B is called the control bit, while S₁ and S₂ are the target bits. The rule is described as follows. If ${K_{B}^{i}}$ is equal to 00, 01, 10 or 11, Bob performs the unitary operations in S₁ and S₂, i.e., $I^{S_{1}} \otimes I^{S_{2}}$, $I^{S_{1}} \otimes X^{S_{2}}$, $X^{S_{1}} \otimes I^{S_{2}}$ or $X^{S_{1}} \otimes X^{S_{2}}$, where the new sequences $S_{1}^{\ast }$ and $S_{2}^{\ast }$ are obtained. According to $K_{C} =\{{K_{C}^{i}} \vert i = 1,2,\mathellipsis ,n\}$, Charlie performs four unitary operations U₀₀, U₀₁, U₁₀ and U₁₁ in S₅. Then Charlie obtains a new sequence $S_{5}^{\ast }$. Charlie (Bob) prepares enough decoy states and randomly inserts them into $S_{5}^{\ast }$ ($S_{1}^{\ast }$ and $S_{2}^{\ast } )$. Charlie (Bob) sends the mixed sequence(s) $S_{5}^{\ast \ast }$ ($S_{1}^{\ast \ast }$ and $S_{2}^{\ast \ast } )$ to Bob (Charlie).

• Step. 6  After receiving the sequence, Bob and Charlie begin to check eavesdropping. The whole process is similar to that in Step 3.

• Step. 7  Bob and Charlie remove the decoy states. Charlie announces the positions corresponding to the states performed operation U₁₁ in $S_{5}^{\ast }$. Subsequently, Bob performs Z-basis or X-basis on every state in $S_{5}^{\ast }$. Charlie performs Z-basis on each state in $S_{1}^{\ast }$ and $S_{2}^{\ast }$. At this moment, Bob and Charlie could gain secret keys from each other. Bob (Charlie) randomly inserts enough decoy states into $S_{5}^{\ast }$ ($S_{1}^{\ast }$ and $S_{2}^{\ast } )$. Hence Bob and Charlie send the mixed sequences $S_{1}^{\ast \prime }$, $S_{2}^{\ast \prime }$ and $S_{5}^{\ast \prime }$ to Alice.

• Step. 8  Alice, Bob and Charlie perform eavesdropping check as demonstrated in Step 3.

• Step. 9  After receiving sequences $S_{1}^{\ast \prime }$, $S_{2}^{\ast \prime }$, $S_{5}^{\ast \prime }$, Alice announces ${V_{A}^{i}} ={K_{A}^{i}} \oplus {M_{A}^{i}}$ via the classical authentication channel. Since Bob and Charlie know the initial states of the seven-qubit entangled states, they can compute the final shared secret key $K=\{{K_{B}^{i}} {K_{C}^{i}} {K_{A}^{i}} \vert i = 1,2,\mathellipsis ,n\}$. Besides, Alice removes the decoy states and measures $S_{1}^{\ast \prime }$, $S_{2}^{\ast \prime }$, $S_{5}^{\ast \prime }$ with correct bases. Finally, Alice obtains the final shared secret key, too.

Fig. 1

Three-party quantum key agreement protocol

4 Security Analysis

In this section, it will be shown that the proposed three-party QKA protocol is secure under some common attacks.

4.1 Trojan Horse Attack

Since the same states are transmitted more than once in the channel, the protocol may be subject to Trojan horse attack. Gisin et al. [27] pointed out how an eavesdropper gains information of the shared secret key with Trojan horse attack. To avoid this attack, each participant should install two quantum optical devices, i.e., the wavelength quantum filter and the photon number splitter (PNS). Specifically, the wavelength quantum filter can filter out Eve’s invisible photons [28], and PNS can discover the delay photons by dividing photons [29, 30]. The proposed three-party quantum key agreement protocol could resist Trojan horse attack if the two quantum optical devices are installed.

4.2 Intercept-Resend Attack

Suppose that Eve successfully intercepts the transmitted sequences of particles and resends the prepared fake sequences. First of all, since only sequences S₁, S₂, S₄ and S₅ are transmitted in quantum channel while S₃, S₆ and S₇ are kept home by Alice, Eve cannot intercept all states to acquire the final shared secret key. Secondly, since participants will randomly insert decoy states into the encoded states before their transmission, Eve does not know the positions and the measurement bases of the random decoy states before the sender’s announcement. Participants calculate the error rate by the eavesdropping check method, then Eve’s attack behavior will be detected with a probability $1-\left ({\textstyle {3 \over 4}} \right )^{m}$ (m denotes the number of decoy states used to detect in this attack). Therefore, it is impossible for Eve to obtain the final shared secret key with intercept-resend attack without being detected.

4.3 Entangling Attack

The entangling attack means that Eve intercepts the particles transmitted and entangles an ancillary system |ε〉 prepared beforehand with it. Finally, Eve resends intercepted particles to the receiver and measures the ancillary system to obtain useful information about the final shared secret key. To perform the entangling attack, Eve intercepts the particles in the sequences $S_{1}^{\prime }$, $S_{2}^{\prime }$, $S_{4}^{\prime }$, $S_{5}^{\prime }$, $S_{1}^{\ast }$, $S_{2}^{\ast }$, $S_{5}^{\ast }$, $S_{1}^{\ast \prime }$ , $S_{2}^{\ast \prime }$ and $S_{5}^{\ast \prime }$, and entangles them with the ancillary system |ε〉. Subsequently, Eve resends intercepted sequences to the receiver and measures the ancillary system. Since the decoy states involved in our protocol are random in four states, i.e., |0〉, |1〉, |+〉 and |−〉, without loss of generality, Eve’s unitary operator U_e should satisfy

$$\begin{array}{@{}rcl@{}} U_{e} \vert 0\rangle \vert \varepsilon \rangle =a\vert 0\rangle \vert e_{00} \rangle +b\vert 1\rangle \vert e_{01} \rangle \end{array} $$

(7)

$$\begin{array}{@{}rcl@{}} U_{e} \vert 1\rangle \vert \varepsilon \rangle =c\vert 0\rangle \vert e_{10} \rangle +d\vert 1\rangle \vert e_{11} \rangle \end{array} $$

(8)

$$\begin{array}{@{}rcl@{}} U_{e} \vert +\rangle \vert \varepsilon \rangle &=&\frac{1}{\sqrt 2} (a\vert 0\rangle \vert e_{00} \rangle +b\vert 1\rangle \vert e_{01} \rangle +c\vert 0\rangle \vert e_{10} \rangle +d\vert 1\rangle \vert e_{11} \rangle ) \\ &=&\frac{1}{2}[\vert +\rangle (a\vert e_{00} \rangle +b\vert e_{01} \rangle +c\vert e_{10} \rangle +d\vert e_{11} \rangle )]\\ &&+\frac{1}{2}[\vert -\rangle (a\vert e_{00} \rangle -b\vert e_{01} \rangle +c\vert e_{10} \rangle -d\vert e_{11} \rangle )] \end{array} $$

(9)

$$\begin{array}{@{}rcl@{}} U_{e} \vert -\rangle \vert \varepsilon \rangle &=&\frac{1}{\sqrt 2} (a\vert 0\rangle \vert e_{00} \rangle +b\vert 1\rangle \vert e_{01} \rangle -c\vert 0\rangle \vert e_{10} \rangle -d\vert 1\rangle \vert e_{11} \rangle ) \\ &=&\frac{1}{2}[\vert +\rangle (a\vert e_{00} \rangle +b\vert e_{01} \rangle -c\vert e_{10} \rangle -d\vert e_{11} \rangle )] \\ &&+\frac{1}{2}[\vert -\rangle (a\vert e_{00} \rangle -b\vert e_{01} \rangle -c\vert e_{10} \rangle +d\vert e_{11} \rangle )] \end{array} $$

(10)

where |a|² + |b|² = 1 and |c|² + |d|² = 1. If Eve passes the eavesdropping detection without being detected in Steps. (3), (6) and (8), she must ensure the conditions such as a = d = 1, b = c = 0 and |e₀₀〉 = |e₁₁〉. Thus, only if Eve’s ancillary states and the decoy states are in state |0〉 or |1〉, eavesdropper will not be detected. However, since Eve can’t distinguish |e₀₀〉 from |e₁₁〉 and must disturb the random decoy states in the two states |+〉 and |−〉, she cannot obtain any useful information about the participants’ secret key with the entangling attack.

4.4 Participant Attack

Since dishonest participants grasp a part of shared secret key information, they may collaborate to predetermine the final shared secret key without being detected. Then they decide the final shared secret key by changing subkey. To resist participant attack, the protocol should employ delayed measurement technique [6] and quantum authentication technique [31, 32]. In other words, all participants obtain the final shared secret key simultaneously and fairly. For example, suppose that Bob and Charlie are dishonest participants, and they want to determine the final shared secret key. Until Alice announces ${V_{A}^{i}}$, Bob and Charlie cannot derive ${K_{A}^{i}}$ from the known ${M_{A}^{i}}$. In addition, Alice is an honest participant necessary to work out K with the measurement results of $S_{1}^{\ast \prime }$, $S_{2}^{\ast \prime }$ and $S_{5}^{\ast \prime }$ after announcing ${V_{A}^{i}}$. It is impossible for the participants to obtain the final shared secret key in advance.

4.5 Information Leakage

Since Alice announces measurement results of S₃ and ${V_{A}^{i}}$, Eve may attempt to gain the final shared secret key. However, Eve does not know the initial states of the seven-qubit entangled states, and sequence S₃ does not carry any useful information about the secret key. Even if Eve luckily obtains the secret key of Alice, there is still no information leakage problem in the proposed three-party QKA protocol, since the final shared secret key has 2⁶ⁿ possible outcomes.

5 Comparison

Cabello [33] put forward the qubit efficiency η in quantum key distribution protocol.

$$ \eta =\frac{c}{q+b} $$

(11)

where c indicates the length of the final shared secret key generated, q indicates the total number of used qubits, i.e. the quantum states and decoy particles prepared by each participant, b is the total number of classical bits exchanged for decoding the message. A simple comparison with similar QKA protocols from the aspects of quantum resource, the length of the shared secret key, qubit efficiency is shown in Table 1. To generate 6n bits of shared secret key in our three-party QKA protocol, the qubit efficiency is:

$$ \eta =\frac{6n}{(7n + 10m)+(n + 2n)} $$

(12)

where q = 7n + 10m, b = n + 2n, m denotes the total number of decoy particles. In addition, 7n denotes that Alice prepares n seven-qubit entangled states, n + 2n is that Alice announces the measurement results of S₃ and ${V_{A}^{i}}$. If m is same as n, then η will be up to 30%. It is obvious that our three-party QKA protocol has higher efficiency.

Table 1 Comparison of QKA protocols

6 Conclusion

In conclusion, a new three-party quantum key agreement protocol based on the seven-qubit entangled states is investigated. In this three-party QKA protocol, each participant adopts different encryption methods to establish a secret key. The negotiation process of the protocol is more diverse and flexible. It is demonstrated that this proposed three-party QKA protocol can effectively resist outside and participants attacks and has higher qubit efficiency due to the multi-qubit entanglement states.