1 Introduction

Material integrity evaluation is of central importance in non-destructive testing (NDT). In elastic materials, e.g., metal alloys, there will be permanent changes when an elastic material is overloaded or loaded cyclically for a long time which will eventually result in generation of fatigue cracks. To prevent the material from failing, it is essential to diagnose or even quantify its stress–strain state which can be generally categorized into two regimes. In the elastic regime, stress varies with strain in a linear and reversible pattern so that elastic solids can restore their original shape after load removal. In this case, the material remains intact and robust. In tensile testing particularly, when the external load exceeds the material’s elastic limit, plastic deformation occurs and the material can no longer maintain its original elastic properties. In this case, materials can be regarded as fatigue hazards and thus require replacement.

In order to implement such diagnosis in-situ, remotely and non-destructively, we explore the application of frequency-domain laser ultrasound (FDLU). As a novel and totally non-contact NDT approach, based on amplitude adjustable fiber-coupled diode laser source irradiation and an inexpensive ultrasonic transducer, FDLU can be implemented without high-performance bulky pulsed laser system instrumentation and exhibits more flexibility than conventional pulsed laser ultrasound methods. Therefore, it has excellent potential for portable industrial use. Some applications on materials diagnosis [1,2,3] and imaging [4] have been reported with promising results for further field testing. The present research developed a full theory for the semi-infinite aluminum FDLU pressure signal which was subsequently validated experimentally through monitoring the stress–strain state of aluminum 6061 used in the aerospace industry with a water-coupled transducer.

2 Experimental Setup and Methodology

2.1 FDLU Instrumentation

Frequency-domain laser ultrasonic and photothermal signals have been studied theoretically and experimentally in the past [1,2,3,4,5]. However, applications of the theory have been limited because it only considers the acoustic radiation directivity with direct contact detection approach. In this work, the FDLU frequency dependence is studied in a non-contact configuration using an aluminum sample (schematic shown in Fig. 1a) with water as the coupling medium. The laser and the water-coupled transducer were aligned at the same location of sample surface. A high-frequency lock-in amplifier captured the harmonic electric signal from the transducer converted from the acoustic pressure and outputted demodulated amplitude and phase signals. The function generator and lock-in amplifier were synchronized and controlled by a computer with data acquisition modules.

2.2 Materials and Methods

According to thermoelastic theory, deformation will set in when an elastic body is under an increasing tensile force. When the external tension becomes constant, the deformation stops and the whole system reaches dynamic equilibrium. In this condition, elongation parallel to the direction of the external force is always accompanied by vertical constriction. The elastic body becomes thinner and necked under tensile load. In addition, the change of elastic moduli and wave velocity due to a high compression or tension has been studied in the field of seismology [6,7,8]. These stress–strain-dependent features suggest a possible change in the photoacoustic (laser ultrasonic) signal which is directly related to the elasticity of the sample.

For our laser ultrasonic stress–strain evaluation, an in-house designed tensile rig with a water-tight tank was assembled. The main part of the rig was made of hardened stainless steel with sufficient tensile strength and corrosion resistance. The experimental configuration is shown in Fig. 1b. The sample was made of aluminum T6061 T-6 alloy which is commonly used in the aerospace industry. A piece of adhesive strain gauge (KYOWA\(^{\circledR }\), sensitivity: 10\(^{-6})\) was affixed on the back surface of the sample to measure the actual strain. An 808 nm diode laser operated at 1 W laser power (RMS) output and 1 MHz frequency with the focused immersion ultrasonic transducer of nominal 1 MHz central frequency fixed at 48 mm above the sample. The 1 MHz modulation frequency was set to be high enough, resulting in a thermal diffusion length of only a few microns and thus thermal-wave penetration effects were suppressed. Furthermore, the large laser beam size (diameter \(\sim \)2 mm) adopted in the experiment provided a heat source whose dimension was much larger than the magnitude of tensile deformation. To check the reliability of the rig and the signal-to-noise ratio (SNR) of the FDLU signal dependence of strain, the first tests were restricted within the elastic regime. Some more tests were also conducted into the plastic regime based on our reliable tensile rig.

3 Theory

A 3-D azimuthally symmetric thermoelastic model was developed with the following assumptions:

  1. a)

    The cross section and thickness of the sample are much larger than the wavelength of any elastic wave modes (compressional wave has a wavelength of 6.7 mm at 1 MHz);

  2. b)

    The front surface of the sample is stress-free, and the water column pressure above the sample is neglected;

  3. c)

    The laser beam intensity has a Gaussian spatial distribution.

In metals, light absorption takes place within a very shallow subsurface layer so that a surface thermoelastic source assumption is a reasonable approximation [9]. The frequency-domain thermal-wave equation in cylindrical coordinates (see Fig. 2a) under harmonic excitation is:

$$\begin{aligned} -k\nabla ^{2}\tilde{T}(r,z,\omega )+i\omega \rho C\tilde{T}(r,z,\omega )=I_0 (\pi r_0^2 )^{-1}\delta (z)\exp \left( {-r^{2}/r_0^2 } \right) . \end{aligned}$$
(1)

\(\tilde{T}\) is the harmonic temperature variation; \(k,\rho ,C\) are the thermal conductivity, density, and specific heat capacity of aluminum, respectively; \(\omega \) is the angular modulation frequency; and \(I_{0}\) is the laser intensity. Taking the Hankel transform of order zero of \(\tilde{T}\) with respect to coordinate r, the solution for the thermal-wave field in the Bessel–Fourier (Hankel) domain (spatial frequency coordinate \(\lambda \)), denoted as \(\hat{{T}}\), can be found:

$$\begin{aligned} \hat{{T}}(\lambda ,z,\omega )=I_0 (2\alpha \pi k)^{-1}\exp \left( {-{r_0^2 \lambda ^{2}}/4-\alpha z} \right) , \end{aligned}$$
(2)

where \(\alpha ^{2}=\lambda ^{2}+i\omega \rho C/k\). Inside the metal, the stress–strain relation follows the generalized Hooke’s Law described in the form of scalar and vector displacement potential components [10],

$$\begin{aligned} \nabla \left[ {\left( {\hat{{\lambda }}+2\hat{{\mu }}} \right) \nabla ^{2}\tilde{\varphi }+\rho \omega ^{2}\tilde{\varphi }-3\hat{{B}}\beta \tilde{T}} \right] +\nabla \times \left( {\hat{{\mu }}\nabla ^{2}{\tilde{{\varvec{\uppsi }} }}+\rho \omega ^{2}{\tilde{{\varvec{\uppsi }} }}} \right) =\mathbf{0}. \end{aligned}$$
(3)

\(\hat{{\lambda }},\hat{{\mu }}\) are Lame’s first and second constants, respectively; \(\hat{{B}}=\hat{{\lambda }}+\frac{2}{3}\hat{{\mu }}\) is the bulk modulus; and \(\beta \) is the linear coefficient of expansion of aluminum. The term \(-3\hat{{B}}\beta \tilde{T}\) represents the thermal expansion due to light absorption. Note that the displacement vector is given by \({\tilde{\mathbf{u}}}=\nabla \tilde{\varphi }+\nabla \times {\tilde{{\varvec{\uppsi }}}}\), and when the surface is stress-free, Eq. 3 reduces to the Helmholtz Eq. 4(a, b) with the following boundary conditions, Eq. 4(c, d) [10]

$$\begin{aligned}&{\partial ^{2}\hat{{\varphi }}^{H_0 }}/{\partial z^{2}}-\sigma ^{2}\hat{{\varphi }}^{H_0 }=\left( {3-4{c_s^2 }/{c_l^2 }} \right) \beta \hat{{T}}(\lambda ,z); \end{aligned}$$
(4a)
$$\begin{aligned}&{\partial ^{2}\hat{{\psi }}^{H_1 }}/{\partial z^{2}}-\gamma ^{2}\hat{{\psi }}^{H_1 }=0; \end{aligned}$$
(4b)
$$\begin{aligned}&\hat{{\tau }}_{zz}^{H_0 } =\hat{{\mu }}\left[ \zeta ^{2}\hat{{\varphi }}^{H_0 }(\lambda ,0)+2\lambda {(\partial \hat{{\psi }}^{H_1 }}/{\partial z})_{z=0}\right. \nonumber \\&\left. \qquad \qquad +\,(3{c_l^2 }/{c_s^2 -4})\beta \hat{{T}}(\lambda ,0) \right] =\hbox {3}B\beta \hat{{T}}(\lambda ,0); \end{aligned}$$
(4c)
$$\begin{aligned}&\hat{{\tau }}_{zr}^{H_1 } =\hat{{\mu }}\left[ {-2\lambda ({\partial \hat{{\varphi }}^{H_0 }}/{\partial z})_{z=0} -\zeta ^{2}\hat{{\psi }}^{H_1 }(\lambda ,0)} \right] =0; \end{aligned}$$
(4d)

where \(c_l =\sqrt{{(\hat{{\lambda }}+2\hat{{\mu }})}/\rho },c_s =\sqrt{{\hat{{\mu }}}/\rho }\) are the longitudinal and transverse wave velocities, respectively. The other symbols are defined as: \(\sigma ^{2}=\lambda ^{2}-{\omega ^{2}}/{c_l^2 },\gamma ^{2}=\lambda ^{2}-{\omega ^{2}}/{c_s^2 }\),\(\zeta ^{2}=2\lambda ^{2}-{\omega ^{2}}/{c_s^2 }\). The superscripts \(H_{0}, H_{1}\) refer to the Hankel transform of the Bessel function of the first kind of order zero and order one, respectively. Since the model is azimuthally symmetric, consistent with a Gaussian laser beam, the vector potential has only one azimuthal component (denoted as \(\psi \)). Solving Eqs. 4, we obtain the displacement potentials in the Hankel domain:

$$\begin{aligned} \hat{{\varphi }}^{H_0 }(\lambda ,z,\omega )= & {} \left[ \frac{4\lambda ^{2}\kappa \gamma \alpha -\zeta ^{4}\kappa }{\alpha (\alpha ^{2}-\sigma ^{2})(\zeta ^{4}-4\lambda ^{2}\gamma \sigma )}\exp \left( {-\sigma z} \right) \right. \nonumber \\&\left. +\frac{\kappa }{\alpha (\alpha ^{2}-\sigma ^{2})}\exp \left( {-\alpha z} \right) \right] \exp \left( {-{r_0^2 \lambda ^{2}}/4} \right) ; \end{aligned}$$
(5a)
$$\begin{aligned} \hat{{\psi }}^{H_1 }(\lambda ,z,\omega )= & {} \frac{2\lambda \kappa \zeta ^{2}}{\alpha (\alpha +\sigma )(\zeta ^{4}-4\lambda ^{2}\gamma \sigma )}\exp \left( {-{r_0^2 \lambda ^{2}}/4-\gamma z} \right) ; \end{aligned}$$
(5b)

where \(\kappa =\left( {3-4{c_s^2 }/{c_l^2 }} \right) \beta I_0 (2\pi k)^{-1}\) is a constant related to the material properties and the laser intensity. To obtain the displacement field in the spatial frequency domain, it is necessary to take the inverse Hankel transforms of \(\hat{{\varphi }}^{H_0 }\) and \(\hat{{\psi }}^{H_1 }\) with respect to \(\lambda \),

$$\begin{aligned} \tilde{\varphi }(r,z,\omega )= & {} \int _0^{+\infty } {\lambda \hat{{\varphi }}^{H_0 }} J_0 (\lambda r)d\lambda ; \end{aligned}$$
(6a)
$$\begin{aligned} \tilde{\psi }(r,z,\omega )= & {} \int _0^{+\infty } {\lambda \hat{{\psi }}^{H_1 }} J_1 (\lambda r)d\lambda . \end{aligned}$$
(6b)

Next, we consider the Hankel transform of the ultrasonic pressure distribution in the coupling medium, water. As the thermal diffusivity of water is small (on the order of 10\(^{-7}\) cm\(^{2} \cdot \mathrm{s}^{-1}\)), its temperature variation is neglected, and thus, the coupling fluid can be regarded as an isothermal medium. The pressure variation \(\tilde{p}\) satisfies the normal wave equation (viscous losses are neglected) [11],

$$\begin{aligned} \nabla ^{2}\tilde{p}+(\omega /v_0 )^{2}\tilde{p}=\rho _0 \omega ^{2}\delta (z)\mathbf{n}\cdot (\nabla \tilde{\varphi }+\nabla \times {\tilde{{\varvec{\uppsi }}}}). \end{aligned}$$
(7)

The Dirac delta function represents the appropriate velocity boundary condition at the sample–water interface; n is the outward unit normal vector.

Case 1. Semi-infinite water layer

In this case, the ultrasonic pressure is a traveling wave without boundary reflections. The pressure in water has a traveling waveform shape (along the negative z-direction), i.e., \(p(\lambda ,z,t)=A(\lambda )\exp (ik_z z+i\omega t)\). The solution of the pressure field in the Hankel domain is

$$\begin{aligned} \hat{{p}}(\lambda ,z,\omega )=\frac{\omega ^{2}}{\alpha \cdot \Omega }\rho _0 (2\lambda ^{2}-\zeta ^{2})\frac{\kappa \zeta ^{2}}{(\alpha +\sigma )(\zeta ^{4}-4\lambda ^{2}\gamma \sigma )}\exp \left( {\Omega z-{r_0^2 \lambda ^{2}}/4} \right) , \end{aligned}$$
(8)

where \(\Omega ^{2}=\lambda ^{2}-\omega ^{2}/v_0^2 \). This solution neglects the influence of the immersion transducer.

Case 2. Effect of ultrasonic transducer location with respect to the sample

As the lateral dimension of the transducer (\(\sim \)19 mm) is much larger than the laser spot size (\(\sim \)2 mm) and the wavelength of the pressure wave in water (\(\sim \)1.5 mm) at 1 MHz, the reflection of the pressure wave due to the transducer should be taken into account, assuming the transducer is placed in the water at a distance \(D_w \) away from the sample with its surface parallel to the sample surface. The influence of the transducer can be described by a boundary condition introducing finite acoustic impedance. Given that the focal length of the transducer is much longer than its radius, its surface curvature is neglected: \(\rho _0^{-1}{} \mathbf{n}\cdot \nabla \tilde{p}=-i\omega Z_T^{-1}\tilde{p}\) at \(z=-D_w \). Here, \(Z_{T}\) is the acoustic impedance of the transducer active surface area. The Hankel transform solution then becomes

$$\begin{aligned} \begin{aligned} \hat{{p}}(\lambda ,z,\omega )&=\frac{\rho _0 \omega ^{2}}{\alpha \cdot \Omega }\left[ {\frac{\kappa \zeta ^{2}(2\lambda ^{2}-\zeta ^{2})}{(\alpha +\sigma )(\zeta ^{4}-4\lambda ^{2}\gamma \sigma )}} \right] \left( {\frac{Z\Omega -i\rho _0 \omega }{Z\Omega +i\rho _0 \omega }e^{2\Omega D_w }-1} \right) ^{-1} \\&\qquad \cdot \left[ {e^{-\Omega z}+\frac{Z\Omega -i\rho _0 \omega }{Z\Omega +i\rho _0 \omega }e^{\Omega (z+2D_w )}} \right] \exp \left( {-{r_0^2 \lambda ^{2}}/4} \right) . \end{aligned} \end{aligned}$$
(9)

Finally, the real spatial pressure field can be obtained by applying a numerical inverse Hankel transform to Eqs. 8 and 9.

4 Results and Discussion

4.1 Theoretical Analysis

Figure 2a shows the metal surface displacement distribution. As the source term includes only scalar displacement potential, and shear motion is generated from mode conversion at the metal surface, both direct generation and mode conversion contribute to the surface normal and tangential displacements. The normal displacement is largest at, and in the area adjacent to, the illumination center and this is the direct result of thermal expansion owing to the laser power absorption. Since the water coupling medium cannot support shear modes of motion, the acoustic pressure is only related to the normal displacement of the metal surface; therefore, the highest acoustic signal is captured above the laser beam incidence spot, i.e., \(\theta =90^{\circ }\). The presence of the transducer redistributes the pressure wave energy and broadens the acoustic beam. The obvious differences can be seen upon comparison of the two wavefront fields in Fig. 2b as the partial reflection distorts and reshapes the pressure fields.

The results are compared with theory from Eqs. 8 and 9. As shown in Fig. 2c, the calculated result is more reliable and shows a pattern similarity to the experimental signal when the pressure wave reflection of the transducer is considered. This characteristic becomes very important when selecting the best location or modulation frequency for the transducer and laser. The frequency response of the transducer also needs to be corrected under the current FDLU configuration when modulated with multi-frequency excitation waveforms. The computed results which include reflections were slightly shifted (approx. 0.6 %) with respect to the experimental response which could be due to the following reasons: (1) discrepancy introduced by neglecting the focused transducer surface curvature; (2) inaccurate transducer position between calculation and experiment.

4.2 FDLU Tensile Test

The 1 MHz laser-induced signal was demodulated by a lock-in amplifier using a time constant of 100 ms. The lock-in signals were captured and digitized 300 times within 1 min and subsequently averaged. The amplitude and phase components of the FDLU signals and their standard deviations are depicted in Fig. 3a. Both amplitude and phase exhibit good reproducibility and reversibility during the tests within the elastic regime. The phase performance is better than the amplitude. With a standard deviation up to only 0.5\(^{\circ }\) despite a small hysteresis, the phase is consistently reversible within the elastic regime. Both amplitude and phase show that the FDLU signal returns to the initial level after the removal of the external load. Figure 3b depicts the full history of the strain-dependent signal from unstressed state to fracture. As the commercial adhesive strain gauge failed after the actual strain exceeded its operating range at a point in the plastic regime, the rest of the strain values were undetermined. The amplitude shows unstable features when the sample underwent plastic deformation as a result of the large surface deformation. The phase trace is smoother and indicates two different regions of mechanical strength: The inflection point defines the elastic limit, about 3500 \(\upmu \)m/m, for this material [12].

Fig. 1
figure 1

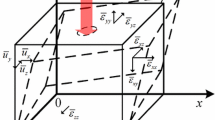
(a) Diagram of FDLU methodology; (b) experimental setup for frequency-scan FDLU testing sample (aluminum, cubic volume: 80 \(\times \) 80 \(\times \) 80 mm\(^{3})\). Frequency scanning range 940 kHz–1 MHz; laser power density: 32 \(\hbox {W}\cdot \hbox {cm}^{-2}\), beam size: 2 mm in diameter, transducer: 19.05 mm PANAMETRICS v314, 1 MHz nominal frequency response, focal length 48.26 mm. Tensile test dog-bone sample (waist at center, thickness \(\times \) width \(\times \) length: 2 \(\hbox {mm}\times 5\hbox { mm} \times 12.5 \hbox { mm}\))

Full size image
Fig. 2
figure 2

(a) Surface displacement of the semi-infinite aluminum sample calculated from Eq. 6; (b) calculated ultrasonic pressure field and wavefronts from the numerical inverse Hankel transform of (1) Eqs. 8, 2 and 9 (transducer at \(z = -48\) mm, \(f = 1\) MHz); (c) frequency-scan experimental results and theoretical simulations calculated from Eqs. 8 and 9; (laser power: 1 W, beam size: 2 mm in diameter)

Full size image
Fig. 3
figure 3

(a) Strain-dependent FDLU signal recorded from two sets of tensile stretching and releasing procedures within the elastic regime; phase and amplitude channels. (b) Full history of FDLU signal from the stress-free state to fracture; amplitude and phase channels

Full size image

A complete quantitative explanation of the FDLU signal is difficult, as the geometry of the dog-bone sample is complex and finite. Multiple reflections occur at each boundary, and it is impossible to find an analytical solutions under such conditions. However, the source of the signal generation can be generally analyzed qualitatively as the result of two aspects, namely the surface vertical displacement and elastic property change. In agreement with independent measurements, deformation occurs when the sample is elongated through tensile stressing. For infinitesimal deformation and cubic materials, the Poisson ratio is \(\nu \approx {\delta l^{\prime }}/{\delta l}; {\delta l^{\prime }}({\delta l)}\) is the deformation perpendicular (parallel) to the direction of stress. The tensile deformation will increase the distance between transducer and sample surface, and this contribution to the phase lag increase can be estimated as \(\delta \varphi _1 \approx 2\pi \delta l^{\prime }/\lambda _0 ; \lambda _0\) is the ultrasonic wavelength in water. Next, the elastic parameters are stress dependent, a phenomenon known as acoustoelasticity [13]. The elastic-wave-velocity stress dependence is expressed as \(\delta c/c=f(\tau )\), where f is a function that determines the external stress-induced relative change of wave velocity, so the second contribution to the phase can be estimated as \(\delta \varphi _2 \approx 2\pi f(\tau )l_0 /\lambda _1 \); \(l_0 \), \(\lambda _1 \) are sample thickness and longitudinal wavelength in the sample, respectively. So far the effects of surface displacement and elastic property change were not possible to separate by only using a single modulated frequency. An alternative investigation procedure is the multi-frequency/frequency-modulated pulse compression FDLU approach using a linear frequency modulation (LFM) chirp [14,15,16]. By cross-correlating the received chirp to the generating signal, this methodology allows time delay analysis in the time-domain which can be a good quantitative solution to this issue.

5 Conclusions

A flexible FDLU experimental setup based on fiber-coupled laser and immersion transducers has been built. A semi-infinite aluminum sample was tested experimentally by means of FDLU and analyzed with a liquid–solid thermoelastic interface theoretical model. The frequency-scan results indicated that the presence of the transducer can seriously affect the power spectrum of the pressure wave field in water, which showed good agreement with the theoretical computation using an acoustic impedance matching boundary condition. Based on the present setup, a non-commercial rig was made and configured on the FDLU tester for the purpose of tensile testing. Strain dependence of the FDLU at a specific frequency was investigated using a strain gauge as an independent measure of the applied stress in the rig. Within the elastic regime, the FDLU signal showed good reproducibility and reversibility with excellent SNR; for tests beyond the elastic regime, the phase exhibited distinct elastic and plastic regimes and was more stable than amplitude. Although the FDLU theory presented in this work can give a reasonable prediction of the frequency-dependent signal, it is unable to quantify the signal changes due to tensile stressing; therefore, a qualitative explanation of the signal strain dependence was introduced. The entire FDLU signal strain history indicates the existence of an elastic limit during the tensile testing. The FDLU technique makes it possible to monitor the stress–strain relation in a solid material remotely, instead of having to resort to contact measurements. The mechanical properties of the material can be further estimated from the analysis of the signal and thus allow the evaluation of its reliability. Compared to pulsed laser ultrasonic techniques that may require bulky apparatus [17,18,19,20,21] and to pure ultrasonic detection that requires a contacting piezoelectric device, the FDLU test setup exhibits very good and reproducible responses in mechanical evaluation studies, benefiting from a fiber-coupled diode laser as part of a potentially portable instrument for in-field evaluation of mechanical components and structures.