1 Introduction

Photothermoacoustic (PTA) techniques enjoy a wide variety of applications in the field of nondestructive testing of solids and fluids [1,2,3,4]. These methodologies generally involve two physical processes: laser illumination of, and photon absorption by, a sample, followed by energy conversion in the form of thermal diffusion (photothermal, PT) or through further thermoelastic energy conversion into acoustic (ultrasonic) wave generation due to thermal expansion (photoacoustic ultrasound, PAUS). Either modality can be used in materials evaluation by means of thermal or acoustic/ultrasonic detection measurements. PTA applications have been extended to mechanical property diagnostics, specifically stress–strain assessment [5,6,7,8,9,10,11], which is conventionally conducted by X-ray diffraction [12]. PTA approaches have the advantage of relying on a laser source and thermal infrared or acoustic/ultrasonic detectors; therefore, they are user-friendly and avoid potentially harmful radiation. In recent years, many experimental implementations of PT and PAUS evaluations on metallic [7,8,9] and composite materials [10] have been published and most of them focused on the PTA signal or image features when the sample was experimentally tensile loaded to plasticity. However, a comprehensive PTA theory correlating the signal to the elastic and thermal properties change has not been systematically developed. The complexity of the stress/strain-related problem lies in complicated tensor formalisms and anisotropic thermal and elastic property analyses. Fortunately, with the help of the finite element method (FEM), an effective discrete and numerical approach, tensor analysis can be largely simplified. In this paper we propose a linear elastic PTA theory considering static external loading and we obtain general analytical expressions on which the FEM analysis is based. The presented FEM-simulated results are compared with some frequency-domain PT and PAUS experimental results. The paper concludes with a comparison between these two approaches when used as nondestructive testing modalities.

2 Theoretical Analysis

2.1 Linear Photothermal Diffusion Theory with Material Pre-stressing

The reason for discussing the linear theory is to simplify the modeling. The validity of a linear model is confined within the range of small perturbations resulting in linear signal generation with laser intensity and a concomitant linear stress–strain relation. Laser radiation absorption is the fundamental reason leading to PTA signal generation which must be treated with photothermal diffusion wave theory in the first place. Prior evidence [5, 13] has shown that under tensile loading, thermal conductivity would evolve into a tensor. Here we consider a purely tensile or compressive load that introduces uniform stress distribution inside the solid so that the loading is still confined within the elastic regime and the solid exhibits a linear stress–strain relation. A model of a pre-stressed elastic sample is shown in Fig. 1. According to the law of conservation of energy, heat absorption Q per unit time within an elastic body is equal to the sum of net heat flux across the surface and the volume heat source g, i.e.,

$$ \int_{V'} {\frac{\partial Q}{\partial t}dV'} = \int_{V'} {T\frac{\partial S}{\partial t}dV'} = - \oint_{S'} {{\mathbf{k}}\nabla T \cdot {\mathbf{n}}_{s'} dS'} + \int_{V'} {gdV'} . $$
(1)

S′ and V′ represent the boundary surface and volume, respectively, of the deformed elastic material; k = kij is the thermal conductivity tensor and is assumed to be symmetric and independent of coordinates; and ns′ is an outward unit normal vector. S is the volumetric entropy density given in the following form [14]:

$$ S(T) = S_{0} (T) + I_{1} \delta_{ij} (3\lambda + 2\mu )\alpha_{l} . $$
(2)

S0(T) is the system entropy in the absence of external loading; λ and μ are Lamé’s first and second constants. δij is the Kronecker delta function with δij = 1 for i = j, and δij = 0 otherwise, αl is the linear thermal expansion coefficient, and I1 is the overall strain invariant that includes both static and dynamic stress. For harmonic modulation, the entropy change due to deformation arises either from static stressing which always reaches dynamic equilibrium, or from modulated laser radiation which is too small to consider [15]. Therefore, this term is negligible and only S0(T) should be considered. Equation 1 takes on the generalized differential form

$$ \rho C_{V} \frac{\partial T}{\partial t} - \sum\limits_{i,j} {\frac{\partial }{{\partial x_{i} }}\left( {k_{ij} \frac{\partial T}{{\partial x_{j} }}} \right)} = g, $$
(3)

where ρ and CV are the density and specific heat capacity of the material with respect to its non-deformed state on which all the differential operators apply. The temperature field should be that of the deformed system. Following an analysis in seismology [16], a Lagrangian coordinate system X(X1, X2, X3) can be defined. The original coordinate system x(x1, x2, x3) is converted into the new system with the following coordinate translation relations:

$$ X_{1} = x_{1} + \bar{u}_{1} ,\quad X_{2} = x_{2} + \bar{u}_{2} ,\quad X_{3} = x_{3} + \bar{u}_{3} . $$
(4)

Here \( \bar{u}:(\bar{u}_{1} ,\bar{u}_{2} ,\bar{u}_{3} ) \) is the initial displacement vector subject to pre-stress tensor \( \bar{\sigma }_{ij} \) with i, j = 1,2,3. Applying a coordinate transformation and using the chain rule for differentiation, the second term of Eq. 3 becomes [11]:

$$ \sum\limits_{i,j} {\frac{\partial }{{\partial x_{i} }}\left( {k_{ij} \frac{\partial T}{{\partial x_{j} }}} \right)} = \sum\limits_{i,j,l} {\frac{{\partial \left( {k_{ij} J_{jl} {{\partial T} \mathord{\left/ {\vphantom {{\partial T} {\partial X_{l} }}} \right. \kern-0pt} {\partial X_{l} }}} \right)}}{{\partial x_{i} }}} = \sum\limits_{i,j,l,m} {(2 - \delta_{ij} )k_{lm} J_{il} J_{jm} \frac{{\partial^{2} T}}{{\partial X_{i} \partial X_{j} }}} $$
(5a)

with the following definitions:

$$ \begin{aligned} J_{ij} & = \delta_{ij} (1 + \bar{\omega }_{ij} ) + (\bar{\varepsilon }_{ij} - \bar{\omega }_{ij} ), \\ \bar{\varepsilon }_{ij} & = ({{\partial \bar{u}_{i} } \mathord{\left/ {\vphantom {{\partial \bar{u}_{i} } {\partial x_{j} }}} \right. \kern-0pt} {\partial x_{j} }} + {{\partial \bar{u}_{j} } \mathord{\left/ {\vphantom {{\partial \bar{u}_{j} } {\partial x_{i} }}} \right. \kern-0pt} {\partial x_{i} }})/2, \\ \bar{\omega }_{ij} & = ({{\partial \bar{u}_{i} } \mathord{\left/ {\vphantom {{\partial \bar{u}_{i} } {\partial x_{j} }}} \right. \kern-0pt} {\partial x_{j} }} - {{\partial \bar{u}_{j} } \mathord{\left/ {\vphantom {{\partial \bar{u}_{j} } {\partial x_{i} }}} \right. \kern-0pt} {\partial x_{i} }})/2. \\ \end{aligned} $$
(5b)

Here, Jij is the Jacobian, \( \bar{\varepsilon }_{ij} \) is the symmetric initial strain tensor, and \( \bar{\omega }_{ij} \) is an antisymmetric initial rotational tensor equal to 0 if no torsion is exerted on the material. For the case of axial loading only, the Jacobian explicitly becomes a diagonal matrix, i.e., Jij = 0 for i ≠ j. In the case of a two-dimensional thermal wave in the frequency domain, the use of coordinate notation x and y instead of X1 and X2 modifies Eq. 3 as follows:

$$ i\omega \rho C_{V} T - \left. {\left[ {k_{xx} J_{11}^{2} \frac{{\partial^{2} T}}{{\partial x^{2} }} + k_{yy} J_{22}^{2} \frac{{\partial^{2} T}}{{\partial y^{2} }}} \right. + (k_{xy} + k_{yx} )J_{11} J_{22} \frac{{\partial^{2} T}}{\partial x\partial y}} \right] = g. $$
(6)
Fig. 1
figure 1

Pre-stressed linear deformation photoacoustic model

Full size image

Equation 6 suggests that initial stressing will result in anisotropic thermal wave diffusion by changing the effective thermal conductivity components while the properties such as ρ and CV are constant. In the frequency domain, the temperature field is always associated with a characteristic length, namely the thermal diffusion length which is proportional to \( f^{ - 1/2} \). If the thermal diffusion length is comparable with the geometric dimension of the sample, the stress-induced thermal anisotropy becomes significant and detectable. However, when the modulation frequency is high enough in the US frequency range (MHz), the corresponding diffusion length is usually negligible compared with geometric dimensions. In such cases, PAUS effects need to be considered, as purely photothermal approaches normally do not apply in the MHz range due to the very large attenuation of the PT signal to below the noise level of the instrumentation.

2.2 Linear Photoacoustic Ultrasonic Theory with Material Pre-stressing

Again, the assumption of weak excitation source still stands followed by a linear stress–strain relation and thermoelastic conversion. For a stress-free elastic material, various acoustic wave modes can propagate independently, which indicates that linear elastic deformation seems to have no impact on acoustic waves [17]. Such an idealized situation is based on a proper infinitesimal strain/deformation assumption and is applicable for microscale deformations associated with elastic waves. When static external loading is exerted on a material confined within the elastic deformation regime, the increased loading magnitude can change the elastic isotropy and wave propagation pattern. The sample is regarded as undergoing two processes sequentially: static elongation due to external loading followed by laser incidence and elastic wave generation. The PAUS signal generation is associated with the latter process either in the time domain or in the frequency domain. For pre-stressed solids, the balance of forces with respect to the original coordinates yields:

$$ \sum\limits_{j} {\frac{{\partial \bar{\sigma }_{ij} }}{{\partial x_{j} }}} = {\mathbf{0}}. $$
(7)

An incident laser excitation is regarded as a perturbation and is associated with a dynamic counterbalance stress tensor δσij generated by thermal expansion. The linear stress–strain approximation for such a small displacement is given as [18]

$$ \delta \sigma_{ij} = \lambda (\delta \varepsilon_{11} + \delta \varepsilon_{22} + \delta \varepsilon_{33} )\delta_{ij} + 2\mu \delta \varepsilon_{ij} , $$
(8)

where δεij is the laser-induced elastic strain. As both static and dynamic stress/strain tensors are involved in the deformed system, Hooke’s law cannot be applied directly. Instead, the free energy function Ft of the system is introduced [17]:

$$ F_{t} = \tfrac{1}{2}\sum\limits_{i,j} {\sigma_{ij} \varepsilon_{ij} } $$
(9a)
$$ \sigma_{ij} = \frac{{\partial F_{t} }}{{\partial \varepsilon_{ij} }} = \bar{\sigma }_{ij} + \delta \sigma_{ij} . $$
(9b)

σij and εij are total stress and strain, respectively, in the deformed state. The free energy function includes the work done by thermal expansion in which the thermoelastic coupling coefficient is a function of static load [19, 20] and thus becomes a tensor, i.e., \( \alpha_{l} (\delta_{ij} + h\bar{\varepsilon }_{ij} ) \). The work We done during the expansion is expressed as

$$ W_{e} = - \sum\limits_{i,j} {\left[ {\left( {3B + \lambda h\bar{I}_{1} } \right)\delta_{ij} + 2\mu h\bar{\varepsilon }_{ij} } \right]\alpha_{l} \delta \varepsilon_{ij} T} . $$
(10)

In Eq. 10, h is the coupling coefficient between static/initial strain \( \bar{\varepsilon }_{ij} \) and thermoelasticity, B is bulk modulus of the material, and T is the temperature change due to laser heating. The thus generated expansion stress tensor \( \sigma_{ij}^{e} \) is written as

$$ - \sigma_{ij}^{e} = \left( {\frac{{\partial W_{e} }}{{\partial \delta \varepsilon_{ij} }}} \right)_{S} = \delta_{ij} \alpha_{l} (3\lambda + 2\mu + \lambda h\bar{I}_{1} )T + 2\mu \alpha_{l} h\bar{\varepsilon }_{ij} T, $$
(11)

where \( \bar{I}_{1} = \bar{\varepsilon }_{11} + \bar{\varepsilon }_{22} + \bar{\varepsilon }_{33} \) is the first invariant of the initial strain. Equation 11 assumes an adiabatic condition and carries a subscript S. All the stress tensors from Eqs. 9b and 11 form a new equilibrium state and thus should satisfy Hooke’s law in the frequency domain with respect to the original coordinate system, i.e.,

$$ \begin{aligned} \sum\limits_{j} {\frac{{\partial \sigma_{ij} }}{{\partial x_{j} }}} & = \sum\limits_{j} {\frac{{\partial \delta \sigma_{ij} }}{{\partial x_{j} }}} \\ & = - \omega^{2} \rho \delta u_{i} + \sum\limits_{j} {\frac{\partial }{{\partial x_{j} }}\left[ {\delta_{ij} (3\lambda + 2\mu + \lambda h\bar{I}_{1} )\alpha_{l} T + 2\mu h\bar{\varepsilon }_{ij} \alpha_{l} T} \right]} . \\ \end{aligned} $$
(12)

δui(X1, X2, X3) is the displacement vector transformed into the deformed state. Introducing a coordinate transformation similar to Eq. 4, combining Eqs. 8 and 12, and considering a linear strain–displacement relation, we obtain:

$$ \frac{{\partial \delta u_{i} }}{{\partial x_{j} }} = \sum\limits_{k} {\frac{{\partial \delta u_{i} }}{{\partial X_{k} }}\frac{{\partial X_{k} }}{{\partial x_{i} }}} = \sum\limits_{j} {J_{ij} \frac{{\partial \delta u_{i} }}{{\partial X_{j} }}} $$
(13a)
$$ \begin{aligned} & 2\mu \sum\limits_{l,j} {\frac{{\partial \left( {J_{lj} \delta \varepsilon_{il} } \right)}}{{\partial X_{j} }}} + \lambda \sum\limits_{j} {\frac{{\partial \left( {J_{ij} I_{1} } \right)}}{{\partial X_{j} }}} \\ & \quad - \alpha_{l} \left[ {\frac{\partial }{{\partial x_{i} }}\left( {3\lambda T + 2\mu T + \lambda h\bar{I}_{1} T} \right) + 2\mu h\sum\limits_{j} {\frac{{\partial \left( {\bar{\varepsilon }_{ij} T} \right)}}{{\partial x_{j} }}} } \right] + \rho \omega^{2} \delta u_{i} = 0. \\ \end{aligned} $$
(13b)

Again, Jij is the Jacobian and I1 = δε11 + δε22 + δε33. Equations 13 are adequate to describe the PAUS waves propagating within a linearly pre-stressed alloy although they have a very complicated form. The temperature term involves contributions from work sources such as the vibration source and should be obtained by solving Eq. 6.

To simplify the discussion and enhance physical insight, a plane stress–strain problem with purely uniform stretch is considered so that the Jacobian matrix becomes symmetric. In practice, since the frequency is up to the MHz range, the diffusion length is on the order of micrometers and only the surface-temperature-gradient-induced momentum needs to be considered, with no anisotropic diffusion. The thermoelastic source/inhomogeneous term in Eq. 13b is then simplified:

$$ - \alpha_{l} \left. {\left[ {\left( {3\lambda + 2\mu + \lambda h\bar{I}_{1} } \right)\sum\limits_{j} {J_{ij} \frac{\partial T}{{\partial X_{j} }}} + 2\mu h\sum\limits_{l,j} {\bar{\varepsilon }_{il} J_{lj} \frac{\partial T}{{\partial X_{j} }}} } \right]} \right|_{{X_{3} = 0}} . $$
(14)

For a two-dimensional stress–strain problem, the homogeneous part of the wave Eq. 13b is expressed in terms of coordinates x and y instead of X1 and X2:

$$ \begin{aligned} - \rho \omega^{2} \delta u_{x} & = (\lambda + 2\mu )\left( {J_{11} \frac{{\partial \delta \varepsilon_{xx} }}{\partial x} + J_{12} \frac{{\partial \delta \varepsilon_{xx} }}{\partial y}} \right) \\ & \quad + 2\mu \left( {J_{12} \frac{{\partial \delta \varepsilon_{xy} }}{\partial x} + J_{22} \frac{{\partial \delta \varepsilon_{xy} }}{\partial y}} \right) + \lambda \left( {J_{11} \frac{{\partial \delta \varepsilon_{yy} }}{\partial x} + J_{12} \frac{{\partial \delta \varepsilon_{yy} }}{\partial y}} \right) \\ \end{aligned} $$
(15a)
$$ \begin{aligned} - \rho \omega^{2} \delta u_{y} & = (\lambda + 2\mu )\left( {J_{12} \frac{{\partial \delta \varepsilon_{yy} }}{\partial x} + J_{22} \frac{{\partial \delta \varepsilon_{yy} }}{\partial y}} \right) \\ & \quad + 2\mu \left( {J_{11} \frac{{\partial \delta \varepsilon_{xy} }}{\partial x} + J_{12} \frac{{\partial \delta \varepsilon_{xy} }}{\partial y}} \right) + \lambda \left( {J_{12} \frac{{\partial \delta \varepsilon_{xx} }}{\partial x} + J_{22} \frac{{\partial \delta \varepsilon_{xx} }}{\partial y}} \right). \\ \end{aligned} $$
(15b)

Again, no torsion is assumed here, so that J12 = J21. The coupled Eq. 15 has lost the advantage of symmetry and can be regarded as a relative change in stiffness. Referring to the classical wave equation [21], the target sample becomes acoustically anisotropic with an equivalent rigidity given by:

$$ {\mathbf{R}} = \left[ {\begin{array}{*{20}c} {R_{xxxx} } & {R_{xxyy} } & {R_{xxxy} } & {R_{xxyx} } \\ {R_{yyxx} } & {R_{yyyy} } & {R_{yyxy} } & {R_{yyyx} } \\ {R_{xyxx} } & {R_{xyyy} } & {R_{xyxy} } & {R_{xyyx} } \\ {R_{yxxx} } & {R_{yxyy} } & {R_{yxxy} } & {R_{yxyx} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {(\lambda + 2\mu )J_{11} } & {\lambda J_{11} } & {2\mu J_{12} } & 0 \\ {\lambda J_{22} } & {(\lambda + 2\mu )J_{22} } & 0 & {2\mu J_{12} } \\ {(\lambda + 2\mu )J_{12} } & {\lambda J_{12} } & {2\mu J_{22} } & 0 \\ {\lambda J_{12} } & {(\lambda + 2\mu )J_{12} } & 0 & {2\mu J_{11} } \\ \end{array} } \right]. $$
(16)

In the above form, the symmetric condition \( R_{ijkl} = R_{ijlk} = R_{jikl} = R_{klij} \) is no longer valid except when J12 = 0 which stands for axial tensile/compressive loading only.

In summary, Eqs. 6 and 15 show the complete form of anisotropic PT and PAUS theories, respectively, with temperature and surface displacement as independent variables. The existence of the factor i in Eq. 6 results in the well-known spatially exponentially decreasing temperature field. Such a feature is an intrinsic part of thermal wave physics and requires a low experimental modulation frequency for deep subsurface penetration. However, if low frequency is applied to Eq. 15, the left-hand side becomes small approaching zero and results in a quasi-static motion with no elastic wave involvement. As a result, PT and PAUS have to be based on two very different testing modalities.

3 Results and Analysis

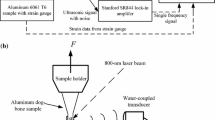
To generate simulations of changes in FD-PTA signals due to stressing, a physical finite element model was built with Comsol Multiphysics® software. A 20 mm × 2 mm planar aluminum sample model was considered. A Gaussian-shaped laser beam was harmonically modulated and directed toward the center of the upper surface, thereby generating an internal temperature gradient which could lead to PT diffusion and PAUS wave generation and propagation.

We focus on the low frequency range (~ Hz) first where PT effects are dominant, with a large diffusion area on the same order as the geometrical dimension of the sample. Based on Eq. 6, the diffusion field of the stressed sample can be simulated by an FEM of thermal diffusion module. A square element mapping method was adopted for the complete mesh, and mesh size was set small enough to have 25 to 80 elements in a single diffusion length. For axial loading, the cross-terms of the thermal conductivity tensor vanish in Eq. 6 and the conductivity change occurs only in the diagonal/orthogonal components with J12 = 0, J11 ≠ J22. Simulated results are shown in Fig. 2. The complex temperature field can be visualized in terms of its real (Fig. 2a) and imaginary (Fig. 2b) parts. For the presence of initial loading, during the FEM analysis \( \bar{\varepsilon }_{xx} \) is assumed to change from − 0.015 to 0.02 with \( \bar{\varepsilon }_{xx} = - \bar{\varepsilon }_{yy} \). This results in the thermal wave field along the two axes exhibiting anisotropy. The gradual shift of the thermal wave phase shown in Fig. 2c reflects the relative change among the stress tensor components and can thus be used as a stress/strain gauge, as experimentally proven in Ref. [11]. Figure 2d shows the result of a lock-in thermographic phase image obtained at 5 Hz under various loading levels in Ref. [13]. The phase distributions are depicted along the half-way midline of the thermal wave field (see the inset) under different loading conditions. In this specific case, while the strain changes from 0 to − 0.015, the FEM simulation shows phase changes similar to the ones in Fig. 2d obtained with lock-in thermography imaging when the experimental strain changed from 0 μm·m−1 to 2000 μm·m−1 [13]. Such observation indicates that the theory has successfully modeled the thermal anisotropy occurring in the stressed sample. In fact, the application of FEM becomes the only approach when dealing with a finite and complicated sample geometry where no analytical solutions to the anisotropic thermal diffusion equation exist.

Fig. 2
figure 2

Simulated and experimental PT signal at 5 Hz modulation. Real part (a) and imaginary part (b) of the thermal wave field (arbitrary units); (c) simulation of PT phase distribution along half of the upper surface (\( \bar{\varepsilon }_{xx} = - \bar{\varepsilon }_{yy} \) is assumed; the strain is unitless); (d) PT experimental result of phase distribution in an aluminum sample under tensile loading [12]. The insets are a magnification of the regions labeled with dashed-line boxes

Full size image

When the modulation frequency moves into the ultrasonic range (~ MHz), PAUS effects become significant and the FEM acoustic module needs to be based on Eqs. 14 and 15. In order that the effects of thermal diffusion and thermoelastic wave propagation might be clearly identified and spatially resolved, two groups of finite element meshes were introduced: a refined (min. grid size < 200 μm2) mesh grid, designated for thermal wave simulations, and a normal mapped (ave. grid size: 0.04 mm2) mesh grid shown in Fig. 3a that was sufficient for elastic wave simulations. For axial loading, the rigidity matrix becomes symmetric, but remains anisotropic. In the FEM simulation, the strain is changed from − 0.01 to 0.01 with the assumption of \( \bar{\varepsilon }_{xx} = - \bar{\varepsilon }_{yy} \). The phase of the vertical component of the harmonic displacement field on the upper surface with anisotropic rigidity is depicted in Fig. 3b in which a distinctive phase shift occurs along with the initial stress/strain change. To obtain a better insight of the phase shift, two specific locations (x = 5 mm and 11 mm) were chosen and the local phase change with respect to initial strain is illustrated in the insets. The phase change patterns at the two locations exhibit different trends which indicate the existence of anisotropy within the sample. Experimentally, the frequency-domain laser ultrasound test was conducted on a test specimen under uniaxial tensile loading described in Ref. [8]. As redrawn in Fig. 3c, a gradually decreasing ultrasonic phase signal was obtained from the experiment which shares similar trends to the bottom-left inset of Fig. 3b. The reason for the larger phase shift range observed in the experimental data is that apart from the effect of changing elasticity of the stretched material, the vertical contraction or Poisson’s displacement due to loading increases the distance between sample surface and transducer which introduces an additional phase shift. Such deformation effect was not possible to exclude from the experimental data. Nonetheless, by considering the insets of Fig. 3b, FEM analysis based on the foregoing theory shows a linear phase change with respect to strain value which should contribute to the experimental signal change.

Fig. 3
figure 3

(a) The FEM model of a plane stress–strain problem; (b) simulated PA phase signal changes with \( \bar{\varepsilon }_{xx} \) and \( \bar{\varepsilon }_{yy} \) at the middle part of the upper surface (insets: bottom-left: phase vs. \( \bar{\varepsilon }_{xx} \) at x = 5 mm, top-right: phase vs. \( \bar{\varepsilon }_{xx} \) at x = 11 mm; the correlation \( \bar{\varepsilon }_{xx} = - \bar{\varepsilon }_{yy} \) is assumed for simulation; the strain is unitless); (c) frequency-domain PA experimental results of an aluminum sample under tensile loading, redrawn from Ref. [9]

Full size image

Compared with the PAUS approach used in this work, PT is entirely based on optical signal generation and thermophotonic detection, thereby being a truly non-contacting method, as opposed to the PAUS transducer requirements for an impedance matching coupling fluid. As regards the magnitude of phase change, PAUS shows a much larger phase shift in experimental and simulated results. However, spurious phase shifts due to the stress-induced displacements occur in PAUS which complicate the analysis. On the other hand, PT signals are functions of thermophysical parameters only; they are simpler and less sensitive to displacements, plus there are no thermal wave mode conversions of the types encountered with ultrasound. As a result, the thermal anisotropy is more easily quantifiable and the overall signal interpretation becomes considerably simpler and more straightforward.

4 Conclusions

A frequency-domain PTA methodology was developed and applied to the detection of changes in the stress–strain behavior of metal alloys by evaluating their thermal/elastic parameters. The theory is based on equilibrium coordinate transformation and involves the initial (unstressed) stress/strain tensor as an important variable. By focusing on widely different frequency ranges in the thermal wave diffusion and ultrasonic regimes, respectively, the FD-PTA theory predicts and derives the anisotropic thermal diffusion and laser ultrasound equations from a common set of physical considerations following optical excitation and light absorption. It indicates the existence of anisotropy in both thermal conductivity and elastic modulus resulting from the mechanically induced stress/strain. To estimate the impact of the stress–strain relation change, an FEM model was used to perform multi-field simulations in terms of harmonic temperature (thermal wave) and vertical displacement (elastic wave) distributions on a 2-D plane sample at two frequency ranges based on the foregoing modified anisotropic PT and PAUS theories. The results indicated that by adopting FEM-aided analysis, the stress–strain condition of finite and complex geometric solids can be evaluated by PTA methodologies. Compared with PAUS, PT represents a theoretically and experimentally simpler and more straightforward means of evaluating stress–strain behavior of alloys.