Keywords

1 Introduction

There are basically two types of approach in structural health monitoring (SHM) namely global approach and local approach. In global approach the changes in the vibrational properties of the structure caused by the damage are measured. This approach is only effective in dealing with large defects because the effects of small defects on the global vibrational properties are often below the noise level in large structures. On the other hand, in local approach the changes in the characteristics of ultrasonic waves propagating across the defects are measured and analyzed to detect and characterize them. This approach is effective in detecting small defects but it requires a dense network of sensors [1].

The existing conventional ultrasonic methods include the pulse-echo, the pitch-catch and through transmission. In the pulse-echo method, defects are detected in the form of additional echoes. In the pitch-catch method, wave dispersion and attenuation due to diffused damage in the material are used as flaw indicators. For thickness-wise inspection, the wave path traverses only a small portion of the material volume; hence, the transducer is mechanically moved along the surface to scan and interrogate the entire material volume. However, the previously mentioned methods are not so sensitive to detect micro cracks in material, delaminations in composite structure and unable to predict structural health of a joint or debonding of stiffeners, where contact surfaces play an important role. In the recent years nonlinear vibration and acoustic phenomena for SHM have emerged to be a promising technique for the detection of microcracks/flaws/delaminations/dislocations/disbondsetc in structural components. The nonlinear acoustical phenomena can be related to various imperfections of atomic lattices (intrinsic or material nonlinearity) and/or non-symmetric thermo-elastic behavior of interfaces (e.g. cracks, contacts, and rubbing surfaces). Intrinsic or material nonlinearity is global type nonlinearity while cracks, contacts, rubbing surfaces are local type nonlinearity. The later has demonstrated a great interest of theoretical and applied research for the last 15 years [2].

Previous experimental work on different materials (e.g., polymer, CL Lexan polycarbonate, nylon, adhesive layers and aluminum alloy) demonstrate that nonlinear phenomena are generally more sensitive to small damage severities than classical linear approaches (depending on velocity, attenuation, etc.) [3]. The features related to nonlinear effects have been investigated so far include: time-domain signal distortions, generation of higher harmonics, resonance frequency shifts, signal modulations, slow dynamics, and nonlinear dissipation. Despite many research works, there is still very little understandings of what physical mechanisms related to these nonlinearities are and the question still remains why material sensitivity of nonlinear effects is so strong if compared with linear responses. There are two major difficulties associated with these problems. The first one is the diversity of nonlinear mechanisms proposed. Similar nonlinear effects can be manifested by different mechanism and vice versa. For example, energy dissipation can be modeled using frictional, hysteretic or thermo-elastic mechanisms. Hysteresis in turn involves both elasticity and dissipation, and could be linear or nonlinear. The second one is, the various experimental evidence related to these nonlinear mechanisms have been observed. It is often very difficult, if not impossible, to separate all these mechanisms involved. It is also important to note that nonlinearities may result not only from cracks but also from other non-damage related effects such as: friction between elements at structural joints or boundaries, overloads, material connections between transducers and monitored surfaces, electronics and instrumentation measurement.

This article describes different types of nonlinearities present in damaged structures and different nonlinear wave interaction techniques developed over the last few years to estimate nonlinearity (damage) in structures in an effort to develop efficient techniques for health monitoring of stiffened plate using nonlinear elastic wave and embedded piezoelectric network.

2 Theoretical Background

Experimental evidence for the highly nonlinear behavior of micro cracked and damaged materials has existed for years from experiments of static stress–strain behavior and dynamic nonlinear wave interaction [4]. Those experiments imply that the dynamic elastic behavior of most solid materials cannot be described by a linear theory. Nonlinear elastic behavior may manifest itself in the generation of harmonics upon dynamic wave propagation, nonlinear attenuation, resonance frequency shift and slow time effects; while, hysteresis and discrete memory are commonly observed in static tests and persist even in low-strain dynamic experiments [5]. Micro-inhomogeneities such as cracks, voids, and contacts have a complex compliance and the local nonlinear forces may entirely dominate the relatively small atomic nonlinearity. Therefore, the theoretical description of nonlinear mesoscopic elastic materials contains terms that describe classical nonlinearity, as well as hysteresis, and discrete memory. The full theory of these effects has not been constructed yet. However, the approaches described below provide at least a qualitative explanation of much of the experimental evidence.

2.1 Classical Theory

The classical theory begins with the expansion of the elastic strain energy in powers of the strain tensor, \( \epsilon _{ij} \). The expansion coefficients designate the components of the second-order elastic tensor and the third-order elastic tensor. The equation of motion in Lagrangian coordinate x and time t is given as [6]:

$$ \rho \frac{{\partial^{2 } }}{{\partial t^{2 } }}(u_{i} ) = \frac{{\partial \sigma_{ij} }}{{\partial x_{j} }} $$
(1)

where, \( u_{i} \) is the displacement vector, ρ is the material density, \( \sigma_{ij} \) is the stress tensor. Now, for one-dimensional case and for non-linear elasticity the above equation of motion can be expressed as [7]

$$ \rho \frac{{\partial^{2 } u }}{{\partial t^{2 } }} = k_{0} \left[ {1 + \beta \frac{\partial u}{\partial x} + \delta \left( {\frac{\partial u}{\partial x}} \right)^{2} + \cdots \cdots \cdot } \right]\frac{{\partial^{2 } u }}{{\partial x^{2 } }} $$
(2)

where the stress field is expressed as

$$ \begin{aligned} \sigma \left( x \right) & = k_{0} \left[ {1 + \beta \frac{\partial u}{\partial x} + \delta \left( {\frac{\partial u}{\partial x}} \right)^{2} + \cdots \cdots \cdot } \right]\frac{\partial u}{\partial x} \\ & = k_{0} \left[ {1 + \beta \epsilon + \delta \epsilon^{2} + \cdots \cdots \cdot } \right]\epsilon \\ \end{aligned} $$
(3)

where

\( \epsilon = \frac{\partial u}{\partial x} \) is the strain field, \( k_{0} \) is the linear elastic modulus, and \( \beta \) and \( \delta \) are non linear parameters are the measures of cubic and quartic anharmonicities [8]. These parameters are the linear combinations of the elastic constants [6].

Now, considering a time-harmonic plane (displacement) wave A 1cos(kX 1 − ωt), where A 1 is the amplitude, k is the wave number, and ω is the angular frequency. Assuming that the nonlinearity in the solid is small (for \( \beta \) only), then the solution to Eq. (2) for this time-harmonic wave is obtained by a perturbation analysis as [6]

$$ \begin{aligned} u_{1} & = - \frac{1}{8}\beta k^{2} A_{1}^{2} X_{1 } + A_{1} \cos \left( {kX_{1 } {-}\omega t} \right) + \frac{1}{8}\beta k^{2} A_{1}^{2} X_{1 } \cos \left\{ {2\left( {kX_{1 } {-}\omega t} \right)} \right\} + \cdots \\ & = A_{0 } + A_{1} \cos \left( {kX_{1 } {-}\omega t} \right) + A_{2} \cos \left\{ {2\left( {kX_{1 } {-}\omega t} \right)} \right\} + \cdots \\ \end{aligned} $$
(4)
$$ \beta = \frac{{8A_{2} }}{{k^{2} A_{1}^{2} X_{1 } }} $$
(5)

Therefore, it is noted that the amplitude of the second-harmonic displacement is proportional to the acoustic nonlinearity parameter and a subharmonic; that is, the static displacement is induced by the material nonlinearity. The acoustic nonlinearity parameter can be determined experimentally by measuring the absolute amplitudes of the fundamental (\( A_{1} \)) and the second-harmonic (\( A_{2} \)) displacement signals.

2.2 Hysteresis

The Classical nonlinear theory explained above cannot explain the nonlinear behavior generated by local nonlinear forces due to damage presence (such as cracks, voids and contacts). This evidence was found experimentally by several authors [4, 8, 9]. In order to include nonlinear behaviours like classical nonlinearity, as well as hysteresis and discrete memory, a stress dependence on strain time derivative (i.e.,\(\;\dot{\epsilon } \)) can be added in the nonlinear classical stress–strain relationship. A theoretical description is given by the nonlinear mesoscopic elastic model as presented below.

$$ \sigma = \mathop \smallint \nolimits k(\epsilon ,\dot{\epsilon })d\epsilon $$
(6)
$$ \begin{aligned} k\left( {\epsilon ,\dot{\epsilon }} \right) & = k_{0} \left[ {1 + \left( { \beta \epsilon + \delta \epsilon^{2} + \cdots } \right) + \propto \{\Delta \epsilon + \epsilon \left( t \right)sign\left( {\dot{\epsilon }} \right) + \cdots \} } \right] \\ & = k_{0} \left[ {1 + nonlinear\;classical\;terms + nonlinear\;nonclassical\;terms } \right] \\ \end{aligned} $$
(7)

where, k is the combination of nonlinear classical and hysteretic (or non-classical) modulus wherein \( k_{0} \) is the linear modulus, \( \Delta \epsilon \) is the strain amplitude change over the previous period (i.e., \( \epsilon \) is a function of time), \( \dot{\epsilon } = d\epsilon /dt \) is the strain rate, \( sign\left( {\dot{\epsilon }} \right) = 1 \) if \( \dot{\epsilon } > 0 \) and \( sign\left( {\dot{\epsilon }} \right) \) = −1 if \( \dot{\epsilon }\,<\,0,\;\beta \) and \( \delta \) are classical nonlinear coefficients and \( \propto \) is a material hysteresis measure and they can be negative. The increase in \( \alpha \) reflects an increase in the nonlinear hysteretic behavior of the material Experimental and numerical studies proved that for purely hysteretic materials (\( \beta ,\delta = 0, \propto \ne 0 \)) and for mono frequency harmonic excitation, the third harmonic is generated which is quadratic with the fundamental amplitude (Eq. 8) [5, 10–12]. Hysteresis also causes the linear decrease in the resonance frequency (Eq. 9) and a linear increase in the modal damping ratio (Eq. 10) with the increase in strain levels. Hysteresis does not affect the level of even harmonics [5].

$$ \Delta \epsilon_{3f} = c_{1 }\Delta \epsilon^{2} $$
(8)
$$ \frac{{f_{0} - f}}{{f_{0} }} = c_{2} \Delta \epsilon $$
(9)
$$ \frac{{\xi - \xi_{0}}}{{\xi_{0}}} = c_{3} \Delta\epsilon $$
(10)

where, \( f_{0} \) = initial resonance frequency, f = resonance frequency at a particular strain level, \( \xi_{0} \) = initial damping ratio, \( \xi \) = damping ratio at a particular strain level, \( c_{1,} \;c_{2 } \) and \( c_{3} \) are the coefficients proportional to the hysteresis parameter, \( \propto \).

2.3 Contacts

Experimental data on a cracked medium exhibiting high acoustic nonlinearity is a commonly observed phenomenon. This is due to the appearance of the nonlinearity parameters in the elastic modulus for the cracked medium for opening and closing of the cracks [13, 14]. Crack produces rough surfaces which are in contact. If observed on a microscopic scale, all machined surfaces are also rough, and the contact between surfaces is restricted to discrete areas at the tip of the surface asperities. The contact between the two nominally flat, but imperfect (or non-bonded), surfaces is no exception. In this respect, all the bolted joints also develop partial contact at their imperfect interfaces, unless the bolted joints are glued [15]. At these imperfect interfaces a true contact area is generated (a fraction of the nominal contact area). The true contact area is known to be smaller than the nominal contact area. This true contact area varies with the contact pressure. The behavior of the crack or the imperfect contact surfaces can be described using the model in which the interface is represented as an elastic contact of two rough surfaces, pressed one to the other under the action of internal stresses in the surrounding solid or due to the applied pressure [13, 14].

3 FE Simulation of the Stiffened Aluminum Plate

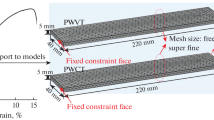
The models of the stiffened aluminum plate for different delamination lengths (100, 150, 200, 250 and 300 mm) are prepared using ANSYS (APDL) 14.0 FE software. The script files are written to do the entire modeling and analysis using APDL commands. A typical figure of the plate for 200 mm delamination is shown in Fig. 1, while the applied loading (20 cycles sine pulse modulated by Hanning window with central frequency of 2 kHz) in Fig. 2. The details of the material property and the geometry, contact surfaces, and the analysis parameters are given in Tables 1,  2, and 3 respectively.

Fig. 1
figure 1

Model of the stiffened aluminum plate in ANSYS (with delamination length of 200 mm)

Full size image
Fig. 2
figure 2

Source signal (2 kHz 20-cycle Hanning pulse)

Full size image
Table 1 Properties of stiffened aluminum plate and applied loading
Full size table
Table 2 Contact surface details
Full size table
Table 3 Analysis parameter details
Full size table

3.1 Numerical Results and Discussion

The total health monitoring work comprises following steps: obtaining time domain data from the simulation, feature (i.e., appearance of harmonics) extraction from the data by performing FFT of the time domain signal and damage severity study by plotting damage index corresponding to the delamination length. The damage index (DI) is defined as the normalized second harmonic amplitude with respective to the carrier frequency amplitude. The typical time domain signals and the corresponding FFTs for the delamination lengths of 100, 200, 250 and 300 mm are shown in Fig. 3. In this figure, higher harmonics at 4, 6, 8, 10 and 12 kHz of the 2 kHz carrier frequency are shown. The final result in Fig. 4 shows the increase in the nonlinearity (DI) with the increase in the delamination length.

Fig. 3
figure 3

Typical time domain signals for the delamination length of 100, 200, 250, 300 mm (a, c, e, g) and corresponding FFT of the signals (b, d, f, h)

Full size image
Fig. 4
figure 4

Delamination length versus damage severity

Full size image

4 Conclusions

Since material strength is often reduced by micro defects, which are usually too small to detect by linear ultrasonic techniques (e.g., by measuring the change in attenuation, velocity, etc.), but can increase the acoustic nonlinearity significantly much earlier than the change in the linear parameters of the material. So, very small damage (e.g., micro cracks, contacts, etc.) can be detected by measuring nonlinear acoustic parameters. But to adopt the nonlinear techniques, it is very much important to check that degree of nonlinearity associated with the instruments including PZTs used for the experiments as they are also nonlinear in character. Also the boundary condition is of another concern for those techniques since boundary conditions may induce strong nonlinear effects.

The numerical investigation of the stiffened aluminum plate reveals that the modulation of the elastic wave occurring at the debonding interface between the plate and stiffener due to the wave interaction with the nonlinear contact stiffness. As a consequence, the higher harmonics of the input signal are generated. The corresponding graph for different delamination lengths show that the increase in the nonlinearity parameter (damage index) is due to the increase in the delamination length.

4.1 Scope for Future Research

The present work is the delamination detection of stiffened metallic structures can be extended for damage detection of composite plates as well as to monitor the health of riveted and bolted joint structures. So far only higher harmonics method is adopted for the stiffened plate simulation. The model can also be tested for other nonlinear methods to check how the other methods are sensitive to this type of contact nonlinearity. Experimental validation of the simulation results are required to rely on the methods.