1 Introduction

Gravitational data sets, which are measured using gravimeters based on land, in boreholes or on board satellites, aircraft or marine vessels, are used to estimate locations and shapes of embedded anomalous mass density bodies in the earth. For instance, gravity signal extraction and enhancement techniques (Zhang et al. 2014) can be used to estimate the approximated shapes of anomalous mass bodies in the underground. To more accurately determine depths, volumes and densities of anomalies, elaborate gravity inversion algorithms are employed (Li and Oldenburg 1998). To obtain more comprehensive and less ambiguous models of the earth, gravity data have been jointly inverted with other geophysical data sets, such as seismic data and electromagnetic induction data using constraints that couple the models of the different material parameters structurally or petrophysically (Moorkamp et al. 2011; Roberts et al. 2016). In recent years, rapid improvement in gravimeter efficiency and modern inversion algorithms has enhanced the capability of collecting large gravity data sets over large-scale areas and inverting such data sets for 3D density models (Kamm et al. 2015). These two improvements guarantee the wide application of the gravity methods in different geophysical or geodetic problems, such as mineral exploration (Beiki and Pedersen 2010; Lelièvre et al. 2012; Martinez et al. 2013; Kamm et al. 2015; Abtahi et al. 2016), crustal structure and Moho studies (Van der Meijde et al. 2013; De Castro et al. 2014) and geoid determination (Bajracharya and Sideris 2004).

An accurate gravity modeling solver plays a key role in interpreting or inverting gravity data sets. Generally, the structure of the real earth has complicated geometrical shapes and mass density distributions. Thus, the important question arises of how to efficiently approximate the 3D mass structure of the earth by volume discretization techniques. As an arbitrary mass body can be reasonably well represented by a set of disjoint polyhedral bodies with simple mass distributions, an arbitrary polyhedral body is generally adopted to reduce to maximum extend geometrical discretization errors. Therefore, seeking an accurate gravity modeling solver using 3D polyhedra is an essential step. Currently, different approaches can be adopted to evaluate the gravity anomaly caused by a polyhedral mass body, such as finite element methods (Kaftan et al. 2005; Cai and Cy 2005), finite difference methods (Farquharson and Mosher 2009), finite volume methods (Jahandari and Farquharson 2013) and direct Newton integral methods (Blakely 1996). The finite element, finite difference and the finite volume methods translate the Poisson boundary value problem of the gravity potential into a system of linear equations. Then, linear system solvers are used to obtain the gravity potential. However, the accuracies of the gravity anomalies calculated by these three algorithms do not only depend on the quality of the discretization elements and the accuracies of the solvers for systems of linear equations, but also depend on the accuracies of the numerical techniques to translate the computed gravitational potentials into gravity fields. Therefore, in general, numerical solutions provided by these solvers are less accurate than solutions from direct Newton integral methods. As for the direct Newton integral methods, if we can derive analytic formulae of the gravity anomaly for a polyhedral mass body, the highest accuracies can be achieved. Therefore, to find possible analytic formulae has become an essential topic in gravity modeling problems using direct Newton integral approaches.

When the distance from the observation site to the mass body is much larger than the size of the polyhedral body, a constant mass density can be assigned to each polyhedral body in gravity forward modeling and inversion. Aiming to improve accuracy and efficiency, different analytic formulae were derived for a homogeneous (with constant mass density contrast) polyhedral body (Paul 1974; Barnett 1976; Okabe 1979; Pohanka 1988; Werner 1994; Holstein and Ketteridge 1996; Petrović 1996; Tsoulis and Petrović 2001; Holstein 2002; D’Urso 2013, 2014a; Conway 2015), for a homogeneous prismatic polyhedron (Nagy 1966; Banerjee and Das Gupta 1977; Smith 2000; Nagy et al. 2000; Tsoulis et al. 2003) and for a circular disk or a flat lamina (Conway 2016) during the last four decades.

Seeking simplicity, researchers generally assumed that the earth is composed of 3D anomalies in a layered medium or a succession of strata with horizontally undulating interfaces (e.g., sedimentary basins and underlying bedrock). In each layer, the rock mass density predominantly exhibits depth-dependent variations (García-Abdeslem 1992). Different efforts were made to derive analytic formulae for anomalous masses with internal layering such as exponential depth-dependent mass density variations (Chai and Hinze 1988), quadratic polynomial depth-dependent mass density variations (Rao 1990) and cubic polynomial depth-dependent mass density variations (García-Abdeslem 2005).

However, geological formations can be more complicated so that the above assumption of dominant depth-dependent mass density variations can be inappropriate. Also, exogenetic (e.g., weathering, fluvial, coastal and glacial) and endogenetic processes (e.g., diagenesis of rocks, plate tectonics, volcano eruptions and earthquakes) at different scales generally have changed the mass density structures of crust and mantle into 3D structures with both horizontal and vertical variations in mass density (Martín-Atienza and García-Abdeslem 1999). Therefore, it is critical for us to establish more general density distribution models for the mass bodies in the earth. This leads to the necessity of developing formulae capable of computing gravity responses of a polyhedral body with both horizontal and vertical variations in mass density (Zhou 2009b). Until now, only a few studies have been carried out on this more and more important topic. For instance, for a 3D polyhedral body with linear mass density varying in both horizontal and vertical directions, several authors derived different closed-form solutions by using different techniques (Pohanka 1998; Hansen 1999; Holstein 2003; Hamayun and Tenzer 2009; D’Urso 2014b). For a 3D prismatic body with arbitrary density contrast variations in both horizontal and vertical directions, Zhou (2009a) derived a generalized numerical solution in terms of 1D line integrals for the gravity anomaly. However, singularities exist in these 1D line integrals when the observation point is placed on any of the faces of the rectangular prism or inside the prism. Therefore, more careful treatment should be considered to deal with singularities. More recently, for a 2D polygon body with polynomial density contrast variations in both horizontal and vertical directions, D’Urso (2015) derived singularity-free closed-form solutions using the generalized Gauss theorem, in which the mass density polynomials have up to cubic order.

However, to our best knowledge, there are still no publications that deal with analytic formulae for 3D polyhedral bodies with complicated polynomial mass density variations in both horizontal and vertical directions. In this study, we derive closed-form solutions for a 3D polyhedral body (and a prismatic body as a specific example) with mass density contrast as \(\lambda =ax^m+by^n+cz^t\), where m, n, t are nonnegative integers and a, b, c are coefficients of mass density. Using several simple vector identities and integration by parts, we first transform the volume integrals of the gravity anomalies into a set of surface integrals over each polygon of the polyhedral body. Then, singularity-free analytic formulae are derived for these surface integrals. Finally, we obtain a set of completely singularity-free analytic formulae of gravity anomalies for arbitrary polyhedral bodies with horizontal and vertical polynomial density contrasts. Our analytic formulae are the first to (1) generalize previously published closed-form solutions for cases of constant mass density contrasts (Paul 1974; Barnett 1976; Okabe 1979; Pohanka 1988; Werner 1994; Holstein and Ketteridge 1996; Petrović 1996; Tsoulis and Petrović 2001; D’Urso 2013, 2014a; Conway 2015) and linear mass density contrasts (Pohanka 1998; Hansen 1999; Holstein 2003; Hamayun and Tenzer 2009; D’Urso 2014b, 2016) to higher polynomial order, (2) permit computation of the gravitational potential for a general polyhedral body with quadratic density contrast in all spatial directions using closed-form solutions and (3) permit computation of the vertical gravitational field for a prismatic body with quartic density contrast along the vertical direction using closed-form solutions. Additionally, our analytic formulae are singularity-free, which means the observation site can be located anywhere with respect to the mass body. Consequently, our singularity-free analytic formulae can be used in gravity modeling problems with high accuracy requirements such as terrain correction problems (where the observation sites locate on the earth’s surface) and borehole gravity problems (where the observation sites are very close to the mass targets).

To verify our new analytic formula, a prismatic body with different depth-dependent polynomial variations and a polyhedral body in form of a triangular prism with constant density contrasts are examined. Excellent agreement between the published solutions (Blakely 1996; García-Abdeslem 2005; Tsoulis 2012) and our solutions is obtained.

2 Theory

2.1 Reduction of Order of Singularities

Given a polyhedral body H, a local Cartesian coordinate system is built in a way where the observation site \({\mathbf {r}}^{\prime }\) is coincident with the coordinate origin, that is, \({\mathbf {r}}^{\prime }=(0,0,0)\). Then, the polynomial mass density contrast in body H can be defined as:

$$\begin{aligned} \lambda ({\mathbf {r}})=ax^m+by^n+cz^t, \end{aligned}$$
(1)

where \({\mathbf {r}}=(x,y,z)\) is a source point. The coefficients a, b, c, m, n, t are generally estimated by fitting the gravity responses generated by the mass density function \(\lambda ({\mathbf {r}})\) to the gravity data set collected in the field (Grant and West 1965). The integer values m, n, t are the polynomial orders of the mass density. Then, the gravity potential and the gravity field are expressed as:

$$\begin{aligned} \phi ({\mathbf {r}}^{\prime })&= G\iiint \limits _{H}\frac{\lambda ({\mathbf {r}})}{R}\hbox {d}v, \end{aligned}$$
(2)
$$\begin{aligned} {\mathbf {g}}({\mathbf {r}}^{\prime })&= \nabla _{{\mathbf {r}}^{\prime }} \phi ({\mathbf {r}}^{\prime })= -G\iiint \limits _{H} \lambda ({\mathbf {r}})\nabla _{{\mathbf {r}}} \left( \frac{1}{R}\right) \hbox {d}v, \end{aligned}$$
(3)

where \(R=|{\mathbf {r}}- {\mathbf {r}}^{\prime }|\) and \(G=6.673\times 10^{-11} \,{\text {m}}^3\,{\text {kg}}^{-1}\,{\text {s}}^{-2}\) is the gravitational attraction constant.

2.1.1 Gravitational Potential

Substituting the polynomial mass contrast in Eq. (1) into Eqs. (2) and (3), we have

$$\begin{aligned} \phi ({\mathbf {r}}^{\prime })_{mnt}&= aG\iiint \limits _{H}\frac{x^m}{R}\hbox {d}v + bG\iiint \limits _{H}\frac{y^n}{R}\hbox {d}v + cG\iiint \limits _{H}\frac{z^t}{R}\hbox {d}v \nonumber \\&= aG \phi _{m}^{x} + bG\phi _{n}^{y}+ cG\phi _{t}^{z}, \end{aligned}$$
(4)
$$\begin{aligned} {\mathbf {g}}({\mathbf {r}}^{\prime })_{mnt}&= -aG\iiint \limits _{H} x^m \nabla _{{\mathbf {r}}}\left( \frac{1}{R}\right) \hbox {d}v -bG\iiint \limits _{H} y^n \nabla _{{\mathbf {r}}}\left( \frac{1}{R}\right) \hbox {d}v -cG\iiint \limits _{H} z^t \nabla _{{\mathbf {r}}}\left( \frac{1}{R}\right) \hbox {d}v \nonumber \\&= -aG {\mathbf {g}}_{m}^{x} -bG {\mathbf {g}}_{n}^{y} -cG {\mathbf {g}}_{t}^{z}, \end{aligned}$$
(5)

where \(\phi _{m}^{x}\), \(\phi _{n}^{y}\) and \(\phi _{t}^{z}\) denote the gravity potential contributed from mass distributions along the x-, y- and z-axes, respectively. Similar definitions apply for the three components \({\mathbf {g}}_{m}^{x}\), \({\mathbf {g}}_{n}^{y}\) and \({\mathbf {g}}_{t}^{z}\) of the gravity field.

In Eqs. (2) and (3), when \(R\rightarrow 0\), a weak singularity of order O(1/R) occurs for the gravity potential, and a strong singularity of order \(O(1/R^2)\) needs to be handled in the computation of the gravitational acceleration. To start with, we deal with the x-component \(\phi _{m}^{x}\) of the weakly singular gravity potential. By introducing an unit vector \(\hat{\mathbf {x}}=\{1,0,0\}\) along the x-direction, we find that

$$\begin{aligned} \nabla _{{\mathbf {r}}} R&= \frac{{\mathbf {r}}-{\mathbf {r}}^{\prime }}{R} , \end{aligned}$$
(6)
$$\begin{aligned} \hat{\mathbf {x}} \cdot \nabla _{{\mathbf {r}}} R&= \frac{x}{R}, \end{aligned}$$
(7)
$$\begin{aligned} x^{m-1} \hat{\mathbf {x}} \cdot \nabla _{{\mathbf {r}}} R &= \frac{x^{m}}{R} , \end{aligned}$$
(8)

where the assumption \({\mathbf {r}}^{\prime }=(0,0,0)\) is used. Then, integrating the above Eq. (8) over the entire polyhedral body H, we have

$$\begin{aligned} \iiint \limits _{H}(x^{m-1} \hat{\mathbf {x}} \cdot \nabla _{{\mathbf {r}}} R ) \hbox {d}v = \iiint \limits _{H} \frac{x^{m}}{R}\hbox {d}v . \end{aligned}$$
(9)

Considering the definition of \(\phi _{m}^{x}\) in Eq. (4), we get

$$\begin{aligned} \phi _{m}^{x} = \iiint \limits _{H} (x^{m-1} \hat{\mathbf {x}} \cdot \nabla _{{\mathbf {r}}} R ) \hbox {d}v. \end{aligned}$$
(10)

Similarly, we have the following expressions for \(\phi _{n}^{y}\) and \(\phi _{t}^{z}\):

$$\begin{aligned} \phi _{n}^{y}&= \iiint \limits _{H} (y^{n-1} \hat{\mathbf {y}} \cdot \nabla _{{\mathbf {r}}} R ) \hbox {d}v, \end{aligned}$$
(11)
$$\begin{aligned} \phi _{t}^{z}&= \iiint \limits _{H} (z^{t-1} \hat{\mathbf {z}} \cdot \nabla _{{\mathbf {r}}} R ) \hbox {d}v, \end{aligned}$$
(12)

where \(\hat{\mathbf {y}}=\{0,1,0\}\) and \(\hat{\mathbf {z}}=\{0,0,1\}\) are the unit vectors along the y-axis and the z-axis, respectively.

Now, using these unit vectors \(\hat{\mathbf {x}}\), \(\hat{\mathbf {y}}\) and \(\hat{\mathbf {z}}\), Eqs. (10)–(12) can be further simplified by using the following vector identity:

$$\begin{aligned} \chi {\varvec{\Psi }}\cdot \nabla R + R \nabla \cdot (\chi {\varvec{\Psi }}) = \nabla \cdot (R\chi {\varvec{\Psi }}). \end{aligned}$$
(13)

Setting \({\varvec{\Psi }} = \hat{\mathbf {x}}\) and \(\chi = x^{m-1}\), \({\varvec{\Psi }} = \hat{\mathbf {y}}\) and \(\chi = y^{n-1}\), and \({\varvec{\Psi }} = \hat{\mathbf {z}}\) and \(\chi = z^{t-1}\) in Eq. (13), and using the notation of \(\nabla = \nabla _{{\mathbf {r}}}\), we have

$$\begin{aligned} x^{m-1}\hat{\mathbf {x}}\cdot \nabla R + R \nabla \cdot (x^{m-1} \hat{\mathbf {x}})&= \nabla \cdot (Rx^{m-1}\hat{\mathbf {x}}), \end{aligned}$$
(14)
$$\begin{aligned} y^{n-1}\hat{\mathbf {y}}\cdot \nabla R + R \nabla \cdot (y^{n-1} \hat{\mathbf {y}})&= \nabla \cdot (Ry^{n-1}\hat{\mathbf {y}}), \end{aligned}$$
(15)
$$\begin{aligned} z^{t-1}\hat{\mathbf {z}}\cdot \nabla R + R \nabla \cdot (z^{t-1} \hat{\mathbf {z}})&= \nabla \cdot (Rz^{t-1}\hat{\mathbf {z}}). \end{aligned}$$
(16)

The surface \(\partial H\) of a polyhedral body is composed of N polygons, that is, \(\partial H = \sum _{i=1}^{N} \partial H_{i}\). Substituting Eqs. (14), (15) and (16) into Eqs. (10), (11) and (12), respectively, and using the divergence theorem (Jin 2002), we get

$$\begin{aligned} \phi _{m}^{x}&= \sum _{i=1}^{N} [\hat{\mathbf {n}}_{i} \cdot \hat{\mathbf {x}}] \iint \limits _{\partial H_{i} } R x^{m-1} \hbox {d}s -(m-1) \iiint \limits _{H} x^{m-2} R \hbox {d}v, \end{aligned}$$
(17)
$$\begin{aligned} \phi _{n}^{y}&= \sum _{i=1}^{N} [\hat{\mathbf {n}}_{i} \cdot \hat{\mathbf {y}}] \iint \limits _{\partial H_{i}} R y^{n-1} \hbox {d}s -(n-1) \iiint \limits _{H} y^{n-2} R \hbox {d}v, \end{aligned}$$
(18)
$$\begin{aligned} \phi _{t}^{z}&= \sum _{i=1}^{N} [\hat{\mathbf {n}}_{i} \cdot \hat{\mathbf {z}}] \iint \limits _{\partial H_{i}} R z^{t-1} \hbox {d}s -(t-1) \iiint \limits _{H} z^{t-2} R \hbox {d}v, \end{aligned}$$
(19)

in which \({\mathbf {n}}_{i}\) is the normal vector on polygon \(\partial H_{i}\), \([\hat{{\mathbf {n}}}_{i} \cdot \hat{\mathbf {x}}]\), \([\hat{{\mathbf {n}}}_{i} \cdot \hat{\mathbf {y}}]\) and \([\hat{{\mathbf {n}}}_{i} \cdot \hat{\mathbf {z}}]\) are constant over polygon \(\partial H_{i}\). We now deal with the above volume integral (note \({\mathbf {r}}^{\prime }=(0,0,0)\)):

$$\begin{aligned} H_{m-2,x, R}&= \iiint \limits _{H} x^{m-2} R \hbox {d}v \nonumber \\&= \iiint \limits _{H} x^{m-2} \frac{1}{4} \nabla _{{\mathbf {r}}} \cdot [({\mathbf {r}} - {\mathbf {r}}^{\prime })R] \hbox {d}v \nonumber \\&= \iiint \limits _{H} \nabla _{{\mathbf {r}}} \cdot [x^{m-2}\frac{1}{4}({\mathbf {r}} - {\mathbf {r}}^{\prime })R] \hbox {d}v - \iiint \limits _{H} ({\mathbf {r}} - {\mathbf {r}}^{\prime })R \cdot \nabla _{{\mathbf {r}}} (\frac{1}{4}x^{m-2})\hbox {d}v \nonumber \\&= \mathop{{\int\!\!\!\!\!\int}\mkern-21mu \bigcirc}\limits _{\partial H} \frac{Rx^{m-2}}{4}[({\mathbf {r}} - {\mathbf {r}}^{\prime })\cdot {\mathbf {n}}]\hbox {d}s - \frac{(m-2)}{4}\iiint \limits _{H} x^{m-2} R\hbox {d}v \nonumber \\&= \sum _{i=1}^{N} \frac{-h_{i}}{4} \iint \limits _{\partial H_{i}} x^{m-2}R\hbox {d}s - \frac{m-2}{4} H_{m-2,x,R}. \end{aligned}$$
(20)

Here, \(h_{i}\) is defined as \(h_{i}=[({\mathbf {r}}^{\prime }- {\mathbf {r}})\cdot {\mathbf {n}}_{i}]\), which is constant over the polygon \(\partial H_{i}\), and \({\mathbf {n}}_{i}\) is the normal vector on polygon \(\partial H_{i}\). Therefore, we have

$$\begin{aligned} H_{m-2,x,R} = - \frac{1}{m+2} \sum _{i=1}^{N} h_{i} \iint \limits _{\partial H_{i}} x^{m-2}R\hbox {d}s. \end{aligned}$$
(21)

Similar results can be obtained for \(H_{n-2, y, R}\) and \(H_{t-2, z, R}\) in Eqs. (18) and (19), respectively. Now, we observe that the original expression for the total gravity potential \(\phi\) in Eq. (4) with a weak singularity of O(1 / R) was successfully transformed to regular surface integrals of the form O(R) in Eqs. (17)–(19). This means that even when no analytic formulae exist for the gravity potential \(\phi _{mnt}=-G(a\phi _{m}^{x}+b\phi _{n}^{y}+c\phi _{t}^{z})\) with high orders, standard quadrature rules can still be easily adopted to evaluate the gravity potential with high accuracy.

2.1.2 Gravitational Acceleration

Now, we proceed to the gravity field terms \({\mathbf {g}}_{m}^{x}\), \({\mathbf {g}}_{n}^{y}\) and \({\mathbf {g}}_{t}^{z}\) with strong singularities of order \(O(1/R^{2})\). Since most gravimeters can only measure the vertical component of the gravity field, here, we only discuss the formula to compute the vertical component of the gravity field along the positive z-axis. The formulae to compute the other components along the horizontal x- and y-axes can be derived in a similar way. For simplicity, we use the scalar symbols \(g_{m}^{x}\), \(g_{n}^{y}\) and \(g_{t}^{z}\) to denote the vertical components of \({\mathbf {g}}_{m}^{x}\), \({\mathbf {g}}_{n}^{y}\) and \({\mathbf {g}}_{t}^{z}\). The first step is to transform the strong singularities into weak ones of order O(1 / R) by using the vector identity of Eq. (13) where we assign the unit z-axis vector \(\hat{\mathbf {z}}\) to the arbitrary vector \({\varvec{\Psi }}\), set \(\chi =x^{m}, y^{n}, z^{t}\), and replace R by \(\frac{1}{R}\):

$$\begin{aligned} x^{m} \hat{\mathbf {z}}\cdot \nabla \frac{1}{R} + \frac{1}{R}\nabla \cdot (x^{m}\hat{\mathbf {z}})&= \nabla \cdot \left( x^{m}\hat{\mathbf {z}}\frac{1}{R}\right) , \end{aligned}$$
(22)
$$\begin{aligned} y^{n} \hat{\mathbf {z}}\cdot \nabla \frac{1}{R} + \frac{1}{R}\nabla \cdot (y^{n}\hat{\mathbf {z}})&= \nabla \cdot \left( y^{n}\hat{\mathbf {z}}\frac{1}{R}\right) , \end{aligned}$$
(23)
$$\begin{aligned} z^{t} \hat{\mathbf {z}}\cdot \nabla \frac{1}{R} + \frac{1}{R}\nabla \cdot (z^{t}\hat{\mathbf {z}})&= \nabla \cdot \left( z^{t}\hat{\mathbf {z}}\frac{1}{R}\right) . \end{aligned}$$
(24)

This yields

$$\begin{aligned} g_{m}^{x}&= \iiint \limits _{H} x^{m} \hat{\mathbf {z}} \cdot \nabla \frac{1}{R} \hbox {d}v = \iiint \limits _{H} \nabla \cdot (x^m\frac{1}{R}\hat{\mathbf {z}})\hbox {d}v - \iiint \limits _{H} \frac{1}{R} \nabla \cdot (x^m\hat{\mathbf {z}})\hbox {d}v, \end{aligned}$$
(25)
$$\begin{aligned} g_{n}^{y}&= \iiint \limits _{H} y^{n} \hat{\mathbf {z}} \cdot \nabla \frac{1}{R} \hbox {d}v = \iiint \limits _{H} \nabla \cdot (y^n\frac{1}{R}\hat{\mathbf {z}})\hbox {d}v - \iiint \limits _{H} \frac{1}{R} \nabla \cdot (y^n\hat{\mathbf {z}})\hbox {d}v, \end{aligned}$$
(26)
$$\begin{aligned} g_{t}^{z}&= \iiint \limits _{H} z^{t} \hat{\mathbf {z}} \cdot \nabla \frac{1}{R} \hbox {d}v = \iiint \limits _{H} \nabla \cdot (z^t\frac{1}{R}\hat{\mathbf {z}})\hbox {d}v - \iiint \limits _{H} \frac{1}{R} \nabla \cdot (z^t\hat{\mathbf {z}})\hbox {d}v. \end{aligned}$$
(27)

Using the divergence theorem (Jin 2002), we get

$$\begin{aligned} g_{m}^{x}&= \sum _{i=1}^{N} [ \hat{\mathbf {z}} \cdot {\mathbf {n}}_{i}] \iint \limits _{\partial H_{i}} \frac{x^m}{R} \hbox {d}s , \end{aligned}$$
(28)
$$\begin{aligned} g_{n}^{y}&= \sum _{i=1}^{N} [ \hat{\mathbf {z}} \cdot {\mathbf {n}}_{i}] \iint \limits _{\partial H_{i}} \frac{y^n}{R}\hbox {d}s , \end{aligned}$$
(29)
$$\begin{aligned} g_{t}^{z}&= \sum _{i=1}^{N} [ \hat{\mathbf {z}} \cdot {\mathbf {n}}_{i}] \iint \limits _{\partial H_{i}} \frac{z^{t}}{R}\hbox {d}s - t \phi _{t-1}^{z}, \end{aligned}$$
(30)

in which \({\mathbf {n}}_{i}\) is the normal vector on polygon \(\partial H_{i}\), \([\hat{\mathbf {z}} \cdot \hat{{\mathbf {n}}}_{i}]\) is constant over polygon \(\partial H_{i}\), and \(\phi _{t-1}^{z}\) is the gravity potential caused by a depth-dependent mass density contrast of order \(\lambda ({\mathbf {r}})= z^{t-1}\) (see Eq. 4 for its definition). In the above equations, the original strong singularity of \(O(1/R^{2})\) in the vertical gravity field \(g_{mnt}=-G(ag_{m}^{x}+bg_{n}^{y}+cg_{t}^{z})\) was reduced by one order to a weak singularity of form O(1 / R).

2.2 Closed-form Solutions for Surface Integrals and Final Singularity Removal

In Eqs. (17)–(19) and (28)–(30), we need to evaluate surface integrals of the form \(\iint \limits _{\partial H_{i}} f^{k} R^{q} \hbox {d}s\) where f is either x, y or z, k is an integer, and \(q=-1,1\). If \(q=-1\) and \(R\rightarrow 0\), the surface integral has a singular integrand.

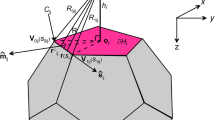
To remove the possible singularity, we set up a local polar coordinate system (\(\rho , \phi\)) on the polygon \(\partial H_{i}\). As shown in Fig. 1, we first project the observation site \({\mathbf {r}}^{\prime }\) onto the plane \(\partial H_{i}\) with the projection point denoted by point \({\mathbf {o}}\). The extent angle at point \({\mathbf {o}}\) is \(\beta ({\mathbf {o}}) = \sum _{j} \beta ({\mathbf {o}})_{j}\), where \(\beta ({\mathbf {o}})_{j}\) is the angular extent of the arc edge \(C_{j}\) or the solid angle (Wilton et al. 1984; Werner 1994), the tangential vector of edge \(C_{j}\) is denoted by \(\hat{\mathbf {e}}_{j}\) and \(\hat{\mathbf {m}}_{j}\) is the normal vector of edge \(C_{j}\), \(\hat{{\mathbf {n}}}_{i}\) is the normal vector of polygon \(\partial H_{i}\), and \(\hat{\mathbf {m}}_{j}\times \hat{\mathbf {e}}_{j}=\hat{{\mathbf {n}}}_{i}\). \(h_i\) is the height of the site \({\mathbf {r}}^{\prime }\) above the polygon \(\partial H_{i}\), i.e., \(h_i = ({\mathbf {r}}^{\prime }-{\mathbf {r}})\cdot \hat{{\mathbf {n}}}_{i}\). Edge \(C_{j}\) is parametrized by a single variable s, \(s=({\mathbf {r}}-{\mathbf {o}})\cdot \hat{\mathbf {e}}_{j}\), \(s_{0}\) and \(s_{1}\) are the parametrized coordinates of two vertices \(v_{0}\) and \(v_{1}\) of edge \(C_{j}\), \(R_{0}\) and \(R_{1}\) are the distances from point \({\mathbf {r}}^{\prime }\) to the vertices \(v_{0}\) and \(v_{1}\), respectively. The distance from the source point \({\mathbf {r}}\in \partial H_{i}\) to the coordinate center \({\mathbf {o}}\) is \(\rho = |{\mathbf {r}} - {\mathbf {o}}|\). Hence, the distance from the site \({\mathbf {r}}^{\prime }\) to the source point \({\mathbf {r}}\) becomes \(R=|{\mathbf {r}}^{\prime }-{\mathbf {r}}| = \sqrt{(h_{i}^2 + \rho ^2)}\). The term \(f^{k}\) could be a complicated function over the polygon; in this study, we derived closed forms only for cases of \(k=0,-1\).

Fig. 1
figure 1

Illustration of the geometrical relationship between the observation site \({\mathbf {r}}^{\prime }\) and an edge \(C_{j}\) of a polygon \(\partial H_{i}\). The point \({\mathbf {o}}\) is the projection point of \({\mathbf {r}}^{\prime }\) onto the polygon \(\partial H_{i}\)

Full size image

First, we have the following identity:

$$\begin{aligned} R^{q} = \nabla _{s}\cdot \frac{1}{q+2} \frac{R^{q+2}}{\rho ^{2}} ({\mathbf {r}} - {{\mathbf {o}}}) , \end{aligned}$$
(31)

in which \(\nabla _{s}\) denotes the surface divergence operation in the local coordinates of the plane.

Proof

Instead of using the local polar coordinate system, here a local 2D Cartesian coordinate system (u, v) is used. Then, assuming u and v are the local coordinates of point \({\mathbf {r}}\), (0, 0) is the 2D local coordinate center \({\mathbf {o}}\), \(R= \sqrt{(u^2 + v^2+h_{i}^2)}\), and \(\rho =\sqrt{u^2+v^2}\), we have

$$\begin{aligned} \nabla _{s}\cdot \frac{1}{q+2} \frac{R^{q+2}}{\rho ^{2}} ({\mathbf {r}} - {\mathbf {o}})&= \frac{1}{q+2} \left\{ \frac{\partial }{\partial u} \left( \frac{R^{q+2}}{\rho ^{2}} u\right) + \frac{\partial }{\partial v} \left( \frac{R^{q+2}}{\rho ^{2}} v\right) \right\} \nonumber \\&= \frac{1}{q+2} \left\{ \frac{(q+2)R^{q+1}\frac{u}{R}\rho ^{2} - R^{q+2} 2 \rho \frac{u}{\rho }}{\rho ^{4}} u \right. \nonumber \\&\quad\left. + \frac{(q+2)R^{q+1}\frac{v}{R}\rho ^{2} - R^{q+2} 2 \rho \frac{v}{\rho }}{\rho ^{4}} v + 2\frac{R^{q+2}}{\rho ^{2}}\right\} \nonumber \\&= \frac{1}{q+2} \left\{ \frac{q+2}{\rho ^{4}} R^{q}\rho ^{4} - \frac{2R^{q+2}}{\rho ^{4}}{\rho ^{2}} + 2 \frac{R^{q+2}}{\rho ^{2}} \right\} \nonumber \\&= R^{q}.\end{aligned}$$
(32)

□

Second, to deal with the weak singularity occurring for \(R\rightarrow 0\), the surface \(\partial H_{i}\) is divided into two regions, one circular region \(\bigcirc _{\epsilon }\) centered at point \({\mathbf {o}}\) with an infinitely small radius \(\epsilon \rightarrow 0\), and the remaining region \(\partial H_{i} - \bigcirc _{\epsilon }\). Hence, for the case \(k=0\),

$$\begin{aligned} I_{R^{q}}= \iint \limits _{\partial H_{i}} R^{q} \hbox {d}s&= \frac{1}{q+2}\iint \limits _{\partial H_{i}-\bigcirc _{\epsilon }} \nabla _{s}\cdot \left( \frac{R^{q+2}}{\rho ^{2}} \left( {\mathbf {r}} - {\mathbf {o}}\right) \right) \hbox {d}s + \iint \limits _{\bigcirc _{\epsilon }} R^{q} \hbox {d}s \nonumber \\&= \frac{1}{q+2} \sum _{j=1}^{M} m_{j} \int _{C_{j}} \frac{R^{q+2}}{\rho ^{2}} \hbox {d}l - \frac{1}{q+2} \frac{\left( \sqrt{h_{i}^2+\epsilon ^2}\right) ^{q+2}}{\epsilon } \int _{\partial \bigcirc _{\epsilon } } \hbox {d}l \nonumber \\&\quad+ \int _{0}^{\beta ({\mathbf {o}})} \int _{0}^{\epsilon } \rho (\sqrt{h_{i}^2+\rho ^2})^{q} \hbox {d}\rho \hbox {d}\phi \nonumber \\&= \frac{1}{q+2} \sum _{j=1}^{M} m_{j} \int _{C_{j}} \frac{R^{q+2}}{\rho ^{2}} \hbox {d}l - \frac{1}{q+2} \frac{\left( \sqrt{h_{i}^2+\epsilon ^2}\right) ^{q+2}}{\epsilon } \epsilon \int _{0}^{\beta ({\mathbf {o}})} \hbox {d}\phi \nonumber \\&\quad+ \frac{\beta ({\mathbf {o}}) }{q+2} (\sqrt{h_{i}^2+\rho ^2})^{q+2} |_{o}^{\epsilon } \nonumber \\&= \frac{1}{q+2} \sum _{j=1}^{M} m_{j} \int _{C_{j}} \frac{R^{q+2}}{\rho ^{2}} \hbox {d}l \nonumber \\&\quad- \frac{\beta ({\mathbf {o}})}{q+2} \left( \sqrt{h_{i}^2+\epsilon ^2}\right) ^{q+2} + \frac{\beta ({\mathbf {o}})}{q+2}\left( \sqrt{h_{i}^2+\epsilon ^2}\right) ^{q+2} - \frac{\beta ({\mathbf {o}})}{q+2} |h_{i}|^{q+2} \nonumber \\&= \frac{1}{q+2} \sum _{j=1}^{M} m_{j} \int _{C_{j}} \frac{R^{q+2}}{\rho ^{2}} \hbox {d}l - \frac{\beta ({\mathbf {o}})}{q+2} |h_{i}|^{q+2} \nonumber \\&= \frac{1}{q+2} \sum _{j=1}^{M} B_{j}^{q+2} - \frac{\beta ({\mathbf {o}})}{q+2} |h_{i}|^{q+2}, \end{aligned}$$
(33)

where, referring to Fig. 1, \(m_{j}=({\mathbf {r}} - {\mathbf {o}}) \cdot \hat{\mathbf {m}}_{j}\) is constant over edge \(C_{j}\), \(\hat{\mathbf {m}}_{j}\) is the normal vector on edge \(C_{j}\), and \(\beta ({\mathbf {o}})\) is the solid angle of \(\bigcirc _{\epsilon }\) centered at point \({\mathbf {o}}\) in the plane \(\partial H_{i}\) (see Eq. 48 in the “Appendix” for its calculation). We also note that when point \({\mathbf {o}}\) is located at a corner or on an edge, the respective distance term \(m_{j}\) vanishes. In the above, we defined a new term \(B_{j}^{q+2} = m_{j} \int _{C_{j}} \frac{R^{q+2}}{\rho ^{2}} \hbox {d}l\) which will be considered in the “Appendix”.

Third, for the surface integrals of form \(\iint _{\partial H_{i}} f^{k} R^{q} \hbox {d}s\) in Eqs. (17)–(19) and (28)–(30) and \(k=1\), we retrieve

$$\begin{aligned} {\mathbf {I}}_{rR_{q}}=\iint \limits _{\partial H_{i}} {\mathbf {r}} R^{q} \hbox {d}s&= ({\mathbf {o}} - {\mathbf {r}}^{\prime }) \iint \limits _{\partial H_{i}} R^{q} \hbox {d}s + \iint \limits _{\partial H_{i}} ({\mathbf {r}}-{\mathbf {o}}) R^{q} \hbox {d}s \nonumber \\&= ({\mathbf {o}} - {\mathbf {r}}^{\prime }) I_{R^{q}} + \iint \limits _{\partial H_{i}-\bigcirc _{\epsilon }} \nabla _{s} \left( \frac{R^{q+2}}{q+2} \right) \hbox {d}s + \iint \limits _{\bigcirc _{\epsilon }} ({\mathbf {r}}-{\mathbf {o}})R^{q} \hbox {d}s \nonumber \\&= ({\mathbf {o}} - {\mathbf {r}}^{\prime }) I_{R^{q}} + \frac{1}{q+2}\sum _{j=1}^{M} \hat{\mathbf {m}}_{j} \int _{C_{j}} R^{q+2} \hbox {d}l \nonumber \\&\quad+ \frac{(\sqrt{h^2+\epsilon ^2})^{q+2}}{q+2} \mathop{{\int\!\!\!\!\!\int}\mkern-21mu \bigcirc}\limits _{\partial \bigcirc _{\epsilon }} \hat{\mathbf {m}}_{j} \hbox {d}l + \int _{0}^{\beta ({\mathbf {o}})} \int _{0}^{\epsilon } \hat{\varvec{\rho }} \rho ^{2} R^{q} \hbox {d}\rho \hbox {d}\phi \nonumber \\&\mathop {=}\limits ^{\epsilon \rightarrow 0} ({\mathbf {o}} - {\mathbf {r}}^{\prime }) I_{R^{q}} + \frac{1}{q+2}\sum _{j=1}^{M} \hat{\mathbf {m}}_{j} \int _{C_{j}} R^{q+2} \hbox {d}l \nonumber \\&= ({\mathbf {o}} - {\mathbf {r}}^{\prime }) I_{R^{q}} + \frac{1}{q+2}\sum _{j=1}^{M} \mathbf {B}_{j}^{q+2}, \end{aligned}$$
(34)

where the term \(\hat{\mathbf {m}}_{j} \int _{C_{j}} R^{q+2} \hbox {d}l\) is denoted by a new variable \({\mathbf {B}}_{j}^{q+2}\) and \(\hat{\varvec{\rho }}\) is a unit vector pointing from point \({\mathbf {o}}\) to point \({\mathbf {r}}\). Note that we have used \({\mathbf {r}}=(x,y,z) = {\mathbf {r}}-{\mathbf {r}}^{\prime } = {\mathbf {r}}-{\mathbf {o}}+ {\mathbf {o}} - {\mathbf {r}}^{\prime }\), where the assumption \({\mathbf {r}}^{\prime }=(0,0,0)\) is used. The term \(I_{R^{q}}\) is given in Eq. (33), and the following identity is used:

$$\begin{aligned} ({\mathbf {r}}-{\mathbf {o}}) R^{q} = \nabla _{s} \left( \frac{R^{q+2}}{q+2} \right) . \end{aligned}$$

To compute the gravity potential and the gravity field, we only have to deal with the cases of \(q=-1,1\). Note, analytic formulae for the scalar term \(B_{j}^{q+2}\) and the vector term \({\mathbf {B}}_{j}^{q+2}\) in Eqs. (33) and (34), respectively, are given in the “Appendix” for the cases \(q=-1\) and \(q=1\).

2.3 Special Cases

2.3.1 Zeroth-Order Density Variation

For \(m=n=t=0\), i.e., spatially homogeneous density, Eq. (4) simplifies to

$$\begin{aligned} \phi _{0}^{x}=\phi _{0}^{y}=\phi _{0}^{z} = \iiint \limits _{H} \frac{1}{R} \hbox {d}v. \end{aligned}$$
(35)

Substituting the vector identity (Hamayun and Tenzer 2009)

$$\begin{aligned} \frac{1}{R} = \frac{1}{2} \nabla _{{\mathbf {r}}} \cdot \frac{{\mathbf {r}}-{\mathbf {r}}^{\prime }}{R} \end{aligned}$$

into Eq. (35) gives

$$\begin{aligned} \phi _{000} = \frac{G(a+b+c)}{2} \iiint \limits _{H} \nabla _{{\mathbf {r}}} \cdot \frac{{\mathbf {r}}-{\mathbf {r}}^{\prime }}{R} \hbox {d}v = -\frac{G(a+b+c)}{2} \sum _{i=1}^{N} h_{i} \iint \limits _{\partial H_{i}} \frac{1}{R}\hbox {d}s, \end{aligned}$$
(36)

where the divergence theorem (Jin 2002) was used. The term \(h_{i}=({\mathbf {r}}^{\prime }-{\mathbf {r}})\cdot \hat{{\mathbf {n}}}_{i}\) for \({\mathbf {r}}\in \partial H_{i}\) is the normal distance from the observation site \({\mathbf {r}}^{\prime }\) to the surface \(\partial H_{i}\) along the direction of \(\hat{{\mathbf {n}}}_{i}\), here \(\hat{{\mathbf {n}}}_{i}\) is the outgoing surface normal vector (Fig. 1). Setting \(m=n=t=0\) in Eqs. (28)–(30), we have

$$\begin{aligned} g_{000} = -G \sum _{i=1}^{N} \{(a+b+c) [\hat{{\mathbf {n}}}_{i} \cdot \hat{\mathbf {z}}] \} \iint \limits _{\partial H_{i} } \frac{1}{R} \hbox {d}s. \end{aligned}$$
(37)

Therefore, by setting \(q=-1\) in Eq. (33), singularity-free analytic expressions for the gravity potential and the gravity field of a homogeneous polyhedral body are developed.

2.3.2 First-Order Density Variation

Now we consider the linear case of \(\lambda ({\mathbf {r}})= {\mathbf {A}}\cdot {\mathbf {r}}\), \({\mathbf {A}}=(a,b,c)\) and \({\mathbf {r}}=(x,y,z)\). Setting \(m=n=t=1\) in Eqs. (17), (18) and (19), we have

$$\begin{aligned} \phi _{111} = \sum _{i=1}^{N} \{ a [\hat{{\mathbf {n}}}_{i} \cdot \hat{\mathbf {x}}] + b [\hat{{\mathbf {n}}}_{i} \cdot \hat{\mathbf {y}}] + c [\hat{{\mathbf {n}}}_{i} \cdot \hat{\mathbf {z}}] \} \iint \limits _{\partial H_{i} } R \hbox {d}s. \end{aligned}$$
(38)

Similarly, setting \(m=n=t=1\) in Eqs. (28)–(30) yields

$$\begin{aligned} g_{111} = -G \sum _{i=1}^{N} [\hat{{\mathbf {n}}}_{i} \cdot \hat{\mathbf {z}}] {\mathbf {A}} \cdot \iint \limits _{\partial H_{i} } {\mathbf {r}} R^{-1} \hbox {d}s + cG\phi _{0}^{z}. \end{aligned}$$
(39)

Setting \(q=1\) in Eq. (33) and \(q=-1\) in Eq. (34), the singularity-free analytic expressions for \(\phi _{111}\) and \(g_{111}\) are obtained.

2.3.3 Second-Order Density Variation

Setting \(m=2,n=2,t=2\), the terms for the gravitational potential in Eqs. (17)–(21) simplify to integrals of the forms \(\iint _{\partial H_{i}} {\mathbf {r}} R \hbox {d}s\) and \(\iint _{\partial H_{i}} R \hbox {d}s\). These expressions can be analytically integrated using \(q=1\) in Eqs. (33) and (34), and hence, the gravity potential \(\phi\) has closed forms. However, for the gravity field, closed forms cannot be derived using the formulae in Eqs. (33) and (34).

2.3.4 Comparison of Available Solutions for Zeroth- to Second-Order Density Variations

In Table 1, we have listed the currently available closed-form solutions for a general polyhedral mass body with constant, linear or quadratic polynomial mass density. Recently, D’Urso (2013, 2014a) has used the distribution theory to derive closed-form solutions for a constant polyhedron and have discussed a way of eliminating singularities. Subsequently, D’Urso (2014b) extended the distribution theory on a general polyhedron with linear mass polynomials. Conway (2015) has employed a vector potential technique to derive closed-form solutions for a constant polyhedron. Compared to these techniques, our approaches have adopted a simple generalized framework to deal with constant and linear cases. To our best knowledge, our new equations are the first to deliver closed-form solutions for the gravitational potential of a general polyhedral body with quadratic density contrast varying in all spatial directions.

Table 1 Comparison of our closed-form solution to other available closed-form solutions for a general polyhedral mass body
Full size table

2.3.5 A Regular Prismatic Body

The surface of a prismatic body is composed of six rectangular surfaces \(\Diamond _{i}\), that is, \(\partial H = \sum _{i=1}^{6} \Diamond _{i}\). In a 3D Cartesian coordinate system with the positive z-axis downward, we arrange the rectangular surfaces as follows: (1) \(\Diamond _{1}\) and \(\Diamond _{2}\) are the two rectangular surfaces perpendicular to the x-axis where the x-coordinate of plane \(\Diamond _{1}\) is less than that of plane \(\Diamond _{2}\); (2) \(\Diamond _{3}\) and \(\Diamond _{4}\) are the two rectangular surfaces perpendicular to the y-axis where the y-coordinate of plane \(\Diamond _{3}\) is less than that of plane \(\Diamond _{4}\); and (3) \(\Diamond _{5}\) and \(\Diamond _{6}\) are the two rectangular surfaces perpendicular to the z-axis where the z-coordinate of plane \(\Diamond _{5}\) is less than that of plane \(\Diamond _{6}\). With this choice, the terms of the gravity potential in Eqs. (17)–(21) become

$$\begin{aligned} \phi _{m}^{x}&= \sum _{i=1}^{2} (-1)^{i} x^{m-1}_{\Diamond _{i}} \iint \limits _{\Diamond _{i} } R \hbox {d}s + \frac{m-1}{m+2} \sum _{i=1}^{6} h_{i} \iint \limits _{\Diamond _{i}} x^{m-2} R \hbox {d}s, \end{aligned}$$
(40)
$$\begin{aligned} \phi _{n}^{y}&= \sum _{i=3}^{4} (-1)^{i} y^{n-1}_{\Diamond _{i}} \iint \limits _{\Diamond _{i}} R \hbox {d}s + \frac{n-1}{n+2} \sum _{i=1}^{6} h_{i} \iint \limits _{\Diamond _{i}} y^{n-2} R \hbox {d}s , \end{aligned}$$
(41)
$$\begin{aligned} \phi _{t}^{z}&= \sum _{i=5}^{6} (-1)^{i} z^{t-1}_{\Diamond _{i}} \iint \limits _{\Diamond _{i}} R \hbox {d}s + \frac{t-1}{t+2} \sum _{i=1}^{6} h_{i} \iint \limits _{\Diamond _{i}} z^{t-2} R \hbox {d}s, \end{aligned}$$
(42)

and the vertical gravity field in Eqs. (28)–(30) consists of the terms

$$\begin{aligned} g_{m}^{x}&= \sum _{i=5}^{6} (-1)^{i} \iint \limits _{\Diamond _{i}} \frac{x^m}{R} \hbox {d}s , \end{aligned}$$
(43)
$$\begin{aligned} g_{n}^{y}&= \sum _{i=5}^{6} (-1)^{i} \iint \limits _{\Diamond _{i}} \frac{y^n}{R}\hbox {d}s , \end{aligned}$$
(44)
$$\begin{aligned} g_{t}^{z}&= \sum _{i=5}^{6} (-1)^{i} z^{t}_{\Diamond _{i}} \iint \limits _{\Diamond _{i}} \frac{1}{R}\hbox {d}s - t \phi _{t-1}^{z}. \end{aligned}$$
(45)

Considering Eqs. (40)–(42) and (33)–(34), and the results discussed in the above special cases, we find that, when \(m\le 3, n\le 3, t\le 3\), all three terms of the gravity potential have analytic expressions. However, based on the results given in Eqs. (33)–(34), closed forms can be derived only if \(m\le 1, n\le 1\) for the \(g_{m}^{x}\) and \(g_{n}^{y}\) terms of the gravity field. Since \(\phi _{t-1}^{z}\) has closed forms in the case of \(t-1\le 3\), \(g_{t}^{z}\) has closed forms if \(t\le 4\). These results for a prismatic body are shown in Table 2 for reference.

Table 2 Lookup table for the availability of analytic formulae of the gravity potential (terms \(\phi _{m}^{x}\), \(\phi _{n}^{y}\), \(\phi _{t}^{z}\) in Eqs. 40–42) and the vertical gravity field (terms \(g_{m}^{x}\), \(g_{n}^{y}\), \(g_{t}^{z}\) in Eqs. 43–45) for a prismatic body
Full size table

As shown in Table 2, for a prismatic body with constant, linear, quadratic and cubic density contrasts varying in both horizontal and vertical directions, our approach can deliver closed-form solutions for the gravitational potential. For the gravitational field, closed-form solutions exist in the cases of constant and linear density contrasts. Compared to previously published methods (Nagy et al. 2000; Rao 1990; García-Abdeslem 2005), one novelty of our approach is that our closed-form solutions are singularity-free which means the observation sites can be outside, inside and on the boundary (edges, corners, faces) of the mass prismatic body.

3 Verification

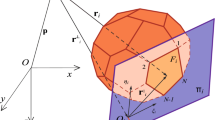
Two synthetic models (as shown in Fig. 2) are used to verify the accuracies of our closed-form solutions. The global Cartesian coordinate system is used to describe the geometries of these two models and locations of testing sites and profiles. Our closed-form formulae use the assumption that the observation site is located at the coordinate origin. Therefore, to compute the gravity signals in these two synthetic models, a coordinate transform from the global Cartesian coordinate system to the local Cartesian coordinate system is needed at each observation site by our closed-form formulae to guarantee that it is at the local coordinate origin.

Fig. 2
figure 2

García-Abdeslem’s (2005) prism model (a). A triangular prism model (b) is constructed from García-Abdeslem’s (2005) prism model with half the volume. Black dots represent observation sites

Full size image

3.1 A Prismatic Body with Vertically Varying Density Contrast

To validate our new singularity-free analytic formulae, first the popular prismatic model is tested. Four different depth-dependent polynomial density contrasts are examined, which are the constant, linear, quadratic and cubic variations. A Cartesian coordinate system is defined in a way that the positive z-axis is downward. The dimension of the prismatic body is \(x=[10\,{\text {km}},20\,{\text {km}}]\), \(y=[10\,{\text {km}},20\,{\text {km}}]\) and \(z=[0\,{\text {km}},8\,{\text {km}}]\) (Fig. 2a). The density contrast function, which is taken from a previous work (García-Abdeslem 2005), is given as:

$$\begin{aligned} \lambda ({{\mathbf {r}}}) = -747.7+203.435z-26.764z^{2}+1.4247z^{3} \end{aligned}$$
(46)

where density is in kg/m\(^{3}\) and z is in km. When the observation site approaches the prism, i.e., the edges, surfaces or corners of the prism, the gravity potential and the gravity field become singular. In the previous work (García-Abdeslem 2005), analytic formulae for depth-dependent density contrasts up to third order were derived. However, these analytic formulae are singular when the observation sites are located on edges or corners.

First, a short measuring profile with three observation sites is arranged on the top surface of the prism, which is perpendicular to an edge with \(x=10\,{\text {km}},z=0\,{\text {km}}\). When the profile is slightly more elevated (with \(z=-0.15\,{\text {m}}\)), the singularity disappears so that we can compare the accuracies of our analytic solutions against the closed-form solutions, which were recomputed by the formula offered by García-Abdeslem (2005). This accuracy comparison for the regular case is shown in Table 3, and an excellent agreement is obtained between these two different closed-form solutions. A slight difference appears at the 14-th significant digit, which is close to the machine precision limitations of the computer. When setting \(z=0\,{\text {km}}\) for the profile as shown in Table 4, a singularity in García-Abdeslem’s (2005) formulae at the edge (at \(x=10\,{\text {km}}\)) impedes computation of a solution [indicated by symbol (–)]. Instead, a smooth solution is obtained by our singularity-free analytic formulae. As observed from Table 4, the smooth transition of our computed vertical gravity field \(g_{00t}\) across the edge implies the correctness of the solution when the observation sites are located on the edge.

Table 3 Comparison of the vertical gravity field (\(g_{00t}\)) computed by our analytic solutions and García-Abdeslem’s (2005) closed-form solutions for the prism model shown in Fig. 2a
Full size table
Table 4 Comparison of the vertical gravity field (\(g_{00t}\)) between our analytic solutions and García-Abdeslem’s (2005) closed-form solutions for the prism model shown in Fig. 2a
Full size table

Secondly, we performed another test, where the observation site is located at one of the corners on the top surface of the prism. Due to the model symmetry, the gravity anomalies at the four top corners have the same values. Therefore, only the case of one corner (\(x=20\,{\text {km}}, y=10\,{\text {km}}, z=0\,{\text {km}}\)) is considered. Similar to the above test, a location at slightly higher elevation (with \(z=-0.15\,{\text {m}}\)) is required for García-Abdeslem’s (2005) analytic expressions. The comparison between our solutions and García-Abdeslem’s solutions is shown in Table 5. Apparently, these two different solutions are identical up to the 14-th significant digit. In the singular case (see Table 6) where the observation site is coincident with the corner, our solutions still show smooth results with respect to the above solutions with a slightly more elevated observation site, implying the correctness of our formulae.

Table 5 Comparison of the vertical gravity field (\(g_{00t}\)) between our analytic solutions and García-Abdeslem’s (2005) closed-form solutions for the prism model shown in Fig. 2a
Full size table
Table 6 Comparison of the vertical gravity field (\(g_{00t}\)) between our analytic solutions and García-Abdeslem’s (2005) closed-form solutions for the prism model shown in Fig. 2a
Full size table

3.2 A Polyhedral Body with Constant Density Contrast

To test the performance of our closed-form approach in the case of arbitrary polyhedral bodies, a complicated triangular prism is selected as shown in Fig. 2b. The triangular prism has half the volume of the prism (cutting in halves the original prism along diagonals of the top and bottom surfaces) and has a mass density of \(2670\,{\text {kg/m}}^3\); only the vertical gravity fields are computed. The triangular surface has a size of \(\frac{1}{2}\times 10\,{\text {km}}\times 10\,{\text {km}}\). Three observation sites are located on the top triangular surface of the anomaly, one at a vertex, one at the mid point of an edge and one at the center of the surface. Hence, singularities might exist.

When the observation site is located at the diagonal edge as shown in Fig. 2b, the vertical gravity field caused by the triangular prism has half  the value of that caused by the prismatic body, due to geometrical symmetries. Therefore, half the value of the well-established Gbox solution (Blakely 1996) can be used as reference. Additionally, the analytic solutions with linear integrals for arbitrary polyhedral bodies from Tsoulis (2012) are also taken as references. The test results are given in Table 7; they show that, using our closed-form formula, the computed \(g_{z}\) of the triangular prism is exactly a factor of 0.5 of \(g_{z}\) caused by the prismatic body. Our closed-form solution has an excellent agreement with that computed by the Gbox code (up to the 15-th significant digit). There is a negligible difference (after the 7-th significant digit) between our closed-form solution and Tsoulis’s (2012) solution. Similar deviations also are observed for the cases that the observation sites are located at the vertex and the center of the surface. The differences between the different solutions are well below instrumental accuracy (0.002–0.010 mGal), demonstrating the generally high accuracy of the compared algorithms.

Table 7 Comparisons of the vertical gravity field computed by our closed-form formula to other approaches for the triangular prism model as shown in Fig. 2b
Full size table

3.3 A Prismatic Body with Quartic Density Contrast

Additionally, we calculate the gravity acceleration for a prismatic body with a quartic density contrast which is

$$\begin{aligned} \lambda ({\mathbf {r}})=z^{4}. \end{aligned}$$
(47)

The profile is along the top surface of the prismatic body (\(y=5\,{\text {km}}\) and \(z=0\,{\text {km}}\)) as shown in Fig. 2a. The reference solutions are calculated by the high-order Gaussian quadrature rule with \(512\times 512\times 512\) quadrature points. As the quadrature points are located inside the prismatic body, solutions of the Gaussian quadrature rule are reasonably well approximating to the solutions. Our closed-form solutions and those of the Gaussian quadrature rule are listed in Table 8. As shown in Table 8, excellent agreements are obtained again and differences occur only at the 11-th significant digit. The testing platform is a personal computer with an Intel core i3 CPU 2.4GHz and 4GB RAM. For 31 observation sites, our closed-form formula takes 0.0055 s and the high-order Gaussian method using \(512\times 512\times 512\) quadrature points takes 171.9481 s. The low-order Gaussian quadrature solution using \(5\times 5\times 5\) quadrature points is also shown in Table 8 which takes 0.0005540 s computation time for 31 observation sites. Although the computational speed of the low-order Gaussian quadrature rule is ten times faster than that of our analytic formula, it has 0.1–0.2% relative errors at observation sites approaching to the center of the top surface. Compared to our closed-form solution, the low-order Gaussian quadrature rule has 0.001–0.039 mGal differences for the vertical gravity field. As these differences are already larger than instrumental accuracy (0.002–0.010 mGal), solutions computed by this low-order Gaussian quadrature rule are undesired.

Table 8 Lists of the vertical gravity field computed using our analytic solution and solutions by the Gaussian quadrature rules with \(512\times 512\times 512\) points and \(5\times 5\times 5\) points for the prism model shown in Fig. 2a with \(\lambda ({\mathbf {r}})=z^{4}\)
Full size table

4 Discussion and Conclusions

In comparison with previously published work, our approaches of computing the gravitational potential and acceleration due to arbitrary polyhedral bodies have adopted a generalized singularity-free framework. This allowed to derive closed-form solutions of the gravitational potential and acceleration for the cases of constant and linear variations in mass density. We are the first to present closed-form solutions of the gravitational potential for a general polyhedral body with quadratic density contrast varying in all directions (x, y and z).

For a prismatic body with density contrasts varying in both horizontal and vertical directions, our approach can deliver closed-form solutions of the gravity potential caused by constant, linear, quadratic and cubic density contrasts. For the gravitational acceleration of a prismatic body, we have shown that closed-form solutions exist in the case of constant and linear variations in density contrast. To our best knowledge, we deliver the first closed-form solutions of the gravitational acceleration for a prismatic body with quartic density contrast, if the density contrast only varies along the z-axis.

In summary, we find:

  1. 1.

    For an arbitrarily polyhedral body, analytic formulae of the gravity potential and the gravity field are available in the case of \(m\le 1\), \(n\le 1\) and \(t\le 1\). For the gravity potential, an analytic formula is also available in the case of \(m=2\), \(n=2\) and \(t=2\).

  2. 2.

    For a prismatic body, an analytic formula exists in the case of \(m\le 3\), \(n\le 3\) and \(t\le 3\) for the gravity potential. For the gravity field, closed-form solutions are available only in the case of \(m\le 1\), \(n\le 1\) and \(t\le 4\).

Since simulation results from closed-form solutions for complicated polyhedral and spatial variations of density contrasts were not available in the literature, a simple prismatic model with a purely depth-dependent polynomial density contrast and a polyhedral body in form of a triangular prism with constant density contrasts had to be considered to verify our new analytic formulae. Excellent agreement between the results of the published analytic formulae and our results is demonstrated, verifying the accuracies of our new analytic expressions of the gravity anomaly.

Due to its ability for dealing with cases of locating observation sites at corners, on edges or on surfaces of a polyhedral body, our new analytic formula is a useful tool to compute the gravity anomaly in the immediate vicinity of the mass source body. It should have high potential in aiding interpretation of gravity data for gravity modeling problems where high accuracy is required, such as terrain correction and borehole gravity problems or in near field computation in associated fast multipole method acceleration techniques.

An interesting aspect of the new formulae is that they allow representing a density distribution with relatively few parameters, since the density is allowed to vary within a single polyhedron. This is an interesting aspect, when it comes to inversion, because these will reduce some of the ambiguities and may require less regularization.