1 Introduction

Loess is a widely-abundant collapsible soil with a microstructure of meta-stable characteristic (Pye 1984; Jefferson et al. 2005). Typically composed of wind-borne sediment, silt-sized particles, this type of soil has some unique physical and chemical characteristics (Smalley 1995; Bell 2013).

In general, loess is highly porous, which results in a low dry density as well as low permeability (Kim & Kang 2013; Liu et al. 2016; Yates et al. 2018). Due to its relatively low shear strength, loess is susceptible to slope failure and other types of failure in construction. Unless properly managed, loess is highly erodible and is susceptible to erosion and gullying. Combined with other factors, such as climate, these properties can greatly influence the behavior of loessial soils in construction and other applications.

Loess is most commonly found in arid and semi-arid regions with low to moderate precipitation rates and strong winds, as these conditions are conducive to the formation and preservation of loess deposits (Li et al. 2020). Russia, the United States, China, Libya, Argentina, Australia and Iran are all known to have this type of soil (Follmer 1996; Zárate 2003; Zhangjian et al. 2007; Nouaouria et al. 2008; Karimi et al. 2009; Yates et al. 2018). Approximately 10 percent of the surface of the earth is covered by loess (Li et al. 2020).

Having a macro-porous characteristic, loess possesses collapsing behavior especially under loading or water inundation which results in construction problems (Yang 1989; Fredlund & Gan 1995; Munoz-Castelblanco et al. 2011). Loess can also collapse when it becomes inundated due to the breakdown of particle connections (Giménez et al. 2012; Wang et al. 2020). As a collapsible soil, construction on loess may make the foundation of the buildings extremely vulnerable to abrupt settlements, absolute and differential, upon saturation of the underlying soil.

As reported in the literature, construction on the base of loess layers have frequently ended in collapsing events in many residential, commercial, and infrastructural projects (Houston et al. 1988; Derbyshire 2001; Jefferson et al. 2003; Sakr et al. 2008; Rabbi et al. 2014).

In general, the potential of collapse refers to the change in the bulk volume of the soil under water inundation, and an experimental approach is used to evaluate this characteristic by compressing and inundating undisturbed soil samples using an oedometer (ASTM 1996).

A number of studies have been dedicated to the effect of different soil parameters on the collapse potential. In general, it can be inferred from the reported results that numerous physical properties of the soil can affect its collapsibility. These parameters include the soil texture and its water content as well as dry density, Atterberg limits and void ratio (Mansour et al. 2008; Bell 2013; Langroudi & Jefferson 2013; Garakani et al. 2015). Regarding the soil micro-structure, the mineral constituents and the number of macro and mini pores along with the bonding material between them can significantly influence the collapse potential (Giménez et al. 2012; Liu et al. 2016; Ma et al. 2017; Xie et al. 2018).

2 Background Review

Within the last two decade, several research papers have been published on the use of modern computational techniques such as artificial neural networks and machine learning methods to solve the problems related to the estimation of collapse potential of collapsible soils.

As one of the earliest studies in this field, Juang & Elton (1997) applied neural network techniques on a dataset composed of the property and collapse potential data for a total of 1044 soil samples. Also, their approach for training employed three main techniques, namely Naïve back-propagation (NBP), backpropagation with momentum and adaptive learning rate, and Levenberg- Marquardt algorithm (LM). The results indicate that their trained network is capable of estimating the collapse potential of soils but since they did not focus on a particular soil type and their dataset contained different types of collapsible soil, the results of their research cannot be applied to a special soil type such as loess.

Furthermore, Basma & Kallas (2004) developed an artificial neural network-based model capable of soil collapsibility behavior prediction. Their proposed network was able to estimate the collapse potential of different soil types with different arrangements and pressure levels. This network includes six neurons as inputs consisting of six main soil properties of the samples.

Also, Habibagahi & Taherian (2004) utilized several neural networks including Generalized Regression Neural Network (GRNN), Recurrent Neural Network (RNN) and Back-Propagation Neural Network (BPNN) for collapse potential estimation. Their findings indicate the significant influence of soil dry density on the collapse potential.

GRNN was also used, along with RBFN, to predict collapsibility potential of different types of soil (Zhang 2011). In comparison with RBFN and the experimental results, GRNN was found to have higher accuracy in estimating the collapse potential of soil.

The use of Multivariate Adaptive Regression Spline (MARS) and BPNN methods in collapse potential estimation were also examined by W. Zhang (2020). Both of these methods exhibit acceptable collapsibility estimation capabilities.

Similarly, Salehi et al. (2015) studied the collapse potential of loess using MLPNN, RBFN and Adaptive Neuro-Fuzzy Inference Systems (ANFIS). The MLPNN was shown to have high prediction capability through LM backpropagation technique. RBFN was also found to be closely accurate but estimations by ANFIS were not just as promising.

Further, Uysal (2020) employed Gene Expression Programming (GEP) technique to estimate collapsibility based on six soil parameters, namely the water content, dry unit weight, inundation stress, sand and clay contents, and the uniformity coefficient. The study also drew a comparison between the GEP-based model and the previously-proposed regression-based models.

In our opinion, the existing models proposed so far in the literature have two major flaws. The first problem is that most of the models were presented based on limited datasets, which usually pertain to a specific geographical area. The second issue is that the models are often presented based on data related to a wide range of collapsible soils, while the different types of collapsible soils possess different characteristics and the results cannot be generalized to them all. Thus, loessial soils have received insufficient attention in this case.

Hence, the purpose of this study is to represent a comparative perspective on well-known supervised machine learning tools including MLPNN, RBFN, and NBC and find a reliable model for estimating the collapse potential of loessial soils.

3 Analysis Methods

This section presents customizations of three supervised machine learning tools including MLPNN, RBFN, and NBC for estimating loess collapse potential. By considering the complexity of data points’ distribution and features of their behaviors, the tools named above were selected to investigate the effect of different classifier properties on results.

With the help of MLPNN, linear separation can be achieved in functions such as AND/OR. However, some of the functions, such as Exclusively-OR (XOR), are not linearly separable. Thus, RBFN was chosen to handle such situations, employing radial functions. In fact, RBFN transforms the input values into a form, which can then be incorporated into the network to achieve linear separability. The reason for studying NBC’s performance in current research, is to employ its high precision classification capability, considering conditional independency and the probabilistic nature of the values of the features.

3.1 MLPNN

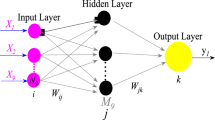
As a multi-layer perceptron neural network, MLPNN is categorized as a feed-forward network with activation thresholds. It is formed by at least three layers of processing nodes including an input layer, a hidden layer, and an output layer. Figure 1 illustrates a simplified MLPNN structure. Using this network, historical data are used for supervised learning aimed at mapping known inputs to outputs (Du & Swamy 2013). It is important to note that, the trained network can then be used to estimate the unknown output through any set of given inputs.

Fig. 1
figure 1

A simple structure of MLPNN (Du & Swamy 2013)

Full size image

In this model, each neuron calculates the weighted sum of all entries. This value is then subtracted from the neuron’s threshold value. The result is passed to an activation function, and finally, the neuron’s outcome is achieved according to Eq. (1) for n neurons (Du & Swamy 2013).

$$ y = \mathop \sum \limits_{i = 1}^{n} W_{i} X_{i} + bias $$
(1)

where i denotes the identification number of the input feature, which ranges from 1 to n, X and W are the value and weight of the input feature, respectively. A brief scheme of neuron is shown in Fig. 2.

Fig. 2
figure 2

A brief scheme of a neuron (Du & Swamy 2013)

Full size image

MLPNN uses the well-known learning algorithm, backpropagation, which was introduced in the 1980s. Backpropagation learns the set of weights iteratively using gradient descent technique to reduce errors and to enhance class prediction precision of the samples.

3.2 RBFN

As a feedforward neural network, RBFN is comprised of three main layers (Haykin 2010):

  • Input layer consisting of sensory or source nodes acquiring data from the environment,

  • Hidden layer which performs a nonlinear transformation on the inputs to obtain the feature space. In general, this layer is of high dimensions making it suitable only for unsupervised learning,

  • Output layer trained in a linear supervised approach which ultimately conveys the network response to the input pattern.

In MLPNN, only linear separability is feasible whereas a function such as XOR is not linearly separable. RBFN uses the radial basis function as an activation function. Neurons’ outputs are inversely proportional to the distance from a location, e.g., the neuron center. The distance metric is usually a Euclidian norm; however, other metrics such as Minkowski and Manhattan are commonly used. The output of the RBFN is a mapping approximation between input and output using a linear combination of radially symmetric functions.

Accordingly, the kth output is given by Eq. (2) (Du & Swamy 2013):

$$ y_{k} \left( x \right) = \mathop \sum \limits_{i = 1}^{n} W_{ki} \Phi_{i} \left( X \right) $$
(2)

where n is the number of inputs, \(k=\mathrm{1,2},\dots ,\) m and m is the number of outputs. Additionally, the Gaussian function \({\Phi }_{i}\left(X\right)\) is defined as Eq. (3) (Haykin 2010).

$$ \Phi_{i} \left( X \right) = \Phi \left( {X - C_{i} } \right) = \Phi \left( {r_{i} } \right) = \exp \left( { - \frac{{r_{i}^{2} }}{{2\sigma_{i}^{2} }}} \right) $$
(3)

where \({C}_{i}\) and \({\sigma }_{i}\ge 0\) are selected centers and widths, and \({r}_{i}\ge 0\).

3.3 NBC

NBC is a probabilistic mathematical classification tool based on the Bayes Theorem and the hypothesis of maximum posteriori. In this method, the values of attributes are assumed to be mutually independent known as “Class Conditional Independence”. This method is considered as “Naïve” as it is used to simplify the calculation task. Class membership of the input pattern can be estimated using this method in a probabilistic way.

Consider a vector \(X=\left({x}_{1},\dots ,{x}_{n}\right)\) is a problem instance with n independent variables. NBC assigns probability depicted in Eq. (4) to this instance for each class \({C}_{k}\) (Murty and Devi 2011):

$$ p\left( {C_{k} |x_{1} , \ldots , x_{n} } \right) $$
(4)

In such a case, conditional probability based on the Bayes theorem can be decomposed as Eq. (5) (Murty and Devi 2011):

$$ p\left( {C_{k} |X} \right) = \frac{{p\left( {C_{k} } \right) p\left( {X|C_{k} } \right)}}{p\left( X \right)} $$
(5)

3.4 Advantages and limitation of the considered models

Advantages and limitations of MLPNN, RBFN, and NBC are thoroughly examined and summarized in detail within Table 1. This table sheds light on the distinctive features and potential drawbacks of each model.

Table 1 Advantages and limitations of MLPNN, RBFN, and NBC (Bishop & Nasrabadi 2006; Du & Swamy 2013)
Full size table

4 Data collection

In order to prepare the dataset, the results of 766 oedometer tests conducted on undisturbed loess samples have been collected from the published literature as primitive raw data. Aside from the measured collapse potential and the inundation stress at which the test was conducted, 4 main soil parameters were collected for each sample including plasticity index, dry unit weight, void ratio, and degree of saturation. Listed in Table A-1 are the details of the compiled dataset, including references, sampling locations, and soil type for each reference based on the USCS.

Figure 3 illustrates the soil type distribution of all samples based on the USCS in the compiled dataset. As shown, the dataset contains four types of soil including CL (clay with low plasticity), ML (silt with low plasticity), SM (silty sand), and ML-CL (clay with low plasticity combined with silt). As can be seen CL is the dominant soil type in the compiled dataset.

Fig. 3
figure 3

Soil type classification of the dataset (Based on the USCS)

Full size image

In addition, Fig. 4 provides a visual representation of the data, illustrating general trends. It is observed that as the degree of saturation and dry unit weight of the samples increase, the collapse potential of the samples decreases. Conversely, with an increase in the void ratio of the samples, the collapse potential shows an upward trend. However, when considering inundation stress and plasticity index, no clear correlation can be identified.

Fig. 4
figure 4

Influence of a Dry unit weight, b Void ratio, c Degree of saturation, d Plasticity index, e Inundation stress on collapse potential of the studied soil samples

Full size image

These findings highlight the complex nature of the collapse potential, indicating the need for more advanced tools and methodologies for analysis. Therefore, in this study, machine learning tools were used to provide a deeper understanding and improved prediction of collapse potential.

A summary of basic statistics is presented in Table 2, including maximum, minimum, average, standard deviation (SD), and coefficient of variation (CV) of the considered variables.

Table 2 Statistical Evaluation of soil parameters in the dataset
Full size table

Based on the information presented in the table, it can be inferred that a majority of the samples exhibit a low dry unit weight. Additionally, the majority of the samples have a comparatively high void ratio as a result of the elevated average value of this parameter (0.76), which can be attributed to the porous characteristics of loess. The table also indicates that the degree of saturation is relatively low, which is expected for loess deposits found in arid areas. The table also demonstrates that the samples are composed of soils with low plasticity, as indicated by the low value of the plasticity index.

Given the comprehensive information regarding soil parameters and inundation stresses, this dataset can be considered highly comprehensive and representative, as the values of different variables span across a wide range without being limited to specific ranges.

5 Model Preparation

In order to prepare the models, the primitive raw data were preprocessed before being fed as input to the models. During the preprocessing of the data, a number of different techniques were applied, including cleaning, integration, reduction, and transformation, based on necessity. These techniques were used to handle the following situations:

  • Noise removal, outlier handling, missing values, and inconsistencies correction,

  • Merging data gathered from various sources into a coherent data store,

  • Reducing data size by aggregating or eliminating redundancies,

  • Normalizing data in some specific ranges or intervals to enhance accuracy and overall performance.

Preprocessed data containing 634 samples were then ready for feeding into the models.

As part of the preparation of the MLPNN and RBFN, the data samples were randomly divided into three parts including 70% as training data, 11% as validation data, and 19% as test data. In order to prepare NBC, the first two parts were combined and fed into the model as training data (81% of the data), and the last part was kept as test data (19% of the data).

In order to prepare MLPNN, a two-hidden-layer feed-forward network with 10 sigmoid neurons in the hidden layer and linear output neurons was selected, and it was trained for 21 epochs. The MLPNN was trained with the Levenberg–Marquardt (LM) backpropagation algorithm except when there is not enough memory. In that case, scaled conjugate gradient backpropagation will be employed. It should be noted that, in the preparation of the model, 5 features (including plasticity index, dry unit weight, void ratio, degree of saturation, and inundation stress) were considered as input parameters while the collapse potential was considered as target or output parameter. In addition, the validation data was used to stop training process in case the network gets overfitted.

For the preparation of the RBFN, both input and output parameters were the same as those for MLPNN. Accordingly, a network with a maximum of 100 neurons was trained, and the spread of RBFs was set to 1.0. Additionally, during the training process, 10 neurons were incrementally added between displays.

To prepare the NBC, the collapse potential values of the samples were classified as targets into five different classes, 1–5, according to Table 3 (ASTM 1996).

Table 3 Collapse potential labels (Based on ASTM, (1996))
Full size table

After classifying the samples as inputs, NBC with normal (Gaussian) distribution parameters was defined for the train data. As a key point, NBC used the same input parameters as MLPNN and RBFN, but its output parameter was the labeled class of collapsibility rather than collapse potential. For the purpose of testing the performance of the model, the NBC was applied to the test data.

6 Evaluation of the Performance of the Proposed Models

In order to assess the performance of the models, it is important to note that the output of MLPNN and RBFN is the collapse potential of soil samples, which is a continuous variable ranging from 0 to more than 10. NBC, however, generates the degree of collapsibility of the samples (In accordance with Table 3), which is an integer ranging from 1 to 5.

Due to the fact that the outputs of the MLPNN and RBFN are continuous values, it is, therefore, necessary to use appropriate performance indices to evaluate their performances such as R2, RMSE, and MAE. The output of NBC, however, is not merely a number, but a class, which makes other criteria such as “Precision” more appropriate for evaluating its performance.

The performance indices are error functions generally defined as the absolute subtraction of targets and model outputs. Learning functions iteratively attempt to reduce error values through techniques such as gradient descent. In general, the closer the outputs are to the targets, the more accurate the model will be. Thus, for some indices, such as R2, high values indicate better performance of the model, while for other indices, such as RMSE and MAE, lower values indicate better performance. As mentioned previously, three popular error indices are R2, MAE, and RMSE as defined by Eqs. (6–8).

$$ {\text{ R}}^{2} = 1 - \frac{{\mathop \sum \nolimits_{{{\text{i}} = 1}}^{{\text{n}}} \left( {{\text{target}}_{{\text{i}}} - {\text{output}}_{{\text{i}}} } \right)^{2} }}{{\mathop \sum \nolimits_{{{\text{i}} = 1}}^{{\text{n}}} \left( {{\text{target}}_{{\text{i}}} - {\text{output}}_{{{\text{avg}}}} } \right)^{2} }} $$
(6)
$$ {\text{MAE}} = { }\frac{{\mathop \sum \nolimits_{{{\text{i}} = 1}}^{{\text{n}}} \left| {{\text{output}}_{{\text{i}}} - {\text{target}}_{{\text{i}}} } \right|}}{{\text{n}}} $$
(7)
$$ {\text{RMSE}} = { }\sqrt {\frac{{\mathop \sum \nolimits_{{{\text{i}} = 1}}^{{\text{n}}} \left( {{\text{output}}_{{\text{i}}} - {\text{target}}_{{\text{i}}} } \right)^{2} }}{{\text{n}}}} $$
(8)

where n is the number of outputs, and \(output_{avg} = {1 \mathord{\left/ {\vphantom {1 n}} \right. \kern-0pt} n}\sum\nolimits_{i = 1}^{n} {output_{i} }\).

Based on the MLPNN and RBFN predictions, Fig. 5 shows the actual values of collapse potential as well as the predicted values for the test dataset (19% of data). Figure 5 illustrates that most of the predicted values of collapse potential by MLPNN and RBFN are in close agreement with the actual values of collapse potential.

Fig. 5
figure 5

Comparison of actual collapse potential values with predicted values based on MLPNN and RBFN models

Full size image

Accordingly, Table 4 presents the calculated MAE, R2, and RMSE for all training, validation, and test datasets for the MLPNN and RBFN.

Table 4 The calculated performance indicators for MLPNN and RBFN models
Full size table

In Table 4, it can be seen that the models perform differently for training and validation datasets due to the random subdivision process. Based on this table, the prediction performance is better for validation set than the training set in terms of the predefined indices. In the context of the test and validation dataset, the high performance of the models can be considered as an indication of their generalization capabilities, as discussed by Cabalar et al. (2012). Regarding the comparison between MLPNN and RBFN, it is evident that MLPNN performs better across all datasets.

In order to compare the performance of RBFN and MLPNN with NBC, the outputs had to be homogenized. Accordingly, Table 3 was once more used to classify the output values of collapse potential for each sample predicted by MLPNN and RBFN.

After classifying the predicted collapse potential values by MLPNN and RBFN, the actual class of soil samples (degree of collapsibility) as well as the predicted class based on MLPNN, RBFN, and NBC are shown in Fig. 6.

Fig. 6
figure 6

Comparison of the predicted class of collapsibility by MLPNN, RBFN, and NBC with the actual class for the test dataset

Full size image

Table 5 shows confusion matrix of predicted classes performed by the used models. A confusion matrix is a widely common performance measurement for machine learning techniques which summarizes a table of the number of actual and predicted classes yielded by a prediction model. The rows in this table indicate the number of samples predicted in each class using three different models, including MLPNN, RBFN, and NBC. Additionally, the columns indicate the amount of data for each actual class. The diagonal cells in the confusion matrix were bolded to visually indicate where the model's predictions aligned with the actual classes.

Table 5 Confusion matrix of predicted classes performed by the used models
Full size table

In the next step, the Precision criterion was selected as an appropriate criterion to compare the performance of the three mentioned models in predicting the degree of collapsibility of samples.

Precision is a machine learning evaluation metric that measures the proportion of correct predictions among all predictions made by a model. In other words, it is an indicator of how accurate a model is at making correct predictions. Alternatively, precision is the percentage of correct predictions that are actually borne out by the model. Precision can be calculated by knowing the number of true positive predictions (TP) and false positive predictions (FP) made by the model. It is then possible to calculate Precision in the following manner (Powers 2020):

$$ Precision = \frac{TP}{{\left( {TP + FP} \right)}} $$
(9)

In order to evaluate the performance of the mentioned models using Precision, the actual degree of collapsibility was compared to the predicted degree of collapsibility by MLPNN, RBFN, and NBC, and if the predictions matched, the prediction was considered TP, whereas if not, they were considered FP. Figure 7 shows the calculated Precision values for each model.

Fig. 7
figure 7

Measured values of Precision for MLPNN, NBC, and RBFN model

Full size image

In this figure, it can be seen that the MLPNN correctly predicted the degree of collapsibility of loess in 86.6% of samples (104 samples from 120) which is a high accuracy level.

7 Conclusion

In this paper, a comparative classification and prediction of the collapse potential of loessial soils was conducted using three well-known supervised machine learning approaches, namely MLPNN, RBFN, and NBC. The preprocessed data utilized in this study comprised 634 samples with 5 input features including dry unit weight, plasticity index, void ratio, degree of saturation, and inundation stress, along with an output parameter named collapse potential. By using the same train, validation, and test data for the MLPNN and RBFN, it was determined that both models are capable of predicting the collapse potential of loess when considering the aforementioned input parameters. MLPNN, however, had better performance than RBFN in predicting collapse potential of loess based on low calculated performance indices (RMSE, MAE, and R2). Furthermore, by utilizing the Precision criterion and confusion matrix, MLPNN was proven to be more accurate than RBFN and NBC in predicting the degree of collapsibility of loessial soils. To conclude, MLPNN performed well when used to predict the level of collapsibility of loess, or in other words when classifying the level of potential collapse risk of loess based on ASTM (1996).