1 Introduction

Soil liquefaction is a catastrophic flow failure of soil that causes severe damage to adjacent structures and can be set in by dynamic or monotonic undrained loading in saturated loose sandy soil. Liquefaction under undrained monotonic loading is called static liquefaction, accompanied by excessive positive pore pressure and low shear strength at high strains; consequently, the mean effective stress approaches zero. An approach for assessing static liquefaction susceptibility is to evaluate soil strain-softening behavior under undrained monotonic triaxial testing. For this purpose, the brittle index, IB, is defined as the ratio of post-peak loss of strength of a strain-softening soil, which can be calculated as follows (Bishop 1967):

$$I_{B} = \frac{{q_{p} - q_{ss} }}{{q_{p} }}$$
(1)

As presented in Fig. 1, qp is the peak undrained shear strength (also known as the onset of static liquefaction), and qss is the steady-state undrained shear strength. The brittleness index ranges from 0 to 1. Higher values of the brittle index reveal the susceptibility to static liquefaction in soil. Therefore, in terms of undrained behavior, soils with IB = 1 are considered full liquefied soils, while soils with IB = 0 are considered non-liquefied soils. Previous studies found that IB is a helpful benchmark for assessing static liquefaction susceptibility (Keramatikerman et al. 2018; Sadrekarimi 2020; Talamkhani and Naeini 2021).

Fig. 1
figure 1

Static liquefaction in monotonic triaxial test

Full size image

The occurrence of instabilities in some sites of sandy soils has drawn the attention of researchers toward its behavior (Ishihara 1993). The static liqueafaction of saturated sands containing plastic fines was dominated by some soil characteristics, such as the fines content, the plasticity of fines fraction, sand gradation, and void ratio of soil. Through experimental studies, several researchers have found that fines content and void ratio influence the undrained behavior of clayey sands in undrained monotonic triaxial tests (Georgiannou et al. 1990; Pitman et al. 1994; E Ovando-Shelley 1997; Bouferra and Shahrour 2004; Abedi and Yasrobi 2010; Naeemifar and Yasrobi 2012). Indeed, Papadopoulou and Tika (2016) introduced the plasticity of the clay particles as a dependent factor in altering the undrained behavior of clayey sand. From the perspective of sand gradation, Rahman and Lo (2008) revealed a dependency between static liquefaction behavior and host sand gradation.

In the scale of analytical and theoretical studies, the static liquefaction of sandy soils has also been investigated. Almost all of them focused on predicting the onset of liquefaction or the point in which soil exhibits an instable behavior at peak strength. A number of studies have employed mathematical equations derived from constitutive behavior models of sandy soils to predict the onset of liquefaction (Mróz et al. 2003; Park and Byrne 2004; Rahman and Lo 2012; Buscarnera and Whittle 2013). These constitutive models for sand behavior rely on state parameters of sand which are affected by stress and density. Prediction of the onset of static liquefaction using these constitutive models bears some challenges and limitations: these models are defined for some specific sand and calibrating these models for other types of sandy soils, particularly sands with plastic fines, has its challenges, may cause errors and imprecisions.

Further, empirical methods based on in-situ tests, including standard penetration test (SPT) and cone penetration test (CPT), have also been used to evaluate the triggering of static liquefaction (Stark and Mesri 1994; Olson and Stark 2002, 2003; Mesri 2007). These methods rely on a correlation of static liquefaction with overburden stress and strength parameters obtained from CPT and SPT tests. Obviously, performing in-situ tests are the requirements of these methods, for which there are associated costs and resources.

To propose a solution for the demanding and incalibrated methods of theoretical approaches and also the costly and time-consuming approaches of emprical methods, Sadrekarimi (2020) conducted an analytical study to predict the onset of static liqueafaction of sandy soils containing plastic and non-plastic fines. In his study, a series of correlations between normalized pore water pressure and the brittle index of sandy soils with different fines content and fines plasticity were performed to derive equations for estimating the normalized pore water pressure at steady state. These analytical interpretations were therefore exempt from fines content and soil initial state.

Recently, considering the practical and efficient application of machine learning techniques in a wide range of engineering areas (Savvides and Papadrakakis 2021; Goodarzi et al. 2021; Savvides and Papadopoulos 2022; Al Bodour et al. 2022), this state-of-the-art approaches are being utilized to predict liquefaction susceptibility of soil (Muduli and Das 2014; Kohestani et al. 2015; Atangana Njock et al. 2020; Kumar et al. 2021; Hanandeh et al. 2022). For static liquefaction assessment, Sabbar et al. (2019) employed two types of artificial neural network models to predict the potential of static liquefaction of clean sands with the ratio of qss/qpeak (Fig. 1). They considered nine input parameters concerning particle size and initial states of clean sand. The model they developed predicted the static liquefaction of clean sand with reasonable accuracy with a root mean squared error of 0.17 for the testing set. It should be noted that the approach they adopted was only applicable to clean sands.

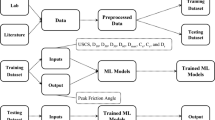
Considering the destructive impacts of static liquefaction to the enviromental and human life, predicting the static liquefaction can prevent and cut these damages. Sandy soils containing plastic fines, as one of the susceptible soils to this hazard, neccesitates more attentions for further studies. Given that the current theoretical and empirical methods for assessing static liquefaction do not incorporate some influential features and condition of soil in liquefaction potential, which have been demonstrated by previous experimental studies, efficient and new approaches should be harnessed to resolve this inconsistency. Using machine learning as a means of predicting engineering properties and nonlinear mechanical behavior would be a useful solution to this problem. In order to extend the application of machine learning algorithms, this study aims to evaluate the competency of six algorithms in predicting static liquefaction of saturated sands containing plastic fines. Further, a sensitivity analysis is also performed to determine the relative importance of each feature in static liquefaction of sand with plastic fine.

2 Methodology

2.1 Dataset

The dataset contains 114 isotropic undrained monotonic triaxial tests conducted on saturated sands containing plastic fines that were compiled from previous studies (Lagunas 1992; Pitman et al. 1994; Bouferra and Shahrour 2004; Derakhshandi et al. 2008; Md. Rahman 2009; Abedi and Yasrobi 2010; Naeemifar and Yasrobi 2012; Papadopoulou and Tika 2016; Chou et al. 2016; Talamkhani 2018). Based on the literature, eight parameters were introduced as the input parameters to the algorithms, which can be classified into three classes: (a) host sand characteristics; (b) plastic fines characteristics; (c) soil condition.

Sand is characterized in regards to its physical dimension and gradation. In this study, two characteristics of sand, including the average grain size of host sand (D50) and the coefficient of uniformity of host sand (Cu), were incorporated into the input parameters.

Plastic fines were introduced to the algorithms using four input parameters consisting of the fines content (Fc), the liquid limit of clay fines (LL), the plasticity index of fines (PI), and the plasticity deviation of fines (ΔPI). The parameter of ΔPI denotes the plasticity deviation from the A-line in Casagrande's classification chart, which equation is as follows (Das 2013):

$$\Delta PI = PI - 0.73\left( {LL - 20} \right)$$
(2)

Das and Khaled (2014) and Khan et al. (2016) found that ΔPI is an influential parameter in predicting the shear strength of clayey soil. Hence, in the present study, ΔPI was considered one of the input parameters that attributes to plastic fines. The plasticity distribution of the fines fraction of the database is depicted in Fig. 2. A significant fraction (90%) of the fines is classified as clay, so a small proportion (10%) of the fines is plastic silt. Moreover, from the liquid limit point of view, only 36% percent have LL values greater than 50, classified as a high plasticity clay or silt, and the remaining are low plasticity fines.

Fig. 2
figure 2

Plasticity distribution of fines portion within the database

Full size image

Two decisive parameters associated with the condition of soil, including the intergranular void ratio (eg) and the effective confining pressure (σ´c), were considered in this study. The parameter of eg is the void ratio concerning sandy soil containing fine particles, which is defined as follows (Thevanayagam 1998):

$$e_{g} = \frac{{e + F_{c} }}{{1 - F_{c} }}$$
(3)

where e is the global void ratio and Fc is the fines content. The idea of the intergranular void ratio proposes that the fines occupy the voids created among the sand grains, so the behavior of sand with a modest quantity of fines could be dictated by the intergranular void ratio in preference to the global void ratio (Thevanayagam and Mohan 2000; Belkhatir et al. 2010, 2011).

On the other hand, the brittle index, IB, is used as the target. Figures 3 and 4 respectively depict the frequency histograms of input and target features throughout the dataset.

Fig. 3
figure 3

Frequency of inputs in the dataset

Full size image
Fig. 4
figure 4

Frequency of target in the dataset

Full size image

In order to validate the models, the dataset was divided into two subsets: the training set (70%) and the testing set (30%). The models were constructed first by learning from the training data; then, their performance was evaluated using the test data. Table 1 shows the statistical characteristics of both the input and target parameters of the training and testing sets.

Table 1 Statistical description of training and testing sets
Full size table

2.2 Overview of the Employed Methods

In the present study, six methods, such as backpropagation multi-layer perceptron (BP-MLP), support vector regression (SVR), lazy K-star (LKS), decision table (DT), random forest (RF), and M5, were implemented to predict the brittle index of sand and plastic fine mixtures. Algorithms and mathematical features of the utilized methods are presented briefly in the following sections.

2.2.1 Backpropagation Multi-Layer Perceptron (BP-MLP)

Artificial neural networks (ANN) is a high-reputed method for predicting engineering properties in the geotechnical field of study, which is derived from the biological neural network (McCulloch and Pitts 1943). ANN architecture involves an input layer, one or more hidden layers, and one output layer. Each layer can include several neurons. Hidden layers connected to the input and output layers using weighted connections are incorporated to achieve accurate predictions.

Backpropagation multi-layer perceptron (BP-MLP) is a type of ANN that consists of one or more hidden layers (Rumelhart et al. 1986). It is trained with a backpropagated algorithm to estimate the optimized cost function. The value of each neuron is computed using a sigmoid activation function from the connected neurons in the previous layer. The activation function, g, is a sigmoid function for computing the hidden layer neurons, as follows:

$$g\left( X \right) = \frac{1}{{1 + e^{ - X} }}$$
(4)

It is important to note that output is computed by a linear function with the last hidden layer. The predicted value is compared to the actual value in a backpropagation procedure. If the mean squared error is greater than the desired error, the process is repeated until the mean squared error is optimized (Fu 1994).

2.2.2 Support Vector Regression (SVR)

Support vector regression (SVR) is a linear or hyperplane method for regression problems to cope with complex non-linearity of numerical data, which is accompanied by using kernel functions (Vapnik 1995; Smola and Schölkopf 2004). In the SVR algorithm, first, an error limit, ϵ, is introduced, then the goal is to find a function that has at most a deviation ϵ from the target values while being as flat as possible. To put it another way, the sensitivity to error is not essential until it is lower than ϵ; but any deviation greater than this will be rejected. Having a loss function with error limit of ϵ, the optimization problem can be solved through a standard dualization technique using Lagrange multipliers (Smola and Schölkopf 2004).

In non-linear problems, a kernel function can be utilized to locate the data into a higher-dimensional feature space where linear regression is conducted. The utilization of appropriate kernel function, depending on the dataset, contributes to reaching the precise prediction. In this study, the Pearson universal kernel (PUK) is employed in the SVR process, which outperformed better than other kernel functions (Üstün et al. 2006).

2.2.3 Lazy K-Star (LKS)

K-star is an instance-based classifier that the class of a test instance is determined by analogous training instances and defined by some similarity function (Cleary and Trigg 1995). The most straightforward instance-based learners are nearest neighbor algorithms (Cover and Hart 1967). These algorithms retrieve the single most comparable instance from the training set using a domain-specific distance function.

Using an entropy-based distance function, the K-star differs from other instance-based learners. The K-Star is a type of nearest-neighbor technique based on transformations using a generalized distance function. The method, which involves calculating the distance between two instances, is based on information theory. Thus, the distance between instances may be characterized as the complexity of transforming one instance into another. In order to define the length of the shortest string connecting the two instances, the Kolmogorov criterion between two instances was defined (Li and Vitányi 1993), which concentrates on just the shortest one out of the numerous potential transformations. Incidentally, the key point is that any sequence can have a probability.

2.2.4 Decision Table (DT)

The decision table is a straightforward learning algorithm that sometimes, depending on the dataset, can surpass other complex decision tree algorithms, attempting to predict a minimum set of features. The performance of DT is based on a decision table, assisted by the features, which searches for the best matches through the table for a given instance. This table, known as decision table majority (DTM), is made up of two components: (1) a schema, which is a collection of features included in the table; (2) a body, which is made up of labeled instances from the space specified by the features in the schema (Kohavi 1995). Development of DTM necessitates using a search algorithm to determine which features should be included in the schema; thus, the particle swarm optimization method (PSO) by using a continuous search space is used in this study to locate these features (Moraglio et al. 2007). It should be mentioned that only the assorted features in the schema are incorporated, and the others are ignored.

2.2.5 Random Forest (RF)

Random forest (RF) is a robust technique for solving regression, unsupervised learning, and classification issues originally presented by Breiman (2001). An extensive number of regression trees are combined parallelly during the training process of the RF, each of which depends on a random vector that has particular characteristics. The accuracy of the RF significantly depends on the strength of the individual trees. A randomly divided subset of the training set is used to build each tree. The RF then aggregates all the trees using the bootstrap aggregating (bagging) technique (Breiman 1996). Bagging formulates each classifier in the ensemble using a randomly generated set of data that each classifier contributes an equal vote for identifying unlabeled instances. By lowering the variation associated with prediction, bagging may increase the accuracy.

2.2.6 M5

M5 is a tree-based model accompanied by a multivariate linear model at the leaves to predict accurately (Quinlan 1992). A decision tree is built in which a splitting criterion is used to minimize the variation along each branch. The splitting procedure is based on the standard deviation of class values that reaches a node, indicating the error and calculating the expected reduction due to testing each attribute. Finally, multivariate linear regression is utilized to construct a linear model for each node based on the selected attributes for the nodes. A pruning technique, incidentally, is employed to minimize the estimated error (Wang and Witten 1997).

2.3 Accuracy Assessment

In this research, the performance of models in predicting the brittle index was controlled through three indicators, including R, RMSE, and MAE.

R is the correlation coefficient that measures the linear correlation between actual and predicted values. The R value ranges from 0 to 1, and the higher value represents the better performance of the model. The correlation coefficient R can be obtained as follows:

$$R = \frac{{\mathop \sum \nolimits_{i - 1}^{m} \left( {y_{i} - \overline{y}} \right)(p_{i} - \overline{p})}}{{\sqrt {\mathop \sum \nolimits_{i = 1}^{m} (y_{i} - \overline{y})^{2} } \sqrt {\mathop \sum \nolimits_{i = 1}^{m} (p_{i} - \overline{p})^{2} } }}$$
(5)

where: \({y}_{i}\) and \({p}_{i}\) are the actual and predicted values of the output, respectively; \(\overline{y}\) and \(\overline{p}\) are average of the actual and predicted output, respectively; m represents the number of instances.

RMSE is the abbreviation of root mean squared error, a measurement of produced error. Accordingly, a lower RMSE means a higher level of accuracy. The RMSE can be calculated as follows:

$$\mathrm{RMSE}=\sqrt{\frac{1}{\mathrm{m}}\left({\sum }_{\mathrm{i}=1}^{\mathrm{m}}({\mathrm{y}}_{\mathrm{i}}-{\mathrm{p}}_{\mathrm{i}}{)}^{2}\right)}$$
(6)

MAE stands for mean absolute error, indicating the average absolute error of predictions in all instances. The lower value of MAE reveals higher accuracy for a model. It can be calculated as the following equation:

$$\mathrm{MAE}=\frac{1}{\mathrm{m}}{\sum }_{\mathrm{i}=1}^{\mathrm{m}}\left|{\mathrm{y}}_{\mathrm{i}}-{\mathrm{p}}_{\mathrm{i}}\right|$$
(7)

2.4 Models Configuration

Throughout this study, all models were developed through WEKA 3.9.5, which is based on Java scripts (Witten and Frank 2002). As seen in the previous section, some models include hyperparameters that can affect the performance of each model. These parameters were selected based on two criteria: (a) precision; (b) quality of the correlations. In other words, the configurations of models were selected to make a prediction with high precision and proper fitting to avoid overfitting and underfitting. The process of hyperparameter tuning includes a series of test and trial of various configuration for each method with regards to bias and variance of train and test sets. The main goal of each series is to find the model that produces predictions with the least possible bias and variance. To put it simply, the optimum models are ones that are not significantly dependent on training data and are capable of producing accurate predictions for test data. To this end, the accuracy of models with various hyperparameters was monitored to find the optimized model with the highest accuracy for both test and training sets (primarily the test set). The hyperparameters of the optimized algorithm for each method are presented in Table 2.

Table 2 Hyperparameters of models
Full size table

3 Results and Discussion

3.1 Models Performance

Tables 3 and 4 provide a summary of the results of all methods using R, RMSE, and MAE for the training and testing sets, respectively. As shown in these tables, tested methods are sorted based on their accuracy. According to each accuracy criterion (R, RMSE, and MAE), all methods are graded such that a method with the highest level of accuracy would receive a higher score than other methods (with a high value of R and a low value of RMSE and MAE); otherwise, it would receive a lower score. As a means of clarifying the effectiveness of the methods, the results are presented with a color intensity model, in which a higher level of accuracy is indicated by a rich green color and a lower level of accuracy by a pale green color. The overall score of each method was equal to the sum up of all subscores corresponding to the method. Finally, all methods are sorted in respect of their overall scores.

Table 3 Performance ranking of all models for the training set
Full size table
Table 4 Performance ranking of all models for the testing set
Full size table

Remarkably, it can be seen from that all methods predicted training set with very strong correlations with the experimental values, as the values of R ranged between 0.90 to 0.99 (Schober and Schwarte 2018). Indeed, in terms of RMSE and MAE, the models showed high accuracy that the values of RMSE corresponding to the training set experienced values between 0.034 and 0.132. Moreover, the values of MAE were between 0.019 to 0.099. Among all methods, the LKS, SVR, and RF models outperform other methods in predicting the training set.

As shown in Table 4, the utilized methods were successful in predicting the testing set with satisfactory accuracy. There was a strong correlation between the predicted and actual value of IB in all methods which predicted the testing set with an R parameter ranging from 0.82 to 0.92. The values of RMSE and MAE corresponding to the testing set provide complementary evidence for the suitability of employed methods. The values of the MAE parameter were found in a range of 0.092 to 0.134 for testing set, which means that the brittle index of a soil can be predicted with an average error of 0.092 to 0.134. In other words, the post-peak loss of strength of the clayey sand can be predicted with an average error of 10% for static liquefaction potential. Furthermore, the values of the RMSE parameter range from 0.133 to 0.178. (Fig. 5)

Fig. 5
figure 5

Experimental and predicted value of brittle index using SVM and LKS methods for: a training set, b testing set

Full size image

By comparing the performance of all methods and their ranking, outperformed predictions were made through SVR and LKS. In order to clarify the performance of SVR and LKS, distribution of predicted values of these two models are plotted against actual values in Fig. 6. Parallel to the line of equality (1:1), error limits with ΔIB = 0.3 are also shown on both sides. As can be seen in Fig. 5, most of the test set falls within the error limit, indicating that almost all of the test set is predicted with an error of less than 0.3. In other words, using SVR or LKS methods to predict the brittle index of soil, the predicted value would have an error less than 0.3. This error threshold appears acceptable for estimating the behavior of clayey sands under monotonic loading when considering static liquefaction. To illustrate the distribution of errors for SVR or LKS methods, Figs. 7 and 8 show the error graphs for the training and testing sets, respectively. There is a normal distribution of error within the dataset, and most of the samples have lower errors. Few predictions, however, produced errors greater than 0.3, which may be the result of laboratory error occurring during the testing of the samples due to the high sensitivity of monotonic triaxial testing.

Fig. 6
figure 6

Experimental versus predicted brittle index of SVM and LKS for: a training set, b testing set

Full size image
Fig. 7
figure 7

Error graphs of the training set: a error magnitude of SVR and LKS, b distribution of error in SVR, c distribution of error in LKS

Full size image
Fig. 8
figure 8

Error graphs of the testing set: a error magnitude of SVR and LKS, b distribution of error in SVR, c distribution of error in LKS

Full size image

Despite the superior performance of LKS to SVR in predicting the training set, both methods made almost similar estimations for the testing set. By comparing the distribution of error in Figs. 7 and 8, the similarity of the prediction can be corroborated. The LKS predicted the testing sets reasonably, while the difference between the precision of testing and training sets marks a degree of overfitting of the LKS model for this study. In addition, the difference between R values for training and testing sets is less in the SVR than in the LKS. This indicates that the SVR method is properly fitted.

3.2 Model Reliability

To determine the superiority and reliability of the algorithms, a reliability analysis is also performed. The Friedman analysis of variance by ranking was performed on the static liquefaction predictions of all utilized models (Shen et al. 2022). In this approach, for z models, the models are ranked based on the errors produced by their predictions from 1 (least error) to z (highest error). For a database with m data, the average ranking (Rj) for model j can be computed as follows:

$${\mathrm{R}}_{\mathrm{j}}=\frac{1}{\mathrm{m}}\sum_{\mathrm{i}=1}^{\mathrm{m}}{\mathrm{r}}_{\mathrm{i}}^{\mathrm{j}}$$
(8)

where \({r}_{i}^{j}\) denotes the ranking of the ith data for model j.

In this study, the average rankings of all utilized models for the test set data were calculated that are plotted in Fig. 9. As can be seen, the two models of SVR and LKS hold the lowest Friedman rank among the other models throughout the test set which demonstrates their superior reliability. To find out whether this variation in performance is significant or not, chi-square is used to evaluate the distribution of rank in the Friedman ranks. Chi-square (\({\upchi }_{\mathrm{r}}^{2}\)) can be calculated using as follows:

Fig. 9
figure 9

Variation of Friedman rank for utilized algorithms on testing data

Full size image
$${\upchi }_{\mathrm{r}}^{2}=\frac{12\mathrm{m}}{\mathrm{z}(\mathrm{z}+1)}\left[\sum_{\mathrm{j}=1}^{\mathrm{z}}{\mathrm{R}}_{\mathrm{j}}^{2}-\frac{\mathrm{z}{(\mathrm{z}+1)}^{2}}{4}\right]$$
(9)

This equation relies on the null hypothesis with z–1 degrees of freedom for z models. According to Sheskin (2011), the null hypothesis would be rejected if the computed value of \({\upchi }_{\mathrm{r}}^{2}\) is equal to or greater than the critical chi-square at a prespecified level of significance. For a distribution of data with 5 degrees of freedom and 0.95 degree of significance, the critical chi-square is equal to 11.07. Considering that the value of \({\upchi }_{\mathrm{r}}^{2}\) of this study is equal to 11.32, the null hypothesis can be rejected, so a significant difference is found between the applied models.

3.3 Sensitivity Analysis

In order to determine the relative importance of brittle index to each input feature, a sensitivity analysis of the features was conducted. In this study, the Cosine amplitude method (CAM) is employed to explore the relative importance of input variables affecting the IB of clayey sand. In this approach, the sensitivity degree of input is obtained by setting an equation between input and output data pairs. For a set of data with n variable and m instances, the sensitivity degree, Ri, of the ith variable is calculated as the following equation (Yang and Zhang 1997):

$${\mathrm{R}}_{\mathrm{i}}=\frac{{\sum }_{\mathrm{k}=1}^{\mathrm{m}}{\mathrm{x}}_{\mathrm{ik}}{\mathrm{y}}_{\mathrm{k}}}{\sqrt{{\sum }_{\mathrm{i}=1}^{\mathrm{m}}{\left({\mathrm{x}}_{\mathrm{ik}}\right)}^{2}.{\sum }_{\mathrm{i}=1}^{\mathrm{m}}{\left({\mathrm{y}}_{\mathrm{k}}\right)}^{2}.}}$$
(10)

where xik denotes the value of the ith variable for kth instance, and yk is the dependent parameter of kth instance. In other words, xik is an array of the input matrix (X) with n × m dimension and yk is an array of the target matrix (Y) with m × 1 dimension, so these matrices are defined as follows:

$${\mathrm{X}}_{114\times 8}=\left[\begin{array}{cccccccc}{\mathrm{x}}_{\mathrm{1,1}}& {\mathrm{x}}_{\mathrm{1,2}}& {\mathrm{x}}_{\mathrm{1,3}}& {\mathrm{x}}_{\mathrm{1,4}}& {\mathrm{x}}_{\mathrm{1,5}}& {\mathrm{x}}_{\mathrm{1,6}}& {\mathrm{x}}_{\mathrm{1,7}}& {\mathrm{x}}_{\mathrm{1,8}}\\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ {\mathrm{x}}_{\mathrm{114,1}}& {\mathrm{x}}_{\mathrm{114,2}}& {\mathrm{x}}_{\mathrm{114,3}}& {\mathrm{x}}_{\mathrm{114,4}}& {\mathrm{x}}_{\mathrm{114,5}}& {\mathrm{x}}_{\mathrm{114,6}}& {\mathrm{x}}_{\mathrm{114,7}}& {\mathrm{x}}_{\mathrm{114,8}}\end{array}\right]$$
(11)
$${\mathrm{Y}}_{8\times 1}=\left[\begin{array}{c}{\mathrm{y}}_{1}\\ \vdots \\ {\mathrm{y}}_{114}\end{array}\right]$$
(12)

In this technique, if the value of Ri is near one, high dependence can be recognized. On the contrary, the value of Ri near zero indicates the independency of that input variable.

The results of the CAM analysis conducted on experimental results and all methods are presented in Fig. 10. For experimental results, five parameters, including D50, Cu, PI, LL, and, eg, ranging from 0.76 to 0.82, showed larger values of Ri than the others, which indicate that the brittle index depends greatly on these parameters. In other words, the static liquefaction of clayey sand is consistent with the gradation of the host sand, the plasticity of clay fraction, and the intergranular void ratio. The index of Ri corresponding to LL has the greatest value among all variables. On the other hand, the experimental Ri values corresponding to ΔPI are around 0.41, demonstrating a low correlation between ΔPI and IB. It should be noted that previous studies have found that ΔPI is an influential parameter in predicting the shear behavior of clay (Das 2013; Khan et al. 2016), whereas the feature importance analysis shows a weak relationship between static liquefaction and ΔPI of clayey sand. Additionally, the variables Fc and σ’c have values of Ri equal to 0.609 and 0.641 for experimental outputs, so a medium influence of fines content and confining pressure on the brittle index can be interpreted.

Fig. 10
figure 10

Importance of the input features resulted from CAM analysis for experimental and developed models predicted values

Full size image

By comparing the values of Ri related to different models from Fig. 10, it can be noted that SVR and LKS have the slightest difference from the experimental values, indicating the superiority of these methods in predicting the brittle index.

The results of sensitivity analysis underline the importance of some characteristics of sand containing plastic fine in static liquefaction. However, as mentioned earlier in the literature review of this study, current approaches for estimating static liquefaction of sand containing plastic fines mainly rely on initial states of soil or are calibrated for a specific soil (Rahman and Lo 2012; Sadrekarimi 2020); thus, the sand physical characteristics are not incorporated in their approach. Further, the plasticity of the plastic fines and their content are not considered in any previously established method of estimating static liquefaction. However, as seen in this section, these features are influential in the static liquefaction of clayey sand, even the relative importance of parameters related to host sand gradation (D50 and Cu) and plasticity of plastic fines (PI and LL) are higher than the parameters related to initial state of soil (eg and σ’c). In summary, sensitivity analysis reveals the importance of soil physics and plasticity in static liquefaction which has previously been ignored.

4 Brittle Index Estimation

There are several practical benefits to using machine learning techniques, such as presenting equations, matrices, or trees for estimating targets without using computer-based programs so that new input can be applied to the equations to estimate the targets. The backpropagation multi-layer perceptron and the M5 are two methods of this study that yield equations for calculating brittle index. Presented in this section are the methods for estimating the brittle index using these two methods. It should be noted that when the computed brittle index returns a negative number, the behavior should be considered stable with IB = 0. On the other hand, computed IB > 1 should be considered as a full-liquefied soil with IB = 1. Further, the units of the input parameters are according to Table 1.

4.1 Backpropagation Multi-Layer Perceptron

As stated in previous sections, BP-MLP utilized a network of neurons to estimate the target. The network is defined by equations and matrices, so new input data can be given to the mathematical equations to calculate the target. As indicated in Fig. 11, a BP-MLP network compromising eight inputs, one hidden layer with four neurons, and output is harnessed for predicting the brittle index. As seen in Fig. 11, the hidden layer is calculated by the weight vector of w(1) connected to the input layer, and the output layer is obtained from the weight vector of w(2) connected to the hidden layer. These two weight factors obtained from the BP-MLP models are as below:

Fig. 11
figure 11

The backpropagation multi-layer perceptron architecture

Full size image
$${\mathrm{w}}^{(1)}={\left[\begin{array}{ccccccccc}1.60& 1.14& 5.45& 8.37& -0.59& -1.03& 0.85& 0.68& 0.56\\ -2.24& 0.32& 0.94& -2.82& 2.43& 1.69& 0.92& -4.67& 2.38\\ -5.16& 2.84& -4.9& -3.34& -3.94& -0.79& -3.60& -1.51& -0.04\\ -3.45& 2.15& -0.01& -1.12& -1.17& 0.62& 2.48& -0.78& -1.37\end{array}\right]}_{4\times (\mathrm{n}+1)}$$
(13)
$${\mathrm{w}}^{(2)}={\left[\begin{array}{ccccc}0.97& -1.84& -1.14& -2.39& 1.58\end{array}\right]}_{1\times (4+1)}$$
(14)

It can be seen that w(1) is a matrix with 4 × (n + 1) dimension that n is the number of input features, which equals 8 in this study, and 4 is the number of hidden layer neurons. It should be noted that one extra column in matrix w(1) refers to the bias of the neurons (bi). Needless to say, the weight vector w(2) connects 4 hidden neurons to one output, so it is a 1 × (4 + 1) matrix. The hidden neuron values can be calculated from the sigmoid function of the linear multiplication of w(1) and the matrix of the input layer (X), so it means:

$$\mathrm{X}=\left[\begin{array}{ccccccccc}1& {\mathrm{D}}_{50}& {\mathrm{C}}_{\mathrm{u}}& \mathrm{Fc}& \mathrm{PI}& \mathrm{LL}& \mathrm{\Delta PI}& {\mathrm{e}}_{\mathrm{g}}& {\upsigma }_{\mathrm{c}}^{\mathrm{^{\prime}}}\end{array}\right]$$
(15)
$${\mathrm{z}}^{(1)}=\mathrm{X}\times {\left({\mathrm{w}}^{(1)}\right)}^{\mathrm{T}}$$
(16)
$$\mathrm{h}=\mathrm{g}({\mathrm{z}}^{(1)})$$
(17)

where the formulation of the sigmoid function, g, is defined in Eq. (3). Eventually, the value of brittle index can be obtained from the linear multiplication of w(2) and hidden layer (h) matrices, as follows:

$$\mathrm{h}=\left[\begin{array}{ccccc}1& {\mathrm{h}}_{1}& {\mathrm{h}}_{2}& {\mathrm{h}}_{3}& {\mathrm{h}}_{4}\end{array}\right]$$
(18)
$${\mathrm{I}}_{\mathrm{B}}=\mathrm{h}\times {\left({\mathrm{w}}^{(2)}\right)}^{\mathrm{T}}$$
(19)

4.2 M5

One of the advantages of M5 methods is formulating a decision tree consisting of linear regression functions at terminal leaves. The M5 tree produced by the dataset of this study is depicted in Fig. 12. The M5 tree for estimating the brittle index relies on two parameters of fines content, Fc, and coefficient of uniformity of host sand, Cu, and includes four linear models (LM) in four-terminal leaves. For calculating brittle index of a new datum, as an input, we should move downward from the head of the M5 tree to find the appropriate linear models based on the conditions (written in diamonds). At the first stage, the fines content of soil is the determining factor: for soil with Fc higher than 0.175, LM1 should be employed for calculating IB. If not, the coefficient of uniformity should be considered: for soil with Cu greater than 1.75 (in addition to Fc ≤ 0.175), LM2 should be employed for computing IB. If not, the fines content again comes out as the determining factor: for soils with Fc higher than 0.125 (in addition to.

Fig. 12
figure 12

The Generated tree based on the M5 model

Full size image

Fc ≤ 0.175 and Cu ≤ 1.75), LM3 should be used and for ones with Fc lower than 0.125; otherwise, LM4 should be used.

5 Conclusion and Future Works

This study compiled a dataset from ten research papers reported undrained monotonic triaxial test results of sand containing plastic fines. The database incorporated 114 test results, including properties of host sand, plastic fines, and test conditions. The database was utilized in six different machine learning methods, including BP-MLP, SVR, LKS, DT, RF, and M5, for the purpose of predicting static liquefaction potential based on brittle index. A color intensity rating with the total ranking of all models concerning three error criteria of R, RMSE, and R was carried out.

An acceptable level of accuracy was found in all methods as the values of R corresponding to testing sets were in ranges of 0.82 to 0.92. Based on the total ranking, the SVR and LKS methods were found to be more accurate than the others, which predicted testing set with R, RMSE, and MAE values were respectively equal to 0.92, 0.135, and 0.096 for the SVR model and 0.908, 0.133, and 0.098 for the LKS model.

The sensitivity analysis highlighted the importance of the characteristics of host sand and plastic fines in static liquefaction. The features D50, Cu, PI, LL, and eg have a greater influence on the brittle index of clayey sand. Brittle index is less affected by the variables Fc and σ’c. Indeed, it was seen that ΔPI of the plastic fines had the least impact on the static liquefaction of clayey sand.

This study has shown that machine learning techniques are capable of predicting static liquefaction of sand containing plastic fines, which suggests that these algorithms, or some more complex algorithms, can be used to predict static liquefaction of other soils with similar vulnerabilities. Silty sand or sand containing non-plastic fines are some of those materials that have been known as one the most vulnerable soils to static liquefaction (Lade and Yamamuro 2011). Further, mine tailings (Macedo and Vergaray 2022) and losses (Yan et al. 2020) are the other static liquefaction susceptible soils. Developing machine learning algorithms may significantly contribute to the geotechnical community to identify and predict the static liquefaction of vulnerable sites.