Abstract
As known, in a Winkler type of analysis the soil medium underneath the foundation is violently replaced by a row of parallel springs having constant ks. For the effective calculation of the latter, which is called the modulus of subgrade reaction, the two elastic constants of the soil (the elastic modulus, E and the Poisson’s ratio, ν) must be known. Although for homogenous soils this generally seems not to be a problem, the same does not stand for stratified mediums or mediums with linearly increasing modulus with depth. In addition, in a Winkler type of analysis, the proper pair of elastic constant values of soil should be selected. This refers to a Poisson’s ratio value equal to zero corresponding to the deformation pattern of springs (compression with no lateral expansion) and the respective modulus. In the present paper a method for calculating the equivalent elastic constants for the above mentioned mediums is proposed based on the theory of elasticity combining the principle of superposition. Various cases are considered, since the equivalent modulus, Eeq, depends on the rigidity and the shape of the footing. As shown, the derived Eeq values not only return reliable settlement results, but also settlement profiles that are similar to those corresponding to the original soil mediums.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Since 1949, according to the best knowledge of the author (Pantelidis 2019), eighteen methods calculating the equivalent modulus of elasticity (\(E_{eq}\)) of stratified mediums have been proposed; indeed, eight of them after 2000 indicating that this research topic remains open. Parallelly, it makes sense that these methods refer exclusively to stratified soil mediums, although soil mediums with linearly increasing modulus with depth are often met in practice. In brief, Odemark’s (1949), de Barros’s (1966), Sridharan et al.’s (1990), Hirai and Kamei’s (2003, 2004), Hirai’s (2008), Abu-Farsakh and Chen’s (2012) methods are based on the concept of the flexural rigidity of thin slabs, Egorov and Nichiporovich (1961), Barden (1962), Gorbunov-Possadov and Malikova (1973), Sadrekarimi and Akbarzad (2009), Brahma and Mukherjee (2010), Budhu (2011) approached the problem from the mathematical mean point of view, Salamon (1968), Wardle and Gerrard (1972) and Gerrard (1982) suggested methods based on stress–strain relationships of the theory of elasticity while Ueshita and Meyerhof (1967), Fraser and Wardle (1985) and HariBharghav et al. (2017) proposed methods purely based on the theory of elastic settlement analysis. The comprehensive review of these methods offered recently by the author (Pantelidis 2019) clearly shows that there is still not a reliable method.
In the present paper a method for calculating both \(E_{eq}\) and \(\nu_{eq}\) of stratified soil mediums or homogenous mediums with linearly increasing modulus with depth is proposed. This method is based on the theory of elasticity.
2 Derivation of the Proposed Equivalent Elastic Moduli
2.1 Derivation of the Proposed Equivalent Elastic Modulus for Flexible Rectangular Footings
According to Boussinesq (1885), the normal stress increase at any point in a homogenous, elastic and isotropic semi-infinite medium due to a concentrated load \(P\) on its surface is:
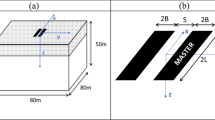
where \(L_{1} = \sqrt {x^{2} + y^{2} + z^{2} } ,\;r = \sqrt {x^{2} + y^{2} }\) and \(\nu\) is the Poisson’s ratio (see Das 2007). The notation followed is shown in Fig. 1.
Considering a rectangular, uniformly loaded area which extends from \(x_{1}\) to \(x_{2}\) and from \(y_{1}\) to \(y_{2}\) (in the x- and y- direction respectively) on the surface of the elastic medium, the increase in the normal stress at any point in the medium in question will be:
The differentials dx and dy of the variables \(x\) and \(y\) are included in \(\Delta \sigma_{i}\) as \(P = q{\text{d}}y{\text{d}}x\) (recall Eqs. 1 to 3; q is the uniform loading). Consequently, from Hooke’s law, the unit vertical strain is:
Using Eqs. 1 to 3, the latter can be rewritten as follows:
The settlement, \(\rho\), at the foundation level corresponding to a layer extending from \(z = 0\) (level of foundation) to \(z = H\), derives from the integration of Eq. 6 between these limits, that is:
The problem has been solved by Steinbrenner (1934) for a general \(B \times L\) footing. The solution can be found in any geotechnical engineering book, usually, combined with Fox’s (1948) embedment depth factor \(I_{E}\). More specifically,
where,
Also, \(a^{\prime} = 4,\;B^{\prime} = {B \mathord{\left/ {\vphantom {B 2}} \right. \kern-\nulldelimiterspace} 2},\;m_{1} = {L \mathord{\left/ {\vphantom {L B}} \right. \kern-\nulldelimiterspace} B}\) and \(n_{1} = {H \mathord{\left/ {\vphantom {H {({B \mathord{\left/ {\vphantom {B 2}} \right. \kern-\nulldelimiterspace} 2})}}} \right. \kern-\nulldelimiterspace} {({B \mathord{\left/ {\vphantom {B 2}} \right. \kern-\nulldelimiterspace} 2})}}\) for the settlement at the center of foundation and \(a^{\prime} = 1,\;B^{\prime} = B,\;m_{1} = {L \mathord{\left/ {\vphantom {L B}} \right. \kern-\nulldelimiterspace} B}\) and \(n_{1} = {H \mathord{\left/ {\vphantom {H B}} \right. \kern-\nulldelimiterspace} B}\) for the settlement at the corner of foundation.
Apparently, there is an equivalent homogenous soil medium with elastic constants \(\left( {E_{eq} ,v_{eq} } \right)\) producing under identical loading conditions the same settlement with the original soil medium. Equating these settlements (note: for the stratified medium the principle of superposition is necessary to be applied; see Barnes 2016)
and solving the latter as for \(E_{eq}\), the following expression is obtained:
where, \(h_{i}\) is the vertical distance extending from the level of foundation to the bottom of the \(i\)-th layer (that is, it is not the thickness of the \(i\)-th layer); there are \(n\) such layers. Also, it is \(I_{s} \left( {h_{0} ,v_{1} } \right) = 0\). Equation 16 has two unknowns, namely, \(E_{eq}\) and \(\nu_{eq}\); however as shown later, the two unknowns can easily be reduced to one, the equivalent modulus \(E_{eq}\). Finally, from Eq. 16 it is inferred that, \(E_{eq}\) depends on the point considered on the plan-view of footing, as the parameter \(n_{1}\) in the \(I_{s}\) factor depends on the location of this point (recall Eqs. 12–14). By suitably applying the principle of superposition on the foundation level (see Barnes 2016), Eq. 16 can be used so that the \(E_{eq}\) value to be calculated at any point on the plan-view of footing.
It is noted that, Eq. 16 stands for any \(I_{s}\) factor derived from a settlement equation of the form:
2.2 Derivation of the Proposed \(E_{eq}\) for Circular Footings
2.2.1 Circular Flexible Footings
In a similar way, the settlement at the center of a flexible circular footing is:
where
and \(r_{1}\) is the radius of footing and \(H\) is the thickness of the compressible medium measured from the foundation level.
Equations 18 and 19 (ignoring the \(I_{E}\) factor) derives from the following single integral:
where, the term \(x^{2} + y^{2}\) in Eq. 6 has been replaced by \(r^{2}\). \(E_{eq}\) is then obtained from Eq. 16 using the \(I_{s}\) factor of Eq. 19.
2.2.2 Circular rigid footings
The settlement of a rigid circular footing is (see Kézdi and Rétháti 1988):
where \(\alpha = \arctan ({{r_{1} } \mathord{\left/ {\vphantom {{r_{1} } H}} \right. \kern-\nulldelimiterspace} H})\) and \(r_{1}\) and \(H\) as before. Equation 21 is rewritten in the form of Eq. 17 as follows:
where,
\(E_{eq}\) is then obtained from Eq. 16 using the \(I_{s}\) factor of Eq. 23.
2.3 Derivation of the Proposed \(E_{eq}\) for Flexible Rectangular Footings Founded on Soil Medium with Linearly Increasing Elastic Modulus
Considering now that, a flexible rectangular footing rests on “Gibson’s soil” (Gibson 1967), that is, on a soil with elastic modulus linearly increasing with depth as follows:
Equation 6 then becomes:
where, \(E_{s,0}\) is the soil modulus immediately below the footing, \(k\) is the rate of increase of the modulus per unit depth and \(z\) is the depth measured from the foundation level.
On the other hand, the strain at depth \(z\) for the equivalent homogenous medium is:
Assuming, now, that the soil medium has thickness \(H\), the equivalent elastic modulus, \(E_{eq}\), derives from the numerical solution of the equation below:
The results are given in chart form in Fig. 2 for various aspect ratio of footing \({L \mathord{\left/ {\vphantom {L B}} \right. \kern-\nulldelimiterspace} B}\) and \(\nu_{eq} =\)\(\nu\) (assuming that all layers have the same Poisson’s ratio value) or \(\nu_{eq} =\) 0. \(H\) in Fig. 2 is the influence depth of footing as proposed by Terzaghi et al. (1996), i.e.:
Recalling Eq. 24, the depth where the elastic modulus of soil is equal to the equivalent one is:
\({{E_{eq} } \mathord{\left/ {\vphantom {{E_{eq} } {E_{0} }}} \right. \kern-\nulldelimiterspace} {E_{0} }}\) versus \({k \mathord{\left/ {\vphantom {k {E_{0} }}} \right. \kern-\nulldelimiterspace} {E_{0} }}\) charts for various \({L \mathord{\left/ {\vphantom {L B}} \right. \kern-\nulldelimiterspace} B}\) cases for \(\nu_{eq} =\)\(\nu\) (left) and \(\nu_{eq} =\) 0 (right). \(\nu\) ranges from 0.1 to 0.5 (from the lower to the upper curve) with 0.1 interval
In this respect, \({{z_{eq} } \mathord{\left/ {\vphantom {{z_{eq} } {z_{l} }}} \right. \kern-\nulldelimiterspace} {z_{l} }}\) versus \({k \mathord{\left/ {\vphantom {k {E_{0} }}} \right. \kern-\nulldelimiterspace} {E_{0} }}\) charts for various \({L \mathord{\left/ {\vphantom {L B}} \right. \kern-\nulldelimiterspace} B}\) cases for \(\nu_{eq} =\)\(\nu\) (0.1 ≤ \(\nu\) ≤ 0.5) are given in Fig. 3. It is noted that, Eqs. 25 and 26 refer to the center of footing.
\({{z_{eq} } \mathord{\left/ {\vphantom {{z_{eq} } {z_{l} }}} \right. \kern-\nulldelimiterspace} {z_{l} }}\) versus \({k \mathord{\left/ {\vphantom {k {E_{0} }}} \right. \kern-\nulldelimiterspace} {E_{0} }}\) charts for various \({L \mathord{\left/ {\vphantom {L B}} \right. \kern-\nulldelimiterspace} B}\) cases for \(\nu_{eq} =\)\(\nu\). \(\nu\) ranges from 0.1 to 0.5 (from the lower to the higher curve) with 0.1 interval
3 Application Examples
3.1 Schmertmann’s (1970) Stratified Medium
The multilayer soil profile used by Schmertmann’s (1970; “Figure 6”) is also used here. This consists of eleven (horizontal) soil strata over bedrock; the thickness and modulus of each soil stratum is given in Table 1. A perfectly flexible, a smooth rigid and a rough rigid circular footing of 2.6 m diameter resting on the surface of the stratified medium were considered. Each one of these footings carries uniform load of 200 kPa. The Poisson’s ratio value for all strata is the same and equal to 0.4. The derived homogenous equivalent soil mediums were compared against the original stratified medium in a finite element analysis framework using Rocscience’s RS2. The criterion used was that a homogenous soil medium is equivalent to a stratified one if under the same loading conditions, the two footings over them yield the same settlement. Prior to running the finite element models, the validity of the models was checked against analytical results (see Appendix).
Considering that \(\nu_{eq} =\) 0.4, Eq. 16 (with the use of the \(I_{s}\) factor of Eq. 19) gave \(E_{eq} =\) 9132 kPa; for \(\nu_{eq} =\) 0 it was found that \(E_{eq} =\) 11,108 kPa. The settlement values obtained are summarized in Table 2. As shown, the error due to the use of the equivalent elastic constants is negligible. It is very interesting that, as shown in Fig. 4, not only the maximum settlement values do not differ but also the whole settlement profiles of the equivalent mediums are almost similar to the original one. Indeed, the same profile is taken using any \((\nu_{eq} ,E_{eq} )\) pair of values derived from Eq. 16; these pair of values are shown in Fig. 5. In the same figure, the relative difference \((R_{d} )\) in \(E_{eq}\) is also given; the following formula for \(R_{d}\) was used:
Comparison of settlement profiles derived from Schmertmann’s (1970) original example medium and its equivalent both for \(\nu_{eq} =\) 0.4 (\(E_{eq} =\) 9132 kPa) and 0 (\(E_{eq} =\) 11,108 kPa)
It is a common practice, however, a study to be restricted to a specific influence zone depth (recall Eq. 28), due to the phenomenon of cementation of soils. Cementation refers to the additional bonding between particles through certain extraneous chemical substances present and hence exhibit higher resistance against deformation (Nagaraj et al. 1995); it contributes to the shear strength of a soil only where the shear strain is kept at low levels (0.001%; see Budhu 2011). Considering an influence zone depth equal to two times the footing diameter (value suggested for circular and square footings; see Schmertmann et al. 1978 and Terzaghi et al. 1996), the equivalent modulus of elasticity, \(E_{eq}\), for the example studied herein is 8336 kPa and 10,580 kPa for \(\nu_{eq} =\) 0.4 and 0 respectively; the variation of \(E_{eq}\) with the ‘(normalized) influence zone depth’ for the present example is also given (see Fig. 6) for both \(\nu_{eq} =\) 0.4 and 0.
Some more examples are given in Table 3 for comparison purposes. From the table in question it is inferred that footing rigidity also affects the \(E_{eq}\) value; in this respect, \(E_{eq}\) is greater for rigid footings. The effect of footing area on \(E_{eq}\) is also shown; the difference in \(E_{eq}\) between footings of different footprint area is attributed to the fact that, as known, bigger footings have greater influence zone depth (bigger stress bulb) and thus, the \(E_{eq}\) value is affected by the deeper strata. Moreover, as shown in Table 3, the effect of the footing point (on plan-view) considered on \(E_{eq}\) is significant for square (flexible) footings and negligible for (flexible) long footings. It is additionally noted that, the relative difference between any \(\nu_{eq} =\) \(v\) case and the \(\nu_{eq} =\) 0 case can be taken by the simple empirical formula \(R_{d} = \nu^{2}\); that is, the same \(R_{d}\) value is obtained for any \(BxL\) footing, footing width or location on footing’s plan-view (see Table 3). The \(E_{eq}\) value corresponding to \(\nu_{eq} =\) 0 and infinite influence zone depth can be taken by the following equation:
For comparison purposes “Bowles” (Egorov and Nichiporovich 1961; Bowles 1996) \(E_{eq}\) value is also given in Table 3:
where \(H_{i}\) and \(E_{i}\) are the thickness and modulus of the i-th layer.
“Bowles” method is probably the most widely used method among practitioners; it is noted however that, it does not consider the effect of the Poisson’s ratio of soils, the footing shape and size, the location on the plan-view of footing and more importantly, the vertical distance of each soil layer from the foundation level. In every case, for the example cases considered herein, Bowles’ \(E_{eq}\) value is very high and thus, on the non-conservative side (see Table 3). Finally, for circular flexible footings, the diameter seems to affect the relative difference in a neither significant nor negligible manner, whilst for rigid circular footings, the footing diameter plays less significant role.
3.2 Reducing the Elastic Modulus of a Homogenous Medium to a Value Suitable for a Winkler Spring Analysis
One of the important outcomes of the present paper is that, since the actual deformation pattern of soil mediums defers from the respective one assuming an array of Winkler springs, it is mandatory that, the elastic modulus of soil in a Winkler’s spring analysis be modified as to correspond to a \(\nu =\) 0 medium, even when the soil is homogenous. The \(\nu_{eq} = 0\) value corresponds to compression with no lateral expansion, that is, to the deformation pattern of springs. For example, if the soil below a circular foundation of diameter 2.6 m is homogenous with \(v\) = 0.2 and \(E_{s} =\) 5000 kPa, the correct \(E_{s}\) value for a Winkler type analysis, according to Eq. 16 (for \(n =\) 1), is 5332 kPa if \({{z_{l} } \mathord{\left/ {\vphantom {{z_{l} } {2r}}} \right. \kern-\nulldelimiterspace} {2r}} =\) 2, and 5208 kPa if \({{z_{l} } \mathord{\left/ {\vphantom {{z_{l} } {2r}}} \right. \kern-\nulldelimiterspace} {2r}} =\)∞ (both values stand for \(v\) = 0); the 5208 kPa value can alternatively be obtained from Eq. 31, i.e. 5000/(1–0.22) = 5208. If, now, the soil below the same foundation had \(v\) = 0.4 and \(E_{s} =\) 5000 kPa, the correct \(E_{s}\) value would be 6346 kPa for \({{z_{l} } \mathord{\left/ {\vphantom {{z_{l} } {2r}}} \right. \kern-\nulldelimiterspace} {2r}} =\) 2 and 5952 kPa for \({{z_{l} } \mathord{\left/ {\vphantom {{z_{l} } {2r}}} \right. \kern-\nulldelimiterspace} {2r}} =\)∞ (again both values stand for \(v\) = 0).
4 Summary and Conclusions
The two elastic constants of soil are essential parameters for assessing the rigidity of shallow foundations (e.g. Gupta 2007), calculating the critical column spacing (e.g. ACI Committee 336, Ulrich et al. 1988) and calculating the modulus of subgrade reaction of soil, \(k_{s}\) (e.g. Vesic 1961). The latter is used as the spring constant in a Winkler type analysis. These springs must effectively represent the deformability of the ground in every case, that is, in homogenous soils, stratified mediums or homogenous soils with linearly increasing modulus; an effective representation involves the use of the \(E_{eq}\) value corresponding to \(\nu_{eq}\) = 0 so that the equivalent soil to be consistent with the deformation pattern of Winkler’s springs (compression with no lateral expansion). This paper presents a method for the determination of the equivalent elastic constants, \(E_{eq}\) and \(\nu_{eq}\), of the above-mentioned cases. The method in question is based on the theory of elasticity combining the principle of vertical and horizontal superposition. Flexible rectangular footings over stratified mediums or over homogenous mediums with linearly varying modulus, as well as rigid and flexible circular footings over stratified mediums were considered. The results are presented either as closed-form expressions or in chart form. A number of application examples are also given. As shown, the derived \(E_{eq}\) values not only return reliable settlement results (reliable as for the “equivalency”), but also settlement profiles that are similar to those corresponding to the original soil mediums.
References
Abu-Farsakh MY, Chen Q (2012) Evaluation of the base/subgrade soil under repeated loading: phase II, in-box and ALF cyclic plate load tests. Louisiana Transportation Research Center
Barden L (1962) Distribution of contact pressure under foundations. Geotechnique 12:181–198
Barnes G (2016) Soil mechanics: principles and practice. Palgrave Macmillan, London
Barros ST (1966) Deflection factor charts for two and three layer elastic system. Highw Res Rec 145:83–108
Boussinesq J (1885) Application des potentiels à l’étude de l’équilibre et du mouvement des solides élastiques: principalement au calcul des déformations et des pressions que produisent, dans ces solides, des efforts quelconques exercés sur une petite partie de leur surface. Gauthier-Villars, Paris
Bowles LE (1996) Foundation analysis and design. McGraw-Hill, New York
Brahma P, Mukherjee S (2010) A realistic way to obtain equivalent Young’s modulus of layered soil. In: Indian geotechnical conference, Bombay, India, pp 305–308
Budhu M (2011) Soil mechanics and foundations, 3rd edn. Firewall Media, Hoboken
Das BM (2007) Fundamentals of geotechnical engineering. 3rd edn., Thomson-Engineering.
Egorov KE, Nichiporovich AA (1961) Research on the deflection of foundations. In: Proceedings of the 5th international conference on soil mechanics and foundation engineering, pp 861–866
Fox L (1948) The mean elastic settlement of a uniformly loaded area at a depth below the ground surface. In: 2nd international conference on soil mechanics and foundation engineering, p 129
Fraser RA, Wardle LJ (1985) Numerical analysis of rectangular rafts on layered foundations. Golden Jubil Int Soc Soil Mech Found Eng Commem, vol 223
Gerrard CM (1982) Equivalent elastic moduli of a rock mass consisting of orthorhombic layers. Int J Rock Mech Min Sci Geomech Abstr 19:9–14
Gibson RE (1967) Some results concerning displacements and stresses in a non-homogeneous elastic half-space. Géotechnique 17:58–67. https://doi.org/10.1680/geot.1967.17.1.58
Gorbunov-Possadov MI, Malikova TA (1973) Calculation of structures on elastic foundation. (In Russian). Stroiizdat, Moskow
Gupta SC (2007) Raft foundations: design and analysis with a practical approach. New Age International
HariBharghav M, Madhav MR, Padmavathi V (2017) Estimation of Deformation Moduli of Reinforced Foundation Beds from Load Tests. In: Indian Geotech Conf 2017 GeoNEst
Hirai H (2008) Settlements and stresses of multi-layered grounds and improved grounds by equivalent elastic method. Int J Numer Anal Methods Geomech 32:523–557
Hirai H, Kamei T (2003) A method to calculate settlement, stress and allowable stress of multi-layered ground. J StructConstrEng 573:81–88
Hirai H, Kamei T (2004) A method to calculate settlement, stress, failure and allowable stress of multi-layered ground by equivalent thickness theory. J Struct Constr Eng 69:79–86
Kézdi A, Rétháti L (1988) 4 Soil Mechanics of Earthworks, Foundations and Highway Engineering, Handbook of Soil Mechanics, Volume 3. Elsevier
Nagaraj T, Srinivasa B (1994) Analysis and prediction of soil behaviour. Taylor & Francis, Abingdon-on-Thames
Nagaraj T, Srinivasa B, Vatsala A (1995) Analysis and prediction of soil behaviour. New Age Publications, India
Odemark N (1949) Investigations as to the Elastic Properties of Soils and Design of Pavements According to the Theory of Elasticity
Pantelidis L (2019) The equivalent modulus of elasticity of layered soil mediums for designing shallow foundations with the Winkler spring hypothesis: a critical review. EngStruct 201:109452. https://doi.org/10.1016/j.engstruct.2019.109452
Sadrekarimi J, Akbarzad M (2009) Comparative study of methods of determination of coefficient of subgrade reaction
Salamon MDG (1968) Elastic moduli of a stratified rock mass. Int J Rock Mech Min Sci Geomech Abstr 5:519–527
Schmertmann JH (1970) Static cone to compute static settlement over sand. J Soil Mech Found Div 96:1011–1043
Schmertmann JH, Hartman JP, Brown PR (1978) Improved strain influence factor diagrams. J GeotechGeoenvironEng 104(8):1131–1135
Sridharan A, Gandhi N, Suresh S (1990) Stiffness coefficients of layered soil systems. J GeotechEng 116:604–624
Steinbrenner SW (1934) Tafeln zur setzungsberechnung. Die StraBe 1
Terzaghi K, Peck RB, Mesri G (1996) Soil mechanics in engineering practice. Wiley, Hoboken
Ueshita K, Meyerhof GG (1967) Deflection of multilayer soil systems. J Soil Mech Found Div 93(5):257–282
Ulrich EJ, Shukla SN, Baker CN Jr, Ball SC, Bowles JE, Colaco JP, Davisson XI et al (1988) Suggested analysis and design procedures for combined footings and mats. J Am Concr Inst 86:304–324
Vesic AB (1961) Beams on elastic subgrade and the Winkler’s hypothesis. In: Proceedings of the fifth international conference on soil mechanics and foundation engineering
Wardle LJ, Gerrard CM (1972) The “equivalent” anisotropic properties of layered rock and soil masses. Rock Mech Rock Eng 4:155–175
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix: Numerical Modeling and Validation with Analytical Modeling
Appendix: Numerical Modeling and Validation with Analytical Modeling
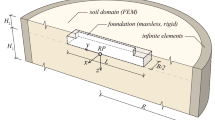
The numerical modeling carried out using Rocscience’s RS2 (v9.028) was checked against analytical modelling. A flexible circular footing (axisymmetric model) having radius equal to one meter was considered (Fig.
7). The mesh used is shown in Fig. 7; this extends 15 m horizontally and 10 m vertically, while the geometry consists of 5651, 6-noded, triangular elements (77 nodes per square meter on average). The nodes of the external boundaries were fixed, while the nodes along the axis of rotation were free to slide in the vertical direction indicating a perfectly smooth boundary. The model of Fig. 7 refers to a homogenous soil with E = 10,000 kPa and ν = 0.499. The surcharge is uniform and equal to 100 kPa, simulating a circular, flexible footing. Perfectly elastic conditions were considered. The maximum settlement obtained (at the center of the footing), was equal to 0.013458 m (shown in Fig. 7). The analytical modelling, on the other hand, gave 0.013507 m (use of Eq. 18 with \(I_{E}\) = 1).
Rights and permissions
About this article
Cite this article
Pantelidis, L. The Equivalent Modulus of Elasticity of Soil Mediums for Designing Shallow Foundations. Geotech Geol Eng 39, 3863–3873 (2021). https://doi.org/10.1007/s10706-021-01732-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10706-021-01732-z