A simplified approach to account for through-soil interaction between two adjacent shallow foundations

Abstract

Neighbouring buildings, even though disconnected from the structural viewpoint, may interact through the underlying soil especially when they are founded on very soft soils. Despite some pioneering studies since the early 1970’s, structure–soil–structure interaction has yet to be further investigated to reveal the effects that could be exerted on both the static and dynamic response of nearby structures. The present work aims at expanding the theoretical knowledge on this phenomenon through an extensive parametric study based on a truly 3D continuum approach solved through the Flac3D finite difference software. The impedance functions of two closely-spaced shallow foundations have been numerically calculated by varying the distance between the nearby footings and the subsoil configuration (homogeneous or layered). The numerical results have elucidated important effects of cross interaction between two neighbouring foundations. The static stiffness reduces, and this effect is increasingly significant as the foundations are closer whatever the subsoil conditions are. The dynamic coefficients increase with respect to those corresponding to the single footing over halfspace. Such effect is less important for the layer-over-halfspace soil configuration, for which the dynamic coefficients are mainly affected by the frequency response of the stratum. Finally, in the realm of the sub-structure approach, a novel simplified design approach, based on group factors for closely-spaced shallow foundations, was proposed to compute the soil-foundation impedance matrix englobing the foundation–foundation interaction in addition to the soil–foundation interaction.

1 Introduction

In densely urbanized areas of modern metropolises or in the historic centres of ancient cities or villages, buildings might be built at very close distance, so that a mutual interaction could arise among them through the underlying soil. The response of a given building in a group might be much different from the response of the same building in isolation. In literature this phenomenon is called Structure–soil–structure interaction (SSSI) or cross-soil–structure interaction (CSSI).

For decades the scientific community has focused its attention exclusively on the phenomenon of common soil–structure interaction (SSI) problems, thus disregarding the presence of multiple structures on the same soil deposit. Studies on SSI started in-between the late 60 s and early 70 s of the last century with the pioneering studies of Parmelee (1967), Parmelee et al. (1969), Perelman et al. (1968) and Sarrazin et al. (1972). The above authors started to highlight the strong modification that the dynamic response of single-storey structures could have had due to soil-foundation compliance. These first studies were later extended by Velestos and Meek (1974) and Bielak (1975), who proposed the use of one-degree-of-freedom simplified models (replacement oscillator) equivalent to the analysed structure on a compliant base. Successively, Gazetas (1983, 1991) collected several closed-form equations providing in a straightforward manner the impedance matrix for shallow and piled foundations. Wolf (1985) proposed different analytical or numerical strategies for handling SSI problems in a reliable and effective way, thus avoiding an overly conservative design. Other aspects regulating the SSI mechanism, such as kinematic effects, foundation embedment and soil layering have been detailed later on by Todorovska (1992), Avilés et al. (1996–1998) and Mylonakis et al. (2006). It is worth noting that in the all-cited studies the impedance function of the soil-foundation system always has been referred to a foundation placed “alone” on a given soil deposit.

While a large part of the scientific community was devoted to investigate the common problem of soil–structure interaction for single buildings, a few authors have begun to research the more general problem of structure–soil–structure interaction to reveal the existence of a possible dynamic coupling between neighbouring structures through the underlying and/or the surrounding soil (Karabalis and Huang 1970; Warburton et al. 1971; Luco and Contesse 1973; Kobori et al. 1973; Lee and Wesley 1973; Chang-Liang 1974; Wong and Trifunac 1975; Roesset and Gonzales 1977). In the above cited literature papers, as typical of a new-born research vein, plenty of acronyms were used to refer to the same phenomenon, such as “through soil coupling” (TSC) by Lee and Wesley (1973) or “dynamic cross interaction” (DCI) by Kobori et al. (1973) or “structure–soil–structure interaction” (SSSI) by Luco and Contesse (1973).

In the early Seventies, even though considered surely worth of investigation, the topic of SSSI was too complex for being solved numerically with the computation tools available at that time so, with exception of a few pioneering numerical studies, the issue of SSSI has been set aside with respect to the usual problem of soil–structure interaction with a single structure (building) accounted for.

Some years later, Qian and Beskos (1995) investigated the cross-interaction phenomenon between two or four 3D rigid shallow foundations through a boundary element method. Foundations of arbitrary shape subjected to harmonic external force excitation were considered. It was found that for the vertical and horizontal stiffnesses, cross-interaction increases with the number of foundations in the group, lower distance among them and low input frequencies, while for the rocking and torsional stiffnesses, cross-interaction is again significant for small foundation–foundation distance, but increases for higher frequencies and does not depend much on the number of foundations. Qian and Beskos (1995) concluded their study by criticizing the assertion of the old ATC-3 regulations (1984) (….“that neglecting coupling effects between footings could lead to conservative results”) by showing that this is no longer true for a small group of four footings in certain bands of input frequencies. In a following paper, Qian and Beskos (1996) extended their study to the case of two rigid shallow foundations, in which the active foundation was loaded by obliquely incident harmonic P, SV, SH and R waves. An extensive parametric study was carried out considering different angles of wave incidence, input frequency of the plane wave, separation distance between the two foundations and the amount of mass in each foundation. Because of wave transmission, both translational and rotational displacements of the downstream (passive) foundation were found to be out of phase with respect to those of the active foundation. The effects of cross interaction between adjacent foundations were significant for small foundation separation and caused additional displacements that would have not appeared for a single foundation. Unfortunately, most of the results by Qian and Beskos (1995–1996) refer only to a homogeneous halfspace with the primary foundation subjected to harmonic input (seismic or external loads) and affected by the presence of the load-free second foundation. Further improvements of the aforementioned works also accounted for foundation flexibility (Qian et al. 1996; Tham et al. 1998). In general, in the low-frequency range the passive footing of the system seemed to be insensitive to the load distribution on the active footing but cross interaction could become considerable at higher frequency.

Betti (1997) analysed the dynamic response of two embedded square foundations by adopting a direct boundary element formulation combined to the substructure deletion method (Betti and Abdel-Ghaffar 1994). For given values of foundation depth and spacing among nearby foundations, both impedance function and foundation input motion of the target foundation in a group were found to be different from the values corresponding to the same foundation considered individually on the same subsoil. In the low-frequency range, translational, rocking and torsional components of the impedance matrix showed clear effects of cross-interaction (up to 30 per cent), which tended to disappear as the frequency and distance between the adjacent foundations increased. Cross-interaction was considered a substantial contribution to superstructure response and should not be neglected in practice.

In the last two decades, thanks to important advancements in computational tools, the SSSI issue has been resumed and the corresponding literature vein started receiving more attention than in the past as testified by many papers published in literature, most of which based on numerical studies, extended to nearby buildings also founded on piles (Padron et al. 2008; Bordón et al. 2019).

Alexander et al. (2013) investigated the role that a tall structure, newly built, could exert on the dynamic response of an existing one of lower height. By representing the two structures through simple discrete models equipped with rotational springs at their base, so that the two degrees of freedom of swaying and rocking were activated, cross interaction through soil was represented by a third rotational spring connecting the foundations of the nearby buildings. By assuming structures and soil to behave linearly elastic, it appeared that under seismic loading the taller structure exacerbated the swaying response of the lower building that actually acted as a tuned mass damper for the taller one. The main outcome of the Alexander et al. (2013) study was the identification of an optimal structure–structure distance so that the smaller and older building could not be injured by the new-built taller construction. As an extension of the above-cited work, through a simplified analytical formulation Aldaikh et al. (2018) obtained closed-form expressions to evaluate in a direct manner (without the addition of 2D F.E.M. analyses) the rotational stiffness coupling two or three identical adjacent foundations resting on a linear elastic half-space. Unfortunately, only the static value of the rotational coupling stiffness was provided as function of the center–center foundation spacing.

Knappet (2015) carried out both experimental and numerical investigations on pairs of adjacent structures. Experimental tests were conducted using a model scale of 1:50 and tested at 50 g using the 3.5 m radius beam centrifuge at University of Dundee (UK). Under a sequence of accelerometric input signals of increasing amplitude, the height and mass of the adjacent structure strongly affected the structural drift and co-seismic settlements of the target building model. For all the analysed cases, an increase in permanent rotation of the master building due to cross interaction through the underlying soil was found.

Starting from small groups of buildings, the SSSI topic has recently been extended also to the urban scale with larger group of buildings either having similar dynamic features or very different. While it is common practice to determine the seismic response of single structures, the higher building density in metropolitan cities or old historic centres inevitably requires accounting for the interaction and consequent coupling of adjacent constructions through the underlying soil. In Tsogka and Wirgin (2003), a 2D model of an idealized city composed of ten homogeneous blocks (structures) was developed. The blocks were considered not equally spaced, of different sizes and placed on a soft soil layer over bedrock. Under seismic loading, the analysis with multiple blocks provided for much higher ground displacement compared to the case of no blocks or single block on the same soil deposit. This statement was later corroborated by Bybordiani and Arici (2019) who performed detailed finite element analyses with 5-, 15-, and 30-story structures representing building clusters placed on a viscoelastic medium. In case of very closely spaced multi-story structures or groups of buildings with high stiffness contrasts, neglecting cross interaction effects might lead to a significant underestimation of the actual seismic demand.

Vicencio and Alexander (2021) have recently explored the 3D multi-building SSSI through a numerically simplified reduced-order model that is a generalization of the 2D approach previously published (Alexander et al. 2013). For 3D configurations of identical buildings having a L or square plan, huge detrimental effects were obtained for buildings parallel to the direction of the seismic excitation. For the considered cases, the corner buildings did not suffer the most detrimental effects of SSSI.

The above state-of-art has elucidated the key factors controlling the mutual interaction between adjacent structures via the underlying soil, such as the relative inertial and dynamic characteristics of adjacent buildings, the foundation–foundation distance, soil layering and mechanical characteristics, and plan configuration of the group of buildings in 3D arrangements. Some other aspects of SSSI are not yet truly understood and research advances on this topic are needed.

As for the analysis approaches, SSSI problems, as common problems of SSI, have mostly been solved through two approaches (Stewart et al. 1998; Wolf 1985): the direct methodology in which the entire interacting system (superstructure, foundation and soil) is analysed in one step through numerical procedures based on spatial discretization of the domain (FEM, BEM or a combination of both) and the substructure (impedance) method in which each interacting subsystem (soil + foundation and the superstructure on a compliant base) is solved in separate steps and later assembled to obtain the final solution in the realm of the superposition principle (Kausel et al. 1976; Mylonakis et al. 2006). In particular, after the evaluation of the foundation input motion (FIM) in step 1, the system impedance function describing the force/moment or displacement/rotation relationships is researched in step 2. The dynamic analysis of the superstructure resting on the impedances coming from step 2 and subjected to the input motion from step 1 is finally conducted.

Even though nowadays the direct approach is surely more affordable in terms of computational demand than some years ago, the substructure method still represents the favourite analysis approach to handle SSI problems in practical design.

By taking advantage of the substructure approach in breaking down a complex interaction between soil and structure into more manageable problems, to provide a step forward on the challenging issue of SSSI, the present study aims to encompass the effects of cross-interaction between closely-spaced buildings directly in the different terms of the impedance function of the target structure. By a rigorous 3D continuum approach, solved through the finite difference method with the software FLAC3D (Itasca 2004), simple schemes of two rigid shallow foundations interacting through the underlying soil were analysed under dynamic excitation. In the parametric study, both soil configuration (homogeneous or stratified) and distance between footings were changed and the different components of the soil-foundation impedance matrix computed. Finally, closed-form equations and abaci were proposed to obtain a suite of modifiers (group factors) for each term of the soil-foundation impedance matrix to account for foundation–foundation interaction through the underlying soil. With respect to former studies on the same issue, the paper tries to shed lights on the static and dynamic response of the two-foundation system placed on different subsoil configurations and proposes an innovative approach to allow engineers to solve practical SSSI problems in a cost-effective manner.

2 Method of analysis

2.1 Problem statement

As stated above, a prerequisite of the uncoupled substructure approach is the computation of the frequency-dependant impedance function, linking the i-th component of the harmonic force vector to the component j of the foundation displacement vector at steady state:

$$\overline{K}_{ij} = \frac{{F_{i} exp\left( {i\omega t} \right)}}{{u_{j} exp\left( {i\omega t +\phi } \right)}}$$

(1)

where ω is the angular exciting frequency, linked to the input frequency by the well-known relation ω = 2πf, and ϕ the phase delay between force and displacement.

Due to phase delay, the impedance is a complex function whose real part reflects the dependence on the stiffness and inertia of the soil, while the imaginary part is associated to radiation and material damping of the soil. Both the real and the imaginary part may conveniently be expressed as the product of a “static” contribution, ${K}_{ij}$ and ${C}_{ij}$, and a frequency-dependent (dynamic) coefficient, ${k}_{ij} \left(\omega \right)$ and ${c}_{ij}\left(\omega \right),$ as follows:

$$\overline{K}_{ij} = k_{ij} \left( \omega \right)K_{ij} + i\omega c_{ij} \left( \omega \right)C_{ij}$$

(2)

The degrees of freedom (d.o.f.) of a foundation are six, thus the displacement vector has six components:

$${\text{U}} = [{\text{u}}_{{\text{x}}} ,{\text{ u}}_{{\text{y}}} ,{\text{ u}}_{{\text{z}}} ,\uptheta_{{\text{x}}} ,\uptheta_{{\text{y}}} ,\uptheta_{{\text{z}}} ]$$

(3)

where u_x, u_y and u_z are the translations along the two horizontal and the vertical axes while θ_x, θ_y, and θ_z are the rotations around each of the three foundation axes.

Similarly, the force vector is composed by the forces acting along the three axes F_x, F_y and F_z and the moments around the three axes, M_x, M_y and M_z:

$${\text{F}} = \left[ {{\text{F}}_{{\text{x}}} ,{\text{ F}}_{{\text{y}}} ,{\text{ F}}_{{\text{z}}} ,{\text{ M}}_{{\text{x}}} ,{\text{ M}}_{{\text{y}}} ,{\text{ M}}_{{\text{z}}} } \right]$$

(4)

Consequently, the impedance terms in Eq. 1 provides for a 6 × 6 matrix. If the foundation is shallow, the force F_i acting along the i-th direction produces only a displacement u_j along the same direction; similarly, the moment M_i only produces a rotation around the i-th direction. The impedance matrix, hence, is diagonal:

$$\overline{K} = \left[ {\begin{array}{*{20}c} {\overline{K}_{xx} } & 0 & 0 \\ 0 & {\overline{K}_{yy} } & 0 \\ 0 & 0 & {\overline{K}_{zz} } \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ \end{array} \begin{array}{*{20}c} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ {\overline{K}_{rx} } & 0 & 0 \\ 0 & {\overline{K}_{ry} } & 0 \\ 0 & 0 & {\overline{K}_{rz} } \\ \end{array} } \right]$$

(5)

In case of two interacting rigid foundations, the displacement and force vectors in Eqs. (3) and (4) are composed of 12 terms, corresponding to the six d.o.fs of both the slave (s) and the master (m) foundation:

$${\text{F}} = \left[ {{\text{F}}_{{{\text{xs}}}} ,{\text{ F}}_{{{\text{ys}}}} ,{\text{ F}}_{{{\text{zs}}}} ,{\text{ M}}_{{{\text{xs}}}} ,{\text{ M}}_{{{\text{ys}}}} ,{\text{ M}}_{{{\text{zs}}}} ,{\text{ F}}_{{{\text{xm}}}} ,{\text{ F}}_{{{\text{ym}}}} ,{\text{ F}}_{{{\text{zm}}}} ,{\text{ M}}_{{{\text{xm}}}} ,{\text{ M}}_{{{\text{ym}}}} ,{\text{ M}}_{{{\text{zm}}}} } \right]$$

(6)

$${\text{U}} = [{\text{ u}}_{{{\text{xs}}}} ,{\text{ u}}_{{{\text{ys}}}} ,{\text{ u}}_{{{\text{zs}}}} ,\uptheta_{{{\text{xs}}}} ,\uptheta_{{{\text{ys}}}} ,\uptheta_{{{\text{zs}}}} ,{\text{ u}}_{{{\text{xm}}}} ,{\text{ u}}_{{{\text{ym}}}} ,{\text{ u}}_{{{\text{zm}}}} ,\uptheta_{{{\text{xm}}}} ,\uptheta_{{{\text{ym}}}} ,\uptheta_{{{\text{zm}}}} ]$$

(7)

The impedances are consequently arranged into a 12 × 12 matrix that can ideally be split into 4 sub-matrices as reported in Gonzales (1977) and more recently in Aldaikh et al. (2018):

$$\left[ {\begin{array}{*{20}c} {K_{ss} } & {K_{sm} } \\ {K_{ms} } & {K_{mm} } \\ \end{array} } \right]$$

(8)

The 6 × 6 submatrices ${K}_{ss}$ and ${K}_{mm}$ control the displacements of the slave and the master foundations respectively when they are subjected to direct load, while the 6 × 6 submatrices ${K}_{sm}$ and ${K}_{ms}$ link the displacements of each footing to the loads applied to the other.

The impedance matrix, for single or multiple foundations, may be obtained from experimental or numerical simulations of the foundation response under harmonic loads.

To date, very few are the cases in which the impedances have been derived experimentally, through forced vibration tests, e.g. Lin et al. (1984), Wong et al. (1988), de Barros et al. (1995), Tileylioglu et al. (2011) and more recently Amendola et al. (2021). Conversely, analytical expressions fitting numerical results obtained through different discretization procedures (F.E.M., B.E.M. or both) were provided by several authors, including Gazetas (1991), Pais and Kausel (1988) and Mylonakis et al. (2006). In most cases, the published solutions refer to a rigid arbitrary-shaped foundation placed on an ideal halfspace. Additional formulations are available in literature to account for the variation of the shear stiffness with depth (Gazetas 1991; Vrettos 1999), foundation embedment (e.g., Apsel and Luco 1987) or flexibility (e.g., Iguchi and Luco 1982).

For two or more nearby foundations, the impedance matrices were evaluated analytically by Warburton et al. (1971) for the case of adjacent rigid cylindrical foundations on a halfspace and numerically through finite or boundary element formulations by Gonzalez (1977), Betti (1997) Karabalis and Mohammadi (1998), Sbartai (2016), Aldaikh et al. (2018), among others.

Most of literature works focus on the diagonal terms of the ${K}_{sm}$ (or ${K}_{ms}$) submatrix in Eq. 8, which are expected to be the most affected by SSSI. For two nearby shallow foundations, the submatrices ${K}_{ss}$ and ${K}_{mm}$ are still diagonal as it happens for the single foundation in Eq. 5. If also the submatrices ${K}_{sm}$ and ${K}_{ms}$ are diagonal, each term of the load vector consequently depends on two stiffness components as shown hereinafter for the translational equilibrium of the master footing along x:

$$F_{xm} = K_{xm} u_{xm} + K_{xsm} u_{xs}$$

(9)

If the same displacement is applied to both foundations, the force–displacement relationship becomes:

$$F_{xm} = (K_{xm} + K_{xsm} )u_{x} = K_{xm,group} u_{x}$$

(10)

The same applies also to the other degrees of freedom of the foundation.

Under the above simplified assumptions, the target foundation may still be modelled as “isolated” but endowed at its base with modified stiffnesses $({K}_{ij,group}$) accounting for the presence of its twin. For design convenience, this procedure could be easily implemented in commercially available softwares, which typically only allow the insertion of the springs associated with the main diagonal of the stiffness matrix (Eq. 8) and not those along the secondary diagonal, ${K}_{sm}$ and ${K}_{ms}$.

2.2 Numerical model description and validation

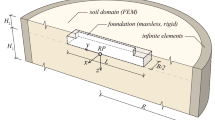
Figure 1 shows the reference schemes considered in this numerical study. They consist of two infinitely rigid foundations with their length parallel to the horizontal x-axis and placed on a layer over halfspace (Fig. 1a). In the parameter study, the layer thickness H has been varied between 3 and 50 m, with the latter value corresponding to the limit case of a homogeneous halfspace.

Fig. 1

Soil configuration (a) and geometrical features of the two footings (b)

The geometric characteristics of the two foundations are shown in Fig. 1b: both foundations were assumed to be rectangular, with their length (2L) equal to 10 m and width (2B) equal to 2 m. The edge-to-edge foundation distance S was varied between 0.5 and 4 m so that the ratio S/B ranges between 0.5 and 4. All the analysed cases are listed in Table 1, while the adopted values of soil density, ρ, bulk modulus, K, and shear modulus, G, are listed in Table 2.

Table 1 Analyzed reference schemes

Table 2 Soil parameters adopted in the numerical study

With reference to Table 2, it is worth pointing out that very low values of the shear wave velocity, V_s, were deliberately assigned to the soil layers to maximize through-soil interaction between adjacent foundations (and structures). In addition, if one considers that the soil volume interacting with an oscillating foundation is characterized by a depth almost comparable to the foundation width (Stewart et al. 2003), it is not unlikely that the shear wave velocity of the shallower layers could be very low even though the bearing capacity of the soil-foundation system might not be reached. This could be the case of very old masonry buildings made of 2 ÷ 3 floors and built without the same prescriptions imposed to new constructions by modern technical codes.

Since it is mandatory modelling the soil as a continuum to properly analyse cross-interaction between the adjacent foundations, the 3D soil domain shown in Fig. 1a was implemented in FLAC3D and discretized through the finite difference technique (Itasca 2004). A grid spacing, Δ, respecting the rule of Kuhlemeyer and Lysmer (1973) ($\Delta <{V}_{s}/8{f}_{max}$) was selected so that input frequencies up to a maximum value f_max = 25 Hz could be reliably propagated throughout a soil with shear wave velocity V_s. The infinite extension of the soil in depth and along the lateral sides of the analysis domain was simulated by means of viscous dashpots. These elements provide for normal and shear stresses that are proportional to the P- and S-wave velocity of the connected soil elements, respectively. As a linear visco-elastic isotropic constitutive law was assigned to the soil, viscous damping was inserted in the model through the Rayleigh formulation and set to a very low value (1%) so that the overall damping was that generated by wave scattering from the oscillating foundation, i.e. radiation damping.

As the foundation was assumed to be rigid, a uniform displacement field was imposed to all the nodes of the foundation base. Since displacements could not be directly controlled in FLAC3D (Itasca 2004), it was necessary to prescribe nodal velocities as loading conditions. To this aim, a harmonic velocity along the x-, y- or z-direction was applied to the grid points of the foundation footprint to obtain the corresponding displacements (swaying), u_x, u_y and u_z. Similarly, the harmonic rotations θ_x and θ_y were imposed by applying nodal velocities varying with a linear distribution with respect to the x and y axis of the footing and null in correspondence of its centroid. Further details on the developed loading procedure may be found in Zeolla et al. (2021, 2022a, b).

The frequency of the harmonic oscillation (f = ω/2π) was alternatively set equal to 1, 3, 5, 7, 9, 11 and 13 Hz to cover the likely frequency band of interest in the engineering field. An additional case, corresponding to a null excitation frequency, was simulated to obtain numerically the static stiffness that appears in the real part of the impedance function in Eq. 2.

For any input frequency and oscillation mode of the foundation, two sets of analyses were performed. In the first, a harmonic oscillation only on the master foundation (without its neighbour) was applied while in the second the same harmonic oscillation on both foundations was imposed. This choice is certainly a simplification of reality but representative of situations in which groups of structures having similar dynamic properties have been built. This could be the case, for example, of the historic centres of ancient cities or metropolitan areas of modern megacities.

During each computation, the displacement of the master foundation as well as the stress state at the foundation-soil interface were recorded. The translational displacements in Eq. 3 were assumed to be equal to that of the foundation centroid, while the rotations θ_x and θ_y were obtained as the ratio between the vertical displacements at the opposite edges of the foundation footprint and the half-size (in x and y direction) of the foundation itself.

The contact stresses at the foundation footprint were later summed to compute the corresponding resultant forces. In particular, for the vertical d.o.f. the resultant force was obtained as:

$$F_{z} = \sum\limits_{{i = 1}}^{N} {\Delta \sigma _{{zzi}} } A_{i}$$

(11)

where ${A}_{i}$ is the area of the i-th mesh elements of the loaded footprint and ${\Delta \sigma }_{zzi}$ the corresponding contact pressure due to external loading. By switching the axis z with x or y and Δσ_zzi with Δσ_zxi or Δσ_zyi, Eq. 11 may be adopted to compute the first and second terms of the force vector in Eq. 4, i.e. F_x or F_y, respectively.

The moments M_x and M_y were obtained by multiplying each addendum of Eq. 11 by the distance of the central node of the mesh element from the rotation axis of the foundation.

Since a velocity (therefore, a displacement) was imposed to excite the foundations, it turned out more convenient to compute firstly the soil-foundation flexibility matrix (inverse of Eq. 1) from the ratio between the Fourier transform of each displacement component and the Fourier transform of the associated force component. Then, the impedance was obtained as the inverse of flexibility in the complex domain.

In the static regime (i.e., null excitation frequency), it was easier to obtain the static stiffness directly as the ratio between the force and the corresponding displacement.

Finally, the frequency-dependent dynamic coefficients k_ij(ω) in Eq. 2 were calculated by dividing the real parts of the impedance by the corresponding static stiffnesses, while the dynamic damping coefficients c_ij(ω) were obtained by dividing the imaginary part by: (1) $\omega \rho {V}_{La}A$ and $\omega \rho {V}_{S}A$ for the vertical and horizontal mode, respectively; (2) $\omega \rho {V}_{La}{I}_{x}$ or $\omega \rho {V}_{La}{I}_{y}$ for the rotational along x and y axis, respectively. In the above two equations, ${V}_{La}$ is the Lysmer's analog wave velocity, ${V}_{S}$ the shear wave velocity, $A$ the area of the footing, ${I}_{x}$ and ${I}_{y}$ the moments of inertia around the x- and y- axis of the soil-foundation contact surface, respectively.

2.3 Validation of the developed numerical procedure

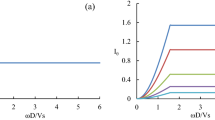
The numerical procedure described above was validated against the analytical impedance functions provided in literature (Gazetas 1991) for a single rigid foundation placed on an elastic halfspace characterized by the soil properties listed in Table 2. For all d.o.fs of the foundation, Fig. 2 provided the comparison between analytically and numerically-computed dynamic stiffness and damping coefficients versus the following dimensionless frequency:

$$a_{0} = \omega B/V_{s}$$

(12)

Fig. 2

Numerical (present study) versus analytical (Gazetas 1991) dynamic coefficients (stiffness and damping) for a single foundation on an elastic halfspace

In the investigated range of a₀, the dynamic stiffness computed numerically were in good agreement with the analytical solutions proposed in literature. The best-fitting was achieved as a result of a detailed sensitivity study in which the effects of different factors were considered, among which the Rayleigh damping assigned to the soil, mesh spacing and amplitude of the imposed motion. Mesh quality, in particular, affected the prediction of the swaying coefficients along the two horizontal axes and the rocking mode around y. At higher frequencies, to reduce the mismatch between numerically and analytically-predicted results a more refined discretization step along x and y was required with element size Δx of the order of λ/16 for the horizontal swaying modes and of λ/24 for the rocking oscillation mode, being λ the soil wavelength. This choice assured a satisfying result accuracy and reasonable computation time. The percentage difference between numerical and analytical predictions is around 10% (for both dynamic stiffness and damping terms) for the horizontal swaying along y, and lower than 19% for swaying along x and rocking around y.

3 Numerical results

The objective of this section is to present the numerical results obtained through the above-outlined formulation to gain insight into the dynamic response of shallow foundations, which are placed in a group but do not belong to a system of interconnected footings. The quantities of interest are the stiffness and damping terms of the impedance functions of a given foundation that may interact with a neighbouring one through the underlying soil. So, by adding the contribution of foundation–foundation interaction into the different terms of the impedance functions, the substructure approach could be effective in handling even more complex problems of SSSI without the enormous computational effort of rigorous 3D analyses. The goal is to suggest a simple physically motivated procedure that accounts for through-soil interaction among buildings.

To highlight the general trends obtained for a small group of two foundations, the real and imaginary part of the vertical impedance for a shallow foundation placed alone on the halfspace or with another identical one are shown in Fig. 3. The first thing that may be observed is that in the whole range of dimensionless frequencies a₀ the dynamic response of the target foundation in a group is different from that of the same foundation considered isolated and this difference for some oscillation modes could exacerbate at higher frequencies as function of the spacing between the two nearby foundations. In other words, if there had been no cross interaction between the foundations, the real and imaginary part of the master footing in a group would have coincided with those of the single foundation (black line) and denoted a more frequency-independent response.

Fig. 3

Real (a) and imaginary (b) part of the vertical impedance of a foundation placed alone or in couple on an elastic halfspace

Figure 3a highlighted that in the low-frequency (a₀ → 0) range the in-group foundation had stiffness much lower than that corresponding to the single foundation and this response had great similarity with the static response of group of piles (Poulos 1971). Moreover, for S/B = 0.5 and 1 the stiffness trends first slightly decrease up to a certain frequency (a₀ = 0.8) and then start increasing. Conversely, for S/B = 2 a more wavy pattern may be observed with a decrease up to a₀ = 0.5 and an abrupt increase up to a₀ = 1.2 due to prevailing out-of-phase soil vibrations. In particular, the transition between the two response modes occurs at smaller frequency as the distance between the two foundations increases (e.g., S/B = 2). Albeit to a lesser extent, the same considerations can also be referred to the imaginary part (radiation damping) of the impedance function (Fig. 3b). What is not doubtful from the above results is the evidence of cross interaction between two shallow foundations starting from low frequencies of excitation and the more frequency-dependent response with respect to the same foundation considered in isolation. The interaction starts to dominate at frequency exceeding a certain limit in a way that is reminiscent of what happens in pile groups for different pile spacing (Kaynia and Kausel 1982; Gazetas and Makris 1991).

In order to gain a deeper insight into the different mechanisms regulating cross interaction effects between nearby foundations through the underlying soil, the in-group foundation response under static (a₀ → 0) and dynamic (a₀ > 0) excitation loading will be detailed hereinafter.

3.1 Static stiffness

For the two soil configurations considered in this study, halfspace and layer-over-half-space, in Fig. 4 the static stiffnesses associated to the swaying and rocking oscillating modes of the standing-alone foundation were compared to those of the same foundation in presence of its twin loaded with an identical displacement field. For consistency with earlier literature studies, the translational stiffnesses (K_zz, K_yy, and K_xx) were normalized by the shear modulus of the soil, G, and the semi-width of the foundation, B, while the rotational stiffnesses (K_rx and K_ry) were divided by G and B cubed. For the layer-over-half-space configuration, the shear modulus of the top layer was, instead, adopted. In addition, for the foundation group the clear (edge-to-edge) spacing S between the two footings along the y axis (Fig. 1b) was divided by the foundation half-width B so that the overall results were presented in terms of spacing ratio, S/B.

Fig. 4

Dimensionless low-frequency stiffnesses of double versus single footing: translational (a) and rotational (b) modes

From Fig. 4 it emerged that when the master footing was close to an identical one (clone), its static stiffnesses decreased with respect to the values corresponding to the same foundation in isolation. The stiffness reduction is lower as the distance between the two foundations, S/B, increased. For S/B = 4, the cross interaction between the two foundations was found to be still important. For the translational modes, the maximum stiffness reduction in the vertical direction was equal to about 33% for the closest foundation pair (i.e., K_zz for S/B = 0.5) on halfspace, while it was equal to almost 20% for the rotational modes. For the case of layer over halfspace, the maximum variations, obtained for the subsoil scheme with H/B = 10, were equal to 25.4% for the horizontal modes (i.e., K_yy for S/B = 1) and 20.6% for the rotational ones. In the layer-over-halfspace case, obviously, the thinner the deformable layer, the higher the stiffness.

For the rocking stiffness K_rx, two graphs were provided in Fig. 4b. The upper plot corresponds to the case of foundations rotating in the same direction around their own x-axis while the lower plot corresponds to the case of nearby foundations rotating in the opposite sense. In the first case, there was an increase of K_rx and this latter effect increased with decreasing the distance between the two foundations (S/B → 0) since the clone foundation exerted a sort of constraint on the master one. On the contrary, if the two foundations rotated in the opposite sense around their own x-axis, K_rx decreased and a slighter dependence on S/B was observed. The above numerical outcomes corroborated what could be expected from the theory of elasticity and Boussinesq solutions for computing the overburden stresses induced by foundation external loading.

For the horizontal degrees of freedom, the static stiffnesses K_xx and K_yy of the master foundation in a group resulted less influenced by the relative distance, S/B. This response could be explained considering the different stress bulb increments (i.e. the zone below the foundation where stresses and strains are significant) induced by the horizontal or vertical loading underneath the single foundation or the couple of foundations. With reference to the stress contours and iso-surfaces shown in Fig. 5, it could be observed that the stress bulbs associated to the horizontal mode (Fig. 5e–g) were less wide than those induced by vertical loading (Fig. 5b–d). In addition, the further apart the two foundations were, the more the stress bulbs moved apart and tended not to overlap, thus leading to a reduction in lateral cross interaction. Finally, in the simplified assumption of perfect bonding between soil and foundation, even though the stress bulbs associated to the rocking modes (Fig. 5h–m) were small compared to the swaying modes, cross interaction was found to affect also the rotational degrees of freedom K_rx of the master foundation if the two foundations rotate in the same sense. This was the only one case in which the static stiffnesses of the in-group foundation increased (Fig. 4b).

Fig. 5

Cross-sectional view (a) of the incremental stress bulbs under the single or double foundation with different S/B for the vertical (b–d), horizontal (e–g) and rocking modes (h–m)

3.2 Dynamic coefficients

3.2.1 Homogeneous halfspace

With reference to the halfspace, in Fig. 6 the dynamic coefficients obtained from the single and double footing system have been plotted against the dimensionless frequency a₀.

Fig. 6

Dynamic stiffness (a) and damping (b) coefficients for the in-group foundation on a homogeneous halfspace

Unlike the static stiffness discussed in the previous section, the dynamic coefficients appeared to be less affected by the foundation–foundation distance S/B. Only at higher frequencies, a systematic increase of the stiffness coefficients started to occur. Such an effect could be attributed to the interference between the wave fields radiated from the two oscillating footings. Closer the foundations, the higher the frequency at which their wave fields interfered. Likewise, the dynamic stiffness coefficient departed from the solution corresponding to the single foundation at frequencies that were lower with increasing S/B.

The damping coefficients appeared to be slightly affected by the presence of the second foundation. With exception of c_rx, the damping coefficients for a footing in a group were slightly higher than those corresponding to the single foundation (black curve) and increased with frequency at least up to a₀ = 1.

3.2.2 Layer over halfspace

With reference to a soil deposit corresponding to a layer-over-halfspace configuration, Fig. 7 showed the frequency-dependent dynamic stiffness and damping coefficients for the single foundation (coloured curves). For the sake of comparison, the solution corresponding to the same foundation placed on the halfspace (H/B = ∞) was superimposed. As enhanced in previous studies (e.g., Gazetas 1983), when the foundation was placed on a layered subsoil, the dynamic stiffness coefficients exhibited a rather wavy trend with the presence of peaks and valleys caused by the waves radiated from the foundation, partially reflected by the stiffer halfspace and returned back into the softer layer. As the H/B ratio increased, the fluctuations flattened more and more so that for H/B = 10 the computed stiffness coefficients matched the curves corresponding to the halfspace solution.

Fig. 7

Dynamic stiffness (a) and damping (b) coefficients for the single foundation on a layered soil deposit

With reference to k_yy, the first valleys were found at a₀ = 0.50, 0.28, and 0.15 for H/B = 3, 5, and 10, respectively. These values of a₀ correspond to an oscillation frequency of 4.3 Hz, 2.4 Hz, and 1.3 Hz, which are the first shear frequency of each soil configuration in free-field conditions. When it was excited close to its fundamental frequency, the subsoil offered a lower reluctancy to be displaced so that a minimum for the stiffness dynamic coefficient was obtained. Subsequent valleys occurred around frequencies that were close to but different from the higher natural frequencies of the subsoil in shear. This mismatch could be related to multiple reflections of P, S, and Rayleigh waves due to soil layering. Similar considerations could be drawn for k_xx.

In the case of vertical and rocking oscillations, the first valleys occurred at values of a₀ corresponding to the fundamental frequencies of the layer under vertical P-waves (a₀ $\cong$ 1.3, 0.60 and 0.30 corresponding to f $\cong$ 9, 5 and 3 Hz for H/B = 3, 5, and 10, respectively).

The dynamic damping coefficients, instead, showed a less wavy pattern. At lower frequencies (approximately a₀ < 0.5) there was a reduction in radiation damping especially for smaller values of H/B. At higher frequencies, the halfspace solution was approached, in particular for H/B = 10 and rocking motions.

Once the response of a standing-alone foundation on a layered soil deposit had been clarified, the mutual interaction between two foundations resting on a layer over halfspace was elucidated. For S/B = 1 and 2, the dynamic stiffness and damping coefficients of the master foundation in group are shown in Figs. 8 and 9, respectively. As expected, the twin oscillating footings exasperated the interference phenomena already observed for the single foundation (Fig. 7) and a stronger dependence from the oscillation frequency a₀ was observed. Likewise, the dimensionless frequency at which the presence of an additional foundation could affect the results of the master foundation decreased with increasing S/B as already highlighted in Fig. 6.

Fig. 8

Dynamic stiffness (a) and damping (b) coefficients for the double foundation with S/B = 1 on a layered soil deposit with different H/B

Fig. 9

Dynamic stiffness (a) and damping (b) coefficients for the double foundation with S/B = 2 on a layered soil deposit with different H/B

4 Discussion

In the previous section, it was observed that for a given foundation both static terms and dynamic coefficients of the impedance functions might be affected by the presence of a nearby structure due to the interference between the wave fields generated by the motion of the footings. Worst the case of two foundations placed on a layered soil deposit rather than on halfspace.

In case of the halfspace, the change in static stiffness of the master foundation in a group with respect to the same foundation in isolation was mainly controlled by the size of the pressure bulb under the foundation itself. As the vertical and lateral extension of the pressure bulbs for the swaying modes was greater than for the rotational ones (Fig. 5), it turned out that a close twin footing had a greater influence on the translational modes of the master foundation (Fig. 4). Moreover, the cross interaction among close foundations was found to modify also the dynamic coefficients in relation to the foundation–foundation spacing ratio, S/B. The different patterns of the dynamic coefficients shown in Figs. 8 and 9 significantly cleared up when an alternative dimensionless frequency parameter b_o linked the quantity (B + S) was introduced:

$$b_{0} = \omega \left( {nB + S} \right)/V_{s}$$

(13)

in which the coefficient n was related to the oscillation mode of the foundation. In particular, n = 1 for foundation oscillations in the z-direction, n = 4 for swaying along y and n = 2 for rocking around x (Fig. 10).

Fig. 10

Dynamic stiffness (a) and damping (b) coefficients versus b₀ = ω(nB + S)/V_s for the double foundation on homogeneous halfspace

Unless a factor of 2π, the new expression of b₀ in Eq. 13 contains the ratio between the soil wavelength (2πV_S/ω) and a geometric parameter controlling the foundation–foundation lateral interaction. Obviously, such consideration only applied to the in-plane interaction of the couple of footings according to scheme of Fig. 1; hence, in Fig. 10 k_xx and k_ry were not shown.

From Fig. 10 it could be observed that the dynamic coefficients along z collapsed into an almost unique curve. Hence, given the shear wave velocity of the halfspace, the vertical oscillation of the master footing was found to be affected in the same manner by a closer foundation oscillating at a higher or lower frequency provided that the b₀ ratio is the same. The same applies to k_rx, meanwhile some differences still persist in k_yy.

In case of a layered soil deposit (soft layer over halfspace), for which the thickness of the upper layer could exacerbate the interference phenomena among radiated (from both foundations) and reflected (from the layer-halfspace interface) waves, the same adimensionalization procedure adopted for the halfspace, as expected, proved to be not effective. Conversely, a better trend could be envisaged by replacing in Eq. 13 the quantity (nB + S) with the layer thickness H. The new trends obtained in Fig. 11 corroborated the fact that in the performed parameter study, for the selected soil/foundation geometrical configurations and mechanical properties assigned to the soil deposit, the effect of wave reflection in the upper soft layer prevailed with respect to the cross interaction between the two oscillating foundations.

Fig. 11

Dynamic stiffness (a) and damping (b) coefficients versus a₀ = ωH/V_s for the double foundation on a layer over halfspace

5 Operative indications

The results illustrated above have furtherly been processed to derive some operational guidance. With reference to all patterns shown in Figures from 6, 7, 8, 9, it is possible to derive the values of a₀ below which the different curves may be considered equal from an engineering viewpoint (i.e., due to SSSI the dynamic stiffness coefficients differ by a maximum of 10%), so that the dynamic stiffness coefficients of the single foundation may still be used. In case of an elastic halfspace (Fig. 6), the threshold value of a₀ is 0.6 for all directions of oscillation, except for the swaying mode along y and rocking around x, for which the values of 0.7 and 1 were deduced, respectively.

In case of a layered subsoil (Figs. 8, 9), the frequency threshold values a₀ depend on the thickness of the deformable layer and direction of oscillation. Specifically, for vertical oscillation and rocking around y, the values of a₀ are 0.1, 0.3 and 0.6 for H/B = 3, 5 and 10, respectively. For horizontal swaying, it may be assumed 0.1 for all configurations, while for rocking around x the value can be assumed equal to 1.

The same conclusions are not valid for the damping coefficients, as their trends differ from case to case.

In the next paragraph, an operative procedure has been proposed to modify the static part of the stiffness terms of the impedance function to account for cross interaction between two closely-spaced foundations through the underlying soil.

5.1 Stiffness modifiers to account for cross interaction between close foundations

The presence of a twin foundation in the neighbourhood of a target one may be condensed into the following expression:

$$F_{ii, group} = F_{ii, single} \left( {1 - \alpha_{ij} } \right)$$

(14)

where ${F}_{ii, single}$ and ${F}_{ii, group}$ are the resultant forces underneath the master foundation in case it is alone or in group and α_ij is the cross-interaction modifier. As an example, the contribution α_xxF_xx,single is that associated with K_xsm in Eq. 10.

The forces in Eq. 14 may be substituted with the product of the displacement u_ij and the corresponding stiffness components, ${K}_{ii, single}$ and ${K}_{ii, group}$. Being the displacement field applied to the standing-alone foundation equal to the displacement applied to the couple, Eq. 14 may easily be rearranged into the following equation providing stiffness interaction modifiers:

$$\alpha_{ij} = \left( {K_{ij, single} - K_{ij, group} } \right)/K_{ij, single}$$

(15)

It is worth pointing out that the α_ij factors proposed in Eq. 15 resemble the stiffness (not displacement) interaction coefficients suggested for pairs of piles in former works by Poulos (1971) or Poulos and Randoph (1983) with the difference that for nearby shallow foundations the α_ij factors are not aimed at computing the stiffness of the group but the stiffness of individual foundations in a group. With this clarification in mind, the variation of the interaction coefficients α_ij against the foundation–foundation spacing for the different degrees of freedom of the foundation are shown in Fig. 12. As already observed in terms of normalized stiffnesses, the interaction coefficients reduce as the spacing S/B increases, while the rocking mode around the x-axis shows two different trends depending on the rotation sense (same or opposite). The α-values are lower for the stratum-over-halfspace configuration and converge to the halfspace solution as the ratio H/B increases.

Fig. 12

Interaction modifiers versus the foundation–foundation spacing ratio, S/B

For each set of analyses, the results obtained were later interpolated with suitable functions through the Matlab tool. The best fitting was found with the exponential law:

$$\alpha_{ij} = a_{ij} {\text{exp}}[b_{ij} (S/B)]\;\;{\text{with}}\;\;{\text{S}}/{\text{B}} \in \left[ {0.{5};\infty } \right[$$

(16)

in which a_ij and b_ij represent the regression coefficients.

The function is defined starting from S/B = 0.5 up to infinity where the interaction modifier approaches to 0, i.e. the response of the master foundation is unaffected by the motion of its twin.

For any oscillation mode of the foundation, the obtained coefficients were plotted as a function of H/B and again fitted through exponential functions:

$${\text{a}}_{{{\text{ij}}}} = {\text{c}}_{{{\text{1a}}}} {\text{exp}}\left( {{\text{d}}_{{{\text{1a}}}} \left( {{\text{H}}/{\text{B}}} \right)} \right) + {\text{c}}_{{{\text{2a}}}} {\text{exp}}\left( {{\text{d}}_{{{\text{2a}}}} \left( {{\text{H}}/{\text{B}}} \right)} \right) + {\text{c}}_{{{3}a}}$$

(17)

$${\text{b}}_{{{\text{ij}}}} = {\text{c}}_{{{\text{1b}}}} {\text{exp}}\left( {{\text{d}}_{{{\text{1b}}}} \left( {{\text{H}}/{\text{B}}} \right)} \right) + {\text{c}}_{{{\text{2b}}}} {\text{exp}}\left( {{\text{d}}_{{{\text{2b}}}} \left( {{\text{H}}/{\text{B}}} \right)} \right) + {\text{c}}_{{{3}b}}$$

(18)

in which the asymptotes c_3a and c_3b correspond to the values of a_ij and b_ij in case of an elastic halfspace (H/B = ∞).

The resulting functions have been plotted in Fig. 13 while the regression coefficients appearing in Eqs. 17 and 18 are respectively listed in Tables 3 and 4 together with the corresponding coefficients of determination, R².

Fig. 13

Best fitting functions of coefficients a_ij and b_ij against layer-over-halfspace thickness, H/B

Table 3 Exponential law coefficients for Eq. 17 together with R²

Table 4 Exponential law coefficients for Eq. 18 together with R²

The calibrated expressions provide for an effective and rapid tool for quantifying the impedance functions in case of through-soil interaction between close shallow foundations. In practice, the impedance of a standing-alone foundation can firstly be estimated through the usual analytical formulas or charts and then modified by means of the SSSI modifiers in Eq. 16, with the a_ij and b_ij coefficients derived for every H/B ratio through Eqs. 17 and 18.

6 Conclusions

By means of a 3D continuous approach, solved numerically with the finite difference technique, the static and dynamic through-soil interaction between two closely-spaced shallow foundations was investigated. In the parametric study, two subsoil configurations, i.e. an elastic halfspace and a layer over halfspace, were considered together with different values of the foundation–foundation spacing.

The extensive parametric analyses highlighted different important aspects worthy of being considered into a more refined design of buildings located in densely urbanized and seismic areas. First, in case of two identical nearby foundations, a reduction of the low-frequency (static) stiffness of the master foundation was observed for almost all degrees of freedom. For smaller values of the foundation–foundation spacing, the cross interaction contribution was more pronounced and new stiffness interaction coefficients were proposed to modify the original static stiffness of the master foundation in presence of its neighbour.

With reference to the dynamic field, two different responses were envisaged. In the low-frequency range, the dynamic stiffness and damping coefficients of the master foundation in group fairly followed the trends of the dynamic coefficients corresponding to the foundation considered alone. Conversely, at higher frequencies of oscillation, the two sets of curves (single and double foundation) departed each other and important group effect was found due to the interference phenomena among the wave fields generated by the two oscillating footings.

In case of nearby foundations placed on a more complex soil deposit, e.g. a layer over halfspace, cross-interaction phenomena among the foundations were superimposed to multiple wave reflections and refractions within the upper layer so that the computed dynamic stiffness and damping coefficients showed a more wavy trends with respect to the frequency of oscillation, with peaks and valleys almost corresponding to the natural frequencies of the layered deposit.

In short, the cross-interaction between adjacent foundations could definitely induce beneficial or detrimental effects on the superstructure dynamic response, depending on the oscillation mode considered (translational or rotational) and other key factors, such as the footing vibration frequency, the soil natural frequency, and the foundation–foundation spacing. In the case of an elastic halfspace, the last three factors were condensed in a new dimensionless frequency parameter b₀.

The design implications of the performed parametric study could be crucial since the highlighted through-soil interaction between two nearby foundations could lead to a completely different (more conservative or not) design with respect to the standard procedure in which SSI is solved considering the foundation in isolation. SSSI could, for instance, affect the estimation of the fundamental period of the coupled system and consequently the seismic demand of the superstructure.

As a final remark, it should be noted that the aforementioned conclusions were figured out by adopting simplified assumptions regarding the soil deposit (halfspace or single layer over halfspace), soil constitutive law (linear elastic), shape of the foundation (rectangular with L >> B), perfect bonding between the foundation and the soil during the vibration, type of foundation group made of just two shallow rigid foundations not belonging to the same footing system and loaded equally and simultaneously. This choice is certainly a simplification of reality but representative of groups of structures having similar dynamic properties as, for example, it is likely to occur in small historic centres or in modern metropolitan areas. As a future perspective, the performed parametric study could be enriched by implementing more geometrical schemes for soil layering, foundation shape and group configuration. Accordingly, some of the outcomes of the study may not be valid in conditions deviating significantly from those assumed and discussed throughout the paper.