1 Introduction

Recent rapid development in a broad range of thermal management, especially the miniaturizations of modern devices, demands higher accuracy in quantifying the transient heat transportation process (Chen 2021; Wang and Han 2012a). The constitutive law of classical Fourier’s heat conduction theory, which is established on the scaling relation between heat flux and temperature gradient empirically, has been successfully employed in most conventional engineering applications, especially these concerning macroscopic temporal or spatial scales. However, for some extreme cases, like the thermal processes involving very low temperatures, ultrafast heating, micro/nano systems, or heat conduction in biological composites with complex inner structures, Fourier’s law may break down and fail to estimate the accurate temperature level (Wang and Li 2013). For instance, as the ultrafast laser pulse duration shortened to picosecond or femtosecond, noticeable discrepancies emerged between the prediction of Fourier’s law and experimental measurement of the surface temperature of gold films heated by laser beams (Qiu and Tien 1992), which is attributed to the fact that the processing period becomes comparable to the time for building local thermal equilibrium and thus the heat transportation speed cannot be neglected anymore.

The parabolic governing equation of Fourier’s law inherently implies heat travels at an infinite speed and any disturbance at one point can be detected instantaneously at any distance within the body (Onsager 1931), which was noticed by Onsager as early as 1931. In 1944, Peshkov first observed the thermal wave (second sound) in helium II below 2.19 Kevin (Peshkov 1944). Afterward, the thermal wave heat transportation phenomena were observed in solid He (Ackerman et al. 1966), NaF (McNelly et al. 1970; Jackson et al. 1970), semimetal bismuth (Narayanamurti and Dynes 1972), and SrTiO3 (Hehlen et al. 1995). Particularly, except for these findings at very low temperatures, recent experimental progress in observing the thermal wavelike motion was made in graphite over 100 K (Huberman et al. 2019) and 200 K (Ding et al. 2022). Apparently, these abnormal thermal behaviors cannot be explained by Fourier’s law. In order to take the thermal wave propagation into consideration, Cattaneo and Vernottee independently proposed the C–V model by introducing a thermal relaxation time and assuming the establishment of the heat flux was behind the temperature gradient by a finite time (Cattaneo 1958; Vernotte 1958), which is an intrinsic material property and determined by the energy carrier’s collisions.

Although C–V theory is able to measure the thermal inertia effect, some physical contradictions and shortcomings exist in this model. For example, the temperature solution of C–V theory would predict very steep wave fronts and overshooting problems, i.e., the thermal level can exceed the initial and boundary temperatures, which implies the heat transfer from cold area to hot one occurs and violates the second law of thermodynamics (Yu et al. 2016). Based on C–V theory, Tzou (1995) proposed the famous Dual-phase-lag model via introducing another thermal relaxation time into the temperature gradient, which can remove the discontinuous sharp wave fronts (Yu et al. 2016). By considering the microstructural interactions and the certain time for achieving the local thermal equilibrium, DPL theory accommodates the electron–phonon interactions in metals and predicts well with the experimental measurements in ultrafast laser heating of gold films (Tzou 2014). Another situation where the C–V theory is not applicable is the very low temperature condition, where the ballistic transport takes effect. The C–V model fails to describe the thermal behaviors in the non-metallic Bi or NaF pure crystals (Zhukovsky and Srivastava 2017). The ballistic heat transport is more likely to occur in nano-sized structures, like nanofilms or nanowires, where the mean free path of phonons or electrons approaches or exceeds the characteristic dimensions. By solving the linearized Boltzmann equation, Guyer and Krumhansl (1966a, b) derived the nonlocal formulation of C–V model, which incorporates Fourier’s diffusion, thermal wave as well as ballistic transportation. The so-called G–K model prompted the establishment of phonon hydrodynamics (Xu 2021, 2022). It agrees well with the experimental observations for heat conduction in semiconductors and is capable to predict the effective thermal conductivities of nanowires or silicon films. Schwarzwälde et al. (2018) solved the G–K equation for thermal flux with a slip boundary condition and demonstrated its ability in capturing the experimental data for effective thermal conductivity of rectangular nanowires. Beardo et al. (2019) adopted the finite element method to study the G–K model and discovered it agreed well with the experimental measurements of thermal conductivity of compact and holey silicon thin films in a wide range of sizes and temperatures. Beyond its successful applications in very low temperature conditions or nano areas, recent findings suggest G–K model can explain the unclassical heat conduction for macroscopic samples at room temperature. Ván et al. (2017) conducted a series of heat pulse experiments at room temperature with macroscopic-sized samples, like rocks, metal foams, and porous materials, and noticed the measured transient temperatures did not follow Fourier’s law but can be well explained by the G–K model.

It is well-known that microcracks and other imperfections can be easily induced in the materials’ fabrication process or loading period, especially during cyclic heating and cooling. The existence of cracks would disturb the original temperature field and arouses potential overheating in materials, which should be avoided especially for the small-sized structures. The intense thermal energy accumulations around the crack tip may elevate the thermal stresses to the extent of exceeding the thermal fracture resistance. Therefore, extensive studies (Jin and Noda 1994; Itou 2000; Choi 2017; Jesch-Weigel et al. 2023) concerning the crack problem under thermal loading were performed. In the past decade, non-Fourier heat conduction received increasing attention and was adopted to solve the transient thermal and fracture problems in various materials. Wang and Han (2012b) utilized the hyperbolic C–V heat conduction theory to study the heat conduction near an interface crack in bi-layered media made of platinum and quartz glass. They found the relaxation time has a pronounced effect on the thermal propagations by converting the diffusing behavior to wave behavior. Fu et al. (2014) adopted the C–V theory to illustrate the thermoelastic analysis of a long solid cylinder with a circumferential crack. Guo et al. (2016) employed the DPL theory to study the inertia effect for heated crack and thermally insulated crack, which corresponded to the model I and II crack problem, respectively. The axisymmetric problem of a penny-shaped crack embedded in an infinite body was solved by Laplace transform and Hankel transform. Zhang and Li (2017) applied the fractional C–V heat conduction theory to solve the circumferential crack problem in a hollow cylinder, where the inner surface was subjected to a thermal shock and the outer surface was adiabatic. Wen et al. (2022) studied the transient temperature response influenced by the oblique cracks in composites by DPL theory. The finite difference method coupled with an extended boundary correction algorithm was employed to solve the crack problem in fiber-reinforced materials at the macroscale.

It is worth noting the above studies of crack problems are confined to the C–V theory or DPL model, while the research investigating the transient heat conduction in the cracked medium by G–K model has not been reported yet. The interplay mechanism of crack’s disturbance and G–K heat conduction remains unknown, which is indispensable in revealing the transient thermal behaviors concerning time lagging and the nonlocal effects. In this work, we consider the crack problem under impulsive and cyclic loading by G–K model. The Fourier transform and Laplace transform are utilized to reduce the problem to a group of singular integral equations, then the Laplace numerical inversion is applied to obtain the transient temperatures.

2 The problem and basic equations

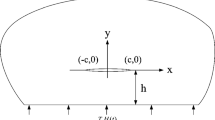
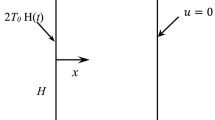
As shown in Fig. 1, consider a typical crack problem under sudden thermal shock. The strip contains a completely thermal insulated Griffith crack of length 2c, which prohibits the penetrations of heat flows across the crack faces and thus perturbing the one-dimension heat conduction. For simplicity, the coordinate system is established along the crack line with the origin locates at the crack’s midpoint. Initially, the whole strip is at the ambient temperature \(T_{0}\). Since \(t = 0\), sudden thermal shocks are exerted on the top surface \(y = h_{1}\), while its bottom surface \(y = - h_{2}\) keeps at the ambient temperature \(T_{0}\).

Fig. 1
figure 1

The cracked strip subjected to thermal shocks

Full size image

The Heaviside step function type impulsive thermal shock as well as cyclic thermal loading are examined in this work, hence the top surface boundary conditions are expressed by:

$$ T(y = h_{1} ,t) = \left\{ {\begin{array}{ll} {T_{S} H(t),} & {Impulsive\;Loading} \\ {T_{S} + (T_{S} - T_{0} )\sin \left( {\frac{2\pi }{{t_{p} }}t} \right),} & {Cyclic\;Loading} \\ \end{array} } \right. $$
(1)

where \(H(t)\) is the Heaviside step function and \(t_{p}\) is the period of sine thermal loading. And the bottom surface boundary condition is:

$$ T(y = - h_{2} ,t) = T_{0} $$
(2)

To capture the two-dimensional transient heat conduction process, Fourier’s law provides a satisfactory evaluation for most macroscopic problems. However, for extreme conditions involving very low temperature, ultrafast heating process, or heat conduction in micro/nano systems, the typical Fourier’s law breaks down. In this work, we employ the Guyer–Krumhansl model to investigate the transient heat conduction problem in the cracked medium, which obeys (Xu 2021, 2022):

$$ \tau_{R} \frac{{\partial {\mathbf{q}}}}{\partial t} + {\mathbf{q}} + k\nabla T = \xi^{2} \left[ {\nabla^{2} {\mathbf{q}} + 2\nabla (\nabla \cdot {\mathbf{q}})} \right] $$
(3)

where \(\tau_{R}\) is the relaxation time, \(\xi\) is the thermal nonlocal length, \(\nabla^{2}\) is the Laplace operator. It is worth noting that when \(\xi = 0\), the model is reduced to C–V theory, and when \(\tau_{R} = \xi = 0\), it can be degraded into Fourier’s law. To obtain the governing equation of the temperature field for G–K model, consider the local energy balance equation without internal heating source:

$$ - \nabla \cdot {\mathbf{q}} = \rho c_{v} \frac{\partial T}{{\partial t}} $$
(4)

where \(\rho\) is mass density and \(c_{v}\) is specific heat. Substitute Eq. (4) into Eq. (3), and then take the divergence of both sides, the heat flux vector can be eliminated. Hence the governing equation in terms of temperature can be obtained as:

$$ \frac{\partial T}{{\partial t}} + \tau_{R} \frac{{\partial^{2} T}}{{\partial t^{2} }} = \frac{k}{{\rho c_{v} }}\nabla^{2} T + 3\xi^{2} \frac{\partial }{\partial t}\nabla^{2} T $$
(5)

At the crack line, the temperature and its gradient are continuous except for the crack segment, hence the governing equation needs to satisfy the following thermal boundary conditions besides Eqs. (1) and (2):

$$ \begin{array}{ll} {\frac{\partial T(x,0)}{{\partial y}} = 0} & {(\left| x \right| \le c)} \\ {T(x,0^{ + } ) = T(x,0^{ - } ),\;\;\frac{{\partial T(x,0^{ + } )}}{\partial y} = \frac{{\partial T(x,0^{ - } )}}{\partial y}} & {(\left| x \right| > c)} \\ \end{array} $$
(6)

For the sake of convenience, the non-dimension variables are introduced:

$$ (x^\prime ,y^\prime ,h_{1} ^\prime ,h_{2}^ \prime ,\xi ^\prime ,c^\prime ) = \frac{{(x,y,h_{1} ,h_{2} ,\xi ,c)}}{{l_{c} }},\;\;\;T^\prime = \frac{{T - T_{0} }}{{T_{S} - T_{0} }}\;,\;\;(t^\prime ,\tau_{R} ^\prime ,t_{p} ^\prime ) = \frac{{(t,\tau_{R} ,t_{p} )}}{{l_{c}^{2} /\alpha }} $$
(7)

where \(l_{c}\) is the characteristic length, \(\alpha = k/\rho c_{v}\) is the thermal diffusivity. Then Eq. (5) can be rewritten to:

$$ \frac{\partial T^{\prime} }{{\partial t^{\prime} }} + \tau_{R} ^{\prime} \frac{{\partial^{2} T^{\prime} }}{{\partial t^{\prime 2} }} = (1 + 3\xi ^{ \prime 2} \frac{\partial }{\partial t})\nabla^{2} T^{\prime} $$
(8)

3 Solution procedures

In this section, the partial differential Eq. (8) is solved by the integral transform method. The employed Fourier transform and Laplace transform are formulated as:

$$ g(s) = \int\limits_{0}^{\infty } {g(t)} \;e^{ - st} dt,\;\;g(t) = \frac{1}{2\pi i}\int\limits_{Br}^{{}} {g(p)} \;e^{st} ds $$
(9)
$$ f(x) = \int\limits_{ - \infty }^{\infty } {f(w)} \;e^{ - iwx} dw,\;\;f(w) = \frac{1}{2\pi }\int\limits_{ - \infty }^{\infty } {f(x)} e^{iwx} dx $$
(10)

where Br is the Bromwich path, \(s,\;w\) are the Laplace and Fourier transform variables, respectively. Utilizing Laplace transform, the dimensionless governing equation is transformed to:

$$ \frac{{\partial^{2} T^{\prime} }}{{\partial x^{\prime 2} }} + \frac{{\partial^{2} T^{\prime} }}{{\partial y^{\prime 2} }} = \frac{{1 + \tau_{R} ^{\prime} s}}{{1 + 3\xi ^{\prime 2} s}}sT^{\prime} $$
(11)

And the boundary conditions at the top and bottom surfaces in the Laplace transformation space are:

$$ T^{\prime} (y^{\prime} = h_{1} ^{\prime} ,s) = \left\{ {\begin{array}{ll} {1/s,} & {Impulsive\;Loading} \\ {\frac{1}{s} + \frac{{2\pi /t_{p} ^{\prime} }}{{(2\pi /t_{p} ^{\prime})^{2} + s^{2} }},} & {Cyclic\;Loading} \\ \end{array} \;\;\;\;\;} \right. $$
(12)
$$ T^{\prime} (y^{\prime} = - h_{2} ^{\prime} ,s) = 0 $$
(13)

while the remaining boundary conditions keep the same with Eq. (6).

For the crack problem, the solution of Eq. (11) can be obtained with the help of the superposition principle (Jin and Noda 1994), shown as:

$$ T^{\prime} (s) = T_{1} ^{\prime} (s) + T_{2} ^{\prime} (s) $$
(14)

where \(T_{1}^ {\prime} (s)\) denotes the temperature solution for the strip subjected to the same boundary conditions but containing no crack, and satisfying the following ordinary differential equation and the boundary conditions:

$$ \frac{{d^{2} T_{1} ^{\prime} }}{{dy^{\prime 2} }} = \frac{{1 + \tau_{R} ^{\prime} s}}{{1 + 3\xi ^{\prime 2} s}}sT_{1} ^{\prime} $$
(15)
$$ T_{1} ^{\prime} (y^{\prime} = h_{1} ^{\prime} ,s) = \left\{ {\begin{array}{*{20}c} {1/s,} & {Impulsive\;Loading} \\ {\frac{1}{s} + \frac{{2\pi /t_{p} ^{\prime} }}{{(2\pi /t_{p} ^{\prime} )^{2} + s^{2} }},} & {Cyclic\;Loading} \\ \end{array} \;\;\;\;\;} \right. $$
(16)
$$ T_{1} ^{\prime} (y^{\prime} = - h_{2} ^{\prime} ,s) = 0 $$
(17)

Therefore, the solution is expressed by:

$$ T_{1} ^{\prime} (s) = \vartheta_{1} (s)e^{ - qy^{\prime} } + \vartheta_{2} (s)e^{qy^{\prime} } ,\;\;\;\;\;\;q = \sqrt {s\frac{{1 + \tau_{R} ^{\prime} s}}{{1 + 3\xi ^{\prime 2} s}}} $$
(18)

For the impulsive loading,

$$ \vartheta_{1} (s) = - \frac{{e^{{ - qh_{1} ^{\prime} }} e^{{ - 2qh_{2} ^{\prime} }} }}{{s(1 - e^{{ - 2q(h_{1} + h_{2} )^{\prime} }} )}},\;\vartheta_{2} (s) = \frac{{e^{{ - qh_{1} ^{\prime} }} }}{{s(1 - e^{{ - 2q(h_{1} + h_{2} )^{\prime} }} )}} $$
(19)

For the cyclic loading,

$$ \vartheta_{1} (s) = - \frac{{e^{{ - qh_{1} ^{\prime} }} e^{{ - 2qh_{2} ^{\prime} }} }}{{1 - e^{{ - 2q(h_{1} + h_{2} )^{\prime} }} }}\left( {\frac{1}{s} + \frac{{2\pi /t_{p} ^{\prime} }}{{(2\pi /t_{p} ^{\prime} )^{2} + s^{2} }}} \right),\;\vartheta_{2} (s) = \frac{{e^{{ - qh_{1} ^{\prime} }} }}{{1 - e^{{ - 2q(h_{1} + h_{2} )^{\prime} }} }}\left( {\frac{1}{s} + \frac{{2\pi /t_{p} ^{\prime} }}{{(2\pi /t_{p} ^{\prime} )^{2} + s^{2} }}} \right) $$
(20)

\(T_{2} ^{\prime} (s)\) represents the thermal responses of the cracked strip without considering the thermal loadings, which satisfies:

$$ \frac{{\partial^{2} T_{2} ^{\prime} }}{{\partial x^{ \prime 2} }} + \frac{{\partial^{2} T_{2} ^{\prime} }}{{\partial y^{\prime 2} }} = \frac{{1 + \tau_{R} ^{\prime} s}}{{1 + 3\xi ^{ \prime 2} s}}sT_{2} ^{\prime} $$
(21)
$$ \begin{array}{*{20}c} {\frac{{\partial T_{2} ^{\prime} (x^{\prime} ,0)}}{\partial y^{\prime} } = - \frac{{dT_{1} ^{\prime} (y^{\prime} = 0)}}{dy^{\prime} }} & {(\left| {x^{\prime} } \right| \le c^{\prime} )} \\ {T_{2} ^{\prime} (x^{\prime} ,0^{ + } ) = T_{2} ^{\prime} (x^{\prime} ,0^{ - } ),\;\;\frac{{\partial T_{2} ^{\prime} (x^{\prime} ,0^{ + } )}}{\partial y^{\prime} } = \frac{{\partial T_{2} ^{\prime} (x^{\prime} ,0^{ - } )}}{\partial y^{\prime} }} & {(\left| {x^{\prime} } \right| > c^{\prime} )} \\ \end{array} $$
(22)

Using Fourier transform and considering these boundary conditions, the solutions are of the form:

$$ \begin{gathered} T_{2} ^{\prime} (x^{\prime} ,y^{\prime} ,s) = \int\limits_{0}^{\infty } {[B_{1} (w,s)e^{ - ry^{\prime} } + B_{2} (w,s)e^{ry^{\prime} } ]} \;e^{ - iwx^{\prime} } {\text{d}}w \hfill \\ T_{2} ^{\prime} (x^{\prime} ,y^{\prime} ,s) = \int\limits_{0}^{\infty } {[B_{3} (w,s)e^{ - ry^{\prime} } + B_{4} (w,s)e^{ry^{\prime} } ]\;} e^{ - iwx^{\prime} } {\text{d}}w \hfill \\ \end{gathered} $$
(23)

where \(r = \sqrt {s\frac{{1 + \tau_{R} ^{\prime} s}}{{1 + 3\xi ^{\prime 2} s}} + \xi^{2} }\) and

$$ \begin{gathered} B_{2} (w,s) = - B_{1} (w,s)e^{{ - 2rh_{1} ^{\prime} }} \\ B_{3} (w,s) = - B_{4} (w,s)e^{{ - 2rh_{2} ^{\prime} }} \\ B_{4} (w,s) = - \frac{{1 + e^{{ - 2rh_{1} ^{\prime} }} }}{{1 + e^{{ - 2rh_{2} ^{\prime} }} }}B_{1} (w,s) \\ \end{gathered} $$
(24)

In order to solve the only unknown term \(B_{1} (w,s)\), introduce the temperature jump function (Hu and Chen 2013) across the crack face:

$$ \psi (x^{\prime} ,s) = \frac{{\partial T_{2} ^{\prime} (x^{\prime} ,0^{ + } ,s)}}{\partial x^{\prime} } - \frac{{\partial T_{2} ^{\prime} (x^{\prime} ,0^{ - } ,s)}}{\partial x^{\prime} } $$
(25)

Considering the boundary conditions, we have

$$ \psi (x^{\prime} ,s) = 0,\;\;\;\;\;\;\;\;\;\left| {x^{\prime} } \right| > c^{\prime} $$
(26)
$$ \int\limits_{ - c^{\prime} }^{c^{\prime} } {\psi (x^{\prime} ,s)} dx^{\prime} = 0 $$
(27)

Plug Eq. (23) into Eq. (25), and apply the inverse Fourier transform, the unknown term is derived as:

$$ B_{1} (w,s) = \frac{i}{4\pi w}\frac{{1 + e^{{ - 2rh_{2} ^{\prime} }} }}{{1 - e^{{ - 2r(h_{1} ^{\prime} + h_{2} ^{\prime} )}} }}\int\limits_{ - c^{\prime} }^{c^{\prime} } {\psi (\tau ,s)e^{iw\tau } {\text{d}}} \tau $$
(28)

Substituting the above equation into Eq. (23) and considering the boundary condition (22), the whole problem can be reduced to the following singular integral equation:

$$ \int\limits_{ - c^{\prime} }^{c^{\prime} } {\psi (\tau ,s)} [\frac{1}{\tau - x^{\prime} } + K(x^{\prime} ,\tau ,s)]d\tau = 2\pi q(\vartheta_{1} - \vartheta_{2} ),\;\;\left| {x^{\prime} } \right| < c^{\prime} $$
(29)

And the kernel function is:

$$ K(x^{\prime} ,\tau ,s) = \int\limits_{0}^{\infty } {\left[ {1 + \frac{1}{w}\left( {\frac{{( - r - re^{{ - 2rh_{1} ^{\prime} }} )(1 + e^{{ - 2rh_{2} ^{\prime} }} )}}{{1 - e^{{ - 2r(h_{1} ^{\prime} + h_{2} ^{\prime} )}} }}} \right)} \right]\;\sin [w(x^{\prime} - \tau )]} \;dw $$
(30)

To solve the above singular integral equation, introduce:

$$ \overline{x} = \frac{x^{\prime} }{{c^{\prime} }},\;\overline{\tau } = \frac{\tau }{c^{\prime} } $$
(31)

Then Eq. (27) and Eqs. (29–30) become:

$$ \int\limits_{ - 1}^{1} {\psi (\overline{x} ,s)} d\overline{x} = 0 $$
(32)
$$ \int\limits_{ - 1}^{1} {\psi (\overline{\tau } ,s)} [\frac{1}{{c\prime (\overline{\tau } - \overline{x} )}} + K(\overline{x} ,\overline{\tau } ,s)]c^{\prime} d\overline{\tau } = 2\pi q(\vartheta_{1} - \vartheta_{2} ),\;\;\left| {\overline{x} } \right| < 1 $$
(33)
$$ K(\overline{x} ,\overline{\tau } ,s) = \int\limits_{0}^{\infty } {\left[ {1 + \frac{1}{w}\left( {\frac{{( - r - re^{{ - 2rh_{1} \prime }} )(1 + e^{{ - 2rh_{2} \prime }} )}}{{1 - e^{{ - 2r(h_{1} \prime + h_{2} \prime )}} }}} \right)} \right]\;\sin [c\prime w(\overline{x} - \overline{\tau } )]} \;dw $$
(34)

Till now, the solution of the above singular integral equation can be expressed in the form of (Hu and Chen 2013):

$$ \psi (\overline{\tau } ,s) = \frac{{\Psi (\overline{\tau } ,s)}}{{\sqrt {1 - \overline{\tau }^{2} } }},\;\;\;\;\left| {\overline{\tau } } \right| \le 1 $$
(35)

Then Eqs. (32–33) can be converted to a series of algebraic equations by employing the Lobatto–Chebyshev method (Hu and Chen 2013):

$$ \sum\limits_{k = 1}^{n} {\frac{\pi }{n}\Psi (\tau_{k} ,s)} \left[ {\frac{1}{{c\prime (\tau_{k} - x_{r} )}} + k(x_{r} ,\tau_{k} ,s)} \right]c\prime = 2\pi q(\vartheta_{1} - \vartheta_{2} ) $$
(36)
$$ \sum\limits_{k = 1}^{n} {\frac{\pi }{n}\;} \Psi (\tau_{k} ,s) = 0 $$
(37)

where \(\tau_{k} (k = 1,2,...,n) = \cos \frac{(2k - 1)\pi }{{2n}}\) and \(x_{r} (r = 1,2,...,n - 1) = \cos \frac{r\pi }{n}\).

By plugging the numerical results into Eq. (28), the unknown term \(B_{1} (w,s)\) can be determined and the temperature field in the Laplace domain can be evaluated by integrations shown in Eqs. (23) and (18). To acquire the transient temperatures in the time domain, the fast Laplace inversion method proposed by Durbin (1974) is employed:

$$ T(t) = \frac{{2e^{at} }}{P}\left[ { - \frac{1}{2}{\text{Re}} \{ T(a)\} + \sum\limits_{k = 0}^{NSUM} {\left( {{\text{Re}} \{ T(a + ik\frac{2\pi }{P})\} \cos (k\frac{2\pi }{P}t) - {\text{Im}} \{ T(a + ik\frac{2\pi }{P})\} \sin (k\frac{2\pi }{P}t)} \right)} } \right] $$
(38)

In the present work, the parameters in the above algorithm are selected as: \(P = 20,\) \(aP = 6,\;NSUM = 500\) during calculations.

4 Verification

The calculation process is implemented by MATLAB software. For concision, the hats of dimensionless variables are removed and all the variables shown in this section and the next one are non-dimensional. As mentioned in the introduction part, the study of transient heat conduction in the cracked medium by the G–K model has not been reported yet. To guarantee the correctness of our solution, the verification is made by comparing the present numerical results with Li’s work (Li et al. 2016) for Fourier’s case. In their work, they assumed the impulsive thermal loading was exerted on the bottom surface and the top free surface was kept at the ambient temperature. By adopting the same geometry sizes and letting \(\tau_{R} = \xi = 0\), a good agreement is observed in Fig. 2, which presents the transient temperatures of the two midpoints of the crack face. It is worth noting that the temperature of the upper and lower midpoints of the present work correspond to the lower and upper midpoints for Li’s work, respectively.

Fig. 2
figure 2

Verification of the transient temperatures of two midpoints of the crack face

Full size image

5 Numerical results and discussions

In this section, by comparing the transient temperatures calculated from the above solution, the coupled effect of the crack’s perturbance and G–K model is explored. The characteristic length is selected as \(l_{c} = h_{1}\). Unless otherwise specified, the non-dimensional variables are supposed to be \(h_{1} = 1,\;h_{2} = 2,\;c = 1\) for the geometry and \(t_{p} = 4\) for the period of cyclic loading. The transient thermal responses of Fourier’s law, C–V theory and G–K model are illustrated graphically for the strip subjected to impulsive thermal loading as well as cyclic loading. Parametric studies are conducted to analyze the impacts of the thermal relaxation time, nonlocal length, and crack length on temperature evolutions.

To begin with, the crack’s perturbance is examined for different heat conduction theories. As mentioned in the second part, G–K model can be degenerated to the C–V model by letting the nonlocal length equal to zero, while Fourier’s law corresponds to the case where both the nonlocal length and the relaxation time are zeros. Figures 3 and 4 illustrate the transient temperatures of the origin point (x = 0, y = 0) influenced by the crack’s perturbance under impulsive loading and cyclic loading, respectively. Summation of Eqs. (18) and (23) gives out the solution for temperatures influenced by the crack, while Eq. (18) alone presents the one-dimensional heat conduction problem without the crack but under the same thermal boundary conditions. In these figures, the parameters for the G–K model are assumed to be \(\tau_{R} = 1,\;\xi = 1\) while these of the C–V model are \(\tau_{R} = 1,\;\xi = 0\). The crack’s disturbance shows a significant influence on the transient temperatures, where obvious thermal jumps occur between the upper crack face and lower crack face. By comparing Fig. 3a with b, the existence of a crack obstructs the heat flow across it and elevates the thermal level of the upper crack midpoint but depresses the temperatures of the lower crack midpoint. For the impulsive loading, Fourier’s law indicates the temperatures always increase gradually to the steady values and the C–V model predicts there is a delayed time before the temperature starts to grow and very steep wave fronts occur, which is unrealistic since this implies almost infinite temperature gradients. Another abnormal behavior is the severe overshooting, as found in the upper crack midpoint, where the peak value reaches 1.3 and is higher than the exerted thermal loading. This demonstrates that the crack’s obstruction enhances the non-Fourier C–V effect since no overshooting is found in Fig. 3a. The occurrence of overshooting means heat can flow from cold area to hot area, and this unphysical result can be well eliminated by introducing the nonlocal length in G–K model, where the temperatures grow gradually but the heating rate is higher than that of Fourier’s law in the early stage. Particularly, this interesting finding is also presented in the heat flux experiments (Both et al. 2016), where the G–K model agrees well with the measured data and shows a higher heating rate at the early stage compared to Fourier’s law. For the cyclic thermal loading, the transient temperatures always present wave like oscillations. Compared to Fourier’s law and G–K model, the C–V heat conduction shows the delayed time at the beginning and very significant overshooting. Besides, the negative temperatures appear for the upper crack midpoint, which indicates some heat flow from cold to hot area again. Similar to the finding for impulsive loading, the G–K model displays a higher heating rate at the early stage. In addition, it is noticed for the cyclic loading, the G–K model has some effects on the peak and troughs as well. Compared to Fourier’s law, larger differences between peak and troughs of transient temperatures are discovered for both the cracked strip and uncracked one.

Fig. 3
figure 3

The transient temperatures of the origin (x = 0, y = 0) under different heat conduction theories for impulsive loading

Full size image
Fig. 4
figure 4

The transient temperatures of the origin (x = 0, y = 0) under different heat conduction theories for cyclic loading

Full size image

Subsequently, the temperature distributions along the y-axis are presented for different time instants, as given by Figs. 5 and 6. The C–V responses are compared to the G–K solutions to further highlight G–K model’s advantages. For the impulsive loading, the temperatures of the top surface at four time instants keep at one, which is the dimensionless exerted Heaviside step function. As to the cyclic loading, the temperatures of the top surface at four time instants obey the sine function’s variation. The temperatures of the bottom surface keep at zero, which is consistent with the dimensionless ambient temperature. These findings confirm the presupposed thermal boundary conditions. It is worth noticing the considerable temperature gradient occurs around the crack face. At \(t = 2\), the C–V model predicts severe overshooting problems for both impulsive loading and cyclic loading. Negative temperatures are observed for the cyclic loading at \(t = 4\). These unphysical predictions spatially are eliminated again by G–K model, as shown in Figs. 5b and 6b.

Fig. 5
figure 5

The temperature distributions along the y-axis for (a) C–V theory, (b) G–K theory under impulsive loading

Full size image
Fig. 6
figure 6

The temperature distributions along the y-axis for (a) C–V theory (b) G–K theory under cyclic loading

Full size image

To illustrate the nonclassical transient heat process governed by G–K model, the influences of the relaxation time and the nonlocal length are considered in contrast to Fourier’s heat condition. Figure 7 depicts the transient temperatures of the crack’s midpoints for impulsive loading with the variation of different relaxation times and nonlocal lengths, and it is found they do not influence the steady values. Compared to Fourier’s result, G–K model plays a vital role in determining the temperatures at the early stage. For \(t < 2\), the G–K’s prediction can be even several times higher than Fourier’s one, which demonstrates the necessity to consider these unconventional thermal processes. Evidently, the increase of thermal relaxation time would “relax” the heating rate at the early stage, while the nonlocal length presents the opposite effect. Figures 8 and 9 reveal the transient temperatures of crack’s midpoints for cyclic loading influenced by different thermal relaxation times and nonlocal lengths, respectively. G–K model results in the phase lag phenomena in the thermal waves. In addition to these similar findings of relaxation effects governed by the relaxation times and nonlocal lengths in the impulsive loading, it is noted the two parameters alter peak and troughs values for the cyclic loading, especially for the lower crack midpoints, as shown in Figs. 8b and 9b. Besides, for different combinations of the relaxation times and nonlocal length, G–K model demonstrates it enhances the temperature differences between peak and troughs compared to Fourier’s law.

Fig. 7
figure 7

The transient temperatures of crack’s midpoints for impulsive loading with different (a) thermal relaxation times (b) nonlocal lengths

Full size image
Fig. 8
figure 8

The transient temperatures of crack’s (a) upper midpoint (b) lower midpoint for different thermal relaxation times under cyclic loading

Full size image
Fig. 9
figure 9

The transient temperatures of crack’s (a) upper midpoint (b) lower midpoint for different nonlocal lengths under cyclic loading

Full size image

Furthermore, to give a better presentation of the transient temperature evolution process of G–K model, the whole temperature fields with isothermals of the cracked strip under impulsive and cyclic loading are illustrated in Figs. 10 and 11, respectively. The relaxation time and nonlocal length are supposed to be \(\tau_{R} = 1,\;\xi = 1\). The crack obstructs the heat flow and intense thermal energies accumulate around the crack face. The maximum temperature gradient exists between the midpoints of crack faces, and large temperature gradients can also be observed at the two crack tips. For the impulsive loading, the heat flow from the top surface to the bottom surface and heat the whole strip gradually. However, for the cyclic loading, due to the variations of exerted boundary conditions at the top surface, the temperatures below the crack face can be higher than those above the upper crack face.

Fig. 10
figure 10

Temperature evolution with isothermals at different time instants for the impulsive loading

Full size image
Fig. 11
figure 11

Temperature evolution with isothermals at different time instants for the cyclic loading

Full size image

Finally, the impacts of the crack length on the temperatures are explored. Figure 12 plots the transient temperatures of crack’s midpoints with the variation of different crack lengths. Figure 13 shows the temperature’s spatial distribution along the x-axis for different crack lengths at one fixed time instant. It is discovered that the larger crack length enhances the temperature jumps between upper and lower crack faces. The increase in crack length elevates the temperature of the upper crack face but lower that of the lower crack face. Server thermal concentrations occur with larger crack length, which suggests more attention should be paid to avoid overheating in small-sized systems and the associated fracture risk. Besides, the heating rates of the upper crack midpoint in the early stage seem to be not affected by the crack lengths for both types of thermal loadings. However, a larger crack length tends to decrease the heating rate of lower crack midpoints for the early stages. In addition, Fig. 13 indicates that the larger crack length lowers the thermal level at the extension line except for the crack segment.

Fig. 12
figure 12

The transient temperatures of crack’s midpoints for different crack lengths under (a) impulsive loading (b) cyclic loading

Full size image
Fig. 13
figure 13

The temperature distribution along x-axis for different crack lengths under (a) impulsive loading (b) cyclic loading

Full size image

6 Conclusions

The purpose of this article is to investigate the transient heat conduction process in the cracked medium by the nonclassical G–K model. The integral transforms technique and the singular integral equations are employed to solve the complex boundary value problems. By the comparisons of thermal responses determined by Fourier’s law, C–V equation and G–K model, the interplay mechanism of the relaxation time, nonlocal length and the crack’s obstruction are examined. Some conclusions are drawn:

  1. (1)

    The crack obstructs the heat flow across the crack face, and elevates the thermal level of the upper crack midpoint but depresses the temperature of the lower crack midpoint.

  2. (2)

    The unphysical results predicted by the C–V equation can be well eliminated by introducing the nonlocal length in the G–K model.

  3. (3)

    The increase of thermal relaxation time would “relax” the heating rate at the early stage, while the nonlocal length presents the opposite effect.

  4. (4)

    The temperatures below the crack face can be higher than those above the upper crack face for the cyclic thermal loading.

  5. (5)

    It is discovered that the larger crack length enhances the temperature jumps between upper and lower crack faces.