1 Introduction

With the rapid development of material science and advanced manufacturing techniques, a wide variety of new functional composites materials, such as polymer matrix composites, nanocomposites hydrogels and soft elastomers, have been invented and put into application extensively in a broad range of fields, like biomedical, tissue, drug delivery, aerospace, mechanical, civil, and nuclear engineering, automotive and aeronautical industry [1,2,3,4,5,6,7]. To assess the safety factors or lifetime, one common aspect which should be taken into consideration is their performance under external thermal loading. For example, to overcome the drawback of low thermal conductivity of polymers, by inserting particles of ultra-high thermal conductivities into the polymer matrix, this kind of polymer-based composites has been commonly fabricated and used in various industries [8,9,10]. Another example is the widespread usage of enormous kinds of biomaterials, which are designed to mimic or replace biological materials and are inevitably to be exposed to heating and cooling, like laser or other modern thermo-therapeutics in biomedical treatments [11, 12].

In order to assure the lifetime, safety and reliability of these composites, the analysis of the heat transfer and transient thermal stress distributions are of paramount importance. Microcracks may develop in the manufacturing of these composites or during the external thermal or mechanical loading process, especially at the interfaces of multiphases due to the differences in the mechanical properties between interphases and matrix [13], in which case the concentration of thermal stresses and high temperature gradients would be induced around the cracks. As to the thermo-elastic analysis of crack problems in various materials, there have been extensive theoretical researches, such as the investigations of FGMs [14,15,16] or piezoelectric materials [17,18,19]. However, two main limitations lie in these previous reports. One is only the classical Fourier’s law concerned in the analysis of heat conduction, which indicates the infinite thermal wave propagation speed and violates the physical fact. The other is neglection of the viscous effect of mechanical properties in deriving the thermal stresses. With the increasing high demanding of accuracy in engineering problems, especially the fast-growing usage of the viscoelastic composites, these aspects cannot be ignored anymore.

To overcome the deficiency of the classical Fourier Law and take the finite speed of thermal waves into consideration, Cattaneo and Vernotte [20, 21] proposed the hyperbolic heat conduction model, by introducing the “thermal relaxation time”, which is a material constant of the time lag of heat flux, usually decided by the collision frequency of the molecules. Since then, numerous scientific works have been developed for the non-Fourier heat conduction, such as [22,23,24,25,26,27,28,29]. As to the heat conduction in cracked media and associated fracture analysis, since 2010s, there have been several reports concerning the non-Fourier effect [30,31,32,33,34,35,36,37,38]. In these reports, some extreme thermal conditions were assumed, such as high heating rates, very high or low temperature, or heat conduction in nanosystem, which are caused by the fact that the thermal relaxation time for most materials is very small, in the order of picoseconds. However, as to the composites or biological materials, due to the particular complex inner structures, experiments [39, 40] show the order of thermal relaxation time can be up to the order of 10 s, which indicates non-Fourier effects should be considered even in conventional thermal conditions for these materials.

Although the hyperbolic heat conduction theory has exhibited some success in the past decades, some researchers [41,42,43,44] pointed out that it introduces additional non-physical effects. One obvious error is that it could give negative absolute temperature. Similarly, the same effect can be observed in the crack problems, like the negative temperature distribution around cracks in [30, 31]. Due to the fact there is no negative temperature in both the initial condition and the external thermal loading, the appearance of negative absolute temperature shows the heat flowing from cold to hot regions around the crack, which violates the second law of thermodynamics. To circumvent this kind of problem, Zhang et al. [45] introduced the fractional calculus to the conventional hyperbolic heat conduction model. By comparing several types of fractional heat conduction equations in the one-dimensional thermal problem, they found a series of favorable results in eliminating the negative temperatures. As an extension of the integer order in partial differential equations, fractional calculus has been widely discussed in various applications like fluid mechanics, viscoelasticity and biological engineering [46,47,48,49]. Unlike the integer order, time-fractional order differentiation is a non-local operator, which indicates the next state of system depends on both the current state and the historical states. Whether the time-fractional single-phase lag heat equation can predict nonnegative absolute temperatures around cracks would be an interesting topic. In this article, we employed the simplest fractional single-phase lag model to investigate the two-dimensional heat transfer in a cracked material.

To depict the relationship between stress and strain, the linear theory of elasticity succeeds in various applications, especially for materials like metals and concrete. However, classical elasticity does not apply to the new synthetic composite materials. For these viscoelastic materials, significant creep or stress relaxation behavior may exist even under room temperature. Usually, the stress and strain depend on their historical variation, and the deformation is a time-dependent process. From the knowledge of linear viscoelasticity, the viscous effect of materials would be much more significant under elevated temperature. Therefore, there has been a lot of research concerning thermo-viscoelasticity, such as [50,51,52]. However, most work only focused on the one-dimensional heat transfer in uncracked materials. There are very few works investigating the thermal fracture behavior of viscoelastic materials. As to cracked viscoelastic materials, the heat conduction would always be two-dimensional since the existence of a crack could disturb the temperature field. It would be interesting to see what kind of transient fracture behaviors could be predicted if we extend the non-Fourier effect into viscoelastic materials. With the increasing application of soft composites, the viscoelastic fracture analysis under thermal loading has become an important topic.

In the present article, instead of focusing on one specific material, we analyze the general crack problem under the framework of the fractional thermo-viscoelasticity. By employing the Laplace transform, the time dependency of the heat conduction equation as well as the viscoelastic constitutive equation is eliminated. Coupled with Fourier transform and the singular integral equations, the governing, partial differential equations (PDEs) are solved numerically. The closed form expressions of both temperature and stress fields are derived, and thereafter, the transient stress intensity factors are shown graphically.

Fig. 1
figure 1

Geometry and loading of the crack problem

Full size image

2 Formulation of the problem

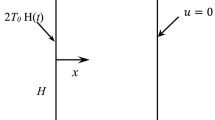
As shown in Fig. 1, consider a crack of length 2c parallel to the free surface of a half infinite plane with homogeneous viscoelastic properties. The initial temperature of the plane is assumed to be \(T_1 \) uniformly. The free surface is subjected to a uniform thermal shock \(T_0 H(t)\), where H(t) is the Heaviside function. The crack is assumed to be partially thermally insulated, and the distance to the free surface is h. Like in the popular usage of uncoupled thermal-elastic theory in crack problems, only the temperature field is assumed to influence the viscoelastic thermal stress. In addition, the inertia effect and body force are neglected. Unlike the linear elastic materials, the significant relaxation phenomena with time should be considered in the viscoelastic materials, so the transient material properties [53, 54] are assumed to be:

$$\begin{aligned} E(t)=E_0 f_1 (t),\,\, \upsilon (t)=\upsilon _0 f_2 (t),\,\, \lambda (t)=\lambda _0 f_3 (t), \end{aligned}$$
(1)

where \(E(t), \upsilon (t), \lambda (t)\) are the Young’s modulus, Poisson’s ratio and thermal expansion coefficient, respectively. \(E_0 ,\upsilon _0 ,\lambda _0 \) are the initial constants and \(f_1 (t), f_2 (t), f_3 (t)\) are the relaxation functions. In the following sections, the governing equations for both heat transfer and viscoelastic thermal stresses are presented in detail.

2.1 Heat conduction

For a viscoelastic composite with complex inner structures, the thermal relaxation time is usually much higher compared to common materials. To incorporate the non-Fourier heat transfer and eliminate the negative temperatures, the time-fractional single-phase lag heat conduction model is investigated in this article, as follows:

$$\begin{aligned} \mathbf{q}(X,t)+\frac{\tau _q ^{\alpha }}{\alpha !}\frac{\partial ^{\alpha }{} \mathbf{q}(X,t)}{\partial t^{\alpha }}=-k\nabla T(X,t), \end{aligned}$$
(2)

where k is the thermal conductivity, \(\mathbf{q}\) is heat flux, \(\tau _q \) is the thermal relaxation time, t is time, \(\nabla \) is the gradient operator, X is the position ; the Caputo fractional derivative of order \(\alpha \) is defined as:

$$\begin{aligned} \frac{\partial ^{\alpha }f(X,t)}{\partial t^{\alpha }}=\left\{ {{\begin{array}{ll} \frac{1}{\Gamma (1-\alpha )}\int \limits _0^t (t-\tau )^{-\alpha }\frac{\partial f(X,\tau )}{\partial \tau }{\mathrm{d}}\tau ,&{}\quad 0<\alpha <1, \\ \frac{\partial f(X,t)}{\partial t},&{}\quad \alpha =1, \\ \end{array} }} \right. \end{aligned}$$
(3)

where \(\Gamma (.)\) is the gamma function. The equation of energy conservation in the absence of inner heat source reads:

$$\begin{aligned} -\nabla \cdot \mathbf{q}=\rho c_p \frac{\partial T}{\partial t}, \end{aligned}$$
(4)

where \(\rho \) is the mass density and \(c_p \) is the specific heat. Substituting Eq. (2) into (4), the governing equation for the temperature field is obtained as

$$\begin{aligned} a\nabla ^{2}T=\frac{\partial T}{\partial t}+\frac{\tau _q ^{\alpha }}{\alpha !}\frac{\partial ^{1+\alpha }T}{\partial t^{1+\alpha }}, \end{aligned}$$
(5)

where \(a=\frac{k}{\rho c_P }\) is the thermal diffusivity and \(\nabla ^{2}=\frac{\partial }{\partial x^{2}}+\frac{\partial }{\partial y^{2}}\).

The initial and boundary conditions for the thermal field are:

$$\begin{aligned} \begin{aligned} T&=T_1 , \;\frac{\partial T}{\partial t}=0, \;(t=0), \\ T(x,-h)&=T_0 , \;(t>0,\left| x \right| <\infty ), \\ T&=T_1 , \;(y\rightarrow \infty ), \\ \frac{\partial T}{\partial y}&=V[T(x,0^{+})-T(x,0^{-})], \;(y=0,\left| x \right| \le 1), \\ T(x,0^{+})&=T(x,0^{-}), \;(\left| x \right|>1), \\ \frac{\partial T(x,0^{+})}{\partial y}&=\frac{\partial T(x,0^{-})}{\partial y}, \;(\left| x \right| >1), \\ \end{aligned} \end{aligned}$$
(6)

where the quantity V is the dimensionless thermal conductivity of the crack surface [55,56,57,58], \(V=0\) corresponds to complete thermal insulation and \(V\rightarrow \infty \) corresponds to complete thermal conduction.

Introducing the dimensionless variables:

$$\begin{aligned} \overline{T} =(T-T_1 )/(T_0 -T_1 ), \;\overline{t} =t/(c^{2}/a),\,\, (\overline{x} ,\overline{y} ,\overline{h} )=(x,y,h)/c, \;\overline{\tau } =\tau _q /(c^{2}/a), \end{aligned}$$
(7)

the dimensionless governing equation becomes

$$\begin{aligned} \nabla ^{2}T=\frac{\partial T}{\partial t}+\frac{\tau ^{\alpha }}{\alpha !}\frac{\partial ^{1+\alpha }T}{\partial t^{1+\alpha }}. \end{aligned}$$
(8)

Hereafter, the hats of the dimensionless variables are omitted for simplicity. The dimensionless initial and boundary conditions of the temperature field are:

$$\begin{aligned} \begin{aligned} T&=0, \;\frac{\partial T}{\partial t}=0, \;(t=0), \\ T(x,-h)&=1, \;(t>0,\left| x \right| <\infty ), \\ T&=0, \;(y\rightarrow \infty ), \\ \frac{\partial T}{\partial y}&=V[T(x,0^{+})-T(x,0^{-})], \;(y=0,\left| x \right| \le 1), \\ T(x,0^{+})&=T(x,0^{-}), \;(\left| x \right|>1), \\ \frac{\partial T(x,0^{+})}{\partial y}&=\frac{\partial T(x,0^{-})}{\partial y}, \;(\left| x \right| >1). \\ \end{aligned} \end{aligned}$$
(9)

2.2 Viscoelastic stress field

In this article, the thermo-viscoelastic problem under plane stress condition is considered. Thus, \(\sigma _{zz} =\sigma _{zx} =\sigma _{zy} =0\). The equilibrium equation is \(\sigma _{ij,j} =0\), strain-displacement relationship is \(\varepsilon _{ij} =\frac{1}{2}(u_{i,j} +u_{j,i} )\), and the two-dimensional compatibility equation is:

$$\begin{aligned} \frac{\partial ^{2}\varepsilon _x }{\partial y^{2}}+\;\frac{\partial ^{2}\varepsilon _y }{\partial x^{2}}=2\frac{\partial ^{2}\varepsilon _{xy} }{\partial x\partial y}. \end{aligned}$$
(10)

Unlike the classical elasticity, the constitutive law of viscoelasticity [59] reads:

$$\begin{aligned} \begin{aligned} s_{ij}&=\int \limits _0^t {G_1 (X,t-\tau )} \frac{{\mathrm{d}}e_{ij} }{{\mathrm{d}}\tau }{\mathrm{d}}\tau , \\ \sigma _{kk}&=\int \limits _0^t {G_2 (X,t-\tau )} \frac{{\mathrm{d}}\varepsilon _{kk} }{{\mathrm{d}}\tau }{\mathrm{d}}\tau -3\int \limits _0^t {\varphi (X,t-\tau )} \frac{{\mathrm{d}}T}{{\mathrm{d}}\tau }{\mathrm{d}}\tau \\ \end{aligned} \end{aligned}$$
(11)

with

$$\begin{aligned} s_{ij} =\sigma _{ij} -\frac{1}{3}\sigma _{kk} \delta _{ij,} \;\;e_{ij} =\varepsilon _{ij} -\frac{1}{3}\varepsilon _{kk} \delta _{ij}, \end{aligned}$$

where \(s_{ij} \) and \(e_{ij} \) are deviatoric components of the stress and strain tensors, \(G_1 (X,t)\) and \(G_2 (X,t)\) are the shear and the bulk relaxation functions and \(\varphi (X,t)\) is the thermal relaxation function. To avoid the convolution in the above equation and eliminate the time dependency, the Laplace transform is employed:

$$\begin{aligned} \begin{aligned} f^{*}(X,p)&=\int \limits _0^\infty {f(X,t)\exp (-pt){\mathrm{d}}t}, \\ f(X,t)&=\frac{1}{2\pi i}\int \limits _{Br} {f^{*}(X,p)\exp (pt){\mathrm{d}}p}, \\ \end{aligned} \end{aligned}$$
(12)

where p is the Laplace transform variable, the superscript “*” denotes the variables in the Laplace domain and “Br” stands for the Bromwich path. Considering the following relationship [54, 59] in the Laplace domain:

$$\begin{aligned} G_1 ^{*}=\frac{E^{*}}{1+p\upsilon ^{*}},\,\, G_2 ^{*}=\frac{E^{*}}{1-2p\upsilon ^{*}}, \;\varphi ^{*}=pG_2 ^{*}\lambda ^{*}, \end{aligned}$$
(13)

the above constitutive equations can be reduced to:

$$\begin{aligned} \begin{aligned} \varepsilon _x ^{*}&=\frac{1}{pE^{*}}(\sigma _x ^{*}-p\upsilon ^{*}\sigma _y ^{*})+p\lambda ^{*}T^{*},\\ \varepsilon _y ^{*}&=\frac{1}{pE^{*}}(\sigma _y ^{*}-p\upsilon ^{*}\sigma _x ^{*})+p\lambda ^{*}T^{*},\\ \varepsilon _{xy} ^{*}&=\frac{1+p\upsilon ^{*}}{pE^{*}}\sigma _{xy} ^{*}. \\ \end{aligned} \end{aligned}$$
(14)

Coupled with the time-dependent material properties from Eq. (1), we have

$$\begin{aligned} \begin{aligned}&\frac{\partial u^{*}}{\partial x}=\frac{1}{pE_0 f_1 (p)}[\sigma _x ^{*}-p\upsilon _0 f_2 (p)\sigma _y ^{*}]+p\alpha _0 f_3 (p)T^{*}, \\&\frac{\partial v^{*}}{\partial y}=\frac{1}{pE_0 f_1 (p)}[\sigma _y ^{*}-p\upsilon _0 f_2 (p)\sigma _x ^{*}]+p\alpha _0 f_3 (p)T^{*}, \\&\frac{\partial u^{*}}{\partial y}+\frac{\partial v^{*}}{\partial x}=\frac{2(1+p\upsilon _0 f_2 (p))}{pE_0 f_1 (p)}\sigma _{xy} ^{*}, \\ \end{aligned} \end{aligned}$$
(15)

where \(f_i (p)\;(i=1,2,3)\) is the Laplace transform of \(f_i (t)\;(i=1,2,3)\).

Introducing the Airy stress function in the Laplace domain \(U^{*}\), the stresses can be expressed as

$$\begin{aligned} \sigma _x ^{*}=\frac{\partial ^{2}U^{*}}{\partial y^{2}},\,\, \sigma _y ^{*}=\frac{\partial ^{2}U^{*}}{\partial x^{2}},\,\, \sigma _{xy} ^{*}=-\frac{\partial ^{2}U^{*}}{\partial x\partial y}. \end{aligned}$$
(16)

Substitute the above equations into the strain compatibility equation, the governing equation is obtained:

$$\begin{aligned} \nabla ^{2}\nabla ^{2}U^{*}+E_0 \lambda _0 p^{2}f_1 (p)f_3 (p)\nabla ^{2}T^{*}=0. \end{aligned}$$
(17)

Let us introduce the following dimensionless variables:

$$\begin{aligned} \begin{aligned} \overline{\sigma _{ij} } ^{*}&=\sigma _{ij} ^{*}/(E_0 \lambda _0 T_0 ), \;\overline{U} ^{*}=U^{*}/(E_0 \lambda _0 T_0 c^{2}),\\ (\overline{u} ^{*},\overline{v} ^{*})&=(u^{*},v^{*})/(c\lambda _0 T_0 ), \;\overline{\varepsilon _{ij} } ^{*}=\varepsilon _{ij} ^{*}/(\lambda _0T_0 ). \\ \end{aligned} \end{aligned}$$
(18)

The above equations can be further reduced to:

$$\begin{aligned} \nabla ^{2}\nabla ^{2}U^{*}+p^{2}f_1 (p)f_3 (p)\nabla ^{2}T^{*}=0, \end{aligned}$$
(19)

and

$$\begin{aligned} \begin{aligned}&\frac{\partial u^{*}}{\partial x}=\frac{1}{pf_1 (p)}[\sigma _x ^{*}-p\upsilon _0 f_2 (p)\sigma _y ^{*}]+pf_3 (p)T^{*}, \\&\frac{\partial v^{*}}{\partial y}=\frac{1}{pf_1 (p)}[\sigma _y ^{*}-p\upsilon _0 f_2 (p)\sigma _x ^{*}]+pf_3 (p)T^{*}, \\&\frac{\partial u^{*}}{\partial y}+\frac{\partial v^{*}}{\partial x}=\frac{2(1+p\upsilon _0 f_2 (p))}{pf_1 (p)}\sigma _{xy} ^{*}. \\ \end{aligned} \end{aligned}$$
(20)

Similarly, the hats of the dimensionless variables are omitted for simplicity.

In this problem, the mechanical boundary conditions in both the time domain and Laplace domain can be expressed as:

$$\begin{aligned} \begin{aligned} \sigma _{xy} (x,-h)&=\sigma _y (x,-h)=0, \;(\left| x \right| <\infty ), \\ \sigma _{xy} (x,0)&=\sigma _y (x,0)=0, \;(\left| x \right| \le 1), \\ \sigma _{xy} (x,0^{+})&=\sigma _{xy} (x,0^{-}), \;\;(\left| x \right|>1), \\ \sigma _y (x,0^{+})&=\sigma _y (x,0^{-}), \;\;(\left| x \right|>1), \\ u(x,0^{+})&=u(x,0^{-}), \;\;\;(\left| x \right|>1), \\ v(x,0^{+})&=v(x,0^{-}), \;\;\;(\left| x \right| >1). \\ \end{aligned} \end{aligned}$$
(21)

3 Solution of the temperature field

Considering the zero initial conditions, application of the Laplace transform to the governing equation (8) leads to

$$\begin{aligned} \nabla ^{2}T^{*}=pT^{*}+\frac{\tau ^{\alpha }}{\alpha !}p^{1+\alpha }T^{*}, \end{aligned}$$
(22)

and the boundary conditions in the Laplace domain are:

$$\begin{aligned} \begin{aligned} T^{*}(x,-h)&=1/p, \;(\left| x \right| <\infty ), \\ T^{*}&=0, \;(y\rightarrow \infty ), \\ \frac{\partial T^{*}}{\partial y}&=V[T(x,0^{+})-T(x,0^{-})], \;(y=0,\left| x \right| \le 1), \\ T^{*}(x,0^{+})&=T^{*}(x,0^{-}), \;(\left| x \right|>1), \\ \frac{\partial T^{*}(x,0^{+})}{\partial y}&=\frac{\partial T^{*}(x,0^{-})}{\partial y}, \;(\left| x \right| >1).\\ \end{aligned} \end{aligned}$$
(23)

To solve the PDE (22) subjected to (23), after employing Fourier transform, the solution of the temperature field in the Laplace domain is:

$$\begin{aligned} \begin{aligned} T^{*}(x,y,p)&=\int \limits _{-\infty }^\infty {D(\xi ,p)} \exp (-my-ix\xi ){\mathrm{d}}\xi +\frac{1}{p}\exp (-q(y+h)),\;\;\;\;y>0, \\ T^{*}(x,y,p)&=\int \limits _{-\infty }^\infty {\frac{-D(\xi ,p)}{1+\exp (-2mh)}\left\{ {\exp (my)-\exp [-m(2h+y)]} \right\} } \exp (-ix\xi ){\mathrm{d}}\xi \\&\quad +\,\frac{1}{p}\exp (-q(y+h)),\qquad y<0, \\ \end{aligned} \end{aligned}$$
(24)

where \(m=\sqrt{p+\xi ^{2}+\frac{\tau ^{\alpha }}{\alpha !}p^{1+\alpha }}\), \(q=\sqrt{p+\frac{\tau ^{\alpha }}{\alpha !}p^{1+\alpha }}\), \(\xi \) is the Fourier transform variable and \(D(\xi ,p)\) is unknown, it will be determined by the following density function:

$$\begin{aligned} \phi ^{*}(x,p)=\frac{\partial T^{*}(x,0^{+},p)}{\partial x}-\frac{\partial T^{*}(x,0^{-},p)}{\partial x}. \end{aligned}$$
(25)

Substituting Eqs. (24) into (25) and applying the inverse Fourier transform, one gets

$$\begin{aligned} D(\xi ,p)=\frac{i[1+\exp (-2mh)]}{4\pi \xi }\int \limits _{-1}^1 {\phi ^{*}(\tau ,p)\exp (i\xi \tau ){\mathrm{d}}} \tau . \end{aligned}$$
(26)

From the continuity condition in the boundary conditions, it is clear that

$$\begin{aligned} \begin{aligned}&\int \limits _{-1}^1 {\phi ^{*}(x,p){\mathrm{d}}x=0}, \\&\phi ^{*}(x,p)=0, \;(\left| x \right| >1). \\ \end{aligned} \end{aligned}$$
(27)

Then substituting Eq. (24) into the boundary conditions on crack faces, with the aid of Eq. (26), the following singular integral equation is obtained:

$$\begin{aligned} \int \limits _{-1}^1 {\phi ^{*}(\tau ,p)} \left[ \frac{1}{\tau -x}+k^{*}(x,\tau ,p)\right] {\mathrm{d}}\tau =\frac{2\pi q}{p}\exp (-qh), \;\;\;\;\left| x \right| \le 1, \end{aligned}$$
(28)

and the kernel function reads:

$$\begin{aligned} k^{*}(x,\tau ,p)=\int \limits _0^\infty {\left\{ {1-\frac{m[1+\exp (-2mh)]+2V}{\xi }} \right\} } \sin [(x-\tau )\xi ]{\mathrm{d}}\xi . \end{aligned}$$
(29)

In order to solve Eqs. (27) and (28), the numerical technique in [60] is employed such that the following algebraic equations are obtained:

$$\begin{aligned}&\sum _{k=1}^n {\frac{1}{n}F^{*}(\tau _k ,p)} \left[ \frac{1}{\tau _k -x_r }+k^{*}(x_r ,\tau _k ,p)\right] =\frac{2\pi q}{p}\exp (-qh), \;\;\;\;\left| x \right| \le 1, \end{aligned}$$
(30)
$$\begin{aligned}&\sum _{k=1}^n {\frac{\pi }{n}} F^{*}(\tau _k ,p)=0, \end{aligned}$$
(31)

where \(\tau _k =\cos \frac{(2k-1)\pi }{2n}, k=1,2,\ldots ,n\); \(x_r =\cos \frac{r\pi }{n}, r=1,2,\ldots ,n-1\), and

$$\begin{aligned} F^{*}(x,p)=\frac{\phi ^{*}(x,p)}{\sqrt{1-x^{2}}}, \;\left| x \right| \le 1. \end{aligned}$$
(32)

Once the above algebraic equations are solved, the inverse Laplace transform of (12) can be performed, and the temperature field in the time domain can be obtained.

4 Solution of the stress field

As mentioned above, the uncoupled, thermo-viscoelastic theory is adopted in the present work. Only the temperature field will affect the stress field, but not vice versa. To avoid the violation of the second law of thermodynamics, the fractional single-phase lag heat conduction theory has been employed to give a more accurate temperature distribution, especially around the cracks. Whether a more accurate thermal stress field and transient fracture behavior will be predicted by the fractional heat conduction theory, will be the focus of this research. In Sect. 3, the temperature field has been determined, so the next step is to investigate the stress field via the following equation:

$$\begin{aligned} \nabla ^{2}\nabla ^{2}U^{*}=-p^{2}f_1 (p)f_3 (p)\nabla ^{2}T^{*}. \end{aligned}$$
(33)

Application of the Fourier transform to Eq. (33) leads to

$$\begin{aligned} \begin{aligned} U^{*}(x,y,p)&=\int \limits _{-\infty }^\infty {(B_1 +B_2 y)\exp (-\left| \xi \right| y-ix\xi )} {\mathrm{d}}\xi -\int \limits _{-\infty }^\infty {C_1 \exp (-my-ix\xi )} {\mathrm{d}}\xi , \\&\quad \,\, y>0 \\ U^{*}(x,y,p)&=\int \limits _{-\infty }^\infty {\{(A_1 +A_2 y)\exp (\left| \xi \right| y)+(A_3 +A_4 y)\exp (-\left| \xi \right| y)\}\exp (-ix\xi )} {\mathrm{d}}\xi \\&\quad -\int \limits _{-\infty }^\infty {\{C_{21} \exp (my)+\left. {C_{22} \exp (-my)} \right\} \exp (-ix\xi )} {\mathrm{d}}\xi ,\qquad y<0,\\ \end{aligned} \end{aligned}$$
(34)

where \(A_1 , A_{2,} A_3 , A_{4, } B_1 , B_2 \) are determined by the mechanical boundary conditions (21). \(C_1 ,C_{21} ,C_{22} \) can be obtained by the particular solution corresponding to the temperature field, as shown in Appendix. Incorporating the dimensionless constitutive Eq. (20) into the relating boundary conditions, the jumps of the displacement components in the Laplace domain at the line \(y=0\) are

$$\begin{aligned} \begin{aligned} \frac{\partial [u^{*}]}{\partial x}&=\frac{1}{pf_1 (p)}[\sigma _x ^{*}]+pf_3 (p)[T^{*}], \\ \frac{\partial ^{2}[v^{*}]}{\partial x^{2}}&=-\frac{1}{pf_1 (p)}\left[ \frac{\partial }{\partial y}\sigma _y ^{*}\right] . \\ \end{aligned} \end{aligned}$$
(35)

The stress components \(\sigma _x ^{*},\sigma _y ^{*},\sigma _{xy} ^{*}\) can be obtained from the Airy stress function via Eq. (16). Substituting the stresses and the temperature jump into the above Eq. (35), we have

$$\begin{aligned} \begin{aligned} \frac{\partial [u^{*}]}{\partial x}&=\int \limits _{-\infty }^\infty {\frac{1}{pf_1 (p)}} \left\{ {\begin{array}{l} -2\left| \xi \right| (B_2 -A_4 )+\xi ^{2}(B_1 -A_3 )+(-2\left| \xi \right| A_2 -\xi ^{2}A_1 )+ \\ m^{2}C_{21} +m^{2}(C_{22} -C_1 ) \\ \end{array}} \right\} \exp (-ix\xi ){\mathrm{d}}\xi \\&\quad +\int \limits _{-\infty }^\infty {pf_3 (p)D(\xi )} \frac{2}{1+e^{-2mh}}\exp (-ix\xi ){\mathrm{d}}\xi , \\ \frac{\partial [v^{*}]}{\partial x}&=\int \limits _{-\infty }^\infty {\left( -\frac{i}{\xi }\right) \frac{1}{pf_1 (p)}} \left\{ {\begin{array}{l} -(\beta +\left| \xi \right| )[\xi ^{2}(B_1 -A_3 )-2\left| \xi \right| (B_2 -A_4 )]+\xi ^{2}(B_2 -A_4 ) \\ +(\beta -\left| \xi \right| )(2\left| \xi \right| A_2 +\xi ^{2}A_1 )-\xi ^{2}A_2 +m^{3}C_{21} -m^{3}(C_{22} -C_1 ) \\ \end{array}} \right\} \exp (-ix\xi ){\mathrm{d}}\xi \\&\quad +\int \limits _{-\infty }^\infty {\left( -\frac{i}{\xi }\right) pf_3 (p)D(\xi )} \frac{2}{1+e^{-2mh}}\exp (-ix\xi ){\mathrm{d}}\xi . \\ \end{aligned} \end{aligned}$$
(36)

Now we introduce two dislocation density functions:

$$\begin{aligned} \psi _1 ^{*}\left( {x,p} \right) =\frac{\partial [u^{*}\left( {x,p} \right) ]}{\partial x}, \;\;\;\;\psi _2 ^{*}\left( {x,p} \right) =\frac{\partial [v^{*}\left( {x,p} \right) ]}{\partial x}. \end{aligned}$$
(37)

By applying the mechanical boundary conditions on crack faces via Eq. (21), the following singular integral equations can be derived:

$$\begin{aligned} \int \limits _{-1}^1 \sum _{j=1}^2 \left[ \frac{\delta _{ij} }{\tau -x} +k_{ij} (x,\tau )\right] \psi _j ^{*}(\tau ,p){\mathrm{d}}\tau =4\pi pf_3 (p)W_i ^{*}(x,p), \;i=1,2, \;\;\;\;-1\le x\le 1 \end{aligned}$$
(38)

with

$$\begin{aligned} \int \limits _{-1}^1 \psi _i ^{*}(x,p){\mathrm{d}}x=0, \;\;\;i=1,2, \end{aligned}$$
(39)

where the expressions of \(k_{ij} (x,\tau ), W_i ^{*}(x,p)\) can be found in the Appendix. To solve the singular integral equations, the Lobatto–Chebyshev method [61] is employed and Eqs. (39) and (39) are transformed to algebraic equations:

$$\begin{aligned} \begin{aligned}&\sum _{i=1}^n {A_i \left[ \frac{1}{\tau _i -x_k }+k_{11} (x_k ,\tau _i )\right] } F_1 ^{*}(\tau _i ,p)+\sum _{i=1}^n {A_i k_{12} (x_k ,\tau _i )} F_2 ^{*}(\tau _i ,p)=4\pi pf_3 (p)W_1 ^{*}(x_k ,p), \\&\sum _{i=1}^n {A_i } F_1 ^{*}(\tau _i ,p)=0, \\&\sum _{i=1}^n {A_i k_{21} (x_k ,\tau _i )} F_1 ^{*}(\tau _i ,p)+\sum _{i=1}^n {A_i \left[ \frac{1}{\tau _i -x_k }+k_{22} (x_k ,\tau _i )\right] } F_2 ^{*}(\tau _i ,p)=4\pi pf_3 (p)W_2 ^{*}(x_k ,p), \\&\sum _{i=1}^n {A_i } F_2 ^{*}(\tau _i ,p)=0, \\ \end{aligned} \end{aligned}$$
(40)

where

$$\begin{aligned} \psi _i ^{*}(\tau ,p)= & {} \frac{F_i ^{*}(\tau ,p)}{\sqrt{1-\tau ^{2}}}, \;(i=1, 2), \left| \tau \right| \le 1, \end{aligned}$$
(41)
$$\begin{aligned} \tau _i= & {} \cos \frac{(i-1)\pi }{n-1}, \;i=1,2,\ldots n; \nonumber \\ x_k= & {} \cos \frac{(2k-1)\pi }{2(n-1)}, \;k=1,2,\ldots n-1; \nonumber \\ A_i= & {} \frac{\pi }{2(n-1)},\,\, i=1,n;\;\;A_i =\frac{\pi }{n-1}, \,\,i=2,3,\ldots n-1. \end{aligned}$$
(42)

According to the literature [14, 30], the stress intensity factors (SIFs) in the Laplace domain are defined as:

$$\begin{aligned} K_I ^{*}=-\frac{\pi }{4}F_2 ^{*}(1,p), K_{II} ^{*}=-\frac{\pi }{4}F_1 ^{*}(1,p). \end{aligned}$$
(43)

5 Numerical results and discussions

In Sects. 3 and 4, the theoretical solutions of dynamic temperature field and the transient stress intensity factors in the Laplace domain have been obtained by solving the singular integral equations. To get the corresponding results in the time domain, the numerical Laplace inversion technique from [62] is employed.

Fig. 2
figure 2

Dimensionless temperature distributions on crack faces and the extension line under the influence of fractional order \(\alpha \) when \(\tau =0.5\) at different time instants a\(t =0.5\); b\( t =1\); c\(t =2\); d\(t=5\)

Full size image

To begin with, the temperature distribution around the crack is shown in Fig. 2. Here, we assume the crack to be completely thermally insulated, i.e., \(V=0\). The dimensionless transient temperature distributions on the crack faces and crack extension line are investigated under the fractional single-phase lag heat conduction theory. When \(\tau =0.5\), the influence of the fractional order \(\alpha \) is shown at four time instants \(t=0.5, 1, 2, 5\), respectively. “UF” denotes the upper crack face, while “LF” denotes the lower crack face. As expected, obvious temperature jumps are observed for all time instants and all fractional orders. With increasing time, the temperature jumps increase at first and then decrease. The largest temperature jump occurs in Fig. 2c at a dimensionless time \(t=2\).

Actually, \(\alpha =1\) corresponds to conventional hyperbolic heat conduction, which leads to the unphysical negative temperature distribution as shown in [30, 31]. This can be confirmed in Fig. 2a. The red lines show that the temperatures on both crack faces and the crack extension line are negative. Because there is no negative temperature in both the initial condition and the external thermal loading, the appearance of negative temperature implies heat flow from cold to hot regions around the crack, which violates the second law of thermodynamics. Another unphysical phenomenon is that the temperature of the upper crack face is higher than that of the lower crack face. The thermal shock is applied at the free surface, as shown in Fig. 1; the lower crack face would be heated at first and the temperature should be always higher than the upper face. Interestingly, when \(\alpha \) is reduced to 0.8 or 0.5, these unphysical phenomena disappear. It is noted that the main difference between the conventional and fractional single-phase lag heat conduction theories happens at the early stage under the thermal shock, as seen in Figs. 2a, b. In Figs. 2c, d, the difference of temperature distributions under different fractional differential orders diminishes with elapsing time.

To further confirm the advantages of the fractional single-phase lag heat conduction theory, the temperature variations of the midpoints of the crack faces versus dimensionless time are shown in Figs. 3, 4 and 5. Similarly, “UF” denotes the midpoint of the upper crack face, while “LF” denotes the midpoint of the lower crack face. “Fourier” corresponds to the classical Fourier law via setting the dimensionless thermal relaxation time to zero. Figure 3 corresponds to the conventional hyperbolic heat conduction theory, where the non-Fourier effect brings a wave-like oscillation in the temperature history. The magnitude of the oscillation will increase with increasing \(\tau \). When \(\tau =5\), very serious temperature overshooting happens, i.e., the maximum of the temperature is much higher than the external thermal loading. Another important feature is the unphysical negative temperature in the early stage. Both the serious overshooting and negative temperatures are caused by the significant wave-like behaviors, which is the relaxation features in conventional hyperbolic theory. As shown in the definition by Eq. (44), the fractional calculus introduces a memory effect and indicates that the current state of heat conduction depends on its historical states. The memory effect is determined by the kernel function \(K(t-\tau )=\frac{(t-\tau )^{-\alpha }}{\Gamma (1-\alpha )}\), while the classical Fourier law can be regarded as “instantaneous memory” with the kernel being Dirac’s delta:

$$\begin{aligned} \frac{\partial ^{\alpha }q}{\partial t^{\alpha }}=\int \limits _0^t {K(t-\tau )\frac{\partial q}{\partial \tau }{\mathrm{d}}\tau } =\int \limits _0^t {\frac{(t-\tau )^{-\alpha }}{\Gamma (1-\alpha )}\frac{\partial q}{\partial \tau }{\mathrm{d}}\tau ,\,\, 0<\alpha <1}. \end{aligned}$$
(44)
Fig. 3
figure 3

The effect of dimensionless thermal relaxation time \(\tau \) on the temperature variation of midpoints of crack faces when fractional order \(\alpha =1\)

Full size image
Fig. 4
figure 4

The effect of dimensionless thermal relaxation time \(\tau \) on the temperature variation of midpoints of crack faces when fractional order \(\alpha =0.8\)

Full size image
Fig. 5
figure 5

The effect of dimensionless thermal relaxation time \(\tau \) on the temperature variation of midpoints of crack faces when fractional order \(\alpha =0.5\)

Full size image

The fractional model’s advantage is the consideration of not only the inherent relaxation characteristic and the wave-like behavior of the conventional hyperbolic model but also the characteristic of the classical Fourier heat conduction. It is noted that wave-like behaviors would disappear when the fractional order is reduced from 1 to 0. Therefore, the significant overshooting and negative temperatures in the early stage are weakened with decreasing fractional order \(\alpha \), as shown in Figs. 4 and 5. When \(\alpha \) is reduced to 0.5, all negative temperatures disappear and there exists only slight temperature overshooting. In addition, with increasing time, the temperature reaches the steady state for different values of \(\tau \). We believe these features are caused by the memory effect. All results demonstrate that the fractional single-phase lag model would be more accurate and more reasonable in predicting the temperature field than the conventional one. Moreover, it should be noticed that the transient temperature would take longer to reach the peak value for smaller fractional order.

Fig. 6
figure 6

The effect of different thermal conductivity V on the temperature distributions around the crack in the steady state when \(\alpha =0.5, \tau =0.5\)

Full size image

The influence of the dimensionless thermal conductivity V of the crack faces on the temperature distributions around the crack is investigated for the steady state, as shown in Fig. 6. From Fig. 5, when \(\alpha =0.5\), the steady-state value of temperature is hardly disturbed by the thermal relaxation time. Here, \(\alpha =0.5, \tau =0.5\) is selected for the graphical comparison here. It is noted that the temperature jumps are declining, and the temperatures of the crack extension line are rising, when V increases from zero to infinity. When V approaches infinity, the crack is completely thermally conducting and the temperature distribution shows no disturbance of the crack.

Then, let us consider the transient fracture behavior of viscoelastic material using the fractional heat conduction theory. Unlike elastic materials, viscoelastic materials always have significant creep or stress relaxation behavior, which will affect the stress intensity factors directly. The fractional single-phase lag theory predicts a more accurate and reasonable temperature field as the preceding figures show. Now, we will further verify that it will also predict more accurately the thermo-mechanical fracture behavior.

As mentioned in Eq. (1), three different relaxation functions of material properties are assumed for viscoelasticity. However, from the theoretical results (see Eq. (40)), it can be found that only \(f_3 (t)\), i.e., the relaxation function of thermal expansion coefficient, will affect the SIFs. The physical explanation is that these relaxation functions are assumed to be independent of spatial coordinates. The stresses can be treated as the sum of mechanical stresses and thermal stresses. The mechanical stresses in the plane will relax at the same speed according to \(f_1 (t),f_2 (t)\), while the thermal stresses are determined by \(f_3 (t)\) as well as the change of temperature, \(\delta T\), which is dependent on the spatial positions. This will be further verified by our future work via considering the space-dependent relaxation functions [63]. In this article, the classical form of viscoelastic relaxation function [53] is assumed as \(f_3 (t)=(\frac{\lambda _\infty }{\lambda _0 }+(1-\frac{\lambda _\infty }{\lambda _0 })e^{-\frac{t}{t_0 }})\), with \(\frac{\lambda _\infty }{\lambda _0 }=0.5, t_0 =1\). In the following analysis, the crack is assumed to be perfectly thermally insulated.

Fig. 7
figure 7

Comparison of SIFs in viscoelastic and elastic materials under the classical Fourier’s Law

Full size image
Fig. 8
figure 8

The effect of dimensionless thermal relaxation time \(\tau \) on the SIFs a\(K_I \) and b\(K_{II} \) when the fractional order \(\alpha =1\)

Full size image

From the previous reports [30, 31], the hyperbolic heat conduction will bring wave-like oscillation to both temperature field and SIFs. To give a clear comparison of the fracture behavior between elastic materials and viscoelastic materials under thermal shock, the classical Fourier heat conduction theory is used when \(\tau =0\). The elastic solution is obtained by setting \(f_3 (t)=1\). An obvious difference can be observed in Fig. 7. \(K_I \) in both materials are positive; nevertheless, \(K_{II} \) are negative with a much larger magnitude, indicating that mode II fracture always plays a dominant role. For elastic materials, the SIFs increase at first and then decrease slowly. However, the SIFs of viscoelastic materials will reach their peak value in a short period and then drop sharply. In addition, the peak value of \(K_{II} \) for viscoelastic materials is higher than that for elastic materials.

When \(\alpha =1\), the fractional heat conduction theory is reduced to the conventional hyperbolic theory, and the influence of the thermal relaxation time on the SIFs in viscoelastic materials is shown in Fig. 8. As expected, significant wave-like oscillations can be observed, and the magnitudes of the oscillation increase with higher thermal relaxation time, which should be a major concern in the application of viscoelastic composites with complex inner structures. However, as Fig. 8 shows, the SIFs can be quite high even when \(t=30\), which is unphysical due to the fact that the modulus of a viscoelastic material will drop to a very low value with enough time elapsed. Fortunately, this unphysical phenomenon can be eliminated with the application of fractional theory, as shown in Figs. 9 and 10. Similar to the temperature results, the fractional calculus shows a pronounced memory effect. With a decrease in the fractional order \(\alpha \), the complex, wave-like oscillations are reduced significantly. When \(t=30\), a steady-state value approaching zero appears for both SIFs after sufficient time for \(\alpha =0.5\). These results verify the accuracy of the fractional single-phase lag heat conduction compared to the conventional one. In addition, different thermal relaxation times exhibit no dramatic influence on the peak values of SIFs. The SIFs always show a quite sharp pulse at the early stage under thermal shock for viscoelastic composites, which should be carefully considered in designing these materials for thermal loading.

Fig. 9
figure 9

The effect of dimensionless thermal relaxation time \(\tau \) on the SIFs a\(K_I \) and b\(K_{II} \) when the fractional order \(\alpha =0.8\)

Full size image
Fig. 10
figure 10

The effect of dimensionless thermal relaxation time \(\tau \) on the SIFs a\(K_I \) and b\(K_{II} \) when the fractional order \(\alpha =0.5\)

Full size image

6 Conclusion

In this article, we firstly extend the non-Fourier heat conduction law to the crack problem of a half-plane under thermal shock within the framework of thermo-viscoelasticity. The fractional single-phase lag heat conduction theory is employed to avoid the unphysical effects associated with the conventional hyperbolic heat conduction. The governing PDEs of the problem are solved by employing the Fourier and Laplace transform, along with the singular integral equations. Finally, we found that the fractional single-phase lag heat conduction has a very good performance in predicting both temperature distribution around cracks and the transient fracture behaviors considering the viscoelastic material properties. As the fractional factor, \(\alpha \), decreases, the negative temperature predicted by the hyperbolic heat conduction disappears. Finally, a sharp pulse of the SIFs at the early stage under thermal shock is observed, which reveals that the fracture risk due to this overshooting needs to be carefully consider in the design and application of viscoelastic composites.