A fracture energy–based viscoelastic–viscoplastic–anisotropic damage model for rate-dependent cracking of concrete

Abstract

A fracture energy-based constitutive model of concrete in the framework of continuum damage mechanics is formulated. Elastic, viscoelastic, and viscoplastic mechanisms are defined in a fictitious undamaged material state, the so-called effective configuration. A linear spring and a linear dashpot characterize the viscoelastic response of concrete. The viscoplastic behavior is also described using a linear spring, a nonlinear dashpot, and a slider with constant frictional resistance. The nonlinear dashpot of the viscoplastic body is formulated using a logarithmic function so that the model can reproduce valid strength magnifications under a wide range of strain rates. As a result, a consistency viscoplastic approach is obtained wherein, in contrast to the so-called overstress viscoplastic laws, the rate effects are induced in the yield surface of the model. A fracture energy-based regularization is employed to adjust the rate of damage growth to obtain mesh-objective results. The directional degradation of concrete is also characterized by a frame-independent tensorial description of damage. Next, a fully implicit return-mapping algorithm based on the Newton–Raphson scheme is proposed. The presented model is then assessed by validating its results with a series of experimental tests. In addition, the mixed-mode fracture of concrete is investigated under different strain rates, verifying the experimentally observed transition of the failure mode from a ductile flexural to a brittle diagonal failure.

1 Introduction

Dissipative mechanisms can occur in solids even when they undergo reversible infinitesimal deformations. In isothermal conditions, those dissipations can be linked to a time-dependent response wherein the deformations are reversible, yet they require time to disappear completely. The inelastic response of solids is also a time-dependent phenomenon. The inertia effects in their microstructure redistribute the stress more uniformly, reducing the stress concentration around the voids and defects. Besides the time-dependent reversible and irreversible deformations, the growth of micro-voids and micro-cracks is another dissipative mechanism in solids, which has more prominent effects when quasi-brittle materials are of interest. This material degradation is anisotropic in nature, meaning that different magnitudes of damage can occur on different planes.

The simultaneous incorporation of viscoelastic, viscoplastic, and damage-growth mechanisms in formulating the mechanical behavior of quasi-brittle solids has been pursued infrequently. Sercombe et al. (1998) proposed a constitutive model using a rate-dependent Rankine-type yield criterion, yet they did not consider the material degradation. Bažant et al. (2000b) formulated a material model based on the microplane theory wherein the viscoelastic response of concrete is resembled using the Maxwell configuration. Gatuingt and Pijaudier-Cabot (2002) reproduced the viscoplastic response of concrete using the Gurson-type criterion of Needleman and Tvergaard (1984). Employing a dynamic elastic modulus in conjunction with a rate-dependent measure of elastic strain energy, Lu and Xu (2004) simulated the dynamic behavior of concrete under different strain rates. Pedersen et al. (2008) utilized the Perzyna overstress model (Perzyna 1971) for considering the viscous hardening pertaining to the Stefan effect (Peschel 1968). They used a simple isotropic formulation to resemble the uniaxial response of concrete in tension and disregarded the effects of unilateral contact.

Concrete shows different responses in tension and compression. This aspect of its behavior hinders describing a smooth admissible elastic limit in the three-dimensional Haigh–Westergaard stress space. Instead of the Lode angle, Lubliner et al. (1989) defined the yield surface of their model using the maximum principal stresses and streamlined the identification of the concrete inelastic response. Lee and Fenves (1998) introduced two damage internal variables to the formulation of Lubliner et al. (1989) and resembled the unilateral effects. Employing the orthogonal projection of Ortiz (1985), Wu et al. (2006) used one damage index for the tensile part of stress and one for its compressive part. Instead of defining different magnitudes of damage in tension and compression, Grassl and Jirásek (2006) used a scalar damage index for both parts. A strain-based damage evolution law was employed by Häussler-Combe and Hartig (2008) for characterizing the distribution of microscopic defects. However, they used the elastic strain tensor for defining the damage indices of their model. Červenka and Papanikolaou (2008) used the smeared crack approach for resembling the tensile behavior of concrete, while the compressive response was governed by the theory of plasticity. Employing damage dissipation potential functions, Cicekli et al. (2007); Voyiadjis et al. (2008) assembled anisotropic damage tensors for the tensile and compressive parts of stress. Grassl et al. (2013) formulated a damage-plastic model by defining an isotopic damage index for each tensile and compressive part. Brünig and Michalski (2017) proposed a constitutive model by utilizing the additive decomposition of the strain tensor. They used the concept of yield surface along with a non-associative flow rule to describe the rate of damage growth. Daneshyar and Ghaemian (2017) proposed a microplane-based plastic-damage formulation. By defining an independent damage internal variable in every possible direction, they assembled fully anisotropic damage tensors for the tensile and compressive parts of stress. All the mentioned works were focused on formulating the concrete behavior in the absence of the rate effects. However, concrete shows rate-dependent responses in both reversible and irreversible regimes. The former manifests itself in stiffness magnification as well as hysteresis loops, and the latter causes strength amplification. These two mechanisms must be included in the concrete response if one is to formulate a constitutive model for general loading conditions.

Similar to concrete, asphalt materials exhibit a rate-dependent response at all deformation stages. Despite their complex heterogeneous mesostructure, phenomenological approaches have been widely used for predicting the mechanical behavior of asphalt concrete since those approaches can be efficiently utilized for practical purposes. In an early attempt toward the continuum modeling of asphalt concrete, Sides et al. (1985) decomposed the strain tensor into elastic, plastic, viscoelastic, and viscoplastic parts. They also conducted a parametric study regarding the dependence of strain components on the number of repetitions and stress magnitudes. Lu and Wright improved the model by modifying its constitutive equations (Lu and Wright 1998) and adding the temperature effects (Lu and Wright 2000). Presenting an associated and a non-associated viscoplastic model, Florea (1994a, 1994b) deduced that the volumetric expansion and rate-dependency of plastic deformations must be considered to reach a rigorous formulation for asphalt concrete. By decomposing the strain tensor into viscoelastic and viscoplastic parts, Uzan (2005) introduced an isotropic damage model with two damage functions in which Schapery’s model (Schapery 1969) describes the viscoelastic part and a strain hardening function governs the viscoplastic part. González et al. (2007) developed a viscoplastic model that uses few mechanical constants which can be easily obtained by simple experiments. Utilizing Schapery’s viscoelasticity and Perzyna’s viscoplasticity, Huang et al. (2011a, 2011b) presented a constitutive model of which the calibration process only needs one creep-recovery test. Further improvements regarding the constitutive modeling of asphalt materials were made by Darabi et al. (2011); Al-Rub and Darabi (2012); Darabi et al. (2012) and Shakiba and coworkers (Shakiba et al. 2013, 2015a, b). Those studies included the different characteristics of asphalt materials such as thermoelasticity, viscoelasticity, viscoplasticity, damage growth, and even moisture effects. Regarding the anisotropy of asphalt concrete, Tashman et al. (2004) used a modified Drucker–Prager yield function in conjunction with Perzyna’s formulation to consider the material viscoplasticity. Yu et al. (2014) developed an anisotropic model to study the effects of direction-dependent damage growth as well as the effects of aggregates directional distribution on the rutting phenomena in asphalt pavements. Zhang et al. (2015) presented a smooth octahedral yield surface based on the generalized Drucker–Prager function that can account for internal friction angles from 0 to 90 degrees. Their model eliminated the limitation of its predecessors regarding the range of internal friction angles. Balieu and Kringos (2015) presented a constitutive model of which the plastic and damage flow rules were extracted within a thermodynamical framework. A second-order tensor was used to define the anisotropic degradation, and the multiplicative decomposition of strain gradient was employed. They utilized their model to emphasize on the anisotropy of damage evolution in asphalt concrete. It should be mentioned that although the heterogeneous mesostructure of concrete and asphalt materials are rather similar, their mechanical characteristics are different to a great extent. Owing to its cementitious binder, concrete is more of a sturdy and solid nature than asphalt materials, making it suitable for construction purposes. On the other hand, asphalt materials are more useful for paving purposes since they are cheaper, softer, and easier to work with. In this regard, each of these two materials demands constitutive models that are specifically formulated based on their applications and indeed their characteristics.

Despite the abundant efforts toward the modeling of damage and cracking processes in quasi-brittle materials, the topic is still an active area of study (see for example Ožbolt and Gambarelli (2018); Jirásek and Allix (2019); Jirásek and Desmorat (2019); Fu et al. (2022); Liu et al. (2022b); Gambarelli and Ožbolt (2020); Sciegaj et al. (2020); Abdullah and Kirane (2021); Konate et al. (2021); Mihai et al. (2021); Liu et al. (2022a)). In particular, many authors have incorporated the rate effects for reproducing reversible and irreversible strains in concrete, such as Coussy and Ulm (1996), Sercombe et al. (1998), and Pedersen and coworkers (Pedersen et al. 2006, 2008, 2013), to name a few. This paper introduces damage-induced anisotropy to their formulations. It has been revealed that isotropic damage models overestimate the intensity of damage, leading to the premature failure of specimens (Jansson and Stigh 1985; Chow and Wang 1987). It also has been shown that this deficiency affects the damaging process to the extent that the resulting crack profiles are influenced (Daneshyar and Ghaemian 2017). The reason lies behind the fact that damage tends to grow on planes that are perpendicular to the principal stresses (Lu and Chow 1990). However, isotropic models ignore the directional dependency of damage so that degradation on a specific plane reduces the load-bearing capacity of the material in all directions. As a result, the weakness of isotropic damage models is uncovered in mixed-mode tests in which the principal cracking plane must rotate during the failure process (Trampczynski et al. 1981; Wang and Chow 1989). Thus, this paper aims to redress this drawback by including the damage anisotropy in conjunction with the viscoelastic and viscoplastic responses of concrete. To this end, an idealized model for describing the elastic, viscoelastic, and viscoplastic responses of concrete is presented first. Then a proper damage growth law is introduced, and the objectivity of the global responses with respect to the width of the fracture process zone is established by linking the rate of damage growth to the fracture energy of concrete. Then, the formulation is generalized for three-dimensional problems, and the numerical aspects regarding the incremental integration of the nonlinear equations are presented. Next, the model is verified by means of a series of experimental tests, and some concluding remarks are presented at the end.

Fig. 1

Rheological model consists of an elastic, a viscoelastic, and a viscoplastic body in the effective (undamaged) configuration

2 Constitutive formulation

2.1 Idealized one-dimensional behavior

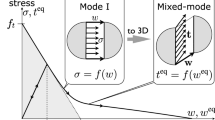
The constitutive behavior of concrete in the effective configuration can be characterized using the elastic, viscoelastic, and viscoplastic responses. These three mechanisms are idealized here by means of the rheological model of Fig. 1. The model consists of a serial arrangement of an elastic, a viscoelastic, and a viscoelastic body. As a result, the additive decomposition of the total strain reads

$$\begin{aligned} \varepsilon = \varepsilon ^e + \varepsilon ^{ve} + \varepsilon ^{vp} , \end{aligned}$$

(1)

where $\varepsilon$, $\varepsilon ^e$, $\varepsilon ^{ve}$, and $\varepsilon ^{vp}$ are the total, elastic, viscoelastic, and viscoplastic strains, respectively. All of the springs are linear as well as the dashpot in the viscoelastic body. On the other hand, the dashpot of the viscoplastic body is nonlinear. In addition, the slider in the viscoplastic body determines the irreversible straining threshold. Since the magnitude of stress is equal in all three bodies, the following expressions hold in the absence of the rate effects:

$$\begin{aligned}&\sigma = E_1\varepsilon ^e , \end{aligned}$$

(2)

$$\begin{aligned}&\sigma = E_2\varepsilon ^{ve} , \end{aligned}$$

(3)

$$\begin{aligned}&\sigma \le \sigma _y + h\varepsilon ^{vp} , \end{aligned}$$

(4)

where $E_1$ and $E_2$ are respectively the stiffness of the elastic and viscoelastic bodies, $\sigma _y$ is the yield stress, and h is a positive constant that is interpreted as the hardening of the viscoplastic body.

Fig. 2

Unloading branches of a typical stress-strain curve based on the damage, plasticity, and damage-plasticity formulations. It is evident that the latter one reproduced a valid unloading slope

The stiffness degradation of concrete is induced by the growth of micro-cracks, whereas the frictional sliding along the faces of those micro-cracks leads to irreversible straining (Jason et al. 2006; Zhu et al. 2010). Both mechanisms manifest themselves in the unloading branch of stress-strain curves. The permanent deformations shift the unloading branch horizontally, whereas the stiffness degradation reduces its slope. The former can be defined by the plasticity theory, and the latter in the framework of damage mechanics. However, as shown in Fig. 2, none of these two theories are adequate in the absence of the other. As can be seen in the figure, a combination of those two is required to reproduce a valid unloading branch. Hence, the underlying mechanisms of damage and plasticity are interwoven and these two phenomena occur concurrently. As a result, the magnitude of the viscoplastic strain controls the damaging process in this model. By assuming an exponential damage growth law, the relation between the effective stress and its macroscopically observed counterpart, the nominal stress, is given by

$$\begin{aligned} \tilde{\sigma }= \exp {(-\alpha \varepsilon ^{vp})}\sigma , \end{aligned}$$

(5)

where $\tilde{\sigma }$ is the nominal stress and $\alpha$ is a constant that controls the rate of damage growth. Note that the tilde denotes a quantity in the damaged configuration in the following.

Numerical treatments of localization and failure problems can be categorized into two classes of discrete and continuum models. Cracks are explicitly modeled by the former one through injecting strong discontinuities within the medium. As a result, special treatments are required to reproduce the energy dissipated across the fracture process zone. Cohesive models replicate this dissipation by means of surface traction acting on the crack faces. The magnitude of this traction is related to the relative displacement of the crack faces through a cohesive law. Assuming a mixed-mode planar problem, the cohesive law must be defined in accordance with the fracture energies of the first and second modes of cracking. Since both normal and tangential relative displacements exist, their corresponding traction vectors are required to replicate the actual energy dissipation. On the other hand, continuum models preserve the continuity of the medium even for completely degraded regions. This postulation streamlines the spatial discretization process but hinders the description of the constitutive model. Continuum damage models are of this type. They use idealized one-dimensional constitutive laws to characterize the degradation process, while the multidimensional effects are considered through the continuity of stress and strain fields. This approach is similar to that of the plasticity theory wherein a one-dimensional response describes the post-linear regime of the stress-strain curve, and the multidimensional effects are injected by means of the flow rule of the model.

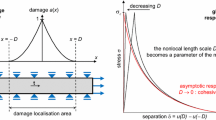
The variations of the effective stress, nominal stress, and damage index with respect to the magnitude of the total strain are plotted in Fig. 3. The area under the nominal stress curve (shaded in gray) represents the energy required for a complete cracking process (Oliver 1989). This process occurs in a finite thickness depending on the microstructure of the material (de Borst 2013). In the nonlocal and gradient-enhanced formulations wherein the governing equations of the system are regularized, this thickness is explicitly defined through a parameter called the characteristic length $\ell$ (de Borst et al. 1995; de Borst and Verhoosel 2016; Iacono et al. 2020). Here, although the rate-dependent inelastic response can lead to increasing the order of time derivatives, the rate effects are not significant in concrete and the field equations remain unregularized. As a result, the localized zone spreads across the width of finite element spaces, and $\ell$ must be defined in accordance with the geometry of elements (Bažant and Oh 1983; Bazoant and Pijaudier-Cabot 1989; Bažant and Pijaudier-Cabot 1988).

Fig. 3

Effective stress and nominal stress curves. The area under the nominal stress–total strain curve from zero to infinity (shaded area) represents the dissipated energy due to a complete cracking process

The classical continuum mechanics concerns continua with perfect structure. The underlying theory is devoid of any parameter incorporating the characteristics of the material microstructure. Hence, no matter whether a medium has dimensions of meters or microns, it is treated the same by the theory (Daneshyar et al. 2022). However, due to its underlying microstructure, the material response is essentially nonlocal. In enriched continua, this feature is incorporated by means of the characteristic length, an internal length parameter the magnitude of which follows from the correlation properties of the material (Askes and Aifantis 2011). The physical meaning of the characteristic length pertains to the phenomenon involved. In gradient elasticity it can be related to the size of unit cells (Fish et al. 2002b, a), dimensions of the representative volume element (Gitman et al. 2005), or dislocation core size (Kioseoglou et al. 2008). In gradient plasticity, it can be described in accordance with the grain size in polycrystals (Menzel and Steinmann 2000) or dislocation spacing (Al-Rub and Voyiadjis 2006). In fracture problems, it represents the width of the fracture process zone, i.e., itself can be linked to the size of aggregates in case of concrete cracking (Bazoant and Pijaudier-Cabot 1989).

With the characteristics length $\ell$ at hand, the energy dissipation during a process of cracking is linked to the fracture energy of concrete, $G_f$, through the following relation:

$$\begin{aligned}{} & {} G_f = \ell \int _{0}^{\infty }{\tilde{\sigma }(e) d\varepsilon } = \ell \nonumber \\{} & {} \int _0^{\varepsilon _y}{\tilde{\sigma }(\varepsilon ) d\varepsilon } + \ell \int _{\varepsilon _y}^{\infty }{\tilde{\sigma }(\varepsilon ) d\varepsilon } , \end{aligned}$$

(6)

where $\varepsilon _y$ is the total strain at the onset of damage. From (2) and (3) we can deduce that

$$\begin{aligned} E_1\varepsilon ^e = E_2\varepsilon ^{ve} . \end{aligned}$$

(7)

In the absence of the viscoplastic strain we have

$$\begin{aligned} d\varepsilon = d\varepsilon ^e + d\varepsilon ^{ve} . \end{aligned}$$

(8)

Hence,

$$\begin{aligned} d\varepsilon = \frac{E_1+E_2}{E_2} d\varepsilon ^e , \end{aligned}$$

(9)

which, by utilizing the relation in (2), can be rewritten as

$$\begin{aligned} d\varepsilon = \frac{E_1+E_2}{E_1E_2} d\sigma = C_a d\sigma , \end{aligned}$$

(10)

where

$$\begin{aligned} C_a = \frac{E_1+E_2}{E_1E_2} \end{aligned}$$

(11)

is the compliance of the equivalent spring for the elastic and viscoelastic bodies. As a result, the first integral on the right-hand side of (6) is computed as

$$\begin{aligned} \int _0^{\varepsilon _y}{\tilde{\sigma }(\varepsilon ) d\varepsilon } = C_a \int _0^{\sigma _y} {\sigma d\sigma } = C_a \frac{\sigma _y^2}{2} . \end{aligned}$$

(12)

On the other hand, the nonlinear branch of the nominal stress is governed by the relation in (4). Thus, based on (2), (3), and (4) we have

$$\begin{aligned}&E_1\varepsilon ^e = \sigma _y + h\varepsilon ^{vp} , \end{aligned}$$

(13)

$$\begin{aligned}&E_2\varepsilon ^{ve} = \sigma _y + h\varepsilon ^{vp} . \end{aligned}$$

(14)

Hence,

$$\begin{aligned}&d\varepsilon ^e = \frac{h}{E_1} d\varepsilon ^{vp} , \end{aligned}$$

(15)

$$\begin{aligned}&d\varepsilon ^{ve} = \frac{h}{E_2} d\varepsilon ^{vp} . \end{aligned}$$

(16)

Using the additive decomposition of the total strain in (1), we have

$$\begin{aligned} d\varepsilon = d\varepsilon ^e + d\varepsilon ^{ve} + d\varepsilon ^{vp} . \end{aligned}$$

(17)

Substituting (15) and (16) into (17) gives

$$\begin{aligned} d\varepsilon = \frac{hE_1 + hE_2 + E_1E_2}{E_1E_2} d\varepsilon ^{vp} = hC_b d\varepsilon ^{vp} , \end{aligned}$$

(18)

where

$$\begin{aligned} C_b = \frac{hE_1 + hE_2 + E_1E_2}{hE_1E_2} \end{aligned}$$

(19)

is the compliance of the equivalent spring for the elastic, viscoelastic, and viscoplastic bodies. Hence, the second integral on the right-hand side of (6) is written in terms of the viscoplastic strain as

$$\begin{aligned}{} & {} \int _{\varepsilon _y}^{\infty }{\tilde{\sigma }(\varepsilon ) d\varepsilon } = hC_b \int _{0}^{\infty }\nonumber \\{} & {} \qquad {\exp {(-\alpha \varepsilon ^{vp})}(\sigma _y + h\varepsilon ^{vp})d\varepsilon ^{vp}} , \end{aligned}$$

(20)

which is computed as follows:

$$\begin{aligned} \int _{\varepsilon _y}^{\infty }{\tilde{\sigma }(\varepsilon ) d\varepsilon } = hC_b \left( \frac{\sigma _y}{\alpha } + \frac{h}{\alpha ^2}\right) . \end{aligned}$$

(21)

By substituting the expressions in (12) and (21) into (6), the unknown constant $\alpha$ is related to the fracture energy of concrete through

$$\begin{aligned} G_f = \ell C_a \frac{\sigma _y^2}{2} + \ell hC_b \left( \frac{\sigma _y}{\alpha } + \frac{h}{\alpha ^2}\right) . \end{aligned}$$

(22)

By introducing

$$\begin{aligned} q = \frac{G_f}{\ell hC_b} - \frac{C_a\sigma _y^2}{2hC_b} , \end{aligned}$$

(23)

the relation in (22) is rewritten as

$$\begin{aligned} q = \frac{\sigma _y}{\alpha } + \frac{h}{\alpha ^2} . \end{aligned}$$

(24)

Rearranging the above relation gives the following second degree algebraic equation for $\alpha$:

$$\begin{aligned} q\alpha ^2 - \sigma _y\alpha - h = 0 . \end{aligned}$$

(25)

As a result, the unknown constant $\alpha$ is computed as

$$\begin{aligned} \alpha = \frac{\sigma _y \pm \sqrt{\sigma _y^2 + 4hq} }{2q} . \end{aligned}$$

(26)

To have an exponential decay, $\alpha$ must be positive. As a result, two possibilities exist based on the sign of q. For the positive values of q, the plus sign in front of the square root is acceptable. On the other hand, for the negative values of q, the numerator is always positive and the denominator is negative, indicating that q must remain positive to have the desired exponential decay. According to the definition of q in (23), the following admissible limit can be defined for the characteristic length $\ell$:

$$\begin{aligned} \ell < \frac{2G_f}{C_a\sigma _y^2} . \end{aligned}$$

(27)

The above requirement can be easily satisfied by defining a proper discretization across the possible crack propagation path. Employing the relation in (26) guarantees the objectivity of the energy dissipation with respect to the spatial discretization of the problem.

2.2 Generalized three-dimensional behavior

2.2.1 Viscoelasticity

According to the idealized rheological model of Fig. 1, the spring and dashpot of the viscoelastic body are connected in parallel. Hence, the equivalent stress of the body can be decomposed into a viscous and a restoring part through (Pedersen et al. 2008):

$$\begin{aligned} \Vert s_{ij}\Vert =\eta \dot{\xi }+ E_2\xi , \end{aligned}$$

(28)

where $s_{ij}$ is the deviatoric part of the effective stress tensor, $\Vert s_{ij}\Vert$ is the Euclidean norm of $s_{ij}$, $\eta$ is the viscosity of the dashpot, which ranges from few megapascal-second to hundreds of gigapascal-second based on the concrete degree of saturation (Pedersen et al. 2008), $\xi$ is the viscoelastic internal variable, and $\dot{\xi }$ is the time-derivative (rate) of $\xi$. Note that the elastic, viscoelastic, and viscoplastic behaviors of concrete are defined in the effective configuration. Hence, for the sake of brevity, the effective stress tensor is simply called the stress tensor hereafter, unless otherwise noted. The evolution of viscoelastic stain, $\dot{\varepsilon }^{ve}$, is given by the following flow rule (Sercombe et al. 1998):

$$\begin{aligned} \dot{\varepsilon }^{ve}_{ij}=\dot{\xi }\frac{s_{ij}}{\Vert s_{ij}\Vert } , \end{aligned}$$

(29)

which implies that the viscoelastic part of strain does not contribute in the volume change of concrete. This property is also observed in laboratory tests (Sercombe et al. 1998).

2.2.2 Viscoplasticity

The overstress viscoplastic models are formulated based on the assumption that the state of stress can be located outside the admissible region defined by the yield surface. As a result, they violate the Kuhn-Tucker conditions and impair the convergence of numerical integration. In addition, the linear behavior of the viscoplastic dashpot in the overstress models does not suffice to provide valid strength magnifications if a wide range of strain rates is of interest. A remedy is to define a rate-dependent yield surface that incorporates both the hardening and strain rate effects. This approach is more appealing from the computational point of view due to its better convergence properties (Wang et al. 1997). As a result, the yield surface of the model is given by (Lee and Fenves 1998)

$$\begin{aligned} F = \sqrt{3J_2} + a I_1 + b \langle \sigma _{max}\rangle - (1-a)\sigma ^-_{d} , \end{aligned}$$

(30)

where $J_2$ is the second invariant of the deviatoric stress tensor, $I_1$ is the first invariant of the stress tensor, $\sigma _{max}$ is the maximum principal stress, $\langle \sigma _{max}\rangle$ returns $\sigma _{max}$ for the positive values and zero for the negative ones, a is a dimensionless material constant, which is equal to 0.12 for most concretes (Lubliner et al. 1989),

$$\begin{aligned} b = (1-a)\frac{\sigma ^-_{d}}{\sigma ^+_{d}}-(1+a) , \end{aligned}$$

(31)

$\sigma ^+_{d}$ is the dynamic strength of concrete in tension, and $\sigma ^-_{d}$ is the dynamic strength of concrete in compression. Note that in the remainder of the text, the minus and plus superscripts denote the compressive and tensile parts of a quantity, respectively. By assuming a logarithmic strength magnification, we have

$$\begin{aligned} \sigma ^\pm _{d} = \big (1+c_1\ln {(c_2\dot{\gamma }^\pm +1)}\big )\sigma ^\pm _{s} , \end{aligned}$$

(32)

where

$$\begin{aligned} \sigma ^\pm _{s} = \sigma ^\pm _{y} + h^\pm \gamma ^\pm \end{aligned}$$

(33)

is the static strength, $\gamma ^\pm$ is the viscoplastic internal variable, $\dot{\gamma }^\pm$ is the time-derivative of $\gamma ^\pm$, $\sigma ^\pm _{y}$ is the yield strength, $h^\pm$ is the hardening parameter, and $c_1$ and $c_2$ are the material constants that define the rate-sensitivity of concrete. Many authors have employed functions similar to those in (32) for describing the rate-dependent response of concrete, such as Bažant et al. (2000a), Bažant et al. (2000b), Ožbolt et al. (2006), and Ožbolt et al. (2011), to name a few. Based on the calibration of Ožbolt et al. (2006), the constants of the logarithmic function are chosen as $c_1=0.032$ and $c_2=500\times 10^{3}$ second. Assuming different strength magnifications, Fig. 4 illustrates the yield surface of the model in the three-dimensional Haigh–Westergaard stress space.

Fig. 4

Yield surface of the model in the three-dimensional space of principal stresses (in MPa) for tensile strength of 2 MPa and compressive strength of 10 MPa under the rate-independent conditions (inner surface), rate-dependent conditions with a magnification factor of 2 (middle surface), and with a magnification factor of 4 (outer surface)

The viscoplastic flow rule of the model is defined by means of a Drucker–Prager type function so that (Lee and Fenves 1998)

$$\begin{aligned} \dot{\varepsilon }^{vp}_{ij}=\dot{\gamma }\Big (\frac{s_{ij}}{\Vert s_{ij} \Vert } + a_p\delta _{ij}\Big ) \end{aligned}$$

(34)

where $a_p$ is the dilation constant. Note that by setting $a_p=0.2$, the non-associative flow rule in (34) reproduces realistic magnitudes of inelastic volumetric expansion.

The yield function F and the rate of viscoplastic internal variable $\dot{\gamma }$ are subjected to the Kuhn–Tucker conditions with the following definition:

$$\begin{aligned} F \le 0,\qquad \dot{\gamma }\ge 0, \qquad \dot{\gamma }F=0 . \end{aligned}$$

(35)

The rate of viscoplastic internal variable $\dot{\gamma }$ is obtained by satisfying the above relations. As a result, the evolution of viscoplastic strain $\dot{\varepsilon }^{vp}_{ij}$ can be computed using the flow rule of the model. With $\dot{\varepsilon }^{vp}_{ij}$ at hand, the rate of tensile and compressive viscoplastic internal variables $\dot{\gamma }^+$ and $\dot{\gamma }^-$ are given by (Lee and Fenves 1998)

$$\begin{aligned}&\dot{\gamma }^+=r(\sigma _{ij})\dot{\varepsilon }^{vp}_{max} , \end{aligned}$$

(36)

$$\begin{aligned}&\dot{\gamma }^-=-\big (1-r(\sigma _{ij})\big )\dot{\varepsilon }^{vp}_{min} , \end{aligned}$$

(37)

where $\dot{\varepsilon }^{vp}_{max}$ and $\dot{\varepsilon }^{vp}_{min}$ are respectively the maximum and minimum principal viscoplastic strain rates and r is a weight function, which is defined by means of the principal values of the stress tensor as follows:

$$\begin{aligned} r(\sigma _{ij})=\frac{\sum ^3_{k=1} \langle \sigma _k\rangle }{\sum ^3_{k=1} |\sigma _k|} . \end{aligned}$$

(38)

2.2.3 Anisotropic damage

Concrete is a heterogeneous solid with an almost isotropic response prior to the onset of damage. Once its degradation begins, it starts to exhibit a direction-dependent response. Since damage tends to grow on the aggregate boundaries, this direction-dependency is more dominant in concrete than in a homogeneous solid.

Tensorial damage growth is formulated here based on the work of Bažant et al. (1996). According to their theory, the virtual work of the stress tensor inside a unit sphere is equal to the virtual work of the traction vectors over the surface of the same sphere. Hence,

$$\begin{aligned} \frac{4\pi }{3}\sigma _{ij}\delta \varepsilon _{ij} = \int _{S_s} { T_i\delta e_i dS_s } , \end{aligned}$$

(39)

where $T_i$ and $\delta e_i$ are the traction and virtual strain vectors, respectively, and $S_s$ denotes the surface of the unit sphere. The virtual strain vector $\delta e_i$ is related to the virtual stain tensor $\delta \varepsilon _{ij}$ through the following kinematic constraint (Jirásek 1999):

$$\begin{aligned} \delta e_i = \delta \varepsilon _{ij}n_j , \end{aligned}$$

(40)

where $n_i$ is the unit outward vector to the surface of the sphere. Employing the kinematic constraint in (40), the relation in (39) yields

$$\begin{aligned} \sigma _{ij}\delta \varepsilon _{ij} = \frac{3}{4\pi }\int _{S_h} {( T_i n_j + T_j n_i)\delta \varepsilon _{ij} dS_h } , \end{aligned}$$

(41)

wherein, due to the symmetry of the traction vectors, the integral on the right-hand side is defined over the surface of a unit hemisphere, $S_h$. As a result, the stress tensor is related to the traction vectors through the following relation:

$$\begin{aligned} \sigma _{ij} = \frac{3}{4\pi }\int _{S_h} {( T_i n_j + T_j n_i) dS_h } . \end{aligned}$$

(42)

On the other hand, by decomposing the stress tensor into its tensile and compressive parts, we have (Wu et al. 2006)

$$\begin{aligned} \sigma _{ij} = \sigma ^+_{ij} + \sigma ^-_{ij} , \end{aligned}$$

(43)

where

$$\begin{aligned} \sigma ^\pm _{ij}=P^\pm _{ijkl}\sigma _{kl} , \end{aligned}$$

(44)

and $P^\pm _{ijkl}$ is a projection tensor with the following tensile and compressive parts:

$$\begin{aligned}&P^+_{ijkl}=\sum ^3_{r=1}H(\sigma _r) n^{(r)}_i n^{(r)}_j n^{(r)}_k n^{(r)}_l , \end{aligned}$$

(45)

$$\begin{aligned}&P^-_{ijkl}=I_{ijkl}-P^+_{ijkl} , \end{aligned}$$

(46)

wherein $n^{(r)}_i$ is the direction of rth principal stress,

$$\begin{aligned} I_{ijkl}=\frac{1}{2}( \delta _{ik}\delta _{jl} + \delta _{jk}\delta _{il} ) \end{aligned}$$

(47)

is the fourth-order identity tensor, and

$$\begin{aligned} H(x) = \left\{ { \begin{array}{*{20}{c}} 1\quad \quad &{}{x > 0}\\ 0\quad \quad &{}{x \le 0} \end{array}} \right. \end{aligned}$$

(48)

is the Heaviside step function. As a result, the relation in (42) can be rewritten for the tensile and compressive parts of the stress tensor as

$$\begin{aligned} \sigma ^\pm _{ij} = \frac{3}{4\pi }\int _{S_h} {( T^\pm _i n_j + T^\pm _j n_i) dS_h } . \end{aligned}$$

(49)

On the other hand, the traction vector $T^\pm _i$ is related to its nominal counterpart, $\tilde{T}^\pm _i$, through the following relation (Jirásek 1999):

$$\begin{aligned} T^\pm _i=\psi ^\pm \tilde{T}^\pm _i , \end{aligned}$$

(50)

where $\psi ^\pm$ is called the inverse integrity, which can be related to the damage index $\varphi ^\pm$ by

$$\begin{aligned} \psi ^\pm = \frac{1}{1-\varphi ^\pm } . \end{aligned}$$

(51)

According to the exponential damage growth law in (5), the inverse integrity $\psi ^\pm$ is defined as

$$\begin{aligned} \psi ^\pm = \exp {(\alpha ^\pm e^{vp\pm })}, \end{aligned}$$

(52)

where

$$\begin{aligned}&\dot{e}^{vp+}=r(\sigma _{ij})\dot{\varepsilon }^{vp}_{ij}n_in_j , \end{aligned}$$

(53)

$$\begin{aligned}&\dot{e}^{vp-}=-\big (1-r(\sigma _{ij})\big )\dot{\varepsilon }^{vp}_{ij}n_in_j . \end{aligned}$$

(54)

Substituting the traction vector $T^\pm _i$ from (50) into (49) results in

$$\begin{aligned} \sigma ^\pm _{ij} = \frac{3}{4\pi }\int _{S_h} {(\psi ^\pm \tilde{T}^\pm _i n_j + \psi ^\pm \tilde{T}^\pm _j n_i) dS_h } . \end{aligned}$$

(55)

On the other hand, the tensile and compressive traction vectors in the damaged configuration are related to the nominal tensile and compressive stress tensors by

$$\begin{aligned} \tilde{T}^\pm _i = \tilde{\sigma }^\pm _{ij}n_j . \end{aligned}$$

(56)

Substituting the above expression into (55) results in

$$\begin{aligned} \sigma ^\pm _{ij} = \frac{3}{4\pi }\int _{S_h} {(\psi ^\pm \tilde{\sigma }^\pm _{ik}n_k n_j + \psi ^\pm \tilde{\sigma }^\pm _{jk}n_k n_i) dS_h } . \end{aligned}$$

(57)

Finally, the effective stress tensors are related to their nominal counterparts by

$$\begin{aligned} \sigma ^\pm _{ij} = \frac{1}{2}( \tilde{\sigma }^\pm _{ik}\psi ^\pm _{kj} + \tilde{\sigma }^\pm _{jk}\psi ^\pm _{ki}) , \end{aligned}$$

(58)

where

$$\begin{aligned} \psi ^\pm _{ij} = \frac{3}{2\pi }\int _{S_h} {\psi ^\pm n_i n_j dS_h } \end{aligned}$$

(59)

is the inverse integrity tensor. The relation between the effective and nominal stress tensors can be rewritten as

$$\begin{aligned} \sigma ^\pm _{ij} = M^\pm _{ijkl}\tilde{\sigma }^\pm _{kl} , \end{aligned}$$

(60)

where

$$\begin{aligned} M^\pm _{ijkl} = \frac{1}{2}( \psi ^\pm _{ik}\delta _{jl} + \psi ^\pm _{jk}\delta _{il}) \end{aligned}$$

(61)

is the fourth-order mapping tensor. According to the stress decomposition in (43) we arrive at

$$\begin{aligned} \sigma _{ij} = M^+_{ijkl}\tilde{\sigma }^+_{kl} + M^-_{ijkl}\tilde{\sigma }^-_{kl} , \end{aligned}$$

(62)

or, equivalently,

$$\begin{aligned} \sigma _{ij} = M_{ijkl}\tilde{\sigma }_{kl} , \end{aligned}$$

(63)

where

$$\begin{aligned} M_{ijkl} = M^+_{ijrs}P^+_{rskl} + M^-_{ijrs}P^-_{rskl} \end{aligned}$$

(64)

is the total fourth-order mapping tensor.

2.3 Return-mapping algorithm

A fully implicit Euler scheme is proposed here to discretize the constitutive equations in the temporal domain. The typical incremental procedure between the time interval $[t_n,t_{n+1}]$ is used to discretize the equations, wherein the subscript n and $n+1$ refer to the previous and current states, respectively. Since the equations are subjected to the Kuhn–Tucker conditions, a two-step algorithm consisting of a viscoelastic predictor and a viscoplastic corrector is required. With the solution of the return-mapping equation at hand, the updated mapping tensor can be computed at the end of the time interval.

2.3.1 Viscoelastic predictor

Given the total strain increment $\varDelta \varepsilon _{ij}$, the trial elastic strain tensor can be defined in the absence of the viscoelastic and viscoplastic responses as follows:

$$\begin{aligned} (\varepsilon ^e_{ij})^{trial}_{n+1} = (\varepsilon ^e_{ij})_{n} + \varDelta \varepsilon _{ij} . \end{aligned}$$

(65)

Assuming a pure viscoelastic loading state, we have

$$\begin{aligned} (\varepsilon ^e_{ij})_{n+1} = (\varepsilon ^e_{ij})^{trial}_{n+1} - \varDelta \varepsilon ^{ve}_{ij} . \end{aligned}$$

(66)

Based on the backward Euler scheme, the viscoelastic flow rule in (29) is discretized as follows:

$$\begin{aligned} \varDelta \varepsilon ^{ve}_{ij}=\varDelta \xi \frac{(s_{ij})_{n+1}}{\Vert s_{ij}\Vert _{n+1}} . \end{aligned}$$

(67)

According to the Hooke’s law, the deviatoric stress tensor is related to the elastic strain tensor through

$$\begin{aligned} (s_{ij})_{n+1} = 2G\Big ((\varepsilon ^e_{ij})_{n+1} - \frac{1}{3}(\varepsilon ^e_{kk})_{n+1}\delta _{ij} \Big ), \end{aligned}$$

(68)

where G is the elastic shear modulus of the material. Substituting the relations in (66) and (67) into the above expression results in

$$\begin{aligned} (s_{ij})_{n+1}= & {} 2G\Big ((\varepsilon ^e_{ij})^{trial}_{n+1}-\frac{1}{3}(\varepsilon ^e_{kk})^{trial}_{n+1}\delta _{ij} - \varDelta \xi \nonumber \\{} & {} \quad \frac{(s_{ij})_{n+1}}{\Vert s_{ij} \Vert _{n+1}} \Big ) . \end{aligned}$$

(69)

The above expression can be rewritten as follows:

$$\begin{aligned} (s_{ij})_{n+1}= (s_{ij})^{trial}_{n+1} - 2G\varDelta \xi \frac{(s_{ij})_{n+1}}{\Vert s_{ij} \Vert _{n+1}} , \end{aligned}$$

(70)

or, equivalently,

$$\begin{aligned} (s_{ij})^{trial}_{n+1} = (s_{ij})_{n+1} \Big ( 1 + \frac{2G\varDelta \xi }{\Vert s_{ij} \Vert _{n+1}} \Big ) . \end{aligned}$$

(71)

By equating the Euclidean norm of the both sides of the above relation we can deduce that

$$\begin{aligned} \Vert s_{ij} \Vert ^{trial}_{n+1} = \Vert s_{ij} \Vert _{n+1} + 2G\varDelta \xi . \end{aligned}$$

(72)

Substituting the above expression into (71) and performing some straightforward manipulations give

$$\begin{aligned} N^{ve}_{ij} :=\frac{(s_{ij})^{trial}_{n+1}}{ \Vert s_{ij} \Vert ^{trial}_{n+1} } = \frac{(s_{ij})_{n+1}}{\Vert s_{ij} \Vert _{n+1}} , \end{aligned}$$

(73)

where $N^{ve}_{ij}$ is the viscoelastic flow direction. The above expression implies the co-linearity of the trial and updated deviatoric stress tensors, which means that $N^{ve}_{ij}$ is a priori known direction. This property substantially streamlines the numerical integration process.

By applying the incremental procedure on the expression in (28), the following discretized relation is obtained:

$$\begin{aligned} \Vert s_{ij} \Vert _{n+1} = \eta \frac{\varDelta \xi }{\varDelta t} + E_2(\xi )_{n+1} , \end{aligned}$$

(74)

wherein

$$\begin{aligned} (\xi )_{n+1}=(\xi )_{n} + \varDelta \xi . \end{aligned}$$

(75)

By substituting the relation in (72) into (74) and employing the above expression we arrive at

$$\begin{aligned} \Vert s_{ij} \Vert ^{trial}_{n+1} - 2G\varDelta \xi = \eta \frac{\varDelta \xi }{\varDelta t} + E_2\Big ( (\xi )_{n} + \varDelta \xi \Big ) . \end{aligned}$$

(76)

Solving the above equation for the increment of viscoelastic internal variable $\varDelta \xi$ gives

$$\begin{aligned} \varDelta \xi = \frac{\Vert s_{ij} \Vert ^{trial}_{n+1} - E_2(\xi )_{n}}{\eta /\varDelta t + 2G + E_2} . \end{aligned}$$

(77)

As a result, the deviatoric stress tensor is updated as follows:

$$\begin{aligned} (s_{ij})_{n+1} = (s_{ij})^{trial}_{n+1} - 2G\varDelta \xi N^{ve}_{ij} . \end{aligned}$$

(78)

On the other hand, the hydrostatic stress is given by

$$\begin{aligned} (p)_{n+1} = (p)^{trial}_{n+1} = K(\varepsilon ^e_{kk})^{trial}_{n+1} , \end{aligned}$$

(79)

where K is the elastic bulk modulus of the material. Finally, the updated stress tensor is computed as follows:

$$\begin{aligned} (\sigma _{ij})_{n+1} = (s_{ij})_{n+1} + (p)_{n+1}\delta _{ij} . \end{aligned}$$

(80)

The updated stress tensor in (80) is obtained by assuming a pure viscoelastic loading state. However, the admissibility of the solution has to be assessed by

$$\begin{aligned} (F)_{n+1} \le 0 , \end{aligned}$$

(81)

which means that the stress state lies within the yield surface and the assumption is correct. As a result, the elastic and viscoelastic solution variables are updated by

$$\begin{aligned}&(\xi )_{n+1} = (\xi )_n + \varDelta \xi , \end{aligned}$$

(82)

$$\begin{aligned}&(\varepsilon ^{ve}_{ij})_{n+1} = (\varepsilon ^{ve}_{ij})_n + \varDelta \varepsilon ^{ve}_{ij} , \end{aligned}$$

(83)

$$\begin{aligned}&(\varepsilon ^e_{ij})_{n+1} = (\varepsilon ^e_{ij})_n + \varDelta \varepsilon _{ij} - \varDelta \varepsilon ^{ve}_{ij} , \end{aligned}$$

(84)

whereas the other variables remain unchanged during the increment.

2.3.2 Viscoplastic corrector

The violation of the stress admissibility indicates that the step is not purely viscoelastic. Hence, the updated elastic strain tensor is defined as

$$\begin{aligned} (\varepsilon ^e_{ij})_{n+1} = (\varepsilon ^e_{ij})^{trial}_{n+1}- \varDelta \varepsilon ^{ve}_{ij}-\varDelta \varepsilon ^{vp}_{ij} . \end{aligned}$$

(85)

According to the viscoplastic flow rule in (34), we have

$$\begin{aligned} \varDelta \varepsilon ^{vp}_{ij}=\varDelta \gamma \Big (\frac{(s_{ij})_{n+1}}{\Vert s_{ij} \Vert _{n+1}} + a_p\delta _{ij}\Big ) . \end{aligned}$$

(86)

Using the increments of viscoelastic and viscoplastic strains, the updated deviatoric stress tensor reads

$$\begin{aligned} \begin{aligned} (s_{ij})_{n+1} =&2G\Big ((\varepsilon ^e_{ij})^{trial}_{n+1}-\frac{1}{3} (\varepsilon ^e_{kk})^{trial}_{n+1}\delta _{ij}\Big ) \\&-2G(\varDelta \xi +\varDelta \gamma )\frac{(s_{ij})_{n+1}}{\Vert s_{ij} \Vert _{n+1}} , \end{aligned} \end{aligned}$$

(87)

or, equivalently,

$$\begin{aligned} (s_{ij})_{n+1}= (s_{ij})^{trial}_{n+1} - 2G(\varDelta \xi +\varDelta \gamma )\frac{(s_{ij})_{n+1}}{\Vert s_{ij} \Vert _{n+1}} . \end{aligned}$$

(88)

As a result, the trial deviatoric stress tensor can be given by

$$\begin{aligned} (s_{ij})^{trial}_{n+1} = (s_{ij})_{n+1} \Big ( 1 + \frac{2G(\varDelta \xi +\varDelta \gamma )}{\Vert s_{ij} \Vert _{n+1}} \Big ) . \end{aligned}$$

(89)

By equating the Euclidean norm of the both sides of the above relation we arrive at

$$\begin{aligned} \Vert s_{ij} \Vert ^{trial}_{n+1} = \Vert s_{ij} \Vert _{n+1} + 2G(\varDelta \xi + \varDelta \gamma ) . \end{aligned}$$

(90)

Substituting the above relation into (89) and performing some algebraic manipulations result in

$$\begin{aligned} N^{vp}_{ij} := \frac{(s_{ij})^{trial}_{n+1}}{ \Vert s_{ij} \Vert ^{trial}_{n+1} } = \frac{(s_{ij})_{n+1}}{ \Vert s_{ij} \Vert _{n+1} } , \end{aligned}$$

(91)

where $N^{vp}_{ij}$ is the viscoplastic flow direction. By utilizing the expression in (90), the equivalent stress of the viscoelastic body in (28) reads

$$\begin{aligned}{} & {} \Vert s_{ij} \Vert ^{trial}_{n+1} - 2G(\varDelta \xi +\varDelta \gamma ) \nonumber \\{} & {} \quad = \eta \frac{\varDelta \xi }{\varDelta t} + E_2\Big ( (\xi )_{n} + \varDelta \xi \Big ) . \end{aligned}$$

(92)

Hence, the increment of the viscoelastic internal variable is obtained as follows:

$$\begin{aligned} \varDelta \xi = \frac{\Vert s_{ij} \Vert ^{trial}_{n+1} - 2G\varDelta \gamma - E_2(\xi )_{n}}{\eta /\varDelta t + 2G + E_2} . \end{aligned}$$

(93)

On the other hand, the updated deviatoric stress tensor in (88) can be rewritten as

$$\begin{aligned} (s_{ij})_{n+1}= (s_{ij})^{trial}_{n+1} - 2G(\varDelta \xi +\varDelta \gamma )N^{vp}_{ij} . \end{aligned}$$

(94)

The hydrostatic stress is also updated as follows:

$$\begin{aligned} (p)_{n+1} = (p)^{trial}_{n+1} - 3Ka_p\varDelta \gamma . \end{aligned}$$

(95)

Consequently, the updated maximum principal stress reads

$$\begin{aligned} \begin{aligned} (\sigma _{max})_{n+1} =&(\sigma _{max})^{trial}_{n+1} - 2G(\varDelta \xi +\varDelta \gamma )N^{vp}_{max} \\&-3Ka_p\varDelta \gamma . \end{aligned} \end{aligned}$$

(96)

In addition, the first invariant of the stress tensor is updated as follows:

$$\begin{aligned} (I_1)_{n+1} = (I_1)^{trial}_{n+1} - 9Ka_p\varDelta \gamma . \end{aligned}$$

(97)

By substituting the updated values into the yield function, the following fully implicit return-mapping equation is obtained:

$$\begin{aligned} \begin{aligned} (F)_{n+1} =&\sqrt{3(J_2)_{n+1}} + a (I_1)_{n+1} \\&+(b)_{n+1} \langle \sigma _{max}\rangle _{n+1} \\&-(1-a)(\sigma ^-_{d})_{n+1} = 0 . \end{aligned} \end{aligned}$$

(98)

According to the Newton–Raphson scheme, the increment of the viscoplastic internal variable is updated through the following relation:

$$\begin{aligned} (\varDelta \gamma )^{k+1} = (\varDelta \gamma )^k - \frac{ (F)^k_{n+1} }{ (F^\prime )^k_{n+1} } , \end{aligned}$$

(99)

wherein the superscripts denote the iteration number. By taking the derivative of the return-mapping equation with respect to $\varDelta \gamma$ we have

$$\begin{aligned} \begin{aligned} F^\prime =&\frac{\partial F}{\partial \varDelta \gamma } + \frac{\partial F}{\partial \varDelta \xi }\frac{\partial \varDelta \xi }{\partial \varDelta \gamma } + \frac{\partial F}{\partial b}\frac{\partial b}{\partial \sigma _d^+} \frac{\partial \sigma _d^+}{\partial \gamma ^+}\frac{\partial \gamma ^+}{\partial \varDelta \gamma } \\&+\frac{\partial F}{\partial b}\frac{\partial b}{\partial \sigma _d^-} \frac{\partial \sigma _d^-}{\partial \gamma ^-}\frac{\partial \gamma ^-}{\partial \varDelta \gamma } + \frac{\partial F}{\partial \sigma _d^-} \frac{\partial \sigma _d^-}{\partial \gamma ^-}\frac{\partial \gamma ^-}{\partial \varDelta \gamma } , \end{aligned} \end{aligned}$$

(100)

where, for briefness, the subscripts and superscripts are dropped. The partial derivatives in the above expression are

$$\begin{aligned} \frac{\partial F}{\partial \varDelta \gamma }= & {} -\sqrt{6}G - 9Ka_pa \nonumber \\{} & {} -(b)^k_{n+1}\big (2GN^{vp}_{max} + 3Ka_p \big )H(\sigma _{max})^k_{n+1} ,\nonumber \\ \end{aligned}$$

(101)

$$\begin{aligned} \frac{\partial F}{\partial \varDelta \xi }= & {} -\sqrt{6}G - (b)^k_{n+1}\big (2GN^{vp}_{max} \big ) H(\sigma _{max})^k_{n+1} ,\nonumber \\ \end{aligned}$$

(102)

$$\begin{aligned} \frac{\partial \varDelta \xi }{\partial \varDelta \gamma }= & {} -\frac{2G}{\eta /\varDelta t + 2G + E_2} , \end{aligned}$$

(103)

$$\begin{aligned} \frac{\partial F}{\partial b}= & {} \langle \sigma _{max}\rangle ^k_{n+1}, \end{aligned}$$

(104)

$$\begin{aligned} \frac{\partial b}{\partial \sigma _d^+}= & {} -(1-a)\frac{ (\sigma ^-_{d})^k_{n+1} }{\big ((\sigma ^+_{d})^k_{n+1}\big )^2} , \end{aligned}$$

(105)

$$\begin{aligned} \frac{\partial b}{\partial \sigma _d^-}= & {} (1-a)\frac{1}{ (\sigma ^+_{d})^k_{n+1} } , \end{aligned}$$

(106)

$$\begin{aligned} \frac{\partial \sigma _d^\pm }{\partial \gamma ^\pm }= & {} \frac{c_1c_2}{c_2\varDelta \gamma ^\pm + \varDelta t}\big (\sigma ^\pm _{y} + h^\pm (\gamma ^\pm )^k_{n+1}\big ) \nonumber \\{} & {} +\bigg (1+c_1\ln {\big (c_2\frac{\varDelta \gamma ^\pm }{\varDelta t}+1\big )}\bigg )h^\pm , \end{aligned}$$

(107)

$$\begin{aligned} \frac{\partial \gamma ^+}{\partial \varDelta \gamma }= & {} r(\sigma _{ij})^k_{n+1}\big (N^{vp}_{max} + a_p \big ) , \end{aligned}$$

(108)

$$\begin{aligned} \frac{\partial \gamma ^-}{\partial \varDelta \gamma }= & {} -\big ( 1-r(\sigma _{ij})^k_{n+1}\big )\big (N^{vp}_{min} + a_p \big ) , \end{aligned}$$

(109)

$$\begin{aligned} \frac{\partial F}{\partial \sigma _d^-}= & {} -(1-a) , \end{aligned}$$

(110)

where

$$\begin{aligned}&\varDelta \gamma ^+ = r(\sigma _{ij})^k_{n+1}\varDelta \gamma \big (N^{vp}_{max} + a_p \big ) , \end{aligned}$$

(111)

$$\begin{aligned}&\varDelta \gamma ^- = -\big ( 1-r(\sigma _{ij})^k_{n+1}\big )\varDelta \gamma \big (N^{vp}_{min} + a_p \big ) . \end{aligned}$$

(112)

Finally, with the increment of viscoplastic internal variable at hand, the solution variables are updated as follows:

$$\begin{aligned}&(\xi )_{n+1} = (\xi )_n + \varDelta \xi , \end{aligned}$$

(113)

$$\begin{aligned}&(\gamma )_{n+1} = (\gamma )_n + \varDelta \gamma , \end{aligned}$$

(114)

$$\begin{aligned}&(\gamma ^\pm )_{n+1} = (\gamma ^\pm )_n + \varDelta \gamma ^\pm , \end{aligned}$$

(115)

$$\begin{aligned}&(\varepsilon ^{ve}_{ij})_{n+1} = (\varepsilon ^{ve}_{ij})_n + \varDelta \varepsilon ^{ve}_{ij} , \end{aligned}$$

(116)

$$\begin{aligned}&(\varepsilon ^{vp}_{ij})_{n+1} = (\varepsilon ^{vp}_{ij})_n + \varDelta \varepsilon ^{vp}_{ij} , \end{aligned}$$

(117)

$$\begin{aligned}&(\varepsilon ^e_{ij})_{n+1} = (\varepsilon ^e_{ij})_n + \varDelta \varepsilon _{ij} - \varDelta \varepsilon ^{ve}_{ij} - \varDelta \varepsilon ^{vp}_{ij} . \end{aligned}$$

(118)

On the other hand, according to the expressions in (53) and (54), we have

$$\begin{aligned}&\varDelta e^{vp+} = r(\sigma _{ij})_{n+1}\varDelta \varepsilon ^{vp}_{ij}n_in_j , \end{aligned}$$

(119)

$$\begin{aligned}&\varDelta e^{vp-} = - \big (1-r(\sigma _{ij})_{n+1}\big )\varDelta \varepsilon ^{vp}_{ij}n_in_j . \end{aligned}$$

(120)

Hence, the viscoplastic strain vector $e^{vp\pm }$ is updated by means of the following relation:

$$\begin{aligned} (e^{vp\pm })_{n+1} = (e^{vp\pm })_n + \varDelta e^{vp\pm }. \end{aligned}$$

(121)

As a result, based on the expressions in (52) and (59), the updated inverse integrity tensor is computed as follows:

$$\begin{aligned} (\psi ^\pm _{ij})_{n+1} = \frac{3}{2\pi }\int _{S_h} {\exp {\big (\alpha ^\pm (e^{vp\pm })_{n+1}\big )} n_i n_j dS_h}.\nonumber \\ \end{aligned}$$

(122)

In practice, the integral on the right-hand side of the above expression is numerically approximated using a cubature method. Hence, the above relation is rewritten as (Daneshyar and Ghaemian 2017, 2020)

$$\begin{aligned} (\psi ^\pm _{ij})_{n+1} \approx \frac{3}{2\pi }\sum _{r=1}^m{\exp {\big (\alpha ^\pm (e^{vp\pm })^{(r)}_{n+1}\big )} n^{(r)}_i n^{(r)}_j \omega ^{(r)}},\nonumber \\ \end{aligned}$$

(123)

where m is the number of cubature points, $(e^{vp\pm })^{(r)}_{n+1}$ is the viscoplastic strain vector of the rth cubature point, $n^{(r)}_i$ is the unit vector to the surface of the sphere at the rth cubature point, and $\omega ^{(r)}$ is the rth cubature weight.

To summarize the proposed incremental procedure, the viscoelastic predictor and viscoplastic corrector algorithms are presented in a pseudo-code format in Algorithms 1 and 2, respectively. It should be mentioned that ABAQUS finite element software is utilized for performing the simulations and the proposed constitutive model is introduced to the software through the user-subroutine UMAT.

3 Uniaxial response

A set of uniaxial experimental tests is simulated here by means of the presented method. To this end, the parameters of the model need be calibrated first. Due to the rate-dependent response of concrete in both reversible and irreversible regimes, a single stress-strain curve does not provide enough information for obtaining a unique set of viscoelastic and viscoplastic parameters. Unlimited combinations of $E_1$, $E_2$, and $\eta$ can reproduce the desired initial slope of the stress-strain curve. However, these three can be adjusted such that the hysteresis loops of the numerical curve conform with the experimental ones. This also stands for the viscoplastic constants $c_1$ and $c_2$ since at least two magnification factors are needed to find the correct combination. In addition, both tensile and compressive responses are required for a full set of parameters. As a result, the parameters of concrete are calibrated by means of the laboratory tests of Gopalaratnam and Shah (1985) and Karsan and Jirsa (1969), which were carried out respectively on the tensile and compressive responses of concrete, and also the comprehensive surveys of Malvar and Ross (1998) and Bischoff and Perry (1991) regarding the tensile and compressive magnification factors of concrete under different strain rates. The calibration procedure starts by adjusting the stress-strain curves with the data reported in Gopalaratnam and Shah (1985) and Karsan and Jirsa (1969). A prescribed strain with a rate of 2 $\mu$strains per second is considered in the tensile test. The compressive test is also simulated using a strain rate of 20 $\mu$strains per second. Note that strength magnification is almost negligible for such low rates. Hence, the viscoplastic constants $c_1$ and $c_2$ do not affect the results. First, a combination of $E_1$, $E_2$, and $\eta$ that gives the desired initial slope is chosen. Then, by performing a trial and error process, a tensile strength of 3.4 MPa and compressive strength of 15 MPa are found in accordance with the peak value of the respective curves. Next, the nonlinear branch of the curves is utilized to find the tensile and compressive fracture energies $G_f^+$ and $G_f^-$, and hardening parameters $h^+$ and $h^-$. Since the tests are one-dimensional and the local response of concrete, i.e., the stress-strain curve, is of interest, the characteristic length must be defined explicitly. Otherwise, by varying the element size, the post-peak branch is affected. Note that the area under the stress-strain curve (whether in tension or compression) is equal to the ratio of the fracture energy to the characteristic length. Hence, these two always appear as a division and their ratio can be considered as an independent parameter. As a result, based on the works of Lee and Fenves (1998), Cicekli et al. (2007), Nguyen and Houlsby (2008), and many others, the characteristic length is set to a reasonable value of 75 mm, and the fracture energies $G_f^+$ and $G_f^-$, and hardening parameters $h^+$ and $h^-$ are found to be 45 N/m, 4350 N/m, 100 Mpa, and 50 Gpa, respectively. Next, by means of a trial and error process, the combination of $E_1$, $E_2$, and $\eta$ that reproduces acceptable hysteresis loops is found to consist of 70 Gpa, 30 Gpa, and 200 Gpa.s. The viscoplastic constants $c_1$ and $c_2$ can be defined by means of the surveys of Malvar and Ross (1998) and Bischoff and Perry (1991). However, based on the calibration of Ožbolt et al. (2006), these two are set to 0.032 and $500\times 10^{3}$ second, respectively, and the obtained magnification factors are validated by means of the surveys of Malvar and Ross (1998) and Bischoff and Perry (1991). The calibrated parameters are presented in Table 1.

Table 1 Parameters of concrete for the uniaxial tests

The tensile stress-strain curve resulted by means of the presented model is plotted against the experimental curve of Gopalaratnam and Shah (1985) in Fig. 5. The initial slopes, as well as the unloading slopes, are in good agreement. The hysteresis loops are also of similar shapes. However, the unloading branch of the experimental curve is steeper during the initial stages of damage growth, while the opposite can be observed for the latter stages. It can be claimed that fracture energies are somehow close since the area under the curves will be evened out if the loading process continues. Figure 6 presents the experimental and numerical compressive curves. Note that the experimental data is extracted from the work of Karsan and Jirsa (1969). The agreement between the initial slopes is acceptable. The area under the curves is also in good agreement and the overall trends are similar. Some discrepancies between the slope of the unloading branches can be observed. The presented model reproduced hysteresis loops, however, the experimental ones are of different shapes. It is worth mentioning that, since countless unknown factors and random phenomena are involved, capturing the exact features of an experimental curve is impossible, especially if a phenomenological model is utilized. However, the overall trends are in good agreement from the viewpoint of an engineer. The stress-strain curve of a cyclic test is plotted against the monotonic response in Fig. 7. Note that the strain rate was 2 $\mu$strains per second in the cyclic test. The crack closing and reopening effects are reproduced by the model.

Fig. 5

Stress-strain curve of the model under the uniaxial tensile loading against the experimental result of Gopalaratnam and Shah (1985)

Fig. 6

Stress-strain curve of the model under the uniaxial compressive loading against the experimental result of Karsan and Jirsa (1969)

Fig. 7

Monotonic and cyclic responses of concrete. The unilateral constraint that prevents penetration between the micro-crack faces causes a sudden change in stiffness during the transition from a tensile to a compressive stress state. The model has properly resembled this behavior

The rate-dependent response of concrete leads to an energy enhancement that manifests itself in the form of strength magnification. The magnitude of this enhancement can be characterized by a magnification factor, which is the ratio of the dynamic strength to the static strength of concrete. Malvar and Ross (1998) and Bischoff and Perry (1991) conducted comprehensive surveys on the tensile and compressive magnification factors of concrete under different strain rates. Their studies are employed in Fig. 8 and 9 to validate the proposed model. It can be seen in the figures that the model has reproduced realistic values of strength magnification in both conditions. It should be mentioned that the experimental values have progressively increased for the strain rates larger than 1 strain per second, while the numerical values have followed a linear trend. By increasing the loading rate of experiments, the inertia effects, which are caused by the stress wave propagation, are pronounced and the shape and configuration of the specimens dominate the magnitude of recorded peak values. Hence, the progressive increase in the experimental data is synthetic and does not pertain to the local constitutive response of concrete, but can be related to the inertia effects at the global structural scale. It has been demonstrated that the local behavior of concrete follows its linear trend when the rate effects are increased, and the rate-dependency of the concrete response is not responsible for this progressive increase (Ožbolt and Reinhardt 2005; Ožbolt et al. 2006; Travaš et al. 2009; Reinhardt et al. 2010; Ožbolt et al. 2011; Ožbolt and Sharma 2012). Here, the numerical tests are one-dimensional and the stress wave propagation is neglected in order to show the local behavior of concrete. If one wants to obtain the same progressive increase, multi-dimensional conditions must be considered and the inertia effects have to be included in the tests.

Fig. 8

Dynamic magnification factor of concrete in tension on a log-log plot against the experimental data of Malvar and Ross (1998)

Fig. 9

Dynamic magnification factor of concrete in compression on a log-log plot against the experimental data of Bischoff and Perry (1991)

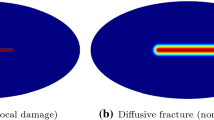
An important feature of the formulation is its ability in reproducing direction-dependent damage growth. This aspect, which is visualized by means of the presented model, is illustrated in Fig. 10. The figure shows damage densities along different directions considering four different loading conditions. Note that the closer a point to the surface, the more damage in that direction. For the uniaxial tension, the prescribed strain is imposed along the $x_3$-axis. It can be observed that the maximum damage growth occurred along that direction. The biaxial tension test is simulated by imposing equal strains along $x_2$ and $x_3$ axes. A donut-shaped distribution is obtained for this case. The prescribed shear strain $\varepsilon _{13}$ is assumed in the uniaxial shear test. The biaxial shear test is also simulated using equal prescribed shear strains $\varepsilon _{13}$ and $\varepsilon _{23}$. Peanut-shaped distributions are reported for the latter two. It is worth mentioning once again that since isotropic formulations are not capable of capturing such details, the rotation of the principal cracking direction, which occurs during mixed-mode tests, is completely neglected, leading to inaccurate or even incorrect results.

Fig. 10

Damage densities along different directions under four different loading conditions

4 Rate-independent mixed-mode cracking

Before proceeding to the rate-independent multidimensional case, the robustness of the model under mixed-mode conditions in the absence of the rate effects is examined here. To this end, the mixed-mode experiments of Gálvez et al. (1998) are chosen. The problem consists of two beams of similar concretes under different mixed-mode conditions. The test setup, which is shown in Fig. 11, was designed such that the cracking modes of the first and second tests are more of an opening and a shearing type, respectively. First, the material properties are calibrated by the load-CMOD curve of the first test, then they are validated by means of the curve of the second test. To this end, the finite element meshes shown in Fig. 12 are employed. Note that square-shaped elements are used across the possible crack propagation path.

Fig. 11

Geometry and boundary conditions of the beams in the rate-independent mixed-mode cracking problem. The beams have 50 mm width, and a notch with 2 mm width is induced at their midspan. By variating the stiffness of the spring k and depth of the notch d, two different setups were defined in Gálvez et al. (1998). For the first test, k was considered to be zero and a notch of a depth of 37.5 mm was considered. The second test was also defined by assuming $k=infty$, meaning that the beam is vertically constrained at the location of the spring, and the notch depth d was assumed to be 45 mm

The calibrated parameters are presented in Table 2. Note that the stiffness of the viscoelastic body $E_2$ is chosen to be 1000 times larger than $E_1$ so that it acts as a penalty factor to bypass the viscoelastic body. It is worth mentioning that all the other parameters do not affect the results, hence they are not reported in the table. The calibration procedure is performed on the first setup of the beams. To this end, $E_1$ is adjusted such that a valid initial slope for the load-CMOD curve is obtained. Then $\sigma _y^+$ is defined in accordance with the peak value of the experimental curve. Finally, the tensile fracture energy $G_f^+$ and tensile hardening $h^+$ are adjusted by means of the post-peak response. Note that the dimensionless constant a and the dilation constant $a_p$ are respectively about 0.12 and 0.2 for most concretes. Poisson’s ratio of concrete is also taken as 0.2 in most applications. Hence, these parameters are not calibrated and the reported values are used. The resulting curve is plotted on the experimental envelope in Fig. 13. With the calibrated parameters at hand, the second setup of which the load-CMOD curve is shown in Fig. 14 is then analyzed. The resulting crack paths are also presented in Fig. 15. It can be seen that by performing the calibration process on the first setup of the tests, the second one is simulated with a good level of accuracy.

Table 2 Parameters of concrete for the tests of Gálvez et al. (1998)

Fig. 12

Finite element meshes of the rate-independent mixed-mode cracking problem for the first type (left) and the second type (right) of the tests

Fig. 13

Comparison of the numerical load-CMOD curve with the experimental envelope for the first setup of the rate-independent mixed-mode problem

Fig. 14

Comparison of the numerical load-CMOD curve with the experimental envelope for the second setup of the rate-independent mixed-mode problem

5 Rate-dependent mixed-mode cracking

The experimental tests revealed that the rate effects influence the concrete response to such an extent that the failure mode of specimens is affected. John and Shah (1990) conducted a comprehensive study regarding this observation, which is revisited numerically in this work. Since their study covers a wide range of strain rates, their results are used here for assessing the robustness of the proposed constitutive model.

5.1 Problem description

The tests are performed on notched beams under different loading rates. The geometry and boundary conditions of the beams are presented in Fig. 16. As shown in the figure, each beam is notched with an offset factor (denoted by $\beta$) ranging from 0 to 1. For $\beta =0$ the notch is located at the midspan, and by increasing $\beta$ the offset is increased to the extent that $\beta =1$ means that the beam is un-notched. Four different strain rates were reported by John and Shah (1990), including 5$\times 10^{-7}$, 1$\times 10^{-4}$, 5$\times 10^{-2}$, and 3$\times 10^{-1}$ strain per second. As explained in John and Shah (1990), these strain rates were defined by means of the initial slope of the experimentally recorded strain-time curve at the location of the notch tip. These four cases with their respective applied velocities, which are obtained by a numerical trial and error process, are presented in Table 3.

Fig. 15

Contours of the maximum principal tensile damage for the first type (left) and the second type (right) of the tests

5.2 Calibration procedure

The parameters of concrete are calibrated in different steps. First the static response of the first mode of cracking (case 1 with the offset factor $\beta =0$) along with the reported values of the elastic modulus, critical stress intensity factor of the first mode of cracking, and critical crack tip opening displacement is used to find the stiffness of the elastic body $E_1$, the stiffness of the viscoelastic body $E_2$, the tensile strength $\sigma _y^+$, the tensile hardening $h^+$, and the tensile fracture energy $G_f^+$. Note that the viscosity parameter $\eta$ must be calibrated simultaneously with $E_1$ and $E_2$ using the four cases since the desired initial slope can be reproduced by unlimited combinations of $E_1$ and $E_2$ if the rate effects be neglected. The viscoplastic parameters are then calibrated by means of peak loads. Once again, the dimensionless constant a, the dilation constant $a_p$, and Poisson’s ratio are chosen to be 0.12, 0.2, and 0.2, respectively. In addition, the parameters that define the compressive response, which include the compressive strength $\sigma _y^-$, the compressive hardening $h^-$, and the compressive fracture energy $G_f^-$ are not applicable here; hence, they are not reported. The only remaining parameter is the characteristics length $\ell$. The ABAQUS solver calls the user-subroutine UMAT for each Gauss point of each element. This subroutine provides a parameter named celent, which is the square root of the area of the element in two-dimensional cases, and the cubic root of the volume of the element in three-dimensional ones. Due to the material softening response, strain localization occurs and the fracture process zone gets limited to the width of the softened element. As a result, the provided parameter can be considered as an estimation of the width of the fracture process zone. As a result, the characteristic length $\ell$ is defined automatically by the ABAQUS solver based on the geometry of the elements. It is worth mentioning that all the calibration process is performed by means of the midspan-notched beam, and the finite element model shown in Fig. 17 is used for this purpose.

Fig. 16

Geometry and boundary conditions of the beams in the rate-dependent mixed-mode cracking problem. The beams have 228.6 mm width, 76.2 mm height, and 25.4 mm thickness. The span of the beams (denoted by l) is 203.2 mm and a notch with 19.05 mm depth and 2 mm width with a semi-circular tip is induced with an offset factor (denoted by $\beta$) ranging from 0 (midspan-notched beam) to 1 (unnotched beam). The beams are loaded by imposing a constant velocity on 20 mm of the middle part of their upper edge

5.2.1 Viscoelastic parameters

The calibration procedure starts by finding the elastic modulus of concrete. At this point, since the viscosity parameter $\eta$ is unknown, unlimited combinations of $E_1$ and $E_2$ can reproduce the desired response. Hence, $E_1$, $E_2$, and $\eta$ have to be calibrated at the same time. Using all four cases, these there parameters are calibrated as 35 MPa, 115 MPa, and 250 MPa.s, respectively. The resulting elastic modulus are compared wth the reported data in Fig. 18, showing that the calibrated parameters provide acceptable elastic response in all four cases.

Table 3 Load cases of the rate-dependent mixed-mode tests. Each case is identified by a strain rate (second column), which is the initial slope of the experimentally recorded strain-time curve at the notch tip (John and Shah 1990). Similar to the reference, the first and last cases are hereafter referred to as the static and impact rates, respectively. Note that the applied velocities (third column) are obtained by a trial and error process using the numerical model

Fig. 17

Finite element model of the midspan-notched beam. The beams are discretized by means of plane stress bi-linear quadrilateral finite elements and a full integration scheme using four Gauss points is employed. Note that square-shaped elements are used across the possible crack propagation path

Fig. 18

Comparison of the numerically- and experimentally-obtained elastic modulus of concrete under different loading rates

5.2.2 Fracture parameters

The two parameter fracture model of Jenq and Shah (1985), which is briefly discussed in the following, is used in the reference (John and Shah 1990) for determining the fracture properties of the beams. According to the linear elastic fracture mechanics, the following relations hold for the three-point bending test of a midspan-notched beam:

$$\begin{aligned}&K_I = \sigma \sqrt{\pi d} f_1 , \end{aligned}$$

(124)

$$\begin{aligned}&\delta _m = \frac{4\sigma d}{E} f_2 , \end{aligned}$$

(125)

$$\begin{aligned}&\delta = \delta _m f_3 , \end{aligned}$$

(126)

where $K_I$ is the stress intensity factor of the first mode of cracking, d is the depth of crack, $\delta _m$ is the crack mouth opening displacement, E is the elastic modulus, $\delta$ is the crack opening displacement, and

$$\begin{aligned}&\sigma = \frac{3pl}{2tw^2} , \end{aligned}$$

(127)

$$\begin{aligned}&f_1 = \frac{1.99-\lambda (1-\lambda )(2.15-3.93\lambda +2.7\lambda ^2)}{\sqrt{\pi }(1+2\lambda )(1-\lambda )^{3/2}} , \end{aligned}$$

(128)

$$\begin{aligned}&f_2 = 0.76 - 2.28\lambda + 3.87\lambda ^2 - 2.04\lambda ^3 + \frac{0.66}{(1-\lambda )^2} , \end{aligned}$$

(129)

$$\begin{aligned}&f_3 = \big ((1-\rho )^2-(1.149\lambda -1.081)(\rho -\rho ^2)\big )^{1/2} , \end{aligned}$$

(130)

where p is the applied load, l, w, and t are respectively the span, height and thickness of the beam, and

$$\begin{aligned}&\lambda = \frac{d_i}{w} , \end{aligned}$$

(131)

$$\begin{aligned}&\rho = \frac{x}{d} , \end{aligned}$$

(132)

wherein $d_i$ is the initial depth of crack (i.e., equal to the depth of the notch) and x is the vertical distance from the bottom edge of the beam. As a result, the relation in (126) gives the crack mouth opening displacement $\delta _m$ for $x=0$ and the crack tip opening displacement $\delta _t$ for $x=d$.

Fig. 19

Typical load-CMOD curve of a three-point bending test

Fig. 20

Finite element meshes of the beam. Note that the elements of the possible crack propagation path have 2 mm side length in the left mesh and 1 mm side length in the right mesh. For briefness, these meshes are simply denoted by the coarse and fine meshes hereafter

The typical load-CMOD response of a three-point bending test is shown in Fig. 19. As shown in the figure, the initial compliance $C_i$ and the critical compliance $C_c$ can be defined on the curve. On the other hand, by substituting the relation in (127) into (125) and performing some algebraic manipulations, the compliance C reads

$$\begin{aligned} C = \frac{\delta _m}{p} = \frac{6ld}{Etw^2} f_2 . \end{aligned}$$

(133)

Hence, the elastic modulus of concrete can be obtained by substituting the initial compliance $C_i$ into the above relation as follows:

$$\begin{aligned} E = \frac{6ld}{C_itw^2} f_2 . \end{aligned}$$

(134)

During the pre-peak nonlinear regime, crack growth occurs within the specimen. Hence, the critical compliance $C_c$ is employed to find the depth of crack at the peak load, $d_c$, as follows:

$$\begin{aligned} d_c = \frac{EC_ctw^2}{6lf_2} . \end{aligned}$$

(135)

Hence, according to the relations in (124) and (125), the critical stress intensity factor of the first mode of cracking $K_{Ic}$ is obtained By

$$\begin{aligned} K_{Ic} = \frac{E\delta _{mc}f_1}{4f_2}\sqrt{\frac{\pi }{d_c}} , \end{aligned}$$

(136)

wherein $\delta _{mc}$ is extracted from the curve. Finally, the critical crack tip opening displacement reads

$$\begin{aligned} \delta _{tc}= & {} \delta _{mc} \big ((1-\rho _c)^2-(1.149\lambda -1.081)\nonumber \\{} & {} \quad \times (\rho _c-\rho ^2_c)\big )^{1/2}, \end{aligned}$$

(137)

where

$$\begin{aligned} \rho _c = \frac{d_i}{d_c} . \end{aligned}$$

(138)

Fig. 21

Comparison of the numerical and experimental load-COD curves. Note that CODs are measured at 1.6 mm above the crack mouth

Fig. 22

Contours of the maximum principal tensile damage for the coarse (left) and fine (right) meshes

The first mode of cracking under the static loading conditions is employed for the calibration process. The elastic modulus of concrete was estimated between 28 and 30 GPa in John and Shah (1990). The critical stress intensity factor of the first mode of cracking was also approximated between 880 and 1000 kPa$\sqrt{\text {m}}$. On the other hand, in plane stress conditions we have (Zehnder 2012)

$$\begin{aligned} G_f = \frac{K_{Ic}^2}{E} . \end{aligned}$$

(139)

Hence, the fracture energy of concrete is estimated between 25 and 35 N/m. Using the static load-COD response of the beam, the tensile strength $\sigma _y^+$, tensile hardening $h^+$, and tensile fracture energy $G^+_f$ are calibrated as 4.5 MPa, 10 MPa, and 25 N/m, respectively. The mesh objectivity of the global responses is also analyzed by means of the meshes shown in Fig. 20. The resulting load-COD curves are plotted on the experimental data in Fig. 21. The crack profiles are also presented in Fig. 22. Although the localized band of the coarse mesh is twice thicker than that of the fine mesh, the post critical branch of the load-COD curves shows no sign of mesh dependency. In addition to the numerical and experimental curves, the values of the elastic modulus E, critical stress intensity factor of the first mode of cracking $K_{Ic}$, and critical crack tip opening displacement $\delta _{tc}$ are compared in Table 4.

5.2.3 Viscoplastic parameters

The final step of the calibration process is to find the viscoplastic constants $c_1$ and $c_2$. Referring to the logarithmic plots in Fig. 8 and 9, the first constant defines the slope of the curve while the second one defines its offset from the horizontal axis. Finding the correct combination of these two constants requires at least two magnification factors. However, John and Shah (1990) only reported the peak loads of the static (case 1) and impact (case 4) rates. As a result, only one magnification factor is available and one of the constants must be chosen arbitrarily. Hence, only the viscoplastic constants $c_1$ is adjusted and the calibrated value of the uniaxial tests (Fig. 8 and 9) is chosen for $c_2$. According to the reference (John and Shah 1990), the peak load of the static and impact loading rates were 1449 and 1718 kPa, respectively. Hence, the magnification factor under the strain rate $\dot{\varepsilon }=0.3$ was 1.1856, which is reproduced numerically by setting $c_1=0.018$ and $c_2=500\times 10^3$ second.

Table 4 Comparison of the experimental and numerical values of the elastic modulus E, critical stress intensity factor of the first mode of cracking $K_{Ic}$, and critical crack tip opening displacement $\delta _{tc}$ under the static loading conditions

Table 5 Parameters of concrete for the rate-dependent mixed-mode problem

5.3 Inertia effects

With all of the required parameters at hand, which are summarized in Table 5, we can investigate the dynamic cracking of concrete by means of the proposed constitutive model. To this end, the effects of wave propagation on the global responses are analyzed first. It has been pointed out by John and Shah (1990) that the wave propagation effects can be neglect for the strain rates under 0.5 strain per second. A similar deduction is made here by loading the midspan-notched beam using the impact strain rate (case 4). For this purpose, the test is simulated twice, once under the quasi-static conditions wherein the inertia effects are neglected, and once under the dynamic conditions with realistic wave propagation effects. The load-COD curves of both simulation are presented in Fig. 23, showing that although the result of the dynamic case is of oscillatory nature, the overall trends are similar. Hence, all of the future simulations are made under the quasi-static assumption.

5.4 Rate effects

The load versus COD responses of the midspan-notched beam assuming different strain rates (the cases of Table 3) are plotted in Fig. 24. The peak values as well as the initial slope of the curves are affected by the loading rate.

Fig. 23

Load-COD curve of case 4 under the quasi-static and dynamic conditions. Although the result of the dynamic case oscillates about the quasi-static response, the overall trends are similar. As a result, the inertia effects can be neglected without losing accuracy. It is also mentioned by John and Shah (1990) that the wave propagation phenomenon does not affect the solutions for the strain rates under 0.5 strain per second

Fig. 24

Load versus COD curve of the concrete beam under different loading rates

Fig. 25

Crack profiles for offset factors of 0.65, 0.70, 0.75, and 0.80 under the static and impact loading rates. The failure mode transition reported in John and Shah (1990) occurred between $\beta =0.65$ and $\beta =0.70$ for the static lading rate, while it happened between $\beta =0.75$ and $\beta =0.80$ for the impact loading rate

5.5 Failure mode transition

It has been experimentally observed by John and Shah (1990) that two possible failure modes exist for a notched beam under mixed-mode conditions. Depending on the notch offset, the failure may occur at the notch tip or at the midspan. They showed that an offset factor exists for which the measured peak load is the same whether the beam fails at either of those two locations. This offset factor, denoted by $\beta _t$, corresponds to a transition stage wherein both failure mechanisms demand equal energies. The mode of failure is more of a brittle one for $\beta <\beta _t$ since a diagonal crack grows from the notch tip and the beam undergoes a tension-shear failure. On the other hand, for $\beta >\beta _t$, a flexural failure occurs wherein the crack grows from the midspan along an almost straight path. John and Shah (1990) also showed that the loading rate affects the failure mechanism so that larger values of $\beta _t$ would be obtained if the rate effects are increased. Here, the reported failure mode transition is studied by means of the presented model. To his end, the geometry of the beam is defined by assuming different locations for the notch, and the beams are loaded under the static and impact strain rates. The crack profiles for offset factors of 0.65, 0.70, 0.75, and 0.80 are reported in Fig. 25. According to the profiles, it can be deduced that the offset factor of the transition stage is somewhere between $\beta =0.65$ and $\beta =0.70$ for the static loading rate, while it is found to be between $\beta =0.75$ and $\beta =0.80$ for the impact loading rate. The peak values are also compared with the predicted values of John and Shah (1990) in Fig. 26. The offset factors of the transition stage, which are at the points where the horizontal lines intersect with the curves, are shown in the figure. Note that John and Shah (1990) used a linear elastic fracture mechanics approach for their predictions. They reported the same failure mode transition, but with slightly smaller values of $\beta _t$.

If the well-posedness of field equations is preserved, e.g., through nonlocal or gradient-enhanced theories, the localized region can run freely across the medium regardless of the element shapes. It should be mentioned that a fine mesh whose elements are small enough to resolve a fracture process zone of width $\ell$ is needed, otherwise, the well-posedness of equations is invalidated. Here, no regularization is assumed and the ill-posedness of the field equations remains untreated. Hence, the crack is obliged to follow a path that conforms with the mesh. In the presented numerical tests, the beams are discretized in a structured fashion and square-shaped elements are used across the possible crack propagation path. Hence, the crack tends to follow a vertical or horizontal line. This tendency can be observed at the latter stages of cracking under the impact loading rates for which straight diagonal cracks are expected. This directional bias can be treated by decreasing the size of elements and/or changing the shape and type of elements.

Fig. 26

Predicted and approximated values of the peak load for different values of $\beta$ under the static and impact loading rates. Note that the predicted curves were obtained based on a linear elastic fracture mechanics approach by John and Shah (1990). The offset factors of the transition stage for both static and impact loading rates are at the points where the horizontal lines intersect with the curves

6 Conclusion

A constitutive model for the rate-dependent cracking of concrete was formulated. The viscoelastic response was included for resembling the dissipative mechanisms pertaining to rate-dependent reversible straining. Rate-dependency was introduced to the yield surface by means of a proper logarithmic function, providing the capability of reproducing valid strength magnifications under a wide range of strain rates. An exponential damage growth function was considered to characterize the degradation of concrete, and the mesh-objectivity of responses was guaranteed by establishing a relation between the fracture energy of concrete and the rate of damage growth. The effective stress tensor was decomposed to the tensile and compressive parts, and damage-induced anisotropy was included by assembling a damage tensor for each part. Next, the temporal discretization of the constitutive equations was pursued by means of a backward Euler scheme, a fully implicit two-step viscoelastic predictor/viscoplastic corrector algorithm was presented, and the iterative procedure of the Newton–Raphson scheme was outlined for finding the solution of the nonlinear return-mapping equation. Finally, the constitutive model was used for simulating some laboratory experiments, which showed the capability of the formulation in reproducing the cracking of concrete under different loading rates. In addition, the experimentally observed transition of the failure mode from a ductile flexural failure to a brittle diagonal failure was properly reproduced by the model.

The presented model benefits from a frame-independent tensorial damage description that is absent in its predecessors. This feature renders the induced mechanical damage anisotropic, providing a more reliable approach with respect to the isotropic ones in terms of predicting the global response and crack profile of specimens. The reason lies in the fact that isotropic models are incapable of distinguishing damage growth direction. As a result, excessive loading along a specific axis affects the material integrity in all directions. Hence, they overestimate damage intensity, especially in mixed-mode conditions. This leads to erroneous stress redistribution and may affect the crack profiles. The presented model, on the other hand, includes the damage-induced anisotropiy through a set of damage tensors. The robustness of this assumption was demonstrated by means of an experimental observation in which two beams of similar concretes are loaded under different mixed-mode conditions.

In conclusion, the different aspects of the presented model are summarized as follows: the stiffness degradation is reproduced through the damage growth, irreversible strains are defined by means of the plasticity theory, the unilateral contact effects are resembled by the stress tensor decomposition, stiffness magnification and strength amplification due to the rate effects are included by considering the viscoelastic and viscoplastic behaviors, and last but not least, the damage-induced anisotropy is added by means of tensorial damage growth.