A nonlocal damage model for plain concrete consistent with cohesive fracture

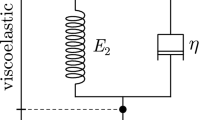
Abstract

A rate-independent damage constitutive law is proposed to describe the fracture of plain concrete under tensile loading. Here, the target scale is the individual crack. In order to deal with localised damage, the model is inherently nonlocal: the gradient of the damage field is explicitly involved in the constitutive equations; it is parameterised by a nonlocal length scale which is interpreted as the width of the process zone. The model is defined so that its predictions are close to those of a cohesive law for vanishing nonlocal length scales. Therefore, the current model is plainly consistent with cohesive zone model analyses: the nonlocal length scale appears as a small parameter which does not need any specific identification. And four parameters—among which the tensile strength and the fracture energy—enable to adjust the softening cohesive response. Besides, a special attention has been paid to the shape of the initial damage surface and to the relation between damage and stiffness. The damage surface takes into account not only the contrast between tensile and compressive strengths but also experimental evidences regarding its shape in multiaxial tension. And the damage–stiffness relation is defined so as to describe important phenomena such as the stiffness recovery with crack closure and the sustainability of compressive loads by damaged structures. Finally, several comparisons with experimental data (global force/opening responses, size dependency, curved crack paths, crack opening profiles) enable to validate qualitatively and quantitatively the pertinence of the constitutive law in 2D and 3D.

1 Introduction

Predicting the fracture of concrete structures has been the subject of many works in the past 40 years. Here, the focus is put on modelling the different stages of fracture under tensile loading, from crack initiation up to potentially large crack propagation. For that purpose, the models at hand can be broadly split in two families: cohesive zone models and continuum damage models.

The former ones have also been named “fictitious crack models” in the pioneering work of Hillerborg et al. (1976) who applied successfully to concrete some ideas introduced by Barenblatt (1959) and Dugdale (1960) for metallic materials. These models explicitly introduce a displacement discontinuity across the (fictitious) crack as a function of the stress applied on the crack faces (the cohesive law). They depend on macroscopic quantities such as the ultimate strength and the fracture energy which are accessible by standardised experiments. Their capabilities have been demonstrated with respect to crack initiation and crack propagation, see for instance Bazant and Planas (1998) and Elices et al. (2002). However, predicting crack paths in 3D still appears as a complex issue in terms of reliability and robustness: a crack orientation criterion has to be stated in complement to the cohesive law while numerical difficulties may arise from the requirement to ensure the geometrical continuity of the cracks. It remains the purpose of on-going work, see Gasser and Holzapfel (2006), Jäger et al. (2008) and Oliver et al. (2014).

On the other hand, continuum damage models are advocated for predicting crack path since they describe the local degradation of concrete through a damage field, hence implicitly giving access to crack patterns whatever their topology, see the seminal articles (Marigo 1981; Bazant and Oh 1983; Mazars 1986). However, strain-softening constitutive relations lead to ill-posed boundary value problems which numerically result in pathological mesh-dependency as soon as damage localisation arises, see for instance Benallal et al. (1993). It has been related to high strain and damage gradients which admittedly appear in fracture process zones and thus preclude using local constitutive laws because the latter are based on a length scale separation assumption which does not hold anymore. Two main classes of enhanced models have been proposed in the literature to control strain and damage gradients. The first one is based on introducing rate-dependency into the constitutive law, see Needleman (1988), Sluys and de Borst (1992) and Suffis et al. (2003). The gradients are indeed limited in the case of dynamic loading thanks to the interaction of viscosity with wave velocity which results in a length scale, but uncontrolled gradients and mesh-dependent localisation are retrieved in the quasi-static limit (de Borst et al. 1993; Forest and Lorentz 2004). In the second class of models, a spatial coupling of the behaviour of neighbour material points of the structure is introduced; the approach is cast under the generic name “nonlocal laws”. Many variants ensure such a coupling:

• The thick level set method where a given damage profile is enforced inside narrow bands the boundaries of which obey a propagation law, see Moës et al. (2011).

• Smoothing local variables through regularisation operators, also known as localisation limiters, usually convolution operators, e.g. Bazant and Pijaudier-Cabot (1988), or differential operators, e.g. the implicit gradient model in Peerlings et al. (1996).

• The introduction of additional kinematic variables the gradient of which are penalised, see Pijaudier-Cabot and Burlion (1996) for micro-void dilation, de Borst and Sluys (1991) and Steinmann and Willam (1991) for Cosserat media or Forest (2009) for a generalisation to micromorphic media.

• The introduction of higher order gradients of displacements (Triantafyllidis and Aifantis 1986; Fernandes et al. 2008).

• The introduction of internal variable gradients (Mühlhaus and Aifantis 1991; Fremond and Nedjar 1996; Svedberg and Runesson 1997; Lorentz and Andrieux 1999; Liebe et al. 2001; Benallal and Marigo 2007; Pham et al. 2011).

Some of these variants are strongly related, see Lorentz and Andrieux (1999, 2003) and Forest (2009). And all of them introduce at least one additional parameter with the dimension of a length, the so-called internal length scale which weights the strength of nonlocal coupling. Because of the latter, the relation between the parameters of the model and experimental measurements—the fracture energy in particular—is not straightforward. Moreover, such models are usually not well adapted to capture the ultimate stage of damage as a crack. It motivates on-going work dedicated to the quite delicate transition from a damage field to a cohesive (or free-surface) crack during the numerical computation, see Simone et al. (2003), Mediavilla et al. (2006), Comi et al. (2007) and Cuvilliez et al. (2012). Despite these drawbacks, acceptable predictions are nevertheless obtained with damage nonlocal models, at least for relatively limited crack propagations, see for instance Pamin (2011) for selected illustrative applications.

As can be seen, the respective qualities of cohesive zone models and continuum damage models are complementary. This article aims at showing in the context of concrete how a nonlocal damage model of the internal variable gradient type may also benefit from the attractive properties of fictitious crack models, that is: (i) describing large crack propagations which includes the access to the current crack opening and the fulfilment of a total degradation with zero residual stress; (ii) controlling the dissipated fracture energy per crack surface unit; (iii) avoiding any specific identification of an internal length. To this end, the key property is the consistency of the damage model with a cohesive law for vanishing internal lengths (i.e. the predictions of both models are close to each other). Numerical simulations and their confrontation with experimental results will assess the robustness and the accuracy resulting from the theoretical properties of the model and the phenomenological choices that have been made to address salient physical characteristics of concrete.

More precisely, the outline is the following. In the next section, a class of gradient damage models is presented and its consistency with cohesive zone models is showed. Then, specific phenomenological refinements are proposed in order to deal with the shape of the softening response in tension, the contrasted behaviour of concrete in tension and compression and the coupling between cracking and directional stiffness. Finally, several numerical simulations are compared to experimental results in order to validate the global force–displacement response, the crack opening distribution and the crack path prediction.

2 Theoretical framework for quasi-brittle damage

A framework for quasi-brittle damage is presented in this section. It is based on nonlocal constitutive equations into which the gradient of damage is explicitly introduced. Such a setting has been given a variational basis in Lorentz and Andrieux (1999) and it has been specialised to damage in Lorentz and Godard (2011). Then the nonlocal constitutive equations are showed to be consistent with a cohesive law under some conditions. Some of the results have already been expressed in Lorentz et al. (2011, 2012) and will be recalled shortly. Here, they are extended to a wider class of constitutive laws in order to encompass the constitutive novelties of the Sect. 3 required by the physical characteristics of concrete.

2.1 Modelling assumptions

The class of constitutive relations considered in this nonlocal setting are restricted to isotropic damage so that the acknowledged anisotropy of concrete fracture results from the localisation of damage at the structure level which implies to model actually each single crack. As stated in Fichant et al. (1999), the assumption of isotropy may prove acceptable for a wide range of applications, provided that stiffness recovery with crack closure is taken into account which is the objective of the Sect. 3.3.

In addition, no damage mechanism in compression is considered in this study which focuses on tensile damage. Therefore there is no need to describe a pre-peak hardening regime. Nevertheless, the dissymmetry between tensile and compressive strengths is modelled so that elastic compressive states are sustained without triggering spurious damage (they may result from self-weight load or prestressing for instance). And the reduction of the tensile strength under partially compressive states should also be taken into account. This calls for a dedicated failure surface in the stress space as introduced in the Sect. 3.2.

Besides, damage-induced inelastic strains are not considered in the model either. Such an assumption is reasonably acceptable when focusing on tensile damage. But complex loading paths such as cyclic loading lay out of the scope of the model.

In addition, only rate-independent dissipative mechanisms are considered in the analysis: coupling creep and damage would need further enhancements. This precludes long lasting load histories.

Finally, as the damage model aims at providing a description of fracture which is consistent with a cohesive zone model, it is not intended to reflect accurately the cracking behaviour at a fine scale and it retains only the macroscopic characteristics of the cohesive law. In practice, a single scalar field—the damage field—parameterises the local stiffness degradation and provides a spatial regularisation of an actual cohesive crack. It can be noticed that this is in strong relation with the framework of phase-field models, already applied in Bourdin et al. (2000, 2008), Del Piero et al. (2007), Miehe et al. (2010) and Sicsic and Marigo (2013) to predict Griffith type crack initiation and propagation according to the formulation in Francfort and Marigo (1998).

2.2 A class of gradient damage models

2.2.1 State equation

Accordingly to the set of assumptions enumerated above, the damage field consists of a single scalar field a which ranges from 0 to 1, the former corresponding to the sound initial state while the latter stands for a complete loss of stiffness in tension. In agreement with the assumption of no inelastic strain, the elastic strain energy ${\mathcal {W}}$ formally reads:

$$\begin{aligned} {\mathcal {W}}\left( \mathbf {u},a \right) =\int \limits _{\Omega }\hbox {w}\left( \mathbf {\upvarepsilon }(\mathbf {u}),a \right) \,d\Omega \end{aligned}$$

(1)

where $\Omega$ denotes the body domain, u the displacement, ${\varvec{{\upvarepsilon }}}$ the infinitesimal strain and w the elastic strain energy density. As there is no viscous effects, the stress simply derives from this energy leading to the state equation:

$$\begin{aligned} {\varvec{{{\upsigma } }}}=\frac{\partial \hbox {w}}{\partial {\varvec{{\upvarepsilon }}}}\left( {{\varvec{{\upvarepsilon }}},a} \right) \end{aligned}$$

(2)

The stress field hence retains its usual interpretation, thanks to the fact that the nonlocal interactions do not explicitly involve the strain field. Consequently, this holds true for the equilibrium equations as well.

According to Pham and Marigo (2013), the energy density function $\hbox {w}$ should fulfil the following properties:

• it is continuously differentiable in order to get a continuous stress–strain response;

• it is positive and decreasing with respect to damage leading to stiffness degradation;

• it is positive homogeneous of degree 2 with respect to the strain so that the stress is positive homogeneous of degree 1 which corresponds to linear radial elasticity;

• it is strictly convex with respect to the strain as long as $a<1$ so that the solution to the elasticity problem (for frozen bounded damage) exists and is unique.

In addition, we restrict our attention to isotropic elasticity, so that $\hbox {w}$ should be isotropic with respect to the strain tensor. In particular, the elastic energy density for the sound material is the usual quadratic isotropic elastic energy $\hbox {w}^{e}\left( {\varvec{\upvarepsilon }} \right)$:

$$\begin{aligned} \hbox {w}\left( {{\varvec{\upvarepsilon }},0} \right) =\hbox {w}^{e}\left( {\varvec{\upvarepsilon }} \right)= & {} \frac{1}{2}{{\varvec{\upvarepsilon }} :\mathbf{E }:{\varvec{\upvarepsilon }} }\nonumber \\= & {} \frac{1}{2}\left[ {\lambda \left( {\hbox {tr}{\varvec{\upvarepsilon }}} \right) ^{2}+2\upmu \; {{\varvec{\upvarepsilon }} :{\varvec{\upvarepsilon }} }} \right] \end{aligned}$$

(3)

with $\mathbf{E}$ the Hooke tensor, $\lambda$ and $\upmu$ the Lamé coefficients (we denote also E the Young modulus and $\upnu$ the Poisson ratio when needed). Finally a complete loss of stiffness in tension is expected for ultimate damage in order to avoid residual cohesive forces across the crack. This requirement is expressed as:

$$\begin{aligned} \left[ {\forall \;i\quad {\upvarepsilon } _i \ge 0} \right] \quad \Rightarrow \quad {{\varvec{{\upsigma }}} }\left( {{\varvec{\upvarepsilon }},1} \right) =0 \end{aligned}$$

(4)

where ${\upvarepsilon } _i$ stands for the eigenvalues of the strain tensor. Note that the expression (4) relies on a minimalist interpretation of tensile states as the strain states for which the extension ratio is positive in any direction ($\mathbf{n}\cdot {\varvec{\upvarepsilon }}\cdot \mathbf{n}\ge 0\;\;\forall \;\mathbf{n})$. Complementary analyses are developed in the Sect. 3.3.

2.2.2 Evolution equation

Next to the definition of the strain energy and the corresponding stress–strain relation, a damage evolution law is stated. The evolution equation is expressed at the scale of the structure, as proposed in Germain et al. (1983) for generalised standard materials:

$$\begin{aligned} -\;\frac{\partial {\mathcal {G}}}{\partial a}\left( {{\varvec{\upvarepsilon }},a} \right) \in \partial {\mathcal {D}}\left( {\dot{a}} \right) \end{aligned}$$

(5)

where the following potentials have been introduced:

$$\begin{aligned}&{\mathcal {G}}\left( {{\varvec{\upvarepsilon }}},a \right) =\int \limits _{\Omega }{\Psi \left( {{\varvec{\upvarepsilon }} },a \right) d\Omega }+\int \limits _{\Omega }{\frac{c}{2} \nabla a\cdot \nabla a \, {d\Omega }}\end{aligned}$$

(6)

$$\begin{aligned}&{\mathcal {D}}\left( {\dot{a}} \right) =\int \limits _{\Omega }{k\,\dot{a}\,d\Omega +{{{\text {I}}}_{{{\mathbb {R}}^{+}}}}\left( {\dot{a}} \right) } \end{aligned}$$

(7)

In (5), a dot denotes time-differentiation, $\partial {\mathcal {D}}$ stands for the subgradient of the dissipation potential ${\mathcal {D}}$ (which extends the notion of derivatives to constitutive laws with thresholds) and the left-hand side term is the driving force associated to damage. $\hbox {I}_{\mathbb {R}^{+}}$ in (7) is the indicator function which is equal to zero for positive damage rate field and else equal to $+\;\infty$. Before commenting the expressions of ${\mathcal {G}}$ and ${\mathcal {D}}$, it should be noted that according to (Lorentz and Andrieux 1999) the evolution equation (5) can be given an equivalent interpretation in terms respectively of a damage threshold g, a consistency condition, a boundary condition along $\partial \Omega$ (the boundary of the body $\Omega$, with $\mathbf{n}$ denoting its normal) and two interface conditions across any surface $\Upsilon$ of normal ${{\varvec{\upnu }} }$ (where $[\![\cdot ]\!]$ denotes the discontinuity across $\Upsilon$):

$$\begin{aligned}&\hbox {g}\left( {{\varvec{\upvarepsilon }},a} \right) \mathop =\limits _{def.} -\;\;\frac{\partial \Psi }{\partial a}\left( {{\varvec{\upvarepsilon }},a} \right) +\mathrm{div}\left( {c \nabla a} \right) -k \end{aligned}$$

(8)

$$\begin{aligned}&\hbox {g}\left( {{\varvec{\upvarepsilon }},a} \right) \le 0;\quad \dot{a}\ge 0;\quad \mathrm{g}\left( {{\varvec{\upvarepsilon }},a} \right) \dot{a}=0\quad \hbox {in }\;\Omega \end{aligned}$$

(9)

$$\begin{aligned}&\nabla a\cdot \mathbf{n}=0\quad \hbox {along }\partial \Omega \end{aligned}$$

(10)

$$\begin{aligned}&[\![a]\!] =0;\quad [\![{c\;\nabla a}]\!] \cdot {{\varvec{\upnu }} }=0\quad \text {across } \Upsilon \end{aligned}$$

(11)

Strictly speaking, the second equality in (11) should be an inequality, see Sicsic et al. (2014). However, the equality holds indeed as soon as the initial damage state is itself consistent with (11), thanks to the positivity of the damage evolution in (9). Therefore, only the equality is retained in (11).

With this more practical expression of the evolution equation at hand, we can now come back to the definitions (6) and (7). First, the indicator function in the dissipation potential enforces that $\dot{a}\ge 0$, that is damage irreversibility; it is retrieved in the consistency condition (9).

The second term in the potential ${\mathcal {G}}$ controls the nonlocal interactions and results in the term div$\left( {c \nabla a} \right)$ in (8). The strictly positive parameter c weights the nonlocal interactions: the larger c, the smoother the damage field. Moreover, it enforces the regularity of the damage field: $a\in \mathrm{H}^{1}\left( \Omega \right)$. In particular, damage discontinuities are precluded, as stated in (11). This has an important consequence: only the gradient of bounded variables should be introduced in (6), as done here since $0\le a\le 1$. Indeed, consider a variable that goes to infinity when a true crack (with displacement discontinuity) appears, for instance the strain or an unbounded damage measure. Were its gradient introduced in (6), it would never reach the infinite value corresponding to a true crack because of the $\mathrm{H}^{1}\left( \Omega \right)$ regularity. Worse, because of the gradient regularisation, the localisation of strain and damage would spread along the initial localisation band, leading to an increasing (and erroneous) band width. This shortcoming is observed with most models based on strain regularisation, see Peerlings et al. (2002), and requires specific treatments such as a varying regularisation weight or an explicit transition to a crack.

Note also that the interface and boundary conditions are stated on the damage field itself and not on its rate, contrarily to other gradient models, e.g. Mühlhaus and Aifantis (1991). Thus, the boundary conditions do not require distinguishing whether the damage/elastic interface reaches the body boundary or not.

The positive parameter k and the function $\Psi \left( {{\varvec{\upvarepsilon }},a} \right)$ defines the current damage threshold via (9). In particular, the domain of reversibility in the strain space should increase with increasing damage for the sake of local stability, see again Pham and Marigo (2013), which implies that ${\partial \Psi }{/}{\partial a}$ is an increasing function of damage, i.e. that the potential $\Psi$ is a convex function of damage.

Finally, it appears that damage initiation is ruled by a local criterion. Indeed, before damage occurs, $a=0$ and $\hbox {div}\left( {c \nabla a} \right) =0$ everywhere in the structure, so that no damage initiates as long as:

$$\begin{aligned}&\forall \;\mathbf{x}\in \Omega \quad {\varvec{\upvarepsilon }}(\mathbf{x})\in {\mathcal {E}}^{0}\quad \quad \hbox {with}\nonumber \\&\quad {\mathcal {E}}^{0} =\left\{ {{\varvec{\upvarepsilon }}\;\;\hbox {s.a.}\;\;-\;\frac{\partial \Psi }{\partial a}\left( {{\varvec{\upvarepsilon }},0} \right) \le k} \right\} \end{aligned}$$

(12)

where ${\mathcal {E}}^{0}$ denotes the initial domain of reversibility in the strain space. In particular, it is independent of the gradient term and its weight factor c. Note that the locus where damage initiates and the corresponding load level are governed by the local criterion, on the contrary of other nonlocal models for which the nonlocal interactions play a role before inception of damage, see Simone et al. (2004).

Fig. 1

Derivation of the asymptotic cohesive law

2.2.3 Energy balance

In this presentation, there is no relation a priori between the strain energy w and the potential $\Psi$ in order to enable some degrees of freedom when coping with the physical characteristics of concrete (Sect. 3). Nevertheless, it can be noticed that the constitutive law belongs to the class of generalised standard materials as soon as $\hbox {w}=\Psi$ for any strain and damage values, see Germain et al. (1983) and Lorentz and Andrieux (1999), which automatically ensures thermodynamic admissibility. Here, the positivity of the rate of fracture energy can also be assessed. Indeed, in isothermal conditions, the elastic Helmholtz strain energy ${\mathcal {W}}$ plus the energy required to damage the material, say ${\mathcal {F}}$, should be equal to the energy provided to the structure. In rate forms, it reads:

$$\begin{aligned} {\mathcal {P}}_\textit{ext} =\dot{{\mathcal {W}}}+\dot{{\mathcal {F}}} \end{aligned}$$

(13)

where ${\mathcal {P}}_{ext}$ denotes the power of external forces. As the equilibrium equations are left unchanged compared to a local model, the rate of fracture energy is given by:

$$\begin{aligned} {\dot{\mathcal {F}}}={{{\mathcal {P}}}_{ext}}-{\dot{\mathcal {W}}}=\int \limits _{\Omega }{\left( -\ \frac{\partial {\text {w}}}{\partial a}\dot{a} \right) d\Omega } \end{aligned}$$

(14)

The density of elastic strain energy is decreasing with respect to damage so that ${\partial }\hbox {w}{/}{\partial a}\le 0$. In addition, the evolution of damage is irreversible: $\dot{a}\ge 0$. Therefore, no energy is retrieved through the damage process, as expected: $\dot{{\mathcal {F}}}\ge 0$.

2.3 Consistency with a cohesive law

The application of a gradient damage model as introduced in the Sect. 2.2 is expected to lead to the concentration of damage in zones of small (but non zero) thickness. The notion of consistency with a cohesive law should then be understood as follows, see also the Fig. 1 for an illustrative explanation.

First, the response of the model in terms of damage and strain distribution along ligaments (lines) transverse to the damage zone (i.e. along its thickness) is idealised as a one-dimensional problem. It consists of a bar subjected to a prescribed displacement at its ends and laterally confined. The progressive development of a damage band is expected up to the ultimate failure of the bar.

Then, the final width of the damage band is interpreted as a length scale which results from the nonlocal effects. And for a given value of this nonlocal length scale, the response of the model can be characterised in a global way through the history of the (homogeneous) stress in the bar versus the opening or separation displacement through the damage band (i.e. the displacement gap between both boundaries of the final damage band).

Finally, it will be showed analytically that the limit of the global responses for vanishing nonlocal length scales is actually the response of a cohesive law in terms of stress versus separation displacement. The convergence is assessed for a nonlocal length scale that goes to zero while macroscopic quantities derived from the model parameters stay constant (e.g. the peak stress and the fracture energy). As will be seen below, such a property is established under additional constitutive assumptions on the form of the elastic energy density $\hbox {w}\left( {{\varvec{\upvarepsilon }},a} \right)$ and the potential $\Psi \left( {{\varvec{\upvarepsilon }},a} \right)$ in (8).

2.3.1 One-dimensional setting: definition of the degradation function

Consider a straight bar of direction $\mathbf{t}$ and of length sufficiently large, i.e. larger than the forthcoming damage band width. It is subjected to a tensile loading while the displacement along its lateral faces is prescribed to remain parallel to $\mathbf{t}$ (confinement), see again the Fig. 1. The strain field can be assumed as:

$$\begin{aligned} {\varvec{\upvarepsilon }}\left( \mathbf{x} \right) ={\upvarepsilon } \left( x \right) \mathbf{t}\otimes \mathbf{t}\quad \hbox {with}\quad \upvarepsilon \ge 0 \end{aligned}$$

(15)

where $\upvarepsilon$ denotes the strain magnitude and x the (longitudinal) position along the bar. The damage field also depends only on x and we assume that it concentrates inside a single band which does not cross the ends of the bar, say the interval $\left[ {-b\;\;b} \right]$ without loss of generality. The band spreads (i.e. b increases) until the damage field reaches its critical value $a=1$ somewhere inside the band, which corresponds to breaking the bar in two pieces. The current damage band is then denoted $\left[ {-D\;\;D} \right]$ where D is taken as the nonlocal length scale. And the separation displacement ${\updelta }$ is defined during the load history as:

$$\begin{aligned} {\updelta } =\int \limits _{-\ D}^{D}{\upvarepsilon \left( x \right) \, dx} \end{aligned}$$

(16)

Consider now the strain energy. For zero damage, the elastic strain energy density is defined according to the Eq. (3):

$$\begin{aligned} \hbox {w}\left( {\upvarepsilon \,\mathbf{t}\otimes \mathbf{t},\;0} \right)= & {} \hbox {w}^{e}\left( {\upvarepsilon \, \mathbf{t}\otimes \mathbf{t}} \right) \,\,\nonumber \\= & {} \frac{E_c }{2}{\upvarepsilon } ^{2} \quad \hbox {with} \,\,E_c =\lambda +2\upmu \end{aligned}$$

(17)

where $E_c$ is the initial one-dimensional confined stiffness. Besides, thanks to the property of positive homogeneity of degree 2 with respect to ${\varvec{\upvarepsilon }}$, the elastic strain energy density reduces to:

$$\begin{aligned} \hbox {w}\left( {{\upvarepsilon } \,\mathbf{t}\otimes \mathbf{t},\;a} \right) =\hbox {A}\left( a \right) \frac{E_c }{2}{\upvarepsilon } ^{2} \end{aligned}$$

(18)

It defines a function $\hbox {A}\left( a \right)$ which quantifies the progressive stiffness reduction and is referred to as the degradation function. It does not depend on $\mathbf{t}$ thanks to the isotropy of w and it should depend on the sign of ${\upvarepsilon }$ but the latter is considered positive in (15) (tension). Since the elastic strain energy is positive and decreasing with damage, it implies that A is a positive and decreasing function. And the continuity of $\mathrm{w}$ at $a=0$ implies that $\hbox {A}\left( 0 \right) =1$.

Finally, the state Eq. (2) leads to the expression of the longitudinal stress field ${\upsigma } =\mathbf{t}\cdot {\varvec{{\upsigma }}}\cdot \mathbf{t}$ in tension through the application of Euler’s identity:

$$\begin{aligned}&2\hbox {w}\left( {{\varvec{\upvarepsilon }},a} \right) ={{\varvec{{\upvarepsilon }}} \mathbf :}\frac{\partial \hbox {w}}{\partial {\varvec{\upvarepsilon }}}\left( {{\varvec{\upvarepsilon }},a} \right) =\left( {\upvarepsilon \,\mathbf{t}\otimes \mathbf{t}} \right) \mathbf{:}{\varvec{{\upsigma }}} =\upvarepsilon {\upsigma } \quad \Rightarrow \nonumber \\&{\upsigma } =\hbox {A}\left( a \right) E_c\, \upvarepsilon \end{aligned}$$

(19)

Moreover, thanks to the isotropy of the strain energy, the stress tensor admits the same eigen-directions as the strain tensor, in particular the direction $\mathbf{t}$. The shear components ${{\upsigma }}_{xy}$ and ${{\upsigma }} _{xz}$ are hence equal to zero. In addition, as the stress components in the plane $y-z$ normal to $\mathbf{t}$ depend only on x (because the strain and the damage depend only on x), the equilibrium equation reduces to:

$$\begin{aligned} \frac{\partial \upsigma }{\partial x}=0 \end{aligned}$$

(20)

Regarding the degradation function, an additional condition is provided through (4). Indeed, thanks to the confinement boundary conditions, all the strain eigenvalues are positive (or equal to zero). This is the condition stated in (4) under which the stress should vanish for ultimate damage (no stiffness recovery in tension). The Eq. (19) then implies that $\hbox {A}\left( 1 \right) =0$.

Finally, the solution of the 1D problem is governed by the evolution equation (9) in one dimension, the interface conditions (11), the stress–strain relation (19) and the equilibrium equation (20) which states that the longitudinal stress component is constant in the bar.

2.3.2 One-dimensional solution in terms of stress: separation response

The solution of the one-dimensional problem and its convergence towards the solution of a cohesive zone model have been established in (Lorentz and Godard 2011; Lorentz et al. 2012) under additional constitutive assumptions. Indeed, the former publications are based on a gradient damage model which belongs to the class of generalised standard materials: it corresponds to the framework of the Sect. 2.2 with the special case $\hbox {w}=\Psi$. In the present 1D case, such a condition would result in:

$$\begin{aligned} \Psi \left( {\upvarepsilon \,\mathbf{t}\otimes \mathbf{t},\;a} \right) =\hbox {A}\left( a \right) \frac{E_c }{2}{\upvarepsilon }^{2} \end{aligned}$$

(21)

We propose here to relax the constraint $\hbox {w}=\Psi$ for general strain tensors while preserving the equality (21). To that end, only the following class of potentials $\Psi$ are considered from now on:

$$\begin{aligned} \forall \;\left( {{\varvec{\upvarepsilon }},a} \right) \quad \Psi \left( {{\varvec{\upvarepsilon }},a} \right) =\hbox {A}\left( a \right) \Gamma \left( {\varvec{\upvarepsilon }} \right) \end{aligned}$$

(22)

where the function $\Gamma$ is positive, isotropic, positive homogeneous of degree 2 and fulfils $\Gamma \left( {\mathbf{t}\otimes \mathbf{t}} \right) ={E_c }/2$ because of (21). Note that as $\Psi$ should be convex with respect to a, the function $\hbox {A}\left( a \right)$ should be convex too.

Thanks to the constitutive choice (22), the results formerly established in 1D for a generalised standard material remain applicable. The main points are recalled hereafter. First, a closed-form expression of the strain field gives access to the separation displacement ${\updelta }$ through (16). In particular, its critical value ${\updelta } _c$ when the damage reaches $a=1$ inside the damage band is finite and not equal to zero if and only if the degradation function $\hbox {A}\left( a \right)$ behaves as $\left( {1-a} \right) ^{2}$ in the neighbourhood of $a=1$. In this case, the strain at failure is a Dirac distribution. Such a form for the degradation function is assumed from now on, as has been done for instance in (Comi 1999; Bourdin et al. 2000; Amor et al. 2009):

$$\begin{aligned} \hbox {A}\left( a \right) \;\;\propto \;\;\left( {1-a} \right) ^{2}\quad \hbox {when}\;\;a\rightarrow 1 \end{aligned}$$

(23)

Moreover, three characteristics of the response of the bar can be calculated: the nonlocal length scale D which is defined as half the final damage band width, the confined peak stress ${\upsigma } _c$ which is actually reached at damage inception (no initial hardening) and the fracture energy per unit area $G_F$ obtained by integration of (14) with respect to the time:

$$\begin{aligned} D=\sqrt{\frac{2 c}{k}};\quad {\upsigma }_c =\sqrt{-\;\;\frac{2E_c k }{{\hbox {A}}^{\prime }\left( 0 \right) }};\quad G_F =\frac{4}{3}k D \end{aligned}$$

(24)

This enables conversely the expression of the internal parameters of the model in terms of these more convenient characteristic values of the fracture process, including in particular the nonlocal length scale D:

$$\begin{aligned} k=\frac{3}{4}\frac{G_F }{D};\quad c=\frac{3}{8}D G_F;\quad {\hbox {A}}^{\prime }\left( 0 \right) =-\;\;\frac{3}{2}\frac{E_c G_F }{\upsigma _c^2 D}\nonumber \\ \end{aligned}$$

(25)

The degradation function $\hbox {A}\left( a \right)$ itself hence appears as an internal characteristic of the model. We choose to rewrite it without loss of generality as:

$$\begin{aligned}&\hbox {A}\left( a \right) =\frac{\left( {1-a} \right) ^{2}}{\left( {1-a} \right) ^{2}+\frac{3}{2}\frac{E_c G_F }{\upsigma _c^2 D} a \bar{{\hbox {A}}}\left( a \right) }\nonumber \\&\quad \Leftrightarrow \bar{{\hbox {A}}}\left( a \right) =\frac{2}{3}\frac{{\upsigma } _c^2 D}{E_c G_F }\frac{\left( {1-a} \right) ^{2}}{ a}\left[ {\frac{1}{\hbox {A}\left( a \right) }\;-\;1} \right] \end{aligned}$$

(26)

where $\bar{{\hbox {A}}}\left( a \right)$ is a continuously differentiable, strictly positive and bounded function so that $\hbox {A}\left( a \right)$ indeed behaves as $\left( {1-a} \right) ^{2}$ in the neighbourhood of $a=1$ and with $\bar{{\hbox {A}}}\left( 0 \right) =1$ so as to fulfil the condition on ${\hbox {A}}'\left( 0 \right)$ in (25). It is referred to as the reduced degradation function. The separation displacement and the stress in the bar admit the following parametric expressions, where $a_0$ denotes the current maximal damage in the bar and the normalised functions $\bar{{{\updelta } }}\left( {a_0 } \right)$ and $\bar{{\upsigma }}\left( {a_0 } \right)$ only depend on the function $\bar{{\hbox {A}}}$:

$$\begin{aligned}&\frac{{\updelta } \left( {a_0 } \right) }{{G_F }{/}{{\upsigma } _c }}=\bar{{{\updelta } }}\left( {a_0 } \right) +D\;\frac{2 {\upsigma }_c^2 }{E_c G_F }\bar{{{\upsigma } }}\left( {a_0 } \right) ;\quad \nonumber \\&\frac{{\upsigma } \left( {a_0 } \right) }{{\upsigma } _c }=\bar{{{\upsigma } }}\left( {a_0 } \right) \end{aligned}$$

(27)

$$\begin{aligned}&\bar{{\updelta } }\left( {{a}_{0}} \right) =\frac{3}{2}\bar{{\upsigma } }\left( {{a}_{0}} \right) \int \limits _{0}^{{{a}_{0}}}{\frac{\bar{\hbox {A}}(a)\,\sqrt{a}}{{{\left( 1-a \right) }^{2}}}{{\left[ 1-\frac{\bar{\hbox {A}}\left( a \right) {{\left( 1-{{a}_{0}} \right) }^{2}}}{\bar{\hbox {A}}\left( {{a}_{0}} \right) {{\left( 1-a \right) }^{2}}} \right] }^{\ -\ \frac{1}{2}}}da}\quad \ ;\ \nonumber \\&\bar{{\upsigma } }\left( {{a}_{0}} \right) =\frac{1-{{a}_{0}}}{\sqrt{\bar{\hbox {A}}\left( {{a}_{0}} \right) }} \end{aligned}$$

(28)

2.3.3 Asymptotic cohesive law

The convergence study corresponds to a vanishing nonlocal length scale D with frozen confined stiffness $E_c$, peak stress ${\upsigma }_c$ and fracture energy $G_F$. This choice affects the type of the asymptotic model: for instance, Bourdin et al. (2000) did not maintain the peak stress constant in their analysis and obtained a convergence towards a Griffith fracture law (with infinite peak stress). In the present case, the response $\left( {{\updelta } ,{\upsigma } } \right)$ provided in (27) evidently admits a cohesive limit $\left( {{\updelta } _{czm}, {\upsigma } _{czm} } \right)$ for vanishing values of D. This response is given in a parametric format, with the functions $\bar{{{\updelta } }}\left( {a_0 } \right)$ and $\bar{{{\upsigma } }}\left( {a_0 } \right)$ defined in (28):

$$\begin{aligned} {\updelta } _{czm} \left( {a_0 } \right)= & {} \frac{G_F }{{\upsigma } _c }\bar{{{\updelta } }}\left( {a_0 } \right) ;\nonumber \\ {\upsigma } _{czm} \left( {a_0 } \right)= & {} {\upsigma } _c \bar{{{\upsigma } }}\left( {a_0 } \right) \quad \hbox {with}\quad 0\le a_0 \le 1 \end{aligned}$$

(29)

If the function $\bar{{\hbox {A}}}$ does not depend on ${\upsigma } _c$ neither on $G_F$, then the cohesive law is deduced from a “master response” or normalised response $\left( {\bar{{{\updelta } }},\bar{{{\upsigma } }}} \right)$ which characterises the shape of the cohesive response.

Fig. 2

Diversity of the stress states in a three-point bending SENB

The graph of such a cohesive response is plotted in red in the Fig. 1 for a given type of function $\bar{{\hbox {A}}}$ which will be detailed later in the Sect. 3.1. It highlights the properties of the cohesive law: perfect adhesion (${\updelta } =0)$ below the initial stress threshold ${\upsigma } _c$ (extrinsic cohesive law, i.e. without initial compliance), then a decrease of the stress with increasing separation displacement when damage occurs (no snap-back) and at last failure with zero stress and a finite critical separation displacement corresponding to a true crack. Thanks to the closed-form expressions (28), the initial softening slope and the final separation ${\updelta } _c$ can be calculated; they respectively read:

$$\begin{aligned}&\left. {\frac{d{\upsigma } _{\mathrm{czm}} }{d{\updelta } _{\mathrm{czm}} }} \right| _{a_0 =0} =\frac{2}{3 \uppi }\;\left( {{\bar{{\hbox {A}}}}'(0)+2} \right) ^{3/2}\frac{{\upsigma }_c^2 }{G_F };\nonumber \\&{\updelta } _c =\frac{3\uppi }{4}\;\sqrt{\bar{{\hbox {A}}}\left( 1 \right) }\;\frac{G_F }{{\upsigma } _c } \end{aligned}$$

(30)

At last, note that several constraints should be fulfilled by the degradation function $\hbox {A}$ (hence also by the function $\bar{{\hbox {A}}})$ in order to ensure its convexity, an increasing damage band width $\hbox {b}\left( {a_0 } \right)$ and a decreasing stress ${\upsigma } \left( {a_0 } \right)$, the latter being a condition of objectivity for the cohesive law (Bazant 2002). These constraints restrict the choice of the function $\bar{{\hbox {A}}}$. In particular, two necessary conditions can be derived whatever the expression of $\bar{{\hbox {A}}}$:

$$\begin{aligned} {\bar{{\hbox {A}}}}'(0)\ge 1;\quad D\le \frac{3}{2\left( {{\bar{{\hbox {A}}}}'(0)+2} \right) }\;\frac{E_c G_F }{{\upsigma } _c^2 } \end{aligned}$$

(31)

The latter sets an upper bound to the nonlocal length scale (half the damage band width) relatively to the cohesive length ${E_c G_F}{/}{{\upsigma } _c^2 }$ introduced in Hillerborg et al. (1976) for concrete and related to the length of the process zone.

2.3.4 Extension to the 2D and 3D cases

The demonstration of convergence towards a cohesive law is rigorous in the confined uniaxial case. However, the distribution of the stress field in a 2D configuration illustrates why the convergence property does not plainly transfer to 2D or 3D cases. Indeed, consider a single-edge notched beam (SENB) subjected to three-point bending. Anticipating the forthcoming developments, the damage model specialised to concrete and summarised in the Sect. 3.4 is applied under a plane-strain assumption. The stress field history is analysed in terms of two quantities: the component of the stress tensor in the direction parallel to the notch ${\upsigma } _{yy}$ and an indicator of biaxiality $\upxi$ which is defined as follows through the eigenvalues of the stress tensor ${\upsigma } _I \ge {\upsigma } _\textit{II}$ in the plane of the simulation:

$$\begin{aligned} {\upsigma } _I= & {} \sqrt{{\upsigma } _I^2 +{\upsigma } _\textit{II}^2 }\;\cos \left[ {\left( {\upxi -1} \right) \frac{\uppi }{4}} \right] ;\nonumber \\ {\upsigma } _\textit{II}= & {} \sqrt{{\upsigma } _I^2 +{\upsigma } _\textit{II}^2 }\;\sin \left[ {\left( {\upxi -1} \right) \frac{\uppi }{4}} \right] \end{aligned}$$

(32)

With this definition, bi-compression (CC), uniaxial compression (C), pure shear (CT), uniaxial tension (T) and biaxial tension (TT) correspond respectively to $\upxi$ equal to –2, –1, 0, 1 and 2. And the confined uniaxial state corresponds to $\upxi \approx 1.3$ when the Poisson ratio $\upnu$ is equal to 0.2. The results are plotted in the Fig. 2 where each point in both graphs corresponds to a given geometrical point of the beam with position $\mathbf{x}$ and at a given time t: the x-axis indicates the corresponding level of damage $a\left( {\mathbf{x},t} \right)$ while the y-axis is $\upsigma _{yy} \left( {\mathbf{x},t} \right)$ in the right-hand side graph and the biaxiality indicator $\upxi \left( {\mathbf{x},t} \right)$ in the left-hand side graph. In order to focus on the damage zone, only the points where damage occurs are actually plotted. Besides, the evolution undergone by the geometrical point P located 10 mm ahead of the notch tip is highlighted in red in the graphs.

This stress history illustrates two limitations which preclude an extension of the convergence property from 1D to 2D or 3D configurations:

• The 1D case should be representative of the real behaviour across the damage band. However, a lateral boundary condition has been stated (longitudinal displacement only) which appears quite arbitrary: why should there be some confinement instead of a free boundary condition, for instance? In fact, the stress history in the Fig. 2 shows that the stress components follow various and complex paths which do not correspond to a single lateral boundary condition in the 1D case. Note however that most damaging points of the beam are close to a “mainstream” path which goes to a value of 1.3 with increasing damage, i.e. a stress state which corresponds indeed to the confined boundary condition. And the mainstream path lies always away from the value 1 which corresponds to a free boundary condition.

• The damage criterion encompassed in the potential $\Psi$ should depend not only on the strain component across the crack (i.e. along $\mathbf{t}$ in the 1D case) but also on the strain components parallel to the crack plane, as stated in Bazant (2002). They are not negligible, see for instance the Fig. 2 for the component ${\upsigma } _{yy}$, in agreement with the results of Linear Fracture Mechanics where the mode I singular stress field in the wake of the crack has the following expression:

  $$\begin{aligned} {\upsigma } _{xx} {=}\frac{K_I }{\sqrt{2\uppi r}};\quad {\upsigma } _{yy} =\frac{K_I }{\sqrt{2\uppi r}};\quad {\upsigma } _{zz} {=}\frac{2 \upnu K_I }{\sqrt{2\uppi r}}\nonumber \\ \end{aligned}$$

  (33)

  where $\upnu$ is the Poisson ratio, x denotes the crack direction, y the load direction normal to the crack, z the crack front direction, $K_I$ the stress intensity factor and r the distance to the crack tip. Although the in-plane components are not negligible, their influence is not included in classical cohesive zone models which hence cannot be the rigorous limit of the damage model in 2D or 3D configurations. Nevertheless, this is true mostly at the beginning of damage, with impact on the tensile strength. When damage growths, the strain component transverse to the crack becomes far larger than the in-plane components (since it tends to a Dirac distribution) and a relatively confined strain state is retrieved.

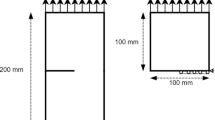
Therefore, even though both limitations preclude an extension of the convergence property to 2D and 3D cases, there is some hope for a reasonable agreement between the asymptotic cohesive law and the nonlocal damage model. It can be assessed numerically in the case of mode I loading in terms of global force–displacement response, crack initiation and crack opening. To this end, a virtual mock-up is considered which consists of a containment wall enclosing a pressurised internal chamber as depicted in the Fig. 3. The thickness of the wall is set to (unusually) large values of 4 m on the left side and 2 m on the right side so that large crack propagations and large crack opening are enabled. In addition, the elliptical shape of the cavity (on the right side) leads to a tensile stress concentration which triggers the crack propagation along the symmetry plane. As a result, the crack path is predictably rectilinear (hence enabling an easy comparison with the cohesive zone model) but the crack history is quite rich: initiation on the right side then on the left side of the cavity, crack propagation on both sides then crack arrest on the left side until the right side crack reaches (unstably) the external boundary of the wall and finally stable crack propagation towards the left side wall boundary. The numerical comparison between cohesive crack and nonlocal damage is conducted again with the model specialised to concrete that will be described in the Sect. 3. However, its precise expression is not necessary here and can be temporarily skipped for the sake of simplicity; just notice the relevant numerical values used in the simulations: $G_F =0.1\;\hbox {N/mm}$, ${\upsigma } _c \approx 3\;\hbox {MPa}$, ${\updelta } _c =0.135\;\hbox {mm}$ and $D=50\;\hbox {mm}$ (for nonlocal damage).

Fig. 3

Numerical mock-up: pressurised internal chamber

The main results are provided in the Fig. 3 for both the nonlocal damage model and the cohesive zone model. First, it can be observed that damage is mostly localised inside a band of constant width $2\times D$ and does not spuriously spread with increasing crack opening. Besides, the global responses in terms of the internal pressure vs. the variation of the cavity volume are indeed close to each other; in particular, the crack histories are qualitatively the same. Moreover, the crack opening displacements are compared for a given loading stage (point A of the global response) where one of the crack has emerged on the external boundary while the other one is still propagating. Again, the displacements are close to each other even inside the active process zone ($0\le {\updelta } \le {\updelta } _c )$.

In conclusion, the nonlocal damage model takes into account all the strain and stress components contrarily to the cohesive zone model which ignores the components parallel to the crack plane. Therefore, the convergence of the nonlocal model toward the cohesive law for vanishing nonlocal length scales seems out of reach, even though mathematical approaches based on the tools and techniques from the calculus of variations will maybe lead in the future to a class of damage models fulfilling this convergence property in 3D (in the sense of $\Gamma$-convergence), see Bourdin et al. (2008) and references therein, or more recently (Freddi and Iurlano 2017). Nevertheless, it can be observed in the Fig. 3 that the numerical responses of both damage and cohesive models remain reasonably close to each other not only with respect to a global force–displacement response but also regarding the crack opening profiles, at least for mode I loading. Both formulations are hence consistent with each other. In addition, it confirms that the nonlocal damage model may give access to reliable crack opening in a straightforward way (displacement discontinuity across the crack surface measured at the distance of ±D), a property which is not straightforward with any nonlocal model, see for instance Dufour et al. (2008).

3 Specialisation to concrete behaviour

In the previous section, a general setting for quasi brittle materials has been presented under the assumptions of isotropic, rate-independent and tension-driven damage. At this stage, three degrees of freedom remain to be defined: the reduced degradation function $\bar{{\hbox {A}}}\left( a \right)$, the strain dependence $\Gamma \left( {\varvec{\upvarepsilon }} \right)$ in (22) and the elastic strain energy density $\hbox {w}\left( {{\varvec{\upvarepsilon }},a} \right)$. These inputs of the damage framework characterise respectively:

• The softening response in radial tensile loading

• The shape of the damage threshold in the strain space

• The effect of partial crack closure on the stress–strain relation

Specific expressions for these functions are proposed in the forthcoming subsections in order to account for the phenomenological characteristics of concrete.

3.1 Softening response

3.1.1 Design of softening functions with respect to experimental softening curves

The choice of a reduced degradation function $\bar{{\mathrm{A}}}$ and the resulting softening stress—separation response is a trade-off between simplicity and realism with respect to concrete behaviour. It is subjected to several constraints among which $\bar{{\mathrm{A}}}\left( 0 \right) =1$ and $\bar{{{\mathrm{A}}'}}\left( 0 \right) \ge 1$. The simplest choice consists of an affine function with a single parameter p:

$$\begin{aligned} \bar{{\mathrm{A}}}\left( a \right) =1+p a\quad \hbox {with}\quad p\ge 1 \end{aligned}$$

(34)

Experimental softening curves have been obtained by Peterson (1981) on the basis of (delicate) tensile experiments. Some results are gathered in the Fig. 4; they concern different types of concrete which differ through their age, their water-cement ratio and the size of their aggregates. A curve fitting is performed with the affine function (34) in order to evaluate the best parameter p for each class of concrete: the softening curves corresponding to the affine function roughly fit the experimental ones, see the dashed lines in the Fig. 4.

Fig. 4

Experimental versus predicted softening curves for different concretes

However, the identification of p clearly results from a trade-off between the initial and the final stage of the softening response since this single parameter characterises the whole normalised softening response. According to Hoover and Bazant (2014), a model where the beginning and the final stage of the softening curve cannot be controlled independently may have limited accuracy when predicting structural responses. Even though the softening law (29) is not covered by their analysis, it hints at somewhat enhancing the expression (34). Therefore, an extended expression is proposed for the function $\bar{{\mathrm{A}}}\left( a \right)$ where an additional parameter q is introduced:

$$\begin{aligned} \bar{{\mathrm{A}}}\left( a \right) =1+p \,a\exp \left( {q^{2}a^{2}} \right) \quad \hbox {with}\quad p\ge 1 \end{aligned}$$

(35)

This specific form results from investigations on polynomial expansions and their effects on the softening curve and the fulfilment of the convexity and damage band enlargement constraints stated in the Sect. 2.3. In particular, q should not be greater than an upper bound $q_{\max } \left( p \right)$ plotted in the Fig. 5. As $q=0$ coincides with the former expression (34), the comparison against the data provided in Peterson (1981) is necessarily better than previously, see indeed the Fig. 4 (plain lines): the simulations are now in satisfactory agreement with the experimental measurements.

3.1.2 Comparison with SENB experimental responses

Even though the use of the more complex degradation function (35) necessarily leads to a better agreement with experimental softening responses, it is interesting to assess how much the burden of calibrating a new parameter q is worth with respect to structural responses. To this end, the quantitative influence of the parameter q is evaluated on a single edge notch beam (SENB), see the Fig. 6 where the experimental results are taken again from Peterson (1981).

Fig. 5

Upper bound for the parameter q

Fig. 6

Effect of the softening law on the response of a SENB (Peterson 1981)

The geometry and the material parameters of the beam—including the tensile strength and the fracture energy—are provided by Peterson (1981) and recalled in the Fig. 6. Therefore, only the parameters p and q remain to be calibrated. The first step is focused on the peak force. A parametric computation the results of which are depicted in the Fig. 6 gives the dependence of the computed peak force with respect to p and q. In particular, it appears that both parameters affect the peak force. As the average experimental value of the latter is equal to 0.763 kN, it narrows the possible combinations of p and q: it corresponds to the black thick line in the left hand side graph in the Fig. 6. For the simple degradation function ($q=0)$, this is enough to identify $p=1.30$. However, the simulated force–displacement response for the beam (red curve in the right hand side graph of the Fig. 6) lies slightly outside the experimental range. When using the enhanced degradation function, a second calibration step is necessary to obtain the best combination of p and q, leading to a peak force of 0.763 kN and the closest numerical response to the average experimental response. After optimisation, it results in the pair p = 1.03 and q = 1.47. Now the corresponding simulated force–displacement response (the black curve in the Fig. 6) lies inside the experimental range.

In conclusion, using the enhanced degradation function somewhat improves the results, as expected since it is an extension of the affine degradation function. Nevertheless, the numerical responses with both functions remain relatively close to each other so that the affine degradation function (34), i.e. setting $q=0$, is probably sufficient for a first guess.

3.2 Damage threshold

Up to now, the evolution of damage has been stated in the context of uniaxial tensile loading only, in relation with the degradation function $\bar{{\mathrm{A}}}\left( a \right)$ involved in the stress–strain relation. Thus, the dependence of the damage evolution with respect to the load direction still remains to be defined. Thanks to the split between radial evolution and direction dependency introduced in (22), the knowledge of the initial domain of reversibility in the strain space—denoted ${\mathcal {E}}^{0}$ and introduced in (12)—provides the information required to complement the definition of the damage evolution law as shown hereafter. The quantitative consequences of the shape of ${\mathcal {E}}^{0}$ on the crack propagation are then highlighted and finally a phenomenological criterion for damage inception is proposed.

3.2.1 Introducing a directional dependency into the damage evolution law

The damage evolution law is characterised by the potential $\Psi$ according to (6). An attractive choice would have consisted in casting the model into the framework of generalised standard materials by setting $\Psi \left( {{\varvec{\upvarepsilon }},a} \right) =\hbox {w}\left( {{\varvec{\upvarepsilon }},a} \right)$. In that way the strain energy density w would have governed the radial evolution of damage and the dependency on the strain direction. Unfortunately, it appears difficult to define a function $\hbox {w}\left( {{\varvec{\upvarepsilon }},a} \right)$ consistent with an acceptable stress–strain relation and at the same time leading to a sufficient contrast between the compressive strength $f_c$ and the tensile strength $f_t$, say ${f_c }{/}{f_t }\approx 10$ for concrete. Therefore, we had to depart from the standard generalised material framework, with practical consequences such as the loss of the tangent operator symmetry or the emergence of challenging questions regarding possible definitions of stability as introduced for instance in Nguyen (1994) and Benallal and Marigo (2007).

A compromise has been introduced in (22) with $\Psi \left( {{\varvec{\upvarepsilon }},a} \right) =\hbox {A}\left( a \right) \Gamma \left( {\varvec{\upvarepsilon }} \right)$: the strain energy still governs the damage evolution in confined uniaxial tension in order to preserve the consistency with a cohesive law for vanishing nonlocal length scales while the directional dependency is taken into account through the separate and independent function $\Gamma \left( {\varvec{\upvarepsilon }} \right)$. We recall that the latter is required to be positive, isotropic, positive homogeneous of degree 2 and normalised through $\Gamma \left( {\mathbf{t}\otimes \mathbf{t}} \right) ={E_c }/2$ for any unit vector $\mathbf{t}$. According to (12), (22) and (25), the initial elastic domain ${\mathcal {E}}^{0}$ is then characterised by:

$$\begin{aligned} {\mathcal {E}}^{0}=\left\{ {{\varvec{\upvarepsilon }}\;\;\hbox {s.a.}\;\;\Gamma \left( {\varvec{\upvarepsilon }} \right) \le \Gamma _c } \right\} \quad \hbox {with}\quad \Gamma _c =\frac{1}{2}\frac{\upsigma _c^2 }{E_c} \end{aligned}$$

(36)

where the threshold value $\Gamma _c$ is consistent with the fact that the strain ${\varvec{\upvarepsilon }}={{\upsigma } _c }{/}{E_c } \mathbf{t}\otimes \mathbf{t}$ lies on the boundary of ${\mathcal {E}}^{0}$ by definition of ${\upsigma } _c$. As ${\varvec{\upvarepsilon }}=0$ belongs to ${\mathcal {E}}^{0}$ since $\Gamma (\mathbf{0})=0$, (36) defines actually the function $\Gamma$ in every strain direction, its values along a given radial direction being set by the condition of positive homogeneity of degree 2.

Fig. 7

Derivation of $\upchi$(${\varvec{{\upvarepsilon }}}$) from a damage surface

In practice, consider that ${\mathcal {E}}^{0}$ is classically described by a damage threshold function $\hbox {f}_{\mathcal {E}} \left( {\varvec{\upvarepsilon }} \right)$, continuous and isotropic, through the condition ${\mathcal {E}}^{0}=\left\{ {{\varvec{\upvarepsilon }}\;;\;\;\hbox {f}_{\mathcal {E}} \left( {\varvec{\upvarepsilon }} \right) \le 0} \right\}$. As in Besson et al. (2001), we introduce a strain measure $\upchi \left( {\varvec{\upvarepsilon }} \right)$ which depends only on ${\mathcal {E}}^{0}$; it is defined by the following implicit relation:

$$\begin{aligned} \forall \;{\varvec{\upvarepsilon }}\quad \hbox {f}_{\mathcal {E}} \left( {\frac{{\varvec{\upvarepsilon }}}{\upchi \left( {\varvec{\upvarepsilon }} \right) }} \right) =0 \end{aligned}$$

(37)

$\upchi$ is positive, isotropic and positive homogeneous of degree 1. A graphical interpretation is provided in the Fig. 7 which shows that $\upchi \left( {\varvec{\upvarepsilon }} \right)$ quantifies how large ${\varvec{\upvarepsilon }}$ is with respect to the amplitude of the damage threshold in the direction of ${\varvec{\upvarepsilon }}$. According to the results detailed in the “Appendix A”, the definition (37) of $\upchi$ is well-posed provided that ${\mathcal {E}}^{0}$ is closed, convex and contains a neighbourhood of the point ${\varvec{\upvarepsilon }}=0$. And ${\mathcal {E}}^{0}$ corresponds to the set of strain tensors such that:

$$\begin{aligned} {\mathcal {E}}^{0}=\left\{ {{\varvec{\upvarepsilon }}\;\;\hbox {;}\;\;\upchi \left( {\varvec{\upvarepsilon }} \right) \le 1} \right\} \end{aligned}$$

(38)

A comparison of (38) with (36) indicates finally that the function $\Gamma$ should be defined as follows:

$$\begin{aligned} \Gamma \left( {\varvec{\upvarepsilon }} \right) =\Gamma _c \;\upchi \left( {\varvec{\upvarepsilon }} \right) ^{2} \end{aligned}$$

(39)

The knowledge of the damage threshold function $\hbox {f}_{\mathcal {E}}$ hence enables the definition of the function $\Gamma \left( {\varvec{\upvarepsilon }} \right)$. If $\hbox {f}_{\mathcal {E}}$ is continuous, convex and $\hbox {f}_{\mathcal {E}} \left( \mathbf{0} \right) <0$, then ${\mathcal {E}}^{0}$ is closed, convex and contains a neighbourhood of the point ${\varvec{\upvarepsilon }}=0$, so that $\upchi$ and $\Gamma$ are also convex and continuous with respect to ${\varvec{\upvarepsilon }}$, according to the “Appendix A”.

This construction can be easily extended to the case where the initial elastic domain is defined in the stress space instead of the strain space (it is then denoted ${\mathcal {S}}^{0})$. Indeed, as stressed by the word “initial”, the definition of the domain is prior to any damage. According to (3), the stress–strain relation hence simply reads ${\varvec{{\upsigma }}}=\mathbf{E:}{{\varvec{\upvarepsilon }}}$ which provides the following relation between ${\mathcal {E}}^{0}$ and ${\mathcal {S}}^{0}$:

$$\begin{aligned} {\mathcal {S}}^{0}=\left\{ {\mathbf{E:}{{\varvec{\upvarepsilon }} }\quad \forall \;{\varvec{\upvarepsilon }}\in {\mathcal {E}}^{0}} \right\} \end{aligned}$$

(40)

In particular, if ${\mathcal {S}}^{0}$ is defined through a function $\hbox {f}_{\mathcal {S}}$ such that ${\mathcal {S}}^{0}=\left\{ {{\varvec{{\upsigma }}}\;\;\hbox {;}\;\;\hbox {f}_{\mathcal {S}} \left( {\varvec{{\upsigma }}} \right) \le 0} \right\}$, then ${\mathcal {E}}^{0}$ is equivalently defined by a function $\hbox {f}_{\mathcal {E}}$ such that ${\mathcal {E}}^{0}=\left\{ {{\varvec{\upvarepsilon }}\;\;\hbox {;}\;\;\hbox {f}_{\mathcal {E}} \left( {\varvec{\upvarepsilon }} \right) \le 0} \right\}$, where both functions are linked by:

$$\begin{aligned} \hbox {f}_{\mathcal {E}} \left( {\varvec{\upvarepsilon }} \right) =\hbox {f}_{\mathcal {S}} \left( {\mathbf{E:}{{\varvec{\upvarepsilon }} }} \right) \end{aligned}$$

(41)

It is then possible to build $\upchi \left( {\varvec{\upvarepsilon }} \right)$ and $\Gamma \left( {\varvec{\upvarepsilon }} \right)$ from (37) and (39).

As an illustration of how to derive the strain measure $\upchi \left( {\varvec{\upvarepsilon }} \right)$ from $\hbox {f}_{\mathcal {E}}$, consider for instance the damage criterion introduced by de Vree et al. (1995) known as the modified von Mises criterion. It relies on a threshold value $\upkappa$ and the ratio $r={f_c }{/}{f_t }$:

$$\begin{aligned}&\hbox {f}_{\mathcal {E}} \left( {\varvec{\upvarepsilon }} \right) =\tilde{{\upvarepsilon } }_{MM} \left( {\varvec{\upvarepsilon }} \right) -\upkappa \nonumber \\&\qquad \hbox {with}\quad \tilde{{\upvarepsilon } }_{\mathrm{MM}} \left( {\varvec{\upvarepsilon }} \right) =\frac{r-1}{2r\left( {1-2\upnu } \right) }\hbox {I}_1 \left( {\varvec{\upvarepsilon }} \right) \nonumber \\&\quad +\frac{1}{2r}\sqrt{\left( {\frac{r-1}{1-2\upnu }\hbox {I}_1 \left( {\varvec{\upvarepsilon }} \right) } \right) ^{2}+\frac{12 r}{\left( {1+\upnu } \right) ^{2}}\hbox {J}_2 \left( {\varvec{\upvarepsilon }} \right) } \end{aligned}$$

(42)

where $\upnu$ is the Poisson ratio, $\hbox {I}_1$ the first strain invariant and $\hbox {J}_2$ the second deviatoric strain invariant. Thanks to the character positive homogeneous of degree 1 of $\tilde{\upvarepsilon }_{MM} \left( {\varvec{\upvarepsilon }} \right)$, the function $\upchi$ simply reads in that case:

$$\begin{aligned} \upchi \left( {\varvec{\upvarepsilon }} \right)= & {} \frac{1}{\upkappa }\tilde{\upvarepsilon }_{\mathrm{MM}} \left( {\varvec{\upvarepsilon }} \right) \quad \hbox {since}\quad \hbox {f}_{\mathcal {E}} \left( {\frac{{\varvec{\upvarepsilon }}}{\upchi \left( {\varvec{\upvarepsilon }} \right) }} \right) \nonumber \\= & {} \tilde{{\upvarepsilon }}_{\mathrm{MM}} \left( {\frac{{\varvec{\upvarepsilon }}}{\upchi \left( {\varvec{\upvarepsilon }} \right) }} \right) -\upkappa =\frac{\tilde{\upvarepsilon }_\mathrm{MM} \left( {\varvec{\upvarepsilon }} \right) }{\upchi \left( {\varvec{\upvarepsilon }} \right) }-\upkappa =0 \end{aligned}$$

(43)

Fig. 8

Effect of the shape of the damage criterion on a structural response

3.2.2 Influence of the shape of the damage surface on crack propagation

It has been shown in the previous subsection how the nonlocal damage setting of the Sect. 2 can be specialised to a given damage threshold function $\hbox {f}_{\mathcal {E}}$. The choice of the latter is ruled by several considerations. First, the boundary of the initial elastic domain is the surface where damage initially occurs. As the model does not describe a preliminary hardening stage, it also coincides with the failure surface. In particular it should reflect the contrast between tensile and compressive strengths. For instance, the criterion introduced in Mazars (1986) is not adapted in our framework since it leads to a contrast ${f_c }{/}{f_t }$ of only 3.5 for a Poisson ratio $\upnu =0.2$.

Moreover, in the context of damage propagation, the local stress state does not reduce to uniaxial tension and a wide range of biaxial stress states are observed, as already pointed out in the Sect. 2.3.4. This fact was also noticed by Jirasek and Bauer (2012) who observed that damage criteria which coincide in uniaxial tension but differ elsewhere in the tensile regime quadrant lead to quantitatively different responses for a structure. In order to assess whether this observation still holds true with the present nonlocal formulation, the modified von Mises damage criterion recalled in (42) is applied to the simulation of a SENB subjected to three-point bending (the other characteristics of the model remain those summarised in the forthcoming Sect. 3.4). The interest—or shortcoming depending on the point of view—of this criterion is the fact that its shape in the tensile quadrant is strongly influenced by the compressive strength even though the tensile strength remains unchanged, see the Fig. 8 for an illustration in plane-stress. The simulation is performed for two values of the ratio ${f_c }{/}{f_t }$, 1.5 and 10. The significant difference observed in the force–deflection curve in the Fig. 8 results from the different shapes of the damage surface in the tensile quadrant (damage in compression with $r=1.5$ is not responsible for the gap between the curves since it happens sufficiently late, cf. the dashed curve in the figure). By the way, note also that the modified von Mises criterion is not able here to reproduce the experimental results when using the realistic ratio ${f_c }{/}{f_t }=10$.

Finally, the previous observations appeal for a reasonably accurate criterion in multiaxial tension while preserving the contrast between compressive and tensile strengths.

3.2.3 An accurate damage criterion for tensile cracking

A damage criterion was proposed by François (2008) which meets both requirements established in the Sect. 3.2.2: reasonably agreeing with experimental observations in multiaxial tension and preventing from early damage in compression. In the stress space, the initial elasticity domain ${\mathcal {S}}^{0}$ reads:

$$\begin{aligned}&{\mathcal {S}}^{0}=\left\{ {{\varvec{{\upsigma }}}\;\;\hbox {;}\;\;\hbox {f}_{\mathcal {S}} \left( {\varvec{{\upsigma }}} \right) \le 0} \right\} \quad \hbox {with}\nonumber \\&\hbox {f}_{\mathcal {S}} \left( {\varvec{{\upsigma }}} \right) =\left\| {\frac{{\varvec{{\upsigma }}}^{\mathrm{D}}+\upbeta _0 \;\mathrm{tr}\left( {\varvec{{\upsigma }}} \right) \;\mathbf{Id}}{{\upsigma } _0 }} \right\| +\left\| {\mathbf{exp}\frac{{\varvec{{\upsigma }}}}{{\upsigma } _0 }} \right\| -{\upgamma }_0\nonumber \\ \end{aligned}$$

(44)

The tensorial function $\mathbf{exp}$ is the exponential of a symmetric tensor and $\left\| \cdot \right\|$ is the usual Euclidean norm ($\left\| \mathbf{T} \right\| ^{2}=\mathbf{T:T})$. The threshold function depends on the parameters ${\upsigma } _0 >0$ (dimension of a stress) and ${\upgamma } _0 >\sqrt{3}$ (dimensionless). According to François (2008), the function $\hbox {f}_{\mathcal {S}}$ fulfils the required conditions: it is continuous, isotropic, convex and $\hbox {f}_{\mathcal {S}} \left( \mathbf{0} \right) <0$. Compared to the original expression in François (2008), a third parameter $\upbeta _0$ is introduced so that the elasticity domain is bounded – even for hydrostatic compression. Even though such stress states lay outside the scope of the study, the boundedness of the domain is convenient on a numerical ground: the function $\upchi \left( {\varvec{\upvarepsilon }} \right)$ is then coercive and the implicit Eq. (37) always admits a unique solution, cf. the “Appendix A”. In practice, $\upbeta _0$ is set to 0.1 so that the weight of the hydrostatic stress remains small except for high triaxialities in compression.

Fig. 9

Damage criteria in biaxial plane-stress

Fig. 10

Parameter identification for the damage criterion in François (2008)

On the contrary of more refined threshold functions, see for instance Willam and Warnke (1975), the criterion here relies on a single tensorial expression and results in a regular convex domain with counterpart a less accurate description in multiaxial compressive states, as can be seen in the Fig. 9 where the experimental results are taken from Lee et al. (2004). This shortcoming is not troublesome for the present purpose since the focus lies on tensile cracking without damage in compression and, if necessary, a slight overestimation of the compressive strength would lead to a better global agreement in multiaxial compression. Besides, a comparison with the modified von Mises criterion (de Vree et al. 1995) and the Mazars criterion (Mazars 1986) is also reported in the Fig. 9 and confirms the interest of the criterion in (François 2008) regarding multiaxial tension and the prevention of early damage in compression. These good properties enable realistic quantitative predictions of structural behaviours, see the results in the Fig. 6 and in the forthcoming validation cases in the Sect. 4.

The identification of the parameters ${\upsigma } _0$ and ${\upgamma } _0$ in (44) may rely on the knowledge of the tensile and compressive strengths. More precisely, it can be noticed from (44) that ${\upgamma } _0$ and ${{\upsigma } _0 }{/}{f_t }$ depend only on the ratio ${f_c }{/}{f_t }$, which should necessarily be greater than 2.8 with this criterion in order to ensure the existence of solutions to the identification procedure. For the sake of convenience, the values of ${\upgamma } _0$ and ${{\upsigma } _0 }{/}{f_t }$ are plotted in the Fig. 10 as functions of the ratio ${f_c }{/}{f_t }$.

3.3 Stress transfer across damage bands and damage/stiffness coupling

When considering the simple strain energy expression $\hbox {w}\left( {{\varvec{\upvarepsilon }},a} \right) =\hbox {A}\left( a \right) \hbox {w}^{e}\left( {\varvec{\upvarepsilon }} \right)$, the completely damaged material ($a=1)$ does no more sustain any stress: its stiffness is equal to zero in any loading direction. This is a shortcoming when compressive load should be transmitted across damaged areas. For instance, a pressurized cavity as depicted in the Fig. 3 should sustain internal pressure beyond the development of damage along the inner wall, damage areas should accommodate self-weight loading, etc. Even though anisotropic damage models a priori provide an adequate setting, relaxing the isotropy assumption of the current model would result in deep impacts on all its properties. Therefore, another direction is followed, less accurate but which should be sufficient for the above-mentioned stakes: damage keeps its former description as a scalar field and the distinction between tensile and compressive states is achieved through the expression of the elastic energy density $\hbox {w}\left( {{\varvec{\upvarepsilon }},a} \right)$ introduced in (1). One speaks then of stiffness recovery.

3.3.1 Isotropic energy split

Several authors considered a split of the initial elastic energy density $\hbox {w}^{e}$ into a tensile part $\hbox {w}^{t}$ and a compressive part $\hbox {w}^{c}$ and assessed that only the tensile part is affected by damage:

$$\begin{aligned} \left\{ {{\begin{array}{l} {\hbox {w}^{e}\left( {\varvec{\upvarepsilon }} \right) \;\; =\hbox {w}^{ t}\left( {\varvec{\upvarepsilon }} \right) +\hbox {w}^{ c}\left( {\varvec{\upvarepsilon }} \right) } \\ {\hbox {w}\left( {{\varvec{\upvarepsilon }},a} \right) =\hbox {A}\left( a \right) \hbox {w}^{ t}\left( {\varvec{\upvarepsilon }} \right) +\hbox {w}^{ c}\left( {\varvec{\upvarepsilon }} \right) } \\ \end{array} }} \right. \end{aligned}$$

(45)

As the degradation function A goes from 1 to 0 with increasing damage, the effect of damage consists of a progressive transition from a sound material with strain energy $\hbox {w}^{e}$ to a fully damaged one (a broken one) with strain energy density $\hbox {w}^{c}$:

$$\begin{aligned} \hbox {w}\left( {{\varvec{\upvarepsilon }},a} \right) =\hbox {A}\left( a \right) \hbox {w}^{e}\left( {\varvec{\upvarepsilon }} \right) +\left[ {1-\hbox {A}\left( a \right) } \right] \hbox {w}^{ c}\left( {\varvec{\upvarepsilon }} \right) \end{aligned}$$

(46)

The expression of w is subjected to several constraints already stated above which result in turn in constraints on $\hbox {w}^{ c}$:

• w is positive, isotropic, strictly convex with respect to ${\varvec{\upvarepsilon }}$ for $a<1$ and continuously differentiable if and only if $\hbox {w}^{ c}$ is positive, isotropic, convex and continuously differentiable;

• w decreases with damage if and only if $\hbox {w}^{ e}\ge \hbox {w}^{ c}$ since the degradation function A is decreasing;

• w is positive homogeneous of degree 2 with respect to the strain if and only if it holds for $\hbox {w}^{ c}$ too.

3.3.2 Residual elastic energy

Actually, distinguishing a tensile state from a compressive one is not straightforward in case of nonzero Poisson ratio. An intuitive and simple distinction can be introduced according to the sign of the strain trace (Comi and Perego 2001; Amor et al. 2009), which is also equal to the sign of the stress trace:

$$\begin{aligned} \hbox {w}^{ c}\left( {\upvarepsilon } \right) =\frac{1}{2}\;\lambda \left\langle {\mathrm{tr}\,{\varvec{\upvarepsilon }}} \right\rangle _- ^{2} \end{aligned}$$

(47)

where the McAuley brackets with minus subscript denote the negative part of a scalar or a symmetric tensor. However, the completely damaged material hence behaves in compression like a perfect fluid and it does not sustain non-hydrostatic stress states. That may result in poor stress transfer, as will be seen hereafter.

Another approach proposed by Fichant et al. (1999) consists in relying on the sign of the stress eigenvalues. They worked at the level of the stress–strain relation which they wrote for the broken material as:

$$\begin{aligned} {\varvec{{\upsigma }}}=\left\langle {\mathbf{E:}{{\varvec{\upvarepsilon }} }} \right\rangle _- \end{aligned}$$

(48)

Unfortunately, the elastic law does not derive from an energy anymore (since there is no symmetry of the tangent operator), a situation which is not handled by the present formalism, see (2). Note also that such a choice raises some questions regarding the existence and uniqueness of elastic solutions and the positivity of the energy dissipation.

This calls for a more complex expression of the ultimate strain energy density $\hbox {w}^{c}$. First, we have stated in (4) that a strain state where all the strain eigenvalues are positive corresponds to a tensile state for which $\hbox {w}^{c}$ should be equal to zero; this is thought to be a minimal requirement for tensile strain states. Therefore, it seems interesting to begin with a focus on the set ${\mathcal {T}}$ of strain states with zero residual energy, named tensile strain states:

$$\begin{aligned} {\mathcal {T}}=\left\{ {{\varvec{\upvarepsilon }}\;;\;\;\hbox {w}^{c}\left( {\varvec{\upvarepsilon }} \right) =0} \right\} \end{aligned}$$

(49)

According to the properties stated in the “Appendix B”, ${\mathcal {T}}$ is a convex cone and its dual convex cone is the set of admissible stress states ${\mathcal {A}}$:

$$\begin{aligned} {\mathcal {A}}=\left\{ {{\varvec{{\upsigma }}}\;;\;\;\forall \;{\varvec{\upvarepsilon }}\in {\mathcal {T}}\;\;{{\varvec{{\upsigma }}} \mathbf{:}{\varvec{\upvarepsilon }} }\le 0} \right\} \end{aligned}$$

(50)

Non-admissible stress states are not sustainable by the material, i.e. the stress energy density is infinite. For instance, if tensile strain states are defined as the strain tensors with positive trace as in (47), then the admissible stress states are indeed reduced to hydrostatic compressive tensors $-p \,\mathbf{Id}$ ($p\ge 0)$ as said above. Actually, the larger ${\mathcal {T}}$, the smaller ${\mathcal {A}}$. Now we make another assumption in order to ensure the sustainability of compressive loading: any stress tensor with all eigenvalues negative should be admissible. In that case, because of (50), there is only a single choice for ${\mathcal {T}}$ and ${\mathcal {A}}$:

$$\begin{aligned} {\mathcal {T}}= & {} \left\{ {{\varvec{\upvarepsilon }}\;;\;\;\forall \;i\;\;{\upvarepsilon }_i \ge 0} \right\} ;\nonumber \\ {\mathcal {A}}= & {} \left\{ {{\varvec{{\upsigma }}}\;;\;\;\forall \;i\;\;{\upsigma } _i \le 0} \right\} \end{aligned}$$

(51)

At this stage, the domains of tensile strains and compressive stresses are defined. We can now focus on actual expressions for the ultimate energy density $\hbox {w}^{c}$. A natural choice would consist in assuming that there is a complete stiffness recovery for any admissible stress state. In terms of stress energy density, this reads $\hbox {w}^{{c}{*}}\left( {\varvec{{\upsigma }}} \right) =\hbox {w}^{{e}{*}}\left( {\varvec{{\upsigma }}} \right)$ for any ${\varvec{{\upsigma }}}\in {\mathcal {A}}$, with $\hbox {w}^{{e}{*}}\left( {\varvec{{\upsigma }}} \right) ={{\varvec{{\upsigma }}} \mathbf{:E}^{-1}\mathbf{:}{\varvec{{\upsigma }}} }{/}{2}$ the elastic stress energy. As $\hbox {w}^{{c}{*}}$ is equal to $+\;\infty$ outside ${\mathcal {A}}$, it is hence completely defined and $\hbox {w}^{c}$ could be obtained through a Legendre transform of $\hbox {w}^{c\;{*}}$. Unfortunately, the corresponding expression is poorly convenient for numerical applications so that we prefer to rely on the following approximation proposed in (Badel et al. 2007):

$$\begin{aligned} \hbox {w}^{c}\left( {\varvec{\upvarepsilon }} \right) =\frac{1}{2}\;\left[ {\lambda \left\langle {\hbox {tr}{\varvec{\upvarepsilon }}} \right\rangle _- ^{2}+2\upmu \left\langle {\varvec{\upvarepsilon }} \right\rangle _- \mathbf{:}\left\langle {\varvec{\upvarepsilon }} \right\rangle _- } \right] \end{aligned}$$

(52)

This expression fulfils (51) and the requirements of the Sect. 3.3.1. It provides a complete stiffness recovery for any strain state such that ${\upvarepsilon }_i \le 0$ for any i. In terms of stress states, the latter is a smaller set than ${\mathcal {A}}$ and that’s why (52) is considered as an approximation of what could have been an optimal $\hbox {w}^{c}$. Nevertheless, when considering stress transfer, the definition of the admissible stress states is thought to be more important than the actual value of the residual energy density.

Fig. 11

Kinematics inside a damaged layer

3.3.3 Stress transfer through damage bands under shear loading

When defining the residual (or compressive) part of the Helmholtz free energy $\hbox {w}^{c}$, the focus has been put on the definition of tensile strain states (with zero residual stiffness) and compressive stress states (i.e. admissible ultimate stress states). One can wonder to what extent such a choice is representative of the macroscopic behaviour of a real crack. In order to answer the question, consider a thin layer of totally damaged material which should be representative of a macroscopic crack. Locally, the damaged layer is subjected to a separation displacement as depicted in the Fig. 11, say $\mathbf{u} ={\updelta } _n \mathbf{n}+{\updelta } _t \mathbf{t}$ where ${\updelta } _n$ and ${\updelta } _t$ denote respectively the components normal and tangential to the “crack”. The “macroscopic discontinuity” results in a strain distribution inside the damaged layer an average estimation of which reads:

$$\begin{aligned} {\varvec{\upvarepsilon }}\sim \frac{1}{h}{} \mathbf{u}\mathop \otimes \limits ^s \mathbf{n}=\frac{{\updelta } _n }{h}{} \mathbf{n}\otimes \mathbf{n}+\frac{{\updelta } _t }{h}{} \mathbf{n}\mathop \otimes \limits ^s \mathbf{t} \end{aligned}$$

(53)

where h is the layer thickness and $\mathop \otimes \limits ^s$ is the symmetrised dyadic product. The minimal strain eigenvalue can be easily calculated :

$$\begin{aligned} {\upvarepsilon }_{min} =\frac{{\updelta } _n -\sqrt{{\updelta } _n^2 +{\updelta } _t^2 }}{2h} \end{aligned}$$

(54)

We recall that a negative value implies some stiffness recovery because of the definition (51) of the tensile strains. As expected, it is strictly negative when ${\updelta } _n <0$: some stiffness is recovered when closing the crack. A more questionable property concerns shear mode loading: the minimal strain eigenvalue is also strictly negative under sliding or tearing, i.e. when ${\updelta } _t \ne 0$, whatever the opening displacement ${\updelta } _n$. It means that stiffness recovery and hence stress transfer are observed as soon as a tangential separation of the crack faces occurs. This is the limitation of an isotropic law when trying to locally reflect the anisotropic behaviour of a crack and it may lead to some locking phenomenon (even though not observed in the forthcoming numerical simulations). Nevertheless, the stiffness recovery and the resulting stress transfer could also somewhat reflect the aggregate interlock as long as the opening displacement remains small, even though we do not claim to actually model the interlock (it is only an artefact of the isotropic modelling).

3.3.4 Stiffness recovery regularisation

It is acknowledged that the brutal stiffness recovery resulting from (52) when a strain eigenvalue becomes negative may raise numerical difficulties, cf. Jefferson and Mihai (2015) which corroborates our own experience. Therefore, we recommend to introduce a progressive stiffness recovery. Even though the motivation here is the numerical robustness, a progressive stiffness recovery with crack closure also stems from experimental evidences (Reinhardt 1984) and micromechanical investigations (Vassaux et al. 2015).

More precisely, the discontinuity of the second order derivative of $\hbox {w}^{c}$ is smoothed by the following positive, convex and $C^{ \infty }$ scalar function, with ${\upgamma } >0$ an additional parameter:

$$\begin{aligned} \hbox {S}\left( x \right) =\left\{ {{\begin{array}{ll} {x^{2}\exp \left( {\frac{1}{\upgamma \,x}} \right) }&{} {\quad \hbox {if }\,x<0} \\ 0&{} {\quad \hbox {if }\,x\ge 0} \\ \end{array} }} \right. \end{aligned}$$

(55)

It exhibits a progressive transition from $x^{2}$ to zero, the smoothing range being parameterized by ${\upgamma }$, and thus provides a regularisation of the function $\left\langle x \right\rangle _-^2$. The compressive strain energy density is then defined as a smooth extension of the potential (52) while the strain energy keeps the expression (46) which implies that the tensile strain energy is also smoothed, see (45):

$$\begin{aligned} \hbox {w}^{ c}\left( \upvarepsilon \right) =\frac{1}{2}\;\left[ {\lambda \;\hbox {S}\left( {\hbox {tr}\,{\varvec{\upvarepsilon }}} \right) +2 \upmu \sum _i {\hbox {S}\left( {{\upvarepsilon }_i } \right) } } \right] \end{aligned}$$

(56)

And the stress–strain relation still derives from (2) :

$$\begin{aligned} {\upsigma } _i= & {} \hbox {A}\left( a \right) \left( {\lambda \hbox {tr}\,{\varvec{\upvarepsilon }}+2 \upmu \;{{\upvarepsilon }}_i } \right) \nonumber \\&+\frac{1}{2}\left[ {1-\hbox {A}\left( a \right) } \right] \left[ {\lambda \;{\hbox {S}}'\left( {\hbox {tr}\,{\varvec{{\upvarepsilon }}}} \right) +2 \upmu \;{\hbox {S}}'\left( {{\upvarepsilon } _i } \right) } \right] \end{aligned}$$

(57)

The required properties should now be checked. $\hbox {w}^{c}$ is positive and isotropic. It is convex: the first term is indeed convex (composition of a convex function with a linear one), the second one is also convex because it is a convex function of the eigenvalues, see Piccolroaz and Bigoni (2009). As S is $C^{ \infty }$ (hence $C^{8})$, $\hbox {w}^{ c}$ is $C^{ 2}$ according to Carlson and Hoger (1986), so that there is no more stiffness discontinuities. Besides, the energy in tension $w^{ t}$ is also positive since $x^{2}-\hbox {S}(x)\ge 0$. Finally, the only issue is the fact that $\hbox {w}^{ c}$ is no more positive homogeneous of degree 2, but only asymptotically positive homogeneous of degree 2: the stress–strain response is not radially linear in compression. Nevertheless, it remains quadratic for tensile strain states, so that the consistency with a cohesive law established in Sect. 2.3 is preserved. The condition of homogeneity of degree 2 can thus be relaxed and the proposal (56) is satisfactory on a theoretical ground.

Fig. 12

Pressurised cavity: impact of the stiffness recovery model

Finally, when returning to the initial objective that is transferring compressive stresses across damage bands, the choice of the parameter ${\upgamma }$ may be ruled by practical considerations. For instance, one can demand that 90% of the stiffness be retrieved when the strain magnitude reaches about ${f_c }/E$; this is the value that will be used in the forthcoming validation numerical simulations, without further precision.

Box 1 Summary of the constitutive relation

3.3.5 Illustration: pressurised cavity

A numerical study now illustrates the importance of ensuring satisfactory stress transfers. It consists of the containment wall enclosing a pressurised internal cavity already introduced in the Sect. 2.3.4 and depicted in the Fig. 3. Three different types of stiffness recovery are considered: (i) no stiffness recovery $\hbox {w}^{c}=0$, (ii) selection of the tensile states through the sign of the trace according to (47) which corresponds to a perfect fluid-type broken material and (iii) selection of the tensile states through the sign of the strain eigenvalues according to our final proposal (56).

The results are presented in the Fig. 12. It appears that without stiffness recovery, the structure cannot sustain any internal pressure as soon as a point of the inner wall is broken: there is not any stress transfer since ${\mathcal {A}}=\left\{ \mathbf{0} \right\}$. With a perfect fluid-type broken material, only hydrostatic compressive stress states are admissible: ${\mathcal {A}}=\mathbb {R}^{-} \mathbf{Id}$. When the damaged zone reaches the outer wall, no more pressure can be sustained (the fluid flows outside). At last, the choice of energy such that any compressive stress states is admissible, i.e. ${\mathcal {A}}=\left\{ {{\varvec{{\upsigma }}}\;;\;\;\forall \;i\;\;\upsigma _i \le 0} \right\}$, enables a reloading of the cavity pressure beyond the first crack going through the wall, in agreement with what is physically expected.

3.4 Summary of the constitutive equations

To sum up, the class of nonlocal damage models presented in the Sect. 2 is specialised to concrete through the expression of the reduced degradation function $\bar{{\hbox {A}}}\left( a \right)$, the damage surface strain dependency $\Gamma \left( {\varvec{{\upvarepsilon }}} \right)$ and the strain energy density $\hbox {w}\left( {{\varvec{{\upvarepsilon }}},a} \right)$. The resulting constitutive equations are gathered in the Box 1. They depend on 6 (optionally 7) material parameters that need to be identified:

• The elasticity Lamé coefficients $\lambda$ and $\upmu$

• The tensile and compressive strengths $f_t$ and $f_c$

• The fracture energy $G_F$

• The softening parameters p and optionally q

Fig. 13

Size and notch effects on three point bending SENB (Hoover et al. 2013)

In addition, a nonlocal length scale D is required; in practice, it is suggested to set it small relatively to the characteristic lengths of the structure. At last, two numerical parameters are introduced (with suggested values): $\upbeta _0$ which ensures that the elasticity domain ${\mathcal {E}}$ is bounded and ${\upgamma }$ which regularises the transition between the stiffness in tension and compression.

4 Validation

The predictive capacities of the model presented in the Sects. 2 and 3 are now assessed by means of several validation test cases with respect to the following characteristics of concrete fracture:

• Prediction of the global force–displacement response with focus on size effects and the transferability from notched to unnotched specimens.

• Prediction of the crack opening profile inside and outside the process zone.

• Prediction of the crack path for rectilinear, then curved and at last nonplanar cracks.

The numerical simulations are led with the finite element software Code_Aster (for the sake of reproducibility, the open-source distribution is available on the official web site www.code-aster.org). Here, we choose to skip the numerical details and to focus on the simulation and experimental results. We just mention that the implementation of the model follows the numerical approach described in Lorentz and Godard (2011) for constitutive laws with gradient of internal variables. When the crack path is unknown a priori, an adaptive mesh refinement strategy is applied according to Lorentz (2010) in order to limit the computation burden: typically, the mesh size is adjusted so that the damage band width ($2\times D$) is discretised by five quadratic elements (size $0.4\times D$, a recommendation based on spatial convergence analyses performed in Lorentz and Godard (2011). And at last, a path-following technique based on the maximal increment of damage is used to adjust the load intensity in order to catch the progressive propagation of the cracks with satisfactory numerical convergence of the solution algorithms, see Lorentz and Badel (2004) for further information. On a practical ground, note that with the target of five elements across the damage band width, the solution algorithms used in Code_Aster (chosen for their robustness rather than their efficiency) and a small degree of parallelism (less than 10 CPUs), the 2D simulations lasted less than an hour while the 3D simulation in the Sect. 4.5 was far longer (several days, the final mesh resulting in about 5 millions of nodal degrees of freedom).

4.1 From notched to unnotched specimen

Hoover et al. (2013) provided a comprehensive set of experimental data based on three point bending of single edge notched beams made of the same concrete. Several beam sizes and crack depths were considered. Here, we focus on three beam sizes and three notch lengths including unnotched specimens, which makes nine combinations. The validation test consists of two steps: first, four of these combinations (2 beam sizes $\times$ 2 notch lengths) enable to fit the parameters of the model; then the behaviour of the five remaining combinations is predicted, including all the unnotched cases. The simulations are compared to the experimental results in terms of force vs. crack mouth opening displacement (CMOD) with a focus on the peak force.

The geometry of the homothetic beams is given in the Fig. 13. The three considered beam depths H are 93 mm (small beams), 215 mm (medium beams) and 500 mm (large beams). And the notch lengths a are equal to 0 (unnotched beams), $0.15\times H$ (intermediate notches) and $0.3\times H$ (deep notches). Only the small and medium beams with intermediate and deep notches are used to fit the parameters, as highlighted in the Fig. 13. More precisely, the elasticity constants and the compressive strength are provided in (Hoover and al. 2013) on the basis of independent experiments: $E=41{,}000\;\hbox {MPa}$, $\upnu =0.17$ and $f_c =56\;\hbox {MPa}$. The nonlocal length scale D is not identified but set to one twentieth of the ligament length, i.e. $0.05\times \left( {H-a} \right)$: as mentioned above, it is not considered as an additional material parameter but taken sufficiently small compared to the structure size in order to be close to the asymptotic CZM model. Finally, only the tensile strength, the fracture energy and the softening parameters p and q need to be estimated. The identification procedure results in the following values: $f_t =5\;\hbox {MPa}$, $G_f =75\;\hbox {N/m}$, $p=1.84$ and $q=1.81$. The value for $f_t$ may seem large but it lies in the range proposed by the fib Model Code (2010), i.e. $f_{tm}\,\pm \,30\%$ with $f_{tm} =0.3\times \left( {f_c -8} \right) ^{2/3}\approx 4\;\hbox {MPa}$.

The results are plotted in the Fig. 13 where the numerical simulations of the force vs. CMOD responses (black thick lines) are compared to the experimental results (orange lines, one for each test). Regarding the four configurations used to adjust the four parameters, the simulations are close to the experimental results. Even though it could have been expected thanks to the identification procedure, it should be pointed out that the agreement covers the whole response. And still more convincing, the blind prediction for the five other configurations also leads to a satisfactory agreement between experimental and numerical responses. In particular, the identification with notched specimen enables realistic predictions for unnotched ones. Actually the worst prediction concerns the peak force of the small unnotched beam (underestimation of the average peak force of about 20%). However, it should be noted that Hoover and Bazant (2014) also encountered some difficulties to fit this particular configuration with a CZM model but succeeded with still smaller specimens which hints maybe at some experimental specificities.

4.2 Opening displacement profile along a crack

Three point bending experiments with different-sized concrete beams are reported in Alam et al. (2013) with a focus on the crack opening profile measured by means of digital image correlation. These experiments provide an opportunity to estimate the accuracy of the present nonlocal model when predicting crack opening displacements.

The geometries of the single edge notched beams are reproduced in the Fig. 14 where three beam depths are considered: 100, 200 and 400 mm. The elasticity constants and the compressive strength are provided in Alam et al. (2013). The nonlocal length scale D is set to 10% of the notch length. At last, the other parameters of the model are identified on the basis of the force vs crack mouth opening displacement curves for the three beam sizes, see again the Fig. 14 for a comparison of the resulting numerical simulation with the experimental curves. In contrast, the measured crack opening profiles are not used in the identification procedure; the corresponding experiment vs. simulation comparisons result from a blind prediction where the opening profiles are computed according to the definition (16) of the separation displacement, i.e. the displacement discontinuity across the crack surface measured at the distance of $\pm \;D$. They are compared with the experimental observations—still in the Fig. 14—for two load levels: when the peak force is reached and when the bending force has decreased up to 60% of the peak force in the softening regime. It appears that the agreement is reasonably satisfactory and better for larger beams. The trend may be explained by the fact that for the smallest beam, the width of the physical process zone is no more negligible with respect to the beam depth, in contradiction with the assumption we made when suggesting that the nonlocal length scale D could be chosen arbitrarily small with respect to the characteristic length of the structure (here 2% of the beam depth). A better agreement could possibly be obtained by adjusting the nonlocal length scale but this lies outside the scope of the present study which focuses on structure sizes for which cohesive zone models yield acceptable predictions.

Fig. 14

Crack opening in three point bending SENB (Alam et al. 2013)

Fig. 15

CLWL-DCB: description and results

4.3 Rectilinear crack path prediction

The crack line wedge loaded double cantilever beam experiment (CLWL-DCB) performed by Kobayashi et al. (1984) exhibits a rectilinear crack path which deviates from the initial notch direction when subjected to non-proportional biaxial loading. Such a specimen thus constitutes a first validation case to check the ability of the damage model to predict crack paths.

The specimen is a thick square plate of concrete the dimension of which is about 50 cm. Its geometry is depicted in the Fig. 15 along with the loading conditions. The latter result from two distinct forces, $P_{1}$ which opens the crack and reflects the penetration of the wedge and $P_{2}$ which is compressive in the diagonal direction; they provide a biaxial stress state. In a first stage, both forces evolve proportionally with a ratio ${P_2 }{/}{P_1 }=0.62$ up to $P_2 =3.65\;\hbox {kN}$. Then the force $P_{2}$ is kept constant while $P_{1}$ is adjusted so as to result in an increasing crack mouth opening displacement (CMOD).

Regarding the concrete characteristics, the compressive strength $f_{c}$ is provided in Kobayashi et al. (1984). Representative values of the stiffness, the fracture energy and the mean tensile strength are deduced through formulas in the fib Model Code (2010), where E, $f_{c}$ and $f_{tm}$ are in MPa and $G_{F}$ in N/m:

$$\begin{aligned}&E=21{,}500\times \left( {\frac{f_c }{10}} \right) ^{1/3};\quad G_F =73\times f_c ^{0.18};\nonumber \\&f_{tm} =0.3\times \left( {f_c -8} \right) ^{2/3} \end{aligned}$$

(58)

The tensile strength in (58) is given with a variability of ±30%. A better agreement with the experimental force–opening response is obtained by a coarse identification of the tensile strength $f_{t}$ inside the interval $\left[ {0.7\times f_{tm} \;\;1.3\times f_{tm} } \right]$. The identification also provides the values of the parameters p and q. The material characteristics are finally gathered in the Fig. 15. Note that the nonlocal length scale D is chosen equal to 10 mm, which is considered sufficiently small with respect to the specimen size.

The computation is performed under a plane-strain assumption. The results are in good agreement with the experimental values, see the Fig. 15. Thanks to the identification, the force–opening response is close to the experimental points, even though the initial (elastic) slope is underestimated by the simulation, a fact also reported in Rots (1988). And the crack path is well predicted: the damage zone is almost superimposed to the experimental crack path.

4.4 Curved crack path prediction

Concrete four-point-shear specimens are known for exhibiting curved crack paths which distinctly differ from what would be obtained with a pure brittle material such as PMMA, see Schlangen (1993) for a review. The crack path is hence influenced by the development of the process zone. And according to Geers et al. (2000), the prediction of the crack path is also highly sensitive to the definition of the damage surface. Therefore, four-point-shear specimens appear to be demanding validation tests. Such an experiment conducted by Schlangen (1993) is studied here to assess the ability of the damage model to predict curved crack path. It consists of a single-edge notched beam (SENB) of height 200 mm and subjected to four-point-shear. The geometry and the loading conditions are summarized in the Fig. 16.

Fig. 16

SENB subjected to four-point-shear: description and results

Fig. 17

Brokenshire torsion test

The material parameters are also given in the Fig. 16. More precisely, the Young modulus, the Poisson ratio, the compressive and the tensile strengths are obtained through standard experiments in Schlangen (1993). The fracture energy $G_{F}$ and the softening parameters p and q are calibrated on the basis of a separate uniaxial tension test, also detailed in Schlangen (1993). As the tensile strength observed in the uniaxial tension test (3.44 Mpa) differs from the tensile strength measured in the Brazilian test (3.1 Mpa), the identification is performed with a normalized stress–stretch curve only, where the stress is normalised by the peak stress value. It appears that the uniaxial tension test is not very discriminating so that several combinations of parameters ($G_{F}, p, q$) would lead to comparable responses: in practice, $G_{F}$ is set here to 100 N/m. At last, considering the characteristic dimensions of the specimen, the nonlocal length scale is set to $D=2.5\,\hbox {mm}$. It should be noticed that none of the material parameters are adjusted with respect to the target four-point-shear experiment: the simulation of the latter is hence predictive, not only in terms of crack path (the purpose of the validation test) but also in terms of quantitative global responses.

The numerical predictions for the four-point-shear test are compared to the experimental measurements, drawn in grey in the Fig. 16. On a quantitative ground, the applied force, the crack-mouth opening displacement (CMOD) and the bending displacement ${\updelta } _2$ are analysed. The latter is depicted in red in the Fig. 16: it is measured as the relative vertical displacement of the right part of the beam (vertical red arrow) compared to a straight stem (red dashed line) glued in two points (red circles) on the left part of the beam. The predicted force—CMOD and force–deflexion curves are close to the experimental ones; in particular, the peak force is slightly over-estimated by 5%. On a qualitative ground, the predicted crack path is also close to the experimental ones the range of which is drawn in grey in the Fig. 16. In particular, the curved crack is nicely retrieved even though the model is isotropic.

4.5 Curved and nonplanar crack path prediction

The last validation test consists of a notched torsion specimen proposed in Brokenshire (1996). The geometry and the loading conditions are depicted in the Fig. 17. The initial orientation of the notch and the mixed-mode loading result in a final curved and nonplanar crack path. The simulation is performed on the basis of the material parameters introduced in (Jefferson et al. 2004) according to the experimental programme and recalled in the Fig. 17. In addition, the values of the softening parameters p and q have been arbitrarily set to 2 and 0. At last, the nonlocal length scale D has been set to one twentieth of the ligament length, i.e. 2.5 mm.

The results of the computation are showed in the Fig. 17. On a quantitative ground, one can notice that the peak force is nicely predicted by the simulation. Moreover, the agreement with the experimental crack mouth opening displacement (CMOD) is satisfactory, lying in the experimental range. Considering the crack mouth sliding displacement (CMSD), a single experimental curve is available, hence unfortunately precluding an estimation of the scattering. Therefore, one can only conclude that the predicted CMSD does not fully agree with the experimental one but the gap between them is not larger (relatively) than the magnitude of the scattering for the CMOD.

On a qualitative ground, the predicted crack path exhibits the same feature than the experimental one (Jefferson et al. 2004): a progressive deviation from the initial crack orientation (slant crack path). However, considering the available experimental data, a photograph of the two broken pieces of the specimen, it is difficult to compare more precisely the crack path, including the shape of the crack front (straight or curved).

5 Conclusion

In conclusion, a constitutive law for plain concrete has been proposed which focuses on rate-independent tensile damage. Because of the assumed isotropy of damage, the model is dedicated to the analysis of structures at the scale of individual cracks. It is built from the beginning as a nonlocal law with the explicit introduction of the gradient of the damage field into the constitutive equations. A special attention has been paid to the consistency with cohesive zone models which explains why the model is focused on localised damage only (i.e. cohesive cracks). This enables to benefit from the amount of validation already available in the literature for concrete cohesive laws and gives access to attractive properties such as a straightforward extraction of the crack opening displacement or the parameterization through standard “engineer” characteristics (tensile strength, fracture energy). In addition, the internal length which results from the nonlocal coupling term is interpreted as the width of the process zone. In our proposal, it plays the role of a “small parameter” and hence it does not need a specific identification. Indeed, it is sufficient to set it small with respect to the characteristic sizes of the structure, thanks to the asymptotic consistency of the model with a cohesive law. Of course, in this case, one cannot expect results at a finer scale than the process zone width.

Several specificities of the behaviour of concrete have been taken into account: the shape of the (cohesive) softening response, the shape of the initial damage surface (which has been showed to play an underestimated though crucial role) and the nature of the coupling between damage and loss of stiffness with a straightforward impact on stiffness recovery with crack closure and more generally the capacity of a damaged structure to sustain compressive loads. The pertinence of these features has been validated through several comparisons with experimental results, including nonplanar three dimensional crack propagation: global predictions (peak force, dissipated energy, crack path, size dependency) and local predictions (crack opening profile) show a reasonably good agreement with the available experimental data.

Appendices

Appendix: Introduction of a distorted norm relative to a closed set

Consider a normed vector space E and a closed set ${\mathcal {D}}\subset E$ which contains the point 0. For any $x\in E$, we introduce the following subset of $\mathbb {R}^{+}$: $I\left( x \right) =\left\{ {t\in \mathbb {R}^{+}\;;\;t x\in {\mathcal {D}}} \right\}$. As $0\in {\mathcal {D}}$, $I\left( x \right)$ is nonempty since $0\in I\left( x \right)$ and we denote $t^{{*}}\left( x \right) \in \bar{{\mathbb {R}}}$ the supremum of $I\left( x \right)$, which is evidently positive. Then, we define the following function $\upchi$ that we named the distorted norm relative to ${\mathcal {D}}$:

Definition

$\upchi$ is the function from E to $\mathbb {R}^{+}$ defined as $\upchi \left( x \right) =t^{{*}}\left( x \right) ^{\;-\;1}$. In particular, it can be noticed that $\upchi \left( 0 \right) =0$.

At this stage, $\upchi$ is not necessarily defined everywhere in E since $t^{{*}}\left( x \right)$ may be equal to 0. Therefore, we introduce the condition that 0 is an interior point of ${\mathcal {D}}$ (there exists an open set containing 0 and contained in ${\mathcal {D}})$.

Property

Under the condition that $0\in \mathrm{int}\left( {\mathcal {D}} \right)$, the domain of the function $\upchi$ denoted dom$\left( \upchi \right)$ is equal to E and there exists a constant $C_U >0$ such that:

$$\begin{aligned} \forall \;x\in E\quad 0\le \upchi \left( x \right) \le C_U \left\| x \right\| \end{aligned}$$

Demonstration

Since $0\in \mathrm{int}\left( {\mathcal {D}} \right)$, there exists $\upeta >0$ such that $\forall \;x\in E\;\;\left\| x \right\| \le \upeta \Rightarrow x\in {\mathcal {D}}$. Therefore, $\forall \;x\in E\backslash \{0\}$ one has $\upeta x/{\left\| x \right\| }\in {\mathcal {D}}$ so that $\upeta /{\left\| x \right\| }\in I\left( x \right)$ and, by definition of $t^{{*}}$, $t^{{*}}\left( x \right) \ge \upeta /{\left\| x \right\| }>0$. Therefore, $\upchi \left( x \right) =1/{t^{{*}}(x)}$ is well defined and $x\in \mathrm{dom}\left( \upchi \right)$. In addition $\upchi \left( 0 \right) =0$. The conclusion follows: $\forall \;x\in E\;\;\upchi \left( x \right) \le C_U \left\| x \right\|$ with $C_U =1/\upeta$.

Property

The function $\upchi$ is positive homogeneous of degree 1:

$$\begin{aligned}&\forall \;x\in \mathrm{dom}\left( \upchi \right) \quad \forall \;\lambda \in \mathbb {R}^{+}\quad \lambda x\in \mathrm{dom}\left( \upchi \right) \quad \hbox {and}\nonumber \\&\quad \upchi \left( {\lambda x} \right) =\lambda \upchi \left( x \right) . \end{aligned}$$

Demonstration

The property holds for $\lambda =0$ since $\upchi \left( 0 \right) =0$. Now, consider any $\lambda >0$ and any $x\in \mathrm{dom}\left( \upchi \right)$. One has:

$$\begin{aligned} t\in I\left( {\lambda x} \right)&\Leftrightarrow \left[ {t\ge 0\;\hbox {and}\;t \lambda x\in {\mathcal {D}}} \right] \\&\Leftrightarrow \left[ {\lambda t\ge 0\;\hbox {and}\;\lambda t x\in {\mathcal {D}}} \right] \Leftrightarrow \lambda t\in I\left( x \right) \end{aligned}$$

Therefore, the relation on the supremum reads $t^{{*}}\left( x \right) =\lambda t^{{*}}\left( {\lambda x} \right)$ so that $\lambda x\in \mathrm{dom}\left( \upchi \right)$ and $\upchi \left( {\lambda x} \right) =\lambda \upchi \left( x \right)$.

In order to exhibit a relation between the set ${\mathcal {D}}$ and the lower level sets $D_\upalpha$ of $\upchi$, defined as $D_\upalpha =\left\{ {x\in \mathrm{dom}(\upchi )\;;\;\;\upchi \left( x \right) \le \upalpha } \right\}$, an additional condition should be introduced: ${\mathcal {D}}$ is star convex with respect to the point 0, that is for any $x\in {\mathcal {D}}$ the segment $\left[ {0\;x} \right]$ is included in ${\mathcal {D}}$.

Property

Under the condition that ${\mathcal {D}}$ is star convex with respect to 0, the lower level sets of $\upchi$ are homothetic to ${\mathcal {D}}$: $\forall \;\upalpha >0\;\;D_\upalpha =\left\{ {\upalpha x\;;\;x\in {\mathcal {D}}} \right\}$. In particular, the set ${\mathcal {D}}$ is equal to the lower level set $D_1$.

Demonstration

First, let us demonstrate that ${\mathcal {D}}=D_1$. If $x\in {\mathcal {D}}$, then $1\in I\left( x \right)$ and hence $t^{{*}}\left( x \right) \ge 1$. Therefore, $x\in \mathrm{dom}\left( \upchi \right)$ and $\upchi \left( x \right) =1/{t^{{*}}\left( x \right) }\le 1$ so that $x\in D_1$. Reciprocally, consider that $x\in D_1$. Then $\upchi \left( x \right) \le 1$ and $t^{{*}}\left( x \right) \ge 1$. We distinguish two cases: $t^{{*}}\left( x \right) =1$ and $t^{{*}}\left( x \right) >1$. In the first case, there exists a sequence $\left( {t_n } \right) \in I\left( x \right) ^{\mathbb {N}}$ which converges towards 1. The sequence $\left( {t_n x} \right)$ hence belongs to ${\mathcal {D}}^{\mathbb {N}}$ and converges towards x. As ${\mathcal {D}}$ is a closed set, $x\in {\mathcal {D}}$. In the second case, there exists $t_1 \in I\left( x \right)$ with $t_1 \ge 1$. Thanks to the condition that ${\mathcal {D}}$ is star convex with respect to 0, $\left[ {0\;\;t_1 x} \right] \subset {\mathcal {D}}$ and in particular $x\in {\mathcal {D}}$ which concludes the demonstration that ${\mathcal {D}}=D_1$.

Now, consider $\upalpha >0$. Thanks to the property that $\upchi$ is positive homogeneous of degree one, one has:

$$\begin{aligned} D_\upalpha= & {} \left\{ {x\in \mathrm{dom}\upchi \;;\;{\upchi (x)}/\upalpha \le 1} \right\} \\= & {} \left\{ {x\in \mathrm{dom}\upchi \;;\;\upchi (x/\upalpha )\le 1} \right\} =\left\{ {\upalpha y\;;\;y\in D_1 } \right\} \end{aligned}$$

As ${\mathcal {D}}=D_1$, this concludes the demonstration.

Property

Under the condition that ${\mathcal {D}}$ is star convex with respect to 0, one has $x/{\upchi \left( x \right) }\;\in \;\mathrm{bd}\left( {\mathcal {D}} \right)$ the boundary of ${\mathcal {D}}$ for any $x\in \mathrm{dom}\left( \upchi \right)$ such that $\upchi \left( x \right) \ne 0$. In particular, if $\upchi \left( x \right) =1$ then $x\in \mathrm{bd}\left( {\mathcal {D}} \right)$.

Demonstration

First, consider the case $\upchi \left( x \right) =1$. Then $t^{{*}}\left( x \right) =1$ which implies that $x\in D$ as demonstrated previously. Moreover, for any ${\upvarepsilon } >0$, $1+{\upvarepsilon } \notin I\left( x \right)$ by definition of the supremum, so that $\left( {1+{\upvarepsilon } } \right) \;x\notin {\mathcal {D}}$. In any neighbourhood of x, one can find a point that belongs to ${\mathcal {D}}$ (the point x itself) and a point that does not belong to ${\mathcal {D}}$. This is a characterisation of the boundary of ${\mathcal {D}}$: $x\in \mathrm{bd}\left( {\mathcal {D}} \right)$.

Consider now the general case $\upchi \left( x \right) \ne 0$. Then $\upchi \left( x \right) >0$ and $\upchi \left( {x/{\upchi (x)}} \right) =1$, thanks to the positive homogeneity of degree one of $\upchi$. We can apply the first part of the demonstration and conclude that $x/{\upchi (x)}\in \mathrm{bd}\left( {\mathcal {D}} \right)$.

Unfortunately, the converse of the previous property does not hold in general: a point $x\in \mathrm{bd}\left( {\mathcal {D}} \right)$ is not necessarily characterised by $\upchi \left( x \right) =1$ so that $x/{\upchi (x)}\in \mathrm{bd}\left( {\mathcal {D}} \right)$ does not necessarily characterises the function $\upchi$. Some additional regularity is required on ${\mathcal {D}}$. A practical case of interest is a convex set ${\mathcal {D}}$, which encompasses the condition of star convexity with respect to zero.

Property

If the set ${\mathcal {D}}$ is convex and if $0\in \mathrm{int}\left( {\mathcal {D}} \right)$, then the boundary of ${\mathcal {D}}$ is characterised by $\upchi \left( x \right) =1$, i.e. $\upchi \left( x \right) =1\Leftrightarrow x\in \mathrm{bd}\left( {\mathcal {D}} \right)$.

Demonstration

As ${\mathcal {D}}$ is convex, the condition of star convexity with respect to 0 is fulfilled and the following implication has been proven above: $\upchi \left( x \right) =1\Rightarrow x\in \mathrm{bd}\left( {\mathcal {D}} \right)$.

Now, let us demonstrate the converse. If $x\in \mathrm{bd}\left( {\mathcal {D}} \right)$ then $x\in {\mathcal {D}}$ (since ${\mathcal {D}}$ is a closed set) and $t^{{*}}\left( x \right) \ge 1$ . Now assume (wrongly) that $t^{{*}}\left( x \right) >1$ so that there exists $\uprho >0$ with $\left( {1+\uprho } \right) x\in {\mathcal {D}}$. In this case, we will show that there exists a neighbourhood of x included in ${\mathcal {D}}$, in contradiction with the assumption that $x\in \mathrm{bd}\left( {\mathcal {D}} \right)$.

Indeed, if $0\in \mathrm{int}\left( {\mathcal {D}} \right)$, there exists $\upeta >0$ such that $\forall \;z\in E\;\;\left\| z \right\| \le \upeta \;\;\Rightarrow \;\;z\in {\mathcal {D}}$. Besides, consider the ball ${\mathcal {B}}$ centred on x with radius $\upeta \uprho /{(1+\uprho )}$. For any point $y\in {\mathcal {B}}$, let us define:

$$\begin{aligned} z=\frac{1+\uprho }{\uprho }\left( {y-x} \right) \end{aligned}$$

Then $\left\| z \right\| \le \upeta$ so that $z\in {\mathcal {D}}$. Moreover, $x,\;y\;\hbox {and}\;z$ are also related through the following equation:

$$\begin{aligned} y=\frac{\uprho }{1+\uprho }z+\frac{1}{1+\uprho }\left( {1+\uprho } \right) x \end{aligned}$$

As $z\in {\mathcal {D}}$ and $\left( {1+\uprho } \right) x\in {\mathcal {D}}$ then $y\in {\mathcal {D}}$ thanks to the convexity of ${\mathcal {D}}$. Thus the neighbourhood ${\mathcal {B}}$ of x is included in ${\mathcal {D}}$, in contradiction with $x\in \mathrm{bd}\left( {\mathcal {D}} \right)$. Therefore, the assumption $t^{{*}}\left( x \right) >1$ is false, which demonstrates that $t^{{*}}\left( x \right) =1$ and $\upchi \left( x \right) =1$.

Corollary

Assume that the set ${\mathcal {D}}$ is convex and contains a neighbourhood of 0. Now consider the following problem for any $x\in E$:

(P) find $\uprho >0$ so that $x/\uprho \in \mathrm{bd}\left( {\mathcal {D}} \right)$

Then the problem (P) admits at most one solution:

• If $\upchi \left( x \right) >0$, the solution exists and is equal to $\upchi \left( x \right)$;

• If $\upchi \left( x \right) =0$, no solution exists.

Demonstration

As ${\mathcal {D}}$ is convex and $0\in \mathrm{int}\left( {\mathcal {D}} \right)$, $x/\uprho \in \mathrm{bd}\left( {\mathcal {D}} \right) \Leftrightarrow \upchi \left( {x/\uprho } \right) =1\Leftrightarrow \uprho =\upchi \left( x \right)$, thanks to the previous property, the fact that the domain of $\upchi$ is E and the positive homogeneity of degree one of $\upchi$. As $\uprho$ should be strictly positive, one has to distinguish two cases: if $\upchi \left( x \right) >0$ then $\uprho =\upchi \left( x \right)$; else there is no solution to the problem (P).

The former corollary provides an alternative definition of the function $\upchi$ for a convex, set ${\mathcal {D}}$ which contains a neighbourhood of the point 0. Indeed, for a given point $x\in E$, $\upchi \left( x \right)$ is equal to the unique solution to the problem (P) when it exists; else, $\upchi \left( x \right) =0$. Moreover, it can be shown that the function $\upchi$ is also convex and continuous in this case.

Property

If the set ${\mathcal {D}}$ is convex and such that $0\in \mathrm{int}\left( {\mathcal {D}} \right)$, then the function $\upchi$ is convex.

Demonstration

First, as $0\in \mathrm{int}\left( {\mathcal {D}} \right)$, $\upchi$ is defined everywhere in E. Then, consider two points $x\in E$ and $y\in E$ and a real $0<\upgamma <1$. We should prove that $\upchi \left( {\upgamma x+\left( {1-\upgamma } \right) y} \right) \le \upgamma \upchi \left( x \right) +\left( {1-\upgamma } \right) \upchi \left( y \right)$. Three cases should be distinguished:

• (a) $\upchi \left( x \right) \ne 0$ and $\upchi \left( y \right) \ne 0$

Let us introduce two additional points:

$$\begin{aligned} {y}'= & {} \frac{\upchi \left( x \right) }{\upchi \left( y \right) }y \\ z= & {} \frac{\upgamma \upchi \left( x \right) }{\upgamma \upchi \left( x \right) +\left( {1-\upgamma } \right) \upchi \left( y \right) }x\nonumber \\&+\,\frac{\left( {1-\upgamma } \right) \upchi \left( y \right) }{\upgamma \upchi \left( x \right) +\left( {1-\upgamma } \right) \upchi \left( y \right) }{y}'\\= & {} \frac{\upchi \left( x \right) \;\;\left[ {\upgamma x+\left( {1-\upgamma } \right) y} \right] }{\upgamma \upchi \left( x \right) +\left( {1-\upgamma } \right) \upchi \left( y \right) } \end{aligned}$$

The definition is licit since $\upchi \left( x \right) \ne 0$ and $\upchi \left( y \right) \ne 0$. Geometrically, the point ${y}'$ is collinear to y and belongs to the same level set of $\upchi$ as x since $\upchi \left( {{y}'} \right) =\upchi \left( x \right)$. And the point z is colinear to $\upgamma x+(1-\upgamma )y$ and belongs to the segment $\left[ {x\;\;{y}'} \right]$. Thanks to the convexity of ${\mathcal {D}}$, the lower level set $D_{\upchi \left( x \right) }$ is also convex because it is homothetic to ${\mathcal {D}}$. And as $x\in D_{\upchi \left( x \right) }$ (by definition) and ${y}'\in D_{\upchi \left( x \right) }$, then $z\in D_{\upchi \left( x \right) }$ which implies that $\upchi \left( z \right) \le \upchi \left( x \right) \ne 0$. One can now conclude:

$$\begin{aligned} \upchi \left( {\upgamma x+\left( {1-\upgamma } \right) y} \right)= & {} \frac{\upgamma \upchi \left( x \right) +\left( {1-\upgamma } \right) \upchi \left( y \right) }{\upchi \left( x \right) }\upchi \left( z \right) \\\le & {} \upgamma \upchi \left( x \right) +\left( {1-\upgamma } \right) \upchi \left( y \right) \end{aligned}$$

• (b) $\upchi \left( x \right) =0$ and $\upchi \left( y \right) \ne 0$

This covers also the case where $\upchi \left( x \right) \ne 0$ and $\upchi \left( y \right) =0$ by permuting x with y. The inequality to be demonstrated then reads:

$$\begin{aligned}&\upchi \left( {\upgamma x+\left( {1-\upgamma } \right) y} \right) \le \left( {1-\upgamma } \right) \upchi \left( y \right) \quad \Leftrightarrow \\&\quad \upchi \left( {\frac{\upgamma }{\left( {1-\upgamma } \right) \upchi \left( y \right) } x+\frac{1}{\upchi \left( y \right) }y} \right) \le 1 \end{aligned}$$

Let us denote:

$$\begin{aligned} \uprho =\frac{\upgamma }{\left( {1-\upgamma } \right) \upchi \left( y \right) }\quad \hbox {and}\quad y_1 =\frac{1}{\upchi \left( y \right) }y \end{aligned}$$

As ${\mathcal {D}}$ is convex (hence star convex with respect to 0) and $\upchi \left( y \right) \ne 0$, it has been showed above that $y_1 \in \mathrm{bd}\left( {\mathcal {D}} \right)$. Moreover, the lower level set $D_1$ is equal to ${\mathcal {D}}$ so that the former inequality is equivalent to $z=\uprho x+y_1 \in {\mathcal {D}}$ which should be demonstrated for any $\uprho >0$, $y_1 \in \mathrm{bd}\left( {\mathcal {D}} \right)$ and x such that $\upchi \left( x \right) =0$.

The demonstration is led in two steps. First, let us introduce a sequence $\left( {t_n } \right) \in ] {0\;\;1} ]^{\mathrm{N}}$ which converges toward 1 and consider the sequence of points $z_n =\uprho x+t_n y_1$ which converges towards z. The expression of $z_n$ can be reformulated as follows:

$$\begin{aligned} z_n =\left( {1-t_n } \right) \frac{\uprho x}{1-t_n }+t_n y_1 \end{aligned}$$

As $\upchi \left( x \right) =0$, $I\left( x \right) ={\mathbb {R}}^{+}$ and hence ${\uprho x}{/}{\left( {1-t_n } \right) }\in {\mathcal {D}}$. Moreover, $y_1 \in {\mathcal {D}}$ since ${\mathcal {D}}$ is closed. Therefore $z_n \in {\mathcal {D}}$ thanks to the convexity of ${\mathcal {D}}$.The next step leads to the conclusion: as $z_n$ converges towards z, $z_n \in {\mathcal {D}}$ and ${\mathcal {D}}$ is closed, $z\in {\mathcal {D}}$, which demonstrates the former inequality.

• (c) $\upchi \left( x \right) =0$ and $\upchi \left( y \right) =0$

In this case, we need to show that $\upchi \left( {\upgamma x+\left( {1-\upgamma } \right) y} \right) =0$, which is equivalent to $I\left( {\upgamma x+\left( {1-\upgamma } \right) y} \right) ={\mathbb {R}}^{+}$. To that purpose, consider any $t>0$. Then:

$$\begin{aligned} t\left( {\upgamma x+\left( {1-\upgamma } \right) y} \right) =\frac{1}{2}\left[ {2\upgamma t x} \right] +\frac{1}{2}\left[ {2\left( {1-\upgamma } \right) t y} \right] \end{aligned}$$

As both terms of the right hand side belong to ${\mathcal {D}}$ since $I\left( x \right) ={\mathbb {R}}^{+}$ and $I\left( y \right) ={\mathbb {R}}^{+}$, the convexity of ${\mathcal {D}}$ enables to conclude that the left hand side also belongs to ${\mathcal {D}}$ for any $t>0$, so that $I\left( {\upgamma x+\left( {1-\upgamma } \right) y} \right) ={\mathbb {R}}^{+}$.

Gathering the three cases (a), (b) and (c) finally shows that the function $\upchi$ is convex.

Corollary

If the set ${\mathcal {D}}$ is convex and such that $0\in \mathrm{int}\left( {\mathcal {D}} \right)$, then the function $\upchi$ fulfils the triangular inequality: $\forall \;x,y\in E\;\;\upchi \left( {x+y} \right) \le \upchi \left( x \right) +\upchi \left( y \right)$ .

Demonstration

The triangular inequality is a straightforward consequence of the convexity and the positive homogeneity:

$$\begin{aligned} \upchi \left( {x+y} \right)= & {} 2 \upchi \left( {\frac{1}{2}x+\frac{1}{2}y} \right) \\\le & {} 2\left( {\frac{1}{2}\upchi (x)+\frac{1}{2}\upchi (y)} \right) =\upchi \left( x \right) +\upchi \left( y \right) \end{aligned}$$

Property

If the set ${\mathcal {D}}$ is convex and such that $0\in \mathrm{int}\left( {\mathcal {D}} \right)$, then the function $\upchi$ is Lipschitz continuous.

Demonstration

Thanks to the triangular inequality, one has for any $x\in E$ and $y\in E$:

Moreover, as $0\in \mathrm{int}\left( {\mathcal {D}} \right)$, it has been shown above that there exists a constant $C_U >0$ such that $0\le \upchi \left( z \right) \le C_U \left\| z \right\|$ for any $z\in E$. In particular, $\upchi \left( {x-y} \right) \le C_U \left\| {y-x} \right\|$ and $\upchi \left( {y-x} \right) \le C_U \left\| {y-x} \right\|$. The previous inequalities hence imply:

$$\begin{aligned} \exists \;C_U >0\quad \forall x,y\in E\quad \left| {\upchi \left( y \right) -\upchi \left( x \right) } \right| \le C_U \left\| {y-x} \right\| \end{aligned}$$

At last, one can explained why $\upchi$ is initially referred to as a norm, thanks to the following properties:

Property

If ${\mathcal {D}}$ is a bounded set, then $\upchi \left( x \right) >0$ for any $x\ne 0$ and there exists a constant $C_L >0$ such that $\forall \;x\in E\quad \upchi \left( x \right) \ge C_L \left\| x \right\|$.

Demonstration

As ${\mathcal {D}}$ is bounded, there exists $M>0$ such that $\forall \;x\in D \quad \left\| x \right\| \le M$. Then, by definition of $I\left( x \right)$, one has for any $x\in E\backslash \left\{ 0 \right\}$ and $t\in I\left( x \right)$: $t\ge 0$ and $t x\in {\mathcal {D}}$. Therefore, $\left\| {t x} \right\| =t\left\| x \right\| \le M$, hence $t\le M/{\left\| x \right\| }$. The latter inequality holds also true for the supremum: $t^{{*}}\left( x \right) \le M/{\left\| x \right\| }$. And finally, by definition of $\upchi$, one has $\upchi \left( x \right) \ge C_L \left\| x \right\|$ with $C_L =1/M$ and in particular $\upchi \left( x \right) >0$. At last, the fact that $\upchi \left( 0 \right) =0$ completes the demonstration.

Property

Assume that the set ${\mathcal {D}}$ is convex, bounded and contains a neighbourhood of 0. Assume in addition that it is symmetric with respect to the point 0, that is $x\in D\Leftrightarrow -x\in D$. Then the function $\upchi$ is a norm.

Demonstration

As $0\in \mathrm{int}\left( {\mathcal {D}} \right)$, $\upchi$ is a mapping from E to ${\mathbb {R}}^{+}$.

As ${\mathcal {D}}$ is bounded, $\upchi \left( x \right) =0\;\;\Leftrightarrow \;\;x=0$.

As ${\mathcal {D}}$ is convex and contains a neighbourhood of 0, the function $\upchi$ fulfils the triangular inequality.

Finally, for any $x\in E$ and $\lambda \ge 0$, one has $\upchi \left( {\lambda x} \right) =\lambda \upchi \left( x \right)$. Moreover, $\upchi \left( {-x} \right) =\upchi \left( x \right)$ thanks to the symmetry of ${\mathcal {D}}$ with respect to 0. Hence $\upchi \left( {-\lambda x} \right) =\lambda \upchi \left( x \right)$. Both equalities can be gathered so that for any $x\in E$ and any $\uprho \in \mathbb {R}$, $\upchi \left( {\uprho x} \right) =\left| \uprho \right| \upchi \left( x \right)$.

This concludes the demonstration that $\upchi$ is a norm.

Note that if ${\mathcal {D}}$ is not bounded, then the function $\upchi$ is only a semi-norm. Besides, if ${\mathcal {D}}$ is not a symmetric set, $\upchi$ is not a norm because $\upchi \left( {-\;x} \right) \ne \upchi \left( x \right)$ a priori, which refers to Minkowski norms (but without the required regularity).

Appendix: Properties of conewise elasticity potentials

Consider a strain energy density ${\varvec{{\upvarepsilon }}}\mapsto \hbox {w}\left( {\varvec{{\upvarepsilon }}} \right)$ which is positive, continuously differentiable, positive homogeneous of degree 2 and convex. Now assume that there exists a set of strain tensors ${\mathcal {C}}$ (not reduced to the point ${\varvec{{\upvarepsilon }}}=0$) where the potential $\hbox {w}$ is equal to zero; this corresponds to a strain domain with zero stiffness.

Property

${\mathcal {C}}$ is a closed convex cone.

Demonstration

Since the function $\hbox {w}$ is continuous and ${\mathcal {C}}$ is the inverse image of the closed set $\left\{ 0 \right\}$ under w, ${\mathcal {C}}$ is closed. Besides, it is a cone thanks to the property of positive homogeneity of $\hbox {w}$. And finally, as ${\mathcal {C}}$ corresponds to the minimisers of a convex function, it is convex.

As the stiffness can be equal to zero, one can expect that some stress states are not admissible. This corresponds to stress tensors for which the dual potential is infinite, where the latter is defined as:

$$\begin{aligned} {\varvec{{\upsigma }}}\mapsto \hbox {w}^{{*}}\left( {\varvec{{\upsigma }}} \right) =\mathop {\sup }\limits _{\varvec{{\upvarepsilon }}} \;\left[ {\varvec{\upsigma }} \mathbf{:}{\varvec{{\upvarepsilon }}} -\hbox {w}\left( {\varvec{{\upvarepsilon }}} \right) \right] \end{aligned}$$

Property

The set of admissible stress tensors corresponding to finite values of the dual potential is the dual cone of ${\mathcal {C}}$, i.e. ${\mathcal {C}}^{{*}}=\left\{ {{\varvec{{\upsigma }}}\;\;\hbox {s.t.}\;\;\forall \;{\varvec{{\upvarepsilon }}}\in {\mathcal {C}}\;\;{{\varvec{\upsigma }} \mathbf{:}{\varvec{\upvarepsilon }} }\le 0} \right\}$. Actually, an additional technical assumption is necessary to show that stress tensors lying on the boundary of ${\mathcal {C}}^{ {*}}$ are admissible: it is detailed in the demonstration and it refers to a nonzero stiffness in any direction normal to C.

Demonstration

• (a) First, consider the case where ${\varvec{{\upsigma }}}$ is such that there exists ${\varvec{{\upvarepsilon }}}\in {\mathcal {C}}$ so that ${ {\varvec{\upsigma }} \mathbf{:}{\varvec{\upvarepsilon }} }>0$. Then the same inequality holds for any $\lambda {\varvec{{\upvarepsilon }}}$ with $\lambda >0$ leading to:

  $$\begin{aligned} \hbox {w}^{{*}}\left( \upsigma \right)\ge & {} \mathop {\sup }\limits _{\lambda >0} \left[ {\lambda { {\varvec{\upsigma }} \mathbf{:}{\varvec{\upvarepsilon }} }-\hbox {w}\left( {\lambda {\varvec{{\upvarepsilon }}}} \right) } \right] \\= & {} +\infty \quad \hbox {since}\quad \hbox {w}\left( {\lambda {\varvec{{\upvarepsilon }}}} \right) =0 \end{aligned}$$

• (b) Conversely, consider the case where ${\varvec{{\upsigma }}}$ is such that ${ {\varvec{\upsigma }} \mathbf{:}{\varvec{\upvarepsilon }} }<0$ for any ${\varvec{{\upvarepsilon }}}\in {\mathcal {C}}$ and decompose ${\varvec{{\upvarepsilon }}}$ as ${\varvec{{\upvarepsilon }}}=\lambda \mathbf{d}$ where $\lambda =\left\| {\varvec{{\upvarepsilon }}} \right\|$ and $\left\| \mathbf{d} \right\| =1$ (i.e. $\mathbf{d}\in {\mathcal {S}}_1$ the unit sphere which is compact since it is closed and bounded in a space of finite dimension). Then, one has:

  $$\begin{aligned}&\hbox {w}^{{*}}\left( {\varvec{{\upsigma }}} \right) =\mathop {\sup }\limits _{\lambda \ge 0} \;\left[ {\lambda {{\varvec{\upsigma }} \mathbf{:d}}_\lambda -\lambda ^{2}\hbox {w}\left( {\mathbf{d}_\lambda } \right) } \right] \quad \hbox {where}\\&\quad \mathbf{d}_\lambda \in \mathop {\arg \max }\limits _{\mathbf{d}\in {\mathcal {S}}_1 } \left[ {\lambda {\varvec{\upsigma }} \mathbf{:d}-\lambda ^{2}\hbox {w}\left( \mathbf{d} \right) } \right] \end{aligned}$$

  $\mathbf{d}_\lambda$ is indeed defined because the function $\mathbf{d}\mapsto \lambda {\varvec{\upsigma }} \mathbf{:d}-\lambda ^{2}\hbox {w}\left( \mathbf{d} \right)$ is continuous and the unit sphere is compact. Moreover, $\mathbf{d}_\lambda \in {\mathcal {S}}_1$ so that one can extract a convergent sequence when $\lambda \rightarrow \infty$, still named $\mathbf{d}_\lambda$ for the sake of simplicity; its limit is denoted $\mathbf{d}_\infty$. If $\mathbf{d}_\infty \notin {\mathcal {C}}$ then $\hbox {w}\left( {\mathbf{d}_\infty } \right) >0$ and by continuity of w, there exist $m>0$ and $\lambda _0$ so that for any $\lambda \ge \lambda _0$, $\hbox {w}\left( {\mathbf{d}_\lambda } \right) >m$. Then:

  $$\begin{aligned} \;\forall \;\lambda\ge & {} \lambda _0 \quad \lambda {{\varvec{\upsigma }} \mathbf{:d}}_\lambda -\lambda ^{2}\hbox {w}\left( {\mathbf{d}_\lambda } \right) \le \lambda \left\| {\varvec{{\upsigma }}} \right\| -\lambda ^{2}m\\\le & {} \frac{\left\| {\varvec{{\upsigma }}} \right\| ^{2}}{4m}\quad \Rightarrow \hbox {w}^{{*}}\left( {\varvec{{\upsigma }}} \right) <+\infty \end{aligned}$$

  And if $\mathbf{d}_\infty \in \mathcal {C}$, then ${ {\varvec{\upsigma }} \mathbf{:d}}_\infty <0$ by assumption. Hence there exist $m>0$ and $\lambda _0$ so that for any $\lambda \ge \lambda _0$, ${{\varvec{\upsigma }} \mathbf{:d}}_\lambda <-\;m$. Then:

  $$\begin{aligned} \;\forall \;\lambda\ge & {} \lambda _0 \quad \lambda {{\varvec{\upsigma }} \mathbf{:d}}_\lambda -\lambda ^{2}\hbox {w}\left( {\mathbf{d}_\lambda } \right) \le \lambda {{\varvec{\upsigma }} \mathbf{:d}}_\lambda \\\le & {} -\;\lambda _0 m\quad \Rightarrow \hbox {w}^{{*}}\left( {\varvec{{\upsigma }}} \right) <+\infty \end{aligned}$$

• (c) The case where the stress tensor belongs to the boundary of the dual cone should now be addressed. With the previous notations, the potentially problematic situation consists of (i) $\mathbf{d}_\infty \in \mathcal {C}$ with (ii) ${{\varvec{\upsigma }} \mathbf{:d}}_\infty =0$ (${\varvec{{\upsigma }}}$ is thus an outer normal of $\mathcal {C}$ in $\mathbf{d}_\infty )$ and (iii) there exists a subsequence (still denoted $\mathbf{d}_\lambda )$ such that ${{\varvec{\upsigma }} \mathbf{:d}}_\lambda >0$ (hence $\mathbf{d}_\lambda \notin {\mathcal {C}})$. In that case, an additional hypothesis of transverse stiffness is required to conclude:

  $$\begin{aligned}&\forall \;\mathbf{d}\in \partial C\cap S_1 \quad \exists \;K>0\quad \exists \;V\in {\mathcal {V}}\left( \mathbf{d} \right) \\&\forall \;\mathbf{{d}'}\in V\cap S_1 \backslash C\quad w\left( {\mathbf{{d}'}} \right) \ge K\left\| {\mathbf{{d}'}-\mathbf{d}} \right\| ^{2} \end{aligned}$$

  where $\partial C$ is the boundary of C and ${\mathcal {V}}\left( d \right)$ denotes the set of neighbourhoods of $\mathbf{d}$; we also recall that $\hbox {w}\left( \mathbf{d} \right) =0$ and $\hbox {w}'\left( \mathbf{d} \right) =0$. The condition refers to a nonzero stiffness in directions normal to C, see Curnier et al. (1995) for its admissibility.

This additional condition is applied to the sequence $\mathbf{d}_\lambda$:

$$\begin{aligned}&\exists \;K>0\quad \exists \;\lambda _0 \ge 0\quad \forall \;\lambda \ge \lambda _0 \quad w\left( {\mathbf{d}_\lambda } \right) \\&\quad \ge K\left\| {\mathbf{d}_\lambda -\mathbf{d}_\infty } \right\| ^{2} \end{aligned}$$

It leads to the following upper bound for any $\lambda \ge \lambda _0$ :

$$\begin{aligned} \lambda {{\varvec{\upsigma }} \mathbf{:d}}_\lambda -\lambda ^{2}\hbox {w}\left( {\mathbf{d}_\lambda } \right)\le & {} \lambda { {\varvec{\upsigma }} \mathbf{:d}}_\lambda -K \lambda ^{2}\left\| {\mathbf{d}_\lambda -\mathbf{d}_\infty } \right\| ^{2}\quad \\= & {} \lambda {\varvec{\upsigma }} \mathbf{:}\left( {\mathbf{d}_\lambda -\mathbf{d}_\infty } \right) -K \lambda ^{2}\left\| {\mathbf{d}_\lambda -\mathbf{d}_\infty } \right\| ^{2} \\\le & {} \lambda \left\| {\varvec{{\upsigma }}} \right\| \left\| {\mathbf{d}_\lambda -\mathbf{d}_\infty } \right\| -K \lambda ^{2}\left\| {\mathbf{d}_\lambda -\mathbf{d}_\infty } \right\| ^{2} \\\le & {} \mathop {\sup \;}\limits _{x\ge 0} \left( {\left\| {\varvec{{\upsigma }}} \right\| x-K x^{2}} \right) \quad =\quad {\left\| {\varvec{{\upsigma }}} \right\| ^{2}}{/}{4K} \\ \end{aligned}$$

It proves that $\hbox {w}^{{*}}\left( {\varvec{{\upsigma }}} \right)$ is finite and concludes the demonstration.