Finite deformation cohesive polygonal finite elements for modeling pervasive fracture

Abstract

We introduce a framework for modeling dynamic fracture problems using cohesive polygonal finite elements. Random polygonal meshes provide a robust, efficient method for generating an unbiased network of fracture surfaces. Further, these meshes have more facets per element than standard triangle or quadrilateral meshes, providing more possible facets per element to insert cohesive surfaces. This property of polygonal meshes is advantageous for the modeling of pervasive fracture. We use both Wachspress and maximum entropy shape functions to form a finite element basis over the polygons. Fracture surfaces are captured through dynamically inserted cohesive zone elements at facets between the polygons in the mesh. Contact is enforced through a penalty method that is applied to both closed cohesive surfaces and general interpenetration of two polygonal elements. Several numerical examples are presented that illustrate the capabilities of the method and demonstrate convergence of solutions.

1 Introduction

Computational simulation of many complex mechanical processes in materials and structures has advanced greatly in recent times. However, simulating and predicting rapid fracture processes remains an elusive goal. Under fast crack growth, fracture is considered pervasive since cracks nucleate and propagate dynamically in complex patterns that branch and coalesce in arbitrary directions. Pervasive fracture is a strongly nonlinear process: in addition to modeling contact, complex constitutive behavior must be accurately captured, including material softening, crack nucleation, and crack growth. Exact solutions exist for benchmark quasi-static fracture problems that simplify investigation of convergence of numerical solutions; however, for dynamic fracture relatively few experimental results are available due to inherent difficulties in observing and measuring a very rapid process. This limits the ability to develop and validate computational methods. Further, measures of convergence and studies of parametric variation of dynamic fracture are limited since the phenomenon inherently has a restricted predictability horizon (Bishop 2009).

Despite these challenges, numerous approaches for modeling pervasive fracture have been utilized, with the finite element method underlying most of this work. Modeling pervasive fracture in standard Galerkin finite element discretizations requires the insertion of evolving fracture surfaces into a pre-determined finite element discretization of a domain of interest. Ideally, these fracture surfaces should have the ability to propagate randomly into the domain. Further, they should be able to freely branch and coalesce as the analysis progresses. To capture these effects, many methods have been used, including finite elements with cohesive surfaces on inter-element boundaries (Xu and Needleman 1994; Camacho and Ortiz 1996), meshfree methods (Li et al. 2002), the extended finite element method (X-FEM) (Moës and Belytschko 2002), hybrid discontinuous Galerkin methods (Radovitzky et al. 2011), and a number of non-Galerkin approaches such as peridynamics (Silling 2003; Ha and Bobaru 2010; Bobaru and Zhang 2015), phase-field approaches (Francfort and Marigo 1998; Borden et al. 2012; Hofacker and Miehe 2013), and lattice models (Kim et al. 2013).

In the context of the finite element method, inter-element surfaces provide a natural network for cracks to manifest. Further, the cohesive zone model over these inter-element surfaces allows crack nucleation effects to be captured. However, with standard, two-dimensional finite elements, element shapes are limited to triangles and quadrilaterals since finite element shape functions are only available on these shapes. While these shapes suffice for many applications, when used in pervasive fracture, they limit the possible fracture network and bias the topology of the cracks, potentially leading to non-natural crack shapes (Bolander and Saito 1998). The effect of finite element mesh dependence on dynamic fracture simulation was investigated by Papoulia et al. (2006), who used pinwheel meshes to address some of the limitations of finite elements in this application.

Recently, the development of generalized barycentric coordinates has permitted more general polygonal element shapes for use with the finite element method. A survey of generalized barycentric coordinates is presented in Floater (2015) and in Anisimov (2017). With polygonal element formulations, an unlimited number of element shapes are available, reducing mesh bias imparted by element selection. Random element shapes provide a non-preferential fracture network and allow for more natural, unbiased cracks to propagate in media. In work by Bishop (2009), Leon et al. (2014), and Spring et al. (2014), random polygonal fracture networks are utilized to model dynamic fracture to great effect. In this paper, we build on these contributions to further demonstrate the capabilities of polygonal finite elements for modeling pervasive fracture.

The remainder of the paper is organized as follows. In Sect. 2, the finite element equations to model fracture with cohesive surfaces are introduced. Polygonal and polyhedral finite element shape functions are also discussed. Section 3 introduces important pervasive fracture modeling considerations, such as meshing, contact, and cohesive element constitutive relationships. In Sect. 4, we describe the nonlinear solution procedure and offer some insight regarding solution time compared to conventional elements. Interesting details of our computer implementation are outlined in Sect. 5 and benchmark fracture problems are presented in Sect. 6. We conclude with some future directions of research in Sect. 7.

2 Polygonal finite element formulation

Polygonal finite elements build on the rich background of finite element technology, making it possible to model new problems within the Galerkin framework. As we will demonstrate in this section, the polygonal finite element formulation used to simulate dynamic fracture shares many common features with standard finite element methodology. The boundary-value problem in both strong and weak form is presented in Sect. 2.1. A finite element approximation is introduced in Sect. 2.2, where we develop the semi-discrete equations of motion. In Sect. 2.3, we depart from standard finite elements and present the shape functions used over polygonal finite element discretizations. Finally, in Sect. 2.4 we discuss methods used to perform numerical integration over polygonal elements.

2.1 Mechanical boundary-value problem with cohesive surfaces

Consider a body $\mathscr {B}$ moving in time $t \in [0, T]$ whose domain is given by $\varOmega$ and whose boundary is given by $\varGamma$. A Lagrangian description of motion is adopted on $\mathscr {B}$, with the position vector in the reference configuration given by $\varvec{X}$ and the position vector in the current configuration given by $\varvec{x}$. Accordingly, the displacement vector on $\mathscr {B}$ is given by $\varvec{u} (\varvec{X}, t) = \varvec{x}(\varvec{X}, t) - \varvec{X}$. The initial configurations of $\varOmega$ and $\varGamma$ at $t = 0$ are denoted $\varOmega _0$ and $\varGamma _0$, respectively. A traction $\bigl ( \varvec{t} (\varvec{X}, t) \bigr )$ is applied on $\varGamma _t \subset \varGamma$, a prescribed displacement $\bigl ( \bar{\varvec{u}} (\varvec{X}, t) \bigr )$ is applied on $\varGamma _u \subset \varGamma$, and a cohesive traction is applied on the cohesive surface $\varGamma _{c} \subset \varGamma$. Furthermore, at $t = 0$ an initial velocity, $\bar{\varvec{v}}$ is given over $\varOmega$. In general, the boundary will contain one of either an applied traction, a prescribed displacement, or a cohesive traction. The boundaries $\varGamma , \varGamma _t, \varGamma _u$, and $\varGamma _{c}$ may change with time, but the properties $\overline{\varGamma _t \cup \varGamma _u \cup \varGamma _{c}} = \varGamma$ and $\overline{\varGamma _t \cap \varGamma _u \cap \varGamma _{c}} = \emptyset$ hold for all $t \in [0,T]$. An example continuum body with a cohesive surface is illustrated in Fig. 1.

Fig. 1

A continuum body with a cohesive surface

As fracture propagates in $\mathscr {B}$, new cohesive surfaces, $\varGamma _c$, are inserted. These cohesive surfaces represent extended crack-tips, or fracture process zones, where cracks have begun to initialize, but are not yet fully formed. This cohesive crack model was first introduced by Dugdale (1960) and Barenblatt (1962) and it provides a natural means of handling crack nucleation, arbitrary crack paths, branching, and fragmentation. It is natural to consider $\varGamma _c$ as the union of two paired surfaces: $\varGamma _{c^+}$ representing the top of the crack and $\varGamma _{c^-}$ representing the bottom of the crack. The jump operator, [[f]], is defined over $\varGamma _c$ and it is the difference in f over the two paired surfaces.

The strong form is presented in the reference configuration, i.e., a total Lagrange formulation. The strong form is: find the deformation $\varvec{u}(\varvec{X}, t)$ that satisfies

$$\begin{aligned} \frac{\partial \varvec{P}}{\partial \varvec{X}} : \varvec{I}&= \rho _0 \ddot{\varvec{u}}\quad \text { in } \varOmega \text { and } \forall t, \end{aligned}$$

(1a)

$$\begin{aligned} \varvec{u}&= \bar{\varvec{u}}\quad \text { on } \varGamma _u \text { and } \forall t, \end{aligned}$$

(1b)

$$\begin{aligned} \varvec{P}\cdot \varvec{n}&= \varvec{t} \quad \text { on } \varGamma _t \text { and } \forall t, \end{aligned}$$

(1c)

$$\begin{aligned} {[}[\varvec{P}\cdot \varvec{n}]]&= \varvec{0} \quad \text { on } \varGamma _c \text { and } \forall t, \text { and} \end{aligned}$$

(1d)

$$\begin{aligned} \dot{\varvec{u}}&= \bar{\varvec{v}} \quad \text { in } \varOmega , \end{aligned}$$

(1e)

where $\varvec{P}$ is the first Piola–Kirchhoff stress tensor, $\varvec{I}$ is the identity matrix, $\rho _0 = \rho _0(\varvec{X})$ is the initial density of the material, and a superposed dot and a superposed double-dot on a quantity denote the first and second time derivatives, respectively.

The strong form of the boundary-value problem can be equivalently stated in a weak form that permits a numerical solution using the finite element method. For the strong form in (1), the weak form (principle of virtual work) is: find the deformation $\varvec{u}(\varvec{X}, t) \in \mathcal {S}$ that satisfies

$$\begin{aligned} \delta W_{\text {ext}}&- \delta W_{\text {int}} - \delta W_{\text {cs}} = \delta K \quad \forall \delta \varvec{u} \in \mathcal {V}, \end{aligned}$$

(2a)

where

$$\begin{aligned} \delta W_{\text {ext}}&= \int _{(\varGamma _0)_t} \varvec{t} \cdot \delta \varvec{u} \, ds ,\\ \delta W_{\text {int}}&= \int _{\varOmega _0} \varvec{P} : \left( \frac{\partial (\delta \varvec{u})}{\partial \varvec{X}} \right) \, d\varvec{X} \nonumber \end{aligned}$$

(2b)

$$\begin{aligned} \delta W_{\text {cs}}&= \int _{(\varGamma _0)_c} \varvec{t}_c \cdot [[\delta \varvec{u}]] \, ds \; \text {, and} \end{aligned}$$

(2c)

$$\begin{aligned} \delta K&= \int _{\varOmega _0} \rho _0 \ddot{\varvec{u}} \cdot \delta \varvec{u} \, d\varvec{X}. \end{aligned}$$

(2d)

In (2), $\mathcal {S}$ and $\mathcal {V}$ are trial and test spaces, which are product Hilbert spaces of degree one that satisfy appropriate initial conditions and Dirichlet boundary conditions; $\delta \varvec{u}$ is the virtual displacement; and $\varvec{t}_c$ is the cohesive traction.

2.2 Semi-discrete equations of motion

Let the domain be discretized into M polygonal elements. We label the domain of the eth element $\varOmega ^e_0$. The finite element approximation of the displacement field (trial function) is

$$\begin{aligned} \varvec{u}_e^h ( \varvec{X}, t )= & {} \sum _{a=1}^n \phi _a ( \varvec{X} ) \varvec{u}_a(t) \nonumber \\&\forall \varvec{X} \in \varOmega ^e_0 \text { and } \forall t \in [0, T] , \end{aligned}$$

(3)

where $\varvec{u}_a(t)$ are nodal values of displacement defined at the n vertices of an element and $\phi _a (\varvec{X})$ are finite element shape functions. The shape functions are used to interpolate nodal values over the polygonal domain $\varOmega ^e_0$, with boundary $\varGamma ^e_0$. The velocity and acceleration fields on $\varOmega ^e_0$ are defined analogously to (3) above.

We substitute (3) into (2) and obtain the following element-level matrices and vectors:

$$\begin{aligned} {(\varvec{f}_{\text {ext}})}_e&= \int _{(\varGamma ^e_0)_t} \varvec{N}^T \varvec{t} \, ds ,\text { and} \end{aligned}$$

(4a)

$$\begin{aligned} {(\varvec{f}_{\text {int}})}_e&= \int _{\varOmega ^e_0} \varvec{B}^T_0 \varvec{S} \, d\varvec{X} , \end{aligned}$$

(4b)

$$\begin{aligned} {(\varvec{f}_{\text {cs}})}_e&= \int _{(\varGamma ^e_0)_c} \begin{bmatrix} \varvec{N}^T \Bigm |_{(\varGamma ^e_0)_{c^-}} \\ - \varvec{N}^T \Bigm |_{(\varGamma ^e_0)_{c^+}} \end{bmatrix} \varvec{t}_c \, ds , \end{aligned}$$

(4c)

$$\begin{aligned} \varvec{M}_e&= \int _{\varOmega ^e_0} \rho _0 \varvec{N}^T \varvec{N} \, d\varvec{X}, \end{aligned}$$

(4d)

where $(\varGamma ^e_0)_t = (\varGamma _0)_t \cap \varGamma ^e_0, (\varGamma ^e_0)_c = (\varGamma _0)_c \cap \varGamma ^e_0$, $\varvec{S} = \varvec{F}^{-1} \cdot \varvec{P}$ is the second Piola–Kirchhoff stress tensor, $\varvec{F}$ is the deformation gradient, $\varvec{N} = \varvec{N} ( \varvec{X} )$ is the standard element shape function vector evaluated in the reference configuration,

$$\begin{aligned} \varvec{B}_0&= \begin{bmatrix} \varvec{B}_0^1&\varvec{B}_0^2&\cdots&\varvec{B}_0^n \end{bmatrix}, \end{aligned}$$

(5a)

$$\begin{aligned} \varvec{B}_0^a&= \varvec{B}^a ( \varvec{X} ) \varvec{F}^T \; \text {, and} \end{aligned}$$

(5b)

$$\begin{aligned} \varvec{B} ( \varvec{X} )&= \begin{bmatrix} \varvec{B}^1 ( \varvec{X} )&\varvec{B}^2 ( \varvec{X} )&\cdots&\varvec{B}^n ( \varvec{X} ) \end{bmatrix} \end{aligned}$$

(5c)

is the standard strain–displacement matrix also evaluated in the reference configuration. After assembling the element-level quantities, we obtain the following semi-discrete equations of motion:

$$\begin{aligned} {\varvec{f}_{\text {ext}} - \varvec{f}_{\text {int}} - \varvec{f}_{\text {cs}} = \varvec{M} \ddot{\varvec{d}}}, \end{aligned}$$

(6)

where $\varvec{d} := \{ \varvec{u}_1, \varvec{u}_2, \ldots , \varvec{u}_N \}^T$ is the vector of nodal displacements.

2.3 Generalized barycentric coordinates

All generalized barycentric coordinates (shape functions) are linearly complete, meaning the following two properties hold for all $\varvec{X} \in \varOmega ^e_0$:

• 1. the coordinates form a partition of unity:

  $\sum _{a=1}^n \phi _a (\varvec{X}) = 1$; and

• 2. the coordinates satisfy linear reproducing conditions:

  $\sum _{a=1}^n \phi _a (\varvec{X}) \varvec{X}_a = \varvec{X}$.

Linear completeness and basic continuity requirements (see Hughes 2000) are required of finite element shape functions to ensure convergence. Additionally, if the coordinates are non-negative, $\phi _a(\varvec{X}) \ge 0$ for all a, the convex hull property for the interpolant is also met. Nonnegativity provides many useful benefits in a Galerkin method, such as a positive-definite mass matrix and suppression of the Runge phenomenon. Wachspress coordinates and maximum entropy coordinates are two examples of generalized barycentric coordinates that satisfy all these requirements, however there are many more (see Floater et al. 2014; Anisimov 2017 for a survey). We will use both in the examples presented in Sect. 6. While we choose to employ Wachspress and maximum entropy coordinates in this paper, other generalized barycentric coordinates have been demonstrated to be suitable for pervasive fracture simulations. See Bishop (2009) for one such example.

2.3.1 Wachspress shape functions

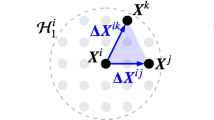
Using ideas from projective geometry, Wachspress (1975) generated a rational finite element basis on convex polygons. On using the formulas presented in Floater et al. (2014), we compute polygonal Wachspress finite element shape functions ($\phi _a(\varvec{X})$ for $a = 1, \ldots , n$) and their derivatives ($\nabla \phi _a(\varvec{X})$ for $a = 1, \ldots , n$) as follows. Consider a polygon $\varOmega _e \subset {\mathbb {R}}^2$ with n vertices, $\varvec{V}_1, \ldots , \varvec{V}_n$, oriented counterclockwise. We assume vertices are in cyclic order, with $\varvec{V}_{n+1} := \varvec{V}_1$ and $\varvec{V}_0 := \varvec{V}_n$. We define an edge of $\varOmega _e$, $e_a$ for $a = 1, \ldots ,n$, as the line segment joining $\varvec{V}_a$ and $\varvec{V}_{a+1}$. Let $\varvec{n}_a$ be the outward normal for the edge $e_a$. For each edge $e_a$, we define $h_a ( \varvec{X} )$ as the perpendicular distance from $\varvec{X}$ to $e_a$ and $\varvec{p}_a ( \varvec{X} ) := \frac{\varvec{n}_a}{h_a ( \varvec{X} )}$. A quadrilateral illustrating some of these values is presented in Fig. 2. The shape function for vertex $\varvec{V}_a$ (i.e., $\phi _a ( \varvec{X} ))$ is defined as

$$\begin{aligned} \phi _a ( \varvec{X} ) = \frac{w_a ( \varvec{X} )}{\sum _{b=1}^n w_b ( \varvec{X} )}, \end{aligned}$$

(7)

where $w_a ( \varvec{X} ) := \det (\varvec{p}_{a-1} ( \varvec{X} ), \varvec{p}_a ( \varvec{X} ))$. The gradient of the shape function associated with vertex $\varvec{V}_a$ (i.e., $\nabla \phi _a ( \varvec{X} ))$ is given by

$$\begin{aligned} \nabla \phi _a ( \varvec{X} ) = \phi _a ( \varvec{X} ) \left( \varvec{R}_a ( \varvec{X} ) - \sum _{b=1}^n \phi _b ( \varvec{X} ) \varvec{R}_b ( \varvec{X} ) \right) , \end{aligned}$$

(8)

where $\varvec{R}_a ( \varvec{X} ) := \varvec{p}_{a-1} ( \varvec{X} ) + \varvec{p}_a ( \varvec{X} )$.

Fig. 2

Computing Wachspress shape functions over a sample polygon

2.3.2 Maximum entropy shape functions

Shannon (1948) introduced the notion of informational entropy as a measure of uncertainty given the probabilities of the possible discrete outcomes of an event. On using Shannon’s work, Jaynes (1957) demonstrated that maximizing entropy provides the least biased probabilities of discrete outcomes when provided insufficient data to determine these probabilities uniquely. Later, Sukumar (2004) recognized the maximum-entropy (max-ent) probability distribution as, in fact, a convex generalized barycentric coordinate that satisfies the linear completeness conditions. While the shape functions in Sukumar (2004) are only valid for convex polytopes, the framework of prior distributions (Kullback and Leibler 1951; Sukumar and Wright 2007) allow max-ent shape functions to be computed over nonconvex polytopes (Hormann and Sukumar 2008).

The maximum entropy shape functions are computed as the solution of the constrained optimization problem:

$$\begin{aligned} \max _{\phi _a( \varvec{X} ) \text { for } a = 1, \ldots , n} - \sum _{a=1}^n \phi _a ( \varvec{X} ) \ln \left( \frac{\phi _a ( \varvec{X} )}{w_a ( \varvec{X} )} \right) \end{aligned}$$

(9a)

subject to

$$\begin{aligned} \sum _{a=1}^n \phi _a ( \varvec{X} ) = 1 \, \text { and} \end{aligned}$$

(9b)

$$\begin{aligned} \sum _{a=1}^n \phi _a ( \varvec{X} ) \varvec{X} = \varvec{X}, \end{aligned}$$

(9c)

where $\phi _a ( \varvec{X} ) \ge 0$ are the shape functions and $w_a ( \varvec{X} ) \ge 0$ are the nodal weight functions. Instead of solving the primal problem posed in (9), we use convex duality to realize an efficient solution via Newton’s method (Arroyo and Ortiz 2006). To compute the shape functions and their gradients, we follow the work of Millán et al. (2015). Using convex duality, we directly seek the solution to the Lagrange multipliers, $\varvec{\lambda } ( \varvec{X} ) \in {\mathbb {R}}^2$. They are computed as

$$\begin{aligned} \varvec{\lambda }^* ( \varvec{X} ) = {\mathop {{{\mathrm{arg\,min}}}}_{\varvec{\lambda }(\varvec{X})}}\,\ln Z(\varvec{X}, \varvec{\lambda }), \end{aligned}$$

(10)

where $\varvec{\lambda }^* ( \varvec{X} )$ represent the value of the Lagrange multipliers at the minimum and

$$\begin{aligned} Z(\varvec{X}, \varvec{\lambda }) = \sum _{b = 1}^n w_b ( \varvec{X} ) \exp \left[ - \varvec{\lambda } ( \varvec{X} ) \cdot ( \varvec{X}_b - \varvec{X} ) \right] \end{aligned}$$

(11)

is the partition function. Given $\varvec{\lambda }^* ( \varvec{X} )$, shape functions are then computed as

$$\begin{aligned} \phi _a ( \varvec{X} ) = \frac{ w_a ( \varvec{X} ) \exp \left[ - \varvec{\lambda }^* ( \varvec{X} ) \cdot ( \varvec{X}_a - \varvec{X} ) \right] }{ Z ( \varvec{X}, \varvec{\lambda }^* ( \varvec{X} ) ) } . \end{aligned}$$

(12)

To simplify the presentation that follows, we define the following functions:

$$\begin{aligned} g_a^*= & {} g_a ( \varvec{X}, \varvec{\lambda }^* ( \varvec{X} ) ) \nonumber \\:= & {} \frac{ \exp \left[ - \varvec{\lambda }^* ( \varvec{X} ) \cdot ( \varvec{X}_a - \varvec{X} ) \right] }{ Z ( \varvec{X}, \varvec{\lambda }^* ( \varvec{X} ) ) } \end{aligned}$$

(13a)

$$\begin{aligned} \varvec{J}^*= & {} \varvec{J} ( \varvec{X}, \varvec{\lambda }^* ( \varvec{X} ) ) \nonumber \\:= & {} \sum _{a=1}^n \phi _a( \varvec{X} ) ( \varvec{X}_a - \varvec{X} ) \otimes ( \varvec{X}_a - \varvec{X} ) \end{aligned}$$

(13b)

$$\begin{aligned} D \varvec{\lambda }^*= & {} D \varvec{\lambda } ( \varvec{X}, \varvec{\lambda }^* ( \varvec{X} ) ) \nonumber \\:= & {} ( \varvec{J}^* )^{-1} \left( \sum _{a=1}^n ( \varvec{X}_a - \varvec{X} ) \otimes g_a^* \nabla w_a ( \varvec{X} ) - \varvec{I} \right) .\nonumber \\ \end{aligned}$$

(13c)

With these definitions, the gradient is computed as

$$\begin{aligned} \nabla \phi _a ( \varvec{X} )= & {} g_a^* \nabla w_a ( \varvec{X} ) - \phi _a ( \varvec{X} ) \nonumber \\&\left[ (\varvec{X}_a - \varvec{X}) \cdot D \varvec{\lambda }^* + \sum _{b=1}^n g_b^* \nabla w_b ( \varvec{X} ) \right] .\nonumber \\ \end{aligned}$$

(14)

2.4 Numerical integration

To numerically integrate the expressions in (4), we apply a triangular integration rule (Dunavant 1985) to the tessellation of a polygon. Tessellations are generated by fanning triangles out from the centroid of the polygon. This tessellation is valid over convex polygons. The shape functions in Sect. 2.3 span affine polynomials; however, they are not polynomials themselves. Since the integration rule is only designed to integrate polynomial functions exactly, the non-polynomial shape functions, $\phi _a ( \varvec{X} )$, are not exactly integrated. This error results in inexact reproduction of linear fields and consequently failure of the patch test. Critically, this error persists even with mesh refinement, which prevents convergence below the magnitude of the quadrature error. Methods to restore polynomial precision using perturbed shape function gradients were first explored in the context of meshfree methods (Krongauz and Belytschko 1997; Chen et al. 2001). These corrected gradients are also applicable to any non-polynomial basis, such as the Wachspress and max-ent shape functions. Further, the correction has been shown to work over polygonal elements as well (Talischi and Paulino 2014; Sukumar 2013; Bishop 2014). Talischi et al. (2015) recognized this correction as a constant factor for linear elements that is proportional to the error in the discrete divergence theorem. We follow the procedure therein to compute corrected gradients. Figure 3 and Table 1 demonstrate satisfaction of the patch test with the correction applied.

Fig. 3

Example of equilibrium patch test passage with gradient correction applied to Wachspress shape functions. In all the above, shape functions are integrated with a three-point rule. Without correction, the patch test is only satisfied to $\mathcal {O}(10^{-5})$ in $\varvec{u}$, whereas with gradient correction, the patch test is satisfied to machine precision. a $| \varvec{u} - \varvec{u}^h |_2$, uncorrected. b $| \varvec{\sigma } - \varvec{\sigma }^h |_F$, uncorrected. c $| \varvec{u} - \varvec{u}^h |_2$, corrected. d $| \varvec{\sigma } - \varvec{\sigma }^h |_F$, corrected

3 Pervasive fracture modeling considerations

In this section, we explore some of the necessary ingredients to model pervasive fracture using polygonal finite elements. To generate polygonal meshes capable of capturing random fracture patterns, we turn to maximal Poisson-disk sampling (MPS). In Sect. 3.1, we describe the MPS algorithm and demonstrate these meshes are not directionally preferential. Pervasive fracture results in unpredictable contact across the entire domain. To handle this, robust contact detection and enforcement are required. These algorithms are outlined in Sect. 3.2. We capture the intermediate stages of crack formation through cohesive elements. In Sect. 3.3, we detail the cohesive surface initiation criteria, the criteria to create a fully-formed crack, and the link between these criteria and fracture mechanics.

3.1 Meshing

3.1.1 Unbiased meshes

Ideally, a pervasive fracture simulation should be able to reproduce any possible crack pattern in the domain. This includes branching cracks (Kobayashi et al. 1974; Ravi-Chandar and Knauss 1984b; Sharon et al. 1995), curved cracks (Ramulu and Kobayashi 1985; Hawong et al. 1987), cracks with surface roughness (Green and Pratt 1974; Rittel and Maigre 1996), and other phenomena observed in fracture testing. For proper convergence with linear finite elements, cracked surfaces can be represented as the union of line segments, ignoring the need to explicitly model a curved crack. Accordingly, the set of all possible cracks in the domain, $\mathcal {C}$, should be capable of reproducing any line segment within the domain. In the discussion that follows, $\mathcal {C}$ will coincide with the inter-element surfaces of a finite element mesh. Therefore, we will use $\mathcal {C}$ to refer to this specific network of possible cracks. A measure of path deviation from a line segment $\ell$ was introduced by Rimoli and Rojas (2015),

$$\begin{aligned} \eta = \frac{L_\mathcal {C}}{L_\ell }, \end{aligned}$$

(15)

where $L_\mathcal {C}$ is the shortest (Euclidean) distance between the two endpoints of $\ell$ along elements in $\mathcal {C}$ and $L_\ell$ is the Euclidean distance between the same two endpoints. Since $\mathcal {C}$ coincides with inter-element facets in the mesh, it can be computed using Dijkstra’s algorithm (Dijkstra 1959). The error in representing a straight line segment is defined as

$$\begin{aligned} \epsilon = \eta - 1. \end{aligned}$$

(16)

As $\epsilon \rightarrow 0$, length deviation from a straight line approaches zero, and accordingly, surface roughness (and the fracture toughness induced from crack path deviation) approaches zero.

Table 1 Max error in norm of displacement and Frobenius norm of stresses for uncorrected and corrected shape function gradients in the equilibrium patch test

The effect of the fracture network $\mathcal {C}$ can also be analyzed from the point of view of the location of initiation of a fracture surface. A crack should be free to initiate and grow from any point in the domain in any direction in the domain. In $\mathcal {C}$, initiation is limited to edges of elements. Therefore, for a fracture network to show no preference for crack direction, randomly directed edges should be present throughout the domain. However, even with a non-preferential fracture network, restricting potential crack paths to $\mathcal {C}$ limits crack growth and initiation directions. This can cause variations in crack initiation locations and directions among different random meshes of the same geometry. Note that variability in macroscopic crack growth patterns are also common in dynamic fracture testing. While these variations are thought to occur due to material inhomogeneities and other test-to-test differences (Spring and Paulino 2018), random spatial variations in $\mathcal {C}$ can be used as a proxy for modeling this material behavior. As part of the examples in Sect. 6, we investigate the variation in crack patterns caused by changes in $\mathcal {C}$. Further, since $\mathcal {C}$ limits potential locations and directions of crack growth, spurious stresses and deformations can be observed where cracks might otherwise form. One such example is shear-induced dilation in mode II dominated fracture. This issue can potentially be ameliorated by introducing surface smoothing into the finite element mesh.

Fig. 4

Assuming rough surfaces orient at 45$^{\circ }$, microscopic surface roughness causes a path deviation of $\eta = 1.41$

While line segments may be sufficient to represent macroscopic crack patterns, it is worth noting that dynamic crack formation can result in microscopic roughness in the cracked surfaces. In finite element implementations, $\mathcal {C}$ is limited to inter-element surfaces in the mesh. These surfaces are generally not on the length scale of observed roughness and would therefore not be captured by $\mathcal {C}$. Further, attempts to capture these surfaces would have a severe effect on the critical timestep in an explicit dynamic finite element analysis. Though the length scale of surface roughness is small (see, for example, Fig. 9 in Kalthoff 2000), its effect on the path deviation can be large, as illustrated in Fig. 4. While microscopic roughness can have significant effects on path deviation, it has minimal effect on the macroscopic crack path, so trends in crack growth can more practically be captured by inter-element fracture surfaces. Roughness effects can then be captured in the crack initiation criteria and friction coefficient used in the finite element formulation. The initiation criteria used herein is discussed in Sect. 3.3.

Since $\mathcal {C}$ is limited to the inter-element facets of a finite element mesh, reducing $\epsilon$ to zero, or equivalently, emanating edges in all directions at every vertex, is all but impossible for any arbitrary line segment, unless on-the-fly mesh modification is permitted. However, if $\mathcal {C}$ exhibits no directional dependence, $\epsilon$ should not be a function of the direction of the line segment $\ell$. Fracture networks that do exhibit directional dependence are said to have mesh-induced anisotropy, whereas meshes that do not are said to be isotropic. We will examine these properties further in Sect. 3.1.3.

3.1.2 Maximal Poisson-disk sampling

Maximal Poisson-disk sampling is a process used to fill a domain ($\varOmega$) with randomly placed, yet evenly distributed set of n points, $\mathcal {P} = \left\{ p_i \right\} _{i=1}^n$, where $p_i$ refers to point i. Points are chosen sequentially, such that choosing a point $p_i$ affects the available placement locations of later points $p_{i+1}, \ldots , p_n$. In this section, we define the domain of available point placement locations after the placement of point $p_i$ as $\varOmega _i \subset \varOmega$. The initial domain (before any points are placed) is $\varOmega _0 := \varOmega$. Once all n points have been placed, $\varOmega _n = \emptyset$. The location of $p_i$ is given by the location vector, $\varvec{x}_i$. The placement of point $p_i$ is subject to the following criteria (Gamito and Maddock 2009):

• 1. the location must be bias-free: For all $\mathcal {D} \subset \varOmega _{i-1}$, we have $P(\varvec{x}_i \in \mathcal {D}) = \dfrac{\text {Vol}(\mathcal {D})}{\text {Vol}(\varOmega _{i-1})}$; and

• 2. the location must be at least a distance r from other disks: $|| \varvec{x}_i - \varvec{x}_j || > r \quad \forall j < i$.

The first criterion ensures points are randomly selected in the domain, a process known as Poisson sampling. However, this does not restrict points from being in close proximity, leading to undesirable clustering of points. Enforcement of the second criterion results in points being more evenly distributed while maintaining randomness. Taken together, criteria one and two are known as Poisson-disk sampling, better known as dart throwing in computer graphics, or the Matérn second process in statistics. To ensure points maximally cover the domain, we introduce a final criterion:

• 3. once all points have been placed, $\forall \varvec{x}\in \varOmega$ there must exist a point $p_i$ such that $|| \varvec{x}- \varvec{x}_i || < r$.

Taken together, these three criteria define maximal Poisson-disk sampling.

Fig. 5

Eliminating short edges in a Voronoi mesh from an MPS point set. a Mesh with short edges highlighted red. b Mesh with collapsed short edges

Generating an MPS point set can be done naïvely by selecting random points in $\varOmega$ and verifying the second criterion is satisfied; however, as $i \rightarrow n, \varOmega _i \rightarrow \emptyset$, reducing the probability of a randomly selected point being in $\varOmega _i$. Recall, to satisfy the third criterion, we must have $\varOmega _n = \emptyset$. To more efficiently generate MPS point sets, we use an algorithm by Ebeida et al. (2011). This algorithm efficiently approximately tracks the shape of $\varOmega _{i-1}$ and selects $p_i$ from this approximate shape, increasing the probability a point selected lies within $\varOmega _{i-1}$.

To improve the efficiency of the finite element solution procedure, r is made a function of location (i.e., $r = r(\varvec{x}))$. This allows selective mesh refinement in areas of $\varOmega$ where small features are present, where large strain gradients are located, and/or where cracks are expected to propagate. If r is constant in areas of crack growth, the randomness of the MPS mesh is retained. An example of an MPS mesh with r used to control mesh density is presented in Fig. 16. Additionally, we permit the specification of critical points throughout the boundary, $\varGamma$. Two points are placed equidistant from a line that contains the critical point, ensuring a node in the finite element mesh is placed on the critical point. Critical points provide two important purposes within the context of finite element analysis: (1) to accurately capture non-convex features on the boundary; and (2) to aid in precise placement of boundary conditions. Since critical points are defined a priori, they can result in mesh-induced anisotropy; accordingly, their usage is kept to a minimum in the examples presented in Sect. 6.

Once $\mathcal {P}$ is generated, it can be used to generate a Voronoi diagram using a tool such as Matlab’s voronoin. To ensure the Voronoi diagram conforms to $\varOmega$, we reflect points near the boundary $\varGamma$ to generate a smooth boundary. While Voronoi meshes generated from MPS point sets generally contain elements with good quality, inevitably, the mesh will contain some short edges. As detailed in Sect. 4, we use explicit central difference time-stepping to solve the semi-discrete equations. Since the critical time step in explicit methods is determined in part by the size of the smallest finite element, having elements with very small edges and faces is detrimental since it reduces the critical time step, thus requiring more iterations to run an analysis. The problem of short edges is not unique to MPS meshes; they are present in polygonal meshes generated from centroidal Voronoi tessellations (CVTs) as well.

Various methods have been proposed to deal with short edges. Sieger et al. (2010) developed a method to remove short edges by solving a minimization problem and more recently, Abdelkader et al. (2017) used local sampling to remove short edges systematically from a mesh. In this work, we follow a simple method introduced by Talischi et al. (2012). Therein, an inner angle $\beta$ is defined as the angle between two consecutive points of a polygon, as measured from the centroid of the polygon. Values of $\beta$ below a certain threshold result in one of the vertices being removed from the mesh. In our implementation, vertices nearest the boundary are retained, such that the overall shape of the boundary $\varGamma$ is not altered. As an added benefit, removed vertices reduce the degrees-of-freedom in the system, speeding up the finite element solution procedure. For meshes generated herein, we removed edges where $\beta < \frac{\pi }{8}$, which resulted in about ten to fifteen percent of the vertices being removed from the mesh. An illustration of the short-edge regularization process is provided in Fig. 5. This process maintains the convexity of each element, so they are still suitable for analysis using both Wachspress and max-ent shape functions. The effects of short edge removal on distribution of edge length are illustrated in Fig. 6.

Fig. 6

A histogram showing the probability of normalized element length in three polygonal mesh types: MPS mesh (blue), centroidal Voronoi tessellation (CVT) mesh with 100 iterations of Lloyd’s algorithm (orange), and MPS mesh with short-edge regularization (green). As illustrated, both MPS and CVT meshes have short edges, though they are more prevalent in MPS meshes. The short edge removal process eliminates all edges with $\beta < \frac{\pi }{8}$

Fig. 7

Boxplots showing error in path ($\epsilon$) as a function of angle of a line segment for three different polygonal mesh types and one triangular mesh type: MPS (blue), CVT with 100 iterations of Lloyd’s algorithm (orange), Delaunay triangulation of MPS points (red), and MPS with short-edge regularization (green)

3.1.3 Mesh quality

In this section, we compare the quality of the fracture network, $\mathcal {C}$, in MPS-generated Voronoi meshes to $\mathcal {C}$ in centroidal Voronoi tessellation (CVT) meshes and meshes produced from the Delaunay triangulation of an MPS point set (MPS triangle mesh). The comparison is based on path deviation and mesh-induced anisotropy, concepts introduced in Sect. 3.1.1. CVT meshes are generated using PolyMesher version 1.1 (Talischi et al. 2012).

Fig. 8

Orientation of edges within a subdomain of a typical MPS mesh, CVT mesh, MPS triangle mesh, and MPS mesh with short-edge regularization. a MPS Voronoi. b CVT. c MPS triangle. d MPS Voronoi, short-edge regularization

To investigate these properties, we generated ten circular meshes using CVT (generated from 100 iterations of Lloyd’s algorithm), MPS triangles, MPS, and MPS with short-edge regularization. In Fig. 7, the relative error in length in reproducing a line segment over $\mathcal {C} \bigl (\epsilon$, defined in (16)$\bigr )$ is computed for various angles around the circle. The line segments traverse the entire diameter of the circle for a length of about 250 times the average inter-element edge length in all four mesh types. As Fig. 7 demonstrates, $\epsilon$ is not sensitive to line segment angle for MPS meshes, MPS triangle meshes, and CVT meshes. Further, the short-edge regularization process did not affect this property. In other words, all four mesh types did not exhibit mesh-induced anisotropy based on this metric. To investigate local mesh anisotropy, frequency of edge direction is plotted in Fig. 8 for edges within a radius of fifty times the average edge length of the mesh. While all three MPS-based meshes demonstrated relatively evenly distributed edge directions, the CVT meshes generally exhibited three preferential directions separated by 60$^{\circ }$. Figure 9 explains this observation—locally, CVT meshes can resemble a hexagonal tiling pattern. Hexagonal tiling is a stable CVT configuration and produces consistent element edge lengths; however, its regularity results in mesh-induced anisotropy. The problem can be alleviated somewhat by relaxing the requirement of a CVT being centroidal, though this has implications on element size regularity in meshes generated using Lloyd’s algorithm.

Examining Fig. 7, it is evident that MPS meshes have smaller deviation in path compared to CVT meshes. Further, the short edge elimination process results in additional reduction in $\epsilon$—approximately 30% less than $\epsilon$ for CVT meshes. Also, of note is the minimal dependence on mesh refinement on the average value of $\epsilon$, as Fig. 10 illustrates. Accordingly, mesh refinement is not a valid strategy to further reduce error in path for both CVT and MPS meshes. While MPS meshes are slightly advantageous to CVT meshes in this regard, it is worth noting $\epsilon$ can be greatly reduced using triangular elements (plotted in Fig. 7) and mesh-modification schemes on polygons, such as element splitting (Leon et al. 2014) and inserting edges perpendicular to the mid-point of existing edges (Spring et al. 2014; Rimoli and Rojas 2015). When applied to CVT meshes, either of these mesh-modifications reduce $\epsilon$ to about 0.05. Also using a triangular meshing scheme reduces $\epsilon$ to about 0.05 as well. Ultimately, a scheme that permits moving vertices and/or inserting new edges may make it possible to eliminate mesh bias entirely. However, such a scheme may result in nonconvex and/or poorly shaped elements. To deal with element quality issues, robust shape functions such as max-ent with appropriately designed prior weight functions or the virtual element method may provide relief.

Fig. 9

Locally, CVT meshes can contain hexagonal tiling leading to mesh-induced anisotropy

Fig. 10

Error in path ($\epsilon$) for four levels of mesh refinement. Ten meshes are generated for each level of mesh refinement, then boxplots are used to show the spread in $\epsilon$. The figure demonstrates $\epsilon$ is largely insensitive to mesh refinement

3.2 Contact

3.2.1 Collision detection

Pervasive fracture modeling presents several challenges in terms of modeling contact. Large-scale fracture processes create new surfaces unpredictably, and furthermore, it is impossible to know beforehand which surfaces come into contact. This makes it unfeasible to define contact surface pairs before the analysis is run. Accordingly, collision detection must occur automatically and over the entire domain. We define contact as a vertex interpenetrated into an element. Therefore, a detection algorithm must identify all interpenetrated vertex/element pairs.

Fig. 11

With the solid gray background grid, the interpenetrated vertex (hollow circle) is not detected since it does not share vertices in the same grid element with any of the vertices of the element it penetrates. However, with the dotted gray background mesh, the interpenetration is detected

Collision detection has many important computational applications outside of solid mechanics and is a topic of intense research in the field of computer graphics. For detailed expositions on the subject, the interested reader is referred to books by Ericson (2005) and van den Bergen (2004). A brute force approach to collision detection would check all possible contact pairs for interpenetration. However, this approach has a machine time complexity of $O(N^2)$, where N is the number of vertices in the finite element mesh. For very large meshes, this can cause a bottleneck in the analysis. To speedup the identification of contact pairs, we use a two-step detection algorithm. The first step employs a uniform background mesh to eliminate pairs not near each other. Element detection is based on the vertices contained in the background mesh element; therefore, the first step is run twice with a shifted background mesh to avoid missed potential contact pairs, such as the case illustrated in Fig. 11. Step two of the algorithm uses the Jordan curve theorem to test if the vertex lies in the element in each of the potential contact pairs. With vertices evenly distributed in each of the background mesh elements, this two-step algorithm reduces machine time complexity to O(N). Further, since penetration detection on each grid element is independent, this portion of the algorithm is well-suited for on-node parallelism using threads or even GPU execution.

3.2.2 Penalty contact semi-discrete equations of motion

Once interpenetrated vertices have been identified, contact enforcement is achieved through a vertex-to-edge (i.e., node-to-surface) penalty approach. Penalization occurs on each of the contact pairs based on two factors (Belytschko et al. 2013):

• 1. the amount of interpenetration of the vertex into the element and

• 2. the relative velocity between the element and the vertex.

The amount of interpenetration is given by $g_n$, the gap normal, and the relative velocity is given by $\dot{g}_n$, the gap rate. A penalty based on relative velocity provides most of the contact force upon initial impact; however, as the rate of interpenetration slows, the relative velocity penalty diminishes. The other penalty term, based on the amount of interpenetration, ensures contact does not persist, even with small/negative relative velocity.

To more formally define $g_n$ and $\dot{g}_n$, we first consider an element/vertex pair in contact. We term the element in the pair $\varOmega _s$ and the vertex $v_s$. $\varOmega _s$ is bounded by n arbitrary edges that lie on the boundary of $\varOmega$ (i.e., $\varGamma$), ${(\varGamma _s)_e} \subset \varGamma$, for $e = 1, \ldots , n$. Each boundary facet has an outward normal $\varvec{n}_e$ that resides in a set of all the element normals, $\mathcal {N}_s = \left\{ \varvec{n}_e \right\} _{e=1}^n$. The location of $v_s$ is given by $\varvec{x}$. Now, we can define the gap normal as

$$\begin{aligned} g_n = \min _{\varvec{n}_e \in \mathcal {N}_s} ( \varvec{n}_e \cdot \varvec{g}_e ), \end{aligned}$$

(17)

where $\varvec{g}_e$ is a vector traveling from $v_s$ to an arbitrary point on the hyperplane where ${(\varGamma _s)_e}$ is located. Typically, a vertex on ${(\varGamma _s)_e}$ is chosen as the arbitrary point. We identify the critical normal vector as

$$\begin{aligned} \varvec{n}_e^* = {\mathop {{{\mathrm{arg\,min}}}}_{\varvec{n}_e \in \mathcal {N}_s}} ( \varvec{n}_e \cdot \varvec{g}_e ) \end{aligned}$$

(18)

and its corresponding boundary as ${(\varGamma _s)_e^*}$. The projection of $\varvec{x}$ onto ${(\varGamma _s)_e^*}$ is

$$\begin{aligned} \varvec{\xi } = \varvec{x}+ g_n \varvec{n}_e^*. \end{aligned}$$

(19)

Now, the gap rate can be defined as

$$\begin{aligned} \dot{g}_n = \left( \dot{\varvec{u}}_s (\varvec{\xi }) - \dot{\varvec{u}}_n (\varvec{x}) \right) \cdot \varvec{n}_e^*, \end{aligned}$$

(20)

where $\dot{\varvec{u}}_s (\varvec{\xi }) = \sum _{a=1}^n \phi _a (\varvec{\xi }) \dot{\varvec{u}}_a (t)$ is the velocity evaluated on ${(\varGamma _s)_e^*}$ and $\dot{\varvec{u}}_n (\varvec{x})$ is the velocity evaluated at $v_s$. With explicit central difference time-stepping, the velocity vector field is tracked and stored throughout the analysis, simplifying computation of these quantities.

With $g_n$ and $\dot{g}_n$ on hand for each contact pair, we enforce contact through the semi-discrete equations of motion:

$$\begin{aligned} {\varvec{f}_{\text {ext}} + \varvec{f}_{\text {con}} - \varvec{f}_{\text {int}} - \varvec{f}_{\text {cs}} = \varvec{M} \ddot{\varvec{d}}}, \end{aligned}$$

(21)

where $\varvec{f}_{\text {ext}}, \varvec{f}_{\text {int}}$, and $\varvec{f}_{\text {cs}}$ are defined in (4) and $\varvec{f}_{\text {con}}$ is the finite element assembly of ${(\varvec{f}_{\text {con}})}_e$, where

$$\begin{aligned} {({(\varvec{f}_{\text {con}})}_e)}_a&= \phi _a (\varvec{\xi }) \left( g_n \tilde{\beta }_1 + \dot{g}_n \tilde{\beta }_2 \right) \varvec{n}_i^* \quad \text { on } {\varGamma _c}_i^* \end{aligned}$$

(22a)

and

$$\begin{aligned} {(\varvec{f}_{\text {con}})}_e&= - \left( g_n \tilde{\beta }_1 + \dot{g}_n \tilde{\beta }_2 \right) \varvec{n}_i^* \quad \text { on } v_c \end{aligned}$$

(22b)

for each contact pair. In (22),

$$\begin{aligned} \tilde{\beta }_i = \beta _i \frac{L_{\text {trib}}}{\overline{L_{\text {edge}}}} , \end{aligned}$$

where $\beta _i$ for $i = 1,2$ are the penalty parameters ($\beta _1$ is the interpenetration penalty and $\beta _2$ is the relative velocity penalty), $L_{\text {trib}}$ is the tributary edge length computed for the vertex, and $\overline{L_{\text {edge}}}$ is the average edge length. Scaling the penalty parameter based on the normalized edge length causes contact forces to be smooth over the entirety of $\varGamma _c$, even with unevenly spaced vertices.

3.3 Cohesive element formulation

To model fracture surfaces, we adopt the cohesive crack model first introduced by Dugdale (1960) and Barenblatt (1962). In the cohesive crack model, a cohesive surface ahead of the crack front is used to model a fracture process zone, wherein the material-dependent critical energy release rate, $\mathcal {G}_c$, must be met for a crack to fully form. The energy release rate is defined as

$$\begin{aligned} \mathcal {G} = \frac{d W_s}{d a}, \end{aligned}$$

(23)

where $W_s$ is the work required to create new surfaces and a represents an incremental length of crack growth. The crack is fully formed when $\mathcal {G} = \mathcal {G}_c$. To track $\mathcal {G}$, we define a traction-separation curve that is active over cohesive surface pairs, $\varGamma _{c^+}$ and $\varGamma _{c^-}$.

Fig. 12

Linear traction-separation curve used on cohesive elements. Gray shaded area is equal to $\mathcal {G}_c$

There are many types of cohesive element formulations that provide a traction-separation law as well as separation criteria over $\varGamma _c$. Two main classes of cohesive elements are the intrinsic cohesive elements and the extrinsic cohesive elements. Intrinsic cohesive elements must be inserted into the finite element mesh before the analysis begins and they contain the elastic portion of the stress-strain curve in their traction-separation law. Xu and Needleman (1994) utilized this form of cohesive element in one of the earliest contributions of modeling dynamic fracture. Extrinsic cohesive elements, on the other hand, are inserted into the mesh as the analysis progresses. These elements are only inserted in edges that meet prescribed criteria. Typically, the traction-separation curve for extrinsic cohesive elements only contains a softening portion. Traction-separation laws can be generated in an ad-hoc manner, or they can be formed from a suitable potential function. They can also be generated using an existing constitutive relationship as discussed in Yang et al. (2005). An overview of traction-separation relationships is presented in Park and Paulino (2013).

In this work, we employ an extrinsic, potential-based, linear traction-separation law devised by Camacho and Ortiz (1996). The relationship is illustrated in Fig. 12. We define ${\delta _\sigma }_{{ crit}}$ as the maximum previous value of $\delta _n$ and $\delta _{{ max}}$ as the maximum $\delta _n$ for which the cohesive surface is active. The normal displacement between the two cohesive surfaces is $\delta _n = [[ \varvec{u} ]] \cdot \bar{\varvec{n}}$, where $\bar{\varvec{n}}$ is the average normal over $\varGamma _{c^+}$ and $\varGamma _{c^-}$. The area under the traction-separation curve is equal to $\mathcal {G}_c$, i.e.,

$$\begin{aligned} \mathcal {G}_c = \frac{\sigma _{\text {max}} \delta _{{ max}}}{2} . \end{aligned}$$

(24)

The cohesive surface is initiated when the average normal traction over an inter-element surface, $t_n = \varvec{n} \cdot \varvec{\sigma } \cdot \varvec{n}$, exceeds $\sigma _{\text {max}}$.

The normal traction ($\sigma$) and shear traction ($\varvec{\tau }$) on the cohesive faces are computed as follows.

• 1. If $\delta _n < 0$:

  $$\begin{aligned} \sigma&= - \delta _n \beta _1 \quad \text { and} \\ \varvec{\tau }&= \varvec{0}, \end{aligned}$$

  where $\beta _1$ is the interpenetration penalty parameter introduced in Sect. 3.2.2.

• 2. If $0 \le \delta _n < {\delta _\sigma }_{{ crit}}$:

  $$\begin{aligned} \sigma&= \sigma _{\text {max}} \left( 1 - \frac{{\delta _\sigma }_{{ crit}}}{\delta _{{ max}}} \right) \frac{\delta _n}{{\delta _\sigma }_{{ crit}}} \quad \text { and} \\ \varvec{\tau }&= || \varvec{\tau _0} || \left( 1 - \frac{{\delta _\sigma }_{{ crit}}}{\delta _{{ max}}} \right) \frac{\delta _n}{{\delta _\sigma }_{{ crit}}} \frac{\varvec{\delta }_\tau }{ || \varvec{\delta }_\tau || }, \end{aligned}$$

  where $\varvec{\tau }_0$ is the tangential traction vector at initialization of the cohesive surface and $\varvec{\delta }_\tau$ is the tangential relative displacement vector between $\varGamma _{c^+}$ and $\varGamma _{c^-}$.

• 3. If $0 \le \delta _n < \delta _{{ max}}$:

  $$\begin{aligned} \sigma&= \sigma _{\text {max}} \left( 1 - \frac{\delta _n}{\delta _{{ max}}} \right) \quad \text { and} \\ \varvec{\tau }&= || \varvec{\tau _0} || \frac{\delta _n}{\delta _{{ max}}} \frac{\varvec{\delta }_\tau }{ || \varvec{\delta }_\tau || }. \end{aligned}$$

These normal and shear tractions are $\varvec{t}_c$ in (4c). A shear initiation criterion and cohesive law are also presented in Camacho and Ortiz (1996); however, they are not required for the brittle fracture examples presented in Sect. 6, so we omit their discussion here.

4 Nonlinear solution procedure

We time-discretize (21) using explicit central difference time-stepping. Explicit finite element analysis is beneficial for pervasive fracture for multiple reasons, such as

• 1. Eliminating the need to linearize the force terms,

• 2. Avoiding deleterious effects on Newton solvers caused by discontinuous linearizations which occur during contact and cohesive surface initiation, and

• 3. Using small time increments, which allow contact conditions and crack nucleation effects to occur more gradually (Belytschko et al. 2013).

We can speedup the analysis through use of a lumped mass matrix wherein all non-zero mass entries are on the diagonal of the matrix. This prevents the need to invert the mass matrix $\varvec{M}$. We use a lumping procedure by Hinton et al. (1976) that ensures all entries of the lumped mass matrix are positive and has been shown to give optimal rates of convergence (Hughes 2000). Additionally, since we are using a total Lagrangian formulation, all integration is done in the initial configuration. Therefore, we can compute and store shape function values and their derivatives at the quadrature points. Since computation of Wachspress and max-ent shape functions are more involved than standard finite element shape functions, storing these values speeds up analysis considerably. As a result, the amount of time spent computing polygonal shape function values is negligible compared to the time required to run an analysis—similar to traditional finite elements. However, since time required to run an analysis is strongly tied to the number of quadrature points, the use of a non-optimal quadrature rule over polygons causes an increase in computation time compared to more optimal finite element quadrature rules. It is anticipated a polygonal quadrature rule with fewer points, such as the one presented in Mousavi et al. (2010), would allow for a more expedient solution. Finally, contact conditions, sudden changes in boundary conditions, and crack surface initiation introduce non-physical shock waves into the domain. To smooth these effects, a small amount of bulk viscosity is introduced into the analysis (Taylor and Flanagan 1986). The steps of the central difference time-stepping algorithm are presented in Algorithm (1).

5 Computer implementation

Pervasive fracture simulation using polygonal finite elements requires a finite element code with robust mesh querying capabilities to enable on-the-fly mesh modification and cohesive surface insertion on arbitrary polygonal elements. To achieve this, we developed a new C++ 14 code. C++ 14 was selected for portability; speed; memory management with smart pointers; a large library of data structures through the standard template library; and nascent support for parallelization through the C++ concurrency API. In Sect. 5.1, we explain the graph-based approach used to store the finite element discretized geometry and some of the benefits it provides. Section 5.2 describes the algorithm used to modify the finite element mesh upon cohesive surface insertion.

5.1 Mesh storage

Geometry information in finite element code is typically stored at the vertex level and at the element level, with a list of ordered vertices representing a single element. While this approach still holds for polygonal finite elements, a more robust storage scheme simplifies mesh operations and generalizes to three dimensions. To implement a more robust mesh, we store geometric entities of all dimensions explicitly with the relationship between entities of different dimension stored as a graph. We term this storage scheme a full representation of a mesh. While using a full representation increases memory requirements for a given mesh (Garimella 2002), there are other speed improvements and algorithmic simplifications we can make from storing this extra data. For example, using a full representation simplifies geometric operations such as determining the entities on the boundary of the domain and splitting edges upon the insertion of a new cohesive surface.

The storage of geometric entities is done as follows:

• 1. Vertex: A reference coordinate and a current coordinate and a std::unordered_set of edges which are connected to the vertex.

• 2. Edge: A std::vector of ordered vertices which make up the edge and a std::unordered_set of faces which are connected to the edge.

• 3. Face: A std::vector of ordered edges with orientation which make up the face.

Querying mesh information is done by traversing different levels of the graph, then adding an entity to a unique set of entities. For example, to determine the list of vertices connected to a face, first the edges connected to the face are retrieved. Then, the vertices connected to the edge are retrieved and unique vertices are added to a list, which is then returned once all edges have been examined. Retrieving mesh information in this fashion ensures that all mesh entities are up-to-date, even after mesh modification procedures. As discussed in Garimella (2002), querying the mesh can be done efficiently through tagging already selected entities.

5.2 Cohesive surface insertion

When an extrinsic cohesive element is added to the domain, a new edge must be added to the finite element mesh. Additionally, the list of edges in each attached face must be updated and, depending on the location of the edge, vertices may need to be added. See Fig. 13 for examples of when new vertices are required and are not required. If new vertices are needed, connecting edge information must be updated as well. Numerous approaches have been proposed to handle the required mesh modifications upon cohesive surface insertion. Bishop (2009) used equivalence classes to determine vertex connectivities—an approach that does not require storing edge information in a graph. Paulino et al. (2008) introduced vertex operations for determining required mesh modifications within an adjacency-based mesh storage scheme that was later used by Leon et al. (2014) and Spring et al. (2014).

For this work, a new cohesive surface insertion scheme is developed that takes advantage of both the full representation of the mesh and the tracking of entities on the boundary of the geometry. After new cohesive edges are identified for a timestep, cohesive surfaces are inserted a single edge at a time. Each edge insertion follows the procedure as follows.

Fig. 13

Two examples of cohesive surface insertion on an edge in the finite element mesh. In (a), no new vertices are created when the edge is inserted, while in (b), two new vertices are created

• 1. Set the edge and attached vertices as being on the boundary of the geometry. Duplicate the edge. Add the new edge to the std::unordered_set in each vertex. Update std::vector and std::unordered_set in the edge/face relationship, assigning the old edge to a face and the new (duplicated) edge to the other face.

• 2. Investigate the two vertices attached to the edge. If a vertex is connected to four edges on the boundary of the geometry, it must be duplicated.

• 3. For a vertex that must be duplicated, order the attached edges by angle from the vertex, determined from the original (reference) coordinates. Create two sets of edges. Add the first edge in the list of ordered edges to the first set and mark the first set as active.

• 4. Loop through the remaining edges. If an edge shares a common face with the previous edge, add it to the active set. Otherwise, mark the other set as active and add the edge to that set.

• 5. Duplicate the vertex and assign different edge sets to the old and duplicated vertex.

This procedure is used for all examples in Sect. 6 and provides robust, fast mesh modification. Further, generalization to three-dimensions is feasible, with the vertex/edge relationship replaced with an edge/face relationship.

Fig. 14

Specimen geometry and boundary conditions for the Kalthoff and Winkler (1987) experiment

Fig. 15

Crack paths for three different meshes of the Kalthoff and Winkler experiment at three levels of mesh refinement (defined by average edge length, $\overline{h}$). Cracks plotted at analysis time $t = {50}\,{\upmu \hbox {s}}$. a $\overline{h} = {2}\,{\hbox {mm}}$. b $\overline{h} = {1}\,{\hbox {mm}}$. c $\overline{h} = {0.5}\,{\hbox {mm}}$

6 Benchmark fracture problems

We verify and validate on our approach to modeling pervasive fracture with several examples of dynamic fracture taken from the open literature. The first simulation is the impact of a notched specimen with a high velocity impactor first studied by Kalthoff and Winkler (1987). The details of this experiment are presented in Sect. 6.1. The second example is a notched glass sheet experiment that results in a branching crack. This study is in Sect. 6.2. Branching effects are further examined in Sect. 6.3, where we reproduce test results of varying applied loading as investigated by Kobayashi et al. (1974). Finally, in Sect. 6.4 we investigate crack growth rates and crack arrest in our simulation by comparison to testing by Ravi-Chandar and Knauss (1984a). A Saint Venant-Kirchhoff hyperelastic material model is assumed for all analyses presented in this section. This material model is sufficient to capture brittle fractures observed in these experiments.

6.1 Kalthoff and Winkler’s experiment

Kalthoff and Winkler (1987) tested doubly notched high-strength steel plates under high velocity impact loading and noted different fracture behavior under different rates of loading. Later, Kalthoff (2000) demonstrated that failure mode also depends on the notch radius. Sharper notches and higher velocity impact tend toward adiabatic shear band formation parallel to the notch whereas blunt notches and relatively low velocity impact induce brittle cracking. We reproduce their results at $v = 32\,\text {m s}^{-1}$, where a brittle crack forms and progresses about 70$^{\circ }$ from the notch. Many authors have simulated this experiment using a variety of numerical methods, such as meshfree methods (Belytschko et al. 1996; Li et al. 2002), X-FEM (Song et al. 2008), peridynamics (Silling 2003), phase field modeling (Hofacker and Miehe 2013; Borden et al. 2012), and cohesive elements (Song et al. 2008; Spring et al. 2014).

Fig. 16

Numerical results for a simulation of Kalthoff and Winkler’s experiment. Element edges are plotted in (b) to demonstrate refinement of the mesh in selected regions. Discontinuous displacements denote the location of cracks in (b). a $\sigma _{yy}$ at $t =$ 34 $\upmu$s. b $u_y$ at $t = {50}$ $\upmu$s

Fig. 17

The three types of typical meshes used to simulate the Kalthoff and Winkler experiment. For each mesh, a 20 mm $\times$ 20 mm patch is illustrated. a MPS polygon mesh, $\overline{h} = {2}\,\text {mm}$. b MPS triangle mesh, $\overline{h} = {1.5}\,\text {mm}$. c Regular triangle mesh, $\overline{h} = {2}\,\text {mm}$

A diagram of the plate geometry is provided in Fig. 14. The plate consists of 18Ni1900 maraging steel with material properties $\rho = 8000$ kg $\hbox {m}^{3}, E = 190$ GPa, and $\nu = 0.3$. The specimen is modeled in plane strain with an implicit thickness of $9\,\text {mm}$. The plate is struck by an impactor traveling at $32\,\text {m s}^{-1}$. The impactor is modeled explicitly, with an implicit cylindrical radius of $25\,\text {mm}$. For the cohesive model, we use the values $\sigma _{\text {max}} = 2000$ MPa and $\mathcal {G}_c = 2.2\times 10^{4}\,\hbox {J\,m}^{2}$. Besides the initial velocity applied to the impactor, no boundary conditions are applied to the model. The analysis was conducted at various levels of mesh refinement, with an average edge length ranging from $h = 2\,\text {mm}$ to $h = 0.5\,\text {mm}$. Element counts range from roughly 3000 elements in the coarsest mesh to about 35,000 in the most refined mesh. Wachspress shape functions are used in all analyses. While critical timestep size is dictated by the speed of wave propagation in elements, crack path dependence on timestep size was observed at timestep sizes below critical. Accordingly, timestep size was reduced until a stable crack path emerged. Timestep sizes ranged from 40 ns in the coarsest mesh to 10 ns in the most refined mesh. The benefit of reducing timestep size is twofold. First, smaller timesteps allow contact forces to be resolved over more intervals, reducing interpenetration without deleterious effects on conditioning. Second, traction-separation law initiation is more gradual with smaller timesteps, reducing shocks imparted by new surface creation.

Overall, all analyses were qualitatively in agreement with each other, in terms of crack path. Figure 15 presents crack paths for analyses conducted at three different levels of mesh refinement after $50\,\upmu \text {s}$ of analysis time. After $50\,\upmu \text {s}$, the impactor is no longer in contact with the specimen and the crack was observed to be no longer growing in all three levels of mesh refinement. In the lowest level of mesh refinement, crack path ranged from 63$^{\circ }$ to 70$^{\circ }$ while in the finest mesh, crack path was roughly 65$^{\circ }$ in all analyses. With mesh refinement, the length of the crack also increased. Reduced average edge length ($\overline{h}$) resulted in easier satisfaction of the cohesive surface initiation criterion, since stresses decay rapidly when traveling away from the crack tip.

Fig. 18

Crack path for a regular triangular mesh with $\overline{h} = {2}$ mm

Fig. 19

Crack paths for three different MPS triangular meshes with $\overline{h} = 1.5$ mm

Results from an analysis with $h = 2\,\text {mm}$ are presented in Fig. 16. The yy-component of Cauchy stress at $t = 34\,\upmu \text {s}$ is plotted in Fig. 16a and y-displacement field at $t = 50\,\upmu \text {s}$ is displayed in Fig. 16b. The location of the crack is visualized through discontinuities in the displacement field in the figures. The simulation demonstrates cracking at roughly a 70$^{\circ }$ angle from the notch, in agreement with observations by Kalthoff and Winkler. The use of a random polygonal mesh allows for the crack to propagate in arbitrary directions, different from what we might expect to occur in a mesh with directional anisotropy.

As a basis of comparison, we also model the Kalthoff and Winkler experiment with two types of triangular meshes: a regular mesh and a mesh formed from MPS-based Delaunay triangulations. Figure 17 compares these two triangular meshes to the MPS polygonal mesh. The crack pattern for a regular triangular mesh with $\overline{h} = 2\,\text {mm}$ is displayed in Fig. 18. As the figure illustrates, this mesh limits the crack to either a 45$^{\circ }$ angle or a 90$^{\circ }$ angle. The crack is also shorter than the crack paths of Fig. 15a, which also possessed an average edge length of $\overline{h} = 2\,\text {mm}$, suggesting the regular mesh pattern caused mesh-induced toughness effects.

Like the MPS polygonal meshes, the MPS-based Delaunay triangulation meshes do not show preferential direction, as demonstrated in Sect. 3.1.3. Crack path in three different simulations with average edge length $\overline{h} = 1.5\,\text {mm}$ is plotted in Fig. 19. Qualitatively, these results largely mirror those produced on polygonal meshes in Fig. 16. The average angle of crack growth slightly differed using triangular meshes and ranged from 58$^{\circ }$ to 60$^{\circ }$. For $\overline{h} = 1.5\,\text {mm}$, approximately 18,000 elements were required in the MPS triangle mesh. By comparison, the polygonal mesh required the same number of elements (around 18,000) for $\overline{h} = 1.0\,\text {mm}$. Since polygonal elements contain more edges per element than triangles, the relative efficiency of generating edges in a polygonal mesh is not a surprise.

Fig. 20

Specimen geometry and boundary conditions for the notched glass experiment

Fig. 21

Crack paths for three different meshes of the notched glass problem at three levels of mesh refinement (defined by average edge length, $\overline{h}$) for max-ent and Wachspress shape functions. Cracks plotted at analysis time $t = 50\,\upmu \text {s}$. a Wachspress, $\overline{h} = 0.64\,\text {mm}$. b Wachspress, $\overline{h} = 0.32\,\text {mm}$. c Wachspress, $\overline{h} = 0.16\,\text {mm}$. d Max-ent, $\overline{h} = 0.64\,\text {mm}$. e Max-ent, $\overline{h} = 0.32\,\text {mm}$. f Max-ent, $\overline{h} = 0.16\,\text {mm}$

Fig. 22

A region of the mesh where crack nucleation begins at $t = 10\,\upmu \text {s}$ but ultimately branching does not occur. Each subfigure illustrates a $6 \times 5\,\text {mm}$ patch within the notched glass domain. a $t = 10\,\upmu \text {s}$. b $t = 15\,\upmu \text {s}$

6.2 Notched glass specimen

The second experiment investigates a pre-notched rectangular glass specimen that displays crack branching under tensile loading. Crack branching has been observed in similar geometric configurations by multiple researchers (Congleton and Petch 1967; Kobayashi et al. 1974; Ravi-Chandar 1998) and it has been simulated using various numerical techniques (Song et al. 2008; Borden et al. 2012). Here, we repeat a simulation by Song et al. (2008) to investigate similarities and differences between our approach and other methods of modeling dynamic fracture.

Figure 20 presents a diagram of the notched glass geometry. For the glass material, $E = 32$ GPa, $\nu = 0.2$, and $\rho = 2450\,\hbox {kg m}^{-3}$. A tensile stress of $\sigma = 1$ MPa is applied to the top and bottom edges of the glass plate. The cohesive surfaces are initiated with $\sigma _{\text {max}} = 3.08$ MPa and crack surfaces are fully formed when $\mathcal {G}_c = 3.0\,\hbox {J\,m}^{-2}$. Plane strain conditions are assumed. The analysis was performed with nine total meshes comprised of three meshes at three levels of mesh refinement, ranging from $h = 0.64\,\text {mm}$ to $h = 0.16\,\text {mm}$ with element counts ranging from about 4000 to 37,000. A crack extending from the notch to the left side of the specimen travels a minimum of 78 edges in the coarsest mesh to a minimum of 312 edges in the most refined mesh. Both Wachspress and max-ent shape functions are used. Timestep size was reduced until a stable crack pattern emerged on each mesh. This required a timestep size of 2.5 ns for the coarsest mesh and 0.6 ns for the finest mesh.

Crack paths for the nine meshes for max-ent and Wachspress shape functions are presented in Fig. 21. Crack branching is observed in all analyses, and while consistent patterns are observed in each of the three similar meshes using the same shape functions, changes in shape function and mesh refinement cause different overall crack patterns to be observed. For example, in the least refined mesh using Wachspress shape functions, a single crack branch is consistently observed after about $28\,\text {mm}$ of crack growth. With max-ent shape functions, the coarsest mesh results in a single branch after anywhere from about $7\,\text {mm}$ to $40\,\text {mm}$ of crack growth. For $\overline{h} = 0.32\,\text {mm}$ and $\overline{h} = 0.16\,\text {mm}$, results are more consistent. For $\overline{h} = 0.32\,\text {mm}$ for both max-ent and Wachspress shape functions, two total branches are observed—one after about $7\,\text {mm}$ of crack growth and a second after roughly $34\,\text {mm}$ of crack growth. Branches at $3\,\text {mm}$ of crack growth and $29\,\text {mm}$ of crack growth are present for both shape functions for meshes at $\overline{h} = 0.16\,\text {mm}$. These results suggest crack path is sensitive to both level of mesh refinement and the selection of shape function, though the effect of shape function on crack path appears to reduce with mesh refinement. In the next example, we will further investigate the sensitivity of these parameters.

Experiments by Sharon et al. (1995, 1996) and Ramulu and Kobayashi (1985) have demonstrated that, in addition to crack branching, local, small-scale branching or microbranching can occur under sufficient crack velocity given this loading and geometry. Microbranching results in a rough crack surface, with crack branches that begin to nucleate but ultimately do not grow as the main crack continues. Polygonal meshes can mimic the microbranching process, as illustrated in Fig. 22. Therein, a branch begins to form as the crack grows through a certain region of the mesh. Ultimately, the branch stops growing as the main crack progresses, though the nucleated surface remains. Microbranching effects grow more pronounced with mesh refinement as more facets are available for branches to form.

Fig. 23

Specimen geometry and boundary conditions for the experiment by Kobayashi et al. (1974)

6.3 Crack branching with changing boundary conditions

In Kobayashi et al. (1974), the effects of boundary conditions on crack branching patterns is investigated. Therein, notched Homalite 100 sheets are subjected to displacement boundary conditions on the top and bottom of the specimen. Various linearly decreasing and constant displacement profiles are applied to test specimens of thickness $3.175\,\text {mm}$ and $9.525\,\text {mm}$ and the resulting crack patterns are reported. In thicker sheets, additional crack branches are observed. In this section, we present analytical results from four simulations that represent those in Kobayashi et al. (1974): linearly decreasing displacements in plane strain and plane stress and constant displacements also in plane strain and plane stress. Plane strain conditions are meant to correspond to a thicker test specimen, while plane stress simulates a thin test specimen. The geometry and boundary conditions for this problem are presented in Fig. 23. The linearly decreasing displacement corresponds to $u_1 = 0.340\,\text {mm}$ and $u_2 = 0.221\,\text {mm}$ and the constant displacement corresponds to $u_1 = u_2 = 0.414\,\text {mm}$ in Fig. 23.

The material properties for Homalite 100 are reported in Kobayashi et al. (1974) as $E = 4.65$ GPa, $\rho = 1197\,\hbox {kg m}^{-3}$, and $\nu = 0.31$. The displacement profiles and stress intensity factors provided are used to calibrate the cohesive model, with values of $\sigma _{\text {max}} = 30$ MPa and $\mathcal {G}_c = 75\,\hbox {J m}^{-2}$ deemed appropriate. Analysis is conducted on six total meshes—three each on two levels of mesh refinement with average edge lengths of $\overline{h} = 1.7\,\text {mm}$ and $\overline{h} = 0.85\,\text {mm}$. A crack traveling from one edge of the specimen to the other must travel a minimum of 150 edges in the coarser mesh and a minimum of 300 edges in the more refined mesh. Displacements are first applied statically, then dynamic crack growth is simulated for $250\,\upmu \text {s}$—roughly the time required for a crack to traverse the length of the geometry in the plane strain, constant load test. A timestep size of 10 ns is used in the coarse mesh while in the refined mesh, timestep size is 5 ns. Wachspress shape functions are used in all analyses.

Fig. 24

Crack paths for analyses simulating experiments by Kobayashi et al. (1974). Cracks plotted at analysis time $t = 250\,\upmu \text {s}$. a Plane strain, constant load, $\overline{h} = 1.7\,\text {mm}$. b Plane strain, constant load, $\overline{h} = 0.85\,\text {mm}$. c Plane strain, linear load, $\overline{h} = 1.7\,\text {mm}$. d Plane strain, linear load, $\overline{h} = 0.85\,\text {mm}$. e Plane stress, constant load, $\overline{h} = 1.7\,\text {mm}$. f Plane stress, constant load, $\overline{h} = 0.85\,\text {mm}$ g Plane stress, linear load, $\overline{h} = 1.7\,\text {mm}$. h Plane stress, linear load, $\overline{h} = 0.85\,\text {mm}$

Fig. 25

Specimen geometry and boundary conditions used by Ravi-Chandar and Knauss (1984a)

Fig. 26

Crack growth versus time for three different meshes run with two different load cases. The load cases are a $\sigma _{\text {max}} = 10$ MPa and b $\sigma _{\text {max}} = 1.5$ MPa. Crack growth versus time is also plotted for similar analyses in Ravi-Chandar and Knauss (dotted lines). a $\sigma _{\text {max}} = 10$ MPa b $\sigma _{\text {max}} = 1.5$ MPa

The crack patterns that emerged from the 24 analyses are presented in Fig. 24. Average number of branches and average branch angle for the various analysis parameters are listed in Table 2. Average branching angle ranges from 37$^{\circ }$ to 46$^{\circ }$—higher than the average of 26$^{\circ }$ that is reported in Kobayashi et al. (1974). In general, more crack branches are present with a constant displacement profile and with plane strain conditions. These findings are in line with those reported in Kobayashi et al. (1974), where $9.525\,\text {mm}$ thick specimen had an average of 7.7 branches and $3.175\,\text {mm}$ thick specimen had an average of 3.7 branches. Further, the number of crack branches varies with mesh refinement; increased refinement causes more crack branches to form. In the analyses, crack growth rate range from 700 to $950\,\text {m s}^{-1}$. Terminal crack velocities in experimentation are reported as approximately $400\,\text {m s}^{-1}$ for all tests. For Homalite 100, Rayleigh wave speed is about $1100\,\text {m s}^{-1}$.

Table 2 Average number of crack branches (where each branch is longer than $15\,\text {mm}$) and average branch angle in dynamic crack growth simulations of experiments by Kobayashi et al. (1974)

6.4 Crack growth rate versus loading

Ravi-Chandar and Knauss (1984a) explored the effects of crack growth rate versus dynamic stress intensity factor in Homalite 100 sheets. In their work, loading is applied directly on the crack faces using electromagnets, which permits a high degree of experimental repeatability. With their load apparatus, traction increases at a constant rate for $25\,\upmu \text {s}$ after which the traction plateaus. After $160\,\upmu \text {s}$, loading is removed, and the experiment is concluded. Crack face tractions are given as follows

$$\begin{aligned} \sigma _0 = {\left\{ \begin{array}{ll} \sigma _{\text {pre}} + \sigma _{\text {max}} t / 25\,\upmu \text {s} &{} t < 25\,\upmu \text {s} \\ \sigma _{\text {pre}} + \sigma _{\text {max}} &{} t \ge 25\,\upmu \text {s} , \end{array}\right. } \end{aligned}$$

where $\sigma _{\text {pre}}$ is the preload caused by the load apparatus applying pressure on the crack faces and $\sigma _{\text {max}}$ is the peak crack face traction. The experiments are conducted on $500\times 300\,\text {mm}$ sheets of Homalite 100 with an initial crack length of roughly $300\,\text {mm}$. The test geometry is illustrated in Fig. 25.

While material properties for Homalite 100 are provided in Kobayashi et al. (1974), we choose to use slightly different properties reported in Ravi-Chandar and Knauss (1982) to account for variations in material. Therein, the relevant material properties are $E =4.55$ GPa, $\rho = 1230\,\hbox {kg m}^{-3}$, and $\nu = 0.31$. Plane stress conditions are assumed. Cohesive parameters from Sect. 6.3 are retained, namely $\sigma _{\text {max}} = 30$ MPa and $\mathcal {G}_c = 75\,\hbox {J m}^{-2}$. Analysis is conducted on three highly refined meshes that contain roughly 30,000 elements and have an average edge length of $\overline{h} = 0.85\,\text {mm}$ in the refined region where crack growth is expected to occur. Two values of $\sigma _{\text {max}}$ are used: $\sigma _{\text {max}} = 10.0$ MPa which is considered the large load case and $\sigma _{\text {max}} = 2.5$ MPa which is considered the small load case. These are within the range of loads used by Ravi-Chandar and Knauss. The preload is estimated to be $\sigma _{\text {pre}} = 0.25$ MPa. A timestep size of 10 ns is used in all analyses. Preload is applied statically after which the dynamic analysis begins and runs for $150\,\upmu \text {s}$ of analysis time (for a total of 15,000 timesteps).

For each of the meshes in the two load cases, the crack growth versus time is plotted in Fig. 26. Experimental results from similar tests in Ravi-Chandar and Knauss (1984a) are also plotted in Fig. 26 for comparison. For the large load case, the three meshes initiate crack growth after 20–$25\,\upmu \text {s}$. After $150\,\upmu \text {s}$, the total crack growth ranges from 85 to $91\,\text {mm}$. The small load case is less consistent—crack growth initiates after anywhere from 85 to $120\,\upmu \text {s}$ of analysis time. Further, the total amount of growth varies from $7\,\text {mm}$ to over $20\,\text {mm}$ after $150\,\upmu \text {s}$. Variations in edge length and orientation are to blame for differences in time to crack initiation and amount of crack growth. In a dynamic analysis where stresses require time to evolve, such as the small load case, variations in mesh edge length can cause appreciable differences in both initiation time and crack growth rate, as Fig. 26b demonstrates. These differences are even apparent in the large load case where crack growth rates are not constant. For example, in mesh 1 with $\sigma _{\text {max}} = 10$ MPa, crack growth halted for about $20\,\upmu \text {s}$ before starting again. In comparison, the two experimental results from Ravi-Chandar and Knauss (1984a) both exhibit constant rates of crack growth over the duration of the analysis. Overall, the average crack growth velocity over the three large load analyses is $694\,\text {m s}^{-1}$. Average crack growth velocity varied quite sharply in the small load case, though over time intervals when crack growth did happen, it occurred at roughly a rate of $600\,\text {m s}^{-1}$. Experimental crack growth rates are roughly $430\,\text {m s}^{-1}$ for the large load case and $157\,\text {m s}^{-1}$ for the small load case.

In all analyses of the large load case, crack branching is observed after 130–$140\,\upmu \text {s}$ of time has elapsed. This approximately coincides with the arrival of stress waves reflected from the boundary of the geometry. Similar branching effects are reported in Ravi-Chandar and Knauss (1984b), though therein, they occur between 80 and $100\,\upmu \text {s}$ after experiment initiation. As in Ravi-Chandar and Knauss (1984b), our results indicate that crack branching effects do not affect the crack growth rate.

7 Concluding remarks

In this paper, we used non-preferential polygonal meshes with the finite element method to simulate pervasive fracture using cohesive elements on inter-element boundaries. The benefits of polygonal meshes have been established in many other contexts. Compared to triangles and quadrilaterals, polygons appear in an arbitrary number of shapes, allowing meshing criteria to be relaxed and simplifying generation of high-quality meshes over complex topologies. Further, generation of random meshes is greatly simplified using polygons. Generating a Voronoi diagram from a randomly distributed pointset, such as one generated from maximal Poisson-disk sampling, provides a mesh whose edges are not oriented in preferential directions. Therefore, if the edges of the polygons are used as a fracture network, as they are in this paper, crack patterns will not exhibit directional bias. Four examples were presented in Sect. 6 that demonstrate not only the lack of directional bias in crack growth predictions, but also demonstrate the flexibility and capabilities of using polygonal finite elements to simulate dynamic fracture. Crack branching and microbranching are observed in Sect. 6.2, consistent with experimental results in literature. The parametric study in Sect. 6.3 illustrated the sensitivity to specimen thickness that is mirrored by Kobayashi et al. (1974).

While polygonal finite element methods provide additional meshing flexibility, they are otherwise compatible with traditional finite elements. Finite element concepts such as nodes, elements, and shape functions still carry the same meaning when moving to polygonal methods. The approach we describe in this paper is largely applicable to regular finite elements, both broadening the applicability of this work and allowing polygonal methods to take advantage of the advances in finite element technology for modeling fracture. However, there are some key differences. Flexible shapes require flexible shape functions; of the many polygonal shape functions available, we simulated dynamic fracture with both Wachspress and max-ent shape functions in Sect. 6.2. While results were not identical, crack patterns exhibited many of the same characteristics suggesting both are equally capable in this scenario. The more flexible max-ent shape functions may be preferred when dealing with nonconvex elements whereas Wachspress shape functions may be preferred on convex elements due to their simplicity. Also, while not a requirement for polygonal finite elements, graph-based storage of the mesh simplifies many of the mesh operations required by cohesive element insertion and generalizes to three dimensions, where reduced representation of polyhedral meshes is not possible.

This paper has demonstrated the benefits of using polygonal finite elements to model pervasive fracture. We continue to build on the promise of this methodology. A three-dimensional code is currently under development and testing, expanding upon the two-dimensional framework already completed. Further, we are exploring the use of the virtual element method (Beirão da Veiga et al. 2013; Wriggers et al. 2017) on polygonal and polyhedral meshes. We are also evaluating the use of other cohesive surface formulations, such as the one proposed in Yang et al. (2005), which does not require explicit definition of a cohesive traction-separation law.