1 Introduction

Dislocations play a key role in different aspects of solid mechanics and can be used to treat different physical phenomena such as plasticity and fracture (Bilby and Eshelby 2006; Hirth and Lothe 1982). Dislocation-based fracture mechanics (Weertman 1996) and the distributed dislocation technique (Hills et al. 1996) has been successfully used to address cracks within the classical theory of elasticity. On the other hand, dislocation (crystal) plasticity has been developed extensively recently (Acharya 2001; Sandfeld et al. 2011; Po et al. 2014). Such formulations of plasticity and fracture can be unified to provide tools for the analysis of materials without any ad hoc assumptions.

Within continuum theory of dislocations (Kröner 1958), dislocations are sources of incompatibility. In our treatment, cracks are represented as a distribution of dislocations. Since dislocation is a source of incompatibility, it is required to employ an incompatible continuum theory for this study. In this connection, it is noted that a discussion on compatibility and incompatibility for generalized continua is given in Eringen (1999). For such generalized continua containing dislocations, disclinations and other structural defects, the classical compatibility (or integrability) conditions for the usual strain tensor are violated.

Classical linear elasticity does not possess an internal length and, thus, no size effects can be predicted and unphysical singularities emerge at dislocation cores and crack tips. Classical dislocation-based approaches also confirm these features of linear elasticity theory. Therein, the singularity of the crack tip stems from the singular fields of the individual dislocations making up the arrays used to represent a macroscopic crack. However, within classical elasticity, the dislocation-based approach does not predict any crack tip plasticity unless an assumption of cohesive zone is considered. It would be valuable to develop a nonsingular fracture theory incorporating crack tip plasticity without any assumption other than the constitutive model of the material.

Continuum mechanics generalization of linear elasticity including higher-order strain or stress gradients have been proposed and extensively used in the literature to account for microstructural effects as they manifest at a continuum macroscopic scale (e.g. Eringen 1999, 2002; Mindlin 1965; Mindlin and Eshel 1968 and references quoted therein). In general, these theories are complex, involve many unknown phenomenological coefficients and they are difficult to be implemented in the solution of related boundary value problems. An exception to this is Eringen’s nonlocal elasticity theory (Eringen 2002) which in its reduced stress gradient form (for a particular type of kernel in the integral constitutive relation) produces analytical nonsingular expressions for the stress field of dislocations and nonsingular stresses (but not nonsingular strains) at the crack tip. Along similar lines, the simple strain gradient elasticity theory (the GradEla model) proposed by the second author (Aifantis 1992) was the first model to provide nonsingular strain at dislocation core and crack tips when boundary conditions do not play a role (e.g. for dislocations in infinite media) or they are simplified and not necessarily identified to those derived from a variational principle (e.g. for cracks in infinite media).

Due to the promising initial results derived for dislocations and cracks by the GradEla model and the applicability of the so-called Ru–Aifantis theorem (Ru and Aifantis 1993), various authors have adopted it and its variational counterpart for studying dislocation, disclination and crack problems (Altan and Aifantis 1997; Georgiadis 2003; Gutkin and Aifantis 1999; Gitman et al. 2010; Unger and Aifantis 1995; Vardoulakis et al. 1996; Lazar et al. 2005; Karlis et al. 2007; Amanatidou and Aravas 2002) within a “compatible” or “incompatible” framework. An early review on combined strain-stress gradient models without attention to characterizing the incompatible distortion field, was provided in Aifantis (2003) and more recent results can be found in Aifantis (2011a) and Askes and Aifantis (2011). The extension of the GradEla model, within an incompatible framework, to derive analytical expressions for both elastic and plastic distortions was given in Lazar and Maugin (2006) for dislocation fields. Analytical expressions for strain fields for mode I, II and III cracks were derived in Aifantis (2009, (2011b, (2014). It is beyond the scope of present contribution to discuss the various features of the stress, strain, and displacement fields produced by the various fracture mechanics analyses based on strain or stress gradient generalizations of elasticity theory. We refer, however, to recent works (Isaksson and Dumont 2014) attempting to make contact of gradient dependent nonsingular solutions to experimental observations and Sciarra and Vidoli (2013), where some asymptotic results for gradient elastic fracture modes are reported. Moreover, the gradient elastic effects associated with the existence of a cohesion type interphase layer is discussed in Lurie and Belov (2014). The same authors have previously developed a higher-order theory of continuous media with conserved dislocations to address hypothesis of Barenblatt about cohesion field near crack tip (Lurie and Belov 2008).

The aforementioned works on gradient elastic cracks do not make use of the fact that a crack can be represented by an array of dislocations (screw for mode III, climb edge for mode I and glide edge for mode II). Such artificial but accurate representation of a crack has been very useful within classical elasticity and confirmed existing results of “singular” linear elastic fracture mechanics, obtained from the solution of related boundary value problems based on standard continuum linear elasticity theory (Bilby and Eshelby 2006; Weertman 1996; Hills et al. 1996). Since the GradEla model and its extension to incompatible framework provides nonsingular dislocation solutions, it should be expected that the adoption of such gradient theory for dislocations may lead to corresponding nonsingular solutions for crack fields.

The first work to employ nonsingular dislocation solutions for continuously distributed dislocation arrays (without applying to crack problems) was Eringen (1985), but it was only recently (Mousavi et al. 2014) that the distributed dislocation technique (DDT) within gradient elasticity was employed to address crack problems. In particular, based on the nonsingular stress component expressions for screw dislocations, cracks of mode III were studied. The standard classical elasticity boundary conditions were used, and corresponding solutions for a single crack and co-linear cracks were presented. The stress field was obtained, but no results were reported for the strain or the crack opening displacement. Later, DDT was employed in Mousavi and Lazar (2015) to study cracks of mode I, II and III within nonlocal elasticity of Helmholtz type. Based on nonsingular stress components for the dislocation fields, nonsingular crack tip stresses were obtained. As expected for nonlocal elasticity, the crack-tip strains remained singular. Recently, nonsingular antiplane fracture theory of anisotropic materials is formulated within nonlocal elasticity (Mousavi and Korsunsky 2015).

The mode III crack within the gradient elasticity theory was revisited recently in Mousavi and Aifantis (2015) by employing the DDT and using the nonsingular stress expressions. Nonsingular elastic stresses were obtained (with the double stresses being singular) and corresponding nonsingular conjugate strains were derived, along with “smooth closure” profiles for the crack faces. In contrast to Mousavi et al. (2014), variationally consistent boundary conditions were used. This work provided an alternative approach to celebrated “Barenblatt’s treatment” of cracks (Barenblatt 1962), without introducing the concept of “cohesive zone” and “intermolecular forces “ahead of the “physical” crack tip. However, in contrast to Altan and Aifantis (1992), where the crack opening displacement (COD) tends asymptotically to zero for large distances ahead at the crack tip, the COD in Mousavi and Aifantis (2015) vanishes at a finite distance ahead of the crack tip, thus defining precisely the length of the cohesive zone. The DDT has also been used to investigate defects within the theory of couple stress elasticity (Gourgiotis and Georgiadis 2007). However, due to the singular stresses for dislocations within the theory of couple stress elasticity, the stress field for mode I, II and III cracks in couple stress elasticity remain singular (in fact, they become more singular than in classical elasticity).

The purpose of this paper is to present the solution to in-plane cracks within an incompatible gradient elasticity framework using a dislocation-based approach. The paper is organized as follows. In Sect. 2, the framework of incompatible first strain gradient elasticity theory is presented. In Sect. 3, the solutions of edge dislocations within such gradient elasticity theory are reviewed from the literature. The stress field of these dislocations will serve as the building blocks for obtaining the stress field of cracks. Section 4 deals with the generalization of the distributed dislocation technique (DDT) from classical elasticity to gradient elasticity by considering equilibrium, boundary and incompatibility conditions. The non-singular stress fields of edge dislocations are used for the in-plane (modes I and II) crack analyses. Numerical examples are presented in Sect. 5. In Sect. 6, the conclusions are given.

2 Fundamentals of strain gradient elasticity

Gradient elasticity is a generalization of linear elasticity which includes higher-order strain or stress gradient terms to account for microstructural effects. Within strain gradient elasticity, the strain energy depends on the elastic strain, and higher order strain tensors defined as spatial gradients either of the displacement field, or of the strain field (Mindlin and Eshel 1968). This general form of the gradient elasticity (Mindlin and Eshel 1968) has been used in different simplified versions such as the one adopted in Aifantis (1992), Ru and Aifantis (1993), Altan and Aifantis (1997) and Altan and Aifantis (1992). We intend to use dislocations for the analysis of cracks, and since dislocations are the source of incompatibility, a suitable framework would be that of incompatible gradient elasticity. Thus, we consider a strain gradient theory in which the strain energy depends on the elastic strain and the first-order strain gradient with variationally consistent boundary conditions (Altan and Aifantis 1997; Aifantis 2011a, 2014), but within an incompatible framework (Lazar et al. 2005; Lazar and Maugin 2006, 2005). Due to the gradient terms, the strain energy contains additional gradient coefficients with the dimension of length. For an isotropic gradient elastic medium, the strain energy density reads (Altan and Aifantis 1997; Lazar and Maugin 2005; Polizzotto 2003),

$$\begin{aligned} W=\frac{1}{2} \tau _{ij}e_{ij}+\frac{1}{2} \tau _{ijk}e_{ij,k}. \end{aligned}$$
(1)

while \(\tau _{ij}\) and \(\tau _{ijk}\) are the stress and double stress tensors, respectively. We employ a comma to indicate partial derivative with respect to rectilinear coordinates. The elastic strain (\(e_{ij}\)) is the symmetric part of the elastic distortion (\(\beta _{ij}\))

$$\begin{aligned} e_{ij}&=\frac{1}{2}\big (\beta _{ij}+\beta _{ji}\big )\,, \end{aligned}$$
(2)

The total distortion (\(\beta _{ij}^T\)) is the gradient of the displacement (\(u_i\)) and is given as a sum of elastic (\(\beta _{ij}\)) and plastic parts \(\beta _{ij}^P\) (deWit 1973)

$$\begin{aligned}&\beta _{ij}^T =\partial _{j}{u_{i}}=\beta _{ij}+\beta _{ij}^P, \end{aligned}$$
(3)

Once the dislocations are the source of the incompatibility, the dislocation density is given by

$$\begin{aligned} \alpha _{ij}=\epsilon _{jkl}\beta _{il,k}=-\epsilon _{jkl}\beta ^{\text {P}}_{il,k}\,. \end{aligned}$$
(4)

The stress and double stress tensors read

$$\begin{aligned}&\varvec{\tau }=\{\tau _{ij}\}=\{C_{ijkl} e_{kl}\}, \end{aligned}$$
(5a)
$$\begin{aligned}&\varvec{\tau }^{(1)}=\{\tau _{ijk}\}=\{\ell ^2 \tau _{ij,k}\}. \end{aligned}$$
(5b)

while \(\ell \) is the gradient coefficient which enrich the current framework to capture the size effect and lead to regularized expressions for stress. For an isotropic material the tensor of elastic moduli (\(C_{ijkl}\)) is

$$\begin{aligned} C_{ijkl}&=\lambda \delta _{ij}\delta _{kl}+\mu (\delta _{ik}\delta _{jl}+\delta _{jk}\delta _{il}), \end{aligned}$$
(6)

while \(\lambda \), \(\mu \) are the Lamé constants and \(\delta _{ij}\) is the Kronecker delta, respectively.

The equilibrium equation of the first gradient elasticity reads (Altan and Aifantis 1997; Polizzotto 2003),

$$\begin{aligned} \partial _{j}({\tau _{ij}-\tau _{ijk,k}})=0. \end{aligned}$$
(7)

Following a variational approach (e.g. Mindlin and Eshel 1968), the natural boundary conditions can be derived. Within first gradient elasticity, the traction (natural) boundary conditions read (e.g. Polizzotto 2013)

$$\begin{aligned}&{\varvec{t}}=\bar{{\varvec{t}}}, \end{aligned}$$
(8a)
$$\begin{aligned}&{\varvec{t}}^{(1)}=\bar{{\varvec{t}}}^{(1)}, \end{aligned}$$
(8b)

where \(\bar{{\varvec{t}}} \) and \(\bar{{\varvec{t}}}^{(1)}\) are the prescribed generalized traction vectors. The generalized tractions \({\varvec{t}}\) and \({\varvec{t}}^{(1)}\) in (8) are given by Polizzotto (2013)

$$\begin{aligned}&{\varvec{t}}=\varvec{n}\cdot \varvec{T}- \big (\bar{{\varvec{\nabla }}}_{(\perp \varvec{n})}+H\varvec{n}\big )\cdot \varvec{S}, \end{aligned}$$
(9a)
$$\begin{aligned}&{\varvec{t}}^{(1)}=\varvec{n}\cdot \varvec{S}. \end{aligned}$$
(9b)

Here \(\bar{{\varvec{\nabla }}}_{(\perp \varvec{n})}\) is the surface gradient (which denotes the tangential gradient over a plane of normal \(\varvec{n}\)), i.e. \(\bar{{\varvec{\nabla }}}_{(\perp \varvec{n})}=\varvec{P}(\varvec{n})\cdot {\varvec{\nabla }}\), while the projection operator is \(\varvec{P}(\varvec{n})=\varvec{I}-\varvec{n}\varvec{n}\) and \(\varvec{I}\) represent the unit dyadic. The symbol \({\varvec{\nabla }}\) denotes the spatial gradient operator, i.e. \({\varvec{\nabla }}{\varvec{x}}=\left\{ \partial _{i} x_j \right\} \) and \(H=-\bar{{\varvec{\nabla }}}_{(\perp \varvec{n})} \cdot \varvec{n}\). In (9), the so-called total stress \(\varvec{T}\) is defined as

$$\begin{aligned} \varvec{T}=\left\{ \tau _{ij}-\tau _{ijk,k}\right\} , \end{aligned}$$
(10)

and the surface stress \(\varvec{S}\) reads

$$\begin{aligned} {\varvec{S}}=\varvec{n}\cdot \varvec{\tau }^{(1)}. \end{aligned}$$
(11)

The non-standard boundary conditions (8) is an important aspect of the gradient theory which should be taken into account, in particular, for crack problems. The boundary conditions (8), in the index notation, read (Gao and Park 2007)

$$\begin{aligned}&t_{i}=(\tau _{ij}-\tau _{ijk,k})n_{j}-\partial _{j}({\tau _{ijk}n_{k}})\nonumber \\&\qquad +\,n_{j}\partial _{l}({\tau _{ijk}n_{k}n_{l}}), \end{aligned}$$
(12a)
$$\begin{aligned}&t_{i}^{(1)}=\tau _{ijk}n_{j}n_{k}. \end{aligned}$$
(12b)

The natural boundary conditions (8) are also derived in Altan and Aifantis (1997) but represented in slightly different forms. For convenience, here we have used the notation presented in Polizzotto (2013). It is also noted that a simplified version of the boundary conditions are used in Altan and Aifantis (1997). In the current study, the natural boundary conditions are enforced in their original form (8).

3 Edge dislocations in gradient elasticity

In first gradient elasticity, (glide and climb) edge dislocations produce non-singular stress and singular double stress fields. The edge dislocation line is assumed to be along the z-axis, while the Burgers vector of a glide dislocation (\(b_x\)) is parallel to the x-axis, and the Burgers vector of a climb dislocation (\(b_y\)) is parallel to the y-axis. In other words, a glide edge dislocation is an edge dislocation that can glide in x-direction while a climb edge dislocation can move only by climb in the x-direction.

3.1 Glide edge dislocation

Within an incompatible gradient elasticity, the stress components of a glide edge dislocation with Burgers vector \(b_x\) read (Lazar et al. 2005; Lazar and Maugin 2005; Lazar 2013)

$$\begin{aligned} \tau _{xx}&= -\gamma \, b_{x}\frac{y}{r^4} \left\{ (y^2+3x^2) +\frac{4\ell ^2}{r^2}(y^2-3x^2)\right. \nonumber \\&\quad \left. -\,2y^2\frac{r}{\ell } K_{1} \big (r/\ell \big ) -2(y^2-3x^2) K_{2}\big (r/\ell \big ) \right\} , \end{aligned}$$
(13a)
$$\begin{aligned} \tau _{yy}&= -\gamma \, b_{x}\frac{y}{r^4} \left\{ (y^2-x^2)-\frac{4\ell ^2}{r^2}(y^2-3x^2)\right. \nonumber \\&\quad \left. -\,\,2x^2\frac{r}{\ell } K_{1}\big (r/\ell \big ) +2(y^2-3x^2) K_{2}\big (r/\ell \big ) \right\} , \end{aligned}$$
(13b)
$$\begin{aligned} \tau _{xy}&= \gamma \, b_{x}\frac{x}{r^4} \left\{ (x^2-y^2)-\frac{4\ell ^2}{r^2}(x^2-3y^2)\right. \nonumber \\&\quad \left. -\,2y^2\frac{r}{\ell } K_{1}\big (r/\ell \big ) +2(x^2-3y^2) K_{2}\big (r/\ell \big ) \right\} \,, \end{aligned}$$
(13c)

where \(\gamma =\mu /[2\pi (1-\nu )]\), \(\nu \) is the Poisson ratio and \(\tau _{zz}=\nu (\tau _{xx}+\tau _{yy})\). The stress field (13) is identical to the stress field reported in Gutkin and Aifantis (1999) for a compatible gradient elasticity. The double stress tensor \(\tau _{ijk}\) may be derived by substituting the stress tensor (13) in (5).

The stress of a glide edge dislocation is zero at the dislocation line and possesses extremum values (maximum and minimum) near the dislocation line. Considering the discontinuity of the dislocation to be along \(y<0\), the displacement field of a glide edge dislocation within first gradient elasticity reads (Lazar and Maugin 2006)

$$\begin{aligned} u_x&= \frac{b_{x}}{4\pi (1-\nu )} \left\{ 2(1-\nu )w(x,y)+\frac{xy}{r^2}\right. \nonumber \\&\quad \left. -\,4\ell ^2\frac{xy}{r^4}+\frac{2xy}{r^2} K_{2}\big (r/\ell \big ) \right\} , \end{aligned}$$
(14a)
$$\begin{aligned} u_y&= -\frac{b_{x}}{4\pi (1-\nu )} \left\{ (1-2\nu )(\ln {r}+K_{0}\big (r/\ell \big ))+\frac{x^2}{r^2}\right. \nonumber \\&\quad \left. -\,2\ell ^2\frac{x^2-y^2}{r^4} +\frac{x^2-y^2}{r^2} K_{2}\big (r/\ell \big ) \right\} \,, \end{aligned}$$
(14b)

Here, w(x, y) is given by

$$\begin{aligned} w&=\arctan \frac{y}{x}-\frac{\pi }{2}+ \frac{1}{2\pi } \int _{-\infty }^{\infty } \int _{-\infty }^{\infty } \frac{k_1}{k_2} \frac{1}{\varvec{k}^2+\frac{1}{\ell ^2}}\nonumber \\&\quad \times \, \exp (i\varvec{k}\cdot {\varvec{x}}) \, \mathrm {d}k_{1} \, \mathrm {d}k_{2}, \end{aligned}$$
(15)

with \(k^2=k_1^2+k_2^2 \), \(\varvec{k}=(k_1,k_2)\) and \({\varvec{x}}=(x,y)\). When \(y\rightarrow 0\), the displacement (14) on the x-axis is given by

$$\begin{aligned} u_x(x,0)&= \frac{b_{x}}{2\pi } w(x,0), \end{aligned}$$
(16a)
$$\begin{aligned} u_y(x,0)&{=} -\frac{b_{x}}{4\pi (1-\nu )} \left\{ (1{-}2\nu )(\ln {|x|}{+}K_{0}\big (|x|/\ell \big ))\right. \nonumber \\&\quad \left. +\,1-\frac{2\ell ^2}{x^2}{+} K_{2}\big (|x|/\ell \big ) \right\} \,, \end{aligned}$$
(16b)

while

$$\begin{aligned} w(x,0)&= -\frac{\pi }{2} \text {sgn} (x) \left\{ 1-\exp (-|x|/\ell )\right\} . \end{aligned}$$
(17)

Within first gradient elasticity, the plastic distortion along \(y=0\) is given by

$$\begin{aligned} \beta _{xx}^P(x,0)=-\frac{b_{x}}{4\ell }. \exp (-|x|/\ell ) \end{aligned}$$
(18)

The dislocation density tensor reads (Lazar et al. 2005; Lazar and Maugin 2006)

$$\begin{aligned} \alpha _{xz}=\frac{b_{x}}{2\pi }\frac{1}{\ell ^2} K_{0}(r/\ell ), \end{aligned}$$
(19)

which is singular.

3.2 Climb edge dislocation

The field components of a climb edge dislocation can be derived following a same procedure outlined for glide edge dislocation. The stress components of a climb edge dislocation with Burgers vector \(b_y\) read (Lazar and Maugin 2005)

$$\begin{aligned} \tau _{xx}&= \gamma \, b_{y}\frac{x}{r^4} \left\{ (x^2-y^2)-\frac{4\ell ^2}{r^2}(x^2-3y^2)\right. \nonumber \\&\quad \left. -\,2y^2\frac{r}{\ell } K_{1}\big (r/\ell \big )+2(x^2-3y^2) K_{2}\big (r/\ell \big ) \right\} , \end{aligned}$$
(20a)
$$\begin{aligned} \tau _{yy}&= \gamma \, b_{y}\frac{x}{r^4} \left\{ (x^2+3y^2)+\frac{4\ell ^2}{r^2}(x^2-3y^2)\right. \nonumber \\&\quad \left. -\,2x^2\frac{r}{\ell } K_{1} \big (r/\ell \big ) -2(x^2-3y^2) K_{2}\big (r/\ell \big ) \right\} , \end{aligned}$$
(20b)
$$\begin{aligned} \tau _{xy}&= \gamma \, b_{y}\frac{y}{r^4} \left\{ (x^2-y^2)-\frac{4\ell ^2}{r^2}(3x^2-y^2)\right. \nonumber \\&\quad \left. +\,2x^2\frac{r}{\ell } K_{1}\big (r/\ell \big )+2(3x^2-y^2) K_{2}\big (r/\ell \big ) \right\} \,, \end{aligned}$$
(20c)

where, again, \(\gamma =\mu /[2\pi (1-\nu )]\), \(\nu \) is the Poisson ratio and \(\tau _{zz}=\nu (\tau _{xx}+\tau _{yy})\). Similarly to a glide edge dislocation, the stress of a climb edge dislocation is zero at the dislocation line and possesses extremum values (maximum and minimum) near the dislocation line. The double stress tensor \(\tau _{ijk}\) can be derived by substituting \(\tau _{ij}\) from (20) into (5).

The displacement field of a climb edge dislocation within first gradient elasticity reads

$$\begin{aligned} u_x&= \frac{b_{y}}{4\pi (1-\nu )} \left\{ (1-2\nu )(\ln {r}+K_{0}\big (r/\ell \big ))\right. \nonumber \\&\quad \left. +\,\frac{y^2}{r^2}-2\ell ^2\frac{y^2-x^2}{r^4}+\frac{y^2-x^2}{r^2} K_{2}\big (r/\ell \big ) \right\} \,, \end{aligned}$$
(21a)
$$\begin{aligned} u_y&= \frac{b_{y}}{4\pi (1-\nu )} \left\{ 2(1-\nu )w(x,y)-\frac{xy}{r^2}+4\ell ^2\frac{xy}{r^4}\right. \nonumber \\&\quad \left. -\,\frac{2xy}{r^2} K_{2}\big (r/\ell \big ) \right\} , \end{aligned}$$
(21b)

while w(x, y) is given in (27). When \(y\rightarrow 0\), the displacement (21) is simplified to

$$\begin{aligned} u_x(x,0)&= \frac{b_{y}}{4\pi (1-\nu )} \left\{ (1-2\nu )(\ln {|x|}+K_{0}\big (|x|/\ell \big ))\right. \nonumber \\&\quad \left. +\,\frac{2\ell ^2}{x^2}- K_{2}\big (|x|/\ell \big ) \right\} \,, \end{aligned}$$
(22a)
$$\begin{aligned} u_y(x,0)&= \frac{b_{y}}{2\pi } w(x,0), \end{aligned}$$
(22b)

where w(x, 0) is given by (17). Within first gradient elasticity, the plastic distortion along \(y=0\) is given by

$$\begin{aligned} \beta _{yx}^P(x,0)=-\frac{b_{y}}{4\ell } \exp (-|x|/\ell ), \end{aligned}$$
(23)

and the dislocation density tensor reads

$$\begin{aligned} \alpha _{yz}=\frac{b_{y}}{2\pi }\frac{1}{\ell ^2} K_{0}(r/\ell ). \end{aligned}$$
(24)

It is noted that the dislocation density within first gradient elasticity is still singular, while second gradient elasticity theory (Lazar et al. 2006) offers a nonsingular dislocation density.

3.3 Edge dislocation in classical elasticity

In the limit for classical elasticity (\(\ell \rightarrow {0}\)), all of the expressions given for the field quantities of the edge dislocations above are reduced to the classical case (deWit 1973). For completeness and in order to compare the classical results with the gradient theory in the following section, the classical field quantities of the edge dislocations are summarized here. The stress field of climb and glide edge dislocations are given by

$$\begin{aligned} \tau _{xx}&= -\gamma \, b_{x}\frac{y}{r^4}(y^2+3x^2) +\gamma \, b_{y}\frac{x}{r^4} (x^2-y^2), \end{aligned}$$
(25a)
$$\begin{aligned} \tau _{yy}&= -\gamma \, b_{x}\frac{y}{r^4} (y^2-x^2)+\gamma \, b_{y}\frac{x}{r^4} (x^2+3y^2), \end{aligned}$$
(25b)
$$\begin{aligned} \tau _{xy}&= \gamma \, b_{x}\frac{x}{r^4} (x^2-y^2)+\gamma \, b_{y}\frac{y}{r^4} (x^2-y^2) \,. \end{aligned}$$
(25c)

The displacement field of edge dislocations reads

$$\begin{aligned} u_x&= \frac{b_{x}}{4\pi (1-\nu )} \left\{ 2(1-\nu )w^0(x,y)+\frac{xy}{r^2} \right\} \nonumber \\&\quad +\,\frac{b_{y}}{4\pi (1-\nu )} \left\{ (1-2\nu )\ln {r}+\frac{y^2}{r^2} \right\} \,, \end{aligned}$$
(26a)
$$\begin{aligned} u_y&= -\frac{b_{x}}{4\pi (1-\nu )} \left\{ (1-2\nu )\ln {r}+\frac{x^2}{r^2}\right\} \nonumber \\&\quad +\,\frac{b_{y}}{4\pi (1-\nu )} \left\{ 2(1-\nu )w^0(x,y)-\frac{xy}{r^2} \right\} \,, \end{aligned}$$
(26b)

with \(w^0(x,y)\) given by

$$\begin{aligned} w^0(x,y)&=\arctan \frac{y}{x}-\frac{\pi }{2}. \end{aligned}$$
(27)

Along the x-axis, the displacement field (27) is simplified to

$$\begin{aligned} u_x(x,0)&= -\frac{b_{x}}{4} \text {sgn}(x)+\frac{b_{y} (1-2\nu )}{4\pi (1-\nu )} \ln {|x|} \,, \end{aligned}$$
(28a)
$$\begin{aligned} u_y(x,0)&= -\frac{b_{x}}{4\pi (1-\nu )} \left\{ (1-2\nu )\ln {|x|}+1\right\} \nonumber \\&\quad -\frac{b_{y}}{4} \text {sgn}(x). \end{aligned}$$
(28b)

The plastic distortion tensor reads

$$\begin{aligned} \beta _{xx}^P(x,0)&= -b_{x} \delta (x) H(-y) \,, \end{aligned}$$
(29a)
$$\begin{aligned} \beta _{yx}^P(x,0)&= -b_{y} \delta (x) H(-y) , \end{aligned}$$
(29b)

which gives rise to the following expressions for dislocation density tensor for edge dislocations

$$\begin{aligned} \alpha _{xz}&= b_{x} \delta (x)\delta (y), \end{aligned}$$
(30a)
$$\begin{aligned} \alpha _{yz}&= b_{y} \delta (x)\delta (y). \end{aligned}$$
(30b)

Once the plane is assumed to contain a dislocation situated at a point with coordinates (\(\eta \), \(\zeta \)), the fields quantities of the plane may be deduced by transforming (x, y) to (\(x-\eta , y-\zeta \)) in the formulation provided above. In the following section, the distributed dislocation technique is generalized to gradient elasticity for the analyses of cracks of mode I and II.

4 Distributed dislocation technique in strain gradient elasticity: in-plane analysis

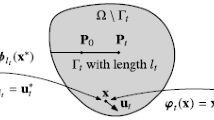
Dislocation is an elementary defect in solids which can be utilized to build composite defects (Weertman 1996) such as dislocation arrays, pile ups, and cracks. In particular, by using the distributed dislocation technique (DDT), an arbitrary configuration of cracks can be modelled (Hills et al. 1996). In this technique, the dislocations are distributed in the location of the crack and the stress field is determined for the cracked medium. The basic idea of DDT is that the field tensor of cracks is determined by the convolution of the field tensor of dislocations with a distribution function. This distribution function is determined using the crack-face boundary conditions. In general, DDT is capable of the analysis of multiple curved cracks. Here, for simplicity, we consider one straight crack. Employing this analysis for multiple inclined cracks is straight forward. Consider a plane weakened by one straight crack of length 2a along x-axis (Fig. 1). The parametric form of the crack is

$$\begin{aligned} x&= \alpha (s)= as \,, \quad -1<s<1 \end{aligned}$$
(31a)
$$\begin{aligned} y&= \beta (s)= 0. \end{aligned}$$
(31b)
Fig. 1
figure 1

Plane weakened by one crack

Full size image

Within the first gradient elasticity framework, the generalized traction boundary conditions is given by (8). In order to accurately model cracks within gradient elasticity, these nonstandard boundary conditions should be taken into account. Accordingly, on the surface of the crack, the normal vector is \(\varvec{n}=\{0,1,0\}\) (Fig.1) and the nonzero generalized tractions (9) on the surface of the crack are

$$\begin{aligned}&t_{x}=\tau _{xy}-\ell ^{2}(\tau _{xx,xy}+\tau _{xy,xx}+\tau _{xy,yy})\,, \end{aligned}$$
(32a)
$$\begin{aligned}&t_{y}=\tau _{yy}-\ell ^{2}(\tau _{xy,xy}+\tau _{yy,xx}+\tau _{yy,yy})\,, \end{aligned}$$
(32b)
$$\begin{aligned}&t_{x}^{(1)}=\ell ^{2}\tau _{xy,y}\,, \end{aligned}$$
(32c)
$$\begin{aligned}&t_{y}^{(1)}=\ell ^{2}\tau _{yy,y}\,, \end{aligned}$$
(32d)

Since these tractions are produced due to the the dislocations, we may use the relations for the stress components of a discrete dislocation (13, 20) (i.e. \(\tau _{xx,x}=-\tau _{xy,y}, \tau _{xy,x}=-\tau _{yy,y}\)) to further simplify the generalized tractions (32). Thus, the generalized tractions (32) on the surface of the crack are simplified to

$$\begin{aligned}&t_{x}=\tau _{xy}-\ell ^{2}\tau _{xy,xx}\,, \end{aligned}$$
(33a)
$$\begin{aligned}&t_{y}=\tau _{yy}-\ell ^{2}\tau _{yy,xx}\,, \end{aligned}$$
(33b)
$$\begin{aligned}&t_{x}^{(1)}=\ell ^{2}\tau _{xy,y}\,, \end{aligned}$$
(33c)
$$\begin{aligned}&t_{y}^{(1)}=\ell ^{2}\tau _{yy,y}\,. \end{aligned}$$
(33d)

For the in-plane analysis of the crack at hand, the crack is represented by a continuous distribution of glide and climb dislocations. Considering (13, 20), the stress components caused by the climb and glide edge dislocations located at a point with coordinates (\(\eta \), \(\zeta \)) read

$$\begin{aligned} \tau _{ls} (x,y)=k_{ls} ^{x} (x,y,\eta ,\zeta ) b_{x}+k_{ls} ^{y} (x,y,\eta ,\zeta ) b_{y} \,, \end{aligned}$$
(34)

where \(k_{ls} ^{i} (x,y,\eta ,\zeta ), l,s \in \lbrace x,y \rbrace \) are the coefficients of \(b_{x}\) and \(b_{y}\), i.e.,

$$\begin{aligned} k_{xx} ^{x}&= -\frac{\gamma Y}{R^4} \left\{ (Y^2+3X^2)+\frac{4\ell ^2}{R^2}(Y^2-3X^2)\right. \nonumber \\&\quad \left. \,-\,2Y^2\frac{R}{\ell } K_{1}\big (R/\ell \big )-2(Y^2-3X^2) K_{2}\big (R/\ell \big ) \right\} \end{aligned}$$
(35a)
$$\begin{aligned} k_{yy} ^{x}&= -\frac{\gamma Y}{R^4} \left\{ (Y^2-X^2)-\frac{4\ell ^2}{R^2}(Y^2-3X^2)\right. \nonumber \\&\quad \left. -\,2X^2\frac{R}{\ell } K_{1}\big (R/\ell \big )+2(Y^2-3X^2) K_{2}\big (R/\ell \big ) \right\} \end{aligned}$$
(35b)
$$\begin{aligned} k_{xy} ^{x}&= \frac{\gamma X}{R^4} \left\{ (X^2-Y^2)-\frac{4\ell ^2}{R^2}(X^2-3Y^2)\right. \nonumber \\&\quad \left. -\,2Y^2\frac{R}{\ell } K_{1}\big (R/\ell \big )+2(X^2-3Y^2) K_{2}\big (R/\ell \big ) \right\} \end{aligned}$$
(35c)
$$\begin{aligned} k_{xx} ^{y}&= \frac{\gamma X}{R^4} \left\{ (X^2-Y^2)-\frac{4\ell ^2}{R^2}(X^2-3Y^2)\right. \nonumber \\&\quad \left. -\,2Y^2\frac{R}{\ell } K_{1}\big (R/\ell \big )+2(X^2-3Y^2) K_{2}\big (R/\ell \big ) \right\} \end{aligned}$$
(35d)
$$\begin{aligned} k_{yy} ^{y}&= \frac{\gamma X}{R^4} \left\{ (X^2+3Y^2)+\frac{4\ell ^2}{R^2}(X^2-3Y^2)\right. \nonumber \\&\quad \left. -\,2X^2\frac{R}{\ell } K_{1}\big (R/\ell \big )-2(X^2-3Y^2) K_{2}\big (R/\ell \big ) \right\} \end{aligned}$$
(35e)
$$\begin{aligned} k_{xy} ^{y}&= \frac{\gamma Y}{R^4} \left\{ (X^2-Y^2)-\frac{4\ell ^2}{R^2}(3X^2-Y^2)\right. \nonumber \\&\quad \left. +\,2X^2\frac{R}{\ell } K_{1}\big (R/\ell \big )+2(3X^2-Y^2) K_{2}\big (R/\ell \big ) \right\} , \end{aligned}$$
(35f)

with \( X=x-\eta , Y=y-\zeta \) and \(R=\sqrt{X^2+Y^2} \).

Next, we consider dislocations with unknown densities \(B_{x} (\xi )\) and \(B_{y}(\xi )\), distributed along an infinitesimal segment \({\mathrm {d}}l~=a {\mathrm {d}}\xi \) on the surface of the crack. For the horizontal crack (Fig. 1) for which \(Y=0\), the in-plane tractions (33) on the surface of the crack due to the presence of this distribution of dislocations are

$$\begin{aligned} t_{x} \big (\alpha (s), \beta (s)\big )&=a{\int _{-1}^{1}{\Big \{ k_{xy}^{x}-\ell ^2 k_{xy,xx}^{x} \Big \} B_{x}(\xi )\, {\mathrm {d}}\xi }}\nonumber \\&\quad +\,a{\int _{-1}^{1}{\Big \{ k_{xy}^{y}-\ell ^2 k_{xy,xx}^{y} \Big \} B_{y}(\xi )\, {\mathrm {d}}\xi }}, \end{aligned}$$
(36a)
$$\begin{aligned} t_{y} \big (\alpha (s), \beta (s)\big )&=a{\int _{-1}^{1}{\Big \{ k_{yy}^{x}-\ell ^2 k_{yy,xx}^{x} \Big \} B_{x}(\xi )\, {\mathrm {d}}\xi }}\nonumber \\&\quad +\,a{\int _{-1}^{1}{\Big \{ k_{yy}^{y}-\ell ^2 k_{yy,xx}^{y} \Big \} B_{y}(\xi )\, {\mathrm {d}}\xi }}\, , \end{aligned}$$
(36b)
$$\begin{aligned} t_{x}^{(1)} \big (\alpha (s), \beta (s)\big )&=a{\int _{-1}^{1}{\ell ^2 k_{xy,y}^{x} B_{x}(\xi )\, {\mathrm {d}}\xi }}\nonumber \\&\quad +\,a{\int _{-1}^{1}{\ell ^2 k_{xy,y}^{y} B_{y}(\xi )\, {\mathrm {d}}\xi }}\, , \end{aligned}$$
(36c)
$$\begin{aligned} t_{y}^{(1)} \big (\alpha (s), \beta (s)\big )&=a{\int _{-1}^{1}{\ell ^2 k_{yy,y}^{x} B_{x}(\xi )\, {\mathrm {d}}\xi }}\nonumber \\&\quad +\,a{\int _{-1}^{1}{\ell ^2 k_{yy,y}^{y} B_{y}(\xi )\, {\mathrm {d}}\xi }}\, . \end{aligned}$$
(36d)

Here the functions \(k_{ls}^{i} (x,y,\eta ,\zeta ), \lbrace l,s,i \rbrace \in \lbrace x,y\rbrace \) are given by (35) with \(Y=0\). The coordinates \(\ (x,y)=(\alpha (s), 0)\) are the parametric form of the points on the crack (31) where \((\eta ,\zeta )=~(\alpha (\xi ), 0) \) are the coordinates of dislocation on the surface of the crack. Due to non-singular dislocation solutions (13, 20), the integral equations (36) are non-singular.

4.1 Mode I crack

For the analysis of a crack along the x-axis in mode I, a far-field uniform traction \(\tau _{yy}^{\infty }=\tau _{yy0}\) is applied to the plane. Hence, the traction at the location of the crack in the defectless plane reads

$$\begin{aligned} \bar{t}_{x}=0\, \,, \quad \bar{t}_{y}=\tau _{yy0}\, \,, \quad \bar{t}_{x}^{(1)}=\bar{t}_{y}^{(1)}=0\,. \end{aligned}$$
(37)

For the distribution of climb edge dislocations, the tractions \(\bar{t}_{x}\) and \(\bar{t}_{y}^{(1)}\) vanish automatically on the crack surface. The remaining traction conditions, i.e.

$$\begin{aligned} \bar{t}_{y}=\tau _{yy0}\, \,, \quad \bar{t}_{x}^{(1)}=0\, \end{aligned}$$
(38)

can be used to determine the density of the dislocations. Using the Bueckner superposition principle (Bueckner 1973), the left-hand side of the integral equations (36) are identical to the traction in (38) with opposite sign, i.e., for mode I,

$$\begin{aligned}&{\int _{-1}^{1}{\Big \{ k_{yy}^{y}-\ell ^2 k_{yy,xx}^{y} \Big \} B_{y}(\xi )\, {\mathrm {d}}\xi }}=-\frac{\tau _{yy0}}{a}\, , \end{aligned}$$
(39a)
$$\begin{aligned}&{\int _{-1}^{1}{\ell ^2 k_{xy,y}^{y} B_{y}(\xi )\, {\mathrm {d}}\xi }}=0\,. \end{aligned}$$
(39b)

The closure requirement implies

$$\begin{aligned} \int _{-1}^{1}{ B_{y}(\xi ){\mathrm {d}}\xi }&=0\,, \end{aligned}$$
(40)

which ensures the single-valuedness of the displacement field field out of the crack. The system of the integral equations (39) and (40) should be solved to determine the climb dislocation density \((B_y)\) for mode I.

4.1.1 Crack opening displacement

The crack opening displacement (COD) is obtained by superposing the displacement field of the dislocations distributed along the crack surface. Considering the density of the dislocations \(B_y(\xi )\) for mode I, the COD reads

$$\begin{aligned} g(x)&=2u_y(x,0)=-a\int _{-1}^{x/a}{B_{y}(\xi )\, {\mathrm {d}}\xi }\nonumber \\&\quad +\,\frac{a}{2}\int _{-1}^{1}{ \text {sgn}(x{-}at) \exp ({-|x{-}a\xi |/\ell }) B_{y}(\xi ) \, {\mathrm {d}}\xi }. \end{aligned}$$
(41)

In the classical limit (\(l\rightarrow {0}\)), the COD reduces to

$$\begin{aligned} g(x)=-a\int _{-1}^{x/a}{B_{y}(\xi )\, {\mathrm {d}}\xi }{=}\frac{2(1-\nu )\tau _{yy0}}{\mu }\sqrt{a^2{-}x^2}. \end{aligned}$$
(42)

In contrast to classical elasticity (42), the COD within gradient elasticity (41) is not limited to the crack surface.

4.1.2 Plastic distortion

The plastic distortion of a discrete dislocation (23) can be superposed to determine the plastic distortion of the plane weakened by a crack. Using the density of the dislocations, the plastic distortion of the plane \(\beta _{yx}^{P,cr}\) along \(y=0\) is obtained as

$$\begin{aligned}&\beta _{yx}^{P,cr}(x,0)=-\frac{a}{4\ell } \int _{-1}^{1}{\left\{ \exp ({-}|x{-}a\xi |/\ell ) \right\} B_y(\xi )\, {\mathrm {d}}\xi }. \end{aligned}$$
(43)

Here and in the following, the superscript “cr” denotes “crack”. In the limit for classical elasticity, the plastic distortion is simplified to

$$\begin{aligned} \beta _{yx}^{P,cr}(x,0^-)=-B_y(x/a). \end{aligned}$$
(44)

According to (44), the classical plastic distortion vanishes outside the crack line while within gradient elasticity, the plastic distortion (43) appears also beyond the crack tip. As demonstrated in the next section, this suggests the emergence of crack tip plasticity without any assumption other than the constitutive model of the material.

4.1.3 Stress field

The stress field of the distributed dislocations reads

$$\begin{aligned}&\tau ^{cr}_{xx}(x,y)=a \int _{-1}^{1}{k_{xx}^y B_{y}(\xi )\, {\mathrm {d}}\xi }\,, \end{aligned}$$
(45a)
$$\begin{aligned}&\tau ^{cr}_{yy}(x,y)=\tau _{yy0} +a \int _{-1}^{1}{k_{yy}^y B_{y}(\xi )\, {\mathrm {d}}\xi }\,, \end{aligned}$$
(45b)
$$\begin{aligned}&\tau ^{cr}_{xy}(x,y)=a \int _{-1}^{1}{k_{xy}^y B_{y}(\xi )\, {\mathrm {d}}\xi }\, , \end{aligned}$$
(45c)

where \(X=x-\alpha (\xi )\), \(Y=y\) and \(R^2=X^2+Y^2\). The stress components (45) are nonsingular. The double stress components can be derived by substituting (45) in (5). As mentioned earlier, for a single dislocation, the double stress is singular within gradient elasticity. Consequently, the double stress tensor of a plane weakened by a crack (being the convolution of the discrete dislocations) is singular. On the other hand, the total stress tensor can be determined by substituting (45) in (10). Since the total stress of a discrete dislocation is singular, it results in singular total stress at crack tips.

4.2 Mode II crack

For a mode II analysis, a plane weakened by a crack along x-axis is assumed to be subjected to the far-field uniform traction \(\tau _{xy}^{\infty }=\tau _{xy0}\). The traction at the location of the crack in the defectless plane is then given by

$$\begin{aligned} \bar{t}_{x}=\tau _{xy0}\, \,, \quad \bar{t}_{y}=0\, \,, \quad \bar{t}_{x}^{(1)}=\bar{t}_{y}^{(1)}=0\,. \end{aligned}$$
(46a)

For the distribution of glide edge dislocations, the tractions \(\bar{t}_{y}\) and \(\bar{t}_{x}^{(1)}\) vanish automatically on the crack surface. The remaining traction conditions are

$$\begin{aligned} \bar{t}_{x}=\tau _{xy0}\, \,, \quad \bar{t}_{y}^{(1)}=0\, \end{aligned}$$
(47)

which can be used to determine the density of the dislocations to represent the crack.

Once the traction in (47), with opposite sign, is substituted in the left-hand side of equations (36), the integral equations

$$\begin{aligned}&{\int _{-1}^{1}{\Big \{ k_{xy}^{x}-\ell ^2 k_{xy,xx}^{x} \Big \} B_{x}(\xi )\, {\mathrm {d}}\xi }}=-\frac{\tau _{xy0}}{a}\,, \end{aligned}$$
(48a)
$$\begin{aligned}&{\int _{-1}^{1}{\ell ^2 k_{yy,y}^{x} B_{x}(\xi )\, {\mathrm {d}}\xi }}=0\, \end{aligned}$$
(48b)

are obtained for mode II. Similar to mode I, the closure requirements should be considered for the analysis of embedded crack, i.e.,

$$\begin{aligned} \int _{-1}^{1}{ B_{x}(\xi ){\mathrm {d}}\xi }&=0\,. \end{aligned}$$
(49)

The solution to the system of integral equations (48) and (49) gives the glide dislocation density \((B_x)\) for mode II.

4.2.1 Crack opening displacement

The COD of a crack of mode II reads

$$\begin{aligned} g(x)&=2u_x(x,0)=-a\int _{-1}^{x/a}{B_{x}(\xi )\, {\mathrm {d}}\xi }\nonumber \\&\quad +\,\frac{a}{2}\int _{-1}^{1}{ \text {sgn}(x{-}at) \exp ({-|x-a\xi |/\ell }) B_{x}(\xi ) \, {\mathrm {d}}\xi } . \end{aligned}$$
(50)

while in the limit for classical elasticity reduces to

$$\begin{aligned} g(x)=-a\int _{-1}^{x/a}{B_{x}(\xi )\, {\mathrm {d}}\xi }. \end{aligned}$$
(51)

4.2.2 Plastic distortion

Considering the plastic distortion of a discrete dislocation (18) and the density of dislocations, the plastic distortion on the plane \(\beta _{xx}^{P,cr}\) along \(y=0\) is obtained as

$$\begin{aligned} \beta _{xx}^{P,cr}(x,0){=}-\frac{a}{4\ell } \int _{-1}^{1}{\left\{ \exp ({-}|x-a\xi |/\ell ) \right\} B_x(\xi )\, {\mathrm {d}}\xi }, \end{aligned}$$
(52)

whereas the classical plastic distortion reads

$$\begin{aligned} \beta _{xx}^{P,cr}(x,0^-)=-B_x(x/a). \end{aligned}$$
(53)

Similarly to mode I, the classical plastic distortion (53) vanishes outside the crack of mode II while within gradient elasticity, the plastic distortion (52) appears also beyond the crack tip.

4.2.3 Stress field

The (nonsingular) stress field of the distributed glide edge dislocations, representing the crack of mode II, reads

$$\begin{aligned}&\tau ^{cr}_{xx}(x,y){=}a \int _{-1}^{1}{k_{xx}^x B_{x}(\xi )\, {\mathrm {d}}\xi }\,, \end{aligned}$$
(54a)
$$\begin{aligned}&\tau ^{cr}_{yy}(x,y)=a \int _{-1}^{1}{k_{yy}^x B_{x}(\xi )\, {\mathrm {d}}\xi }\,, \end{aligned}$$
(54b)
$$\begin{aligned}&\tau ^{cr}_{xy}(x,y)=\tau _{yy0} + a \int _{-1}^{1}{k_{xy}^x B_{x}(\xi )\, {\mathrm {d}}\xi }\,, \end{aligned}$$
(54c)

where \(X=x-\alpha (\xi )\), \(Y=y\) and \(R^2=X^2+Y^2\). The double stress components can be derived by substituting (54) in (5). Similar to the discussion for mode I, the double stress field of a plane weakened by a mode II crack, being the convolution of the discrete dislocations, is singular. Additionally, the (singular) total stress tensor can be derived by substituting (54) in (10).

5 Numerical results

In this section, numerical results are presented for a plane weakened by a crack (Fig. 1). Mode I and II are studied in the following subsections. It is noted that the singular value decomposition technique is used to solve the system of integral equations (Mousavi et al. 2014; Golub and Van Loan 1996).

5.1 Mode I crack

As demonstrated in the previous section, once the plane is under a far-field uniform traction \(\tau _{yy}^{\infty }=\tau _{yy0}\), the crack behaves in mode I. In order to compare gradient elasticity with classical elasticity, the results for the dislocation density are shown in Fig. 2 for \(\tau _{yy0}=\mu \). The classical dislocation density is given by

$$\begin{aligned} B_y(x)=\frac{2(1-\nu )\tau _{yy0}}{\mu }\frac{x}{\sqrt{a^2-x^2}}\,. \end{aligned}$$
(55)
Fig. 2
figure 2

Climb dislocation density for mode I within classical and gradient elasticity, \(\tau _{yy0}=\mu \)

Full size image

It can be seen that the density is singular at the crack tips in which the dislocations are piled up and concentrated. The sign of the singularity in gradient elasticity coincides with the sign of the classical singular density. This is an interesting feature of gradient elasticity, in contrast to the nonlocal elasticity where the singularities possess opposite sign with respect to classical elasticity (Mousavi and Lazar 2015). It is also noted that the nonlocal stress field of a discrete dislocation coincides with the stress field of a discrete dislocation within gradient elasticity. The boundary conditions are the major difference between nonlocal and gradient elasticity which leads to this characteristic distinction. In nonlocal elasticity, the boundary conditions are as simple as classical elasticity, while (as explained in previous sections) the gradient elasticity contains non-classical boundary conditions. Figure 2 demonstrates the dislocation density for gradient coefficients \(\ell =0.1a, 0.4a, 0.8a\). It is noticed that for lower values of gradient coefficient, the classical density is recovered. However, the higher values of gradient coefficients contribute to insignificant changes of the dislocation density with respect to classical one.

Fig. 3
figure 3

Crack opening displacement for mode I within classical and gradient elasticity, \(\tau _{yy0}=\mu \)

Full size image
Fig. 4
figure 4

Plastic distortion \(\beta _{yx}^{P,cr}\) along \(y=0\) for mode I within classical and gradient elasticity, \(\tau _{yy0}=\mu \), \(\ell =0.1a\)

Full size image
Fig. 5
figure 5

Stress component \(\tau _{xx}^{cr}\) for mode I within classical and gradient elasticity, \(\tau _{yy0}=\mu \), \(\ell =0.1a\)

Full size image

The crack opening displacement (COD) is an important aspect of any fracture theory. Figure 3 compares the classical COD (42) with the one in gradient elasticity (41) for \(\ell =0.1a, 0.2a\). The gradient elasticity predicts a smoother closure than the classical one. In other words, a cusp-like closure of the crack faces is observed within gradient elasticity.

In the present model, COD extends beyond the crack surfaces, which is related to the intermolecular forces ahead of the physical crack tip. This extent of COD beyond the physical crack tip demonstrates the similarity of the current treatment with the cohesive zone model (Karihaloo and Xiao 2003) in which the crack opening in the cohesive zone is related to the distribution of cohesive force. In this study, this feature is modelled without the introduction of a cohesive zone. In fact, this is a nice feature of gradient elasticity providing an alternative justification of Barenblatt’s “smooth closure” crack condition. In his seminal work, Barenblatt proposed the idea of the “mathematical” and “physical” crack by introducing internal compressive forces ahead of the mathematical crack tip, acting along a certain distance (the cohesive zone) determined by requiring to eliminate the singularity at the tip of the physical crack (Barenblatt 1962). Gradient elasticity provides a different formulation and explanation of Barenblatt’s problem by introducing the “cohesive forces” directly in the constitutive equation.

Since dislocation is a source of incompatibility, they give rise to plastic distortion. Consequently, an interesting aspect of the dislocation-based approach is its capability to determine the plastic distortion of the plane weakened by cracks. Figure 4 depicts the plastic distortion \(\beta _{yx}^{P,cr}\) (43) along \(y=0\). It is noticed that the classical plastic distortion vanishes out of the crack faces, while the gradient elasticity captures crack-tip plasticity without any extraneous assumption, as in classical Barenblatt’s cohesive fracture theory (Barenblatt 1962).

Fig. 6
figure 6

Stress component \(\tau _{yy}^{cr}\) for mode I within classical and gradient elasticity, \(\tau _{yy0}=\mu \), \(\ell =0.1a\)

Full size image
Fig. 7
figure 7

Glide dislocation Density for mode II within classical and gradient elasticity, \(\tau _{xy0}=\mu \)

Full size image

The stress components \(\tau _{xx}\) and \(\tau _{yy}\) are also shown in Figs. 5 and 6, respectively. As expected, a full-field solution is obtained using the dislocation-based approach. The classical singularity of the stress field is regularized and the stress field is finite at the crack tip. The maximum of the stress field occurs in the vicinity of the crack tip, out of the crack surface. It is noticed that, in contrast to nonlocal elasticity which gives zero nonlocal stress at the crack tips (Mousavi and Lazar 2015), this gradient elasticity solution predicts finite nonzero stress at the crack tips. This distinction is due to different boundary conditions. In nonlocal elasticity, the nonlocal stress should vanish along the crack while within gradient elasticity, it is the generalized tractions (33) which is set equal to zero on the crack surface.

Within classical elasticity, the dislocation-based approach does not predict any crack tip plasticity unless the assumption of cohesive zone is considered. In contrast, it is observed here that the dislocation-based approach within strain gradient elasticity provided the full-field nonsingular stress field as well as the profile for the crack tip plasticity. In other words, a full-field (not asymptotic) nonsingular stress field as well as the profile for the crack tip plasticity is realized without any assumption other than the constitutive model of the material. The knowledge of stress field and crack tip plasticity can serve the attempt to predict plastic failure or brittle fracture. The study of such criteria is in progress.

5.2 Mode II crack

In order to study an in-plane shear problem, the plane (Fig. 1) is assumed to be under a far-field uniform traction \(\tau _{xy}^{\infty }=\tau _{xy0}=\mu \). This gives rise to a crack of mode II. Similarly to the previous section, the dislocation-based approach is applied to obtain the dislocation density, crack opening, plastic distortion and stress field.

Figure 7 demonstrates the dislocation density of classical elasticity and gradient elasticity (\(\ell =0.1a, 0.4a, 0.8a\)). The mode II dislocation density (Fig. 7) behaves qualitatively similarly to the one in mode I (Fig. 2). For lower values of \(\ell \), the density within gradient elasticity approaches to the classical one. However, a distinction between mode I and II is the fact that, in contrast to mode I, here we notice that the higher values of the gradient coefficient contribute to a significant change with respect to classical solution.

The crack opening displacement is depicted in Fig. 8. Similarly to mode I, the gradient elasticity predicts a smoother closure than the classical one.

Fig. 8
figure 8

Crack opening displacement for mode II within classical and gradient elasticity, \(\tau _{xy0}=\mu \)

Full size image
Fig. 9
figure 9

Plastic distortion \(\beta _{xx}^{P,cr}\) along \(y=0\) for mode II within classical and gradient elasticity, \(\tau _{xy0}=\mu \), \(\ell =0.1a\)

Full size image
Fig. 10
figure 10

Stress component \(\tau _{xy}^{cr}\) for mode II within classical and gradient elasticity, \(\tau _{xy0}=\mu \), \(\ell =0.1a\)

Full size image

To study the plasticity induced by the crack, the plastic distortion \(\beta _{xx}^{P,cr}\) (52) is demonstrated along \(y=0\) in Fig. 9. As in the case for mode I, a non-vanishing plastic distortion appears in the vicinity of the crack tip, representing the cohesive zone.

Finally, the only nonzero stress components \(\tau _{xy}\) is shown in Fig. 10. The stress field is nonsingular and possesses finite nonzero values at the crack tip. The maximum of the stress occurs in the vicinity of the crack tip outside the crack surface.

6 Conclusions

In this paper, a dislocation-based approach is applied to analyse the cracks of mode I and II within gradient elasticity. Due to the use of dislocations, an incompatible framework was employed. By properly distributing the dislocations and using the variationally consistent boundary conditions, all field quantities are derived as a convolution of the corresponding field quantities for a discrete dislocation through the so-called dislocation density function.

The dislocation densities of cracks (of mode I and II) are demonstrated and compared to the classical elasticity. The distinctive feature of gradient elasticity in comparison to the nonlocal elasticity is that the “nonlocal” density contains opposite singularity with respect to the “classical” density, while the one in gradient elasticity is consistent with that of classical density.

Due to the regularization of the stress fields of edge dislocations within gradient elasticity, non-singular stresses for cracks are obtained for mode I and II. The crack opening displacement (COD) is also determined and is compared to the classical COD. It is observed that, in comparison to classical elasticity, the crack closure is smoother than in gradient elasticity. Furthermore, the emergence of crack tip plasticity is captured without any extraneous assumption such as in classical Barenblatt’s cohesive fracture theory. This provides an alternative approach to celebrated “Barenblatt’s treatment” of cracks, without the introduction of a cohesive zone and relate to intermolecular forces ahead of the physical crack tip.

A nonsingular dislocation-based fracture theory is of considerable interest since it provides the chance to formulate a unified dislocation-based theory for plasticity and fracture. It is to be noted that dislocation (crystal) plasticity has been developed successfully recently. Such formulation of plasticity can be unified with the dislocation-based fracture to provide tools for the analysis of materials without any ad hoc assumptions.