Panorama Behaviors of Holographic Dark Energy Models in Modified Gravity

Abstract

A class of solutions of field equations in $f(R,T)$ gravity proposed by Harko et. al. (2011) for a Bianchi type I (Kasner form) space–time with dark matter and Holographic Dark Energy (HDE) is mentioned. Exact solutions of field equations are obtained with volumetric power and exponential expansion laws. The negative value of the deceleration parameter represents the present acceleration of the universe. It is observed that EoS parameter of HDE is a decreasing function, converges to the negative value in Power-law model whereas in exponential model, it behaves like cosmological constant. The overall density parameter approaches to some constant values close to 1 which is in agreement with the observational data of the universe. The physical and geometrical parameters of the models are discussed in detail. The statefinder diagnostic pair and jerk parameter are analyzed to characterize completely different phases of the universe.

1 Introduction

Observational data from the Cosmic Microwave Background (CMB), Type Ia Supernovae (SNe) and Large Scale Structure (LSS) indicates that our universe is accelerating and expanding [1,2,3]. Dark Energy (DE) is the bizarre cosmic fluid having strong negative pressure which makes the universe to accelerate and expand. The cosmological constant Λ is the simple candidate of the DE. The quintessence scalar field models [4, 5], the phantom model [6, 7], k-essence[8,9,10], tachyon field [11, 12], Chaplygin gas [13, 14], Holographic Dark Energy [15, 16] are the various important candidates of DE. Modifications of general relativity are attracting more and more attention to explain late time acceleration and dark energy. Due to its ability to explain several issues in cosmology and astrophysics, recently many cosmologists and astrophysicists have studied f (R,T) theory.

In f (R,T) theory, the gravitational Lagrangian is given by an arbitrary function of the Ricci scalar R and the trace T of the stress energy tensor. The f(R,T) gravity model depends on a source term, representing the variation of the matter stress energy tensor with respect to the metric. A general expression for this source term is obtained as a function of the matter Lagrangian Lm so that each choice of Lm would generate a specific set of field equations. Some particular models corresponding to specific choices of the function f(R, T) are also represented, they have also demonstrated the possibility of reconstruction of arbitrary FRW cosmologies by an appropriate choice of a function f(T). In the present model the covariant divergence of the stress energy tensor is non-zero. Hence the motion of test particles is non-geodesic and an extra acceleration due to the coupling between matter and geometry is always present. Katore and Shaikh [17] investigated Kantowaski-Sachs cosmological model with constant deceleration parameter in f (R,T) gravity. Reddy et al. [18] discussed Bianchi type-III dark energy model in f (R,T) gravity. Kaluza-Klein dark energy models are studied by Sahoo and Mishra [19] within the presence of wet dark fluid in f (R,T) gravity. Rao and Papa Rao [20] investigated five dimensional Kaluza-Klein space–time in the presence of anisotropic dark energy in f (R,T) gravity. State finder diagnosis for HDE models are studied by Singh and Pankaj Kumar [21]. Shaikh [22]. discussed a binary mixture of perfect fluid and dark energy in a modified theory of gravity. Shaikh and Katore [23] derived the exact solutions of Hypersurface-Homogeneous universe within the presence of perfect fluid in the framework of f (R, T) theory of gravity. Shaikh and Wankhade [24] investigated cosmological model in f(R,T) theory of gravity with a term Λ. Moraes and Sahoo [25] constructed a cosmological model from the simplest non-minimal matter–geometry coupling. Analysis about compact stellar structures, hydrostatic equilibrium configurations of strange stars, Anisotropic stellar filaments evolving under expansion free condition and the dynamical stability of shearing viscous anisotropic fluid were discussed [26,27,28,29,30,31]. Srivastava and Singh [32] obtained new holographic dark energy model with constant bulk viscosity in modified f (R,T) gravity theory. Moraes et.al [33]. proposed a new exponential shape function in wormhole geometry within modified gravity. Moraes and Sahoo [34] investigated wormholes in exponential f (R, T) gravity.

The Kasner universe is probably the most famous closed-form cosmological solution of GR in vacuum [35]. On the large scale, the Universe seems homogeneous and isotropic. But there is no observational data that guarantees the isotropy in an era prior to recombination. In general, the Kasner solution describes an anisotropic metric in which the space directions are Killing translations, that is, the space–time is invariant under a three-dimensional Abelian translation group [35]. Moreover, a general cosmological singularity is believed to be constructed as an infinite series of consecutive epochs, each of them being a particular Kasner solution with a good accuracy [35]. The Kasner solution is a solution for an anisotropically expanding Universe with scale factors changing as powers of time. The Kasner solution described the evolution of Mixmaster Universe when the effect of the Ricci scalar of the three dimensional spatial hypersurface is negligible because of simplicity and the importance of the Kasner solution. Kasner-like solutions which provide cosmological singularities with inflationary solutions were determined. The Kasner solution plays an important role in study of anisotropy in quantum particle creation, Baryosynthesis, inflation, massive particle survival, magnetic field evolution, primordial nucleosynthesis, temperature isotropy and statics of the microwave background [36].

In the last decades, the holographic dark energy based on holographic principle also used to solve dark energy problem which is a promising approach and helps in finding cosmological features of the vacuum energy density which plays the role of energy density of DE. The holographic dark energy model is successful in explaining the observational data. According to the holographic principle, the number of degrees of freedom in a bounded system should be finite and is related to the area of its boundary [37]. It is argued that this model may solve the cosmological constant problem and some other issues. In the context of the dark energy problem, though the holographic principle proposes a relation between the holographic dark energy density $\rho_{\lambda }$ and the Hubble parameter H as $\rho_{\lambda } = H^{2}$, it does not contribute to the present accelerated expansion of the universe. Using the holographic principle of quantum gravity theory Susskind[38] a viable holographic dark energy model was constructed by Li [39].Cosmological versions of HDE as an emerging model are constructed on the basis of holographic principle [40,41,42,43,44,45]. Interacting modified HDE in the Kaluza-Klein universe is explored by Sharif and Jawad [46]. Samanta [47] studied HDE cosmological model within the presence of quintessence. Minimally interacting HDE are discussed by Sarkar and Mahanta [48], Sarkar [49,50,51] for anisotropic models in general relativity. Jawad et al.[52] discussed MHRDE in Chameleon BD cosmology with non-minimally matter coupling of the scalar field and its thermodynamic consequence. Reddy et.al [53] studied five dimensional spherically symmetric holographic dark energy cosmological models. Rao and Prasanthi [54], Reddy [55], Naidu et al. [56] and Aditya and Reddy [57] explored MHRDE in scalar tensor theories of gravitations. Ricci dark energy model with bulk viscosity has been investigated by Singh and Kumar [58].Sharma and Pradhan [59] analyzed the Tsallis Holographic Dark Energy (THDE) model using the statefinder diagnostic.

The motivation for this study comes from the above investigation and discussion of cosmological models of the universe. The purpose of our work is to study the universe filled with holographic dark energy in the newly established extension of the standard general relativity, which is known as the f(R,T) theory of gravity. In this article we investigate the possibility that an accelerated expansion ought to be possible owing to the presence of matter and holographic Ricci dark energy in the frame work of f (R,T) gravity proposed by Harko et al. [60].We therefore turn our attention to modified gravity theories (MGT) which refute the existence of the “Dark Energy” and “Dark Matter” by presuming them to be purely geometrical in nature. The predictions of the f(R,T) gravity models could lead to some major differences, as compared to the predictions of standard general relativity or other generalized gravity models, in several problems of current interest.

2 Basic Formalism

The $f(R,T)$ theory of gravity is a modification of General Relativity (GR). The field equations of $f(R,T)$ gravity are derived from the Hilbert–Einstein-type variational principle. The action for the modified $f(R,T)$ gravity is

$$S = \frac{1}{16\pi G}\int {\sqrt { - g} \, f(R,T) \, d^{4} x} + \int {\sqrt { - g} \, L_{m} } d^{4} x,$$

(1)

where $f(R,T)$ is an arbitrary function, $R{\kern 1pt} ,{\kern 1pt} {\kern 1pt} T{\kern 1pt} {\kern 1pt} ,{\kern 1pt} {\kern 1pt} L_{m}$ are the Ricci scalar,trace of the stress energy tensor of the matter $T_{ij}$ ($T = g^{ij} T_{ij}$) and Lagrangian density respectively.The $f(R,T)$ gravity field equations are obtained by varying the action S for the function $f(R,T) = R + 2f(T)$ within the presence of perfect fluid [60] as

$$R_{ij} - \frac{1}{2}Rg_{ij} = 8\pi T_{ij} + 2f^{\prime}\left( T \right)T_{ij} + [2pf^{\prime}\left( T \right) + f\left( T \right)]g_{ij} .$$

(2)

here prime denotes differentiation with respect to the argument, $f(T)$ is an arbitrary function of the trace of stress energy tensor of matter and $p$ is the pressure of the matter source, which is a perfect fluid.

3 Metric and Field Equations

In the Bianchi model, the spatial section is flat in which the extension or contraction rate is direction dependent. The investigation of Bianchi models in modified theories of gravitation plays a vital role in understanding the possible anisotropic nature of dark energy and its effects on the evolution of the universe. We consider Bianchi type I metric (Kasner form) as follows

$$ds^{2} = dt^{2} - t^{{2q_{1} }} dx^{2} - t^{{2q_{2} }} dy^{2} - t^{{2q_{3} }} dz^{2} ,$$

(3)

where $q_{1} ,q_{2} ,q_{3}$ are three parameters being constants and if at least two of the three are different then the space is anisotropic. Let $S = q_{1} + q_{2} + q_{3} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \theta = q_{1}^{2} + q_{2}^{2} + q_{3}^{3}$ which follows $a = \left( {S^{2} - 2S + \theta } \right){\kern 1pt} {\kern 1pt} {\kern 1pt} t^{ - 2}$. Let us assume

$$f(T) = \mu T,$$

(4)

where $\mu$ is a constant [60]. Here the universe is occupied with matter and a hypothetical isotropic fluid as the holographic dark energy components. The energy momentum tensor for matter and holographic dark energy is defined as

$$T_{\mu \nu } = \rho_{m} u_{\mu } u_{\nu } ;\;\overline{T}_{\mu \nu } = (\rho_{\lambda } + p_{\lambda } )u_{\mu } u_{\nu } + g_{\mu \nu } p_{\lambda } ,$$

(5)

where $\rho_{m}$ and $\rho_{\lambda }$ are the energy densities of matter and holographic dark energy respectively and $p_{\lambda }$ is the pressure.Using commoving coordinates system and Eqs. (2),(3), (4) and (5), the field equations can be written as

$$\left[ {q_{1} (s - 1) - \frac{1}{2}(s^{2} - 2s + \theta )} \right]t^{ - 2} = 8\pi p_{\lambda } - [ - 3p_{\lambda } + \rho_{m} + \rho_{\lambda } ]\mu ,$$

(6)

$$\left[ {q_{2} (s - 1) - \frac{1}{2}(s^{2} - 2s + \theta )} \right]t^{ - 2} = 8\pi p_{\lambda } - [ - 3p_{\lambda } + \rho_{m} + \rho_{\lambda } ]\mu ,$$

(7)

$$\left[ {q_{3} (s - 1) - \frac{1}{2}(s^{2} - 2s + \theta )} \right]t^{ - 2} = 8\pi p_{\lambda } - [ - 3p_{\lambda } + \rho_{m} + \rho_{\lambda } ]\mu ,$$

(8)

$$\left[ {(s - \theta ) - \frac{1}{2}(s^{2} - 2s + \theta )} \right]t^{ - 2} = - 8\pi (\rho_{m} + \rho_{\lambda } ) - [ - p_{\lambda } + 3\rho_{m} + 3\rho_{\lambda } ]\mu ,$$

(9)

where a dot here in after denotes ordinary differentiation with respect to cosmic time “t” only.

4 Isotropization

Define $a = \left( {t^{{q_{1} }} t^{{q_{2} }} t^{{q_{3} }} } \right)^{\frac{1}{3}}$ as the average scale factor so that the Hubble parameter in our model may be defined as

$$H = \frac{{\dot{a}}}{a} = \frac{1}{3}\sum\limits_{i = 1}^{3} {H_{i} } ,$$

(10)

where a is the mean scale factor and $H_{i} = \frac{{\dot{a}_{i} }}{{a_{i} }}$ are directional Hubble’s factors in the direction of $x^{i}$ respectively. The anisotropy parameter of the expansion $\Delta$ is defined as

$$\Delta = \frac{1}{3}\sum\limits_{i = 1}^{3} {\left( {\frac{{H_{i} - H}}{H}} \right)^{2} }$$

(11)

in the $x,y,z$ directions, respectively. The scalar expansion and shear scalar are given by

$$\theta = 3H$$

(12)

$$\sigma^{2} = \frac{3}{2}\Delta H^{2}$$

(13)

The deceleration parameter is defined as

$$q = \frac{d}{dt}\left( \frac{1}{H} \right) - 1.$$

(14)

The holographic dark energy density is given by

$$\rho_{\lambda } = 3(\alpha H^{2} + \beta \dot{H}),$$

(15)

with $M_{p}^{ - 2} = 8\pi G = 1.$

The continuity equation can be obtained as

$$\dot{\rho }_{m} + \dot{\rho }_{\lambda } + 3H(\rho_{m} + \rho_{\lambda } + p_{\lambda } ) = 0.$$

(16)

The continuity equation of the matter is

$$\dot{\rho }_{m} + 3H\rho_{m} = 0.$$

(17)

The continuity equation of the holographic dark energy is

$$\dot{\rho }_{\lambda } + 3H(\rho_{\lambda } + p_{\lambda } ) = 0.$$

(18)

The barotropic equation of state is

$$p_{\lambda } = \omega_{\lambda } \rho_{\lambda } .$$

(19)

Using Eqs. (15), (18) and (19), the EoS HDE parameter is obtained as

$$\omega_{\lambda } = - 1 - \frac{{2\alpha H\dot{H} + \beta \ddot{H}}}{{3H(\alpha H^{2} + \beta \dot{H})}}.$$

(20)

4.1 Statefinder Parameters

State finder parameters {r, s} are defined as (Sahni et al.[61])

$$r = \frac{\dddot a}{{aH^{3} }},\;s = \frac{r - 1}{{3\left( {q - \frac{1}{2}} \right)}}$$

(21)

These parameters can be expressed in terms of Hubble parameter and its derivatives with respect to cosmic time as

$$r = 1 + \frac{{3\dot{H}}}{{H^{2} }} + \frac{{\ddot{H}}}{{H^{3} }}{\kern 1pt} ,\;s = \frac{{ - 2(3H\dot{H} + \ddot{H})}}{{3H(3H^{2} + 2\dot{H})}}.$$

(22)

When $(r,s) = (1,1)$, we have cold dark matter (CDM) limit while $(r,s) = (1,0)$ gives ΛCDM limit. When $r < 1$ we have quintessence DE region and for $s > 0$ phantom DE regions.

4.2 Jerk Parameter

In cosmology cosmic jerk parameter j, is used to describe models close to ΛCDM, which is a dimensionless quantity containing the third order derivative of the average scale factor with respect to the cosmic time. It is defined as (Chiba and Nakamura [62])

$$j(t) = \frac{1}{{H^{3} }}\frac{\dddot a}{a},$$

(23)

where a is the cosmic scale factor, H is the Hubble parameter and the dot denotes differentiation with respect to the cosmic time. In terms of the deceleration parameter can be expressed as

$$j(t) = q + 2q^{2} - \frac{{\dot{q}}}{H}.$$

(24)

4.3 Stability Factor

The stability or instability of the model depends upon the sign of $c_{s}^{2} = \frac{{dp_{\lambda } }}{{d\rho_{\lambda } }}$, where $dp_{\lambda }$ and $d\rho_{\lambda }$ are pressure and density of dark energy, respectively. The models with $c_{s}^{2} > 0$ are stable where as models with $c_{s}^{2} < 0$ are unstable.

4.4 Solutions of the Field Equations

Using Eqs. (6) and (7), we obtain

$$(q_{1} - q_{2} )(s - 1)t^{ - 2} = 0.$$

(25)

Equations (25) can be written as

$$\frac{d}{dt}\left( {\frac{{q_{1} }}{t} - \frac{{q_{2} }}{t}} \right) + \left( {\frac{{q_{1} }}{t} - \frac{{q_{2} }}{t}} \right)\frac{s}{t} = 0,$$

(26)

After mathematical manipulation, it yields

$$\frac{d}{dt}\left( {\frac{{q_{1} }}{t} - \frac{{q_{2} }}{t}} \right) + \left( {\frac{{q_{1} }}{t} - \frac{{q_{2} }}{t}} \right)\frac{{\dot{V}}}{V} = 0.$$

(27)

Integrating the above equation, we obtain

$$\frac{{q_{1} }}{{q_{2} }} = d_{1} \exp \left( {x_{1} \int {\frac{1}{V}dt} } \right),$$

(28)

where $d_{1}$ and $x_{2}$ are constants of integrations.

The metric potentials $t^{{q_{1} }} ,t^{{q_{2} }} ,t^{{q_{3} }}$ in the explicit form can be written as

$$t^{{q_{1} }} = D_{1} V^{\frac{1}{3}} \exp \left( {X_{1} \int {\frac{1}{V}dt} } \right)$$

(29)

$$t^{{q_{2} }} = D_{2} V^{\frac{1}{3}} \exp \left( {X_{2} \int {\frac{1}{V}dt} } \right),$$

(30)

$$t^{{q_{3} }} = D_{3} V^{\frac{1}{3}} \exp \left( {X_{3} \int {\frac{1}{V}dt} } \right),$$

(31)

where $D_{i} (i = 1,2,3)$ and $X_{i} (i = 1,2,3)$ satisfy the relation $D_{1}^{{}} D_{2} D_{3} = 1$ and $X_{1} + X_{2} + X_{3} = 0$.

Since field Eqs. (6)–(9) are highly nonlinear equations having five unknowns, an extra condition is needed to solve the system completely. Here two different volumetric expansion laws are used, i.e.

$$V = a_{1} t^{b}$$

(32)

and

$$V = \alpha_{1} e^{{\beta_{1} t}} ,$$

(33)

where a₁, b, $\alpha_{1} ,\beta_{1}$ are constants. In power law model given by Eq. (32), for $0 < b < 1$ the universe decelerates whereas it accelerates for $b > 1$. Accelerated volumetric expansion is exhibited by the exponential law model as expressed by Eq. (33).

5 Regime I—Model for Power Law

Using Eq. (32) in (29)-(31), the scale factors are obtained as follows

$$t^{{q_{1} }} = D_{1} a_{1}^{\frac{1}{3}} t^{\frac{b}{3}} \exp \left\{ {\frac{{X_{1} }}{{a_{1} (1 - b)}}t^{1 - b} } \right\},$$

(34)

$$t^{{q_{2} }} = D_{2} a_{1}^{\frac{1}{3}} t^{\frac{b}{3}} \exp \left\{ {\frac{{X_{2} }}{{a_{1} (1 - b)}}t^{1 - b} } \right\},$$

(35)

$$t^{{q_{3} }} = D_{3} a_{1}^{\frac{1}{3}} t^{\frac{b}{3}} \exp \left\{ {\frac{{X_{3} }}{{a_{1} (1 - b)}}t^{1 - b} } \right\},$$

(36)

where $D_{i} (i = 1,2,3)$ and $X_{i} (i = 1,2,3)$ satisfy the relation $D_{1}^{{}} D_{2} D_{3} = 1$ and $X_{1} + X_{2} + X_{3} = 0$.

We observe that the spatial volume V is zero at $t = 0$. Therefore the model starts evolving with a big-bang type singularity at $t = 0$. It can be seen that at an initial epoch $t = 0$, both the scale factors vanish [63]. The scale factors increase with increasing time. Therefore the model has an initial singularity. The mean Hubble’s parameter H, anisotropic parameter, expansion scalar, shear scalar and deceleration parameter are given by

$$H = \frac{b}{3t}.$$

(37)

$$\Delta = \frac{{3X^{2} }}{{a_{1}^{2} b^{2} t^{{2\left( {b - 1} \right)}} }}.$$

(38)

$$\theta = \frac{b}{t}.$$

(39)

$$\sigma^{2} = \frac{{X^{2} }}{{2a_{1}^{2} t^{2b} }},\;{\text{where}}\;X^{2} \; = \;2X_{1}^{2} \; + \;X_{2}^{2} \; = \;{\text{constant}}$$

(40)

$$q = \frac{3}{b} - 1.$$

(41)

At an initial stage of expansion, the Hubble parameter and shear scalar are infinitely large while with the expansion of the universe $H{\kern 1pt} {\kern 1pt} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} \sigma$ both decreases [64].The graphical confirmation of shear scalar and Hubble parameter are shown in Figs. 1and 2. Figure 3 depicts that the anisotropy parameter is also a function of cosmic time. It tends to infinite as $t \to 0$ and vanishes at $t \to \infty$[65]. From Fig. 4, we observe that when $t \to 0{\kern 1pt} {\kern 1pt} {\kern 1pt} ,\theta \to \infty$ and this indicates the inflationary scenario at early stages of the universe [66, 67]. It can be observed from the from Fig. 5 that the deceleration goes from positive to negative region independent of cosmic time t showing a signature flipping and approaches the present value $q_{0} = - 0.725$ which matches with the observed value of Cunha et.al.[68]. In recent times from the observational data, the constraints of the deceleration parameter is in the range $- 1 < q < 0$ [69, 70].The negative value of the deceleration parameter represents the present acceleration of the universe.

Fig. 1

Variation of Hubble parameter against cosmic time for $b = 2$

Fig. 2

Variation of shear scalar against cosmic time for $X = 0.5,a_{1} = 1,b = 2$

Fig. 3

Variation of anisotropic parameter against cosmic time for $X = 0.5,a_{1} = 1,b = 2$

Fig. 4

Variation of scalar expansion against cosmic time for $b = 2$

Fig. 5

Variation of deceleration parameter against b

The holographic dark energy density, EoS parameter, pressure and matter energy density are derived as

$$\rho_{\lambda } = \frac{b(\alpha b - 3\beta )}{{3t^{2} }}.$$

(42)

$$\omega_{\lambda } = \frac{2}{b} - 1.$$

(43)

$$p_{\lambda } = \frac{b(\alpha b - 3\beta )}{{3t^{2} }}\left( {\frac{2}{b} - 1} \right).$$

(44)

$$\rho_{m} = \frac{{k_{1} }}{{a_{1} t^{b} }}$$

(45)

Figure 6 depicts the variation of the Equation of State (EoS) parameter of HDE versus b. It is observed that EoS parameter of HDE is a decreasing function and converges to the negative value. By mere observation, it is clear that EoS parameter of HDE in early stages was positive (matter-dominated universe) and with the evolution of the universe passes through phantom region $w < - 1$ and approaches to $w = - 1$ in the future, which is mathematically equivalent to the cosmological constant. Thus, the early matter dominated phase later on converted to DE phase.

Fig. 6

Variation of EoS parameter of HDE against $b$

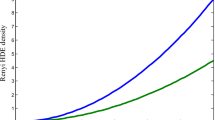
Equation (44) shows that the pressure $p$ of the universe is an increasing function of cosmic time t. At an initial epoch, the HDE pressure begins from a large negative value and tends to zero at late time for $b > 2$. The accelerated expansion of the universe is due to the fact of DE i.e. negative pressure. Thus the derived model is in good agreement with the cosmological observations in accordance with the behavior of the pressure. Figures 7 and 8 represent the behavior of energy density of HDE and matter energy density respectively versus cosmic time t. It can be seen from the graphs that HDE energy density and matter energy density decreases as the cosmic time increases. The energy densities are positive throughout the evolution of the model. The matter density parameter $\Omega_{m}$,holographic dark energy density parameter $\Omega_{\lambda }$, overall density parameter and coincidence parameter are found to be

$$\Omega_{m} = \frac{{3k_{1} t^{2 - b} }}{{a_{1} b^{2} }}$$

(46)

$$\Omega_{\lambda } = \frac{\alpha b - 3\beta }{b}.$$

(47)

$$\Omega = \Omega_{m} + \Omega_{\lambda } = \frac{{3k_{1} t^{2 - b} }}{{a_{1} b^{2} }} + \frac{\alpha b - 3\beta }{b}$$

(48)

$$\overline{r} = \frac{{\rho_{m} }}{{\rho_{\lambda } }} = \frac{{\frac{{k_{1} }}{{a_{1} t^{b} }}}}{{\frac{b(\alpha b - 3\beta )}{{3t^{2} }}}}.$$

(49)

Fig. 7

Variation of energy density of HDE against cosmic time for$,b = 2,\alpha = 2.5,\beta = 1$

Fig. 8

Variation of matter energy density against cosmic time for $k_{1} = 1,a_{1} = 1,b = 2$

Figure 9 represents the behavior of overall density parameter versus cosmic time. With the cosmic evolution, the overall density parameter decreases with cosmic time. For proper choice of the constants, the overall density parameter approaches to some constant values close to 1 which is in agreement with the observational data of the universe. The coincidence parameter is an increasing function of time t. Thus the universe is dominated by HDE at early epoch of the universe and at later the universe is dominated by matter. This result is in good accordance with the actual universe.

Fig. 9

Variation of overall density parameter against cosmic time for $\alpha = 2.5,\beta = 1,a_{1} = 1,b = 1.2$

The statefinder parameters, jerk parameter are obtained as

$$r = \frac{{9s^{2} - 9s + 2}}{2}$$

(50)

$$j(t) = \frac{{b^{2} - 9b + 18}}{{b^{2} }}$$

(51)

From Eqs. (42) and (44), it is observed that the ratio $c_{s}^{2} = \frac{{dp_{\lambda } }}{{d\rho_{\lambda } }}$ is independent of cosmic time and totally depends upon the value of b.

The behaviour of the statefinder parameters are displayed in Fig. 10.We can see that the curve passes through the point $\left\{ {r = 1,s = 0} \right\}$ which corresponds to the ΛCDM model.The jerk parameter is positive throughout the evolution of the universe as depicted in Fig. 11. This shows that the universe exhibits a smooth transition of the universe from early deceleration to the present accelerated phase which is in agreement with the present scenario and observations of modern cosmology.The stability factor is independent of cosmic time. Figure 12 gives the graphical representation of the satbility factor versus b for the proper choice of constants. The model satisfies the inequality $0 \le C_{s}^{2}$ at late time evolution of the universe so that the model do not admit superluminal fuctuations during late time [71].

Fig. 10

Variation of $r$ against $s$

Fig. 11

Variation of jerk parameter vs $b$

Fig. 12

Variation of stability factor against $b$

6 Regime II- Model for Exponential Law

Using Eq. (33) in (29)–(31), the scale factors are expressed as

$$t^{{q_{1} }} = D_{1} \alpha_{1}^{\frac{1}{3}} e^{{\frac{{\beta_{1} t}}{3}}} \exp \left\{ {\frac{{ - X_{1} }}{{\alpha_{1} \beta_{1} }}e^{{ - \beta_{1} t}} } \right\},$$

(52)

$$t^{{q_{2} }} = D_{2} \alpha_{1}^{\frac{1}{3}} e^{{\frac{{\beta_{1} t}}{3}}} \exp \left\{ {\frac{{ - X_{2} }}{{\alpha_{1} \beta_{1} }}e^{{ - \beta_{1} t}} } \right\},$$

(53)

$$t^{{q_{3} }} = D_{3} \alpha_{1}^{\frac{1}{3}} e^{{\frac{{\beta_{1} t}}{3}}} \exp \left\{ {\frac{{ - X_{3} }}{{\alpha_{1} \beta_{1} }}e^{{ - \beta_{1} t}} } \right\},$$

(54)

where $D_{i} (i = 1,2,3)$ and $X_{i} (i = 1,2,3)$ satisfy the relation $D_{1}^{{}} D_{2} D_{3} = 1$ and $X_{1} + X_{2} + X_{3} = 0$.

The spatial volume is finite at $t = 0$. It expands exponentially as t increases and becomes infinitely large as $t \to \infty$. It can be seen that the scale factor admits constant values at the time t = 0, afterwards they evolve with time without any type of singularity and finally diverge to infinity. This is consistent with the big-bang scenario [72,73,74,75]. The mean Hubble’s parameter H, anisotropic parameter, expansion scalar, shear scalar and deceleration parameter are given by

$$H = \frac{{\beta_{1} }}{3}.$$

(55)

$$\Delta = \frac{{3X^{2} e{}^{{ - 2\beta_{1} t}}}}{{\alpha_{1}^{2} \beta_{1}^{2} }}.$$

(56)

$$\theta = \beta_{1} .$$

(57)

$$\sigma^{2} = \frac{{X^{2} e^{{ - 2\beta_{1} t}} }}{{2\alpha_{1}^{2} }},\;{\text{where}}\;X^{2} \; = \;2X_{1}^{2} \; + \;X_{2}^{2} \; = \;{\text{constant}}$$

(58)

$$q = - 1.$$

(59)

The derivative of mean Hubble parameter with respect to cosmic time vanishes implies the rapid rate of expansion of universe. Thus to describe the dynamics of the late time evolution, the derived model can be considered. At an initial epoch of the universe, the anisotropy parameter of the expansion is infinite and decreases with time and ultimately becomes zero as $t \to \infty$ as shown in Fig. 13. Thus anisotropy of the fluid does not support the anisotropy of expansion. The expansion scalar $\theta$ exhibits the constant value which shows uniform exponential expansion. The behavior shown in Fig. 14 specifies that the shear scalar is the function of cosmic time. It is infinite at an initial stage $\left( {t = 0} \right)$, decreases with time, and vanishes for large value of cosmic time $\left( {t = \infty } \right)$.

Fig. 13

Variation of anisotropic parameter against cosmic time for $X = 0.5,\alpha_{1} = 1,\beta_{{}} = 2$

Fig. 14

Variation of shear scalar against cosmic time for $X = 0.5,\alpha_{1} = 1,\beta_{{}} = 2$

The universe decelerates for positive value of deceleration parameter whereas it accelerates for negative one [76]. Equation (59) indicates that the universe is accelerating which is consistent with the present day observations that universe is undergoing the accelerated expansion. In the derived model we have $\frac{dH}{{dt}} = 0 \Rightarrow q = - 1.$ The holographic dark energy density, EoS parameter, pressure and matter energy density are derived as

$$\rho_{\lambda } = \frac{{\alpha_{1} \beta_{1}^{2} }}{3}.$$

(60)

$$\omega_{\lambda } = - 1.$$

(61)

$$p_{\lambda } = - \frac{{\alpha_{1} \beta_{1}^{2} }}{3}.$$

(62)

$$\rho_{m} = \frac{{k_{2} }}{{\alpha_{1} e^{{\beta_{1} t}} }}$$

(63)

The physical behavior of holographic dark energy density is constant. It is observed that HDE pressure is negative, which is the cause of the accelerated expansion of the universe. With appropriate choices of constants and other physical parameters, the behavior of matter energy density is shown in Fig. 15.It is observed that the matter energy density decreases with time and tends to zero at $t \to \infty$.The matter density parameter $\Omega_{m}$, holographic dark energy density parameter $\Omega_{\lambda }$, overall density parameter and coincidence parameter are found to be

$$\Omega_{m} = \frac{{3k_{2} }}{{\alpha_{1} \beta_{1}^{2} e^{{\beta_{1} t}} }}$$

(64)

$$\Omega_{\lambda } = \alpha_{1} .$$

(65)

$$\Omega = \Omega_{m} + \Omega_{\lambda } = \frac{{3k_{2} }}{{\alpha_{1} \beta_{1}^{2} e^{{\beta_{1} t}} }} + \alpha_{1} .$$

(66)

$$\overline{r} = \frac{{\rho_{m} }}{{\rho_{\lambda } }} = \frac{{\frac{{k_{2} }}{{\alpha_{1} e^{{\beta_{1} t}} }}}}{{\frac{{\alpha_{1} \beta_{1}^{2} }}{3}}}.$$

(67)

Fig. 15

Variation of matter energy density against cosmic time for $k_{2} = 0.5,\alpha_{1} = 1,\beta_{{}} = 2$

The overall density parameter approaches to 1, as depicted in Fig. 16, which describes the flatness of universe and confirms the present cosmological data of the universe.

Fig. 16

Variation of overall density parameter against cosmic time for $k_{2} = 0.5,\alpha_{1} = 1,\beta_{{}} = 2$

It is clear that the coincidence parameter is the decreasing function of time. It is very large at the early epoch of the universe but decreases monotonically at later time. Hence this universe is dominated by matter at early stages of the universe.

The statefinder parameters and jerk parameter are found as

$$r\; = \;1\;{\text{and}}\;s\; = \;0$$

(68)

$$j(t) = 1$$

(69)

For $r \to \infty {\kern 1pt} {\kern 1pt} ,{\kern 1pt} {\kern 1pt} s \to - \infty$, the universe starts from an asymptotic Einstein static era and for $\left( {r = 1{\kern 1pt} {\kern 1pt} ,{\kern 1pt} {\kern 1pt} s = 0} \right)$ goes to the Λ CDM model and a fixed newton’s gravitational constant. The cold dark matter model containing no radiation is represented for $\left( {r = 1{\kern 1pt} {\kern 1pt} ,{\kern 1pt} {\kern 1pt} s = 1} \right)$. Equation (68) is similar to the $\Lambda$ CDM cosmological model for which the statefinder parameters are $\left\{ {r,s} \right\} = \left\{ {1,0} \right\}$.

The jerk parameter which is equal to 1 indicates a flat LCDM model.

7 Discussion and Concluding Remarks

In this article, we have studied the Bianchi type-I (Kasner form) universe in $f(R,T)$ gravity in presence of matter and holographic dark energy. Here, we have discussed two models namely power law model and exponential law model. The observations obtained from these two models are presented below:

8 Regime I—Power Law Volume Expansion Model

The model starts evolving with a big-bang type singularity at $t = 0$.The expansion scalar, shear scalar and the Hubble parameter are infinite at time $t = 0$ and for large values of t they tend to zero. The deceleration goes from positive to negative region independent of cosmic time t and approaches the present value $q_{0} = - 0.725$. The model changes its evolution from early decelerated phase to present accelerating phase, which is in good agreement with recent observational data. HDE energy density and matter energy density decrease as the cosmic time increases. The model would give an empty space for large time.The jerk parameter is positive throughout the evolution of the universe. The temporal evolution of jerk parameter where the positivity of jerk parameter ensures an accelerated expansion. The EoS parameter for our model assumes values close to -1 at present epoch which is in remarkable agreement with the latest Planck measurements [77].

9 Regime II—Exponential Volume Expansion Law Model

The scale factor admits constant values at the time t = 0, afterwards they evolve with time without any type of singularity and finally diverge to infinity. This is consistent with the big-bang scenario.q = -1 indicates that the universe is accelerating which is consistent with the present day observations that universe is undergoing the accelerated [78,79,80]. For this model $q = - 1$ and $\frac{dH}{{dt}} = 0$, which implies the greatest values of the Hubble parameter and the fastest rate of expansion of the universe. Thus, this model may represent the inflationary era in the early universe and the very late time of the universe.It is observed that the matter energy density decreases with time and then tends to zero at $t \to \infty$[81]. We observe that the jerk parameter is positive throughout the evolution and is finally equal to one. It follows that our models are consistent with recent observations. It is assumed that the accelerated expansion of the universe is due to some kind of energy matter with negative pressure known as dark energy. Hence, the nature of pressure in our model is in a good agreement with the current observation. The overall density parameter approaches to 1 which describes the flatness of universe and confirms the present cosmological data of the universe. It is interesting to observe that the holographic dark energy EoS parameter behaves like cosmological constant, this is mathematically equivalent to cosmological constant which is a suitable candidate to represent the behavior of DE in the derived model at late times and resembles with the values obtained for holographic dark energy [82,83,84,85,86,87].This work can be extended to the other two classes of $f(R,T)$ gravity and also the other modified theories of gravity.