1 Introduction

In decision making processes, ranking constitutes a crucial step for choosing among alternatives after their evaluation. In multi-attribute decision making (MADM) problems we have n alternatives which are assessed against m criteria. The evaluations that result from these assessments provide the final ranking values of the alternatives, so that the alternative with the highest ranking value is usually considered as the best of the alternatives, that is, the one with best performance.

Rankings have experienced an increasing popularity. An example of this can be found in Higher Education with the university rankings or league tables. Most visible international rankings are The Academic Ranking of World Universities (ARWU) by Shanghai Jiao Tung University, commonly known as the Shanghai index and the World University Ranking by Times Higher Education (THESQS). As has been widely acknowledged in the related literature, university rankings are controversial but influential. Despite their limitations, university rankings have some effect on decision making regarding higher education institutions: on the choice of a convenient place by students, on recruitment decisions by employers, on university policies, motivating the competitiveness among them, etc. See Witte and Hudrlikova (2013) for a discussion.

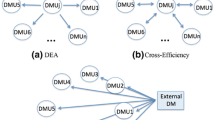
In this paper we are concerned with the assessment of performance of DMUs involved in production processes. Specifically, the focus is on the evaluation of their relative efficiency in the use of several inputs to produce several outputs by means of DEA models. DEA provides efficiency scores in the form of the classical ratios of a weighted sum of outputs to a weighted sum of inputs. One of the key issues of this methodology lies in the fact that the individual circumstances of the DMUs (there are often considerable variations in goals, policies, etc., among units) can be considered in the analysis through a DMU-specific assignment of input and output weights. Specifically, the DEA efficiency scores provide a self-evaluation of DMUs based on the inputs and output weights that show them in their best possible light. However, this attractive feature of DEA may become a problem if we are interested in ranking the DMUs. Since the DMUs are evaluated with DMU-specific weights, which means that the importance attached to each of the inputs and outputs often varies depending on the unit that is being evaluated, it has been widely claimed in the literature that the DEA efficiency scores cannot be used for purposes of ranking DMUs (see, e.g., Cooper and Tone 1997; Sinuany-Stern and Friedman 1998; Kao and Hung 2005; Ramón et al. 2010 for discussions).

Cross-efficiency evaluation, as introduced in Sexton et al. (1986) and Doyle and Green (1994), arose as an extension of DEA aimed at ranking DMUs. The idea behind the cross-efficiency evaluation is to apply one DMU’s perspective to others, by using its DEA weights in the evaluations. That is, the efficiency of each unit is assessed with the weights of all the DMUs instead of with only its own weights. Each of these assessments, which are called the cross-efficiencies, is defined as the classical efficiency ratio of a weighted sum of outputs to a weighted sum of inputs. Eventually, the cross-efficiency score of a given unit is calculated as the average of the cross-efficiencies of such unit obtained with the weights of all the DMUs. Cross-efficiency evaluation provides thus a peer-evaluation of the DMUs, instead of a self-evaluation, which makes it possible to derive an ordering. We highlight the parallelism between the cross-efficiency evaluation and MADM problems. Cross-efficiency evaluation can be seen as a MADM problem in which the DMUs are the alternatives and the DEA weights of each of them act as the criteria used in the evaluations.

The literature has emphasized the following two as the principal advantages of the cross-efficiency evaluation (see, for example, Anderson et al. 2002): (1) it provides an ordering of the DMUs and (2) it eliminates unrealistic weighting schemes without requiring the elicitation of weight restrictions. Doyle and Green (1994) have also highlighted the interpretation of the cross-efficiency evaluation as peer-appraisal. As a result, these authors suggest that cross-efficiency evaluation has less of the arbitrariness of additional constraints and has more of the right connotations of a democratic process, as opposed to authoritarianism (externally imposed weights) or egoism (self-appraisal, DEA).

Cross-efficiency evaluation has received much attention in the related literature. In fact, “cross-efficiency evaluation and ranking” is identified as one of the four research fronts in DEA in the study carried out by Liu et al. (2016), which applies a network clustering method in order to group the DEA literature over the period 2000 to 2014. We also note that this methodology has been widely applied for ranking performance of DMUs in many different contexts. See, among others, the applications in Oral et al. (1991) to R&D projects, in Green et al. (1996) to preference voting, in Chen (2002) to the electricity distribution sector, in Lu and Lo (2007) to economic-environmental performance, in Ruiz et al. (2013) and Gutiérrez and Ruiz (2013) to sport, and in Lim et al. (2014) to portfolio selection.

Since the seminal article by Charnes et al. (1978), DEA has been progressively enhanced with numerous extensions of the basic methodology. In many cases, these were intended to address the problems and needs that arose in its use in practice. In particular, DEA was initially developed to be used with crisp data. Nevertheless, several fuzzy formulations of the classical DEA models have been proposed in order to deal with imprecise data (see Kao and Liu 2000; Guo and Tanaka 2001; León et al. 2003; Lertworasirikul et al. 2003a, b). What is more, some of the DEA enhancements above mentioned have in turn been extended to fuzzy approaches. For example, see the fuzzy approaches in Liu and Chuang (2009) to DEA/AR models, in Zerafat Angiz et al. (2010) to non-radial models or Lozano (2014) to network DEA. See Hatami-Marbini et al. (2011) and Emrouznejad et al. (2014) for a couple of updated reviews of Fuzzy Data Envelopment Analysis (FDEA) methods.

In this paper, we propose a fuzzy cross-efficiency evaluation to be used in the case of having inputs and/or outputs which are fuzzy numbers. This issue has been previously addressed in Sirvent and León (2014) in the related literature. Sirvent and León (2014) point out that rankings of DMUs based on the ordering of fuzzy efficiencies can be criticized for the same reasons as those resulting from crisp DEA efficiency scores, which justifies the need of a fuzzy cross-efficiency evaluation. They also claim that, unlike in crisp DEA, it is not possible to set out a general approach to the cross-efficiency evaluation in FDEA because there exist many different definitions of efficiency in FDEA. Thus, each fuzzy approach to the cross-efficiency evaluation will depend on the specific features of the FDEA model used for the measurement of efficiency.

The fuzzy cross-efficiency evaluation in Sirvent and León (2014) is based on the fuzzy DEA model by Guo and Tanaka (2001). This model is developed for symmetrical triangular fuzzy inputs and outputs, and follows the fuzzy ranking approach to solve fuzzy linear programming problems. For a given possibility level h in between 0 and 1 pre-specified by the decision-maker, it provides an efficiency score which is a non-symmetrical triangular fuzzy number. Sirvent and León select this FDEA model because it defines fuzzy efficiency in a ratio form in terms of input and output weights, so the cross-efficiencies can be defined analogously. Thus, the fuzzy cross-efficiency evaluation is consistent with the DEA efficiency assessment in the sense that the cross-efficiency of a given DMU calculated with its own input and output weights coincides with its fuzzy DEA efficiency score.

We propose here a fuzzy cross-efficiency evaluation based on the fuzzy DEA model in Lertworasirikul et al. (2003a). This efficiency model is developed for the more general case of fuzzy inputs and outputs being normal and convex, and is solved by following a possibility approach in which fuzzy constraints are treated as fuzzy events. By using possibility measures and specifying the corresponding acceptable levels of possibility for the constraints, the resulting FDEA model is transformed into a possibility linear programming problem, which provides a possibilistic efficiency score for every DMU at the pre-specified possibility levels. We prove some results that allow us to define the fuzzy cross-efficiencies in a ratio form by using the input and output weights provided by this fuzzy efficiency model, so the fuzzy cross-efficiency evaluation is also consistent with the original fuzzy efficiency measurement. The ranking of DMUs results thus from the ordering of the cross-efficiency scores, which are real numbers for a given possibility level. In Sirvent and León (2014) the cross-efficiency scores for each possibility level are triangular fuzzy numbers, so a method for ranking fuzzy numbers is needed in order to derive an ordering.

The existence of alternate optima for the weights in the DEA models is the main difficulty with the cross-efficiency evaluation, because the cross-efficiency scores and the rankings of units may change depending on the used weights. In order to deal with this issue, we develop both a benevolent and an aggressive fuzzy formulation which are aimed at making a choice of weights among the alternate optima, if any, of the FDEA model by Lertworasirikul et al.

The paper unfolds as follows: In Sect. 2 we briefly describe the standard (crisp) cross-efficiency evaluation methodology. In Sect. 3 we propose a fuzzy cross-efficiency evaluation based on the fuzzy DEA model in Lertworasirikul et al. (2003a) above mentioned. Section 4 extends to the context of the fuzzy cross-efficiency evaluation in this paper the crisp benevolent and aggressive approaches to the choice of weights. The examples in Sect. 5 illustrate the proposal that is made. Last section concludes.

2 Data envelopment analysis and cross-efficiency evaluation

Throughout the paper we assume that we have n DMUs that use m inputs to produce s outputs. These can be described by means of the vectors (\(\hbox {X}_\mathrm{j},\hbox \mathrm{Y}_{j}), \hbox {j}=1,{\ldots },\hbox {n}\). For the calculation of cross-efficiencies, the standard cross-efficiency evaluation uses the weights provided by the CCR DEA model for each DMU. Thus, the input and output weights are the optimal solutions of the following problem, which yields the efficiency score of a given DMU\(_{0}\)

$$\begin{aligned} {\begin{array}{lll} {\hbox {Max}}&{} \quad {\uptheta _0 =\frac{{\hbox {u}^{\prime }}\hbox {Y}_0 }{{\hbox {v}^{\prime }}\hbox {X}_0 }}&{} \\ {\hbox {s.t.:}}&{} \quad {\frac{{\hbox {u}^{\prime }}\hbox {Y}_\mathrm{j} }{{\hbox {v}^{\prime }}\hbox {X}_\mathrm{j} }\le 1\hbox { }}&{} {\hbox {j}=1,\ldots ,\hbox {n}} \\ &{}\quad {\hbox {v}\ge 0_\mathrm{m} ,\;\hbox {u}\ge 0_\mathrm{s} }&{} \\ \end{array} } \end{aligned}$$
(1)

This is the CCR model in its ratio form. By using the results on linear fractional programming in Charnes and Cooper (1962), (1) can be converted into the following linear problem (which is the so-called dual multiplier formulation)

$$\begin{aligned} {\begin{array}{ll} {\hbox {Max}}&{} \quad {\uptheta _0 ={\hbox {u}^{\prime }}\hbox {Y}_0 } \\ {\hbox {s.t.:}}&{} \quad {{\hbox {v}^{\prime }}\hbox {X}_0 =1} \\ &{} {-{\hbox {v}^{\prime }}\hbox {X}_\mathrm{j} +{\hbox {u}^{\prime }}\hbox {Y}_\mathrm{j} \le 0}\quad {\hbox {j}=1,\ldots ,\hbox {n}} \\ &{}\quad {\hbox {v}\ge 0_\mathrm{m},\;\hbox {u}\ge 0_\mathrm{s}} \\ \end{array} } \end{aligned}$$
(2)

In standard cross-efficiency evaluations we use the optimal solutions of (2) to calculate the cross-efficiencies. To be specific, if \((\hbox {v}_\mathrm{d} ,\hbox {u}_\mathrm{d} )\) is an optimal solution of (2) for a given DMU\(_\mathrm{d}\), then the cross-efficiency of DMU\(_\mathrm{j}\), \(\hbox {j}=1,{\ldots },\hbox {n}\), obtained with the weights of DMU\(_\mathrm{d}\) is the following

$$\begin{aligned} \hbox {E}_{\mathrm{dj}} =\frac{\hbox {u}_\mathrm{d} ^{\prime }\hbox {Y}_\mathrm{j} }{\hbox {v}_\mathrm{d} ^{\prime }\hbox {X}_\mathrm{j} } \end{aligned}$$
(3)

Then, the cross-efficiency score of DMU\(_\mathrm{j}\), \(\hbox {j}=1,{\ldots },\hbox {n}\), is usually defined as the average of its cross-efficiencies obtained with the weights of all the DMUs. That is, the cross-efficiency score of DMU\(_\mathrm{j}\) is defined as

$$\begin{aligned} \bar{{\hbox {E}}}_\mathrm{j} =\frac{1}{\hbox {n}}{\mathop {\sum }\limits _{\mathrm{d}=1}^\mathrm{n}} \hbox {E}_{\mathrm{dj}} , \quad \hbox {j}=1,\ldots ,\hbox {n}. \end{aligned}$$
(4)

The cross-efficiency score \(\bar{{\hbox {E}}}_\mathrm{j} \) provides a peer-evaluation of DMU\(_\mathrm{j}\), and these values can be used for ranking the DMUs.

It should be noted that the main difficulty with the cross-efficiency evaluation is the possible existence of alternate optima for the DEA weights in (2), which may lead to different cross-efficiency scores, and consequently to different rankings of units, depending on the choice of weights that each DMU makes. As a potential remedy, it has been suggested the use of alternative secondary goals to the choice of weights among the alternate optima. Examples of this approach are the well-known benevolent and aggressive formulations (Doyle and Green 1994) below, which seek to find the optimal weights that maximize/minimize the efficiency of the other DMUs while maintaining that of the DMU under evaluation (see Liang et al. 2008; Wang and Chin 2010 for other proposals)

$$\begin{aligned} {\begin{array}{lll} {\hbox {Max/Min}} &{} \;{{\hbox {u}^{\prime }}{\mathop {\sum }\limits _{\mathrm{j}\ne \mathrm{d}}} {\hbox {Y}_\mathrm{j}}} &{} \\ {\hbox {s.t.:}} &{} {{\begin{array}{l} {{\hbox {v}^{\prime }}{\mathop {\sum }\limits _{\mathrm{j}\ne \mathrm{d}}} {\hbox {X}_\mathrm{j}} =1} \\ \end{array} }} &{} \\ &{} {-\uptheta _\mathrm{d} {\hbox {v}^{\prime }}\hbox {X}_\mathrm{d} +{\hbox {u}^{\prime }}\hbox {Y}_\mathrm{d} =0} &{} \\ &{} {-{\hbox {v}^{\prime }}\hbox {X}_\mathrm{j} +{\hbox {u}^{\prime }}\hbox {Y}_\mathrm{j} \le 0} &{} {\hbox {j}=1,\ldots ,\hbox {n},\;\hbox {j}\ne \hbox {d}} \\ &{} {\hbox {v}\ge 0_\mathrm{m} ,\;\hbox {u}\ge 0_\mathrm{s} } &{} \\ \end{array} } \end{aligned}$$
(5)

where \(\uptheta _\mathrm{d} \) is the optimal value of problem (2) when evaluating DMU\(_\mathrm{d}\).

3 Possibility cross-efficiency evaluation

As can be seen from Sect. 2, in order to carry out a cross-efficiency evaluation, we first need a DEA formulation, which yields a self-evaluation of the efficiency of each DMU through weights that show it in its best possible light, and then define the cross-efficiencies with those DEA DMU-specific weights, in order to provide evaluations of the different units from the point of view of that DMU’s performance. We develop here a cross-efficiency evaluation to be used when fuzzy inputs and outputs are considered. Specifically, the proposal that is made is developed in the context of the possibility approach followed by Lertworasirikul et al. (2003a) to measure efficiency with DEA. Thus, we start with the following possibility linear programming problem which evaluates the efficiency of a given DMU\(_{0}\)

$$\begin{aligned} {\begin{array}{ll} {(\hbox {PCCR})} &{}\quad {\hbox {Max}} \qquad {\bar{{\hbox {f}}}_0 } \\ &{}\quad {\hbox {s.t.:}} \qquad {\uppi ({\hbox {u}^{\prime }}\tilde{\hbox {Y}}_0 \ge \bar{{\hbox {f}}}_0 )\ge \upbeta } \\ &{}\qquad \qquad \quad {\uppi ({\hbox {v}^{\prime }}\tilde{\hbox {X}}_0 =1)\ge \upgamma } \\ &{}\qquad \qquad \quad {\uppi (-{\hbox {v}^{\prime }}\tilde{\hbox {X}}_\mathrm{j} +{\hbox {u}^{\prime }}\tilde{\hbox {Y}}_\mathrm{j} \le 0)\ge \upalpha _\mathrm{j} }\quad {\hbox {j}=1,\ldots ,\hbox {n}} \\ &{}\qquad \qquad \quad {\hbox {v}\ge 0_\mathrm{m} ,\hbox {u}\ge 0_\mathrm{s} } \\ \end{array} } \end{aligned}$$
(6)

where \(\tilde{\hbox {X}}_\mathrm{j} \) and \(\tilde{\hbox {Y}}_\mathrm{j}\) represent the vectors of fuzzy inputs and fuzzy outputs of each DMU\(_\mathrm{j}\), \(\hbox {j}=1,{\ldots },\hbox {n}\), \(\upbeta , \upgamma , \upalpha _{1},\ldots , \upalpha _\mathrm{n} \in \) [0,1] are pre-specified acceptable levels of possibility for the objective and the constraints, respectively, and \(\uppi (A)\) denotes the possibility of the fuzzy event A. We can see in (6) that Lertworasirikul et al. (2003a) deal with the uncertainty in both the fuzzy objective and the fuzzy constraints of the fuzzy version of model (2) by using possibility measures and specifying the corresponding acceptable levels of possibility.

As in the crisp case, the optimal value \(\bar{{\hbox {f}}}_0 \) of \({\hbox {u}^{\prime }}\tilde{\hbox {Y}}_0 \) is used here to determine if the DMU\(_{0}\) under assessment is efficient in the possibilistic sense at a given possibility level. Let \(\upalpha ^{\prime }\) be the set of \(\upbeta , \upgamma , \upalpha _{1},\ldots ,\upalpha _\mathrm{n}\), then:

Definition 1

A given DMU\(_{0}\) is said to be \(\upalpha ^{\prime }\)-possibilistic efficient if, and only if, \(\bar{{\hbox {f}}}_0 \) is larger than or equal to 1 at the \(\upalpha ^{\prime }\) possibility level; otherwise, DMU\(_{0}\) is \(\upalpha ^{\prime }\)-possibilistic inefficient.

To make comprehensive efficiency comparisons among DMUs in terms of the values \(\bar{{\hbox {f}}}^{\prime }\mathrm{s}\), we should consider the same set \(\upalpha ^{\prime }\) for all the DMUs.

Throughout this section we assume fuzzy inputs and fuzzy outputs being normal and convex. In that case, Lertworasirikul et al. show that model PCCR can be solved by considering

$$\begin{aligned} {\begin{array}{ll} {(\hbox {PCCR1})} &{}\quad {\hbox {Max}} \qquad {\bar{{\hbox {f}}}_0 } \\ &{}\quad {\hbox {s.t.:}} \qquad {({\hbox {u}^{\prime }}\tilde{\hbox {Y}}_0 )_\upbeta ^\mathrm{U} \ge \bar{{\hbox {f}}}_0 } \\ &{}\qquad \qquad \quad {({\hbox {v}^{\prime }}\tilde{\hbox {X}}_0 )_\upgamma ^\mathrm{U} \ge 1} \\ &{}\qquad \qquad \quad {({\hbox {v}^{\prime }}\tilde{\hbox {X}}_0 )_\upgamma ^\mathrm{L} \le 1} \\ &{}\qquad \qquad \quad {(-{\hbox {v}^{\prime }}\tilde{\hbox {X}}_\mathrm{j} +{\hbox {u}^{\prime }}\tilde{\hbox {Y}}_\mathrm{j} )_{\upalpha _\mathrm{j} }^\mathrm{L} \le 0} \quad \,{\hbox {j}=1,\ldots ,\hbox {n}} \\ &{}\qquad \qquad \quad {\hbox {v}\ge 0_\mathrm{m} ,\;\hbox {u}\ge 0_\mathrm{s} } \end{array} } \end{aligned}$$
(7)

where \(({\hbox {u}^{\prime }}\tilde{\hbox {Y}}_0 )_\upbeta ^\mathrm{U} \) denotes the upper bound of the \(\upbeta \)-level set of \({\hbox {u}^{\prime }}\tilde{\hbox {Y}}_0 , ({\hbox {v}^{\prime }}\tilde{\hbox {X}}_0 )_\upgamma ^\mathrm{U} \) and \(({\hbox {v}^{\prime }}\tilde{\hbox {X}}_0 )_\upgamma ^\mathrm{L} \) denote the upper and lower bounds of the \(\upgamma \)-level set of \({\hbox {v}^{\prime }}\tilde{\hbox {X}}_0 \), respectively, and \((-{\hbox {v}^{\prime }}\tilde{\hbox {X}}_\mathrm{j} +{\hbox {u}^{\prime }}\tilde{\hbox {Y}}_\mathrm{j} )_{\upalpha _\mathrm{j} }^\mathrm{L} \) the lower bound of the \(\upalpha _\mathrm{j}\)-level set of \(-{\hbox {v}^{\prime }}\tilde{\hbox {X}}_\mathrm{j} +{\hbox {u}^{\prime }}\tilde{\hbox {Y}}_\mathrm{j} , \hbox {j}=1,\ldots ,\hbox {n}\) (see the original paper for more details).

Once we have chosen the model that establishes the fuzzy DEA framework of the proposed approach, the key issue is therefore in how to define the cross-efficiencies, that is, the efficiencies of the different units obtained with the DEA weights that PCCR1 provides for each DMU. In the standard crisp cross-efficiency evaluation, we can use the optimal weights of (2) in order to define the cross-efficiencies as a ratio of a weighted sum of outputs to a weighted sum of inputs, because the efficiency score of DMU\(_{0}\) provided by that model can be expressed in a ratio form \(\uptheta _0 ={{\hbox {u}^{\prime }}\hbox {Y}_0 }/{{\hbox {v}^{\prime }}\hbox {X}_0 ,}\) as a result of the normalization constraint, \({\hbox {v}^{\prime }}\hbox {X}_0 =1\). However, the possibilistic efficiency score \(\bar{{\hbox {f}}}_0 \) provided by model PCCR1 is not directly expressed as a ratio and, in addition, the constraint of normalization involves two restrictions in this fuzzy model, \(({\hbox {v}^{\prime }}\tilde{\hbox {X}}_0 )_\upgamma ^\mathrm{U} \ge 1\) and \(({\hbox {v}^{\prime }}\tilde{\hbox {X}}_0 )_\upgamma ^\mathrm{L} \le 1\).

The following two lemmas provide some keys that will allow us to give a definition of consistent cross-efficiencies in the context of an efficiency measurement carried out with PCCR1:

Lemma 1

Let \((\bar{{\hbox {f}}}_0 ,\hbox {v},\hbox {u})\) be an optimal solution of model PCCR1 for a given DMU\(_{0}\), then \(({\hbox {v}^{\prime }}\tilde{\hbox {X}}_0 )_\upgamma ^\mathrm{L} =1\) holds.

Proof

By contradiction, suppose that \(({\hbox {v}^{\prime }}\tilde{\hbox {X}}_0 )_\upgamma ^\mathrm{L} =\hbox {k}<1\).

Let us define: \(\hat{{\hbox {v}}}=\frac{\hbox {v}}{\hbox {k}},\;\hat{{\hbox {u}}}=\frac{\hbox {u}}{\hbox {k}}\) and \(\hat{{\hbox {f}}}_0 =(\hat{{{\hbox {u}^{\prime }}}}\tilde{\hbox {Y}}_0 )_\upbeta ^\mathrm{U} \). Then, \((\hat{{\hbox {f}}}_0 ,\hat{{\hbox {v}}},\hat{{\hbox {u}}})\) is a feasible solution of PCCR1 since:

$$\begin{aligned} ({\hat{\hbox {v}}^{\prime }}\tilde{\hbox {X}}_0 )_\upgamma ^\mathrm{U}= & {} \frac{({\hbox {v}^{\prime }}\tilde{\hbox {X}}_0 )_\upgamma ^\mathrm{U} }{\hbox {k}}\ge \frac{1}{\hbox {k}}>1,\\ ({\hat{\hbox {v}}^{\prime }}\tilde{\hbox {X}}_0 )_\upgamma ^\mathrm{L}= & {} \frac{({\hbox {v}^{\prime }}\tilde{\hbox {X}}_0 )_\upgamma ^\mathrm{L} }{\hbox {k}}=1, \hbox {and}\\ (-{\hat{\hbox {v}}^{\prime }}\tilde{\hbox {X}}_\mathrm{j} +{\hat{\hbox {u}}^{\prime }}\tilde{\hbox {Y}}_\mathrm{j} )_{\upalpha _\mathrm{j} }^\mathrm{L}= & {} \frac{(-{\hbox {v}^{\prime }}\tilde{\hbox {X}}_\mathrm{j} +{\hbox {u}^{\prime }}\tilde{\hbox {Y}}_\mathrm{j} )_{\upalpha _\mathrm{j} }^\mathrm{L} }{\hbox {k}}\le 0, \hbox {j}=1,\ldots ,\hbox {n}. \end{aligned}$$

In addition, it satisfies \(\hat{{\hbox {f}}}_0 =(\hat{{{\hbox {u}^{\prime }}}}\tilde{\hbox {Y}}_0 )_\upbeta ^\mathrm{U} =\frac{({\hbox {u}^{\prime }}\tilde{\hbox {Y}}_0 )_\upbeta ^\mathrm{U} }{\hbox {k}}\ge \frac{\bar{{\hbox {f}}}_0 }{\hbox {k}}>\bar{{\hbox {f}}}_0 \), which contradicts the optimality of \((\bar{{\hbox {f}}}_0 ,\hbox {v},\hbox {u})\). Therefore, \(({\hbox {v}^{\prime }}\tilde{\hbox {X}}_0 )_\upgamma ^\mathrm{L} =1\).\(\square \)

Lemma 2

Let \((\bar{{\hbox {f}}}_0 ,\hbox {v},\hbox {u})\) be an optimal solution of model PCCR1 for a given DMU\(_{0}\), then \(\bar{{\hbox {f}}}_0 =({\hbox {u}^{\prime }}\tilde{\hbox {Y}}_0 )_\upbeta ^\mathrm{U}\) holds.

Proof

By contradiction, suppose that \(\bar{{\hbox {f}}}_0<({\hbox {u}^{\prime }}\tilde{\hbox {Y}}_0 )_\upbeta ^\mathrm{U} \). Then, \((\hat{{\hbox {f}}}_0 ,\hbox {v},\hbox {u})\) with \(\hat{{\hbox {f}}}_0 =({\hbox {u}^{\prime }}\tilde{\hbox {Y}}_0 )_\upbeta ^\mathrm{U} \), is a feasible solution of PCCR1 satisfying \(\hat{{\hbox {f}}}_0 >\bar{{\hbox {f}}}_0 \), which contradicts the optimality of \((\bar{{\hbox {f}}}_0 ,\hbox {v},\hbox {u})\). Therefore, \(\bar{{\hbox {f}}}_0 =({\hbox {u}^{\prime }}\tilde{\hbox {Y}}_0 )_\upbeta ^\mathrm{U} \). \(\square \)

The two previous lemmas show that the first and third constraints of model PCCR1 are binding at the optimum. Therefore, the possibilistic efficiency score \(\bar{{\hbox {f}}}_0\) of DMU\(_{0}\) is actually a ratio, which is an important result we enunciate in the following proposition:

Proposition 1

$$\begin{aligned} \bar{{\hbox {f}}}_0 =\frac{({\hbox {u}^{\prime }}\tilde{\hbox {Y}}_0 )_\upbeta ^\mathrm{U} }{({\hbox {v}^{\prime }}\tilde{\hbox {X}}_0 )_\upgamma ^\mathrm{L}} \end{aligned}$$
(8)

Taking into account this result, we define the possibilistic cross-efficiencies and the possibilistic cross-efficiency scores as follows:

Definition 2

If \((\bar{{\hbox {f}}}_\mathrm{d} ,\hbox {v}_\mathrm{d} ,\hbox {u}_\mathrm{d} )\) is an optimal solution of model PCCR1 for a given DMU\(_\mathrm{d}\) at the possibility level \(\upalpha ^{\prime }=(\upbeta ,\upgamma ,\upalpha _1 ,\ldots ,\upalpha _\mathrm{n} )\), then the possibilistic cross-efficiency of DMU\(_\mathrm{j}, \hbox {j}=1,{\ldots },\hbox {n}\), at the possibility level \(\upalpha ^{\prime }\), obtained with the weights of DMU\(_\mathrm{d}\), is defined as the ratio:

$$\begin{aligned} \hbox {E}_{\mathrm{dj}}^\mathrm{P} =\frac{({\hbox {u}^{\prime }}_\mathrm{d} \tilde{\hbox {Y}}_\mathrm{j} )_\upbeta ^\mathrm{U} }{({\hbox {v}^{\prime }}_\mathrm{d} \tilde{\hbox {X}}_\mathrm{j} )_\upgamma ^\mathrm{L}} \end{aligned}$$
(9)

Definition 3

Let \(\hbox {E}_{\mathrm{dj}}^\mathrm{P}, \hbox {d}=1,{\ldots },\hbox {n}\), be the cross-efficiencies of a given DMU\(_\mathrm{j}\) at the possibility level \(\upalpha ^{\prime }=(\upbeta ,\upgamma ,\upalpha _1,\ldots ,\upalpha _\mathrm{n} )\), then the possibilistic cross-efficiency score of DMU\(_\mathrm{j}\), \(\hbox {j}=1,{\ldots },\hbox {n}\), at the possibility level \(\upalpha ^{\prime }\), is defined as

$$\begin{aligned} {\bar{\hbox {E}}}_\mathrm{j}^\mathrm{P} =\frac{1}{\mathrm{n}}\sum _{\mathrm{d}=1}^{\mathrm{n}} \hbox {E}_{\mathrm{dj}}^{\mathrm{P}} ,\quad \hbox {j}=1,\ldots ,\hbox {n}. \end{aligned}$$
(10)

Note in Definition 3 that in order to make a comprehensive aggregation of possibilistic cross-efficiencies when defining the possibilistic cross-efficiency score of a given DMU\(_\mathrm{j}\), the involved possibilistic cross-efficiencies are required to be calculated all at the same possibility level \(\upalpha ^{\prime }=(\upbeta ,\upgamma ,\upalpha _1,\ldots ,\upalpha _\mathrm{n} )\). The possibilistic cross-efficiency scores \(\bar{{\hbox {E}}}_\mathrm{j}^\mathrm{P} ,\hbox {j}=1,\ldots ,\hbox {n},\) provide a peer-evaluation of units and can be used to rank the DMUs. Note that, for a given possibility level, these cross-efficiency scores are real numbers, while those in Sirvent and León (2014) are triangular fuzzy numbers. As a result, rankings of DMUs at a given possibility level with our approach involve the ordering of real numbers, while in Sirvent and León (2014) a method for ranking fuzzy numbers must be chosen to that end.

In the following two propositions we enunciate a couple of suitable properties of the proposed possibilistic approach to the fuzzy cross-efficiency evaluation, which mimic what actually happens in the standard crisp cross-efficiency evaluation.

Proposition 2

For every DMU\(_\mathrm{d}, \hbox {d}=1,{\ldots },\hbox {n}, \hbox {E}_{\mathrm{dd}} =\bar{{\hbox {f}}}_\mathrm{d} \), at any possibility level.

That is, the proposed cross-efficiency evaluation is consistent with the efficiency measurement provided by PCCR1. The notion of “consistency” in cross-efficiency evaluations is introduced in this paper as a desirable property that requires the cross-efficiency of each unit calculated with its own DEA weights to coincide with its DEA self-evaluation. It seems reasonable that when evaluating a DMU from its own perspective this unit is rated with the efficiency score provided by the model used as the basis for the cross-efficiency evaluation. For example, the standard crisp cross-efficiency evaluation, which is performed on the basis of model (2) and where the cross-efficiencies are calculated as in (3), is consistent, because \(\uptheta _\mathrm{d}^{*} =\hbox {E}_{\mathrm{dd}} , \hbox {d}=1,{\ldots },\hbox {n}\).

Proposition 3

For every DMU\(_\mathrm{j}, \hbox {j}=1,{\ldots },\hbox {n}, \bar{{\hbox {E}}}_\mathrm{j} \le \bar{{\hbox {f}}}_\mathrm{j}\), at any possibility level.

That is, the possibilistic cross-efficiency scores cannot be larger than the corresponding possibilistic DEA efficiency scores (self-evaluations), which is consistent with the idea that DEA, even in this possibility approach, shows the DMU under assessment in the best possible light.

4 Alternative secondary goals

As mentioned in Sect. 2, the possible existence of alternate optima for the weights when solving the CCR model is the main difficulty with cross-efficiency evaluations, because this may lead to different cross-efficiency scores, and consequently to different rankings, depending on the choice of weights that is made. Following the same approach as in the crisp case, which is based on the choice of DEA weights among alternate optima by using some alternative secondary goal, we develop here a couple of fuzzy formulations which are aimed at making a choice of weights among the alternative optimal solutions of PCCR1, if any. Specifically, we extend to the fuzzy context the well-known benevolent and aggressive formulations (5) proposed in Doyle and Green (1994).

The benevolent formulation by Doyle and Green (1994) selects weights that maintain the self-efficiency score of the unit under assessment while enhancing the efficiency of the “composite” DMU created by aggregating the inputs and outputs of the remaining n-1 units. Likewise, the aggressive formulation also maintains the self-efficiency score while diminishing the efficiency of the composite DMU. In the fuzzy context of the possibility approach by Lertworasirikul et al., we propose the following fuzzy benevolent formulation, which selects the input and output weights of a given DMU\(_\mathrm{d}\) to be used in the calculation of the cross-efficiencies (9) at the possibility level \(\upalpha ^{\prime }=(\upbeta ,\upgamma ,\upalpha _1 ,\ldots ,\upalpha _\mathrm{n} )\):

$$\begin{aligned} {\begin{array}{llll} {(\hbox {PB})} &{}\quad {\hbox {Max}} &{}\quad {\bar{{\hbox { g}}}} &{} \\ &{}\quad {\hbox {s.t.:}} &{}\quad {{\begin{array}{l} {\left( {\hbox {u}^{\prime }}{\mathop {\sum }\limits _{\mathrm{j}\ne \mathrm{d}}} {\tilde{\hbox {Y}}_\mathrm{j} } \right) _\upbeta ^\mathrm{U} \ge \bar{{\hbox {g}}}} \\ \end{array} }} &{} \\ &{} &{}\quad {\left( {\hbox {v}^{\prime }}{\mathop {\sum }\limits _{\mathrm{j}\ne \mathrm{d}}} {\tilde{\hbox {X}}_\mathrm{j}} \right) _\upgamma ^\mathrm{U} \ge 1} &{} \\ &{} &{}\quad {\left( {\hbox {v}^{\prime }}{\mathop {\sum }\limits _{\mathrm{j}\ne \mathrm{d}}} {\tilde{\hbox {X}}_\mathrm{j}} \right) _\upgamma ^\mathrm{L} \le 1} &{} \\ &{} &{}\quad {({\hbox {u}^{\prime }}\tilde{\hbox {Y}}_\mathrm{d} ) _\upbeta ^\mathrm{U} -\bar{{\hbox {f}}}_\mathrm{d} ({\hbox {v}^{\prime }}\tilde{\hbox {X}}_\mathrm{d} ) _\upgamma ^\mathrm{L} =0} &{} \\ &{} &{}\quad {(-{\hbox {v}^{\prime }}\tilde{\hbox {X}}_\mathrm{j} +{\hbox {u}^{\prime }}\tilde{\hbox {Y}}_\mathrm{j} ) _{\upalpha _\mathrm{j} }^\mathrm{L} \le 0} &{} {\hbox {j}=1,\ldots ,\hbox {n}} \\ &{} &{}\quad {\hbox {v}\ge 0_\mathrm{m} ,\;\hbox {u}\ge 0_\mathrm{s}} &{} \end{array} } \end{aligned}$$
(11)

where \(\bar{{\hbox {f}}}_\mathrm{d}\) is the efficiency of DMU\(_\mathrm{d}\) provided by PCCR1 at the same possibility level \(\upalpha ^{\prime }\), and \({\sum _{\mathrm{j}\ne \mathrm{d}}} {\tilde{\hbox {Y}}_\mathrm{j}}\) and \({\sum _{\mathrm{j}\ne \mathrm{d}}} {\tilde{\hbox {X}}_\mathrm{j}} \) are, respectively, the outputs and inputs of the composite DMU. As it happens in the crisp case, PB selects the optimal solutions of PCCR1 that maximize the efficiency of the composite DMU.

PB is a crisp model that can give rise to programming problems which are either linear or nonlinear depending on the form of the membership functions of the fuzzy inputs and outputs. In the particular case of being trapezoidal membership functions, this model becomes the following linear programming model

$$\begin{aligned} {\begin{array}{llll} &{}\quad {\hbox {Max}} \quad {\bar{{\hbox {g}}}} &{} \\ {\hbox {s.t.:}} &{}\quad {{\begin{array}{l} {(1-\upbeta )\left( {\hbox {u}^{\prime }}{\mathop {\sum }\limits _{\mathrm{j}\ne \mathrm{d}}} {\tilde{\hbox {Y}}_\mathrm{j} } \right) _0^\mathrm{U} +\upbeta \left( {\hbox {u}^{\prime }}{\mathop {\sum }\limits _{\mathrm{j}\ne \mathrm{d}}} {\tilde{\hbox {Y}}_\mathrm{j} } \right) _1^\mathrm{U} \ge \bar{{\hbox {g}}}} \\ \end{array} }} &{} \\ &{}\quad {(1-\upgamma )\left( {\hbox {v}^{\prime }}{\mathop {\sum }\limits _{\mathrm{j}\ne \mathrm{d}}} {\tilde{\hbox {X}}_\mathrm{j}} \right) _0^\mathrm{U} +\upgamma \left( {\hbox {v}^{\prime }}{\mathop {\sum }\limits _{\mathrm{j}\ne \mathrm{d}}} {\tilde{\hbox {X}}_\mathrm{j} } \right) _1^\mathrm{U} \ge 1} &{} \\ &{}\quad {(1-\upgamma )\left( {\hbox {v}^{\prime }}{\mathop {\sum }\limits _{\mathrm{j}\ne \mathrm{d}}} {\tilde{\hbox {X}}_\mathrm{j} } \right) _0^\mathrm{L} +\upgamma \left( {\hbox {v}^{\prime }}{\mathop {\sum }\limits _{\mathrm{j}\ne \mathrm{d}}} {\tilde{\hbox {X}}_\mathrm{j} } \right) _1^\mathrm{L} \le 1} &{} \\ &{}\quad {(1-\upbeta )({\hbox {u}^{\prime }}\tilde{\hbox {Y}}_\mathrm{d} )_0^\mathrm{U} +\upbeta ({\hbox {u}^{\prime }}\tilde{\hbox {Y}}_\mathrm{d} ) _1^\mathrm{U} -\bar{{\hbox {f}}}_\mathrm{d} ((1-\upgamma )({\hbox {v}^{\prime }}\tilde{\hbox {X}}_\mathrm{d} ) _0^\mathrm{L} +\upgamma ({\hbox {v}^{\prime }}\tilde{\hbox {X}}_\mathrm{d} )_1^\mathrm{L} )=0} &{} \\ &{}\quad {(1-\upalpha _\mathrm{j} )((-{\hbox {v}^{\prime }}\tilde{\hbox {X}}_\mathrm{j} )_0^\mathrm{L} \!+\!({\hbox {u}^{\prime }}\tilde{\hbox {Y}}_\mathrm{j} )_0^\mathrm{L} )\!+\!\upalpha ((-{\hbox {v}^{\prime }}\tilde{\hbox {X}}_\mathrm{j} )_1^\mathrm{L} \!+\!({\hbox {u}^{\prime }}\tilde{\hbox {Y}}_\mathrm{j} )_1^\mathrm{L} )\le 0}\qquad \,\, {\hbox {j}=1,\ldots ,\hbox {n}}&{} \\ &{}\qquad \quad \quad {\hbox {v}\ge 0_\mathrm{m},\;\hbox {u}\ge 0_\mathrm{s} } &{} \end{array} }\nonumber \\ \end{aligned}$$
(12)

where \(\tilde{\hbox {a}}=(\tilde{\hbox {a}}_0^\mathrm{L} ,\tilde{\hbox {a}}_1^\mathrm{L} ,\tilde{\hbox {a}}_1^\mathrm{U} ,\tilde{\hbox {a}}_0^\mathrm{U} )\) denotes a trapezoidal fuzzy number with a trapezoidal membership function with support \([\tilde{\hbox {a}}_0^\mathrm{L} ,\tilde{\hbox {a}}_0^\mathrm{U} ]\) and kernel \([\tilde{\hbox {a}}_1^\mathrm{L} ,\tilde{\hbox {a}}_1^\mathrm{U} ]\).

Analogously, a fuzzy aggressive formulation can be developed by minimizing instead of maximizing the objective in (11) and replacing the first constraint of that model with \(({\hbox {u}^{\prime }}{\sum _{\mathrm{j}\ne \mathrm{d}}} {\tilde{\hbox {Y}}_\mathrm{j}} )_\upbeta ^\mathrm{L} \le \bar{{\hbox {g}}}\). For inputs and outputs being trapezoidal fuzzy numbers, the resulting formulation would be a model like (12), which minimizes its objective and has \((1-\upbeta )({\hbox {u}^{\prime }}{\sum _{\mathrm{j}\ne \mathrm{d}}} {\tilde{\hbox {Y}}_\mathrm{j} } )_0^\mathrm{L} +\upbeta ({\hbox {u}^{\prime }}{\sum _{\mathrm{j}\ne \mathrm{d}}} {\tilde{\hbox {Y}}_\mathrm{j} } )_1^\mathrm{L} \le \bar{{\hbox {g}}}\) as its first constraint.

5 Illustrative examples

In this section we illustrate the use of the methodology proposed here with different data sets that have been previously utilized in the related literature.

Table 1 Data
Full size table

5.1 Example 1

The data of this example, which are recorded in Table 1, have been taken from Guo and Tanaka (2001). The sample consists of 5 DMUs (A, B, C, D and E) with two fuzzy inputs and two fuzzy outputs. These fuzzy inputs and outputs are symmetrical triangular fuzzy numbers denoted by the pairs (a, c) where \(a\in {\mathbb {R}}\) is the center and \(c\ge 0\) is the spread. This example has also been used in Lertworasirikul et al. (2003a) to illustrate their possibility approach to the DEA efficiency evaluation, as well as in many other FDEA papers.

Since we have triangular fuzzy numbers, which are normal and convex, we use model PCCR1 in order to obtain the DEA weights in this example. For the analysis, we set \(\upbeta = \upgamma = \upalpha _\mathrm{A} = \upalpha _\mathrm{B} = \upalpha _\mathrm{C} = \upalpha _\mathrm{D} = \upalpha _\mathrm{E} = \upalpha \), and make the following choices of \(\upalpha = 0, 0.25, 0.5, 0.75\) and 1. Then, we analyze the results for these different specifications of the possibility levels [that is actually the same choice of \(\upalpha ^{\prime }\)s made in the DEA efficiency analysis in Lertworasirikul et al. (2003a)]. Table 2 provides the possibilistic DEA efficiency scores at these possibility levels. We can see that DMUs B, D and E are possibilistically efficient at all the possibility levels considered, while DMUs A and C are so only for lower possibility levels.

Table 2 Possibilistic DEA efficiency scores at different possibility levels
Full size table
Table 3 Possibilistic cross-efficiency scores at different possibility levels
Full size table
Table 4 Optimal weights provided by PCCR1 at possibility level \(\upalpha = 0\)
Full size table

Table 3 shows the possibilistic cross-efficiency scores at the different possibility levels considered. We note that the weights used for that purpose are the unique optimal solution obtained when solving model PCCR1, except for \(\upalpha =1\). In this latter case, we have used the weights provided by model PB, which coincides with model (5) because we have triangular numbers. To illustrate the way to compute the cross-efficiency scores, Table 4 records the optimal weights \((\hbox {v}_\mathrm{d} ,\hbox {u}_\mathrm{d})\) provided by PCCR1 for the 0-possibility level (just as a representative case). Table 5 records the matrix of possibilistic cross-efficiencies obtained from these optimal weights, and the associated possibilistic cross-efficiency scores (in its last row), which are calculated as the average of the cross-efficiencies in the corresponding column.

Table 5 Possibilistic cross-efficiencies and cross-efficiency scores at possibility level \(\upalpha \) = 0
Full size table

As it happens with the possibilistic efficiencies in Table 2, the possibilistic cross-efficiency scores of each DMU in Table 3 are lower as the possibility level increases. Moreover, we can see that, as Proposition 3 states, the possibilistic cross-efficiency scores are lower than the corresponding possibilistic DEA efficiencies. In addition, these two tables also show that, when \(\upalpha =1\), the cross-efficiency evaluation allows to discriminating between the DMUs that have been rated with a possibilistic efficiency equals 1.

Table 6 Data
Full size table
Table 7 Possibilistic cross-efficiency scores at different possibility levels
Full size table

From the cross-efficiency scores in Table 3 we can derive a ranking of DMUs for each of the possibility levels. We can see that DMU D ranks 1st for all the possibility levels, which shows that it is the most efficient unit, while DMU A always ranks bottom, so it appears to be the least efficient one. In fact, for \(\upalpha ^{\prime }\)s higher than or equal to 0.5, the peer evaluation provided by the cross-efficiency evaluation yields the following full ranking of DMUs: D, B, E, C and A. For \(\upalpha =0.25\), only DMUs C and E would exchange their position, whereas for \(\upalpha =0\) DMUs B, C and E would be 4th, 2nd and 3rd, respectively.

Table 8 Data
Full size table
Table 9 Possibilistic cross-efficiency scores at different possibility levels
Full size table

5.2 Other examples

With the only purpose of gaining more insight into the influence in practice of the alternate optima for the weights on our approach to the cross-efficiency evaluation, we have repeated the analysis in Example 1 with the data sets in Saati et al. (2002) (Table 6) and in Liu (2008) (Table 8). The inputs and outputs in these data sets are either triangular or degenerated fuzzy numbers. In both cases, the possibilistic cross-efficiency scores, which are reported in Tables 7 and 9, respectively, are again associated with the unique optimal solution for the weights provided by model PCCR1 (except again for \(\upalpha =1\), like in example 1, where the benevolent formulation has been used).

These examples show that the problem with the alternate optima for the weights, which is one of the key issues in the cross-efficiency evaluation in the crisp case, appears to have less influence in practice with the fuzzy approach proposed here. This is because model PCCR1 seems to have frequently a unique optimal solution for the weights (except, obviously, if the \(\upalpha \)-cuts consist of only one point, as is the case when \(\upalpha =1\) if we have triangular fuzzy inputs and outputs, because in those cases PCCR1 and the crisp CCR model coincide).

6 Conclusions

Cross-efficiency evaluation is an extension of DEA that arose as a response to the need of ranking DMUs involved in production processes regarding their efficiency. However, in many real applications, the data cannot be measured with precision, and the analysts have to deal with imprecise inputs and outputs. This is why we have proposed here a fuzzy cross-efficiency evaluation for the case of inputs and outputs being normal and convex fuzzy numbers. To be specific, we have developed a possibility approach that has made it possible to define consistent cross-efficiencies. Rankings of DMUs at a given possibility level result from the ordering of the corresponding possibilistic cross-efficiency scores, which are real numbers. It is worth highlighting the results that have been obtained in our examples. In particular, these seem to show that, in practice, the problems with the alternate optima for the weights appears to have less influence with the proposed possibilistic approach to the fuzzy cross-efficiency evaluation. As a future research, we would like to investigate the possible extension of other existing FDEA models for use in cross-efficiency evaluations.