Abstract
Probabilistic linguistic term set solves the problem of probabilistic distribution of linguistic terms. Due to the objective and subjective factors such as the decision makers’experience and preference, the credibility of the linguistic terms is different. However, current studies on PLTSs ignore this difference. In this paper, we first propose a novel concept called Z probabilistic linguistic term set (ZPLTS). As an extension of existing tools, it takes advantage of the fact that Z-number can represent both information and corresponding credibility. At the same time, we discuss the normalization, operational rules, ranking method and distance measure for ZPLTSs. Then, we propose a new weight calculation method, an aggregation-based method and an extended TOPSIS method, and apply them to multi-attribute group decision making in Z probabilistic linguistic environment. Finally, a numerical example and some comparisons with other methods illustrate the necessity and effectiveness of the proposed method.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
The world we live in is full of uncertainty, while traditional values cannot express the uncertainty and complexity. Therefore, Zadeh (1965) proposed fuzzy sets to represent this uncertain fuzzy concept. With the development of the discipline and its application in decision making, Zadeh proposed linguistic variables (Zadeh 1975) to represent linguistic information more conveniently and clearly. Linguistic variables such as “a little bit”, “very well” and “unlikely” are closer to decision maker’s (DM’s) intentions than numerical values, which helps in decision making.
The decision making of linguistic information has been studied extensively. Herrera et al. (1996, 1997) established a series of group decision making models under linguistic evaluation. Xu (2004) extended the traditional single linguistic variable into an interval linguistic variable and proposed the uncertain linguistic variable. Multi-attribute group decision making (MAGDM) has a wide range of applications in uncertain linguistic environments. Based on the distance and similarity theory Xian and Sun (2014), further proposed the Euclidean and Minkowski ordered weighted average distance operators (FLIEOWAD and FLIOWAMD) and applied to linguistic group decision making.
There are decision preferences in decision making, and a single linguistic term cannot accurately express this preference. To express DMs’ hesitation, Rodriguez et al. (2012) proposed hesitant fuzzy linguistic term sets (HFLTSs) based on the hesitant fuzzy sets (HFSs) (Torra 2010) and linguistic term sets (LTSs) (Zadeh 1975), which can express several possible linguistic terms simultaneously. The TOPSIS method of HFLTSs (Beg and Rashid 2013) and correlation operators (Wei et al. 2014) were also proposed and applied to decision making. Subsequently, Wang (2015) developed extended hesitant fuzzy linguistic term sets (EHFLTSs) based on HFLTSs. Scholars found that the weights of the linguistic information given by different DMs should be different in actual decision making. Therefore, Pang (Pang et al. 2016) proposed the PLTS to present possible linguistic terms and corresponding probabilistic information. Gou and Xu (2016) explored its operational rules. Bai et al. (2017) and Xian et al. (2019) put forward different methods to rank PLTSs. Since PLTSs are in line with the actual situation of decision making, it is also widely used in GDM Xing Li and Liao 2018. To show the preference of DMs, Zhang et al. (2016) proposed the probabilistic linguistic preference relation (PLPR) and applied it to risk assessment. Hu et al. (2020) made a comprehensive analysis of the current research status, applications and future development directions related to PLTSs.
The above concepts all assume that the uncertain information is true and reliable. But in the real world, information released by government departments is obviously more reliable than it transmitted by individuals. This is due to the different credibility of the information. In view of the defect that the credibility of the information is ignored in the fuzzy domain, Zadeh (2011) proposed Z-numbers. A Z-number is expressed as \(Z=(A,B)\), where A is the evaluation and B is the credibility of A. For example, when evaluating the quality of a product, we use a Z-number (good, sure) to express “the DM is sure the quality is good”. “Good” is the evaluation and “sure” is its credibility. Kang et al. (2016) proposed a multi-attribute decision making (MADM) method to solve the supplier selection problem. Yaakob and Gegov (2016) combined the TOPSIS method with Z-numbers. Xiao (2014) applied Z-numbers to MADM. Z-number has also been studied to represent linguistic information, Wang et al. (2017) and Xian et al. (2019) respectively proposed the linguistic Z-number and the \(\mathrm{{{\mathcal {Z}}}}\) linguistic variable to represent the linguistic evaluation information containing credibility.
In decision making, the information credibility is influenced by two aspects: DM’s objective experience and subjective decision preference. DMs have different experience and familiarity with different fields involved. The evaluation credibility of familiar fields is higher, while that of unfamiliar fields is lower. Some DMs are accustomed to giving higher evaluations, while others are usually lower. Therefore, the credibility of the evaluation information is obviously different.
However, in the group decision making (GDM) research on PLTSs, most of the current studies focus on the representation of the linguistic terms and the calculation of the probability distribution, without considering the influence of the information credibility. Due to the subjective or objective reasons mentioned above, we often encounter the situation that the credibility of the evaluation information is different. For example, there are ten experts assessing the risk of a project, seven of them evaluate it as “high”, and three of them evaluate it as “very high”. Four of the ten experts are senior experts with years of experience in risk assessment, and their credibilities of the assessment are “very likely”; six of the ten experts are young and inexperienced, and their credibilities are “likely”. In this case, the decision information is expressed as: \((\{high(0.7),\;very\;high(0.3)\}, \{(likely(0.4),\;very\;likely(0.6))\})\).
In the above example, if we do not consider the credibility of the information, then they are completely credible by default. Obviously, incomplete decision information may lead to inaccurate final decision results. In addition, the existing methods to calculate attribute weights, such as the maximum deviation method, do not take the information credibility into consideration. It is more in line with people’s decision making habits to assign higher weights to the attributes with high credibility. In this paper, we propose a novel concept, Z probabilistic linguistic term set (ZPLTS). It combines the advantage that Z-numbers can represent information credibility, and solves the problem of inaccurate decision results caused by lack of information credibility in PLTS group decision problems. As a new linguistic information representation tool, ZPLTS can simultaneously represent multiple possible linguistic terms, probability distribution and information credibility, making decision information more complete.
The main contributions of this paper are:
First, inspired by Z-numbers, we propose the concept called ZPLTS. ZPLTS can not only represent the linguistic evaluation of DMs, but also show the hesitant decision information and preference of DMs. The normalization, operational rules, ranking method and distance measure are also proposed.
Second, combining with the characteristics of the information credibility, a weight calculation method based on the credibility is proposed.
Finally, we build a MAGDM model based on ZPLTSs, including the operators method and the extended TOPSIS method.
The distribution of the rest of the paper is as follows: In Sect. 2, we review some concepts of PLTSs and Z-numbers. The concept of ZPLTSs is proposed in Sect. 3. The normalization, operational rules, ranking method and distance are also put forward in this section. In Sect. 4, a MAGDM model is proposed to solve the decision making problems under Z probabilistic linguistic environment. We take a numerical example and conduct a comparative analysis to discuss the necessity and validity of what we proposed in Sect. 5. Section 6 concludes.
2 Preliminaries
In this section, we first review some concepts used in the following.
2.1 Linguistic term sets
Definition 1
(Xu 2005) Let \(S = \{ {s_i}|i = - \varsigma , \ldots , - 1,0,1, \ldots ,\varsigma \}\) be a LTS, \({s_i}\) presents the possible value of a linguistic varible.
Example 1
Let \(\varsigma =3,2\) , respectively. S and \(S^{\prime }\) are express as
2.2 Hesitant fuzzy linguistic term sets
On the basis of LTSs, the hesitant psychology of DMs was taken into consideration. DMs may evaluate several linguistic term values in the actual decision making. Then the concept of HFLTSs was put forward.
Definition 2
(Rodriguez et al. 2012) \(S = \{ {s_i}|i = - \varsigma , \ldots , - 1,0,1, \ldots ,\varsigma \}\) is a LTS, and \({b_S}\) is a HFLTS. \({b_S}\) is an ordered finite subset of the consecutive linguistic terms of S.
Example 2
Continue to Example 1, \(b_S\) and \(b_{{S^{\prime }}}\) are expressed as follows:
\({b_S} = \{ {s_{ - 1}} = slight\;bad,\;{s_1} = slight\;good\}\).
\({b_{{S^{\prime }}}} = \{ s_0^{\prime } = \;fair,\;{s_1^{\prime }} = slight\;possible\;good,\;s_2^{\prime } = possible\}\).
If we simplify them, we obtain \({b_S} = \{ {s_{ - 1}},\;{s_0}\}\), \({b_{{S^{\prime }}}} = \{ s_0^{\prime },\;{s_1^{\prime }},\;s_2^{\prime }\} \).
2.3 Probabilistic linguistic term sets
In HFLTSs, each linguistic variable has the same weight. However, preference exists in actual decision problems. To express the preference of DMs, Pang Pang et al. (2016) proposed PLTSs to make decision information more realistic and complete.
Definition 3
(Pang et al. 2016) \(S = \{ {s_i}|i = - \varsigma , \ldots , - 1,0,1, \ldots ,\varsigma \}\) is a LTS, then a PLTS is defined as
where \(L^{(m)}\) is a linguistic term, \(p^{(m)}\) is its probability, and \({\# L(p)}\) denotes the number of all different linguistic terms in L(p).
The operational rules of PLTSs are defined as follows:
Definition 4
(Gou and Xu 2016) Let \({L_1}(p)\) and \({L_2}(p)\) be two PLTSs, \(\chi \) is a real number and \(\chi > 0\). Then,
where \(g:[ - \varsigma ,\varsigma ] \rightarrow [0,1],\;g({s_i}) = \frac{i}{{2\varsigma }} + \frac{1}{2} = \sigma \); \({g^{ - 1}}:[0,1] \rightarrow [ - \varsigma ,\varsigma ],\;{g^{ - 1}}(\sigma ) = {s_{(2\sigma - 1)\varsigma }} = {s_i}\).
2.4 Z-number
Zadeh (2011) proposed Z-numbers by adding credibility to the traditional evaluation.
Definition 5
(Zadeh 2011) A Z-number is denoted as \(Z = (A,B)\), which is an ordered pair of fuzzy numbers. The first component, A, is a description or restriction of a value, and B is a measure of the credibility of A.
3 Z probabilistic linguistic term sets
To solve the problem of ignoring information credibility in the existing study of PLTSs, we propose ZPLTSs. In this section, the definition, relative operational rules, ranking method, normalization and distance are put forward.
3.1 The concept of ZPLTSs
In GDM, as the example illustrated in Sect. 1, ignoring credibility will lead to inaccurate results for decision making in probabilistic linguistic environment. Therefore, each DM gives the corresponding credibility while evaluating, which is a linguistic Z-number. Then, the evaluation and the credibility of multiple DMs are summarized to form two PLTSs, respectively, thus forming a novel ZPLTS. It contains three kinds of decision information: possible linguistic terms, probabilistic distribution, and credibility.
Definition 6
X is a non-empty set, then a ZPLTS \({\hat{Z}}^\# \) is defined as:
where \({\hat{Z}}\) is a Z probabilistic linguistic value (ZPLV).
Definition 7
Let \({L_A}(p)\) and \({L_B}(p)\) be two PLTSs, then a ZPLV is defined as
where
\(S = \{ {s_i}|i = - \varsigma , \ldots , - 1,0,1, \ldots ,\varsigma \}\) and \(S' = \{ {s'_j}|j = - \zeta , \ldots , - 1,0,1, \ldots ,\zeta \}\) are two LTSs.
Remark 1
(1) If \({L_{{\hat{B}}}}(p) = \{ {s'_\zeta }(1)\} \), then the credibility is the highest, the concept of the credibility can be ignored. A ZPLV is reduced to a PLTS, and it is expressed as:
(2) If \(\# {L_{{\hat{A}}}}({p_{{\hat{A}}}}) = \# {L_{{\hat{B}}}}({p_{{\hat{B}}}}) = 1\) and \({p_{{\hat{A}}}}^{(m)} = {p_{{\hat{B}}}}^{(n)} = 1\), then both \({\hat{A}}\) and \({\hat{B}}\) have only one linguistic term, and the probabilities are 1. Then, a ZPLV is reduced to a linguistic Z-number (Wang et al. 2017), and it is expressed as:
where \(i = - \varsigma , \ldots , - 1,0,1, \ldots ,\varsigma \) and \(j = - \zeta , \ldots , - 1,0,1, \ldots ,\zeta \).
Example 3
Continue to Example 1. Assume that there are four experts evaluating a product, and their evaluations and corresponding credibilities are: \((good,slight\; possible)\), \((very\;good,possible)\), (good, fair), and (good, possible). Then, represent them by the linguistic terms in Example 1 and obtain four linguistic Z-numbers: \(({s_2},{{s'}_1})\), \(({s_3},{{s'}_2})\), \(({s_2},{{s'}_0})\), \(({s_2},{{s'}_2})\). Summarize them to a ZPLTS and obtain \((\{ {s_2}(0.75),{s_3}(0.25)\} ,\{ {{s'}_0}(0.25),{{s'}_1}(0.25),{{s'}_2}(0.5)\} )\).
3.2 The normalization of ZPLVs
For the normalization of ZPLVs, both \({L_{{\hat{A}}}}(p)\) and \({L_{{\hat{B}}}}(p)\) in ZPLVs should be normalized. The process is divided into two parts: one is the normalization of the probability distribution, and the other is the normalization of the number of linguistic terms.
The first is the normalization of the probability. When the sums of probabilities in \({L_{{\hat{A}}}}(p)\) and \({L_{{\hat{A}}}}(p)\) are less than 1, the remaining probabilities need to be further allocated.
Definition 8
Let \({\hat{Z}} = ({L_{{\hat{A}}}}(p),{L_{{\hat{B}}}}(p))\) be a ZPLV with \(\sum \limits _{m = 1}^{\# {L_{{\hat{A}}}}({p_{{\hat{A}}}})} {{p_{{\hat{A}}}}^{(m)} < 1} \) and \(\sum \limits _{n = 1}^{\# {L_{{\hat{B}}}}({p_{{\hat{B}}}})} {{p_{{\hat{B}}}}^{(n)} < 1} \), then the associated ZPLV is:
where
\(m = 1,2, \ldots ,\# {L_{{\hat{A}}}}({p_{{\hat{A}}}})\) and \(n = 1,2, \ldots ,\# {L_{{\hat{B}}}}({p_{{\hat{B}}}})\).
Next is the normalization of the number of linguistic terms. In order to facilitate the calculation of the distance between ZPLVs, we need to make the number of linguistic terms in \({L_A}(p)\) and \({L_B}(p)\) equal.
Definition 9
Let \({{\hat{Z}}_1} = ({L_{{\hat{A}}1}}(p),{L_{{\hat{B}}1}}(p))\) and \({{\hat{Z}}_2} = ({L_{{\hat{A}}2}}(p),{L_{{\hat{B}}2}}(p))\) be two ZPLVs. \(\# {L_{{\hat{A}}1}}({p_{{\hat{A}}1}})\) and \(\# {L_{{\hat{A}}2}}({p_{{\hat{A}}2}})\) are the numbers of linguistic terms in \({L_{{\hat{A}}1}}(p)\) and \({L_{{\hat{A}}2}}(p)\), respectively. \(\# {L_{{\hat{B}}1}}({p_{{\hat{B}}1}})\) and \(\# {L_{{\hat{B}}2}}({p_{{\hat{B}}2}})\) are the numbers of the linguistic terms in \({L_{{\hat{B}}1}}(p)\) and \({L_{{\hat{B}}2}}(p)\), respectively. If \(\# {L_{{\hat{A}}1}}({p_{{\hat{A}}1}}) > \# {L_{{\hat{A}}2}}({p_{{\hat{A}}2}})\), then
-
(1)
add \(\# {L_{{\hat{A}}1}}({p_{{\hat{A}}1}}) - \# {L_{{\hat{A}}2}}({p_{{\hat{A}}2}})\) linguistic terms to \({L_{{\hat{A}}2}}(p)\), and the added linguistic terms are any linguistic terms in \({L_{{\hat{A}}2}}(p)\);
-
(2)
let the probabilities of the added linguistic terms be 0.
Similarly, when \(\# {L_{{\hat{B}}1}}({p_{{\hat{B}}1}}) > \# {L_{{\hat{B}}2}}({p_{{\hat{B}}2}})\), the steps for their normalization are like these.
3.3 Basic operational rules of ZPLVs
Inspired by Xian et al. (2019) and Gou and Xu (2016), the operational rules of ZPLVs are defined in this part.
Definition 10
Let \({{\hat{Z}}_1} = ({{\hat{A}}_1},{{\hat{B}}_1}) = ({L_{{\hat{A}}1}}(p),{L_{{\hat{B}}1}}(p))\) and \({{\hat{Z}}_2} = ({{\hat{A}}_2},{{\hat{B}}_2}) = ({L_{{\hat{A}}2}}(p),{L_{{\hat{B}}2}}(p))\) be two ZPLVs, where
and
then some basic operational rules are as follows:
Theorem 1
Let \(\;{\hat{Z}},{{\hat{Z}}_1},{{\hat{Z}}_2}\) be three ZPLVs, and \(\chi ,{\chi _1},{\chi _2}\) are three real numbers. Then
\((1)\;{{\hat{Z}}_1} + {{\hat{Z}}_2} = {{\hat{Z}}_2} + {{\hat{Z}}_1}\);
\((2)\;{{\hat{Z}}_1} \otimes {{\hat{Z}}_2} = {{\hat{Z}}_2} \otimes {{\hat{Z}}_1}\);
\((3)\;\chi ({{\hat{Z}}_1} + {{\hat{Z}}_2}) = \chi {{\hat{Z}}_1} + \chi {{\hat{Z}}_2}\);
\((4)\;{({{\hat{Z}}_1} \otimes {{\hat{Z}}_2})^\chi } = {{\hat{Z}}_1}^\chi \otimes {{\hat{Z}}_2}^\chi \);
\((5)\;{\chi _1}{\hat{Z}} + {\chi _2}{\hat{Z}} = ({\chi _1} + {\chi _2}){\hat{Z}}\), when \({{\varepsilon ^{(m)}},{\varepsilon ^{(n)}} \in g({L_{{\hat{A}}}})}\) and \(m=n\);
\((6)\;{{\hat{Z}}^{{\chi _1}}} \otimes {{\hat{Z}}^{{\chi _2}}} = {{\hat{Z}}^{{\chi _1} + {\chi _2}}}\), when \({{\varepsilon ^{(m)}},{\varepsilon ^{(n)}} \in g({L_{{\hat{A}}}})}\), \({{\varepsilon ^{(h)}},{\varepsilon ^{(k)}} \in g({L_{{\hat{B}}}})}\), \(m=n\) and \(h=k\).
Proof
The proofs of (1) and (2) are obvious, so we omit the proofs here.
(5) When \({{\varepsilon ^{(m)}},{\varepsilon ^{(n)}} \in g({L_{{\hat{A}}}})}\) and \(m=n\), then
(6) When \({{\varepsilon ^{(m)}},{\varepsilon ^{(n)}} \in g({L_{{\hat{A}}}})}\), \({{\varepsilon ^{(h)}},{\varepsilon ^{(k)}} \in g({L_{{\hat{B}}}})}\), \(m=n\) and \(h=k\).Then
\(\square \)
Example 4
Let \( {{\hat{Z}}_1} = ({{\hat{A}}_1},{{\hat{B}}_1}) = ({L_{{\hat{A}}1}}(p),{L_{{\hat{B}}1}}(p)) = (\{ {s_0}(0.2),{s_1}(0.4),{s_3}(0.4)\} , \{ {s'_{ - 2}}(0.1), {s'_0}(0.4)\} ) \text {and} {{\hat{Z}}_2} = ({{\hat{A}}_2},{{\hat{B}}_2}) = ({L_{{\hat{A}}2}}(p),{L_{{\hat{B}}2}}(p)) = (\{ {s_{ - 1}}(0.4),{s_0}(0.6)\} ,\{ {s'_1}(0.5),{s'_2}(0.5)\} ) \) be two ZPLVs, and \(\chi = 2\).
The normalized \({{{\hat{Z}}}_1}\) and \({{{\hat{Z}}}_2}\) are:
3.4 The comparison method of ZPLVs
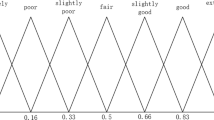
In this section, we propose a comparison method for ZPLVs. First, we define the concept of the score of the ZPLV. We express the linguistic values of A and B in ZPLV through the axes. And then use the area as the score of the ZPLV, as shown in Fig.1.
Definition 11
Let
\(v_{{\hat{A}}}^{(m)}\) and \(v_{{\hat{B}}}^{(n)}\) are the subscripts of \({L_{{\hat{A}}}}^{(m)}\) and \({L_{{\hat{B}}}}^{(n)}\). The score of \({\hat{Z}}\) is
where
The higher the score of the ZPLV is, the larger the ZPLV is. However, it is also possible for the scores of two ZPLVs to be equal, as shown in Fig.2. Therefore, we introduce another concept, the deviation degree of the ZPLV.
The definition of the deviation degree of the ZPLV is as follows:
Definition 12
Let
\({v_{{\hat{A}}}}^{(m)}\) and \({v_{{\hat{B}}}}^{(n)}\) are the subscripts of \({L_{{\hat{A}}}}^{(m)}\) and \({L_{{\hat{B}}}}^{(n)}\). The score of \({\hat{Z}}\) is \(S({\hat{Z}}) = ({\bar{\alpha }} + \varsigma )({{\bar{\alpha }} ^{\prime }} + \varsigma )\), where \({\bar{\alpha }} = \frac{{\sum \limits _{m = 1}^{\# {L_{{\hat{A}}}}({p_{{\hat{A}}}})} {{v_{{\hat{A}}}}^{(m)}} {p_{{\hat{A}}}}^{(m)}}}{{\sum \limits _{m = 1}^{\# {L_{{\hat{A}}}}({p_{{\hat{A}}}})} {{p_{{\hat{A}}}}^{(m)}} }}\) and \({{\bar{\alpha }} ^{\prime }} = \frac{{\sum \limits _{n = 1}^{\# {L_{{\hat{B}}}}({p_{{\hat{B}}}})} {{v_{{\hat{B}}}}^{(n)}} {p_{{\hat{B}}}}^{(n)}}}{{\sum \limits _{n = 1}^{\# {L_{{\hat{B}}}}({p_{{\hat{B}}}})} {{p_{{\hat{B}}}}^{(n)}} }}\).
The deviation degree of \({\hat{Z}}\) is
Then, the comparison method of ZPLVs is summarized as follows:
Definition 13
Let \({{\hat{Z}}_1}\) and \({{\hat{Z}}_2}\) be two ZPLVs, then
-
(1)
If \(S({{\hat{Z}}_1}) > S({{\hat{Z}}_2})\), then \({{\hat{Z}}_1} > {{\hat{Z}}_2}\).
-
(2)
If \(S({{\hat{Z}}_1}) < S({{\hat{Z}}_2})\), then \({{\hat{Z}}_1} < {{\hat{Z}}_2}\).
-
(3)
If \(S({{\hat{Z}}_1}) = S({{\hat{Z}}_2})\), then
- (\(\dot{1}\)):
-
If \(D({{\hat{Z}}_1}) > D({{\hat{Z}}_2})\), then \({{\hat{Z}}_1} < {{\hat{Z}}_2}\).
- (\(\dot{2}\)):
-
If \(D({{\hat{Z}}_1}) < D({{\hat{Z}}_2})\), then \({{\hat{Z}}_1} > {{\hat{Z}}_2}\).
- (\(\dot{3}\)):
-
If \(D({{\hat{Z}}_1}) = D({{\hat{Z}}_2})\), then \({{\hat{Z}}_1} \approx {{\hat{Z}}_2}\).
- (\(\dot{4}\)):
-
If \({L_{{\hat{A}}1}}(p) = {L_{{\hat{B}}1}}(p)\) and \({L_{{\hat{A}}2}}(p) = {L_{{\hat{B}}2}}(p)\), then \({{\hat{Z}}_1} = {{\hat{Z}}_2}\).
Example 5
Continue to Example 4, compare \({{\hat{Z}}_1}\) and \({{\hat{Z}}_2}\). We calculate the score and the deviation degree of them, respectively.
With the same method, we obtain
3.5 The distance between ZPLVs
The distance between ZPLVs is based on the deviation degree of ZPLVs and the modified Euclidean distance.
Definition 14
Let \( {{\hat{Z}}_1} = ({{\hat{A}}_1},{{\hat{B}}_1}) = ({L_{{\hat{A}}1}}(p),{L_{{\hat{B}}1}}(p)) = (\{ {L_{{\hat{A}}1}}^{(m)}({p_{{\hat{A}}1}}^{(m)})|m = 1,2, \ldots ,\# {L_{{\hat{A}}1}}({p_{{\hat{A}}1}})\} ,\{ {L_{{\hat{B}}1}}^{(n)} ({p_{{\hat{B}}1}}^{(n)})|n = 1,2, \ldots ,\# {L_{{\hat{B}}1}}({p_{{\hat{B}}1}})\} )\) and \( {{\hat{Z}}_2} = ({{\hat{A}}_2},{{\hat{B}}_2}) = ({L_{{\hat{A}}2}}(p),{L_{{\hat{B}}2}}(p)) = (\{ {L_{{\hat{A}}2}}^{(h)}({p_{{\hat{A}}2}}^{(h)})|h = 1,2, \ldots , \# {L_{{\hat{A}}2}}({p_{{\hat{A}}2}})\} ,\{ {L_{{\hat{B}}2}}^{(k)}({p_{{\hat{B}}2}}^{(k)})|k = 1,2, \ldots ,\# {L_{{\hat{B}}2}}({p_{{\hat{B}}2}})\} ) \) be two ZPLVs. \( \# {L_{{\hat{A}}1}}({p_{{\hat{A}}1}}) = \# {L_{{\hat{A}}2}}({p_{{\hat{A}}2}}) \text {and} \# {L_{{\hat{B}}1}}({p_{{\hat{B}}1}}) = \# {L_{{\hat{B}}2}}({p_{{\hat{B}}2}}), \) then the distance between \({{\hat{Z}}_1}\) and \({{\hat{Z}}_2}\) is
Theorem 2
Let \({{\hat{Z}}_1},{{\hat{Z}}_2},{{\hat{Z}}_3}\) be three ZPLVs, then they satisfy the next three theorems:
-
(1)
\(d({{\hat{Z}}_1},{{\hat{Z}}_2}) \ge 0;\)
-
(2)
\(d({{\hat{Z}}_1},{{\hat{Z}}_2}) = d({{\hat{Z}}_2},{{\hat{Z}}_1});\)
-
(3)
If \({{\hat{Z}}_1} \le {{\hat{Z}}_2} \le {{\hat{Z}}_3}\), then \( d({{{\hat{Z}}}_1},{{{\hat{Z}}}_2}) \le d({{{\hat{Z}}}_1},{{{\hat{Z}}}_3}) \text {and}\,d({{{\hat{Z}}}_2},{{{\hat{Z}}}_3}) \le d({{{\hat{Z}}}_1},{{{\hat{Z}}}_3}). \)
Proof
(1) and (2) are obvious.
(3)
For \({{\hat{Z}}_2} \le {{\hat{Z}}_3}\), so
Therefore, \( d({{{\hat{Z}}}_1},{{{\hat{Z}}}_2}) \le d({{{\hat{Z}}}_1},{{{\hat{Z}}}_3}). \)
Similarly, \( d({{{\hat{Z}}}_2},{{{\hat{Z}}}_3}) \le d({{{\hat{Z}}}_1},{{{\hat{Z}}}_3}). \) \(\square \)
Example 6
Continue to Example 4, the distance between the normalized \({{{\hat{Z}}}_1}\) and \({{{\hat{Z}}}_2}\) is:
4 MAGDM with ZPLTSs
Assume that there are a discrete set of alternatives \(X = \{ {x_1},{x_2}, \ldots ,{x_s}\} (s \ge 2)\) and a set of attributes \(C = \{ {c_1},{c_2}, \ldots ,{c_t}\} (t \ge 2)\). The weighting vector of attributes is \(W = {({\omega _1},{\omega _2}, \ldots ,{\omega _t})^T}\), where \({\omega _\theta } \in [0,1]\), \(\theta = 1,2, \cdots ,t\), and \(\sum \limits _{\theta = 1}^t {{\omega _\theta }} = 1\). The attribute weights are unknown. According to the evaluation and the corresponding credibility given by DMs, we can obtain ZPLVs. All of the ZPLVs constitute the ZPLV decision matrix and it is denoted as R.
where \( {{\hat{Z}}_{\gamma \theta }} = ({{\hat{A}}_{\gamma \theta }},{{\hat{B}}_{\gamma \theta }}) = ({L_{{{{\hat{A}}}_{\gamma \theta }}}}(p),{L_{{{{\hat{B}}}_{\gamma \theta }}}}(p)) = (\{ {L_{{{{\hat{A}}}_{\gamma \theta }}}}^{(m)}({p_{{{{\hat{A}}}_{\gamma \theta }}}}^{(m)})|m = 1,2, \ldots ,\# {L_{{{{\hat{A}}}_{\gamma \theta }}}}({p_{{{{\hat{A}}}_{\gamma \theta }}}})\} , \{ {L_{{{{\hat{B}}}_{\gamma \theta }}}}^{(n)}({p_{{{{\hat{B}}}_{\gamma \theta }}}}^{(n)})| \) \(n = 1,2, \ldots ,\# {L_{{{{\hat{B}}}_{\gamma \theta }}}}({p_{{{{\hat{B}}}_{\gamma \theta }}}})\} )\). It represents the decision information of attribute \(\theta (\theta = 1,2, \ldots ,t)\) of alternative \(\gamma (\gamma = 1,2, \ldots ,s)\). \({L_{{{{\hat{A}}}_{\gamma \theta }}}}^{(m)}\) is the mth value of \({L_{{{{\hat{A}}}_{\gamma \theta }}}}({p_{{{{\hat{A}}}_{\gamma \theta }}}})\), \({p_{{{{\hat{A}}}_{\gamma \theta }}}}^{(m)}\) is the corresponding probability, \(\# {L_{{{{\hat{A}}}_{\gamma \theta }}}}({p_{{{{\hat{A}}}_{\gamma \theta }}}})\) is the number of different linguistic terms in \({L_{{{{\hat{A}}}_{\gamma \theta }}}}({p_{{{{\hat{A}}}_{\gamma \theta }}}})\). \({L_{{{{\hat{B}}}_{\gamma \theta }}}}^{(n)}\) is the nth value of \({L_{{{{\hat{B}}}_{\gamma \theta }}}}({p_{{{{\hat{B}}}_{\gamma \theta }}}})\), \({p_{{{{\hat{B}}}_{\gamma \theta }}}}^{(n)}\) is the corresponding probability, \(\# {L_{{{{\hat{B}}}_{\gamma \theta }}}}({p_{{{{\hat{B}}}_{\gamma \theta }}}})\) is the number of different linguistic terms in \({L_{{{{\hat{B}}}_{\gamma \theta }}}}({p_{{{{\hat{B}}}_{\gamma \theta }}}})\).
4.1 Calculation method for attribute weights based on the credibility
The determination of the attribute weights is a very important part in MAGDM. However, due to the complexity and the uncertainty of the decision environment, the attribute weights are often unknown. Therefore, we propose a method to determine the attribute weights in Z probabilistic linguistic (ZPL) environment based on the credibility of the information. The main idea of this method is that the higher the credibility of the evaluation information is, the more credible the information is, and the higher the weight is given to it.
The information credibility of the attribute \(\theta \) is labeled as:
where \({L_{{{{\hat{B}}}_\theta }}}^{(f)}\) is the fth value of \({L_{{{{\hat{B}}}_\theta }}}({p_{{{{\hat{B}}}_\theta }}})\), \({p_{{{{\hat{B}}}_\theta }}}^{(f)}\) is the corresponding probability, \(\# {L_{{{{\hat{B}}}_\theta }}}({p_{{{{\hat{B}}}_\theta }}})\) is the number of different linguistic terms in \(\# {L_{{{{\hat{B}}}_\theta }}}({p_{{{{\hat{B}}}_\theta }}})\) and \({v_{{{{\hat{B}}}_\theta }}}^{(f)}\) is the subscript of \({L_{{{{\hat{B}}}_\theta }}}^{(f)}\). And
Using the score of PLTSs in Pang et al. (2016), the score of \({L_{{{{\hat{B}}}_\theta }}}({p_{{{{\hat{B}}}_\theta }}})\) is:
where \( {{\bar{\alpha }} _{_\theta }} = {{\sum \limits _{f = 1}^{\# {L_{{{{\hat{B}}}_\theta }}}({p_{{{{\hat{B}}}_\theta }}})} {{p_{{{{\hat{B}}}_\theta }}}^{(f)}{v_{{{{\hat{B}}}_\theta }}}^{(f)}} } \Big / {\sum \limits _{f = 1}^{\# {L_{{{{\hat{B}}}_\theta }}}({p_{{{{\hat{B}}}_\theta }}})} {{p_{{{{\hat{B}}}_\theta }}}^{(f)}} }}. \)
Then the attribute weight \({\omega _\theta }\) is:
where \({g({{s'}_{{{{\bar{\alpha }} }_{_\theta }}}})}\) is calculated by the equation mentioned in Definition 4. It’s easy to prove \({\omega _\theta } > 0\).
By normalizing \({\omega _\theta }(\theta = 1,2, \ldots ,t)\) so that its sum is 1, the following equation is obtained:
In this way, we obtain the attribute weight vector \(W = {({\omega _1},{\omega _2}, \ldots ,{\omega _t})^T}\). It is used in the following operators and the extended TOPSIS method for ZPLVs.
4.2 Some aggregate operators based on ZPLTSs
In decision making, information aggregation is an indispensable part. To integrate ZPLTSs in decision making, we propose three operators to aggregate decision information.
4.2.1 ZPLWA operator
First, we propose the Z probabilistic linguistic weighted averaging (ZPLWA) operator.
Definition 15
Let \({{\hat{Z}}^\# }\) be a ZPLTS, \({{\hat{Z}}_\theta } = ({{\hat{A}}_\theta },{{\hat{B}}_\theta }) \in {{\hat{Z}}^\# }\), \(\theta = 1,2, \ldots ,t\). A ZPLWA operator aggregation is as follows:
where \({\omega _\theta }\) is calculated by the method proposed in Sect. 4.1, \({\omega _\theta }\in [0,1]\), and \(\sum \limits _{\theta = 1}^t {{\omega _{\theta } } = 1} \).
Theorem 3
\( {{\hat{Z}}_\theta } = ({{\hat{A}}_\theta },{{\hat{B}}_\theta }) = ({L_{{\hat{A}}\theta }}({p_{{\hat{A}}\theta }}),{L_{{\hat{B}}\theta }}({p_{{\hat{B}}\theta }})) = (\{ {L_{{\hat{A}}\theta }}^{(m)}({p_{{\hat{A}}\theta }}^{(m)})|m = 1,2, \ldots , \# {L_{{\hat{A}}\theta }}({p_{{\hat{A}}\theta }})\} ,\{ {L_{{\hat{B}}\theta }}^{(n)}({p_{{\hat{B}}\theta }}^{(n)})|n = 1,2, \ldots ,\# {L_{{\hat{B}}\theta }}({p_{{\hat{B}}\theta }})\} ), \) then their aggregated value by using the ZPLWA operator is also a ZPLV, and
Proof
For \(t = 2\), \( {\omega _1}{{{\hat{Z}}}_1} + {\omega _2}{{{\hat{Z}}}_2} = {\omega _1}({{{\hat{A}}}_1},{{{\hat{B}}}_1}) + {\omega _2}({{{\hat{A}}}_2},{{{\hat{B}}}_2})\; = {\omega _1}({L_{{\hat{A}}1}}(p),{L_{{\hat{B}}1}}(p)) + {\omega _2}({L_{{\hat{A}}2}}(p),{L_{{\hat{B}}2}}(p)) = \left( {\omega _1}{L_{{\hat{A}}1}}(p) + {\omega _2}{L_{{\hat{A}}2}}(p),\frac{{{L_{{\hat{B}}1}}(p) + {L_{{\hat{B}}2}}(p)}}{2}\right) . \)
When \(t = k\), we have
When \(t = k + 1\), we have
Therefore, this equation holds for all t. \(\square \)
Theorem 4
(Monotonicity) Let \(({{\hat{Z}}_1},{{\hat{Z}}_2}, \ldots ,{{\hat{Z}}_t})\) and \(({{\hat{Z}}^*}_1,{{\hat{Z}}^*}_2, \ldots ,{{\hat{Z}}^*}_t)\) be two ZPLTSs. If \({{\hat{Z}}_\theta } < {{\hat{Z}}^*}_\theta \) for all \(\theta = 1,2, \ldots ,t\), then
Proof
\({{\hat{Z}}_\theta } < {{\hat{Z}}^*}_\theta \) holds for all \(\theta = 1,2, \ldots ,t\) . Therefore, \({\phi _{ZPLWA}}({{\hat{Z}}_1},{{\hat{Z}}_2}, \ldots ,{{\hat{Z}}_t}) < {\phi _{ZPLWA}}({{\hat{Z}}^*}_1,{{\hat{Z}}^*}_2, \ldots ,{{\hat{Z}}^*}_t)\). \(\square \)
Theorem 5
(Idempotency) If \({{\hat{Z}}_\theta },{\hat{Z}} \in {{\hat{Z}}^\# }\) and \({{\hat{Z}}_\theta } = {\hat{Z}}\), \(\theta = 1,2, \ldots ,t\) , then
Proof
Since for all \(\theta = 1,2, \ldots ,t\), we have \({{\hat{Z}}_\theta } = {\hat{Z}}\),
According to \(\sum \limits _{\theta = 1}^t {{\omega _\theta } = 1} \),
\(\square \)
Theorem 6
(Boundedness) Let \({{\hat{Z}}_m} = \min ({{\hat{Z}}_1},{{\hat{Z}}_2}, \ldots ,{{\hat{Z}}_t})\), \({{\hat{Z}}_M} = \max ({{\hat{Z}}_1},{{\hat{Z}}_2}, \ldots ,{{\hat{Z}}_t})\). Then
Proof
For \({{\hat{Z}}_m} \le {{\hat{Z}}_\theta } \le {{\hat{Z}}_M}\), \(\theta = 1,2, \ldots ,t\), and \(\sum \limits _{\theta = 1}^t {{\omega _\theta } = 1} , \)
Therefore, \({{\hat{Z}}_m} \le {\phi _{ZPLWA}}({{\hat{Z}}_1},{{\hat{Z}}_2}, \ldots ,{{\hat{Z}}_t}) \le {{\hat{Z}}_M}\). \(\square \)
Remark 2
When \({\omega _\theta } = \frac{1}{t}\), the ZPLWA operator is reduced to the Z probabilistic linguistic averaging (ZPLA) operator.
4.2.2 ZPLWG operator
Second, we propose the Z probabilistic linguistic weighted geometric (ZPLWG) operator.
Definition 16
Let \({{\hat{Z}}^\# }\) be a ZPLTS, \({{\hat{Z}}_\theta } = ({{\hat{A}}_\theta },{{\hat{B}}_\theta }) \in {{\hat{Z}}^\# }\), \(\theta = 1,2, \ldots ,t\). A ZPLWG operator aggregation is as follows:
where \({\omega _\theta }\) is calculated by the method proposed in Sect. 4.1, \({\omega _\theta }\in [0,1]\), and \(\sum \limits _{\theta = 1}^t {{\omega _{\theta } } = 1} \).
Theorem 7
then their aggregated value by using the ZPLWG operator is also a ZPLV, and
Theorem 8
(Monotonicity) Let \(({{\hat{Z}}_1},{{\hat{Z}}_2}, \ldots ,{{\hat{Z}}_t})\) and \(({{\hat{Z}}^*}_1,{{\hat{Z}}^*}_2, \ldots ,{{\hat{Z}}^*}_t)\) be two ZPLTSs. If \({{\hat{Z}}_\theta } < {{\hat{Z}}^*}_\theta \) for all \(\theta = 1,2, \ldots ,t\), then
Theorem 9
(Idempotency) If \({{\hat{Z}}_\theta },{\hat{Z}} \in {{\hat{Z}}^\# }\) and \({{\hat{Z}}_\theta } = {\hat{Z}}\), \(\theta = 1,2, \ldots ,t\), then
Theorem 10
(Boundedness) Let \({{\hat{Z}}_m} = \min ({{\hat{Z}}_1},{{\hat{Z}}_2}, \ldots ,{{\hat{Z}}_t})\), \({{\hat{Z}}_M} = \max ({{\hat{Z}}_1},{{\hat{Z}}_2}, \ldots ,{{\hat{Z}}_t})\). Then
Remark 3
When \({\omega _\theta } = \frac{1}{t}\), the ZPLWG operator is reduced to the Z probabilistic linguistic geometric(ZPLG) operator.
4.2.3 ZPLWD operator
Finally, we propose the Z probabilistic linguistic weighted distance (ZPLWD) operator.
In ZPLVs, there is a positive ideal solution when \({\hat{A}}\) and \({\hat{B}}\) are both the largest, that is, the highest evaluation and the highest credibility.
Definition 17
Let \(R = {[{{\hat{Z}}_{\gamma \theta }}]_{s \times t}}\) be a ZPLV decision matrix, where
Then the positive ideal solution of the alternatives is \({{\hat{Z}}^ + } = ({\hat{Z}}_1^ + ,{\hat{Z}}_2^ + , \cdots ,{\hat{Z}}_t^ + )\), where
and \(({({L_{{{{\hat{A}}}_\theta }}}^{(m)})^ + },{({L_{{{{\hat{B}}}_\theta }}}^{(n)})^ + }) = ({s_{\mathop {\max }\limits _\gamma \{ p_{\gamma \theta }^{(m)}v_{\gamma \theta }^{(m)}\} }}, {s'_{\mathop {\max }\limits _\gamma \{ p_{\gamma \theta }^{(n)}v_{\gamma \theta }^{(n)}\} }})\), \(v_{\gamma \theta }^{(m)}\) and \(v_{\gamma \theta }^{(n)}\) are the subscripts of \({L_{{{{\hat{A}}}_{\gamma \theta }}}}^{(m)}\) and \({L_{{{{\hat{B}}}_{\gamma \theta }}}}^{(n)}\), respectively.
Definition 18
Let \({{\hat{Z}}^\# }\) be a ZPLTS, \({{\hat{Z}}_\theta } = ({{\hat{A}}_\theta },{{\hat{B}}_\theta }) \in {{\hat{Z}}^\# }\), and \(\theta = 1,2, \ldots ,t\). A ZPLWD operator aggregation is as follows:
where \({{\hat{Z}}_\theta }^ + \) is the positive ideal solution, which is calculated by Definition 17. \({\omega _\theta }\) is calculated by the method proposed in Section 4.1, \({\omega _\theta }\in [0,1]\), and \(\sum \limits _{\theta = 1}^t {{\omega _{\theta } } = 1} \).
Their aggregated value by using the ZPLWD operator is the distance between \({x_\gamma }\) and the optimal alternative, and it is labeled as \(d({x_\gamma },{Z^ + })\). \(d({{\hat{Z}}_\theta },{{\hat{Z}}_\theta }^ + )\) can also be abbreviated to \({d_\theta }\).
Theorem 11
(Monotonicity) Let \(({{\hat{Z}}_1},{{\hat{Z}}_2}, \ldots ,{{\hat{Z}}_t})\) and \(({{\hat{Z}}^*}_1,{{\hat{Z}}^*}_2, \ldots ,{{\hat{Z}}^*}_t)\) be two ZPLTSs. If \({d_\theta } < {d_\theta }^*\) for all \(\theta = 1,2, \ldots ,t\), then
Theorem 12
(Idempotency) If \({{\hat{Z}}_\theta },{\hat{Z}} \in {{\hat{Z}}^\# }\) and \({d_\theta } = d\), \(\theta = 1,2, \ldots ,t\), then
Theorem 13
(Boundedness) Let \({d_m} = \min ({d_1},{d_2}, \ldots ,{d_t})\), \({d_M} = \max ({d_1},{d_2}, \ldots ,{d_t})\). Then
4.3 An extended TOPSIS method for ZPLTSs
We propose a series of operators in the last section, but the aggregation process leads to increased computational complexity and loss of decision information. In order to overcome these shortcomings, we propose an extended TOPSIS method for ZPLTs to solve MAGDM problems in Z probabilistic linguistic environment environment. The main idea of the TOPSIS method is to find an ideal solution which is the closest to the positive ideal solution and the farthest from the negative ideal solution.
Definition 19
Let \(R = {[{{\hat{Z}}_{\gamma \theta }}]_{s \times t}}\) be a ZPLV decision matrix. Then the attribute values vector of the alternative \({x_\gamma }(\gamma = 1,2, \ldots ,s)\) is \({{\hat{Z}}_\gamma } = ({{\hat{Z}}_{\gamma 1}},{{\hat{Z}}_{\gamma 2}}, \ldots ,{{\hat{Z}}_{\gamma t}})\).
The definition of the positive ideal solution is proposed in Definition 17. The negative ideal solution requires the worst evaluation and the highest credibility.
Definition 20
Let \(R = {[{{\hat{Z}}_{\gamma \theta }}]_{s \times t}}\) be a ZPLV decision matrix, where \( {{\hat{Z}}_{\gamma \theta }} = ({L_{{{{\hat{A}}}_{\gamma \theta }}}}({p_{{{{\hat{A}}}_{\gamma \theta }}}}),{L_{{{{\hat{B}}}_{\gamma \theta }}}}({p_{{{{\hat{B}}}_{\gamma \theta }}}})) = (\{ {L_{{{{\hat{A}}}_{\gamma \theta }}}}^{(m)}({p_{{{{\hat{A}}}_{\gamma \theta }}}}^{(m)})|m = 1,2, \ldots , \# {L_{{{{\hat{A}}}_{\gamma \theta }}}}({p_{{{{\hat{A}}}_{\gamma \theta }}}})\} ,\{ {L_{{{{\hat{B}}}_{\gamma \theta }}}}^{(n)}({p_{{{{\hat{B}}}_{\gamma \theta }}}}^{(n)})|n = 1,2, \ldots , \# {L_{{{{\hat{B}}}_{\gamma \theta }}}}({p_{{{{\hat{B}}}_{\gamma \theta }}}})\} ). \) Then the negative ideal solution of the alternatives is \({{\hat{Z}}^ - } = ({\hat{Z}}_1^ - ,{\hat{Z}}_2^ - , \cdots ,{\hat{Z}}_t^ - )\), where \( {\hat{Z}}_\theta ^ - = ({L_{{{{\hat{A}}}_\theta }}}^ - ({p_{{{{\hat{A}}}_\theta }}}),{L_{{{{\hat{B}}}_\theta }}}^ + ({p_{{{{\hat{B}}}_\theta }}})) = (\{ {({L_{{{{\hat{A}}}_\theta }}}^{(m)})^ - }|m = 1,2, \ldots , \# {L_{{{{\hat{A}}}_{\gamma \theta }}}}({p_{{{{\hat{A}}}_{\gamma \theta }}}})\} ,\{ {({L_{{{{\hat{B}}}_\theta }}}^{(n)})^ + }|n = 1,2, \ldots , \# {L_{{{{\hat{B}}}_{\gamma \theta }}}}({p_{{{{\hat{B}}}_{\gamma \theta }}}})\} )\ and\ ({({L_{{{{\hat{A}}}_\theta }}}^{(m)})^ - },{({L_{{{{\hat{B}}}_\theta }}}^{(n)})^ + })= ({s_{\mathop {\min }\limits _\gamma \{ p_{\gamma \theta }^{(m)}v_{\gamma \theta }^{(m)}\} }},{s'_{\mathop {\max }\limits _\gamma \{ p_{\gamma \theta }^{(n)}v_{\gamma \theta }^{(n)}\} }}), {v_{\gamma \theta }^{(m)}} \) and \({v_{\gamma \theta }^{(n)}}\) are the subscripts of \({L_{{{{\hat{A}}}_{\gamma \theta }}}}^{(m)}\) and \({L_{{{{\hat{B}}}_{\gamma \theta }}}}^{(n)}\), respectively.
The distance between \({x_\gamma }\) and the positive ideal solution is:
where
\({\omega _\theta }\) is calculated by the method proposed in Sect. 4.1.
The distance between \({x_\gamma }\) and the negative ideal solution is:
where
\({\omega _\theta }\) is calculated by the method proposed in Sect. 4.1.
It is not difficult to see that the smaller \(d_{\min }^ +\) is, the larger \(d_{\max }^ -\) is, the better the alternative is.
The smallest distance between \({x_\gamma }\) and the positive ideal solution is:
The largest distance between \({x_\gamma }\) and the negative ideal solution is:
Then, the closeness coefficient of the alternative \({x_\gamma }(\gamma = 1,2, \ldots ,s)\) is:
The best alternative is:
4.4 A MAGDM model based on ZPLTSs
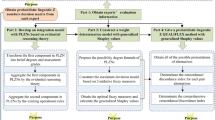
ZPLTS can be widely used in MAGDM because it can not only show the preference of DMs, but also represent information in a more comprehensive way. We build a MAGDM model based on ZPLTSs in this section. The flow chart of the model is shown in Fig.3.
In a MAGDM problems, assume there are a discrete set of alternatives \(X = \{ {x_1},{x_2}, \ldots ,{x_s}\} (s \ge 2)\), a set of DMs \(D = \{ {d_1},{d_2}, \ldots ,{d_\eta }\} (\eta \ge 2)\), and a set of attributes \(C = \{ {c_1},{c_2}, \ldots ,{c_t}\} (t \ge 2)\). Each DM give a ZPLV decision matrix \({R^\eta }(\eta = 1,2, \cdots ,q)\) to evaluate every attributes of different alternatives. \({R^\eta } = {[{{\hat{Z}}^\eta }_{\gamma \theta }]_{s \times t}}\) and \( {{\hat{Z}}^\eta }_{\gamma \theta } = ({{\hat{A}}^\eta }_{\gamma \theta },{{\hat{B}}^\eta }_{\gamma \theta }) = ({L^\eta }_{{{{\hat{A}}}_{\gamma \theta }}}({p^\eta }_{{{{\hat{A}}}_{\gamma \theta }}}),{L^\eta }_{{{{\hat{B}}}_{\gamma \theta }}}({p^\eta }_{{{{\hat{B}}}_{\gamma \theta }}})) = (\{ {L^\eta }{_{{{{\hat{A}}}_{\gamma \theta }}}^{(m)}}({p^\eta }{_{{{{\hat{A}}}_{\gamma \theta }}}^{(m)}})|m = 1,2, \ldots ,\# {L^\eta }_{{{{\hat{A}}}_{\gamma \theta }}}({p^\eta }_{{{{\hat{A}}}_{\gamma \theta }}})\} , \{ {L^\eta }{_{{{{\hat{B}}}_{\gamma \theta }}}^{(n)}}({p^\eta }{_{{{{\hat{B}}}_{\gamma \theta }}}^{(n)}})|n = 1,2, \ldots ,\# {L^\eta }_{{{{\hat{B}}}_{\gamma \theta }}}({p^\eta }_{{{{\hat{B}}}_{\gamma \theta }}})\} ). \)
Step 1. Combine all of the DMs’ evaluations and corresponding credibilities to construct the final ZPLV decision matrix \(R = {[{{\hat{Z}}_{\gamma \theta }}]_{s \times t}}\).
Step 2. Calculate the attribute weight vector by Eq. (16). If DMs choose the method of the operators, then go to Step 3. If DMs choose the extended TOPSIS method, then go to Step 5.
Step 3. DMs choose the appropriate operator according to the actual situation.
(1) Calculate the ZPLTS \({{\hat{Z}}_{x\gamma }}(\gamma = 1,2, \ldots ,s)\) of the alternative \({x_\gamma }\) by the ZPLWA operator.
(2) Calculate the ZPLTS \({{\hat{Z}}_{x\gamma }}(\gamma = 1,2, \ldots ,s)\) of the alternative \({x_\gamma }\) by the ZPLWG operator.
(3) Calculate the distance \(d({x_\gamma },{{\hat{Z}}^ + })\) between each alternative and the positive ideal solution by the ZPLWD operator.
Step 4. If DMs choose the ZPLWA operator and the ZPLWG operator, then rank \({\hat{Z}}_{x\gamma }\) with the ranking method proposed in Sect. 3.3. If DMs choose the ZPLWD operator, then the smaller \(d({x_\gamma },{{\hat{Z}}^ + })\) is, the better the alternative is. Select the best alternative(s) and go to Step 9.
Step 5. Determine the positive ideal solution \({{\hat{Z}}^ +}\) and the negative ideal solution \({{\hat{Z}}^ - }\) by Definitions 17 and 20.
Step 6. Calculate the distance \(d_\gamma ^ +\) between \({x_\gamma }\) and the positive ideal solution by Eq. (33). And calculate the distance \(d_\gamma ^ -\) between \({x_\gamma }\) and the positive ideal solution by Eq. (34).
Step 7. Calculate \(d_{\min }^ + \) and \(d_{\max }^ - \) by Eq. (35) and Eq. (36), respectively.
Step 8. Obtain \(C({x_\gamma })\) of each alternative by Eq. (37) and select the best one(s) by Eq. (38).
Step 9. End.
The MAGDM model contains two methods: the operators, and the extended TOPSIS method. It is easy to see from Fig.3 that the steps of the operators are relatively simple. The extended TOPSIS method reduce the loss of decision information. Each method has its advantages, so DMs can choose according to their needs.
5 Illustrative example and discussion
We illustrate ZPLTSs with a numerical example from (Pang et al. 2016).
5.1 A numerical example
A company plan a project in the next following years, and there are three projects to choose. Five company employers decide one integrated optimal project to be the development plan of the company. Assessment to evaluate mainly from the following four aspects:
-
(1)
Financial perspective(\({c_1}\));
-
(2)
The customer satisfaction(\({c_2}\));
-
(3)
Internal business process perspective(\({c_3}\));
-
(4)
Learning and growth perspective(\({c_4}\)).
DMs provide the decision information represented by ZPLVs according to their experience, which includes the evaluation and the corresponding credibility. The evaluation is based on the LTS
and the credibility is based on the LTS
Five linguistic decision matrixes provided by five DMs are listed in Table 1–5. Next, we use the operators and the extended TOPSIS method to calculate.
5.1.1 The aggregate operators
Step 1. The linguistic decision matrixes of five DMs are summarized into a ZPLV decision matrix. For example, for the first attribute of the first alternative, the evaluation information given by five DMs are \(({s_0},{s'_2})\), \(({s_1},{s'_3})\), \(({s_{ 1}},{s'_2})\), \(({s_1},{s'_3})\), and \(({s_0},{s'_3})\). For there are two \({s_0}\) and three \({s_1}\), the probabilities of \({s_0}\) and \({s_1}\) are 0.4 and 0.6. Similarly, the probabilities of \({s'_2}\) and \({s'_3}\) are 0.4 and 0.6. Therefore, the summarized ZPLV is \((\{ {s_0}(0.4),{s_1}(0.6)\} ,\{ {s'_2}(0.4),{s'_3}(0.6)\} )\). The ZPLV decision matrix is shown in Table 6. Then, normalize Table 6 to obtain the normalized matrix shown in Table 7.
Step 2. Calculate the attribute weight vector by Eq. (16).
Step 3. Select the optimal project with the operators based on ZPLTSs.
(1) Aggregate \({{\hat{Z}}_\gamma }(\gamma = 1,2,3)\) with the ZPLWA operator and select the optimal project.
Therefore, \({x_{1}}\) is the optimal project.
(2) Aggregate \({{\hat{Z}}_\gamma }(\gamma = 1,2,3)\) with the ZPLWG operator and select the optimal project.
Therefore, \({x_{1}}\) is the optimal project.
(3) Aggregate \({{\hat{Z}}_\gamma }(\gamma = 1,2,3)\) with the ZPLWD operator and select the optimal project.
Determaine the positive ideal solution.
Aggregate with the ZPLWD operator.
Therefore, \({x_{1}}\) is the optimal project.
5.1.2 The extended TOPSIS method
Step 1. Construct the ZPLV decision making matrix as Table 7.
Step 2. Calculate the attribute weight vector by Eq. (16).
Step 3. Determine \({{\hat{Z}}^ +}\) and \({{\hat{Z}}^ -}\) by Definitions 17 and 20.
Step 4. Calculate \(d_\gamma ^ + \) and \(d_\gamma ^ - \) by Eq. (33) and Eq. (34).
Step 5. Calculate \(d_{\min }^ + \) and \(d_{\max }^ - \) by Eq. (35) and Eq. (36).
Step 6. Obtain \(C({x_\gamma })\) of each project by Eq. (37) and select the best one by Eq. (38).
Therefore, \({x_1}\) is the optimal project.
5.2 Analysis and discussion
5.2.1 Comparison with particular ZPLVs
In this section, we explore the impact of the information credibility on ranking results. In the numerical example above, we set all of the credibilities as \(\{ {s'_3}(1),{s'_3}(0),{s'_3}(0)\} \), and then the normalized ZPLV decision matrix is constructed as Table 8. At this time, the credibility is the maximum, which can be ignored as ZPLVs degenerate into PLTSs. Repeat the calculation in the previous section, and the obtained results are compared with those obtained in Sect. 5.1, as shown in Table 9.
As can be seen from Table 9, the attribute weight vectors are the same. This is because all of the credibilities are equal. When the credibility of each evaluation is different, just like the example in Sect. 5.1, the obtained attribute weights are different. However, other weighting methods (such as the maximum deviation method) ignore the important role of the information credibility.
Except for attribute weights, the change of the credibility also lead to the changes of the ranking and the optimal alternative. These also prove the necessity of the ZPLTs and the ZPLVs proposed in this paper.
5.2.2 Comparison with PLTSs
We use PLTSs (Pang et al. 2016) to calculate the above example as a comparison. The processes are follows:
First, we take the probabilistic linguistic weighted averaging (PLWA) operator as an example.
Step 1. Construct a probabilistic linguistic decision making matrix and normalize it. The normalized matrix is shown in Table 10.
Step 2. Calculate the attribute weight vector by the maximizing deviation method.
Step 3. Aggregate \({{\tilde{Z}}_\gamma }(\omega )\) with the PLWA operator:
Then,
Step 4. The score of each alternative is
Step 5. Rank and select the optimal project.
Therefore, \({x_3}\) is the optimal project.
Then, the extended TOPSIS method with PLTSs is used to calculate the numerical example.
Step 1. Construct a probabilistic linguistic decision making matrix and normalize it. The normalized matrix is shown in Table 10.
Step 2. Calculate the attribute weight vector by the maximizing deviation method.
Step 3. Determine the PIS \(L{(p)^ + }\) and the NIS \(L{(p)^ - }\).
Step 4. Calculate the deviation degree \(d({x_\gamma },L{(p)^ + })\) between each project and the deviation degree \(d({x_\gamma },L{(p)^ - })\) between each project and the NIS.
Step 5. Calculate \({d_{\max }}({x_\gamma },L{(p)^ + })\) and \({d_{\min }}({x_\gamma },L{(p)^ - })\).
Step 6. Obtain the improved closeness coefficient \(C({x_\gamma })\) of each project and select the best one.
Therefore, \({x_1}\) is the optimal project.
The ranking results of PLTSs are compared those of ZPLVs when the credibility is the highest. The comparison results are shown in Table 11.
The attribute weights calculated by this paper are different from those calculated by Pang (Pang et al. 2016). This is due to the different emphasis of the two methods. This paper emphasizes the influence of the credibility on weights, and the maximum deviation method emphasizes the deviation degree of the evaluation.
Table 11 shows that the ranking and the optimal alternative obtained by both the operator method and the extended TOPSIS method are the same. This is because ZPLVs can degenerate to PLTSs under special circumstances(that is, when the credibility is the highest). The results in the table further confirm the theory. ZPLVs in this paper can not only represent the evaluation and probability in traditional PLTSs, but also the corresponding credibility. The diversity of information representation is an advantage over PLTSs.
5.2.3 Comparison with other linguistic representation method
We compare several linguistic representation methods in this section, including HFLTS, EHFLTS, PLTS, uncertain probabilistic linguistic term set (UPLTS) (Jin et al. 2019), linguistic Z-number, \(\mathrm{{{\mathcal {Z}}}}\) linguistic variable and ZPLTS proposed in this paper. The comparison aspects including the characteristics, the probability information, and the credibility. The comparison results are shown in Table 12.
As can be seen from Table 12, the ZPLTS can not only include the linguistic evaluation and the probability of preference, but also represent the credibility of information, making the decision information more complete and the decision result more accurate. A single PLTS or Z-number will not do the trick.
6 Conclusion
In GDM of PLTSs, only considering the linguistic terms and the probability distribution but ignoring the credibility of the information will lead to the loss of decision information, thereby affecting the accuracy of the decision results. Therefore, in this paper, we propose the ZPLTS in combination with the existing linguistic representation tools. The normalization, calculation, comparison method and distance measure are studied. Then we put forward a new weight calculation method based on the credibility, and put forward a MAGDM model based on ZPLTSs in combination with the correlation operators and the extended TOPSIS method. Finally, a numerical example and comparisons with other methods are given to prove its effectiveness.
In the future, we will discuss the new method to calculating probabilistic distribution in ZPLTSs. The current algorithm defaults to the same weight for all DMs. In addition, it is of great significance to further study the relevant theories of ZPLTSs and explore its application in public health emergency decision making.
References
Bai, C. Z., Zhang, R., Qian, L. X., & Wu, Y. N. (2017). Comparisons of probabilistic linguistic term sets for multi-criteria decision making. Knowledge-Based Systems,119((C)), 284–291.
Beg, I., & Rashid, T. (2013). Topsis for hesitant fuzzy linguistic term sets. International Journal of Intelligent Systems, 28(12), 1162–1171.
Gou, X. J., & Xu, Z. S. (2016). Novel basic operational laws for linguistic terms, hesitant fuzzy linguistic term sets and probabilistic linguistic term sets. Information Sciences, 372, 407–427.
Herrera, F., Herrera-viedma, E., & Verdegay, J. L. (1996). A model of consensus in group decision making under linguistic assessments. Fuzzy Sets & Systems, 78(1), 73–87.
Herrera, F., Herrera-viedma, E., & Verdegay, J. L. (1997). A rational consensus model in group decision making using linguistic assessments. Fuzzy Sets & Systems, 88(1), 31–49.
Jin, C., Wang, H., & Xu, Z. S. (2019). Uncertain probabilistic linguistic term sets in group decision making. International Journal of Fuzzy Systems, 21(4), 1241–1258.
Kang, B. Y., Yong, H., Deng, Y., & Zhou, D. Y. (2016). A new methodology of multicriteria decision-making in supplier selection based on z-numbers. Mathematical Problems in Engineering, 1, 1–17.
Liao, H. C., Mi, X. M., & Xu, Z. S. (2020). A survey of decision-making methods with probabilistic linguistic information: bibliometrics, preliminaries, methodologies, applications and future directions. Fuzzy Optimization and Decision Making, 19, 81–134.
Pang, Q., Wang, H., & Xu, Z. S. (2016). Probabilistic linguistic term sets in multi-attribute group decision making. Information Sciences, 369, 128–143.
Rodriguez, R. M., Martinez, L., & Herrera, F. (2012). Hesitant fuzzy linguistic term sets for decision making. IEEE Transactions on Fuzzy Systems, 20(1), 109–119.
Torra, V. (2010). Hesitant fuzzy sets. International Journal of Intelligent Systems, 25(6), 529–539.
Wang, H. (2015). Extended hesitant fuzzy linguistic term sets and their aggregation in group decision making. International Journal of Computational Intelligence Systems, 8(1), 14–33.
Wang, J. Q., Cao, Y. X., & Zhang, H. Y. (2017). Multi-criteria decision-making method based on distance measure and choquet integral for linguistic z-numbers. Cognitive Computation, 9(6), 827–842.
Wei, C. P., Zhao, N., & Tang, X. J. (2014). Operators and comparisons of hesitant fuzzy linguistic term sets. IEEE Transactions on Fuzzy Systems, 22(3), 575–585.
Wu, X. L., & Liao, H. C. (2018). An approach to quality function deployment based on probabilistic linguistic term sets and Oreste method for multi-expert multi-criteria decision making. Information Fusion, 43, 13–26.
Xian, S. D., Chai, J. H., & Yin, Y. B. (2019). A visual comparison method and similarity measure for probabilistic linguistic term sets and their applications in multi-criteria decision making. International Journal of Fuzzy Systems, 21(4), 1154–1169.
Xian, S. D., Chai, J. H., & Guo, H. L. (2019). Z linguistic-induced ordered weighted averaging operator for multiple attribute group decision-making. International Journal of Intelligent Systems, 34(2), 271–296.
Xian, S. D., & Sun, W. J. (2014). Fuzzy linguistic induced Euclidean OWA distance operator and its application in group linguistic decision making. Journal of Intelligent Systems, 29(5), 478–491.
Xiao, Z. Q. (2014). Application of z-numbers in multi-criteria decision making. International Conference on Informative & Cybernetics for Computational Social Systems, 91–95.
Xu, Z. S. (2004). Uncertain linguistic aggregation operators based approach to multiple attribute group decision making under uncertain linguistic environment. Information Sciences, 168(1), 171–184.
Xu, Z. S. (2005). Deviation measures of linguistic preference relations in group decision making. Omega-international Journal of Management Science, 33(3), 249–254.
Yaakob, A. M., & Gegov, A. (2016). Interactive topsis based group decision making methodology using z-numbers. International Journal of Computational Intelligence Systems, 9(2), 311–324.
Zadeh, L. A. (1965). Fuzzy sets. Information & Control, 8(3), 338–353.
Zadeh, L. A. (1975). The concept of a linguistic variable and its application to approximate reasoning. Information Sciences, 8(3), 199–249.
Zadeh, L. A. (2011). A note on z-numbers. Information Sciences, 181(14), 2923–2932.
Zhang, Y. X., Xu, Z. S., Wang, H., & Liao, H. C. (2016). Consistency-based risk assessment with probabilistic linguistic preference relation. Applied Soft Computing, 49(C), 817–833.
Acknowledgements
This work was supported by the Chongqing Research and Innovation Project of Graduate Students (No. CYS19254), Graduate Teaching Reform Research Program of Chongqing Municipal Education Commission (No. YJG183074) and the Chongqing Social Science Planning Project (No. 2018YB SH085).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Chai, J., Xian, S. & Lu, S. Z probabilistic linguistic term sets and its application in multi-attribute group decision making. Fuzzy Optim Decis Making 20, 529–566 (2021). https://doi.org/10.1007/s10700-021-09351-2
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10700-021-09351-2