1 Introduction

In today’s competitive world, products’ life cycles have become shorter, and firms are required to more frequently introduce new products to their customers. Usually, placing a new product into the market requires the participation of several firms. Each firm wants to get as much profit as possible regardless of the whole system’s profits, automatically leading to a decentralization of decisions. Most of the literature on supply chain management highlights the disadvantages of decentralization and underlines the benefits of cooperation in mitigating its inefficiency on the whole system.

In this paper, we pursue this research field by investigating a supply chain that consists of two capacitated suppliers and a customer who faces the offer of a new product procurement contract. The customer decides on how to allocate the new product demand volume between the two suppliers. The suppliers compete for the new product offer by choosing base stock inventory levels in a way to maximize their profits. Moreover, each of the three players decides on accepting or rejecting the deal according to its profitability.

To model competition between players, we have applied game theory. In particular, we use the Nash equilibrium concept to determine players’ strategies. According to this concept, we suppose that players have equivalent dominance power. This is the case when large companies negotiate with large-sized suppliers. It is also the case when medium or small-sized firms interact with each other.

Considering the centralized system performances (where the supply chain is optimized as a whole) as a benchmark, we highlight the inefficiency of the decentralization of decisions and show that it may lead to the loss of the new product offer. To improve the decentralized system performances, we derive coordination arrangements between partners that make the decentralized system perform as well as the centralized one. We give simple and feasible conditions that allow each player to earn higher profits under coordination.

The remainder of the paper is structured as follows. In the second section, we present the related literature review. In Sect. 3, we describe our model. We then analyze the decentralized and centralized system performances in Sect. 4, while in Sect. 5, we expose the coordination arrangements. Our analyses are illustrated through a numerical example in Sect. 6. Finally, we present conclusions and research perspectives in Sect. 7.

2 Literature review

In the last 2 decades, several studies have focused on the interaction between supply chain actors in the context of production/inventory systems. In particular, some of these papers considered interactions within the same firm. For example, Benjaafar et al. (2004) investigated the multiple manufacturing facilities system. These authors gave a solution procedure to obtain the optimal demand allocation parameters and optimal base stock levels that each facility has to keep. Arda (2008) analyzed a model that includes a make to stock producer who allocates demand to several facilities experiencing make to order queues. Benjaafar et al. (2008) treated the case of multiple demand sources and multiple distribution centers and focused on how to allocate each demand to the different distribution centers.

A second stream of papers considered the competition and collaboration between independent actors. These papers can be classified into two families. In the first family, the authors focus on the competition within a two-stage supply chain. Players are generally competing on inventory positioning (Cachon and Zipkin 1999; Jemai and Karaesmen 2007), on transfer payments between players (Arda and Hennet 2008), on sub-contracting decisions (Saharadis et al. 2009), on order sequencing and on due date quotations (Kaminsky and Kaya 2009).

In the second family of papers, the authors consider competition between actors in the same supply chain stage. Ha et al. (2003) presented the competition between two suppliers serving one customer whose allocation decision depends on the suppliers’ mean delivery time in a deterministic environment. Cachon and Zhang (2007) investigated a model in which a customer has to split demand volume between two make to order servers that are competing on their capacities. They exposed some demand allocation frameworks that exist in the literature and studied suppliers’ responses at the equilibrium for each framework. Benjaafar et al. (2007) presented a way of stressing competition between identical suppliers by means of the proportional demand allocation scheme. According to this allocation scheme, each supplier gets more demand volume if he offers a better service level. Bernstein and de Véricourt (2008) studied a system that includes two suppliers and two customers. Each customer proposes a new item and allocates all its demand volume to the supplier who offers the highest backorder penalty. The authors studied the suppliers’ competition and analyzed their choices at equilibrium. Ching et al. (2011) generalized the model of Benjaafar et al. (2007) by including a penalty scheme for the suppliers who do not meet the promised delivery time. For identical supply chain structures, Elahi (2013) compared service level and inventory level competitions and showed that the latter creates a higher service level for the buyer. Elahi and Blake (2014) used laboratory experiments to examine those theoretical results. Ernez-Gahbiche et al. (2016a) considered competition between two suppliers on an external new product offer. Ernez-Gahbiche et al. (2016b) analyzed competition between coalitions of suppliers on a new product deal. They modeled their problem through a Stackelberg game where the customer dominates the supply chain.

All these papers treated the interaction between supply chain members with two forms. Some papers treated systems where the customer is leader in the game. For instance, Arda and Hennet (2008) analyzed a system where a customer decides on the backorder penalty that his supplier is charged for unmet demand. Caldentey and Wein (2003) and Jemai and Karaesmen (2007) treated the case where the customer decides on each actor’s stock position. The Stackelberg game is the tool offered by game theory to model such situations. Generally, the idea of dominance between supply chain actors stands when a large company operates with small or medium-sized companies. Some other papers focus on models where players have equivalent dominance power with respect to each other. This is the case when a large company negotiates with another company that has almost the same power or when medium-sized firms or small firms interact with each other. In the earlier mentioned references, we note the research works of Jemai and Karaesmen (2007) in the case of a two-stage supply chain (Cachon and Zhang 2007) in the case of two suppliers and (Benjaafar et al. 2007) in the case of multiple suppliers. The Nash equilibrium is the tool offered by game theory to model such situations.

Some of the earlier mentioned references shed light on the contract coordination that players may agree to adopt to cope with decentralization inefficiency (see for example Jemai and Karaesmen 2007; Arda and Hennet 2008; Caldentey and Wein 2003; Cachon and Zipkin 1999). Cachon (2000) conducted an extensive literature review about coordination arrangements.

Our paper is in the field of the papers presented above since it addresses competition and coordination between two suppliers and one customer. Our major contributions are threefold:

  • We consider a more general framework. Indeed, the presented papers considering multi-suppliers’ model generally focus on the downstream stage performances. However, in our model, the customer is considered as an actor and participates in the game. Moreover, the earlier mentioned papers considered that supply chain actors accept the demand volume that they are allocated and do not discuss the possibility of refusal. In this paper, we introduce the acceptance variable as a decision parameter. The literature that studied the problem of admitting or rejecting the offer of a new item is limited. However, we do acknowledge the model of Carr and Duenyas (2000) that gives the supplier the ability to accept or to reject orders, which makes their problem a scheduling one. What distinguishes this paper from theirs is that this paper examines the possibilities of accepting or rejecting a new product offer.

  • We consider a one-stage game where each player concurrently decides on its strategies. Indeed, there is interdependence between participation and operational parameters. Participation decisions depend on each player’s profits, which in turn depend on the players’ operational decisions. We propose a further refinement similar to some related papers in the literature that consider multi-stage game modeling where decisions are made according to some order and decisions in a stage serve as game parameters in the following stages. For example, Anupindi et al. (2001) and Granot and Sošic (2003) considered multi-stage models where the first stage concerns decentralized decisions and the second stage concerns cooperative decisions. Furthermore (El Ouardighi 2014) analyzed a two-stage system where in the first stage players choose the type of contract that they will establish together, and in the second stage players implement their management decisions.

  • For the considered model, we derive Nash equilibria between the three players and obtain interesting insights on the interactions between them. We propose a transfer payment contract that allows the decentralized system to behave as the centralized one. We also provide conditions under which collaboration is beneficial for all of the players.

3 Modeling assumptions and notations

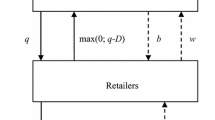
We consider a customer who faces the offer of a new product procurement contract. He determines how to allocate the new product’s demand volume between two different capacity suppliers in a way that would maximize his own profits. The suppliers may differ in the new item’s sale prices and supply costs. They compete to attract the customer based on base stock level guarantees. Furthermore, each of the three actors has the option of accepting or refusing the new product deal.

Demand occurs according to a Poisson process with rate λ. Since our work is in the Business to Business (B to B) context, we consider a system with backorders. Therefore, all orders that cannot be satisfied are backordered. The customer incurs a backorder penalty cost B per unit backordered and earns P for each product unit sold. The customer is charged a sale price pi and transportation costs tci for each unit purchased from supplier-i. Unit processing times at each supplier facility are stochastic, independent and exponentially distributed with mean \( \frac{1}{{\mu_{i} }} \) at supplier-i, i ∈ {1, 2}. Each supplier-i is charged production costs ci, holding costs hi per item per unit time and a backorder penalty bi per item per unit time. The penalty is paid to the customer.

The three actors simultaneously decide on their strategies, and a competition is drawn between them. Each supplier-i, i ∈ {1, 2} has to decide on a pair of decisions (Ai, si), where Ai is a binary variable expressing supplier-i’s acceptance (Ai = 1) or refusal (Ai = 0) of the customer’s offer, and si is the base stock level supplier-i decides to install. The customer has to decide on a triplet of decisions (A0, α1, α2) where A0 is a binary variable revealing the customer’s acceptance or refusal of the new product offer, and αi ∈ [0, 1] is the percentage of demand allocated to supplier-i.

None of the two suppliers are allocated a demand volume if the customer refuses the offer. However, all demand volume is allocated to suppliers if the customer accepts the offer. We resume these assumptions by letting α1 + α2 = A0. A supplier-i is not allocated a demand volume if he refuses the offer. Therefore, we suppose that αi ≤ Ai. We suppose that the unprofitability of the deal is the only reason of refusal.

We denote the ρi(αi) supplier-i utilization rate as:

$$ \rho_{i} \left( {\alpha_{i} } \right) = \frac{{\alpha_{i} \lambda }}{{\mu_{i} }},\quad \forall i\, \in \,\left\{ {1, \, 2} \right\} $$
(1)

Each supplier’s system stability requires that ρi(αi) < 1. If we satisfy this constraint ∀i ∈ {1, 2}, then we satisfy the whole system stability: λ < μ1 + μ2. However, 0 ≤ αi ≤ 1, and thus we can resume these constraints by imposing that \( \alpha_{1} \in \left[ {0,1} \right] \cap \left] {1 - \frac{{\mu_{2} }}{\lambda },\frac{{\mu_{1} }}{\lambda }} \right[ \), and we denote this interval by J.

$$J=\left[ {0,1} \right] \cap \left] {1 - \frac{{\mu_{2} }}{\lambda },\frac{{\mu_{1} }}{\lambda }} \right[.$$
(2)

Since the arrival of demand is a Poisson process and service time has an exponential distribution, the production inventory system of each supplier can be modeled as an M/M/1 queue. The average inventory and backorder levels were established by Buzacott and Shanthikumar (1993) who showed that the two corresponding expressions are respectively of the form:

$$ \bar{X}_{i} = s_{i} - \frac{{\rho_{i} \left( {\alpha_{i} } \right)}}{{1 - \rho_{i} \left( {\alpha_{i} } \right)}}\left( {1 - \left( {\rho_{i} \left( {\alpha_{i} } \right)} \right)^{{s_{i} }} } \right) $$
(3)
$$ \bar{Y}_{i} = \frac{{\left( {\rho_{i} \left( {\alpha_{i} } \right)} \right)^{{s_{i} + 1}} }}{{1 - \rho_{i} \left( {\alpha_{i} } \right)}} $$
(4)

Let ξ = ((A0, α1, α2), (A1, s1), (A2, s2)) be an example of players’ strategies. We define πi(ξ) as the profit function of supplier-i, i ∈ {1, 2} and π0(ξ) as the profit function of the customer. Then:

$$ \pi_{0} \left( \xi \right) = A_{0} \mathop \sum \limits_{i = 1}^{2} A_{i} \left( {\left( {P - p_{i} - tc_{i} } \right)\alpha_{i} \lambda - \left( {B - b_{i} } \right)\bar{Y}_{i} } \right) $$
(5)
$$ \pi_{1} \left( \xi \right) = A_{0} A_{1} \left( {\left( {p_{1} - c_{1} } \right)\alpha_{1} \lambda - b_{1} \bar{Y}_{1} } \right) - h_{1} \bar{X}_{1} $$
(6)
$$ \pi_{2} \left( \xi \right) = A_{0} A_{2} \left( {\left( {p_{2} - c_{2} } \right)\alpha_{2} \lambda - b_{2} \bar{Y}_{2} } \right) - h_{2} \bar{X}_{2} $$
(7)

Since players operate in a stochastic environment, we suppose that the customer and both suppliers are risk neutral. This assumption is widely used in the literature related to our paper (see Benjaafar et al. 2007; Elahi 2013).

4 Decentralized versus centralized system optimal performances

The performances of the decentralized system are measured with respect to the centralized system ones since they are the best performances the decentralized system can ever reach. In this section, we analyze the Nash equilibria resulting from the competition between the two suppliers and the customer. Then, we study the centralized system performances.

4.1 The decentralized system

In this section, we develop the decentralized system performances. First, we present a brief definition of the Nash equilibrium. Second, we determine all Nash equilibria resulting from our game through Propositions 1, 2 and 3. Then, we partially characterize the influence of some system parameters on the obtained equilibria.

Each supplier has to express his acceptance or refusal of the new product offer and has to decide on the base stock level to install. On the other hand, the customer has to decide on whether he accepts or rejects the new product offer and on the demand allocation scheme between suppliers.

As defined by Osborne and Rubinstein (2011), a Nash equilibrium is an action profile \( a^{*} = \{ a_{1}^{*} , \ldots ,a_{n}^{*} \} \) that has the property that no player j can do better by choosing an action different from \( a_{j}^{*} \), given that every other player k adheres to \( a_{k}^{*} \).

In the case of our Nash game, unlike most of the models treated in the literature, each player’s action contains more than one decision variable. In fact, each supplier-i decides on the couple (Ai, si) and the customer decides on (A0, α1, α2).

Next, we show the existence of Nash equilibria and we determine all of them. We denote \( \upxi^{*} = ((A_{0}^{*} ,\alpha_{1}^{*} ,\alpha_{2}^{*} ),(A_{1}^{*} ,s_{1}^{*} ),(A_{2}^{*} ,s_{2}^{*} )) \) as a Nash equilibrium.

We adopt the following classifications:

  • \( {\mathbb{E}}^{0} \) is the set of Nash equilibria corresponding to the refusal of the deal by the customer.

    $$ {\mathbb{E}}^{0} = \left\{ { \xi^{0} = \left( {\left( {A_{0}^{*} ,\alpha_{1}^{*} ,\alpha_{2}^{*} } \right),\left( {A_{1}^{*} ,s_{1}^{*} } \right),\left( {A_{2}^{*} ,s_{2}^{*} } \right)} \right){ \setminus }A_{0}^{*} = 0} \right\}. $$

  • \( {\mathbb{E}}^{1} \) is the set of Nash equilibria where the demand volume is allocated to only one supplier.

    $$ {\mathbb{E}}^{1} = \left\{ {\xi^{1} = \left( {\left( {A_{0}^{*} ,\alpha_{1}^{*} ,\alpha_{2}^{*} } \right),\left( {A_{1}^{*} ,s_{1}^{*} } \right),\left( {A_{2}^{*} ,s_{2}^{*} } \right)} \right){ \setminus }A_{0}^{*} = 1\,\, {\text{and}}\,\, \alpha_{1}^{*} = 1 \,\,{\text{or}}\,\, \alpha_{2}^{*} = 1} \right\}. $$

  • \( {\mathbb{E}}^{2} \) is the set of Nash equilibria where the demand volume is split between the two suppliers.

    $$ {\mathbb{E}}^{2} = \left\{ {\xi^{2} = \left( {\left( {A_{0}^{*} ,\alpha_{1}^{*} ,\alpha_{2}^{*} } \right),\left( {A_{1}^{*} ,s_{1}^{*} } \right),\left( {A_{2}^{*} ,s_{2}^{*} } \right)} \right) { \setminus }A_{0}^{*} = 1 \,\,{\text{and}}\,\, \alpha_{i}^{*} \in \left] {0,1} \right[ \forall i \in \left\{ {1,2} \right\}} \right\}. $$

  • It is clear that the set of all Nash equilibria is \( {\mathbb{E}} = {\mathbb{E}}^{0} \cup {\mathbb{E}}^{1} \cup {\mathbb{E}}^{2} \).

  • In the next proposition, we characterize the set \( {\mathbb{E}}^{0} \).

Proposition 1

$$ {\mathbb{E}}^{0} = \left\{ {\xi^{0} = \left( {\left( {0,0,0} \right),\left( {0,0} \right),\left( {0,0} \right)} \right)} \right\}. $$
(8)

Proof

See the “Appendix”.□

If the customer turns down the offer, the rest of the supply chain members refuse it as well.

In the next proposition, we characterize Nash equilibria where all demand volume is allocated to one supplier.

Proposition 2

$$ {\mathbb{E}}^{1} = {\mathbb{E}}_{a}^{1} \cup {\mathbb{E}}_{b}^{1} $$

where

$$ \begin{aligned} {\mathbb{E}}_{a}^{1} & = \left\{ {\begin{array}{*{20}l} {\xi_{a}^{1} = \left( {\left( {1, 1, 0} \right), (1, s_{1}^{*} ), \left( {0, 0} \right)} \right)} \hfill & {\,\,if\,\,\pi_{1} \left( {\xi_{a}^{1} } \right) > 0\,\,and\,\,\pi_{0} \left( {\xi_{a}^{1} } \right) > 0,} \hfill \\ \emptyset \hfill & {\,\,otherwise.} \hfill \\ \end{array} } \right. \\ {\mathbb{E}}_{\text{b}}^{1} & = \left\{ {\begin{array}{*{20}l} {\xi_{b}^{1} = \left( {\left( {1,0,1} \right),\left( {0,0} \right),\left( {1,s_{2}^{*} } \right)} \right)} \hfill & {\,\, if\,\,\pi_{2} \left( {\xi_{b}^{1} } \right) > 0\,\,and\,\,\pi_{0} \left( {\xi_{b}^{1} } \right) > 0,} \hfill \\ \emptyset \hfill & {\,\,otherwise.} \hfill \\ \end{array} } \right. \\ \end{aligned} $$
$$ s_{1}^{*} = \left\lfloor {\frac{{{\text{Log}}\left( {\frac{{h_{1} }}{{h_{1} + b_{1} }}} \right)}}{{{\text{Log}}\left( {\rho_{1} \left( 1 \right)} \right)}}} \right\rfloor , \quad s_{2}^{*} = \left\lfloor {\frac{{{\text{Log}}\left( {\frac{{h_{2} }}{{h_{2} + b_{2} }}} \right)}}{{{\text{Log}}\left( {\rho_{2} \left( 1 \right)} \right)}}} \right\rfloor $$
(9)

ρ1(1) and ρ2(1) are given by (1).

Proof

See the “Appendix”.□

Proposition 2 determines all Nash equilibria where the entire demand is allocated to a single supplier. Note that this set is composed of two types of equilibria: the equilibria where demand is fully assigned to supplier-1 (the set \( {\mathbb{E}}_{{a}}^{{{1}}} \)), and those where demand is fully assigned to supplier-2 (the set \( {\mathbb{E}}_{{b}}^{{{1}}} \)). Note that unlike the set \( {\mathbb{E}}^{{{0}}} \), the set \( {\mathbb{E}}^{{{1}}} \) may be empty depending on the values of the problem’s parameters.

By the Nash equilibria resulting from Proposition 2, our model returns to a one supplier–one customer supply chain. It aligns the problem handled by Jemai and Karaesmen (2007) if we consider that players accept the affair and that (in their model) the customer does not hold inventory.

In the next proposition, we characterize the Nash equilibria where the new product offer is accepted by players and demand volume is shared between both suppliers such that \( \upalpha_{i}^{*} \, \in \,]0, \, 1[\,\,\forall i\, \in \,\left\{ {1, \, 2} \right\} \). Let \( \upalpha_{2} = 1 -\upalpha_{1} \) and \( g\left( {{\text{s}}_{1} ,{\text{s}}_{2} ,{\alpha}_{1} } \right) \) be the derivative of the profit function \( {\pi}_{0} \) with respect to \( {\alpha}_{1} \). Then, we obtain:

$$ g\left( {s_{1} ,s_{2} ,\alpha_{1} } \right) = \frac{{\partial \pi_{0} }}{{\partial \alpha_{1} }} = \mathop \sum \limits_{i = 1}^{2} \left( { - 1} \right)^{i} \left\{ {\left( {p_{i} + tc_{i} } \right) \lambda + \frac{{\left( {B - b_{i} } \right) \lambda \left( {\rho_{i} \left( {\alpha_{i} } \right)} \right)^{{s_{i} }} \left( {1 + s_{i} \left( {1 - \rho_{i} \left( {\alpha_{i} } \right)} \right)} \right)}}{{\left( {1 - \rho_{i} \left( {\alpha_{i} } \right)} \right)^{2} \mu_{i} }}} \right\}. $$

Proposition 3

Let\( \hat{s}_{1} \left( {\upalpha_{1} } \right) = \left\lfloor {\frac{{Log\left( {\frac{{h_{1} }}{{h_{1} + b_{1} }}} \right)}}{{Log\left( {\rho_{1} \left( {{\alpha}_{1} } \right)} \right)}}} \right\rfloor \)and\( \hat{s}_{2} \left( {{{\upalpha}}_{1} } \right) = \left\lfloor {\frac{{Log\left( {\frac{{h_{2} }}{{h_{2} + b_{2} }}} \right)}}{{Log\left( {\rho_{2} \left( {1 -{\alpha}_{1} } \right)} \right)}}} \right\rfloor \).

If the equation\( g\left( {\hat{s}_{1} \left( {{\alpha}_{1} } \right),\hat{s}_{2} \left( {{\alpha}_{1} } \right),{\alpha}_{1} } \right) = 0 \)has no roots with respect to\( {\alpha}_{1} , \)then\( {\mathbb{E}}^{2} = \emptyset \).

Otherwise

Let\( \upalpha_{1}^{*} \)be a root of the equation\( g\left( {\hat{s}_{1} \left( {\upalpha_{1} } \right),\hat{s}_{2} \left( {{\alpha}_{1} } \right),{\alpha}_{1} } \right) = 0 \), and let\( s_{1}^{*} = \hat{s}_{1} \left( {{\alpha}_{1}^{*} } \right) \)and\( s_{2}^{{*}} = \hat{s}_{2} \left( {{\alpha}_{1}^{*} } \right) \).

For each root\( \alpha_{1}^{*} \), we denote\( \xi = \left( {\left( {1,\alpha_{1}^{*} ,1 - \alpha_{1}^{*} } \right),\left( {1,s_{1}^{*} } \right),\left( {1,s_{2}^{*} } \right)} \right) \).

  • If \( b_{1} > B,b_{2} < B \) and \( \mu_{1} > \lambda \) , then \( {\mathbb{E}}^{2} \) is the set of all ξ such that:

    1. 1.

      \( {\alpha}_{1}^{*} \, \in \,\left] {0, \, 1} \right[, \)

    2. 2.

      \( \frac{{\partial {\text{g}}}}{{\partial{\alpha}_{1} }}\left( {s_{1}^{*} ,s_{2}^{*} ,\alpha_{1}^{*} } \right) < 0 \),

    3. 3.

      \( {\pi}_{i} \left({\xi}\right) > 0 \,\,\forall i\, \in \,\left\{ {0, \, 1, \, 2} \right\}, \) and

    4. 4.

      \( \pi_{0} \left( \xi \right) \ge \pi_{0} \left( {\left( {1,1,0} \right),\left( {1,s_{1}^{*} } \right),\left( {1,s_{2}^{*} } \right)} \right). \)

  • If \( b_{1} < B, b_{2} > B \) and \( \mu_{2} > \lambda , \) then \( {\mathbb{E}}^{2} \) is the set of all ξ such that:

    1. 1.

      \( {\alpha}_{1}^{*} \, \in \,\left] {0, \, 1} \right[, \)

    2. 2.

      \( \frac{{\partial {\text{g}}}}{{\partial{\alpha}_{1} }}\left( {s_{1}^{*} ,s_{2}^{*} ,\alpha_{1}^{*} } \right) < 0 \),

    3. 3.

      \( {\pi}_{\text{i}} \left( {{\upxi}} \right) > 0 \,\,\forall i\, \in \,\left\{ {0, \, 1, \, 2} \right\}, \) and

    4. 4.

      \( \pi_{0} \left( \xi \right) \ge \pi_{0} \left( {\left( {1,0,1} \right),\left( {1,s_{1}^{*} } \right),\left( {1,s_{2}^{*} } \right)} \right). \)

  • If (\( b_{1} > B \)and\( \mu_{1} \le \lambda \)) or (\( b_{2} > B \)and\( \mu_{2} \le \lambda \)), then\( {\mathbb{E}}^{2} = \emptyset \).

  • Otherwise, \( {\mathbb{E}}^{2} \) is the set of all \( \xi \) such that

    1. 1.

      \( \alpha_{1}^{*} \, \in \,\left] {0, \, 1} \right[, \)

    2. 2.

      \( \frac{\partial g}{{\partial \alpha_{1} }}\left( {s_{1}^{*} ,s_{2}^{*} ,\alpha_{1}^{*} } \right) < 0 \)

    3. 3.

      \( \pi_{i} \left( {\xi^{2} } \right) > 0 \,\,\forall i\, \in \,\left\{ {0, \, 1, \, 2} \right\}. \)

Proof

See the “Appendix”.□

To determine the set \( {\mathbb{E}}^{2} \), we first have to determine the roots of the equation \( g(\hat{s}_{1} (\alpha_{1} ),\hat{s}_{2} (\alpha_{1} ),\alpha_{1} ) = 0 \). These roots are obtained numerically by means of an iterative algorithm that simply searches the solutions in the interval J through a small increment.

The set of all Nash equilibria is then \( {\mathbb{E}} = {\mathbb{E}}^{0} \cup {\mathbb{E}}^{1} \cup {\mathbb{E}}^{2} \). Note that at least there is a Nash equilibrium since \( {\mathbb{E}}^{0} \ne \emptyset \). However, as shown in Propositions 1, 2 and 3, there may be several Nash equilibria.

In the next lemma, we partially characterize the influence of some system parameters on the obtained equilibria.

Lemma 1

Recall that\( {\mathbb{E}}_{a}^{1} \)is the Nash equilibrium set where supplier-1 gets the whole demand volume and\( {\mathbb{E}}_{b}^{1} \)is the one where supplier-2 gets the whole demand volume.

  • ∃ μ01 > λ such that if\( \mu_{1} \le \mu_{01} , \)then\( {\mathbb{E}}_{\text{a}}^{1} = \emptyset \).

  • ∃ μ02 > λ such that if\( \mu_{2} \le \mu_{02} , \)then\( {\mathbb{E}}_{\text{b}}^{1} = \emptyset \).

There is no Nash equilibrium where all demand volume is allocated to supplier-i if his service capacity is less than some threshold μ0i, i ∈ {1, 2}.

Proof

See the “Appendix”.□

Remark

Let us note that in the study led here, we supposed that λ < μ1 + μ2 (see Sect. 3). Indeed, it is obvious that should the opposite occur, the affair can be only lost because we supposed that all of the demand must be satisfied in the case of acceptance. While it is out of our hypothesis indicated in Sect. 3, we can write that if λ ≥ μ1 + μ2, then \( {\mathbb{E}} = {\mathbb{E}}^{0} \).

We illustrate the results of Remarks 1 and 2 in Fig. 1 where we present all the possible Nash equilibria according to suppliers’ production capacities.

Fig. 1
figure 1

Possibilities of suppliers 1’s and 2’s shares of the new product deal as function of μ1 and μ2

Full size image

Lemma 2

When the whole supply chain is relatively loaded, the relaxation of the base stocks to their continuous form\( s_{i}^{*} \approx \hat{s}_{i} = \frac{{{\text{Log}}\left( {\frac{{h_{i} }}{{h_{i} + b_{i} }}} \right)}}{{{\text{Log}}\left( {\rho_{i} \left( {\alpha_{i} } \right)} \right)}} \)is known to be a good approximation in the literature (see Buzacott and Shanthikumar 1993). In this case, we can determine the earlier production capacity thresholds analytically as:

$$ \mu_{0i} = max\left\{ {\lambda \left( {1 + \frac{{b_{i} }}{{h_{i} }}} \right)^{{\frac{{h_{i} }}{{\left( {p_{i} - c_{i} } \right)\lambda }}}} , \lambda + \frac{{B - b_{i} }}{{P - p_{i} - tc_{i} }}\frac{{h_{i} }}{{h_{i} + b_{i} }} } \right\},\,\,\forall \,\,i\, \in \,\left\{ {1, \, 2} \right\}. $$
(10)

Proof

See the “Appendix”.□

4.2 Performances of the centralized system

To underline the impact of decentralization on system performances, we study the centralized system where the suppliers and the customer decisions are optimized in a centralized manner. The whole system receives the entire demand from the customer according to a Poisson process with rate λ, earns P per unit sold and pays a backorder penalty B per unit backordered per unit time. Each supplier-i incurs production and holding costs ci and hi, respectively. The unit transportation costs from supplier-i is tci.

In the centralized system, we have to determine the base stock level of each supplier-i sic, the amount of demand volume that will be allocated to him αicλ and the binary variable Ac that reveals the decision of acceptance Ac = 1 or refusal Ac = 0 of the new product offer by the whole system. The deal is refused by the system if it is not profitable.

Since the arrival of demand is a Poisson process and service time has an exponential distribution, the production inventory system of each supplier can be modeled as an M/M/1 queue. The average inventory \( \bar{X}_{ic} \) and backorder \( \bar{Y}_{ic} \) levels were established by Buzacott and Shanthikumar (1993) who showed that the two corresponding expressions are respectively of the form \( \bar{X}_{ic} = s_{ic} - \frac{{\rho_{i} (\alpha_{ic} )}}{{1 - \rho_{i} (\alpha_{ic} )}}\left( {1 - \rho_{i} (\alpha_{ic} )^{{s_{ic} }} } \right) \) and \( \bar{Y}_{ic} = \frac{{\rho_{i} (\alpha_{ic} )^{{s_{ic} + 1}} }}{{1 - \rho_{i} (\alpha_{ic} )}} \), where ρi(αic) is supplier-i’s utilization rate \( \rho_{i} \left( {\alpha_{ic} } \right) = \frac{{\alpha_{ic} \lambda }}{{\mu_{i} }}\,\, \forall \,i\, \in \,\left\{ {1, \, 2} \right\} \). To afford stability for each supplier’s production system, we impose that \( \alpha_{1c} \in {\text{J}} \).

The centralized system profits are denoted by πc. It consists of the system turnover minus the sum of the production and holding costs of suppliers and the backorder costs of the customer.

Our object is to maximize πc, which we can express as follows:

$$ \pi_{c} \left( {A_{c} ,\alpha_{1c} ,\alpha_{2c} ,s_{1c} , s_{2c} } \right) = A_{c} \left( {P \lambda - \mathop \sum \limits_{i = 1}^{2} \left( {\left( {c_{i} + tc_{i} } \right)\alpha_{ic } \lambda + B\bar{Y}_{ic} } \right)} \right) - \mathop \sum \limits_{i = 1}^{2} h_{i} \bar{X}_{ic} $$
(11)

where \( A_{c} = \left\{ {\begin{array}{*{20}l} 1 \hfill & {\,\,{\text{if}}\,\, \pi_{c} \left( {1,\alpha_{1c} ,\alpha_{2c} ,s_{1c} , s_{2c} } \right) > 0} \hfill \\ 0 \hfill & {\,\,{\text{otherwise}}} \hfill \\ \end{array} } \right. \).

Proposition 4

Let

$$ \hat{s}_{ic} \left( {\alpha_{ic} } \right) = \left\lfloor {\frac{{Log\left( {\frac{{h_{i} }}{{h_{i} + B}}} \right)}}{{Log\left( {\rho_{i} \left( {\alpha_{ic} } \right)} \right)}}} \right\rfloor \,\,if\,\,\alpha_{1c} \, \ne \,0\,\,and\,\,\hat{s}_{ic} \, = \,0\,\, \, otherwise\,\,\forall i\, \in \,\left\{ {1, \, 2} \right\} $$
(12)

and \( \tilde{\alpha }_{1c} = ArgMax_{{\alpha_{1c} \in {\text{J}}}} \pi_{c} \left( {1,\alpha_{1c} ,1 - \alpha_{1c} ,\hat{s}_{1c} \left( {\alpha_{1c} } \right),\hat{s}_{2c} \left( {1 - \alpha_{1c} } \right)} \right) \)

  • If\( \pi_{c} \left( {1,\tilde{\alpha }_{1c} ,1 - \tilde{\alpha }_{1c} ,\hat{s}_{1c} \left( {\tilde{\alpha }_{1c} } \right),\hat{s}_{2c} \left( {1 - \tilde{\alpha }_{1c} } \right)} \right) > 0 \), then\( A_{c}^{*} = 1, \alpha_{1c}^{*} = \tilde{\alpha }_{1c} , \alpha_{2c}^{*} = 1 - \tilde{\alpha }_{1c} ,s_{1c}^{*} = \hat{s}_{1c} \left( {\tilde{\alpha }_{1c} } \right) \), and\( s_{2c}^{*} = \hat{s}_{2c} \left( {1 - \tilde{\alpha }_{1c} } \right) \)

  • If\( \pi_{c} \left( {1,\tilde{\alpha }_{1c} ,1 - \tilde{\alpha }_{1c} ,\hat{s}_{1c} \left( {\tilde{\alpha }_{1c} } \right),\hat{s}_{2c} \left( {1 - \tilde{\alpha }_{1c} } \right)} \right) \le 0 \), then\( A_{c}^{*} , s_{ic}^{*} = 0 \)and\( \alpha_{ic}^{*} = 0\,\,\forall \,i\, \in \,\left\{ {1, \, 2} \right\} \).

Proof

See the “Appendix”.□

s1c and s2c in (11) are replaced with their expressions given by (12), and the resulting function depends only on αc. Since it is difficult to analytically characterize the values of \( \hat{\alpha }_{c} \), we constructed an algorithm that increases \( \hat{\alpha }_{c} \) with a small increment in each iteration and saves the highest corresponding πc value.

4.3 Comparison between the decentralized and the centralized systems

In this section, we study the system’s inefficiency due to decentralization of decisions. \( \pi_{d}^{*} \) denotes the whole decentralized system’s profits and Ad is a binary variable that expresses whether the offer is accepted (Ad = 1 if \( \pi_{d}^{*} > 0 \)) or refused (Ad = 0 if \( \pi_{d}^{*} \le 0 \)). Let \( \pi_{c}^{*} \) be the optimal centralized system profit. When \( \pi_{c}^{*} > 0 \), we define the competition penalty CP as the relative loss of the decentralized system with regard to the centralized one.

$$ CP = \frac{{\pi_{c}^{*} - \pi_{d}^{*} }}{{\pi_{c}^{*} }} \times 100 $$
(13)

In the next proposition, we derive some comparisons between centralized and decentralized systems.

Proposition 5

Regardless of the Nash equilibrium that results from the decentralized system, we have the following results:

  • \( \pi_{d}^{*} \le \pi_{c}^{*} , \)

  • If \( A_{c}^{*} = 0 \) then \( A_{d}^{*} = 0 \) , and

  • In addition, if the system parameters are such that

    $$ \begin{aligned} \mu_{1} & > \lambda > \mu_{2} \,\,and\,\,p_{1} + \frac{{h_{1} Exp\left( 1 \right)}}{{\mu_{1} }} Log\left( {\frac{{h_{1} }}{{h_{1} + b_{1} }} \frac{{\mu_{1} }}{{\lambda - \mu_{2} }}} \right) \\ & < c_{1} < P - tc_{1} - \frac{{h_{1} }}{\lambda }\frac{{Log\left( {\frac{{h_{1} }}{{h_{1} + B}}} \right)}}{{Log\left( {\frac{\lambda }{{\mu_{1} }}} \right)}} \\ \end{aligned} $$
    (14)

    then, the deal is accepted in the centralized model and refused in the decentralized one (i.e., \( A_{c}^{*} = 1 \) and \( A_{d}^{*} = 0 \) ). Consequently, CP = 100%.

Proof

See the “Appendix”.□

Proposition 5 shows that the offer can never be accepted in the decentralized system if it is refused in the centralized one. Inversely, the offer can be refused in the decentralized system (because of competition). Nevertheless, it is profitable for the system when it is managed in a centralized manner. In this case, the loss caused by competition is as high as 100%. Let us note that condition (14) is sufficient but not necessary. In fact, the offer can be refused in the decentralized system and accepted in the centralized one in other different situations. These cases will be detailed numerically.

5 Coordination of the decentralized system

As shown in Proposition 5, decentralized operations lead to a high loss of efficiency for the supply chain. This loss can reach 100%. In this section, we design contractual arrangements between players that allow the decentralized system to perform as efficiently as the centralized one while letting each player independently manage his system. First, we provide transfer payments between players. Second, we investigate some constraints on the transfer payment parameters so that players get higher profits after coordination.

Our coordination mechanism involves contracts that consist of a linear transfer payment from the customer to supplier-1 (Tr1) and from the customer to supplier-2 (Tr2):

$$ Tr_{1} \left( \xi \right) = A_{0} A_{1} \left( {\left( {1 - \zeta_{1} } \right)\left( {\left( {P - c_{2} - tc_{2} } \right)\alpha_{2} \lambda - h_{2} \bar{X}_{2} - B\bar{Y}_{2} } \right) + \zeta_{1} h_{1} {\bar{\text{X}}}_{1} } \right) $$
$$ Tr_{2} \left( \xi \right) = A_{0} A_{2} \left( {\left( {1 - \zeta_{2} } \right)\left( {\left( {P - c_{1} - tc_{1} } \right)\alpha_{1} \lambda - h_{1} \bar{X}_{1} - B\bar{Y}_{1} } \right) + \zeta_{2} h_{2} {\bar{\text{X}}}_{2} } \right) $$

where ξ = ((A0, α1, α2), (A1, s1), (A2, s2)) is an example of players strategies, and \( \upzeta_{1} \) and \( \upzeta_{2} \) are the contract parameters where \( \upzeta_{1} \) and \( \upzeta_{2} \, \in \,\left[ {0, \, 1} \right] \).

Through these transfer payments, the customer pays each supplier a holding cost subsidy and a part of the whole system’s profits.

Since suppliers’ sale prices are such that \( c_{1} < p_{1} < P - tc_{1} \) and \( c_{2} < p_{2} < P - tc_{2} \), they can be written as follows:

$$ p_{1} = \eta_{1} \left( {P - tc_{1} - c_{1} } \right) + c_{1} $$
$$ p_{2} = \eta_{2} \left( {P - tc_{2} - c_{2} } \right) + c_{2} $$

where η1 and η2 are in the interval ]0, 1[.

The new profits of the players are as follows:

$$ \pi_{0c} \left( \xi \right) = A_{0} \mathop \sum \limits_{i = 1}^{2} \left( {A_{i} \left( {\left( {1 - \eta_{i} } \right)\left( {P - tc_{i} - c_{i} } \right)\alpha_{i} \lambda - \left( {B - b_{i} } \right)\bar{Y}_{i} } \right)} \right) - \mathop \sum \limits_{i = 1}^{2} Tr_{i} \left( \xi \right) $$
(15)
$$ \pi_{1c} \left( \xi \right) = A_{0} A_{1} \left( {\left( {\eta_{1} \left( {P - tc_{1} - c_{1} } \right)} \right)\alpha_{1} \lambda - b_{1} \bar{Y}_{1} } \right) - h_{1} \bar{X}_{1} + Tr_{1} \left( \xi \right) $$
(16)
$$ \pi_{2c} \left( \xi \right) = A_{0} A_{2} \left( {\left( {\eta_{2} \left( {P - tc_{2} - c_{2} } \right)} \right)\alpha_{2} \lambda - b_{2} \bar{Y}_{2} } \right) - h_{2} \bar{X}_{2} + Tr_{2} \left( \xi \right) $$
(17)

In the next proposition, we present the set of possible contracts ((ζ1, ζ2), (η1, η2)) such that there is a Nash equilibrium that aligns the centralized system’s optimal performances.

Let \( \xi_{c}^{*} = \left( {1,\alpha_{1c}^{*} ,\alpha_{2c}^{*} ,s_{1c}^{*} , s_{2c}^{*} } \right) \) be the optimal centralized system solution.

Proposition 6

If

  • \( \zeta_{1} = 1 - \frac{{b_{1} }}{B} \) and \( \zeta_{2} = 1 - \frac{{b_{2} }}{B} \)

  • η1 = 1 − ζ1and η2 = 1 − ζ2

  • ζ1 < 1, ζ2 < 1 and ζ1 + ζ2 > 1

then,\( \xi^{*} = ((A_{c}^{*} , \alpha_{1c}^{*} , \alpha_{2c}^{*} ), (1, s_{1c}^{*} ), (1, s_{2c}^{*} )) \)is a Nash equilibrium of the decentralized system after coordination. In this case, CP = 0%.

Proof

See the “Appendix”. □

The transfer payment arrangements allow for the perfect coordination of the supply chain. Note that our coordination contract is applicable in the case of one supplier by simply supposing that the other supplier refuses the offer. In this case, our coordination contract is a holding cost subsidy by the customer to the supplier. This kind of contract was detailed by Cachon and Zipkin (1999).

To participate to this consortium, each player needs to obtain higher profits after coordination.

In the next proposition, we present some expressions of suppliers’ backorder penalties b1 and b2 such that each player gets better profits after coordination.

Recall that \( \pi_{c}^{*} \) is the optimal centralized system’s profits. \( \pi_{i}^{*} \) denotes the profits of player-i at the Nash equilibrium before coordination and \( \pi_{ic}^{*} \) denotes his profits at the equilibrium after coordination, where i ∈ {0, 1, 2}. Let \( \pi_{d}^{*} = \sum_{i = 0}^{2} \pi_{i}^{*} \).

Proposition 7

If\( b_{1}^{co} \)and\( b_{2}^{co} \)are such that

$$ b_{1}^{co} > B\frac{{\pi_{1}^{*} }}{{\pi_{c}^{*} }} $$
(18)
$$ b_{2}^{co} > B\frac{{\pi_{2}^{*} }}{{\pi_{c}^{*} }} $$
(19)
$$ b_{1}^{co} + b_{2}^{co} < B\left( {1 - \frac{{\pi_{0}^{*} }}{{\pi_{c}^{*} }}} \right) $$
(20)

then,\( \pi_{ic}^{*} \ge \pi_{i}^{*} \,\,\forall \,i\, \in \,\left\{ {0, \, 1, \, 2} \right\} \).

Proof

See the “Appendix”. □

As shown in Proposition 7, an adequate choice of backorder penalties contributes to better profits for each player. Consequently, it is interesting for all the players to accept the coordination contracts.

The choice of parameters \( b_{1}^{co} \) and \( b_{2}^{co} \) impacts the allocation of savings between players. In the next corollary, we provide a condition that allows an equal distribution of the additional benefits thanks to coordination.

Corollary

By letting

$$ b_{1}^{co} = \frac{B}{{ \pi_{c}^{*} }}\left( {\pi_{1}^{*} + \frac{{ \pi_{c}^{*} - \pi_{d}^{*} }}{3}} \right) \,\,and \,\,b_{2}^{co} = \frac{B}{{ \pi_{c}^{*} }}\left( {\pi_{2}^{*} + \frac{{ \pi_{c}^{*} - \pi_{d}^{*} }}{3}} \right) $$
(21)

Then, players’ profits increase at the same amount, i.e.,\( \pi_{1c}^{*} - \pi_{1}^{*} = \pi_{2c}^{*} - \pi_{2}^{*} = \pi_{0c}^{*} - \pi_{0}^{*} \).

Proof

See the “Appendix”. □

We note that the conditions in (21) satisfy constraints (18)–(20). Therefore, each player’s profits are higher with coordination. Moreover, profits increase at the same amount.

6 Numerical results

In this section, we numerically illustrate our principle results and give some insights.

6.1 Example 1: Study of the loss due to competition

To measure the gap between the centralized and the decentralized policies, we first consider an example where the two suppliers are identical except for their production capacities. The demand’s arrival rate is λ = 50 pallets/year where a pallet contains 1000 items.

The suppliers’ unit production costs are c1 = c2 = 8 €/item. The suppliers’ sale prices are p1 = p2 = 10 €/item. The customer’s sale price is P = 12.5 €/item. The transportation costs are tc1 = tc2 = 150 €/pallet. The unit inventory holding costs are h1 = h2 = 38 €/Pallet/week. The customer’s backorder penalty is B = 480 €/Pallet/week. The suppliers’ backorder penalties are b1 = b2 = b, where b = B/3. This value will be varied in the next numerical example.

Figure 2 shows the competition penalty (CP%) as a function of \( \frac{{\mu_{1} }}{{\mu_{1} + \mu_{2} }} \) for several values of the system load ρ, where \( \rho \, = \,\frac{\lambda }{{\mu_{1} + \mu_{2} }} \). We note that for symmetry reasons \( \frac{{\mu_{1} }}{{\mu_{1} + \mu_{2} }} \) takes values in the interval [0.5; 1]. We note that when several Nash equilibria exist, we report the Nash equilibrium that corresponds to the lowest CP value.

Fig. 2
figure 2

Competition penalty (CP%) as a function of supplier-1’s relative production capacity

Full size image

These curves show that the loss due to decentralization can be very important (between 20 and 100% in most of the cases). Recall that a 100% loss means that the offer is lost in the competitive case while it is accepted in the centralized one.

From these curves, it appears that CP is increasing with respect to the system load ρ. For ρ = 98%, the system becomes so loaded that the deal is refused in both the decentralized and the centralized cases. The overall profits will be zero in both cases.

To analyze the shape of the CP curves, we consider the example of ρ = 93%. This curve has three ranges. The first one is approximately \( 50\% \le \frac{{\mu_{1} }}{{\mu_{1} + \mu_{2} }} \le 60\% \). In this range, the production capacities of the two suppliers are almost identical. The offer will be shared between the two suppliers. The corresponding competition penalty is approximately 50%. In the second range (\( 60\% \le \frac{{\mu_{1} }}{{\mu_{1} + \mu_{2} }} \le 95\% \)), supplier-2 has a low capacity. Supplier-1’s production capacity is relatively large but not large enough to allow him to get the deal alone. Competition makes both suppliers refuse the offer, and thus, CP is equal to 100%. In the third range (approximately \( 95\% \le \frac{{\mu_{1} }}{{\mu_{1} + \mu_{2} }} \le 100\% \)), the offer is not lost because the production capacity of supplier-1 is very important and enables him to get the whole offer alone. The loss resulting from competition is also high in this range since, in the centralized system, supplier-2 is allocated a small amount of demand, which significantly reduces the costs. However, the impact of supplier-2 on this loss is reduced when his capacity is lower. This is why CP decreases when \( \frac{{\mu_{1} }}{{\mu_{1} + \mu_{2} }} \) approaches 100%.

6.2 Example 2: Supply chain coordination

We now consider a second example where the two suppliers are different in terms of production costs, transportation costs and sale prices. We suppose that the demand arrival rate is λ = 50,000 items/year. Suppliers’ production capacities are μ1 = μ2 = 52,000 items/year. The customer’s sale price is P = 12.5 €/item. The system backorder penalty is B = 480 €/Pallet/week. The unit inventory holding costs are h1 = h2 = 38€/Pallet/week. The suppliers’ production costs are c1 = 8 €/item and c2 = 6.5 €/item. The transportation costs are tc1 = 150 €/pallet and tc2 = 187 €/pallet. The suppliers’ sale prices (p1 and p2) and backorder penalties (b1 and b2) will be varied (see Tables 1, 2, 3).

Table 1 Competition versus coordination optimal performances \( \left( {b = \frac{B}{3}} \right) \)
Full size table
Table 2 Competition versus coordination optimal performance (b = B)
Full size table
Table 3 Competition versus coordination optimal performances (b = 3B)
Full size table

In these tables, we give players’ strategies at the Nash equilibrium (\( \alpha_{1}^{*} , \alpha_{2}^{*} , s_{1}^{*} , s_{2}^{*} \)) and their corresponding profits (\( \pi_{1}^{*} , \pi_{2}^{*} , \pi_{0}^{*} \)). We also give their decisions at the equilibrium under coordination (\( \alpha_{1c}^{*} , \alpha_{2c}^{*} , s_{1c}^{*} , s_{2c}^{*} \)) and the corresponding profits (\( \pi_{1c}^{*} , \pi_{2c}^{*} , \pi_{0c}^{*} \)). We follow the expressions of the corollary in the choice of \( b_{1}^{co} \) and \( b_{2}^{co} \) in the three tables. Finally, we present the competition penalty (CP). We note that when several Nash equilibria exist, we report the Nash equilibrium that maximizes the total supply chain profits.

Again, the loss due to competition is important and varies between 30 and 100% in most of the cases. These tables also show the huge interest of coordination in improving the profits of the three players. For example, for (p2 = 13 and b = b), the profits of supplier-1 increases from 17 to 75 M€/year, supplier-2’s profits grow from 0 to 58 M€/year and the customer’s profits rise from 67 to 125 M€/year.

It is also interesting to note the gap between competition and coordination optimal strategies. In the centralized case, the optimal allocation of demand between the two suppliers is (\( \alpha_{1c}^{*} \, = \,18\% \) and \( \alpha_{2c}^{*} \, = \,82\% \)) regardless of p2 and \( \frac{b}{B} \). In the decentralized case, because of competition, the demand allocation is very different. In some cases, it is fully assigned to the first supplier, and in some others it is fully assigned to the second supplier or it can be divided between the two suppliers in several demand allocation schemes (see columns \( \alpha_{1}^{*} \) and \( \alpha_{2}^{*} \)). The gaps between base stock levels are also very wide. Under coordination, the total base stock level is \( (s_{1c}^{*} \, + \,s_{2c}^{*} )\, = \,12 \) pallets. Under competition, the total base stock level \( \left( {s_{1}^{*} \, + \,s_{2}^{*} } \right) \) varies between 4 and 9 pallets if \( b = \frac{B}{3} \), between 66 and 71 pallets if b = B and 98 pallets if b = 3B.

This shows that base stock level varies significantly with respect to the penalty costs imposed by the customer and that the competition scheme can lead to over storage for high values of b and vice versa.

Looking at the evolution of \( \pi_{2}^{*} \) and \( \pi_{2c}^{*} \) with respect to p2, it appears that supplier-2’s sale price must be almost equal to supplier-1’s sale price, although c2 < c1. Indeed, a lower price will allow supplier-2 to get a higher portion of demand volume, but it will reduce his profit margin.

On the other hand, it appears that the customer has no interest in charging suppliers a high backorder penalty (see for example \( \pi_{0}^{*} \) and \( \pi_{0c}^{*} \) if p2 = 7). Note that, in most cases of this example, the penalty costs are also increasing with respect to \( \frac{{\text{b}}}{{\text{B}}} \): (CP(b > B) > CP(b = B) > CP(b < B).

7 Conclusion and perspectives

We have investigated a supply chain with two capacitated suppliers and a downstream customer who faced the offer of a new product deal. The customer decides how to allocate demand volume between suppliers according to their base stock levels’ commitment. In addition, each of the three players decides to accept or to refuse the concerned deal. In the case where all players manage their own systems in a decentralized manner, we showed that the game has pure Nash equilibria and we characterized them all. In addition, we analyzed the impact of different parameters on the system’s whole profits.

We showed that the decentralized system may be inefficient, and this inefficiency can be significant. In some cases the offer is lost, while it is accepted if the system is managed in a centralized manner. We presented linear transfer payments between the customer and each of the two suppliers that led to a perfect coordination of the supply chain. However, we allow each part to separately manage its system.

The last part of this paper was devoted to a numerical study where we underlined the impact of decentralization on the players’ systems’ performances and where we studied the benefit of our coordination arrangement.

It would be interesting to investigate the case where the customer holds inventory. In this case, the customer decides on the demand distribution and the stock to install. The multiple suppliers’ case could represent an interesting extension of our research work as well.

Finally, it would also be interesting to let suppliers cooperate and decide on how to divide demand volume between them. Some interesting insights may be drawn by comparing results with the optimal centralized system performances.