Incentives in experiments with objective lotteries

Abstract

Azrieli et al. (J Polit Econ, 2018) provide a characterization of incentive compatible payment mechanisms for experiments, assuming subjects’ preferences respect dominance but can have any possible subjective beliefs over random outcomes. If instead we assume subjects view probabilities as objective—for example, when dice or coins are used—then the set of incentive compatible mechanisms may grow. In this paper we show that it does, but the added mechanisms are not widely applicable. As in the subjective-beliefs framework, the only broadly-applicable incentive compatible mechanism (assuming all preferences that respect dominance are admissible) is to pay subjects for one randomly-selected decision.

1 Introduction

Consider an experiment in which subjects make two choices. The first is to choose from the set $\{$apple,left shoe$\}$, and the second is to choose from the set $\{$banana,right shoe$\}$. Most subjects would prefer the apple over the left shoe and the banana over the right shoe. But when both choices are paid then subjects may choose the shoes instead, because they prefer a pair of shoes over having both an apple and a banana. In other words, complementarities between choice objects may distort subjects’ choices when multiple decisions are given. An experimenter might infer incorrectly that the left shoe is preferred to the apple and that the right shoe is preferred to the banana. In this case we say that the payment mechanism is not incentive compatible (IC) because it did not incentivize subjects to reveal their true preference in each individual problem separately.¹

A proposed solution to the problem of complementarities (due to Allais 1953) is to pay for one randomly-selected decision. We call this the Random Problem Selection (RPS) mechanism.² With this mechanism subjects cannot receive both shoes, and therefore have no incentive to choose the shoe in either decision problem. Although this solves the complementarities problem, it introduces randomness. And there are examples of preferences over lotteries for which the RPS mechanism is not IC.³ Thus, exact conditions under which this mechanism is incentive compatible were not well understood. Neither was it known whether other mechanisms can be used to guarantee truthful revelation of choices in experiments with multiple decisions.

In our earlier work (Azrieli et al. 2018) we filled this gap by studying experiment incentives in a general framework in which subjects are permitted to have any subjective belief over random outcomes. Assuming state-wise monotonicity (which requires that subject’s preference respects dominance) and nothing else, we showed that the RPS mechanism is the only incentive compatible mechanism that can be applied to any experiment. There can be contrived examples of experiments for which other mechanisms are incentive compatible, but these are almost never seen in practice.

But what if an experiment consists entirely of objective lotteries? For example, suppose the experimenter flips a fair coin to determine which problem is paid. In this case allowing subjects to have any belief distribution over random outcomes may be too permissive. But if we restrict beliefs to equal the objective probabilities then we restrict the model, and in doing so we may open the door for additional incentive compatible mechanisms. Thus, it is important to study whether the set of incentive compatible mechanisms grows when we assume objective lotteries, and whether any of the new mechanisms would have broad applicability.

In this paper we assume objective probabilities and that all preferences which respect stochastic dominance are admissible. In this framework we show that the set of IC mechanisms is strictly larger than that characterized by Azrieli et al. (2018). But the newly-identified mechanisms are again only applicable in certain contrived experiments. In almost every real-world experiment the RPS mechanism is the unique incentive compatible mechanism under our assumptions.

As in Azrieli et al. (2018), we model an experiment as a list of decision problems, i.e. a list of sets of choice objects from which the subject should choose. The subject announces a chosen object from each decision problem. The experimenter then maps that announced vector of choices into a payment, which may be random. For example, the RPS mechanism takes the announced vector of choices and randomly chooses one of them for payment.

A crucial observation in this analysis is that the choice objects and the payment objects in an experiment are typically non-overlapping sets. In the example above the set of all choice objects would be $\{$apple,banana,left shoe,right shoe$\}$. The experimenter is interested in learning the subject’s preferences over those choice objects, which we denote by $\succ$.⁴ But the subject actually is being paid lotteries over these choice objects. Thus, the set of payment objects is a set of lotteries over the choice objects.⁵ Which choice objects the subject chooses in the experiment will therefore be driven by their preferences over payment objects (lotteries), not their preference over choice objects. We denote the preference over payment objects (lotteries) by $\succeq ^*$. In the experiment the subject chooses (or “announces”) the choice objects that map into her most-preferred payment object (according to $\succeq ^*$). We say that the payment mechanism is incentive compatible if what she announces coincides with her most-preferred choice objects according to $\succ$. In other words, incentive compatibility ensures that the subject will reveal truthfully her most-preferred choice in every problem.

We refer to $\succeq ^*$ as an extension of $\succ$. For us to study incentive compatibility we must make some assumptions about how $\succeq ^*$ relates to $\succ$. If they are not related—meaning every extension is admissible—then no mechanism can be incentive compatible. This is Proposition 0 of Azrieli et al. (2018). A natural restriction on extensions is that they satisfy monotonicity with respect to first order stochastic dominance (FOSD), relative to the underlying preference $\succ$. Formally, an extension is monotonic if lottery f is preferred to lottery g whenever f dominates g in the sense of FOSD. Monotonicity places no restrictions on lotteries that are not ranked by dominance.

We show in Theorem 1 that, as long as all admissible extensions are monotonic, the RPS mechanism is IC. In other words, if a subject’s preferences are such that she never prefers a dominated gamble, then any RPS mechanism provides her the right incentives to truthfully reveal her favorite element in each decision problem. The logic is simple: any time a subject switches from telling the truth to lying on any decision problem, they shift probability away from their most-preferred object and onto a less-preferred item. The resulting lottery is therefore stochastically dominated by the lottery induced by truth-telling. Notice that expected utility is not needed for this argument; the RPS mechanism is incentive compatible as long as monotonicity is satisfied.⁶

Monotonicity is satisfied by nearly every decision-theoretic model of choice under uncertainty. Indeed, it is often viewed as normative, and models that violate monotonicity are often dismissed as implausible; see Quiggin (1982), for example. Thus we view monotonicity as a minimal assumption on $\succeq ^*$, though we discuss its limitations in the sequel and more extensively in Azrieli et al. (2018).

Assuming all monotonic extensions are admissible (and that beliefs coincide with objective probabilities), we characterize the class of all IC mechanisms for any given experiment. The main result of this paper, Theorem 2, shows that, in a certain sense, any IC mechanism resembles the RPS mechanism, but that the class of IC mechanisms may extend beyond the RPS mechanism in certain contrived experiments.

To understand how incentive compatibility could extend beyond the RPS mechanism in some experiments, consider the following example. Let $D_1=\{x,y\}$, $D_2=\{y,z\}$ and $D_3=\{x,z\}$ be the three decision problems in some experiment. Now, for every (strict) preference over $\{x,y,z\}$, if the subject truthfully announces her choices, then her favorite alternative from the set $E=\{x,y,z\}$ will also be revealed. Below we will call sets with this property surely identified sets. We can imagine an RPS-like mechanism that not only pays for choices in the actual decision problems, but also might pay for the inferred choice from this surely identified set E. For instance, consider the distribution $\lambda$ over subsets of $\{x,y,z\}$ given by $\lambda (D_1) = \lambda (D_2) = \lambda (D_3) = 0.3$ and $\lambda (E)=0.1$. And suppose the subject has preferences $x\succ y \succ z$. If she announces truthfully in each $D_i$ then their message vector will be (x, y, x), and the experimenter can use that to infer that x is also her most-preferred element in E. The mechanism will therefore pay x with probability $\lambda (D_1)+\lambda (D_3)+\lambda (E)=0.7$ and y with probability $\lambda (D_2)=0.3$. If the subject misrepresents and instead announces (y, y, x), then y would be inferred to be the most-preferred in E, so the subject would instead receive x with probability 0.3 and y with probability 0.7. This is strictly dominated by the truth-telling lottery, so any subject who respects dominance will not choose it. Indeed, any non-truthful message will result in a dominated lottery, so the mechanism is incentive compatible under monotonicity.⁷

Still, we can generalize even further by allowing $\lambda$ to put negative weight on some of the sets. For instance, set $\lambda (D_1) = \lambda (D_2) = \lambda (D_3) = 0.4$ and $\lambda (E)=-\,0.2$. For our subject with $x\succ y\succ z$ reporting truthfully in this mechanism pays x with probability 0.6 and y with probability 0.4. Misrepresenting by announcing (y, y, z) would again switch those probabilities, leading to a dominated lottery. However, if we choose the weights to be $\lambda (D_1) = \lambda (D_2) = \lambda (D_3) = 0.6$ and $\lambda (E)=-\,0.8$, then the resulting mechanism will not be incentive compatible, since the revealed second-best alternative (y) is now paid with a higher probability than the revealed first-best alternative (x). Thus, some restrictions must be placed on $\lambda$ in order for incentive compatibility to hold in the resulting mechanism. Theorem 2 shows that, in any experiment, any IC mechanism can be represented by a particular $\lambda$ as above, and precisely describes the restrictions on $\lambda$ that guarantee incentive compatibility.

It is illuminating to compare this characterization to the one obtained in our previous paper (Azrieli et al. 2018). In that work we characterize incentive compatibility of experiments under monotonicity, but when mechanisms map choices to acts instead of objective lotteries.⁸ Monotonicity in that framework means that if f is preferred to g in every possible state of the world, then f is preferred to g; otherwise their ranking is not restricted. The acts framework allows for more general extensions of preferences: Subjects may have their own subjective beliefs about the likelihood of different outcomes of the randomization device, or they may even have preferences which are not probabilistically sophisticated (Machina and Schmeidler 1992); e.g., they may be uncertainty averse. This might apply when subjects view the experimenter’s randomization as ambiguous. The assumption of the current paper that subjects view payments as lotteries can be thought of as an additional restriction on the set of admissible extensions in the acts framework. Since the experimenter can use this additional knowledge about extensions to construct IC mechanisms, one would expect that the class of IC mechanisms will be larger in the case of lotteries. In Sect. 5 we show that this is indeed the case: If a mechanism is IC in the acts framework, and one puts some (full-support) distribution over the state space of the randomization device, then the resulting lottery mechanism is IC. However, there are IC mechanisms in the lotteries environment that cannot be generated by any IC acts mechanism; in fact, these are exactly the mechanisms whose distribution $\lambda$ uses negative weights.

Although the set of IC mechanisms grows when we restrict attention to objective lotteries, the new mechanisms all require the existence of surely identified sets, such as $E=\{x,y,z\}$ in the example above. But most experiments do not have surely identified sets, because most experiments have no overlap between decision problems. In that case the only incentive compatible mechanism (assuming all preferences that respect stochastic dominance) is the RPS mechanism.⁹ Thus, we view our result as confirming the conclusion of Azrieli et al. (2018): under our stochastic dominance assumption, in practice, the RPS mechanism is the only incentive compatible mechanism. Nothing is gained by assuming objective probabilities.

Behaviorally, we speculate that mechanisms that pay based on surely-identified sets or that use negative weights are excessively complicated and may lead to more confusion and mistakes by subjects.¹⁰ Thus, even if an experiment does have surely identified sets, we see no particular reason to use anything other than the simple RPS mechanism. Indeed, we believe the practical implication of our characterization is that the RPS mechanism is the only IC mechanism any experimenter would want to use, assuming monotonicity. Any other mechanism is either not incentive compatible or adds unnecessary complications.

In Sect. 6 we consider the particular case of experiments in which the choice objects are themselves lotteries over money. In this set-up an RPS mechanism generates a compound lottery, where in the first ‘upper’ stage a decision problem is randomly chosen for payment, and in the second ‘lower’ stage a dollar amount is randomly chosen according to the lottery that the subject chose in the realized decision problem of the first stage. Examples in the literature (Holt 1986, e.g.) show that if the subject reduces compound lotteries according to the laws of probability and has Rank-Dependent Utility (RDU) preferences over lotteries over money, then the RPS may not be IC. Our framework and results make it easy to see the source of the failure: Reduction of compound lotteries together with monotonicity imply the independence axiom. Since RDU preferences typically violate independence, if one assumes reduction then it must be the case that monotonicity does not hold. Our Theorem 1 cannot be applied then, and the RPS may not be IC. In fact, we show that if subjects reduce compound lotteries and if all RDU preferences are admissible then no IC mechanism exists. Fortunately, empirical evidence suggests that it is rare for subjects to satisfy reduction but violate expected utility (Halevy 2007), so such violations of monotonicity may not be a large concern.

The issue of complementarities (paying both the left shoe and the right shoe) was addressed in Azrieli et al. (2018). There we showed that an incentive compatible mechanism can never pay in ‘bundles’ unless the researcher is willing to assume that subjects’ preferences exhibit no complementarities. But that conclusion holds whether we allow for subjective beliefs or objective probabilities, so the result is exactly the same in the current framework of objective lotteries. If the experimenter is going to pay for multiple decision problems (thus forming a bundle) then complementarities must be assumed away. We therefore restrict attention to non-bundle payments in this paper.¹¹

We do find that experimenters have lacked a convention for which payment mechanism to use. In our survey of papers published in 2011, we found that only 25% use the RPS mechanism, while 56% pay for every decision. Almost all of the remainder pay for some number of randomly-selected decisions (13%) or use a mechanism that is not incentive compatible under any standard assumptions (6%). Our goal is to provide a theoretical framework in which experimenters can understand exactly what assumptions justify one payment mechanism over another, and to understand exactly those conditions under which the RPS mechanism is incentive compatible.

We review empirical tests of monotonicity and the RPS mechanism in the concluding section. Monotonicity violations appear to occur most frequently when multiple decisions are shown on one screen, or when a single decision problem is repeated multiple times. In other settings monotonicity appears to be satisfied.¹²

From a theoretical perspective, our work is probably closest to the classic work of Gibbard (1977), who characterizes strategy-proof random mechanisms (using objective lotteries) when only ordinal preferences can be elicited. He characterizes these mechanisms as a kind of random-dictatorship, whereby a ‘dictator’ is an agent that solely determines the outcome. Our paper is comparable to the special case in which there is only one agent present. Gibbard does not, however, uncover the special structure of these dictatorial mechanisms in the form that we uncover, presumably because his interest was in understanding the implications of strategy-proofness across agents. Another important difference between the papers is that in Gibbard’s framework agents report their entire ranking over alternatives, while we consider the more general case in which the favorite alternatives in several subsets are reported. Finally, Gibbard requires only weak incentive compatibility, while we require that truth-telling be the unique optimum.

2 The framework

There is a finite set X of choice objects. The decision maker (also called the subject) has a strict preference relation $\succ$ over X which is asymmetric and negatively transitive.¹³ The relation $\succ$ is not complete because it is not reflexive (it is not true that $x\succ x$), so we use $x \succeq y$ to mean that either $x\succ y$ or $x=y$. For any $x\in X$, let $L(x,\succ ) = \{y\in X:\, x\succeq y\}$ and $U(x,\succ ) = \{y\in X:\, y\succeq x\}$ be the (weak) lower- and upper-contour sets of x according to $\succ$, respectively. The $\succ$-dominant element of any set $E\subseteq X$ is denoted by ${\text {dom}}_\succ (E)$. That is, ${\text {dom}}_\succ (E)$ is the unique element of E satisfying ${\text {dom}}_\succ (E)\succeq y$ for all $y\in E$.

The researcher has an exogenously-given list of k decision problems, denoted $D=(D_1,\ldots ,D_k)$, where $D_i\subseteq X$ for each $i\in \{1,\ldots ,k\}$. Let ${\mathscr {D}}=\{D_1,\ldots ,D_k\}$ represent the set of decision problems. We assume throughout that each $D_i\in {\mathscr {D}}$ is non-trivial, meaning $|D_i|>1$, and that the same decision problem does not appear more than once, meaning $D_i\ne D_j$ whenever $i\ne j$. These assumptions are made only to simplify notation and can easily be relaxed.

The subject is asked to choose an element from each $D_i$. The announced choice vector (or, the subject’s message) is denoted by $m=(m_1,\ldots ,m_k)$. The space of all possible messages is $M=\times _i D_i$. For each $i\in \{1,\ldots ,k\}$, let $\mu _i(\succ )={\text {dom}}_\succ (D_i)$ be the $\succ$-dominant element of $D_i$, and denote $\mu (\succ ) = (\mu _1(\succ ),\ldots ,\mu _k(\succ ))$. We refer to $\mu (\succ )$ as the truthful message for $\succ$.

We assume that an objective randomization device can be used to determine payoffs, so that payments are given by lotteries. Denote by $\Delta (X)$ the set of all probability distributions over X. If $f\in \Delta (X)$ then f(x) is the probability with which $x\in X$ is selected according to f. A (payment) mechanism$\varphi :M\rightarrow \Delta (X)$ takes the announced choice $m\in M$ and awards the subject with the lottery $\varphi (m)\in \Delta (X)$. Thus, $\varphi (m)(x)$ denotes the probability with which x is awarded when the decision maker announces m.

We refer to the pair $(D,\varphi )$ as an experiment; D completely specifies the choices the subject must face, and $\varphi$ describes how they are paid for those choices. Since D determines the domain of a mechanism, there is little distinction between an experiment $(D,\varphi )$ and its associated mechanism $\varphi$; when it causes no confusion, we refer to experiments and mechanisms interchangeably.

We assume that the subject’s preferences $\succ$ extend to the space of lotteries $\Delta (X)$. An extension of $\succ$ to $\Delta (X)$ is denoted by $\succeq ^*$, and we assume that any admissible extension is complete and transitive. Although $\succ$ is strict, $\succeq ^*$ may not be. The asymmetric part of $\succeq ^*$ is denoted by $\succ ^*$. An extension $\succeq ^*$ is assumed to agree with $\succ$ on the space of degenerate lotteries. We let ${\mathscr {E}}(\succ )$ denote the set of admissible extensions of $\succ$. Think of ${\mathscr {E}}$ as capturing the assumptions the experimenter is willing to make about the subject’s preferences over lotteries. For example, if the experimenter assumes that the subject is a risk-averse expected utility maximizer, then ${\mathscr {E}}(\succ )$ is the set of extensions $\succeq ^*$ that have an expected utility representation with a concave cardinal utility index $u:X\rightarrow {\mathbb {R}}$ that ordinally agrees with $\succ$ (meaning, $u(x)>u(y)$ if and only if $x\succ y$).¹⁴

Definition 1

(Incentive compatibility) A mechanism $\varphi$ is incentive compatible with respect to ${\mathscr {E}}$ if, for every preference $\succ$, every extension $\succeq ^*\in {\mathscr {E}}(\succ )$, and every $m \ne \mu (\succ )$, we have that $\varphi (\mu (\succ ))\succ ^*\varphi (m)$.

In other words, incentive compatible experiments induce the subject to announce truthfully, treating each decision problem as though it were in isolation. Note that whether or not a mechanism (or experiment) is incentive compatible depends crucially on ${\mathscr {E}}$. When there is no confusion, we drop the reference to ${\mathscr {E}}$ and simply refer to $\varphi$ as incentive compatible.

In some experiments subjects are paid for all of their decisions, or for some randomly-selected subset of decisions. In those cases, payment objects are ‘bundles’ of choice objects. Technically, they are subsets of $\bigcup _i D_i$. Our framework already accommodates bundles; simply expand X to include all non-empty subsets of $\bigcup _i D_i$ and allow $\varphi$ to select lotteries that put positive probability on these subsets. However, we will show that paying anything outside of $\bigcup _i D_i$ cannot be incentive compatible without making assumptions about how $\succ$ behaves outside of $\bigcup _i D_i$. For the case of bundles, one would need to assume no complementarities in $\succ$. We explore this in our previous work.

3 Incentive compatibility of the RPS mechanism

Without making further assumptions on the correspondence ${\mathscr {E}}$, there do not exist incentive compatible mechanisms when the number of decision problems is $k\ge 2$; see Proposition 0 in Azrieli et al. (2018) for the proof. Unless otherwise specified, we assume that extensions $\succeq ^*$ respect first-order stochastic dominance with respect to the underlying preference $\succ$.

Definition 2

(First-order stochastic dominance) Fix $\succ$. The lottery fdominates the lottery g with respect to $\succ$ (denoted $f\sqsupseteq g$) if, for every $x\in X$,

$$\sum _{\{x'\in X:x'\succeq x\}}f(x')\ge \sum _{\{x'\in X:x'\succeq x\}}g(x').$$

If there is strict inequality for at least one x then we say fstrictly dominatesg with respect to $\succ$ ($f\sqsupset g$).¹⁵

Definition 3

(Monotonic extension) An extension $\succeq ^*$ of $\succ$ is monotonic if $f\sqsupseteq g$ implies $f \succeq ^* g$ and $f\sqsupset g$ implies $f \succ ^* g$. The collection of all monotonic extensions of $\succ$ is denoted by ${\mathscr {E}}^\mathrm {mon}(\succ )$.

Monotonicity is satisfied by nearly every model in decision theory; indeed, many authors view it as normative.¹⁶

The following simple lemmas will be useful for some of the following results. The proofs are omitted.

Lemma 1

Assume${\mathscr {E}}(\succ ) \subseteq {\mathscr {E}}^\mathrm {mon}(\succ )$for every$\succ$. If for every$\succ$and every$m\ne \mu (\succ )$we have that$\varphi (\mu (\succ ))\sqsupset \varphi (m)$, then$\varphi$is incentive compatible with respect to${\mathscr {E}}$.

Lemma 2

A mechanism$\varphi$is incentive compatible with respect to${\mathscr {E}}^\mathrm {mon}$if and only if, for every preference$\succ$and every$m\ne \mu (\succ ), \varphi (\mu (\succ ))\sqsupset \varphi (m)$.

Remark

The conclusion of Lemma 2 continues to hold even if the set of admissible extensions ${\mathscr {E}}(\succ )$ does not contain all monotonic extensions, as long as this set is ‘sufficiently rich’. For example, if any expected utility extension is admissible then the lemma is still true.

A common payment mechanism is one in which a single decision problem is randomly selected, and the subject is paid with her choice at that problem. We call such a mechanism a Random Problem-Selection (RPS) Mechanism. Formally,

Definition 4

(Random problem-selection mechanism) A mechanism $\varphi$ is a random problem-selection mechanism (RPS) if there exists a full-support probability distribution $\lambda$ over ${\mathscr {D}}$ such that for every alternative $x\in X$,

$$\varphi (m)(x) = \sum _{\{i :\, m_i=x\}} \lambda (D_i).$$

(1)

Theorem 1

If${\mathscr {E}}(\succ ) \subseteq {\mathscr {E}}^\mathrm {mon}(\succ )$for every$\succ$and$\varphi$is an RPS mechanism, then$\varphi$is incentive compatible with respect to${\mathscr {E}}$.

Proof

Follows immediately from Lemma 1, and from the obvious fact that lying in an RPS mechanism induces a lottery that is strictly dominated by the lottery obtained by truth-telling. $\square$

4 Characterization of incentive compatible mechanisms

In this section we provide a complete characterization of incentive compatible mechanisms when all monotonic extensions are admissible (or when the set of admissible extensions is sufficiently rich, see the Remark after Lemma 2). Recall that, by Lemma 2, incentive compatibility in this set-up is equivalent to the property that the lottery obtained by truth-telling strictly dominates any lottery that can be obtained by lying.

The example in the introduction illustrates how incentive compatibility can extend beyond the RPS mechanism. We now introduce notations and definitions required to formally state and prove the characterization result.

4.1 Surely identified sets

Let $M_R=\left\{ m\in M: (\exists \succ )\ m =\mu (\succ )\right\}$ be the set of rationalizable messages. $M_{NR}=M\setminus M_R$ is then defined as the set of non-rationalizable messages.

Definition 5

Fix any rationalizable message $m=(m_1,\ldots ,m_k)\in M_R$. For every $x, y\in X$, say that x is directly revealed preferred to y under m if there is $1\le i\le k$ such that $m_i=x$ and $y\in D_i$, or if $x=y$. Denote the transitive closure of this relation by R(m), and say that x is revealed preferred to y under choices m if xR(m)y.

The relation R(m) is reflexive, transitive and antisymmetric, but it need not be complete. Denote by $L(x,m) = \{y\in X : x R(m) y\}$ and $U(x,m) = \{y\in X : y R(m) x\}$ the sets of elements that are revealed to be worse than x and better than x under choices m, respectively. Clearly, $L(x,m)\subseteq L(x,\succ )$ and $U(x,m)\subseteq U(x,\succ )$ when $m=\mu (\succ )$, with strict inclusions for some x when R(m) is not a complete relation.

Let ${\text {dom}}_m(E)$ be the R(m)-dominant element of E, if one exists. Notice that if $m=\mu (\succ )$, then either ${\text {dom}}_m(E)$ does not exist or else ${\text {dom}}_m(E)={\text {dom}}_\succ (E)$.

Definition 6

(Surely identified sets) A non-empty set $E\subseteq X$ is surely identified (SI) if, for every $m\in M_R$, ${\text {dom}}_m(E)$ exists. In other words, E is SI if, for any order $\succ$, the message $m=\mu (\succ )$ identifies the most-preferred element of E, so that ${\text {dom}}_m(E)={\text {dom}}_\succ (E)$.

For example, if $D_1=\{x,y\}$, $D_2=\{y,z\}$, and $D_3=\{x,z\}$, then $E=\{x,y,z\}$ is surely identified, since any rationalizable message identifies the entire (strict) relation $\succ$ over E, and therefore identifies the most-preferred element of E.

Let $SI({\mathscr {D}})$ be the collection of surely identified sets for the given set of decision problems ${\mathscr {D}}$.¹⁷ Obviously, any $D_i$ is in $SI({\mathscr {D}})$. All singleton sets (of the form $\{x\}$) are also surely identified. But there can be other sets in $SI({\mathscr {D}})$, such as E above. A characterization of surely identified is given by the following lemma, whose proof can be found in the “Appendix”.

Lemma 3

$E\in SI({\mathscr {D}})$if and only ifEis either a singleton, or for every pair$\{x,y\}\subseteq E$, there exists$D\in {\mathscr {D}}$for which$\{x,y\}\subseteq D \subseteq E$.

4.2 Weighted set-selection mechanisms

We can now define a generalization of RPS mechanisms called weighted set-selection (WSS) mechanisms. These mechanisms randomly select from the surely identified sets and pay the revealed-most-preferred element from that set (assuming m is rationalizable). Thus, the probability that x is paid under message m is simply the probability that an SI set E is drawn such that ${\text {dom}}_m(E)=\{x\}$.

Definition 7

(Weighted set-selection mechanisms) A mechanism $\varphi :M\rightarrow \Delta (X)$ is a weighted set-selection mechanism (WSS) if there exists some $\lambda :SI({\mathscr {D}})\rightarrow {\mathbb {R}}$ such that for every rationalizable $m\in M_R$ and every alternative $x\in X$,

$$\varphi (m)(x) = \sum _{\left\{ E:\,{\text {dom}}_m(E)=\{x\}\right\} } \lambda (E).$$

The requirement that $\varphi (m)$ be a well-defined lottery places some restrictions on the weighting function $\lambda$. For example, it cannot put negative weight on any singleton set: If $\lambda (\{x\})<0$ and there is no other $E\in SI({\mathscr {D}})$ for which ${\text {dom}}_m(E)=\{x\}$, then $\varphi (m)(x)=\lambda (\{x\})<0$, which is forbidden. Furthermore, we have that

$$\begin{aligned} \sum _x \varphi (m)(x)&= \sum _x \left[ \sum _{\{E\in SI({\mathscr {D}}):\,{\text {dom}}_m(E)=\{x\}\}} \lambda (E)\right] \\ &= \sum _{E\in SI({\mathscr {D}})} \lambda (E),\end{aligned}$$

so it must be that $\sum _{E\in SI({\mathscr {D}})} \lambda (E)=1$. These observations prove the following lemma.

Lemma 4

A weighted set-selection mechanism must be associated with a weighting function $\lambda$ that satisfies

• (1) $\sum _{E\in SI({\mathscr {D}})} \lambda (E) = 1$, and

• (2) $\lambda (\{x\})\ge 0$for every$x\in X$.

Remark

A weighted set-selection mechanism uniquely determines the vector $\lambda$ that represents it. That is, if $\lambda$ and $\lambda '$ are two different weighting vectors then the corresponding mechanisms $\varphi$ and $\varphi '$ differ on $M_R$. This can be seen by considering a minimal (with respect to inclusion) SI set E for which $\lambda (E)\ne \lambda (E')$, and an order $\succ$ which ranks all elements of E below every other element of X. The top element of E according to $\succ$ is chosen with different probabilities under $\varphi$ and $\varphi '$ when the choices are $\mu (\succ )$. Thus, given the collection ${\mathscr {D}}$, there is a one-to-one correspondence between WSS mechanisms and the vectors $\lambda$ that define them.

4.3 Switch positivity

We now formalize a condition on $\lambda$ called switch positivity that is precisely what’s needed to guarantee incentive compatibility of a WSS mechanism. To gain understanding for switch positivity, consider the example given in Table 1. The four decision problems are shown on the left, along with the set $E_1$, which is surely identified, and the set $E_2$, which is not. The $\lambda$ functions for four different WSS mechanisms are given, labeled $\lambda ^1$ through $\lambda ^4$, with $\lambda ^2$ being an RPS mechanism. Since $E_2$ is not surely identified, no WSS mechanism can put weight on $E_2$. On the right are four example preferences. The truthful announcement vector for each preference is listed at the bottom.

Comparing $\mu (\succ ^x)$ and $\mu (\succ ^y)$, we see that these preferences are only distinguished in this experiment by their choice from $D_1$. Thus, to distinguish these two preferences, an incentive compatible WSS mechanism must provide incentives to answer $D_1$ truthfully. The mechanism given by $\lambda ^1$ (which has $\lambda ^1(D_1)=0$) does not provide such incentives. This is because announcing $\mu (\succ ^x)$ and $\mu (\succ ^y)$ would both give the same lottery (which pays x, y, and b each with 1 / 3 chance). Thus, neither preference has a strict incentive to tell the truth; deviating to the other preference’s truthful announcement has no cost.

An easy way to restore incentive compatibility is to put strictly positive weight on $D_1$, which is exactly what the RPS mechanism $\lambda ^2$ does.

Table 1 Examples to demonstrate the switch positivity condition

But there is an alternative way to restore incentive compatibility in this example: put weight on $E_1$ instead of $D_1$. This is done in $\lambda ^3$. Now announcing $\mu (\succ ^x)=(x,x,y,b)$ gives a 1 / 2 chance of receiving x (1 / 4 from $D_2$ and 1 / 4 from $E_1$), while announcing $\mu (\succ ^y)=(y,x,y,b)$ gives a 1 / 2 chance of receiving y (1 / 4 from $D_3$ and 1 / 4 from $E_1$). Thus, each type has a strict incentive to tell the truth in $D_1$, even though $\lambda ^3(D_1)=0$.

From this we see that both $D_1$ and $E_1$ could be used to distinguish between $\succ ^x$ and $\succ ^y$. Since $\succ ^x$ and $\succ ^y$ differ only in that they switch the ordering of x and y, we refer to both $D_1$ and $E_1$ as switch test sets for x and y. And a natural condition for incentive compatibility is that at least one of these switch test sets must have positive weight.

In fact, we can derive a slightly weaker condition. Consider $\lambda ^4$, which has $\lambda ^4(D_1)>0$ but $\lambda ^4(E_1)<0$. Because $\lambda (E_1)+\lambda (D_1)>0$ the mechanism will also distinguish between $\succ ^x$ and $\succ ^y$, since announcing $x\in D_1$ will, on net, increase the probability that x is paid by $1/2-1/4=1/4$, while announcing $y\in D_1$ will, on net, increase the probability of y by $1/2-1/4=1/4$. Putting these cases together, we can say that incentive compatibility requires that $\lambda (D_1)+\lambda (E_1)>0$. In other words, the sum of weights on all switch test sets for x and y must be positive. We call this the switch positivity condition.

We do not need switch positivity to apply to all x and y because we do not need to distinguish all possible x and y pairs. Consider the preferences $\succ ^a$ and $\succ ^b$. There are no decision problems containing both a and b. Thus, $\mu (\succ ^a)=\mu (\succ ^b)$. Furthermore, there are no surely identified sets containing both a and b (recall $E_2$ is not surely identified), so this particular experiment is simply not designed to distinguish between $\succ ^a$ and $\succ ^b$. There is no need to put positive weight on switch test sets for a and b. Therefore, we can refine our switch positivity condition to apply only to those pairs x and y that have surely-identified switch test sets.

In the above example the switch in ordering between x and y occurred at the top of the preference ranking. But a similar example could be constructed where the switch between x and y happens in the middle of the ordering. As long as the decision problems contain none of the elements ranked above x and y, the resulting condition on $\lambda$ is the same, though we must specify that the switch test set does not contain any of those higher-ranked elements. Formally, if A is the set of elements ranked below x and y, then the switch test set must be a subset of $A\cup \{x,y\}$. In this case we call it a switch test set for x and y against A, and require that switch positivity hold for all A. For example, if $A=\emptyset$ (meaning x and y are at the bottom) then the only surely identified switch test set for x and y against $A=\emptyset$ is $D_1=\{x,y\}$, and so switch positivity would require that $\lambda (D_1)>0$.

We now have our complete notion of switch test sets and the needed switch positivity condition.

Definition 8

(Switch test set) Let $x,y\in X$ and $A\subseteq X\setminus \{x,y\}$. A set $E\subset X$ is a switch test set for x and y against A if $E\in SI({\mathscr {D}})$ and $\{x,y\}\subseteq E\subseteq A\cup \{x,y\}$. Let T(x, y, A) denote the collection of switch test sets for x and y against A.

Definition 9

(Switch positivity) A weighted set-selection mechanism $\varphi$ (with associated weighting vector $\lambda$) satisfies switch positivity if, for every $x,y\in X$ and $A\subseteq X\setminus \{x,y\}$ such that $T(x,y,A)\ne \emptyset$, it holds that

$$\sum _{ \{E\in T(x,y,A)\} } \lambda (E) > 0.$$

Remark

If the collection T(x, y, A) is not empty, then it contains at least one of the decision problems in ${\mathscr {D}}$. In the example above, $D_1\in T(x,y,\{x,y,a\})$. Indeed, $E\in T(x,y,A)$ means that $\{x,y\}\subseteq E \subseteq A\cup \{x,y\}$. Since E is surely identified, Lemma 3 implies that there is $D\in {\mathscr {D}}$ such that $\{x,y\}\subseteq D \subseteq E$. It follows that $D\in T(x,y,A)$ as well.

4.4 Dealing with non-rationalizable messages

Switch positivity is clearly necessary for incentive compatibility because it guarantees that a subject with preference $\succ$ will not “imitate” the preference $\succ ^{xy}$ by announcing $\mu (\succ ^{xy})$ (the optimal choices for $\succ ^{xy}$) instead of $\mu (\succ )$. But we also need to ensure that the subject has no incentive to announce any non-rationalizable messages. Because we allow for all monotonic extensions, the only way to accomplish this is to ensure that, for every $\succ$ and $m'\in M_{NR}$, $\varphi (m')$ is dominated by $\varphi (\mu (\succ ))$.

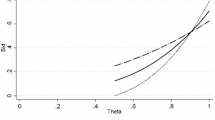
To visualize this requirement, return to the example of $D_1=\{x,y\}$, $D_2=\{y,z\}$, and $D_3=\{x,z\}$, and consider Fig. 1. Let $\varphi$ be any incentive compatible mechanism. Start with the preference $x\succ y\succ z$ for which truth-telling generates the lottery $\varphi (\mu (\succ ))$. This point is denoted as xyz in the figure. If a lottery $\varphi (m')$ is to be dominated by $\varphi (\mu (\succ ))$ (for preference $\succ$) then it must put less weight on x and more weight on z. In the figure, $\varphi (m')$ must be in the cone emanating to the northeast from the point xyz, as indicated by two dashed lines. Thus, every $m'\in M_{NR}$ needs to map into some $\varphi (m')$ in this cone.

But for preference $y\succ ' x\succ ' z$, we must have that every $\varphi (m')$ maps into the cone emanating to the northwest from the truth-telling lottery yxz. In general, for any preference $\succ$, we must have that every $\varphi (m')$ be in the cone of dominated lotteries for that preference. There are six such cones (one for each $\succ$), and the intersection of those cones is the dark gray area labeled $\Phi _{NR}$. Incentive compatibility requires that $\varphi (m')\in \Phi _{NR}$ for each $m'\in M_{NR}$. Note that the six vertices must be excluded from $\Phi _{NR}$ because incentive compatibility requires that all non-rationalizable messages be strictly dominated; if one non-rationalizable maps into the same lottery as some truthful message, then an a subject with that preference will be indifferent between the truthful message and the equivalent non-rationalizable message. Strict incentive compatibility rules this out.

Fig. 1

In $\Delta (X)$, the lotteries stochastically dominated by the point $\varphi (\mu (\succ ))$ when $x\succ y \succ z$ (labeled xyz) are shown in light gray. The lotteries that are dominated by the truthful announcement for every $\succ$ are shown in dark gray ($\Phi _{NR}$)

Formally, let $\varphi (M_R)$ be the set of lotteries that can be obtained by announcing any rationalizable message and $co(\varphi (M_R))$ be the convex hull of that set. We denote $\Phi _{NR} = co(\varphi (M_R))\setminus \varphi (M_R)$. Incentive compatibility requires that if $m'\in M_{NR}$ then $\varphi (m')\in \Phi _{NR}$.¹⁸

4.5 The characterization theorem

Theorem 2

A mechanism $\varphi :M \rightarrow \Delta (X)$ is incentive compatible with respect to ${\mathscr {E}}^\mathrm {mon}$ if and only if it is a weighted set-selection mechanism such that

• (1) $\varphi$ satisfies switch positivity; and

• (2) if$m\in M_{NR}$then$\varphi (m)\in \Phi _{NR}$.

The proof of this theorem—provided in the appendix—proceeds in three steps: First, we characterize a set of restrictions on the lotteries $\varphi (m)$ that are equivalent to incentive compatibility. Second, we show how an incentive compatible $\varphi$ can be represented via a supermodular capacity, and how the restrictions on lotteries imposed by incentive compatibility translate into certain restrictions on that capacity. Third, we show that the capacity can be translated into a weighting vector $\lambda$—so that $\varphi$ is in fact a weighted set-selection mechanism—and how the restrictions on the capacity imply that $\varphi$ must satisfy switch positivity. Finally, we ‘close the loop’ by proving that any weighted set-selection mechanism satisfying these two conditions is in fact incentive compatible.

In most experiments there are no surely identified sets beyond the original decision problems (except for the singletons sets $\{x\}_{x\in X}$, which are always surely identified). Assuming there are no other surely identified sets and that no $D_i$ can be surely identified from the other decision problems, switch positivity implies that every decision problem must have positive weight, that singleton sets may have positive or zero weight, and that every other set must have zero weight. In other words, the only incentive compatible mechanisms are RPS mechanisms, but with the added possibility that some alternatives are paid with fixed probabilities that do not depend on the subject’s messages.

Corollary 1

If no sets outside of$(D_1,\ldots ,D_k)$are surely identified, and if no$D_i$is surely identified from the other decision problems, then$\varphi :M\rightarrow \Delta (X)$is incentive compatible if and only if it is an ‘extended’ RPS mechanism that may also put positive weight on singleton sets. Formally,$\varphi$is incentive compatible if and only if it is associated with a probability distribution$\lambda$ over ${\mathscr {D}}\cup \{x\}_{x\in X}$such that$\lambda (D_i)>0$for each$D_i\in {\mathscr {D}}$and$\lambda (\{x\})\ge 0$for each$x\in X$.

Recall that our framework can handle the case of bundle payments (for example, paying the subject all of their choices) by expanding X to include subsets of $\bigcup _i D_i$. But incentive compatibility requires that one use a WSS mechanism, and WSS mechanisms can only put positive probability on items in $SI({\mathscr {D}})$. And $SI({\mathscr {D}})$ cannot contain these bundles. Without explicit assumptions on complementarities, sets containing bundles will not be surely identified and therefore cannot be paid in any incentive compatible mechanism. See Azrieli et al. (2018) for an assumption on complementarities that does make paying for multiple decisions incentive compatible.

5 Lotteries versus acts: a comparison of characterizations

In this section we compare IC mechanisms in the objective lotteries framework of the current paper to IC mechanisms in the more general acts set-up of our previous paper (Azrieli et al. 2018). As explained in the introduction, we would like to show that there are more IC mechanisms when the subject views the randomization device as generating objective lotteries.

To formalize this idea, we must be able to compare directly a mechanism $\phi$ in the acts framework to a mechanism $\varphi$ in the lotteries framework. In the acts framework (ignoring bundle payments), a mechanism is a function $\phi :M\rightarrow X^\Omega$, where $\Omega$ is a finite state space and $X^\Omega$ is the set of all acts, i.e. mappings from $\Omega$ to X. To convert acts into lotteries, let $\rho$ be a probability measure over $\Omega$.¹⁹ We say that $(\Omega ,\rho , \phi )$generates$\varphi$ if, for each $m\in M$ and $x\in X$,

$$\varphi (m)(x) = \rho \left( \{\omega \in \Omega : \phi (m)(\omega )=x\}\right) .$$

If the above equality holds for every rationalizable message $m\in M_R$ then we say that $(\Omega ,\rho , \phi )$ generates $\varphi$ on rationalizable messages.

Proposition 1

If$\phi$is an incentive compatible act-mechanism (defined on some state space$\Omega$), and$\rho$is a full-support probability distribution over$\Omega$, then the lotteries-mechanism$\varphi$generated by$(\Omega ,\rho , \phi )$is incentive compatible.

The proof of this proposition follows from the discussion in the introduction and is therefore omitted.

We now consider the opposite direction, taking an IC lotteries-mechanism and studying the equivalent act-mechanism that generates it. But the following example shows that (1) there can be many act-mechanisms that generate a given IC lotteries-mechanism, and (2) some of those act-mechanisms may not be IC. In other words, the converse of Proposition 1 does not hold generally.

Example 1

Let $X=\{x,y,z\}$. Suppose $k=3$ with $D_1=\{x,y\}$, $D_2=\{y,z\}$, and $D_3=\{z,x\}$.²⁰

In the lotteries framework, consider an RPS mechanism $\varphi$ with $\lambda (D_i)=1/3$ for each i. The subject receives their revealed-most-preferred element of X with probability 2 / 3 and their revealed-second-most-preferred element with probability 1 / 3. A non-rationalizable message results in the uniform lottery over X.

This mechanism can be generated by an RPS mechanism $\phi$ in the acts framework, where $\Omega =\{\omega _1,\omega _2,\omega _3\}$—each corresponding to a decision problem—and a distribution $\rho$ with $\rho (\omega _i)=1/3$ for each i. Here, both mechanisms are incentive compatible in their respective frameworks.

But $\varphi$ can also be generated by the following non-incentive-compatible act-mechanism $\phi$ and distribution $\rho$: Let $\Omega =\{\omega _1,\omega _2,\omega _3\}$ and $\rho (\omega _i)=1/3$ for each i. For rationalizable message m, set $\phi (m)(\omega _1)=\phi (m)(\omega _2)={\text {dom}}_m(X)$ and $\phi (m)(\omega _3)$ equal to the revealed-second-most-preferred element of X. For non-rationalizable message m set $\phi (m)(\omega _1)=x, \phi (m)(\omega _2)=y,$ and $\phi (m)(\omega _3)=z$. This mechanism is not incentive compatible in the acts framework because beliefs are subjective: A subject who believes $\omega _3$ will occur with high enough probability will prefer to reveal their true favorite element as if it were their second-most-preferred.

The next example further demonstrates that there are incentive compatible lotteries-mechanisms that cannot be generated by any incentive compatible acts-mechanism (even when restricted to rationalizable messages). Thus, in this sense, the set of IC mechanisms is strictly larger in the lotteries framework.

Example 2

Let $X=\{x,y,z\}$. Suppose $k=4$ with $D_1=\{x,y\}$, $D_2=\{y,z\}$, $D_3=\{z,x\}$, and $D_4=\{x,y,z\}$.

In the lotteries framework, consider a mechanism with $\lambda (D_i)=0.4$ for each $i\in \{1,2,3\}$ and $\lambda (D_4)=-0.2$. This mechanism pays the revealed-most-preferred element of X with probability 0.6 and the revealed-second-most-preferred element with probability 0.4. Also, set $\varphi (m)$ to be the uniform distribution over X whenever m is non-rationalizable. By Theorem 2 this mechanism is incentive compatible.

However, this mechanism cannot be generated by any incentive compatible mechanism in the acts framework. To prove this, suppose that $(\Omega , \rho , \phi )$ generates $\varphi$, where $\phi$ is incentive compatible. By Theorem 1 in Azrieli et al. (2018), each $\omega \in \Omega$ corresponds to some decision problem (or to a singleton) and pays the selected item from that problem. Consider first $\succ$ with $z\succ x\succ y$. Since $\varphi (\mu (\succ ))(x)=0.4$, the set of $\omega$’s corresponding to $D_1$ or to the singleton $\{x\}$ must have $\rho$-probability of 0.4. But, by a symmetric argument, the same is true for $D_2$ and $\{y\}$ and to $D_3$ and $\{z\}$. But then $\sum _\omega \rho (\omega )\ge 1.2$, a contradiction.

The difficulty in generating $\varphi$ from an incentive compatible $\phi$ in Example 2 comes from $\lambda$ assigning negative weights to certain SI sets. In fact, this exactly characterizes the cases where $\varphi$ cannot be generated by an incentive compatible $\phi$.

Proposition 2

Assume that$\varphi$is an incentive compatible lotteries-mechanism.

• (1) If the associated weighting vector$\lambda$ of $\varphi$is non-negative, then there exists an incentive compatible acts-mechanism$\phi$ (on some $\Omega$) and a probability$\rho$on$\Omega$such that$(\Omega , \rho , \phi )$generates$\varphi$on rationalizable messages.

• (2) If the associated weighting vector$\lambda$ of $\varphi$contains negative elements, then$\varphi$cannot be generated by any incentive compatible acts-mechanism$\phi$(even when restricted to rationalizable messages).

For (1), the construction of the first mechanism in Example 1 can be generalized to any lotteries mechanism with non-negative $\lambda$ to get a generating incentive compatible acts-mechanism. The proof of (2) is similar to the proof that $\varphi$ cannot be generated by an incentive compatible acts-mechanism in Example 2. The details are omitted.

6 Choice from lotteries, reduction, and RDU preferences

Many experimental tests of decision-theoretic models ask the subject to make choices from menus of lotteries whose outcomes are dollar payments. In this case, payments in the RPS mechanism represent two-stage lotteries, where the ‘upper’ stage refers to the random draw of a decision problem, and the ‘lower’ stage refers to the draw of a dollar amount according to the chosen lottery from that problem.

It is possible that the subject ‘reduces’ compound lotteries into one-stage lotteries according to the laws of probability, and thus that her preferences over the space of single stage lotteries (over money) completely determine her preferences over compound lotteries. The following example—adapted from Holt (1986)—shows that incentive compatibility of the RPS mechanism can fail when non-expected utility models (in the lower stage) are combined with the reduction of compound lotteries.

Definition 10

(Rank-dependent utility) A subject has rank-dependent utility (RDU) preferences if a simple lottery $f=(x_1,p_1;x_2,p_2;\ldots ;x_n,p_n)\in \Delta ({\mathbb {R}})$ (with $x_1<x_2<\cdots <x_n$) is evaluated according to the functional

$$U_q(f) = \sum _{s=1}^n u(x_s)\left[ q(\sum _{r=1}^s p_r) - q(\sum _{r=1}^{s-1} p_r) \right] ,$$

where $u:{\mathbb {R}}\rightarrow {\mathbb {R}}$ is increasing, $q:[0,1]\rightarrow [0,1]$ is increasing, strictly concave over (0, 0.5) and strictly convex over (0.5, 1), $q(0)=0$, and $q(1)=1$.

Example 3

Let $l=(\$0,1/2;\$3,1/2)$ be an equiprobable lottery between $\$0$ and $\$3$, and consider $D_1=\{l,\$1\}$ and $D_2=\{l,\$2\}$. If a subject has rank-dependent utility with $u(x)=x^{3/4}$, $q(1/4)=1/3$, $q(1/2)=1/2$, and $q(3/4)=2/3$, then $\$2\succ ^* l \succ ^* \$1$. Thus, the truthful announcement is $m^*=(l,\$2)$. Now consider an RPS mechanism for lotteries that puts equal probability on each $D_i$ being chosen. Announcing $m^*$ gives the lottery $\varphi (m^*)=(\$0,1/4;\$2,1/2;\$3,1/4)$, assuming compound lotteries are reduced to single-stage lotteries. Announcing $m'=(1,2)$ gives the lottery $\varphi (m')=(\$1,1/2;\$2,1/2)$. Plugging in the values of u and q, we find that $U(\varphi (m'))>U(\varphi (m^*))$, so incentive compatibility is violated.

The reason the RPS mechanism fails in this example stems from the well-known fact that reduction of compound lotteries, when combined with our monotonicity assumption, implies the Von Neumann-Morgenstern independence axiom on the space of single stage lotteries.²¹ Consequently, if a model of preferences violates independence (as the RDU model does), but the reduction of compound lotteries is assumed, then that model must violate monotonicity. Without monotonicity, Theorem 1 cannot be applied and there is no guarantee that the RPS mechanism is incentive compatible.

In fact, we now show that for the decision problems in Example 3 there is no incentive compatible payment mechanism if any RDU preference is admissible. We need to slightly modify our framework in order to accommodate this example. Let $\Delta ({\mathbb {R}})$ be the set of all simple (finite support) lotteries on ${\mathbb {R}}$. A degenerate lottery that pays $\$x$ with probability 1 is denoted by $\delta _x$. The subject faces the two decision problems from Example 3, $D_1=\{l,\delta _1\}$ and $D_2=\{l,\delta _2\}$, where l is the lottery that pays 0 or 3 with equal probabilities.

We assume that the subject has RDU preferences over $\Delta ({\mathbb {R}})$, represented by a functional $U_q$ (for some u and q) as in Definition 10. Notice that this allows the subject to be indifferent between some of the lotteries. We therefore need to modify the definition of incentive compatibility to allow for weak preferences. We do that by requiring that, whenever a message is truthful, the output of the mechanism is (weakly) preferred to any other possible outcome, with strict preference whenever the other message is not truthful.

Since we assume that the subject reduces compound lotteries, her preferences over the compound lotteries induced by the mechanism are already captured by her functional $U_q$. Thus, a mechanism can be described by a function $\varphi :M \rightarrow \Delta ({\mathbb {R}})$. Notice that we allow the mechanism to pay with arbitrary (simple) lotteries, not necessarily lotteries over $\{0,1,2,3\}$.

Proposition 3

In the set-up described above, there exists no incentive compatible mechanism for the decision problems$D_1=\{l,\delta _1\}$and$D_2=\{l,\delta _2\}$.

The proof of this proposition appears in the “Appendix”. While the proposition is stated for a particular pair of decision problems, we believe that this impossibility result is typical, and that for most experiments there will be no incentive compatible mechanism. Thus, either reduction of compound lotteries or the domain of admissible preferences must be relaxed in order to get positive results.

7 Empirical tests of the RPS mechanism

Consider the following simple test of the RPS mechanism. In treatment A, subjects face $(D_1,\ldots ,D_k)$ and are paid via the RPS mechanism. In treatment B subjects see only one $D_i$ (for some $i\in \{1,\ldots ,k\}$) and are paid for that one choice. If there are differences in the choice frequencies in $D_i$ between treatments then one might infer that the RPS mechanism (and, thus, monotonicity) failed. There are several papers that have taken this approach, including Beattie and Loomes (1997), Cubitt et al. (1998, Experiment 2), Cox et al. (2014, 2015), Harrison and Swarthout (2014) and Freeman et al. (2016). Results among them are mixed.

There is a potential confound in the above design, however: subjects in treatment A see more choice objects than those in treatment B, and seeing these other options might alter their preferences over $D_i$. For example, the decoy effect or compromise effect might alter preferences. If this is the case then differences in $D_i$ across treatments may not necessarily indicate a monotonicity failure.

One possible way to fix the confound is to have the subjects in treatment B make choices from all k decision problems (just as in treatment A), but knowing that only their choice from $D_i$ will be paid. To our knowledge, there are four papers that take this approach: Starmer and Sugden (1991), Cubitt et al. (1998, Experiment 3), Cox et al. (2015) and Brown and Healy (2018). Results here are also mixed. Starmer and Sugden (1991) find that the RPS mechanism is incentive compatible in one test, but not the other.²² Cubitt et al. (1998) and Cox et al. (2015) find no significant violation of incentive compatibility.²³ Finally, Brown and Healy (2018) find significant a difference when all decisions are shown as one list on a single computer screen, but no significant difference when decisions are shown on sperate screens and in a random order. Indeed, this organizes the past results: the Starmer and Sugden (1991) rejection occurs when choices are presented in a list, but the other two studies—which find no rejection—present choices in a separated format. Thus, we conjecture that the list presentation causes monotonicity violations and recommend separating decisions wherever possible.

Camerer (1989) uses the RPS mechanism in his experiment, and then, once the payment state is realized, surprises subjects by asking if they’d like to change their decision in the paid decision problem. Less than three percent of subjects opt to change, suggesting that the RPS mechanism is incentive compatible.²⁴ Hey and Lee (2005b) ask whether their data fit better a model where subjects treat each question in isolation, or treat all as one large lottery. They assume several functional forms of preferences over lotteries, but find the data fit better the hypothesis that each decision is treated in isolation.²⁵

Loomes (1998) and Rubinstein (2002) document a violation of monotonicity caused by irrational diversification. Imagine a die with four red faces and two blue faces. If subjects are asked to bet six times on six different rolls of the die, many will bet on red four times and bet on blue two times. Assuming they truly prefer the bet on red, the two bets on blue give a lottery that is stochastically dominated.²⁶

Similarly, consider a dictator who must give $1 to either Ann or Bob. Suppose he prefers to give to Ann, but if given the choice twice might choose to give to Ann in one problem and Bob in another. The random choice of which problem gets paid provides an ex-ante fair division between Ann and Bob. This was first suggested by Diamond (1967), and evidence of this kind of preference has been documented by Bolton and Ockenfels (2010) and Cappelen et al. (2013), for example. Both fairness concerns and a preference for mixing suggest that monotonicity is more likely to be violated when the same question is asked repeatedly.

In developing prospect theory (Kahneman and Tversky 1979), it was found that subjects remove common components of compound lotteries. This ‘isolation effect’ has often been used as a justification for incentive compatibility of the RPS mechanism (Cubitt et al. 1998; Wakker et al. 1994). Indeed, isolation is equivalent to monotonicity (assuming transitivity), so isolation can be an appropriate justification for using the RPS mechanism.

Recall that monotonicity and reduction together imply expected utility, so monotonicity may be questionable if reduction holds. Reduction has found little empirical support, however (see Camerer 1995, p. 656 for a survey). For example, Loomes et al. (1991), Starmer and Sugden (1991), Cubitt et al. (1998, Experiment 1) and Beattie and Loomes (1997) all run experiments using the RPS mechanism in which two different messages m and $m'$ lead to the same simple lottery if reduction is assumed. In their data, subjects choose one message significantly more often than the other, clearly indicating that m and $m'$ are evaluated differently in many subjects’ preferences. Snowball and Brown (1979), Schoemaker (1989) and Bernasconi and Loomes (1992) also observe violations of reduction. Halevy (2007) finds that subjects who respect reduction seem to be rare, and seem to be exactly those for whom independence (and, therefore, monotonicity) is a reasonable assumption.

Appendices

Appendix 1: Proof of Lemma 3

For all of the appendices, recall that $x\succeq y$ indicates that either $x\succ y$ or $x=y$.

Suppose that $E\in SI({\mathscr {D}})$, and that E is not a singleton. Let $\{x,y\}\subseteq E$ be arbitrary. Consider the following two linear orders, $\succeq$ and $\succeq '$, which are identical except in their ranking of x and y (which are adjacent): They rank all elements of $X\backslash E$ above all elements of E, and they rank x and y above all elements of $E\backslash \{x,y\}$. However, $x\succ y$ and $y\succ ' x$. It is clear that if there is no $D\in {\mathscr {D}}$ such that $\{x,y\}\subseteq D \subseteq E$, then for all $D\in {\mathscr {D}}$, we have ${\text {dom}}_{\succeq }D={\text {dom}}_{\succeq '}D$, yet ${\text {dom}}_{\succeq }E=x\ne y ={\text {dom}}_{\succeq '}E$, contradicting sure identification.

Conversely, suppose that for every pair $\{x,y\}\subseteq E$, there exists $D\in {\mathscr {D}}$ for which $\{x,y\}\subseteq D\subseteq E$. Suppose by means of contradiction that there exist $\succeq$ and $\succeq '$ for which for all $D\in {\mathscr {D}}$, ${\text {dom}}_{\succeq }D={\text {dom}}_{\succeq '}D$, but ${\text {dom}}_{\succeq }E\ne {\text {dom}}_{\succeq '}E$. Let $w={\text {dom}}_{\succeq }E$ and $z={\text {dom}}_{\succeq '}E$. There exists $D'\in {\mathscr {D}}$ for which $\{w,z\}\subseteq D'\subseteq E$. As a consequence, $w={\text {dom}}_{\succeq }D'$ and $z={\text {dom}}_{\succeq '}D'$, contradicting the fact that ${\text {dom}}_{\succeq }D={\text {dom}}_{\succeq '}D$ for all $D\in {\mathscr {D}}$.

Appendix 2: Proof of Theorem 2

2.1 Step 1: Restrictions on $\varphi$

Recall that $L(x,\succeq )$ and $U(x,\succeq )$ are the lower- and upper-contour sets of x according to $\succeq$, respectively. Let $r(x,\succeq ) = |U(x,\succeq )|$ be the rank of x in $\succeq$. Two elements x, y are adjacent in $\succeq$ if $|r(x,\succeq )-r(y,\succeq )|=1.$ A switch of x, y in an order $\succeq$ is the replacement of the order of x, y, where x, y are adjacent in $\succeq$. Denote the obtained order by $\succeq ^{xy}$.²⁷

Lemma 5

$\varphi$is incentive compatible with respect to${\mathscr {E}}^\mathrm {mon}$if and only if it has the following two properties:

• (1) For every$\succeq$and everyx, ywith$r(x,\succeq )=r(y,\succeq )-1$,

  • (a) $\varphi (\mu (\succeq ))(z) = \varphi (\mu (\succeq ^{xy}))(z)$for every$z\ne x,y$.

  • (b) $\varphi (\mu (\succeq ))(x) > \varphi (\mu (\succeq ^{xy}))(x)$and$\varphi (\mu (\succeq ))(y) < \varphi (\mu (\succeq ^{xy}))(y)$whenever$\mu (\succeq )\ne \mu (\succeq ^{xy})$.

• (2) $\varphi (m)\in \Phi _{NR}$whenever$m\in M_{NR}$.

Proof

Assume $\varphi$ is incentive compatible and fix some $\succeq$ and some x, y with $r(x,\succeq )=r(y,\succeq )-1$. If $\mu (\succeq )=\mu (\succeq ^{xy})$ then the conditions are trivially true. Now assume that they differ. Let $z\ne x,y$ be some other element of X. Assume first that $r(z,\succeq )< r(x,\succeq )$, so z is ranked above x (and y) according to $\succeq$. Incentive compatibility implies that $\varphi (\mu (\succeq ))(U(z,\succeq )) \ge \varphi (\mu (\succeq ^{xy}))(U(z,\succeq ))$ and that $\varphi (\mu (\succeq ^{xy}))(U(z,\succeq ^{xy})) \ge \varphi (\mu (\succeq ))(U(z,\succeq ^{xy}))$. But since $U(z,\succeq ) = U(z,\succeq ^{xy})$ we get that they are equal, that is $\varphi (\mu (\succeq ))(U(z,\succeq )) = \varphi (\mu (\succeq ^{xy}))(U(z,\succeq ))$. The same argument applies to any z ranked above x (according to $\succeq$), which proves that $\varphi (\mu (\succeq ))(z) = \varphi (\mu (\succeq ^{xy}))(z)$ for any such z. A similar argument proves the assertion for elements z ranked below y. It follows that we must have $\varphi (\mu (\succeq ))(x) > \varphi (\mu (\succeq ^{xy}))(x)$ (and therefore $\varphi (\mu (\succeq ))(y) < \varphi (\mu (\succeq ^{xy}))(y)$) in order for $\varphi (\mu (\succeq )) \sqsupset \varphi (\mu (\succeq ^{xy}))$ to hold. This concludes the proof of property 1.

As for property 2, whenever $m\in M_{NR}$ incentive compatibility implies that $\varphi (\mu (\succeq )) \sqsupset \varphi (m)$ for every $\succeq$. First, this implies that $\varphi (m) \ne \varphi (\mu (\succeq ))$ for every $\succeq$. Second, assume that $\varphi (m)$ is not in $\Phi _{NR}$. Then by the separation theorem there is a vector $u\in {\mathbb {R}}^X$ such that $\sum _x u(x) \varphi (m)(x) > \sum _x u(x) \varphi (\mu (\succeq ))(x)$ for every $\succeq$. By boundedness of the set $\Phi _{NR}$, we can choose u such that $u(x)\ne u(y)$ whenever $x\ne y$. Let $\succeq _u$ be the order over X defined by u (formally, $u(x)>u(y)$ implies $x\succ y$). Then an expected utility maximizer with utilities $u(\cdot )$ prefers to report the non-rationalizable choices m over her true choices $\mu (\succeq _u)$. But this means $\varphi (\succeq _u)$ does not first-order stochastically dominate $\varphi (m)$ according to $\succeq _u$, a contradiction.

Conversely, assume that properties 1 and 2 are satisfied. Fix some $\succeq$ and consider some rationalizable deviation $m\in M_R$, $m\ne \mu (\succeq )$. Let $\succeq '\in \mu ^{-1}(m)$. Consider a minimal sequence of switches that starts at $\succeq$ and ends at $\succeq '$. This means that x and y are switched somewhere a long the path if and only if $x\succ y$ but $y\succ ' x$. Then property 1 implies that after any switch along the way we get a lottery that is dominated (relative to $\succeq$) by the previous one. This shows that $\varphi (\mu (\succeq ))$ dominates $\varphi (\mu (\succeq '))=\varphi (m)$. Finally, if $m\in M_{NR}$ then by property 2 and the above argument $\varphi (m)$ is a convex combination of lotteries that are dominated (relative to $\succeq$) by $\varphi (\mu (\succeq ))$, so it is dominated as well. This proves the lemma. $\square$

2.2 Step 2: Capacity representation

A capacity is a set function $v:2^X\rightarrow {\mathbb {R}}$ such that $v(\emptyset )=0$. A capacity v is normalized if $v(X)=1$ and monotone if $A\subseteq B$ implies $v(A)\le v(B)$.

Definition 11

A capacity v satisfies switch positivity if for every $x,y\in X$ and $A\subseteq X\setminus \{x,y\}$ the following holds: If $T(x,y,A)\ne \emptyset$ then $v(A\cup \{x,y\})+v(A) > v(A\cup \{x\})+v(A\cup \{y\})$; otherwise, $v(A\cup \{x,y\})+v(A) = v(A\cup \{x\})+v(A\cup \{y\})$.

If v satisfies switch positivity then it is supermodular, meaning $v(A\cup B)+v(A\cap B) \ge v(A) +v(B)$ for every $A,B\subseteq X$.

Lemma 6

If a mechanism$\varphi$is incentive compatible with respect to${\mathscr {E}}^\mathrm {mon}$then there exists a normalized and monotone capacityvthat satisfies switch positivity such that$\varphi (m)(x) = v(L(x,m)) - v(L(x,m)\setminus \{x\})$for every$m\in M_R$ and every $x\in X$.

Proof

Given $A\subseteq X$, consider some order $\succeq$ which ranks A at the bottom. Define $v(A) = \varphi (\mu (\succeq ))(A):= \sum _{x\in A} \varphi (\mu (\succeq ))(x)$. Notice first that, under incentive compatibility, v is well-defined in the sense that it does not depend on the particular order $\succeq$ used. Indeed, this follows from property (1a) in Lemma 5. It is also clear that v is normalized and monotone.

We now claim that v satisfies switch positivity. To see this, take any x, y and $A\subseteq X\setminus \{x,y\}$. Consider some order $\succeq$ with $L(x,\succeq )=A\cup \{x\}$ and $L(y,\succeq )=A\cup \{x,y\}$. We have $v(A\cup \{x\}) = \varphi (\mu (\succeq ))(A\cup \{x\})$ and $v(A\cup \{y\}) = \varphi (\mu (\succeq ^{xy}))(A\cup \{y\})$, so

$$\begin{aligned}v(A\cup \{x\}) + v(A\cup \{y\}) &= \varphi (\mu (\succeq ))(A\cup \{x\}) + \varphi (\mu (\succeq ^{xy}))(A\cup \{y\}) \\ &=v(A) + \varphi (\mu (\succeq ))(A) + \varphi (\mu (\succeq ))(x) + \varphi (\mu (\succeq ^{xy}))(y).\end{aligned}$$

Now, if $T(x,y,A)\ne \emptyset$ then $\mu (\succeq )\ne \mu (\succeq ^{xy})$ (see Remark 4.3), so by property (1b) of Lemma 5 we have $\varphi (\mu (\succeq ^{xy}))(y) < \varphi (\mu (\succeq ))(y)$. Thus,

$$\begin{aligned}v(A\cup \{x\}) + v(A\cup \{y\})&< v(A) + \varphi (\mu (\succeq ))(A) + \varphi (\mu (\succeq ))(x) + \varphi (\mu (\succeq ))(y)\\ &= v(A) + v(A\cup \{x,y\}),\end{aligned}$$

as required. On the other hand, if $T(x,y,A)=\emptyset$ then $\mu (\succeq )=\mu (\succeq ^{xy})$, so we get

$$\begin{aligned} v(A\cup \{x\}) + v(A\cup \{y\}) &= v(A) + \varphi (\mu (\succeq ))(A) + \varphi (\mu (\succeq ))(x) + \varphi (\mu (\succeq ))(y)\\ &= v(A) + v(A\cup \{x,y\}). \end{aligned}$$

Finally, we need to show that $\varphi (m)(x) = v(L(x,m)) - v(L(x,m)\setminus \{x\})$ whenever $m\in M_R$. Fix $m\in M_R$ and some $x\in X$. We claim that there is $\succeq \in \mu ^{-1}(m)$ such that $L(x,m)=L(x,\succeq )$. Since $L(x,m)\subseteq L(x,\succeq )$ for all $\succeq \in \mu ^{-1}(m)$, it is sufficient to show that the reverse inclusion holds for some $\succeq \in \mu ^{-1}(m)$. To see this, start with an arbitrary $\succeq \in \mu ^{-1}(m)$ and consider the set $L(x,\succeq )\setminus L(x,m)$. If this set is empty we are done. Otherwise, take the highest ranked element (according to $\succeq$) in this set, say y. Then for any z ranked between y and x (including $z=x$) it cannot be that zR(m)y, so by a sequence of switches we can put y above x without changing the resulting choices. By repeating this procedure for every element in $L(x,\succeq )\setminus L(x,m)$ we get the desired order, say $\succeq '$. For this order we have

$$\begin{aligned}v(L(x,m)) - v(L(x,m)\setminus \{x\}) &= v(L(x,\succeq ')) - v(L(x,\succeq ')\setminus \{x\})\\ &= \varphi (m)(L(x,\succeq ')) - \varphi (m)(L(x,\succeq ')\setminus \{x\})\\ &= \varphi (m)(x), \end{aligned}$$

as needed. $\square$

2.3 Step 3: Weighting vector representation

Lemma 7

Given$\varphi$, if there exists a normalized and monotone capacityvthat satisfies switch positivity such that$\varphi (m)(x) = v(L(x,m)) - v(L(x,m)\setminus \{x\})$for every$m\in M_R$and every$x\in X$, then$\varphi$is a weighted set-selection mechanism that satisfies switch positivity.

Proof

Let v be a normalized and monotone capacity that satisfies switch positivity and represents $\varphi$ as in the assertion of the lemma. As is well known (see Gilboa and Schmeidler 1995, e.g.), any capacity can be uniquely represented as a linear combination of the ‘unanimity capacities’. That is, there is a unique vector $\{\lambda (E)\}_{E\subseteq X, E\ne \emptyset }$ such that $v(A) = \sum _{E\subseteq A} \lambda (E)$ for every $A\subseteq X$.

We first show that if B is not SI then $\lambda (B)=0$. If B is not SI then by Lemma 3 there are $x,y\in B$ such that for no $1\le i\le k$ it holds that $\{x,y\} \subseteq D_i \subseteq B$. This in turn implies that $T(x,y,B\setminus \{x,y\})$ is empty (see Remark 4.3). Since v satisfies switch positivity we get that

$$\sum _{\{E :\, \{x,y\} \subseteq E \subseteq B\}} \lambda (E) = v(B) - v(B\setminus \{x\}) - v(B\setminus \{y\}) + v(B\setminus \{x,y\}) =0.$$

But if $\{x,y\} \subseteq D_i \subseteq B$ for no i then for every set E in the sum on the left it is also true that $\{x,y\} \subseteq D_i \subseteq E$ for no i, which implies that every such E is not SI. By induction on the size of B we can therefore prove that $\lambda (B)=0$.

We next check that the vector $\lambda$ satisfies switch positivity. Take any $x,y\in X$ and $A\subseteq X\setminus \{x,y\}$. By the last paragraph,

$$\sum _{ \{E\in T(x,y,A)\}} \lambda (E) = v(A\cup \{x,y\}) - v(A\cup \{x\}) - v(A\cup \{y\}) + v(A).$$

If $T(x,y,A)\ne \emptyset$ then since v satisfies switch positivity we have that $v(A\cup \{x,y\}) - v(A\cup \{x\}) - v(A\cup \{y\}) + v(A)>0$. Thus, $\lambda$ satisfies switch positivity.

The last thing to check is that $\lambda$ in fact represents the weighted set-selection mechanism $\varphi$ as in Definition 7. This follows from (for $m\in M_R$)

$$\varphi (m)(x)= v(L(x,m)) - v(L(x,m)\setminus \{x\}) = \sum _{\left\{ E:\, x\in E \subseteq L(x,m) \right\} } \lambda (E) = \sum _{\left\{ E:\, {\text {dom}}_m(E)=x \right\} } \lambda (E).$$

$\square$

2.4 Step 4: Weighted set-selection mechanisms are incentive compatible

Lemma 8

If$\varphi$is a weighted set-selection mechanism that satisfies switch positivity and satisfies$\varphi (m)\in \Phi _{NR}$whenever$m\in M_{NR}$then$\varphi$is incentive compatible with respect to${\mathscr {E}}^\mathrm {mon}$.

Proof

To check that $\varphi$ is incentive compatible we use Lemma 5. It follows immediately from the definition of a weighted set-selection mechanism that in a switch of adjacent two elements x, y the probability of any other element z being selected is not affected. Further, we have just showed above that the probability of x goes strictly up after a switch that increases the rank of x and changes the truthful message. This proves property 1 of Lemma 5. Property 2 of Lemma 5 is satisfied by assumption. $\square$

Appendix 3: Proof of Proposition 3

It will be convenient to think of any lottery f as a function $f:{\mathbb {R}}\rightarrow {\mathbb {R}}$, with f(x) being the probability assigned to x by f. For instance, the lottery l in the proposition is identified with the function $l(0)=l(3)=1/2$ and $l(x)=0$ otherwise. Addition of lotteries and multiplication of lotteries by scalars are performed pointwise (yielding functions which are not necessarily lotteries). The expected utility of a lottery f for a subject with utility function u (defined on dollar amounts) is denoted by $u\cdot f$.

The proof is broken into two claims:

Claim 1

If$\varphi$is incentive compatible then there is$a\in (0,1/2]$such that$\varphi (\delta _1,\delta _2)- \varphi (l,\delta _2) = -a \delta _0 + 2a \delta _1 -a \delta _3$.

Proof

Consider some strictly increasing utility function u such that $1/2u(0)+1/2u(3)=u(1)$. Then an expected utility maximizer (a special case of RDU preferences) with utility function u is indifferent between l and $\delta _1$, so both announcements $(\delta _1,\delta _2)$ and $(l,\delta _2)$ are truthful. By incentive compatibility this decision maker must also be indifferent between $\varphi (\delta _1,\delta _2)$ and $\varphi (l,\delta _2)$, that is $u \cdot \varphi (\delta _1,\delta _2) = u \cdot \varphi (l,\delta _2)$.

First, it cannot be true that there is $x\in {\mathbb {R}}\setminus \{0,1,3\}$ such that $\varphi (\delta _1,\delta _2)(x) \ne \varphi (l,\delta _2)(x)$. Indeed, let u be as above, and change the values of u in a small neighborhood of x (small enough that it does not affect any other point in the support of the two lotteries) to get a new increasing function ${\tilde{u}}$ that still satisfies $1/2{\tilde{u}}(0)+1/2{\tilde{u}}(3)={\tilde{u}}(1)$. Then it cannot be true that both equalities $u \cdot \varphi (\delta _1,\delta _2) = u \cdot \varphi (l,\delta _2)$ and ${\tilde{u}} \cdot \varphi (\delta _1,\delta _2) = {\tilde{u}} \cdot \varphi (l,\delta _2)$ hold simultaneously, a contradiction.

Thus, there are $a,b,c \in {\mathbb {R}}$ such that $\varphi (\delta _1,\delta _2)- \varphi (l,\delta _2) = a \delta _0 + b \delta _1 +c \delta _3$. Consider a utility function u with $u(0)=1, u(1)=2$ and $u(3)=3$. By the same argument as above we get that $u \cdot \varphi (\delta _1,\delta _2) = u\cdot \varphi (l,\delta _2)$, which implies $a+2b+3c=0$. By considering another function u with $u(0)=1, u(1)=3$ and $u(3)=5$ gives $a+3b+5c=0$. Solving these two equations gives $b=-2a$ and $c=a$.

To conclude, we showed that $\varphi (\delta _1,\delta _2)- \varphi (l,\delta _2) = -a \delta _0 + 2a \delta _1 -a \delta _3$ for some $a\in {\mathbb {R}}$. The fact that $a>0$ follows by looking at an expected utility maximizer with the utility function $u(x)=x$ (who strictly prefers the lottery l over $\delta _1$). The fact that $a\le 1/2$ is obvious. $\square$

The proof of the above claim only considered EU preferences. The following claim makes use of RDU preferences which do not satisfy independence.

Claim 2

If$\varphi$is incentive compatible then$\varphi (\delta _1,\delta _2)=\delta _1$and$\varphi (l,\delta _2)=l$.

Proof

Let u be the function $u(x)=0$ for $x<1$, $u(1)=1$, and $u(x)=3$ for $x>1$. Consider an RDU decision maker with utility function u and a probability weighting function q satisfying $q(0)=0, q(1/2)=1/2, q(1)=1$. Any such decision maker prefers the lottery l over $\delta _1$ and prefers $\delta _2$ over l. Thus, for incentive compatibility, any such decision maker must prefer $\varphi (l,\delta _2)$ over $\varphi (\delta _1,\delta _2)$, that is $U_q(\varphi (l,\delta _2)) > U_q(\varphi (\delta _1,\delta _2))$.

By the definition of u we have that

$$U_q(h) = 1[q(H(1))-q(H(1-))] + 3[1-q(H(1))]$$

for every lottery h with cdf H. Denote by F the cdf of the lottery $\varphi (l,\delta _2)$ and by G the cdf of $\varphi (\delta _1,\delta _2)$. Then incentive compatibility requires that

$$U_q(\varphi (l,\delta _2)) - U_q(\varphi (\delta _1,\delta _2)) = 2[q(G(1))-q(F(1))] - [q(F(1-))-q(G(1-))]>0$$

(2)

for every q as above.

By the previous claim, there is $0<a\le 1/2$ such that $G(1)-F(1)= F(1-)-G(1-)=a$. We claim now that incentive compatibility can only hold if $a=1/2$., i.e. if $G(1)=1, F(1)=F(1-)=1/2$ and $G(1-)=0$. Indeed, in any other case it is possible to choose q (strictly increasing, $q(0)=0$, $q(1)=1$, $q(1/2)=1/2$) such that $q(G(1))-q(F(1))$ is much smaller than $q(F(1-))-q(G(1-))$, which violates (2). The precise construction of such q depends on which of the intervals [0, 1 / 2] or [1 / 2, 1] each one of these four numbers belongs to, but it is straightforward in all cases. For instance, assume that $G(1-)\in [0,1/2]$ and $F(1-), F(1), G(1)$ are all in (1 / 2, 1]. Then we can find q such that $q(F(1-)), q(F(1))$ and q(G(1)) are all close to 1, while $q(G(1-))$ is at most 1/2. Other cases are treated similarly. $\square$

To conclude the proof, notice that the same arguments can be applied to the choices in the second decision problem. That is, incentive compatibility requires that $\varphi (l,l)=l$ and $\varphi (l,\delta _2)=\delta _2$. Since we cannot have $\varphi (l,\delta _2)=l$ and $\varphi (l,\delta _2)=\delta _2$ at the same time, we conclude that an incentive compatible mechanism does not exist.