Following van Inwagen (1990: 29), the binary mereological predicate ‘is composed of’ is generally defined as follows

(1):

x is composed of the ys = df x is a sum of the ys and the ys are pairwise disjoint (i.e., no two of them have any parts in common),

where

(2):

x is a sum of the ys = df the ys are all parts of x and every part of x has a part in common with at least one the ys.

This predicateFootnote 1 has played a central role in the debate on the special composition question and on related metaphysical issues concerning the mereological structure of objects. In this note we show that the characterization in (1) is nonetheless inadequate. We do so by constructing a mereological model M where everything qualifies as composed of atoms even though some elements in the domain are gunky, i.e., can be divided indefinitely into smaller and smaller proper parts.

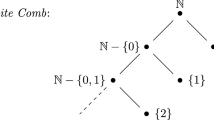
To this end, let G be a nonempty open interval on the real line, \( {\mathbb{R}} \), and let A be a countably infinite set of points of \( {\mathbb{R}} \) such that G ∩ A = ∅. For definiteness, we may identify G with the open interval \( (0,1) = \{ x \in {\mathbb{R}}:0 < x < 1\} \) and A with the set of all natural numbers, \( {\mathbb{N}} \). Next, define two functions α and β as follows:

(i):

for every open subinterval I = (x, y) of G, let α(I) = (x, (x + y)/2) and β(I) = ((x + y)/2, y);

(ii):

for every infinite subset P of A, let α(P) = {n ∈ P: f P (n) is even} and β(P) = {n ∈ P: f P (n) is odd}, where f P is the mapping of P into \( {\mathbb{N}} \) such that f P (n) = m if and only if n is the m-th element of P (relative to the natural linear ordering induced by ≤).

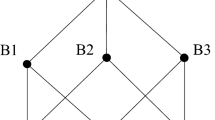
Thus, intuitively, given an open interval I ⊆ G, α(I) and β(I) are the two disjoint open subintervals corresponding to the left and right halves of I, respectively, separated by I’s midpoint. Similarly, given a countably infinite set P ⊆ A, α(P) and β(P) are the two disjoint countably infinite subsets corresponding to the even-valued and the odd-valued halves of P, respectively, relative to f P . See Fig. 1 for an illustration of the progressive “splitting” of G = (0, 1) and \( A = {\mathbb{N}} \) resulting from repeatedly applying α and β.

Fig. 1
figure 1

Progressive “splitting” of G and A by repeated application of α and β

Full size image

Third, for every n ≥ 0, define the set D n by induction:

$$ \begin{aligned} D_{0} = & \{ G \cup A\} \\ D_{k + 1} = & \{\upalpha(I) \cup\upalpha(P):I \subseteq G,P \subseteq A,I \cup P \in D_{k} \} \cup \{\upbeta(I) \cup\upbeta(P):I \subseteq G,P \subseteq A,I \cup P \in D_{k} \} . \\ \end{aligned} $$

Thus, each D k+1 will contain exactly 2k+1 elements, half of which will be of the form α(I) ∪ α(P) and the other half of the form β(I) ∪ β(P) for all I and P such that I ∪ P is an element of D k . With G = (0, 1) and \( A = {\mathbb{N}} \), the beginning of the sequence will look like this:

$$ \begin{array}{*{20}l} {D_{0} :} \hfill & {\{ \{ x \in {\mathbb{R}}:0 < x < 1\;{\text{or}}\;x \in {\mathbb{N}}\} \} } \hfill & = \hfill & {\{ (0,1) \cup \{ 0,1,2, \ldots \} \} } \hfill \\ {D_{1} :} \hfill & {\{ \{ x \in {\mathbb{R}}:0 < x < 1/2\;{\text{or}}\;x = 2y\;{\text{for}}\;{\text{some}}\;y \in {\mathbb{N}}\} ,} \hfill & = \hfill & {\{ (0,1/2) \cup \{ 0,2,4, \ldots \} ,} \hfill \\ {} \hfill & {\{ x \in {\mathbb{R}}:1/2 < x < 1\;{\text{or}}\;x = 2y + 1\;{\text{for}}\;{\text{some}}\;y \in {\mathbb{N}}\} \} } \hfill & {} \hfill & {(1/2,1) \cup \{ 1,3,5, \ldots \} \} } \hfill \\ {D_{2} :} \hfill & {\{ \{ x \in {\mathbb{R}}:0 < x < 1/4\;{\text{or}}\;x = 4y\;{\text{for}}\;{\text{some}}\;y \in {\mathbb{N}}\} ,} \hfill & = \hfill & {\{ (0,1/4) \cup \{ 0,4,8, \ldots \} ,} \hfill \\ {} \hfill & {\{ x \in {\mathbb{R}}:1/4 < x < 2/4\;{\text{or}}\;x = 4y + 2\;{\text{for}}\;{\text{some}}\;y \in {\mathbb{N}}\} ,} \hfill & {} \hfill & {(1/4,2/4) \cup \{ 2,6,10, \ldots \} ,} \hfill \\ {} \hfill & {\{ x \in {\mathbb{R}}:2/4 < x < 3/4\;{\text{or}}\;x = 4y + 1\;{\text{for}}\;{\text{some}}\;y \in {\mathbb{N}}\} ,} \hfill & {} \hfill & {(2/4,3/4) \cup \{ 1,5,9, \ldots \} ,} \hfill \\ {} \hfill & {\{ x \in {\mathbb{R}}:3/4 < x < 1\;{\text{or}}\;x = 4y + 3\;{\text{for}}\;{\text{some}}\;y \in {\mathbb{N}}\} \} } \hfill & {} \hfill & {(3/4,1) \cup \{ 3,7,11, \ldots \} \} } \hfill \\ \vdots \hfill & \vdots \hfill & {} \hfill & {} \hfill \\ \end{array} $$

Finally, we construct a mereological structure M as follows:

(i):

the domain of M, D M , is the set {{a}: a ∈ A} ∪ U n≥0 D n;

(ii):

the parthood predicate is interpreted in M as set inclusion, i.e., as the binary relation {〈x, y〉 ∈ D M  × D M : x ⊆ y}.

Now, it is easily checked that M has the following two properties. On the one hand, every element x ∈ D M has some singletons from the set {{a}: a ∈ A} as parts. This means that M satisfies the Atomicity axiom, as usually formulated:

(3):

Atomicity Everything has atomic parts,

where

(4):

y is atomic = df y has no proper parts (i.e., no parts other than itself).

On the other hand, every non-atomic element x ∈ D M can be divided indefinitely into proper parts of the form γ0(…(γ n (G))…) ∪ γ0(…(γ n (A))…), where each γ i is either α or β. Thus, every such element has gunky parts, too, where:

(5):

y is gunky = df every part of y has proper parts.

This is unpleasant. It is tempting to say that M shows the inadequacy of (3) vis-à-vis the atomistic intuition that this principle is meant to express. However, note that any non-atomic x ∈ D M does in fact count as being composed of atoms in the sense of (1). This follows directly from the fact that, as long as parthood is reflexive and transitive, (3) logically entails

(6):

Everything is composed of atoms.

(See Varzi 2015, §3.4.) But the truth of (6) in M can also be checked directly against the definitions in (1) and (2). For let x be an element of D M of the form I ∪ P and let the ys be the singletons of the points in P. Clearly, each of the ys is part of x. Conversely, if z is any part of x, then either z is one of the ys or z is an item of the form I′ ∪ P′, with I′ ⊆ I and P′ ⊆ P, and in either case it follows that z overlaps at least one of the ys. This means that x is a sum of the ys in the sense of (2). And since the ys are pairwise disjoint (trivially), it follows that x counts as composed of the ys in the sense of (1). Thus—here is the moral we wish to draw—not only is M a non-atomistic model of the Atomicity axiom (3), which is bad enough.Footnote 2 M is also a counterexample to the classical definition of composition in (1), since its domain contains elements that count as composed of atoms even though the atoms are not enough to generate them.

We leave it to the reader to determine whether the culprit is, as it often happens, the relevant notion of mereological sum, as defined in (2). For our part, we prefer to conclude with a remark concerning the sort of mereology that is needed to block the problem. To this end, note first of all that M satisfies the following principle:

(7):

Strong supplementation If x is not part of y, then x has a part that is disjoint from y.

(Proof: Pick any x, y ∈ D M and suppose x \( \nsubseteq \) y. By definition of D M , either x = {a} for some a ∈ A, or x ∈ D n for some n ≥ 0. In the first case, it follows immediately that {a} ⊆ x and {a} ∩ y = ∅. In the second case, x must be a subset of G ∪ A obtained by applying α and/or β. Since x \( \nsubseteq \) y, it follows that either x ∩ G \( \nsubseteq \) y or x ∩ A \( \nsubseteq \) y. But the inductive definition of D n implies that x ∩ G ⊆ y if and only if x ∩ A ⊆ y.Footnote 3 Thus, x ∩ A \( \nsubseteq \) y, which means that we can again pick some a ∈ A such that {a} ⊆ x and {a} ∩ y = ∅. In both cases, we have found an atom {a} ∈ D M that is a part of x and disjoint from y.)

It is a known fact that (7) together with the partial-order properties of parthood (all of which are satisfied in M) entails

(8):

Extensionality If x and y are non-atomic and have the same proper parts, then x = y.

(See Simons 1987, pp. 28–29.) It follows, therefore, that so-called Extensional Mereology—the theory obtained by adding (7) to the partial-order axioms—is not strong enough to block the problem, i.e., to guarantee that Atomicity and Composition behave as intended. By contrast, it is easy to see that M does not satisfy the following principle:

(9):

Universalism For any ys there is a z that is a sum of the ys.

(For instance, given any two points a 1, a 2 ∈ A, the atoms {a 1}, {a 2} are in D M but their sum {a 1} ∪ {a 2} is not.) Principle (9) is also known as Unrestricted Composition, and together with (7) yields the theory known as General Extensional Mereology, also known as Classical Mereology (from Leśniewski 1927–1930 and Leonard and Goodman 1940, modulo plural quantification). Such a theory is, therefore, strong enough to do the job, and it is easy to see why. For, given (9), any element x ∈ D M of the form I ∪ P can be split into its gunky and atomistic parts: one can first form the sum, z, of the atoms in P and then take the difference of x minus z, i.e., effectively, the sum of all parts of x that are disjoint from z, which is precisely the gunky part I of x.

It is an open question whether models like M can also be ruled out by weaker theories, i.e., theories properly included between Extensional Mereology and Classical Mereology. What is clear, however, is that short of some principle governing mereological summation, the notion of ‘composition’ that has shaped the recent debate on atomism and on other fundamental mereological issues is defective.