1 Introduction

Assessment of sediment transport in rivers plays a vital role in water resource planning and management. Often, the sediment transport process defines the course of the river. Basically, it is so dynamic and complex that makes it challenging to model and predict sediment loads accurately. Generally, the sediment load in a river depends on numerous factors, such as shear stress, sediment size, sediment gradation, moisture condition, distance of major sediment source, surface runoff, vegetal cover in the catchment, and discharge in the river (Delmas et al., 2011; Gupta et al., 2023; Nagy et al., 2002; Zakwan & Ara, 2022). Nevertheless, the data of all variables mentioned above are seldom available (Guguloth & Pandey, 2023) or require extensive field campaigns (Niazkar et al., 2019). Therefore, sediment load is conventionally estimated by developing sediment rating curves, wherein sediment load is assumed to be a function of river discharge.

Application of simple sediment ratings may not always yield reliable estimates of sediment loads, and as such, several researchers have questioned their reliability (Aytek & Kişi, 2008; Zakwan & Ahmad, 2021). Regarding inaccuracies in simple sediment ratings, Ferguson (1986) proposed the application of a correction factor along with simple sediment ratings for a better prediction of sediment loads. Furthermore, Zakwan and Ahmad (2021) employed a monthly index number in the simple sediment rating equation for a better prediction of sediment loads in Ganga river.

In addition to efforts devoted to improving the mathematical sediment ratings, the advent of machine learning (ML) and artificial intelligence (AI) techniques provided another ray of hope to the researchers to tackle the complex process of sediment transport with only discharge data as an input. Initially, Jain (2008) applied artificial neural network (ANN) for estimating the sediment load. Thereafter, several other researchers have found that ANN can provide reliable estimates of sediment loads (Adib & Mahmoodi, 2017; Gupta et al. 2021). Furthermore, Fadaee et al. (2020) utilized hybrid butterfly and genetic algorithms to estimate the sediment load and reported it to be more reliable than conventional sediment ratings. Moreover, Nhu et al. (2020) used novel random subspace ANN and compared the estimates of sediment load with hybrid support vector machine models, revealing the superiority of random subspace model over the hybrid ones. Additionally, Singh and Ali (2020) employed ANN to model sediment loads and emphasized on the need for development of a unique ANN architecture for each problem because they cannot be generalized. They suggested that even for the gauging sites on the same river, different ANN architectures may be found suitable. Also, Sharghi et al. (2021) employed emotional neural network to estimate the uncertainty in sediment ratings. Also, Sharafati et al. (2020) compared performances of three ensemble techniques to model the sediment ratings and found that random forest regression is the best ensemble technique to estimate the sediment load. In addition, Mohammadi et al. (2021) applied hybrid particle swarm optimization algorithm, differential evolution along with multi-layer-perceptron network to model the sediment ratings and reported high accuracy of the approach. Li et al. (2022) applied the wavelet decomposition on stage, discharge, and sediment load data of Yangtze River to obtain the integrated sediment load ratings and reported a significant improvement in the sediment load estimation as compared to simple rating curves. Achite et al. (2022) evaluated performances of various ML models and found that dynamic evolving neural-fuzzy inference systems is the most accurate for predicting suspended sediment loads. Khosravi et al. (2022) compared the performance of soil water assessment tool with that of random forest for prediction of suspended sediment loads and concluded the superiority of the latter for such estimations. Recently, Latif et al. (2023) compared various machine learning and deep learning algorithms to predict sediment load and found that application of ANN may be illusionary as during training stage it may over fit the data and the results may not be so promising during the real-time prediction.

The above literature survey suggests that there is a continuous scope of assessment of AI, ML, and hybridized models to improve the accuracy of predicted sediment loads. In this regard, the present article explores the capabilities of ensemble machine learning approach to estimate the sediment load. To be more precise, two-parameter and four-parameter rating curves, ANN, multi-gene genetic programming (MGGP), a hybrid MGGP-based model were combined linearly and nonlinearly to develop empirical and ML-based ensemble models. Their performances were evaluated for three time scales of two measuring stations.

2 Materials and methods

2.1 Datasets

The data adopted in this study are discharge and corresponding sediment discharge measured at two ground-based stations, named Botovo and Donji Miholjac on lower part of Drava River Basin, Croatia. To be more specific, the former is upstream of the latter with an approximate 150 km distance, while their average elevations are 121.55 m and 88.50 m above mean sea level, which corresponds to an average slope of 0.0002.

The original data, which were previously utilized in the literature (Niazkar & Zakwan, 2021), include pairs of discharge (Q) and sediment discharge (Qs) for each gauging site. Apart from the daily sediment discharge data, two additional datasets with different time scales were created by considering 10-daily and monthly averages of the discharge and sediment load values. The box blots of the data are depicted in Fig. 1. As shown, six sediment discharge data (two stations and three time scales) were used in this study.

Fig. 1
figure 1

Box plots of the data used in this study in terms of a daily, b 10-daily, and c monthly scales

Full size image

In order to estimate sediment discharge, 75% of each dataset was exploited as the training data for calibrating different estimation models (Shivashankar et al., 2022; Singh et al., 2022). On the other hand, the rest of the data was used in a bid to conduct a comparative analysis among different estimation models, while the measurements were considered as benchmark values. Regarding the data division, Table 1 summarizes the number of data, minimum, maximum, and average of the six training and testing datasets. As shown, each set of daily, 10-daily, and monthly data consists of 10,957, 1080, and 360, respectively. Moreover, the maximum and minimum Qs is 26,454.4 t/year and 0.5 t/year for Botovo and 18,774.7 t/year and 0.2 t/year for Donji Miholjac, respectively. Furthermore, Q varies in the range of 2345–103 m3/s at the first station and between 2166 m3/s and 175 m3/s at the second station, respectively. Finally, Table 1 indicates that the data acquire a wide range of values.

Table 1 Statistical characteristics of the sediment discharge data used in this study
Full size table

2.2 Empirical methods

Generally, sediment rating curve is presented by a two-parameter (2P) sediment rating equation, which is presented in Eq. (1):

$$S = { }a\left( Q \right)^{b}$$
(1)

where S is sediment discharge, Q is discharge, and a and b are constant coefficients, which can be calibrated using historical records.

Additionally, in the present study, a four-parameter (4P) model has also been used to address the scatter in the sediment discharge relationship as presented by Eq. (2):

$$S = \left\{ {\begin{array}{*{20}c} {cQ^{d} } & {Q < Q_{{{\text{avg}}}} } \\ {{ }eQ^{f} } & {Q > Q_{{{\text{avg}}}} } \\ \end{array} } \right.$$
(2)

where c, d, e, and f are constant coefficients and Qavg is the average discharge of the historical records.

According to Eqs. (1) and (2), the 4P model is an improved version of the 2P model, while the former considers more coefficients to associate sediment loads with discharges using a discharge-based threshold. The idea of considering a threshold for sediment estimation was originated from the theory of sediment transport and incipient motion. Similar considerations were assumed in a few sediment transport formulas available in the literature (Asadi et al., 2021). Hence, the aim of applying the 4P model is to improve the flexibility of the 2P model, while their performances will be explored later in this study.

2.3 Optimization algorithms

The 2P and 4P ratings were separately calibrated by two optimization techniques, called Generalized Reduced Gradient (GRG) and the Modified Honey Bee Mating Optimization (MHBMO) algorithms. Application of different optimization algorithms was carried out with the aim of addressing whether type of optimization algorithm can have an influence on sediment estimation models. As a result, four estimation models were developed: (1) 2P-MHBMO, (2) 2P-GRG, (3) 4P-MHBMO, and (4) 4P-GRG. The first two methods were used in another study for the daily sediment estimation (Niazkar & Zakwan, 2021), whereas applications of the first two methods for 10-daily and monthly and the two last ones for all cases were conducted for the first time in this study. In the following, a summary of the two optimization algorithms is presented:

The MHBMO algorithm has been previously applied to solve various problems in water resources management (Niazkar, 2020). In essence, it is a zero-order search-based optimization algorithm that basically mimics the nature mating process of honey bees, whose community consists of the queen, drones, and workers, while the first two are the best solution in each generation and possible random values for calibration coefficients, i.e., a and b in Eq. (1) and c, d, e, and f in Eq. (2). At the beginning of the algorithm, the first generation is produced randomly, while the queen is the individual with the lowest objective function, which is the root-mean-square errors between estimated and measured sediment loads. In order to find the optimum values of the calibration parameters, a new generation is produced by the mating process between the queen and drones. The generation reproduction continues until a stopping criterion is met. In this study, the controlling parameters of the MHBMO algorithm were set in accordance with a previous study on estimating daily sediment rating curves in the literature (Niazkar & Zakwan, 2021).

Generalized Reduced Gradient (GRG) is a gradient-based optimization technique. GRG solver is available as a plug-in in Microsoft Excel and is widely used in solving nonlinear problems. GRG algorithm looks for the optimal solution of the problem in the search space based on quasi-Newton method; however, in very complex nonlinear problems it relies on conjugate gradient technique. Application of GRG requires an objective function along with predefined nonlinear relationship and initial values of decision variables. The search space can be reduced by applying reasonable constrain depending upon the physical understanding of the problem; as an example, the coefficients (a and b) in sediment ratings are necessarily non-negative, so providing a non-negativity constrain can help in reducing search space and run time. Multistart option is also available in GRG solver to look after multiple starting points to address the chances of getting trapped in local optimum (Zakwan, 2016).

2.4 Machine learning techniques

The ML techniques used in the present study for estimating sediment ratings are presented as follows:

2.4.1 Artificial neural networks

ANN is a widely used machine learning technique in the domain of water resource problems. It employs a flow of data within a structure, which basically consists of three main layers. The first and last layers are input and output layers, whose neurons store input and output data, respectively. The third is named hidden layer, whose objective is to find a suitable relationship to relate input with output data. For this purpose, the neurons in a layer are only connected to those in other layers and cannot transfer information among one single layer. This constraint provides the flow transfer from two adjacent layer, while the repetition of the back-and-forth flow of data enables ANN to reach an estimation model with a desirable precision.

This study exploited a feed-forward backpropagation architecture to develop a sediment estimation model. Furthermore, the input layer and output layer entail one neuron each, which are dimensionless discharge (\(\overline{{Q_{i} }}\)) and dimensionless sediment discharge (\(\overline{{Q_{s,i} }}\)), respectively. The former and latter can be obtained by \(\overline{{Q_{i} }} = \frac{{Q_{i} - Q_{{{\text{min}}}} }}{{Q_{{{\text{max}}}} - Q_{{{\text{min}}}} }}\) and \(\overline{{Q_{s,i} }} = \frac{{Q_{s,i} - Q_{{s,{\text{min}}}} }}{{Q_{{s,{\text{max}}}} - Q_{{s,{\text{min}}}} }}\), respectively, where \(\overline{{Q_{i} }}\) is the ith discharge, \(Q_{{{\text{max}}}}\) is the maximum discharge, \(Q_{\min }\) is the minimum discharge, \(Q_{{s{,}\;i}}\) is the ith sediment discharge, \(Q_{{s{,}\;\max }}\) is the maximum sediment discharge, \(Q_{{s{,}\;\min }}\) is the minimum sediment discharge, respectively. After running ANN, the dimensionless sediment loads estimated by ANN will be turned to sediment discharges, which can be compared with the measured values.

2.4.2 Multi-gene genetic programming

MGGP is a modified version of genetic programming (GP), which is an ML model. Basically, GP is an estimation model that assumes a tree-like structure for any mathematical equation and exploits genetic algorithm (GA) to minimize the objection function, which is basically the estimation error of the GP-based model. The tree structure of GP and MGGP includes nodes, which can be categorized based on their content and location to (i) root node, (ii) function node, and (iii) terminal node. Each node stores one component of a mathematical equation, while the model can build up based on the content and connections between the nodes of an estimation model.

Both GP and MGGP mimic natural selection concept like GA, whereas they can develop ML-based estimation models unlike GA. The main difference between GP and MGGP is the way they define a single individual (an estimation model or a mathematical equation) in a population. The former presumes that an individual is one gene or tree, whereas an individual in the latter can consist of more than one gene or one tree. To be more specific, MGGP gives a weight to each tree and sums the weighted trees with a bias to make an individual, whereas GP considers only one tree to drive each individual. This difference may help to capture the trend of a more complicated phenomenon, like sediment transport.

In the current study, GPTIPS was used to run MGGP in MATLAB. The controlling parameters of MGGP were set as suggested in the literature (Niazkar, 2023). Like the data used for learning ANN models, \(\overline{{Q_{i} }}\) and \(\overline{{Q_{s,\;i} }}\) were utilized by MGGP as input and output data, and consequently, the MGGP-based estimation models are a function of \(\overline{{Q_{s,\;i} }}\) Finally, MGGP was run for more than 50 times for each case, while the best results were reported as the final MGGP results.

2.4.3 Hybrid MGGP-GRG

MGGP is a powerful tool to develop estimation models. Nevertheless, it was seen that coefficients of MGGP-based models can be further modified. For this purpose, Niazkar and Zakwan (2021) combined MGGP with GRG and presented a novel hybrid MGGP-GRG technique to model discharge ratings. First, the structure of the best-fitted estimation model is developed by MGGP. Later, coefficients of the MGGP based can be further improved/optimized using the GRG algorithm. Thus, the hybrid MGGP-GRG has twofold benefits: (i) It exploits the capability of a powerful ML model, i.e., MGGP, to develop the construction of the methodical formula of the estimation model, and (ii) it uses GRG to optimize coefficients of the MGGP-based estimation model. This hybrid method has been utilized for developing discharge rating curves (Niazkar & Zakwan, 2021) and estimating infiltration rates (Niazkar & Zakwan, 2021).

2.5 Ensemble methods

In this study, there are two types of methods, i.e., empirical and ML methods, for developing total sediment loads. In order to improve their performances, they were combined to obtain four ensemble methods: (i) linear empirical-based ensemble model, (ii) linear ML-based ensemble model, (iii) nonlinear empirical-based ensemble model, (iv) nonlinear ML-based ensemble model. In other words, empirical and ML methods were combined by using linear and nonlinear ensemble approaches, which are presented in the following:

Linear ensemble approach: This method calculates a simple algebraic average of estimation models. To be more specific, the sediment load for the ith data estimated by the linear ensemble model (\({\text{Q}}_{s,i}^{{{\text{lem}}}}\)) can be obtained by Eq. (3):

$${\text{Q}}_{s,i}^{{{\text{lem}}}} { } = { }\frac{1}{M}\mathop \sum \limits_{j = 1}^{M} \,Q_{s,i}^{j}$$
(3)

where \(Q_{s,i}^{j}\) is the sediment load estimated by one of empirical/ML methods for the ith data, M is 4 for empirical-based ensemble and 3 for ML-based ensemble models, respectively. As shown in Eq. (3), the weight of each method is assumed as equal in the linear ensemble model.

Nonlinear ensemble approach: This approach uses the estimations of empirical/ML models an input for training an ANN model, which will provide the final estimations of nonlinear ensemble methods. In other words, the ANN model is utilized to determine the weight associated with each model in the nonlinear ensemble model.

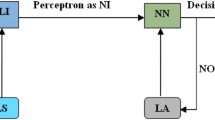
For a better clarification, the flowchart of the ensemble methods is illustrated in Fig. 2. As shown, the input data at the left side of the figure are discharge, which is used as an input for all empirical and ML-based models. The sediment loads estimated by the former, i.e., GRG (2P), GRG (4P), MHBMO (2P), and MHBMO (4P), are used as an input to train and ANN model for developing the nonlinear empirical-based ensemble model. Thus, the ANN output is the final estimation of the empirical-based ensemble model. Likewise, as shown in Fig. 2, the sediment loads predicted by the ML-based models, i.e., ANN, MGGP, and MGGP-GRG, are utilized as an input for an ANN model to develop the nonlinear ML-based ensemble model. Similarly, the output of the ANN model is the final sediment loads estimated by the nonlinear ML-based ensemble model. Finally, it should be noted that all the four ensemble methods shown in Fig. 2 were separately used for estimating sediment loads for three times scales, i.e., daily, 10-daily, and monthly.

Fig. 2
figure 2

Flowchart of ensemble methods

Full size image

2.6 Performance metrics

To evaluate the performance of sediment estimation models, six metrics were used in the comparative analysis. The indices are (1) Root-Mean-Square Errors (RMSE), (2) Mean Absolute Error (MAE), (3) Mean Absolute Relative Error (MARE), (4) Maximum Absolute Relative Error (MXARE), (5) Relative Error (RE), and (6) Determination Coefficient (R2). They are given in Eq. (4) to (9), respectively (Niazkar, 2020):

$${\text{RMSE}}\;{ = }\;\sqrt {\frac{{\sum\nolimits_{i = 1}^{N} {\left( {Q_{s,i}^{{{\text{obs}}}} - Q_{s,i}^{{{\text{est}}}} } \right)^{2} } }}{N}}$$
(4)
$${\text{MAE = }}\frac{{\sum\nolimits_{i = 1}^{N} {\left| {Q_{s,i}^{{{\text{obs}}}} - Q_{s,i}^{{{\text{est}}}} } \right|} }}{N}$$
(5)
$${\text{MARE = }}\frac{1}{N}\sum\nolimits_{i = 1}^{N} {\left| {\frac{{Q_{s,i}^{{{\text{obs}}}} - Q_{s,i}^{{{\text{est}}}} }}{{Q_{s,i}^{{{\text{obs}}}} }}} \right|}$$
(6)
$${\text{MXARE = max }}\left( {\left| {\frac{{Q_{s,i}^{{{\text{obs}}}} - Q_{s,i}^{{{\text{est}}}} }}{{Q_{s,i}^{{{\text{obs}}}} }}} \right|} \right) \, \quad {\text{for }}i = {1,} \cdots {,}N$$
(7)
$${\text{RE = }}\frac{{Q_{s,i}^{{{\text{obs}}}} - Q_{s,i}^{{{\text{est}}}} }}{{Q_{s,i}^{{{\text{obs}}}} }} \, \quad {\text{for }}i = {1,} \cdots {,}N$$
(8)
$$R^{{2}} { = }\left\{ {\frac{{\sum\nolimits_{i = 1}^{N} {\left[ {\left( {Q_{s,i}^{{{\text{obs}}}} - \frac{{\sum\nolimits_{i = 1}^{N} {Q_{s,i}^{{{\text{obs}}}} } }}{N}} \right)\left( {Q_{s,i}^{{{\text{est}}}} - \frac{{\sum\nolimits_{i = 1}^{N} {Q_{s,i}^{{{\text{est}}}} } }}{N}} \right)} \right]} }}{{\sum\nolimits_{i = 1}^{N} {\left[ {\left( {Q_{s,i}^{{{\text{obs}}}} - \frac{{\sum\nolimits_{i = 1}^{N} {Q_{s,i}^{{{\text{obs}}}} } }}{N}} \right)^{2} \left( {Q_{s,i}^{{{\text{est}}}} - \frac{{\sum\nolimits_{i = 1}^{N} {Q_{s,i}^{{{\text{est}}}} } }}{ + }} \right)^{{2}} } \right]} }}} \right\}^{2}$$
(9)

where \(Q_{s,i}^{{{\text{obs}}}}\) is the ith of the observed sediment load, \(Q_{s,i}^{{{\text{ests}}}}\) is the ith of the estimated sediment load, and N is the amount of data.

3 Results and discussion

For the comparative analysis, daily, 10-daily, and monthly sediment discharge data of two gauging sites were utilized to compare the estimates obtained from different techniques. The results are presented and discussed in the following:

3.1 Results of empirical methods

Tables 2 and 3 show the values calibrated for 2P and 4P models, respectively. As shown, for the daily and monthly time scales, the values calibrated by MHBMO for the parameters of 2P and 4P models are quite the same or close to the corresponding values calibrated by GRG at both stations. For instance, a and b of the 2P model were obtained by the MHBMO algorithm and GRG equal to 0.0207 and 1.7148 for the daily sediment data at the Botovo station, respectively. On the contrary, the MHBMO algorithm and GRG yielded different values for the 10-daily data for 2P and 4P models at both stations. Thus, it is expected that GRG (2P) performs quite the same as and MGBMO (2P) for estimating daily and monthly sediment loads at two stations. Likewise, GRG (4P) and MHBMO (4P) obtained quite the same values of calibration parameters for predicting daily and monthly sediment discharges at Botovo and Donji Miholjac, whereas they reach different values for the calibration parameters of the models for estimating 10-daily sediment loads, as shown in Table 3. Furthermore, the performance of 2P and 4P models should be compared for each time scale and case study using metrics to evaluate performances of GRG (2P), MGBMO (2P), GRG (4P), and MHBMO (4P) for estimating total sediment discharges.

Table 2 Calibration parameters of two-parameter empirical models for estimating sediment loads in different time scales
Full size table
Table 3 Calibration parameters of four-parameter empirical models for estimating sediment loads in different time scales
Full size table

3.2 Comparison of empirical and ML methods

To assess performances of empirical and ML models, measured sediment loads were set as benchmark solutions, while different metrics were calculated for sediment discharge estimations. Tables 4 and 5 present the empirical and ML-based estimation models with the best metric value are listed for various cases (i.e., train and test data, five metrics, and three time scales) for Botovo and Donji Miholjac stations, respectively. According to Table 4, MGGP-GRG achieved the best value for 15 out of 30 cases, while MGGP yield to 10 out of 30 cases. This indicates that MGGP-GRG and MGGP perform better than other models for estimating sediment loads for Botovo. Moreover, Table 4 indicates that 2P and 4P models resulted in the best metric performances for 1 and 6 out of 30 cases, which shows the superiority of 4P models in comparison with 2P. In addition, ANN is repeated 4 times in the 30 cases shown in Table 4.

Table 4 List of empirical and ML-based methods with the best performance in terms of each metric for estimating total sediment loads in Botovo
Full size table
Table 5 List of empirical and ML-based methods with the best performance in terms of each metric for estimating total sediment loads in Donji Miholjac
Full size table

For the second measuring station, i.e., Donji Miholjac, the ML-based estimation models performed better than empirical ones, as shown in Table 5. To be more precise, MGGP-GRG, MGGP, and ANN achieved the best metric value for 11, 1, and 11 cases out of 30 cases, respectively. On the other hands, 2P and 4P models yielded best metric performance for 3 and 5 out of 30 cases, respectively.

In order to summarize the performances of different models reported in Tables 4 and 5, the number of times that the name of one method is mentioned in Tables 4 and 5 is summed and inserted into Table 6 to rank different models in light of estimating sediment discharges for two measuring stations, train and test parts of data, and three different time scales. Table 6 shows that the comparative analysis reveals that ML-based models perform better than empirical ones for estimating sediment loads for different time scales because MGGP-GRG, MGGP, and ANN got the first three ranks in Table 6. Additionally, Table 6 obviously shows that enhancing MGGP with GRG can improve sediment discharge estimations. Also, Table 6 indicates that 4P models resulted in more rigorous sediment estimations than those of 2P models.

Table 6 Ranking analysis of empirical and ML-based methods for total sediment estimation
Full size table

3.3 Results of daily sediment loads

In order to further improve the prediction of sediment loads, empirical and ML-based models were combined separately to develop empirical and ML-based ensemble methods, respectively. Figure 3 depicts the performances of different ensemble methods for estimating daily sediment loads for the first and second measuring stations using five metrics. As shown, the lowest (i.e., best) RMSE and MAE values for Botovo were obtained by the empirical-based nonlinear ensemble model (i.e., 1050.1 and 448.9) and ML-based nonlinear ensemble model (i.e., 1031.2 and 440.5) for the train and test data, respectively. Furthermore, the best RMSE and MAE results for Donji Miholjac were achieved by the ML-based nonlinear ensemble model (i.e., 971.3 and 507.3) and the empirical-based nonlinear ensemble model (i.e., 943.3) and the ML-based nonlinear ensemble model (i.e., 505.5), respectively. In addition, the comparative analysis in terms of R2 for estimating daily sediment loads demonstrates the empirical-based nonlinear ensemble model (i.e., 0.4835) and the ML-based nonlinear ensemble model (i.e., 0.4712) for the train and test data of Botovo, respectively. Comparing R2 values for daily sediment data of Donji Miholjac indicates that the ML-based nonlinear ensemble model (i.e., 0.3053) and the empirical-based nonlinear ensemble model (i.e., 0.3037) perform slightly better than the other ensemble models for the train and test data, respectively. Moreover, Fig. 3 clearly shows that the ML-based nonlinear ensemble model outperformed other models in respect of MARE for both measuring stations. Additionally, the empirical-based nonlinear ensemble model reaches the lowest MXARE for the train data of Botovo (i.e., 127.17) and Donji Miholjac (i.e., 939.1), respectively, whereas the ML-based nonlinear ensemble model reaches better MXARE for the test data of Botovo (i.e., 60.3) and Donji Miholjac (i.e., 542.6), respectively.

Fig. 3
figure 3

Comparison of different ensemble methods for estimating daily total loads based on different metrics

Full size image

3.4 Results of 10-daily sediment loads

Figure 4 compares the performance of different ensemble models for estimating 10-daily sediment discharges for the two case studies. As shown, the ML-based nonlinear ensemble model achieved the best RMSE values for the train data of Botovo (i.e., 579.4) and for the train (i.e., 664.98) and test data (i.e., 651.5) of Donji Miholjac, respectively. On the other hand, with a slight difference with the result of the ML-based nonlinear ensemble model, the empirical-based nonlinear ensemble obtained the lowest RMSE (i.e., 650.1). Moreover, the ML-based linear ensemble model and the empirical-based nonlinear ensemble model obtained the lowest MAE (i.e., 343.5 and 354.6) for the train and test data of Botovo, respectively. In addition, the former model yielded the best MAE values for the train and the test data (i.e., 422.2 and 431.6) of Donji Miholjac, respectively. Furthermore, the ML-based nonlinear ensemble model outperformed other ensemble models in terms of R2 for the train and test data of both stations, while the empirical-based nonlinear ensemble model obtained quite the same R2 as the ML-based nonlinear ensemble model for the test data of Botovo. Also, Fig. 4 indicates that the empirical-based nonlinear ensemble model reaches the lowest MARE and MXARE for the train and test data of both stations, except that the ML-based linear ensemble model achieved a better MXARE than the empirical-based nonlinear ensemble model for the test data of Botovo.

Fig. 4
figure 4

Comparison of different ensemble methods for estimating 10-daily total loads based on different metrics

Full size image

3.5 Results of monthly sediment loads

Figure 5 illustrates the comparative analysis of different ensemble models for estimating monthly sediment discharges for Botovo and Donji Miholjac stations. According to Fig. 5, the ML-based simple average ensemble model (i.e., 556.5, 255.0, and 0.759) and the empirical-based nonlinear ensemble model (i.e., 549.1, 378.6, and 0.589) achieved the lowest RMSE and MAE and highest R2 for the train and test monthly sediment data of Botovo, respectively. Additionally, the ML-based nonlinear ensemble model (i.e., 544.6 and 0.470) and the empirical-based simple average ensemble model (i.e., 603.6 and 0.374) obtained the best RMSE and R2 for the train and test monthly sediment data of Donji Miholjac, respectively. Furthermore, Fig. 5 indicates that the ML-based simple average ensemble model (i.e., 376.5) and the empirical-based simple average ensemble model (i.e., 603.6) reach the best MAE for the train and test monthly sediment data of Donji Miholjac, respectively. Also, the ML-based simple average ensemble model yielded the lowest MARE for the train and test data at both stations. Moreover, Fig. 5 shows that the empirical-based nonlinear ensemble model achieved the lowest MXARE for the train (i.e., 603.6) and test (i.e., 603.6) data of the first station, whereas the ML-based simple average ensemble model and the empirical-based simple average ensemble model obtained the lowest MXARE for the train (i.e., 28.48) and test (i.e., 15.90) data of the second station, respectively.

Fig. 5
figure 5

Comparison of different ensemble methods for estimating monthly total loads based on different metrics

Full size image

According to Tables 4, 5, and 6 and Figs. 3, 4, and 5, different sediment estimation models can be identified as the most robust one based on different metrics. Nevertheless, based on the comparative analysis, it is obvious that application of ensemble models can improve the estimation of sediment models for the daily, 10-daily, and monthly time scales. Additionally, the difference between performances of ML and those of empirical models indicates that ML-based estimation models, particularly MGGP-GRG, can enhance estimating sediment loads.

4 Conclusions

Sediment ratings are an integral part of water resource engineering. The present study examines the capability of a four-parameter (4P) sediment rating equation and application of ensemble ML models to estimate the sediment load. The model parameters obtained from MHBMO and GRG were the same. Therefore, either of the optimization technique can be applied for estimating the parameters of sediment ratings. Among single models employed in the present study, MGGP-GRG provided the best fitness statistics in more than 50% of the cases considered here. Additionally, the ranking analysis demonstrated that combining MGGP with GRG enhances the performance of MGGP because MGGP-GRG and MGGP models were took the first and third ranking places. Furthermore, ensemble-based models improved the estimates of sediment load at daily, 10-daily, and monthly scales. In particular, ML-based simple average ensemble model and the empirical-based nonlinear ensemble model achieved the lowest RMSE and best R2 for monthly sediment data at Botovo. Thus, the application of ensemble models is recommended for dealing with complex sediment ratings.