An efficient hybrid method based on cubic B-spline and fourth-order compact finite difference for solving nonlinear advection–diffusion–reaction equations

Abstract

This paper proposes an efficient hybrid numerical method to obtain approximate solutions of nonlinear advection–diffusion–reaction (ADR) equations arising in real-world phenomena. The proposed method is based on finite differences for the approximation of time derivatives while a combination of cubic B-splines and a fourth-order compact finite difference scheme is used for spatial discretization with the help of the Crank–Nicolson method. Since desired accuracy and order of convergence cannot be reached using the traditional cubic B-spline method, to overcome this, the second-order derivatives are approximated using the unknowns and their first derivative approximations with the compact support. Thus, instead of expressing the second-order derivative in second-order accuracy, it is represented by the convergence of order four in the present method. The computed results revealed that this combined approach improves the accuracy of solutions of nonlinear ADR equations in comparison to up-to-date literature even using relatively larger step sizes. Besides, this method is seen to be capable of capturing the behavior of the models with very small viscosity values. The stability of the proposed method has been discussed by considering the matrix stability approach and it has been shown that the method is stable. In addition to the fact that the proposed method obtains sufficiently accurate solutions, another main superiority is its simplicity and applicability, which requires minimum computational effort.

1 Introduction

Nonlinear advection–diffusion–reaction (ADR) equations play an important role in representing various physical or biological phenomena arising in engineering and science. Therefore, researchers focus their attention on capturing the behaviors of these problems which is a challenging issue. Since obtaining an analytical solution for such problems is not easy due to the complexity of the transport process, researchers have attempted to investigate the behaviors of these problems by developing various numerical techniques. In this paper, a new hybrid numerical method has been proposed for the following ADR equation:

$$\begin{aligned} u_t+\alpha u^{\mu }u_x-vu_{xx}=F(u), \quad a\le x \le b,\quad t \ge 0, \end{aligned}$$

(1)

subject to the initial condition

$$\begin{aligned} u(x,0)=g(x), \quad a \le x \le b, \end{aligned}$$

(2)

and the boundary conditions

$$\begin{aligned} u(a,t)= & {} g_1(t), \end{aligned}$$

(3)

$$\begin{aligned} u(b,t)= & {} g_2(t), \quad 0 \le t \le T, \end{aligned}$$

(4)

where v, $\alpha$, and F(u) are the eddy viscosity, the velocity component of the fluid, and source/sink in terms of u, respectively. The terms g(x), $g_1(t)$, and $g_2(t)$ are known functions and the subscripts x and t represent differentiations with respect to space and time, respectively. The advection term $u_x$ depicts the transportation of the quantity u by the velocity field. The diffusion term $u_{xx}$ describes the dissemination of the quantity u.

In the literature, various numerical techniques based on finite difference methods [1, 2], Galerkin methods [3, 4], spectral collocation methods [5], and decomposition methods [6, 7] have been developed for numerical simulation of nonlinear ADR equations up to now. In addition, the aim of accurately capturing the behavior of these problems encountered in various fields of science and engineering has always prompted researchers to develop new various techniques such as a lattice Boltzmann method [8], high-order splitting methods [9], a finite volume and Fourier pseudospectral method [10], 2N order compact finite difference method [11], a meshless semi-analytical collocation technique [12], and a new heuristic method [13].

In the last decades, B-spline functions have attracted the attention of many researchers to find out effective numerical solutions to linear and nonlinear partial differential equations. The cubic B-spline collocation methods which use B-splines as basis functions are well-known efficient approximation methods. These methods with some special properties such as smoothness, local support of spline curve, good approximation rate, computationally fast, and numerical consistency are convenient to apply to differential equations. These methods are also able to approximate analytical solutions up to a certain smoothness [14]. Therefore, spline methods provide the flexibility to get the approximation at any point in the domain with more accurate results compared to some other standard methods. The earliest studies about the theory of standard cubic B-spline methods, their properties, and some applications to ordinary and partial differential equations can be found in the books of Prenter [15] and Rubin [16]. More recently, various efficient methods based on various versions of B-splines and combined with other numerical techniques have been developed to capture the behavior of ADR equations accurately. For instance, hybrid B-spline collocation methods based on possessing a free parameter were proposed for various forms of ADR equations by Wasim et al. [14] and for a generalized nonlinear Klien–Gordon equation by Mat Zin [17]. Although those remarkable methods represented the behavior of the problems successfully, the lack of a technique for predicting an optimal parameter can be a drawback for those methods. In the study of Mittal and Jain [18], the cubic B-spline functions have needed to be modified into a set of basis functions for handling their problems. In addition to those studies, various kinds of B-spline collocation methods were also applied to deal with several nonlinear ADR equations [19,20,21,22,23,24,25,26]. Despite many advantages of the cubic B-spline collocation methods, the desired accuracy and order of convergence cannot be achieved compared to some competitors in solving differential equations. To overcome this, they are combined with other robust techniques in the literature such as compact finite difference methods which become one of the most popular techniques for solving partial differential equations arising in many applications. Compact finite difference methods have higher accuracy even when using larger mesh sizes. Thus, the system of equations has a small bandwidth coefficient matrix that can be solved efficiently. Besides, high-order compact finite difference methods consider not only the value of the function but also those of its first derivatives as unknowns at each discretization point [27]. Although the solutions of the ADR equations can be obtained through some effective numerical techniques, in terms of the aforementioned reasons, the need of obtaining flexible and computationally efficient solutions of the problems where it is difficult to control precision and stability motivated us to propose a new hybrid method based on combining with the standard cubic B-spline and a fourth-order compact finite difference method.

In this paper, a new numerical scheme by combining the standard cubic B-spline and a fourth-order compact finite difference scheme is proposed to capture the behavior of the Burgers, Burgers–Fisher, Burgers–Huxley, and Fisher’s equations. Firstly, these equations have been discretized by the Crank–Nicolson and the forward finite difference methods for spatial and temporal domains, respectively, and then, the combined method has been applied for spatial derivatives. In this technique, spatial second derivative approximations are approached by the fourth-order compact finite difference scheme in which second derivative approximations of the unknowns are eliminated with the unknowns themselves and their first derivative approximations while retaining the fourth-order accuracy. Hence, the second-order derivative is represented by the convergence of order four by this approach, while it has second-order accuracy in the standard cubic B-spline method. Thus, with the aforementioned advantages of the cubic B-spline and fourth-order compact finite difference methods, the combination of these methods aims to pull up the capacity of the algorithm to achieve higher accuracy with minimal computational effort. The computed results for each equation have been evaluated in terms of accuracy, flexibility, and computational efficiency depending on the dynamics of the problems with their different set of parameters by comparing them with up-to-date techniques in the literature. The calculations for the strong form of the Burgers equations revealed that the proposed method is in very good agreement with the exact solution and that the proposed method is superior to the cubic B-spline collocation method presented in the study of Dag et al. [28] and other compared techniques in the literature even when using fewer spatial and temporal elements. Moreover, the current scheme can capture the behavior of the model with very small viscosity efficiently and accurately. For the Burgers-Fisher and Burgers-Huxley equations, considerable improvement has been reached even if sometimes it is at a moderate level even using fewer spatial or temporal elements which reduces the computational complexity, CPU time, and memory space. Finally, implementing the proposed method to the Fisher’s equation has demonstrated that the current scheme produces more accurate solutions than the standard cubic B-spline method [29] and the wavelet-Galerkin approach [30]. Besides, the current scheme solutions for the Fisher’s equation have been found to be in reasonable agreement with other compared methods and is successful to represent the behavior of the problem having small viscosity. In addition, the proposed method provides much flexibility to implement complicated problems by importing second derivative terms with a high-order compact finite difference formula. The stability analysis of the method has been discussed by the matrix stability analysis and concluded that the present method is stable. Furthermore, the current scheme is quite easy to produce computer codes in any programming language and has not been implemented in any other study including ADR equations so far.

2 The proposed method

In this section, a new combining method based on the cubic B-spline and fourth-order compact finite difference methods will be constructed for the nonlinear ADR equations. Cubic B-splines are chosen as the basis function in the collocation methods due to the higher smoothness and sparse nature of matrices corresponding to splines. These methods which have some special properties such as smoothness, good approximation rate, computationally fast, numerically consistent, and ability to produce the shape of the data with the second order of continuity produce efficient algorithms for obtaining solutions of partial differential equations. Another important advantage of this method is that it is able to approximate the analytical curve up to a certain smoothness, providing the flexibility to obtain an approximation at any point in the domain [14]. In addition, the fourth-order compact finite difference method used in the proposed scheme is preferred in terms of solving various differential equations with providing low computational effort by using a small number of grid points.

Now, to construct the new combined method, let us introduce the cubic B-spline and the fourth-order compact finite difference method and derive the second-order derivative approximation which includes the unknowns themselves and their first derivatives only.

Firstly, a uniform partition of the domain $[a,b] \times [0,T]$ is considered by the knots $x_i$, $i=0,1,2\ldots ,N$ and $t^n$, $n=0,1,2,\ldots ,M$ such that $x_i=a+ih$ and $t^n=n\textrm{d}t$, $h=\frac{b-a}{N}$ and $\textrm{d}t=\frac{T}{M}$. The numerical solutions of the nonlinear ADR problem (1)–(4) are approximated by the cubic B-spline interpolation as follows:

$$\begin{aligned} u(x,t)\approx V_N(x,t)=\sum _{i=-1}^{N+1}\delta _i(t)B_i(x), \end{aligned}$$

(5)

where $\delta _i$ is time-dependent parameter and $B_i$ represents the well-known cubic B-spline functions given the following relationship [15]:

$$\begin{aligned} B_i(x)=\frac{1}{h^3} {\left\{ \begin{array}{ll} \left( x-x_{i-2}\right) ^3, &{} \left[ x_{i-2},x_{i-1}\right] ,\\ h^3+3h^2 \left( x-x_{i-1}\right) +3h\left( x-x_{i-1}\right) ^2-3\left( x-x_{i-1}\right) ^3, &{} \left[ x_{i-1},x_{i}\right] ,\\ h^3+3h^2\left( x_{i+1}-x\right) +3h\left( x_{i+1}-x\right) ^2-3\left( x_{i+1}-x\right) ^3, &{} \left[ x_{i},x_{i+1}\right] ,\\ \left( x_{i+2}-x\right) ^3, &{} \left[ x_{i+1},x_{i+2}\right] ,\\ 0,&{}\textrm{otherwise},\\ \end{array}\right. } \end{aligned}$$

where $h=x_{i+1}-x_i, i=-1,\ldots ,N+1$. The variation of $V_N(x,t)$ over typical element $\left[ x_i,x_{i+1}\right]$ is expressed by

$$\begin{aligned} V_N(x,t)=\sum _{j=i-1}^{i+2}\delta _j(t)B_j(x). \end{aligned}$$

(6)

By using the interpolating conditions, the values at the knots of V(x, t) and its two derivatives $V'(x,t)$ and $V''(x,t)$ at the knots are stated in terms of time-dependent parameters $\delta _i$ as follows:

$$\begin{aligned} V_i=V(x_i)=\delta _{i-1}+4\delta _i+\delta _{i+1}, \end{aligned}$$

$$\begin{aligned} V_i^{'}=V'(x_i)=\frac{3}{h}\left( \delta _{i+1}-\delta _{i-1}\right) , \end{aligned}$$

(7)

$$\begin{aligned} V_i''=V''(x_i)=\frac{6}{h^2}\left( \delta _{i-1}-2\delta _i+\delta _{i+1}\right) . \end{aligned}$$

The space and time derivatives in Eq. (1) are discretized by using the Crank–Nicolson and the finite difference schemes:

$$\begin{aligned} \frac{V^{n+1}-V^n}{\textrm{d}t}+\alpha \frac{(V^{\mu }V_{x})^{n+1}+(V^{\mu }V_{x})^{n}}{2}-v\frac{V_{xx}^{n+1}+V_{xx}^n}{2}=\frac{F^{n+1}(V)+F^n(V)}{2}. \nonumber \\ \end{aligned}$$

(8)

The nonlinear terms in Eq. (8) can be linearized by using the following formula [16]

$$\begin{aligned} (V^\mu V_x)^{n+1}=\left( V^{\mu }\right) ^n V_x^{n+1}+\mu (V^{\mu -1})^nV_x^nV^{n+1}-\mu (V^\mu )^nV_x^n. \end{aligned}$$

Hence, Eq. (8) transforms to the following form:

$$\begin{aligned}{} & {} \frac{V^{n+1}-V^n}{\textrm{d}t}+\alpha \frac{(V^\mu )^n V_{x}^{n+1}+\mu (V^{\mu -1})^n V_x^n V^{n+1}-\mu (V^\mu )^n V_x^n+(V^\mu V_x)^n}{2}\nonumber \\{} & {} \qquad -v\frac{V_{xx}^{n+1}+V_{xx}^n}{2} =\frac{F^{n+1}(V)+F^n(V)}{2}. \end{aligned}$$

(9)

Now, to construct the new proposed scheme, let us introduce the fourth-order compact finite difference approximation for the first and second derivatives, respectively, as follows:

$$\begin{aligned}{} & {} \frac{1}{4}V_{i-1}'+V_i'+\frac{1}{4}V_{i+1}'=\frac{1}{h}\left[ -\frac{3}{4}V_{i-1}+\frac{3}{4}V_{i+1}\right] , \end{aligned}$$

(10)

$$\begin{aligned}{} & {} \frac{1}{10}V_{i-1}''+V_{i}''+\frac{1}{10}V_{i+1}''=\frac{1}{h^2}\left[ \frac{6}{5}V_{i-1}-\frac{12}{5}V_i+\frac{6}{5}V_{i+1}\right] , \end{aligned}$$

(11)

where $V'_i$ and $V''_i$ are the first- and second-order derivative approximations of unknown V at point $x_i$, respectively. In Eq. (10), the second-order derivative terms can be obtained by applying the first operator again:

$$\begin{aligned} \frac{1}{4}V_{i-1}''+V_i''+\frac{1}{4}V_{i+1}''=\frac{1}{h}\left[ -\frac{3}{4}V_{i-1}'+\frac{3}{4}V_{i+1}'\right] . \end{aligned}$$

(12)

Eliminating $V_{i-1}''$ and $V_{i+1}''$ from Eqs. (11) and (12), the second derivative is obtained as the following form [27]:

$$\begin{aligned} V_i''=2\frac{V_{i+1}-2V_i+V_{i-1}}{h^2}-\frac{V_{i+1}'-V_{i-1}'}{2h}. \end{aligned}$$

(13)

Thus, the second derivative that is constructed by unknowns themselves and their first derivatives only has been represented by the convergence of the fourth order by this formula in the proposed method. Thus, in the solution of Eq. (9) while Eq. (7) is used for approximating unknown V and its first and second derivatives for boundary points, Eq. (13) will be used instead of the second derivative given in Eq. (7) for interior points.

3 Implementation of the method

In this section, the proposed method will be implemented for the Burgers, Burgers–Fisher, Burgers–Huxley, and Fisher’s equations.

3.1 Algorithm for the Burgers equation

Equation (1) is called the well-known Burgers equation when $F(u)=0$ and $\alpha =\mu =1$. Considering Eq. (9) that is the discretization form of Eq. (1) for the Burgers equation and rearranging the terms and simplifying them, it is expressed as the following form:

$$\begin{aligned} V^{n+1}\left\{ 1+\frac{\textrm{d}t}{2}V_x^n\right\} +\frac{\textrm{d}t}{2}V^{n}V_x^{n+1}-v\frac{\textrm{d}t}{2}V_{xx}^{n+1}=V^n+v\frac{\textrm{d}t}{2}V_{xx}^n. \end{aligned}$$

(14)

Substituting Eq. (7) into Eq. (14) for the boundary points, $i=0,N$, it is obtained

$$\begin{aligned} \alpha _1\delta _{i-1}^{n+1}+\alpha _2\delta _i^{n+1}+\alpha _3 \delta _{i+1}^{n+1}=\alpha _4 \delta _{i-1}^{n}+\alpha _5 \delta _i^n+\alpha _6\delta _{i+1}^n, \end{aligned}$$

(15)

where

$$\begin{aligned} \alpha _1= & {} 1+\frac{\textrm{d}t}{2}V_x^n-\frac{3\textrm{d}t}{2h}V^n-3v\frac{\textrm{d}t}{h^2},\nonumber \\ \alpha _2= & {} 4+2\textrm{d}tV_x^n+6v\frac{\textrm{d}t}{h^2}, \quad \alpha _3=1+\frac{\textrm{d}t}{2}V_x^n+\frac{3\textrm{d}t}{2h}V^n-3v\frac{\textrm{d}t}{h^2},\nonumber \\ \alpha _4= & {} 1+3v\frac{\textrm{d}t}{h^2}, \quad \alpha _5=4-6v\frac{\textrm{d}t}{h^2}, \quad \alpha _6=1+3v\frac{\textrm{d}t}{h^2}. \end{aligned}$$

(16)

Substituting the approximate value V and its first derivative $V'$ in Eq. (7) and second-order derivative $V''$ in Eq. (13) into Eq. (14) for interior points, $i=1,\ldots ,N-1$, it is obtained

$$\begin{aligned}{} & {} \beta _1\delta _{i-2}^{n+1}+\beta _2\delta _{i-1}^{n+1}+\beta _3\delta _{i}^{n+1}+\beta _4\delta _{i+1}^{n+1}+\beta _5\delta _{i+2}^{n+1}=\beta _6\delta _{i-2}^{n}+\beta _7\delta _{i-1}^{n}\nonumber \\ {}{} & {} \quad +\beta _8\delta _{i}^{n}+\beta _9\delta _{i+1}^{n}+\beta _{10}\delta _{i+2}^{n}, \end{aligned}$$

(17)

where

$$\begin{aligned}{} & {} \beta _1=-v\frac{\textrm{d}t}{4h^2}, \quad \beta _2=1+\frac{\textrm{d}t}{2}V_x^n-\frac{3\textrm{d}t}{2h}V^n-2v\frac{\textrm{d}t}{h^2}, \quad \beta _3=4+2\textrm{d}tV_x^n+\frac{9}{2}v\frac{\textrm{d}t}{h^2}, \nonumber \\{} & {} \beta _4=1+\frac{\textrm{d}t}{2}V_x^n+\frac{3\textrm{d}t}{2h}V^n-2v\frac{\textrm{d}t}{h^2}, \quad \beta _5=\beta _1, \quad \beta _6=-\beta _1, \quad \beta _7=1+2v\frac{\textrm{d}t}{h^2}, \nonumber \\{} & {} \beta _8=4-\frac{9}{2}v\frac{\textrm{d}t}{h^2},\quad \beta _9=\beta _7, \quad \beta _{10}=-\beta _1. \end{aligned}$$

(18)

3.2 Algorithm for the Burgers–Fisher equation

Equation (1) is called the Burgers–Fisher equation when $F(u)=\beta u(1-u^\mu )$ and $v=1$. These terms are evaluated in Eq. (9) and rearranging the other terms by using linearization and simplifications, it is obtained

$$\begin{aligned}{} & {} V^{n+1}\left\{ 1+\alpha \frac{ \textrm{d}t}{2}\mu (V^{\mu -1})^n V_x^n -\beta \frac{ \textrm{d}t}{2}+\beta \frac{ \textrm{d}t}{2}\left( 1+\mu \right) \left( V^{\mu }\right) ^n\right\} +\alpha \frac{ \textrm{d}t}{2}(V^\mu )^nV_x^{n+1}-\frac{\textrm{d}t}{2}V_{xx}^{n+1} \nonumber \\{} & {} \qquad = V^n\left\{ 1+\beta \frac{ \textrm{d}t}{2}-\beta \frac{ \textrm{d}t}{2}\left( 1-\mu \right) \left( V^\mu \right) ^n\right\} +\alpha \frac{ \textrm{d}t}{2}\left( \mu -1\right) (V^\mu )^n V_x^n+\frac{\textrm{d}t}{2}V_{xx}^n. \end{aligned}$$

(19)

Considering Eq. (7) into Eq. (19), Eq. (15) is obtained for the boundary points, $i=0,N$, and its coefficients are given as follows:

$$\begin{aligned}{} & {} \alpha _1=1+\alpha \frac{ \textrm{d}t}{2}\mu L_1^{\mu -1}L_2-\beta \frac{ \textrm{d}t}{2}+\beta \frac{ \textrm{d}t}{2}\left( 1+\mu \right) L_1^\mu -\alpha \frac{3\, \textrm{d}t}{2h}L_1^\mu -3\frac{\textrm{d}t}{h^2}, \nonumber \\{} & {} \alpha _2= 4+2\alpha \, \textrm{d}t \mu L_1^{\mu -1}L_2-2\beta \, \textrm{d}t +2\beta \, \textrm{d}t\left( 1+\mu \right) L_1^{\mu }+6\frac{\textrm{d}t}{h^2}, \nonumber \\{} & {} \alpha _3=1+\alpha \frac{ \textrm{d}t}{2}\mu L_1^{\mu -1}L_2-\beta \frac{ \textrm{d}t}{2}+\beta \frac{ \textrm{d}t}{2}\left( 1+\mu \right) L_1^\mu +\alpha \frac{3\, \textrm{d}t}{2h}L_1^\mu -3\,\frac{\textrm{d}t}{h^2}, \nonumber \\{} & {} \alpha _4=1+\beta \frac{ \textrm{d}t}{2}-\beta \,\frac{ \textrm{d}t}{2}\left( 1-\mu \right) L_1^{\mu }-\alpha \frac{3\, \textrm{d}t}{2 h}\left( \mu -1\right) L_1^{\mu }+3\frac{\textrm{d}t}{h^2}, \nonumber \\{} & {} \alpha _5= 4+2\beta \, \textrm{d}t -2 \beta \, \textrm{d}t \left( 1-\mu \right) L_1^{\mu }-6\frac{\textrm{d}t}{h^2}, \nonumber \\{} & {} \alpha _6= 1+\beta \frac{ \textrm{d}t}{2}-\beta \frac{ \textrm{d}t}{2}\left( 1-\mu \right) L_1^{\mu }+\alpha \frac{3\, \textrm{d}t}{2h}(\mu -1)L_1^{\mu }+3\frac{\textrm{d}t}{h^2}. \end{aligned}$$

(20)

Evaluating Eq. (7) for approximate value V and its first derivative $V'$ and Eq. (13) for second derivative $V''$ into Eq. (19), Eq. (17) is obtained for interior points, $i=1,\ldots ,N-1$, and its coefficients are given by

$$\begin{aligned}{} & {} \beta _1=-\frac{\textrm{d}t}{4h^2},\,\, \beta _2=1\!+\!\alpha \frac{ \textrm{d}t}{2} \mu L_1^{\mu -1} L_2\!-\!\beta \frac{ \textrm{d}t}{2}+\beta \frac{ \textrm{d}t}{2}(1+\mu )L_1^{\mu }\!-\!\alpha \frac{3\, \textrm{d}t}{2h}L_1^\mu \!-\!\frac{2\,\textrm{d}t}{h^2}, \nonumber \\{} & {} \beta _3=4+2\alpha \, \textrm{d}t \mu L_1^{\mu -1}L_2-2\beta \, \textrm{d}t+2 \beta \, \textrm{d}t (1+\mu )L_1^\mu -\frac{9}{2}\frac{\textrm{d}t}{h^2}, \nonumber \\{} & {} \beta _4=1+\alpha \frac{ \textrm{d}t}{2} \mu L_1^{\mu -1} L_2-\beta \frac{ \textrm{d}t}{2}+\beta \frac{ \textrm{d}t}{2}(1+\mu )L_1^{\mu }+\alpha \frac{3\, \textrm{d}t}{2h}L_1^\mu -2\frac{\textrm{d}t}{h^2}, \nonumber \\{} & {} \beta _5=\beta _1, \quad \beta _6=-\beta _1, \nonumber \\{} & {} \beta _7=4+2\beta \, \textrm{d}t-2\beta \, \textrm{d}t(1-\mu )L_1^\mu -\frac{9}{2}\frac{\textrm{d}t}{h^2}, \nonumber \\{} & {} \beta _8=1+\beta \frac{\textrm{d}t}{2}-\beta \frac{\textrm{d}t}{2}(1-\mu )L_1^{\mu }-\alpha \frac{3\,\textrm{d}t}{2h}(\mu -1)L_1^{\mu }+2\frac{\textrm{d}t}{h^2}, \nonumber \\{} & {} \beta _9=1+\beta \frac{\textrm{d}t}{2}-\beta \frac{\textrm{d}t}{2}(1-\mu )L_1^{\mu }+\alpha \frac{3\,\textrm{d}t}{2h}(\mu -1)L_1^{\mu }+2\frac{\textrm{d}t}{h^2},\,\, \beta _{10}=-\beta _1.\!\! \end{aligned}$$

(21)

3.3 Algorithm for the Burgers–Huxley equation

Equation (1) is called the Burgers–Huxley equation when $F(u)=\beta u(1-u^\mu )(u^\mu -\gamma )$ and $v=1$. Considering these terms into Eq. (9) and after the linearization and simplifications, Eq. (9) transforms to the following form:

$$\begin{aligned}{} & {} V^{n+1}\left\{ 1+\alpha \frac{ \textrm{d}t}{2} \mu (V^{\mu -1})^n V_x^n\!-\beta \frac{ \textrm{d}t}{2}(\mu \!+\!1)(V^\mu )^n+\gamma \beta \frac{ \textrm{d}t}{2} +\beta \frac{ \textrm{d}t}{2}(2\mu \!+\!1)(V^{2\mu })^n \right. \nonumber \\{} & {} \qquad \left. -\beta \gamma \frac{ \textrm{d}t}{2}(\mu +1)(V^\mu )^n\right\} +\,\,\alpha \frac{ \textrm{d}t}{2}(V^\mu )^n V_x^{n+1}-\frac{\textrm{d}t}{2}V_{xx}^{n+1} \nonumber \\{} & {} \quad =V^n\left\{ 1+\beta \frac{ \textrm{d}t}{2}(1-\mu )(V^\mu )^n-\gamma \beta \frac{ \textrm{d}t}{2}-\beta \frac{\textrm{d}t}{2}(1-2\mu )(V^{2\mu })^n \right. \nonumber \\{} & {} \qquad \left. +\beta \gamma \frac{\textrm{d}t}{2}(1-\mu )(V^\mu )^n\right\} +\frac{\textrm{d}t}{2}(V_{xx})^n -\,\,\alpha \frac{ \textrm{d}t}{2}(1-\mu )(V^\mu )^n V_x^n. \end{aligned}$$

(22)

Evaluating Eq. (7) for approximate value V and its first derivative $V'$ and Eq. (13) for second derivative $V''$ into Eq. (22), Eq. (15) is obtained for the boundary points, $i=0,N$, and its coefficients are obtained in the following form:

$$\begin{aligned}{} & {} \alpha _1= 1+\alpha \frac{ \textrm{d}t}{2}\mu L_1^{\mu -1}L_2-\beta \frac{ \textrm{d}t}{2}(\mu +1)L_1^\mu +\beta \gamma \frac{ \textrm{d}t}{2}+\beta \frac{ \textrm{d}t}{2}(2\mu +1)L_1^{2\mu }\nonumber \\ {}{} & {} \quad -\beta \gamma \frac{ \textrm{d}t}{2}(\mu +1)L_1^{\mu }-\alpha \frac{3\, \textrm{d}t}{2 h}L_1^\mu -3\frac{\textrm{d}t}{h^2}, \nonumber \\{} & {} \alpha _2=4+2\alpha \, \textrm{d}t\mu L_1^{\mu -1}L_2-2\beta \, \textrm{d}t(\mu +1)L_1^\mu +2\gamma \beta \, \textrm{d}t +2 \beta \, \textrm{d}t(2\mu +1)L_1^{2\mu } \nonumber \\ {}{} & {} \quad -2\beta \gamma \, \textrm{d}t (\mu +1)L_1^\mu +6\frac{\textrm{d}t}{h^2}, \nonumber \\{} & {} \alpha _3=1+\alpha \frac{ \textrm{d}t}{2}\mu L_1^{\mu -1}L_2-\beta \frac{ \textrm{d}t}{2}(\mu +1)L_1^\mu +\beta \gamma \frac{ \textrm{d}t}{2}+\beta \frac{ \textrm{d}t}{2}(2\mu +1)L_1^{2\mu }\nonumber \\ {}{} & {} \quad -\beta \gamma \frac{ \textrm{d}t}{2}(\mu +1)L_1^{\mu }+\alpha \frac{3\, \textrm{d}t}{2 h}L_1^\mu -3\frac{\textrm{d}t}{h^2}, \nonumber \\{} & {} \alpha _4=1+\beta \frac{ \textrm{d}t}{2}(1-\mu )L_1^\mu -\gamma \beta \frac{ \textrm{d}t}{2}-\beta \frac{ \textrm{d}t}{2}(1-2\mu )L_1^{2\mu }+\beta \gamma \frac{ \textrm{d}t}{2}(1-\mu )L_1^\mu \nonumber \\ {}{} & {} \quad +\alpha \frac{3\, \textrm{d}t}{2h}(1-\mu )L_1^\mu +3\frac{\textrm{d}t}{h^2}, \nonumber \\{} & {} \alpha _5=4+2\beta \, \textrm{d}t (1-\mu ) L_1^{\mu }-2\gamma \beta \, \textrm{d}t-2\beta \, \textrm{d}t (1-2\mu )L_1^{2\mu }\nonumber \\{} & {} \quad +2\beta \gamma \, \textrm{d}t(1-\mu )L_1^{\mu }-6\frac{\textrm{d}t}{h^2}, \nonumber \\{} & {} \alpha _6=1+\beta \frac{ \textrm{d}t}{2}(1-\mu )L_1^\mu -\beta \gamma \frac{ \textrm{d}t}{2}-\beta \frac{ \textrm{d}t}{2}(1-2\mu )L_1^{2\mu }+\beta \gamma \frac{ \textrm{d}t}{2}(1-\mu )L_1^\mu \nonumber \\{} & {} \quad -\alpha \frac{3\, \textrm{d}t}{2h}(1-\mu )L_1^\mu +3\frac{\textrm{d}t}{h^2}. \end{aligned}$$

(23)

For the interior points, the coefficients of Eq. (17) for the Burgers–Huxley equation are given by

$$\begin{aligned} \beta _1= & {} -\frac{\textrm{d}t}{4h^2}, \nonumber \\ \beta _2= & {} 1+\frac{\alpha \, \textrm{d}t}{2}\mu L_1^{\mu -1}L_2-\beta \frac{\textrm{d}t}{2}(\mu +1)L_1^{\mu }+\beta \gamma \frac{ \textrm{d}t}{2}+\beta \frac{ \textrm{d}t}{2}(2\mu +1)L_1^{2\mu } \nonumber \\ {}{} & {} \quad -\beta \gamma \frac{ \textrm{d}t}{2}(\mu +1)L_1^{\mu }-\alpha \frac{3\, \textrm{d}t}{2h}L_1^\mu -2\frac{\textrm{d}t}{h^2}, \nonumber \\ \beta _3= & {} 4+2\alpha \, \textrm{d}t \mu L_1^{\mu -1}L_2-2\beta \, \textrm{d}t(\mu +1)L_1^{\mu }+2\gamma \beta \, \textrm{d}t +2 \beta \, \textrm{d}t(2\mu +1)L_1^{2\mu } \nonumber \\ {}{} & {} \quad -2\gamma \beta \, \textrm{d}t (\mu +1)L_1^{\mu } +\frac{9\,\textrm{d}t}{2h^2}, \nonumber \\ \beta _4= & {} 1+\alpha \frac{ \textrm{d}t}{2}\mu L_1^{\mu -1}L_2-\beta \frac{\textrm{d}t}{2}(\mu +1)L_1^{\mu }+\beta \gamma \frac{ \textrm{d}t}{2}+\beta \frac{ \textrm{d}t}{2}(2\mu +1)L_1^{2\mu }\nonumber \\ {}{} & {} \quad -\beta \gamma \frac{ \textrm{d}t}{2}(\mu +1)L_1^{\mu }+\alpha \frac{3\, \textrm{d}t}{2h}L_1^\mu -2\frac{\textrm{d}t}{h^2}, \nonumber \\ \beta _5= & {} \beta _1, \quad \beta _6=-\beta _1, \nonumber \\ \beta _7= & {} 1+\beta \frac{\textrm{d}t}{2}(1-\mu )L_1^\mu -\gamma \beta \frac{\textrm{d}t}{2}-\beta \frac{\textrm{d}t}{2}(1-2\mu )L_1^{2 \mu }+\gamma \beta \frac{\textrm{d}t}{2}(1-\mu )L_1^{\mu }\nonumber \\ {}{} & {} \quad +\alpha \, \frac{3\,\textrm{d}t}{2h}(1-\mu )L_1^\mu +2\frac{\textrm{d}t}{h^2}, \nonumber \\ \beta _8= & {} 4+2\beta \, \textrm{d}t (1-\mu ) L_1^\mu -2 \gamma \beta \, \textrm{d}t-2\beta \, \textrm{d}t (1-2\mu )L_1^{2\mu } \nonumber \\{} & {} \quad +2\gamma \beta \, \textrm{d}t(1-\mu )L_1^{\mu }-\frac{9\,\textrm{d}t}{h^2}, \nonumber \\ \beta _9= & {} 1+\beta \frac{\textrm{d}t}{2}(1-\mu )L_1^\mu -\gamma \beta \frac{\textrm{d}t}{2}-\beta \frac{\textrm{d}t}{2}(1-2\mu )L_1^{2\mu }+\gamma \beta \frac{\textrm{d}t}{2}(1-\mu )L_1^{\mu }\nonumber \\ {}{} & {} \quad -\alpha \frac{3\,\textrm{d}t}{2h}(1-\mu )L_1^\mu +2\frac{\textrm{d}t}{h^2}, \nonumber \\ \beta _{10}= & {} -\beta _1. \end{aligned}$$

(24)

3.4 Algorithm for the Fisher’s equation

Equation (1) is called the Fisher’s equation when $\alpha =0$ and $F(u)=u \left( \beta -\gamma u\right)$. Evaluating Eq. (9) with these terms, it is obtained

$$\begin{aligned} V^{n+1}\left\{ 1-\beta \frac{ \textrm{d}t}{2}+\gamma \, \textrm{d}t V^n\right\} -v\frac{\textrm{d}t}{2}V_{xx}^{n+1}=V^n\left\{ 1+\beta \frac{ \textrm{d}t}{2}\right\} +v\frac{\textrm{d}t}{2}V_{xx}^n. \end{aligned}$$

(25)

Substituting Eq. (7) for approximate value V and its first derivative $V'$ and Eq. (13) for second derivative $V''$ into Eq. (25), Eq. (15) is obtained for the boundary points, $i=0,N$, and its coefficients are as follows:

$$\begin{aligned}{} & {} \alpha _1=1-\beta \frac{ \textrm{d}t}{2}+\gamma \, \textrm{d}t\, L_1-3v\frac{\textrm{d}t}{h^2}, \quad \quad \quad \alpha _2=4-2\beta \, \textrm{d}t+4 \gamma \, \textrm{d}t\, L_1+6v\frac{\textrm{d}t}{h^2}, \\{} & {} \alpha _3= 1-\beta \frac{ \textrm{d}t}{2}+\gamma \, \textrm{d}t\, L_1-3v\frac{\textrm{d}t}{h^2}, \quad \quad \quad \alpha _4=1+\beta \frac{ \textrm{d}t}{2}+3v\frac{\textrm{d}t}{h^2}, \quad \quad \quad \\{} & {} \alpha _5=4+2\beta \, \textrm{d}t-6v\frac{\textrm{d}t}{h^2}, \quad \quad \quad \quad \quad \quad \quad \quad \alpha _6=1+\beta \frac{ \textrm{d}t}{2}+3v\frac{\textrm{d}t}{h^2}. \end{aligned}$$

For interior points, $i=1,\ldots ,N-1$, Eq. (17) is obtained and its coefficients are given by

$$\begin{aligned} \beta _1= & {} -v\frac{\beta }{4h^2}, \quad \quad \beta _2=1-\beta \frac{ \textrm{d}t}{2}+\gamma \, \textrm{d}t\, L_1-2v\frac{\textrm{d}t }{h^2}, \quad \quad \beta _3=4-2 \beta \, \textrm{d}t+4\gamma \, \textrm{d}t\, L_1+v\frac{9\,\textrm{d}t}{2h^2},\quad \quad \quad \\ \beta _4= & {} 1-\beta \frac{ \textrm{d}t}{2}+\gamma \, \textrm{d}t\, L_1-2v\frac{ \textrm{d}t}{h^2}, \quad \quad \beta _5=\beta _1, \quad \quad \beta _6=-\beta _1, \quad \quad \beta _7=1+\beta \frac{ \textrm{d}t}{2}+2v\frac{\textrm{d}t}{h^2}, \\ \beta _8= & {} 4+2\beta \, \textrm{d}t -v\frac{9\,\textrm{d}t}{2h^2}, \quad \quad \beta _9=1+\beta \frac{ \textrm{d}t}{2}+2v\frac{\textrm{d}t}{h^2}, \quad \quad \quad \beta _{10}=-\beta _1. \end{aligned}$$

Here, $L_1=\delta _{i-1}^n+4\delta _i^n+\delta _{i+1}^n$, $L_2=\frac{3}{h}\left( \delta _{i+1}^n-\delta _{i-1}^n\right)$.

Note that Eqs. (15) and (17) generate a system of $(N+1)$ equations in $(N+3)$ unknowns $d^n=\left\{ \delta _{-1}^n, \delta _0^n, \delta _1^n,\ldots , \delta _N^n, \delta _{N+1}^n\right\}$ for the Burgers, Burgers–Fisher, Burgers–Huxley, and Fisher’s equations as follows:

$$\begin{aligned}{} & {} \alpha _1\delta _{-1}^{n+1}+\alpha _2\delta _{0}^{n+1}+\alpha _3\delta _1^{n+1} =\alpha _4\delta _{-1}^{n}+\alpha _5\delta _{0}^{n}+\alpha _6\delta _{1}^{n}, \quad i=0, \nonumber \\{} & {} \beta _1\delta _{i-2}^{n+1}+\beta _2\delta _{i-1}^{n+1}+\beta _3\delta _{i}^{n+1}+\beta _4\delta _{i+1}^{n+1}+\beta _5\delta _{i+1}^{n+1}\nonumber \\{} & {} \quad =\beta _6\delta _{i-2}^n+\beta _7\delta _{i-1}^n+\beta _8\delta _{i}^n+\beta _9\delta _{i+1}^n+\beta _{10}\delta _{i+2}^n, \quad i=1,\ldots ,N-1, \nonumber \\{} & {} \alpha _1\delta _{N-1}^{n+1}+\alpha _2\delta _N^{n+1}+\alpha _3\delta _{N+1}^{n+1}=\alpha _4\delta _{N-1}^n+\alpha _5\delta _{N}^n+\alpha _6\delta _{N+1}^n,\quad i=N. \end{aligned}$$

(26)

System (26) can be converted into the following matrix form:

$$\begin{aligned} A\varvec{d}^{n+1}=B\varvec{d}^n, \end{aligned}$$

(27)

where

$A=A_{ij}=\begin{bmatrix} \alpha _1 &{} \alpha _2 &{} \alpha _3\\ \beta _1 &{} \beta _2 &{} \beta _3&{}\beta _4&{}\beta _5\\ &{}\beta _1&{}\beta _2&{}\beta _3&{}\beta _4&{}\beta _5\\ &{}&{}\ddots &{}\ddots &{}\ddots &{}\ddots &{}\ddots \\ &{}&{}&{}&{}\beta _1&{}\beta _2&{}\beta _3&{}\beta _4&{}\beta _5\\ &{}&{}&{}&{}&{}&{}\alpha _1&{}\alpha _2&{}\alpha _3\\ \end{bmatrix}$,

$B=B_{ij}=\begin{bmatrix} \alpha _4 &{} \alpha _5 &{} \alpha _6\\ \beta _6 &{} \beta _7 &{} \beta _8&{}\beta _9&{}\beta _{10}\\ &{}\beta _6&{}\beta _7&{}\beta _8&{}\beta _9&{}\beta _{10}\\ &{}&{}\ddots &{}\ddots &{}\ddots &{}\ddots &{}\ddots \\ &{}&{}&{}&{}\beta _6&{}\beta _7&{}\beta _8&{}\beta _9&{}\beta _{10}\\ &{}&{}&{}&{}&{}&{}\alpha _4&{}\alpha _5&{}\alpha _6\\ \end{bmatrix}$ and

$$\begin{aligned} \varvec{d}^n=\left( \delta _{-1}, \delta _{0}, \delta _{1},\ldots ,\delta _N, \delta _{N+1}\right) ^\textrm{T}. \end{aligned}$$

To obtain a consistent system, the $\delta _{-1}^n$ and $\delta _{N+1}^n$ are eliminated using the boundary conditions:

$$\begin{aligned}{} & {} U(x_0)=\delta _{-1}^{n+1}+4\delta _0^{n+1}+\delta _1^{n+1}=g_1(t^{n+1})\Rightarrow \delta _{-1}^{n+1}=g_1(t^{n+1})-4\delta _0^{n+1}-\delta _1^{n+1}, \nonumber \\{} & {} U(x_N)=\delta _{N-1}^{n+1}+4\delta _N^{n+1}+\delta _{N+1}^{n+1}=g_2(t^{n+1}) \Rightarrow \delta _{N+1}^{n+1}=g_2(t^{n+1})-4\delta _N^{n+1}-\delta _{N-1}^{n+1}.\nonumber \\ \end{aligned}$$

(28)

Substituting equalities (28) into the combined system (26), it is obtained $(N+1)\times (N+1)$ matrix system as follows:

$$\begin{aligned} \tilde{A}\varvec{d^{n+1}}=\tilde{B}\varvec{d^{n}}+b, \end{aligned}$$

(29)

where

$\tilde{A}=\tilde{A}_{ij}=\begin{bmatrix} \kappa _1&{}\kappa _2&{}&{} \\ \kappa _3&{} \kappa _4 &{}\kappa _5 &{}\kappa _6&{}\\ -\eta _1&{}\eta _2&{}\eta _3&{}\eta _4&{}-\eta _1\\ &{}-\eta _1&{}\eta _2&{}\eta _3&{}\eta _4&{}-\eta _1&{}\\ &{}&{}-\eta _1&{}\eta _2&{}\eta _3&{}\eta _4&{}-\eta _1&{}&{}\\ &{}&{}&{}\ddots &{}\ddots &{}\ddots &{}\ddots &{}\ddots &{}\\ &{}&{}&{}&{}&{}&{}-\eta _1&{}\eta _1&{}\omega _1&{}\omega _2\\ &{}&{}&{}&{}&{}&{}&{}&{}\omega _3&{}\omega _4\\ \end{bmatrix}$,

$\tilde{B}=\tilde{B}_{ij}=\begin{bmatrix} \xi _1&{} &{} \\ \xi _2&{}\xi _3 &{}\xi _4 &{}\xi _5&{}\\ \eta _1&{}\psi _1&{}\psi _2&{}\psi _1&{}\eta _1\\ &{}\eta _1&{}\psi _1&{}\psi _2&{}\psi _1&{}\eta _1&{}\\ &{}&{}\eta _1&{}\psi _1&{}\psi _2&{}\psi _1&{}\eta _1&{}&{}\\ &{}&{}&{}\ddots &{}\ddots &{}\ddots &{}\ddots &{}\ddots &{}\\ &{}&{}&{}&{}&{}\eta _1&{}\psi _1&{}\xi _3&{}\xi _2\\ &{}&{}&{}&{}&{}&{}&{}&{}\xi _1\\ \end{bmatrix}$,

   and

$$\begin{aligned} b=b_j=\left( b_1, b_2, 0,\ldots ,0,b_3,b_4\right) . \end{aligned}$$

Here, the entries of $A_{ij}$, $B_{ij}$, and $b_j$ are determined according to the type of the equation. The obtained system can be solved by using the Thomas algorithm. To evaluate variables $\delta _i^{n+1}$ for a particular time level, the initial vector $d^{0}$ is obtained from the initial condition (2).

4 Stability of the proposed method

Stability plays a very important role in the theory of numerical methods. Up to now, various techniques have been proposed to analyze the stability of numerical methods to be confident of the calculated predictions. Among them, von Neumann stability analysis which is based on the Fourier series analysis is the most common technique used to determine stability. Although this technique can be employed directly on linear problems with constant coefficients, it is not valid to estimate the stability of linear problems with variable coefficients and nonlinear problems. However, researchers have developed many ways to apply the von Neumann technique to these challenging problems with some constraints that change according to the specific nature of the problem to be confident in their predictions. While some authors linearize the nonlinear terms of the problem [14, 17, 24, 31,32,33,34,35,36,37] or freeze the coefficient [21, 26, 38,39,40] by applying the von Neumann techniques, some other authors adopted matrix stability [20, 22, 41,42,43,44,45] and other techniques [46, 47] by keeping the originality of their problems with some defects.

Though nonlinear advection–diffusion–reaction equations that are considered in this study are quite common, the von Neumann stability analysis does not directly apply to such nonlinear equations in the standard sense since the stability conditions are complicated and varying. Therefore, in this study, the matrix stability analysis which preserves the nonlinearity of the problem has been performed to analyze the stability of the proposed scheme.

Now, the stability of the present scheme for the numerical integration performed by the Crank–Nicolson method will be discussed using the matrix stability technique by computing the eigenvalues of the coefficient matrix. The proposed scheme for Eq. (1) can be rewritten in compact form as in Eq. (29):

$$\begin{aligned} \tilde{A}\varvec{d^{n+1}}=\tilde{B}\varvec{d^n}+{b}, \end{aligned}$$

(30)

where $\tilde{A}$ and $\tilde{B}$ are the real matrices and $\tilde{b}$ is the column vector. Now, let us introduce the numerical error vector $\epsilon$ as

$$\begin{aligned} \epsilon ^{n}=u_{exact}^n-u_{app}^n, \end{aligned}$$

(31)

where $u_{exact}$ and $u_{app}$ are exact and approximate solutions, respectively. Hence, Eq. (30) is rewritten as [48]

$$\begin{aligned} \tilde{A}\epsilon ^{n+1}=\tilde{B}\epsilon ^{n}. \end{aligned}$$

(32)

Equation (32) can be written, by assuming that A is nonsingular, as follows:

$$\begin{aligned} \varepsilon ^{n+1}=\tilde{A}^{-1}\tilde{B}\varepsilon ^{n}\implies \varepsilon ^{n+1}=C\varepsilon ^n, \end{aligned}$$

(33)

where $C=\tilde{A}^{-1}\tilde{B}$. Here, the stability of the scheme depends on estimate of the coefficient matrix C. For a stable method, matrix C should satisfy the Lax–Richtmyer criterion [49]

$$\begin{aligned} ||C|| \le 1. \end{aligned}$$

(34)

In addition, the following inequality

$$\begin{aligned} \rho (C) \le ||C|| \end{aligned}$$

(35)

is always satisfied for any matrix. Here, $\rho (C)$ is the largest eigenvalue of matrix C. Thus, the condition for the stability of system (30) is obtained by considering inequalities (34) and (35) as follows:

$$\begin{aligned} \rho (C) \le 1. \end{aligned}$$

(36)

As can be realized from the previous section and Eq. (29), the entries of matrix C vary depending on some factors such as $\alpha , \beta , \mu , \gamma$, spatial and temporal steps sizes, h and dt, and time-dependent parameter $\delta _i^n$. As far as is known, there is no certain technique to establish a relationship between these factors in the solution of these problems. However, during the calculations, it is observed that the entries of matrix C do not vary rapidly and do not change much with varying these factors. Thus, since the properties of the matrix do not change with different spatial and temporal points, to prove the stability of the proposed scheme, the entries of matrix C can be fixed at certain spatial and temporal points, generally, in maximum values, as a technique commonly used. Thus, for the stability of the proposed scheme given in Eq. (29), $|\rho (C)| \le 1$ should be fulfilled for all i as $t \rightarrow \infty$ [48]. The computed eigenvalues have been presented in Fig. 1 for all examples in Sect. 5. Since Fig. 1 indicates that $max|\rho (C)| \le 1$ for all examples, the proposed scheme satisfies the criteria of stability.

Fig. 1

Eigenvalues of matrix C for Examples 1–5

5 Numerical results and analysis

In this section, the proposed method is applied to the Burgers, Burgers–Fisher, Burgers–Huxley, and Fisher’s equations, respectively. The accuracy of the method for these equations is measured by using the absolute error given in the following formula:

$$\begin{aligned} \text {Absolute error}=|V_\mathrm{{exact}}(x_i,t^n)-V_\mathrm{{app}}(x_i,t^n)|, \end{aligned}$$

(37)

where $V_\mathrm{{exact}}$ and $V_\mathrm{{app}}$ are the exact and approximate solutions, respectively. The numerical order of convergence (OC) is obtained by using the following formula:

$$\begin{aligned} OC=\frac{Log(L_{\infty }(N)/L_{\infty }(2N))}{Log(2N/N)}, \end{aligned}$$

(38)

where $L_{\infty }=\textrm{max}_i|V_{\text {exact}}(x_i,t^n)-V_\mathrm{{app}}(x_i,t^n)|$ and N is number of partition of problem domain. The theoretical convergence analysis of nonlinear ADR equations, which are solved by B-spline methods, can be found in the works [31,32,33,34,35] and therein references.

Numerical results obtained by the proposed method have been compared with the exact solution and available literature solutions. The numerical computations have been performed using the software MATLAB 2021. CPU times are measured by the ”tic-toc” Matlab function.

5.1 Example 1 [28]

Consider the nonlinear Burgers equation by taking $\alpha =\mu =1$ and $F(u)=0$ in Eq. (1) over the domain [0, 1] with the initial condition

$$\begin{aligned} u(x,0)=\textrm{sin}(\pi x),\quad 0\le x\le 1, \end{aligned}$$

(39)

and Dirichlet boundary conditions

$$\begin{aligned} u(0,t)=u(1,t)=0, \quad t>0. \end{aligned}$$

(40)

The exact solution is

$$\begin{aligned} u(x,t)=2\pi v \frac{\sum _{n}^{\infty }a_n\textrm{exp}(-n^2 \pi ^2 vt)n\textrm{sin}(n\pi x)}{a_0+\sum _{n=1}^{\infty }a_n \textrm{exp}(-n^2 \pi ^2 vt)\textrm{cos}(n\pi x)} \end{aligned}$$

(41)

with the following Fourier coefficients:

$$\begin{aligned} a_0= & {} \int _{0}^{1}\textrm{exp}\left\{ -\left( 2 \pi v\right) ^{-1}\left[ 1-\textrm{cos}(\pi x)\right] \right\} \textrm{d}x, \\ a_n= & {} 2\int _{0}^{1}\textrm{exp}\left\{ -\left( 2 \pi v\right) ^{-1}\left[ 1-\textrm{cos}(\pi x)\right] \right\} \textrm{cos}(n \pi x)\textrm{d}x,\quad n=1,2,3,\ldots \end{aligned}$$

In order to compute the exact solutions given by Eq. (41), the infinite series solutions have been truncated after 500 terms for all calculations. The numerical solutions of Example 1 obtained by the proposed method have been compared with the exact solution, cubic B-spline collocation method [28], and other up-to-date techniques [41, 50,51,52] in Tables 1–4. Tables 1, 2, and 3 reveal that the proposed scheme converges to the exact solution very fast and is more accurate than the standard cubic B-spline method presented in the work of Dag et al. [28] even when using larger spatial and temporal step sizes, and in this way, it reduces the computational time and complexity. In Table 2, the comparisons of the proposed method solutions with the exact solution and some recently developed techniques [41, 50] are given at different time levels and spatial points for $v=0.1$. It is observed from the table that the computed results by the current scheme are in reasonable agreement with the solutions in the work of Singh and Gupta [41] for $N=40$ and $\textrm{d}t=0.004$. Besides, when using smaller time increments $\textrm{d}t=0.001$ in the proposed scheme, both methods produce the same accurate solutions. In addition, the results of the current scheme are more accurate than those obtained from the solutions presented in the work of Jiwari et al. [50]. Similarly, Table 3 presents the comparisons of the current scheme with the exact solution and the literature solutions [50, 51] at different time levels and spatial points for $v=0.01$. As seen from the table that the current scheme is far more accurate than the literature [28, 51], and for five decimal places, it is compatible with Jiwari [50].

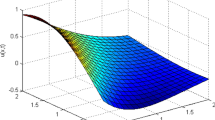
The exact and numerical behaviors of Example 1 for $v=0.1$ and $v=0.01$ are illustrated in Fig. 2. It is seen from the figure, the solutions become smaller as time increases due to the effect of the nonlinear term. The numerical behaviors of the problem exhibited in Fig. 2 are very close to the exact solution and similar to those in the compared studies [28, 41, 50].

Table 1 Comparison of the proposed method solutions with the exact and cubic B-spline solutions [28] for various mesh sizes and $v=1$ at $t=0.1$ in Example 1

Table 2 Comparison of the proposed method solutions with the exact and available literature solutions at different temporal and spatial points for $v=0.1$ in Example 1

Table 4 lists comparisons of the solutions obtained by the proposed method and some up-to-date good techniques [50,51,52] in the literature for smaller viscosity values $v=0.003$ and $v=0.004$. Although many numerical methods in the literature fail for these viscosity values, the presented method solutions are in good agreement with the exact solution. Also, the present scheme revealed that one can find similar or sometimes better results than the compared methods even using larger spatial or temporal step sizes. The findings presented in all tables have clearly revealed that less computational time and memory space could be accomplished when using larger spatial or temporal sizes by the proposed method. Also, in addition to the commendable contribution of the aforementioned references in the tables for improving the accuracy of the solutions of Eq. (1), the proposed method provides flexibility in implementation by avoiding some of the additional efforts of the compared methods such as reducing ordinary differential equations, requiring to be modified into a set of basis functions [41] and selecting an optimal parameter [50].

Table 3 Comparison of the proposed method solutions with the exact and available literature solutions at different temporal and spatial points for $v=0.01$ in Example 1

Fig. 2

Simulation of behaviors of the Burgers equation in Example 1 for different time points when $v=0.1$ (left) and $v=0.01$ (right)

Table 4 Comparison of the proposed method solutions with the exact and available literature solutions at different temporal and spatial points for $v=0.003$ and $v=0.004$ in Example 1

Table 5 Order of convergence when $t=3$ for different values of N in Example 1

Due to the slow rate of convergence of series solutions, the analytical solutions of the Burgers equations considered in this study which include small viscosity values diverge. Therefore, computationally intensive numerical techniques are required to obtain the solution of such problems. In the work of Jiwari [53], it is indicated that many numerical schemes in the literature fail to capture the physical behavior of the Burgers equation for very small viscosity values. Recently, Jiwari [53], Seydaoglu [51], and Verma et al. [54] presented numerical techniques which produce accurate solutions for small viscosity values. In this work, it has been seen that the proposed method is successful to capture the behavior of the Burgers equation for $v=0.001$ and even a very small value $v=0.0005$. Figures 3 and 4 illustrate the behavior of the numerical solutions of Example 1 for small viscosity values $v=0.001$ and $v=0.0005$ at different time points and these graphs are similar to studies [51, 53, 54]. As clearly seen from the figures, the approximate solutions have a steep descent and as time increases, approximate solutions decrease. The order of convergence is presented in Table 5 for different values of N and it is seen that the convergence rate reaches 4 in $||.||_{\infty }$.

Fig. 3

Simulation of behaviors of the Burgers equation in Example 1 for $\textrm{d}t=0.01$, $N=400$ (left) and $\textrm{d}t=0.01$, $N=800$ (right) at different time t when $v=0.001$ and $v=0.0005$, respectively

Fig. 4

Simulation of the approximate solution in Example 1 for $\textrm{d}t=0.01$,$N=400$ (left) and $\textrm{d}t=0.01$, $N=800$ (right) when $v=0.001$ and $v=0.0005$, respectively

5.2 Example 2 [37]

The next Burgers equation over the domain [0, 1] with the initial condition

$$\begin{aligned} u(x,0)=4x(1-x),\quad 0\le x\le 1 \end{aligned}$$

(42)

and Dirichlet boundary conditions

$$\begin{aligned} u(0,t)=u(1,t)=0, \quad t>0. \end{aligned}$$

(43)

The exact solution for this example is given by Eq. (41) with the Fourier coefficients

$$\begin{aligned}{} & {} a_0=\int _{0}^{1}\textrm{exp}\left\{ -x^2 (3v)^{-1}\left( 3-2x\right) \right\} \textrm{d}x, \\{} & {} a_n=2\int _{0}^{1}\textrm{exp}\left\{ -x^2 (3v)^{-1}\left( 3-2x\right) \right\} \textrm{cos}(n\pi x)\textrm{d}x. \end{aligned}$$

After the numerical experiments have been tried for various mesh sizes, all calculations have been performed for values of $N=20, 40$ and $M=100, 1000$. Table 6 exhibits the comparisons of proposed method solutions with the exact and some good techniques in the literature for various mesh sizes and $v=0.1$ at different spatial and temporal points. As clearly seen from the table, the numerical solutions approximate the exact solution up to seven decimal places when the mesh size is $N=40$ and $\textrm{d}t=0.01$ and are more accurate than the compared methods. Besides, even using fewer temporal and spatial elements in the proposed method, while obtained solutions are the same or sometimes better than those in Erdogan et al. [55], they are more accurate as compared to the literature [37, 50, 56]. Also, the current scheme produces the same accurate solutions as the work of Singh and Gupta [41] for the mesh size values $N=20$ and $\textrm{d}t=0.001$. Thus, the computed results revealed that the proposed method approximates the exact solution very well than the other recently developed techniques even using larger spatial and temporal step sizes. Similarly, a comparison of the proposed method with the exact solution and up-to-date good techniques [37, 41, 50, 55, 56] in the literature is presented in Table 7 for $v=0.01$. The currently obtained solutions for $N=40$ and $\textrm{d}t=0.01$ are seen to be more accurate than the literature [37, 50, 55, 56] even using smaller spatial or temporal elements compared to the works [37, 50, 56]. Compared to the reference [55], it is seen from the table that the proposed method produces better results even using a far less number of elements. The current scheme is in very good agreement with the exact solution and reference [41] for the mesh size values $N=40$ and $\textrm{d}t=0.001$.

Table 6 Comparison of the proposed method solutions with the exact and available literature solutions at different temporal and spatial points for $v=0.1$ in Example 2

Table 7 Comparison of the proposed method solutions with the exact and available literature solutions at different temporal and spatial points for $v=0.01$ in Example 2

Fig. 5

Simulation of behaviors of the Burgers equation in Example 2 for different time points when $v=0.1$ (left) and $v=0.01$ (right)

The behaviors of the problem obtained by the proposed method are depicted in Fig. 5 for $v=0.1$ and $v=0.01$. As seen in Fig. 5, the numerical solutions and exact solutions are very close to each other. When analyzing figures, it is seen that the peaks of the solution decrease as time increases.

In Table 8, the proposed method has been compared with a hybrid method [53], LRBF-DQM [50], and TGFEM [52] for smaller viscosity values $v=0.003$ and $v=0.004$. As indicated before, for these values of viscosity, the numerical methods in the literature fail or do not reach the desired accuracy. As seen from the table, the presented method solutions are in good agreement with the exact solution and produce the same or more accurate solutions than compared with other solutions in the table even using larger spatial step sizes. Figures 6 and 7 show the physical behavior of numerical solutions obtained by the proposed method for very small viscosity values $v=0.001$ and $v=0.0005$ at different time levels. It is seen from the figures that the proposed scheme produces accurate and reliable results for small viscosity values.

Table 8 Comparison of the proposed method solutions with the exact and available literature solutions at different temporal and spatial points for $v=0.003$ and $v=0.004$ in Example 2

5.3 Example 3 [11]

Consider the Burgers–Fisher equation by taking $v=1$ and $F(u)=\beta u(1-u^\mu )$ in Eq. (1) subject to initial condition

$$\begin{aligned} u(x,0)=\left( \frac{1}{2}+\frac{1}{2}tanh\left( \left( \frac{-\alpha \mu }{2(1+\mu )}\right) x\right) \right) ^\frac{1}{\mu },\quad 0 \le x \le 1, \end{aligned}$$

(44)

and boundary conditions

$$\begin{aligned}{} & {} u(0,t)=\left( \frac{1}{2}-\frac{1}{2}\textrm{tanh} \left( \left( \frac{-\alpha \mu }{2(1+\mu )}\right) \left( \frac{\alpha }{1+\mu }+\frac{\beta (1+\mu )}{\alpha }\right) t\right) \right) ^\frac{1}{\mu }, \end{aligned}$$

(45)

$$\begin{aligned}{} & {} u(1,t)=\left( \frac{1}{2}+\frac{1}{2}\textrm{tanh}\left( \left( \frac{-\alpha \mu }{2\left( 1+\mu \right) }\right) \left( 1-\left( \frac{\alpha }{1+\mu }+\frac{\beta (1+\mu )}{\alpha }\right) t\right) \right) \right) ^\frac{1}{\mu }.\qquad \end{aligned}$$

(46)

The exact solution is given

$$\begin{aligned} u(x,t)=\left( \frac{1}{2}+\frac{1}{2}\textrm{tanh}\left( \frac{-\alpha \mu }{2\left( \mu +1\right) }\left( x-\left( \frac{\alpha }{\mu +1}+\frac{\beta (\mu +1)}{\alpha }\right) t\right) \right) \right) ^\frac{1}{\mu }, \quad t \ge 0.\nonumber \\ \end{aligned}$$

(47)

Fig. 6

Simulation of behaviors of the Burgers equation in Example 2 for $\textrm{d}t=0.01$, $N=400$ (left) and $\textrm{d}t=0.01$, $N=800$ (right) at different time t when $v=0.001$ and $v=0.0005$, respectively

Fig. 7

Simulation of the approximate solution in Example 2 for $\textrm{d}t=0.01$,$N=400$ (left) and $\textrm{d}t=0.01$, $N=800$ (right) when $v=0.001$ and $v=0.0005$, respectively

In this example, in order to test the accuracy and efficiency of the proposed method, a comparison of the absolute errors of the proposed scheme and up-to-date techniques in the literature is given in Tables 9, 10, and 11.

The absolute errors of the proposed method and contemporary methods [11, 47, 57, 58] in the literature are presented for $\alpha =\beta =1$ and $\mu =2,4$ when $h=0.1$ and $\textrm{d}t=0.0001$ at different time levels with step sizes in Table 9. The superiority of the proposed scheme is shown by comparing it with the literature solutions [47, 57] in Table 9. Besides, as clearly seen in the table, although the solutions obtained by the proposed method are less accurate than the compared methods [11, 58] at the starting points, it should be noted that the solutions are highly accurate at the middle points and endpoints with the effect of the fourth-order formula and the error decreases with a decrease in time. The evaluation of computed solutions with spatial and temporal variables for the values in Table 9 is illustrated in Fig. 8.

The pointwise absolute errors of the proposed method and up-to-date developed methods in the literature are listed for $\alpha =\beta =0.001$, $\mu =2,8$, and $h=0.1$ in Table 10. It can be noticed from the table that the current method provides more accurate solutions than those obtained in the literature [57, 58] even using larger temporal step sizes. Besides, as compared to the other references [11, 26], although the proposed method produces less accurate solutions at the starting points of the domain, it is more accurate in the middle points and endpoints. In other words, solutions are less accurate than the other compared methods at the starting points, but they are highly accurate at the middle points and endpoints. It can be concluded from these results observed in Tables 9 and 10, using the fourth-order compact formula in interior points has increased the accuracy of the solution of these points. Contrary to this, due to the domination of the relatively low-order cubic B-spline in the starting points, in these points, it is obtained a less accurate solution by comparison with the interior points. Also, as the time increases, the error decreases as seen in the table.

In Table 11, the absolute errors of the proposed and up-to-date literature [11, 47] solutions are listed for $\alpha =1$, $\beta =0$, $\mu =3,8$, and $h=0.1$. It is noticed from the table that the proposed method produces the same or sometimes more accurate solutions, especially at the middle and endpoints of the domain even using larger temporal step sizes. Figure 9 shows the behavior of Example 3 for values in Table 11.

Table 9 Absolute error comparison of the proposed method and available literature solution at different temporal and space points for $\alpha =\beta =1$ and $\mu =2,8$ in Example 3

Table 10 Absolute error comparison of the proposed method and available literature solution at different temporal and space points for $\alpha =\beta =0.001$ and $\mu =1,4$ in Example 3

Table 11 Absolute error comparison of the proposed method and available literature solution at different temporal and space points for $\alpha =1$, $\beta =0$, and $\mu =3,8$ in Example 3

Fig. 8

Simulations of the exact (left) and proposed method (right) solutions for the generalized Burgers–Fisher equation with $\alpha =\beta =1$, $\mu =2, h=0.1$, and $\textrm{d}t=0.001$

Fig. 9

Simulations of the exact (left) and proposed scheme (right) for the generalized Burgers–Fisher equation with $\alpha =1$, $\beta =0$, $\mu =3, h=0.1$, and $\textrm{d}t=0.001$

5.4 Example 4 [11]

Now, let us consider the generalized Burgers–Huxley equation by taking $v=1$ and $F(u)=\beta u\left( 1-u^\mu \right) \left( u^\mu -\gamma \right)$ in Eq. (1) subject to the initial condition

$$\begin{aligned} u(x,0)=\left( \frac{\gamma }{2}+\frac{\gamma }{2}\textrm{tanh}\left( \frac{-\alpha \mu +\mu \sqrt{\alpha ^2+4\beta (1+\mu )}}{4(1+\mu )}\gamma x\right) \right) ^\frac{1}{\mu }, \quad 0\le x\le 1,\nonumber \\ \end{aligned}$$

(48)

and boundary conditions

$$\begin{aligned} u(0,t)= & {} \left( \frac{\gamma }{2}-\frac{\gamma }{2}\textrm{tanh}\left( \frac{-\alpha \mu +\delta \sqrt{\alpha ^2+4\beta (1+\mu )}}{4(1+\mu )} \right. \right. \nonumber \\ {}{} & {} \quad \left. \left. \left( \frac{\alpha \gamma }{1+\mu }-\frac{\left( 1+\mu -\gamma \right) \left( -\alpha +\sqrt{\alpha ^2+4\beta (1+\mu )}\right) }{2(1+\mu )}\right) t\right) \right) ^\frac{1}{\mu }, \nonumber \\ \end{aligned}$$

(49)

$$\begin{aligned} u(1,t)= & {} \left( \frac{\gamma }{2}+\frac{\gamma }{2}\textrm{tanh}\left( \frac{-\alpha \mu +\mu \sqrt{\alpha ^2+4\beta (1+\mu )}}{4(1+\mu )} \right. \right. \nonumber \\ {}{} & {} \quad \left. \left. \left( 1-\left( \frac{\alpha \gamma }{1+\mu }-\frac{\left( 1+\mu -\gamma \right) \left( -\alpha +\sqrt{\alpha ^2+4\beta (1+\mu )}\right) }{2(1+\mu )}\right) t\right) \right) \right) ^\frac{1}{\mu }.\nonumber \\ \end{aligned}$$

(50)

The exact solution is

$$\begin{aligned} u(x,t)= & {} \left( \frac{\gamma }{2}+\frac{\gamma }{2}\textrm{tanh}\left( \frac{-\alpha \mu +\mu \sqrt{\alpha ^2+4\beta (1+\mu )}}{4(1+\mu )} \right. \right. \nonumber \\ {}{} & {} \quad \left. \left. \left( x-\left( \frac{\alpha \gamma }{1+\mu }-\frac{\left( 1+\mu -\gamma \right) \left( -\alpha +\sqrt{\alpha ^2+4\beta (1+\mu )}\right) }{2(1+\mu )}\right) t\right) \right) \right) ^\frac{1}{\mu }. \nonumber \\ \end{aligned}$$

(51)

Tables 12, 13, and 14 illustrate the comparison of the absolute errors of the proposed method and up-to-date techniques in the literature solutions for different values of $\alpha$, $\beta$, $\gamma$, and $\mu$ at different temporal and spatial points.

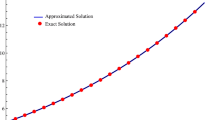
For comparison purposes, the absolute errors of the proposed method and up-to-date good techniques [11, 14, 25, 59] have been presented for $\alpha =\beta =1$, $\gamma =0.001$, and $\mu =1,2$ at different time levels and spatial points in Table 12. The obtained results are more accurate than Inan and Bahadir [59] and are in reasonable agreement with other compared methods [11, 14, 25] for both values $\mu =1$ and $\mu =2$ even with using a larger temporal mesh size. Also, it can be noticed from the table that the order of errors is the same for all compared methods. Furthermore, it can be observed that the larger temporal size does not affect the accuracy of the current method and it still approximates as adequately as literature solutions. Figure 10 illustrates the behavior of the exact and numerical solution results, and as clearly seen in the figure, there is a close agreement between the two solutions.

Table 13 represents the absolute errors of the proposed method and available literature solutions at different time levels with spatial steps for $\alpha =0$, $\beta =1$, and $\gamma =0.001$. It is concluded from the table that the current scheme is very well compatible with the literature solutions. In addition, as seen from the table, when it is used larger temporal size the accuracy of the suggested scheme is not disturbed so much.

Finally, the absolute errors of the proposed method and hybrid B-spline collocation method [14] are listed at different space points and time levels for $\alpha =5$, $\beta =10$, and various $\gamma$ values in Table 14. The comparisons demonstrated that the proposed method produces the same accurate solution with the reference [14] by using larger temporal mesh sizes. Therefore, it is concluded that the proposed method is more efficient and economical than the compared method. Although, in addition to this, the work of Wasim [14] captures the behavior of the problem accurately, a lack of a technique for predicting the optimal parameter used in the method can be a defect in the flexibility of their method.

Table 12 Absolute error comparisons of the proposed method and available literature solution at different temporal and spatial points for $\alpha =\beta =1$ and $\gamma =0.001$ in Example 4

Table 13 Absolute error comparisons of the proposed method and available literature solution at different temporal and spatial points for $\alpha =0,\beta =1$, and $\gamma =0.001$ in Example 4

Fig. 10

Simulations of the exact (left) and proposed method (right) solutions for the generalized Burgers–Huxley equation with $\alpha =\beta =1$, $\gamma =0.001$, $\mu =1, h=0.1$ and $\textrm{d}t=0.0001$ at $t=0.01$

Fig. 11

Numerical behavior of the proposed method solutions and exact solutions for the Fisher’s equation

Fig. 12

Simulations of the proposed method (left) and exact (right) solutions for the Fisher’s equation with the viscosity value $v=1$

5.5 Example 5 [29]

Let us consider the Fisher’s equation by taking $\alpha =0$ and $F(u)=\beta u(1-\gamma u)$ with the following initial condition

$$\begin{aligned} u(x,0)=-\frac{1}{4}\frac{\beta }{\gamma }\left[ \textrm{sech}^2\left( -\sqrt{\frac{\beta }{24v}}x\right) -2\textrm{tanh}\left( -\sqrt{\frac{\beta }{24v}}x\right) -2\right] , \end{aligned}$$

(52)

and boundary conditions

$$\begin{aligned} \lim _{x\rightarrow -\infty } u(x,t)=0.5 \quad \text {and} \quad \lim _{x \rightarrow \infty } u(x,t)=0. \end{aligned}$$

(53)

The exact solution is

$$\begin{aligned} u(x,t)=- \frac{1}{4}\frac{\beta }{\gamma }\left[ \textrm{sech}^2\left( \pm \sqrt{\frac{\beta }{24v}}x+\frac{5\beta }{12}t\right) -2\textrm{tanh}\left( -\sqrt{\frac{\beta }{24v}}x+\frac{5\beta }{12}t\right) -2\right] .\nonumber \\ \end{aligned}$$

(54)

The behavior of the Fisher’s equation depends on infection rate $\beta u(1-\gamma u)$. The infection rate is measured by $\beta u$, while the nonlinear term $-\beta \gamma u^2$ represents the diffusion rate. Wazwaz [60] proposed an analytical solution for this problem and the solution indicates a shock-like traveling wave. The amplitude of the wave is proportional to $\frac{\beta }{\gamma }$. The numerical solutions of the equation have been presented in Tables 15 and 16 for the parameters $\gamma =v=1$, $\beta =1/2$ in $\left[ -30,30\right]$, when $t=2$ and $t=4$ with $h=1$ and $\textrm{d}t=0.1$. It is seen from the tables that while the proposed method produces more accurate solutions than the wavelet-Galerkin approach [30] and the standard cubic B-spline method [29], it is in reasonable agreement with other compared literature [18, 61, 62].

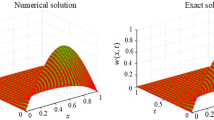
Figure 11 illustrates the behaviors of the exact and present method solutions and pointwise error graphs for $v=1$ at times $t=1,2,3,4,5$ (Fig. 11a, b) and for $v=0.1$ at times $t=0.1,0.2,0.3,0.4,0.5$ (Fig. 11c, d). As indicated in the figure, the currently obtained solutions and exact solution profiles are very close. In addition, Figs. 12 and 13 show the surface behaviors of the exact and numerical solutions for $v=1$ and $v=0.1$, respectively and it can be observed that numerical and exact behaviors look similar.

Table 14 Absolute error comparisons of the proposed method and available literature solution at different temporal and spatial points for $\alpha =5,\beta =10$ and $\mu =2$ in Example 4

Table 15 Comparison of the proposed method with the exact and available literature solution at different temporal and spatial points at $t=2$ in Example 5

Table 16 Comparison of the proposed method with the exact and available literature solution at different temporal and spatial points at $t=4$ in Example 5

6 Conclusion

In this study, a new hybrid method based on the combination of the cubic B-spline method and fourth-order compact finite difference scheme has been introduced for the spatial discretization of the ADR equations. Since the desired accuracy cannot be reached using the cubic B-spline method, the second-order derivatives have been obtained by the fourth-order compact finite difference scheme in which second derivatives are approximated with the unknowns and their first derivatives. Thus, the second-order derivatives are represented by the fourth-order convergence in the proposed method. The combined method has been applied to the Burgers, Burgers–Fisher, Burgers–Huxley, and Fisher’s equations after the equations have been discretized with help of the Crank–Nicolson scheme. The numerical results are in very good agreement with the exact solutions and quite satisfactory and competent with contemporary literature solutions. Furthermore, the solutions of some equations have superior performance even when relatively large temporal and spatial step sizes are used in computations and, thus, this reduces the computational complexity, computational time, and memory space. In addition, the proposed method can capture the physical behavior of the Burgers equation in the presence of very small viscosity values accurately and efficiently. The stability of the proposed method has been discussed by the matrix stability analysis and it is concluded that the method is stable. The convergence of the solution has been measured by an error norm and it is confirmed that the present method is convergent. Furthermore, the proposed method is easy to implement and provides much flexibility with the minimal computational effort to deal with challenging problems by altering the second-order approach with the high-order compact finite difference. Therefore, it is concluded that the new hybrid method that has computationally efficient and economical properties is a good alternative for investigating the nonlinear partial differential equations.

Fig. 13

Simulations of the proposed method (left) and exact (right) solutions for Fisher’s equation with the viscosity value $v=0.1$