The numerical study of advection–diffusion equations by the fourth-order cubic B-spline collocation method

Abstract

A fourth-order numerical method based on cubic B-spline functions has been proposed to solve a class of advection–diffusion equations. The proposed method has several advantageous features such as high accuracy and fast results with very small CPU time. We have applied the Crank–Nicolson method to solve the advection–diffusion equation. The stability analysis is performed, and the method is shown to be unconditionally stable. Error analysis is carried out to show that the proposed method has fourth-order convergence. The efficiency of the proposed B-spline method has been checked by applying on ten important advection–diffusion problems of three types, having Dirichlet, Neumann and periodic boundary conditions. Considered examples prove the mentioned advantages of the method. The computed results are also compared with those available in the literature, and it is found that our method is giving better results.

Introduction

Consider the one-dimensional convection–diffusion equation

$$\begin{aligned} \frac{\partial u}{\partial t}+\epsilon \frac{\partial u}{\partial x}=\gamma \frac{\partial ^2 u}{\partial x^2},a< x< b \,\ \text {and} \,\ 0 < t \le T, \end{aligned}$$

(1.1)

where $\epsilon$ and $\gamma$ are convection and diffusion coefficients, respectively. The initial condition is defined by

$$\begin{aligned} u(x,0)=\psi (x). \end{aligned}$$

(1.2)

The boundary conditions are as follows:

• (a) The Dirichlet boundary conditions are given by

  $$\begin{aligned} u(a,t)=f_1(t), \,\ u(b,t)=f_2(t), \end{aligned}$$

  (1.3)

• (b) The Neumann boundary conditions are defined by

  $$\begin{aligned} \frac{\partial u}{\partial x}(a,t)=g_1(t) , \,\ \frac{\partial u}{\partial x}(b,t)=g_2(t), \end{aligned}$$

  (1.4)

  and

• (c) The periodic boundary conditions can be written as

  $$\begin{aligned} u(a,t)=u(b,t). \end{aligned}$$

  (1.5)

  If the boundary conditions are periodic, then the total heat(mass) is conserved, i.e.,

  $$\begin{aligned} m(t)&= \int ^{b}_{a}u(x,t)\mathrm{d}t\nonumber \\ &= \hbox {k}\,(\hbox {constant}). \end{aligned}$$

  (1.6)

The advection–diffusion equation represents many problems of physics, chemistry and biology. It describes physical phenomena in which energy is transformed during two processes, namely advection and diffusion. It presents advection and diffusion of quantities such as mass, energy, heat, etc. The advection–diffusion equation can be used to depict water transfer in soils [1], transportation of pollutants in the atmosphere [2], diffusion of pollutants in rivers and stream [3], transfer of energy [4] and fluid [5] through the medium. Different numerical methods have been given to solve advection–diffusion equations due to wide applicability of this equation in different areas. Rizwan and Uddin presented second-order space and time nodal method [6]. Different numerical methods have been given by Dehghan for finding numerical solutions for this equation. Most of his methods are based on finite difference implicit or explicit schemes and are used to solve one- and three-dimensional advection–diffusion equations. Dehghan presented the weighted finite difference scheme [5] and high-order compact scheme [7] for the numerical study of the advection–diffusion equation. Other methods given by Dehghan can be seen in [8,9,10,11]. The advection–diffusion equation was studied numerically by Salkuyeh [12]. Karahan [13, 14] developed finite difference methods to solve this equation numerically. Zhang and Ding [15] developed a new difference scheme to get numerical solutions. Several spline-based methods have been given to solve (1.1) such as spline functions [16], exponential cubic spline [17], cubic B-splines [18, 19], cubic B-spline differential quadrature method [20], redefined splines [4], B-spline finite element [21, 22], the Taylor–Galerkin method [22] and the Taylor–Galerkin finite element method [23]. In the classical method of B-spline collocation, we just replace the unknown function and its derivatives by spline approximations for the function and its derivatives, respectively, and apply the Crank–Nicolson scheme or Runge–Kutta methods to get solutions at the grid points. The B-spline approximations of the unknown function u and its first derivative are of the fourth order, and those for the double derivative are of the second order.

In this work, we have introduced two different end conditions for the double derivatives to develop a fourth-order method having a higher order of convergence. In short, we have improved approximation for the double derivative by using different end conditions which resulted in very good numerical solutions. The fourth-order approximation for $u^{''}(x)$ can be obtained by taking one more term in the Taylor series expansion. A collocation method is applied to find the solution. One of the advantages of the method is that the solution can be obtained at any point of the domain.

The rest of the paper is organized as follows. In “Cubic B-spline functions” section, we have discussed the properties of spline functions. In “Implementation of the method” section, the implementation of the method to (1.1) has been explained. In “Error analysis” section, the convergence has been checked. “ Stability analysis” section contains the stability analysis followed by “Numerical experiments” section which contains test problems taken from the literature. A conclusion has been added in “Conclusion” section to briefly summarize the outcomes of the research work.

Cubic B-spline functions

A spline is a function that is piecewise defined by polynomial functions and possesses a high degree of smoothness at the places where polynomial pieces connect. A B-spline is a spline function that has minimal support with respect to given degree smoothness and domain partition. The cubic B-spline functions are defined as follows

$$\begin{aligned} B_j(x)=\frac{1}{h^3} {\left\{ \begin{array}{ll} (x-x_{j-2})^3 &{} {x}\in [x_{j-2},x_{j-1}),\\ (x-x_{j-2})^3-4(x-x_{j-1})^3, &{} {x}\in [x_{j-1},x_j),\\ (x_{j+2}-x)^3-4(x_{j+1}-x)^3, &{} {x} \in [x_{j},x_{j+1}),\\ (x_{j+2}-x)^3 &{} {x}\in [x_{j+1},x_{j+2}),\\ 0 &{} \text {otherwise} \end{array}\right. } \end{aligned}$$

(2.1)

where $\big \{B_{-1}(x),B_0(x),B_1(x),B_2(x),\ldots ,B_N(x),B_{N+1}(x)\big \}$ forms a basis over the considered interval.

Consider a uniform partition of the problem domain $a\le x \le b$ by the knots $x_i$, $i=0,1,2 \ldots N$ such that $x_{i}-x_{i-1}=h$ is the length of each interval.

In the cubic B-spline collocation method, we approximate exact solution u(x, t) by S(x, t) in the form [24]

$$\begin{aligned} S(x,t)=\displaystyle \sum _{j=-1}^{N+1} c_j(t)B_j(x), \end{aligned}$$

(2.2)

where $c_j(t)$’s are time-dependent quantities which we determine from the boundary conditions and collocation from the differential equation. We assume that the approximate solution S(x, t) satisfies the following interpolatory and boundary conditions

$$\begin{aligned} S(x_j,t)&= u(x_j,t), \,\ 0 \le j\le N, \end{aligned}$$

(2.3)

$$\begin{aligned} S^{''}(x_j,t)&= u^{''}(x_j,t)-\frac{1}{12}h^2u^{(4)}(x_j,t), \,\ j=0, \,\ N. \end{aligned}$$

(2.4)

If u(x, t) is sufficiently smooth and S(x, t) is the unique cubic spline interpolant satisfying the above end conditions, then we have from [25]

$$\begin{aligned} S^{'}(x_j,t) &= u^{'}(x_j,t)+O(h^4), \,\ 0\le j \le N\,\nonumber \\ S^{''}(x_j,t)&= u^{''}(x_j,t)-\frac{1}{12}h^2u^{(4)}(x_j,t)+O(h^4), \,\ 0\le j \le N. \end{aligned}$$

(2.5)

The approximate values S(x, t) and their first-order derivatives at the knots are defined by using finite difference and Taylor expansions as follows

$$\begin{aligned} u^{(4)}(x_j,t)&= \frac{S^{''}(x_{0},t)-5S^{''}(x_{1},t)+4S^{''}(x_{2},t)-S^{''}(x_{3},t)}{h^2}\nonumber \\& \quad +\,O(h^2), \,\ j=0, \end{aligned}$$

(2.6)

$$\begin{aligned} u^{(4)}(x_j,t)&= \frac{S^{''}(x_{j-1},t)-2S^{''}(x_{j},t)+S^{''}(x_{j+1},t)}{h^2}\nonumber \\& \quad +\,O(h^2), \,\ 1 \le j \le N-1, \end{aligned}$$

(2.7)

$$\begin{aligned} u^{(4)}(x_j,t)&= \frac{S^{''}(x_{N},t)-5S^{''}(x_{N-1},t)+4S^{''}(x_{N-2},t)-S^{''}(x_{N-3},t)}{h^2}\nonumber \\& \quad +\,O(h^2), \,\ j=N. \end{aligned}$$

(2.8)

Using (2.7)–(2.9) in (2.5)–(2.6), we get

$$\begin{aligned} u^{'}(x_j,t)&= S^{'}(x_j,t)+O(h^4), \,\ 0 \le j \le N, \end{aligned}$$

(2.9)

$$\begin{aligned} u^{''}(x_0,t)&= \frac{14S^{''}(x_{0},t)-5S^{''}(x_{1},t)+4S^{''}(x_{2},t)-S^{''}(x_{3},t)}{12}\nonumber \\&+O(h^4), \,\ j=0, \end{aligned}$$

(2.10)

$$\begin{aligned} u^{''}(x_j,t)&= \frac{S^{''}(x_{j-1},t)+10S^{''}(x_{j},t)+S^{''}(x_{j+1},t)}{12}+O(h^4), \,\ 1 \le j \le N-1, \end{aligned}$$

(2.11)

$$\begin{aligned} u^{''}(x_N,t)&= \frac{14S^{''}(x_{N},t)-5S^{''}(x_{N-1},t)+4S^{''}(x_{N-2},t)-S^{''}(x_{N-3},t)}{12}\nonumber \\&+O(h^4), \,\ j=N. \end{aligned}$$

(2.12)

(2.11) to (2.13) can be written as

$$\begin{aligned} u^{''}(x_0,t)&= \frac{14\displaystyle \sum\nolimits _{j=-1}^{N+1} c_j(t)B^{''}_j(x_0)-5\displaystyle \sum\nolimits _{j=-1}^{N+1} c_j(t)B^{''}_j(x_1)+4\displaystyle \sum\nolimits _{j=-1}^{N+1} c_j(t)B^{''}_j(x_2)-\displaystyle \sum\nolimits _{j=-1}^{N+1} c_j(t)B^{''}_j(x_3)}{12}, \end{aligned}$$

(2.13)

$$\begin{aligned} u^{''}(x_j,t)&= \frac{\displaystyle \sum\nolimits _{j=-1}^{N+1} c_j(t)B^{''}_j(x_{j-1})+10\displaystyle \sum\nolimits _{j=-1}^{N+1} c_j(t)B^{''}_j(x_j)+\displaystyle \sum\nolimits _{j=-1}^{N+1} c_j(t)B^{''}_j(x_{j+1})}{12}, \,\ 1 \le j \le N-1, \end{aligned}$$

(2.14)

$$\begin{aligned} u^{''}(x_N,t)&= \frac{14\displaystyle \sum\nolimits _{j=-1}^{N+1} c_j(t)B^{''}_j(x_N)-5\displaystyle \sum\nolimits _{j=-1}^{N+1} c_j(t)B^{''}_j(x_{N-1})+4\displaystyle \sum\nolimits _{j=-1}^{N+1} c_j(t)B^{''}_j(x_{N-2})-\displaystyle \sum\nolimits _{j=-1}^{N+1} c_j(t)B^{''}_j(x_{N-3})}{12}, \,\ j=N. \end{aligned}$$

(2.15)

Using (2.1)–(2.2), (2.14)–(2.16) can be further simplified to get

$$\begin{aligned} u^{''}(x_0,t)&= \frac{14c_{-1}-33c_0+28c_1-14c_2+6c_3-c_4}{2h^2}, \end{aligned}$$

(2.16)

$$\begin{aligned} u^{''}(x_j,t)&= \frac{c_{j-2}+8c_{j-1}-18c_j+8c_{j+1}+c_{j+2}}{2h^2},\end{aligned}$$

(2.17)

$$\begin{aligned} u^{''}(x_N,t)&= \frac{14c_{N+1}-33c_{N}+28c_{N-1}-14c_{N-2}+6c_{N-3}-c_{N-4}}{2h^2}. \end{aligned}$$

(2.18)

We will use these formulae in the next section.

Implementation of the method

Applying the Crank–Nicolson scheme to Eq. (1.1), it can be written as

$$\begin{aligned} \frac{u^{n+1}-u^n}{\Delta t}+\epsilon \frac{u_x^{n+1}+u_x^n}{2}=\gamma \frac{u_{xx}^{n+1}+u_{xx}^n}{2}. \end{aligned}$$

(3.1)

Separating the terms of advanced and initial level, we get

$$\begin{aligned} u^{n+1}+\frac{\epsilon \Delta t u_x^{n+1}}{2}-\frac{\gamma \Delta t u_{xx}^{n+1}}{2}=u^{n}-\frac{\epsilon \Delta t u_x^{n}}{2}+\frac{\gamma \Delta t u_{xx}^{n}}{2}. \end{aligned}$$

(3.2)

For $j=0$,

$$\begin{aligned}&(c^{n+1}_{-1}+4c^{n+1}_0+c^{n+1}_1)+3\frac{\epsilon \Delta t}{2h}(c^{n+1}_1-c^{n+1}_{-1}) \nonumber \\&\qquad -\frac{\gamma \Delta t}{4h^2}(14c^{n+1}_{-1}-33c^{n+1}_0+28c^{n+1}_1-14c^{n+1}_2\nonumber \\&\qquad +6c^{n+1}_3-c^{n+1}_4).\nonumber \\&\quad =(c^{n}_{-1}+4c^{n}_0+ c^{n}_1)-3\frac{\epsilon \Delta t}{2h}(c^{n}_1-c^{n}_{-1})\nonumber \\&\qquad +\frac{\gamma \Delta t}{4h^2}(14c^{n}_{-1}-33c^{n}_0+28c^{n}_1-14c^{n}_2+6c^{n}_3-c^{n}_4). \end{aligned}$$

(3.3)

For $1 \le j \le N-1$,

$$\begin{aligned}&(c^{n+1}_{j-1}+4c^{n+1}_{j}+c^{n+1}_{j+1})+3\frac{\epsilon \Delta t}{2h}(c^{n+1}_{j+1}-c^{n+1}_{j-1})\nonumber \\&\qquad -\frac{\gamma \Delta t}{4h^2}(c^{n+1}_{j-2}+8c^{n+1}_{j-1}-18^{n+1}c_j+8c^{n+1}_{j+1}+c^{n+1}_{j+2})\nonumber \\&\quad =(c^{n}_{j-1}+4c^{n}_{j}+ c^{n}_{j+1})-3\frac{\epsilon \Delta t}{2h}(c^{n}_{j+1}-c^{n}_{j-1})\nonumber \\&\qquad +\frac{\gamma \Delta t}{4h^2}(c^{n}_{j-2}+8c^{n}_{j-1}-18^{n}c_j+8c^{n}_{j+1}+c^{n}_{j+2}), \end{aligned}$$

(3.4)

for $j=N$, we have

$$\begin{aligned}&(c^{n+1}_{N-1}+4c^{n+1}_{N}+c^{n+1}_{N+1})+3\frac{\epsilon \Delta t}{2h}(c^{n+1}_{N+1}-c^{n+1}_{N-1})\nonumber \\&\qquad -\frac{\gamma \Delta t}{4h^2}(14c^{n+1}_{N+1}-33c^{n+1}_N+28c^{n+1}_{N-1}\nonumber \\&\qquad -14c^{n+1}_{N-2}\nonumber \\&\qquad +6c^{n+1}_{N-3}-c^{n+1}_{N-4})\nonumber \\&\quad =(c^{n}_{N-1}+4c^{n}_{N}+c^{n}_{N+1})-3\frac{\epsilon \Delta t}{2h}(c^{n}_{N+1}-c^{n}_{N-1})\nonumber \\&\qquad +\frac{\gamma \Delta t}{4h^2}(14c^{n}_{N+1}-33c^{n}_N+28c^{n}_{N-1}-14c^{n}_{N-2}\nonumber \\&\qquad +6c^{n}_{N-3}-c^{n}_{N-4}). \end{aligned}$$

(3.5)

Rearranging the terms for $j=0$, we may write

$$\begin{aligned}&s_1c^{n+1}_{-1}+s_2c^{n+1}_0+s_3c^{n+1}_1+s_4c^{n+1}_2+s_5c^{n+1}_3+s_6c^{n+1}_4\\&\quad =v_1c^{n}_{-1}+v_2c^{n}_0+v_3c^{n}_1+v_4c^{n}_2+v_5c^{n}_3+v_6c^{n}_4, \end{aligned}$$

where

$$\begin{aligned} s_1&= 1-\frac{3\epsilon \Delta t}{2h}-\frac{7\gamma \Delta t}{2h^2},\\ s_2&= 4+\frac{33\gamma \Delta t}{4h^2},\\ s_3&= 1+\frac{3\epsilon \Delta t}{2h}-\frac{7\gamma \Delta t}{h^2},\\ s_4&= \frac{7\gamma \Delta t}{2h^2},\\ s_5&= -\frac{3\gamma \Delta t}{2h^2},\\ s_6&= \frac{\gamma \Delta t}{4h^2}, \end{aligned}$$

and

$$\begin{aligned} v_1&= 1+\frac{3\epsilon \Delta t}{2h}+\frac{7\gamma \Delta t}{2h^2},\\ v_2&= 4-\frac{33\gamma \Delta t}{4h^2},\\ v_3&= 1-\frac{3\epsilon \Delta t}{2h}+\frac{7\gamma \Delta t}{h^2},\\ v_4&= -\frac{7\gamma \Delta t}{2h^2},\\ v_5&= \frac{3\gamma \Delta t}{2h^2},\\ v_6&= -\frac{\gamma \Delta t}{4h^2}, \end{aligned}$$

and for $j=1,2 \ldots N-1,$ we get

$$\begin{aligned}&-x_1c^{n+1}_{j-2}+x_2c^{n+1}_{j-1}+x_3c^{n+1}_{j}+x_4c^{n+1}_{j+1}-x_1c^{n+1}_{j+2}\nonumber \\&\quad = x_1c^{n}_{j-2}+x_5c^{n}_{j-1}+x_6c^{n}_{j}+x_7c^{n}_{j+1}+x_1c^{n}_{j+2}, \end{aligned}$$

(3.6)

where $x_1=\frac{\gamma \Delta t}{4h^2},$

$$\begin{aligned} x_2&= 1-\frac{3\epsilon \Delta t}{2h}-\frac{2\gamma \Delta t}{h^2},\\ x_3&= 4+\frac{9\gamma \Delta t}{2h^2},\\ x_4&= 1+\frac{3\epsilon \Delta t}{2h}-\frac{2\gamma \Delta t}{h^2},\\ x_5&= 1+\frac{3\epsilon \Delta t}{2h}-\frac{2\gamma \Delta t}{h^2},\\ x_6&= 4-\frac{9\gamma \Delta t}{2h^2},\\ x_7&= 1+\frac{3\epsilon \Delta t}{2h}+\frac{2\gamma \Delta t}{h^2}. \end{aligned}$$

for $j=N$,

$$\begin{aligned}&t_1c^{n+1}_{N-5}+t_2c^{n+1}_{N-4}+t_3c^{n+1}_{N-3}+t_4c^{n+1}_{N-2}+t_5c^{n+1}_{N-1}+t_6c^{n+1}_N\\&\quad =e_1c^{n}_{N-5}+e_2c^{n}_{N-4}+e_3c^{n}_{N-3}+e_4c^{n}_{N-2} +e_5c^{n}_{N-1}+e_6c^{n}_{N} \end{aligned}$$

where

$$\begin{aligned} t_1&= \frac{\gamma \Delta t}{4h^2},\\ t_2&= -\frac{3\gamma \Delta t}{2h^2},\\ t_3&= \frac{7\gamma \Delta t}{2h^2}\\ t_4&= 1-\frac{3\epsilon \Delta t}{2h}-\frac{7\gamma \Delta t}{h^2},\\ t_5&= 4+\frac{33\gamma \Delta t}{4h^2},\\ t_6&= 1+\frac{3\epsilon \Delta t}{2h}-\frac{7\gamma \Delta t}{2h^2}, \end{aligned}$$

and

$$\begin{aligned} e_1&= -\frac{\gamma \Delta t}{4h^2},\\ e_2&= \frac{3\gamma \Delta t}{2h^2},\\ e_3&= -\frac{7\gamma \Delta t}{2h^2},\\ e_4&= 1+\frac{3\epsilon \Delta t}{2h}+\frac{7\gamma \Delta t}{h^2},\\ e_5&= 4-\frac{33\gamma \Delta t}{4h^2},\\ e_6&= 1-\frac{3\epsilon \Delta t}{2h}+\frac{7\gamma \Delta t}{2h^2}. \end{aligned}$$

Thus, we get the following system

$$\begin{aligned} Ac^{n+1}=Bc^{n}, \end{aligned}$$

(3.7)

where $c=[c_{-1},c_0,c_1,c_2 \ldots c_{N},c_{N+1}]^T$

$$\begin{aligned} A&= \begin{pmatrix} s_1 &{} s_2 &{} s_3 &{} s_4 &{} s_5&{} s_6 &{} &{} &{}\\ -x_1 &{} x_2 &{} x_3 &{} x_4 &{}-x_1 &{} &{} &{} &{}\\ &{}-x_1 &{} x_2 &{} x_3 &{} x_4 &{}-x_1 &{} &{} &{} \\ .. &{} .. &{} .. &{} .. &{} .. &{} .. &{} ..&{} &{}\\ &{}&{}&{}&{}-x_1 &{} x_2 &{} x_3 &{} x_4 &{}-x_1 \\ &{} &{} &{} t_1&{}t_2 &{} t_3&{} t_4 &{} t_5 &{} t_6\\ \\ \end{pmatrix},\\ \hbox {and}\,\, B= & {} \begin{pmatrix} v_1 &{} v_2 &{} v_3 &{} v_4 &{} v_5&{} v_6 &{} &{} &{}\\ x_1 &{} x_5 &{} x_6 &{} x_7 &{}x_1 &{} &{} &{} &{}\\ &{}x_1 &{} x_5 &{} x_6 &{} x_7 &{}x_1 &{} &{} &{} \\ .. &{} .. &{} .. &{} .. &{} .. &{} .. &{} ..&{} &{}\\ &{}&{}&{}&{}x_1 &{} x_5 &{} x_6 &{} x_7 &{}x_1 \\ &{} &{} &{} e_1&{}e_2 &{} e_3&{} e_4 &{} e_5 &{} e_6\\ \\ \end{pmatrix}. \end{aligned}$$

We have $N+1$ equations in $N+3$ unknowns. It may be observed that $c_{-1}$ and $c_{N+1}$ can be eliminated with the help of the Dirichlet or Neumann boundary conditions to get $N+1$ equations in $N+1$ unknowns. In the case of the periodic boundary condition, we solve for $c_{0}$...$c_{N-1}$ only. The system obtained on eliminating $c_{-1}$ and $c_{N+1}$ can be solved at any desired time level starting with the initial vector $[c^{(0)}_{0},c^{(0)}_{1},c^{(0)}_{2} \ldots c^{(0)}_{N-1},c^{(0)}_{N}]^T$. The initial vector can be determined by using the B-spline approximation of the initial condition of the problem.

Error analysis

In this section, we have found an error bound for the presented method. From (2.1), we get the following expressions

$$\begin{aligned} S(x_i)&= c_{i-1}+4c_i+c_{i+1}, \end{aligned}$$

(4.1)

$$\begin{aligned} S^{'}(x_i)&= \frac{3}{h}(c_{i+1}-c_{i-1}), \end{aligned}$$

(4.2)

$$\begin{aligned} S^{'}(x_i)&= \frac{6}{h^2}(c_{i-1}-2c_i+c_{i+1}), \end{aligned}$$

(4.3)

$$\begin{aligned}{}[S^{'}(x_{i-1})+4S^{'}(x_{i})+S^{'}(x_{i+1})]&= \frac{3}{h}[u(x_{i+1})-u(x_{i-1})], \end{aligned}$$

(4.4)

$$\begin{aligned} h^2S^{''}(x_i)&= 6[u(x_{i+1})-u(x_{i})]\nonumber \\&-2h[2u^{'}(x_i)+u^{'}(x_{i+1})]. \end{aligned}$$

(4.5)

Then, as given in [26], we can use the operator notation $E(S(x_i))=S(x_{i+1})$ and $E=e^{hD}$ where $D\equiv d/dx$. We obtain the following expressions

$$\begin{aligned} e^{hD}+e^{-hD}&= 2\left( 1+\frac{h^2D^2}{2!}+\frac{h^4D^4}{4!}+\frac{h^6D^6}{6!}+\cdots \right) \end{aligned}$$

(4.6)

$$\begin{aligned} e^{hD}-e^{-hD}&= 2\left( hD+\frac{h^3D^3}{3!}+\frac{h^5D^5}{5!}+\frac{h^7D^7}{7!}+\cdots \right) \end{aligned}$$

(4.7)

Using the above relations in (4.4) and (4.5), we obtain

$$\begin{aligned} h[E^{-1}+4+E]S^{'}(x_i)&= \frac{3}{h}(E-E^{-1})u(x_i) \end{aligned}$$

(4.8)

$$\begin{aligned} h^2S^{''}(x_i)&= 6[E-1]u(x_i)-2h(2+E)u^{'}(x_i) \end{aligned}$$

(4.9)

Now, using (4.6)–(4.7) in (4.8), we obtain

$$\begin{aligned}&\left[ 4+2\left( 1+\frac{h^2D^2}{2!}+\frac{h^4D^4}{4!}+\frac{h^6D^6}{6!}+\cdots \right) \right] S^{'}(x_i)\nonumber \\&\quad =\frac{6}{h}\left[ hD+ \frac{h^3D^3}{3!}+\frac{h^5D^5}{5!}+\frac{h^7D^7}{7!}+\cdots \right] u(x_i) \end{aligned}$$

(4.10)

which can be simplified to get

$$\begin{aligned}&S^{'}(x_i)=\frac{6}{h}\left[ hD+ \frac{h^3D^3}{3!}+\frac{h^5D^5}{5!}+\frac{h^7D^7}{7!}+\cdots \right] \nonumber \\&\quad \left[ 4+2\left( 1+\frac{h^2D^2}{2!}+\frac{h^4D^4}{4!} +\frac{h^6D^6}{6!}+\cdots \right) \right] ^{-1}u(x_i) \end{aligned}$$

(4.11)

We further simplify the above to get

$$\begin{aligned} S^{'}(x_i)&= \left( D-\frac{h^4D^5}{180}+\cdots \right) u(x_i) \end{aligned}$$

(4.12)

$$\begin{aligned} S^{'}(x_i)&= \left( u^{'}(x_i)-\frac{h^4u^{(5)}(x_i)}{180}+\cdots \right) +O(h^6) \end{aligned}$$

(4.13)

From (4.9) and (4.13), we obtain

$$\begin{aligned} h^2 S^{''}(x_i)&= 6[e^{hD}-1]u(x_i)-2h[2+e^{hD}]\left[ u^{'}(x_i)\right. \nonumber \\&\left. -\frac{1}{180}h^4u^{(5)}(x_i)+\cdots \right] \end{aligned}$$

(4.14)

Expanding $e^{hD}$ and rearranging the terms of the above equation, we obtain

$$\begin{aligned} S^{''}(x_i)=\left( u^{''}(x_i)-\frac{h^2u^{(4)}(x_i)}{12}+\frac{h^4u^{(6)}(x_i)}{360}...\right) +O(h^6) \end{aligned}$$

(4.15)

Error analysis of convection–diffusion equation

As discussed above, we have applied the following approximations

$$\begin{aligned} S^{'}(x_i)&= u^{'}(x_i)-\frac{1}{180}h^4u^{(5)}(x_i)+O(h^6) \end{aligned}$$

(4.16)

$$\begin{aligned} S^{''}(x_i)&= u^{''}(x_i)-\frac{h^2u^{(4)}(x_i)}{12}+\frac{1}{360}h^4u^{(6)}(x_i)+O(h^6) \end{aligned}$$

(4.17)

Truncation error associated with the time discretization of convection–diffusion equation can be found by the typical finite difference formulation. Consider

$$\begin{aligned} u_t=f(u,u_x,u_{xx}) \end{aligned}$$

(4.18)

We discretize the time derivative by finite difference to get

$$\begin{aligned} \frac{u^{n+1}_i-u^{n}_i}{\Delta t}=\frac{f^n+f^{n+1}}{2} \end{aligned}$$

(4.19)

We apply the Taylor series expansion

$$\begin{aligned} (u_t)_i=f_i+\frac{1}{12}\Delta t^2 f_{tt}+\cdots \end{aligned}$$

(4.20)

The truncation error of convection–diffusion equation is

$$\begin{aligned} e_i=(u_t)_i+\epsilon (u_x)_i-\gamma (u_{xx})_i \end{aligned}$$

(4.21)

Substituting the values of errors introduced by space and time approximations, the truncation error of convection–diffusion equation may be given by

$$\begin{aligned} e_i=\Bigg (\frac{1}{12}\Bigg )\Delta t^2f_{tt}-\epsilon \frac{1}{180}h^4u^{(5)}_i-\gamma \frac{1}{360}h^4u^{(6)}_i+O(\Delta t^3,h^6) \end{aligned}$$

(4.22)

Hence, the final truncation error is

$$\begin{aligned} e_i=O(\Delta t^2)+O(h^4) \end{aligned}$$

(4.23)

Hence, the spline approximation used in the proposed method with uniformly distributed interior points is $O(\Delta t^2+h^4)$accurate.

Stability analysis

To check the stability of the scheme derived by the Crank–Nicolson and the fourth-order B-spline method, we have applied the Fourier-series (von Neumann) method. As discussed in “Cubic B-spline functions” section, applying the Crank–Nicolson on (1.1), we obtain the following difference scheme

$$\begin{aligned}&-x_1c^{n+1}_{j-2}+x_2c^{n+1}_{j-1}+x_3c^{n+1}_{j}+x_4c^{n+1}_{j+1}-x_1c^{n+1}_{j+2}\nonumber \\&\quad = x_1c^{n}_{j-2}+x_5c^{n}_{j-1}+x_6c^{n}_{j}+x_7c^{n}_{j+1}+x_1c^{n}_{j+2} \end{aligned}$$

(5.1)

where $x_i$’s have values as given in the previous section. Substituting $c^n_j=A\xi ^n exp(ij\phi h)$, where $i=\sqrt{-1}$, A is amplitude, h is step length and $\phi$ is mode number, we get

$$\begin{aligned} \xi =\frac{x_1e^{-2\phi i h}+x_5e^{-\phi i h}+x_6+x_7 e^{\phi i h}+x_1 e^{2\phi i h}}{-x_1e^{-2\phi i h}+x_2e^{-\phi i h}+x_3+x_4 e^{\phi i h}-x_1 e^{2\phi i h}} \end{aligned}$$

(5.2)

We further simplify (5.2) by substituting values of $x_i$’s. We thus get the following expression

$$\begin{aligned} \xi =\frac{4h^2(\mathrm{cos}(\phi h)+2)-\gamma \Delta t(9-8\mathrm{cos}(\phi h)-\mathrm{cos}(2 \phi h))-6i\epsilon h \Delta t \mathrm{sin}(\phi h)}{4h^2(\mathrm{cos}(\phi h)+2)+\gamma \Delta t(9-8\mathrm{cos}(\phi h)-\mathrm{cos}(2 \phi h))+6i\epsilon h \Delta t \mathrm{sin}(\phi h)} \end{aligned}$$

(5.3)

which may be written as

$$\begin{aligned} \xi =\frac{X_1-iY}{X_2+iY} \end{aligned}$$

(5.4)

where $X_1=4h^2(\mathrm{cos}(\phi h)+2)-\gamma \Delta t(9-8\mathrm{cos}(\phi h)-\mathrm{cos}(2 \phi h))$

$$\begin{aligned} X_2&= 4h^2(\mathrm{cos}(\phi h)+2)+\gamma \Delta t(9-8\mathrm{cos}(\phi h)-\mathrm{cos}(2 \phi h) \end{aligned}$$

and $Y=6\epsilon h \Delta t \mathrm{sin}(\phi h)$

which gives $|\xi |^2=\frac{X_1^2+Y^2}{X_2^2+Y^2}$

For stability, we must have $|\xi | \le 1$.

That is,$\frac{X_1^2+Y^2}{X_2^2+Y^2}\le 1$

Hence, for stability, we need to show that $X_1^2\le X_2^2$

We note that $X_1^2-X_2^2=(X_1+X_2)(X_1-X_2)=(8h^2(\mathrm{cos}(\phi h)+2))\big [-2\gamma \Delta t(9-8\mathrm{cos}(\phi h)-\mathrm{cos}(2 \phi h))\big ]\le 0$

Hence, the difference scheme is stable for any value of $\Delta t$ and any value of $\Delta x$. That is, the difference scheme is unconditionally stable.

Numerical experiments

We apply the cubic B-spline based method to 11 problems taken from the literature which have been categorized into problems having Dirichlet, Neumann and periodic boundary conditions. The accuracy of the method has been calculated by using maximum absolute error norms given by

$$\begin{aligned} L_{\infty }=\Vert u^{\mathrm{exact}}-U^{N}\Vert _{\infty } = \mathrm{max}|u_{i}^{\mathrm{exact}}-u^{N}_{i}| \end{aligned}$$

(6.1)

where $U^{N}$ stands for numerical solution. $u_{i}^{exact}$ and $U^{N}_{i}$ represent exact solution and numerical solution at the knot $x_{i}$, respectively. The rate of convergence for the method has been calculated using the following formula

$$\begin{aligned} r=\frac{ \ln (E(N_2)/E(N_1))}{ \ln (N_1/N_2)} \end{aligned}$$

(6.2)

where $E(N_1)$ and $E(N_2)$ represent maximum absolute error with number of grid points $N_1$ and $N_2$, respectively. The Peclet number is defined by

$P_e=$heat transport by convection/heat transport by diffusion=$\frac{\epsilon }{\gamma }$. The obtained results are presented in tabular form and illustrated in graphs also.

Problems having Dirichlet boundary conditions

Example 1

We consider the advection–diffusion problem [9] in (0, 2) with exact solution

$$\begin{aligned} u(x,t)=\mathrm{exp}(-\gamma t)\mathrm{sin}(x-\epsilon t) \end{aligned}$$

(6.3)

Boundary conditions are taken from the exact solution, and initial condition is

$$\begin{aligned} \psi (x)=\mathrm{sin}(x) \end{aligned}$$

(6.4)

This problem is solved with $\Delta t=0.001$ for different values of N. Computed results for $N=120$ at $t=1.0$ for different values of $P_e$ are reported in Table 1 and compared with those obtained with $\Delta t=0.00078125$ by the fourth-order method given by Dehghan [9]. It may be noticed that our method is giving good results even at high Peclet number. Table 2 shows the results for different values of $\gamma$ and $\epsilon =1.0$. Absolute errors for different values of N at $t=1.0$, $\epsilon =1.0$ and $\gamma =0.001$ are reported in Table 3. It can be observed that solutions are very accurate and the CPU time is very small. Numerical solutions are depicted in Figs. 1 and 2 with $\gamma =1.0$, $t \le 2$ and $\gamma =0.001$, $t \le 1$, respectively.

Fig. 1

Plot of numerical solutions of Example 1 at $t \le 2$ with $N=20 \epsilon =1,\gamma =1.0$ and $\Delta t=0.001$

Fig. 2

Plot of numerical solutions of Example 1 at $t \le 1$ with $N=10,\epsilon =1,\gamma =0.001$ and $\Delta t=0.001$

Table 1 Absolute errors for Example 1 at $t=1.0$ at different values of $P_e$

Table 2 Absolute errors of Example 1 with $\epsilon =1.0$ and different values of $\gamma$

Table 3 Maximum absolute errors for Example 1 at $t=1.0$ with different values of n for $\epsilon =1.0$ and $\gamma =0.001$

Example 2

We consider the advection–diffusion Eq. (1.1) in (0, 1) with $\epsilon =1.0$, $\gamma =0.1$ and following initial condition

$$\begin{aligned} u(x,0)=exp(5x)\left[ cos\left( \frac{\pi x}{2}\right) +.25sin\left( \frac{\pi x}{2}\right) \right] \end{aligned}$$

(6.5)

The exact solution [9] of this advection–diffusion equation is given by

$$\begin{aligned} u(x,t)&= \mathrm{exp}(5(x-t/2))\mathrm{exp}\left( -\frac{\pi ^2t}{40}\right) \nonumber \\&\quad \left[ \mathrm{cos}\left( \frac{\pi x}{2}\right) +.25\mathrm{sin}\left( \frac{\pi x}{2}\right) \right] \end{aligned}$$

(6.6)

Absolute errors with $\Delta t=0.01$ for different values of h at $t=2$ are reported in Table 4. It is observed that our results are better than those given by Dehghan [9]. In Table 6, absolute errors at $t=5.0$ are given and also compared with the errors obtained by Mittal and Jain [4]. We can conclude from the table that the results obtained by the present method are better than those obtained by redefined B-splines. Numerical results obtained for $t\leqslant 2$ are depicted in Fig. 3 for $N=20$ and $\Delta t=0.01$ (Figs. 4, 5).

Fig. 3

Plot of numerical solutions of Example 2 with $N=20$ and $\Delta t=0.01$

Fig. 4

Plot of numerical solutions of Example 3 with $N=20$ and $\Delta t=0.1$

Fig. 5

Plot of numerical solutions of Example 4 with $N=50,\Delta t=0.001$,$\epsilon =1.0$ and $\gamma =1.0$

Table 4 Absolute errors for Example 2 at $t=2.0$

Example 3

We consider (1.1) with the steady-state solution [27] given by

$$\begin{aligned} u(x,t)=\frac{e^{\epsilon x/\gamma }-1}{e^{\epsilon /\gamma }-1},0< x < 1 \end{aligned}$$

(6.7)

Initial and boundary conditions are taken from the exact solution(4.6). Numerical solutions at $t=1.0,t=5.0$ and $t=10.0$ are reported in Table 5 with $\Delta t=0.1$ and $N=300$.   Numerical solutions have been plotted in Fig. 4 against the values of x and t. CPU time has been estimated to be 1 second. Maximum absolute errors, rate of convergence and CPU time at different values of N are represented in Table 6. We observe that CPU time is very small even at large values of N.

Table 5 Absolute errors of Example 3 with $\Delta t=0.1$ and $N=300$

Table 6 Maximum absolute errors and rate of convergence for Example 3 at $t=1.0$ with different values of n

Example 4

We consider (1.1) in (0, 1) with the following boundary conditions

$$\begin{aligned} u(0,t)=\frac{1}{s}\mathrm{exp}\left( -50\frac{t^2}{s}\right) \hbox { and }u(1,t)=\frac{1}{s}exp\left( -50\frac{(1-t)^2}{s}\right) \end{aligned}$$

and with the initial condition given by

$$\begin{aligned} u(x,0)=\frac{1}{s}\mathrm{exp}\left( \frac{-50x^2}{s}\right) \end{aligned}$$

(6.8)

The exact solution [4] of the problem is

$$\begin{aligned} u(x,t)=\frac{1}{s}\mathrm{exp}\left( -50\frac{(x-t)^2}{s}\right) \end{aligned}$$

(6.9)

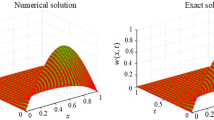
where $s=1+200\gamma t$. Absolute errors at different grid points are given in Table 7 at time levels of $t=0.5$, $t=1.0$ and $t=5.0$ with $N=10$. Results obtained by the present method are compared with those obtained by Nazir et al [28] in Table 8. Our solutions are found to be better than the solutions given in [4, 29] and [28]. Numerical and exact solutions have been plotted in Fig. 5. We can see that numerical results coincide with the exact results.

Table 7 Absolute errors for Example 4 with $\epsilon =1.0$ , $\gamma =1.0$ and, $\Delta t= 0.001$

Table 8 Absolute errors of Example 4 with $\epsilon =1.0$ and $\gamma =1.0$

Example 5

We consider problem [30] with an analytical solution of a Gaussian pulse of unit height with its center at $x=1$ in a domain [0, 9]. Its analytical solution is given by

$$\begin{aligned} u(x,t)=\frac{1}{\sqrt{4t+1}}\mathrm{exp}\left[ \frac{x-x_0-\epsilon t}{\gamma (4t+1)}\right] \end{aligned}$$

(6.10)

The initial condition is obtained from the exact solution by taking $t=0$. The boundary conditions are given by $u(0,t)=u(9,t)=0$. We performed numerical simulations up to time $t=5$ with $\epsilon =.008$ and $\gamma =.5$, and results are reported in Table 9 and compared with those given in [30]. We found that the fourth-order method is giving better results than QRTDQ and QNTDQ with very small CPU time.

Table 9 A comparison of maximum absolute ($L_{\infty }$) errors and CPU time with different values of N for Example 5

Problems having Neumann boundary conditions

Example 6

We consider the advection–diffusion equation with the boundary conditions

$$\begin{aligned} \left( \frac{\partial u}{\partial x}\right) _{(a,t)}&= \mathrm{exp}(-\gamma t)\mathrm{cos}(a-\epsilon t) \,\ and \,\ \nonumber \\ \left( \frac{\partial u}{\partial x}\right) _{(b,t)}&= \mathrm{exp}(-\gamma t)\mathrm{cos}(b-\epsilon t) \end{aligned}$$

(6.11)

and with the initial condition defined by

$$\begin{aligned} u(x,0)=\mathrm{sin}(x) \end{aligned}$$

(6.12)

The problem has the exact solution [28] of the form

$$\begin{aligned} u(x,t)=\mathrm{exp}(-\gamma t)\sin (x-\epsilon t) \end{aligned}$$

(6.13)

We consider this problem in (0, 2). Absolute errors at grid points for different Peclet numbers are illustrated in Table 10. It may be seen that excellent results have been obtained. Table 11 contains absolute errors and CPU time for different values of N at $t=1.0$. Space and time graphs of numerical and exact solutions are given in Figs. 6 and 7 for $\gamma =0.01$ and $\gamma =0.001$, respectively. In Fig. 8, numerical and exact solutions are depicted up to time $t=5.0$ with $\epsilon =\gamma =1.0$. It may be seen that approximate solutions are very close to the exact solutions.

Fig. 6

Numerical and exact solutions of Example 6 with $N=40,\Delta t=0.001$,$\epsilon =1.0$ and $\gamma =0.01$ up to $t\le 20$

Fig. 7

Numerical and exact solutions of Example 6 with $N=40,\Delta t=0.001$,$\epsilon =1.0$ and $\gamma =0.001$ up to $t\le 20$

Fig. 8

Plot of numerical solutions of Example 6 with $N=40,\Delta t=0.001$,$\epsilon =1.0$ and $\gamma =1.0$

Table 10 Absolute errors for Example 6 at $t=1.0$ with $\Delta t=0.001$ and $N=120$

Table 11 Maximum absolute errors for Example 6 at $t=1.0$ with different values of n

Example 7

Let us consider the advection–diffusion Eq. (1.1) with the following exact solution [22]

$$\begin{aligned} u(x,t)=e^{\alpha x+\beta t},\quad 0< x < 1 \end{aligned}$$

(6.14)

Boundary conditions are defined as follows

$$\begin{aligned} \left( \frac{\partial u}{\partial x}\right) _{(0,t)}=\alpha e^{\beta t},\left( \frac{\partial u}{\partial x}\right) _{(1,t)}=\alpha e^{\alpha +\beta t} \end{aligned}$$

(6.15)

Initial condition is given by

$$\begin{aligned} u(x,0)=e^{\alpha x} \end{aligned}$$

(6.16)

This problem has been solved by taking $\alpha =0.02854797991928$, $\beta =-0.0999$, $\Delta t=0.001$ , $N=40$, $\epsilon =3.5$ and $\gamma =0.022$. Excellent results have been obtained which are presented in tabular form (Table 12) and compared with the solutions obtained by Mittal and Jain [22]. It is noticed that our method is better than the methods given in [22].

Table 12 Comparison of absolute errors for Example 7

Example 8

Consider (1.1) with the exact solution [22]

$$\begin{aligned} u(x,t)=e^{\alpha x+\beta t}, \,\ 0< x <1 \end{aligned}$$

(6.17)

where $\alpha =1.17712434446770$, $\beta =-0.09$, $\Delta t=0.001$, $N=80$, $\epsilon =0.1$ and $\gamma =0.2$. Initial and Neumann boundary conditions are taken from the exact solution. We computed results for different values of parameters which are reported in Table 13. Our results are better than the results obtained by [22].

Table 13 Comparison of absolute errors for Example 8

Example 9

We consider the following Neumann boundary conditions for (1.1) in (0, 1)

$$\begin{aligned} \left( \frac{\partial u}{\partial x}\right) _{(0,t)}=-ac \,\ \mathrm{exp}(bt),\left( \frac{\partial u}{\partial x}\right) _{(1,t)}=-ac \,\ \mathrm{exp}(bt-c) \end{aligned}$$

(6.18)

Initial condition is $u(x,0)=a \,\ exp(-cx)$, and the exact solution is [31]

$$\begin{aligned} u(x,t)=a e^{bt-cx} \end{aligned}$$

(6.19)

where $c=\frac{-\epsilon +\sqrt{\epsilon ^2+4\gamma b}}{2\gamma }$, $a=1.0$ and $b=0.1$. We carried out numerical experiments by taking different values of $\epsilon$ and $\gamma$. Results obtained for $\Delta t=0.001$ and $h=0.1$ are reported in Table 14. It may be observed that results are very good. Computed results up to time $t=1$ are depicted in Fig. 9. It may be found that the space and time graph is the same as illustrated by [22, 31].

Fig. 9

Plot of numerical solutions of Example 9 with $N=10,\Delta t=0.001$,$\epsilon =1.0$ and $\gamma =0.001$

Table 14 Absolute errors for Example 9 at $N=10$ with $\epsilon =1.0$ and $\gamma =0.001$

Periodic problems

Example 10

We consider the advection–diffusion Eq. (1.1) with the exact solution given by

$$\begin{aligned} u(x,t)=e^{-\gamma t}\mathrm{sin}(2\pi (x-\epsilon t)),0< x < 1 \end{aligned}$$

(6.20)

This equation represents a decaying traveling wave. The initial condition is taken from the exact solution of the problem. The boundary conditions are periodic in the considered interval and may be given as

$$\begin{aligned} u(0,t)=u(1,t) \end{aligned}$$

(6.21)

Computed results are illustrated in Fig. 10 and presented in Table 15. Figure 10 depicts exact and numerical solutions at $t=0.1$, 0.2, 0.3, 0.4 and $t=0.5$. It may be observed that numerical solutions are very close to the exact values. We calculated the value of m(t) and found that it is a constant for different time levels.

$$\begin{aligned} m(t)&= \int ^{b}_{a}u(x,t)\mathrm{d}t\nonumber \\&= 0.0025\hbox { for }\hbox {t}=0.5\hbox { and }\hbox {t}=1.0 \end{aligned}$$

(6.22)

Fig. 10

Plot of numerical solutions of Example 10 with $N=50,\Delta t=0.001$,$\epsilon =1.0$ and $\gamma =10^{-6}$

Table 15 Absolute errors for Example 10 at $N=50$ with $\epsilon =1.0$ and $\Delta t=0.001$

Example 11

We consider the periodic problem [32] with the boundary condition

$$\begin{aligned} u(0,t)=u(1,t),0<t<T \end{aligned}$$

(6.23)

and with the initial condition $u(x,0)=cos(2\pi x)$,$0<x<1$. The problem has exact solution given by

$$\begin{aligned} u(x,t)=e^{-4\pi ^t}cos(2\pi (x-t)),0<x<1 \end{aligned}$$

(6.24)

The computed absolute errors at $t=0.1,0.2$ and $t=0.3$ are given in Table 16. Figure 11 depicts the numerical and the exact results with $\epsilon =1.0$ and $\gamma =0.001$ at $t=0.1$ and $t=0.2$. It may be seen that the results obtained by the proposed method are very good.

Fig. 11

Plot of numerical solutions of Example 11 with $N=10,\Delta t=0.001$,$\epsilon =1.0$ and $\gamma =0.001$

Table 16 Absolute errors for Example 11 at $N=100$ with $\epsilon =1.0$ and $\gamma =1.0$

We evaluated m(t) for t$=0.1$, 0.2 and 0.3.

$$\begin{aligned} m(t)&= \int ^{b}_{a}u(x,t)\mathrm{d}t\nonumber \\ m(t)&= 1.87E-08\hbox { for t} = 0.1, 0.2\hbox { and }0.3. \end{aligned}$$

(6.25)

Conclusion

• (a) The proposed method produces very accurate results with very small CPU time.

• (b) The stability analysis is performed by using the von Neumann’s method, and proposed spline-based fourth-order method has been shown to be unconditionally stable.

• (c) The convergence analysis has been carried out, and it is shown that the proposed method is $O(\Delta t^2+h^4)$ accurate.

• (d) The method is stable, so the time step can be taken large compared with some other known methods. This allows one to find solution at a high level of time.

• (e) Ten important convection–diffusion problems have been studied and shown to have very accurate solutions.

• (f) The obtained results are presented in tables and depicted in figures also. We can observe that the method is applicable for convection-dominated problems as well as for diffusion-dominated problems.

• (g) The method can solve very efficiently a large class of partial differential equations having the Dirichlet, Neumann or periodic boundary conditions.

• (h) We would like to extend our research work in this direction by taking hyperbolic and two-dimensional problems.