1 Introduction

The Swift–Hohenberg equation was first proposed by Swift and Hohenberg [19, 20] to model the onset and evolution of roll patterns in Rayleigh–B\(\acute{e}\)nard convection. Since then, it has attracted considerable attention in several related fields, for instance, as a model for the study of pattern formation [5] and biological materials [12]. It is the gradient flow with the energy

$$\begin{aligned} E(u)=\int _{\Omega } \left( \frac{1}{2}(\Delta u+\frac{a}{2} u)^2+\Phi (u) \right) d{{\varvec{x}}}, \end{aligned}$$
(1.1)

where \(\Omega \in {\mathbb {R}}^2\), \(a>0\) is a physical parameter and

$$\begin{aligned} \Phi (u)=-\frac{\varepsilon }{2} u^2-\frac{g}{3} u^3+\frac{u^4}{4}, \end{aligned}$$

\(\varepsilon >0\) and \(g\ge 0\) are constants with physical significance.

The chemical potential is defined by the variational derivative of the energy, i.e.

$$\begin{aligned} \mu :=\frac{\delta E}{\delta u}=\left( \Delta +\frac{a}{2}\right) ^2 u+\Phi '(u). \end{aligned}$$
(1.2)

Then the gradient flow follows

$$\begin{aligned} u_t=-\mu =-\left( \Delta +\frac{a}{2}\right) ^2 u-\Phi '(u). \end{aligned}$$
(1.3)

For easy presentation of the analysis, we assume a periodic boundary condition for all the variables throughout the paper. With the periodic boundary condition, the Eq. (1.3) is energy dissipative, and the dissipation rate is

$$\begin{aligned} \frac{d}{dt} E(u)=-\int _{\Omega } (u_t)^2 d{{\varvec{x}}}\le 0. \end{aligned}$$

There have been various numerical methods to simulate the Swift–Hohenberg Eq. (1.3) recently. For example, in [29], the authors presented a large time-stepping numerical method for the Swift–Hohenberg equation by adding an extra artificial term to preserve the unconditional energy stability. In [13], Lee presented first- and second-order semi-analytical Fourier spectral methods as an accurate and efficient approach for solving the Swift–Hohenberg equation based on the operator splitting method. In [14], Liu and Yin developed discontinuous Galerkin (DG) methods for spatial discretization, and the invariant energy quadratization (IEQ) method for the temporal discretization. They further proposed a multi-stage algebraically stable Runge–Kutta method and could achieve high order accuracy in both space and time in [15]. Several numerical results were presented to illustrate the efficiency of the proposed numerical schemes, but no convergence or error analyses were discussed. Qi and Hou [17] proposed and analyzed a second-order energy stable numerical scheme for the Swift–Hohenberg equation, with a mixed finite element approximation in space, and they presented an optimal error estimate for the scheme.

For spatial discretization, we will develop the high-order local discontinuous Galerkin (LDG) methods for the Swift–Hohenberg equation, since the LDG method has arbitrary high-order accuracy, easy parallelization, the flexibility for arbitrary hp adaptivity and simple treatment of boundary conditions. However, to the best knowledge of the authors, optimal error estimates of the semi-discrete and fully-discrete DG schemes for the Swift–Hohenberg equation are lacking in the existing literature. Our contribution here is that we establish the energy stability and optimal error estimates of the semi-discrete LDG scheme. The novelty of the error analysis is that we construct the energy equality for both the primal variable and auxiliary variables to eliminate or control troublesome terms in the error equations. To estimate the nonlinear term, we show the boundness of the LDG solution with similar techniques in [10].

The LDG method considered in this paper is an extension of the DG method, which was first designed for solving linear transport equation by Reed and Hill [18] and later extended to Runge–Kutta DG (RKDG) methods for nonlinear conservation laws by Cockburn, Shu [3]. As a method developed to solve partial differential equations (PDEs) with higher-order derivatives, the LDG method was first constructed by Cockburn and Shu for convection-diffusion equations in [2]. The main idea of LDG methods is to rewrite the higher-order differential equation as a first order system by introducing auxiliary variables, then apply the traditional DG method on the system. Besides, the auxiliary variables can be locally eliminated, which is a key advantage of the scheme. Optimal error estimates of LDG methods were also obtained for the fourth order time-dependent bi-harmonic type equations [7], high order waves equations [28] and the Allen-Cahn equation [9]. For more details about LDG methods, we refer the readers to the review article [27] and the references therein.

The Swift–Hohenberg equation contains fourth-order spacial derivatives, and explicit time discretization suffers from extremely small time step restriction for stability. In this paper, we will develop a first-order linear scheme based on the scalar auxiliary variable (SAV) approach [11, 22, 23] for the Swift–Hohenberg equation. By introducing a scalar auxiliary variable to the nonlinear part of energy functional, the SAV approach has a modified energy dissipation property for a large class of gradient flows. In addition, the SAV approach leads to linear equations with constant coefficients thus it is remarkably easy to implement. Coupled with the LDG method, we will construct a fully-discrete LDG scheme and prove its energy stability and optimal convergence rate. To derive the optimal error estimates, \({\mathcal {O}}(h^{k+1}+\Delta t)\), we adopt a technique of the elliptic projection to deal with troublesome terms caused by auxiliary variables and jump terms of LDG schemes. In addition, we establish an extra energy equality to handle the nonlinear term of the SAV approach.

To improve the temporal accuracy, we employ the semi-implicit SDC method [8, 24] iteratively. The SDC method was first developed by Dutt et al. [6]. Then, a semi-implicit SDC method was introduced by Minion [16] to solve equations containing both stiff and nonstiff components. It is based on first-order time integration methods, which are corrected iteratively, with the order of accuracy increased by one for each additional iteration. Combining with the SAV method, the semi-implicit SDC method can be linear, high-order accurate and energy stable in our numerical tests.

The organization of the paper is as follows. In Sect. 2, we will develop the LDG method for the Swift–Hohenberg equation and prove its energy stability and optimal error estimate in \(L^2\) norm. In Sect. 3, we first present a first-order linear temporal scheme based on the SAV approach, prove its unconditional energy stability and optimal error estimate when coupled with the LDG spatial discretization. Then, we employ the semi-implicit SDC method to achieve high-order temporal accuracy. Sect. 4 contains various numerical experiments to test the performance of the fully-discrete high-order scheme. Finally, we give concluding remarks and optimal error estimates for the elliptic projection in Sect. 5 and in the appendix, respectively.

2 Energy Stability and Error Estimate of the Semi-discrete LDG Method

In this section, we will develop the semi-discrete LDG scheme for the Swift–Hohenberg equation and establish its energy stability and error estimate.

2.1 The LDG Method and Its Energy Stability

Let \({\mathcal {T}}_h=\{K\}\) be a shape-regular subdivision of \(\Omega \). For example, K is a rectangle for Cartesian meshes. \({\mathcal {E}}_h\) denotes the union of the boundary faces of elements \(K \in {\mathcal {T}}_h\), and \({\mathcal {E}}_0={\mathcal {E}}_h{\setminus }\partial \Omega \). Associated with this mesh, we define the DG finite element spaces

$$\begin{aligned} V_{h}=&\Bigl \{\varphi :\;\;\;\varphi \vert _K\in {\mathcal {Q}}^k(K),\;\;\;\; \; \forall K\in {\mathcal {T}}_{h}\Bigr \},\\ \Sigma _h =&\Bigl \{{\varvec{\eta } }=(\eta _1, \eta _2)^T :\;\;\; \eta _l\vert _{ K }\in {\mathcal {Q}}^k(K), \;\;l=1, 2,\;\;\; \forall K \in {\mathcal {T}}_{h}\Bigr \}, \end{aligned}$$

where \({\mathcal {Q}}^k(K)\) denotes the space of tensor product of polynomials of degree at most \(k\ge 0\) on \(K \in {\mathcal {T}}_h\) in each variable. For one-dimensional case, we have \({\mathcal {Q}}^k(K)={\mathcal {P}}^k(K)\), which is the space of polynomials of degree at most k defined on K. Set

$$\begin{aligned} (u,v)_{K}=\int _{K}uvd{{\varvec{x}}},\;\; ({{\varvec{s}}},{\varvec{\theta } })_{K}=\int _{K}{{\varvec{s}}}\cdot {\varvec{\theta } }d{{\varvec{x}}},\;\; , <u, {\varvec{\theta } }\cdot {{\varvec{n}}}>_{\partial K}=\int _{\partial K}u{\varvec{\theta } }\cdot {{\varvec{n}}}ds, \end{aligned}$$

which are the standard inner products in \(L^{2}(K)\) and \(L^{2}(\partial K)\), respectively. The associate \(L^{2}\) norm is defined by

$$\begin{aligned} \Vert v\Vert _{K}^{2}=(v,v)_{K},\;\;\Vert {{\varvec{s}}}\Vert _{K}^{2}=({{\varvec{s}}},{{\varvec{s}}})_{K},\;\;\Vert v\Vert ^{2}_{\partial K}=<v,v>_{\partial K} \end{aligned}$$

and \(\Vert v\Vert ^{2}=\sum \limits _{K}\Vert v\Vert _{K}^{2}\), \(\Vert {{\varvec{s}}}\Vert ^{2}=\sum \limits _{K}\Vert {{\varvec{s}}}\Vert _{K}^{2}\), \(\Vert v\Vert ^{2}_{{\mathcal {E}}_h}=\sum \limits _{K}\Vert v\Vert _{\partial K}^{2}.\)

To develop the LDG scheme, we first rewrite the Eq. (1.3) as a first order system

$$\begin{aligned} u_t&= -\nabla \cdot {{\varvec{s}}}-\frac{a}{2} q-p, \end{aligned}$$
(2.1a)
$$\begin{aligned} {{\varvec{s}}}&=\nabla q, \end{aligned}$$
(2.1b)
$$\begin{aligned} q&= \nabla \cdot {\varvec{\omega }}+\frac{a}{2} u, \end{aligned}$$
(2.1c)
$$\begin{aligned} {\varvec{\omega }}&= \nabla u, \end{aligned}$$
(2.1d)
$$\begin{aligned} p&=\Phi '(u). \end{aligned}$$
(2.1e)

The LDG scheme to solve the system (2.1) is as follows: find \(u_h, q_h, p_h \in V_h\), and \({{\varvec{s}}}_h, {\varvec{\omega }}_h \in \Sigma _h\), such that, for all test functions \(\varphi _1, \varphi _2, \varphi _3 \in V_h\), and \({\varvec{\theta } }_1, {\varvec{\theta } }_2 \in \Sigma _h\), we have

$$\begin{aligned} ((u_h)_t,\varphi _1)_K&=({{\varvec{s}}}_h,\nabla \varphi _1)_K-<{\widehat{{{\varvec{s}}}}}_h \cdot {{\varvec{n}}},\varphi _1>_{\partial K}-\frac{a}{2}(q_h,\varphi _1)_K-(p_h,\varphi _1)_K, \end{aligned}$$
(2.2a)
$$\begin{aligned} ({{\varvec{s}}}_h,{\varvec{\theta } }_1)_K&=-(q_h, \nabla \cdot {\varvec{\theta } }_1)_K+<{\widehat{q}}_h, {\varvec{\theta } }_1 \cdot {{\varvec{n}}}>_{\partial K}, \end{aligned}$$
(2.2b)
$$\begin{aligned} (q_h, \varphi _2)_K&=-({\varvec{\omega }}_h, \nabla \varphi _2)_K+<{\widehat{{\varvec{\omega }}}}_h \cdot {{\varvec{n}}}, \varphi _2>_{\partial K}+\frac{a}{2}(u_h,\varphi _2)_K, \end{aligned}$$
(2.2c)
$$\begin{aligned} ({\varvec{\omega }}_h,{\varvec{\theta } }_2)_K&=-(u_h, \nabla \cdot {\varvec{\theta } }_2)_K+<{\widehat{u}}_h, {\varvec{\theta } }_2 \cdot {{\varvec{n}}}>_{\partial K}, \end{aligned}$$
(2.2d)
$$\begin{aligned} (p_h,\varphi _3)_K&=(\Phi '(u_h),\varphi _3)_K. \end{aligned}$$
(2.2e)

The “hat” terms in (2.2) in the cell boundary terms from integration by parts are the so-called numerical fluxes. To properly define the numerical fluxes, we need to introduce the following notations.

Let e be an interior face shared by the “left” and “right” elements \(K_L\) and \(K_R\) and define the normal vectors \({{\varvec{n}}}_L\) and \({{\varvec{n}}}_R\) on e pointing exterior to \(K_L\) and \(K_R\), respectively. For our purpose, “left” and “right” can be uniquely defined for each face according to any fixed rule. For example, we choose \({{\varvec{n}}}_0\) as a constant vector. The left element \(K_L\) to the face requires that \({{\varvec{n}}}_L \cdot {{\varvec{n}}}_0<0\), and the right one \(K_R\) requires \({{\varvec{n}}}_R \cdot {{\varvec{n}}}_0 \ge 0\). If \(\psi \) is a function on \(K_L\) and \(K_R\), but possibly discontinuous across e , let \(\psi _L\) denote \((\psi |_{K_L})|_e\) and \(\psi _R\) denote \((\psi |_{K_R})|_e\), the left and right trace, respectively.

In the following proof of the energy stability and error estimate, we can see the simple alternating numerical fluxes can guarantee the energy stability, such as

$$\begin{aligned} {\widehat{{{\varvec{s}}}}}_h=({{\varvec{s}}}_h)_{R},\;\;\;\;\;\;\; {\widehat{q}}_h=(q_h)_{L},\;\;\;\;\;\;\; {\widehat{{\varvec{\omega }}}}_h=({\varvec{\omega }}_h)_{R},\;\;\;\;\;\;\; {\widehat{u}}_h=(u_h)_{L}. \end{aligned}$$
(2.3)

In addition, we can see the above choice of fluxes is not unique. The crucial part is taking \({\widehat{{{\varvec{s}}}}}_h\) and \({\widehat{u}}_h\), also \({\widehat{{\varvec{\omega }}}}_h\) and \({\widehat{q}}_h\) from opposite sides. For the convenience of presentation, we introduce some LDG operators. Denote

$$\begin{aligned} H^{-}_{K}(r,{{\varvec{v}}})&=(r, \nabla \cdot {{\varvec{v}}})_K-<r_{L}, {{\varvec{v}}}\cdot {{\varvec{n}}}>_{\partial K},\\ H^{+}_{K}({{\varvec{v}}},r)&=({{\varvec{v}}},\nabla r)_K-<{{\varvec{v}}}_{R} \cdot {{\varvec{n}}},r>_{\partial K}. \end{aligned}$$

Summing up over K, we define \((\cdot ,\cdot )= \sum \limits _{K}(\cdot ,\cdot )_K\), \(<\cdot ,\cdot>=\sum \limits _{K}<\cdot ,\cdot >_{\partial K}\) and

$$\begin{aligned} H^{-}(r,{{\varvec{v}}})=\sum _{K}H^{-}_{K}(r,{{\varvec{v}}}),\;\;H^{+}({{\varvec{v}}},r)=\sum _{K}H^{+}_{K}({{\varvec{v}}},r). \end{aligned}$$

With the special choice of the flux (2.3) and the periodic boundary conditions, we have the property

$$\begin{aligned} H^{-}(r,{{\varvec{v}}})=-H^{+}({{\varvec{v}}},r). \end{aligned}$$
(2.4)

Next, we will prove its energy dissipation.

Proposition 2.1

(Energy stability for the semi-discrete LDG scheme). The solution to the LDG scheme (2.2) with the numerical fluxes (2.3) satisfies the energy stability

$$\begin{aligned} \frac{d}{dt} \int _{\Omega } \left( \frac{1}{2} (q_h)^2+\Phi (u_h) \right) d{{\varvec{x}}}\le 0. \end{aligned}$$
(2.5)

Proof

First, we take the time derivative of (2.2c) and (2.2d), choose the test functions \(\varphi _2=q_h\) and \({\varvec{\theta } }_2=-{{\varvec{s}}}_h\) separately to obtain

$$\begin{aligned} ((q_h)_t, q_h)_K&=-H^{+}_{K}(({\varvec{\omega }}_h)_t, q_h)+\frac{a}{2}((u_h)_t,q_h)_K, \end{aligned}$$
(2.6)
$$\begin{aligned} -(({\varvec{\omega }}_h)_t,{{\varvec{s}}}_h)_K&=H^{-}_{K}((u_h)_t, {{\varvec{s}}}_h). \end{aligned}$$
(2.7)

For other equations in scheme (2.2), we choose the test functions

$$\begin{aligned} \varphi _1=(u_h)_t,\;\;\;\;\;\;\; {\varvec{\theta } }_1=({\varvec{\omega }}_h)_t,\;\;\;\;\;\;\; \varphi _3=-(u_h)_t, \end{aligned}$$

respectively, to get

$$\begin{aligned} ((u_h)_t,(u_h)_t)_K&=H^{+}_{K}({{\varvec{s}}}_h,(u_h)_t)-\frac{a}{2}(q_h,(u_h)_t)_K-(p_h,(u_h)_t)_K, \end{aligned}$$
(2.8)
$$\begin{aligned} ({{\varvec{s}}}_h,({\varvec{\omega }}_h)_t)_K&=-H^{-}_{K}(q_h, ({\varvec{\omega }}_h)_t), \end{aligned}$$
(2.9)
$$\begin{aligned} -(p_h,(u_h)_t)_K&=-(\Phi '(u_h),(u_h)_t)_K. \end{aligned}$$
(2.10)

Combining Eqs. (2.6)–(2.10), we find

$$\begin{aligned}&\frac{d}{dt} \int _{K} \left( \frac{1}{2} (q_h)^2+\Phi (u_h) \right) d{{\varvec{x}}}+\int _{K}((u_h)_t)^2 d{{\varvec{x}}}\nonumber \\&\quad =-H^{+}_{K}(({\varvec{\omega }}_h)_t, q_h)-H^{-}_{K}(q_h, ({\varvec{\omega }}_h)_t)+H^{-}_{K}((u_h)_t, {{\varvec{s}}}_h)+H^{+}_{K}({{\varvec{s}}}_h,(u_h)_t). \end{aligned}$$
(2.11)

Finally, summing up (2.11) over K and by the property (2.4), we have

$$\begin{aligned} \frac{d}{dt} \int _{\Omega } \left( \frac{1}{2} (q_h)^2+\Phi (u_h) \right) d{{\varvec{x}}}+\int _{\Omega }((u_h)_t)^2 d{{\varvec{x}}}=0, \end{aligned}$$
(2.12)

which implies the energy stability result (2.5). \(\square \)

2.2 Error Estimate of the Semi-discrete LDG Method

In this subsection, we will present the optimal error estimate of the LDG scheme (2.2). Before stating the convergence results, we first give some projections and properties.

2.2.1 Projections and Properties

First, the one-dimensional Gauss-Radau projections \(P^{\pm }u\) of a function u are defined as follows. For any \(v\in P^{k-1}(K_{j})\), \(k\ge 1\), and an arbitrary subinterval \(K_{j}=(x_{j-1},x_{j})\), there hold

$$\begin{aligned}&(P^{-}u,v)_{K_{j}}=(u,v)_{K_{j}},\quad P^{-}u\left( x_{j}\right) =u\left( x_{j}\right) , \end{aligned}$$
(2.13)
$$\begin{aligned}&(P^{+}u,v)_{K_{j}}=(u,v)_{K_{j}},\quad P^{+}u\left( x_{j-1}\right) =u\left( x_{j-1}\right) . \end{aligned}$$
(2.14)

For Cartesian meshes in two dimension, we define the projection \(P^{-}\) for scalar functions on a two-dimensional rectangle element \(I\otimes J=[x_{i-1},x_{i}]\times [y_{j-1},y_{j}]\) as

$$\begin{aligned} P^{-}=P^{-}_{x}\otimes P^{-}_{y}, \end{aligned}$$
(2.15)

where the subscripts x and y indicate the one-dimensional projections defined by (2.13).

Denote the standard \(L^{2}\) projection in x and y direction by \(\pi _{x}\), \(\pi _{y}\), respectively. The projection \(\Pi ^{+}\) for a vector-valued function \({\varvec{\theta } }= (\theta _{1}(x, y),\theta _{2}(x, y))\) is defined by

$$\begin{aligned} \Pi ^{+}:\big [H^{1}(\Omega )\big ]^{2}\longrightarrow \big [{\mathcal {Q}}^{k}(I \otimes J)\big ]^{2},\,\,\,\, {\varvec{\theta } }\longmapsto \Pi ^{+}{\varvec{\theta } }=\big (P^{+}_{x}\otimes \pi _{y}\theta _{1},\pi _{x}\otimes P^{+}_{y}\theta _{2}\big ), \end{aligned}$$
(2.16)

where \(P^{+}_x\) and \(P^{+}_y\) are the one-dimensional projections defined in (2.14). Note that the projection \(\Pi ^{+}{\varvec{\theta } }\) satisfies the following properties, for any \(\varphi \in {\mathcal {Q}}^{k}(I \otimes J)\),

$$\begin{aligned} \int _{I}\int _{J}\big (\Pi ^{+}{\varvec{\theta } }-{\varvec{\theta } }\big )\cdot \nabla \varphi dydx&=0, \end{aligned}$$
(2.17a)
$$\begin{aligned} \int _{J}\big (\Pi ^{+}{\varvec{\theta } }(x_{i-1},y)-{\varvec{\theta } }(x_{i-1},y)\big )\cdot {{\varvec{n}}}\varphi \big (x_{i-1}^{+},y\big )dy&=0, \end{aligned}$$
(2.17b)
$$\begin{aligned} \int _{I}\big (\Pi ^{+}{\varvec{\theta } }(x,y_{j-1})-{\varvec{\theta } }(x,y_{j-1})\big )\cdot {{\varvec{n}}}\varphi \big (x,y_{j-1}^{+}\big )dx&=0. \end{aligned}$$
(2.17c)

In addition, we have the following approximation properties of the projections mentioned above,

$$\begin{aligned} |P^{-}u-u|_{H^{m}({\mathcal {T}}_{h})}+h^{1/2-m}\Vert P^{-}u-u\Vert _{{\mathcal {E}}_h}&\le Ch^{\min \{r,k+1\}-m}\Vert u\Vert _{H^{r}(\Omega )}, \end{aligned}$$
(2.18a)
$$\begin{aligned} |\Pi ^{+}{\varvec{\theta } }-{\varvec{\theta } }|_{H^{m}({\mathcal {T}}_{h})}+h^{1/2-m}\Vert (\Pi ^{+}{\varvec{\theta } }-{\varvec{\theta } })\cdot {{\varvec{n}}}\Vert _{{\mathcal {E}}_h}&\le Ch^{\min \{r,k+1\}-m}\Vert {\varvec{\theta } }\Vert _{H^{r}(\Omega )}, \end{aligned}$$
(2.18b)

for \(0\le m\le \min \{r,k+1\}\). Here the positive constant C is independent of h. The projection \(P^{-}\) on the Cartesian meshes defined by (2.15) has the following superconvergence property (see [4], Lemma 3.6). For more details about the projections, we refer readers to [1, 7].

Lemma 2.2

Suppose \((u,{\varvec{\theta } })\in H^{k+2}(\Omega )\otimes \Sigma _h\), then the projection \(P^{-}\) defined by (2.15) satisfies

$$\begin{aligned} |(u-P^{-}u,\nabla \cdot {\varvec{\theta } })-\langle u-\widehat{P^{-}u},{\varvec{\theta } }\cdot {{\varvec{n}}}\rangle |\le C h^{k+1}\Vert u\Vert _{H^{k+2}(\Omega )}\Vert {\varvec{\theta } }\Vert , \end{aligned}$$
(2.19)

where the “hat” term is the numerical flux.

2.2.2 Error Equations

Denote

$$\begin{aligned} e_{r}=r-r_{h},\,\,\,\,e_{{{\varvec{z}}}}={{\varvec{z}}}-{{\varvec{z}}}_{h} \end{aligned}$$

for \(r=u\), q, p and \({{\varvec{z}}}={{\varvec{s}}}\), \({\varvec{\omega }}\). Let P and \(\Pi \) be the projections defined in the above subsection. By adding and subtracting projections Pr and \(\Pi {{\varvec{z}}}\), we divide the error into

$$\begin{aligned} e_{r}=r-Pr +Pr-r_{h}=\eta _{r}+\zeta _{r},\,\,\,\,e_{{{\varvec{z}}}}={{\varvec{z}}}-\Pi {{\varvec{z}}}+\Pi {{\varvec{z}}}-{{\varvec{z}}}_{h}=\eta _{{{\varvec{z}}}}+\zeta _{{{\varvec{z}}}}. \end{aligned}$$

Here we take the projections \((P, \Pi ) = (P^{-}, P^{+})\) defined by (2.13)–(2.14) for the one-dimensional space, and take \((P, \Pi ) = (P^{-}, \Pi ^{+})\) defined by (2.15)–(2.16) for two-dimensional Cartesian meshes. Note that the exact solutions \(u, q, p, {{\varvec{s}}}, {\varvec{\omega }}\) of the problem (2.1) also satisfy (2.2). We obtain the error equations

$$\begin{aligned} ((\zeta _{u})_t,\varphi _1)_K&=H^{+}_{K}(\zeta _{{{\varvec{s}}}},\varphi _1)-\frac{a}{2}(e_q,\varphi _1)_K-(e_p,\varphi _1)_K-((\eta _{u})_t,\varphi _1)_K, \end{aligned}$$
(2.20a)
$$\begin{aligned} (\zeta _{{{\varvec{s}}}},{\varvec{\theta } }_1)_K&=-H^{-}_{K}(\zeta _q, {\varvec{\theta } }_1)-(\eta _{{{\varvec{s}}}},{\varvec{\theta } }_1)_K -H^{-}_{K}(\eta _q, {\varvec{\theta } }_1), \end{aligned}$$
(2.20b)
$$\begin{aligned} (\zeta _q, \varphi _2)_K&=-H^{+}_{K}(\zeta _{\varvec{\omega }}, \varphi _2)+\frac{a}{2}(e_u,\varphi _2)_K-(\eta _q, \varphi _2)_K, \end{aligned}$$
(2.20c)
$$\begin{aligned} (\zeta _{\varvec{\omega }},{\varvec{\theta } }_2)_K&=-H^{-}_{K}(\zeta _u,{\varvec{\theta } }_2)-(\eta _{\varvec{\omega }},{\varvec{\theta } }_2)_K-H^{-}_{K}(\eta _u,{\varvec{\theta } }_2), \end{aligned}$$
(2.20d)
$$\begin{aligned} (e_p,\varphi _3)_K&=(\Phi '(u)-\Phi '(u_h),\varphi _3)_K \end{aligned}$$
(2.20e)

for any \(\varphi _1, \varphi _2, \varphi _3 \in V_h\), and \({\varvec{\theta } }_1, {\varvec{\theta } }_2 \in \Sigma _h\). Here we use the property (2.17) of the projections, i.e., \(H^{+}_{K}(\eta _{{\varvec{s}}}, \varphi _1)=0\) and \(H^{+}_{K}(\eta _{\varvec{\omega }}, \varphi _2)=0\).

2.2.3 Optimal Error Estimates in \(L^{2}\) Norm

To deal with the nonlinear term in the analysis, we show the estimate for the numerical solution \(u_{h}\). Along the same idea as that in [10], the following lemma is required and thus we need to introduce the “discrete Laplacian” operator [21] firstly.

For the second-order elliptic problem with a periodic boundary condition

$$\begin{aligned} - \Delta u=f, \end{aligned}$$
(2.21)

where f is a given function, the LDG discrete Laplacian operator can be derived through its first order version

$$\begin{aligned} \nabla u&={{\varvec{z}}}, \\ -\nabla \cdot {{\varvec{z}}}&=f. \end{aligned}$$

Multiplying the first and second equations by the test functions \({\varvec{\theta } }\) and \(\vartheta \), respectively, and integrating on K, we define the LDG “discrete Laplacian” \(\Delta _h\) as follows: given \(u_h \in V_h\), find \(-\Delta _h u_h \in V_h\) such that

$$\begin{aligned} ({{\varvec{z}}}_h,{\varvec{\theta } })_K&=-(u_h, \nabla \cdot {\varvec{\theta } })_K+<{\widehat{u}}_h, {\varvec{\theta } }\cdot {{\varvec{n}}}>_{\partial K}, \end{aligned}$$
(2.22)
$$\begin{aligned} (-\Delta _hu_h, \vartheta )_K&=({{\varvec{z}}}_h,\nabla \vartheta )_K-<{\widehat{{{\varvec{z}}}}}_h \cdot {{\varvec{n}}}, \vartheta >_{\partial K}, \end{aligned}$$
(2.23)

where \({\widehat{u}}_h=(u_h)_L\), \({\widehat{{{\varvec{z}}}}}_h=({{\varvec{z}}}_h)_R\). The well-posedness of the operator can be obtained in \(V_h^0:=\{v\in V_h:(v,1)=0\}\).

Lemma 2.3

[21] For any \(u_h\in V_h^{0}\), we have

$$\begin{aligned} \Vert u_h\Vert _{\infty }\le C(1+\Vert {{\varvec{z}}}_{h}\Vert )\sqrt{\log (1+\Vert \Delta _{h}u_h\Vert )}, \end{aligned}$$

where \({{\varvec{z}}}_h\) satisfies (2.22).

Next we can obtain the estimate for the numerical solution.

Lemma 2.4

The solution of the LDG scheme (2.2) satisfies

$$\begin{aligned} \Vert u_{h}\Vert \le C, \,\,\,\,\Vert q_{h}\Vert \le C,\,\,\,\,\Vert {\varvec{\omega }}_{h}\Vert \le C,\,\,\,\,\Vert u_{h}\Vert _{\infty }\le C, \end{aligned}$$

where \(C>0\) is independent of h.

Proof

Applying Cauchy’s inequality, we have

$$\begin{aligned} \frac{d}{dt}(u_{h},u_{h})=2(u_h,(u_h)_t)\le 2(u_h,u_h)+\frac{1}{2}((u_h)_t,(u_h)_t). \end{aligned}$$

Thus the energy equality (2.12) turns out to be

$$\begin{aligned} \frac{d}{dt} \int _{\Omega } \left( \frac{1}{2} (q_h)^2+(u_h)^2+\Phi (u_h) \right) d{{\varvec{x}}}+\frac{1}{2}\int _{\Omega }((u_h)_t)^2 d{{\varvec{x}}}\le 2(u_h,u_h). \end{aligned}$$

By Gronwall’s inequality, we derive

$$\begin{aligned}&\left( \frac{1}{2} (q_h,q_h)+(u_h,u_h)+(\Phi (u_h),1) \right) (t)\\&\le e^{2t}\left( \frac{1}{2} (q_h,q_h)+(u_h,u_h)+(\Phi (u_h),1)\right) (0)\le C. \end{aligned}$$

where the last inequality holds because of the choice of the initial condition. By Young’s inequality, we have

$$\begin{aligned} \int _{\Omega } u_h^3d{{\varvec{x}}}\le \int _{\Omega }\left( \frac{\delta }{2}u_h^4+\frac{1}{2\delta }u_h^2\right) d{{\varvec{x}}}, \end{aligned}$$

which implies

$$\begin{aligned} \int _{\Omega }\Phi (u_h) d{{\varvec{x}}}\ge \left( \frac{1}{4}-\frac{g\delta }{6}\right) \int _{\Omega } u_h^4d{{\varvec{x}}}-\left( \frac{g}{6\delta }+\frac{\varepsilon }{2}\right) \int _{\Omega }u_h^2d{{\varvec{x}}}. \end{aligned}$$

Thus

$$\begin{aligned} \frac{1}{2} (q_h,q_h)+(u_h,u_h)+(\Phi (u_h),1)\!\ge \int _{\Omega } \left( \frac{1}{2}q_h^2+\left( 1-\frac{g}{6\delta }-\frac{\varepsilon }{2}\right) u_h^2+\!\left( \frac{1}{4}-\frac{g\delta }{6}\right) u_h^4\right) d{{\varvec{x}}}. \end{aligned}$$

Choose \(\delta \) such that

$$\begin{aligned} 1-\frac{g}{6\delta }-\frac{\varepsilon }{2}>0,\quad \frac{1}{4}-\frac{g\delta }{6}\ge 0, \end{aligned}$$

which yields

$$\begin{aligned} \Vert u_{h}\Vert \le C, \,\,\,\,\Vert q_{h}\Vert \le C. \end{aligned}$$

Taking the test functions \(\varphi _2=u_{h}\), \({\varvec{\theta } }_2={\varvec{\omega }}_h\) in (2.2c)–(2.2d) derives

$$\begin{aligned} (q_h,u_{h})_K&=-({\varvec{\omega }}_h, \nabla u_{h})_K+<{\widehat{{\varvec{\omega }}}}_h \cdot {{\varvec{n}}}, u_{h}>_{\partial K}+\frac{a}{2}(u_h,u_{h})_K,\\ ({\varvec{\omega }}_h,{\varvec{\omega }}_h)_K&=-(u_h, \nabla \cdot {\varvec{\omega }}_h)_K+<{\widehat{u}}_h, {\varvec{\omega }}_h \cdot {{\varvec{n}}}>_{\partial K}. \end{aligned}$$

Adding them together and summing up over K, we get

$$\begin{aligned} \Vert {\varvec{\omega }}_h\Vert ^{2}=\frac{a}{2}(u_h,u_{h})-(q_h,u_{h})\le \frac{a+1}{2}\Vert u_h\Vert ^{2}+\frac{1}{2}\Vert q_h\Vert ^{2}\le C. \end{aligned}$$

Note that the “discrete Laplacian” operator \(\Delta _{h}u_h\) is defined by

$$\begin{aligned} (\Delta _{h}u_h,v)_K&=-({\varvec{\omega }}_h, \nabla v)_K+<{\widehat{{\varvec{\omega }}}}_h \cdot {{\varvec{n}}}, v>_{\partial K}\\&=(q_h,v)_K-\frac{a}{2}(u_h,v)_K, \,\,\,\,v\in V_h, \end{aligned}$$

where the second equality is by (2.2c). Taking \(v=\Delta _{h}u_h\) in the above equation leads to

$$\begin{aligned} \Vert \Delta _{h}u_h\Vert \le \frac{a}{2}\Vert u_{h}\Vert +\Vert q_{h}\Vert \le C. \end{aligned}$$

Applying Lemma 2.3, we obtain

$$\begin{aligned} \Vert u_{h}\Vert _{\infty }\le C(1+\Vert {\varvec{\omega }}_{h}\Vert )\sqrt{\log (1+\Vert \Delta _{h}u_h\Vert )}\le C, \end{aligned}$$

which completes the proof. \(\square \)

We would like to assume the exact solution of Eq. (1.3) has the following smoothness:

$$\begin{aligned} u\in L^{\infty }(0,T; H^{k+4}),\quad u_t\in L^{\infty }(0,T; H^{k+3}). \end{aligned}$$
(2.24)

Now we are ready to derive the optimal error estimate of the semi-discrete LDG scheme (2.2).

Theorem 2.5

Let \(u_{h}\) be the numerical solution of the scheme (2.2), and u be the exact solution of equation (1.3). Suppose u satisfies the smoothness assumption (2.24), then there exists a constant C, such that

$$\begin{aligned} \Vert u(\cdot ,T)-u_{h}(\cdot ,T)\Vert \le Ch^{k+1}, \end{aligned}$$
(2.25)

where C is independent of h, \(u_{h}\) and dependent on k, the final time T, \(\Vert u\Vert _{L^{\infty }(0,T; H^{k+4}(\Omega ))}\) and \(\Vert u_t\Vert _{L^{\infty }(0,T; H^{k+3}(\Omega ))}\).

Proof

Taking the test functions \(\varphi _1=\zeta _{u}\), \({\varvec{\theta } }_1=\zeta _{{\varvec{\omega }}}\), \(\varphi _2=\zeta _q\), \({\varvec{\theta } }_2=-\zeta _{{{\varvec{s}}}}\), \(\varphi _3=-\zeta _{u}\) in the error Eq. (2.20), respectively, and adding them together, we have

$$\begin{aligned} ((\zeta _{u})_t,\zeta _{u})_K+(\zeta _q, \zeta _q)_K=RHS, \end{aligned}$$

where

$$\begin{aligned} RHS=&-((\eta _{u})_t,\zeta _{u})_K-(\eta _{{{\varvec{s}}}},\zeta _{{\varvec{\omega }}})_K -(\eta _q, \zeta _q)_K+(\eta _{\varvec{\omega }},\zeta _{{{\varvec{s}}}})_K-\frac{a}{2}(\eta _q,\zeta _{u})_K+\frac{a}{2}(\eta _u,\zeta _q)_K\\&+H^{+}_{K}(\zeta _{{{\varvec{s}}}},\zeta _{u})+H^{-}_{K}(\zeta _u,\zeta _{{{\varvec{s}}}})-H^{-}_{K}(\zeta _q, \zeta _{{\varvec{\omega }}})-H^{+}_{K}(\zeta _{\varvec{\omega }}, \zeta _q) \\&-H^{-}_{K}(\eta _q, \zeta _{{\varvec{\omega }}})+H^{-}_{K}(\eta _u,\zeta _{{{\varvec{s}}}})-(\Phi '(u)-\Phi '(u_h),\zeta _{u})_K. \end{aligned}$$

Summing up over K and by the property (2.4), we obtain the first energy equality in the form of \(\zeta _{u}\) and \(\zeta _{q}\),

$$\begin{aligned} ((\zeta _{u})_t,\zeta _{u})+(\zeta _q, \zeta _q)={S_1}, \end{aligned}$$
(2.26)

where

$$\begin{aligned} S_1=&-((\eta _{u})_t,\zeta _{u})-(\eta _{{{\varvec{s}}}},\zeta _{{\varvec{\omega }}}) -(\eta _q, \zeta _q)+(\eta _{\varvec{\omega }},\zeta _{{{\varvec{s}}}})-\frac{a}{2}(\eta _q,\zeta _{u})+\frac{a}{2}(\eta _u,\zeta _q)\\&-H^{-}(\eta _q, \zeta _{{\varvec{\omega }}})+H^{-}(\eta _u,\zeta _{{{\varvec{s}}}})-(\Phi '(u)-\Phi '(u_h),\zeta _{u}). \end{aligned}$$

Taking the time derivative of (2.20d), we have

$$\begin{aligned} ((\zeta _{\varvec{\omega }})_t,{\varvec{\theta } }_2)_K&=-H^{-}_{K}((\zeta _u)_t,{\varvec{\theta } }_2)-((\eta _{\varvec{\omega }})_t,{\varvec{\theta } }_2)-H^{-}_{K}((\eta _u)_t,{\varvec{\theta } }_2). \end{aligned}$$
(2.27)

Choosing test functions \(\varphi _1=-\zeta _{q}\), \({\varvec{\theta } }_1=\zeta _{{{\varvec{s}}}}\), \(\varphi _2=(\zeta _u)_t\) in the error Eqs. (2.20a)–(2.20c), \({\varvec{\theta } }_2=\zeta _{{\varvec{\omega }}}\) in (2.27), and \(\varphi _3=\zeta _{q}\) in (2.20e), we derive

$$\begin{aligned} ((\zeta _{u})_t,-\zeta _{q})_K&=H^{+}_{K}(\zeta _{{{\varvec{s}}}},-\zeta _{q})-\frac{a}{2}(e_q,-\zeta _{q})_K-(e_p,-\zeta _{q})_K-((\eta _{u})_t,-\zeta _{q})_K, \\ (\zeta _{{{\varvec{s}}}},\zeta _{{{\varvec{s}}}})_K&=-H^{-}_{K}(\zeta _q, \zeta _{{{\varvec{s}}}})-(\eta _{{{\varvec{s}}}},\zeta _{{{\varvec{s}}}})_K -H^{-}_{K}(\eta _q, \zeta _{{{\varvec{s}}}}),\\ (\zeta _q, (\zeta _u)_t)_K&=-H^{+}_{K}(\zeta _{\varvec{\omega }}, (\zeta _u)_t)+\frac{a}{2}(e_u,(\zeta _u)_t)_K-(\eta _q, (\zeta _u)_t)_K,\\ ((\zeta _{\varvec{\omega }})_t,\zeta _{{\varvec{\omega }}})_K&=-H^{-}_{K}((\zeta _u)_t,\zeta _{{\varvec{\omega }}})-((\eta _{\varvec{\omega }})_t,\zeta _{{\varvec{\omega }}})_K-H^{-}_{K}((\eta _u)_t,\zeta _{{\varvec{\omega }}}),\\ (e_p,\zeta _{q})_K&=(\Phi '(u)-\Phi '(u_h),\zeta _{q})_K. \end{aligned}$$

Adding them together, summing up over K and by the property (2.4), we obtain the second energy equality in the form of \(\zeta _{{{\varvec{s}}}}\) and \(\zeta _{{\varvec{\omega }}}\),

$$\begin{aligned} ((\zeta _{\varvec{\omega }})_t,\zeta _{{\varvec{\omega }}})+(\zeta _{{{\varvec{s}}}},\zeta _{{{\varvec{s}}}})-\frac{a}{2}(\zeta _q,\zeta _{q})-\frac{a}{2}(\zeta _u,(\zeta _u)_t)={S_2}, \end{aligned}$$
(2.28)

where

$$\begin{aligned} S_2&=((\eta _{u})_t,\zeta _{q})-(\eta _{{{\varvec{s}}}},\zeta _{{{\varvec{s}}}})-(\eta _q, (\zeta _u)_t)-((\eta _{\varvec{\omega }})_t,\zeta _{{\varvec{\omega }}})+\frac{a}{2}(\eta _q,\zeta _{q})+\frac{a}{2}(\eta _u,(\zeta _u)_t) \\&\quad -H^{-}(\eta _q, \zeta _{{{\varvec{s}}}})-H^{-}((\eta _u)_t,\zeta _{{\varvec{\omega }}})+(\Phi '(u)-\Phi '(u_h),\zeta _{q}). \end{aligned}$$

Then, \( a \times (2.26)+ (2.28)\) gives

$$\begin{aligned} \frac{a}{2}((\zeta _{u})_t,\zeta _{u})+\frac{a}{2}(\zeta _q, \zeta _q)+((\zeta _{\varvec{\omega }})_t,\zeta _{{\varvec{\omega }}})+(\zeta _{{{\varvec{s}}}},\zeta _{{{\varvec{s}}}})=T_{1}+T_{2}+T_{3}+T_{4}, \end{aligned}$$
(2.29)

where

$$\begin{aligned} T_{1}=&-a((\eta _{u})_t,\zeta _{u})-a(\eta _{{{\varvec{s}}}},\zeta _{{\varvec{\omega }}}) -a(\eta _q, \zeta _q)+a(\eta _{\varvec{\omega }},\zeta _{{{\varvec{s}}}})-\frac{a^{2}}{2}(\eta _q,\zeta _{u})+\frac{a^{2}}{2}(\eta _u,\zeta _q)\\&+((\eta _{u})_t,\zeta _{q})-(\eta _{{{\varvec{s}}}},\zeta _{{{\varvec{s}}}})-((\eta _{\varvec{\omega }})_t,\zeta _{{\varvec{\omega }}})+\frac{a}{2}(\eta _q,\zeta _{q}),\\ T_{2}=&-(\eta _q, (\zeta _u)_t)+\frac{a}{2}(\eta _u,(\zeta _u)_t),\\ T_3=&-aH^{-}(\eta _q, \zeta _{{\varvec{\omega }}})+aH^{-}(\eta _u,\zeta _{{{\varvec{s}}}}) -H^{-}(\eta _q, \zeta _{{{\varvec{s}}}})-H^{-}((\eta _u)_t,\zeta _{{\varvec{\omega }}}).\\ T_4=&-a(\Phi '(u)-\Phi '(u_h),\zeta _{u})+(\Phi '(u)-\Phi '(u_h),\zeta _{q}). \end{aligned}$$

By Cauchy–Schwarz inequality, the approximation properties (2.18) and the linearity of the projections, we get

$$\begin{aligned} T_{1}\le Ch^{k+1}(\Vert \zeta _{u}\Vert +\Vert \zeta _{q}\Vert +\Vert \zeta _{{{\varvec{s}}}}\Vert +\Vert \zeta _{{\varvec{\omega }}}\Vert ). \end{aligned}$$

As for the term \(T_3\), Lemma 2.2 implies that

$$\begin{aligned} T_{3}\le Ch^{k+1}(\Vert \zeta _{{{\varvec{s}}}}\Vert +\Vert \zeta _{{\varvec{\omega }}}\Vert ). \end{aligned}$$

Considering the nonlinear term \(T_4\), we apply Lagrange’s mean value theorem to obtain

$$\begin{aligned} T_4&=-a(\Phi ''(\xi )(u-u_h),\zeta _{u})+(\Phi ''(\xi )(u-u_h),\zeta _{q})\\&\le C \biggl (|(u-u_h,\zeta _{u})|+|(u-u_h,\zeta _{q})|\biggr ), \end{aligned}$$

where \(\xi \) is between u and \(u_{h}\). Here we use the fact that \(\Vert u_h\Vert _{\infty }\le C\) derived in Lemma 2.4 and \(\Phi (u)\) is a polynomial of u. Note that \(u-u_h=\zeta _{u}+\eta _{u}\). The estimate of \(T_4\) turns out to be

$$\begin{aligned} T_4&\le C (\Vert \eta _{u}\Vert \Vert \zeta _{u}\Vert +\Vert \zeta _{u}\Vert ^{2}+\Vert \eta _{u}\Vert \Vert \zeta _{q}\Vert +\Vert \zeta _{u}\Vert \Vert \zeta _{q}\Vert )\\&\le C\Vert \zeta _{u}\Vert ^{2}+\frac{a}{4}\Vert \zeta _{q}\Vert ^{2}+Ch^{2k+2}. \end{aligned}$$

Here the approximation properties (2.18) are used again. Combine the estimates of \(T_1\), \(T_3\), \(T_4\) and the energy equality (2.29) together to get

$$\begin{aligned}&\frac{d}{dt}\left( \frac{a}{4}\Vert \zeta _{u}\Vert ^{2}+\frac{1}{2}\Vert \zeta _{\varvec{\omega }}\Vert ^{2}\right) +\frac{a}{2}\Vert \zeta _q\Vert ^2+\Vert \zeta _{{{\varvec{s}}}}\Vert ^{2}\nonumber \\&\quad \le C\Vert \zeta _{u}\Vert ^{2}+\frac{1}{4}\Vert \zeta _{\varvec{\omega }}\Vert ^{2}+\frac{a}{2}\Vert \zeta _{q}\Vert ^{2}+\Vert \zeta _{{{\varvec{s}}}}\Vert ^{2}+Ch^{2k+2}+T_2. \end{aligned}$$
(2.30)

For the term \(T_2\), using integration by parts with respect to t, we have

$$\begin{aligned} \int _{0}^{T}T_2dt&=\int _{0}^{T}\left[ \frac{a}{2}(\eta _u,(\zeta _u)_t)-(\eta _q, (\zeta _u)_t)\right] dt\\&=\left. \left( \frac{a}{2}(\eta _u,\zeta _u)-(\eta _q, \zeta _u)\right) \right| _{0}^{T}-\int _{0}^{T}\left[ \frac{a}{2}((\eta _u)_t,\zeta _u)-((\eta _q)_t, \zeta _u)\right] dt\\&\le \frac{a}{8}\Vert \zeta _{u}(T)\Vert ^{2}+\frac{a}{8}\Vert \zeta _{u}(0))\Vert ^{2}+\int _{0}^{T}\Vert \zeta _{u}\Vert ^{2}dt+Ch^{2k+2}. \end{aligned}$$

Integrating (2.30) with respect to t to obtain

$$\begin{aligned}&\frac{a}{4}\Vert \zeta _{u}(T)\Vert ^{2}+\frac{1}{2}\Vert \zeta _{\varvec{\omega }}(T)\Vert ^{2}\nonumber \\&\quad \le \int _{0}^{T}\left( C\Vert \zeta _{u}\Vert ^{2}+\frac{1}{4}\Vert \zeta _{\varvec{\omega }}\Vert ^{2}+T_2\right) dt+\frac{a}{4}\Vert \zeta _{u}(0)\Vert ^{2}+\frac{1}{2}\Vert \zeta _{\varvec{\omega }}(0)\Vert ^{2}+Ch^{2k+2}. \end{aligned}$$

With the special choice of the initial condition, it is easy to see that

$$\begin{aligned} \Vert \zeta _{u}(0)\Vert \le Ch^{k+1},\,\,\Vert \zeta _{{\varvec{\omega }}}(0)\Vert \le Ch^{k+1}. \end{aligned}$$

Thus

$$\begin{aligned} \frac{a}{8}\Vert \zeta _{u}(T)\Vert ^{2}+\frac{1}{2}\Vert \zeta _{\varvec{\omega }}(T)\Vert ^{2}\le \int _{0}^{T}\left( C\Vert \zeta _{u}\Vert ^{2}+\frac{1}{4}\Vert \zeta _{\varvec{\omega }}\Vert ^{2}\right) dt+Ch^{2k+2}. \end{aligned}$$

Finally, the optimal error estimate (2.25) follows by using Gronwall’s inequality and triangle inequality. \(\square \)

3 Time Discretization

In this section, we first describe a first-order time stepping scheme for the Swift–Hohenberg equation, which is based on the SAV approach. Coupled with the LDG spatial discretization, we then achieve the fully-discrete LDG scheme and prove its energy stability and optimal error estimates. Lastly, we employ the semi-implicit SDC method iteratively to improve the temporal accuracy.

3.1 A Linear Scheme in Time

In order to develop a linear and energy stable scheme, we first describe the SAV approach [23] briefly. Let \(E_1(u)=\int _{\Omega } \Phi (u) d{{\varvec{x}}}\). Then we introduce the scalar variable \(r(t)=\sqrt{E_1(u)+B}\), where B is a constant to ensure \(E_1(u)+B\ge 0\).

Using the variable r, the energy functional (1.1) can be recast as

$$\begin{aligned} E(u,r)=\int _{\Omega } \left( \frac{1}{2}(\Delta u+\frac{a}{2} u)^2\right) d{{\varvec{x}}}+r^2-B. \end{aligned}$$
(3.1)

Then, we have the following equivalent equation

$$\begin{aligned} u_t&=-\left( \Delta +\frac{a}{2}\right) ^2 u-\frac{r}{\sqrt{E_1(u)+B}} \Phi '(u), \end{aligned}$$
(3.2)
$$\begin{aligned} r_t&=\frac{1}{2\sqrt{E_1(u)+B}}\int _{\Omega } \Phi '(u)u_t d{{\varvec{x}}}. \end{aligned}$$
(3.3)

The initial conditions are

$$\begin{aligned} u(t=0)=u_0, \;\;\;\; r(t=0)=\sqrt{E_1(u_0)+B}. \end{aligned}$$

Further, the equivalent equation preserves an energy law, i.e.

$$\begin{aligned} \frac{d}{dt}E(u,r)=-\int _{\Omega } (u_t)^2 d{{\varvec{x}}}\le 0. \end{aligned}$$
(3.4)

Obviously, we hope to construct a linear scheme that preserve the energy law (3.4) in the discrete sense. A first-order SAV scheme can be given as follows

$$\begin{aligned} \frac{u^{n+1}-u^n}{\Delta t}&=-\left( \Delta +\frac{a}{2}\right) ^2 u^{n+1}-\frac{r^{n+1}}{\sqrt{E_1(u^n)+B}} \Phi '(u^n), \end{aligned}$$
(3.5)
$$\begin{aligned} \frac{r^{n+1}-r^n}{\Delta t}&=\frac{1}{2\sqrt{E_1(u^n)+B}}\int _{\Omega } \Phi '(u^n)\frac{u^{n+1}-u^n}{\Delta t} d{{\varvec{x}}}. \end{aligned}$$
(3.6)

Since (3.6) is a simple algebraic equation, we can rewrite it as

$$\begin{aligned} r^{n+1}=r^n+\frac{1}{2\sqrt{E_1(u^n)+B}}\int _{\Omega } \Phi '(u^n)(u^{n+1}-u^n) d{{\varvec{x}}}. \end{aligned}$$

Denote

$$\begin{aligned} b^n=\Phi '(u^n)/\sqrt{E_1(u^n)+B}. \end{aligned}$$

Then the scheme (3.5) can be written as

$$\begin{aligned} \frac{u^{n+1}-u^n}{\Delta t}=-\left( \Delta +\frac{a}{2}\right) ^2 u^{n+1}-b^n\left( r^n+\frac{1}{2}\int _{\Omega }b^n(u^{n+1}-u^n) d{{\varvec{x}}}\right) . \end{aligned}$$
(3.7)

Now, we show an efficient implementation of the scheme (3.5). We derive from (3.7) that

$$\begin{aligned} \left( I+\Delta t\left( \Delta +\frac{a}{2}\right) ^2\right) u^{n+1}+\frac{\Delta t}{2}b^n(b^n,u^{n+1})=u^n-\Delta t b^n r^n+\frac{\Delta t}{2}b^n(b^n,u^n). \end{aligned}$$
(3.8)

Denote the right hand side of (3.8) by \(c^n\). Multiplying (3.8) with \((I+\Delta t(\Delta +\frac{a}{2})^2)^{-1}\), then taking the inner product with \(b^n\), we obtain

$$\begin{aligned} (b^n,u^{n+1})+\frac{\Delta t}{2} \gamma ^n (b^n,u^{n+1})=\left( b^n,\left( I+\Delta t\left( \Delta +\frac{a}{2}\right) ^2\right) ^{-1}c^n\right) , \end{aligned}$$
(3.9)

where \(\gamma ^n=(b^n,(I+\Delta t(\Delta +\frac{a}{2})^2)^{-1}b^n)\). Hence

$$\begin{aligned} (b^n,u^{n+1})=\frac{(b^n,(I+\Delta t(\Delta +\frac{a}{2})^2)^{-1}c^n)}{1+\Delta t \gamma ^n/2}. \end{aligned}$$
(3.10)

The details related to the scheme implementation are summarized in the following algorithm.

Step 1:

Compute \(b^n\) and \(c^n\);

Step 2:

Compute \((b^n,u^{n+1})\) by (3.10);

Step 3:

Compute \(u^{n+1}\) by (3.8) and \(r^{n+1}\) by (3.6), then goto the next step.

3.2 The Fully-Discrete LDG Scheme and Its Energy Stability

In this subsection, we will develop the LDG scheme to solve the linear scheme (3.5)–(3.6). Firstly we rewrite it as a first order system

$$\begin{aligned} \frac{u^{n+1}-u^n}{\Delta t}&= -\nabla \cdot {{\varvec{s}}}^{n+1}-\frac{a}{2} q^{n+1}-r^{n+1}b^n, \end{aligned}$$
(3.11a)
$$\begin{aligned} {{\varvec{s}}}^{n+1}&=\nabla q^{n+1}, \end{aligned}$$
(3.11b)
$$\begin{aligned} q^{n+1}&= \nabla \cdot {\varvec{\omega }}^{n+1} +\frac{a}{2} u^{n+1}, \end{aligned}$$
(3.11c)
$$\begin{aligned} {\varvec{\omega }}^{n+1}&= \nabla u^{n+1}. \end{aligned}$$
(3.11d)

The LDG scheme to solve the linear scheme (3.5)–(3.6) becomes the following: find \(u_{h}^{n+1}, q_{h}^{n+1}\) \(\in V_h\) and \({{\varvec{s}}}_{h}^{n+1}, {\varvec{\omega }}_{h}^{n+1} \in \Sigma _h\) such that, for all test functions \(\varphi _1, \varphi _2 \in V_h\) and \({\varvec{\theta } }_1, {\varvec{\theta } }_2 \in \Sigma _h\), we have

$$\begin{aligned} \frac{1}{\Delta t}(u_{h}^{n+1}-u^n_{h},\varphi _1)_K&=H^{+}_{K}({{\varvec{s}}}_{h}^{n+1},\varphi _1)-\frac{a}{2}(q_{h}^{n+1},\varphi _1)_K-(r^{n+1}_{h}b^n_{h},\varphi _1)_K, \end{aligned}$$
(3.12a)
$$\begin{aligned} ({{\varvec{s}}}^{n+1}_{h},{\varvec{\theta } }_1)_K&=-H^{-}_{K}(q^{n+1}_{h},{\varvec{\theta } }_1), \end{aligned}$$
(3.12b)
$$\begin{aligned} (q^{n+1}_{h}, \varphi _2)_K&=-H^{+}_{K}({\varvec{\omega }}^{n+1}_{h},\varphi _2)+\frac{a}{2}(u_{h}^{n+1},\varphi _2)_K, \end{aligned}$$
(3.12c)
$$\begin{aligned} ({\varvec{\omega }}^{n+1}_{h},{\varvec{\theta } }_2)_K&=-H^{-}_{K}(u^{n+1}_{h},{\varvec{\theta } }_2), \end{aligned}$$
(3.12d)

where

$$\begin{aligned} r^{n+1}_{h}&=r^n_{h}+\frac{1}{2\sqrt{E_1(u^n_{h})+B}}\int _{\Omega } \Phi '(u^n_{h})(u^{n+1}_{h}-u^n_{h}) d{{\varvec{x}}},\nonumber \\ b^n_{h}&=\Phi '(u^n_{h})/\sqrt{E_1(u^n_{h})+B}. \end{aligned}$$
(3.13)

The numerical fluxes are

$$\begin{aligned} {\widehat{{{\varvec{s}}}}}_{h}^{n+1}=({{\varvec{s}}}^{n+1}_{h})_{R},\;\;\;\;\;\;\; {\widehat{q}}^{n+1}_{h}=(q^{n+1}_{h})_{L},\;\;\;\;\;\;\; {\widehat{{\varvec{\omega }}}}_{h}^{n+1}=({\varvec{\omega }}^{n+1}_{h})_{R},\;\;\;\;\;\;\; {\widehat{u}}^{n+1}_{h}=(u^{n+1}_{h})_{L}.\nonumber \\ \end{aligned}$$
(3.14)

Next, we will prove its energy dissipation.

Proposition 3.1

(Energy stability for the fully-discrete LDG scheme). The solution to the LDG scheme (3.12) with the numerical fluxes (3.14) satisfies the energy stability

$$\begin{aligned} E_h(q^{n+1}_{h},r^{n+1}_{h})+\frac{1}{\Delta t} \int _{\Omega } (u^{n+1}_{h}-u^n_{h})^2 d{{\varvec{x}}}\le E_h(q^n_{h},r^n_{h}), \end{aligned}$$
(3.15)

where

$$\begin{aligned} E_h(q_h,r_h)=\frac{1}{2}\int _{\Omega } q_h^2 d{{\varvec{x}}}+r_h^2. \end{aligned}$$

Proof

Let \({\mathcal {D}} u\) denote \(u^{n+1}_{h}-u^n_{h}\). For (3.12c) and (3.12d), subtracting the equations at time level \(t^n\) from the equations at time level \(t^{n+1}\), choosing the test function \(\varphi _2=q^{n+1}_{h}\) and \({\varvec{\theta } }_2=-{{\varvec{s}}}^{n+1}_{h}\), we obtain

$$\begin{aligned} ({\mathcal {D}}q, q^{n+1}_{h})_K&=-H^{+}_{K}({\mathcal {D}}{\varvec{\omega }}, q^{n+1}_{h})+\frac{a}{2}({\mathcal {D}}u,q^{n+1}_{h})_K, \end{aligned}$$
(3.16)
$$\begin{aligned} -({\mathcal {D}}{\varvec{\omega }},{{\varvec{s}}}^{n+1}_{h})_K&=H^{-}_{K}({\mathcal {D}}u, {{\varvec{s}}}^{n+1}_{h}), \end{aligned}$$
(3.17)

where \({\mathcal {D}}q:=q^{n+1}-q^n\) and \({\mathcal {D}}{\varvec{\omega }}:={\varvec{\omega }}^{n+1}-{\varvec{\omega }}^n\). For (3.12a) and (3.12b), taking the test functions as \(\varphi _1={\mathcal {D}}u\) and \({\varvec{\theta } }_1={\mathcal {D}} {\varvec{\omega }}\), we have

$$\begin{aligned} \frac{1}{\Delta t}({\mathcal {D}}u,{\mathcal {D}}u)_K&=H^{+}_{K}({{\varvec{s}}}^{n+1}_{h},{\mathcal {D}}u)-\frac{a}{2}(q_{h}^{n+1},{\mathcal {D}}u)_K-(r_{h}^{n+1}b^{n}_h,{\mathcal {D}}u)_K, \end{aligned}$$
(3.18)
$$\begin{aligned} ({{\varvec{s}}}^{n+1}_{h},{\mathcal {D}} {\varvec{\omega }})_K&=-H^{-}_{K}(q^{n+1}_{h}, {\mathcal {D}} {\varvec{\omega }}). \end{aligned}$$
(3.19)

Now combining Eqs. (3.16)–(3.19), we find

$$\begin{aligned}&({\mathcal {D}}q, q^{n+1}_{h})_K+\frac{1}{\Delta t}({\mathcal {D}}u,{\mathcal {D}}u)_K+(r_{h}^{n+1}b^{n}_h,{\mathcal {D}}u)_K\nonumber \\&\quad = -H^{+}_{K}({\mathcal {D}}{\varvec{\omega }}, q^{n+1}_{h})-H^{-}_{K}(q^{n+1}_{h}, {\mathcal {D}} {\varvec{\omega }}) +H^{-}_{K}({\mathcal {D}}u, {{\varvec{s}}}^{n+1}_{h})+H^{+}_{K}({{\varvec{s}}}^{n+1}_{h},{\mathcal {D}}u). \end{aligned}$$
(3.20)

Summing up (3.20) over K and by the property (2.4), we get

$$\begin{aligned} \int _{\Omega } {\mathcal {D}}q q_{h}^{n+1} d{{\varvec{x}}}+\frac{1}{\Delta t}\int _{\Omega }({\mathcal {D}}u)^2 d{{\varvec{x}}}+\int _{\Omega }r_{h}^{n+1}b^{n}_h {\mathcal {D}}u d{{\varvec{x}}}=0. \end{aligned}$$
(3.21)

Multiplying the Eq. (3.13) with \(2 r^{n+1}_{h}\), we obtain

$$\begin{aligned} 2 r^{n+1}_{h}(r^{n+1}_{h}-r^n_{h})=\int _{\Omega } r^{n+1}_{h}b_{h}^{n}{\mathcal {D}} u d{{\varvec{x}}}. \end{aligned}$$
(3.22)

Combining Eqs. (3.21) and (3.22) and using the identity

$$\begin{aligned} a(a-b)=\frac{1}{2}(a^2-b^2+(a-b)^2), \end{aligned}$$

we have the discrete energy stability

$$\begin{aligned} \frac{1}{2} \int _{\Omega } (q^{n+1}_{h})^2 d{{\varvec{x}}}+(r^{n+1}_{h})^2+\frac{1}{\Delta t} \int _{\Omega } ({\mathcal {D}}u)^2 d{{\varvec{x}}}\le \frac{1}{2} \int _{\Omega } (q^{n}_{h})^2 d{{\varvec{x}}}+(r^{n}_{h})^2. \end{aligned}$$

\(\square \)

Note that

$$\begin{aligned} \Vert u_{h}^{n+1}\Vert ^2\le \Vert u_{h}^{n+1}-u_h^n\Vert ^2+\Vert u_{h}^{n}\Vert ^2. \end{aligned}$$

It follows from the discrete energy stability (3.15) that

$$\begin{aligned} \frac{1}{2} \Vert q_{h}^{n+1}\Vert ^2+(r^{n+1}_{h})^2+\frac{1}{\Delta t} \Vert u_{h}^{n+1}\Vert ^2 \le \frac{1}{2} \Vert q_{h}^{n}\Vert ^2+(r^{n}_{h})^2+\frac{1}{\Delta t} \Vert u_{h}^{n}\Vert ^2. \end{aligned}$$

Then by special initial solutions, we can easily get

$$\begin{aligned} \Vert u_{h}^{n}\Vert \le C,\;\;\;\;\Vert u_{h}^{n}\Vert _{\infty }\le C. \end{aligned}$$
(3.23)

The second inequality can be proved by the essentially same procedure as that in Lemma 2.4.

3.3 Optimal Error Estimates of the Fully-Discrete LDG Scheme

To obtain the optimal error estimates of the first-order fully-discrete LDG scheme (3.12), we would like to introduce the elliptic projection [7], which plays an important role in our analysis. Firstly, we assume the exact solution of Eq. (1.3) is sufficiently smooth with bounded derivatives,

$$\begin{aligned} u\in L^{\infty }(0,T;H^{k+4}),\;\;u_{t}\in L^{\infty }(0,T;H^{k+1}),\;\;u_{tt}\in L^{\infty }(0,T;L^{2}). \end{aligned}$$
(3.24)

Then suppose \(u,{{\varvec{s}}},q,{\varvec{\omega }}\) are the exact solution of the first order system (2.1), we define the elliptic projection \(U_{h},Q_{h}\in V_h\), \(\varvec{S}_{h}, \varvec{W}_{h}\in \Sigma _{h}\) satisfying

$$\begin{aligned} H^{+}(\varvec{S}_h,\varphi _1)&=H^{+}({{\varvec{s}}},\varphi _1), \end{aligned}$$
(3.25a)
$$\begin{aligned} (\varvec{S}_h,{\varvec{\theta } }_1)+H^{-}(Q_h,{\varvec{\theta } }_1)&=({{\varvec{s}}},{\varvec{\theta } }_1)+H^{-}(q,{\varvec{\theta } }_1), \end{aligned}$$
(3.25b)
$$\begin{aligned} (\varvec{Q}_h,\varphi _2)+H^{+}(\varvec{W}_h,\varphi _2)&=(q,\varphi _2)+H^{+}({\varvec{\omega }},\varphi _2), \end{aligned}$$
(3.25c)
$$\begin{aligned} (\varvec{W}_h,{\varvec{\theta } }_2)+H^{-}(U_h,{\varvec{\theta } }_2)&=({\varvec{\omega }},{\varvec{\theta } }_2)+H^{-}(u,{\varvec{\theta } }_2), \end{aligned}$$
(3.25d)

for any \(\varphi _1,\varphi _2\in V_h\), \({\varvec{\theta } }_1,{\varvec{\theta } }_2\in \Sigma _{h}\). Following [7], we assume \((u-U_h,1)=0\) to ensure the problem (3.25) is well-defined. In addition, we consider the adjoint problem

$$\begin{aligned} {\varvec{\theta } }=\nabla \sigma ,\;\;\varphi =\nabla \cdot {\varvec{\theta } },\;\;{\varvec{\zeta } }=\nabla \varphi ,\;\;z=\nabla \cdot {\varvec{\zeta } }, \end{aligned}$$
(3.26)

and assume the elliptic regularity result (see, e.g., [7])

$$\begin{aligned} \Vert {\varvec{\zeta } }\Vert _{H^1(\Omega )}+\Vert \varphi \Vert _{H^2(\Omega )}+\Vert {\varvec{\theta } }\Vert _{H^3(\Omega )}+\Vert \sigma \Vert _{H^4(\Omega )}\le C_{*}\Vert z\Vert , \end{aligned}$$
(3.27)

then we derive the approximation property of the elliptic projection.

Lemma 3.2

Suppose u, q are the exact solution of the first order system (2.1) and \(U_h,Q_h\) are the elliptic projection (3.25), there hold

$$\begin{aligned} \Vert u-U_h\Vert +\Vert q-Q_h\Vert \le Ch^{k+1}, \end{aligned}$$
(3.28)

where \(C>0\) is independent of h, \(\Delta t\), but depends on the regularity of u and the elliptic regularity constant \(C_{*}\).

Remark 3.3

The proof will be obtained by the aid of the duality argument and the projections defined by (2.13)–(2.14) for the one-dimensional space and (2.15)–(2.16) for two-dimensional Cartesian meshes. It is very similar to [7], in which the \(L^{2}\) projection for triangular meshes is considered and only the optimal error estimate of u in (3.28) is obtained. The details of the proof will be shown in the Appendix.

Denote the error between the exact solution and the numerical solution of the fully-discrete LDG scheme (3.12) by \(e_{u}^{n}=u({{\varvec{x}}},t^n)-u_{h}^{n}\), \(e_{{{\varvec{s}}}}^{n}={{\varvec{s}}}({{\varvec{x}}},t^n)-{{\varvec{s}}}_{h}^{n}\). As usual, we divide the error into

$$\begin{aligned} e_{u}^{n}=u({{\varvec{x}}},t^n)-U_{h}^{n} +U_{h}^{n}-u_{h}^{n}=R_{u}^{n}+\xi _{u}^{n},\,\,\,\,e_{{{\varvec{s}}}}^{n}={{\varvec{s}}}({{\varvec{x}}},t^n)-\varvec{S}_h^n+\varvec{S}_h^n-{{\varvec{s}}}_{h}^{n}=R_{{{\varvec{s}}}}^{n}+\xi _{{{\varvec{s}}}}^{n}, \end{aligned}$$

where \(U_{h}^{n}\), \(\varvec{S}_h^n\) are the elliptic projections (3.25) of \(u({{\varvec{x}}},t^n)\) and \({{\varvec{s}}}({{\varvec{x}}},t^n)\), respectively. Similar notations are used for q and \({\varvec{\omega }}\). By the approximation property in Lemma 3.2, we have

$$\begin{aligned} \Vert R_{u}^{n}\Vert +\Vert R_{q}^{n}\Vert \le Ch^{k+1}, \;\;\Vert R_{u}^{n+1}-R_{u}^{n}\Vert \le C\Delta th^{k+1}. \end{aligned}$$
(3.29)

Next we consider the error equation of the fully-discrete LDG scheme (3.12). It is easy to verify that

$$\begin{aligned} u(t^{n+1})&=u(t^n)-\Delta t\nabla \cdot {{\varvec{s}}}(t^{n+1})-\frac{a}{2}\Delta t q(t^{n+1})-\Delta tr(t^{n+1})b(t^{n})+\rho _{1}^{n}, \end{aligned}$$
(3.30)
$$\begin{aligned} r(t^{n+1})&=r(t^n)+\frac{1}{2}(b(t^n),u(t^{n+1})-u(t^{n}))+\rho _{2}^{n}. \end{aligned}$$
(3.31)

Here we omit the spacial variable \({{\varvec{x}}}\) for simplicity and \({{\varvec{s}}}\), q are the auxiliary variables (2.1b)–(2.1d), \(b(t^n)=\Phi '(u(t^n))/\sqrt{E_1(u(t^n))+B}\). \(\rho _{1}\) and \(\rho _{2}\) are the local truncation errors in time satisfying

$$\begin{aligned} \Vert \rho _{1}^{n}\Vert \le C(\Delta t)^{2},\;\;\Vert \rho _{2}^{n}\Vert \le C(\Delta t)^{2}. \end{aligned}$$
(3.32)

Multiply the test function \(\varphi _{1}\in V_h\) on both sides of (3.30) and integrate the equation by parts to yield

$$\begin{aligned} \big (u(t^{n+1}),\varphi _{1}\big )=&\big (u(t^n),\varphi _{1}\big )+\Delta tH^{+}\big ({{\varvec{s}}}(t^{n+1}),\varphi _{1}\big )-\frac{a}{2}\Delta t \big (q(t^{n+1}),\varphi _{1}\big )\\&-\Delta t\big (r(t^{n+1})b(t^{n}),\varphi _{1}\big )+\big (\rho _{1}^{n},\varphi _{1}\big ). \end{aligned}$$

Subtracting the above equation from the first equality of the scheme (3.12) gives the error equations for \(\xi _u^{n}\) as follows

$$\begin{aligned} \big (\xi _u^{n+1}-\xi _u^{n},\varphi _{1}\big )=&-\big (R_u^{n+1}-R_u^{n},\varphi _{1}\big )+\Delta tH^{+}\big (\xi _{{{\varvec{s}}}}^{n+1},\varphi _{1}\big )-\frac{a}{2}\Delta t \big (e_{q}^{n+1},\varphi _{1}\big )\nonumber \\&-\Delta t\big (r(t^{n+1})b(t^{n})-r_{h}^{n+1}b_h^n,\varphi _{1}\big )+(\rho _{1}^{n},\varphi _{1}). \end{aligned}$$
(3.33)

Note that the auxiliary variables q, \({{\varvec{s}}}\), \({\varvec{\omega }}\) also satisfy the scheme (3.12) and we have

$$\begin{aligned} \big (\xi _{{\varvec{s}}}^{n+1},{\varvec{\theta } }_1\big )&=-H^{-}\big (\xi _q^{n+1},{\varvec{\theta } }_1\big ), \end{aligned}$$
(3.34a)
$$\begin{aligned} \big (\xi _q^{n+1},\varphi _2\big )&=-H^{+}\big (\xi _{\varvec{\omega }}^{n+1},\varphi _2\big )+\frac{a}{2}\big (e_u^{n+1},\varphi _2\big ), \end{aligned}$$
(3.34b)
$$\begin{aligned} \big (\xi _{\varvec{\omega }}^{n+1},{\varvec{\theta } }_2\big )&=-H^{-}\big (\xi _u^{n+1},{\varvec{\theta } }_2\big ). \end{aligned}$$
(3.34c)

Here we use the definition of the elliptic projection (3.25). For the error \(e_{r}^{n}=r(t^n)-r^n\), we have

$$\begin{aligned} e_r^{n+1}&=e_r^n+\frac{1}{2}\big (b\big (t^n\big ),u\big (t^{n+1}\big )-u\big (t^{n}\big )\big )-\frac{1}{2}\big (b_h^n,u_h^{n+1}-u_h^{n}\big )+\rho _{2}^{n}\nonumber \\&=e_r^n+\frac{1}{2}\big (b\big (t^n\big )-b_h^n,u\big (t^{n+1}\big )-u\big (t^{n}\big )\big )+\frac{1}{2}\big (b_h^n,e_u^{n+1}-e_u^{n}\big )+\rho _{2}^{n}. \end{aligned}$$
(3.35)

Now we give the optimal error estimates in the following theorem.

Theorem 3.4

Let \(u_{h}^{n}\) be the numerical solution of the scheme (3.12), and u be the exact solution of equation (1.3). Suppose u satisfies the smoothness assumption (3.24), then there exists a constant \(C>0\) such that

$$\begin{aligned} \Vert u\big ({{\varvec{x}}},t^n\big )-u_{h}^{n}\Vert \le C\big (h^{k+1}+\Delta t\big ), \end{aligned}$$
(3.36)

where C is independent of h and \(u_{h}^{n}\) and dependent on the regularity of u and \(C_{*}\).

Proof

Taking the test function \(\varphi _{1}=\xi _u^{n+1}\) in (3.33), we obtain the first energy equality in the form of \(\xi _u\)

$$\begin{aligned} \frac{1}{2}\Vert \xi _u^{n+1}\Vert ^{2}-\frac{1}{2}\Vert \xi _u^{n}\Vert ^{2}+\frac{1}{2}\Vert \xi _u^{n+1}-\xi _u^n\Vert ^{2}={\mathcal {T}}_1+{\mathcal {T}}_2+{\mathcal {T}}_3, \end{aligned}$$

where

$$\begin{aligned} {\mathcal {T}}_1&=-\big (R_u^{n+1}-R_u^{n},\xi _u^{n+1}\big )+\big (\rho _{1}^{n},\xi _u^{n+1}\big ),\\ {\mathcal {T}}_2&=\Delta tH^{+}\big (\xi _{{{\varvec{s}}}}^{n+1},\xi _u^{n+1}\big )-\frac{a}{2}\Delta t \big (e_{q}^{n+1},\xi _u^{n+1}\big ),\\ {\mathcal {T}}_3&=-\Delta t\big (r(t^{n+1})b(t^{n})-r_{h}^{n+1}b_h^n,\xi _u^{n+1}\big ). \end{aligned}$$

The terms will be estimated separately. Adopting the Cauchy–Schwarz inequality, the property of the elliptic projection (3.29) and (3.32), we obtain

$$\begin{aligned} {\mathcal {T}}_1\le C\Delta th^{k+1}\Vert \xi _u^{n+1}\Vert +C(\Delta t)^{2}\Vert \xi _u^{n+1}\Vert . \end{aligned}$$
(3.37)

For the second term, by (2.4) and (3.34), we have

$$\begin{aligned} H^{+}\big (\xi _{{{\varvec{s}}}}^{l},\xi _u^{m}\big )&=-H^{-}\big (\xi _u^{m},\xi _{{{\varvec{s}}}}^{l}\big )=\big (\xi _{\varvec{\omega }}^m,\xi _{{{\varvec{s}}}}^{l}\big )=-H^{-}\big (\xi _{q}^{l},\xi _{\varvec{\omega }}^{m}\big )\nonumber \\&=H^{+}\big (\xi _{\varvec{\omega }}^{m},\xi _{q}^{l}\big )=-\big (\xi _{q}^{m},\xi _{q}^{l}\big )+\frac{a}{2}\big (e_u^m,\xi _{q}^{l}\big ),\;\;\forall m,l=n,n+1. \end{aligned}$$
(3.38)

Thus

$$\begin{aligned} {\mathcal {T}}_2&=-\Delta t\Vert \xi _{q}^{n+1}\Vert ^2+\frac{a}{2}\Delta t\big (e_u^{n+1},\xi _{q}^{n+1}\big )-\frac{a}{2}\Delta t \big (e_{q}^{n+1},\xi _u^{n+1}\big )\nonumber \\&=-\Delta t\Vert \xi _{q}^{n+1}\Vert ^2+\frac{a}{2}\Delta t\big (R_u^{n+1},\xi _{q}^{n+1}\big )-\frac{a}{2}\Delta t \big (R_{q}^{n+1},\xi _u^{n+1}\big )\nonumber \\&\le -\Delta t\Vert \xi _{q}^{n+1}\Vert ^2 +C\Delta th^{k+1}\big (\Vert \xi _{q}^{n+1}\Vert +\Vert \xi _u^{n+1}\Vert \big ), \end{aligned}$$
(3.39)

where the property (3.29) is used. For the nonlinear term, we can obtain

$$\begin{aligned} {\mathcal {T}}_3&=-\Delta t\left( r(t^{n+1})(b(t^{n})-b_h^n),\xi _u^{n+1}\right) -\Delta t\left( (r(t^{n+1})-r_{h}^{n+1})b_h^n,\xi _u^{n+1}\right) \\&\le \Delta t|r(t^{n+1})|\Vert b(t^{n})-b_h^n\Vert \Vert \xi _u^{n+1}\Vert +\Delta t|e_r^{n+1}|\Vert b_h^n\Vert \Vert \xi _u^{n+1}\Vert . \end{aligned}$$

With the definition of \(b(t^n)\), \(b_h^n\) and through some calculations, we derive

$$\begin{aligned} b(t^{n})-b_h^n&=\frac{\Phi '(u(t^n))}{\sqrt{E_1(u(t^n))+B}}-\frac{\Phi '(u_h^n)}{\sqrt{E_1(u_h^n)+B}}\\&=\frac{\Phi '(u_h^n)}{\sqrt{E_1(u_h^n)+B}\sqrt{E_1(u(t^n))+B}}\frac{E_1(u_h^n)-E_1(u(t^n))}{\sqrt{E_1(u_h^n)+B}+\sqrt{E_1(u(t^n))+B}}\\&\quad +\frac{\Phi '(u(t^n))-\Phi '(u_h^n)}{\sqrt{E_1(u(t^n))+B}}, \end{aligned}$$

which leads to

$$\begin{aligned} \Vert b(t^{n})-b_h^n\Vert&\le C\Vert \Phi '(u(t^n))-\Phi '(u_h^n)\Vert +C\Vert E_1(u_h^n)-E_1(u(t^n))\Vert \nonumber \\&\le C\Vert \Phi ''(\eta _{1})(u(t^n)-u_h^n)\Vert +C\Vert \Phi '(\eta _2)(u_h^n-u(t^n))\Vert \nonumber \\&\le C(\Vert R_u^n\Vert +\Vert \xi _u^n\Vert ). \end{aligned}$$
(3.40)

Here the first and last inequalities have used the boundness (3.23) and \(\eta _1\), \(\eta _2\) lie between \(u_h^n\) and \(u(t^n)\). It follows from \(r(t^{n+1})<C\) and (3.29) that

$$\begin{aligned} {\mathcal {T}}_3&\le C\Delta t(h^{k+1}+\Vert \xi _u^n\Vert )\Vert \xi _u^{n+1}\Vert +\Delta t\Vert b_h^n\Vert |e_r^{n+1}|\Vert \xi _u^{n+1}\Vert . \end{aligned}$$
(3.41)

Combine the estimates (3.37)–(3.41) to yield

$$\begin{aligned} \frac{1}{2}\Vert \xi _u^{n+1}\Vert ^{2}-\frac{1}{2}\Vert \xi _u^{n}\Vert ^{2}+\frac{1}{2}\Vert \xi _u^{n+1}-\xi _u^n\Vert ^{2}\le {\mathcal {R}}_{1} \end{aligned}$$
(3.42)

where

$$\begin{aligned} {\mathcal {R}}_1&=-\Delta t\Vert \xi _{q}^{n+1}\Vert ^2+C\Delta th^{k+1}\Vert \xi _q^{n+1}\Vert +C\Delta t(h^{k+1}+\Vert \xi _u^n\Vert +\Delta t)\Vert \xi _u^{n+1}\Vert \\&\quad +\Delta t\Vert b_h^n\Vert |e_r^{n+1}|\Vert \xi _u^{n+1}\Vert \\&\le \Delta t\Vert \xi _u^{n+1}\Vert ^{2}-\frac{1}{2}\Delta t\Vert \xi _{q}^{n+1}\Vert ^2+\frac{1}{2}\Delta t\Vert b_h^n\Vert ^{2}|e_r^{n+1}|^{2}+C\Delta t(h^{2k+2}+\Vert \xi _u^n\Vert ^{2}+(\Delta t)^2). \end{aligned}$$

Taking the test function \(\varphi _{1}=(\xi _u^{n+1}-\xi _u^{n})/\Delta t\) in (3.33), multiplying \(2e_r^{n+1}\) on both sides of (3.35) and adding them together, we obtain the second energy equality

$$\begin{aligned} \frac{1}{\Delta t}\Vert \xi _u^{n+1}-\xi _u^n\Vert ^{2}+(e_r^{n+1})^2-(e_r^{n})^2+(e_r^{n+1}-e_r^n)^2={\mathcal {L}}_1+{\mathcal {L}}_2+{\mathcal {L}}_3+{\mathcal {L}}_4, \end{aligned}$$

where

$$\begin{aligned} {\mathcal {L}}_1&=-\frac{1}{\Delta t}(R_u^{n+1}-R_u^{n},\xi _u^{n+1}-\xi _u^n)+\frac{1}{\Delta t}(\rho _{1}^{n},\xi _u^{n+1}-\xi _u^n)+2\rho _{2}^{n}e_r^{n+1},\\ {\mathcal {L}}_2&=H^{+}(\xi _{{{\varvec{s}}}}^{n+1},\xi _u^{n+1}-\xi _u^n)-\frac{a}{2}(e_{q}^{n+1},\xi _u^{n+1}-\xi _u^n),\\ {\mathcal {L}}_3&=-(r(t^{n+1})b(t^{n})-r_{h}^{n+1}b_h^n,\xi _u^{n+1}-\xi _u^n)+e_r^{n+1}(b_h^n,e_u^{n+1}-e_u^{n}),\\ {\mathcal {L}}_4&=e_r^{n+1}(b(t^n)-b_h^n,u(t^{n+1})-u(t^{n})). \end{aligned}$$

Using the Cauchy–Schwarz inequality and the approximation properties (3.29), (3.32), we have

$$\begin{aligned} {\mathcal {L}}_1\le Ch^{k+1}\Vert \xi _u^{n+1}-\xi _u^n\Vert +C\Delta t\Vert \xi _u^{n+1}-\xi _u^n\Vert +C(\Delta t)^{2}|e_r^{n+1}|. \end{aligned}$$
(3.43)

By the property (3.38), we derive

$$\begin{aligned} {\mathcal {L}}_2&=-(\xi _{q}^{n+1}-\xi _q^n,\xi _{q}^{n+1})+\frac{a}{2}(e_u^{n+1}-e_u^n,\xi _{q}^{n+1})-\frac{a}{2}(e_{q}^{n+1},\xi _u^{n+1}-\xi _u^n)\nonumber \\&=-(\xi _{q}^{n+1}-\xi _q^n,\xi _{q}^{n+1})+\frac{a}{2}(R_u^{n+1}-R_u^n,\xi _{q}^{n+1})-\frac{a}{2} (R_{q}^{n+1},\xi _u^{n+1}-\xi _u^n)\nonumber \\&\le -(\xi _{q}^{n+1}-\xi _q^n,\xi _{q}^{n+1}) +Ch^{k+1}(\Delta t\Vert \xi _{q}^{n+1}\Vert +\Vert \xi _u^{n+1}-\xi _u^n\Vert ), \end{aligned}$$
(3.44)

where the approximation property (3.29) of the elliptic is used again. For the term \({\mathcal {L}}_3\), some calculations yield

$$\begin{aligned} {\mathcal {L}}_3&=-\left( r(t^{n+1})(b(t^{n})-b_h^n),\xi _u^{n+1}-\xi _u^n\right) -(e_r^{n+1}b_h^n,\xi _u^{n+1}-\xi _u^n)+e_r^{n+1}(b_h^n,e_u^{n+1}-e_u^{n})\nonumber \\&\le |r(t^{n+1})|\Vert b(t^{n})-b_h^n\Vert \Vert \xi _u^{n+1}-\xi _u^n\Vert +|e_r^{n+1}|\Vert b_h^n\Vert \Vert R_u^{n+1}-R_u^n\Vert \nonumber \\&\le C(h^{k+1}+\Vert \xi _u^n\Vert )\Vert \xi _u^{n+1}-\xi _u^n\Vert +C\Delta th^{k+1}|e_r^{n+1}|. \end{aligned}$$
(3.45)

Here we use the estimate (3.40) and (3.29). Similarly, we have

$$\begin{aligned} {\mathcal {L}}_4\le C|e_r^{n+1}|(h^{k+1}+\Vert \xi _u^n\Vert )\Vert u(t^{n+1})-u(t^{n})\Vert \le C\Delta t|e_r^{n+1}|(h^{k+1}+\Vert \xi _u^n\Vert ). \end{aligned}$$
(3.46)

Then by the estimates (3.43)–(3.46), the second the energy equality turns out to be

$$\begin{aligned} LHS\le {\mathcal {R}}_2, \end{aligned}$$
(3.47)

where

$$\begin{aligned} LHS=&\frac{1}{\Delta t}\Vert \xi _u^{n+1}-\xi _u^n\Vert ^{2}+(e_r^{n+1})^2-(e_r^{n})^2+(e_r^{n+1}-e_r^n)^2\\&+\frac{1}{2}\Vert \xi _{q}^{n+1}\Vert ^2-\frac{1}{2}\Vert \xi _{q}^{n}\Vert ^2+\frac{1}{2}\Vert \xi _{q}^{n+1}-\xi _q^n\Vert ^2,\\ {\mathcal {R}}_2=&C(h^{k+1}+\Delta t+\Vert \xi _u^n\Vert )\Vert \xi _u^{n+1}-\xi _u^n\Vert +Ch^{k+1}\Delta t\Vert \xi _{q}^{n+1}\Vert \\&+C\Delta t(h^{k+1}+\Vert \xi _u^n\Vert +\Delta t)|e_r^{n+1}|\\ \le&\frac{1}{\Delta t}\Vert \xi _u^{n+1}-\xi _u^n\Vert ^{2}+\frac{1}{2}\Delta t\Vert \xi _{q}^{n+1}\Vert ^2+\frac{1}{2}\Delta t|e_r^{n+1}|^2\\&+C\Delta t(h^{2k+2}+(\Delta t)^2+\Vert \xi _u^n\Vert ^2). \end{aligned}$$

Note that

$$\begin{aligned} \Vert \xi _u^{n+1}\Vert ^{2}\le 2(\Vert \xi _u^{n}\Vert ^{2}+\Vert \xi _u^{n+1}-\xi _u^n\Vert ^{2}),\;\;|e_r^{n+1}|^{2}\le 2(|e_r^{n}|^{2}+(e_r^{n+1}-e_r^{n})^{2}). \end{aligned}$$

Add the energy inequalities (3.42), (3.47) together to get

$$\begin{aligned}&\Vert \xi _u^{n+1}\Vert ^{2}-\Vert \xi _u^{n}\Vert ^{2}+\Vert \xi _u^{n+1}-\xi _u^n\Vert ^{2}+2(e_r^{n+1})^2-2(e_r^{n})^2+2(e_r^{n+1}-e_r^n)^2\\&\quad +\Vert \xi _{q}^{n+1}\Vert ^2-\Vert \xi _{q}^{n}\Vert ^2+\Vert \xi _{q}^{n+1}-\xi _q^n\Vert ^2\le {\mathcal {R}}_{3}, \end{aligned}$$

where

$$\begin{aligned} {\mathcal {R}}_3&\le 4\Delta t\Vert \xi _u^{n+1}-\xi _u^n\Vert ^{2}+2\Delta t(1+\Vert b_h^n\Vert ^{2})|e_r^{n+1}-e_r^n|^{2}\\&\quad +C\Delta t(h^{2k+2}+(\Delta t)^2+\Vert \xi _u^n\Vert ^2+(e_r^n)^2). \end{aligned}$$

If

$$\begin{aligned} 4\Delta t<1,\;\;\Delta t(1+\Vert b_h^n\Vert ^{2})<1, \end{aligned}$$

we can get the estimate by using the discrete Gronwall’s inequality

$$\begin{aligned} \Vert \xi _u^{n}\Vert ^{2}+\Vert \xi _{q}^{n}\Vert ^2+2(e_r^{n})^2\le C(h^{2k+2}+(\Delta t)^2). \end{aligned}$$

By the triangle inequality and (3.29), we complete the proof. \(\square \)

3.4 The Semi-implicit SDC Method

The linear scheme proposed above is unconditionally energy stable. However, it is only first-order accurate in time, while the LDG method is high-order accurate in space. To obtain high-order accuracy in both space and time, we will employ the semi-implicit SDC method iteratively to improve the temporal accuracy.

The semi-implicit SDC method is based on a first-order scheme, for example the SAV method (3.12) here. An advantage of the SDC method is that it is a one step method and can be constructed easily and systematically for any order of accuracy. More details for the semi-implicit SDC method can be found in [16, 26].

We do the SDC procedure in every interval \([t^n,t^{n+1}]\). We divide the time interval \([t^n,t^{n+1}]\) into P subintervals by choosing the points \(t^{n,m}\) for \(m=0,1,\ldots ,P\) such that \(t^n=t^{n,0}<t^{n,1}<\cdots<t^{n,m}<\cdots <t^{n,P}=t^{n+1}\). Let \(\Delta t^{n,m}=t^{n,m+1}-t^{n,m}\) and \(u_k^{n,m}\) denotes the kth order approximation to \(u(t^{n,m})\). The points \(\{t^{n,m}\}_{m=0}^P\) can be chosen to be the Chebyshev Gauss–Lobatto nodes on \([t^n,t^{n+1}]\) to avoid the instability of approximation at equispaced nodes for high order accuracy. Starting from \(u^n\) and \(r^n\), we give the algorithm to calculate \(u^{n+1}\) and \(r^{n+1}\) in the following.

Compute the initial approximation

\(u^{n,0}_1=u^n\) and \(r^{n,0}_1=r^n\).

Use the first-order scheme (3.12) to compute a first-order accurate approximate solution \(u_1\) and \(r_1\) at the nodes \(\{t^{n,m}\}_{m=1}^P\), i.e.

For \(m=0,\ldots ,P-1\)

$$\begin{aligned} u_1^{n,m+1}&=u_1^{n,m}+\Delta t^{n,m}\left( -\left( \Delta +\frac{a}{2}\right) ^2 u_1^{n,m+1}-\frac{r_1^{n,m+1}}{\sqrt{E_1(u_1^{n,m}+B)}}\Phi '(u_1^{n,m})\right) , \end{aligned}$$
(3.48)
$$\begin{aligned} r_1^{n,m+1}&=r_1^{n,m}+\frac{1}{2\sqrt{E_1(u_1^{n,m})+B}} \int _{\Omega } \Phi '(u_1^{n,m}) (u_1^{n,m+1}-u_1^{n,m})d{{\varvec{x}}}. \end{aligned}$$
(3.49)

Compute successive corrections

For \(k=1,\ldots ,K\)

\(u^{n,0}_{k+1}=u^n\) and \(r^{n,0}_{k+1}=r^n\).

For \(m=0,\ldots ,P-1\)

$$\begin{aligned} u_{k+1}^{n,m+1}&=u_{k+1}^{n,m}+\Delta t^{n,m}\left( -\left( \Delta +\frac{a}{2}\right) ^2 u_{k+1}^{n,m+1}-\frac{r_{k+1}^{n,m}}{\sqrt{E_1(u_{k+1}^{n,m})+B}}\Phi '(u_{k+1}^{n,m}) \right. \nonumber \\&\quad +\left. \left( \Delta +\frac{a}{2}\right) ^2u_{k}^{n,m+1}+\frac{r_{k}^{n,m}}{\sqrt{E_1(u_{k}^{n,m})+B}}\Phi '(u_{k}^{n,m})\right) +I_m^{m+1}(F(u_k,r_k)), \end{aligned}$$
(3.50)
$$\begin{aligned} r_{k+1}^{n,m+1}&=\sqrt{E_1\left( u_{k+1}^{n,m+1}\right) +B}, \end{aligned}$$
(3.51)

where

$$\begin{aligned} F(u_k,r_k)=-\left( \Delta +\frac{a}{2}\right) ^2 u_k-\frac{r_k}{\sqrt{E_1(u_k)+B}}\Phi '(u_k). \end{aligned}$$

Here, \(I_m^{m+1}(F(u_k,r_k))\) is the integral of the P-th degree interpolating polynomial on the \(P+1\) points \((t^{n,m},F(u^{n,m}_k,r^{n,m}_k))_{m=0}^P\) over the subinterval \([t^{n,m},t^{n,m+1}]\), which is the numerical quadrature approximation of

$$\begin{aligned} \int _{t^{n,m}}^{t^{n,m+1}}F(u(t),r(t))dt. \end{aligned}$$

Finally we have \(u^{n+1}=u^{n,P}_{K+1}\) and \(r^{n+1}=r^{n,P}_{K+1}\).

Remark 3.5

(Local truncation error) The local truncation error obtained with the above semi-implicit SDC scheme [26] is

$$\begin{aligned} {\mathcal {O}}(\tau ^{\min [K+1,P+1]}), \end{aligned}$$

where \(\tau =\max \limits _{n,m} \Delta t^{n,m}\).

4 Numerical Experiments

In this section, we present some numerical experiments using the LDG spatial discretization and the semi-implicit SDC temporal discretization for the Swift–Hohenberg equation. In all examples, we assume periodic boundary conditions. We first perform an accuracy test, which shows the expected accuracy in time and space. Then, we present an example to show the energy stability of the first-order scheme and the semi-implicit SDC scheme, and to illustrate the advantage of the high-order SDC method. Lastly, we present some long time simulations to verify the energy stability and show the effectiveness of the proposed schemes.

Example 4.1

(Accuracy tests and efficiency of the proposed numerical methods) Consider the Swift–Hohenberg equation in the square domain \(\Omega =[0,2\pi ]^2\). For the tests, we choose a suitable source term such that the exact solution is taken as

$$\begin{aligned} u(x,y,t)=e^{-2t} \sin (x)\sin (y). \end{aligned}$$

Choose the parameters \(\varepsilon =0.025\), \(g=0\) and \(a=2\).

To test the temporal accuracy of the first-order scheme (3.12), we use the meshes \(N=64\) and \({\mathcal {P}}^2\) approximation to ensure that the spatial discretization error is small enough, and the temporal discretization error is dominant in the numerical test. The time step refinement path is taken to be \(\Delta t=\Delta t_0/2^m\), \(\Delta t_0=0.1\) and \(m=1,2,3,4\). The \(L^2\) and \(L^{\infty }\) errors and orders of convergence are presented in Table 1, which shows first-order accurate in time and agrees with the theoretical result.

Table 1 Temporal accuracy test
Full size table
Table 2 Spatial accuracy test. \(L^2\) and \(L^{\infty }\) errors and orders of convergence at \(T=0.1\)
Full size table
Table 3 Spatial and temporal accuracy test. \(L^2\) and \(L^{\infty }\) errors and orders of convergence at \(T=0.5\) with \(\Delta t=0.2 \Delta x\)
Full size table
Table 4 Total CPU time for the Swift–Hohenberg equation using various time-stepping methods
Full size table
Fig. 1
figure 1

Energy evolution of the first-order scheme and the third-order semi-implicit SDC scheme

Full size image
Fig. 2
figure 2

Numerical results of the Swift–Hohenberg equation using the third-order SDC method and the piecewise \({\mathcal {P}}^2\) polynomial basis with \(\varepsilon =0.3, g=0.0\)

Full size image

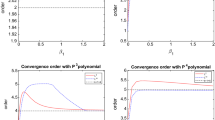
To test the spatial accuracy numerically, we set the time step as \(\Delta t=10^{-4}\) to ensure that the spatial discretization error is dominant. The mesh sizes are set to be \(\Delta x=\Delta y=2\pi /N\) with \(N=8,16,32,64\). The \(L^2\) and \(L^{\infty }\) errors and convergence rate at \(T=0.1\) are reported in Table 2, which shows \((k+1)\)-th orders of accuracy for \({\mathcal {P}}^k\) approximation and agrees with the theoretical result.

The \(L^2\) and \(L^{\infty }\) errors and accuracy of the third-order SDC scheme are presented in Table 3. The error is expected to be at the order of \(\min \{{\mathcal {O}}(\Delta t^3), {\mathcal {O}}(\Delta x^{k+1})\}\) for \({\mathcal {P}}^k\) approximation. Namely, high order accuracy in both space and time is easy to achieve for our proposed LDG and SDC methods with larger time step sizes.

Fig. 3
figure 3

Numerical results of the Swift–Hohenberg equation using the third-order SDC method and the piecewise \({\mathcal {P}}^2\) polynomial basis with \(\varepsilon =0.1, g=1.0\)

Full size image
Fig. 4
figure 4

Energy evolution of the third-order SDC method

Full size image

For the sake of comparison of efficiency, we document the CPU time of the third-order SDC method and the first-order method for solving the Swift–Hohenberg equation. We choose \({\mathcal {P}}^2\) polynomial for spatial discretization, and the suitably chosen \(\Delta t\) which yields an \(L^{\infty }\) error at the level of \(10^{-5}\) for both methods. The results are contained in Table 4. Comparing the CPU times, we notice that the third-order SDC method requires less time.

Example 4.2

(Energy stability test) In this example, we perform stability tests to verify the energy stability, the initial condition is taken as

$$\begin{aligned} u(x,y,0)=rand(x,y), \end{aligned}$$

where rand(x, y) is a random number between 0 and 1. The computational domain is \(\Omega =[0,100]^2\). Choose the parameters \(\varepsilon =0.3\), \(g=0\) and \(a=2\).

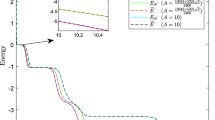
Figure 1a presents the energy evolution of the first-order scheme (3.12) with three different time step sizes, i.e. \(\Delta t=0.05,0.005,0.0005\). We can see the energy curves decay with all time step sizes, which agrees with the theoretical result of the unconditional energy stability. In addition, the energy curves are far away from the energy trace with \(\Delta t=0.0005\) if we use \(\Delta t=0.05,0.005\) due to the low-accuracy of the first-order scheme (3.12). Thus, to obtain more accurate numerical solutions, a smaller time step is necessary. However, our semi-implicit SDC scheme can enhance the accuracy, we can see from Fig. 1b that the energy curve of the third-order SDC scheme with \(\Delta t=0.05\) is better coincident with the energy trace with \(\Delta t=0.0005\).

Example 4.3

(Long time simulations) In this example, we will show the long time simulations of the Swift–Hohenberg equation with the random initial data between 0 and 1. The computational domain is \(\Omega =[0,100]^2\). We take \(a=2\). For other parameters, we use the values \(\varepsilon =0.3, g=0.0\) and \(\varepsilon =0.1, g=1.0\), separately.

We adopt the third-order SDC method and the piecewise \({\mathcal {P}}^2\) polynomial basis. The computed mesh is composed of \(128 \times 128\) elements with uniform mesh. The time step is \(\Delta t=0.05\). In Fig. 2, we show the contour plots of u with \(\varepsilon =0.3, g=0.0\). While for \(\varepsilon =0.1, g=1.0\), the corresponding results are contained in Fig. 3. The numerical results compare very well with the numerical calculations performed by Liu and Yin [15].

The energy evolution for both cases are presented in Fig. 4, we can see the energy is decreasing in time, which shows that the SDC method based on the first-order SAV scheme can maintain the energy stability.

5 Concluding Remarks

In this paper, we studied the LDG method for the Swift–Hohenberg equation and proved the energy stability for the semi-discrete and fully-discrete schemes. In addition, we derived the optimal convergence rates for the semi-discrete and fully-discrete LDG schemes. The LDG methods are high-order accurate in space, while the proposed linear scheme is only first-order accurate in time, which motives us to develop high-order temporal discretization methods. Thus, we employed the semi-implicit SDC method to improve the temporal accuracy based on the first-order SAV scheme. Numerical experiments verified the theoretical analysis and capabilities of the LDG and semi-implicit SDC methods.