1 Introduction

In this paper, we explore the following nonlinear singular two-point boundary value problem

$$\begin{aligned}&\left( x^{\alpha }u'\right) '=f(x,u),\quad \ 0<x<1,\quad \ 0\le \alpha <\infty , \end{aligned}$$
(1.1)

where f(x, u) may be weakly singular at \(x=0\) and is continuously differentiable with respect to u. We consider two kinds of boundary conditions

$$\begin{aligned}&u(0)=A,\quad \ \sigma u(1)+\gamma u'(1)=B,\quad \ \sigma \ge 0,\quad \ \gamma \ge 0\quad \ \mathrm {and}\ \sigma +\gamma > 0,\quad \ \mathrm {for} \ 0\le \alpha <1, \end{aligned}$$
(1.2)
$$\begin{aligned}&u'(0)=0,\quad \ \sigma u(1)+\gamma u'(1)=B,\quad \ \sigma >0,\quad \ \gamma \ge 0,\quad \ \mathrm {for} \ 0\le \alpha <\infty . \end{aligned}$$
(1.3)

We note that Eq. (1.1) is called weakly singular when \(0<\alpha <1\) and strongly singular when \(\alpha \ge 1\) [1]. For the weakly singular case, we can impose all kinds of boundary conditions, but for the strongly singular case, we can only impose \(u'(0)=0\) at the left boundary [2]. For a more general second-order singular differential equation, the existence and uniqueness of the solution have been explored by Kiguradze and Shekhter [3].

Nonlinear singular differential equations (1.1) occur frequently in several areas of science and engineering [4, 5], such as gas dynamics, chemical reaction, atomic calculation, and physiological studies. Some famous models include the Emden–Fowler equation [6, 7], the Lane–Emden equation [8], which are used in mathematical physics and chemical physics, and the Thomas–Fermi equation in atomic physics describing the electron distribution in an atom [7, 9,10,11,12]. In mathematics, linear or nonlinear elliptic equations with spherically symmetry naturally reduce to singular differential equations (1.1) with boundary condition (1.3) using spherical coordinate [13].

The solution of singular differential equation is usually not sufficiently smooth at the singularity [14], which will deteriorate the accuracy of the standard numerical methods. Jamet [2] proved this assertion when standard three-point finite difference scheme with a uniform mesh was used to solve the singular two-point boundary value problem (1.1) with Dirichlet boundary condition when \(0<\alpha <1\). Ciarlet et al. [15] obtained a similar conclusion when a suitable Rayleigh–Ritz–Galerkin method was used to solve the problem. Chawla and Katti [16] proposed a three-point difference method of second order under appropriate conditions by constructing an integral identity for this kind of singular two-point boundary value problem. Followed this integral identity, a lot of finite difference methods with second or fourth order accuracy were constructed for weakly or strongly singular differential equations, see, for example, [1, 17,18,19,20,21]. Another treatment for singularity was proposed by Gustafsson [22], who solved the problem by first writing the series solution in the neighborhood of the singularity and then employing several standard difference schemes in the remaining part of the interval. As for the further development of this method, see [23, 24]. Recently, Roul et al. [25] designed a high-order compact finite difference method for a general class of nonlinear singular boundary value problems with Neumann and Robin boundary conditions. Some kinds of collocation methods including cubic or quartic B-spline, Jacobi interpolation, and Chebyshev series were also used to numerically solve singular differential equations [26,27,28,29,30,31,32,33,34,35,36,37]. As stated by Russel and Shampine [31], collocation with piecewise polynomial functions is an effective method for solving singular problems with smooth solutions, although the coefficients are singular. But for the problem with non-analytic solution, the accuracy becomes lower [36]. Hence, some modifications should be adopted for these problems. For instance, nonpolynomial bases are used in collocation space [34] or singularity is removed by splitting the interval into two subintervals [26], or graded mesh is used in finite element method [38]. It is worth mentioning that Huang et al. [30] derived the convergence order of Legendre and Chebyshev collocation methods for a singular differential equation (\(\alpha =1\) and linear case in (1.1)) and Guo et al. [33] developed the convergence theory of Jacobi spectral method for differential equations possessing two-endpoint singularities.

Besides numerical methods, many semi-analytical methods were also developed to obtain approximate series solutions for singular problems, see, for example, the homotopy perturbation method (HPM) [39], the homotopy analysis method (HAM) [40,41,42,43], and the (improved) Adomian decomposition method (ADM) [44, 45]. These methods transformed the singular differential equations to the Fredholm integral ones using Green’s function and then obtained recursive schemes based on HPM, HAM, or ADM. We note that the transformed integral equations can also be discretized by numerical method [46].

The first thing to effectively solve singular differential equation is describing the singular behavior of the solution at its singularity. A useful tool is the Puiseux series, a generalization of Taylor’s series, which may contain negative and fractional exponents and logarithms [47,48,49]. In [50], this kind of series was called psi-series. We note that if the Puiseux series or psi-series contains only fractional exponents, it is also called fractional Taylor’s series [51, 52]. For the singular differential equation (1.1) with Dirichlet boundary conditions, Zhao et al. [53] first derived the series expansion of the solution about zero with a parameter for the case \(0<\alpha <1\), and then designed an augmented compact finite volume method to solve the equation. In this paper, we consider the equation with mixed boundary conditions for the case \(0\le \alpha <\infty \). We aim to explore the singular behavior of the solution at \(x=0\) by deriving the fractional Taylor’s expansion for the solution about zero. The main idea is first transforming the differential equation (1.1) to an equivalent Fredholm integral equation, and then obtaining the fractional series expansion via Picard iteration. The key point is implementing the series expansion for the nonlinear function f(x, u(x)) about \(x=0\) by symbolic computation. We note that the obtained series expansion contains an unknown parameter, which is essentially determined by the right boundary condition. Since the series expansion may not be convergent at \(x=1\), we should resort to some other methods to solve the singular differential equation, such as Chebyshev collocation method [30, 54,55,56,57]. Certainly, the series expansion can help us to find a suitable variable transformation such that the solution of (1.1) is sufficiently smooth, even though the equation is still singular. For the transformed equation, the Chebyshev collocation method could get accurate numerical solution if we evaluate the function values near the singularity with very small roundoff errors. Once the numerical values at nodes are obtained, their interpolation can give an accurate approximation to the unknown parameter in the series expansion.

As stated above, the methods for solving singular differential equations usually fall into two categories, one is series expansion method and the other is numerical method. The series expansion method can automatically recognize the singular behavior of the solution when generating the series solution, but it usually costs much time, whereas the numerical method is usually fast, but it cannot recognize the singular feature of the solution. For singular equation, it needs to introduce special techniques to treat the singularity. The method in this paper combines the advantages of the above two classes of methods. We note that our series expansion method is different from those of ADM, HPM, and HAM. What we obtained is exactly the truncated series of the solution about zero, which accurately reflects the singular behavior of the solution. We also optimize the iterative procedures so that the series decomposition has high efficiency. Based on this series expansion, we are easy to know how to perform a suitable variable transformation to make the solution be sufficiently smooth. For the transformed differential equation, all kinds of traditional numerical methods such as finite difference method, finite element method, and finite volume method can be effectively used. That is to say, we develop a common technique such that the existing numerical methods can be effectively simplified. In this paper, we only use Chebyshev collocation method to obtain numerical solutions with high accuracy for singular differential equations.

The outline of the paper is as follows. In Sect. 2, we derive the truncated fractional series for the solution about zero via Picard iteration for the equivalent Fredholm integral equation. In Sect. 3, we first transform the singular differential equation to the one with smooth solution based on the series expansion, and then discretize the transformed differential equation by Chebyshev collocation method. In Sect. 4, we discuss the convergence of the Chebyshev collocation method by taking the corresponding linear equation as an example. In Sect. 5, some typical examples are provided to show that the series expansion generating algorithm is feasible and the Chebyshev collocation method is accurate for these kinds of nonlinear singular differential equations. In Sect. 6, we apply the method to the Thomas–Fermi equation and the Emden–Fowler equation over finite interval and derive the fractional series expansions for the solution about the two endpoints. We end with a concise conclusion in Sect. 7.

2 The singular series expansion for the solution about zero

In this section, we consider the nonlinear singular differential equation (1.1) with the boundary condition (1.2) or (1.3). In order to guarantee the existence and uniqueness of the solution, we need to impose some additional conditions for the function f(x, u), which will be given later. In the following, we first transform the singular two-point boundary value problem to an equivalent Fredholm integral equation of the second kind using Green’s function and then formulate the finite-term truncation of the fractional Taylor’s series for the solution about \(x=0\).

For the boundary value problem (1.1), (1.2), by introducing the Green’s function [44]

$$\begin{aligned} G(x,\xi )= {\left\{ \begin{array}{ll} \displaystyle \frac{\xi ^{1-\alpha }}{1-\alpha }\left[ \frac{\sigma x^{1-\alpha }}{\sigma +\gamma (1-\alpha )}-1\right] ,\quad \ 0\le \xi \le x,\\ \displaystyle \frac{x^{1-\alpha }}{1-\alpha }\left[ \frac{\sigma \xi ^{1-\alpha }}{\sigma +\gamma (1-\alpha )}-1\right] ,\quad \ x\le \xi \le 1, \end{array}\right. } \end{aligned}$$
(2.1)

we can obtain an equivalent Fredholm integral equation

$$\begin{aligned}&u(x)=A+\frac{B-\sigma A}{\sigma +\gamma (1-\alpha )}x^{1-\alpha }+\int _{0}^{1}G(x,\xi )f(\xi ,u(\xi ))\mathrm {d}\xi . \end{aligned}$$
(2.2)

For the boundary value problem (1.1), (1.3), by introducing the Green’s function [45]

$$\begin{aligned} G(x,\xi )= {\left\{ \begin{array}{ll} \displaystyle \frac{x^{1-\alpha }-1}{1-\alpha }-\frac{\gamma }{\sigma },\quad \ 0\le \xi \le x,\\ \displaystyle \frac{\xi ^{1-\alpha }-1}{1-\alpha }-\frac{\gamma }{\sigma },\quad \ x\le \xi \le 1, \end{array}\right. }\ \mathrm {for}\ \alpha \ne 1, \end{aligned}$$
(2.3)

or

$$\begin{aligned} G(x,\xi )= {\left\{ \begin{array}{ll} \log x-\displaystyle \frac{\gamma }{\sigma },\quad \ 0\le \xi \le x,\\ \log \xi -\displaystyle \frac{\gamma }{\sigma },\quad \ x\le \xi \le 1, \end{array}\right. }\ \mathrm {for}\ \alpha =1, \end{aligned}$$
(2.4)

we can also obtain an equivalent Fredholm integral equation

$$\begin{aligned}&u(x)=\frac{B}{\sigma }+\int _{0}^{1}G(x,\xi )f(\xi ,u(\xi ))\mathrm {d}\xi . \end{aligned}$$
(2.5)

Remark 1

Under the assumptions for \(\sigma \) and \(\gamma \) in (1.2) and (1.3), it is easy to show that the Green’s functions defined by (2.1), (2.3), and (2.4) are all nonpositive for \(x,\xi \in [0,1]\).

Next, we try to derive the fractional Taylor’s expansion for u(x) about \(x=0\) with the form

$$\begin{aligned}&u(x)=A+a_0x^{1-\alpha }+\sum _{j=1}^{\infty }a_jx^{\alpha _j},\quad \ 1-\alpha<\alpha _1<\alpha _2<\cdots \rightarrow \infty . \end{aligned}$$
(2.6)

Suppose that f(x, u) is infinitely differentiable with respect to u and possesses the following Taylor’s expansion about \(u=A\):

$$\begin{aligned}&f(x,u)=f(x,A)+\sum \limits _{i=1}^{\infty }\frac{1}{i!}\frac{\partial ^i f(x,A)}{\partial u^i}(u-A)^i. \end{aligned}$$
(2.7)

We further assume that \({\partial ^i f(x,A)}/{\partial u^i}\), \(i=0,1,\ldots , \infty \) hold the following fractional Taylor’s expansions about \(x=0\):

$$\begin{aligned}&\frac{\partial ^i f(x,A)}{\partial u^i}=\sum \limits _{j=1}^{\infty }\eta _{i,j}x^{\rho _{i,j}},\quad \ -1<\rho _{i,1}<\rho _{i,2}<\cdots \rightarrow \infty . \end{aligned}$$
(2.8)

Here, we impose another condition for \(\rho _{i,j}\), which is \(\rho _{0,1}\le \rho _{1,1}\le \rho _{2,1}\le \cdots \). Substituting (2.6), (2.8) into (2.7), we can show that f(x, u(x)) possesses the following series expansion:

$$\begin{aligned}&f(x,u(x))=\sum _{j=1}^{\infty }c_jx^{\beta _j},\quad \ -1<\beta _1=\rho _{0,1}<\beta _2<\cdots \rightarrow \infty . \end{aligned}$$
(2.9)

Since we only need to obtain a finite-term series expansion for u(x) about \(x=0\), we further denote the expansions of u(x) and f(x, u(x)), respectively, as

$$\begin{aligned}&u(x)=A+a_0x^{1-\alpha }+\sum _{j=1}^{M}a_jx^{\alpha _j}+r_{u,M}(x),\quad \ 1-\alpha<\alpha _1<\alpha _2<\cdots <\alpha _M, \end{aligned}$$
(2.10)
$$\begin{aligned}&f(x,u(x))=\sum _{j=1}^{M}c_jx^{\beta _j}+r_{f,M}(x),\quad \ -1<\beta _1=\rho _{0,1}<\beta _2<\cdots <\beta _M, \end{aligned}$$
(2.11)

where M is a suitably large integer and the remainders \(r_{u,M}(x)=x^{\alpha _{M+1}}z_{u,M}(x)\) (\(\alpha _{M+1}>\alpha _{M}\)), \(r_{f,M}(x)=x^{\beta _{M+1}}z_{f,M}(x)\) (\(\beta _{M+1}>\beta _{M})\), and both \(z_{u,M}(x)\), \(z_{f,M}(x)\) are continuous over [0, 1]. We note that the coefficient \(a_0\) in (2.10) is a free parameter to be determined for the problem (1.1) with (1.2), but it vanishes for the problem (1.1) with (1.3), where in this problem, A is a free parameter to be determined.

First, we discuss the problem (1.1) with (1.2). Substituting (2.10) and (2.11) into (2.2), we obtain

$$\begin{aligned} A+a_0x^{1-\alpha }+\sum _{j=1}^{M}a_jx^{\alpha _j}+r_{u,M}(x)&=A+\frac{(B-\sigma A)x^{1-\alpha }}{\sigma +\gamma (1-\alpha )}+\sum _{j=1}^{M}c_j\int _{0}^{1}G(x,\xi )\xi ^{\beta _j}\mathrm {d}\xi \\&\quad +\int _{0}^{1}G(x,\xi )r_{f,M}(\xi )\mathrm {d}\xi . \end{aligned}$$

Using the Green’s function (2.1), a straightforward computation shows

$$\begin{aligned} A+a_0x^{1-\alpha }+\sum _{j=1}^{M}a_jx^{\alpha _j}+r_{u,M}(x)&=A+\frac{\left( B-\sigma A\right) x^{1-\alpha }}{\sigma +\gamma \left( 1-\alpha \right) }+\sum _{j=1}^{M}\frac{c_jx^{2-\alpha +\beta _j}}{\left( 1+\beta _j\right) \left( 2-\alpha +\beta _j\right) }\nonumber \\&\quad -\sum _{j=1}^{M}\frac{c_j\left( \sigma +\gamma \left( 2-\alpha +\beta _j\right) \right) x^{1-\alpha }}{\left( \sigma +\gamma \left( 1-\alpha \right) \right) \left( 1+\beta _j\right) \left( 2-\alpha +\beta _j\right) }\nonumber \\&\quad +\int _{0}^{1}G(x,\xi )r_{f,M}(\xi )\mathrm {d}\xi . \end{aligned}$$
(2.12)

Noticing Remark 1, the last term on the right-hand side of (2.12) is estimated by

$$\begin{aligned}&\left| \int _{0}^{1}G(x,\xi )r_{f,M}(\xi )\mathrm {d}\xi \right| \le \frac{C_{f,M} x^{1-\alpha }}{(1+\beta _{M+1})(2-\alpha +\beta _{M+1})} \left[ 1+\frac{\gamma (1+\beta _{M+1})}{\sigma +\gamma (1-\alpha )}-x^{1+\beta _{M+1}}\right] , \end{aligned}$$
(2.13)

where \(C_{f,M}=\max _{x\in [0,1]}|z_{f,M}(x)|\). The estimation (2.13) means that the last integral on the right-hand side of (2.12) does not generate the terms in front of it except the one like \(x^{1-\alpha }\). Hence, equating the powers and coefficients of like powers of x on both sides of (2.12) yields

$$\begin{aligned}&\alpha _j=2-\alpha +\beta _j,\quad \ a_j=\displaystyle \frac{c_j}{(1+\beta _j)(2-\alpha +\beta _j)},\quad \ j=1,2,\ldots ,M. \end{aligned}$$
(2.14)

Second, we consider the problem (1.1) with (1.3). Noting that for this problem, \(a_0=0\) in (2.10), we have from (2.5)

$$\begin{aligned}&A+\sum _{j=1}^{M}a_jx^{\alpha _j}+r_{u,M}(x)=\frac{B}{\sigma }+\sum _{j=1}^{M}c_j\int _{0}^{1}G(x,\xi )\xi ^{\beta _j}\mathrm {d}\xi +\int _{0}^{1}G(x,\xi )r_{f,M}(\xi )\mathrm {d}\xi . \end{aligned}$$
(2.15)

For the case \(\alpha \ne 1\), by substituting the Green’s function (2.3) into (2.15), we can obtain

$$\begin{aligned} A+\sum _{j=1}^{M}a_jx^{\alpha _j}+r_{u,M}(x)&=\frac{B}{\sigma }-\sum _{j=1}^{M}\frac{c_j}{1+\beta _j}\left( \frac{\gamma }{\sigma }+ \frac{1}{2-\alpha +\beta _j}\right) +\sum _{j=1}^{M}\frac{c_jx^{2-\alpha +\beta _j}}{(1+\beta _j)(2-\alpha +\beta _j)}\nonumber \\&\quad +\int _{0}^{1}G(x,\xi )r_{f,M}(\xi )\mathrm {d}\xi . \end{aligned}$$
(2.16)

For the case \(\alpha =1\), substituting the Green’s function (2.4) into (2.15) yields

$$\begin{aligned} A+\sum _{j=1}^{M}a_jx^{\alpha _j}+r_{u,M}(x)&=\frac{B}{\sigma }-\sum _{j=1}^{M}\frac{c_j}{1+\beta _j}\left( \frac{\gamma }{\sigma }+ \frac{1}{1+\beta _j}\right) +\sum _{j=1}^{M}\frac{c_jx^{1+\beta _j}}{(1+\beta _j)^2}+\int _{0}^{1}G(x,\xi )r_{f,M}(\xi )\mathrm {d}\xi . \end{aligned}$$

Obviously, the above equation is a special case of (2.16) when \(\alpha =1\). Hence, we only consider the general case (2.16) in the following. For (2.16), we should further assume that \(\beta _1>\alpha -1\) since \(u'(0)=0\). Equating the powers and coefficients of like powers of x on both sides of (2.16) yields

$$\begin{aligned}&\alpha _j=2-\alpha +\beta _j,\quad \ a_j=\displaystyle \frac{c_j}{(1+\beta _j)(2-\alpha +\beta _j)},\quad \ j=1,2,\ldots ,M. \end{aligned}$$
(2.17)

Comparing (2.14) with (2.17), we know the singular expansions for u(x) about \(x=0\) are very similar for the two different boundary conditions \(u(0)=A\) (\(0\le \alpha <1\)) and \(u'(0)=0\).

From (2.14) and (2.17), we know the key point to derive the singular expansion for u(x) about \(x=0\) is determining the power exponents \(\beta _j\) and the coefficients \(c_j\) of the truncated fractional series for f(x, u(x)) in (2.11). This can be achieved by symbolic computation, for instance, using the Series command of Mathematica. For the nonlinear equation, we need to implement a Picard iteration to recover the \(\beta _j\) and \(c_j\) step by step. Since \(a_0\) in (2.12) and A in (2.16) cannot be determined by these equations, we take them as free parameters when implementing the iterations. Concretely, we have the following series expansion algorithm.

Step 1: Let \(u_0(x)=A+a_0 x^{1-\alpha }\) for the problem (1.1) with (1.2), where \(a_0\) is a free parameter to be determined or let \(u_0(x)=A\) for the problem (1.1) with (1.3), where A is a free parameter to be determined.

Step 2: For \(j=1,2,\ldots ,M\), implement the fractional series expansion for \(f(x,u_{j-1}(x))\) about \(x=0\) by symbolic computation. We assume that

$$\begin{aligned} f(x,u_{j-1}(x))=\sum \limits _{k=1}^{j}c_k x^{\beta _k}+r_{f,j}(x), \end{aligned}$$
(2.18)

where \(r_{f,j}(x)=x^{\beta _{j+1}}z_{f,j}(x)\) (\(\beta _{j+1}>\beta _{j})\) is the remainder and the coefficients \(c_k\), \(k=1,2,\ldots ,j\), are related with \(a_0\) (for boundary condition (1.2)) or A (for boundary condition (1.3)). Then let

$$\begin{aligned}&\alpha _j=2-\alpha +\beta _j,\quad \ a_j=\frac{c_j}{\alpha _j(1+\beta _j)},\quad \ u_j(x)=u_{j-1}(x)+a_jx^{\alpha _j}, \end{aligned}$$
(2.19)

and repeat for \(j+1\). Finally, we obtain a truncated series

$$\begin{aligned} u_M(x)=A+a_0x^{1-\alpha }+\sum _{j=1}^{M}a_jx^{\alpha _j}. \end{aligned}$$
(2.20)

Theorem 1

Suppose that f(x, u) is infinitely differentiable with respect to u and \({\partial ^i f(x,A)}/{\partial u^i}\), \(i=0,1,\ldots , \infty \), hold the fractional Taylor’s expansions with respect to x as in (2.8), where \(A=u(0)\). We further assume that in (2.9), \(\beta _1=\rho _{0,1}>-1\) for the problem (1.1), (1.2), and \(\beta _1=\rho _{0,1}>\alpha -1\) for the problem (1.1), (1.3). Then the power exponents \(\beta _k\) and the coefficients \(c_k\) in the fractional series expansion of \(f(x,u_{j-1}(x))\), \(k = 1, 2, \ldots , j\) do not change as j increases.

Proof

Performing Taylor’s expansion for \(f(x, u_j(x))\) about u at \(u_{j-1}(x)\), noticing (2.8), we have from (2.18) and (2.19)

$$\begin{aligned} f(x, u_j(x))&= f(x, u_{j-1}(x)) + \frac{\partial f}{\partial u} (x, u_{j-1}(x)) (u_j(x)-u_{j-1}(x)) + \cdots \\&= \sum _{k=1}^j c_k x^{\beta _k}+\left( \frac{\partial f(x,A)}{\partial u} +\frac{\partial ^2 f(x,A) }{\partial u^2} (u_{j-1}(x)-A)+\cdots \right) a_j x^{2-\alpha +\beta _j} + \cdots \\&=\sum _{k=1}^j c_k x^{\beta _k}+a_j\sum \limits _{k=1}^{\infty }\eta _{1,k}x^{2-\alpha +\beta _j+\rho _{1,k}}+\cdots , \end{aligned}$$

where the exponents of x in the omitting part are all greater than \(2-\alpha +\beta _j+\rho _{1,1}\). By our assumptions about \(\rho _{1,k}\), we have

$$\begin{aligned} 2-\alpha +\beta _j+\rho _{1,1}\ge 2-\alpha +\rho _{0,1}+\beta _j=2-\alpha +\beta _1+\beta _j. \end{aligned}$$

For the problem (1.1) with (1.2), since \(0 \le \alpha < 1\) and \(\beta _1>-1\), we know \(2-\alpha +\beta _1+\beta _j > \beta _j\). For the problem (1.1) with (1.3), since \(\beta _1>\alpha -1\), we obtain \(2-\alpha +\beta _1+\beta _j>1+\beta _j >\beta _j\). Therefore, we can conclude that \(\beta _k\) and \(c_k\), \(k = 1, 2, \ldots , j\) do not change as j increases for these two different boundary conditions. The proof is complete. \(\square \)

Theorem 2

Under the conditions imposed on f(x, u) in Theorem 1, \(u_M(x)\) given in (2.20) is exactly the truncated fractional Taylor’s series for u(x) about \(x=0\), but contains an unknown parameter \(a_0\) for the problem (1.1), (1.2) or A for the problem (1.1), (1.3) (in this case \(a_0=0\)).

Proof

We only prove the case for the problem (1.1), (1.2). Define

$$\begin{aligned}&e_M(x)=u_M(x)-A-\frac{B-\sigma A}{\sigma +\gamma (1-\alpha )}x^{1-\alpha }-\int _{0}^{1}G(x,\xi )f(\xi ,u_{M-1}(\xi ))\mathrm {d}\xi , \end{aligned}$$
(2.21)

then combining (2.12), (2.18)–(2.20), and using Theorem 1 yield

$$\begin{aligned}&e_M(x)=\left( a_0-\frac{B-\sigma A}{\sigma +\gamma (1-\alpha )}+ \sum _{j=1}^{M}\frac{a_j(\sigma +\gamma \alpha _j)}{\sigma +\gamma (1-\alpha )}\right) x^{1-\alpha } -\int _{0}^{1}G(x,\xi )r_{f,M}(\xi )\mathrm {d}\xi . \end{aligned}$$
(2.22)

Further, the estimation (2.13) implies

$$\begin{aligned}&\int _{0}^{1}G(x,\xi )r_{f,M}(\xi )\mathrm {d}\xi \rightarrow 0, \ M\rightarrow \infty , \end{aligned}$$

for suitably small x since \(\beta _{M+1}\rightarrow \infty \) by our assumption. Then letting \(M\rightarrow \infty \) in (2.22) yields

$$\begin{aligned}&e_M(x)\rightarrow \left( a_0-\frac{B-\sigma A}{\sigma +\gamma (1-\alpha )}+ \sum _{j=1}^{\infty }\frac{a_j(\sigma +\gamma \alpha _j)}{\sigma +\gamma (1-\alpha )}\right) x^{1-\alpha }. \end{aligned}$$

By choosing \(a_0\) such that the coefficient of \(x^{1-\alpha }\) equals to zero, we assert that \(e_M(x)\rightarrow 0\) as \(M\rightarrow \infty \) for suitably small x. Hence, by letting \(M\rightarrow \infty \) in (2.21), we know \(u_\infty (x)=A+a_0x^{1-\alpha }+\sum _{j=1}^{\infty }a_jx^{\alpha _j}\) is the series solution for u(x) about \(x=0\), and of course, \(u_M(x)\) is exactly the truncated fractional Taylor’s series for u(x) about \(x=0\). A similar argument can be conducted for the problem (1.1), (1.3). The proof is complete. \(\square \)

Remark 2

Theorems 1, 2 actually give the conditions for f(x, u) such that the boundary value problem has a unique series solution, which are (2.8) holding for f(x, A) and \(\beta _1>-1\) for the problem (1.1), (1.2), \(\beta _1>\alpha -1\) for the problem (1.1), (1.3). These conditions can be easily checked since \(f(x, A)= \eta _{0,1} x^{\beta _1}+\cdots \).

Remark 3

In this section, we first assume that u(x) possesses the fractional Taylor’s expansion (2.6). In the proof of Theorem 2, we show the Picard iteration has truly generated this expansion under the assumptions for f(x, u), which means that the assumption (2.6) is reasonable.

Remark 4

The truncated series expansion \(u_M(x)\) contains an unknown parameter \(a_0\) for the left boundary condition \(u(0)=A\) or A for the case \(u'(0)=0\), which should be determined by the right boundary condition \(\sigma u(1)+\gamma u'(1)=B\). As is well known, the Taylor’s expansion is very good near the center of expansion, but the error may increase rapidly as the variable moves away. This is true for \(u_M(x)\). Even though we cannot expect to determine these parameters accurately by the right boundary condition except that the series is convergent fast at \(x=1\), the expansion \(u_M(x)\) at least provides the information about the singular behavior of the solution, which may help us to design numerical methods with high precision for solving singular differential equations.

Remark 5

We write a Mathematica function Pesbvp[f,\(\alpha \),M,A,a0] to implement the series expansion algorithm, where f is the given function f(x, u), M is the maximal exponent of the series to be recovered, and a0,A are the undetermined parameters corresponding to the boundary condition \(u(0)=A\) (in this case, A is known) and \(u^\prime (0)=0\), respectively.

Remark 6

If f(x, u) is singular at \(x=1\), we can also use the method in this section to derive the series expansion for u(x) about \(x=1\).

3 Chebyshev collocation method

The results in Sect. 2 reveal that the singular equation (1.1) with boundary condition (1.2) or (1.3) has generally insufficiently smooth solution, which will lead to the decrease of accuracy when high-order collocation methods are directly used to solve it. In this section, we show that this difficulty can be effectively overcome after a suitable smoothing transformation is performed.

From the truncated fractional power series \(u_M(x)\) in (2.20), we can reasonably assume that \(u(x)=A+\sum _{j=0}^M a_j x^{\beta \rho _j}+\cdots \), where \(0<\beta \le 1\) and \(\rho _j\), \(j=0,1,\ldots ,M\) are all integers. Hence, taking the variable transformation \(t=x^{\beta }\) can make the solution sufficiently smooth about t. By letting \(s=2t-1\) and \(v(s)=u(x)\), we can transform Eq. (1.1) into

$$\begin{aligned}&\frac{\mathrm{d}^2v}{{\mathrm{d}s}^2}+p(s)\frac{\mathrm{d}v}{\mathrm{d}s}=g(s,v),\quad \ -1<s<1, \end{aligned}$$
(3.1)

where

$$\begin{aligned} p(s)=\frac{\alpha +\beta -1}{\beta (s+1)},\quad \ g(s,v)=\frac{1}{4\beta ^2}\left( \frac{s+1}{2}\right) ^{-\frac{\alpha +2(\beta -1)}{\beta }} f\left( \left( \frac{s+1}{2}\right) ^{\frac{1}{\beta }},v\right) . \end{aligned}$$

Meanwhile, the boundary condition (1.2) is converted to

$$\begin{aligned}&v(-1)=A,\quad \ \sigma v(1)+2\beta \gamma v'(1)=B, \end{aligned}$$
(3.2)

and the boundary condition (1.3) is converted to

$$\begin{aligned}&v'(-1)=0,\quad \ \sigma v(1)+2\beta \gamma v'(1)=B. \end{aligned}$$
(3.3)

We note that Eq. (3.1) is still singular, but its solution is sufficiently smooth. In order to obtain an accurate numerical solution, we solve it by the Chebyshev collocation method [54,55,56,57].

We first divide the interval \([-1,1]\) into n subintervals and select the nodes as the Chebyshev–Gauss–Lobatto points \(s_j=\cos \left( \pi j/n\right) \), \(j=0,1,\ldots ,n\), which are the extreme points of the Chebyshev polynomial \(T_n(s)=\cos n\arccos s\). Then, for v(s), \(s\in [-1,1]\), we construct a Lagrange interpolating polynomial \(v_n(s)\) of degree n using the nodes \(s_j\), \(j=0,1,\ldots ,n\), which is

$$\begin{aligned}&v_n(s)=\sum _{j=0}^nl_j(s)v(s_j), \end{aligned}$$
(3.4)

where the Lagrange basis functions \(l_j(s)\) read as

$$\begin{aligned}&l_j(s)=\prod _{k=0,k\not =j}^{n}\frac{s-s_k}{s_j-s_k},\quad \ j=0,1,\ldots ,n. \end{aligned}$$

Finally, replacing v(s) in (3.1) with \(v_n(s)\) and forcing the resulting equation to be held at the interior collocation points, we get a collocation scheme

$$\begin{aligned}&\frac{\mathrm{d}^2v_n(s_i)}{{\mathrm{d}s}^2}+p(s_i)\frac{\mathrm{d}v_n(s_i)}{\mathrm{d}s}=g(s_i,v_n(s_i)),\quad \ i=1,2,\ldots ,n-1. \end{aligned}$$
(3.5)

In the following, we show that (3.5) is equivalent to a system of nonlinear equations. Differentiating the Lagrange interpolation (3.4) m times, we have

$$\begin{aligned} v_n^{(m)}(s)=\sum _{j=0}^nl_j^{(m)}(s)v(s_j). \end{aligned}$$

Let \(s=s_i\), then

$$\begin{aligned}&v_n^{(m)}(s_i)=\sum _{j=0}^nl_j^{(m)}(s_i)v(s_j),\quad \ i=0,1,\ldots ,n. \end{aligned}$$
(3.6)

By introducing the following notations:

$$\begin{aligned} V_n^{(m)}= \begin{pmatrix} v_n^{(m)}(s_0) \\ v_n^{(m)}(s_1) \\ \vdots \\ v_n^{(m)}(s_n) \\ \end{pmatrix},\ V= \begin{pmatrix} v(s_0) \\ v(s_1) \\ \vdots \\ v(s_n) \\ \end{pmatrix},\ D^{(m)}= \begin{pmatrix} l_0^{(m)}(s_0)&{}\quad l_1^{(m)}(s_0)&{}\quad \ldots &{}\quad l_n^{(m)}(s_0)\\ l_0^{(m)}(s_1)&{}\quad l_1^{(m)}(s_1)&{}\quad \ldots &{}\quad l_n^{(m)}(s_1)\\ \vdots &{}\quad \vdots &{}\quad \ddots &{}\quad \vdots \\ l_0^{(m)}(s_n)&{}\quad l_1^{(m)}(s_n)&{}\quad \ldots &{}\quad l_n^{(m)}(s_n) \end{pmatrix}, \end{aligned}$$

the formula (3.6) is equivalent to \(V_n^{(m)}=D^{(m)}V\), where \(D^{(m)}\) is called a differentiation matrix, which plays an important role in the collocation method. When \(m=1\), denote \(D^{(1)}\) by D, whose entries can be explicitly formulated as [54]

$$\begin{aligned} d_{ij}=\frac{\widetilde{c}_i(-1)^{i+j}}{\widetilde{c}_j(s_i-s_j)},\quad \ i\not =j,\quad d_{ii}=-\frac{s_i}{2(1-s_i^2)},\quad \ i\not =0, n,\quad d_{00}=-d_{nn}=\frac{2n^2+1}{6}, \end{aligned}$$

where \(\widetilde{c}_i=1\) \((i=1,2,\ldots , n-1)\) and \(\widetilde{c}_0=\widetilde{c}_n=2\). It can be straightforwardly shown that \(D^{(m)}=D^{m}\) when \(m>1\).

Denote the solution of (3.5) by \(v_j\), \(j=0,1,\ldots ,n\). Using the differentiation matrices, (3.5) can be converted to a system of nonlinear equations

$$\begin{aligned}&\sum _{j=1}^{n-1}\{(D^{2})_{ij}+p(s_i)(D)_{ij}-\left[ (D^{2})_{i0}+p(s_i)(D)_{i0}\right] \widetilde{\alpha }_{0j}\}v_j \nonumber \\&\qquad = g(s_i,v_i) -\left[ (D^{2})_{i0}+p(s_i)(D)_{i0}\right] \widetilde{c}_+-\left[ (D^{2})_{in}+p(s_i)(D)_{in}\right] \widetilde{c}_-,\quad \ i=1,2,\ldots ,n-1, \end{aligned}$$
(3.7)

where the parameters \(\widetilde{c}_+\), \(\widetilde{\alpha }_{0j}\), \(\widetilde{c}_-\), \(\widetilde{\alpha }_{nj}\) are evaluated by

$$\begin{aligned}&\widetilde{c}_+=\frac{B-\widetilde{d} A}{\widetilde{c}},\quad \ \widetilde{c}_-=A,\quad \ \widetilde{\alpha }_{0j}=\frac{2\beta \gamma (D)_{0j}}{\widetilde{c}},\quad \ j=1,2,\ldots ,n-1,\\&\widetilde{c}:=\sigma +2\beta \gamma (D)_{00},\quad \ \widetilde{d}:=2\beta \gamma (D)_{0n} \end{aligned}$$

via the boundary condition (3.2). Then

$$\begin{aligned}&v_0=\widetilde{c}_+ -\sum _{j=1}^{n-1}\widetilde{\alpha }_{0j}v_j,\quad \ v_n=A. \end{aligned}$$
(3.8)

Similarly, for the problem (3.1) with the boundary condition (3.3), we have

$$\begin{aligned} \sum _{j=1}^{n-1}\left\{ (D^{2})_{ij}+p(s_i)(D)_{ij}\right\} v_j&=g(s_i,v_i) -\left[ (D^{2})_{i0}+p(s_i)(D)_{i0}\right] v_0 -\left[ (D^{2})_{in}+p(s_i)(D)_{in}\right] v_n, \end{aligned}$$
(3.9)

where

$$\begin{aligned}&v_0=\widetilde{c}_+-\sum _{j=1}^{n-1}\widetilde{\alpha }_{0j}v_j,\quad \ v_n=\widetilde{c}_--\sum _{j=1}^{n-1}\widetilde{\alpha }_{nj}v_j \end{aligned}$$
(3.10)

with the parameters \(\widetilde{c}_+\), \(\widetilde{\alpha }_{0j}\), \(\widetilde{c}_-\), \(\widetilde{\alpha }_{nj}\) being defined by

$$\begin{aligned}&\widetilde{c}_+=\frac{\widetilde{b}B}{\widetilde{c}\widetilde{b}-\widetilde{a}\widetilde{d}},\quad \ \widetilde{c}_-=\frac{\widetilde{a}B}{\widetilde{a}\widetilde{d}-\widetilde{c}\widetilde{b}},\\&\widetilde{\alpha }_{0j}=\frac{\widetilde{d}(D)_{nj}-2\beta \gamma \widetilde{b}(D)_{0j}}{\widetilde{a}\widetilde{d}-\widetilde{c}\widetilde{b}},\quad \ \widetilde{\alpha }_{nj}=\frac{2\beta \gamma \widetilde{a}(D)_{0j}-\widetilde{c}(D)_{nj}}{\widetilde{a}\widetilde{d}-\widetilde{c}\widetilde{b}}.\\&\widetilde{a}:=(D)_{n0},\ \widetilde{b}:=(D)_{nn},\quad \ \widetilde{c}:=\sigma +2\beta \gamma (D)_{00},\quad \ \widetilde{d}:=2\beta \gamma (D)_{0n}. \end{aligned}$$

The system of the nonlinear equations (3.7) or (3.9) can be solved by Newton’s iterative method with an initial guess, then (3.8) or (3.10) is used to compute \(v_0\) and \(v_n\). We now discuss how to choose the initial values for Newton’s method. For the first boundary condition, we can use the known conditions \(u(0)=A\), \(u(1)=B\) to construct a linear interpolation to determine the initial values. For the other boundary conditions, we first use the condition \(\sigma u(1)+ \gamma u'(1)=B\) to determine the parameter \(a_0\) or A in (2.20) for \(u_M(x)\), then the deduced \(u_M(x)\) is used to evaluate the initial values. As we have mentioned in Remark 4, this technique is not accurate for determining the parameter, but it is enough to obtain the initial values for iteration. We note that we can also simply generate the initial values randomly in practical computation. Since the collocation method has high accuracy, we set machine precision (\(2.22045\times 10^{-16}\)) as the stop criteria for Newton’s method.

By using the computational values \((s_i,v_i)\), \(i=0,1,\ldots ,n\), we can construct a Lagrange interpolant \(v_n(s)=\sum _{j=0}^{n}v_j l_j(s)\). By letting \(\widetilde{l}_j(x)= l_j(2x^{\beta }-1)\), we obtain \(u_n(x)=\sum _{j=0}^{n}v_j\widetilde{l}_j(x)\), which is the interpolating approximation of u(x) based on the Chebyshev–Gauss–Lobatto points. Expanding \(u_n(x)\) about \(x=0\), we can also determine the unknown parameter \(a_0\) or A in the truncated series expansion \(u_M(x)\) with high precision.

Remark 7

Although the solution of (3.1) is smooth, the equation is still singular. In order to avoid the cancellation of significant digits, we should treat the singular parts carefully. For instance, when evaluating \(p(s_i)\) in (3.1), we should rewrite

$$\begin{aligned}&p(s_i)=\frac{\alpha +\beta -1}{2\beta }\sec ^2\left( \frac{\pi i}{2n}\right) ,\quad \ s_i=\cos \left( \frac{\pi i}{n}\right) ,\quad \ i=1,2,\ldots ,n-1. \end{aligned}$$

4 Convergence analysis

The implementation of collocation method is simple, but its convergence analysis is not easy. Canuto, Quarteroni, Shen, et al. [55,56,57] constructed the framework for analyzing the convergence of collocation method in weighted Sobolev spaces and Huang [30], Guo [33] conducted the convergence analysis of spectral collocation methods for singular differential equations. In this section, we only consider the linear case of Eq. (3.1) with homogeneous Dirichlet boundary conditions, which is rewritten as

$$\begin{aligned}&\frac{\mathrm{d}^2v}{{\mathrm{d}s}^2}+\frac{\kappa }{1+s}\frac{\mathrm{d}v}{\mathrm{d}s}=g(s),\quad \ -1<s<1,\ v(-1)=0,\quad \ v(1)=0. \end{aligned}$$
(4.1)

where \(\kappa = \frac{\alpha +\beta -1}{\beta }\) (\(0\le \alpha <1\)) and \(\widetilde{g}=(1+s)g(s)\) is sufficiently smooth about \(s\in [-1,1]\).

Denote \(v_n(s)\) by the collocation solution to (4.1) corresponding with the Chebyshev–Gauss–Lobatto points \(s_i\), \(i=0,1,\ldots ,n\), then

$$\begin{aligned}&v_n^{\prime \prime }(s_i)+\frac{\kappa }{1+s_i}v_n^{\prime }(s_i)=g(s_i),\quad \ i=1,2,\ldots ,n-1,\quad \ v_n(s_0)=v_n(s_n)=0, \end{aligned}$$
(4.2)

where the Lagrange interpolating polynomial \(v_n(s)\) of degree n reads

$$\begin{aligned}&v_n(s)=\sum _{j=0}^n l_j(s)v_j, \end{aligned}$$

and \(v_j\) is the approximation of \(v(s_j)\). Denote by

$$\begin{aligned}&\varPhi _{n,0}=\{\phi \in \mathcal {P}_n,\ \phi (-1)=\phi (1)=0 \}, \end{aligned}$$

where \(\mathcal {P}_n\) is the polynomial space of degree less than or equal to n. By introducing the Chebyshev weight function \(\omega (x)=(1-x^2)^{-1/2}\), we know the Chebyshev–Gauss–Lobatto quadrature formula holds [55]

$$\begin{aligned}&\int _{-1}^1\phi (s)\omega (s)\mathrm {d}s=\sum _{i=0}^n \omega _i \phi (s_i) \quad \ \mathrm {for} \ \phi (s)\in \mathcal {P}_{2n-1}, \end{aligned}$$
(4.3)

where \(\omega _0=\omega _n=\frac{\pi }{2n}\), \(\omega _i=\frac{\pi }{n}, \ i=1,2,\dots , n-1\).

For \(\forall \phi (s)\in \varPhi _{n,0}\), multiplying the equation in (4.2) by \((1+s_i)\omega _i \phi (s_i)\), summing over the range of i from 1 to \(n-1\), and noting that \( \phi (s_0)=\phi (s_n)=0\), we have

$$\begin{aligned}&\sum _{i=0}^n (1+s_i) \omega _i \phi (s_i)v_n^{\prime \prime }(s_i)+\kappa \sum _{i=0}^n \omega _i \phi (s_i)v_n^{\prime }(s_i)=\sum _{i=0}^n \omega _i \phi (s_i)\widetilde{g}(s_i). \end{aligned}$$
(4.4)

Noting that \(v_n(s)\) is a polynomial of degree n, we know from (4.3) that Eq. (4.4) is equivalent to

$$\begin{aligned}&\int _{-1}^1\omega (s)\phi (s)(1+s)v_n^{\prime \prime }(s)\mathrm{d}s+\kappa \int _{-1}^1\omega (s)\phi (s)v_n^{\prime }(s)\mathrm{d}s=\sum _{i=0}^n \omega _i \phi (s_i)\widetilde{g}(s_i), \end{aligned}$$
(4.5)

which yields by integrating by parts for the first integral in (4.5)

$$\begin{aligned}&\int _{-1}^1(1+s)v_n^{\prime }(s)(\omega (s)\phi (s))^\prime \mathrm{d}s-(\kappa -1)\int _{-1}^1\omega (s)\phi (s)v_n^{\prime }(s)\mathrm{d}s=-\sum _{i=0}^n \omega _i \phi (s_i)\widetilde{g}(s_i). \end{aligned}$$
(4.6)

By introducing the following notations:

$$\begin{aligned} a_\omega (v,\phi )&=\int _{-1}^1(1+s)v^{\prime }(\omega \phi )^\prime \mathrm{d}s,\quad \ b_\omega (v,\phi )=\int _{-1}^1\omega (s)\phi (s)v^{\prime }(s)\mathrm{d}s, \end{aligned}$$
(4.7)
$$\begin{aligned} (\widetilde{g},\phi )_{\omega }&=\int _{-1}^1\omega (s)\widetilde{g}(s)\phi (s)\mathrm{d}s,\quad \ (\widetilde{g},\phi )_{\omega ,n}=\sum _{i=0}^n \omega _i \phi (s_i)\widetilde{g}(s_i), \end{aligned}$$
(4.8)

Eq. (4.6) is written as

$$\begin{aligned}&a_\omega (v_n,\phi )-(\kappa -1)b_\omega (v_n,\phi )=-\,(\widetilde{g},\phi )_{\omega ,n}\quad \ \forall \phi \in \varPhi _{n,0}. \end{aligned}$$
(4.9)

Analogously, the boundary value problem (4.1) can be transformed to

$$\begin{aligned}&a_\omega (v,\phi )-(\kappa -1)b_\omega (v,\phi )=-\,(\widetilde{g},\phi )_{\omega }\quad \ \forall \phi \in \varPhi _{n,0}. \end{aligned}$$
(4.10)

Then, subtracting (4.9) from (4.10) gives the error equation

$$\begin{aligned}&a_\omega (v-v_n,\phi )-(\kappa -1)b_\omega (v-v_n,\phi )=-\,\left[ (\widetilde{g},\phi )_{\omega }-(\widetilde{g},\phi )_{\omega ,n} \right] \quad \ \forall \phi \in \varPhi _{n,0}. \end{aligned}$$
(4.11)

Generally, it is convenient to estimate the error \(v-v_n\) in weighted Sobolev spaces. Denote \(I=(-1,1)\), and let \(\omega ^{(\gamma ,\delta )}(s)=(1-s)^\gamma (1+s)^\delta \) be the Jacobi weight. For this weight, we define weighted \(L^2\) space

$$\begin{aligned}&L^2_{\omega ^{(\gamma ,\delta )}}(I)=\{v|\ v \hbox { is measurable and } \Vert v\Vert _{\omega ^{(\gamma ,\delta )}}<\infty \} \end{aligned}$$

with inner product and norm

$$\begin{aligned}&(u,v)_{\omega ^{(\gamma ,\delta )}}=\int _I u(s) v(s) \omega ^{(\gamma ,\delta )}(s)\mathrm{d}s,\quad \ \Vert v\Vert _{\omega ^{(\gamma ,\delta )}}=\sqrt{(v,v)_{\omega ^{(\gamma ,\delta )}}}. \end{aligned}$$

For any integer \(m\ge 0\), we set

$$\begin{aligned}&H^m_{\omega ^{(\gamma ,\delta )}}(I)=\left\{ v\in L^2_{\omega ^{(\gamma ,\delta )}}(I)|\ v^{(k)}\in L^2_{\omega ^{(\gamma ,\delta )}}(I), \ 0\le k\le m \right\} \end{aligned}$$

with norm and semi-norm

$$\begin{aligned}&\Vert v\Vert _{m,\omega ^{(\gamma ,\delta )}}=\left( \sum \limits _{k=0}^m \Vert v^{(k)}\Vert ^2_{\omega ^{(\gamma ,\delta )}}\right) ^{1/2},\quad \ |v|_{m,\omega ^{(\gamma ,\delta )}}= \Vert v^{(m)}\Vert _{\omega ^{(\gamma ,\delta )}}. \end{aligned}$$

We also set \(H^1_{\omega ^{(\gamma ,\delta )},0}(I)=\{v\in H^1_{\omega ^{(\gamma ,\delta )}}(I)|\ v(-1)=v(1)=0\}\). We note that when \(\gamma =\delta =-\frac{1}{2}\), the Jacobi weight \(\omega ^{(\gamma ,\delta )}(s)\) degenerates to Chebyshev weight \(\omega (s)=(1-s^2)^{-1/2}\), and the notations for spaces and norms are correspondingly simplified. In the following, we provide some useful lemmas.

Lemma 1

([33], Lemma 3.7) If \(\rho \le \gamma +2\), \(\tau \le \delta +2\), and \(-1<\rho ,\tau <1\), then for any \(v\in H^1_{\omega ^{(\rho ,\tau )},0}(I)\), we have \(\Vert v\Vert _{\omega ^{(\gamma ,\delta )}}\le c |v|_{1,\omega ^{(\rho ,\tau )}}\), where c is a positive constant.

Lemma 2

([30], Lemma 3.6) For \(v,\phi \in H^1_{\omega ,0}(I)\), we have for \(a_\omega (v,\phi )\) defined in (4.7)

$$\begin{aligned}&\frac{1}{4}|v|^2_{1,\omega ^{(-1/2,1/2)}}+\frac{3}{8}\int _I\frac{v^2(s)\omega (s)}{1-s}\mathrm {d}s -\frac{1}{8}\int _I\frac{v^2(s)\omega (s)}{1+s}\mathrm {d}s \le a_\omega (v,v)\le |v|^2_{1,\omega ^{(-1/2,1/2)}}, \end{aligned}$$
(4.12)
$$\begin{aligned}&\left| a_\omega (v,\phi )\right| \le 3|v|_{1,\omega ^{(-1/2,1/2)}}|\phi |_{1,\omega ^{(-1/2,1/2)}}. \end{aligned}$$
(4.13)

Lemma 3

For \(v,\phi \in H^1_{\omega ,0}(I)\), we have for \(b_\omega (v,\phi )\) defined in (4.7)

$$\begin{aligned}&b_\omega (v,v)=-\frac{1}{4}\int _I\frac{v^2(s)\omega (s)}{1-s}\mathrm {d}s +\frac{1}{4}\int _I\frac{v^2(s)\omega (s)}{1+s}\mathrm {d}s, \end{aligned}$$
(4.14)
$$\begin{aligned}&\left| b_\omega (v,\phi )\right| \le c|v|_{1,\omega ^{(-1/2,1/2)}}|\phi |_{1,\omega ^{(-1/2,1/2)}}. \end{aligned}$$
(4.15)

Proof

From the definition of \(b_\omega (v,\phi )\), noting that \(v(-1)=v(1)=0\), we know

$$\begin{aligned} b_\omega (v,v)&=\frac{1}{2}\int _I\omega (s)\frac{\mathrm {d}v^2}{\mathrm {d}s}\mathrm {d}s =-\frac{1}{2}\int _Iv^2(s)\frac{\mathrm {d}\omega (s)}{\mathrm {d}s}\mathrm {d}s =-\frac{1}{2}\int _I\frac{s}{1-s^2}v^2(s)\omega (s)\mathrm {d}s\\&=-\frac{1}{4}\int _I\frac{v^2(s)\omega (s)}{1-s}\mathrm {d}s +\frac{1}{4}\int _I\frac{v^2(s)\omega (s)}{1+s}\mathrm {d}s. \end{aligned}$$

As for (4.15), by using Cauchy inequality, we have

$$\begin{aligned} \left| b_\omega (v,\phi )\right|&=\left| \int _I(1+s)\omega (s)\frac{\phi (s)}{1+s}v^{\prime }(s)\mathrm{d}s\right| \\&\le \left( \int _I(1+s)\omega (s)(v^{\prime }(s))^2\mathrm{d}s\right) ^{1/2}\left( \int _I\frac{\phi ^2(s)\omega (s)}{1+s}\mathrm {d}s\right) ^{1/2}. \end{aligned}$$

In Lemma 1, taking \(\gamma =-\frac{1}{2}\), \(\delta =-\frac{3}{2}\), \(\rho =-\frac{1}{2}\), \(\tau =\frac{1}{2}\) implies

$$\begin{aligned}&\int _I\frac{\phi ^2(s)\omega (s)}{1+s}\mathrm {d}s\le c^2 |\phi |^2_{1,\omega ^{(-1/2,1/2)}}. \end{aligned}$$

Hence, (4.15) holds. The proof is complete. \(\square \)

Lemma 4

([33], Lemma 3.16) For the orthogonal projection \(P^0_{n,\gamma ,\delta }\): \(H_{\omega ^{(\gamma ,\delta )},0}^1(I)\rightarrow \varPhi _{n,0}\) defined by \(((v-P^0_{n,\gamma ,\delta }v)^\prime ,\phi ^\prime )_{\omega ^{(\gamma ,\delta )}}=0\), \(v\in H_{\omega ^{(\gamma ,\delta )},0}^1(I)\), \(\forall \phi \in \varPhi _{n,0}\), there holds

$$\begin{aligned}&\Vert v-P^0_{n,\gamma ,\delta }v\Vert _{1,\omega ^{(\gamma ,\delta )}}\le c\, n^{1-m}\Vert v\Vert _{m,\omega ^{(\gamma ,\delta )},*} \le c\, n^{1-m}\Vert v\Vert _{m,\omega ^{(\gamma ,\delta )}},\ m>1. \end{aligned}$$
(4.16)

where \(c>0\) is a constant and the definition of the norm \(\Vert v\Vert _{m,\omega ^{(\gamma ,\delta )},*}\) can be found in [33].

Lemma 5

([56, 57]) For all \(\phi \in \varPhi _{n,0}\) and \(v\in H_{\omega }^m(I)\), \(m\ge 1\), there holds

$$\begin{aligned}&|(v,\phi )_{\omega }-(v,\phi )_{\omega ,n}|\le c\, n^{-m}\Vert v\Vert _{m,\omega }\Vert \phi \Vert _{\omega }. \end{aligned}$$

In Lemma 1, by taking \(\gamma =\delta =-\frac{1}{2}\), \(\rho =-\frac{1}{2}\), \(\tau =\frac{1}{2}\), we know \(\Vert \phi \Vert _{\omega }\le c |\phi |_{1,\omega ^{(-1/2,1/2)}}\) for \(\phi \in \varPhi _{n,0}\). Hence

$$\begin{aligned}&|(\widetilde{g},\phi )_{\omega }-(\widetilde{g},\phi )_{\omega ,n}|\le c\, n^{-m}\Vert \widetilde{g}\Vert _{m,\omega }|\phi |_{1,\omega ^{(-1/2,1/2)}}. \end{aligned}$$
(4.17)

Now we state the convergence result of the Chebyshev collocation method. We note that \(C_1\), \(C_2\) and c are general positive constants in this section, which may have different values in different places.

Theorem 3

Suppose that \(v(s)\in H^1_{\omega ,0}(I)\cap H^m_{\omega ^{(-1/2,1/2)}}(I)\) is the solution of the singular differential equation (4.1) (\(0\le \alpha <1\)) and \(v_n(s)\in \varPhi _{n,0}\) is the collocation solution to (4.1) corresponding with \(n+1\) Chebyshev–Gauss–Lobatto points. If \(\kappa ={\alpha +\beta -1}/{\beta }\) satisfies \(-\frac{1}{2}\le \kappa \le \frac{1}{2}\) (or equivalently \(\frac{1}{2}\beta \le 1-\alpha \le \frac{3}{2}\beta \)), then there exist two positive constant \(C_1\), \(C_2\) such that the error \(v-v_n\) is estimated by

$$\begin{aligned}&|v-v_n|_{1,\omega ^{(-1/2,1/2)}} \le C_1\, n^{1-m}\Vert v\Vert _{m,\omega ^{(-1/2,1/2)}} +C_2\, n^{-m}\Vert \widetilde{g}\Vert _{m,\omega }, \end{aligned}$$
(4.18)

where \(\widetilde{g}=(1+s)g(s)\) is sufficiently smooth.

Proof

For \(\forall \psi \in \varPhi _{n,0}\), we rewrite the error equation (4.11) as

$$\begin{aligned}&a_\omega (\psi -v_n,\phi )-(\kappa -1)b_\omega (\psi -v_n,\phi )\\&\qquad =-a_\omega (v-\psi ,\phi )+(\kappa -1)b_\omega (v-\psi ,\phi ) -\left[ (\widetilde{g},\phi )_{\omega }-(\widetilde{g},\phi )_{\omega ,n} \right] \ \forall \phi \in \varPhi _{n,0}. \end{aligned}$$

Taking \(\phi =\psi -v_n\) and using (4.13), (4.15), (4.17), we have

$$\begin{aligned}&a_\omega (\psi -v_n,\psi -v_n)-(\kappa -1)b_\omega (\psi -v_n,\psi -v_n)\nonumber \\&\quad \le \left( 3|v-\psi |_{1,\omega ^{(-1/2,1/2)}} +c|\kappa -1| |v-\psi |_{1,\omega ^{(-1/2,1/2)}} + c\, n^{-m}\Vert \widetilde{g}\Vert _{m,\omega }\right) |\psi -v_n|_{1,\omega ^{(-1/2,1/2)}}. \end{aligned}$$
(4.19)

From (4.12) and (4.14), we know when \(-\frac{1}{2}\le \kappa \le \frac{1}{2}\)

$$\begin{aligned}&a_\omega (\psi -v_n,\psi -v_n)-(\kappa -1)b_\omega (\psi -v_n,\psi -v_n)\nonumber \\&\quad \ge \frac{1}{4}|\psi -v_n|^2_{1,\omega ^{(-1/2,1/2)}} +\frac{1+2\kappa }{8}\int _I\frac{(\psi (s)-v_n(s))^2\omega (s)}{1-s}\mathrm {d}s\nonumber \\&\qquad +\frac{1-2\kappa }{8}\int _I\frac{(\psi (s)-v_n(s))^2\omega (s)}{1+s}\mathrm {d}s\nonumber \\&\quad \ge \frac{1}{4}|\psi -v_n|^2_{1,\omega ^{(-1/2,1/2)}}. \end{aligned}$$
(4.20)

Combining (4.19) with (4.20) yields

$$\begin{aligned}&|\psi -v_n|_{1,\omega ^{(-1/2,1/2)}} \le C_1|v-\psi |_{1,\omega ^{(-1/2,1/2)}}+C_2\, n^{-m}\Vert \widetilde{g}\Vert _{m,\omega }. \end{aligned}$$

Taking \(\psi =P^0_{n,-1/2,1/2}v\) defined in Lemma 4, we know

$$\begin{aligned}&|P^0_{n,-1/2,1/2}v-v_n|_{1,\omega ^{(-1/2,1/2)}} \le C_1\, n^{1-m}\Vert v\Vert _{m,\omega ^{(-1/2,1/2)}}+C_2\, n^{-m}\Vert \widetilde{g}\Vert _{m,\omega }. \end{aligned}$$
(4.21)

Further using the triangle inequality

$$\begin{aligned} |v-v_n|_{1,\omega ^{(-1/2,1/2)}}\le |v-P^0_{n,-1/2,1/2}v|_{1,\omega ^{(-1/2,1/2)}}+|P^0_{n,-1/2,1/2}v-v_n|_{1,\omega ^{(-1/2,1/2)}} \end{aligned}$$

and Lemma 4, we know (4.18) holds. The theorem is proved. \(\square \)

Theorem 3 tells us that the accuracy of the collocation method depends upon the smoothness of the solution and the source term. In order to increase the accuracy of the scheme, it is necessary to perform a smooth transformation as done in Sect. 3. In this section, we only discuss a special linear case for \(0\le \alpha <1\). We note that the case includes the most important one \(\beta =1-\alpha \) corresponding to \(\kappa =0\). As for the other cases, we are going to explore in the future.

Remark 8

As stated in [33], the semi-norm \(|v|_{1,\omega ^{(-1/2,1/2)}}\) is a norm of the space \(H^1_{\omega ^{(-1/2,1/2)},0}(I)\), which is equivalent to the norm \(\Vert v\Vert _{1,\omega ^{(-1/2,1/2)}}\). Hence, (4.18) also holds for this norm.

5 Numerical examples

In this section, we present three examples to show the performance of our proposed methods. All the experiments are performed on a Laptop with Intel Core i5-6200U CPU (2.30 GHz) and 8 GB RAM by using Mathematica.

Example 1

Solve the following linear strongly singular two-point boundary value problem using our method, the Adomian decomposition method (ADM) [45], and the optimal homotopy analysis method (OHAM) [41]

$$\begin{aligned} \begin{aligned} (xu')'&=g(x)u:=\frac{9}{4}\left( \sqrt{x}+x^2\right) u,\quad u'(0)&=0,\quad \ \frac{1}{2}u(1)+\frac{1}{3}u'(1)=4\mathrm {e}. \end{aligned} \end{aligned}$$
(5.1)

We know its exact solution is \(u(x)=4\mathrm {e}^{x^{3/2}}\).

In this example, \(\alpha =1\), but \(g(x)=\frac{9}{4}\left( \sqrt{x}+x^2\right) \) involves a term \(\sqrt{x}\). Hence the solution is not sufficiently smooth at \(x=0\). By implementing the series expansion method, we obtain the truncated fractional power series expansion for u(x) about \(x=0\) with a parameter \(A=u(0)\), denoted by

$$\begin{aligned} u_p(x)=A+Ax^{3/2}+\frac{A}{2}x^3+\frac{A}{6}x^{9/2}+\frac{A}{24}x^6+\frac{A}{120}x^{15/2}+\frac{A}{720}x^9, \end{aligned}$$

from which we know the transformation \(s=2\sqrt{x}-1\) can make the solution u(x) infinitely smooth. By discretizing the transformed equation (3.1) using the Chebyshev collocation method with \(n=18\), we obtain a fractional Lagrange interpolation

$$\begin{aligned} \begin{aligned} u_{tc}(x)&=4- 4.57551\times {10}^{-14}\sqrt{x} + 3.42666\times {10}^{-8}x + 4x^{3/2} +1.17129\times {10}^{-4}x^2 \\&\quad - 0.00222858 x^{5/2} + 2.02614 x^3 -0.20533 x^{7/2} + 1.13593 x^4 - 3.90777 x^{9/2} + 13.6913 x^5 \\&\quad -30.8144 x^{11/2} + 52.5145 x^6 - 66.8327 x^{13/2} +63.2231 x^7 -43.0473 x^{15/2} + 20.0611 x^8 \\&\quad - 5.74558 x^{17/2}+ 0.776323 x^9. \end{aligned} \end{aligned}$$

Comparing this approximate solution with \(u_p(x)\), we know the parameter \(A=4\) in the fractional series expansion \(u_p(x)\), which leads to

$$\begin{aligned} u_p(x)=4+4x^{3/2}+2x^3+\frac{2}{3}x^{9/2}+\frac{1}{6}x^6+\frac{1}{30}x^{15/2}+\frac{1}{180}x^9. \end{aligned}$$

As a comparison, we also solve this example using ADM and OHAM. Since Eq. (5.1) is equivalent to

$$\begin{aligned} u(x)=u(0)+\int _0^xt^{-1}\int _0^t g(\xi )u(\xi )\mathrm {d}\xi \, \mathrm {d}t, \end{aligned}$$

the Adomian iteration reads

$$\begin{aligned}&y_0(x)=A,\ y_i(x)=\int _0^x t^{-1}\int _0^t g(\xi )y_{i-1}(\xi )\mathrm {d}\xi \,\mathrm {d}t,\quad \ i=1,2,\ldots , \end{aligned}$$

from which the m-th approximate solution of ADM is \(u_m^{\mathrm {adm}}(x)=\sum _{i=0}^m y_i(x)\). We note that the parameter A is determined by the right boundary condition. A direct computation shows

$$\begin{aligned} u_6^{\mathrm {adm}}(x)&= 4 + 4 x^{3/2} + 2 x^3 + \frac{2}{3} x^{9/2} + \frac{1}{6} x^6 + \frac{1}{30} x^{15/2} + 0.00555556 x^9 \\&\quad + 0.000793494 x^{21/2} + 0.0000988595 x^{12} + 0.0000107118 x^{27/2}\\&\quad + 9.54922\times 10^{-7} x^{15} + 6.01026\times 10^{-8} x^{33/2} + 1.8838\times 10^{-9} x^{18}. \end{aligned}$$

The OHAM is based on the integral equation (2.5). By introducing an optimal parameter h, the OHAM reads

$$\begin{aligned}&y_0(x)=\frac{B}{\sigma },\ y_1(x)=-h\int _{0}^{1}G(x,\xi )g(\xi )y_0(\xi ))\mathrm {d}\xi ,\\&y_i(x)=(1+h)y_{i-1}(x)-h\int _{0}^{1}G(x,\xi )g(\xi )y_{i-1}(\xi )\mathrm {d}\xi ,\quad \ i=2,3,\ldots , \end{aligned}$$

from which the m-th approximate solution of OHAM is \(u_m^{\mathrm {oham}}(x)=\sum _{i=0}^m y_i(x)\). The parameter h is determined by minimizing the error

$$\begin{aligned}&\int _0^1\left[ u_m^{\mathrm {oham}}(x)-\frac{B}{\sigma }-\int _{0}^{1}G(x,\xi )g(\xi )u_m^{\mathrm {oham}}(\xi )\mathrm {d}\xi \right] ^2\mathrm {d}x. \end{aligned}$$

When \(m=6\), we obtain the optimal \(h=-0.394885\) and the approximate solution

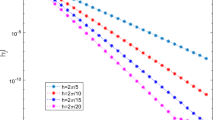
$$\begin{aligned} u_6^{\mathrm {oham}}(x)&= 3.98385 + 4.02531 x^{3/2} + 2.03473 x^3 + 0.667562 x^{9/2} + 0.151846 x^6 + 0.0254998 x^{15/2}\\&\quad + 0.00321373 x^9 + 0.000299202 x^{21/2} + 0.0000228003 x^{12} + 1.15048\times 10^{-6} x^{27/2}\\&\quad + 5.57005\times 10^{-8} x^{15} + 1.23837\times 10^{-9} x^{33/2} + 3.88143\times 10^{-11} x^{18}. \end{aligned}$$

We note that when \(h=-1\), the OHAM degenerates to the improved Adomian decomposition method [45], but it is not convergent for this example. In order to discuss the accuracy of these approximations, we plot their absolute errors with logarithmic scale, as shown in Fig.1.

Fig. 1
figure 1

The absolute errors of the approximate solutions to the exact solution in Example 1

Full size image

It can be seen from Fig. 1 that the Chebyshev collocation method with smoothing transformation has the highest accuracy even though the highest degree of \(u_{tc}(x)\) is only half compared with the ones of the other two methods and the OHAM has the lowest accuracy in this example. Since the standard OHAM is not convergent fast, Roul et al. [42] further designed a domain decomposition OHAM to accelerate the convergence. As we expected, the series expansion \(u_{p}(x)\) approximates u(x) with high precision only over a small interval near \(x=0\). When the variable x moves away from \(x=0\) to \(x=1\), the accuracy decreases gradually. In the computation, we also record the CPU time for these methods. For our method, the total CPU time for generating \(u_p(x)\) and calculating \(u_{tc}(x)\) is only 0.03125 seconds, whereas the ADM and OHAM cost 8.04688 and 99.6719 seconds, respectively. Obviously, our method is much faster than the other two methods. Although both the iteration procedures of the ADM and OHAM are very simple, they cost much time since many integrals are evaluated analytically by symbolic computation in their iterations.

Example 2

Solve the following nonlinear singular two-point boundary value problem:

$$\begin{aligned} \begin{aligned}&\left( x^{1/2}u'\right) '=f(x,u):=\frac{2}{\sqrt{x}(2-x)}-\frac{\sqrt{u}}{(2-x)^{3/2}},\\&u(0)=A:=\frac{\pi ^2}{4},\ u(1)=0. \end{aligned} \end{aligned}$$
(5.2)

Its exact solution is \(u(x)=\left( \arcsin (1-x)\right) ^2\).

For this example, f(x, u) is obviously weakly singular at \(x=0\). Even so, we can also use the series expansion Mathematica function Pesbvp[f,1/2,10,A,\(a_0\)] to obtain

$$\begin{aligned} u_p(x)&= \frac{\pi ^2}{4}+a_0\sqrt{x}+2x-\frac{\pi }{6 \sqrt{2}}x^{3/2}+\left( \frac{1}{6}-\frac{a_0}{6 \sqrt{2} \pi }\right) x^2+\left( -\frac{1}{5 \sqrt{2} \pi }-\frac{3 \pi }{80\sqrt{2}}+\frac{a_0^2}{10 \sqrt{2} \pi ^3}\right) x^{5/2}\\&\quad +\bigg [\frac{7}{180}+a_0 \left( \frac{2 \sqrt{2}}{15 \pi ^3}-\frac{1}{20 \sqrt{2} \pi }\right) -\frac{\sqrt{2}a_0^3}{15 \pi ^5}\bigg ] x^3 \\&\quad +\bigg [\frac{2 \sqrt{2}}{21 \pi ^3}-\frac{5}{63 \sqrt{2} \pi }-\frac{5 \pi }{448 \sqrt{2}}-\frac{a_0}{252 \pi ^2}+a_0^2\left( -\frac{2 \sqrt{2}}{7 \pi ^5}+\frac{1}{28 \sqrt{2}\pi ^3}\right) +\frac{5 a_0^4}{21 \sqrt{2} \pi ^7}\bigg ]x^{7/2} \\&\quad +\bigg [\frac{53}{4480}-\frac{1}{120 \pi ^2}+a_0 \left( -\frac{3\sqrt{2}}{7 \pi ^5}+\frac{5}{42 \sqrt{2} \pi ^3}-\frac{15}{896 \sqrt{2} \pi }\right) +\frac{17a_0^2}{1680\pi ^4}\\&\quad +a_0^3 \left( \frac{5 \sqrt{2}}{7 \pi ^7}-\frac{3}{56\sqrt{2} \pi ^5}\right) -\frac{a_0^5}{2 \sqrt{2} \pi ^9}\bigg ] x^4+\cdots . \end{aligned}$$

Based on this series expansion, we choose the smoothing transformation \(s=2\sqrt{x}-1\). By applying the Chebyshev collocation method with \(n=20\) to the transformed equation (3.1), we can obtain the Chebyshev interpolation

$$\begin{aligned} \begin{aligned} u_{tc}(x)&=2.4674-4.44288\sqrt{x} + 2x - 0.370241 x^{3/2} + 0.333357 x^2 -0.0838254 x^{5/2}\\&\quad + 0.0961995 x^3 - 0.0946874 x^{7/2} +0.506482 x^4 - 2.42262 x^{9/2} + 9.22243 x^5 \\&\quad - 26.9487 x^{11/2}+60.9291 x^6 - 106.786 x^{13/2} + 144.658 x^7+\cdots +0.683452x^{10}, \end{aligned} \end{aligned}$$

which is an approximate solution to u(x). Since \(u_{tc}(x)\) and \(u_p(x)\) are both accurate when x is small, we can conclude that \(a_{0}=-4.442882938175524\) in the series expansion \(u_p(x)\). Thus

$$\begin{aligned} \begin{aligned} u_p(x)&=2.4674-4.44288\sqrt{x} + 2x - 0.37024 x^{3/2} + 0.333333 x^2 -0.0833041 x^{5/2}\\&\quad + 0.0888889 x^3 - 0.0247929 x^{7/2} +0.0285714 x^4 - 0.00843646 x^{9/2} + 0.0101587x^5\\&\quad - 0.00310615x^{11/2} +0.003848 x^6 - 0.00120463 x^{13/2} +\cdots +0.000110849x^{10}. \end{aligned} \end{aligned}$$

For comparison, we apply the Chebyshev collocation method (taking \(n=20\)) directly to solve the problem (5.2) and obtain an approximate solution

$$\begin{aligned} \begin{aligned} u_c(x)&=2.4674 - 55.407 x + 2542.05 x^2 - 80553.5 x^3 + 1.60707\times 10^6 x^4 - 2.13328\times 10^7 x^5 \\&\quad + 1.98344\times 10^8 x^6 - 1.34265\times 10^9 x^7 + 6.80723\times 10^9 x^8 +\cdots + 1.01071\times 10^9 x^{20}. \end{aligned} \end{aligned}$$

The absolute errors of the approximate solutions \(u_{tc}(x)\), \(u_{p}(x)\), and \(u_{c}(x)\) are plotted in Fig. 2 with logarithmic scale.

Fig. 2
figure 2

The absolute errors of the approximate solutions to the exact solution in Example 2

Full size image

It can be seen from Fig. 2 that the approximate solution \(u_{c}(x)\) has very low precision of about \(10^{-1}\) order. After smoothing transformation, the solution \(u_{tc}(x)\) achieves a very high precision, whose accuracy is about \(10^{-13}\) order. In addition, the fractional power series \(u_{p}(x)\) is a good approximation to u(x) when \(x\le 0.25\), but it gradually becomes less accurate as x tends to 1.

We further explore the convergence order of the Chebyshev collocation method for the transformed equation using different n, and the results are shown in Table 1, where in this table, the maximal absolute error \(E_n=\max _{0\le x\le 1}|u(x)-u_{tc}(x)|\) and the order is defined by \(\log E_n/\log E_{2n}\). From Table 1, we know the order is about 0.5, which means \(E_n=O\left( \exp (-\theta n)\right) \) (\(\theta >0\)). Rubio [58] called this convergence as exponential convergence. We note that we only discuss the algebraic convergence in Sect. 4. In addition, we can also see that the CPU time increases slowly as n increases to two times.

Table 1 Convergence order and CPU time in Example 2
Full size table

Example 3

Solve the nonlinear strongly singular two-point boundary value problem

$$\begin{aligned} \begin{aligned}&\left( x^{3/2}u'\right) '=-\frac{4}{9}\pi ^2x^{13/6}u-\frac{11}{9}\pi x^{5/6}\sqrt{1-u^2},\\&u'(0)=0,\ u(1)+3u'(1)=-2\pi , \end{aligned} \end{aligned}$$
(5.3)

with the exact solution \(u(x)=\cos \left( \pi x^{4/3}/2\right) \).

This example is a strongly singular problem. By means of the proposed series expansion method, we obtain the truncated fractional series expansion for u(x) about \(x=0\)

$$\begin{aligned} \begin{aligned} u_p(x)&=A-\frac{\pi }{2} \sqrt{1-A^2} x^{4/3}-\frac{A \pi ^2}{8}x^{8/3}+\frac{\pi ^3}{48} \sqrt{1-A^2} x^4+\frac{A \pi ^4}{384}x^{16/3}\\&\quad -\frac{\pi ^5}{3840}\sqrt{1-A^2}x^{20/3}-\frac{A \pi ^6}{46080}x^8+\frac{\pi ^7 \sqrt{1-A^2} x^{28/3}}{645120}+\frac{\pi ^8 A x^{32/3}}{10321920}. \end{aligned} \end{aligned}$$

Hence, we choose the smoothing transformation \(s=2x^{2/3}-1\). By applying the Chebyshev collocation method with \(n=20\) to the new equation, we can formulate a Lagrange interpolation

$$\begin{aligned} \begin{aligned} u_{tc}(x)&=1+ 3.59234\times {10}^{-14}x^{2/3} - 8.57432\times {10}^{-11} x^{4/3} +4.70386 \times {10}^{-9} x^2 - 1.2337 x^{8/3} \\&\quad + 1.90657 \times {10}^{-6} x^{10/3} -1.99629 \times {10}^{-5} x^4 +0.000148541 x^{14/3} + 0.252854 x^{16/3}\\&\quad + 0.00339015 x^6 - 0.0108396 x^{20/3}+ 0.0269292 x^{22/3} - 0.073067 x^8 + 0.0788706 x^{26/3}\\&\quad - 0.0921944 x^{28/3} + 0.0821393 x^{10} - 0.053415 x^{32/3} + 0.0255147 x^{34/3} - 0.00784089 x^{12} \\&\quad + 0.00132846 x^{38/3} - 0.000099176 x^{40/3}. \end{aligned} \end{aligned}$$

From this approximate solution, we know the parameter \(A=1\) in the series expansion \(u_p(x)\), which leads to

$$\begin{aligned} u_p(x)=1-\frac{\pi ^2}{8} x^{8/3}+\frac{\pi ^4}{384} x^{16/3}-\frac{\pi ^6}{46080} x^{8}+\frac{\pi ^8}{10321920} x^{32/3}. \end{aligned}$$

We can also directly solve Eq. (5.3) using the Chebyshev collocation method (taking \(n=20\)) to obtain an approximate solution \(u_c(x)\). The absolute errors of the three approximate solutions \(u_{tc}(x)\), \(u_{p}(x)\), and \(u_{c}(x)\) to the exact solution u(x) are plotted in Fig. 3.

Fig. 3
figure 3

The absolute errors of the approximate solutions to the exact solution in Example 3

Full size image

We can see from Fig. 3 that the approximate solution \(u_{c}(x)\) has the accuracy \(10^{-6}\) since the exact solution is twice continuously differentiable over the interval [0, 1]. By using smoothing transformation, the solution \(u_{tc}(x)\) achieves the accuracy \(10^{-14}\). For this example, the series expansion \(u_{p}(x)\) has very high accuracy when \(x\le 0.2\), but it becomes less accurate as \(x\rightarrow 1\).

The three examples in this section demonstrate that the Chebyshev collocation method can be applied directly to solve the singular two-point boundary value problem, but the approximate solution is not accurate due to the low regularity of the exact solution u(x) at \(x=0\). Obviously, the smoother the solution is, the higher accuracy will be achieved for the Chebyshev collocation method. With the proposed series decomposition method, we can give an accurate description of the singular behavior of the solution using the fractional series expansion. Then, a suitable smoothing transformation is taken for the equation so that the solution is sufficiently smooth. For the transformed equation, the accuracy of the Chebyshev collocation method can be improved significantly. In addition, the Lagrange interpolation of the Chebyshev collocation solution can also determine the unknown parameter \(a_0\) or A in the fractional series expansion with high precision. In most cases, the fractional series expansion approximates u(x) with high precision only in the neighborhood of \(x=0\). When the variable x is away from the point \(x=0\), the series expansion gradually becomes less accurate.

6 Applications to the Thomas–Fermi equation and Emden–Fowler equation

In this section, we apply our method to solve the Thomas–Fermi equation and Emden–Fowler equation over finite interval. We first consider the Thomas–Fermi equation. It is used to model the potentials and charge densities in atoms [7, 9,10,11,12]. The equation is

$$\begin{aligned}&u^{\prime \prime }=\frac{u^{3/2}}{\sqrt{x}},\quad \ x>0. \end{aligned}$$
(6.1)

There are three kinds of boundary conditions of interest for this equation [9, 10]. Here, we only consider the ion case

$$\begin{aligned}&u(0)=1,\quad \ u(1)=0. \end{aligned}$$
(6.2)

By implementing the Mathematica function Pesbvp[f,0,10,1,a0], we obtain the series expansion with an undetermined parameter \(a_0\) for the solution u(x) about \(x=0\)

$$\begin{aligned} u_{p,l}(x)&=1+a_0 x+\frac{4}{3} x^{3/2} +\frac{2 a_0}{5} x^{5/2} +\frac{1}{3} x^3 +\frac{3 a_0^2}{70} x^{7/2} +\frac{2 a_0}{15} x^4+\left( \frac{2}{27}-\frac{a_0^3}{252}\right) x^{9/2} \nonumber \\&\quad + \frac{a_0^2}{175} x^5 + \left( \frac{31 a_0}{1485}+\frac{a_0^4}{1056}\right) x^{11/2} +\left( \frac{4}{405}+\frac{4 a_0^3}{1575}\right) x^6\nonumber \\&\quad +\left( \frac{557 a_0^2}{100100}-\frac{3 a_0^5}{9152}\right) x^{13/2} +\cdots + \left( \frac{51356 a_0}{103378275}-\frac{99856 a_0^4}{70945875}+\frac{256 a_0^7}{1044225}\right) x^{10}. \end{aligned}$$
(6.3)

Next, we discuss the asymptotic behavior of u(x) about \(x=1\). Since \(u(1)=0\), we can reasonably let \(u(x)=(1-x)^\beta w(x)\), where \(\beta >0\) and \(w(1)=b_0\ne 0\). Substituting it into (6.1) yields

$$\begin{aligned}&w^{\prime \prime }-\frac{2\beta }{1-x}w^\prime +\frac{\beta (\beta -1)}{(1-x)^2}w=\frac{(1-x)^{\beta /2}}{\sqrt{x}}w^{3/2}. \end{aligned}$$
(6.4)

Noting that \(w(x)=b_0+(1-x)^{\beta _1}g(x)\), \(\beta _1>0\), we can deduce that the third term on the left-hand side of (6.4) must vanish, which means \(\beta =1\). Hence, Eq. (6.4) becomes

$$\begin{aligned}&\left( (1-x)^2w^{\prime }\right) ^\prime =f(x,w):=\frac{(1-x)^{5/2}}{\sqrt{x}}w^{3/2},\quad \ w(0)=1,\quad \ w(1)=b_0\ne 0. \end{aligned}$$
(6.5)

Obviously, f(x, w) is infinitely differentiable with respect to w at \(w=b_0\). Hence, w(x) possesses the fractional power series about \(x=1\). Substituting \(w(x)=b_0+b_1(1-x)^{\gamma _1}+\cdots \) into (6.5), we can deduce \(\gamma _1=\frac{5}{2}\), which means we can impose a right boundary condition \(w^\prime (1)=0\) for Eq. (6.5). Hence, we can obtain the series expansion of w(x) about \(x=1\) by using our decomposition method for Eq. (6.5) at \(x=1\), denoted by \(w_p(x)\). Further by letting \(u_{p,r}(x)=(1-x)w_p(x)\), we have

$$\begin{aligned} u_{p,r}(x)&= b_0 (1-x) +\frac{4 b_0^{3/2}}{35}(1-x)^{7/2} +\frac{2 b_0^{3/2}}{63}(1-x)^{9/2} +\frac{b_0^{3/2}}{66} (1-x)^{11/2} +\frac{b_0^2}{175} (1-x)^6 \nonumber \\&\quad +\frac{5 b_0^{3/2}}{572} (1-x)^{13/2} +\frac{b_0^2}{315} (1-x)^7 +\frac{7 b_0^{3/2}}{1248} (1-x)^{15/2} +\frac{16 b_0^2}{8085} (1-x)^8 \nonumber \\&\quad +\frac{b_0^{3/2} (25725+1408 b_0)}{6664000} (1-x)^{17/2} +\frac{4 b_0^2}{3003} (1-x)^9 +\cdots +\frac{128 b_0^2}{135135} (1-x)^{10}, \end{aligned}$$
(6.6)

where \(b_0\) is a parameter to be determined.

Remark 9

In history, many researchers studied the series expansions of the solution for the Thomas–Fermi equation. As early as 1930, Baker [59] obtained the series expansion (6.3) for the Cauchy problem of the Thomas–Fermi equation. Hille [10] proved the convergence of this series and obtained the radius of convergence. Hille also discussed the series expansion (6.6). Here, we reproduce these series expansions by our method.

From (6.3) and (6.6), we know the solution u(x) is not smooth enough at the two endpoints, but we can take a variable substitution \(t=2\sqrt{1-\sqrt{1-x}}-1\) in (6.1) such that the solution \(v(t)=u(x)\), \(t\in [-1,1]\) is sufficiently smooth. Correspondingly, the equation (6.1) with boundary condition (6.2) is transformed to

$$\begin{aligned}&v^{\prime \prime }+\frac{-1+6t+3t^2}{(1-t^2)(3+t)}v^{\prime }=\frac{(1-t^2)(1-t)(3+t)^2}{4\sqrt{7-2t-t^2}} v^{3/2},\quad \ -1<t<1,\nonumber \\&\quad v(-1)=1,\quad \ v(1)=0. \end{aligned}$$
(6.7)

By taking \(n=20\) in the Chebyshev collocation method, we obtain an approximate solution to the transformed Thomas–Fermi equation (6.7). Taking \(t=2\sqrt{1-\sqrt{1-x}}-1\) again, we obtain

$$\begin{aligned} u_{tc}(x)&=0.48501 - 0.700536 t + 0.0268687 t^2 + 0.136627 t^3 - 0.00556901 t^4 + 0.0792602 t^5 \nonumber \\&\quad - 0.00887676 t^6 - 0.0158342 t^7 + 0.00163158 t^8 - 0.0000678796 t^9 + 0.00123403 t^{10} \nonumber \\&\quad + 0.000680707 t^{11} - 0.000282336 t^{12} - 0.00013135 t^{13} - 0.0000289612 t^{14} + 1.90737\times 10^{-7} t^{15}\nonumber \\&\quad + 0.0000156853 t^{16} + 2.01339\times 10^{-6} t^{17} - 2.85306\times 10^{-6} t^{18} - 7.09989\times 10^{-7} t^{19}\nonumber \\&\quad + 2.07261\times 10^{-9} t^{20}, \ t\rightarrow 2\sqrt{1-\sqrt{1-x}}-1. \end{aligned}$$
(6.8)

In order to show the accuracy of the approximate solution, we introduce an error function

$$\begin{aligned}&e_{tc}(x)=u_{tc}^{\prime \prime }(x)-\frac{\left( u_{tc}(x)\right) ^{3/2}}{\sqrt{x}}, \end{aligned}$$

which is plotted in Fig. 4 in logarithmic scale. In this figure, we also plot the error computed by directly applying the Chebyshev collocation method to the original Thomas–Fermi equation (6.1) (\(e_c(x)\), dashed line). Obviously, the transformed approximate solution is more accurate than the one obtained by direct Chebyshev collocation method, which further shows our singular transformation is successful.

Fig. 4
figure 4

The errors of the approximate solutions in logarithmic scale for the Thomas–Fermi equation

Full size image

By expanding \(u_{tc}(x)\) as fractional power series about \(x=0\) and \(x=1\), respectively, we know \(a_0=-1.9063841613597106\) in (6.3) and \(b_0=0.8365830238318072\) in (6.6). Hence, we can plot the errors \(|u_{tc}(x)-u_{p,l}(x)|\), \(|u_{tc}(x)-u_{p,r}(x)|\) with logarithmic scale, shown in Fig. 5.

Fig. 5
figure 5

The errors between the collocation solution and the series expansions for the Thomas–Fermi equation

Full size image

It can be seen from Fig. 5 that the collocation solution \(u_{tc}(x)\) approximates the series expansions \(u_{p,l}(x)\), \(u_{p,r}(x)\) as \(x\rightarrow 0\), \(x\rightarrow 1\), respectively. Hence, it is a good approximation to the Thomas–Fermi equation (6.1) with boundary condition (6.2) over the whole interval [0, 1].

Now we consider the Emden–Fowler equation, which can be imposed initial or boundary conditions [6, 7, 12, 43]. Here, we only discuss the first boundary value problem, which reads [6]

$$\begin{aligned}&\left( x^{\alpha }u'\right) '+x^\theta u^\rho =0,\quad \ 0<x<1, \end{aligned}$$
(6.9)
$$\begin{aligned}&u(0)=0,\quad \ u(1)=0, \end{aligned}$$
(6.10)

where \(\alpha \) and \(\rho \) are real numbers satisfying \(0<\alpha <1\), \(\rho >0\). Obviously, this equation has a trivial solution \(u=0\). Here, we explore the positive solution. By introducing a variable transformation \(y=x^{1-\alpha }\) and letting \(v(y)=u(x)\), we obtain

$$\begin{aligned}&v''(y)+\frac{1}{(1-\alpha )^2}y^\mu v^\rho (y)=0,\quad \ 0<y<1, \end{aligned}$$
(6.11)
$$\begin{aligned}&v(0)=0,\quad \ v(1)=0, \end{aligned}$$
(6.12)

where \(\mu ={\alpha +\theta }/{1-\alpha }\). Here, we further require that \(\mu \ge 0\). Now we discuss the asymptotic behaviors of v(y) about \(y=0,1\). Since \(v(0)=0\), we can reasonably assume that \(v(y)=y^\beta w_l(y)\), where \(\beta >0\) and \(w_l(0)=a_0>0\). Substituting it into (6.11) yields

$$\begin{aligned}&w_l^{\prime \prime }+\frac{2\beta }{y}w_l^\prime +\frac{\beta (\beta -1)}{y^2}w_l+\frac{1}{(1-\alpha )^2}y^{\mu +(\rho -1)\beta } w_l^\rho =0. \end{aligned}$$
(6.13)

The fact \(w_l(0)=a_0>0\) implies \(w_l(y)=a_0+y^{\gamma _1}g(y)\), where \(\gamma _1>0\), g(y) is continuous over [0, 1] and \(g(0)\ne 0\). Substituting this expression of \(w_l(y)\) into (6.13) yields

$$\begin{aligned}&y^{\gamma _1}g^{\prime \prime }(y)+2(\gamma _1+\beta )y^{\gamma _1-1}g^\prime (y) +\gamma _1(\gamma _1+2\beta -1)y^{\gamma _1-2}g(y)+\frac{\beta (\beta -1)}{y^2}\left[ a_0+y^{\gamma _1}g(y)\right] \nonumber \\&\quad +\frac{a_0^\rho }{(1-\alpha )^2}y^{\mu +(\rho -1)\beta }\left[ 1+\frac{\rho }{a_0}y^{\gamma _1}g(y)+\left( {\begin{array}{c}\rho \\ 2\end{array}}\right) \frac{y^{2\gamma _1}g^2(y)}{a_0^2}+\cdots \right] =0. \end{aligned}$$
(6.14)

For Eq. (6.14), the only term involving \(y^{-2}\) (the smallest exponent about y) must be vanished. Hence \(\beta =1\). Further, since the coefficient of the term involving \(y^{\gamma _1-2}\) is not equal to zero (\(\gamma _1(\gamma _1+1)>0\), \(g(0)\ne 0\)), we must set \(\gamma _1-2=\mu +\rho -1\Rightarrow \gamma _1=\mu +\rho +1\) to make the terms involving \(y^{\gamma _1-2}\) be zero. Since \(\gamma _1=\mu +\rho +1>1\), we can impose a left boundary condition \(w_l^\prime (0)=0\) on Eq. (6.14). Finally, we obtain a boundary value problem from (6.13)

$$\begin{aligned}&\left( y^2w_l^{\prime }\right) ^\prime +\frac{1}{(1-\alpha )^2}y^{\mu +\rho +1} w_l^\rho =0,\quad \ w_l^\prime (0)=0,\quad \ w_l(1)=0. \end{aligned}$$
(6.15)

Analogously, we can show \(v(y)=(1-y) w_r(y)\) and \(w_r(y)\) satisfies

$$\begin{aligned}&\left( (1-y)^2w_r^{\prime }\right) ^\prime +\frac{1}{(1-\alpha )^2}y^{\mu }(1-y)^{\rho +1} w_r^\rho =0,\quad \ w_r(0)=0,\quad \ w_r^\prime (1)=0. \end{aligned}$$
(6.16)

Obviously, (6.15) and (6.16) are standard equations in Sect. 2, but (6.16) is singular at the right boundary \(y=1\). Hence, we can generate the series expansions of \(w_l(y)\) and \(w_r(y)\) about \(y=0\) and \(y=1\), respectively, by the algorithm in Sect. 2. In the following, we show that the exponents of the series expansion for v(y) about \(y=0\) can be directly determined from (2.14) for the problem (6.11), (6.12). From the above deduction, we can suppose that \(v(y)=a_0 y+\sum _{j=1}^{\infty }a_j y^{\alpha _j}\). By substituting \(v_0(y)=a_0 y\) into (2.18), we know \(\beta _1=\mu +\rho \), and hence \(\alpha _1=2+\mu +\rho \). Further let \(v_1(y)=a_0 y+a_1 y^{\alpha _1}\), then the binomial expansion of \(v_1(y)^\rho \) implies \(\beta _2=1+2(\mu +\rho )\), which deduces \(\alpha _2=3+2(\mu +\rho )\). Recursively, we can conclude that \(\alpha _j=j+1+j(\mu +\rho )\), \(j=1,2,\ldots \). By similar arguments, we know the exponents of the series expansion for v(y) about \(y=1\) have the form \(\{1\}\cup \{i+j \rho \}\) \((i\ge 2, j=1,2,\ldots i-1)\). We only consider the case that both \(\mu \) and \(\rho \) are rational numbers. Let \(\mu +\rho ={\xi _0}/{\eta _0}\) and \(\rho ={\xi _1}/{\eta _1}\), where \(\xi _0\), \(\eta _0\) and \(\xi _1\), \(\eta _1\) are coprime numbers, respectively. Then the variable substitution \(t=\left( 1-(1-y)^{1/\eta _1}\right) ^{1/\eta _0}\) can make the solution of Eq. (6.11) sufficiently smooth, which yields by letting \(w(t)=v(y)\)

$$\begin{aligned}&w''(t)+\frac{(\eta _0 \eta _1-1)t^{\eta _0}-\eta _0+1}{t\left( 1-t^{\eta _0}\right) }w'(t)+q(t) w^\rho (t)=0,\quad \ 0<t<1, \end{aligned}$$
(6.17)
$$\begin{aligned}&w(0)=0,\quad \ w(1)=0, \end{aligned}$$
(6.18)

where

$$\begin{aligned}&q(t)=\frac{\left[ \eta _0\eta _1t^{\eta _0-1}(1-t^{\eta _0})^{\eta _1-1}\right] ^2}{(1-\alpha )^2}\left[ 1-(1-t^{\eta _0})^{\eta _1}\right] ^\mu . \end{aligned}$$

We choose \(\alpha =\frac{1}{2}\), \(\theta =-\frac{1}{3}\), and \(\rho =\frac{1}{3}\) in (6.9), then a computation yields \(\eta _0=\eta _1=3\) in (6.17). By applying the Chebyshev collocation method to Eq. (6.17) with boundary condition (6.18), we obtain the approximate solution by taking \(n=20\)

$$\begin{aligned} u_{tc}(x)&=0.18215 + 0.303731 t - 0.407715 t^2 - 1.08104 t^3 - 0.127282 t^4 + 1.36295 t^5 + 1.15084 t^6 \nonumber \\&\quad - 0.495033 t^7 - 1.31964 t^8 - 0.494441 t^9 + 0.56986 t^{10} + 0.657761 t^{11} + 0.0845911 t^{12} - 0.2992 t^{13}\nonumber \\&\quad - 0.208823 t^{14} + 0.033786 t^{15} + 0.0922835 t^{16} + 0.015476 t^{17} - 0.0175699 t^{18} - 0.00399044 t^{19}\nonumber \\&\quad + 0.0013115 t^{20}, \ t\rightarrow 2\left( 1-(1-\sqrt{x})^{1/3}\right) ^{1/3}-1, \end{aligned}$$
(6.19)

which is plotted in Fig. 6.

Fig. 6
figure 6

The approximate solution of the Emden–Fowler equation

Full size image
Fig. 7
figure 7

The errors of the approximate solutions in logarithmic scale for the Emden–Fowler equation

Full size image

Finally, the logarithmic absolute errors of the approximate solutions obtained by the Chebyshev collocation method to (6.17) (\(e_{tc}(x)\), solid line) and (6.9) (\(e_{c}(x)\), dashed line) are plotted in Fig. 7, which show that the given singular transformation improves the computational accuracy significantly. Here, we note that the error \(e_{tc}(x)\) is defined by

$$\begin{aligned}&e_{tc}(x)=\left( x^{\alpha }u_{tc}'(x)\right) '+x^\theta u_{tc}^\rho (x). \end{aligned}$$

Remark 10

The solutions of the Thomas–Fermi equation and the Emden–Fowler equation are not sufficiently smooth at the two endpoints. For these kinds of problems, we tactically perform a smoothing transformation reflecting the singular behaviors of the solution at the two endpoints such that the solution is sufficiently smooth over the whole interval. Hence, the Chebyshev collocation method can be effectively used to solve these problems with high accuracy.

7 Conclusions

Nonlinear singular two-point boundary value problem is an important model equation, which has wide applications in many branches of mathematics, physics, and engineering. Since the solution of the equation is not sufficiently smooth at the one or two endpoints of the interval, the computational accuracy is low when standard numerical algorithms are used to solve the problem. In this paper, we design a simple method to recover the truncated fractional series expansion for the solution about the endpoint, which accurately describes the singular behavior of the solution. Although the series expansion involves an undetermined parameter, the singular feature of the solution is known. By taking a simple variable transformation, the solution is sufficiently smooth, and hence, the Chebyshev collocation method can be used to effectively solve the transformed differential equation, which has been confirmed by convergence analysis. Numerical examples illustrate the high efficiency of the algorithm, which shows that the computational accuracy improves significantly compared with the direct implementation of the Chebyshev collocation method to the original differential equation. The method is capable of solving the problems with two-endpoint singularities. As some applications, the Thomas–Fermi equation and the Emden–Fowler equation over finite interval are solved by the proposed algorithm with high accuracy.