Solution of Riemann problems for hyperbolic systems of conservation laws modeling two-phase flow in general stream tube geometries

Abstract

This paper describes a procedure for the analytical solution of Riemann problems for multi-component, two-phase flow in general stream tube geometries in porous media. The procedure is first described for a scalar hyperbolic conservation law modeling waterflooding of an oil reservoir. Thereafter, it is easy to generalize the procedure to Riemann problems for multi-component, two-phase systems of hyperbolic conservation laws, for which the associated 1D Riemann problem has a known solution. The procedure is described for both constant flow rate and constant boundary pressures as imposed Riemann data. In the latter case, the flow rate is time-dependent and its novel analytical solution is constructed in this paper, clearly demonstrating a non-trivial impact of the flow geometry on the solution.

1 Introduction

In this paper we will first consider the immiscible displacement of oil by water in an isotropic and homogeneous porous tube as depicted in Fig. 1a and b. The entire stream tube volume is composed of a space filling family of non-intersecting, time-independent, smooth streamlines connecting the inlet boundary $\partial {\varOmega }_\mathrm{{i}}$ and outlet boundary $\partial {\varOmega }_\mathrm{{o}}$. For an isotropic medium (for which the permeability is a scalar as opposed to a rank 2 tensor for an anisotropic medium) the equipotential surfaces are everywhere perpendicular to the streamlines. Therefore, we choose the arc length of an arbitrary streamline in the tube as the space variable x, which uniquely defines the surface A(x) and, therefore, the propagation of waves within a stream tube. We will see later that the geometry A(x) influences this propagation. In Fig. 2 we have shown four streamlines orthogonal to the equipotential surface A(x). In numerical stream tube simulation, an elliptic (time independent) pressure equation is first solved numerically based on which the stream tubes are generated. When the boundary conditions or the flow field change, this is repeated and stream tubes are re-generated.

Fig. 1

a 3D stream tube, b 2D stream tube

Fig. 2

Stream line geometry A(x) in an isotropic medium.

Changing flow fields occur for example when new wells in an oil reservoir are opened or old wells are closed. At such instances, the entire flow field including the stream tubes must be re-generated. Depending on the accuracy required, stream tubes may also have to be re-generated even without such large-impact type of changes. An example on this occurs during the propagation of an unstable displacement front. However, frequent updating of the stream tubes counteracts the advantage of computational efficiency over conventional simulation methods.

We will treat the displacement within fixed stream tubes by analytical means by first considering the corresponding 1D Riemann problem. A general discussion of Riemann problems can be found in Refs. [1, 2]. When the flow rate is constant, this 1D Riemann solution can be applied in the tube using appropriate scaled dimensionless variables, as shown in Sect. 3. If we instead consider the situation when the pressures on the inlet and outlet boundaries $\partial {\varOmega }_\mathrm{{i}}, \partial {\varOmega }_\mathrm{{o}}$ are given constants, the flow rate in the tube will no longer be constant and a dimensionless analysis will not provide the solution directly. Nevertheless, one of the main results of this paper is to construct the Riemann solution for the tube also for the case of constant pressure boundaries through the determination of the time-dependent flow rate.

A solution of a 1D Riemann problem with $A(x)=\textit{constant}$ for waterflooding of an oil reservoir and with a constant flow rate was described in Ref. [3]. The model for this process is a scalar hyperbolic conservation law for which the global Riemann problem with constant flow rate has a unique solution in the weak sense. This follows for example as a special case of the model considered in Ref. [4]. For a constant flow rate, the fluid pressure in the waterflooding process will vary with time, since the mobility of the fluid system changes as the two different fluids progress through the medium, i.e. the pressure distribution required to maintain the constant rate will be different at different times. If instead of using a constant flow rate the pressures on the boundaries $\partial {\varOmega }_\mathrm{{i}}$, $\partial {\varOmega }_\mathrm{{o}}$ are kept constant, the flow rate will change as the fluid system moves through the medium. This flow rate q(t) was determined in closed form in Ref. [5] for constant A(x). Since it was also shown there that the elementary waves for the Riemann problems with constant rate and constant boundary pressures are identical (modulo propagation velocities), it follows that the global 1D Riemann problem for waterflooding with constant pressure boundaries and $A(x)=\textit{constant}$ has a unique solution.

In the case when the medium (oil reservoir) is a stream tube as in Fig.1a and the flow rate q in the tube is constant, the flow velocity q / A(x) varies with x. As we shall see in Sect. 3, this enables the use of scaled dimensionless variables which transforms the Riemann problem for the tube to a 1D Riemann problem with a known solution. In the case of constant pressures on $\partial {\varOmega }_\mathrm{{i}}$, $\partial {\varOmega }_\mathrm{{o}}$, q varies with time. The solution of this problem is constructed in this paper. This is precisely formulated and proved in Sect. 4. In Sect. 4, we also generalize this main result to two-phase, multi-component Riemann problems in the tube, for which the associated 1D Riemann problem has a known solution. These multi-component flows are in general governed by non-strictly hyperbolic systems of conservation laws, which are not genuinely non-linear in the sense of Lax [2].

In Sect. 5, the theory of Sect. 4 is applied to three special cases: Linear flow, showing that the theory of this paper reduces to known 1D solutions; Radial flow; Spherical flow. We also give calculated examples.

2 Riemann problems for flow in porous media

Consider a system of non-linear conservation laws

$$\begin{aligned} c_t+[uf(c)]_x=0, \end{aligned}$$

(1)

where $(x,t)\in {\mathbb {R}} \times {\mathbb {R}}^+$, $c(x,t)=(c_1,c_2,\ldots ,c_n) \in {\mathbb {R}}^n$, $u\in {\mathbb {R}}$ and $f=(f_1,f_2,\ldots ,f_n):{\mathbb {R}}^n \rightarrow {\mathbb {R}}^n$ is twice continuously differentiable. The flow of $n+1$ fluid components with $\sum ^{n+1}_{i=1} c_i=1$ and $\sum ^{n+1}_{i=1} f_i=1$ in a porous medium can in general be represented in the form (1) when $c_i$ represents component concentrations. In other words the model for $n+1$ components reduces to an $n \times n$ system since only n of the components $c_i$, $f_i$ are independent. Such flows must in general be driven by a pressure gradient $p_x$ that balances the resistance to flow (friction), i.e. the total flow rate q is given by

$$\begin{aligned} q=-\lambda (c)A(x)p_x. \end{aligned}$$

(2)

The volumetric flux is then $u=q(t)/A(x)$.

In other words, the system of conservation laws (1) in general is incomplete as a model if (2) is omitted. Equation (2) is Darcy’s Law for flow without gravity. The pressure p is continuous and piecewise smooth (with possible discontinuous $p_x$ at locations x of shocks in c). The quantity $\lambda (c) \in {\mathbb {R}}^+$ is the total mobility of the fluid system. The oil and water pressures are assumed equal (p) throughout the paper. We will discuss these physical aspects in more detail in Sect. 3. Here, our intention is to relate Riemann problems for porous media flows to standard mathematical texts such as Ref. [1], where Eq. (2) is not discussed as part of a complete model, i.e. it is silently assumed that u is constant in (1).

In Eq. (1), $uf_i(c)=u_i$ represents the volumetric flux (velocity) of component i as a fraction $f_i(c)$ of the total volumetric flux for the entire fluid system. A constant rate Riemann problem for the above model is an initial-boundary value problem of the following form with $u=\textit{constant}$:

$$\begin{aligned} \begin{aligned}&c_t+[uf(c)]_x = 0,\\&u = -\lambda (c)p_x,\\&c(x,0) = c_R;\ 0 \le x\le L,\\&c(0,t) = c_L;\ t \ge 0. \end{aligned} \end{aligned}$$

(3)

A constant pressure boundary Riemann problem is

$$\begin{aligned}&c_t+[uf(c)]_x = 0,\nonumber \\&u = -\lambda (c)p_x,\nonumber \\&c(x,0) = c_R;\ 0 \le x\le L,\nonumber \\&c(0,t) = c_L;\ t \ge 0,\nonumber \\&p(x,0) =p_R,\ 0\le x\le L;\ p(L,t) =p_R, t\ge 0, \nonumber \\&p(0,t) =p_L;\ t\ge 0. \end{aligned}$$

(4)

In (3) and (4), $c_L,\ c_R \in {\mathbb {R}}^n$ and $p_L,\ p_R \in {\mathbb {R}}^+$ are constant. When $A(x)=\textit{constant}$, these Riemann problems are 1D. For the constant rate problem, u is then also constant, and we may assume $u \equiv 1$ without loss of generality. Problem (3) for $A(x)=\textit{constant}$ and constant rate q can then be solved by first solving

$$\begin{aligned} \begin{aligned}&c_t+[f(c)]_x = 0,\\&c(x,0) = c_R,\\&c(0,t) = c_L, \end{aligned} \end{aligned}$$

(5)

and if a solution is obtained, the pressure can subsequently be evaluated as

$$\begin{aligned} p(x,t)=p_{L}-\int _{0}^{x} \frac{\text {d}x}{\lambda (c(x,t))}. \end{aligned}$$

(6)

However, problem (4) for constant pressure boundaries does not yield u constant even if $A(x)=\textit{constant}$. Although u is always constant as a function of x for incompressible flows, it will be a function of time for constant pressure boundaries. The explicit construction of u(t) of (4) for constant pressure boundaries with $A(x)=\textit{constant}$ is given in Ref. [5]. It is also proved there that the solutions of (4) and (5) are identical if represented in the state space of weak solutions, although the parameterizations are different because $u \equiv 1$ for (5) and $u=u(t)$ for (4). In other words, to solve the constant pressure boundary Riemann problem (4) for $A(x)=\textit{constant}$, one would first solve (5) where u(t) can be constructed as in Ref. [5], and subsequently obtaining the pressure from (6).

In this paper we consider flow in stream tubes with arbitrary A(x). We will see in Sect. 3 that the solution of the constant rate Riemann problem (3) can be obtained using scaled variables.

The final question to be answered then becomes: Can the constant pressure boundary Riemann problem (4) be solved in the case of a general stream tube geometry (with variable A(x))? We will prove in Sect. 4 that the answer is affirmative. However, the solution cannot be obtained simply by using scaled variables as for the constant rate Riemann problem (3). This is summarized in Theorem 1 of Sect. 4 for a scalar conservation law and by Theorem 2 for systems.

The relationship between the method for solving Riemann problems (3) and (4) for $A=\textit{constant}$ and general A(x) is summarized in Table. 1.

Table 1 Summary of theories

The complete theory of Riemann problems for strictly hyperbolic, genuinely non-linear systems with local data was described in Ref. [2]. The hyperbolic models for porous media flow are typically not strictly hyperbolic and genuinely non-linear, and the solution of Riemann problems may not be possible to represent by a wave train with elementary waves corresponding to distinct eigenvalues. This means that global solutions of Riemann problems (4) for porous media flow must be constructed on a case by case basis by varying $u_L,\ u_R$ and $p_L,\ p_R$ systematically until all cases are covered as required by a global solution. Although the existence of known global Riemann solutions for non-strictly hyperbolic systems is limited, a brief summary of such literature is given below.

In Ref. [6] and references therein, the Riemann problem for polymer flooding of an oil reservoir was analyzed. The polymer is added to the water phase to increase the viscosity of the water. This was generalized to polymer flooding with non-linear polymer adsorption on rock surface in Refs. [7, 8]. The latter is a generalization of Ref. [9] where a single-phase multi-component Riemann problem with non-linear adsorbing components was solved. Similar problems for two-phase flow with components partitioning between two phases were analyzed in Refs. [10, 11]. Analyses of Riemann problems for three phase flow was presented in Ref. [12]. Such systems may also be parabolic/elliptic in certain regions of state space.

3 Streamline simulation using Riemann solutions

Streamline modeling has gained its popularity in the oil and gas industry because of computational efficiency and flow visualization for communication between injection and production wells (well placement). It is based on a decoupling of the flow problem assuming incompressible fluids and rock, and also dispersion-free flow (i.e negligible mechanical dispersion and capillary dispersion). In the near-well regions where flow velocities are large, convection will dominate, assuming zero capillary pressure (as in this paper) is adequate. In inter-well regions this may not be true. In such cases, the results of this paper may nevertheless be used within individual stream tubes by employing an operator splitting scheme, where the results of this paper is used on the convective part and a numerical solution on the dispersive (diffusive) part [13]. In addition to zero capillary pressure, equal densities between injected fluid (water) and displaced fluid (oil) is assumed. A discussion on the practical implications of this decoupling can be found in Ref. [14]. In particular, see Ref. [15] on inclusion of gravity effects in streamline modeling. The method of stream tube simulation belongs to a larger class of methods, namely those that use a fixed-flow field in any given time interval to advance fluid motions during that time interval according to the given flow field. Another example on this approach is front tracking [16], which also uses analytical solutions of Riemann problems to advance fluid motions.

Based on the above assumptions the pressure p decouples from the other unknown quantities (fluid saturation of oil ($s_o$) and water ($s_w$)). The pressure equation reduces to the material balance equation for incompressible flow

$$\begin{aligned} \nabla \cdot u=0, \end{aligned}$$

(7)

where $u \in {\mathbb {R}}^3$ is the total volumetric flux $u_\mathrm{{o}} +u_\mathrm{{w}}$ of oil and water given by Darcy’s Law (including gravity)

$$\begin{aligned} u=-\lambda \nabla {\varPhi };\ {\varPhi }=p-\rho gz, \end{aligned}$$

(8)

where $\lambda$ is the total fluid mobility, $\rho$ is fluid density, g is the acceleration of gravity, ${\varPhi }:{\mathbb {R}}^3\rightarrow {\mathbb {R}}$ is continuous and piecewise differentiable and z is depth below a horizontal plane. In an isotropic medium,

$$\begin{aligned} \lambda (s)=K \left[ \frac{k_\mathrm{{rw}}(s)}{\mu _\mathrm{{w}}}+\frac{k_\mathrm{{ro}}(s)}{\mu _\mathrm{{o}}}\right] , \end{aligned}$$

(9)

where $s=s_\mathrm{{w}},\ s_\mathrm{{w}}+s_\mathrm{{o}}=1;k_\mathrm{{r}}:[0,1]\rightarrow [0,1]$ is relative permeability; $\mu$ is phase viscosity and $K \in {\mathbb {R}}^{+}$ is absolute permeability. The equation ${\varPhi }=\textit{constant}$ defines a level surface A in the tube, and $\lambda \nabla {\varPhi }\perp A$, since the medium is isotropic. Therefore, all streamlines are perpendicular to A. This is not true in an anisotropic medium since then K is a rank 2 tensor. In particular, $\partial {\varOmega }_\mathrm{{i}}$ and $\partial {\varOmega }_\mathrm{{o}}$ are level surfaces of ${\varPhi }$. If $x\in {\mathbb {R}}$ is the arc length along any one streamline in the tube, A(x) is the area of the unique level surface at x, and the unique flow velocity associated with x is $u=q/A(x)$. The stream tubes can be numerically generated in different ways. For one such approach, see Ref. [17]. For a comprehensive treatment of streamline simulation see Ref. [18].

The next step in streamline simulation is to solve the displacement problem within each stream tube, thereby reducing a 3D flow problem to a number of simpler problems along stream tubes. For this, one approach is to use existing solutions of Riemann problems. As mentioned above, for constant flow rates in the stream tubes such solutions exist. For constant pressure boundaries, this paper provides new analytical solutions which can be used in stream tubes, thereby expanding the applicability of streamline simulation.

For the case when the injection flow rate is kept constant over time, we can define scaled variables

$$\begin{aligned} \xi =\frac{V(x)}{V};\ \tau =\frac{\int _{0}^{t}q(t)\text {d}t}{V}, \end{aligned}$$

(10)

where $V(x)=\int _{0}^{x} A(x) \text {d}x;\ V=V(L)=\int _{0}^{L} A(x)\text {d}x$.

The conservation of water within the stream tube is described by

$$\begin{aligned} s_{{t}}+\frac{1}{A(x)}[A(x)u_\mathrm{{w}}]_{x}=0, \end{aligned}$$

(11)

where $s \in [0,1]$ is water saturation and $u_\mathrm{{w}} \in {\mathbb {R}}$ is water velocity. We define the fractional flow function $f(s) \in [0,1]$ of water by $f=u_\mathrm{{w}}/(u_\mathrm{{o}}+u_\mathrm{{w}})=u_\mathrm{{w}}/u$ where $u_\mathrm{{w}}, u_\mathrm{{o}}$ and u is water, oil, and total fluid velocity, respectively. Supported by a vast amount of experimental evidence (see Ref. [19]), f is a smooth, monotonically increasing function (in the absence of gravity) with the following additional properties: $f'(0)=f'(1)=0$; there exists a unique ${\bar{s}} \in (0,1)$ such that $f''({\bar{s}})=0, f''({\bar{s}})>0$ for $s\in (0,{\bar{s}})$ and $f''({\bar{s}})<0$ for $s \in ({\bar{s}},1)$. A typical f is shown in Fig. 3. Specifically, the function plotted is based on the parameters from calculation example Case 1 shown in Table 1.

From Darcy’s Law $u=-\lambda p_x$ it follows that f is related to the phase mobilities by

$$\begin{aligned} f(s)=\frac{\lambda _\mathrm{{w}}(s)}{\lambda _\mathrm{{w}}(s)+\lambda _\mathrm{{o}}(s)}, \end{aligned}$$

(12)

where $\lambda _\mathrm{{w}}(s)=-Kk_\mathrm{{rw}}(s)/\mu _\mathrm{{w}}$ and $\lambda _\mathrm{{o}}(s)=-Kk_\mathrm{{ro}}(s)/\mu _\mathrm{{o}}$; $k_\mathrm{{rw}}, k_\mathrm{{ro}}$ being the relative permeability of water and oil, respectively. See also Eq. (9).

The conservation of oil is modeled by $q=\textit{constant}$ as a function of x, since fluids are assumed incompressible. If we consider the case when q is also constant as a function of t as in (3), (11) becomes

$$\begin{aligned} s_{{t}}+\frac{1}{A(x)}[A(x)uf(s)]_x = s_{{t}}+\frac{1}{A(x)}[qf(s)]_x = s_{{t}}+\frac{q}{A(x)}[f(s)]_x=s_{{t}}+uf(s)_x=0. \end{aligned}$$

(13)

Using the transform (10), the model (11) reduces to

$$\begin{aligned} s_{\tau }+f(s)_\xi =0. \end{aligned}$$

(14)

This is a 1D conservation law, for which the (constant rate) Riemann problem (5) with $s=c$ has an analytical solution. This can then be applied within each stream tube. The same is true if q(t) is known.

The transform (10) is applicable as a practical procedure only if q is constant both in space and time. If the pressures on the boundaries $\partial {\varOmega }_\mathrm{{i}}, \partial {\varOmega }_\mathrm{{o}}$ are given constants, then $q=q(t)$ is a function of time, although it remains constant as a function of x because of the incompressibility assumption. The main result of this paper is to solve the constant pressure boundary Riemann problem (4) and determine q(t) for any given stream tube geometry A(x). To keep boundary pressures constant is a very common operating strategy both in field application and laboratory experiments. Thereby, the applicability of the streamline approach is extended to also allow constant pressure boundaries.

Fig. 3

Fractional flow function

Fig. 4

Saturation profiles

4 Solution of the Riemann problem with constant pressure boundaries and arbitrary stream tube geometry

In Sect. 3, we briefly discussed the solution of the Riemann problem for

$$\begin{aligned} s_{{t}}+u(x)f_x=0, \end{aligned}$$

(15)

with data

$$\begin{aligned} s(x,0)&=s_R, \end{aligned}$$

(16)

$$\begin{aligned} s(0,t)&=s_L, \end{aligned}$$

(17)

where

$$\begin{aligned} u(x)=\frac{q_0}{A(x)}, \end{aligned}$$

(18)

with $q_0>0$ being a given constant flow rate in a stream tube geometry represented by A(x). Denoting this solution $s_0(x,t)$ we can write

$$\begin{aligned} s_0(x,t)=S_0(\xi ,\tau )=S_0\left( \frac{\xi }{\tau }\right) , \end{aligned}$$

(19)

where

$$\begin{aligned} \xi =\frac{V(x)}{V(L)}; \ \tau =\frac{q_0t}{V(L)}, \end{aligned}$$

(20)

and $S_0$ is the self similar solution of the Riemann problem for

$$\begin{aligned} s_{\tau }+f_{\xi }=0 \end{aligned}$$

(21)

with data

$$\begin{aligned} s(\xi ,0)&=s_R, \end{aligned}$$

(22)

$$\begin{aligned} s(0,\tau )&=s_L. \end{aligned}$$

(23)

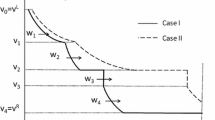
This is the constant rate Riemann problem (5), which, as discussed above, has a unique solution $S_0$. This solution is depicted in Fig. 4 for the case $s_L>s_R$, and consists of a leading shock with shock saturation $s^*$ and a trailing smooth wave connecting $s^*$ to $s_L$.

If instead we impose given constant pressures on the boundaries $\partial {\varOmega }_\mathrm{{o}},\ \partial {\varOmega }_\mathrm{{i}}$, the flow rate in the stream tube will be time-dependent and hence, the above solutions $s_0$, $S_0$ are not explicit in t since q(t) is not known.

In this section we prove the following

Theorem 1

The stream tube constant pressure boundary Riemann problem for

$$\begin{aligned}&s_t+u(x,t)f_x=0, \end{aligned}$$

(24)

$$\begin{aligned}&u=-\lambda (c)p_x. \end{aligned}$$

(25)

with constant data

$$\begin{aligned} s(x,0)&=s_R;\ x\in [0,L], \end{aligned}$$

(26)

$$\begin{aligned} s(0,t)&=s_L;\ t \geqslant 0, \end{aligned}$$

(27)

$$\begin{aligned} p(x,0)&=p_R,\ 0 \le x \le L;\ p(L,t)=p_R,\ t \geqslant 0, \end{aligned}$$

(28)

$$\begin{aligned} p(0,t)&=p_L;\ t \geqslant 0. \end{aligned}$$

(29)

and where

$$\begin{aligned} u(x,t)=\frac{q(t)}{A(x)}, \end{aligned}$$

(30)

has a unique solution, s(x,t), q(t), p(x,t).

Proof of Theorem 1

This proof is constructive and the solution for q(t) and s(x, t) is given by (38) together with (60), and (50) together with (64). Once q(t) and s(x, t) have been determined, the pressure p(x, t) is easily determined by integration of Darcy’s Law (25).

As for $u=\textit{constant}$ it is straight forward to see that the characteristics are given by

$$\begin{aligned} \frac{\text {d}x}{\text {d}t}=u(x,t)f'(s), \end{aligned}$$

(31)

and that s is constant on these (non-linear) characteristics.

Recall that $s_0$ is used for the constant rate solution of (15)–(17) and s is used for the unknown function in Theorem 1. Also, we let $v_0(\sigma ,t)$, $v(\sigma ,t)$ be the corresponding propagation velocity for any saturation value $\sigma$, using an arbitrary $q_0$ in (18). (If $\sigma$ is inside a shock, these velocities are the corresponding shock velocities). Furthermore, let $x_0(\sigma ,t)$ and $x(\sigma ,t)$ be the position of the saturation value $\sigma$ on $s_0$ and s at time t, respectively.

The outline of the proof is as follows:

• 1. We first relate s uniquely to $s_0$ for any given flow rate q(t) and any given constant rate $q_0$.

• 2. As we have seen in (21), $s_0$ can be uniquely represented by a self similar solution $S_0$, and from this fact and 1. above, a relationship between s and $S_0$ is established.

• 3. It is then verified that the relationship between s and $S_0$ is independent of the arbitrary constant rate $q_0$, as it must be to provide uniqueness.

• 4. The unique relationship between s and $S_0$ does depend on q(t). The main part of the proof is therefore to determine the flow rate q(t) in closed form from given model parameters, upon successful completion the proof is complete.

• 1. We first relate s uniquely to $s_0$ for any given flow rate q(t) and any given constant rate $q_0$. Then,

  $$\begin{aligned} \frac{\text {d}x(\sigma ,t)}{\text {d}t}=v(\sigma ,t);\quad \frac{\text {d}x_0(\sigma ,t)}{\text {d}t}=v_0(\sigma ,t), \end{aligned}$$

  (32)

  or

  $$\begin{aligned} \frac{\text {d}x(\sigma ,t)}{\text {d}t}=f'(\sigma )\frac{q(t)}{A(x(\sigma ,t))};\quad \frac{\text {d}x_0(\sigma ,t)}{\text {d}t}=f'(\sigma )\frac{q_0}{A(x_0(\sigma ,t))}, \end{aligned}$$

  (33)

  i.e.

  $$\begin{aligned} V(x(\sigma ,t))=f'(\sigma )\int _{0}^{t}q(\tau )\text {d}\tau ; V(x_0(\sigma ,t))=f'(\sigma )q_0t . \end{aligned}$$

  (34)

  Since V is a monotonically increasing function of x, we can then express $x(\sigma ,t)$ in terms of $x_0(\sigma ,t)$ as

  $$\begin{aligned} x(\sigma ,t)=Z(t)x_0(\sigma ,t), \end{aligned}$$

  (35)

  where (since we temporarily assumed q(t) is known), Z(t) is the known function

  $$\begin{aligned} Z(t)=\frac{V^{-1}\left[ f'(\sigma )\int ^{t}_{0} q(\tau ) \text {d}\tau \right] }{V^{-1}[f'(\sigma )q_0t]}. \end{aligned}$$

  (36)

  Therefore,

  $$\begin{aligned} s(x(\sigma ,t),t)=s_0\left( \frac{x(\sigma ,t)}{Z(t)},t\right) . \end{aligned}$$

  (37)

• 2. We also have (see (21))

  $$\begin{aligned} s_0\left( \frac{x(\sigma ,t)}{Z(t)},t\right) =S_0(\xi ,\tau )=S_0 \left( \frac{\xi }{\tau }\right) , \end{aligned}$$

  (38)

  where (see (10))

  $$\begin{aligned} \xi =\frac{V\left( \frac{x(\sigma ,t)}{Z(t)}\right) }{V(L)};\quad \tau =\frac{q_0t}{V(L)}. \end{aligned}$$

  (39)

• 3. Therefore,

  $$\begin{aligned} \frac{\xi }{\tau }=\frac{V(x_0(\sigma ,t))}{q_0t}=f'(\sigma ) \end{aligned}$$

  (40)

  on rarefactions and $\xi /\tau$ = shock velocity for shocks. The second equality in (40) where $q_0$ cancels follows from (37).

  This leaves s independent of the constant $q_0$, and determines s(x, t) once q(t) is known.

• 4. We next determine q(t), leaving (37) as the unique solution s(x, t). We denote the shock position at time t by $x^*(t)$ and the time when the shock reaches $x=L$ by $t^*$. Furthermore, $s^*$ denotes the saturation value on the upstream side of the shock. Also, the location of a given $s\in [s^*,s_{L}]$ at time t is denoted x(s, t). We first prove two lemmas.

$\square$

Lemma 1

Let $t \leqslant t^*$, then for any $s \in [s^*,s_L]$,

$$\begin{aligned} \int _{0}^{x(s,t)} \frac{\text { d }x}{A(x)\lambda (\sigma (x,t))}=-\frac{V(x(s,t))}{f'(s)} {\mathcal {J}}(s,t), \end{aligned}$$

(41)

where

$$\begin{aligned} {\mathcal {J}}(s,t)= \int _{s}^{s_L} \frac{f''(\sigma )\text { d }\sigma }{A^2\left[ V^{-1} \left\{ V(x(s,t))\frac{f'(\sigma )}{f'(s)} \right\} \right] \lambda (\sigma )}. \end{aligned}$$

(42)

Proof of Lemma 1

We know that the propagation velocity of any $\sigma \in [s,s_L]$ is given by

$$\begin{aligned} \frac{\text {d}x(\sigma ,t)}{\text {d}t}=\frac{q(t)}{A(x(\sigma ,t))}f'(\sigma ), \end{aligned}$$

(43)

which, integrated from 0 to t, gives

$$\begin{aligned} V(x(\sigma ,t))=f'(\sigma ) {\varPsi }(t), \end{aligned}$$

(44)

since q is constant with respect to x. In (44), ${\varPsi }=\int ^{t}_{0}q(\tau )\text {d}\tau$. Then,

$$\begin{aligned} x(\sigma ,t)=V^{-1} \left\{ f'(\sigma ){\varPsi }(t) \right\} . \end{aligned}$$

(45)

Differentiating (44) with respect to $\sigma$,

$$\begin{aligned} A(x(\sigma ,t))\frac{\text {d}x(\sigma ,t)}{\text {d}\sigma }=f''(\sigma ){\varPsi }(t). \end{aligned}$$

(46)

Starting with the left hand side of (41), we then get

$$\begin{aligned} \int _{0}^{x(s,t)}\frac{\text {d}x}{A(x)\lambda (\sigma (x,t))}=-{\varPsi }(t)\int _{s}^{s_L}\frac{f''(\sigma )\text {d}\sigma }{A^2[x(\sigma ,t)]\lambda (\sigma )}. \end{aligned}$$

(47)

Using (45), this becomes

$$\begin{aligned} -{\varPsi }(t) \int _{s}^{s_L}\frac{f''(\sigma )\text {d}\sigma }{A^2\left[ V^{-1} \left\{ {\varPsi }(t)f'(\sigma ) \right\} \right] \lambda (\sigma )}. \end{aligned}$$

(48)

From (44) we also have

$$\begin{aligned} {\varPsi }(t)=\frac{V(x(s,t))}{f'(s)}. \end{aligned}$$

(49)

Using this in (47), (48), we get (41), (42) which proves the Lemma. $\square$

Lemma 2

Let $s>s^*$ be arbitrary and let $t_s>t^*$ be the time when $x(s,t_s)=L$. Let $x(s,t^*)$ be the location of s at time $t^*$. Then,

$$\begin{aligned} t_{s}=t^{*}-\frac{V(L)^{2}-V(x(s,t^{*}))^{2}}{2\triangle pf'(s)^{2}} {\mathcal {J}}(s), \end{aligned}$$

(50)

where $\Delta p=p_L-p_R$ and ${\mathcal {J}}(s)$ is

$$\begin{aligned} {\mathcal {J}}(s)= \int _{s}^{s_L} \frac{f''(\sigma )\text { d }\sigma }{A^2\left[ V^{-1} \left\{ V(L)\frac{f'(\sigma )}{f'(s)} \right\} \right] \lambda (\sigma )}. \end{aligned}$$

(51)

Proof of Lemma 2

Recall that s(x, t) is the saturation $s \in [s^*,s_L]$ at location $x<x^*$, at time t. The variables in the Lemma are illustrated in Fig. 4 together with s at $t<t^*$.

From Darcy’s Law (2)

$$\begin{aligned} q(t)=-\lambda (s) A(x)p_x, \end{aligned}$$

(52)

integration of (52) from $x=0$ to $x=L$ at an arbitrary t between $t^*$ and $t_s$ gives

$$\begin{aligned} \Delta p=q(t) \int _{0}^{L}\frac{\text {d}x}{A(x)\lambda (\sigma (x,t))}. \end{aligned}$$

(53)

According to Lemma 1,

$$\begin{aligned} \Delta p=-q(t)\frac{V(x(s,t))}{f'(s)} {\mathcal {J}}(s), \end{aligned}$$

(54)

where ${\mathcal {J}}$ is given by (51). We also have from (44),

$$\begin{aligned} \text {d}V(x(s,t))=q(t)f'(s)\text {d}t. \end{aligned}$$

(55)

Combining (54), (55),

$$\begin{aligned} V\text {d}V=-\frac{\Delta p f'(s)^2}{{\mathcal {J}}(s)}\text {d}t. \end{aligned}$$

(56)

Integrating this from $t^*$ to $t_s$,

$$\begin{aligned} \frac{1}{2}[V^2(x(s,t^*))-V^2(L)]=\frac{\Delta p f'(s)^2}{{\mathcal {J}}(s)}(t_s-t^*), \end{aligned}$$

(57)

from which Lemma 2 follows. $\square$

We now proceed with the proof of Theorem 1. At any time, Darcy’s Law integrated from $x=0$ to $x=L$ is

$$\begin{aligned} \Delta p=q(t)\int _{0}^{L}\frac{\text {d}x}{A(x)\lambda (\sigma (x,t))}. \end{aligned}$$

(58)

Assume first $t<t^*$, i.e. $x(s,t) <L$. Then, (58) is

$$\begin{aligned} \Delta p=q(t)\left[ \int _{0}^{x(s^*,t)} \frac{\text {d}x}{A(x)\lambda (\sigma (x,t))}+\frac{1}{\lambda _{R}} \int _{x(s^*,t)}^{L}\frac{\text {d}x}{A(x)}\right] , \end{aligned}$$

(59)

where $\lambda _R=\lambda (s_R)$ is constant. The first term is for the smooth part of the solution, the second term is for the constant state $s_R$.

Using Lemma 1, this can be written

$$\begin{aligned} q(t)=\frac{\Delta p}{-\frac{V(x(s^{*},t))}{f'(s^{*)}}{\mathcal {J}}(s^*)+\frac{1}{\lambda _{R}}\int _{x(s^*,t)}^{L}\frac{\text {d}x}{A(x)}}. \end{aligned}$$

(60)

This defines q(t) for $t \leqslant t^*$.

It remains to determine q(t) for $t>t^*$, in which case the shock is no longer present in the stream tube. First, we need to determine $t^*$ from (60). For this, let $x^*$ be an arbitrary given shock location in [0, L] and let the time when the shock ($s^*$) is at this location be $t(x^*)$. From (60), we can calculate $q(t(x^*))$ explicitly, since $V(x^*)$ and ${\mathcal {J}}(s^*)$ are known, see (42). We then have

$$\begin{aligned} \frac{\text {d}t(x^*)}{\text {d}x^*}=\frac{A(x^*)}{f'(s^*)q(t(x^*))}. \end{aligned}$$

(61)

At $x^*=0$, $A(0)=Area(\partial {\varOmega }_\mathrm{{i}}) \ne 0$. From (60) we see that $q(t(x^*))$ is smooth and bounded. The ordinary differential equation (61) with initial data $t(0)=0$, therefore, has a unique solution $t(x^*)$, and $t^*=t(L)$. Having determined $t^*$ uniquely, Lemma 2 yields the time $t_s$ when an arbitrary $s\in [s^*,s_L]$ reaches $x=L$, i.e. when $x(s,t_s)=L$. Also,

$$\begin{aligned} \Delta p=q(t_{s})\int _{0}^{x(s,t_s)}\frac{\text {d}x}{A(x)\lambda (\sigma )}, \end{aligned}$$

(62)

which by Lemma 1 can be written

$$\begin{aligned} \Delta p=-q(t_s) \frac{V(x(s,t_s))}{f'(s)}{\mathcal {J}}(s)=-q(t_s) \frac{V(L)}{f'(s)} {\mathcal {J}}. \end{aligned}$$

(63)

Combining (57) and (63), we find

$$\begin{aligned} q(t_{s})=\frac{V^{2}(L)-V^{2}(x(s,t^{*}))}{2V(L)f'(s)(t_{s}-t^{*})}. \end{aligned}$$

(64)

Since $t_s$ in known from Lemma 2 and s is arbitrary, this defines the flow rate for $t_s>t^*$.

The flow rate for an arbitrary $s\in [s^*,s_L]$ and the time when s reaches $x=L$ are uniquely given by (50) and (64) for $t>t^*$, i.e. after the shock has reached $x=L$. This completes the proof of Theorem 1, since the case $t\le t^*$ was completed previously.

We also note that the flow rate is continuous at $s=s^*$. To see this we write $V^2-V(x(s,t))^2=(V+V(x(s,t)))(V-V(x(s,t)))$ and we find from (60) that

$$\begin{aligned} {\lim }_{s\rightarrow s^{*}}q(t_s)=\frac{\text {d}V}{\text {d}t}\frac{1}{f'(s)} \Big |_{s=s^*}. \end{aligned}$$

(65)

which is the same as (61) since $\text {d}V/\text {d}t=(\text {d}x^*/\text {d}t)A(x^*)$. However, q(t) is in general not differentiable at $t=t^*$, see Ref. [5] where the 1D Riemann problem (4) with A(x)=constant was solved for any two-phase, multi-component hyperbolic $n \times n$ system of conservation laws for the case of constant boundary pressures, provided that the associated 1D Riemann problem (5) with constant flow rate has a known solution. With reference to Ref. [5], it is shown how q(t) can be determined before and after each elementary wave of the $n \times n$ Riemann problem (with $A(x)=\textit{constant}$) reaches $x=L$. Following the same procedure as in Ref. [5]; however, with calculation of q(t) replaced by the techniques used in this paper, we can formulate the following more general result:

Theorem 2

If the Riemann problem for a hyperbolic system of conservation laws modeling flow in 1D has a known solution for the case of a constant flow rate, the associated Riemann problem for an arbitrary stream tube also has solutions both with constant flow rate and with constant pressure boundaries. These solutions are unique if the associated 1D constant rate Riemann solutions are unique.

5 Application to special geometries

In this section we demonstrate the theory developed above to three special situations. Firstly, we want to demonstrate that the stream tube solution of the waterflooding Riemann problem reduces to the 1D solution for the case when $A(x)=constant$, i.e. a linear flow geometry. Secondly, we consider a radial geometry, typically encountered when water is injected in a vertical well into a horizontal isotropic oil reservoir. Thirdly, we consider spherical flow, which may occur in a local water injectivity test or a fluid sampling test with oil/water flow. These examples have one thing in common, namely the analytical basic solution $S_0$ of the 1D Riemann problem for waterflooding, (21)–(23).

In the previous Sects. 1– 4, we used scaled water saturations $s\in (0,1)$ given by

$$\begin{aligned} s=\frac{s-s_\mathrm{{wc}}}{1-s_\mathrm{{wc}}-s_\mathrm{{or}}}, \end{aligned}$$

(66)

where $s_\mathrm{{wc}}$ is irreducible water saturation and $s_\mathrm{{or}}$ is residual oil saturation, satisfying $0 \le s_\mathrm{{wc}} \le 1-s_\mathrm{{or}} \le 1$. In the calculated examples below, we used non-zero values for $s_\mathrm{{wc}}$ and $s_\mathrm{{or}}$, see Tables 1 and 2.

Table 2 Parameters for radial geometry sample case

For a Riemann problem with a constant flow rate $q_0$, the only influence from the geometry A(x) on the velocity is the trivial one, i.e. $u=q_0/A(x)$.

When the boundary pressures are constant there is a non-trivial influence on the velocity u(t) from the basic 1D Riemann solution even when $A=\textit{constant}$ [5].

In this paper, we have considered the Riemann problems with arbitrary geometries and constant boundary pressures. As we can see from (60), (64), in these cases, q(t) also varies with time in a non-trivial manner. This is exemplified in the specific cases of radial and spherical flow below and the calculated examples.

In the case of general A(x) (including radial and spherical flow below), we have to evaluate the integrals ${\mathcal {J}}$ in (60), given by (42). This is done by the following numerical procedure before the shock reaches $x=L$. First, we choose an equidistant partitioning $(x_{i-1},x_i]$ of [0, L], where $x_i$ is the position of the shock saturation $s^*$ at times $t_i$. Second, we calculate the times $t_i$ from (61) using the forward Euler method (or any other ODE solver). Then the discrete functional dependency of t on q(t) is calculated from (60) using the given partition points $x_i$ for $x^*$, together with $t_i$ obtained as the solution of (61).

We observe from (60) that as the shock approaches $x=L$, the influence from the initial state $s_R$ on the flow rate vanishes as the second term in the denominator approaches zero. From (64) we observe that after the shock has left the medium, the influence of $s_R$ on the flow rate is absent, since $x(s,t^*)<L$ for $t_s>t^*$.

As we saw in the discussion of (65), the two rates q(t) for $t<t^*$ and $q(t_s)$ for $t_s>t^*$ meet continuously at $t^*$.

5.1 Linear geometry

Linear flow occurs for example in laboratory core floods with long cores of constant cross section $A(x)=A_0$. Then in (60), (42),

$$\begin{aligned} {\mathcal {J}}(s^*)=\frac{1}{{A_0}^2} \int _{s^*}^{s_L}\frac{{f''(\sigma )\text {d}\sigma }}{\lambda (\sigma )}, \end{aligned}$$

(67)

and

$$\begin{aligned} q(t)=\frac{\Delta p}{-\frac{A_{0}x^{*}}{f'(s^{*})}\frac{1}{A_{0}^{2}} \int _{s^*}^{s_L}\frac{f''(\sigma )\text {d} \sigma }{\lambda (\sigma )}+\frac{1}{\lambda _R}\frac{L-x^*}{A_0}}, \end{aligned}$$

(68)

or

$$\begin{aligned} u(t)=\frac{\Delta p f'(s^*)}{-x^* \int _{s^*}^{s_L} \frac{f''(\sigma )\text {d} \sigma }{\lambda (\sigma )}+\frac{L-x^*}{\lambda _R}}, \end{aligned}$$

(69)

where $x^*=x(s^*,t)$. This is the same solution as derived in Ref. [5], where calculated examples of linear flow are also presented.

5.2 Radial geometry

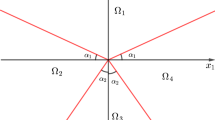
This geometry is shown in Fig. 5 for an arbitrary angle $\alpha \in [0,2 \pi ]$.

Fig. 5

Radial geometry

In this case we put $x=r-r_\mathrm{{w}}$, where $r_\mathrm{{w}}$ is the well bore radius, i.e. $\ x=0$ on $\partial {\varOmega }_\mathrm{{i}}$. Then, $A(x)=\alpha h (x+r_\mathrm{{w}}), V(x)=\alpha h(x^2/2 + r_\mathrm{{w}} x)$ and $V^{-1}(y)=\sqrt{r_\mathrm{{w}}^2 + 2y/\alpha h}-r_\mathrm{{w}}$.

Substituting in (60), (42) and re-arranging, we arrive at

$$\begin{aligned} q(t)=\frac{2\triangle p \alpha h}{-\left[ (x^{*}+r_\mathrm{{w}})^{2} -r_\mathrm{{w}}^{2}\right] {\mathcal {J}}(S^*)+ \frac{1}{\lambda _{R}} \ln \left( \frac{r_\mathrm{{e}}}{x^{*}+r_\mathrm{{w}}}\right) }, \end{aligned}$$

(70)

where

$$\begin{aligned} {\mathcal {J}}(s^*)= \int _{s^*}^{s_L} \frac{f''(\sigma ) \text {d}\sigma }{\left\{ r_\mathrm{{w}}^{2}f'(s^{*})+ \left[ (x^{*}+r_\mathrm{{w}})^{2} -r_\mathrm{{w}}^{2}\right] f'(\sigma )\right\} \lambda (\sigma )}. \end{aligned}$$

(71)

Fig. 6

a Flow rate solution of radial flow case (viscoscity ratio = 0.20). b Consistency between the radial flow and spherical flow cases

It is clear from (71) that the geometry of the problem has a non-trivial impact on the solutions. This is also seen from the calculated example below where we used $\alpha =2\pi$, i.e. the stream tube is the entire circular disk with streamlines being the radii. Two cases are calculated: $\mu _\mathrm{{w}}/\mu _\mathrm{{o}}=0.2$ for Case 1 and $\mu _\mathrm{{w}}/\mu _\mathrm{{o}}=5.00$ for Case 2. For the sample calculation, parameters are shown in Table 2. The analytical solutions are shown in Figs. 6a and 7. For the numerical solution, we used an explicit first order upwind scheme using equidistant space and time discretization $x_j=j \Delta x$ ($j=0,\ldots ,M$) and $t^n=n \Delta t$ ($n=0,\ldots ,N$).

First, the initial flow rate $q^0$ is calculated using (2) and the fact that $\lambda =\lambda _R=\textit{constant}$ initially,

$$\begin{aligned} q^0=\frac{p_L-p_R}{\lambda _R \int _{0}^{L}\frac{\text {d}x}{A(x)}}. \end{aligned}$$

(72)

The initial velocities, saturations, and pressures are, respectively,

$$\begin{aligned} u^0_j&=\frac{q^0}{A(x_j)}, \end{aligned}$$

(73)

$$\begin{aligned} s_o^0&=s_L,\ s_j^0=s_R \ (j=1,\ldots ,M), \end{aligned}$$

(74)

$$\begin{aligned} p_o^0&=p_L,\ p_j^0=p_R \ (j=1,\ldots ,M). \end{aligned}$$

(75)

These quantities are updated on each time step, see (6), (15), (2), respectively:

$$\begin{aligned} p_j^{n+1}&=p_L-\sum _{i=0}^{j}\frac{u_i^n}{\lambda \left( s_i^n\right) }\Delta x, \end{aligned}$$

(76)

$$\begin{aligned} s_j^{n+1}&=s_j^n-u_j^n\frac{\Delta t}{\Delta x}\left[ f \left( s_j^n\right) - f\left( s_{j-1}^n \right) \right] , \end{aligned}$$

(77)

$$\begin{aligned} u_j^{n+1}&= \frac{\lambda \left( s_j^{n+1}\right) \left[ p_{j+1}^{n+1}-p_{j-1}^{n+1}\right] }{2\Delta x}. \end{aligned}$$

(78)

Using this, the time step must satisfy the Couraut–Friedrich–Lewy condition $\Delta t< \Delta x/u_j^n\ (j=1,\ldots ,M; \ n=1,\ldots ,N)$.

Fig. 7

Flow rate solution of radial flow case (viscosity ratio = 5.00)

Fig. 8

Spherical geometry

When water is the least viscous fluid ($\mu _\mathrm{{w}}/\mu _\mathrm{{o}}=0.2$), the flow rate increases with time as the most viscous fluid (oil) is exiting the system in Fig. 6a. When the injected fluid (water) is the most viscous ($\mu _\mathrm{{w}}/\mu _\mathrm{{o}}=5.00$), the total flow rate decreases with time as the amount of water between the inlet and outlet boundaries increases in Fig. 7. We also observe in Fig. 6a that the numerical solution approaches the analytical solutions as the grid is refined and that a very fine grid is required to give a satisfactory result.

It is observed that the rates of change in flow velocities are different in these two cases. This is because for viscosity ratio 0.20 (Fig. 6a) the effect of viscosity and relative permeability of the fluids are counteractive on the velocity change, while in the case of viscosity ratio 5.0 (Fig. 7) these effects are both enhancing the velocity change.

Table 3 Parameters for spherical geometry sample case

5.3 Spherical flow

This geometry is depicted in Fig. 8 for a semi-sphere ($\alpha =2\pi$).

Fig. 9

Flow rate solution of spherical flow case (viscosity ratio = 0.25)

We put $x=r-r_\mathrm{{w}}$, i.e. $\ x=0$ on $\partial {\varOmega }_\mathrm{{i}}$. In this case we get $A(x)=\alpha (x+r_\mathrm{{w}})^2$; $\alpha \in \ (0,4\pi ], V(x)=(\alpha /3)[(x+r_\mathrm{{w}})^3-r_\mathrm{{w}}^3]$ and $V^{-1}(y)=\root 3 \of {r_\mathrm{{w}}^{3}+3y/\alpha }-r_\mathrm{{w}}$. Substituting in (60), (42),

$$\begin{aligned} q(t)=\frac{2\triangle p\alpha h}{-\frac{\left[ \left( x^*+r_\mathrm{{w}}\right) ^{3} -r_\mathrm{{w}}^{3}\right] }{f'(s^{*})} {\mathcal {J}}(s^*)+ \frac{1}{\lambda _{R}} \left[ \frac{1}{r_\mathrm{{e}}}-\frac{1}{x^{*}+r_\mathrm{{w}}}\right] }, \end{aligned}$$

(79)

where

$$\begin{aligned} {\mathcal {J}}(s^*)= \int _{s^*}^{s_L}\frac{f''(\sigma ) \text {d}\sigma }{\left[ r_\mathrm{{w}}^{3}+ \left( \left( x^*+r_\mathrm{{w}} \right) ^{3} -r_\mathrm{{w}}^{3}\right) \frac{{f'(\sigma )}}{f'(s^{*})}\right] ^{\frac{4}{3}}\lambda (\sigma )}. \end{aligned}$$

(80)

The analytical solution of the spherical case using the entire sphere as a stream tube is shown in Fig. 8 and the calculation parameters are shown in Table 3. The flow rate will also level out and stay bounded as indicated in Fig. 9. Qualitatively, the behavior displayed in Fig. 9 is analogous to the low viscosity case for radial flow shown in Fig. 6a and b: as the less mobile fluid is displaced from the medium by the more mobile fluid, the flow rate increases. Eventually in both cases, the shock will break through at the outer boundary at $t=t_{BT}$. At this point in time, the derivative of q(t) is discontinuous. This is because the fluid saturations change discontinuously at $t_{BT}$, and hence also the fractional flow function f. The pace of these evolutions are different in the radial case (Fig. 6a) and the spherical case (Fig. 9). This is because of the data used in these cases, the volume of the medium in the spherical case is larger than in the radial case. Furthermore, the area of the inflow boundary is smaller than the inflow area for the radial case while the boundary pressures are the same. Together, these differences will cause a slower evolution in the spherical case compared to the radial case.

A comprehensive analysis of the solution properties, including parametric studies, is beyond the scope of the paper, where the main objective was to develop new analytical solutions to practical Riemann problems in general stream tube geometries. For the purpose of illustrating the complexity of the analytical solutions, a few calculated examples accompanied by qualitative discussions were presented.