Two-Dimensional Riemann Problems: Transonic Shock Waves and Free Boundary Problems

Abstract

We are concerned with global solutions of multidimensional (M-D) Riemann problems for nonlinear hyperbolic systems of conservation laws, focusing on their global configurations and structures. We present some recent developments in the rigorous analysis of two-dimensional (2-D) Riemann problems involving transonic shock waves through several prototypes of hyperbolic systems of conservation laws and discuss some further M-D Riemann problems and related problems for nonlinear partial differential equations. In particular, we present four different 2-D Riemann problems through these prototypes of hyperbolic systems and show how these Riemann problems can be reformulated/solved as free boundary problems with transonic shock waves as free boundaries for the corresponding nonlinear conservation laws of mixed elliptic-hyperbolic type and related nonlinear partial differential equations.

1 Introduction

We are concerned with global solutions of multidimensional (M-D) Riemann problems for nonlinear hyperbolic systems of conservation laws, focusing on their global configurations and structures. In this paper, we present some recent developments in the rigorous analysis of two-dimensional (2-D) Riemann problems involving transonic shock waves (shocks, for short) through several prototypes of hyperbolic systems of conservation laws and discuss some further M-D Riemann problems and related problems for nonlinear partial differential equations (PDEs). These Riemann problems can be reformulated as free boundary problems with transonic shocks as free boundaries for the corresponding nonlinear conservation laws of mixed elliptic-hyperbolic type and related nonlinear PDEs.

The study of Riemann problems has an extensive history, which dates back to the pioneering work of Riemann [74] in 1860. For the one-dimensional (1-D) Riemann problem, a theory has been established for the appropriate amplitude of the Riemann data for general strictly hyperbolic systems (cf. [55, 66]) and for general Riemann data for the compressible Euler equations (cf. [12, 70, 79, 88, 89] and the references cited therein). The 1-D Riemann problem has been essential in the development of the 1-D mathematical theory of hyperbolic conservation laws and associated shock capturing methods for the construction and computation of global entropy solutions; see [35, 42, 44, 54, 55, 57, 66, 78] and the references cited therein. More importantly, general global entropy solutions can be locally approximated by the Riemann solutions that are regarded as fundamental building blocks of the entropy solutions (cf. [35, 42, 55, 79]). Moreover, the Riemann solutions usually determine the large-time asymptotic behaviors and global attractors of general entropy solutions of the Cauchy problem. On the other hand, it is the simplest Cauchy problem (initial value problem) whose solutions have fine explicit structures.

The M-D Riemann problems are more challenging mathematically, and the corresponding M-D Riemann solutions are of much richer global configurations and structures; see [9,10,11,12, 34, 35, 43, 44, 56, 76, 94] and the references cited therein. Thus, the Riemann solutions often serve as standard test models for analytical and numerical methods for solving nonlinear hyperbolic systems of conservation laws and related nonlinear PDEs. Theoretical results for first-order scalar conservation laws are available in [12, 29, 45, 65, 80, 87, 93] and the references cited therein. During recent decades, some significant developments for the 2-D Riemann problems for first-order hyperbolic systems and second-order hyperbolic equations of conservation laws have been made. Zhang and Zheng [94] first considered the 2-D four-quadrant Riemann problem that each jump between two neighboring quadrants projects exactly one planar fundamental wave, and predicted that there are a total of 16 genuinely different configurations of the Riemann solutions for polytropic gas. Schulz-Rinne [75] proved that one of them is impossible. In Chang et al. [9, 10], it is first observed that, when two initially parallel slip lines are present, it makes a true difference whether the vorticity waves generated have the same or opposite sign, which, along with Lax and Liu [56], leads to the classification with a total 19 genuinely different configurations of the Riemann solutions for the compressible Euler equations for polytropic gas, via characteristic analysis; also see [52, 59, 76]. On the other hand, experimental and numerical results have shown that many new configurations may arise from other types of Riemann problems. In particular, the angles between two discontinuities separated by sectorial regions in the initial Riemann data and the boundaries in the lateral Riemann data play essential roles in forming the global Riemann solution configurations, besides the strengths of jumps in the initial Riemann data; see [3, 5, 34, 36, 38, 39, 44, 68, 81,82,83,84, 91]. In this paper, we present four different 2-D Riemann problems involving transonic shocks through the prototypes of nonlinear hyperbolic PDEs and demonstrate how these Riemann problems can be reformulated and then solved rigorously as free boundary problems for nonlinear conservation laws of mixed elliptic-hyperbolic type and related nonlinear PDEs. Special attention has been paid to whether/how different initial or boundary setups of the Riemann problems affect the global Riemann solution configurations. These are achieved by developing further the nonlinear method and related ideas/techniques introduced in Chen and Feldman [20,21,22] for solving free boundary problems with transonic shocks as free boundaries for nonlinear conservation laws of mixed elliptic-hyperbolic type and related nonlinear PDEs; also see [14, 23].

The organization of this paper is as follows: In Sect. 2, we first show how the solutions of M-D Riemann problems for hyperbolic conservation laws can be formulated as the self-similar solutions for nonlinear conservation laws of mixed elliptic-hyperbolic type and then we introduce the notion of Riemann solutions in the self-similar coordinates in the distributional sense. In Sect. 3, we present the first 2-D Riemann problem, Riemann Problem I, involving two shocks and two vortex sheets for the pressure gradient system and show how Riemann Problem I can be reformulated/solved as a free boundary problem with transonic shocks as free boundaries for a second-order nonlinear conservation law of mixed elliptic-hyperbolic type and related nonlinear PDEs. In Sect. 4, we present the second 2-D Riemann problem, Riemann Problem II—the Lighthill problem for shock diffraction by convex cornered wedges through the nonlinear wave equations, and show how Riemann Problem II can be solved as another free boundary problem. Even though both the origin and form of the nonlinear wave equations are different from those of the pressure gradient system, the same arguments for solving the Riemann problem apply for the pressure gradient system to obtain similar results without additional analytical obstacles; the same is true for the Riemann problem in Sect. 3 for the nonlinear wave equations. In Sect. 5, we present the third 2-D Riemann problem, Riemann Problem III—the Prandtl-Meyer problem for unsteady supersonic flow onto solid wedges through the Euler equations for potential flow, and show how Riemann Problem III can be reformulated/solved as a free boundary problem for a second-order nonlinear conservation law of mixed elliptic-hyperbolic type. Then, in Sect. 6, we present the fourth 2-D Riemann problem, Riemann Problem IV—the von Neumann problem for shock reflection-diffraction by wedges for the Euler equations for potential flow, and show how Riemann Problem IV can be solved again as a free boundary problem. We give our concluding remarks and discuss several further M-D Riemann problems and related problems for nonlinear PDEs in Sect. 7.

2 Multidimensional (M-D) Riemann Problems and Nonlinear Conservation Laws of Mixed Elliptic-Hyperbolic Type

In this section, we first show how the solutions of the M-D Riemann problems for nonlinear hyperbolic conservation laws can be formulated as the self-similar solutions for nonlinear conservation laws of mixed elliptic-hyperbolic type, and then introduce the notion of Riemann solutions in the self-similar coordinates in the distributional sense.

Consider both the M-D first-order quasilinear hyperbolic systems of conservation laws of the form:

$$\begin{aligned} \partial _t{\varvec{U}}+\nabla _{\mathbf {x}}\cdot {\varvec{F}}=0 \qquad \,\, \text{ for } t\in \mathbb {R}_+=[0,\infty ) \text{ and } \, \mathbf {x}\in \mathbb {R}^n \end{aligned}$$

(1)

with ${\varvec{U}}\in \mathbb {R}^m$ and the nonlinear mapping ${\varvec{F}}{:} \mathbb {R}^m\rightarrow \mathbb {R}^m\times \mathbb {R}^n$, and the M-D second-order quasilinear hyperbolic equations of conservation laws of the form:

$$\begin{aligned} \partial _t G_0(\partial _t\Phi, \nabla _\mathbf {x}\Phi) +\nabla _{\mathbf {x}}\cdot {\varvec{G}}(\partial _t\Phi, \nabla _\mathbf {x}\Phi )=0 \qquad \,\, \text{ for } t\in \mathbb {R}_+ \text{ and } \, \mathbf {x}\in \mathbb {R}^n \end{aligned}$$

(2)

with $\Phi \in \mathbb {R}$ and the nonlinear mapping $(G_0, {\varvec{G}}){:} \mathbb {R}^{n+1}\rightarrow \mathbb {R}\times \mathbb {R}^n$.

A prototype of (1) is the full Euler equations in the conservation form (1) with

$$\begin{aligned} {{\varvec{U}}}:=(\rho,\rho \mathbf {u},\rho E)^\top,\quad {\varvec{F}}:=(\rho \mathbf {u},\rho \mathbf {u}\otimes \mathbf {u}+pI, (\rho E+p)\mathbf {u})^\top, \end{aligned}$$

(3)

where $\rho >0$ is the density, $\mathbf {u}\in \mathbb {R}^n$ the velocity, p the pressure, and $E=\frac{|\mathbf {u}|^2}{2}+e$ the total energy per unit mass with the internal energy e given by $e=\frac{p}{(\gamma -1)\rho }$ for the adiabatic constant $\gamma >1$ for polytropic gases.

A prototype of (2) can be derived from the Euler equations for potential flow, which is governed by the conservation law of mass and the Bernoulli law for the density function $\rho$ and the velocity potential $\Phi$ (i.e., $\mathbf{u}=\nabla_{\mathbf{x}}\Phi$):

$$\begin{aligned} \partial _t\rho + \nabla _{\mathbf {x}}\cdot (\rho \nabla _{\mathbf {x}}\Phi )=0,\quad \,\, \partial _t\Phi +\frac{1}{2}|\nabla _{\mathbf {x}}\Phi |^2+h(\rho )=B, \end{aligned}$$

(4)

where B is the Bernoulli constant and $h(\rho )$ is given by

$$\begin{aligned} h(\rho )=\frac{\rho ^{\gamma -1}-1}{\gamma -1} \qquad \,\, \text{ for } \text{ the } \text{ adiabatic } \text{ exponent } \gamma >1. \end{aligned}$$

(5)

By (4)–(5), $\rho$ can be expressed as

$$\begin{aligned}\rho (\partial _t\Phi,\nabla _\mathbf{x}\Phi)=h^{-1}\ (B-\partial _t\Phi -\frac{1}{2}|\nabla _\mathbf{x}\Phi |^2\ ).\end{aligned}$$

(6)

Then system (4) can be rewritten as the second-order nonlinear wave equation as in (2) with

$$\begin{aligned} (G_0, {\varvec{G}})=(\rho (\partial _t\Phi, \nabla _\mathbf{x}\Phi ), \rho (\partial _t\Phi, \nabla _\mathbf{x}\Phi )\nabla _\mathbf{x}\Phi ) \end{aligned}$$

(7)

and $\rho (\partial _t\Phi, \nabla _\mathbf{x}\Phi )$ determined by (6).

A standard Riemann problem for (1) is a special Cauchy problem

$$\begin{aligned} {\varvec{U}}|_{t=0} = {\varvec{U}}_0(\mathbf {x}) \end{aligned},$$

(8)

so that the initial data function ${\varvec{U}}_0(\mathbf {x})$ is invariant under the self-similar scaling in $\mathbf {x}$:

$$\begin{aligned} {\varvec{U}}_0(\alpha \mathbf {x})={\varvec{U}}_0(\mathbf {x}) \qquad \,\, \text{ for } \text{ any } \alpha >0, \end{aligned}$$

that is, ${\varvec{U}}_0(\mathbf {x})$ is constant along the ray originating from $\mathbf {x}=0$; in other words, ${\varvec{U}}_0$ depends only on the angular directions of the rays originating from $\mathbf {x}=0$ in $\mathbb {R}^n$.

A lateral Riemann problem for (1) is a special initial-boundary problem in an unbounded domain $\mathcal {D}$ that contains the origin and is invariant under the self-similar scaling (i.e., if $\mathbf {x}\in \mathcal {D}$, then $\alpha \mathbf {x}\in \mathcal {D}$ for any $\alpha >0$) so that the initial data and boundary data are also invariant under the self-similar scaling.

Since system (1) is invariant under the time-space self-similar scaling, the standard/lateral Riemann problems are also invariant under the time-space self-similar scaling:

$$\begin{aligned} (t, \mathbf {x})\rightarrow \left(\alpha t, \alpha \mathbf {x}\right)\qquad \,\, \text{ for } \text{ any } \alpha >0. \end{aligned}$$

(9)

Thus, we seek self-similar solutions of the Riemann problems

$$\begin{aligned} {\varvec{U}}(t,\mathbf {x})={\varvec{V}}(\frac{\mathbf {x}}{t}). \end{aligned}$$

(10)

Denote ${\varvec{\xi }}=\frac{\mathbf {x}}{t}$ as the self-similar variables. Then ${\varvec{V}}({\varvec{\xi }})$ is determined by

$$\begin{aligned} \mathrm{D}\cdot {\varvec{F}}({\varvec{V}})-{\varvec{\xi }}\cdot \mathrm{D}{\varvec{V}}=0, \end{aligned}$$

that is,

$$\begin{aligned} \mathrm{D}\cdot ({\varvec{F}}({\varvec{V}})-{\varvec{V}}\otimes {\varvec{\xi }})+n\,{\varvec{V}}=0, \end{aligned}$$

(11)

where $\mathrm{D}=(\partial _{\xi _1}, \cdots, \partial _{\xi _n})$ is the gradient with respect to the self-similar variables ${\varvec{\xi }}=(\xi _1,\cdots, \xi _n)\in \mathbb {R}^n$, and ${\varvec{V}}\otimes {\varvec{\xi }}=(V_i\xi _j)_{1\leqslant i,j\leqslant n}$. Even though system (1) is hyperbolic, system (11) generally is of mixed elliptic-hyperbolic type, even composite-mixed elliptic-hyperbolic type. In particular, for a bounded solution ${\varvec{V}}({\varvec{\xi }})$, system (11) may be purely hyperbolic in the far-field, i.e., outside a large ball in the ${\varvec{\xi }}$-coordinates, but generally is of mixed type or composite-mixed type in a bounded domain containing the origin, ${\varvec{\xi }}=\mathbf {0}$.

For the full Euler system (1) with (3), the self-similar solutions are governed by the following system:

$$\begin{aligned} \left\{ \begin{aligned}&\mathrm{div}(\rho \mathbf {v}) + n\rho =0,\\&\mathrm{div} (\rho \mathbf {v}\otimes \mathbf {v})+ \mathrm{D}p +(n+1)\rho \mathbf {v}=0,\\&\mathrm{div}\big ((\frac{1}{2}\rho |\mathbf {v}|^2+\frac{\gamma p}{\gamma -1})\mathbf {v}\big ) +n\big (\frac{1}{2}\rho |\mathbf {v}|^2+\frac{\gamma p}{\gamma -1}\big )=0, \end{aligned} \right. \end{aligned}$$

(12)

where $\mathbf {v}=\mathbf {u}-{\varvec{\xi }}$ is the pseudo-velocity with ${\varvec{V}}=(\rho, \rho \mathbf {v}, \frac{1}{2}\rho |\mathbf {v}|^2+ \rho e)^\top$.

The weak solutions of system (11) can be defined as follows:

Definition 1

(Weak Solutions) A function ${\varvec{V}}\in L_{\mathrm{loc}}^\infty (\Lambda )$ in a domain $\Lambda \subset \mathbb {R}^n$ is a weak solution of system (11) in $\Lambda$, provided that

$$\begin{aligned} \int _\Lambda \big (({\varvec{F}}({\varvec{V}})-{\varvec{V}}\otimes {\varvec{\xi }})\cdot \mathrm{D}\zeta ({\varvec{\xi }})- n\,{\varvec{V}}\zeta ({\varvec{\xi }})\big )\, \mathrm{d}{\varvec{\xi }}=0 \quad \,\, \text{ for any } \zeta \in C_0^1(\Lambda ). \end{aligned}$$

(13)

It can be shown that any weak solution of system (11) in the ${\varvec{\xi }}$-coordinates in the sense of Definition 1 is a weak solution of system (1) in the $(t,\mathbf {x})$-coordinates. Then any co-dimension-one $C^1$-discontinuity S satisfies the Rankine-Hugoniot conditions along S in the ${\varvec{\xi }}$-coordinates:

$$\begin{aligned} ([{\varvec{F}}({\varvec{V}})]- [{\varvec{V}}]\otimes {\varvec{\xi }})\cdot {\varvec{\nu }}_{\mathrm{s}}=0, \end{aligned}$$

or equivalently,

$$\begin{aligned}{}[({\varvec{F}}({\varvec{V}})-{\varvec{V}}\otimes {\varvec{\xi }})\cdot {\varvec{\nu }}_{\mathrm{s}}]=0, \end{aligned}$$

(14)

where ${\varvec{\nu }}_{\mathrm{s}}$ can be either of the unit normals to S, and $[\,\cdot \,]$ denotes the difference between the traces of the corresponding quantities on the two sides of the co-dimension-one surface S.

Similarly, the Riemann problems for (2) are invariant under the time-space self-similar scaling:

$$\begin{aligned} (t, \mathbf {x},\Phi (t,\mathbf {x}))\rightarrow (\alpha t, \alpha \mathbf {x}, \frac{\Phi (\alpha t, \alpha \mathbf {x})}{\alpha }) \,\,\qquad \text{ for any } \alpha >0. \end{aligned}$$

(15)

Thus, we seek self-similar solutions of the Riemann problem:

$$\begin{aligned} \Phi (t,\mathbf {x})=t\phi (\frac{\mathbf {x}}{t}). \end{aligned}$$

(16)

Then $\phi ({\varvec{\xi }})$ is determined by

$$\begin{aligned} \mathrm{div}\,{\varvec{G}}(\phi -{\varvec{\xi }}\cdot \mathrm{D}\phi, \mathrm{D}\phi )-{\varvec{\xi }}\cdot \mathrm{D}G_0(\phi -{\varvec{\xi }}\cdot \mathrm{D}\phi, \mathrm{D}\phi ) =0, \end{aligned}$$

that is,

$$\begin{aligned} \mathrm{div}\big ({\varvec{G}}(\phi -{\varvec{\xi }}\cdot \mathrm{D}\phi, \mathrm{D}\phi )- G_0(\phi -{\varvec{\xi }}\cdot \mathrm{D}\phi, \mathrm{D}\phi ){\varvec{\xi }}\big ) + n G_0(\phi -{\varvec{\xi }}\cdot \mathrm{D}\phi, \mathrm{D}\phi )=0. \end{aligned}$$

(17)

Again, even though (2) is hyperbolic, (17) generally is of mixed elliptic-hyperbolic type. In particular, for a gradient bounded solution $\phi ({\varvec{\xi }})$, (17) may be purely hyperbolic in the far-field, i.e., outside a large ball in the ${\varvec{\xi }}$-coordinates, but generally is of mixed type in a bounded domain containing the origin.

For the Euler equations (2) for potential flow with (6)–(7), the self-similar solutions are governed by the following second-order quasilinear PDE for the pseudo-velocity $\varphi =\phi -\frac{1}{2}|{\varvec{\xi }}|^2$:

$$\begin{aligned} \mathrm{div}(\rho (|\mathrm{D}\varphi |^2, \varphi )\mathrm{D}\varphi )+ n\rho (|\mathrm{D}\varphi |^2, \varphi )=0, \end{aligned}$$

(18)

where $\rho (|\mathrm{D}\varphi |^2, \varphi )=\big (B_0-(\gamma -1)(\frac{1}{2}|\mathrm{D}\varphi |^2+\varphi )\big )^{\frac{1}{\gamma -1}}$ with $B_0=(\gamma -1)B+1$.

The weak solutions of (17) can be defined as follows:

Definition 2

A function $\phi \in W^{1,\infty }_{\mathrm{loc}}(\Lambda )$ in a domain $\Lambda \subset \mathbb {R}^n$ is a weak solution of system (17) in $\Lambda$, provided that

$$\begin{aligned} &\int _\Lambda \big ( \big({\varvec{G}}(\phi -{\varvec{\xi }}\cdot \mathrm{D}\phi, \mathrm{D}\phi )- G_0(\phi -{\varvec{\xi }}\cdot \mathrm{D}\phi, \mathrm{D}\phi ){\varvec{\xi }}\big )\cdot \mathrm{D}\zeta ({\varvec{\xi }}) \nonumber \\&\quad\quad-n G_0(\phi -{\varvec{\xi }}\cdot \mathrm{D}\phi, \mathrm{D}\phi )\zeta ({\varvec{\xi }})\big )\, \mathrm{d}{\varvec{\xi }}=0 \end{aligned}$$

(19)

for any $\zeta \in C_0^1(\Lambda )$.

Similarly, it can shown that any weak solution of (17) in the ${\varvec{\xi }}$-coordinates in the sense of Definition 2 is a weak solution of (2) in the $(t,\mathbf {x})$-coordinates. Then any co-dimension-one $C^1$-discontinuity S satisfies the Rankine-Hugoniot conditions along S in the ${\varvec{\xi }}$-coordinates:

$$\begin{aligned}{}[\phi ]=0, \qquad [{\varvec{G}}(\phi -{\varvec{\xi }}\cdot \mathrm{D}\phi, \mathrm{D}\phi )- G_0(\phi -{\varvec{\xi }}\cdot \mathrm{D}\phi, \mathrm{D}\phi ){\varvec{\xi }}]\cdot {\varvec{\nu }}_{\mathrm{s}}=0, \end{aligned}$$

or equivalently,

$$\begin{aligned}{}[\phi ]=0, \qquad [({\varvec{G}}(\phi -{\varvec{\xi }}\cdot \mathrm{D}\phi, \mathrm{D}\phi )- G_0(\phi -{\varvec{\xi }}\cdot \mathrm{D}\phi, \mathrm{D}\phi ){\varvec{\xi }})\cdot {\varvec{\nu }}_{\mathrm{s}}]=0, \end{aligned}$$

where ${\varvec{\nu }}_{\mathrm{s}}$ is either of the unit normals to S.

3 Two-Dimensional (2-D) Riemann Problem I:  Two Shocks and Two Vortex Sheets for the Pressure Gradient System

In this section, we present the first 2-D Riemann problem, Riemann Problem I, through the pressure gradient system that is a hyperbolic system of conservation laws.

The pressure gradient system takes the following form:

$$\begin{aligned} {\left\{ \begin{array}{ll} u_t+p_{x_1}=0,\\ v_t+p_{x_2}=0,\\ E_t+(pu)_{x_1}+(pv)_{x_2}=0, \end{array}\right. } \end{aligned}$$

(20)

where $E=\frac{|\mathbf {u}|^2}{2}+p$ with $\mathbf {u}=(u,v)$. System (20) can be written in form (2) with

$$\begin{aligned} {\varvec{U}}=(\mathbf {u},E)^\top, \,\,\, {\varvec{F}}_1=\big(E-\frac{{|\mathbf {u}|^2}}{2}\big)(1, 0, u)^\top, \,\,\, {\varvec{F}}_2=\big(E-\frac{|\mathbf {u}|^2}{2}\big)(0, 1, v)^\top . \end{aligned}$$

(21)

There are two mechanisms for the fluid motion: the inertia and the pressure differences. Corresponding to a separation of these two mechanisms, the full Euler equations (1) with (3) in gas dynamics can be split into two subsystems of conservation laws: the pressure gradient system and the pressureless Euler system, respectively; also see [1, 28, 62] and the references cited therein for this and similar flux-splitting ideas which have been widely used to design the so-called flux-splitting schemes and their high-order accurate extensions. Furthermore, system (20) can also be deduced from system (1) with (3) under the physical regime whereby the velocity is small and the adiabatic gas constant $\gamma$ is large; see [95]. An asymptotic derivation of system (20) has also been presented by Hunter as described in [97]. We refer the reader to [59, 98] for further background on system (20).

3.1 2-D Riemann Problem I: Two Shocks and Two Vortex Sheets

We now consider the following Riemann problem:

Problem 1

(2-D Riemann Problem I: Two Shocks and Two Vortex Sheets) Seek a global solution of system (20) with Riemann initial data that consist of four constant states in four sectorial regions $\Omega _i$ with symmetric sectorial angles (see Fig. 1):

$$\begin{aligned} (p,\mathbf {u})(0,\mathbf {x})=(p_i,\mathbf {u}_i) \qquad \,\, \text{ for } \,\,\mathbf {x}\in \Omega _i, \, i=1,2,3,4 \end{aligned},$$

(22)

such that the four initial constant states are required to satisfy the following conditions:

$$\begin{aligned} {\left\{ \begin{array}{ll} \text { a forward shock }S_{41}^{+} \text { is formed between states } (1) \text { and } (4),\\ \text { a backward shock }S_{12}^{-} \text { is formed between states }(1) \text { and }(2),\\ \text { a vortex sheet }J_{23}^{+} \text { is formed between states } (2) \text { and }(3),\\ \text { a vortex sheet }J_{34}^{-} \text { is formed between states } (3) \text { and } (4). \end{array}\right. } \end{aligned}$$

(23)

Fig. 1

Riemann Problem I: Riemann initial data (cf. [31, 96])

This Riemann problem with the assumption that the angle $\alpha _1=\alpha _2$ is close to zero initially was first analyzed in Zheng [96], for which the two shocks bend slightly and the diffracted shock $\Gamma _{\mathrm{shock}}$ does not meet the inner sonic circle $C_2$. In the recent work [31], this Riemann problem has been solved globally for the general case; that is, the angle between the two shocks is not necessarily close to $\uppi$.

3.2 Reformulation of Riemann Problem I

As discussed earlier, we seek self-similar solutions in the self-similar coordinates with the form

$$\begin{aligned} (p,\mathbf {u})(t,\mathbf {x})=(p,\mathbf {u})({\varvec{\xi }}) \qquad \text { with } {\varvec{\xi }}=\frac{\mathbf {x}}{t},\,t>0. \end{aligned}$$

In the ${\varvec{\xi }}$-coordinates, system (20) can be rewritten in form (11) with (21). The four waves in Riemann Problem I can be obtained by solving four 1-D Riemann problems in the self-similar coordinates ${\varvec{\xi }}$, which form the following configuration as shown in Fig. 2:

Fig. 2

Riemann Problem I: Riemann solution configuration (cf. [31])

More precisely, let $\xi _2=f(\xi _1)$ be a $C^1$-discontinuity curve of a bounded discontinuous solution of system (11) with (21). From the Rankine-Hugoniot relations on $\xi _2=f(\xi _1)$,

$$\begin{aligned} {\left\{ \begin{array}{ll} \big (\xi _1f'(\xi _1)-f(\xi _1)\big )[u]-f'(\xi _1)[p]=0,\\ \\ \big (\xi _1 f'(\xi _1)-f(\xi _1)\big )[v]+[p]=0,\\ \\ \big (\xi _1 f'(\xi _1)-f(\xi _1)\big )[E]-f'(\xi _1)[pu]+[pv]=0, \end{array}\right. } \end{aligned}$$

we find that $\xi _2=f(\xi _1)$ can be one of the two nonlinear discontinuities:

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{\mathrm{d}f(\xi _1)}{\mathrm{d}\xi _{1}}=\sigma _{\pm }=-\frac{[u]}{[v]} =\frac{\xi _{1} f(\xi _{1}){\pm }\sqrt{\overline{p}( \xi _{1}^{2}+ |f(\xi _{1})|^{2} -\overline{p})}}{\xi _{1}^{2}-\overline{p}},\\ \\ {[}p{]}^2=\overline{p}([u]^2+[v]^2), \end{array}\right. } \end{aligned}$$

(24)

or a vortex sheet (linearly degenerate discontinuity):

$$\begin{aligned} {\left\{ \begin{array}{ll} \sigma _{0}=\frac{f(\xi _{1})}{\xi _{1}}=\frac{[v]}{[u]},\\ \\ {[}p{]}=0, \end{array}\right. } \end{aligned}$$

(25)

where $\overline{p}$ is the average of the pressure on the two sides of the discontinuity.

A nonlinear discontinuity is called a shock if it satisfies (24) and the entropy condition: pressure p increases across it in the flow direction; that is, the pressure ahead of the wave-front is larger than that behind the wave-front. There are two types of shocks $S^{\pm }$:

• $S=S^{+}$ if $\mathrm{D}p$ and the flow direction form a right-hand system;

• $S=S^{-}$ if $\mathrm{D}p$ and the flow direction form a left-hand system.

A discontinuity is called a vortex sheet if it satisfies (25). There are two types of vortex sheets $J^{\pm }$ determined by the signs of the vorticity:

$$\begin{aligned} J^{\pm }{:} \quad \text {curl}\,\mathbf {u}=\pm \infty . \end{aligned}$$

It can be shown that, for fixed $(p_1,\mathbf {u}_1)$ and $p_2=p_3=p_4$ satisfying $p_1>p_2$, there exist states $\mathbf {u}_i, i=2,3,4$, depending on angles $(\alpha _1,\alpha _2)$ continuously such that the conditions in (23) for the Riemann initial data hold.

Fig. 3

The Riemann data and the global solution when $\alpha _1=0$ (cf. [31])

There is a critical case when $\alpha _1=0$. Then the Riemann initial data satisfy

$$\begin{aligned} p_1>p_2=p_3=p_4, \quad u_1=u_2=u_3=u_4,\quad v_1>v_2=v_3=v_4. \end{aligned}$$

The global Riemann solution is a piecewise constant solution with two planar shocks $S_{12}^{-}$ for $\xi _1<0$ and $S_{41}^{+}$ for $\xi _1>0$ on the line, $\xi _2=-\sqrt{\overline{p}}$, with

$$\begin{aligned}{}[v]=-\frac{[p]}{\sqrt{\overline{p}}}, \quad \, [u]=0\,\,\qquad \text{ for } \overline{p}=\frac{p_1+p_2}{2}, \end{aligned}$$

and two vortex sheets $J_{23}^{+}$ and $J_{34}^{-}$, as shown in Fig. 3. The two planar shocks $S_{12}^{-}$ and $S_{41}^{+}$ are both tangential to the circle, $|{\varvec{\xi }}|=\sqrt{\overline{p}}$, with the tangent point on the circle as the end-point. It follows from the expression of $J_{23}^{+}$ given in (25) that $p_2=p_3$ on both sides of $J_{23}^{+}$. At the point where $J_{23}^{+}$ intersects with $S_{12}^{-}$, we see that $J_{23}^{+}$ does not affect the shock owing to $p_2=p_3$. The intersection between $J_{34}^{-}$ and $S_{41}^{+}$ can be handled in the same way.

We now consider the general case: $\alpha _1\in (0,\frac{\uppi} {2})$. From system (11) with (21), we can derive the following second-order nonlinear equation for p:

$$\begin{aligned} (p-\xi _1^{2})p_{\xi _1\xi _1}-2\xi _1\xi _2 p_{\xi _1\xi _2}+(p-\xi _2^{2})p_{\xi _2\xi _2} +\frac{(\xi _1 p_{\xi _1}+\xi _2 p_{\xi _2})^{2}}{p} -2(\xi _1 p_{\xi _1}+\xi _2 p_{\xi _2})=0. \end{aligned}$$

(26)

Equation (26) is of the mixed hyperbolic-elliptic type, which is hyperbolic when $|{\varvec{\xi }}|>\sqrt{p}$ and elliptic when $|{\varvec{\xi }}|<\sqrt{p}$ with the transition boundary—the sonic circle $|{\varvec{\xi }}|=\sqrt{p}$. Furthermore, in the polar coordinates: $(r,\theta )=(|{\varvec{\xi }}|, \arctan (\frac{\xi _2}{\xi _1})),$ (26) becomes

$$\begin{aligned} Qp{:}=(p-r^{2})p_{rr}+\frac{p}{r^{2}}p_{\theta \theta }+\frac{p}{r}p_{r}+\frac{1}{p}\big ((r p_{r})^{2}-2r p p_{r}\big )=0, \end{aligned}$$

(27)

which is hyperbolic when $p<r^2$ and elliptic when $p>r^2$. The sonic circle is given by $r=r(\theta )=\sqrt{p(r(\theta ),\theta )}$.

In the ${\varvec{\xi }}$-coordinates, the four waves come from the far-field (at infinity, corresponding to $t=0$) and keep planar waves before the two shocks meet the outer sonic circle $C_1$ of state (1):

$$\begin{aligned} C_1{:}=\{\,{\varvec{\xi }}{:}\,|{\varvec{\xi }}|=\sqrt{p_1}\,\}. \end{aligned}$$

When the two shocks $S_{12}^{-}$ and $S_{41}^{+}$ meet the sonic circle $C_1$ at points $P_3$ and $P_1$, respectively, the key issue is whether they bend and meet to form a diffracted shock, denoted by $\Gamma _{\mathrm{shock}}$; see Fig. 2. Since the whole configuration is symmetric with respect to the $\xi _2$-axis, $\Gamma _{\mathrm{shock}}$ must be perpendicular to $\xi _1=0$ at point $P_2$ where the two diffracted shocks meet. It is not known a priori whether the diffracted shock may degenerate partially into a portion of the inner sonic circle $C_2$ of state (2). Once this case occurs, $p=p_2$ on the sonic circle, which satisfies the oblique derivative condition on the diffracted shock automatically. Observe that the two vortex sheets $J_{23}^{+}$ and $J_{34}^{-}$ and the diffracted shock $\Gamma _{\mathrm{shock}}$ have no influence on each other during the intersection, as pointed out earlier by Zhang et al. [92]. Therefore, from now on, we first ignore the two vortex sheets and focus mainly on the diffracted shock.

On $\Gamma _{\mathrm{shock}}$, the Rankine-Hugoniot conditions in the polar coordinates must be satisfied:

$$\begin{aligned} {\left\{ \begin{array}{ll} r[u]-\big (\cos \theta +\frac{1}{r}\frac{\mathrm{d}r}{\mathrm{d}\theta }\sin \theta \big )[p]=0,\\ r[v]-\big (\sin \theta -\frac{1}{r}\frac{\mathrm{d}r}{\mathrm{d}\theta }\cos \theta \big )[p]=0,\\ r[E]-\big (\cos \theta +\frac{1}{r}\frac{\mathrm{d}r}{\mathrm{d}\theta }\sin \theta \big )[pu] -\big (\sin \theta - \frac{1}{r}\frac{\mathrm{d}r}{\mathrm{d}\theta }\cos \theta \big )[pv]=0. \end{array}\right. } \end{aligned}$$

(28)

Owing to $[pu]=\overline{p}\,[u]+\overline{u}\,[p],$ with $\overline{p}$ as the average of the two neighboring states of p, we eliminate [u] and [v] in the third equation in (28) to obtain

$$\begin{aligned} \Big (\frac{\mathrm{d}r}{\mathrm{d}\theta }\Big )^2=\frac{r^2(r^2-\overline{p})}{\overline{p}}. \end{aligned}$$

The shock diffraction can also be regarded to be generated from point $P_2$ in two directions, which implies that $r^{\prime }(\theta )>0$ for $\theta \in [\frac{3\uppi }{2},\theta _{1}]$ and $r^{\prime }(\theta )<0$ for $\theta \in [\theta _{3},\frac{3\uppi }{2}]$, where $\theta _{i}$ are denoted as the $\theta$-coordinates of points $P_i$, $i=1,3$, respectively. Thus, we choose

$$\begin{aligned} \frac{\mathrm{d}r}{\mathrm{d}\theta }=g(p(r(\theta ),\theta ),r(\theta )):= {\left\{ \begin{array}{ll} r\sqrt{\frac{r^2-\overline{p}}{\overline{p}}}\qquad \,\, &{}\text {for}\,\, \theta \in \big[\frac{3\uppi }{2},\theta _{1}\big],\\ -r\sqrt{\frac{r^2-\overline{p}}{\overline{p}}}\qquad \,\, &{}\text {for}\,\, \theta \in \big[\theta _{3},\frac{3\uppi }{2}\big]. \end{array}\right. } \end{aligned}$$

(29)

It follows from (24), or (28), that $[p]^2=\overline{p}\,\big ([u]^2+[v]^2\big ).$ Then taking the derivative $r^\prime (\theta )\partial _r+\partial _\theta$ on both sides of this equation along the shock yields the derivative boundary condition on $\Gamma _{\mathrm{shock}}=\{(r(\theta ),\theta ){:}\, \theta _3\leqslant \theta \leqslant \theta _1\}$:

$$\begin{aligned} \beta _1 p_r+\beta _2 p_\theta =0, \end{aligned}$$

(30)

where ${\beta }=(\beta _1,\beta _2)$ is a function of $(p,p_2,r(\theta ),r^\prime (\theta ))$ with

$$\begin{aligned} \beta _1=2r^\prime (\theta )\Big (\frac{r^2-\overline{p}}{r^2}-\frac{[p]}{4\overline{p}} +\frac{\overline{p}(r^2-p)}{r^2p}\Big ), \quad \beta _2=\frac{4(r^2-\overline{p})}{r^2}-\frac{[p]}{2\overline{p}}. \end{aligned}$$

(31)

The obliqueness becomes

$$\begin{aligned} \mu :=(\beta _1,\beta _2)\cdot (1,-r^\prime (\theta ))=-2r^\prime (\theta )\bigg (1-\frac{\overline{p}}{p}\bigg ). \end{aligned}$$

Note that $\mu$ vanishes at point $P_2$ where $r^\prime (\frac{3\uppi }{2})=0$ and

$$\begin{aligned} \beta _1=0,\qquad \beta _2=-\frac{[p]}{2\overline{p}}<0, \end{aligned}$$

owing to $p>p_2$.

Let $\Gamma _{\mathrm{sonic}}$ be the larger portion $\widehat{P_1P_3}$ of the sonic circle $C_1$ of state (1). On $\Gamma _{\mathrm{sonic}}$, p satisfies the Dirichlet boundary condition

$$\begin{aligned} p=p_1. \end{aligned}$$

(32)

Let $\Omega$ be the bounded domain enclosed by $\Gamma _{\mathrm{sonic}}$ and $\Gamma _{\mathrm{shock}}$. Then Riemann Problem I (Problem 1) can be reformulated into the following free boundary problem.

Problem 2

(Free Boundary Problem) Seek a solution $(p(r,\theta ), r(\theta ))$ such that $p(r, \theta )$ and $r(\theta )$ are determined by (27) in $\Omega$ and the free boundary conditions (29)–(31) on $\Gamma _{\mathrm{shock}}$ (the derivative boundary condition), in addition to the Dirichlet boundary condition (32) on $\Gamma _{\mathrm{sonic}}$.

3.3 Global Solutions of Riemann Problem I:  Free Boundary Problem, Problem 2

To solve Riemann Problem I, it suffices to deal with the free boundary problem, Problem 2, which has been solved as stated in the following theorem.

Theorem 1

([31])  There exists a global solution $(p(r,\theta ), r(\theta ))$ of Problem 2 in domain $\Omega$ with the free boundary

$$\begin{aligned} \Gamma _{\mathrm{shock}}{:}=\{(r(\theta ),\theta ){:}\, \theta _{3}\leqslant \theta \leqslant \theta _{1}\} \end{aligned}$$

such that

$$\begin{aligned} p\in C^{2,\alpha }(\Omega )\cap C^{0,1}(\overline{\Omega }), \qquad r\in C^{2,\alpha }((\theta _{3},\theta _{1}))\cap C^{1,1}([\theta _{3},\theta _{1}]), \end{aligned}$$

where $\alpha \in (0,1)$ depends only on the Riemann initial data. Moreover, the global solution $(p(r,\theta ),r(\theta ))$ satisfies the following properties:

• (i) $p>p_2$ on the free boundary $\Gamma _{\mathrm{shock}}$; that is, $\Gamma _{\mathrm{shock}}$ does not meet the sonic circle $C_2$ of state (2);

• (ii) the free boundary $\Gamma _{\mathrm{shock}}$ is convex in the self-similar coordinates;

• (iii) the global solution $p(r,\theta )$ is $C^{1,\alpha }$ up to the sonic boundary $\Gamma _{\mathrm{sonic}}$ and Lipschitz continuous across $\Gamma _\mathrm{sonic}$;

• (iv) the Lipschitz regularity of the solution across $\Gamma _{\mathrm{sonic}}$ from the inside of the subsonic domain is optimal.

There are three main difficulties for the proof of Theorem 1:

• (i) the diffracted shock $\Gamma _{\mathrm{shock}}$ is a free boundary, which is not known a priori whether it coincides with the inner sonic circle $C_2$ of state (2);

• (ii) on the sonic boundary $\Gamma _{\mathrm{sonic}}$, owing to $p_1=r^2$, the ellipticity of (27) degenerates;

• (iii) at point $P_2$ where the diffracted shock $\Gamma _{\mathrm{shock}}$ meets the $\xi _2$-axis: $\xi _1=0$, the obliqueness of derivative boundary condition fails, since

  $$\begin{aligned} (\beta _1,\beta _2)\cdot (1,-r^{\prime }(\theta ))=0. \end{aligned}$$

In the proof of Theorem 1, we first assume that $p\geqslant p_2+\delta$ holds on $\Gamma _{\mathrm{shock}}$ for some $\delta >0$; that is, $\Gamma _{\mathrm{shock}}$ cannot coincide with the sonic circle $C_2$ of state (2), which is eventually proved. For the third difficulty, we may express this as a one-point Dirichlet condition $p(P_2)=\hat{p}$ by solving

$$\begin{aligned} 2r(\theta _2)=p(r(\theta _2),\theta _2)+p_2. \end{aligned}$$

More precisely, the existence proof is divided into four steps.

• (i) Since (27) degenerates on the sonic boundary, the differential operator Q in (27) is replaced by the regularized operator:

  $$\begin{aligned} Q^{\varepsilon }=Q+\varepsilon \Delta _{\varvec{\xi }}. \end{aligned}$$

  The free boundary $\Gamma _{\mathrm{shock}}$ is first fixed, then the equation and the derivative boundary condition are linearized, and the existence of a solution of the linear fixed mixed-type boundary problem is established for the regularized equation in the polar coordinates.

• (ii) Based on the estimates of solutions of the linear fixed boundary problem obtained in Step (i), the existence of a solution of the nonlinear fixed boundary problem is proved via the Schauder fixed point theorem.

• (iii) The existence of a solution of the free boundary problem with the oblique derivative boundary condition for the regularized elliptic equation is established by using the Schauder fixed point argument again. It follows that the free boundary never meets the sonic circle $C_2$ of state $p_2$.

• (iv) Finally, the limiting solution as the elliptic regularization parameter $\varepsilon$ tends to 0 is proved to be a solution of Problem 2.

In Theorem 1, a global solution p of the second-order equation (26) in $\Omega$ is constructed, which is piecewise constant in the supersonic domain. Moreover, p is proved to be Lipschitz continuous across the degenerate sonic boundary $\Gamma _{\mathrm{sonic}}$ from $\Omega$ to the supersonic domain. To recover velocity $\mathbf {u}=(u, v)$, we consider the first two equations in system (11) with (21). We can rewrite these equations in the radial variable r as

$$\begin{aligned} \frac{\partial \mathbf {u}}{\partial r}=\frac{1}{r}\mathrm{D}p, \end{aligned}$$

and integrate from the boundary of the subsonic domain toward the origin. It is direct to see that $\mathbf {u}$ is at least Lipschitz continuous across $\Gamma _{\mathrm{sonic}}$. Furthermore, $\mathbf {u}$ has the same regularity as p inside $\Omega$ except origin $r=0$. However, $\mathbf {u}$ may be multi-valued at the origin (i.e., $r=0$). Therefore, we have

Theorem 2

 ([31])   Let the Riemann initial data satisfy (23). Then there exists a global solution $(p, \mathbf {u})(r,\theta )$ with the 2-D shock

$$\begin{aligned} \Gamma _{\mathrm{shock}}=\{(r(\theta ), \theta ){:}\, \theta _{3}\leqslant \theta \leqslant \theta _{1}\} \end{aligned}$$

such that

$$\begin{aligned} (p, \mathbf {u})\in C^{2,\alpha }(\Omega ), \quad p\in C^{0,1}(\overline{\Omega }), \quad r\in C^{2,\alpha }((\theta _{3},\theta _{1}))\cap C^{1,1}([\theta _{3},\theta _{1}]), \end{aligned}$$

and $(\textit{p}, \mathbf {u})$ are piecewise constant in the supersonic domain. Moreover, the global solution $(\textit{p}, \mathbf {u})$ with shock $\Gamma _\mathrm{shock}$ satisfies properties (i)–(ii) in Theorem 1 and

• (a) $(p, \mathbf {u})$ is $C^{1,\alpha }$ up to the sonic boundary $\Gamma _{\mathrm{sonic}}$ and Lipschitz continuous across $\Gamma _\mathrm{sonic}$;

• (b) the Lipschitz regularity of both solution $(p, \mathbf {u})$ across $\Gamma _{\mathrm{sonic}}$ from the subsonic domain $\Omega$ and shock $\Gamma _{\mathrm{shock}}$ across points $\{P_1, P_3\}$ is optimal.

More details can be found in [31]. Similar results can be obtained for the nonlinear wave system introduced in Sect. 4 below by using the same approach and related techniques/methods. Furthermore, Riemann Problem I for the Euler equations for potential flow has also been solved recently in [16].

4 Two-Dimensional (2-D) Riemann Problem II: the Lighthill Problem for Shock Diffraction for the Nonlinear Wave System

In this section, we present the second Riemann problem, Riemann Problem II—the Lighthill problem for shock diffraction by 2-D convex cornered wedges in the compressible fluid flow (Lighthill [63, 64]), through the nonlinear wave system; also see [4, 17, 38, 39].

The nonlinear wave system consists of three conservation laws, which takes the form

$$\begin{aligned} {\left\{ \begin{array}{ll} \rho _{t}+m_{x_1}+n_{x_2}=0,\\ m_{t}+p_{x_1}=0,\\ n_{t}+p_{x_2}=0\end{array}\right. } \end{aligned}$$

(33)

for $(t,\mathbf {x})\in [0,\infty )\times \mathbb {R}^2$, where $\rho$ stands for the density, p for the pressure, and (m, n) for the momenta in the $\mathbf {x}$-coordinates. The pressure-density constitutive relation is

$$\begin{aligned} p(\rho )=\frac{\rho ^\gamma }{\gamma } \qquad \,\, \text{ for } \gamma >1, \end{aligned}$$

(34)

by scaling without loss of generality. Then the sonic speed $c=c(\rho )$ is determined by

$$\begin{aligned} c(\rho ):=\sqrt{p'(\rho )}=\rho ^{\frac{\gamma -1}{2}}, \end{aligned}$$

which is a positive, increasing function for all $\rho >0$. System (33) can be written in form (1) with

$$\begin{aligned} {\varvec{U}}=(\rho, m, n)^\top, \quad {\varvec{F}}_1=(m, p,0)^\top, \quad {\varvec{F}}_2=(n, 0, p)^\top . \end{aligned}$$

(35)

The 2-D nonlinear wave system (33) is derived from the compressible isentropic gas dynamics by neglecting the inertial terms, i.e., the quadratic terms in the velocity; see [7].

4.1 Riemann Problem II: the Lighthill Problem for Shock Diffraction by Convex Cornered Wedges

Let $S_0$ be the vertical planar shock in the $(t, \mathbf{x})$-coordinates, with the left constant state $U_{1}=(\rho _{1},m_{1},0)$ and the right state $U_{0}=(\rho _{0},0,0)$, satisfying

$$\begin{aligned} m_1=\sqrt{\big (p(\rho _{1})-p(\rho _{0})\big )(\rho _{1}-\rho _{0})}>0, \qquad \rho _1>\rho _0. \end{aligned}$$

When $S_0$ passes through a convex cornered wedge:

$$\begin{aligned} W{:}=\{\mathbf {x}=(x_1, x_2)\,{:}\, x_2<0, x_1\leqslant x_2\,\mathrm{cot}\,\theta _{\mathrm{w}}\}, \end{aligned}$$

shock diffraction occurs, where the wedge angle $\theta _{\mathrm{w}}$ is between $-\uppi$ and 0; see Fig. 4. Then the shock diffraction problem can be formulated as follows:

Fig. 4

Riemann Problem II: the Lighthill problem (cf. [17])

Problem 3

(Riemann Problem II: the Lighthill Problem for Shock Diffraction)  Seek a solution of system (33)–(34) with the initial condition at $t=0$:

$$\begin{aligned} {\varvec{U}}|_{t=0} ={\left\{ \begin{array}{ll} (\rho _0, 0, 0) \quad &{} \text{ in } \big\{-\uppi +\theta _{\mathrm{w}}\leqslant \arctan (\frac{x_2}{x_1} )\leqslant \frac{\uppi} {2}\big\},\\ (\rho _1, m_1, 0) \quad &{} \text{ in } \big\{x_1<0, x_2>0\big\}, \end{array}\right. } \end{aligned}$$

(36)

and the slip boundary condition along the wedge boundary $\partial W$:

$$\begin{aligned} (m, n)\cdot {\varvec{\nu }}_{\mathrm{w}}\mid _{\partial W}=0, \end{aligned}$$

(37)

where ${\varvec{\nu }}_{\mathrm{w}}$ is the exterior unit normal to $\partial W$ (see Fig. 4).

4.2 Reformulation of Riemann Problem II

Notice that Problem 3 is invariant under the self-similar scaling: $(t, \mathbf{x})\rightarrow (\alpha t, \alpha \mathbf{x})$ for $\alpha \ne 0$. In the self-similar ${\varvec{\xi }}$-coordinates, system (33)–(34) can be rewritten in form (11) with (35). In the polar coordinates $(r,\theta ), r=|{\varvec{\xi }}|$, the system can be further written as

$$\begin{aligned} \partial _{r}\begin{pmatrix} r\rho - m\cos \theta -n\sin \theta \\ rm-p(\rho )\cos \theta \\ rn-p(\rho )\sin \theta \end{pmatrix}+\partial _{\theta } \begin{pmatrix} m\sin \theta -n\cos \theta \\ p(\rho )\sin \theta \\ -p(\rho )\cos \theta \end{pmatrix} =\begin{pmatrix} \rho +\frac{\cos \theta }{r}m+\frac{\sin \theta }{r}n \\ m+\frac{\cos \theta }{r}p(\rho )\\ n+\frac{\sin \theta }{r}p(\rho ) \end{pmatrix}. \end{aligned}$$

(38)

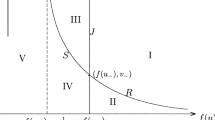
The location of the incident shock $S_0$ for large $r\gg 1$ is

$$\begin{aligned} \xi _1=\xi _1^0:=\sqrt{\frac{p(\rho _1)-p(\rho _0)}{\rho _1-\rho _0}}>0. \end{aligned}$$

(39)

Then Problem 3 can be reformulated as a boundary value problem in an unbounded domain (see Fig. 5): seek a solution of system (11) with (35), or equivalently (38), with the asymptotic boundary condition when $r\rightarrow \infty$:

$$\begin{aligned} (\rho, m, n)\rightarrow {\left\{ \begin{array}{ll} (\rho _0, 0, 0)\, &{}{\mathrm{in}} \{\xi _1>\xi _1^0, \xi _2>0\}\cup \big\{-\uppi +\theta _{\mathrm{w}}\leqslant \arctan (\frac{\xi _2}{\xi _1} )\leqslant 0\big\},\\ (\rho _1, m_1, 0) \, &{}{\mathrm{in} \{\xi _1<\xi _1^0,\xi _2>0\}}, \end{array}\right. } \end{aligned}$$

(40)

and the slip boundary condition along the wedge boundary $\partial W$:

$$\begin{aligned} (m, n)\cdot {\varvec{\nu }}_{\mathrm{w}}\mid _{\partial W}=0. \end{aligned}$$

(41)

Fig. 5

Shock diffraction configuration (cf. [17])

For a smooth solution $U=(\rho,m,n)$ of system (11) with (35), we may eliminate m and n in (33) to obtain a second-order nonlinear equation for $\rho$:

$$\begin{aligned} \big ((c^{2}-\xi _1^{2})\rho _{\xi _1}-\xi _1\xi _2\rho _{\xi _2}+\xi _1\rho \big )_{\xi _1} +\big ((c^{2}-\xi _2^{2})\rho _{\xi _2}-\xi _1\xi _2\rho _{\xi _1}+\xi _2\rho \big )_{\xi _2} -2\rho =0. \end{aligned}$$

(42)

Correspondingly, (42) in the polar coordinates $(r, \theta ), r=|{\varvec{\xi }}|$, takes the form

$$\begin{aligned} \big ((c^{2}-r^{2})\rho _{r}\big )_{r}+\frac{c^{2}}{r}\rho _{r} +\bigg (\frac{c^{2}}{r^{2}}\rho _{\theta }\bigg )_{\theta }=0. \end{aligned}$$

(43)

In the self-similar ${\varvec{\xi }}$-coordinates, as the incident shock $S_0$ passes through the wedge corner, $S_0$ interacts with the sonic circle $\Gamma _{\mathrm{sonic}}$ of state (1): $r=r_1$, and becomes a transonic diffracted shock $\Gamma _{\mathrm{shock}}$, and the flow in domain $\Omega$ behind the shock and inside $\Gamma _{\mathrm{sonic}}$ becomes subsonic.

Consider system (38) in the polar coordinates. Then the Rankine-Hugoniot relations, i.e., the jump conditions, are

$$\begin{aligned}{}[p][\rho ]=[m]^2+[n]^2, \qquad \frac{\mathrm{d} r}{\mathrm{d}\theta }= r\frac{\sqrt{r^2-\bar{c}^2(\rho,\rho _0)}}{\bar{c}(\rho,\rho _0)} \end{aligned}$$

with $\bar{c}(\rho,\rho _0)=\sqrt{\frac{p(\rho )-p(\rho _0)}{\rho -\rho _0}}$, where the plus branch has been chosen so that $\frac{\text{d}r}{\text{d}\theta }>0$. Differentiating the first equation above along $\Gamma _{\text {shock}}$ and using the equations obtained above, we have

$$\begin{aligned} \beta _1\rho _r+\beta _2\rho _{\theta }=0 \qquad \text { on } \Gamma _{\text {shock}}{:}=\{(r(\theta ),\theta ){:}\,\theta \in [\theta _{\mathrm{w}}, \theta _1]\}, \end{aligned}$$

(44)

where $\beta =(\beta _1,\beta _2)$ is a function of $(\rho _0, \rho, r(\theta ), r'(\theta ))$ with

$$\begin{aligned} \beta _{1}=r'(\theta )\big (c^{2}(r^2-\bar{c}^2)-3\bar{c}^2(c^{2}-r^2)\big ),\quad \beta _{2}=3c^{2}(r^{2}-\bar{c}^2)-\bar{c}^2(c^{2}-r^{2}). \end{aligned}$$

Then the obliqueness becomes

$$\begin{aligned} \mu :=\beta \cdot (1,-r'(\theta ))=-2r^2(c^2-\bar{c}^{2})r'(\theta ) \ne 0, \end{aligned}$$

where $(1,-r'(\theta ))$ is the outward normal to $\Omega$ on $\Gamma _{\text {shock}}$. Note that $\mu$ becomes zero when $r'(\theta )=0$, i.e., $r=\bar{c}(\rho,\rho _0)$, where

$$\begin{aligned} \beta _1=0, \qquad \beta _2=-\bar{c}^2(c^2-r^2)<0, \end{aligned}$$

since $c^2(\rho )>\bar{c}^2(\rho,\rho _0)=r^2$ if $\rho >\rho _0$.

The second condition on $\Gamma _{\text {shock}}$ is the shock equation

$$\begin{aligned} \frac{\mathrm{d} r}{\mathrm{d}\theta }=r\frac{\sqrt{r^2-\bar{c}^2(\rho,\rho _0)}}{\bar{c}(\rho,\rho _0)}:=g(r,\theta,\rho (r,\theta )), \qquad \,\,\, r(\theta _1)=r_1, \end{aligned}$$

(45)

where $(r_1,\theta _1)$ are the polar coordinates of $P_1=(\xi _1^0,\xi _2^0)$.

At point $P_2$, $r'(\theta _{\mathrm{w}})=0$, (44) does not satisfy the oblique derivative boundary condition. We may alternatively express this as a one-point Dirichlet condition by solving $r(\theta _{\mathrm{w}})=\bar{c}(\rho (r(\theta _{\mathrm{w}}), \theta _{\mathrm{w}}),\rho _0)$. To deal with this equation, we use the notation:

$$\begin{aligned} a=(\bar{c}_{b})^{-1}(r)\qquad \text {when}\,\, \bar{c}_b:=\bar{c}(a,b)=r \,\,\, \text{ for } \text{ fixed } b, \end{aligned}$$

(46)

so that

$$\begin{aligned} \rho (P_1)=\bar{\rho }=(\bar{c}_{\rho _0})^{-1}(r(\theta _{\mathrm{w}})). \end{aligned}$$

(47)

The boundary condition on the wedge is the slip boundary condition, i.e., $(m,n)\cdot {\varvec{\nu }}_{\mathrm{w}}=0$. Differentiating it along the wedge and combining this with the second and third equations in (33), we conclude that $\rho$ satisfies

$$\begin{aligned} \rho _{{\varvec{\nu }}_{\mathrm{w}}}=0\qquad \text { on } \Gamma _0:=\partial \Omega \cap (\{\theta =\uppi \}\cup \{\theta =\theta _{\mathrm{w}}\}). \end{aligned}$$

(48)

The Dirichlet boundary condition on $\Gamma _{\mathrm{sonic}}$ is

$$\begin{aligned} \rho =\rho _1\qquad \text { on } \Gamma _{\text {sonic}}:=\partial \Omega \cap \partial B_{c_1}(0). \end{aligned}$$

(49)

On the Dirichlet boundary $\Gamma _{\mathrm{sonic}}$, (43) becomes degenerate elliptic from the inside of $\Omega$.

With the derivation of the free boundary conditions on $\Gamma _\mathrm{shock}$ and the fixed boundary conditions on $\Gamma _{\mathrm{sonic}}\cup \Gamma _0$, Problem 3 is further reduced to the following free boundary problem for (43) in domain $\Omega$, with (m, n) correspondingly determined by (38).

Problem 4

(Free Boundary Problem) Seek a solution $(\rho (r, \theta ), r(\theta ))$ such that $\rho (r,\theta )$ and $r(\theta )$ are determined by (43) in domain $\Omega$ and the free boundary conditions (44)–(47) on $\Gamma _\mathrm{shock}=\{(r(\theta ),\theta ){:}\, \theta _{\mathrm{w}}\leqslant \theta \leqslant \theta _1\}$, in addition to the Neumann boundary condition (48) on wedge $\Gamma _0$ and the Dirichlet boundary condition (49) on the degenerate boundary $\Gamma _\mathrm{sonic}$, that is the sonic circle of state (1) (cf. Fig. 5).

4.3 Global Solutions of Riemann Problem II: Free Boundary Problem, Problem 4

To solve Riemann Problem II, it suffices to deal with the free boundary problem, Problem 4, which has been solved as stated in the following theorem.

Theorem 3

([17])   Let the wedge angle $\theta _{\mathrm{w}}$ be between $-\uppi$ and 0. Then there exists a global solution, a density function $\rho (r,\theta )$ in domain $\Omega$, and a free boundary $\Gamma _\mathrm{shock}=\{(r(\theta ),\theta ){:}\, \theta _{\mathrm{w}}\leqslant \theta \leqslant \theta _1\}$, of Problem 4 such that

$$\begin{aligned} \rho \in C^{2+\alpha }(\Omega )\cap C^{\alpha }(\overline{\Omega }), \quad r\in C^{2+\alpha }([\theta _{\mathrm{w}},\theta _1))\cap C^{1,1}([\theta _{\mathrm{w}},\theta _1]). \end{aligned}$$

Moreover, solution $(\rho (r,\theta ), r(\theta ))$ satisfies the following properties:

• (i) $\rho > \rho _0$ on the free boundary $\Gamma _{\mathrm{shock}}$; that is, $\Gamma _{\mathrm{shock}}$ is separated from the sonic circle $C_0$ of state (0);

• (ii) the free boundary $\Gamma _{\mathrm{shock}}$ is strictly convex up to point $P_1$, except point $P_2$, in the self-similar ${\varvec{\xi }}$-coordinates;

• (iii) the density function $\rho (r,\theta )$ is $C^{1,\alpha }$ up to $\Gamma _{\mathrm{sonic}}$ and Lipschitz continuous across $\Gamma _{\mathrm{sonic}}$;

• (iv) the Lipschitz regularity of $\rho (r,\theta )$ across $\Gamma _{\mathrm{sonic}}$ and at $P_1$ from the inside is optimal.

Similar to the proof of Theorem 1, Theorem 3 is established in two steps. First, the regularized approximate free boundary problem for (43) involving two small parameters $\varepsilon$ and $\delta$ is solved. Then the limits: $\varepsilon \rightarrow 0$ and $\delta \rightarrow 0$ are proved to yield a solution of Problem 4, i.e., (43)–(49), with the optimal regularity.

In Theorem 3, a global solution $\rho$ of (43) in $\Omega$ is constructed, by combining this function with $\rho =\rho _1$ in state (1) and $\rho =\rho _0$ in state (0). That is, the global density function $\rho$ that is piecewise constant in the supersonic domain is Lipschitz continuous across the degenerate sonic boundary $\Gamma _{\mathrm{sonic}}$ from $\Omega$ to state (1). To recover the momentum vector function (m, n), we can integrate the second and third equations in (38). These can also be written in the radial variable r,

$$\begin{aligned} \frac{\partial (m,n)}{\partial r}=\frac{1}{r} \mathrm{D}p(\rho ) \end{aligned}$$

(50)

and integrated from the boundary of the subsonic domain toward the origin.

It has been proved that the limit of $\mathrm{D}\rho$ does not exist at $P_1$ as ${\varvec{\xi }}$ in $\Omega$ tends to ${\varvec{\xi }}^0$, but $|\mathrm{D}c(\rho )|$ has an upper bound. Thus, $p(\rho )$ is Lipschitz, which implies that (m, n) is at least Lipschitz across the sonic circle $\Gamma _{\mathrm{sonic}}$. Furthermore, (m, n) has the same regularity as $\rho$ inside $\Omega$, except for origin $r=0$. However, (m, n) may be multi-valued at origin $r=0$. Therefore, we have

Theorem 4

([17])   Let the wedge angle $\theta _{\mathrm{w}}$ be between $-\uppi$ and 0. Then there exists a global solution $(\rho, m, n)(r,\theta )$ with the diffracted shock $\Gamma _{\mathrm{shock}}=\{(r(\theta ),\theta ){:}\, \theta _{\mathrm{w}}\leqslant \theta \leqslant \theta _1\}$ of Problem 4 such that

$$\begin{aligned} (\rho, m, n)\in C^{2+\alpha }(\Omega ), \quad \rho \in C^{\alpha }(\overline{\Omega }), \quad r\in C^{2+\alpha }([\theta _\mathrm{w},\theta _1))\cap C^{1,1}([\theta _{\mathrm{w}},\theta _1]), \end{aligned}$$

and $(\rho, m, n)=(\rho _1, m_1, 0)$ in domain $\{\xi _1<\xi _1^0,\, r>r_1\}$ and $(\rho _0, 0,0)$ in domain $\{\xi _1>\xi _1^0,\, \xi _2>\xi _2^0\}\cup \{r>r(\theta ),\,\theta _{\mathrm{w}}\leqslant \theta \leqslant \theta _1\}$. Moreover, solution $(\rho,m,n)(r,\theta )$ with the diffracted shock $\Gamma _{\mathrm{shock}}$ satisfies properties (i)–(ii) in Theorem 3 and

• (i) $(\rho,m,n)$ is $C^{1,\alpha }$ up to $\Gamma _{\mathrm{sonic}}$ and Lipschitz continuous across $\Gamma _{\mathrm{sonic}}$;

• (ii) the Lipschitz regularity of solution $(\rho,m,n)$ across $\Gamma _{\mathrm{sonic}}$ and at $P_1$ from the inside is optimal;

• (iii) the momentum vector function (m, n) may be multi-valued at the origin.

In particular, Theorem 3 implies the following facts.

• (a) The optimal regularity of $(\rho, m, n)(r, \theta )$ across $\Gamma _{\mathrm{sonic}}$ and at $P_1$ from the inside is $C^{0,1}$, i.e., the Lipschitz continuity.

• (b) The diffracted shock $\Gamma _{\mathrm{shock}}$ is definitely not degenerate at point $P_2$. This had been an open question even when the wedge angle is $\frac{\uppi }{2}$ as in [50], though it was physically plausible.

• (c) The diffracted shock $\Gamma _{\mathrm{shock}}$ away from point $P_2$ is strictly convex and has a jump at point $P_1$ from a positive value to zero, while the strict convexity of $\Gamma _{\mathrm{shock}}$ fails at $P_2$.

More details can be found in [17]. Similar results can be obtained for the pressure gradient equation introduced in Sect. 3 above. In [24], the loss of regularity of solutions of Problem 3 for the potential flow equation (4)–(5), or (2) with (6), has been shown, which implies that the solution configuration for this case is much more complicated.

5 Two-Dimensional (2-D) Riemann Problem III: the Prandtl-Meyer Problem for Unsteady Supersonic Flow onto Solid Wedges for the Euler Equations for Potential Flow

Now we present the third Riemann problem, Riemann Problem III, for the Prandtl-Meyer problem for unsteady supersonic flow onto solid wedges for the Euler equations for potential flow in form (2) with (6)–(7), or (4)–(5); see also [3, 37, 71, 73].

5.1 2-D Riemann Problem III: the Prandtl-Meyer Problem for Unsteady Supersonic Flow onto Solid Wedges for Potential Flow

Consider a supersonic flow with the constant density $\rho _{0}>0$ and velocity $\mathbf{u}_{0}=(u_0, 0)$, $u_0> c_0:=c(\rho _0)$, which impinges toward a symmetric wedge:

$$\begin{aligned} W{:}= \big \{(x_1,x_2){:}\, |x_2|< x_1 \tan \theta _{\mathrm{w}}, x_1 > 0\big \} \end{aligned}$$

(51)

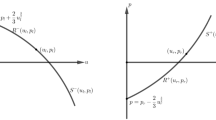
at $t = 0$. If $\theta _{\mathrm{w}}$ is less than the detachment angle $\theta _{\mathrm{w}}^{\mathrm{d}}$, then the well-known shock polar analysis demonstrates that there are two different steady weak solutions: the steady solution $\bar{\Phi }$ of weaker shock strength and the steady solution of stronger shock strength, both of which satisfy the entropy condition and the slip boundary condition (see Fig. 6); see also [3, 14, 34]. Then the dynamic stability of the steady transonic solution $\bar{\Phi }$ of weaker shock strength for potential flow can be formulated as the following problem:

Fig. 6

The shock polar in the $\mathbf {u}$-plane and uniform steady (weak/strong) shock flows (see [14])

Problem 5

(Riemann Problem III: the Prandtl-Meyer Problem for Unsteady Supersonic Flow onto Solid Wedges) Given $\gamma >1$, fix $(\rho _{0}, u_0)$ with $u_0>c_0$. For a fixed $\theta _{\mathrm{w}}\in (0,\theta _{\mathrm{w}}^{\mathrm{d}})$, seek a global entropy solution $\Phi \in W^{1,\infty }_{\mathrm{loc}}({\mathbb {R}}_+\times ({\mathbb {R}}^2{\setminus } W))$ of (2) with (6)–(7) and $B=\frac{u_0^2}{2}+h(\rho _{0})$ so that $\Phi$ satisfies the initial condition at $t=0$:

$$\begin{aligned} (\rho,\Phi )|_{t=0}=(\rho _{0}, u_0 x_1) \qquad \,\,\, \text {for}\;\;\mathbf {x}\in {\mathbb {R}}^2\setminus W, \end{aligned}$$

(52)

and the slip boundary condition along the wedge boundary $\partial W:$

$$\begin{aligned} \nabla _\mathbf{x}\Phi \cdot {\varvec{\nu }}_{\mathrm{w}} |_{\partial W}=0, \end{aligned}$$

(53)

where ${\varvec{\nu }}_{\mathrm{w}}$ is the exterior unit normal to $\partial W$. In particular, we seek a solution $\Phi \in W^{1,\infty }_\mathrm{loc}({\mathbb {R}}_+\times ({\mathbb {R}}^2{\setminus } W))$ that converges to the steady solution $\bar{\Phi }$ of weaker oblique shock strength corresponding to the fixed parameters $(\rho _{0}, u_0, \gamma, \theta _{\mathrm{w}})$ with $\bar{\rho }=h^{-1}(B-\frac{1}{2}|\nabla \bar{\Phi }|^2)$, when $t\rightarrow \infty$, in the following sense: for any $R>0$, $\Phi$ satisfies

$$\begin{aligned} \lim _{t\rightarrow \infty } \Vert (\nabla _\mathbf{x}\Phi (t,\cdot )-\nabla _\mathbf{x}\bar{\Phi }, \rho (t,\cdot )-\bar{\rho })\Vert _{L^1(B_R(\mathbf{0})\setminus W)}=0 \end{aligned}$$

(54)

for $\rho (t,\mathbf{x})$ given by (6).

Since the initial data in (52) do not satisfy the boundary condition (53), a boundary layer is generated along the wedge boundary starting at $t=0$, which forms the Prandtl-Meyer reflection configurations; see [3] and the references cited therein.

To define the notion of weak solutions of Problem 5, it is noted that the boundary condition can be written as $\rho \nabla _\mathbf{x}\Phi \cdot {\varvec{\nu }}_{\mathrm{w}}=0$ on $\partial W$, which is the spatial conormal condition for (2) with (6)–(7). Then we have

Definition 3

(Weak Solutions of Problem 5: Riemann Problem III) A function $\Phi \in W^{1,1}_{\mathrm{loc}}({\mathbb {R}}_+\times ({\mathbb {R}}^2{\setminus } W))$ is called a weak solution of Problem 5 if $\Phi$ satisfies the following properties:

• (i) $B-\big( \partial _t\Phi +\frac{1}{2}|\nabla _\mathbf {x}\Phi |^2\big) \geqslant h(0+) \;\;{(a.e.)} \,{\rm{in}}\,{\mathbb {R}}_+\times ({\mathbb {R}}^2{\setminus } W)$ ,

• (ii) for $\rho (\partial _t \Phi, \nabla _\mathbf {x}\Phi )$ determined by (6),

  $$\begin{aligned} (\rho (\partial _t\Phi, |\nabla _\mathbf {x}\Phi |^2), \rho (\partial _t\Phi, |\nabla _\mathbf {x}\Phi |^2)|\nabla _\mathbf {x}\Phi |)\in (L^1_{\mathrm{loc}}({\mathbb {R}}_+\times \overline{{\mathbb {R}}^2\setminus W}))^2, \end{aligned}$$

• (iii) for every $\zeta \in C^\infty _c({{\mathbb {R}}_+}\times {\mathbb {R}}^2)$,

  $$\begin{aligned}&\int _0^\infty \int _{{\mathbb {R}}^2\setminus W}\Big (\rho (\partial _t\Phi, |\nabla _{\mathbf {x}}\Phi |^2)\partial _t\zeta +\rho (\partial _t\Phi, |\nabla _{\mathbf {x}}\Phi |^2) \nabla_{\mathbf{x}} \Phi \cdot \nabla_{\mathbf{x}}\zeta \Big ) \,\mathrm{d}\mathbf {x}\mathrm{d}t\\&+\int _{{\mathbb {R}}^2\setminus W}\rho _0\zeta (0, \mathbf {x})\,\mathrm{d}\mathbf {x}=0. \end{aligned}$$

Since $\zeta$ does not need to be zero on $\partial \Lambda$, the integral identity in Definition 3 is a weak form of equation (2) with (6)–(7) and the boundary condition $\rho \nabla _\mathbf{x}\Phi \cdot {\varvec{\nu }}_{\mathrm{w}}=0$ on $\partial W$. A weak solution is called an entropy solution if it satisfies the entropy condition that is consistent with the second law of thermodynamics (cf. [22, 34, 35, 55]). In particular, a piecewise smooth solution is an entropy solution if the discontinuities are all shocks.

5.2 Reformulation of Riemann Problem III

Notice that (2) with (6)–(7) is invariant under the self-similar scaling (15), so that it admits self-similar solutions in form (16). Then the pseudo-potential function $\varphi =\phi -\frac{1}{2}|{\varvec{\xi }}|^2$ satisfies the following equation:

$$\begin{aligned} \mathrm{div}(\rho (|\mathrm{D}\varphi |^2,\varphi )\mathrm{D}\varphi )+2\rho (|\mathrm{D}\varphi |^2,\varphi )=0 \end{aligned}$$

(55)

for

$$\begin{aligned} \rho (|\mathrm{D}\varphi |^2,\varphi )= \bigl (B_0- (\gamma -1)(\frac{1}{2}|\mathrm{D}\varphi |^2+\varphi )\bigr )^{\frac{1}{\gamma -1}}, \end{aligned}$$

(56)

where $B_0=(\gamma -1)B+1$. Equation (55) written in the non-divergence form is

$$\begin{aligned} (c^2-\varphi _{{\xi _{1}}}^2)\varphi _{{\xi _{1}}{\xi _{1}}}-2\varphi _{\xi _{1}}\varphi _{\xi _{2}}\varphi _{{\xi _{1}}{\xi _{2}}} +(c^2-\varphi _{{\xi _{2}}}^2)\varphi _{{\xi _{2}}{\xi _{2}}}+2c^2-|\mathrm{D}\varphi |^2=0, \end{aligned}$$

(57)

where the sonic speed $c=c(|\mathrm{D}\varphi |^2,\varphi )$ is determined by

$$\begin{aligned} c^2(|\mathrm{D}\varphi |^2,\varphi )= \rho ^{\gamma -1}(|\mathrm{D}\varphi |^2,\varphi ) =B_0-(\gamma -1)\big (\frac{1}{2}|\mathrm{D}\varphi |^2+\varphi \big ). \end{aligned}$$

(58)

Equation (55) is a nonlinear PDE of mixed elliptic-hyperbolic type. It is elliptic at ${\varvec{\xi }}$ if and only if

$$\begin{aligned} |\mathrm{D}\varphi |<c(|\mathrm{D}\varphi |^2,\varphi ) \end{aligned}$$

(59)

and is hyperbolic if the opposite inequality holds.

One class of solutions of (55) is that of constant states which are the solutions with the constant velocity $\mathbf {v}\in \mathbb {R}^2$. Then the pseudo-potential of the constant state $\mathbf {v}$ satisfies $\mathrm{D}\varphi =\mathbf {v}-{\varvec{\xi }}$ so that

$$\begin{aligned} \varphi ({\varvec{\xi }})=-\frac{1}{2}|{\varvec{\xi }}|^2+\mathbf {v}\cdot {\varvec{\xi }}+C, \end{aligned}$$

(60)

where C is a constant. For such $\varphi$, the expressions in (56) and (58) imply that the density and sonic speed are positive constants $\rho$ and c, i.e., independent of ${\varvec{\xi }}$. Then, from (59)–(60), the ellipticity condition for the constant state $\mathbf {v}$ is

$$\begin{aligned} |{\varvec{\xi }}-\mathbf {v}|<c. \end{aligned}$$

Thus, (55) is elliptic inside the sonic circle with center $\mathbf {v}$ and radius c, and hyperbolic outside this circle.

Moreover, if density $\rho$ is a constant, then the solution is also a constant state; that is, the corresponding pseudo-potential $\varphi$ is of form (60).

Since the problem involves transonic shocks, we have to consider weak solutions of (55), which admit shocks. A shock is a curve across which $\mathrm{D}\varphi$ is discontinuous. If $\Lambda ^+$ and $\Lambda ^-(:=\Lambda \setminus \overline{\Lambda ^+})$ are two nonempty open subsets of a domain $\Lambda \subset {\mathbb {R}}^2$, and ${S}:=\partial \Lambda ^+\cap \Lambda$ is a $C^1$-curve across which $\mathrm{D}\varphi$ has a jump, then $\varphi \in W^{1,1}_{\mathrm{loc}}\cap C^1(\Lambda ^{\pm }\cup S)\cap C^2(\Lambda ^{\pm })$ is a global weak solution of (55) in $\Lambda$ if and only if $\varphi$ is in $W^{1,\infty }_{\mathrm{loc}}(\Lambda )$ and satisfies (55) and the Rankine-Hugoniot conditions on S:

$$\begin{aligned}&\varphi |_{\Lambda ^+\cap S}=\varphi |_{\Lambda ^-\cap S}, \end{aligned}$$

(61)

$$\begin{aligned}&\rho (|\mathrm{D}\varphi |^2, \varphi )\mathrm{D}\varphi \cdot {\varvec{\nu }}_\mathrm{s}|_{\Lambda ^+\cap S} =\rho (|\mathrm{D}\varphi |^2, \varphi )\mathrm{D}\varphi \cdot {\varvec{\nu }}_{\mathrm{s}}|_{\Lambda ^-\cap S}. \end{aligned}$$

(62)

A piecewise smooth solution with the discontinuities is called an entropy solution of (55) if it satisfies the entropy condition: density $\rho$ increases in the pseudo-flow direction of $\mathrm{D}\varphi |_{\Lambda ^+\cap S}$ across the discontinuity. Then such a discontinuity is called a shock.

As the upstream flow has the constant velocity $\mathbf {u}_0=(u_0,0)$, the corresponding pseudo-potential $\varphi _{0}$ has the expression of

$$\begin{aligned} \varphi _{0}=-\frac{1}{2}|{\varvec{\xi }}|^2+u_0\xi _1 \end{aligned}$$

(63)

directly from (60) with the choice of B in Problem 5. Since the symmetry of the domain and the upstream flow in Problem 5 with respect to the $x_1$-axis, Problem 5 can then be reformulated as the following boundary value problem in the domain:

$$\begin{aligned} \Lambda :={\mathbb {R}}^2_+\setminus \{{\varvec{\xi }}{:} \,\xi _2\leqslant \xi _1\tan \theta _\mathrm{w},\, \xi _1\geqslant 0\} \end{aligned}$$

in the self-similar coordinates ${\varvec{\xi }}$, which corresponds to domain $\{(t, \mathbf{x}){:}\, \mathbf{x}\in {\mathbb {R}}^2_+\setminus W,\, t>0\}$ in the $(t, \mathbf{x})$-coordinates, where ${\mathbb {R}}^2_+=\{{\varvec{\xi }}{:} \,\xi _2>0\}:$  seek a solution $\varphi$ of (55) in the self-similar domain $\Lambda$ with the slip boundary condition

$$\begin{aligned} \mathrm{D}\varphi \cdot {\varvec{\nu }}_{\mathrm{w}}|_{\partial \Lambda }=0 \end{aligned}$$

(64)

and the asymptotic boundary condition

$$\begin{aligned} \varphi -\varphi _0\longrightarrow 0 \end{aligned}$$

(65)

along each ray $R_\theta :=\{ \xi _1=\xi _2 \cot \theta, \xi _2 > 0 \}$ with $\theta \in (\theta _{\mathrm{w}}, \uppi )$ as $\xi _2\rightarrow \infty$ in the sense that

$$\begin{aligned} \lim _{r\rightarrow \infty } \Vert \varphi - \varphi _0\Vert _{C(R_{\theta }\setminus B_r(0))} = 0. \end{aligned}$$

(66)

Fig. 7

Self-similar solutions for $\theta _{\mathrm{w}}\in (0, \theta _{\mathrm{w}}^{\mathrm{s}})$ in the self-similar coordinates ${\varvec{\xi }}$ (cf. [3])

Fig. 8

Self-similar solutions for $\theta _{\mathrm{w}}\in [\theta _\mathrm{w}^{\mathrm{s}},\theta _{\mathrm{w}}^{\mathrm{d}})$ in the self-similar coordinates ${\varvec{\xi }}$ (cf. [3])

Given $M_0>1$, $\rho _1$ and $\mathbf {u}_1$ are determined via the shock polar as shown in Fig. 6 for steady potential flow. For any wedge angle $\theta _{\mathrm{w}}\in (0,\theta _{\mathrm{w}}^{\mathrm{s}})$, line $v=u\tan \theta _{\mathrm{w}}$ and the shock polar intersect at a point $\mathbf {u}_1=(u_1,v_1)$ with $|\mathbf {u}_1|>c_1$ and $u_{1}<u_0$; while, for any $\theta _{\mathrm{w}}\in [\theta _{\mathrm{w}}^{\mathrm{s}}, \theta _{\mathrm{w}}^{\mathrm{d}})$, they intersect at a point $\mathbf {u}_1$ with $u_{1}>u_{\mathrm{d}}$ and $|\mathbf {u}_1|<c_1$ where $u_{\mathrm{d}}$ is the u-component of the unique detachment state $\mathbf {u}_{\mathrm{d}}$ when $\theta _{\mathrm{w}}=\theta _{\mathrm{w}}^{\mathrm{d}}$. The intersection state $\mathbf {u}_1$ is the velocity for steady potential flow behind an oblique shock ${S}_0$ attached to the wedge vertex with angle $\theta _\mathrm{w}$. The strength of shock ${S}_0$ is relatively weak compared to the shock given by the other intersection point on the shock polar, hence ${S}_0$ is called a weak oblique shock and the corresponding state $\mathbf {u}_1$ is a weak state. Moreover, such a state $\mathbf {u}_1$ depends smoothly on $(u_0, \theta _{\mathrm{w}})$ and is supersonic when $\theta _{\mathrm{w}}\in (0,\theta _{\mathrm{w}}^{\mathrm{s}})$ and subsonic when $\theta _{\mathrm{w}}\in [\theta _{\mathrm{w}}^{\mathrm{s}}, \theta _{\mathrm{w}}^{\mathrm{d}})$.

Once $\mathbf {u}_1$ is determined, by (61)–(63), the pseudo-potential $\varphi _1$ below the weak oblique shock ${S}_0$ is

$$\begin{aligned} \varphi _1=-\frac{1}{2}|{\varvec{\xi }}|^2+ \mathbf {u}_1\cdot {\varvec{\xi }}. \end{aligned}$$

(67)

We seek a global entropy solution with two types of Prandtl-Meyer reflection configurations whose occurrence is determined by the wedge angle $\theta _{\mathrm{w}}$ in the two different cases: One contains a straight weak oblique shock ${S}_0$ attached to the wedge vertex O and connected to a normal shock ${S}_1$ through a curved shock $\Gamma _{\mathrm{shock}}$ when $\theta _{\mathrm{w}}<\theta _{\mathrm{w}}^\mathrm{s}$, as shown in Fig. 7; the other contains a curved shock $\Gamma _{\mathrm{shock}}$ attached to the wedge vertex and connected to a normal shock ${S}_1$ when $\theta _\mathrm{w}^{\mathrm{s}}\leqslant \theta _{\mathrm{w}}<\theta _{\mathrm{w}}^{\mathrm{d}}$, as shown in Fig. 8, in which the curved shock $\Gamma _{\mathrm{shock}}$ is tangential to the straight weak oblique shock ${S_0}$ at the wedge vertex. To achieve these, we need to compute the pseudo-potential function $\varphi$ below ${S_0}$.

By (61)–(64), the pseudo-potential $\varphi _2$ below the normal shock ${S}_1$ is of the form

$$\begin{aligned} \varphi _2=-\frac{1}{2}|{\varvec{\xi }}|^2+ \mathbf {u}_2\cdot {\varvec{\xi }}+ k_2 \end{aligned}$$

(68)

for constant state $\mathbf {u}_2$ and constant $k_2$; see (60). Then it follows from (56) and (67)–(68) that the corresponding densities $\rho _1$ and $\rho _2$ are constants in the form

$$\begin{aligned} \rho _k^{\gamma -1}=\rho _0^{\gamma -1}+\frac{\gamma -1}{2}\big (u_0^2-|\mathbf {u}_k|^2\big )\qquad \,\, \text{ for } k=1,2. \end{aligned}$$

(69)

Denote $\Gamma _{\mathrm{wedge}}:=\partial W\cap \partial \Lambda$, and the sonic arcs $\Gamma _{\mathrm{sonic}}^1:=P_1P_4$ on Fig. 7 and $\Gamma _{\mathrm{sonic}}^2:=P_2P_3$ on Figs. 7–8. The sonic circle $\partial B_{c_1}(\mathbf {u}_1)$ of the uniform state $\varphi _1$ intersects line ${S_0}$, where $c_1=\rho _1^{\frac{\gamma -1}{2}}$ by (58). For the supersonic case $\theta _{\mathrm{w}}\in (0,\theta _{\mathrm{w}}^{\mathrm{s}})$, there are two arcs of this sonic circle between ${S_0}$ and $\Gamma _{\mathrm{wedge}}$ in $\Lambda$. Note that $\Gamma _{\mathrm{sonic}}^1$ tends to point O as $\theta _{\mathrm{w}} \nearrow \theta _{\mathrm{w}}^{\mathrm{s}}$ and is outside of $\Lambda$ for the subsonic case $\theta _{\mathrm{w}}\in [\theta _{\mathrm{w}}^{\mathrm{s}}, \theta _{\mathrm{w}}^{\mathrm{d}})$. Similarly, the sonic circle $\partial B_{c_2}(\mathbf {u}_2)$ of the uniform state $\varphi _2$ intersects line ${S_1}$, where $c_2=\rho _2^{\frac{\gamma -1}{2}}$. There are two arcs of this circle between ${S_1}$ and the line containing $\Gamma _{\mathrm{wedge}}$. Notice that $\varphi _1>\varphi _2$ on $\overline{\Gamma _\mathrm{sonic}^1}$ and $\varphi _1<\varphi _2$ on $\overline{\Gamma _\mathrm{sonic}^2}$. Then Problem 5 can be further reformulated into the following free boundary problem:

Problem 6

(Free Boundary Problem) For $\theta _{\mathrm{w}}\in (0, \theta _{\mathrm{w}}^{\mathrm{d}})$, find a free boundary (curved shock) $\Gamma _{\mathrm{shock}}$ and a function $\varphi$ defined in domain $\Omega$, as shown in Figs. 7–8, such that $\varphi$ satisfies

• (i) (55) in $\Omega$,

• (ii) $\varphi =\varphi _{0}$ and $\rho \mathrm{D}\varphi \cdot {\varvec{\nu }}_{\mathrm{s}}=\rho _0 \mathrm{D}\varphi _{0}\cdot {\varvec{\nu }}_{\mathrm{s}}$ on $\Gamma _{\mathrm{shock}}$,

• (iii) $\varphi =\hat{\varphi }$ and $\mathrm{D}\varphi =\mathrm{D}\hat{\varphi }$ on $\Gamma _\mathrm{sonic}^1\cup \Gamma _{\mathrm{sonic}}^2\,\,$ when $\theta _{\mathrm{w}}\in (0, \theta _{\mathrm{w}}^{\mathrm{s}})$ and on $\Gamma _{\mathrm{sonic}}^2\cup \{O\}$ when $\theta _{\mathrm{w}}\in [\theta _{\mathrm{w}}^{\mathrm{s}}, \theta _{\mathrm{w}}^\mathrm{d})$ for $\hat{\varphi }:=\max (\varphi _1, \varphi _2)$,

• (iv) $\mathrm{D}\varphi \cdot {\varvec{\nu }}_{\mathrm{w}}=0$ on $\Gamma _{\mathrm{wedge}}$,

where ${\varvec{\nu }}_{\mathrm{s}}$ and ${\varvec{\nu }}_{\mathrm{w}}$ are the unit normals to $\Gamma _{\mathrm{shock}}$ and $\Gamma _{\mathrm{wedge}}$ pointing to the interior of $\Omega$, respectively.

It can be shown that $\varphi _1>\varphi _2$ on $\Gamma _{\mathrm{sonic}}^1$, and the opposite inequality holds on $\Gamma _{\mathrm{sonic}}^2$. This justifies the requirements in Problem 6(iii) above. The conditions in Problem 6(ii)–(iii) are the Rankine-Hugoniot conditions (62)–(61) on $\Gamma _{\mathrm{shock}}$ and $\Gamma _{\mathrm{sonic}}^1\cup \Gamma _{\mathrm{sonic}}^2$ or $\Gamma _{\mathrm{sonic}}^2\cup \{O\}$, respectively.

5.3 Global Solutions of Riemann Problem III: Free Boundary Problem, Problem 6

To solve Riemann Problem III, it suffices to solve the free boundary problem, Problem 6, for all the wedge angles $\theta _\mathrm{w}\in (0, \theta _{\mathrm{w}}^{\mathrm{d}})$. To obtain a global solution from $\varphi$ that is a solution of Problem 6 such that $\Gamma _{\mathrm{shock}}$ is a $C^1$-curve up to its endpoints and $\varphi \in C^1({\overline{\Omega }})$, we consider two cases:

For the supersonic case $\theta _{\mathrm{w}}\in (0, \theta _{\mathrm{w}}^\mathrm{s})$, we divide domain $\Lambda$ into four separate domains; see Fig. 7. Denote by ${{S}_{0,\mathrm{seg}}}$ the line segment $OP_1\subset S_0$, and by ${{S}_{1,\mathrm{seg}}}$ the portion (half-line) of $S_1$ with left endpoint $P_2$ so that ${{S}_{1,\mathrm{seg}}}\subset \Lambda$. Let $\Omega _{{S}}$ be the unbounded domain below curve $\overline{{{S}_{0,\mathrm{seg}}}\cup \Gamma _{\mathrm{shock}}\cup {{S}_{1,\mathrm{seg}}}}$ and above $\Gamma _{\mathrm{wedge}}$ (see Fig. 7). In $\Omega _{{S}}$, let $\Omega _1$ be the bounded domain enclosed by ${S}_0, \Gamma ^1_{\mathrm{sonic}}$, and $\Gamma _{\mathrm{wedge}}$. Set $\Omega _{2}:=\Omega _{{S}}{\setminus } \overline{\Omega _1\cup \Omega }$. Define a function $\varphi _*$ in $\Lambda$ by

$$\begin{aligned} \varphi _*= {\left\{ \begin{array}{ll} \varphi _{0}&{} \qquad \text { in }\Lambda \setminus \Omega _{{S}},\\ \varphi _1&{} \qquad \text { in }\Omega _1,\\ \varphi &{} \qquad \text { in }\Gamma ^1_{\mathrm{sonic}}\cup \Omega \cup \Gamma ^2_{\mathrm{sonic}},\\ \varphi _2&{}\qquad \text { in }\Omega _2. \end{array}\right. } \end{aligned}$$

(70)

By Problem 6(ii)–(iii), $\varphi _*$ is continuous in $\Lambda \setminus \Omega _S$ and $C^1$ in $\overline{\Omega _{{S}}}$. In particular, $\varphi _*$ is $C^1$ across $\Gamma ^1_\mathrm{sonic}\cup \Gamma ^2_{\mathrm{sonic}}$. Moreover, using Problem 6(i)–(iii), we obtain that $\varphi _*$ is a global entropy solution of (55) in $\Lambda$.

For the subsonic case $\theta _{\mathrm{w}}\in [\theta _{\mathrm{w}}^{\mathrm{s}}, \theta _{\mathrm{w}}^{\mathrm{d}})$, domain $\Omega _1\cup \Gamma ^1_{\mathrm{sonic}}$ in $\varphi _*$ reduces to one point $\{O\}$; see Fig. 8. The corresponding function $\varphi _*$ is a global entropy solution of (55) in $\Lambda$.

Definition 4

(Admissible Solutions) Let $\theta _{\mathrm{w}}\in (0, \theta _{\mathrm{w}}^{\mathrm{d}})$. A function $\varphi \in C^{0,1}({\overline{\Lambda }})$ is an admissible solution of Problem 6 if $\varphi$ is a solution of Problem 6 extended to $\Lambda$ by (70) and satisfies the following properties:

• (i) The structure of solution is of the form:

  • if $\theta _{\mathrm{w}}\in (0, \theta _{\mathrm{w}}^{\mathrm{s}})$, then $\varphi$ has the configuration shown on Fig. 7 such that $\Gamma _{\mathrm{shock}}$ is $C^{2}$ in its relative interior and

    $$\begin{aligned}&\varphi \in C^{0,1}(\Lambda )\cap C^1(\Lambda \setminus (\overline{{{S}_{0,\mathrm{seg}}}}\cup {\overline{\Gamma _{\mathrm{shock}}}}\cup \overline{{{S}_{1,\mathrm{seg}}}})),\\&\varphi \in C^{1}(\overline{\Omega })\cap C^2({\overline{\Omega }}\setminus (\overline{{{S}_{0,\mathrm{seg}}}}\cup \overline{{{S}_{1,\mathrm{seg}}}}))\cap C^3(\Omega ); \end{aligned}$$

  • if $\theta _{\mathrm{w}}\in [ \theta _{\mathrm{w}}^{\mathrm{s}}, \theta _{\mathrm{w}}^{\mathrm{d}})$, then $\varphi$ has the configuration shown on Fig. 8 such that $\Gamma _{\mathrm{shock}}$ is $C^{2}$ in its relative interior and

    $$\begin{aligned}&\varphi \in C^{0,1}(\Lambda )\cap C^1(\Lambda \setminus (\Gamma _{\mathrm{shock}}\cup \overline{{{S}_{1,\mathrm{seg}}}})),\\&\varphi \in C^{1}(\overline{\Omega })\cap C^2({\overline{\Omega }}\setminus (\{O\}\cup \overline{{{S}_{1,\mathrm{seg}}}}))\cap C^3(\Omega ); \end{aligned}$$

• (ii) (55) is strictly elliptic in ${\overline{\Omega }}\setminus \,\overline{\Gamma _{\mathrm{sonic}}}$:  $|\mathrm{D}\varphi |<c(|\mathrm{D}\varphi |^2, \varphi )$ in ${\overline{\Omega }}\setminus \,\overline{\Gamma _{\mathrm{sonic}}}$;

• (iii) $0<\partial _{{\varvec{\nu }}_{\mathrm{s}}}\varphi \leqslant \partial _{{\varvec{\nu }}_{\mathrm{s}}}\varphi _0$ on $\Gamma _{\mathrm{shock}}$, where ${\varvec{\nu }}_{\mathrm{s}}$ is the unit normal to $\Gamma _{\mathrm{shock}}$ pointing to the interior of $\Omega$;

• (iv) the inequalities hold:

  $$\begin{aligned} \max \{\varphi _{1}, \varphi _{2}\}\leqslant \varphi \leqslant \varphi _0 \qquad \text{ in } \Omega ; \end{aligned}$$

  (71)

• (v) the monotonicity properties hold:

  $$\begin{aligned} \mathrm{D}(\varphi _0-\varphi )\cdot \mathbf {e}_{{S}_1}\geqslant 0, \quad \mathrm{D}(\varphi _0-\varphi )\cdot \mathbf {e}_{{S}_0}\leqslant 0 \qquad \,\,\,\, \text{ in } \Omega, \end{aligned}$$

  (72)

  where $\mathbf {e}_{{S}_0}$ and $\mathbf {e}_{{S}_{1}}$ are the unit vectors along lines ${S}_0$ and ${S}_1$ pointing to the positive $\xi _1$-direction, respectively.

The monotonicity properties in (72) imply that

$$\begin{aligned} \mathrm{D}(\varphi _1-\varphi )\cdot \mathbf{e}\leqslant 0 \qquad \,\, \text{ in } {\overline{\Omega }}\,\, \text{ for } \text{ all } {} \mathbf{e}\in \overline{\text{Cone}(-\mathbf {e}_{{S}_1}, \mathbf {e}_{{S}_0})}, \end{aligned}$$

(73)

where $\text{Cone}(-\mathbf {e}_{{S}_1}, \mathbf {e}_{{S}_0}) =\{-a\,\mathbf {e}_{{S}_1}+b \,\mathbf {e}_{{S}_0}{:}a, b>0\}$. Notice that $\mathbf {e}_{{S}_0}$ and $\mathbf {e}_{{S}_1}$ are not parallel if $\theta _{\mathrm{w}}\ne 0$. Then we have the following theorem:

Theorem 5

([3]) Let $\gamma >1$ and $u_{0}>c_0$. For any $\theta _{\mathrm{w}}\in (0, \theta _{\mathrm{w}}^{\mathrm{d}})$, there exists a global entropy solution $\varphi$ of Problem 6 such that the following regularity properties are satisfied for some $\alpha \in (0,1)$:

• (i) if $\theta _{\mathrm{w}}\in (0, \theta _{\mathrm{w}}^{\mathrm{s}})$, the reflected shock $\overline{{{S}_{0,\mathrm{seg}}}}\cup \Gamma _{\mathrm{shock}}\cup \overline{{{S}_{1,\mathrm{seg}}}}$ is $C^{2,\alpha }$-smooth, and $\varphi \in C^{1,\alpha }({\overline{\Omega }})\cap C^\infty ({\overline{\Omega }}{\setminus } (\overline{\Gamma _{\mathrm{sonic}}^1}\cup \overline{\Gamma _\mathrm{sonic}^2}))$;

• (ii) if $\theta _{\mathrm{w}}\in [\theta _{\mathrm{w}}^{\mathrm{s}}, \theta _{\mathrm{w}}^{\mathrm{d}})$, the reflected shock $\overline{\Gamma _{\mathrm{shock}}}\cup \overline{{{S}_{1,\mathrm{seg}}}}$ is $C^{1,\alpha }$ near O and $C^{2,\alpha }$ away from O, and $\varphi \in C^{1,\alpha }({\overline{\Omega }})\cap C^\infty ({\overline{\Omega }}{\setminus } (\{O\}\cup \overline{\Gamma _\mathrm{sonic}^2}))$.

Moreover, in both cases, $\varphi$ is $C^{1,1}$ across the sonic arcs, and $\Gamma _{\mathrm{shock}}$ is $C^\infty$ in its relative interior. Furthermore, $\varphi$ is an admissible solution in the sense of Definition 4, so $\varphi$ satisfies the additional properties listed in Definition 4.

To achieve this, for any small $\delta >0$, the required uniform estimates of admissible solutions with wedge angles $\theta _{\mathrm{w}} \in [0, \theta _{\mathrm{w}}^{\mathrm{d}}-\delta ]$ are first obtained. By using these estimates, the Leray-Schauder degree theory can be applied to obtain the existence in the class of admissible solutions for each $\theta _{\mathrm{w}} \in [0, \theta _{\mathrm{w}}^{\mathrm{d}}-\delta ]$, starting from the unique normal solution for $\theta _{\mathrm{w}}=0$. Since $\delta >0$ is arbitrary, the existence of a global entropy solution for any $\theta _{\mathrm{w}}\in (0,\theta _{\mathrm{w}}^{\mathrm{d}})$ can be established. More details can be found in [3]; see also [22] and related references cited therein.

Recently, we have also established the convexity of transonic shocks for the Prandtl-Meyer reflection configurations.

Theorem 6

([25]) If a solution of the Prandtl-Meyer problem is admissible in the sense of Definition 4, then its domain $\Omega$ is convex, and the shock curve $\Gamma _{\mathrm{shock}}$ is a strictly convex graph. That is, $\Gamma _{\mathrm{shock}}$ is uniformly convex on any closed subset of its relative interior. Moreover, for the solution of Problem 6 extended to $\Lambda$ by (70) (with the appropriate modification for the subsonic/sonic case) with pseudo-potential $\varphi \in C^{0,1}(\Lambda )$ satisfying Definition 4$(\mathrm{i})-(\mathrm{iv})$, the shock is strictly convex if and only if Definition 4$(\mathrm{v})$ holds.

With the convexity of reflected-diffracted transonic shocks, the uniqueness and stability of global regular shock reflection-diffraction configurations have also been established in the class of admissible solutions; see [26] for the details.

The existence results in [3] indicate that the steady weak supersonic/transonic shock solutions are the asymptotic limits of the dynamic self-similar solutions, the Prandtl-Meyer reflection configurations, in the sense of (66) in Problem 5 for all $\theta _{\mathrm{w}}\in (0, \theta _{\mathrm{w}}^{\mathrm{d}})$ and all $\gamma >1$.

On the other hand, it is shown in [36] and [3] that, for each $\gamma >1$, there is no self-similar strong Prandtl-Meyer reflection configuration for the unsteady potential flow in the class of admissible solutions. This means that the situation for the dynamic stability of the steady oblique shocks of stronger strength is more sensitive.

6 Two-Dimensional (2-D) Riemann Problem IV: the von Neumann Problem for Shock Reflection-Diffraction for the Euler Equations for Potential Flow

In this section, we present some recent developments in the analysis of the fourth Riemann problem, Riemann Problem IV—the von Neumann problem for shock reflection-diffraction by wedges for the Euler equations for potential flow in form (4)–(5), or (2) with (6)–(7).

6.1 2-D Riemann Problem IV: the von Neumann Problem for Shock Reflection-Diffraction by Wedges

When a vertical planar shock perpendicular to the flow direction and separating two uniform states (0) and (1), with constant velocities $\mathbf {u}_0= (0, 0)$ and $\mathbf {u}_1=(u_1, 0), u_1>0$, and constant densities $\rho _0<\rho _1$ (state (0) is ahead or to the right of the shock, and state (1) is behind the shock), hits a symmetric wedge W in (51) head-on at time $t = 0$, a reflection-diffraction process takes place when $t > 0$. Mathematically, the shock reflection-diffraction problem is a 2-D lateral Riemann problem in domain ${\mathbb {R}}^2\setminus \overline{W}$.

Problem 7

(Riemann Problem IV—the von Neumann Problem for Shock Reflection-Diffraction by Wedges) Piecewise constant initial data, consisting of state (0) on $\{x_1>0\}\setminus \overline{W}$ and state (1) on $\{x_1 < 0\}$ connected by a shock at $x_1=0$, are prescribed at $t = 0$. Seek a solution of (2) with (6)–(7) for $t\geqslant 0$ subject to the initial data and the boundary condition $\nabla_{\mathbf{x}}\Phi \cdot {\varvec{\nu }}_{\mathrm{w}}=0$ on $\partial W$.

Similarly to Definition 3, we can define the notion of weak solutions of Problem 7, by noting that the boundary condition can be written as $\rho \nabla_{\mathbf{x}}\Phi \cdot {\varvec{\nu }}_{\mathrm{w}}=0$ on $\partial W$, which is the spatial conormal condition for (2) with (6)–(7).

The mathematical analysis of the shock reflection-diffraction by wedges was first proposed by von Neumann in [83,84,85]. The complexity of reflection-diffraction configurations was first reported by Mach [68] in 1878, who observed two patterns of reflection-diffraction configurations: regular reflection (two-shock configuration; see Figs. 9–10) and Mach reflection (three-shock/one-vortex-sheet configuration). It has been found later that the reflection-diffraction configurations can be much more complicated than what Mach originally observed; see also [5, 22, 34, 44, 46, 81] and the references cited therein.

6.2 Reformation of Riemann Problem IV

Problem 7 is invariant under self-similar scaling (15), so it also admits self-similar solutions determined by (55)–(56), along with the appropriate boundary conditions. By the symmetry of the problem with respect to the $\xi _1$-axis, we consider only the upper half-plane $\{\xi _2>0\}$ and prescribe the boundary condition: $\varphi _{{\varvec{\nu }}}=0$ on the symmetry line $\{\xi _2=0\}$. Then Problem 7 is reformulated as a boundary value problem in the unbounded domain

$$\begin{aligned} \Lambda {:}={\mathbb {R}}^2_+\setminus \{{\varvec{\xi }}{:}\,|\xi _2|\leqslant \xi _1 \tan \theta _{\mathrm{w}}, \xi _1>0\} \end{aligned}$$

in the self-similar coordinates, where $\mathbb {R}^2_+:=\mathbb {R}^2\cap \{\xi _2>0\}$. The incident shock in the ${\varvec{\xi }}$-coordinates is the half-line: $S_0=\{\xi =\xi _1^0\}\cap \Lambda$, where

$$\begin{aligned} \xi _1^0:=\rho _1\sqrt{\frac{2(c_1^2-c_0^2)}{(\gamma -1)(\rho _1^2-\rho _0^2)}}=\frac{\rho _1u_1}{\rho _1-\rho _0}, \end{aligned}$$

(74)

which is determined by the Rankine-Hugoniot conditions between states (0) and (1) on $S_0$. Then Problem 7 for self-similar solutions becomes the boundary value problem: seek a solution $\varphi$ of (55)–(56) in the self-similar domain $\Lambda$ with the slip boundary condition $\mathrm{D}\varphi \cdot {\varvec{\nu }}|_{\partial \Lambda }=0$ and the asymptotic boundary condition at infinity:

$$\begin{aligned} \varphi \rightarrow \bar{\varphi }= {\left\{ \begin{array}{ll} \varphi _0 \qquad \textit{ for }\,\,\, \xi _1>\xi _1^0, \xi _2>\xi _1 \tan \theta _{\mathrm{w}},\\ \varphi _1 \qquad \textit{ for }\,\,\, \xi _1<\xi _1^0, \;\xi _2>0, \end{array}\right. } \qquad \textit{ when } |{\varvec{\xi }}|\rightarrow \infty, \end{aligned}$$

where $\varphi _0=-\frac{1}{2}|{\varvec{\xi }}|^2$ and $\varphi _1=-\frac{1}{2}|{\varvec{\xi }}|^2+u_1(\xi _1-\xi ^0_1)$.

Similarly, we can define the notion of weak solutions of the boundary value problem by observing that the boundary condition can be written as $\rho \mathrm{D}\varphi \cdot {\varvec{\nu }}|_{\partial \Lambda }=0$, which is the spatial conormal condition for (55)–(56). A weak solution is called an entropy solution if it satisfies the entropy condition: density $\rho$ increases in the pseudo-flow direction of $\mathrm{D}\varphi |_{\Lambda ^+\cap S}$ across any discontinuity curve (i.e., shock).

Fig. 9

Supersonic regular shock reflection-diffraction configuration

Fig. 10

Subsonic regular shock reflection-diffraction configuration

If a solution has one of the regular shock reflection-diffraction configurations as shown in Figs. 9–10 (cf. [22]) and its pseudo-potential $\varphi$ is smooth in the subdomain $\Omega$ between the wedge and the reflected-diffracted shock, then it should satisfy the slip boundary condition on the wedge and the Rankine-Hugoniot conditions with state (1) across the flat shock $S_1=\{\varphi _1=\varphi _2\}$, which passes through point $P_0$ where the incident shock meets the wedge boundary. Define the uniform state (2) with pseudo-potential $\varphi _2({\varvec{\xi }})$ such that

$$\begin{aligned} \varphi _2(P_0)=\varphi (P_0), \qquad \mathrm{D}\varphi _2({P_{0}})= \lim _{P\rightarrow P_0,\; P\in \Omega } \mathrm{D}\varphi (P). \end{aligned}$$

Then the constant density $\rho _2$ of state (2) is equal to $\rho (|\mathrm{D}\varphi |^2, \varphi )({P_{0}}) =\rho (|\mathrm{D}\varphi _2|^2, \varphi _2)({P_{0}})$ via (56). It follows that $\varphi _2$ satisfies the following three conditions at $P_0$:

$$\begin{aligned} \mathrm{D}\varphi _2\cdot {\varvec{\nu }}_{\mathrm{w}}=0, \quad \varphi _2=\varphi _1, \quad \rho (|\mathrm{D}\varphi _2|^2,\varphi _2)\mathrm{D}\varphi _2\cdot {\varvec{\nu }}_{S_1}= \rho _1\mathrm{D}\varphi _1\cdot {\varvec{\nu }}_{S_1} \end{aligned}$$

(75)

for ${\varvec{\nu }}_{S_1}=\frac{\mathrm{D}(\varphi _1-\varphi _2)}{|\mathrm{D}(\varphi _1-\varphi _2)|}$, where ${\varvec{\nu }}_{\mathrm{w}}$ is the outward normal to the wedge boundary.

State (2) can be either supersonic or subsonic at ${P_{0}}$, which determines the supersonic or subsonic type of the configurations. The regular reflection solution in the supersonic domain is expected to consist of the constant states separated by straight shocks (cf. [77, Theorem 4.1]). Then, when state (2) is supersonic at ${P_{0}}$, it can be shown that the constant state (2), extended up to arc $\Gamma _{\mathrm{sonic}}:=P_1P_4$ of the sonic circle of state (2), as shown in Fig. 9, satisfies (55) in the domain, the Rankine-Hugoniot conditions (62)–(61) on the straight shock $P_0P_1$, and the slip boundary condition: $\mathrm{D}\varphi _2\cdot {\varvec{\nu }}_{\mathrm{w}}=0$ on the wedge $P_0P_4$, and is expected to be a part of the configuration. Then the supersonic regular shock reflection-diffraction configuration on Fig. 9 consists of three uniform states (0), (1), (2), and a non-uniform state in domain $\Omega =P_1P_2P_3P_4$, where (55) is elliptic. The elliptic domain $\Omega$ is separated from the hyperbolic domain ${P_{0}}{P_{1}}{P_{4}}$ of state (2) by the sonic arc $\Gamma _{\mathrm{sonic}}$, on which the ellipticity in $\Omega$ degenerates. The subsonic regular shock reflection-diffraction configuration as shown in Fig. 10 consists of two uniform states (0) and (1), and a non-uniform state in domain $\Omega =P_0P_2P_3$, where (55) is elliptic, and $\varphi _{|\Omega }({P_{0}})=\varphi _2({P_{0}})$ and $\mathrm{D}(\varphi _{|\Omega })({P_{0}})=\mathrm{D}\varphi _2({P_{0}})$.

For the supersonic case in Fig. 9, we also use $\Gamma _{\mathrm{shock}}$, $\Gamma _{\mathrm{wedge}}$, and $\Gamma _{\mathrm{sym}}$ for the curved part of $P_1P_2$, the wedge boundary $P_3P_4$, and the symmetry line segment $P_2P_3$, respectively. For the subsonic case in Fig. 10, $\Gamma _{\mathrm{shock}}$, $\Gamma _{\mathrm{wedge}}$, and $\Gamma _{\mathrm{sym}}$ denote $P_0P_2$, $P_0P_3$, and $P_2P_3$, respectively. We unify the notations with the supersonic case by introducing points ${P_{1}}$ and ${P_{4}}$ for the subsonic case as

$$\begin{aligned} {P_{1}}:={P_{0}}, \quad {P_{4}}:={P_{0}}, \quad {\overline{\Gamma _{\mathrm{sonic}}}}:=\{{P_{0}}\}. \end{aligned}$$

(76)

The corresponding solution for $\theta _{\mathrm{w}}=\frac{\uppi }{2}$ is called the normal reflection. In this case, the incident shock normally reflects from the flat wall so that the reflected shock is also a plane $\{\xi _1=\bar{\xi }_1\}$, where $\bar{\xi }_1<0$; see Fig. 11.

Fig. 11

Normal reflection configuration (cf. [22])

As indicated above, a necessary condition for the existence of a regular reflection solution is the existence of the uniform state (2) with pseudo-potential $\varphi _2$ determined by the system of algebraic equations (75) for constants $(u_2, v_2, \rho _2)$ of state (2) across the flat shock $S_1=\{\varphi _1=\varphi _2\}$ separating it from state (1) and satisfying the entropy conditions $\rho _2>\rho _1$. For any fixed densities $0<\rho _0<\rho _1$ of states (0) and (1), it can be shown that there exist a sonic angle $\theta _{\mathrm{w}}^{\mathrm{s}}$ and a detachment angle $\theta _{\mathrm{w}}^{\mathrm{d}}$ satisfying

$$\begin{aligned} 0<\theta _{\mathrm{w}}^{\mathrm{d}}<\theta _{\mathrm{w}}^{\mathrm{s}}<\frac{\uppi }{2} \end{aligned}$$

such that the algebraic system (75) has two solutions for each $\theta _{\mathrm{w}}\in (\theta _{\mathrm{w}}^{\mathrm{d}}, \frac{\uppi }{2})$ which become equal when $\theta _{\mathrm{w}}=\theta _{\mathrm{w}}^{\mathrm{d}}$. Thus, for each $\theta _{\mathrm{w}}\in (\theta _{\mathrm{w}}^{\mathrm{d}}, \frac{\uppi }{2})$, there exist two states (2), weak versus strong, with densities $\rho _2^{\mathrm{weak}}<\rho _2^{\mathrm{strong}}$. The weak state (2) is supersonic at the reflection point ${P_{0}}(\theta _\mathrm{w})$ for $\theta _{\mathrm{w}}\in (\theta _{\mathrm{w}}^{\mathrm{s}}, \frac{\uppi }{2})$, sonic for $\theta _{\mathrm{w}}=\theta _{\mathrm{w}}^{\mathrm{s}}$, and subsonic for $\theta _{\mathrm{w}}\in (\theta _{\mathrm{w}}^{\mathrm{d}}, {\hat{\theta }}_\mathrm{w}^{\mathrm{s}})$ for some ${\hat{\theta }}_{\mathrm{w}}^\mathrm{s}\in (\theta _{\mathrm{w}}^{\mathrm{d}}, \theta _{\mathrm{w}}^{\mathrm{s}}]$. The strong state (2) is subsonic at ${P_{0}}(\theta _{\mathrm{w}})$ for all $\theta _{\mathrm{w}}\in (\theta _{\mathrm{w}}^{\mathrm{d}}, \frac{\uppi }{2})$.

To determine which of the two states (2) for $\theta _{\mathrm{w}}\in (\theta _{\mathrm{w}}^{\mathrm{d}}, \frac{\uppi }{2})$, weak or strong, is physical for the local theory, it was conjectured that the strong shock reflection-diffraction configuration would be non-physical; indeed, it is shown in [21, 22] that the weak shock reflection-diffraction configuration tends to the unique normal reflection in Fig. 11, but the strong one does not, when $\theta _{\mathrm{w}} \rightarrow \frac{\uppi }{2}$. The entropy condition and the definition of weak state (2) imply that $0<\rho _1<\rho _2^{\mathrm{weak}}$. With the weak state (2), the following conjectures were proposed (see von Neumann [83, 84]).

The Sonic Conjecture There exists a supersonic regular shock reflection-diffraction configuration when $\theta _{\mathrm{w}}\in (\theta _{\mathrm{w}}^{\mathrm{s}}, \frac{\uppi }{2})$ for $\theta _{\mathrm{w}}^\mathrm{s}>\theta _{\mathrm{w}}^{\mathrm{d}}$. That is, the supersonicity of the weak state (2) implies the existence of a supersonic regular reflection solution, as shown in Fig. 9.

The Detachment Conjecture There exists a regular shock reflection-diffraction configuration for any wedge angle $\theta _{\mathrm{w}}\in (\theta _{\mathrm{w}}^{\mathrm{d}}, \frac{\uppi }{2})$. That is, the existence of state (2) implies the existence of a regular reflection solution, as shown in Figs. 9–10.

In other words, the von Neumann detachment conjecture above is that the global regular shock reflection-diffraction configuration is possible whenever the local regular reflection at the reflection point is possible.

From now on, for the given wedge angle $\theta _{\mathrm{w}}\in (\theta _{\mathrm{w}}^{\mathrm{d}}, \frac{\uppi }{2})$, state (2) represents the unique weak state (2) and $\varphi _2$ is its pseudo-potential. State (2) is obtained from the algebraic conditions (75) which determines line $S_1$ and the sonic arc $\Gamma _{\mathrm{sonic}}$ when state (2) is supersonic at $P_0$, and the slope of $\Gamma _{\mathrm{shock}}$ at $P_0$ when state (2) is subsonic at $P_0$. Thus, the unknowns are both domain $\Omega$ and pseudo-potential $\varphi$ in $\Omega$, as shown in Figs. 9–10. Then, from (62)–(61), to construct a solution of Problem 7 for the supersonic or subsonic regular shock reflection-diffraction configuration, it suffices to solve the following problem:

Problem 8

(Free Boundary Problem) For $\theta _{\mathrm{w}}\in (\theta _{\mathrm{w}}^{\mathrm{d}}, \frac{\uppi }{2})$, find a free boundary (curved reflected shock) $\Gamma _{\mathrm{shock}}\subset \Lambda \cap \{{\xi _{1}}<\xi _{1{P_{1}}}\}$ and a function $\varphi$ defined in domain $\Omega$ as shown in Figs. 9–10 such that

• (i) (55) is satisfied in $\Omega$ and is strictly elliptic for $\varphi$ in ${\overline{\Omega }}\setminus {\overline{\Gamma _{\mathrm{sonic}}}}$,

• (ii) $\varphi =\varphi _1$ and $\rho \mathrm{D}\varphi \cdot {\varvec{\nu }}_{\mathrm{s}}=\rho _1 \mathrm{D}\varphi _1\cdot {\varvec{\nu }}_{\mathrm{s}}$ on the free boundary $\Gamma _{\mathrm{shock}}$,

• (iii) $\varphi =\varphi _2$ and $\mathrm{D}\varphi =\mathrm{D}\varphi _2$ on $P_1P_4$ in the supersonic case as shown in Fig. 9 and at $P_0$ in the subsonic case as shown in Fig. 9,

• (iv) $\mathrm{D}\varphi \cdot {\varvec{\nu }}_{\mathrm{w}}=0$ on $\Gamma _{\mathrm{wedge}}$, and $\mathrm{D}\varphi \cdot {\varvec{\nu }}_{\mathrm{sym}}=0$ on $\Gamma _{\mathrm{sym}}$,

where ${\varvec{\nu }}_{\mathrm{s}}$, ${\varvec{\nu }}_{\mathrm{w}}$, and ${\varvec{\nu }}_{\mathrm{sym}}$ are the interior unit normals to $\Omega$ on $\Gamma _{\mathrm{shock}}$, $\Gamma _{\mathrm{wedge}}$, and $\Gamma _{\mathrm{sym}}$, respectively.

The conditions in Problem 8(ii) are the Rankine-Hugoniot conditions (62)–(61) on $\Gamma _{\mathrm{shock}}$ between $\varphi _{|\Omega }$ and $\varphi _1$. Since $\Gamma _{\mathrm{shock}}$ is a free boundary and (55) is strictly elliptic for $\varphi$ in ${\overline{\Omega }}\setminus {\overline{\Gamma _{\mathrm{sonic}}}}$, then two conditions (the Dirichlet and oblique derivative conditions) on $\Gamma _{\mathrm{shock}}$ are consistent with one-phase free boundary problems for nonlinear elliptic PDEs of second order.

A careful asymptotic analysis has been made for serval reflection-diffraction configurations; see [44, 47,48,49, 72] and the references cited therein. Large or small scale numerical simulations have also been performed; cf. [5, 44, 90] and the references cited therein. However, most of the fundamental issues for the shock reflection-diffraction phenomena have not been understood, especially the global structures and the transition between the different patterns of shock reflection-diffraction configurations. This is partially because physical/numerical experiments are hampered by many difficulties and have not yielded clear transition criteria between the different patterns. In particular, some different patterns occur when the wedge angles are only fractions of a degree apart, a resolution even by sophisticated experiments and numerical simulations has been unable to reach (cf. [5, 67]). Therefore, the necessary approach to understand fully the shock reflection-diffraction phenomena, especially the transition criteria, is via rigorous mathematical analysis.

6.3 Global Solutions of Riemann Problem IV: Free Boundary Problem, Problem 8

If $\varphi$ is a solution of Problem 8, define its extension from $\Omega$ to $\Lambda$ by

$$\begin{aligned} \varphi ={\left\{ \begin{array}{ll} \, \varphi _0 \qquad \, \text{ for }\,\, \xi _1>\xi _1^0 \text{ and } \xi _2>\xi _1\tan \theta _{\mathrm{w}},\\ \, \varphi _1 \qquad \, \text{ for }\,\, \xi _1<\xi _1^0 \text{ and } \text{ above } \text{ curve } \,\, P_0{P_{1}}{P_{2}},\\ \, \varphi _2 \qquad \, \text{ in } \text{ domain }\,\, P_0{P_{1}}{P_{4}}, \end{array}\right. } \end{aligned}$$

(77)

where we have used the notational convention (76) for the subsonic reflection case, in which domain $P_0{P_{1}}{P_{4}}$ is one point and curve $P_0{P_{1}}{P_{2}}$ is $P_0{P_{2}}$; see Figs. 9–10. Also, the extension by (77) is well-defined because of the requirement that $\Gamma _{\mathrm{shock}}\subset \Lambda \cap \{{\xi _{1}}<\xi _{1{P_{1}}}\}$ in Problem 8.

In the supersonic case, the conditions in Problem 8(iii) are the Rankine-Hugoniot conditions on $\Gamma _{\mathrm{sonic}}$ between $\varphi _{|\Omega }$ and $\varphi _2$. Indeed, since state (2) is sonic on $\Gamma _{\mathrm{sonic}}$, it follows from (62)–(61) that no gradient jump occurs on $\Gamma _{\mathrm{sonic}}$. Then, if $\varphi$ is a solution of Problem 8, its extension by (77) is a global entropy solution in the self-similar coordinates.

Since $\Gamma _{\mathrm{sonic}}$ is not a free boundary, it is not possible in general to prescribe two conditions given in Problem 8(iii) on $\Gamma _{\mathrm{sonic}}$ for a second-order elliptic PDE. In the iteration problem, we prescribe the condition: $\varphi =\varphi _2$ on $\Gamma _{\mathrm{sonic}}$, and then prove that $\mathrm{D}\varphi =\mathrm{D}\varphi _2$ on $\Gamma _{\mathrm{sonic}}$ by exploiting the elliptic degeneracy on $\Gamma _{\mathrm{sonic}}$.

The key obstacle to establish the existence of regular shock reflection-diffraction configurations as conjectured by von Neumann [83, 84] is an additional possibility that, for some wedge angle $\theta _{\mathrm{w}}^{\mathrm{a}}\in (\theta _{\mathrm{w}}^{\mathrm{d}}, \frac{\uppi }{2})$, shock ${P_{0}}{P_{2}}$ may attach to the wedge vertex ${P_{3}}$, as observed by experimental results (cf. [81, Fig. 238]). To describe the conditions of such a possible attachment, we note that

$$\begin{aligned} u_1=(\rho _1-\rho _0) \sqrt{\frac{2(\rho _1^{\gamma -1}-\rho _0^{\gamma -1})}{\rho _1^2-\rho _0^2}}>0,\qquad \rho _1>\rho _0, \,\,\qquad c_1=\rho _1^{\frac{\gamma -1}{2}}. \end{aligned}$$

Then it follows from the explicit expressions above that, for each $\rho _0$, there exists $\rho ^{\mathrm{c}}>\rho _0$ such that

$$\begin{aligned} u_1\leqslant c_1 \quad \text{ if } \rho _1\in (\rho _0, \rho ^{\mathrm{c}}]; \,\, \qquad u_1>c_1 \quad \text{ if } \rho _1\in (\rho ^{\mathrm{c}}, \infty ). \end{aligned}$$

If $u_1\leqslant c_1$, we can rule out the solution with a shock attached to the wedge vertex. This is based on the fact that, if $u_1\leqslant c_1$, then the wedge vertex $P_3=(0,0)$ lies within the sonic circle $\overline{B_{c_1}(\mathbf {u}_1)}$ of state (1), and $\Gamma _{\mathrm{shock}}$ does not intersect $\overline{B_{c_1}(\mathbf {u}_1)}$, as we show below. If $u_1> c_1$, there would be a possibility that the reflected shock could be attached to the wedge vertex, as the experiments show (e.g., [81, Fig. 238]).

To solve the free boundary problem (Problem 8) involving transonic shocks for all the wedge angles $\theta _{\mathrm{w}}\in (\theta _\mathrm{w}^{\mathrm{d}},\frac{\uppi }{2})$, we define the following admissible solutions.

Definition 5

(Admissible Solutions)   Let $\theta _{\mathrm{w}}\in (\theta _{\mathrm{w}}^{\mathrm{d}},\frac{\uppi }{2})$. A function $\varphi \in C^{0,1}({\overline{\Lambda }})$ is an admissible solution of the regular reflection problem if $\varphi$ is a solution of Problem 8 extended to $\Lambda$ by (77) and satisfies the following properties:

• (i) The structure of solution:

  • if $|\mathrm{D}\varphi _2(P_0)|>c_2$, then $\varphi$ is of the supersonic regular shock reflection-diffraction configuration as shown on Fig. 9 and satisfies the conditions that the curved part of reflected-diffracted shock $\Gamma _{\mathrm{shock}}$ is $C^{2}$ in its relative interior; curves $\Gamma _{\mathrm{shock}}$, $\Gamma _{\mathrm{sonic}}$, $\Gamma _{\mathrm{wedge}}$, and $\Gamma _{\mathrm{sym}}$ do not have common points except their endpoints; and

    $$\begin{aligned}&\varphi \in C^{0,1}(\Lambda )\cap C^1(\Lambda \setminus ({S_0}\cup \overline{P_0P_1P_2})),\\&\varphi \in C^{1}(\overline{\Omega })\cap C^{3}({\overline{\Omega }}\setminus ({\overline{\Gamma _{\mathrm{sonic}}}}\cup \{P_2, P_3\})); \end{aligned}$$

  • if $|\mathrm{D}\varphi _2(P_0)|\leqslant c_2$, then $\varphi$ is of the subsonic regular shock reflection-diffraction configuration shown on Fig. 10 and satisfies the conditions that the reflected-diffracted shock $\Gamma _{\mathrm{shock}}$ is $C^{2}$ in its relative interior; curves $\Gamma _{\mathrm{shock}}$, $\Gamma _{\mathrm{wedge}}$, and $\Gamma _{\mathrm{sym}}$ do not have common points except their endpoints; and

    $$\begin{aligned}&\varphi \in C^{0,1}(\Lambda )\cap C^1(\Lambda \setminus ({S_0}\cup {\overline{\Gamma _{\mathrm{shock}}}})),\\&\varphi \in C^{1}(\overline{\Omega })\cap C^3({\overline{\Omega }}\setminus \{P_0, P_3\}). \end{aligned}$$

  Moreover, in both the supersonic and subsonic cases, the extended curve $\Gamma _{\mathrm{shock}}^{\mathrm{ext}}:=\Gamma _{\mathrm{shock}}\cup \{P_0\}\cup \Gamma _{\mathrm{shock}}^-$ is $C^1$ in its relative interior, where $\Gamma _{\mathrm{shock}}^-$ is the reflection of $\Gamma _{\mathrm{shock}}$ with respect to the $\xi _1$-axis.

• (ii) (55) is strictly elliptic in ${\overline{\Omega }}\setminus \,\overline{\Gamma _{\mathrm{sonic}}}$:  $|\mathrm{D}\varphi |<c(|\mathrm{D}\varphi |^2, \varphi )$ in ${\overline{\Omega }}\setminus \,\overline{\Gamma _{\mathrm{sonic}}}$.

• (iii) $\partial _{{\varvec{\nu }}_{\mathrm{s}}}\varphi _1>\partial _{{\varvec{\nu }}_{\mathrm{s}}}\varphi >0$ on $\Gamma _{\mathrm{shock}}$, where ${\varvec{\nu }}$ is the normal to $\Gamma _{\mathrm{shock}}$ pointing to the interior of $\Omega$.

• (iv) Inequalities hold:

  $$\begin{aligned} \varphi _2\leqslant \varphi \leqslant \varphi _1 \qquad \text{ in } \Omega . \end{aligned}$$

  (78)

• (v) The monontonicity properties hold:

  $$\begin{aligned} \partial _{\xi _2}(\varphi _1-\varphi )\leqslant 0, \quad \mathrm{D}(\varphi _1-\varphi )\cdot \mathbf {e}_{S_1}\leqslant 0 \qquad \,\, \text{ in } \Omega \,\, \text{ for } \mathbf {e}_{S_1}=\frac{P_0P_1}{|P_0P_1|}. \end{aligned}$$

  (79)

Notice that (79) implies that

$$\begin{aligned} \mathrm{D}(\varphi _1-\varphi )\cdot \mathbf {e}\leqslant 0 \qquad \text{ in } {\overline{\Omega }}\, \text{ for } \text{ any } \mathbf {e}\in \overline{\text{Cone}(\mathbf {e}_{\xi _2}, \mathbf {e}_{S_1})}, \end{aligned}$$

(80)

where $\text{Cone}(\mathbf{e}_{\xi _2}, \mathbf{e}_{S_1})=\{a\,\mathbf{e}_{\xi _2}+b \,\mathbf{e}_{S_1}{:} a, b>0\}$ with $\mathbf{e}_{\xi _2}=(0,1)$, and $\mathbf{e}_{\xi _2}$ and $\mathbf{e}_{S_1}$ are not parallel if $\theta _{\mathrm{w}}\ne \frac{\uppi }{2}$. Then we establish the following theorem:

Theorem 7

([21, 22]) There are the following two cases:

• (i) If $\rho _0$ and $\rho _1$ are such that $u_1\leqslant c_1$, then the supersonic/subsonic regular reflection solution exists for each wedge angle $\theta _{\mathrm{w}}\in (\theta _{\mathrm{w}}^{\mathrm{d}}, \frac{\uppi }{2})$. That is, for each $\theta _{\mathrm{w}}\in (\theta _\mathrm{w}^{\mathrm{d}}, \frac{\uppi }{2})$, there exists a solution $\varphi$ of Problem 8 such that

  $$\begin{aligned} \Phi (t, {\mathbf {x}}) =t\,\varphi (\frac{\mathbf {x}}{t}) +\frac{|{\mathbf {x}}|^{2}}{2t} \qquad \textit{ for }\,\, \frac{\mathbf {x}}{t}\in \Lambda,\, t>0 \end{aligned}$$

  with

  $$\begin{aligned} \rho (t, \mathbf{x})=\left (\rho _0^{\gamma -1}-(\gamma -1) (\Phi _t +\frac{1}{2}|\nabla _\mathbf{x}\Phi |^2 )\right )^{\frac{1}{\gamma -1}} \end{aligned}$$

  is a global weak solution of Problem 7in the sense of Definition 3satisfying the entropy condition; that is, $\Phi (t, \mathbf{x})$ is an entropy solution.

• (ii) If $\rho _0$ and $\rho _1$ are such that $u_1> c_1$, then there exists $\theta _{\mathrm{w}}^{\mathrm{a}}\in [\theta _{\mathrm{w}}^{\mathrm{d}}, \frac{\uppi }{2})$ so that the regular reflection solution exists for each wedge angle $\theta _{\mathrm{w}}\in (\theta _{\mathrm{w}}^{\mathrm{a}}, \frac{\uppi }{2})$, and the solution is of the self-similar structure described in (i) above. Moreover, if $\theta _{\mathrm{w}}^\mathrm{a}>\theta _{\mathrm{w}}^{\mathrm{d}}$, then, for the wedge angle $\theta _\mathrm{w}=\theta _{\mathrm{w}}^{\mathrm{a}}$, there exists an attached solution, i.e., $\varphi$ is a solution of Problem 8 with ${P_{2}}={P_{3}}$.

The type of regular shock reflection-diffraction configurations (supersonic as in Fig. 9or subsonic as in Fig. 10) is determined by the type of state (2) at ${P_{0}}$.

• (a) For the supersonic and sonic reflection cases, the reflected-diffracted shock ${P_{0}}{P_{2}}$ is $C^{2,\alpha }$-smooth for some $\alpha \in (0,1)$ and its curved part $P_1P_2$ is $C^\infty$ away from $P_1$. Solution $\varphi$ is in $C^{1,\alpha }({\overline{\Omega }})\cap C^\infty (\Omega )$, and is $C^{1,1}$ across the sonic arc which is optimal; that is, $\varphi$ is not $C^2$ across the sonic arc.

• (b) For the subsonic reflection case (Fig. 10), the reflected-diffracted shock ${P_{0}}{P_{2}}$ and solution $\varphi$ in $\Omega$ is in $C^{1,\alpha }$ near $P_0$ and $P_3$ for some $\alpha \in (0,1)$, and $C^\infty$ away from $\{P_0,P_3\}$.

Moreover, the regular reflection solution tends to the unique normal reflection (as in Fig. 11) when the wedge angle $\theta _{\mathrm{w}}$ tends to $\frac{\uppi }{2}$. In addition, for both supersonic and subsonic reflection cases,

$$\begin{aligned} \varphi _2<\varphi <\varphi _1 \qquad \textit{ in } \Omega . \end{aligned}$$

(81)

Furthermore, $\varphi$ is an admissible solution in the sense of Definition 5 below, so that $\varphi$ satisfies further properties listed in Definition 5.

Theorem 7 is proved by solving Problem 8. The first results on the existence of global solutions of the free boundary problem (Problem 8) were obtained for the wedge angles sufficiently close to $\frac{\uppi }{2}$ in [21]. Later, in [22], these results were extended up to the detachment angle as stated in Theorem 7. For this extension, the techniques developed in [21], notably the estimates near the sonic arc, were the starting point. More details can be found in [22]; also see [21].

Furthermore, in [25], we established the convexity of transonic shocks for the regular shock reflection-diffraction configurations.

Theorem 8

([25])  If a solution of the von Neumann problem for shock reflection-diffraction is admissible in the sense of Definition 5, then its domain $\Omega$ is convex, and the shock curve $\Gamma _{\mathrm{shock}}$ is a strictly convex graph. That is, $\Gamma _{\mathrm{shock}}$ is uniformly convex on any closed subset of its relative interior. Moreover, for the solution of Problem 8 extended to $\Lambda$ by (77), with pseudo-potential $\varphi \in C^{0,1}(\Lambda )$ satisfying Definition 5(i)–(iv), the shock is strictly convex if and only if Definition 5$(\mathrm{v})$ holds.

Furthermore, with the convexity of reflected-diffracted transonic shocks, the uniqueness and stability of global regular shock reflection-diffraction configurations have also been established in the class of admissible solutions; see [26] for details.

7 Concluding Remarks

In this paper, we have presented four different 2-D Riemann problems involving transonic shocks through several prototypes of hyperbolic systems of conservation laws and have shown how these Riemann problems can be formulated/solved as free boundary problems with transonic shocks as free boundaries for the corresponding nonlinear conservation laws of mixed elliptic-hyperbolic type and related nonlinear PDEs. In [60, 61], another 2-D Riemann problem including the classical problem of the expansion of a wedge of gas into a vacuum for the isentropic Euler equations has also been solved; also see the recent work by Lai and Sheng [53] and the references cited therein on further related Riemann problems. The other types of 2-D Riemann problems are still wide open, even for the prototypes of hyperbolic systems of conservation laws as discussed in this paper.

For the full Euler equations (1) with (3), the 2-D Riemann problems involve vortex sheets and entropy waves, in addition to shocks and rarefaction waves; see [8,9,10,11, 22, 43, 52, 56, 59, 76, 97] and the references cited therein. Almost all of these Riemann problems for the full Euler equations (1) with (3) are still unsolved. In addition, all the 3-D or higher-D Riemann problems, including M-D wedge problems or M-D conic body problems, are still open; see [15, 18, 19, 27] and the references cited therein for some recent developments for M-D steady problems. The nonlinear methods and related techniques/approaches originally developed in [20,21,22] as presented above for solving 2-D Riemann problems involving 2-D transonic shocks should be useful in the analysis of these longstanding Riemann problems and newly emerging problems for nonlinear PDEs; also see [14, 22, 23] and the references cited therein. Certainly, further new ideas, techniques, and methods still need to be developed to solve these mathematically challenging and fundamentally important problems.