Phenomenological isotropic visco-hyperelasticity: a differential model based on fractional derivatives

Abstract

The rheological equation of a standard linear solid, i.e., the Zener model, is thermodynamically consistent. Thus, it was often used as a starting point for the development of nonlinear viscoelastic models, especially for elastomers. The basic idea of this paper is a generalization of the one-dimensional fractional constitutive equation of the Zener model to large strains. To reduce the number of material parameters of differential models based on the concept of the internal variables and to avoid integral constitutive equations, we develop a differential model based on the concept of dual stress and strain tensors and their derivatives. To this end, we select two couples of dual stress and strain tensors that have been used in finite elasticity. Then we obtain two constitutive models of incompressible isotropic materials called M1 and M2. We show that the M1 model is not suitable for describing the viscoelastic behavior of elastomers. To improve the predictions of the M2 model, we assume that the material is thixotropic. Therefore, the ratio of the relaxation and creep time depends on deformation. Experimental results show that this ratio may be represented as a function of the first invariant of the Cauchy–Green strain tensor. This yields a new constitutive equation whose material parameters were identified using experimental data on relaxation loadings in the literature. Next, we show that the model is able to predict the experimental data for combined loads of tension–torsion. Consequently, the model seems to be efficient at predicting the multiaxial visco-hyperelastic behavior of elastomers. The main advantage of the current model is that it has a differential form with relatively few parameters and is mathematically convenient.

1 Introduction

Elastomeric rubbers are being used increasingly in various industrial applications such as, for example, shock absorbers, engine mounts, tires, and adhesive joints. To design elastomer components using convential finite-element method (FEM) techniques, it is necessary to choose a three-dimensional constitutive equation that would be reliable for predicting the multiaxial behavior of elastomers. The mechanical behavior of such materials is dominated by hyperelastic behavior with a nonlinear response varying with the strain rate owing to viscous effects; the behavior is called visco-hyperelastic. In the literature, essentially two approaches have been developed for describing the viscoelastic behavior of elastomers at large strains: integral and differential formulations. Often, hereditary integral representations are more commonly used. For more details, the nonlinear viscoelastic theories and constitutive models were well summarised in the book by Locket [1] and recent review articles [2, 3].

Finite linear viscoelasticity (FLV) theory is a major foundation for modeling the mechanical behavior of materials, which depends on the strain rate. In fact, FLV theory is a simplification of the phenomenological approach of Coleman and Noll [4], which was based on the concept of rate-dependent functionals with fading memory properties. Thus, the stress may be decomposed into two components: an equilibrium stress corresponding to the stress response at an infinitely slow rate of deformation and a viscosity-induced overstress. The overstress was expressed as an integral over the deformation history and a relaxation function specified as a measure of the material memory [5]. The FLV theory of Coleman and Noll [4] contains, for an isotropic material, 12 relaxation functions and 3 steady-state material functions. This theory is not appealing because of the large number of functions that need to be determined by experimentation. Simplified versions of FLV theory have been developed that consist mainly of decreasing the number of relaxation functions [6–10]. For instance, Pipkin and Rogers [11] motivated the addition of successive terms in integral series representation of the stress in terms of the history of strain till the difference between the test data and the prediction from theory became smaller than a preassigned value. Thus, they derived a nonlinear theory of viscoelasticity. Bernstein et al. [12] proposed the Bernstein–Kearsley–Zapas (BKZ) elastic-fluid model, which was able to predict the stress relaxation of many kinds of rubber. Recently, a modified version of Kaye-Bernstein–Kearsley–Zapas (K-BKZ) theory was used to model the nonlinear viscoelastic behavior of elastomers [13]. The integral models of type K-BKZ are attractive because of their form, which is equivalent to that envisaged by molecular dynamics. They are based on the molecular network concepts that consist of entanglements. The disappearance of the nodes of the network over time is accelerated by the deformation. These models have been used for a long time and successfully in the field of thermoplastic polymer flows, as well as in shear and elongation deformation modes. Jaishankar and McKinley [14] improved K-BKZ theory using fractional derivatives in the framework of complex fluids and soft materials.

Although FLV theory is very general, other less general theories have been used in the literature [15, 16]. Recently, Hoo Fatt and Ouyang [17] proposed a new single integral form for stresses in which the material parameters intervening in the elastic potential depend on time. Ciambella et al. [18] have expressed the second Piola–Kirchhoff stress tensor as a sum of the equilibrium stress and the overstress represented by a convolution integral in which the relaxation function is described by a Mittag–Leffler type. The authors claimed that their model may be a generalization of both differential and fractional models. The complexity of the model requires the use of a sophisticated optimization process for obtaining the material parameters. Christensen [19] used the kinetic theory of rubber elasticity as a starting point for behavior in large deformations and generalized this theory to include the effect of time. He showed that the type of degree of nonlinearity is very different under relaxation conditions from those involved during creep conditions. O’Dowd and Knauss [20] developed an integral constitutive model that describes the principal deformations of polymeric materials under small and large deformations using the conjugate pair of the second Piola–Kirchhoff stress and the Green strain tensors. Recently, multinetwork theories have been developed [21] for polymeric solids and reproduce successfully a variety of physical phenomena. These theories may be applied to elastomeric solids; however, much work remains to be done. In addition, integral models are difficult to implement using conventional FEM techniques [22], and differential constitutive equations are more appropriate for FEM analysis. To formulate differential constitutive equations in large strains, differential models of linear viscoelasticity [23] may be used as basic models. For these models, elastic behavior is represented by a linear spring and the linear viscous element by a dashpot. Thus, many viscoelastic behaviors of polymers can be approximated by changing the number of springs and dashpots and the connection mode of these elements [24]. Let us focus on a rheological model that is capable of predicting relaxation and creep phenomena (nonviscous material). A simple rheological model incorporating both behaviors is the standard linear solid (SLS) model [25, 26]. The SLS model reasonably describes the viscoelastic behavior of elastomers, as it gradually tends to an equilibrium elastic state during a long relaxation test [27–29]. At small deformations, its creep compliance and relaxation modulus may be represented by a Prony series. Thus, several parameters are usually required to reproduce the viscoelastic behavior of elastomers. Consequently, the identification of the material parameters can be an ill-posed problem. To overcome this issue, one reduces the number of material parameters using fractional differential models [30–33].

Recently, the concept of fractional differential has been applied to extend the constitutive equations of Maxwell and Kelvin–Voigt linear models to finite viscoelasticity [34, 35]. The constitutive equations that are deduced from these models are not suitable for predicting the viscoelastic behavior of solids. In fact, they cannot predict either relaxation or creep responses. Adolfsson and Enelund [36] have proposed a fractional finite viscoelastic model that is based on the concept of internal variables. The model was validated numerically by finite elements. The mathematical structure of this model entails high numerical computational costs in order to fix the number of material parameters to identify and experimentally validate the model. Johnson and Quigley [37] have proposed a one-dimensional phenomenological integral model based on the extension of the Maxwell model to large strains. The parameters of this model can be easily determined from the experimental data of tension relaxation tests. The model has many material parameters and can accurately predict experimental data. Kim et al. [38] have implemented this model in finite-element analysis using the multiplicative decomposition of deformation gradients.

Other authors have applied continuum thermodynamics theory and the multiplicative decomposition of the deformation gradient into elastic and viscous parts or internal variable to formulate constitutive equations [5, 39–44]. The decomposition of the deformation gradient into elastic and viscous parts is a conceptual approach, ${\mathbf {F}}={\mathbf {F}}_\mathrm{e}{\mathbf {F}}_\mathrm{v}$. Generally, this decomposition cannot be determined experimentally since neither ${\mathbf {F}}_\mathrm{e}$ nor ${\mathbf {F}}_\mathrm{v}$ is an observable quantity [45]. In the framework of elastoplasticity, the decomposition of the deformation gradient into elastic and plastic terms relies on clear physical assumptions; there is a lack of evidence in the context of viscoelasticity. However, this decomposition has been successfully applied in many nonlinear constitutive equations [26, 46, 47].

An alternative to the models based on continuum thermodynamics is the micromechanics approach. These models are based on the macromolecular chain network concept with cross links. The earlier work of Green and Tobolsky [48] demonstrated that the classical relaxation theories could be expressed in terms of molecular structure theory and chemical rate theory. They obtained a time-dependent behavior from the sum of an elastic component and a strain-history-dependent component. These authors introduced a transient network concept based on the assumption that chains are steadily breaking and reforming. Bergström and Boyce [49] developed a visco-hyperelastic constitutive model to predict the hysteresis of rubber subjected to slow cyclic loads. Reese [50] developed a material model for the thermo-viscoelastic behavior of rubberlike polymers based on transient network theory. Some of these micromechanical models can be found in the literature [51, 52]. However, these micromechanics-based models are extremely difficult to use and rely on assumptions that have been questioned [53].

The aim of this paper is to propose a novel differential visco-hyperelastic model that can predict the multiaxial behavior of incompressible elastomeric solids. To obtain the model, we will extend the one-dimensional fractional rheological equation of the SLS model, i.e., the Zener model, to large strains using the concept of dual stress and strain tensors. The paper is organized as follows. In Sect. 2, we recall the one-dimensional fractional constitutive equation of the SLS model in the framework of linear viscoelasticity. Then the concept of dual variables and their derivatives is applied to this constitutive equation to obtain two constitutive models, called M1 and M2. We will demonstrate that M1 is not appropriate for describing the visco-hyperelastic behavior of elastomers. Model M2 seems qualitatively able to reproduce the shape of a nominal stress curve. Therefore, the material parameters for this model are identified using experimental results found in the literature. Good agreements are shown between these predictions and experimental data of the multiaxial behavior of elastomeric solids. We end with some concluding remarks.

2 Phenomenological finite viscoelasticity

Elastomeric (or rubberlike) materials constitute a family of high polymers that regroups the thermoplastic elastomers (e.g., polyurethanes), natural rubbers (vulcanized natural rubber, carbon black filled natural rubber), and synthetic elastomers (e.g., silicone rubbers, styrene–butadiene rubber, ethylene propylene diene monomer rubber).

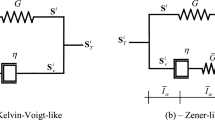
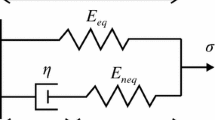
These polymers are widely used for sound and vibration damping. One of the remarkable properties of these materials, besides their high damping ability, is the strong frequency dependence of dynamic properties. Material damping is quantified by the loss factor, defined as the ratio between the imaginary part and the real part of the complex modulus of elasticity in the frequency domain. These materials show a weak frequency dependence of their damping properties over a broad frequency range. This weak frequency dependency is difficult to describe with classical viscoelasticity based on integer derivative operators. Among these models, the standard linear solid (SLS), better known as the Zener model, is probably the most attractive one. This model is built on the parallel coupling of a linear spring and a Maxwell element (a serial coupling of a linear spring and a viscous damper). Its rheological representation is shown in Fig. 1a, and the one-dimensional constitutive equation at any time is

$$\begin{aligned} \sigma (t)+\tau _\mathrm{R} \dot{\sigma }(t)=E_\mathrm{R} \varepsilon (t)+E_\mathrm{R} \tau _\mathrm{c}\dot{\varepsilon }(t), \end{aligned}$$

(1)

where $\sigma (t)$ and $\varepsilon (t)$ are the engineering stress and strain, $E_\mathrm{R}$ is the relaxed magnitude of the elastic modulus (prolonged modulus of elasticity), and the parameters $\tau _\mathrm{R}=\eta /E$ and $\tau _\mathrm{c}=\tau _\mathrm{R}(1+E/E_\mathrm{R})=\tau _\mathrm{R}\xi ^{-1}$ are respectively the relaxation and creep (retardation) time. Equation (1) is not able to correctly represent the viscoelastic behavior of elastomers.

Usually, a large number of derivative operators are required to obtain a reasonably accurate description of observed damping characteristics. Consequently, many material parameters are necessary, and their identification could be problematic. By introducing fractional order derivative operators in the constitutive relations, the number of material parameters can be significantly reduced (Fig. 1b). Thus, Eq. (1) can be generalized as follows:

$$\begin{aligned} \sigma (t)+\tau _\mathrm{R}^\alpha {D}^\alpha \sigma (t)= E_\mathrm{R}\varepsilon (t)+E_\mathrm{R}\tau _\mathrm{c}^\alpha {D}^\alpha \varepsilon (t), \end{aligned}$$

(2)

where ${D}^\alpha \sigma (t)$ and ${D}^\alpha \varepsilon (t)$ are fractional derivatives in the sense of Caputo and Mainardi [54],

$$\begin{aligned} {D}^\gamma f(t) =\left\{ \begin{array}{ll} \frac{1}{\varGamma (1-\gamma )}\int \limits _{0}^{t} \frac{f'(s)}{(t-s)^\gamma } {\mathrm {d}} s &{} \quad \gamma \in \,]0,1[, \\ \frac{{\mathrm {d}}f(t)}{{\mathrm {d}}t} &{} \quad \gamma =1, \end{array}\right. \end{aligned}$$

(3)

where the Gamma function is defined by $\varGamma (z)=\int _{0}^{\infty }u^{z-1}{\mathrm {e}}^{-u} {\mathrm {d}}u$.

Fig. 1

a Standard three-parameter Zener model and b fractional three-parameter Zener model

A number of publications have shown that fractional order viscoelastic models successfully predict the experimental data over a broad frequency range for several polymers using only four material parameters in the uniaxial case [30, 55]. Also, these fractional viscoelastic models can predict the experimental data of the creep and relaxation stress of many polymers [56, 57]. According to [55], the use of Eq. (2) is attractive in the analysis of viscoelastic damped structures. It leads to well-posed equations of motion with causal solutions when used in modal analysis. The finite-element formulations corresponding to these models have been presented to predict the temporal responses of viscoelastic structures. Substantial contributions in this research field have been presented by Padovan [58], Enelund et al. [59], and Schmidt and Gaul [60]. Padovan and Schmidt used a single constitutive equation that involves fractional derivatives acting on the stresses and strains. Consequently, both strain and stress histories need to be stored and included in each time step when integrating the structural response. Enelund et al. have developed a formulation based on internal variables. The fractional derivative was introduced in the evolution law equation of the internal variables. This general three-dimensional formulation has been implemented in a finite-element framework. The advantage of this approach is that only the history of the internal variable must be stored; thus, the computer time and memory are saved. This formulation was subsequently generalized by Adolfsson and Enelund [36] to large strains using the concept of the decomposition of the deformation gradient into elastic and inelastic parts. In the frequency domain, one needs to store the history of displacement owing to the nonlocal character of fractional derivatives. To overcome this drawback, Yuan and Agrawal [61] proposed a numerical scheme. In this scheme, the dynamic of motion of a system containing a fractional term is transformed into a set of differential equations with no fractional derivative terms. Recently, Schmidt and Gaul [62] have proven that this scheme is equivalent to a classical spring–dashpot representation. Furthermore, they have shown that the model of Yuan and Agrawal predicts incorrect asymptotic behavior.

The elastomeric materials are often used in applications where the approximation of small deformations is not valid, so the theory of linear viscoelasticity is not suitable. Moreover, many rubber components that are used as vibration isolators are subjected to small oscillatory loads superimposed on large static deformation. Thus, most dynamic properties of vibration isolators can be described by the linearized steady-state harmonic response. Therefore, Eqs. (1) and (2) cannot be applied in the range of large strains. In the literature, several models have been proposed to extend classical linear viscoelastic models to the nonlinear domain [26]. However, less attention has been devoted to fractional derivative viscoelasticity in combination with large deformations. The main objective of this paper is the extension of Eq. (2) to large strains. To this end, the equilibrium stress response of elastomeric materials must be derived from the strain-energy density function. Thus, Eq. (2) can be rearranged as

$$\begin{aligned} \sigma (t)+\tau _\mathrm{R}^\alpha {D}^\alpha \sigma (t)=\frac{\partial {W}}{\partial {\varepsilon (t)}}+E_\mathrm{R}\xi ^{-1}\tau _\mathrm{R}^\alpha {D}^\alpha \varepsilon (t), \end{aligned}$$

(4)

where W is the strain-energy density function of the elastomeric solid, and $\tau _\mathrm{R}^\alpha \cdot \tau _\mathrm{c}^{-\alpha }=\xi =E_\mathrm{R}/E_\mathrm{NR}<1$, in which $E_\mathrm{NR}=E+E_\mathrm{R}$ is the instantaneous modulus of elasticity (nonrelaxed elastic modulus).

2.1 Differential isotropic visco-hyperelastic model

Let ${\mathbf {F}}=\partial \mathbf {x}/\partial \mathbf {X}$ be the deformation gradient tensor, where $\mathbf {X}$ is the position vector of a material particle in the undeformed configuration and $\mathbf {x}$ is the corresponding position vector in the deformed configuration. The right and left Cauchy–Green strain tensors are denoted by ${\mathbf {C}}={\mathbf {F}}^\mathrm{T}{\mathbf {F}}$ and ${\mathbf {B}}={\mathbf {F}}{\mathbf {F}}^\mathrm{T}$, respectively. The principal invariants of ${\mathbf {C}}$ (or ${\mathbf {B}}$) are given by $I_1({\mathbf {C}})=I_1({\mathbf {B}})=\mathrm{tr}({\mathbf {C}})$, $I_2({\mathbf {C}})=I_2({\mathbf {B}})=(1/2)[I_1^2({\mathbf {C}})-\mathrm{tr}({\mathbf {C}}^2)]$, and $I_3({\mathbf {C}})=I_3({\mathbf {B}})=\mathrm{det}({\mathbf {C}})=(\mathrm{det}({\mathbf {F}}))^2=J^2$ [63].

The generalization of Eq. (4) at finite strains was not considered in the publications of Haupt and Lion [34] and Drozdov [35]. To do that, we apply the concept of dual variables and derivatives corresponding to family 1 of Haupt and Tsakmakis [64]. According to this concept, we introduce the so-called covariant and contravariant Oldroyd derivatives $(\mathop {\bullet }\limits ^{\bigtriangleup })$, $(\mathop {\bullet }\limits ^{\bigtriangledown })$ with respect to the stress configuration

$$\begin{aligned} (\mathop {\bullet }\limits ^{\bigtriangleup })= (\dot{\bullet })+{\mathbf {L}}^\mathrm{T}(\bullet )+(\bullet ){\mathbf {L}},\quad (\mathop {\bullet }\limits ^{\bigtriangledown }) =(\dot{\bullet })-{\mathbf {L}}(\bullet )-(\bullet ){\mathbf {L}}^\mathrm{T}. \end{aligned}$$

(5)

A superscripted dot represents the material time rate, the symbol T denotes the transposed tensor, and ${\mathbf {L}}={\dot{\mathbf {F}}}{\mathbf {F}}^{-1}$ is the velocity gradient.

We select dual stress and strain tensors that are standard in the framework of finite elasticity [65, 66]. The stress and strain tensors form the conjugate pairs $({\mathbf {S}},\mathbf {E})$ and $(\varvec{\tau },\mathbf {A})$. The tensors ${\mathbf {S}}$ and $\mathbf {E}=(1/2)({\mathbf {C}}-\mathbf {I})$ are the second Piola–Kirchhoff stress tensor and Green–Lagrange strain tensor, respectively, and $\mathbf {I}$ is the identity tensor; these tensors operate in the reference configuration. The weighted Cauchy stress tensor (or Kirchhoff stress tensor) is defined by $\varvec{\tau }=J \varvec{\sigma }$, where $\varvec{\sigma }$ is the Cauchy stress tensor and $\mathbf {A}=(1/2)(\mathbf {I}-{\mathbf {B}}^{-1})$ is the Almansi strain tensor; the tensors $\varvec{\tau }$ and $\mathbf {A}$ act in the actual configuration.

The work and the stress power for conjugate pairs $({\mathbf {S}},\mathbf {E})$ and $(\varvec{\tau },\mathbf {A})$ are invariant under the change of configuration

$$\begin{aligned} {\mathbf {S}}:\mathbf {E}=\varvec{\tau }:\mathbf {A}, \quad {\mathbf {S}}:\dot{\mathbf {E}}=\varvec{\tau }: \mathop {\mathbf {A}}\limits ^{\bigtriangleup }, \end{aligned}$$

(6)

where : denotes the scalar product of two second rank tensors.

According to the concept of dual variables, it is not only pairs of variables that are naturally coupled but also their derivatives:

$$\begin{aligned} {\dot{\mathbf {S}}}:\dot{\mathbf {E}}= \mathop {\varvec{\tau }}\limits ^{\bigtriangledown }: \mathop {\mathbf {A}}\limits ^{\bigtriangleup }. \end{aligned}$$

(7)

It seems that the concept of dual variables remains valid even for nonlinear viscoelasticity; the proof can be found in the publications of Hassani et al. [67], Haupt and Lion [34], and Haupt [68]. Indeed, reliable nonlinear viscoelastic models can be formulated using internal variables. The concept of internal variables postulates that the current state at a given point of a dissipative material is specified by the strain tensor, ${\mathbf {C}}$, and a finite number of scalar, vector, or tensor internal variables, $\gamma _1,\gamma _2,\ldots \gamma _m$. The information relative to the whole past of a material is thus contained in the set of internal variables at time t. The free energy of viscoelastic material can be decomposed as follows [63]:

$$\begin{aligned} \psi ({\mathbf {C}},\gamma _1,\gamma _2,\ldots \gamma _m)=W_\mathrm{eq} ({\mathbf {C}})+\sum \limits _{\alpha =1}^{m} Y_\alpha ({\mathbf {C}},\gamma _\alpha ), \end{aligned}$$

(8)

where $W_\mathrm{eq}({\mathbf {C}})$ is the equilibrium free energy (hyperelastic). The second term on the right-hand side is a dissipative free energy responsible for the viscoelastic regime. The scalar-valued functions $Y_\alpha$ represent the so-called configurational energy of the viscoelastic solid and characterize the nonequilibrium state. Each subscripted $\alpha$ is related (conjugate) to $\gamma _\alpha$ by the internal equation

$$\begin{aligned} {\mathbf {Q}}_\alpha =-2\frac{\partial Y_\alpha (\bar{{\mathbf {C}}},\gamma _\alpha )}{\partial \gamma _\alpha }, \end{aligned}$$

(9)

where ${\mathbf {C}}=J^{2/3}\bar{{\mathbf {C}}}$, and $\bar{{\mathbf {C}}}$ is associated with the isochoric deformations of the material.

The set of equations already obtained must be completed by a kinetic relation, which describes the evolution of the material variables. These are of the form

$$\begin{aligned} {\mathbf {Q}}_\alpha =f_\alpha (\bar{{\mathbf {C}}},{\mathbf {Q}}_1, {\mathbf {Q}}_2,\ldots ,{\mathbf {Q}}_m). \end{aligned}$$

(10)

From a phenomenological point of view, the physical microstructure of a material can be represented by internal variables that can be stress or strain tensors and refers to appropriately selected configurations [43]. For internal variables of the strain type, the one-dimensional rheological models of linear viscoelasticity can be extended to finite strains by introducing an intermediate configuration. Within the concept of internal variables, this intermediate configuration is related to the multiplicative decomposition of the deformation gradient, ${\mathbf {F}}={\mathbf {F}}_\mathrm{e}{\mathbf {F}}_\mathrm{v}$, where ${\mathbf {F}}_\mathrm{e}$ and ${\mathbf {F}}_\mathrm{v}$ are elastic and viscous parts, respectively. According to this approach, it is possible to generalize the constitutive equation of the Maxwell model to large strains. Consequently, the second Piola–Kirchhoff stress tensor is decomposed as a sum of the equilibrium hyperelastic stress and the rate-dependent overstress. The stress relation is combined with the evolution equations, and it seems that it is sufficient to provide the thermodynamic consistency of the material response.

The first model, M1, is defined through the second Piola–Kirchhoff stress tensor ${\mathbf {S}}(t)$, stress rate $\mathop {{\mathbf {S}}}\limits ^{\bigtriangledown }\,=\,{\dot{\mathbf {S}}}(t)$, the Green–Lagrange strain tensor $\mathbf {E}(t)$, and strain rate $\mathop {\mathbf {E}}\limits ^{\bigtriangleup }\,\,=\,\dot{\mathbf {E}}(t)$. These dual tensors are defined in Lagrangian configuration. Thus, the model may be qualified as a Lagrangian model, i.e., M1.

The equivalents of Eqs. (1) and (4) at large strains are respectively as follows:

$$\begin{aligned} {\mathbf {S}}(t)+\tau _\mathrm{R}\dot{{\mathbf {S}}}(t)= \frac{\partial {W}}{\partial {\mathbf {E}(t)}}+ 2\mu _0\tau _\mathrm{R}\xi ^{-1}\dot{\mathbf {E}}(t) \end{aligned}$$

(11)

and

$$\begin{aligned} {\mathbf {S}}(t)+\tau _\mathrm{R}^\alpha {D}^\alpha {\mathbf {S}}(t)= \frac{\partial {W}}{\partial {\mathbf {E}(t)}}+2\mu _0\tau _\mathrm{R}^\alpha \xi ^{-1}{D}^\alpha \mathbf {E}(t), \end{aligned}$$

(12)

where $\dot{\mathbf {E}}(t)$ is the Green strain rate operating on the reference configuration. The parameter $\tau _\mathrm{R}$ represents a relaxation time corresponding to the Lagrangian model, i.e., M1, and $\mu _0$ is the shear modulus at small strains.

The second model, M2, operates in the current configuration and may be defined through the Kirchhoff stress tensor $\varvec{\tau }$ and $\mathop {\varvec{\tau }}\limits ^{\bigtriangledown }\,=\, \dot{\varvec{\tau }}-L\varvec{\tau }- \varvec{\tau }L^\mathrm{T}$, which is dual to $\mathop {\mathbf {A}}\limits ^{\bigtriangleup }\,\,=\,\dot{\mathbf {A}}+ {\mathbf {L}}^\mathrm{T}\mathbf {A}+\mathbf {A}{\mathbf {L}}=\mathbf {D}$ [64], where $\mathbf {D}=(1/2)({\mathbf {L}}+{\mathbf {L}}^\mathrm{T})$ is the strain rate tensor. Thus, the equivalent of Eq. (1) at large strains is as follows:

(13)

where the functional represents the equilibrium Cauchy stress tensor, and the constant $\tau _\mathrm{R}$ is a relaxation time of the Eulerian model, i.e., M2.

Equation (13) may be written in the reference configuration as follows:

(14)

$$\begin{aligned}&{\mathbf {S}}(t)+\tau _\mathrm{R}\dot{{\mathbf {S}}}(t)= \frac{\partial {W}}{\partial {\mathbf {E}(t)}}-2\mu _0\tau _\mathrm{R} \xi ^{-1}\dot{{\mathbf {e}}}(t), \end{aligned}$$

(15)

where ${\mathbf {e}}=(1/2)({\mathbf {C}}^{-1}-\mathbf {I})$ is the Piola strain tensor.

We use the concept of fractional derivatives to generalize Eq. (15), obtaining

$$\begin{aligned} {\mathbf {S}}(t)+\tau _\mathrm{R}^\alpha {D}^\alpha {\mathbf {S}}(t) =\frac{\partial {W}}{\partial {\mathbf {E}(t)}}-2\mu _0\tau _\mathrm{R}^\alpha \xi ^{-1} {D}^\alpha {\mathbf {e}}(t). \end{aligned}$$

(16)

In Eqs. (12) and (16), the stress tensor and stress rate are those of the second Piola–Kirchhoff stress tensor. The strain tensor and strain rate are those respectively of the strain tensor of Green–Lagrange and Piola. Consequently, both constitutive equations are formulated in the reference configuration. For numerical reasons [58] and to preserve the principle of objectivity, the constitutive equations need to be written in the reference configuration. Thus, Eqs. (12) and (16) may be well suited for finite-element computations.

The causality principle requires that ${\mathbf {S}}(t)$ vanish for $t<0$ with the initial condition ${\mathbf {S}}(t=0)=0$, and we have $\mathbf {E}(t)={\mathbf {e}}(t)=0$ for $t\le 0$.

Let us recall the definition of the Laplace transform of the Caputo fractional order derivative [69] before solving equations (12) and (16):

$$\begin{aligned} \mathcal {L}[{D}^{\alpha }f(t)]= p^{\alpha }\mathcal {L}[f(t)]-\sum \limits _{k=0}^{n-1}[f^k(0) p^{\alpha -1-k}], \end{aligned}$$

(17)

where n is an integer chosen such that $n-1<\alpha \le n$.

In particular, the case of fractional relaxation is obtained for $n=1$, so Eq. (17) becomes

$$\begin{aligned} \mathcal {L}[{D}^{\alpha }f(t)]=p^{\alpha }\mathcal {L} [f(t)]-f(0)p^{\alpha -1}. \end{aligned}$$

(18)

We apply the Laplace transform to Eq. (12) (see Appendix 1 for details):

$$\begin{aligned} \mathcal {L}\left[ {\mathbf {S}}(t)+\tau _\mathrm{R}^\alpha {D}^ \alpha {{\mathbf {S}}}(t)\right] = \mathcal {L}\left[ \frac{\partial {W}}{\partial {\mathbf {E}(t)}}+ 2\mu _0\tau _\mathrm{R}^\alpha \xi ^{-1}{D}^\alpha {\mathbf {E}}(t)\right] \end{aligned}$$

(19)

and

$$\begin{aligned} {\hat{\mathbf {S}}}(p)=\left( \frac{1}{\tau _\mathrm{R}^{-\alpha }+p^\alpha }\right) \left[ \tau _\mathrm{R}^{-\alpha }\mathcal {L}\left( \frac{\partial W}{\partial \mathbf {E}(t)}\right) +2\mu _0\xi ^{-1}p^\alpha \hat{\mathbf {E}}(p)\right] . \end{aligned}$$

(20)

The inverse Laplace transform of Eq. (20) leads to

$$\begin{aligned} {\mathbf {S}}(t)= & {} {\mathbf {S}}^\mathrm{L}(t)=\tau _\mathrm{R}^{-\alpha }\int \limits _{0}^{t} \frac{\partial W}{\partial \mathbf {E}(s)}(t-s)^{\alpha -1}E_\alpha ,_\alpha \left( -\left( \frac{t-s}{\tau _\mathrm{R}}\right) ^\alpha \right) {\mathrm {d}}s \nonumber \\&+2\mu _0\xi ^{-1}\int \limits _{0}^{t}\dot{\mathbf {E}}(s)E_\alpha ,_1 \left( -\left( \frac{t-s}{\tau _\mathrm{R}}\right) ^\alpha \right) {\mathrm {d}}s. \end{aligned}$$

(21)

Similarly, the solution of Eq. (16) is

$$\begin{aligned} {\mathbf {S}}(t)= & {} {\mathbf {S}}^\mathrm{E}(t)=\tau _\mathrm{R}^{-\alpha } \int \limits _{0}^{t}\frac{\partial W}{\partial \mathbf {E}(s)}(t-s)^{\alpha -1}E_\alpha ,_\alpha \left( -\left( \frac{t-s}{\tau _\mathrm{R}}\right) ^\alpha \right) {\mathrm {d}}s \nonumber \\&-2\mu _0\xi ^{-1}\int \limits _{0}^{t}{\dot{\mathbf {e}}}(s) E_\alpha ,_1\left( -\left( \frac{t-s}{\tau _\mathrm{R}}\right) ^\alpha \right) {\mathrm {d}}s, \end{aligned}$$

(22)

where $E_\alpha ,_1(z)=\sum _{k=0}^{\infty }z^k/\varGamma (\alpha k+1)$ is the Mittag–Leffler function in which $\alpha >0$, $\mid z\mid <\infty$. This function is a generalization of the exponential function, i.e., $E_{1}(z)=\mathrm {exp}(z)$ (Appendix 2). A straightforward generalization of the Mittag–Leffler function $E_\alpha ,_\beta (z)=\sum _{k=0}^{\infty }z^k/\varGamma (\alpha k+\beta )$ was introduced by Humbert and Agarwal [70].

For $z\in R^+$, $0<\alpha \le 1$, and $\beta \ge \alpha$, the generalized Mittag–Leffler function on the negative axis, i.e., $E_\alpha ,_\beta (-z)$, is completely monotone [70].

From a theoretical point of view, the incompressibility constraint facilitates the finding of analytical solutions. Experimentally, all elastomers are compressible (i.e., the bulk modulus is finite), and Poisson’s ratio can approach 1 / 2. In experiments, incompressibility is a good approximation in the framework of plane problems (e.g., simple traction and equibiaxial traction) for vulcanized natural rubber and carbon black filled rubber. For instance, an excellent fit of the experimental data was obtained for carbon black filled natural rubber [71]. Moreover, Charrier et al. [72] proved that the behavior of slightly compressible materials may approximate well that of incompressible materials. We used experimental data from the literature, which were obtained by assuming that the SBR was an incompressible material. Consequently, the incompressibility constraint of the material implies the introduction of a Lagrange multiplier, P(t), so that the Cauchy stress tensor is defined by adding a pressure term, $P(t) \mathbf {I}$.

The Cauchy stress tensor ${\varvec{\sigma }}={\mathbf {F}}{\mathbf {S}}{\mathbf {F}}^\mathrm{T}$ is given by the expression

$$\begin{aligned} {\varvec{\sigma }}^\mathrm{L}(t)= & {} \tau _\mathrm{R}^{-\alpha }{\mathbf {F}}(t) \left[ \int \limits _{0}^{t}\frac{\partial W}{\partial \mathbf {E}(s)}(t-s)^{\alpha -1}E_\alpha ,_\alpha \left( -\left( \frac{t-s}{\tau _\mathrm{R}}\right) ^\alpha \right) {\mathrm {d}}s \right] {\mathbf {F}}^\mathrm{T}(t)\nonumber \\&+\,2\mu _0\xi ^{-1}{\mathbf {F}}(t)\left[ \int \limits _{0}^{t} \dot{\mathbf {E}}(s) E_\alpha ,_1\left( -\left( \frac{t-s}{\tau _\mathrm{R}}\right) ^\alpha \right) {\mathrm {d}}s \right] {\mathbf {F}}^\mathrm{T}(t)-P(t)\mathbf {I} \end{aligned}$$

(23)

and

$$\begin{aligned} {\varvec{\sigma }}^\mathrm{E}(t)= & {} \tau _\mathrm{R}^{-\alpha }{\mathbf {F}}(t)\left[ \int \limits _{0}^{t}\frac{\partial W}{\partial \mathbf {E}(s)}(t-s)^{\alpha -1}E_\alpha ,_\alpha \left( -\left( \frac{t-s}{\tau _\mathrm{R}}\right) ^\alpha \right) \mathrm { d}s \right] {\mathbf {F}}^\mathrm{T}(t)\nonumber \\&-\,2\mu _0\xi ^{-1}{\mathbf {F}}(t)\left[ \int \limits _{0}^{t}{\dot{\mathbf {e}}}(s) E_\alpha ,_1\left( -\left( \frac{t-s}{\tau _\mathrm{R}}\right) ^\alpha \right) {\mathrm {d}}s \right] {\mathbf {F}}^\mathrm{T}(t) -P(t)\mathbf {I}. \end{aligned}$$

(24)

Note that the Green functions $k(t)=\tau _\mathrm{R}^{-\alpha }t^{\alpha -1}E_\alpha ,_\alpha (-(t/\tau _\mathrm{R})^\alpha )$ and $R(t)=E_\alpha ,_1(-(t/\tau _\mathrm{R})^\alpha )$ are monotonically decreasing functions of time, and they can represent phenomena of relaxation. The tensor $\partial W/\partial \mathbf {E}(t)$ depends on the strain-energy density function. $\dot{\mathbf {E}}$ and ${\dot{\mathbf {e}}}$ are respectively the Green strain rate and the Piola rate tensors.

On the right-hand side of Eqs. (23) and (24), the first term can be interpreted as the instantaneous hyperelasticity response of the models; this is viewed as the elastic relaxation function of the material. The second term of Eqs. (23) and (24) is interpreted as overstress; thus, this relaxation function may be related to the material memory [5]. The relaxation functions are not affected by the deformation. However, it seems they are related to different physical processes [16].

2.1.1 Model responses for a step-strain relaxation loading

To prove the consistency of models M1 and M2, we will investigate their predictions in the context of a simple relaxation test. Thus, the deformation gradient is

$$\begin{aligned} {\mathbf {F}}=\lambda {\mathbf {e}}_1\otimes {\mathbf {e}}_1+\frac{1}{\sqrt{\lambda }}({\mathbf {e}}_2\otimes {\mathbf {e}}_2+{\mathbf {e}}_3\otimes {\mathbf {e}}_3), \end{aligned}$$

(25)

where $\lambda =\lambda (t)$ is the stretch ratio, ${\mathbf {e}}_1$ is the extension direction, and ${\mathbf {e}}_2$ and ${\mathbf {e}}_3$ are the transverse directions.

For the relaxation test, the expression of the stretch ratio is $\lambda (t)=(\lambda _0-1)H(t)+1$, where H(t) is a Heaviside unit step function and $\lambda _0$ is the imposed stretch ratio. We may eliminate the unknown variable P(t) using the boundary conditions $\sigma _{11}(t)=\sigma (t)$ and $\sigma _{22}(t)=\sigma _{33}(t)=0$. According to experiments of Goldberg and Lianis [73], Yuan and Lianis [74], and Yuan [75], in the quasi-static regime, the SBR can be considered incompressible and of a Mooney–Rivlin type. The strain-energy density of the Mooney–Rivlin model for incompressible rubber is

$$\begin{aligned} W=c_{10}(I_1({\mathbf {C}})-3)+c_{01}(I_2({\mathbf {C}})-3) =\left( \frac{\mu _0}{2}\right) [\chi (I_1({\mathbf {C}})-3) +(1-\chi )(I_2({\mathbf {C}})-3)], \end{aligned}$$

(26)

where $\mu _0=2(c_{10}+c_{01})>0$ is the constant shear modulus for infinitesimal deformations and $0<\chi \le 1$ is a dimensionless constant. When $\chi =1$, one obtains the neo-Hookean strain-energy density function. One can see that the material parameters $c_{10}=\mu _0\chi /2$ and $c_{01}=\mu _0(1-\chi )/2$ are effectively dependent. We point out that the constants $c_{10}>0$ and $c_{01}\ge 0$ must be positive in order to satisfy the requirement of a positive strain-energy density. The aspects of stability and identification of the material parameters were detailed in the paper by Hartmann [76] by considering the Mooney–Rivlin strain-energy density function.

We deduce from Eqs. (23) and (24) the stress relaxation for models M1 and M2, respectively:

$$\begin{aligned} \sigma ^\mathrm{L}(t)=(\lambda _0^2-\lambda _0^{-1})\left[ 2(c_{10}+c_{01}\lambda _0^{-1})(1-g(t))\right] +\mu _0\xi ^{-1}\left[ \lambda _0^4-\lambda _0^2-\lambda _0^{-2}+\lambda _0^{-1}\right] g(t) \end{aligned}$$

(27)

and

$$\begin{aligned} \sigma ^\mathrm{E}(t)=(\lambda _0^2-\lambda _0^{-1})\left[ 2(c_{10}+c_{01}\lambda _0^{-1})(1-g(t))+\mu _0\xi ^{-1}g(t)\right] , \end{aligned}$$

(28)

where $g(t)=E_\alpha ,_1(-(t/\tau _\mathrm{R})^\alpha )$.

The component of the first Piola–Kirchhoff stress tensor, i.e., $\pi$, can be deduced respectively from Eqs. (27) and (28):

$$\begin{aligned} \pi ^\mathrm{L}(t)= & {} (\lambda _0-\lambda _0^{-2})\left[ 2(c_{10}+c_{01}\lambda _0^{-1})(1-g(t))\right] +\mu _0\xi ^{-1}\left[ \lambda _0^3-\lambda _0-\lambda _0^{-3}+\lambda _0^{-2}\right] g(t), \end{aligned}$$

(29)

$$\begin{aligned} \pi ^\mathrm{E}(t)= & {} (\lambda _0-\lambda _0^{-2})\left[ 2(c_{10}+c_{01}\lambda _0^{-1})(1-g(t))+\mu _0\xi ^{-1}g(t)\right] . \end{aligned}$$

(30)

In experiments and in the case of a simple extension, the nominal stress must be a positive-definite monotonically increasing function of the stretch ratio [77], and its second derivative must be negative. In other words, the slope of the stress isochrones (i.e., the slope of the pertinent nominal stress vs. a measure of deformation curves for fixed t) is a nonincreasing function of the deformation measure [78]. According to Batra [79], the criterion can be applied in the framework of nonlinear elastic (or hyperelastic) materials. We evaluate the second derivative of the nominal stress of models M1 and M2 as follows:

$$\begin{aligned} \frac{{\mathrm {d}}^2\pi ^\mathrm{L}(\lambda _0)}{{\mathrm {d}}\lambda _0^2}= & {} -12\left[ c_{10}\lambda _0 ^{-4}+2c_{01}\lambda _0^{-5}\right] (1-g(t)) +6\mu _0\xi ^{-1}\left[ \lambda _0+\lambda _0^{-4}-2\lambda _0^{-5}\right] g(t), \end{aligned}$$

(31)

$$\begin{aligned} \frac{{\mathrm {d}}^2\pi ^\mathrm{E}(\lambda _0)}{{\mathrm {d}}\lambda _0^2}= & {} -6\left[ \left( 2c_{10}\lambda _0^{-4}+4c_{01}\lambda _0^{-5}\right) (1-g(t))+\mu _0\xi ^{-1}\lambda _0^{-4}g(t)\right] . \end{aligned}$$

(32)

We have

$$\begin{aligned} \frac{{\mathrm {d}}^2\pi ^\mathrm{L}(\lambda _0)}{{\mathrm {d}}\lambda _0^2}\le 0 \quad \Leftrightarrow \quad \frac{\mu _0\xi ^{-1}[\lambda _0^5+1-2\lambda _0^{-1}]}{2[c_{10}+2c_{01}\lambda _0^{-1}]}\le \frac{1-g(t)}{g(t)}. \end{aligned}$$

(33)

For $\lambda _0>1$, $\exists t_0>0$ such that, $\forall t\in [0,t_0]$, $\mu _0\xi ^{-1}[\lambda _0^5+1-2\lambda _0^{-1}]/[2(c_{10}+2c_{01}\lambda _0^{-1})]>[1-g(t)]/g(t)$. This means that the second derivative ${\mathrm {d}}^2\pi ^\mathrm{L}(\lambda _0)/{\mathrm {d}}\lambda _0^2$ is positive when $t\in [0,t_0]$. For model M2 we have

$$\begin{aligned} \forall \lambda _0\ge 1,\qquad \frac{{\mathrm {d}}^2\pi ^\mathrm{E}(\lambda _0)}{{\mathrm {d}}\lambda _0^2}<0. \end{aligned}$$

(34)

The second derivative of the nominal stress of model M2 is always negative, as indicated by Eq. (32). For model M1, the nominal stress is not a concave function of the stretch ratio. This result contradicts experimental data and is thus excluded in the process of material parameter identification in the next section.

2.1.2 Material parameter identification

The material parameters $(c_{10},c_{01},\xi ,\tau _\mathrm{R},\alpha )$ of model M2 are determined using the experimental data of the relaxation tests of Goldberg and Lianis [73] (Appendix 3). These data are obtained by varying both the time and the stretch ratio on SBR specimens. At a slow strain rate, SBR behaves like a Mooney–Rivlin material. The material parameters are considered to be nearly constant during the relaxation tests. Their identification implies the solution of a nonlinear least-squares problem with optimization,

$$\begin{aligned} \min \left( \frac{1}{NM}\sum \limits _{i=1}^{N}\sum \limits _{j=1}^{M} \left[ \sigma _\mathrm{mod}(c_{10},c_{01},\xi ,\tau _\mathrm{R},\alpha ,\lambda _0^i,j) -\sigma _\mathrm{exp}(c_{10},c_{01},\xi ,\tau _\mathrm{R},\alpha ,\lambda _0^i,j)\right] ^2\right) , \end{aligned}$$

where N and M are respectively the number of test and experimental data for each test. $\sigma _\mathrm{exp}$ and $\sigma _\mathrm{mod}$ are respectively the experimental data and theoretical values of the Cauchy stress. The material parameters $(c_{10},c_{01},\xi ,\tau _\mathrm{R},\alpha )$ are determined by a stochastic Monte Carlo technique. The stochastic Monte Carlo technique is implemented in the commercial package MATLAB; tens of thousands of parameter sets were tested and evaluated. The parameters are listed in Table 1.

Table 1 Material parameters of model of Eq. (28)

We checked whether the proposed model could correctly reproduce the experimental data of each relaxation test using the material parameters given in Table 1. The corresponding results are presented in Fig. 2 for different values of the stretch ratio, $\lambda _0 \in \{1.1, 1.2, 1.5, 1.8, 2, 2.5\}$.

Fig. 2

Comparison of constitutive model of Eq. (28) with experimental data for an extension relaxation test of [73]

The relative error (ERR) is calculated as follows:

$$\begin{aligned} \mathrm{ERR}_j=\frac{|\sigma _{\exp (j)}-\sigma _{\mathrm{mod}(j)}|}{|\sigma _{\exp (j)}|}; \end{aligned}$$

(35)

it is plotted versus time in Fig. 3 for different values of the stretch ratio.

At the beginning of the relaxation, one can note that the relative error is rather high. Thus, the model gives good estimates for $\lambda _0=1.5$, but it underestimates experimental results for $\lambda _0<1.5$ and overestimates experimental results for $\lambda _0 >1.5$.

We conclude that the model cannot correctly reproduce experimental data for each relaxation test, and the results of parameter identification of the model are moderate.

Fig. 3

Relative error versus time for different values of $\lambda _0$, logarithmic time scale

The values of the material parameters are probably not suitable; they can depend on the stretch ratio. If this is the case, the Laplace transform cannot be applied to Eq. (16). However, it may be solved numerically [69, 80]. Consequently, the identification of material parameters demands more computation time.

2.2 Novel constitutive equation

To improve the predictions of model M2, we suppose that the material is thixotropic. Many authors have reported that elastomeric materials are thixotropic [46, 47, 81]. For instance, in the framework of a harmonic regime, the complex moduli depend on the strain amplitude [47]. In linear viscoelasticity (Eq. 4), the storage and loss moduli are independent of the deformation amplitude [82]. Therefore, the parameter $\xi =(\tau _\mathrm{R}/\tau _\mathrm{c})^\alpha$ is a constant and does not depend on the strain.

We note that the modulus E should depend on the right Cauchy–Green strain tensor, $E({\mathbf {C}}_\mathrm{e})=E(({\mathbf {F}}_\mathrm{v}^{-1})^\mathrm{T}{\mathbf {C}}{\mathbf {F}}_\mathrm{v}^{-1})$; however, ${\mathbf {F}}_\mathrm{v}$ is not an observable quantity and cannot be measured.

In this work, we take into account the thixotropy by assuming that the parameter $\xi ({\mathbf {C}}(t))=E_\mathrm{R}/[E_\mathrm{R}+E({\mathbf {C}}(t))]$ is a function of the right Cauchy–Green strain tensor, i.e., ${\mathbf {C}}(t)$, and the viscosity depends on the derivative of ${\mathbf {C}}(t)$, i.e., $\eta =\eta ({\dot{\mathbf {C}}}(t))$. However, we assume that the relaxation time is constant, i.e., $\tau _\mathrm{R}=\eta ({\dot{\mathbf {C}}}(t))/E({\mathbf {C}}(t))=\hbox {const}$.

Equation (16) may be written as follows:

$$\begin{aligned} {\mathbf {S}}(t)+\tau _\mathrm{R}^\alpha {D}^\alpha {\mathbf {S}}(t)=\frac{\partial {W}}{\partial {\mathbf {E}(t)}}-2\mu _0\tau _\mathrm{R}^\alpha \xi ^{-1}(t) {D}^\alpha {\mathbf {e}}(t). \end{aligned}$$

(36)

Thus, Eq. (36) is a linear differential equation with constant coefficients and can be solved using the Laplace transform as follows:

$$\begin{aligned} {\hat{\mathbf {S}}}(p)=\Biggl (\frac{1}{\tau _\mathrm{R}^{-\alpha }+p^\alpha }\Biggr )\Biggl [\tau _\mathrm{R}^{-\alpha }\mathcal {L}\biggl (\frac{\partial W}{\partial \mathbf {E}(t)}\biggr ) -2\mu _0\mathcal {L}\biggl (\xi ^{-1}(t){D}^\alpha {\mathbf {e}}(t)\biggr )\Biggr ]. \end{aligned}$$

(37)

Now, one needs to evaluate the inverse Laplace transform of the function on the right-hand side of Eq. (37). We find after calculations (Appendix 1),

$$\begin{aligned} {\mathbf {S}}(t)= & {} \tau _\mathrm{R}^{-\alpha }\int \limits _{0}^{t}\frac{\partial W}{\partial \mathbf {E}(s)}(t-s)^{\alpha -1}E_\alpha ,_\alpha \left( -\left( \frac{t-s}{\tau _\mathrm{R}}\right) ^\alpha \right) {\mathrm {d}}s \nonumber \\&-2\mu _0\int \limits _{0}^{t}\xi ^{-1}(s) {D}^\alpha {\mathbf {e}}(s)(t-s)^{\alpha -1}E_\alpha ,_\alpha \left( -\left( \frac{t-s}{\tau _\mathrm{R}}\right) ^\alpha \right) {\mathrm {d}}s -P(t){\mathbf {C}}^{-1}(t), \end{aligned}$$

(38)

where

$$\begin{aligned} {D}^\alpha {\mathbf {e}}(s)=\frac{1}{\varGamma (1-\alpha )}\int \limits _{0}^{s} \frac{{\mathbf {e}}'(x)}{(s-x)^\alpha } {\mathrm {d}}x. \end{aligned}$$

(39)

The constitutive equation is

$$\begin{aligned} {\varvec{\sigma }}(t)=\tau _\mathrm{R}^{-\alpha }{\mathbf {F}}(t)\left[ \int \limits _{0}^{t}\frac{\partial W}{\partial \mathbf {E}(s)}K(t-s) {\mathrm {d}}s \right] {\mathbf {F}}^\mathrm{T}(t) -2\mu _0{\mathbf {F}}(t)\left[ \int \limits _{0}^{t}\xi ^{-1}(s) {D}^\alpha {\mathbf {e}}(s)K(t-s){\mathrm {d}}s \right] {\mathbf {F}}^\mathrm{T}(t)-P(t)\mathbf {I}, \end{aligned}$$

(40)

where $K(t-s)=(t-s)^{\alpha -1}E_\alpha ,_\alpha (-((t-s)/\tau _\mathrm{R})^\alpha )$.

Equation (40) can also be written in the form

$$\begin{aligned} {\varvec{\sigma }}(t)= & {} 2\tau _\mathrm{R}^{-\alpha }{\mathbf {B}}(t)\left[ \int \limits _{0}^{t}\left( c_{10}+c_{01}I_1({\mathbf {C}})\right) K(t-s) {\mathrm {d}}s \right] -2\tau _\mathrm{R}^{-\alpha }{\mathbf {F}}(t)\left[ \int \limits _{0}^{t}c_{01}{\mathbf {C}}(s) K(t-s) {\mathrm {d}}s \right] {\mathbf {F}}^\mathrm{T}(t)\nonumber \\&-2\mu _0{\mathbf {F}}(t)\left[ \int \limits _{0}^{t}\xi ^{-1}(s) {D}^\alpha {\mathbf {e}}(s)K(t-s){\mathrm {d}}s \right] {\mathbf {F}}^\mathrm{T}(t) -P(t)\mathbf {I} \end{aligned}$$

(41)

in the context of the Mooney–Rivlin model.

To evaluate Eq. (41) in the framework of boundary problems, it is necessary to propose a particular expression for the function $\xi$.

We consider the reduced stress obtained from Eq. (28) with $\lambda _0\ne 1$

$$\begin{aligned} \sigma _\mathrm{R}(t,\lambda _0)=\frac{\sigma (t,\lambda _0)}{\lambda _0^2-\lambda _0^{-1}}=2\bigl (c_{10}+c_{01}\lambda _0^{-1}\bigr )\bigl (1-g(t)\bigr )+\mu _0\xi ^{-1}g(t). \end{aligned}$$

(42)

When the time is near zero, Eq. (42) becomes a function that depends on the shear modulus, i.e., $\mu _0$, and the material parameter $\xi$:

$$\begin{aligned} \sigma _\mathrm{R}(t\rightarrow 0)=\sigma _{R0}\simeq \mu _0\xi ^{-1}; \end{aligned}$$

(43)

thus,

$$\begin{aligned} \frac{\xi }{\mu _0}\simeq \sigma _{R0}^{-1}. \end{aligned}$$

(44)

Using the experimental data of [73], we deduced the graph of the function $\sigma _{R0}^{-1}$, which is shown in Fig. 4 for different imposed values of the stretch ratio $\lambda _0$.

We note that the shear modulus, i.e., $\mu _0$, is constant. Consequently, the material parameter $\xi$ is approximatively a linear function of the stretch ratio.

Fig. 4

Variation in material parameter $\xi$

In three-dimensional space, the material parameter $\xi$ may be approximated by a single function depending on the variable $(I_1({\mathbf {C}})-3)$ as follows:

$$\begin{aligned} \xi ({\mathbf {C}})=A\sqrt{{\mathbf {C}}:\mathbf {I}-3}+\xi _0 \end{aligned}$$

(45)

or

$$\begin{aligned} \xi ({\mathbf {C}})=A\sqrt{I_1({\mathbf {C}})-3}+\xi _0, \end{aligned}$$

(46)

where $\xi _0$ represents the value of $\xi$ at infinitesimal strains and A is a positive constant.

The actual model involves only six material parameters, $(c_{10},c_{01},A,\xi _0,\tau _\mathrm{R},\alpha )$, which are determined using data of the relaxation test loading. It is completely described by the constitutive equation (41).

2.2.1 Identification of material parameters

In the case of relaxation we have

$$\begin{aligned} \xi ({\mathbf {C}})=A\sqrt{\lambda _0^2+2\lambda _0^{-1}-3}+\xi _0, \end{aligned}$$

(47)

and Eq. (41) becomes

$$\begin{aligned} \sigma (t)=\bigl (\lambda _0^2-\lambda _0^{-1}\bigl )\biggl [2(c_{10}+c_{01}\lambda _0^{-1})(1-g(t)) +\mu _0\left( A\sqrt{\lambda _0^2+2\lambda _0^{-1}-3}+\xi _0\right) ^{-1}g(t)\biggr ]. \end{aligned}$$

(48)

We easily obtain from Eq. (48) the second derivative of the nominal stress:

$$\begin{aligned} \frac{{\mathrm {d}}^2\pi (\lambda _0)}{{\mathrm {d}}\lambda _0^2}= & {} -\left( 12c_{10}\lambda _0^{-4}+24c_{01}\lambda _0^{-5}\right) (1-g(t)) \nonumber \\&+\,\mu _0g(t)\left[ (\lambda _0-\lambda _0 ^{-2})\left( \frac{{\mathrm {d}}^2\xi ^{-1}}{{\mathrm {d}}\lambda _0^2}\right) +2(1+2\lambda _0^{-3})\left( \frac{{\mathrm {d}}\xi ^{-1}}{{\mathrm {d}}\lambda _0}\right) -6\lambda _0^{-4}(\xi ^{-1})\right] . \end{aligned}$$

(49)

After some simple algebraic calculations, one deduces a sufficient condition to ensure the concavity of the curve $\pi =\pi (\lambda _0)$:

$$\begin{aligned} \frac{\xi _0}{A}\ge 0.6994. \end{aligned}$$

(50)

We use the previous stochastic Monte Carlo technique to identify the material parameters $(c_{10},c_{01},A,\xi _0,\tau _\mathrm{R},\alpha )$. The nonlinear minimization problem is

$$\begin{aligned} \min \left( \frac{1}{NM}\sum \limits _{i=1}^{N} \sum \limits _{j=1}^{M}\left[ \sigma _\mathrm{mod} (c_{10},c_{01},A,\xi _0,\tau _\mathrm{R},\alpha ,\lambda _0^i,j) -\sigma _\mathrm{exp}(c_{10},c_{01},A,\xi _0,\tau _\mathrm{R}, \alpha ,\lambda _0^i,j)\right] ^2\right) . \end{aligned}$$

The values of $(c_{10},c_{01},A,\xi _0,\tau _\mathrm{R},\alpha )$ thus found are tabulated in Table 2.

Table 2 Material parameters of model of Eq. (48)

The results obtained with the identified parameters in the case of the relaxation test are presented in Fig. 5.

For different values of the stretch ratio, $\lambda _0$, the maximum relative error is less than 2.5 % (Fig. 6). It seems that the results obtained from the identified parameters from our model and the experimental data are in good agreement for all values of the stretch ratio.

The new model is better than the first one because it perfectly fits experimental curves.

Fig. 5

Comparison of constitutive model of Eq. (48) with experimental data for extension relaxation test of [73]

Fig. 6

Relative error versus time for different values of $\lambda _0$ (new model), logarithmic time-scale

2.2.2 Validation of the model using combined tension–torsion tests

In this section, we validate the model by considering an inhomogeneous deformation of tension–torsion loadings.

In cylindrical coordinates, the extension–torsion problem of a solid circular cylinder composed of an incompressible isotropic material is described by

$$\begin{aligned} r=\lambda ^{-{1}/{2}}R, \quad \theta =\varTheta +\psi \lambda Z, \quad z=\lambda Z, \end{aligned}$$

(51)

where $(R,\varTheta ,Z)$ and $(r,\theta ,z)$ are respectively the cylindrical coordinates in the undeformed and in the current configurations, $\lambda$ denotes the axial stretch, and $\psi$ is the angle of twist per unit length.

The deformation gradient tensor ${\mathbf {F}}$ is

$$\begin{aligned} {\mathbf {F}}= \left( \begin{array}{ccc} \frac{1}{\sqrt{\lambda }}\quad &{} 0 &{} \quad 0 \\ 0 &{} \quad \frac{1}{\sqrt{\lambda }} &{} \quad \sqrt{\lambda }\psi R \\ 0 &{} \quad 0 &{} \quad \lambda \end{array} \right) , \end{aligned}$$

(52)

and the components of the tensors ${\mathbf {B}}$, ${\mathbf {C}}$, and ${\mathbf {e}}$ are given by

$$\begin{aligned} {\mathbf {B}}= & {} \left( \begin{array}{ccc} \lambda ^{-1} &{} \quad 0 &{} \quad 0 \\ 0 &{} \quad \lambda ^{-1}+\lambda (\psi R)^2 &{} \quad \lambda ^{3/2}\psi R \\ 0 &{} \quad \lambda ^{3/2}\psi R &{} \quad \lambda ^2 \end{array} \right) , \end{aligned}$$

(53)

$$\begin{aligned} {\mathbf {C}}= & {} \left( \begin{array}{ccc} \lambda ^{-1}&{} \quad 0 &{} \quad 0 \\ 0 &{} \quad \lambda ^{-1} &{}\quad \psi R \\ 0 &{}\quad \psi R &{}\quad \lambda ^2+\lambda (\psi R)^2 \end{array} \right) , \end{aligned}$$

(54)

$$\begin{aligned} {\mathbf {e}}= & {} \frac{1}{2} \left( \begin{array}{ccc} \lambda -1&{} 0 &{} 0 \\ 0 &{}\quad \lambda +(\psi R)^2-1 &{} \quad -\lambda ^{-1}\psi R \\ 0 &{} \quad -\lambda ^{-1}\psi R &{}\quad \lambda ^{-2}-1 \end{array} \right) . \end{aligned}$$

(55)

Equations (51)–(55), together with the constitutive equation of the proposed model, imply that

$$\begin{aligned} {\varvec{\sigma }}= \left( \begin{array}{ccc} \sigma _{rr}&{} 0&{} 0 \\ 0&{}\quad \sigma _{\theta \theta } &{}\quad \sigma _{\theta z} \\ 0 &{} \quad \sigma _{\theta z} &{}\quad \sigma _{zz} \end{array} \right) . \end{aligned}$$

(56)

Yuan and Lianis [74] assumed that the motion was slow in their experiments; thus, it can be considered as quasi-static; that is, the equation of motion (or, here, the equation of equilibrium) becomes

$$\begin{aligned} \mathrm{div}\,{\varvec{\sigma }}=0. \end{aligned}$$

(57)

No external force is applied to the lateral surface of the sample when it is deformed. Thus, on the lateral surface (radius $r=r_0$) we have

$$\begin{aligned} \sigma _{rr}(r=r_0,t)=0. \end{aligned}$$

(58)

The pressure P is independent of $\theta$ and z and is a function of t and r only, i.e., $P=P(r,t)$ (Appendix 4).

To find the Lagrange multiplier, i.e., the pressure P(r, t), in terms of the material parameters, $\lambda (t)$ and $\psi (t)$, we use the constitutive equation of the proposed model, Eqs. (52)–(57), and the boundary condition (see Appendix 4 for more details).

After calculations we obtain

$$\begin{aligned} P(r,t)= & {} 2c_{10}\lambda ^{-1}(t)(1-g(t)) +2c_{01}\tau _\mathrm{R}^{-\alpha }\lambda ^{-1}(t)\left[ \int \limits _{0}^{t}\Bigl (\lambda ^2(s)+\lambda ^{-1}(s)+[r\lambda (s)\psi (s)]^2\Bigr )K(t-s) {\mathrm {d}}s \right] \nonumber \\&-\,2\mu _0\lambda ^{-1}(t)\left[ \int \limits _{0}^{t}\xi ^{-1}(s) {D}^\alpha e_{rr}(s)K(t-s){\mathrm {d}}s \right] +\int \limits _{r}^{r_0}\Biggl \{2c_{10}[\lambda (t)\psi (t)]^2\Bigl (1-g(t)\Bigr )r\nonumber \\&+\,4c_{01}\tau _\mathrm{R}^{-\alpha }[\lambda (t)\psi (t)]^2r\int \limits _{0}^{t}\lambda ^{-1}(s)K(t-s){\mathrm {d}}s -4c_{01}\lambda ^{1/2}(t)\psi (t)\tau _\mathrm{R}^{-\alpha }\int \limits _{0}^{t}\left[ \lambda ^{1/2}(s)\psi (s)r\right] K(t-s){\mathrm {d}}s \Biggr \}{\mathrm {d}}r\nonumber \\&+\,\int \limits _{r}^{r_0}\left\{ 2\mu _0r^{-1}\lambda ^{-1}(t)\left[ \int \limits _{0}^{t}\xi ^{-1}(s) {D}^\alpha e_{rr}(s)K(t-s){\mathrm {d}}s -\int \limits _{0}^{t}\xi ^{-1}(s) {D}^\alpha e_{\theta \theta }(s)K(t-s){\mathrm {d}}s\right] \right. \nonumber \\&-\,4\mu _0\lambda ^{1/2}(t)\psi (t)\left[ \int \limits _{0}^{t}\xi ^{-1}(s) {D}^\alpha e_{\theta z}(s)K(t-s){\mathrm {d}}s\right] \nonumber \\&\left. -\,2\mu _0r[\lambda (t)\psi (t)]^2\left[ \int \limits _{0}^{t}\xi ^{-1}(s) {D}^\alpha e_{zz}(s)K(t-s){\mathrm {d}}s\right] \right\} {\mathrm {d}}r. \end{aligned}$$

(59)

The resultant moment M(t) and axial force N(t) are respectively given by

$$\begin{aligned} M=\int \limits _{0}^{r_0}2\pi r^2\sigma _{\theta z}\;{\mathrm {d}}r \end{aligned}$$

(60)

and

$$\begin{aligned} N=\int \limits _{0}^{r_0}2\pi r\sigma _{zz}\;{\mathrm {d}}r. \end{aligned}$$

(61)

To validate our model, we used the experimental data of [74] obtained from the combined tension and torsion of a cylindrical specimen made of SBR, with the parameters calculated in the previous section for the relaxation test.

For a step in the tension and linear ramp in the torsion, the loading is

$$\begin{aligned} \lambda (s)=1+(\lambda _0-1)H(s), \quad \psi (s)=\dot{\psi }s. \end{aligned}$$

(62)

Substitution of Eq. (62) into Eq. (59) yields

$$\begin{aligned} P(r,t)= & {} \Bigl (1-g(t)\Bigr )\left[ 2c_{10}\lambda _0^{-1}+2c_{01}(\lambda _0+\lambda _0^{-2})\right] -4c_{01}\lambda _0(r\dot{\psi }t)^2\left[ G_2(t)-\frac{1}{\varGamma (3)}\right] \nonumber \\&-\,\mu _0\left[ \frac{1-\lambda _0^{-1}}{\varGamma (1-\alpha )}\int \limits _{0}^{t}\xi ^{-1}(s)s^{-\alpha }K(t-s){\mathrm {d}}s\right] \nonumber \\&+\,\frac{1}{2}(r_0^2-r^2)(\dot{\psi }t)^2\left[ (2c_{10}\lambda _0^2+4c_{01}\lambda _0)(1-g(t))+4c_{01}\lambda _0(G_1(t)-1)\right] \nonumber \\&+\,2\mu _0\int \limits _{r}^{r_0}\left\{ \left[ \frac{-u\dot{\psi }^2}{\varGamma (3-\alpha )}\int \limits _{0}^{t}\xi ^{-1}(s,u)s^{2-\alpha }K(t-s){\mathrm {d}}s\right] +\left[ \frac{u\dot{\psi }^2t}{\varGamma (2-\alpha )}\int \limits _{0}^{t}\xi ^{-1}(s,u)s^{1-\alpha }K(t-s){\mathrm {d}}s\right] \right. \nonumber \\&+\,\left. \left[ \frac{u(\lambda _0^2-1)(\dot{\psi }t)^2}{2\varGamma (1-\alpha )}\int \limits _{0}^{t}\xi ^{-1}(s,u)s^{-\alpha }K(t-s){\mathrm {d}}s\right] \right\} {\mathrm {d}}u, \end{aligned}$$

(63)

where $G_1(t)=E_\alpha ,_2(-(t/\tau _\mathrm{R})^\alpha )$ and $G_2(t)=E_\alpha ,_3(-(t/\tau _\mathrm{R})^\alpha )$.

Substitution of Eq. (62) into the equation of $\sigma _{\theta z}$ yields

$$\begin{aligned} \sigma _{\theta z}(R,t)= & {} \lambda _0^{3/2}(\dot{\psi }t) R\left[ (2c_{10}+4c_{01}\lambda _0^{-1})(1-g(t))+2c_{01}\lambda _0^{-1}(G_1(t)-1)\right] \nonumber \\&-\,2\mu _0\left[ \frac{-\lambda _0^{-1/2}R\dot{\psi }}{2\varGamma (2-\alpha )}\int \limits _{0}^{t}\xi ^{-1}(s)s^{1-\alpha }K(t-s){\mathrm {d}}s +\frac{\lambda _0^{3/2}(\lambda _0^{-2}-1)R\dot{\psi }t}{2\varGamma (1-\alpha )}\int \limits _{0}^{t}\xi ^{-1}(s)s^{-\alpha }K(t-s){\mathrm {d}}s\right] ,\nonumber \\ \end{aligned}$$

(64)

and the resultant applied moment is obtained from Eq. (60); after calculations we obtain

$$\begin{aligned} M(t)= & {} \frac{\pi }{2}(\dot{\psi }t)R_0^4\left[ (2c_{10}+4c_{01}\lambda _0^{-1})[1-g(t)]+2c_{01}\lambda _0^{-1}(G_1(t)-1)\right] \nonumber \\&+2\pi \mu _0\dot{\psi }\left[ \frac{\lambda _0^{-2}}{\varGamma (2-\alpha )}\int \limits _{0}^{R_0}\int \limits _{0}^{t}R^3\xi ^{-1}(s,R)s^{1-\alpha }K(t-s){\mathrm {d}}s {\mathrm {d}}R \right. \nonumber \\&\qquad \qquad \qquad \left. - t\frac{\lambda _0^{-2}-1}{\varGamma (1-\alpha )}\int \limits _{0}^{R_0}\int \limits _{0}^{t}R^3\xi ^{-1}(s,R)s^{-\alpha }K(t-s){\mathrm {d}}s {\mathrm {d}}R \right] , \end{aligned}$$

(65)

where $R_0=r_0\sqrt{\lambda _0}$.

We substitute Eq. (62) into the equation of $\sigma _{zz}$, and using Eq. (63) we obtain

$$\begin{aligned} \sigma _{zz}(R,t)= & {} -\frac{1}{2}(R^2_0-R^2)(\dot{\psi }t)^2\left[ (2c_{10}\lambda _0+4c_{01})(1-g(t)) +4c_{01}(G_1(t)-1)\right] \nonumber \\&-\,2\mu _0\int \limits _{R}^{R_0}\left\{ \left[ \frac{-u\lambda _0^{-1}\dot{\psi }^2}{\varGamma (3-\alpha )}\int \limits _{0}^{t}\xi ^{-1}(s,u)s^{2-\alpha }K(t-s){\mathrm {d}}s\right] \right. \nonumber \\&\left. +\left[ \frac{u\lambda _0^{-1}\dot{\psi }^2t}{\varGamma (2-\alpha )}\int \limits _{0}^{t}\xi ^{-1}(s,u)s^{1-\alpha }K(t-s){\mathrm {d}}s\right] -\left[ \frac{u(\lambda _0^{-1}-\lambda _0)(\dot{\psi }t)^2}{2\varGamma (1-\alpha )}\int \limits _{0}^{t}\xi ^{-1}(s,u)s^{-\alpha }K(t-s){\mathrm {d}}s\right] \right\} {\mathrm {d}}u \nonumber \\&+\,(\lambda _0^2-\lambda _0^{-1})\left[ (2c_{10}+2c_{01}\lambda _0^{-1})(1-g(t))\right] +4c_{01}(R\dot{\psi }t)^2\left[ G_2(t)-\frac{1}{\varGamma (3)}\right] \nonumber \\&+\,\mu _0\left[ \frac{\lambda _0^{2}-\lambda _0^{-1}}{\varGamma (1-\alpha )}\int \limits _{0}^{t}\xi ^{-1}(s)s^{-\alpha }K(t-s){\mathrm {d}}s\right] . \end{aligned}$$

(66)

The tensile force is given by

$$\begin{aligned} N(t)= & {} \pi R_0^2\Biggl ((\lambda _0-\lambda _0^{-2})\left[ (2c_{10}+2c_{01}\lambda _0^{-1})(1-g(t))\right] +\frac{1}{4}(R_0\dot{\psi }t)^2 \nonumber \\&\times \left[ -2\Bigl (c_{10}+2c_{01}\lambda _0^{-1}\Bigr )(1-g(t))+8c_{01}\lambda _0^{-1}\Bigl (G_2(t)-\frac{1}{\varGamma (3)}\Bigr )-4c_{01}\lambda _0^{-1}\Bigl (G_1(t)-1\Bigr )\right] \Biggr )\nonumber \\&-\,4\pi \mu _0\lambda _0^{-2}\Biggl (\int \limits _{0}^{t}\biggl (\int \limits _{0}^{R_0}R\int \limits _{R}^{R_0}u\xi ^{-1}(s,u){\mathrm {d}}u\;{\mathrm {d}}R\biggr )\Biggr \{\frac{-(\dot{\psi })^2}{\varGamma (3-\alpha )}s^{2-\alpha }K(t-s)\nonumber \\&+\,\frac{(\dot{\psi })^2t}{\varGamma (2-\alpha )}s^{1-\alpha }K(t-s) -\frac{(\dot{\psi }t)^2(1-\lambda _0^2)}{2\varGamma (1-\alpha )}s^{-\alpha }K(t-s)\Biggr \}{\mathrm {d}}s\Biggr )\nonumber \\&+\,2\pi \mu _0\frac{\lambda _0-\lambda _0^{-2}}{\varGamma (1-\alpha )}\Biggl [\int \limits _{0}^{R_0}\int \limits _{0}^{t}R\xi ^{-1}(s,R)s^{-\alpha }K(t-s){\mathrm {d}}s\;{\mathrm {d}}R\Biggr ]. \end{aligned}$$

(67)

Lianis [6] simplified the FLV theory of Coleman and Noll [4] using thermodynamic arguments. He proposed a constitutive equation containing only four relaxation functions and three steady-state functions. This simplified theory was successfully applied to predict the behaviors of elastomeric materials in the framework of uniaxial tension and combined tension–torsion [73–75]. In this paper, a special theory of finite viscoelasticity is motivated on the basis of rheological models. So the question arises: Is there a relationship between the theory of FLV and the proposed model? To provide a partial answer, we compare the predictions of our model, those of Lianis theory [6, 7, 74], and experimental data [74] in the context of the combined tension–torsion loadings. Figures 7, 8, 9, and 10 show that the proposed model adequately describes the experimental data. One can see that the predictions of the present model and those of Lianis’ theory are the same. We note, however, that our model has only six material parameters that are derived from a differential form.

Fig. 7

Comparison between predictions of the proposed model, those of Lianis’ theory, and the experimental data of [74] for tension–torsion loadings ($\lambda _0=1.28$, $\dot{\psi }=1.062992$ rad/m-s)

Fig. 8

Comparison between predictions of the proposed model, those of Lianis’ theory, and the experimental data of [74] for tension–torsion loadings ($\lambda _0=1.355, \dot{\psi }=0.600787$ rad/m-s)

Fig. 9

Comparison between predictions of the proposed model, those of Lianis’ theory, and the experimental data of [74] for tension–torsion loadings ($\lambda _0=1.352, \dot{\psi }=0.293307$ rad/m-s)

Fig. 10

Comparison between predictions of the proposed model, those of Lianis’ theory, and the experimental data of [74] for tension–torsion loadings ($\lambda _0=1.459, \dot{\psi }=0.184252$ rad/m-s)

3 Conclusion

In this article, we applied the concept of dual stress and strain and their derivatives to extend the fractional constitutive equation of SLS, i.e., the Zener model, to finite strains. In fact, we used the dual tensors of family 1 [64] by limiting it especially to two couples of stress and strain tensors that are physically significant in the context of finite elasticity. We assumed that the elastomeric solids were isotropic and incompressible. Thus, two models, M1 and M2, were deduced. We showed that M1 was not appropriate for predicting the behavior of elastomers in the context of relaxation loading. Model M2 seems qualitatively to reproduce the nonlinear relaxation behavior of elastomers. Thus, its material parameters were identified using the experimental data of relaxation loadings published in the literature. The agreement between theoretical and experimental results seems to be qualitatively good. To improve quantitatively the predictions of this model, we assumed that the parameter $\xi$ depended on the strain. Then the new material parameters were determined by considering the previous experimental data of relaxation tests. To validate the model, we considered the experimental data of combined tension–torsion loadings found in the literature. For computation, we used earlier numerical values of the new model’s material parameters. This model seems capable of reproducing the behavior of elastomers in the framework of multiaxial loadings.

To our knowledge, the existing visco-hyperelastic models found in the literature are of integral and differential types. The integral models describe the history of medium deformation using integral equations. However, these equations are difficult to generalize for complex problems. For instance, attempts to take into account the accumulation of damage and thixotropic elastomeric materials in terms of integral models add to the complexity of these models and hamper their practical application. The differential models describe the rheological properties of materials in terms of internal variable tensors and, as a rule, assign them the physical meaning of stresses or strains. These models can conveniently be represented with the aid of symbolic diagrams illustrating the mechanical behavior of the medium. Usually, the number of material parameters of these models is quite large, and their identification probably requires complex methods of optimization.

The main advantage of the new model is its differential form with relatively few parameters and may be suitable for implementation in finite-element analysis.

For future work, we envisage studying the stress response of small oscillatory loads superimposed on large static deformations. Thus, we will develop the new model to predict the complex moduli of elastomers. In many applications, these moduli are important in the framework of the design of rubber parts.

Appendices

Appendix 1: Resolution of fractional differential equation

The analytical solution of linear fractional differential equations (FDEs) with constant coefficients can be obtained using the Laplace transform technique.

In the case of relaxation, the Laplace transform formula for the Caputo fractional derivatives involves the value of the function f(t) at the lower terminal $t=0$:

$$\begin{aligned} \mathcal {L}[{D}^{\alpha }f(t)]=p^{\alpha }\mathcal {L}[f(t)]-f(0)p^{\alpha -1}. \end{aligned}$$

(68)

Let us consider the following FDE:

$$\begin{aligned} {\mathbf {S}}(t)+\tau _\mathrm{R}^\alpha {D}^\alpha {\mathbf {S}}(t)=\frac{\partial {W}}{\partial {\mathbf {E}(t)}}-2\mu _0\tau _\mathrm{R}^\alpha \xi ^{-1}(t) {D}^\alpha {\mathbf {e}}(t), \end{aligned}$$

(69)

with the initial condition ${\mathbf {S}}(0)=0$.

Applying the Laplace transform to both sides of this equation, and using the linearity of the Laplace transform, we obtain the following result:

$$\begin{aligned} \mathcal {L}\left[ {\mathbf {S}}(t)\right] +\tau _\mathrm{R}^\alpha \mathcal {L}\left[ {D}^\alpha {{\mathbf {S}}}(t)\right] = \mathcal {L}\left[ \frac{\partial {W}}{\partial {\mathbf {E}(t)}}\right] -2\mu _0\tau _\mathrm{R}^\alpha \mathcal {L}\left[ \xi ^{-1}(t){D}^\alpha {{\mathbf {e}}}(t)\right] . \end{aligned}$$

(70)

Then

$$\begin{aligned} {\hat{\mathbf {S}}}(p) + \tau _\mathrm{R}^\alpha p^\alpha \hat{\mathbf {S}}(p)={\hat{\mathbf {F}}}_1(p)-2\mu _0\tau _\mathrm{R}^ \alpha {\hat{\mathbf {F}}}_2(p), \end{aligned}$$

(71)

where ${\hat{\mathbf {F}}}_1(p)$ and ${\hat{\mathbf {F}}}_2(p)$ denote the Laplace transforms of $\partial {W}/\partial {\mathbf {E}(t)}$ and $\xi ^{-1}(t){D}^\alpha {{\mathbf {e}}}(t)$.

The equation’s solution is

$$\begin{aligned} {\hat{\mathbf {S}}}(p) =\left( \frac{\tau _\mathrm{R}^{-\alpha }}{p^\alpha +\tau _\mathrm{R}^{-\alpha }}\right) {\hat{\mathbf {F}}}_1(p)-2\mu _0\left( \frac{1}{p^\alpha +\tau _\mathrm{R}^{-\alpha }}\right) {\hat{\mathbf {F}}}_2(p). \end{aligned}$$

(72)

The solution in the time–space domain is obtained using the inverse Laplace transform, and we obtain

$$\begin{aligned} {\mathbf {S}}(t)= & {} \tau _\mathrm{R}^{-\alpha }\int \limits _{0}^{t}\frac{\partial W}{\partial \mathbf {E}(s)}(t-s)^{\alpha -1}E_\alpha ,_\alpha \Bigl (-\Bigl (\frac{t-s}{\tau _\mathrm{R}}\Bigr )^\alpha \Bigr ) {\mathrm {d}}s\nonumber \\&-2\mu _0\int \limits _{0}^{t}\xi ^{-1}(s){D}^\alpha {\mathbf {e}}(s)(t-s)^{\alpha -1}E_\alpha ,_\alpha \Bigl (-\Bigl (\frac{t-s}{\tau _\mathrm{R}}\Bigr )^\alpha \Bigr ) {\mathrm {d}}s. \end{aligned}$$

(73)

Application of the Laplace transform to the FDE, in the case of $\xi$ equal to a constant, gives

$$\begin{aligned} {\hat{\mathbf {S}}}(p) =\Bigl (\frac{\tau _\mathrm{R}^{-\alpha }}{p^\alpha +\tau _\mathrm{R}^{-\alpha }}\Bigr ){\hat{\mathbf {F}}}_1(p)-2\mu _0\xi ^{-1}\Bigl (\frac{p^\alpha }{p^\alpha +\tau _\mathrm{R}^{-\alpha }}\Bigr )\hat{ {\mathbf {e}}}(p). \end{aligned}$$

(74)

We have

$$\begin{aligned} \mathcal {L}^{-1}\left[ \left( \frac{p^\alpha }{p^\alpha +\tau _\mathrm{R}^{-\alpha }}\right) {\hat{\mathbf {e}}}(p)\right] =\mathcal {L}^{-1}\left[ \left( \frac{p^{\alpha -1}}{p^\alpha +\tau _\mathrm{R}^{-\alpha }}\right) \Bigr (p {\hat{\mathbf {e}}}(p)\Bigr )\right] . \end{aligned}$$

(75)

We obtain the solution as follows:

$$\begin{aligned} {\mathbf {S}}(t)=\tau _\mathrm{R}^{-\alpha }\int \limits _{0}^{t}\frac{\partial W}{\partial \mathbf {E}(s)}(t-s)^{\alpha -1}E_\alpha ,_\alpha \left( -\Bigl (\frac{t-s}{\tau _\mathrm{R}}\right) ^\alpha \Bigr ) {\mathrm {d}}s -2\mu _0\xi ^{-1}\int \limits _{0}^{t}{\dot{\mathbf {e}}}(s)E_\alpha ,_1\left( -\Bigl (\frac{t-s}{\tau _\mathrm{R}}\right) ^\alpha \Bigr ) {\mathrm {d}}s. \end{aligned}$$

(76)

Appendix 2: Mittag–Leffler function

The function $E_\alpha$, with $\alpha >0$ defined by $E_\alpha (z)=\sum _{k=0}^{\infty }z^k/\varGamma (\alpha k+1)$, is called the Mittag–Leffler function of order $\alpha$. This function provides a simple generalization of the exponential function, i.e., $E_1(z)=\mathrm {exp}(z)$.

When $0<\alpha \le 1$, the Mittag–Leffler function on the negative axis is completely monotone and is capable of representing phenomena of relaxation. The graph of the function $E_\alpha (-x^\alpha )$, with $x=(t/\tau _\mathrm{R})\ge 0$, is illustrated in Fig. 11 for different values of $\alpha$.

Fig. 11

Mittag–Leffler function for different values of $\alpha$

Appendix 3: Lianis material functions for SBR circular bar at $0\,^{\circ }$C [73]

The Lianis constitutive equation for an isotropic incompressible viscoelastic material is given by

$$\begin{aligned} {\varvec{\sigma }}(t)= & {} \left[ a+\Bigl (I_1({\mathbf {B}})-3\Bigl )b+cI_1({\mathbf {B}})\right] {\mathbf {B}}-c{\mathbf {B}}^2+2\int \limits _{-\infty }^{t}\varphi _0(t-\tau ){\dot{\mathbf {C}}}_t(\tau ){\mathrm {d}}\tau \nonumber \\&+\int \limits _{-\infty }^{t}\varphi _1(t-\tau )[{\mathbf {B}}{\dot{\mathbf {C}}}_t(\tau )+{\dot{\mathbf {C}}}_t(\tau ){\mathbf {B}}]{\mathrm {d}}\tau + \int \limits _{-\infty }^{t}\varphi _2(t-\tau ) [{\mathbf {B}}^2{\dot{\mathbf {C}}}_t(\tau )+ {\dot{\mathbf {C}}}_t(\tau ){\mathbf {B}}^2]{\mathrm {d}}\tau \nonumber \\&+{\mathbf {B}}\int \limits _{-\infty }^{t}\varphi _3(t-\tau ) I_1({\mathbf {B}}{\dot{\mathbf {C}}}_t(\tau )){\mathrm {d}}\tau - P(t)\mathbf {I}, \end{aligned}$$

(77)

where a, b, c are constants corresponding to the equilibrium stress, and the $\varphi _k(u)$ are relaxation functions that approach zero as $u\rightarrow \infty$.

For a SBR at $0\,^{\circ }$C, the constants a, b, c were found to be $a=29.5$ psi, $b=0$, $c=51.07$ psi, where 1 psi = $6.8948 \times 10^3$ Pa, and the Lianis material functions were related by

$$\begin{aligned} \varphi _1(t)=\varphi _3(t)=-2\varphi _2(t). \end{aligned}$$

(78)

The relaxation functions $\varphi _k(t)$ are tabulated in Table 3.

Table 3 Lianis material functions for SBR at $0\,^{\circ }$C

Appendix 4: Tension–torsion of a circular cylinder

In cylindrical coordinates and for the extension–torsion of a solid circular cylinder made of an incompressible isotropic material, we have

$$\begin{aligned} {\mathbf {F}}= & {} \left( \begin{array}{c@{\quad }c@{\quad }c} \frac{1}{\sqrt{\lambda }} &{} 0 &{} 0 \\ 0 &{} \frac{1}{\sqrt{\lambda }} &{} \sqrt{\lambda }\psi R \\ 0 &{} 0 &{} \lambda \end{array} \right) , \end{aligned}$$

(79)

$$\begin{aligned} {\mathbf {B}}= & {} \left( \begin{array}{c@{\quad }c@{\quad }c} \lambda ^{-1} &{} 0 &{} 0 \\ 0 &{} \lambda ^{-1}+\lambda (\psi R)^2 &{} \lambda ^{3/2}\psi R \\ 0 &{} \lambda ^{3/2}\psi R &{} \lambda ^2 \end{array}\right) , \end{aligned}$$

(80)

$$\begin{aligned} {\mathbf {C}}= & {} \left( \begin{array}{c@{\quad }c@{\quad }c} \lambda ^{-1}&{} 0 &{} 0 \\ 0 &{} \lambda ^{-1} &{} \psi R \\ 0 &{} \psi R &{} \lambda ^2+\lambda (\psi R)^2 \end{array}\right) , \end{aligned}$$

(81)

$$\begin{aligned} {\mathbf {e}}= & {} \frac{1}{2} \left( \begin{array}{c@{\quad }c@{\quad }c} \lambda -1&{} 0 &{} 0 \\ 0 &{} \lambda +(\psi R)^2-1 &{} -\lambda ^{-1}\psi R \\ 0 &{} -\lambda ^{-1}\psi R &{} \lambda ^{-2}-1 \end{array}\right) . \end{aligned}$$

(82)

The equation of equilibrium is given by

$$\begin{aligned} \mathrm{div}\,{\varvec{\sigma }}=0. \end{aligned}$$

(83)

Equations (79)–(82), together with the constitutive equation of the proposed model, imply that

$$\begin{aligned} {\varvec{\sigma }}= \left( \begin{array}{c@{\quad }c@{\quad }c} \sigma _{rr} &{} 0 &{} 0 \\ 0 &{} \sigma _{\theta \theta } &{} \sigma _{\theta z} \\ 0 &{} \sigma _{\theta z} &{} \sigma _{zz} \end{array}\right) , \end{aligned}$$

(84)

where the nonzero components of the Cauchy stress tensor are given by

$$\begin{aligned} \sigma _{rr}(t)= & {} 2\tau _\mathrm{R}^{-\alpha }B_{rr}(t)\left[ \int \limits _{0}^{t}\left( c_{10}+c_{01}I_1({\mathbf {C}})\right) K(t-s) {\mathrm {d}}s \right] -2\tau _\mathrm{R}^{-\alpha }c_{01}F_{rr}^2(t)\left[ \int \limits _{0}^{t}C_{rr}(s) K(t-s) {\mathrm {d}}s \right] \nonumber \\&-2\mu _0F_{rr}^2(t)\left[ \int \limits _{0}^{t}\xi ^{-1}(s) {D}^\alpha e_{rr}(s) K(t-s) {\mathrm {d}}s \right] -P(t), \end{aligned}$$

(85)

$$\begin{aligned} \sigma _{\theta \theta }(t)= & {} 2\tau _\mathrm{R}^{-\alpha }\left\{ B_{\theta \theta }(t)\left[ \int \limits _{0}^{t}\left( c_{10}+c_{01}I_1({\mathbf {C}})\right) K(t-s) {\mathrm {d}}s \right] -2\tau _\mathrm{R}^{-\alpha }c_{01}\left\{ F_{\theta \theta }^2(t) \left[ \int \limits _{0}^{t}C_{\theta \theta }(s) K(t-s) {\mathrm {d}}s \right] \right. \right. \nonumber \\&\left. +2F_{\theta \theta }(t)F_{\theta z}(t)\left[ \int \limits _{0}^{t}C_{\theta z}(s) K(t-s) {\mathrm {d}}s \right] +F_{\theta z}^2(t)\left[ \int \limits _{0}^{t}C_{zz}(s) K(t-s) {\mathrm {d}}s \right] \right\} \nonumber \\&-2\mu _0\left\{ F_{\theta \theta }^2(t)\left[ \int \limits _{0}^{t} \xi ^{-1}(s) {D}^\alpha e_{\theta \theta }(s)K(t-s){\mathrm {d}}s \right] +2F_{\theta \theta }(t)F_{\theta z}(t)\left[ \int \limits _{0}^{t} \xi ^{-1}(s) {D}^\alpha e_{\theta z}(s) K(t-s) {\mathrm {d}}s \right] \right. \nonumber \\&\left. +F_{\theta z}^2(t)\left[ \int \limits _{0}^{t}\xi ^{-1}(s) {D}^\alpha e_{zz}(s) K(t-s) {\mathrm {d}}s \right] \right\} -P(t), \end{aligned}$$

(86)

$$\begin{aligned} \sigma _{zz}(t)= & {} 2\tau _\mathrm{R}^{-\alpha }B_{zz}(t)\left[ \int \limits _{0}^{t} \Bigl (c_{10}+c_{01}I_1({\mathbf {C}})\Bigr )K(t-s) {\mathrm {d}}s \right] -2\tau _\mathrm{R}^{-\alpha }c_{01}F_{zz}^2(t)\left[ \int \limits _{0}^{t} C_{zz}(s) K(t-s) {\mathrm {d}}s \right] \nonumber \\&-2\mu _0F_{zz}^2(t)\left[ \int \limits _{0}^{t}\xi ^{-1}(s) {D}^\alpha e_{zz}(s) K(t-s) {\mathrm {d}}s \right] -P(t), \end{aligned}$$

(87)

$$\begin{aligned} \sigma _{\theta z}(t)= & {} 2\tau _\mathrm{R}^{-\alpha }B_{\theta z}(t) \left[ \int \limits _{0}^{t}\Bigl (c_{10}+c_{01}I_1({\mathbf {C}})\Bigr ) K(t-s) {\mathrm {d}}s \right] -2\tau _\mathrm{R}^{-\alpha }c_{01}\left\{ F_{\theta \theta }(t)F_{zz}(t) \left[ \int \limits _{0}^{t}C_{\theta z}(s) K(t-s) {\mathrm {d}}s \right] \right. \nonumber \\&\left. +F_{\theta z}(t)F_{zz}(t)\left[ \int \limits _{0}^{t}C_{zz}(s) K(t-s) {\mathrm {d}}s \right] \right\} -2\mu _0\left\{ F_{\theta \theta }(t)F_{zz}(t)\left[ \int \limits _{0}^{t} \xi ^{-1}(s) {D}^\alpha e_{\theta z}(s) K(t-s) {\mathrm {d}}s \right] \right. \nonumber \\&\left. +F_{\theta z}(t)F_{zz}(t)\left[ \int \limits _{0}^{t}\xi ^{-1}(s) { D}^\alpha e_{zz}(s) K(t-s) {\mathrm {d}}s \right] \right\} , \end{aligned}$$

(88)

where $I_1({\mathbf {C}})=\lambda ^2+2\lambda ^{-1}+\lambda (\psi R)^2$.

Substituting (84) into (83), one obtains

$$\begin{aligned}&\frac{\partial \sigma _{rr}}{\partial r}+\frac{\partial \sigma _{rz}}{\partial z}+\frac{\partial \sigma _{\theta r}}{r\partial \theta }+\frac{\sigma _{rr}-\sigma _{\theta \theta }}{r}= \frac{\partial \sigma _{rr}}{\partial r}+\frac{\sigma _{rr}-\sigma _{\theta \theta }}{r}=0, \end{aligned}$$

(89)

$$\begin{aligned}&\frac{\partial \sigma _{r\theta }}{\partial r}+\frac{\partial \sigma _{z\theta }}{\partial z}+\frac{\partial \sigma _{\theta \theta }}{r\partial \theta }+2\frac{\sigma _{r\theta }}{r}= \frac{\partial P}{\partial \theta }=0, \end{aligned}$$

(90)

$$\begin{aligned}&\frac{\partial \sigma _{rz}}{\partial r}+\frac{\partial \sigma _{z\theta }}{r\partial \theta }+\frac{\partial \sigma _{zz}}{\partial z}+\frac{\sigma _{rz}}{r}=\frac{\partial P}{\partial z}=0. \end{aligned}$$

(91)

We see that Eq. (90) implies that ${\partial } P/{\partial } \theta =0$ and Eq. (91) implies that $\partial P/\partial z=0$. This means that P is independent of $\theta$ and z and is a function of t and r only. Then (89) becomes

$$\begin{aligned} \frac{\partial \sigma _{rr}}{\partial r}+\frac{1}{r}(\sigma _{rr}- \sigma _{\theta \theta })=0. \end{aligned}$$

(92)

The integration of (92) leads to

$$\begin{aligned} \int \limits _{r}^{r_0}{\mathrm {d}}\sigma _{rr}=\sigma _{rr}(r_0,t)- \sigma _{rr}(r,t)=-\int \limits _{r}^{r_0}\frac{1}{r}(\sigma _{rr}- \sigma _{\theta \theta }){\mathrm {d}}r. \end{aligned}$$

(93)

We have

$$\begin{aligned} \sigma _{rr}(r=r_0,t)=0. \end{aligned}$$

(94)

One can deduce from Eq. (93) that

$$\begin{aligned} \sigma _{rr}(r,t)=\int \limits _{r}^{r_0}\frac{1}{r}(\sigma _{rr}- \sigma _{\theta \theta }){\mathrm {d}}r. \end{aligned}$$

(95)

According to Eqs. (85) and (86), one can write the following relations:

$$\begin{aligned} \sigma _{rr}(r,t)= & {} T_1(r,t)-P(r,t), \end{aligned}$$

(96)

$$\begin{aligned} \sigma _{\theta \theta }(r,t)= & {} T_2(r,t)-P(r,t), \end{aligned}$$

(97)

where

$$\begin{aligned} T_1(r,t)= & {} 2\tau _\mathrm{R}^{-\alpha }B_{rr}(t)\left[ \int \limits _{0}^{t} \Bigl (c_{10}+c_{01}I_1({\mathbf {C}})\Bigr )K(t-s) {\mathrm {d}}s\right] -2\tau _\mathrm{R}^{-\alpha }c_{01}F_{rr}^2(t)\left[ \int \limits _{0}^{t}C_{rr} (s) K(t-s) {\mathrm {d}}s \right] \nonumber \\&-2\mu _0F_{rr}^2(t)\left[ \int \limits _{0}^{t}\xi ^{-1}(s) {D}^\alpha e_{rr}(s) K(t-s) {\mathrm {d}}s \right] , \end{aligned}$$

(98)

$$\begin{aligned} T_2(r,t)= & {} 2\tau _\mathrm{R}^{-\alpha }B_{\theta \theta }(t)\left[ \int \limits _{0}^{t}\Bigl (c_{10}+ c_{01}I_1({\mathbf {C}})\Bigr )K(t-s) {\mathrm {d}}s\right] -2\tau _\mathrm{R}^{-\alpha }c_{01}\left\{ F_{\theta \theta }^2(t) \left[ \int \limits _{0}^{t}C_{\theta \theta }(s) K(t-s) {\mathrm {d}}s \right] \right. \nonumber \\&\left. +2F_{\theta \theta }(t)F_{\theta z}(t)\left[ \int \limits _{0}^{t}C_{\theta z}(s) K(t-s) {\mathrm {d}}s \right] +F_{\theta z}^2(t)\left[ \int \limits _{0}^{t}C_{zz}(s) K(t-s) { \mathrm {d}}s \right] \right\} \nonumber \\&-2\mu _0\left\{ F_{\theta \theta }^2(t)\left[ \int \limits _{0}^{t} \xi ^{-1}(s) {D}^\alpha e_{\theta \theta }(s)K(t-s){\mathrm {d}}s \right] +2F_{\theta \theta }(t)F_{\theta z}(t)\left[ \int \limits _{0}^{t}\xi ^{-1}(s) {D}^ \alpha e_{\theta z}(s)K(t-s){\mathrm {d}}s \right] \right. \nonumber \\&\left. +F_{\theta z}^2(t)\left[ \int \limits _{0}^{t}\xi ^{-1}(s) {D}^\alpha e_{zz}(s) K(t-s) {\mathrm {d}}s \right] \right\} . \end{aligned}$$

(99)

Thus, Eq. (95) gives

$$\begin{aligned} \sigma _{rr}(r,t)=\int \limits _{r}^{r_0}\frac{1}{r}(T_1-T_2){\mathrm {d}}r. \end{aligned}$$

(100)

Substituting Eqs. (100) into (96), we can easily find the Lagrange multiplier, i.e., the pressure P(r, t), in terms of the material parameters $\lambda (t)$ and $\psi (t)$:

$$\begin{aligned} P(r,t)=T_1(r,t)-\int \limits _{r}^{r_0}\frac{1}{r} [T_1(r,t)-T_2(r,t)]{\mathrm {d}}r. \end{aligned}$$

(101)

After calculations we obtain

$$\begin{aligned} P(r,t)= & {} 2c_{10}\lambda ^{-1}(t)(1-g(t)) +2c_{01}\tau _\mathrm{R}^{-\alpha }\lambda ^{-1}(t)\left[ \int \limits _{0}^{t}\Bigl (\lambda ^2(s)+\lambda ^{-1}(s)+[r\lambda (s)\psi (s)]^2\Bigr )K(t-s){\mathrm {d}}s \right] \nonumber \\&-\,2\mu _0\lambda ^{-1}(t)\left[ \int \limits _{0}^{t}\xi ^{-1}(s) {D}^\alpha e_{rr}(s)K(t-s){\mathrm {d}}s \right] +\int \limits _{r}^{r_0}\Biggl \{2c_{10}[\lambda (t)\psi (t)]^2 \Bigl (1-g(t)\Bigr )r\nonumber \\&+\,4c_{01}\tau _\mathrm{R}^{-\alpha }[\lambda (t)\psi (t)]^2r\int \limits _{0}^{t} \lambda ^{-1}(s)K(t-s){\mathrm {d}}s -4c_{01}\lambda ^{1/2}(t)\psi (t)\tau _\mathrm{R}^{-\alpha }\int \limits _{0}^{t}[\lambda ^{1/2}(s)\psi (s)r]K(t-s){\mathrm {d}}s \Biggr \}{\mathrm {d}}r\nonumber \\&+\,\int \limits _{r}^{r_0}\left\{ 2\mu _0r^{-1}\lambda ^{-1}(t) \left[ \int \limits _{0}^{t}\xi ^{-1}(s) {D}^\alpha e_{rr}(s)K(t-s){\mathrm {d}}s -\int \limits _{0}^{t}\xi ^{-1}(s) {D}^\alpha e_{\theta \theta }(s)K(t-s){\mathrm {d}}s\right] \right. \nonumber \\&-\,4\mu _0\lambda ^{1/2}(t)\psi (t)\left[ \int \limits _{0}^{t}\xi ^{-1}(s) {D}^\alpha e_{\theta z}(s)K(t-s){\mathrm {d}}s\right] \nonumber \\&\left. -\,2\mu _0r[\lambda (t)\psi (t)]^2\left[ \int \limits _{0}^{t}\xi ^{-1}(s) {D}^ \alpha e_{zz}(s) K(t-s) {\mathrm {d}}s\right] \right\} {\mathrm {d}}r. \end{aligned}$$

(102)