Rayleigh-Type Waves in Nonlocal Micropolar Thermoelastic Half-Space Containing Void Pores

Abstract

Propagation of Rayleigh-type waves is investigated in a half-space composed of nonlocal micropolar thermoelastic material containing void pores. Dispersion relation is derived for a mechanically stress-free and thermally insulated boundary surface of the half-space. The particle motion during the propagation of the waves is found to follow elliptical path. Numerical computations for a specific material are performed to analyze the characteristics of propagating Rayleigh-type waves in detail. Comparison between the phase speed and corresponding attenuation coefficient in some particular cases is also carried out. The effect of various parameters on the characteristics of waves in question is also studied.

1 Introduction

Eringen [1] was the first who developed the theory of micropolar elasticity and presented governing equations for a uniform micropolar elastic material. Micropolar theory of elasticity is a generalization of classical theory of elasticity and a special class of the theory of micromorphic solids. In classical theory of elasticity, the particles of elastic body undergo translation during the deformation and the interaction between two adjacent portions of the body is governed by a force stress only. In micropolar theory of elasticity, the particles of the body are allowed to undergo rotation about their center of mass, in addition to the translation. And the interaction between two adjacent portions of the micropolar body is governed not only by a force stress, but also by a couple stress. The micropolar theory of elasticity is found to be adequate for the bodies having granular sized particles, that is, the bodies whose particles are dumb-bell shaped. The microstructure of such bodies is found to affect the propagation of elastic waves particularly in the vibrational problems of high frequency and/or small wavelength. The development of micropolar theory of elasticity is of great importance in the field of continuum mechanics. Parfitt and Eringen [2] studied the possibility of plane wave propagation in micropolar elastic medium and found that there exist four basic waves propagating with distinct speeds comprising of a longitudinal displacement wave, an independent longitudinal micro-rotational wave and two sets of coupled transverse waves. Each set of coupled transverse waves consist of a transverse displacement wave and a transverse micro-rotation wave perpendicular to it. They have also studied the reflection phenomenon of these plane waves from the stress-free flat boundary surface of a micropolar elastic solid half-space. Later, Tomar and Gogna [3–5] studied the reflection and transmission of plane waves at the interface of two dissimilar micropolar elastic solid half-spaces.

The classical theory of elasticity was also extended by Cowin and his co-worker [6, 7] by incorporating a uniform distribution of voids and developing the nonlinear and linear theories of elastic materials with voids. Elastic materials with voids are porous materials, in which the voids (pores) are small vacuous pores containing nothing of mechanical and energetic significance and these pores are not interconnected. The underlying idea of their theory was stemmed from the theory of granular material developed by Goodman and Cowin [8]. They have derived the constitutive relations and equations of motion for a uniform elastic materials with voids. Later, Puri and Cowin [9] studied the propagation of plane waves in elastic materials with voids and found that there exist three basic waves, two of them are coupled longitudinal waves and the third one is a lone transverse wave. The coupled longitudinal waves depend on void parameters and one of these waves arises in the medium due to the presence of voids. Whereas, the lone transverse wave is not influenced by the presence of voids and propagates with the speed of classical transverse wave. Iesan [10] developed the linear theory of thermoelastic elastic materials with voids and studied the acceleration waves. Later, Iesan [11] also presented the theory of micropolar elastic material with voids and studied shock waves. The interaction between the two adjacent portions of micropolar elastic body containing voids is governed by the force stress, couple stress and equilibrated stress. Following Lebon [12] law of heat conduction, Passarella [13] introduced a theory of micropolar thermoelasticity for materials with voids and obtained the constitutive relations and equations of motion. Ciarletta et al. [14] developed basic equations of the linear theory of micropolar thermoelasticity for isotropic and homogeneous materials with voids by taking into account the thermal relaxation time and studied plane waves and vibrations. They have also studied some existence theorems concerning the non-trivial solutions of interior homogeneous boundary value problems.

Eringen [15] developed the theory of nonlocal elasticity and presented the constitutive relations for nonlocal anisotropic elastic material. The underlying idea of nonlocal theory of elasticity is that it integrates long range forces between the atoms of the continuum. Therefore, in the continuum body, the stress at a point $\mathbf{x}$ not only depends on the strain at that point, but also on the strains at all the surrounding points ${\mathbf{x}}'$ of that point. According to Eringen [15], the nonlocal constitutive relation incorporates the classical constitutive relation in a weighted integral taken over the entire volume $V$ of the body as

$$ {\boldsymbol {\tau}}({\mathbf{x}})= \int _{V} k({\mathbf{x'}}, {\mathbf{x}}, \zeta ){ \mathbf{D}}~{\mathbf{e}}({\mathbf{x'}}) dV({\mathbf{x'}}), \qquad \qquad \forall ~~{\mathbf{x'}}, {\mathbf{x}} \in V. $$

The weight function $k({\mathbf{x'}}, {\mathbf{x}}, \zeta )$ is called nonlocal kernel function, which describes the influence of nonlocality and a measure for the dependence of stresses ${\boldsymbol {\tau}}({\mathbf{x}})$ to the strains ${\mathbf{e}}({\mathbf{x'}})$. The quantity ${\mathbf{D}}$ is a matrix of constitutive coefficients. In isotropic elastic medium, the kernel function $k({\mathbf{x'}}, {\mathbf{x}}, \zeta )$ is a distance function $k(|{\mathbf{x'}}-{\mathbf{x}}|, \zeta )$, which is chosen such that (i) it reached to maximum at ${\mathbf{x'}}={\mathbf{x}}$, (ii) attenuates to the large distances between ${\mathbf{x'}}$ and ${\mathbf{x}}$, (iii) behaves analogous to Dirac delta function. The quantity $\zeta$ is a ratio of the internal characteristic length ($l$), e.g., lattice parameter, size of the particle/void, to the external characteristic length ($L$), e.g., wavelength, size of the sample of the material. When $L$ is sufficiently large than $l$, then the results obtained using classical theory are found to be adequate with those obtained experimentally. But when these lengths are comparable, that is, $L\approx l$, then the classical theory fails to yield the satisfactory results. In elastic solids possessing micropolarity and/or voids, the external and internal characteristic lengths are comparable and hence, the nonlocal theory can be best suitable model for the elastic solids possessing micropolarity and/or voids. In view of the suitability of micropolar elastic solids, Eringen [16] developed the nonlocal theory of micropolar elasticity and derived the constitutive relations and equations of motion. He has also obtained the dispersion relation for the propagation of plane waves in the nonlocal mocropolar elastic medium. Later, Singh et al. [17] developed the nonlocal theory of elastic materials with voids within the context of Eringen’s theory of nonlocal elasticity. They have obtained the constitutive relations and equations of motion for an isotropic material. They have also studied the propagation of plane waves and found that there exist three plane waves propagating in the medium, whose speeds depend on the nonlocality parameter. Sarkar and Tomar [18] developed the theory of nonlocal thermoelastic materials with voids and derived the constitutive relations and equations of motion. Kumar and Tomar [19] developed the theory of nonlocal micropolar thermoelastic material with voids and studied the possibility of plane wave propagation within the context of Lord-Shulman theory of generalized thermoelasticity [20]. They found that there exist five waves propagating in the medium, out of which three are coupled longitudinal waves and remaining two are coupled transverse waves. Kumar and Tomar [21] have also studied the reflection phenomenon of coupled plane waves from the stress-free boundary surface of the half-space composed of nonlocal micropolar thermoelastic material with voids. Following Iesan [11] and Eringen [22], they assumed that there is no interaction of micro-rotation with the void and thermal parameters, and postulated the reflection of four waves comprising of two coupled longitudinal waves and two coupled transverse waves when a set of coupled waves is made incident against the stress-free boundary surface of the half-space. Some other papers in the pertinent area of research are given by Khurana and Tomar [23], Sarkar et al. [24], Biswas [25], Mondal and Sarkar [26] and Singh et al. [27].

Lord Rayleigh [28] was the first who discovered the existence of a type of waves propagating near the boundary surface of a Cauchy elastic half-space and go on decaying very fast with the distance away from the surface. Since then these waves are known as Rayleigh waves in the literature. The study of these waves are found to be of great importance in the field of earthquake sciences and in several other areas. Using the theory of elastic material with voids, Chandrasekharaiah [29] explored the possibility of propagation of Rayleigh surface waves in the elastic half-space having uniform distribution of void pores and investigated the effect of void parameters on Rayleigh waves. Kaur et al. [30] also studied the Rayleigh-type surface waves in nonlocal elastic half-space with voids and noticed the effect of nonlocality together with void parameters on the speed of propagating Rayleigh-type surface waves. Khurana and Tomar [31] have studied Rayleigh-type surface waves in nonlocal micropolar elastic half-space and found that there exist two modes of Rayleigh-type surface waves. Kumar et al. [32] investigated the propagation of Rayleigh-type surface waves in nonlocal generalized thermoelastic half-space for isothermal and thermally insulated boundaries. Some other papers on the propagation of Rayleigh-type surface waves in different models are given by Singh [33], Kumar et al. [34], Biswas [35] and Abd-Alla et al. [36] including others.

In the present work, the propagation of Rayleigh-type waves is studied in a half-space composed of nonlocal micropolar thermoelastic materials containing voids within the context of Lord-Shulman theory of generalized thermoelasticity. Dispersion relation is derived by assuming that the boundary surface of the half-space is mechanically stress-free and thermally insulated. The path followed by the particles during the propagation of surface waves are found to be elliptical. Dispersion relations for the propagation of Rayleigh-type surface waves in nonlocal elastic material with voids and in nonlocal micropolar thermoelastic material with voids are obtained as special cases of the present formulation. Numerical calculations have been carried out with the help of MATLAB software and the speed of Rayleigh-type surface waves is studied for a particular model. The obtained results are shown graphically against different parameters like angular frequency and nonlocal parameter. The comparison between the speed of Rayleigh-type surface waves in different models have also been shown through graphs and explained. A lone mode of Rayleigh-type wave is found to propagate in the considered model. It is observed that the various parameters such as nonlocality, thermal properties, and micropolarity significantly affect the phase speed and corresponding attenuation coefficient of propagating Rayleigh-type wave. It is also found that in the dissipative medium, the major axis of the ellipse described by the particles during the propagation of Rayleigh-type wave aligns with the coordinate axis.

2 Governing Relations and Equations

Following Kumar and Tomar [19], the stress tensor $(t_{ij})$, the couple stress tensor $(m_{ij})$, the equilibrated stress vector $(h_{i})$, the equilibrated body force $(g)$ and the entropy $(\eta )$ for nonlocal micropolar thermoelastic materials containing void pores are given by

$$ \left (1-\epsilon ^{2} \nabla ^{2}\right )t_{ij}=t^{L}_{ij}=[\lambda 'e_{kk}({ \mathbf{x}})+e' \phi ({\mathbf{x}})-d'\theta ({\mathbf{x}})]\delta _{ij} +(\mu '+K')e_{ij}({ \mathbf{x}})+\mu 'e_{ji}({\mathbf{x}}), $$

(1)

$$ \left (1-\epsilon ^{2} \nabla ^{2}\right )m_{ij}=m^{L}_{ij}=\alpha ' \gamma _{kk}({\mathbf{x}})\delta _{ij}+\beta ' \gamma _{ij}({\mathbf{x}})+ \gamma ' \gamma _{ji}({\mathbf{x}}), $$

(2)

$$ \left (1-\epsilon ^{2} \nabla ^{2}\right )h_{i}=h^{L}_{i}= c'\phi _{,i}({ \mathbf{x}}), $$

(3)

$$ \left (1-\epsilon ^{2} \nabla ^{2}\right )g=g^{L}=-\tau '\dot{\phi}({ \mathbf{x}})-\xi ' \phi ({\mathbf{x}})-e'e_{ii}({\mathbf{x}})+G'\theta ({\mathbf{x}}), $$

(4)

$$ \left (1-\epsilon ^{2} \nabla ^{2}\right )\rho \eta =\rho \eta ^{L}= \zeta '\theta ({\mathbf{x}})+d'e_{ii}({\mathbf{x}})+G'\phi ({\mathbf{x}}), $$

(5)

where $e_{ij}=u_{j,i}-\epsilon _{ijm}\psi _{m}$ is the distortion tensor, $\gamma _{ij}=\psi _{i,j}$ is the curvature tensor, $u_{i}$ is the displacement vector, $\psi _{i}$ is the microrotation vector, $\epsilon _{ijm}$ is the permutation symbol, $\phi =\nu ({\mathbf{x}}, t)-\nu _{R}$ is the change in void volume fraction from the reference void volume $\nu _{R}$, $\theta$ is the change in temperature from the ambient temperature $T_{0}$ and related with the heat flux vector ($Q_{i}$) through the relation

$$ (1-\epsilon ^{2}\nabla ^{2})Q_{i}=\mathcal{K}\theta _{,i}, $$

$\rho$ is the mass density, $\delta _{ij}$ is the Kronecker delta symbol, $\mathcal{K}$ is the coefficient of thermal conductivity, $\epsilon (=e_{0}a)$, is the nonlocality parameter, $a$ being the internal characteristic length and $e_{0}$ is the material constant. The symbols $\lambda '$, $\mu '$, $e'$, $K'$, $\alpha '$, $\beta '$, $\gamma '$, $c'$, $\tau '$, $\xi '$, $G'$, $\zeta '$ and $d'$ are the local constitutive coefficients. The superscript $L$ on the various symbols represents the local effect, a comma in the subscript denotes the spatial derivative and an over dot denotes the derivative with respect to time variable $t$. Other symbols have their usual meaning. Here, we have assumed that during the deformation processes, the micro-rotation shall remain independent of voids and thermal effects as supported by Iesan [11] and Eringen [22]. Furthermore, there is need to have some extra conditions to be imposed on the nonlocal stresses given by (see Anh and Vinh [37] and Anh et al. [38])

$$ \{t^{L}_{ij},m^{L}_{ij},h^{L}_{i},g^{L},\eta ^{L}\}\equiv 0 \implies \{t_{ij},m_{ij},h_{i},g,\eta \}\equiv 0~\text{in}~V. $$

(6)

Mechanically, these conditions state that if there is no strain in the body everywhere, then there is no stress in the body everywhere. Mathematically, these conditions ensure the uniqueness of various nonlocal stresses, as a solution of (1)-(5), for the given local stresses. Hence, these conditions make the present problem well-posed and the operator $\mathcal{L}\equiv \left (1-\epsilon ^{2}\nabla ^{2}\right )$ to be invertible.

Following Kumar and Tomar [19], the equations of motion for the considered nonlocal micropolar thermoelastic materials containing uniform distribution of voids are given by

$$ \left (\lambda '+\mu ' \right )\nabla \left (\nabla \cdot{\mathbf{u}} \right )+\left (\mu '+ K'\right )\nabla ^{2}{\mathbf{u}}+e'\nabla \phi -d' \nabla \theta +K' \nabla \times {\boldsymbol{\psi}} +\rho \mathcal{L} \left ({\mathbf{f}}-\ddot{{\mathbf{u}}}\right )={\mathbf{0}}, $$

(7)

$$ \left (\alpha '+\beta ' \right )\nabla \left (\nabla \cdot{ \boldsymbol{ \psi}}\right )+\gamma ' \nabla ^{2}{\boldsymbol{ \psi}}+K' \nabla \times {\mathbf{u}}-2K'{\boldsymbol{ \psi}}+\rho \mathcal{L}\left ({ \mathbf{l}}-j\ddot{{\boldsymbol{ \psi}}} \right )={\mathbf{0}}, $$

(8)

$$ c'\nabla ^{2}\phi -\tau ' \dot{\phi}-\xi '\phi -e'\nabla \cdot {\mathbf{u}}+G' \theta +\rho \mathcal{L}\left (l-\chi \ddot{\phi}\right )= 0, $$

(9)

$$ \mathcal{K}\,\nabla ^{2} \theta =\left (1+\tau _{0} \frac{\partial}{\partial t}\right )\left (\rho C_{e}\dot{\theta}+d'T_{0} \nabla \cdot \dot{{\mathbf{u}}}+G'T_{0}\dot{\phi}-\rho \mathcal{L} \mathcal{R}\right ), $$

(10)

where $\mathbf{f}$ is the body force, $\mathbf{l}$ is the body couple, $l$ is the extrinsic equilibrated body force, $\chi$ is the equilibrated inertia and $j$ is the micro-inertia, $\tau _{0}$ is the thermal relaxation time, ℛ is the extrinsic heat supply and $C_{e}$ is the specific heat at fixed strain such that $\rho C_{e}=\zeta '\,T_{0}$.

3 Surface Wave Propagation

Consider a half-space $H$ composed of a nonlocal micropolar thermoelastic materials containing uniform distribution of voids. With reference to a rectangular Cartesian coordinate system, let the $x-y$ plane defines the boundary surface of the half-space while $z$-axis directs vertically downwards into the half-space. The region occupied by the half-space is thus defined by

$$ H=\{(x,\,y,\,z):\,-\infty < x,y < \infty ,\, 0 \leq z < \infty \}. $$

We shall discuss a two-dimensional problem in $x-z$ plane so that

$$ {\mathbf{u}}=(u_{1},0,u_{3})(x,z,t),\quad \boldsymbol{\psi}=(0,\psi ,0)(x,z,t), \quad \phi =\phi (x,z,t),\quad \theta =\theta (x,z,t). $$

Introducing the scalar potential $q$ and solenoidal vector potential $\mathbf{U}$ through Helmholtz decomposition theorem for the displacement vector $\mathbf{u}$, the components of displacement vector are given by

$$ u_{1}=q_{,x}-U_{,z}, \quad u_{3}=q_{,z}+U_{,x}, $$

(11)

where $U$ is the $y$-component of the vector potential $\mathbf{U.}$ In view of these consideration, the equations of motion (7)-(10) are reduced to

$$ \left (\lambda '+2\mu '+K'\right )\nabla ^{2} q+e'\phi -d'\theta = \rho \left (1-\epsilon ^{2}\nabla ^{2}\right )\ddot{q}, $$

(12)

$$ c'\nabla ^{2}\phi -\tau '\dot{\phi}-\xi '\phi -e'\nabla ^{2} q+G' \theta =\rho \chi \left (1-\epsilon ^{2}\nabla ^{2}\right ) \ddot{\phi}, $$

(13)

$$ \mathcal{K} \nabla ^{2}\theta =\left (1+\tau _{0} \frac{\partial}{\partial t}\right )\left (\rho C_{e}\dot{\theta}+d'T_{0} \nabla ^{2}\dot{q}+G'T_{0}\dot{\phi}\right ), $$

(14)

$$ \left (\mu '+K'\right )\nabla ^{2}{ U}+K'\psi = \rho \left (1- \epsilon ^{2}\nabla ^{2}\right )\ddot{{U}}, $$

(15)

$$ \gamma '\nabla ^{2}\psi -K'\nabla ^{2} U-2K' \psi =\rho j \left (1- \epsilon ^{2}\nabla ^{2}\right )\ddot{\psi}. $$

(16)

Note that the equations (12)-(14) are coupled through the potentials $q$, $\phi$ and $\theta$, whereas the equations (15) and (16) are coupled through the potentials $U$ and $\psi$.

For time harmonic steady state wave propagating with speed $v$, the quantities $q$, $\phi$, $\theta$, $U$ and $\psi$ can be taken in the form as

$$ \{q,\phi ,\theta , U, \psi \}=\{\bar{q},\bar{\phi},\bar{\theta}, \bar{U}, \bar{\psi}\}\exp \{-\iota \omega t\}, $$

(17)

where $\bar{q}$, $\bar{\phi}$, $\bar{\theta}$, $\bar{U}$ and $\bar{\psi}$ are the amplitudes, $\omega$ is the angular frequency of the propagating wave related with the wavenumber $k$ through the relation $\omega =kv$. Here, the wavenumber $k$ may be real or complex valued, while the angular frequency $\omega$ will be taken as a real positive quantity. It is expected that (i) when $k$ is real valued, then the speed $v$ will also be real valued, (ii) when $k$ is complex valued, then the speed $v$ will also be complex valued.

Inserting the relation (17) into (12)-(16), one can obtain

$$ \left (A_{1}\nabla ^{6}+\omega ^{2}A_{2}\nabla ^{4}+\omega ^{4}A_{3} \nabla ^{2}+\omega ^{6}A_{4}\right )\bar{q}=0, $$

(18)

$$ \left (B_{1}\nabla ^{4}+\omega ^{2}B_{2}\nabla ^{2}+\omega ^{4}B_{3} \right )\bar{U}=0, $$

(19)

where

$$ A_{1}=k_{4}c_{2}c_{4}\omega ^{2},\quad A_{2}=\omega ^{2}c_{4}(d_{1}d_{2}-c_{2}-k_{4})-k_{4}c_{2}c_{5}+e_{1}e_{2}k_{4}, $$

$$ A_{3}=-[e_{1}(e_{2}+g_{1}d_{2})+d_{1}(e_{2}g_{2}+d_{2}c_{5})-\omega ^{2}c_{4}-k_{4}c_{5}+c_{2}(g_{1}g_{2}-c_{5})], $$

$$ A_{4}=\omega ^{4}(g_{1}g_{2}-c_{5}),\quad B_{1}=\omega ^{2}(\epsilon ^{2} \omega ^{2}-\gamma _{1})(\epsilon ^{2}\omega ^{2}-c^{2}_{t}-k_{1}), \quad B_{3}=\omega ^{2}-2k_{2}, $$

$$ B_{2}=-[\omega ^{2}(\epsilon ^{2}\omega ^{2}-\gamma _{1})+(\omega ^{2}-2k_{2})( \epsilon ^{2}\omega ^{2}-c^{2}_{t}-k_{1})-k_{1}k_{2}], $$

$$ c_{2}=\epsilon ^{2}\omega ^{2}-c^{2}_{l}-k_{1},\,\ c_{4}=\epsilon ^{2} \omega ^{2}-c_{1},\,\ c_{5}=\omega ^{2}-\xi _{1}+\iota \omega \tau _{1}, \,\ e_{1}=e'/\rho ,\,\ c_{1}=c'/\rho \chi, $$

$$ d_{1}=d'/\rho ,\quad e_{2}=e_{1}/\chi ,\quad g_{1}=G'/\rho \chi , \quad d_{2}=d_{1}T_{0}/C_{e},\quad g_{2}=g_{1} \chi T_{0}/C_{e}, $$

$$ k_{4}=-k_{3}/\tau _{2},\quad \omega ^{2}\tau _{2}=\tau _{0}\omega ^{2}+ \iota \omega ,\quad \gamma _{1}=\gamma '/\rho j,\quad k_{1}=K'/\rho , \quad k_{2}=k_{1}/j, $$

$$ k_{3}=\mathcal{K}/\rho C_{e},\quad \xi _{1}=\xi '/\rho \chi ,\quad \tau _{1}=\tau '/\rho \chi ,\quad c^{2}_{l}=(\lambda '+2\mu ')/\rho , \quad c^{2}_{t}=\mu '/\rho . $$

The general solution of equations (18) and (19) can be written as

$$ \bar{q}= \sum _{i=1}^{3} q_{i} \quad \text{and}\quad \bar{U}=\sum _{j=4}^{5} U_{j}, $$

(20)

where each $q_{i}$ and $U_{j}$ satisfies the following Helmholtz equations

$$ \bigg(\nabla ^{2}+\frac{\omega ^{2}}{v^{2}_{i}}\bigg)q_{i}=0 \quad \text{and} \quad \bigg(\nabla ^{2}+ \frac{\omega ^{2}}{v^{2}_{j}}\bigg)U_{j}=0. $$

(21)

The quantities $v^{2}_{i}$ and $v^{2}_{j}$ in equations under (21) are respectively the roots of equations

$$ A_{4}v^{6}-A_{3}v^{4}+A_{2}v^{2}-A_{1}=0 \quad \text{and} \quad B_{3}v^{4}-B_{2}v^{2}+B_{1}=0. $$

(22)

For the waves propagating along positive direction of $x$-axis, the form of potentials $q_{i}$ and $U_{j}$ can be taken as

$$ \{q_{i},U_{j}\}=\{\bar{q}_{i}(z),\bar{U}_{j}(z)\}e^{\iota kx}, $$

(23)

where the amplitudes $\bar{q}_{i}(z)$ and $\bar{U}_{j}(z)$ are functions of $z$. Inserting (23) into (21), the expressions of $\bar{q}_{i}(z)$ and $\bar{U}_{j}(z)$ representing the surface wave solutions are given by

$$ \{\bar{q}_{i}(z),\bar{U}_{j}(z)\} =\{A'_{i}e^{-m_{i}z}, B'_{j}e^{-m_{j}z} \}, $$

(24)

where $A'_{i}$ and $B'_{j}$ are the arbitrary constants and the quantities $m_{i}$ and $m_{j}$ given by

$$ m_{i}=k\sqrt{1-\frac{v^{2}}{v^{2}_{i}}}\quad \text{and}\quad m_{j}=k \sqrt{1-\frac{v^{2}}{v^{2}_{j}}}, $$

must be real and positive. So, we must have

$$ v^{2} < \{v^{2}_{i}, v^{2}_{j}\}. $$

Thus, the complete solutions representing Rayleigh-type surface wave propagating in a positive $x$-axis direction are given by

$$ \left [\{q,\phi ,\theta \},\{U,\psi \}\right ]=\left [\sum _{i=1}^{3}A'_{i} \{1,M_{i},N_{i}\}e^{-m_{i}z},\sum _{j=4}^{5}B'_{j}\{1,Q_{j}\}e^{-m_{j}z} \right ]e^{\iota k\{x-vt\}}, $$

(25)

where $M_{i}'$s, $N_{i}'$s and $Q_{j}'$s obtained from equations (12)-(16) are given by

$$ M_{i}= \frac{(k^{2}-m^{2}_{i})(e_{2}d_{1}+g_{1}c_{2})+g_{1}\omega ^{2}}{d_{1}c_{4}m^{2}_{i}-c_{4}d_{1}k^{2}-c_{5}d_{1}-e_{1}g_{1}}, $$

(26)

$$ N_{i}=\frac{1}{d_{1}}\left (\omega ^{2}-c_{2}m^{2}_{i}+c_{2}k^{2}+e_{1}M_{i} \right ), $$

(27)

$$ Q_{j}=(\epsilon ^{2}\omega ^{2}-c^{2}_{t}-k_{1})(m^{2}_{j}-k^{2})- \omega ^{2}. $$

(28)

Here, it can be easily noticed that while using (11) and (25) into (1)-(5), the vanishing of local stresses implies that all the $A'_{i},~(i=1,2,3)$ and $B'_{j},~(j=4,5)$ must vanish, which results in vanishing of nonlocal stresses. In the following section, we shall obtain the dispersion relation for the propagation of Rayleigh-type waves in question.

4 Dispersion Relation

We assumed that the boundary surface of the half-space is mechanically-stress free and thermally insulated. Therefore, the relevant nonlocal stress components shall vanish at the boundary surface $z=0$. These boundary conditions can be written in mathematical form as: At $z=0$, we have

$$ t_{zx}=t_{zz}=h_{z}=m_{zy}=Q_{z}=0. $$

(29)

The nonlocal stresses can be obtained in term of local stresses by implementing the operator ℒ on both side of (1)-(5). Since the operator ℒ is considered to be invertible, therefore $\mathcal{L}^{-1}\equiv (1-\epsilon ^{2}\nabla ^{2})^{-1}$ exist. Expanding $(1-\epsilon ^{2}\nabla ^{2})^{-1}$ by means of Binomial theorem and assuming that the nonlocal parameter ($\epsilon$) is so small such that $\epsilon ^{3}$ and its higher powers are negligible, we obtain $(1-\epsilon ^{2}\nabla ^{2})^{-1}\approx (1+\epsilon ^{2}\nabla ^{2})$ (see, Eringen [39]). With this, the boundary conditions (29) in terms of potentials are written as

$$ (1+\epsilon ^{2}\nabla ^{2}) \left [(2\mu '+K')q_{,xz}+\mu 'U_{,xx}-( \mu '+K')U_{,zz}-K'\psi \right ]=0, $$

(30)

$$ (1+\epsilon ^{2}\nabla ^{2}) \left [\lambda 'q_{,xx}+(\lambda '+2\mu '+K')q_{,zz}+(2 \mu '+K')U_{,xz}+e'\phi -d'\theta \right ]=0, $$

(31)

$$ \gamma ' (1+\epsilon ^{2}\nabla ^{2}) \psi _{,z}=0, $$

(32)

$$ c' (1+\epsilon ^{2}\nabla ^{2}) \phi _{,z}=0, $$

(33)

$$ (1+\epsilon ^{2}\nabla ^{2}) \theta _{,z}=0. $$

(34)

Using the expressions of potentials given in (25) into the boundary conditions (30)-(34), we obtained a system of five homogeneous equations in five unknown, namely, $A_{i}~(i=1,2,3)$ and $B_{j}~(j=4,5)$. The condition for non-trivial solution of this homogeneous system yields the following dispersion relation given by

$$\begin{aligned} & \prod _{n=1}^{5} \left [1+\epsilon ^{2}(m^{2}_{n}-k^{2}) \right ]\Big[ k^{2}(2\mu '+K')^{2} \prod _{n=1}^{5}m_{n}\big[(Q_{5}-Q_{4}) \{M_{1}(N_{2}-N_{3}) \\ &+M_{2}(N_{3}-N_{1})+M_{3}(N_{1}-N_{2})\}\big]+\big[m_{4}m_{5}(\mu '+K')(Q_{4}m_{5}-Q_{5}m_{4}) \\ &+\mu 'k^{2}(Q_{4}m_{4}-Q_{5}m_{5})+K'Q_{4}Q_{5}(m_{4}-m_{5})\big] \big[m_{2}m_{3}(M_{2}N_{3}-M_{3}N_{2}) \\ &\{\lambda '(m^{2}_{1}-k^{2})+(2\mu '+K')m^{2}_{1}+e'M_{1}-d'N_{1}\}+m_{1}m_{3}(M_{3}N_{1}-M_{1}N_{3}) \\ &\{\lambda '(m^{2}_{2}-k^{2})+(2\mu '+K')m^{2}_{2}+e'M_{2}-d'N_{2}\}+m_{1}m_{2}(M_{1}N_{2}-M_{2}N_{1}) \\ &\{\lambda '(m^{2}_{3}-k^{2})+(2\mu '+K')m^{2}_{3}+e'M_{3}-d'N_{3}\} \big]\Big]=0. \end{aligned}$$

(35)

Equation (35) is the dispersion relation for Rayleigh-type surface waves propagating in the half-space composed of nonlocal micropolar thermoelastic materials containing voids. It can be seen that this dispersion relation provides two equations, one of which, namely,

$$ \prod _{n=1}^{5} \left [1+\epsilon ^{2}(m^{2}_{n}-k^{2})\right ]=0, $$

does not lead to any propagating wave, whereas the other one is expected to yield the speed of a propagating wave. Note that it is not easy to solve the equation (35) analytically due to its complex valued coefficients, but these coefficients are clearly dependent on frequency, nonlocality, void, thermal and micropolar parameters. Thus, one can conclude that the speed of relevant surface wave obtained from (35) shall be dispersive and attenuating in nature.

5 Particle Motion

In this section, we shall determine the nature of path followed by the particles of the medium during the propagation of Rayleigh-type surface waves in the considered half-space. First, we shall obtain the expression of real part of the displacement components $u_{1}$ and $u_{3}$ by inserting the potentials $q$ and $U$ given in (25) into (11) as

$$ \{\Re{(u_{1})},\Re{(u_{3})}\}=-\{|u^{o}_{1}|\sin \theta _{1},|u^{o}_{3}| \cos \theta _{2}\}e^{-\Im{(k)}x}, $$

(36)

where

$$ \theta _{1}=\arg (u^{o}_{1})+\Re{(k)}x-\omega t,\quad \theta _{2}= \arg (u^{o}_{3})+\Re{(k)}x-\omega t, $$

$$ u^{o}_{1}=\sum _{i=1}^{3}kA'_{i}e^{-m_{i}z}-\sum _{j=4}^{5}\iota m_{j}B'_{j}e^{-m_{j}z}, \quad u^{o}_{3}=\sum _{i=1}^{3}m_{i}A'_{i}e^{-m_{i}z}-\sum _{j=4}^{5} \iota kB'_{j}e^{-m_{j}z}. $$

From (36), we obtain

$$ \mathcal{A}_{0}[\Re{(u_{1})}]^{2}-\mathcal{B}_{0}\Re{(u_{1})}\Re{(u_{3})}+ \mathcal{C}_{0}[\Re{(u_{3})}]^{2}=1, $$

(37)

where

$$ \mathcal{A}_{0}=\frac{1}{|u^{o}_{1}|^{2}\mathcal{D}^{2}_{0}},\,\ \mathcal{B}_{0}= \frac{2\sin \theta _{3}}{|u^{o}_{1}||u^{o}_{3}|\mathcal{D}^{2}_{0}}, \,\ \mathcal{C}_{0}=\frac{1}{|u^{o}_{3}|^{2}\mathcal{D}^{2}_{0}},\,\ \mathcal{D}_{0}=(\cos \theta _{3})e^{-\Im{(k)}x},\,\ \theta _{3}= \arg \left (\frac{u^{o}_{1}}{u^{o}_{3}}\right ). $$

Equation (37) gives the locus of the path traced by the particle during the propagation of Rayleigh-type surface wave. This is an equation of conic in standard form, whose discriminant is given by

$$ -\frac{4}{|u^{o}_{1}|^{2}|u^{o}_{3}|^{2}\mathcal{D}^{4}_{0}}\left (1- \sin ^{2}\theta _{3}\right ), $$

(38)

which is negative for all values of $\theta _{3}$, except at $\theta _{3}=\pi /2$. Therefore, for all values of $\theta _{3}\neq \pi /2$, the equation (37) represents an ellipse. Thus, the particle traces elliptical path during the propagation of Rayleigh-type surface waves in half-space.

Next, we shall obtain the tilt angle at which the particle follows the elliptical motion with respect to the vertical axis. For this purpose, we transform equation (37) into standard form of the ellipse by rotating the co-ordinate axis through an angle $\theta _{4}$. The relevant transformation is given by

$$ \begin{bmatrix} \Re{(u_{1})} \\ \Re{(u_{3})} \end{bmatrix} = \begin{bmatrix} \cos \theta _{4} &-\sin \theta _{4} \\ \sin \theta _{4} & ~~\cos \theta _{4} \end{bmatrix} \begin{bmatrix} \Re{(u'_{1})} \\ \Re{(u'_{3})} \end{bmatrix} , $$

(39)

where the angle $\theta _{4}$ is given by

$$ \tan 2\theta _{4}= \textstyle\begin{cases} \mathcal{B}_{0}/(\mathcal{C}_{0}-\mathcal{A}_{0}), &\text{for}~ \mathcal{A}_{0}\neq \mathcal{C}_{0} \\ ~~~~~~~\infty , & \text{for}~\mathcal{A}_{0}=\mathcal{C}_{0} \end{cases}\displaystyle . $$

(40)

Hence, the plane of the ellipse is inclined through an angle $\theta _{4}$ from the vertical axis.

6 Special Cases

In this section, we shall reduce the dispersion relation (35) to corresponding dispersion relation of Rayleigh-type wave propagation in specific media. These particular cases are discussed as follows.

6.1 Nonlocal Thermoelastic Material with Voids

If we neglect micropolar parameters from the model, one would be left with the nonlocal thermoelastic material with voids. It can be observed that in the absence of micropolarity, one of the coupled transverse waves disappears from the medium. Let us consider that the wave propagating with speed $v_{5}$ disappears from the medium together with the micropolar constitutive coefficients, namely, $\alpha '$, $\beta '$, ${\gamma}$ and $K'$. The vanishing of $v_{5}$ implies that the parameter $m_{5}$ and the coupling coefficient $Q_{5}$ approach to infinity. With these considerations, the dispersion relation (35) reduces to

$$\begin{aligned} &\prod _{n=1}^{4} \left [1+\epsilon ^{2}(m^{2}_{n}-k^{2}) \right ]\big[4k^{2}\mu ^{\prime \,2} \prod _{n=1}^{4} m_{n}\{M_{1}(N_{2}-N_{3})+M_{2}(N_{3}-N_{1})+M_{3}(N_{1}-N_{2}) \} \\ &+\mu '(m^{2}_{4}+k^{2}) [m_{2}m_{3}(M_{2}N_{3}-M_{3}N_{2})\{\lambda '(m^{2}_{1}-k^{2})+2 \mu 'm^{2}_{1}+e'M_{1}-d'N_{1}\} \\ &+m_{1}m_{3}(M_{3}N_{1}-M_{1}N_{3})\{\lambda '(m^{2}_{2}-k^{2})+2\mu 'm^{2}_{2}+e'M_{2}-d'N_{2} \} \\ &+m_{1}m_{2}(M_{1}N_{2}-M_{2}N_{1})\{\lambda '(m^{2}_{3}-k^{2})+2\mu 'm^{2}_{3}+e'M_{3}-d'N_{3} \}]\big]=0. \end{aligned}$$

(41)

Equation (41) represents dispersion relation for Rayleigh-type surface waves propagating in the half-space composed of nonlocal thermoelastic material containing voids. Singh [33] has also obtained the dispersion relation for Rayleigh-type surface waves by using local boundary conditions in a nonlocal thermoelastic half-space containing voids for thermally insulated boundary surface, whereas we have obtained the dispersion relation for thermally insulated case by using nonlocal boundary conditions. It can be noticed that the reduced dispersion relation (41) is dependent on void, thermal and nonlocal parameters.

6.2 Nonlocal Micropolar Elastic Material with Voids

To achieve this model, we shall ignore the thermal parameters from the considered model. Setting the thermal parameters, namely, $d'$, $f'$, $G'$ and $\zeta '$ to zero, we observe that one of the coupled longitudinal waves disappears from the medium. This means that one of the speeds, say, $v_{3}$ of coupled longitudinal waves vanishes. We further notice that in this case, the parameter $m_{3}$ and the coupling coefficient $N_{3}$ approach to infinity. With these considerations, the dispersion relation (35) reduces to

$$\begin{aligned} \{1+&\epsilon ^{2}(m^{2}_{1}-k^{2})\} \{1+\epsilon ^{2}(m^{2}_{2}-k^{2}) \} \{1+\epsilon ^{2}(m^{2}_{4}-k^{2})\} \{1+\epsilon ^{2}(m^{2}_{5}-k^{2}) \} \\ \big[k^{2}& K^{2}_{1} m_{1}m_{2}m_{4}m_{5}(Q_{5}-Q_{4})(M_{2}-M_{1})+[m_{4}m_{5}( \mu '+K')(Q_{4}m_{5}-Q_{5}m_{4}) \\ +&\mu 'k^{2}(Q_{4}m_{4}-Q_{5}m_{5})+K'Q_{4}Q_{5}(m_{4}-m_{5})] [m_{2}M_{2} \{\lambda '(m^{2}_{1}-k^{2}) \\ &+K_{1}m^{2}_{1}+e'M_{1}\}-m_{1}M_{1}\{\lambda '(m^{2}_{2}-k^{2})+K_{1}m^{2}_{2}+e'M_{2} \}]\big]=0, \end{aligned}$$

(42)

where

$$ K_{1}=2\mu '+K'~\text{and}~M_{i}=\frac{1}{e_{1}}\left [c_{2}(m^{2}_{i}-k^{2})- \omega ^{2}\right ],\qquad (i=1,2). $$

Equation (42) is the dispersion relation for Rayleigh-type surface waves propagating in the half-space composed of nonlocal micropolar elastic material containing voids, which is new and not obtained hitherto. It can be seen that this dispersion relation is dependent on various void, micropolar and nonlocal parameters, therefore, the corresponding speed of Rayleigh-type surface wave is also dependent on these parameters.

6.3 Nonlocal Micropolar Thermoelastic Material

In the absence of void parameters, namely, $e'$, $b'$, $c'$, $\tau '$, $\xi '$ and $G'$, one of the coupled longitudinal waves shall disappear from the medium. Let the wave propagating with speed $v_{2}$ disappears in the absence of void parameters. Also, the parameter $m_{2}$ and the coupling coefficient $M_{2}$ shall approach to infinity in this case. With these consideration, the dispersion relation (35) reduces to

$$\begin{aligned} \prod _{n=1,3,4,5}\{1+\epsilon ^{2}(m^{2}_{n}&-k^{2})\} \\ \big[k^{2}& K^{2}_{1} m_{1}m_{3}m_{4}m_{5}(Q_{5}-Q_{4})(N_{3}-N_{1})\\ +&[m_{4}m_{5}( \mu '+K')(Q_{4}m_{5}-Q_{5}m_{4}) \\ +&\mu 'k^{2}(Q_{4}m_{4}-Q_{5}m_{5})+K'Q_{4}Q_{5}(m_{4}-m_{5})] [m_{3}N_{3} \{\lambda '(m^{2}_{1}-k^{2}) \\ &+K_{1}m^{2}_{1}-d'N_{1}\}-m_{1}N_{1}\{\lambda '(m^{2}_{3}-k^{2})+K_{1}m^{2}_{3}-d'N_{3} \}]\big]=0, \end{aligned}$$

(43)

where

$$ N_{i}=\frac{1}{d_{1}}\left [\omega ^{2}-c_{2}(m^{2}_{i}-k^{2})\right ], \qquad (i=1,3). $$

Equation (43) is the dispersion relation for Rayleigh-type surface wave propagating in the half-space composed of nonlocal micropolar thermoelastic material. The relation (43) is new in the relevant nonlocal theory of elasticity, which contains frequency, thermal and various material parameters. The speed of Rayleigh-type wave obtained from relation (43) is therefore dispersive, attenuating and dependent on various material parameters.

6.4 Nonlocal Thermoelastic Material

To achieve the relevant dispersion relation in this model, we shall set the micropolar parameters, namely, $\alpha '$, $\beta '$, ${\gamma}$ and $K'$ to zero in the dispersion relation (43) obtained in Sect. 6.3. It can be noticed that in the absence of micropolarity, one of the coupled transverse waves disappears from the medium. As discussed in Sect. 6.1, the vanishing of one of the speeds of coupled transverse waves, say, $v_{5}$ implies that the parameter $m_{5}$ and the coupling coefficient $Q_{5}$ approach to infinity. With these consideration, the dispersion relation (43) reduces to

$$\begin{aligned} \prod _{n=1,3,4}\{1+\epsilon ^{2}(m^{2}_{n}&-k^{2})\} \big[4k^{2}\mu ' m_{1}m_{3}m_{4}(N_{3}-N_{1})-(m^{2}_{4}+k^{2}) [m_{3}N_{3} \{\lambda '(m^{2}_{1}-k^{2}) \\ +& 2\mu 'm^{2}_{1}-d'N_{1}\}- m_{1}N_{1}\{\lambda '(m^{2}_{3}-k^{2})+2 \mu 'm^{2}_{3}-d'N_{3}\}]\big]=0, \end{aligned}$$

(44)

where

$$ N_{i}=\frac{1}{d_{1}}\left [\omega ^{2}-(\epsilon ^{2}\omega ^{2}-c^{2}_{l})(m^{2}_{i}-k^{2}) \right ], \qquad (i=1,3). $$

Equation (44) is the dispersion relation for Rayleigh-type surface wave propagating in the half-space composed of nonlocal thermoelastic material. For the local boundary conditions, the dispersion relation (44) matches with the dispersion relation (24) obtained by Kumar et al. [32] apart from notations and representations.

6.5 Nonlocal Elastic Material with Voids

In the absence of micropolar and thermal parameters, the dispersion relation (35) reduces to

$$\begin{aligned} \{1+\epsilon ^{2}(m^{2}_{1}-& k^{2} )\} \{1+\epsilon ^{2}(m^{2}_{2}-k^{2}) \} \{1+\epsilon ^{2}(m^{2}_{4}-k^{2})\} \\ \big[4 k^{2} \mu ^{\prime \,2} & m_{1}m_{2}m_{4}(M_{2}-M_{1})-\mu '(m^{2}_{4}+k^{2}) [m_{2}M_{2}\{\lambda '(m^{2}_{1}-k^{2}) \\ &+K_{1}m^{2}_{1}+e'M_{1}\}-m_{1}M_{1}\{\lambda '(m^{2}_{2}-k^{2})+K_{1}m^{2}_{2}+e'M_{2} \}]\big]=0, \end{aligned}$$

(45)

where $M_{i}'$s are exactly the same as given in Section-6.2.

Equation (45) is the dispersion relation for Rayleigh-type surface waves propagating in the half-space composed of nonlocal elastic material with voids. The form of dispersion relation (45) is not exactly the same analytically as obtained earlier by Kaur et al. [30] for the corresponding problem. The reason for not achieving exactly the same form of dispersion relation is because they consider the local stresses vanish at the boundary of the half-space, while we have considered the nonlocal stresses vanish at the boundary of the half-space. Therefore, there is slight difference between the dispersion relation of the two formulations.

6.6 Classical Cauchy Continuum

In the absence of nonlocal, micropolar, thermal and void parameters, the dispersion relation (35) reduces to

$$ \left (2-\frac{v^{2}}{c^{2}_{t}}\right )^{2}=4\sqrt{1- \frac{v^{2}}{c^{2}_{l}}}\sqrt{1-\frac{v^{2}}{c^{2}_{t}}}. $$

(46)

Equation (46) is the dispersion relation for Rayleigh-type surface waves propagating in a half-space composed of Cauchy elastic medium, which exactly match with the well-known relation for Rayleigh wave in classical elasticity [29].

7 Numerical Results and Discussion

To study the behavior of propagating Rayleigh-type surface wave in the nonlocal micropolar thermoelastic half-space with voids, we shall consider a specific model with specific values of relevant material parameters as listed in Table-1 (Refs. [11, 40]). Using these values, the speed $v$ is computed numerically from the dispersion relation given in (35) using MATLAB software. It is found that the speed of propagating Rayleigh-type surface waves is complex valued as was expected beforehand. The phase speed and the corresponding attenuation coefficient are computed by using the formulae given in Borcherdt [41]

$$ V_{r}= \frac{(\Re (v))^{2}+(\Im (v))^{2}}{\Re (v)}\quad \text{and} \quad Q_{r}=\frac{-\omega \Im (v)}{(\Re (v))^{2}+(\Im (v))^{2}}. $$

(47)

The computations have been kept up to the forty decimal places in the output format in order to have best possible accuracy.

Table 1 Numerical value of material parameters

We have shown the behavior of phase speed and corresponding attenuation coefficient of Rayleigh-type surface wave graphically against the angular frequency ($\omega$) in low and high-frequency ranges.

Figures 1 & 2 depict the behavior of the phase speed ($V_{r}$) and corresponding attenuation ($Q_{r}$) of Rayleigh-type surface wave against angular frequency ($\omega$) in the low-frequency range: $0<\omega \leq 12\times 10^{4}$. It is found that the phase speed increases monotonically in the frequency range: $0<\omega \leq 1.7\times 10^{3}$, to achieve its maxima and then decreases with increase of frequency in the range $1.7\times 10^{3} <\omega \leq 4.1\times 10^{4}$. Thereafter, Rayleigh-type surface wave propagates with constant phase speed in the rest of the considered range of frequency. From Fig. 2, it can be seen that the attenuation coefficient is very small in magnitude throughout the considered range of frequency. The wave is attenuating in the initial range of frequency: $0<\omega \leq 1.5 \times 10^{4}$ and then non-attenuating for further increase in frequency. From Figs. 1 & 2, we conclude that the speed of Rayleigh-type surface wave is dispersive and attenuating in the initial range of frequency, but it becomes non-dispersive and non-attenuating for further increase of frequency in the low-frequency range considered. Also, in the high-frequency range, the Rayleigh-type wave is highly dispersive and attenuating. Note that the dispersive behavior of Rayleigh-type surface wave can be noticed only in the half-space with nonlocality.

Fig. 1

Variation of phase speed ($V_{r}$) against angular frequency ($\omega$) (low-frequency range)

Fig. 2

Variation of attenuation coefficient ($Q_{r}$) against angular frequency ($\omega$) (low-frequency range)

Figures 3 & 4 depict the variation of phase speed and corresponding attenuation coefficient of Rayleigh-type surface wave against frequency in high frequency range: $0\leq \omega \leq 4.8\times 10^{12}$. In this considered high-frequency range, the phase speed decreases continuously and finally die out. The corresponding attenuation coefficient also increases continuously with the increase of frequency. Hence, from Figs. 3 & 4, we conclude that the Rayleigh-type surface wave is highly dispersive and attenuating in high-frequency range. The real part of the speed of propagating wave vanishes at a very high value of angular frequency.

Fig. 3

Variation of phase speed ($V_{r}$) against angular frequency ($\omega$) (high-frequency range)

Fig. 4

Variation of attenuation coefficient ($Q_{r}$) against angular frequency ($\omega$) (high-frequency range)

Figures 5 & 6 show the comparison of phase speeds of Rayleigh-type surface wave and that of the transverse wave having speed $v_{4}$ (counterpart of the classical transverse wave) in the low-frequency range: $0\leq \omega \leq 12\times 10^{4}$ as well as in the high-frequency range: $0\leq \omega \leq 4.8\times 10^{12}$, respectively. It can be noticed that the transverse wave propagates with a faster speed than the speed of Rayleigh-type surface wave, which is similar to the well-establish fact about Rayleigh wave in Cauchy elastic half-space. The phase speed of both the waves approaches to zero at the same value of frequency, namely, $\omega _{c_{1}}=\displaystyle (c_{t}+k_{1})/\epsilon$, after which both Rayleigh-type and transverse waves disappear. From these figures, we conclude that the behavior of Rayleigh-type surface wave and that of the counterpart of the transverse wave is similar.

Fig. 5

Comparison of phase speeds of the counterpart of classical transverse wave and Rayleigh-type surface wave against angular frequency ($\omega$) (low-frequency range)

Fig. 6

Comparison of phase speeds of the counterpart of classical transverse wave and Rayleigh-type surface wave against angular frequency ($\omega$) (high-frequency range)

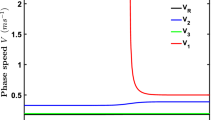
Figures 7 & 8 show the comparison of phase speed and corresponding attenuation coefficient of Rayleigh-type surface wave, respectively, propagating in the half-space composed of nonlocal micropolar thermoelastic materials with voids (NMTEMV), nonlocal micropolar elastic materials with voids (NMEMV), nonlocal thermoelastic materials with voids (NTEMV), nonlocal elastic material (NEM) and classical elastic material (CEM) in low-frequency range. From Fig. 7, it can be noticed that in the absence of micropolar parameters, the phase speed of Rayleigh-type surface wave propagates slower than that of in the medium with non-zero micropolar parameters. Also, due to the presence of void parameters, the phase speed of Rayleigh-type surface wave increases, whereas it propagates with a constant speed in the absence of void parameters in the frequency range: $0\leq \omega \leq 3.5\times 10^{3}$. In low-frequency range, the phase speed of surface wave is independent of nonlocal parameter ($\epsilon$). Also, the thermal parameters have almost negligible effect on the speed of propagating surface wave. This is because the wave with and without thermal parameters propagates with the same phase speed, as shown in Fig. 7. The variation of the attenuation coefficient against the frequency has been depicted on logarithmic scale to have a clear comparison with those in other mediums. From Fig. 8, it can be seen that the Rayleigh-type surface wave is attenuating in low-frequency range: $0\leq \omega \leq 1.1\times 10^{4}$, except that in classical elastic medium. This is because in the classical elastic medium, the Rayleigh-type surface wave is non-attenuating and propagates with real speed. The comparison of the attenuation coefficients of Rayleigh-type wave in NEM and in other media is not shown here because the attenuation coefficient in NEM is also found to be nil for all values of frequency considered. Hence, from Figs. 7 & 8, we conclude that the micropolar parameters enhances the speed of Rayleigh-type wave, while in the presence of void parameters, the Rayleigh-type surface wave becomes dispersive and attenuating in low-frequency range. Also, due to the presence of micropolar parameters, the surface wave is less dispersive as compared to that in the medium without micropolar parameters. It can be noticed that the nonlocal parameter ($\epsilon$) has a negligible effect on the speed of Rayleigh-type surface wave in low-frequency range. Furthermore, it is noticed that in NEM and CEM models, the Rayleigh-type surface wave propagates with real speeds.

Fig. 7

Comparison of phase speeds in different media against angular frequency ($\omega$) (low-frequency range)

Fig. 8

Comparison of attenuation coefficients in different media against angular frequency ($\omega$) on logarithmic scale (low-frequency range)

Figures 9 & 10 show the comparison of the phase speeds of Rayleigh-type surface wave and their corresponding attenuation coefficients, respectively, in different media under very high-frequency range. From Fig. 9, it can be noticed that the phase speed of Rayleigh-type surface wave decreases with increase of angular frequency in nonlocal medium and vanishes at a particular value of frequency. This value of frequency is equal to $\omega _{c_{1}}$ for the medium with micropolarity and $\omega _{c_{2}}=\displaystyle c_{t}/\epsilon$ for the medium without micropolarity. However, in Fig. 9, it is not clearly seen because the difference between these two frequencies is very less in comparison to the number of points on the horizontal axis. The Rayleigh-type surface wave propagates with constant phase speed in the medium without nonlocality. From Fig. 10, it is noticed that the attenuation coefficient of Rayleigh-type surface wave increases in the medium with thermal parameters, whereas in the absence of thermal parameters, the attenuation coefficient remains constant in high-frequency range. The surface wave is attenuating in NMTEMV and NTEMV media, beyond the frequency values $\omega \geq 4.2\times 10^{12}$ and $\omega \geq 3.77\times 10^{12}$, respectively. Hence, from these figures, we conclude that due to the presence of nonlocality, the Rayleigh-type surface wave is highly dispersive in high-frequency range and the wave ceases to propagate beyond a particular value of frequency. In the high-frequency range, the surface wave is highly attenuating in the thermoelastic medium and non-attenuating in the medium without thermal effects. Hence, thermal parameters have significant effect on the attenuation coefficients of the Rayleigh-type surface wave.

Fig. 9

Comparison of phase speeds in different media against angular frequency ($\omega$) (high-frequency range)

Fig. 10

Comparison of attenuation coefficients in different media against angular frequency ($\omega$) (high-frequency range)

Figures 11 & 12 depict the variation of the phase speeds and corresponding attenuation coefficients of Rayleigh-type surface wave, respectively, against the non-dimensional nonlocal parameter $\bar{\epsilon}(={\epsilon ^{2}\omega ^{2}_{0}}/{c^{2}_{l}})$, $\omega _{0}=2\pi \times 2000~s^{-1}$ is the standard angular frequency for a fixed value of frequency $\omega =2\pi \times 5000~s^{-1}$. It is found that the phase speed and corresponding attenuation of Rayleigh-type surface wave decreases with increase of non-dimensional nonlocal parameter $\bar{\epsilon}$. However, the phase speed decreases from $925~ms^{-1}$ to $907~ms^{-1}$ approximately and the rate of decrease of attenuation coefficient is very less (almost negligible) in the considered range of nonlocal parameter $\bar{\epsilon}$. From these figures, we conclude that the phase speed of Rayleigh-type wave is significantly affected, while its attenuation coefficient is hardly affected by the non-locality parameter.

Fig. 11

Variation of phase speed ($V_{r}$) against nonlocal parameter ($\bar{\epsilon}$)

Fig. 12

Variation of attenuation coefficient ($Q_{r}$) against nonlocal parameter ($\bar{\epsilon}$)

The tilt angle ($\theta _{4}$) is obtained from the relation (40) in terms of displacement components, namely, $u_{1}$ and $u_{3}$. Figure 13 depicts the variation of ($\theta _{4}$) against the angular frequency on logarithmic scale at origin and time $t=0$ for dissipative and non-dissipative media. The coefficients $A'_{2}$, $A'_{3}$, $B'_{4}$ and $B'_{5}$ are obtained in terms of coefficient $A'_{1}$, which is taken one unit. From Fig. 13, it can be seen that for the dissipative medium, the tilt is very small (almost nil), whereas for non-dissipative medium, it increases in the initial range of frequency up to $\omega \leq 352$ and then decreases after a certain value of frequency $\omega =352$ and approaches to zero ultimately. From this figure, we conclude that the axis of ellipse traced by the particle during the propagation of Rayleigh-type wave almost coincides with the coordinate axis in the dissipative medium.

Fig. 13

Variation of tilt angle ($\theta _{4}$) against angular frequency ($\omega$) on logarithmic scale

8 Conclusions

In the present paper, we have explored the possibility of propagation of Rayleigh-type surface waves in a half-space composed of nonlocal micropolar thermoelastic solid containing uniform distribution of voids. Only one Rayleigh-type wave is found to propagate in the considered model. From the present study, following conclusions can be inferred:

• 1. Only one Rayleigh-type surface wave can propagate, which is dispersive and attenuating in nature. The dispersive behavior is due to voids present in the medium under low frequency range, whereas, it is due to the nonlocality present in the medium under high-frequency range.

• 2. There exist two cut-off frequencies, one for nonlocal medium with micropolarity and other for nonlocal medium without micropolarity, beyond which the surface wave ceases to propagate.

• 3. The surface wave propagates with a slower speed than that of the transverse wave in the considered medium.

• 4. The micropolarity enhances the speed of Rayleigh-type surface wave, but decreases its dispersiveness in the low frequency range.

• 5. The nonlocality decreases the phase speed of surface wave, but does not affect the attenuation coefficient.

• 6. The path traced out by the particle of the medium during the propagation of Rayleigh-type surface wave is found to be elliptical.