Rayleigh-type waves in magneto-elastic half-space containing voids

Abstract

Rayleigh-type surface waves propagating in a magneto-elastic half-space containing voids are studied. Dispersion equation is derived under suitably constructed boundary conditions, which involves elastic, electro-magnetic, void parameters and angular frequency, but contains radicals, making it difficult to solve analytically. However, under limiting frequencies, the dispersion equation is analyzed and discussed. The effect of various parameters on phase velocity of propagating Rayleigh-type surface waves is investigated and shown graphically for a particular model. The effect of induced electric field on considered surface waves is also studied and explained. It is shown that the particles near the boundary surface move in an elliptic manner. However, if there is no phase difference between the displacement components, then we have a degenerate case. Some special cases of dispersion relation are also deduced from the present formulation.

1 Introduction

Lord Rayleigh [1] discovered a kind of surface waves propagating along the boundary surface of a uniform elastic half-space called Rayleigh waves after his name. The amplitude of these waves confines near the boundary surface of the half-space and decays exponentially with distance into the half-space. The motion of these waves involves a combination of both longitudinal and transverse waves, causing the particles to follow elliptically retrograde motion near the surface (see Love [2]). These waves have vast applications in the areas of geophysics, acoustics, seismology, electronic devices and non-destructive testings for detecting defects. Researchers have investigated the propagation of Rayleigh waves in various different models and under different circumstances, whose papers are available in open literature. They have generally derived dispersion equation and investigated the condition of existence and propagation characteristics. Very few of them are being cited here, viz., Eringen [3] discussed the existence of Rayleigh waves having small wavelengths and propagating in a non-local elastic solid half-space. He discovered that the Rayleigh waves are dispersive in nature and have same attenuation rate as that of classical Rayleigh waves. Abd-Alla [4] developed frequency equation of Rayleigh wave propagation in an orthotropic elastic solid body under the influence of gravity field and initial stress. He claimed that when the solid is subjected to earth’s gravity and initial compression, the velocity of Rayleigh wave increases significantly. Furthermore, in the absence of earth’s gravity field, the classical frequency equation is recovered as a special case for an isotropic, initially unstressed medium. Papers by Chirita [5], Rymarz [6] and Acharya and Mondal [7] are some remarkable contributions in the pertinent area of research. Apart from the study of Rayleigh-type surface waves, Kuznetsov [8] had proved the existence of non-Rayleigh type surface waves in an anisotropic elastic half-spaces. He has also presented an example in the support of his claim.

In the linear theory of elasticity, the deformation of classical elastic material is proportional to the amount of load applied to it. Under classical elasticity, the interaction between adjacent elements of the elastic continuum is governed only by force stress vector, which depends on displacement vector field. The stress–strain relation for classical elastic solid is given by well known generalized Hooke’s law. However, for an elastic material containing void pores, the response to the applied load is not consistent with those of classical elastic solids and affected by the presence of voids. Cowin and his co-worker [9, 10] presented linear and nonlinear theories of elastic material with voids as a generalization to the classical theory of elasticity. They have introduced a new independent kinematic variable known as ’change in void volume fraction,’ in addition to the displacement vector field, by factorizing the bulk density of the body as a product of density of matrix material field and void volume fractional field. Thus, corresponding to this new kinematic variable, they introduced a stress vector called ’equilibrated stress vector’ in their theory. The idea to incorporate voids in the elastic material was stemmed from the continuum theory of granular materials formulated by Goodman and Cowin [11]. Later, Puri and Cowin [12] investigated the existence of plane harmonic waves in a linear elastic material with voids and showed that a lone distortional wave and two coupled dilatational waves may propagate in the medium with distinct speeds. Of the two coupled dilatational waves, one is predominantly a wave carrying change in void volume fraction field and other one is predominantly classical dilatational wave. They analyzed that at high (low) frequencies the predominantly classical elastic wave propagates with the speed of classical dilatational wave (less than the speed of classical dilatational wave). Later, Iesan [13] extended the linear theory of elastic material with voids under thermal interactions and developed basic field equations for a uniform thermo-elastic material with voids. Using Iesan’s theory, Singh and Tomar [14] discussed the propagation and existence of harmonic plane waves in a medium of infinite extent. They inferred that a lone distortional wave and three coupled dilatational waves may propagate in the considered medium, all traveling with distinct speeds. They have also shown that the effect of temperature and voids on the wave speeds can be noticed theoretically from the dispersion relation of coupled dilatational waves.

Chandrasekharaiah [15] explored the possibility of surface wave propagation in a uniform elastic half-space containing voids. He derived the dispersion relations yielding the speed of propagation of various possible waves and revealed that contrary to the classical case, the waves are dispersive in nature. He further added that in a low-frequency domain, the presence of voids brings significant modification in the expression of the phase speeds when compared with those of classical elastic case. Later, Chandrasekharaiah [16] investigated the propagation of Rayleigh waves under the effects of surface stresses and voids in an elastic medium with voids. He concluded that the secular equation is dispersive and this dispersive nature is occurred due to the presence of voids and the stresses exerted by the boundary. He further added that in a low-frequency region when the stresses are caused due to residual surface tension, there exists a critical wavelength beyond which the surface waves propagate with the speed of classical shear waves. However, the surface wave ceases to exist below this critical value of wavelength. He also depicted that the critical wavelength varies with the intensity of surface tension. Kaur et al. [17] have presented the propagation of surface waves in an isotropic homogeneous non-local elastic solid half-space containing voids. They showed that there exists only one mode of Rayleigh-type surface waves, which is dispersive. This surface wave involves void and non-locality parameters. Further, they deduced that during the propagation of Rayleigh-type surface waves, the particles follow elliptic motion. Some remarkable contributions in the field of surface waves containing voids are from Bucur et al. [18], and Chirita [19] among others.

The interaction of deformable bodies with electromagnetic fields has gained popularity among many researchers due to its wide range of applications in magnetically levitated vehicles, magnetic launchers, high energy storage devices, and detecting faults in ferrous metals. Dunkin and Eringen [20] studied the propagation of elastic waves subjected to large magnetic and electric fields interactions. They found that electromagnetic fields have a substantial impact on the phase velocity of elastic waves. They conveyed that the waves get reduced to Alfven waves when the shear modulus is zero. Eringen [21] devised a continuum theory of microstretch elasticity to explore the deformation of materials having interconnected voids and microcracks (such as porous solids, animal bones nano-composites) under electro-magnetic interactions. He developed constitutive relations and governing equations for both anisotropic and isotropic microstretch elastic solids. Matsumoto [22] reviewed the mechanics of deformable bodies under magnetic field. He laid down the conservation laws and electromagnetic field equations to analyze the behavior of electromagnetic deformable materials. He emphasized that the application of magnetic field may cause structural instabilities and damage to the material. Tomar and Kumar [23] developed the governing equations for homogeneous, isotropic elastic material with voids under electromagnetic interactions. They discussed the impact of large magnetic (electric) field on the phase speeds of harmonic plane waves. They conveyed that under large magnetic (electric) field, there may propagate three (five) basic waves, all propagating with distinct speeds. Other useful literature pertaining to mechanical waves under magnetic field includes Ericksen [24], Eringen and Maugin [25] among others.

The aforementioned theories are limited to the study of body wave propagation under the influence of magnetic field. The study of propagation of surface waves through magnetic field received attention since Kaliski and Rogula’s [26] findings. They investigated the existence of Rayleigh-type surface waves for a perfectly conducting half-space, placed in a magnetic field. They assumed that the magnetic permeability of the medium is same as that in the vacuum. They observed the dependence of characteristic equation on the orientation and magnitude of the applied magnetic field. It was found that when the magnetic field is applied normally (or tangentially) to the direction of propagation of Rayleigh waves, the corresponding velocity increases with the intensity of the applied field. Thereafter, in the context of Kaliski and Rogula [26], Tomita and Shindo [27] studied the propagation of Rayleigh waves in a semi-infinite thermally and electrically conducting uniform elastic medium. They obtained approximate solutions for both magneto-elastic and thermo-elastic coupling. They discovered that when a magnetic field is applied parallel to the boundary surface, the magnitude of the characteristic wave speed changes significantly. Further, in the subsequent study, Lee and Its [28] presented a theory to discuss the Rayleigh wave propagation in a conducting medium under the influence of an applied magnetic field. The purpose of their study is to discuss non-destructive testing of materials for their structural and mechanical properties. They investigated the dependence of Rayleigh waves on electromagnetic parameters in tangentially and normally oriented magnetic fields. They conveyed that in a tangentially applied magnetic field, the variation in magnetic permeability results in a sudden change in the wave velocity, whereas in a normally oriented magnetic field, the wave follow asymptotic behavior. A small change is observed in the expression of wave velocity, even under the application of a high-intensity magnetic field. Additionally, it was shown that under a strong magnetic field, there exists a critical value of magnetic permeability beyond which the surface waves cease to exist. Abd-Alla and his co-workers [29] discussed the effects of magnetic field, gravity, and initial stress on the propagation of Rayleigh waves in an orthotropic elastic medium. They observed that the speed of Rayleigh waves decreases with increase in initial stress and magnetic field.

In the present work, the propagation of Rayleigh-type waves in elastic material with voids and subjected to an applied magnetic field has been discussed. For this, admissible boundary conditions are constructed to obtain the secular equation for the propagation of Rayleigh waves. The phase speed and corresponding attenuation coefficients of Rayleigh waves are computed and analyzed at limiting values of frequency. It is observed that there exists a lone Rayleigh-type wave which is dispersive. The effect of induced electric field on the wave propagation is discussed. For a specific model, the dependence of Rayleigh wave speed on the magnetic field, voids, frequency, and electromagnetic parameters have been depicted graphically.

2 Field equations and relations

Following Tomar and Kumar [23], the vectorial form of equations of motion for a homogeneous, isotropic elastic solid containing voids under electromagnetic interactions in the absence of mechanical body forces is given by

$$\begin{aligned}{} & {} (\lambda +\mu )\nabla \nabla \cdot \textbf{u}+\mu \nabla ^2\textbf{u}+a\nabla \nu +\textbf{f}^E=\rho \ddot{\textbf{u}}, \end{aligned}$$

(2.1)

$$\begin{aligned}{} & {} \alpha \nabla ^2\nu -a\nabla \cdot \textbf{u}+d\nabla \cdot \mathcal {E}-\zeta \nu =\rho \kappa \ddot{\nu }, \end{aligned}$$

(2.2)

where $\lambda$ and $\mu$ are conventional Lame’s elastic parameters; $\textbf{u}$ is the displacement vector; $\rho$ is the material mass density; a,  $\alpha$ and $\zeta$ are material parameters due to the presence of voids; $\nu$ represents the change in void volume fraction from the reference state; d is the cross coupling coefficient; $\mathcal {E}$ denotes the electric field vector for the moving frame; $\kappa$ is the equilibrated inertia; superposed dot denotes the time derivative; and $\textbf{f}^E$ denotes the electromagnetic force. The current problem is concerned with the dynamical study of uniform elastic solid medium containing voids under magnetic field. Following Eringen [25], the form of electromagnetic force $\textbf{f}^E$ has been taken as

$$\begin{aligned} \textbf{f}^E=\frac{1}{c}(\textbf{J}\times \textbf{B}), \end{aligned}$$

where $\textbf{J}$ and $\textbf{B}$ are the usual current density vector and magnetic flux vector, respectively, and the symbol c denotes the speed of light. This electromagnetic force is taken as Lorentz’s body force in the problem.

To observe and approximate the material’s response to external forces, we have a set of relations between two or more physical quantities known as constitutive relations. Following Tomar and Kumar [23], the mechanical set of constitutive relations for a uniform magneto-elastic solid containing voids are given by

$$\begin{aligned} \begin{aligned}&t_{ij}=(\lambda e_{kk}+a\nu )\delta _{ij} + 2\mu e_{ij}, \qquad S_i=\alpha \nu _{,i} + d \mathcal {E_i}, \end{aligned} \end{aligned}$$

(2.3)

where $t_{ij}$ denotes the components of stress tensor; $S_i$ denotes the components of equilibrated stress vector; and $e_{ij}$ denotes the components of strain tensor connected with the displacement components $u_i,$ as

$$\begin{aligned} 2e_{ij}=u_{i,j}+u_{j,i}. \end{aligned}$$

(2.4)

Here and after, a comma in the subscript denotes the spatial partial derivative. The electromagnetic part of constitutive relations is given by

$$\begin{aligned} \begin{aligned}&\mathcal {J_i}=\sigma \mathcal {E_i}, \qquad {\mathcal M_i}=-\chi _m B_i,\qquad P_i=-(d\nu _{,i} + \chi ^E \mathcal {E_i}), \end{aligned} \end{aligned}$$

(2.5)

where $\chi ^E$ is the di-electric susceptibility; $\chi _m$ is the magnetic susceptibility; $\sigma$ is the electric conductivity; $P_i$ denotes the components of Polarization vector; and ${\mathcal M_i}$ denotes the components of Magnetization vector.

3 Formulation of problem

With reference to a rectangular cartesian coordinate system Oxyz,  we consider an elastic half-space, say M,  containing evenly distributed voids throughout. Here, it is assumed that the surface of the half-space M coincides with the $x-y$ plane, and the positive direction of $z-$ axis is pointing vertically downward into the half-space. Thus, the region occupied by the half-space is given by $M=\{(x,y,z): -\infty< x,y<\infty , 0\le z<\infty \}.$ To discuss the propagation of surface waves, we shall take the Rayleigh wave propagating in the direction of positive $x-$ axis satisfying the radiation property, i.e., the amplitude of the wave keeps on decaying very fast with depth along the positive direction of $z-$ axis. We shall consider a two-dimensional problem in $x-z$ plane, for which the displacement vector will take the form $\mathbf{{u}}=(u,0,w).$ Since the medium is placed under magnetic field only and applied normal to the $x-z$ plane, therefore, the applied magnetic field $\textbf{H}^0$ is oriented along the positive direction of $y-$ axis, that is, $\textbf{H}^0=(0,H,0).$ This magnetic field will induce magnetic field $\mathbf{{h}}=(0,h,0)$ and electric field $\textbf{e},$ both of small order, whose higher powers can be neglected. Therefore, the expressions of net magnetic field $\textbf{H},$ and electric field $\textbf{E},$ in the medium can be expressed as

$$\begin{aligned} \textbf{H}=\textbf{H}^0+\textbf{h}, \qquad \textbf{E}=\textbf{0}+\textbf{e}, \end{aligned}$$

(3.1)

where the induced electric field $\textbf{e}$ generates electric current in the medium. The flow of current depends on the conductive behavior of the medium. Since the material can be of varying electric conductivity, we shall study the wave characteristics in a high and low electric conductive material separately. Maxwell’s equation for a slowly moving electrically conducting medium in linearized form is given by

$$\begin{aligned} \begin{aligned} \nabla \times \{\textbf{h}, \textbf{e}\}=\frac{1}{c}\{\textbf{J}+\dot{\textbf{e}}, -\mu _m\dot{\textbf{h}}\},\qquad \nabla \cdot \textbf{h}=0, \qquad \textbf{e}=-\frac{\mu _m}{c}(\dot{\textbf{u}}\times \textbf{H}^0), \end{aligned} \end{aligned}$$

(3.2)

where $\mu _m$ is the permeability coefficient, $\chi _m$ has been defined earlier such that $\textbf{B}=\mu _m\textbf{H}$ and $\mu _m=(1+\chi _m)^{-1}.$ Owing to relations in (3.2), one can see that the Lorentz’s body force takes the form $f^E=\mu _m(\nabla \times \textbf{h})\times \textbf{H}^0,$ within the context of linear theory.

Following Dunkin an Eringen [20], the boundary conditions at the surface of magneto-elastic medium are given by

$$\begin{aligned} \begin{aligned} \textbf{n}\times [\![\textbf{E}+ \frac{1}{c}(\dot{\textbf{u}}\times \textbf{B})]\!]= \textbf{0}, \quad \textbf{n} \times [\![\textbf{H} ]\!]=\textbf{0},\\ \textbf{n}\cdot [\![\textbf{B} ]\!]=0, \qquad n_{j}[\![t_{ij}+t_{ij}^E ]\!]=0, \qquad n_{j}[\![S_{j} ]\!]=0, \end{aligned} \end{aligned}$$

(3.3)

where $\textbf{n}$ is the outward unit normal vector and $[\![A ]\!]$ denotes the difference in the values of quantity A,  exterior and interior of the medium. The quantity $t_{ij}^E$ denotes the Maxwell’s electromagnetic stress tensor given by

$$\begin{aligned} t_{ij}^E=B_{i}H_{j}-\frac{1}{2}\left( B^2-2 \mathcal {M}\cdot \textbf{B}\right) \delta _{ij}, \qquad i,j=1,2,3 \end{aligned}$$

(3.4)

where $\delta _{ij}$ is conventional Kronecker delta symbol and $B=|\textbf{B}|.$ The parameters in the exterior of the half-space will be represented by an overhead bar corresponding to the parameters in the magneto-elastic half-space with voids. Moreover, if the half-space is surrounded by vacuum, then all the elastic and void parameters and hence the stress tensors vanish outside the half-space, i.e., ${\bar{t}}_{ij}={\bar{S}}_{j}=0.$ Therefore, the boundary condition (3.3)$_{4}$ and (3.3)$_{5}$ reduce to

$$\begin{aligned} t_{ij}n_{j}=[\![t_{ij}^E ]\!]n_{j}, \qquad S_{j}n_{j}=0. \end{aligned}$$

(3.5)

Introducing the scalar potential p and solenoidal vector potential $\textbf{U}$ through Helmholtz decomposition of vector $\textbf{u},$ the displacement components u and w can be written as

$$\begin{aligned} u=p_{,x}-U_{,z}, \qquad w=p_{,z}+U_{,x}, \end{aligned}$$

(3.6)

where U is the y-component of vector potential $\textbf{U}.$ For Rayleigh waves propagating with speed $c_{R}$ in the positive direction of $x-$ axis, we shall take

$$\begin{aligned} \{p,\nu ,U\}=\{{\hat{p}},{\hat{\nu }},{\hat{U}}\}\exp {(-\gamma z)}\exp \{\iota (kx-\omega t)\}, \end{aligned}$$

(3.7)

where ${\hat{p}},$ ${\hat{\nu }}$ and ${\hat{U}}$ are constants, $\omega$ denotes the angular frequency and k is the wavenumber satisfying the relation given by $\omega =k c_{R}.$ The factor $\exp (-\gamma z)$ will comply the radiation property as $z\rightarrow \infty ,$ provided $\gamma > 0.$ In case, when $\gamma$ is complex valued, then $\exp (-\gamma z)$ will satisfy radiation condition provided $\Re (\gamma )> 0.$ Further, the wavenumber k may be real or complex valued, while the frequency $\omega$ will be considered a positive real quantity always. When k is real valued and $\omega$ being real quantity, the Rayleigh wave speed will be real valued. However, when k is complex valued, then $c_{R}$ will be complex valued for real values of $\omega .$ In such a case, the wavenumber k with positive imaginary part ($\Im (k)>0$) corresponds to the wave propagating in the positive direction of $x-$ axis¹.

Inserting (3.2) and (3.6) into (2.1) and (2.2) and using (3.7), we obtain

$$\begin{aligned}{} & {} \{c_{\ell \ell }^2(\gamma ^2-k^2) + \omega ^2\}{\hat{p}}+c_a^2{\hat{\nu }}=0, \end{aligned}$$

(3.8)

$$\begin{aligned}{} & {} \{c_{t}^2(\gamma ^2-k^2)+\omega ^2\}{\hat{U}}=0, \end{aligned}$$

(3.9)

$$\begin{aligned}{} & {} \{c_{\alpha }^2(\gamma ^2-k^2)-c_{\zeta }^2+\omega ^2\}{\hat{\nu }}-\frac{c_{a}^2}{\kappa }(\gamma ^2-k^2){\hat{p}}=0, \end{aligned}$$

(3.10)

where

$$\begin{aligned} c_{\ell \ell }^2=c_{\ell }^2+R_{H}^2, \,\, c_{\ell }^2=\frac{\lambda +2\mu }{\rho }, \,\, R_{H}^2=\frac{\mu _mH^2}{\rho }, \,\, c_{\alpha }^2=\frac{\alpha }{\rho \kappa }, \,\, c_{\zeta }^2=\frac{\zeta }{\rho \kappa }, \,\, c_{a}^2=\frac{a}{\rho }, \,\, c_{t}^2=\frac{\mu }{\rho }. \end{aligned}$$

Here, the quantities $c_\ell$ and $c_{t}$ are, respectively, the speeds of classical dilatational and transverse waves. Equations (3.8) and (3.10) represent a system of homogeneous equations in two unknowns ${\hat{p}}$ and ${\hat{\nu }},$ and they will provide non-trivial solution if

$$\begin{aligned} D'(\gamma ^2-k^2)^2+B'\omega ^2(\gamma ^2-k^2)+A'\omega ^4=0, \end{aligned}$$

(3.11)

where

$$\begin{aligned} D'=c_{\alpha }^2c_{\ell \ell }^2, \qquad B'=c_{\alpha }^2+c_{\ell \ell }A'+\frac{c_{a}^4}{\kappa \omega ^2}, \qquad A'=1-\frac{c_{\zeta }^2}{\omega ^2}. \end{aligned}$$

(3.12)

Equations (3.9) and (3.11) are, respectively, the linear and quadratic equations in $(\gamma ^2 - k^2).$ The three values of $\gamma ^2$ obtained from roots are given by

$$\begin{aligned} \gamma _{i}^2=k^2m_{i}^2, \qquad m_{i}^2=1-\frac{c_{R}^2}{V_{i}^2}, \qquad i=1,2,3, \end{aligned}$$

(3.13)

where the expressions of $V_i$’s are given by

$$\begin{aligned} V_{1,2}^2=\frac{1}{2A'}\left( B'\pm \sqrt{B'^2-4A'D'}\right) , \quad V_3=c_{t}. \end{aligned}$$

(3.14)

It has been shown earlier in Kumar and Tomar [30] that $V_1$ and $V_2$, respectively, represent the speeds of two coupled dilatational waves and $V_3$ is the speed of transverse wave propagating in an elastic medium with voids subjected to magnetic field. The wave speeds $V_{1,2}^2$ are real valued provided $A' > 0.$ Further, it can be noticed from (3.13) that the quantity $\gamma$ will be real and positive provided $c_{R} < V_{i}.$ Thus, the condition of Rayleigh-type surface waves is given by

$$\begin{aligned} 0< c_{R} < V_{i}. \end{aligned}$$

The expressions of relevant quantities p,  $\nu$, and U for the propagation of Rayleigh-type surface waves are given by

$$\begin{aligned} \{p, \nu \}=\sum _{j=1}^2\{A_{j}, \mathcal {B}_{j}\}\exp {(-km_{j}z)}e^{\iota (kx-\omega t)}, \quad U=A_{3}\exp {(-km_{3}z)}e^{\iota (kx-\omega t)} \end{aligned}$$

(3.15)

where the amplitudes $\mathcal {B}_{1}$ and $\mathcal {B}_{2}$ of the potential $\nu$ are connected with amplitudes $A_{1}$ and $A_{2}$ of potential p via relation

$$\begin{aligned} \mathcal {B}_{j}=\eta _{j}A_{j}, \qquad \eta _{j}=\frac{k^2}{c_{3}^2}\left[ (1-m_{j}^2)c_{\ell \ell }^2-V_{j}^2\right] , \quad j=1,2. \end{aligned}$$

In the following section, we shall develop the dispersion relation for the propagation of Rayleigh-type surface waves in a magneto-elastic half-space containing voids.

4 Boundary conditions and Dispersion relation

We shall assume that the upper space of the half-space M is vacuum so that the boundary surface of the half-space is free from all kinds of stresses. Therefore, the suitable boundary conditions at the interface $z=0$ between the vacuum half-space and the magneto-elastic half-space containing voids (that is, the stress-free boundary surface of the half-space M) will be the vanishing of mechanical and equilibrated stresses. In the present model, the normal vector to the interface is $\textbf{n}=(0,0,1)$ and we shall assume that these boundary conditions hold for all values of x and time t at the interface $z=0.$ Owing to the relations (3.1), (3.3) and (3.5), the boundary conditions at $z=0$ under the interaction of primary magnetic field can be analytically expressed as

$$\begin{aligned}{} & {} (i)\quad t_{31}+t_{31}^E-{{{\bar{t}}}_{31}}^E=0, \quad (ii)\quad t_{33}+ t_{33}^E-{{\bar{t}}_{33}}^E=0, \quad (iii)\quad S_{3}=0, \end{aligned}$$

(4.1)

$$\begin{aligned}{} & {} (iv) \quad H-{\bar{H}}=0, \quad (v)\quad h-{\bar{h}}=0, \end{aligned}$$

(4.2)

where $t_{31}^E$ and $t_{33}^E$ are the components of electromagnetic stress tensor in the elastic half-space and those with overhead bar are the corresponding quantities in the vacuum half-space. Since the medium is surrounded by vacuum, therefore the magnetic susceptibility ${{\bar{\chi }}}_{m}$ in vacuum vanishes, that is, ${{\bar{\chi }}}_m=0,$ and owing to relation ${{\bar{\mu }}}_m=(1+\bar{\chi }_{m})^{-1},$ the permeability coefficient in vacuum becomes ${{\bar{\mu }}}_{m}=1.$ Under these formulations and with the aid of relations (4.2), (3.1) and (3.4) followed by (3.2), the difference in the components of electromagnetic stress tensor inside and outside the elastic half-space can be written as

$$\begin{aligned} t_{31}^E-{{{\bar{t}}}_{31}}^E=0, \qquad t_{33}^E-{\bar{t}_{33}}^E=-(\mu _{m}-1)^2H(\nabla \cdot \textbf{u}). \end{aligned}$$

(4.3)

With the aid of equations (2.3) and (3.6), the boundary conditions given in (4.1) at $z=0$ can be written in terms of p and U as follows

$$\begin{aligned}{} & {} 2p_{,xz}+U_{,xx}-U_{,zz}=0, \end{aligned}$$

(4.4)

$$\begin{aligned}{} & {} H^2\{\mu _m-(1+\mu _m^2)\}\nabla ^2 p+2\mu (U_{,xz}-p_{,xx})+\rho \ddot{p}=0 \end{aligned}$$

(4.5)

$$\begin{aligned}{} & {} c_{\ell \ell }^2\nabla ^2 p_{,z}-\ddot{p}_{,z}=0 \end{aligned}$$

(4.6)

Equations (4.5) and (4.6) have been obtained by eliminating $\nu$ in terms of scalar potential p by manipulating (3.6) and (2.1) under considered assumptions. Further, on inserting the potentials given via (3.15) into the boundary conditions (4.4)-(4.6), we shall obtain a system of three linear homogeneous equations in three unknowns, namely $A_1,$ $A_2$, and $A_3.$ For a nonzero solution of these unknowns, the determinant of their coefficient matrix (say $[m_{ij}]_{3 \times 3}$) must vanish. Therefore, the desired dispersion relation is given by

$$\begin{aligned} m_{31}(m_{12}m_{23}-m_{22}m_{13})-m_{32}(m_{11}m_{23}-m_{13}m_{21})=0, \end{aligned}$$

(4.7)

where

$$\begin{aligned} \begin{aligned} m_{1i}=2-\frac{c_R^2}{c_{t}^2}-\ell _i, \, m_{13}=-2m_{3}, \, m_{2i}=2m_{i}, \, m_{23}=-(1+m_{3}^2), \, m_{3i}=m_{i}n_{i},\\ \ell _{i}=\frac{R_{H}^2}{c_{t}^2}\left[ 1-\frac{1+\mu _{m}^2}{\mu _{m}}\right] (1-m_{i}^2), \qquad n_{i}=\frac{c_{R}^2}{c_{\ell \ell }^2}+m_{i}^2-1, \quad i=1,2. \end{aligned} \end{aligned}$$

(4.8)

The dispersion relation (4.7) can be rewritten as

$$\begin{aligned} \left( 2-\frac{c_{R}^2}{c_{t}^2}\right) ^2=\frac{4m_{1}m_{2}m_{3}(n_{1}-n_{2})-(1+m_{3}^2)(\ell _{1}n_{2}m_{2}-\ell _{2}n_{1}m_{1})}{n_{1}m_{1}-n_{2}m_{2}} \end{aligned}$$

(4.9)

Equation (4.9) provides the speed of Rayleigh-type surface waves in an elastic material with voids under the influence of applied magnetic field. Note that this equation involves material parameters and angular frequency $\omega .$ Therefore, the Rayleigh wave is dispersive and dependent on material characteristics of the model. One can notice that the secular equation (4.9) is an irrational equation in $c_{R},$ which contains real-valued quantities; therefore, the wave speed $c_{R}$ of the wave in question may be real valued. If the speed $c_{R}$ is found to be complex-valued for some real-valued angular frequency $\omega ,$ that is, $c_{R}=\Re (c_{R})+ \iota \Im (c_{R}),$ then the phase speed $V_{R}$ and the corresponding attenuation coefficient $Q_{R}$ of the Rayleigh-type surface wave are given by (see Borcherdt [31])

$$\begin{aligned} V_{R}=\frac{|c_{R}^2|}{\Re (c_{R})}, \qquad Q_{R}=-\frac{\omega \Im (c_{R})}{|c_{R}^2|}, \end{aligned}$$

(4.10)

where $|c_{R}^2|$ denotes the modulus value of $c_{R}^2.$

It can be seen that the secular equation (4.9) involves terms containing surds, therefore, solving it analytically/algebraically will be a challenging task. To obtain a radical free dispersion equation, it has been squared twice and then simplified to a polynomial equation with real coefficients given by

$$\begin{aligned} \sum _{\ell =0}^{10} a_{\ell }z^{\ell }=0, \qquad z \equiv c_{R}^2, \end{aligned}$$

(4.11)

where the expressions of various coefficients $a_\ell , (\ell =1-10)$ are presented in Appendix-1. It is worth noting that not all roots of this polynomial equation satisfy the original secular equation, as some additional roots have been introduced during the rationalization process. Those roots that satisfy the original secular equation are then tested for the radiation property of the wave field. These short listed roots ought to be the wave speeds for possible surface waves in the considered magneto-elastic half-space containing voids.

Since the wave is dispersive in nature, therefore, we can discuss the speed of Rayleigh-type surface waves at limiting low and high frequencies.

(i) Limitly low frequency: When the angular frequency is very low, that is, $\omega \rightarrow 0,$ then following Kumar and Tomar [30], the speeds of various body waves reduce to

$$\begin{aligned} V_{1}^2 \rightarrow c_{\ell \ell }^2-\frac{a^2}{\rho \zeta }, \qquad V_{2}^2 \rightarrow 0, \qquad V_{3}^2=c_{t}^2. \end{aligned}$$

(4.12)

Under these outcomes, the dispersion equation (4.9) in limitly low frequency domain reduces to

$$\begin{aligned} \left( 2-\frac{c_{R}^2}{c_{t}^2}\right) ^2=4\sqrt{1-\frac{c_{R}^2}{V_{1}^2}}\sqrt{1-\frac{c_{R}^2}{c_{t}^2}}-\left( 2-\frac{c_{R}^2}{c_{t}^2}\right) \frac{R_{H}^2}{c_{t}^2}\left[ \frac{1+\mu _{m}^2}{\mu _{m}}-1\right] \frac{c_{R}^2}{V_{1}^2} \end{aligned}$$

(4.13)

Therefore, at limitly low frequency, the Rayleigh-type wave is influenced by the presence of voids. Moreover, the application of the primary magnetic field affects the magnitude of Rayleigh-type wave when compared to the classical Rayleigh wave. Note that in the case when $a=H=0,$ the above dispersion equation (4.13) reduces to the well-known dispersion equation of classical Rayleigh wave.

(ii) Limitly high frequency: When the angular frequency is very high, that is, $\omega \rightarrow \infty ,$ then from (3.14), the wave speeds $V_{i}$ reduce to

$$\begin{aligned} V_{1}^2 \rightarrow c_{\ell \ell }^2, \qquad V_{2}^2 \rightarrow c_{\alpha }^2, \qquad V_{3}^2=c_{t}^2 \end{aligned}$$

It can be verified that at limitly high values of frequency, the quantity $n_{1}$ in dispersion equation (4.9) vanishes. Therefore, the dispersion equation (4.9) in the present case reduces to

$$\begin{aligned} \left( 2-\frac{c_{R}^2}{c_{t}^2}\right) ^2=4\sqrt{1-\frac{c_{R}^2}{c_{\ell \ell }^2}}\sqrt{1-\frac{c_{R}^2}{c_{t}^2}}-\left( 2-\frac{c_{R}^2}{c_{t}^2}\right) \frac{R_{H}^2}{c_{t}^2}\left[ \frac{1+\mu _{m}^2}{\mu _{m}}-1\right] \frac{c_{R}^2}{c_{\ell \ell }^2} \end{aligned}$$

(4.14)

Thus, we notice that at limitly high frequency, the dispersion equation and hence the Rayleigh-type surface wave remain unaffected by the presence of voids in the medium. Moreover, it is the applied magnetic field H,  which brings some significant changes in the speed of Rayleigh-type wave. Note that if applied magnetic field is absent, that is, $H=0,$ then equation (4.14) reduces to the well-known dispersion equation of classical Rayleigh wave.

Next, we shall examine the possibility of propagation of Rayleigh-type wave in the material with low electric conductivity. It can be noticed from the constitutive relation (2.5)$_1,$ that in low conductive material, the net current $\textbf{J}$ is zero. Following Kumar and Tomar [30], the linearized form of Maxwell’s equations for low conductive material are given by

$$\begin{aligned} \begin{aligned} \nabla \times \textbf{h}= \textbf{0}, \qquad \nabla \cdot \textbf{h}= 0,\qquad \nabla \times \textbf{e}=\textbf{0}, \qquad \nabla \cdot \textbf{e}=d\nabla ^2\nu /(1-\chi ^E). \end{aligned} \end{aligned}$$

(4.15)

To derive the dispersion equation in this case, one may carry out a similar analysis as performed earlier for materials with high conductivity. After careful analysis, it is found that the secular equation for Rayleigh-type wave in low electric conductive material can be obtained by replacing the quantities $c_{\ell \ell }^2,$ $\alpha$ and $\ell _{i}~(i=1,2)$ with the quantities $c_{\ell }^2,$ $\mathcal {A}=\alpha +d^2/(1-\chi ^E)$ and 0, respectively. Under these observations, the dispersion equation (4.9) reduces to

$$\begin{aligned} \left( 2-\frac{c_{R}^2}{c_{t}^2}\right) ^2=\frac{4m_{1}m_{2}m_{3}(n_{1}-n_{2})}{n_{1}m_{1}-n_{2}m_{2}}. \end{aligned}$$

(4.16)

It is worth noting that for low electric conductive materials, the dispersion equation contains parameters pertaining to the induced electric field. As a result, the effect of induced electric field on Rayleigh-type surface waves can be noticed. Furthermore, if these parameters are set to zero, the problem reduces to an investigation of Rayleigh-type waves in elastic material with voids.

5 Particle motion

In this section, we shall analyze the path followed by the particles when the Rayleigh-type surface waves progress along the boundary of the half-space. Since the wave motion adheres to the boundary surface, therefore to determine the path described by the particles, we shall obtain the parametric equation of the locus. For this purpose, we substitute the potentials given in (3.15) into the displacement components given in equation (3.6). One may notice that the displacement components u and w, in general, are complex valued. Therefore, there exists a phase difference between these two components. Using Euler’s formula, the parametric representation of the real parts of displacement components is given by

$$\begin{aligned} \{\Re (u), \Re (w)\}=\{|\mathcal {U}|\cos (q+\alpha _1), -|\mathcal {W}|\cos (q+\alpha _2)\}e^{-\Im (k)x}, \end{aligned}$$

(5.1)

where

$$\begin{aligned} \{\mathcal {U}, \mathcal {W}\}=\sum _{i=1}^3\{1, m_i\}kA_{i}e^{-km_{i}z},\quad q=\Re (k)x-\omega t, \qquad \{\alpha _1, \alpha _2\}=\{\arg (\mathcal {U}), \arg (\mathcal {W})\}. \end{aligned}$$

Eliminating the parameter q from the relations given in (5.1), we obtain the path traced by the particles as

$$\begin{aligned} A_{0}\{\Re (u)\}^2+B_{0}\{\Re (u)\Re (w)\}+C_{0}\{\Re (w)\}^2=1, \end{aligned}$$

(5.2)

where

$$\begin{aligned}{} & {} A_{0}=(|\mathcal {U}|D_{0})^{-2}, \qquad B_{0}=2(|\mathcal {U}||\mathcal {W}|D_{0}^2)^{-1}\cos \eta , \qquad C_{0}=(|\mathcal {W}|D_{0})^{-2}, \nonumber \\{} & {} D_{0}= e^{-\Im (k)x}\sin \eta , \qquad \eta =\arg \mathcal {U}-\arg \mathcal {W}=\alpha _1-\alpha _2. \end{aligned}$$

(5.3)

Equation (5.2) is a second-degree equation with real coefficients. If both $\Re (u)$ and $\Re (w)$ are in phase, that is, if $\eta =0$, then this equation represents a degenerate case of line. Further, for $\eta \ne 0,$ one may verify that the quantity $(B_{0}^2-4A_{0}C_{0}) < 0,$ indicating that the path described by the particle is elliptic. Further, to determine the motion as prograde or retrograde, we shall define a polar angle $\theta$ such that $\tan \theta =\Re (w)/\Re (u).$ The time derivative of the angle $\theta$ is given by

$$\begin{aligned} {\dot{\theta }}=\frac{\Re (u)^2}{\Re (u)^2+\Re (w)^2}\frac{|\mathcal {W}|}{|\mathcal {U}|}\frac{\sin \eta }{\cos ^2(q+\alpha _1)}\omega . \end{aligned}$$

(5.4)

From this equation, one may conclude that the orientation of elliptical motion is prograde (retrograde), according as $\sin \eta >0$ $(<0).$ To determine the axes of motion, namely the semi-major axis and semi-minor axis, we shall reduce equation (5.2) to its standard form, that is, removing the mixed term from the equation. This can be achieved by defining some suitable rotation of co-ordinates through an angle $\beta$ (called the angle of rotation) with respect to vertical axis. This rotation of co-ordinates can be presented by a transformation matrix (say T) given by

$$\begin{aligned} T= \begin{bmatrix} \cos \beta &{} -\sin \beta \\ \sin \beta &{} \cos \beta \end{bmatrix} \end{aligned}$$

(5.5)

such that

$$\begin{aligned} \begin{aligned} \Re (u)= \Re (u)'\cos \beta - \Re (w)'\sin \beta ,\quad \Re (w)= \Re (u)'\sin \beta + \Re (w)'\cos \beta , \end{aligned} \end{aligned}$$

(5.6)

where the terms containing prime denote the corresponding variables in the transformed state. On inserting (5.6) into equation (5.2), the transformed equation of ellipse is obtained as

$$\begin{aligned} \frac{\Re (u)'^2}{\mathcal {B}'^2}+\frac{\Re (w)'^2}{\mathcal {C}'^2}=1, \end{aligned}$$

(5.7)

where

$$\begin{aligned} \mathcal {B}'^2=2\left( \frac{A_{0}+C_{0}-\sqrt{B_{0}^2+(A_{0}-C_{0})^2}}{4A_{0}C_{0}-B_{0}^2}\right) , \quad \mathcal {C}'^2=2\left( \frac{A_{0}+C_{0}+\sqrt{B_{0}^2+(A_{0}-C_{0})^2}}{4A_{0}C_{0}-B_{0}^2}\right) . \end{aligned}$$

Here, $\mathcal {B}'$ and $\mathcal {C}'$ represent, respectively, the length of semi-major and semi-minor axes. Further, from (5.3), one can notice that if $\eta =\pi /2,$ then the coefficient $B_{0}=0.$ For this particular case, the lengths $\mathcal {B}'$ and $\mathcal {C}'$ will be $A_{0}^{-1/2}$ and $C_{0}^{-1/2}$, respectively. From (5.7), it is clear that the particles describe elliptic motion in the vertical plane parallel to the direction of propagating Rayleigh-type surface wave.

6 Special cases

Here, we shall recover some earlier known results as special cases of the present formulation.

6.1 Elastic solid with voids

To recover the dispersion equation of Rayleigh-type waves in elastic solid with voids, we shall assume that the half-space is not placed under the primary magnetic field. For this, we shall set the relevant electro-magnetic parameters H and d equal to zero to obtain $R_{H}=0,$ $c_{\ell \ell }=c_{\ell },$ $\ell _{1}=\ell _{2}=0.$ The dispersion equation (4.9) then reduces to

$$\begin{aligned} \left( 2-\frac{c_{R}^2}{c_{t}^2}\right) ^2=\frac{4m_{1}m_{2}m_{3}(n_{1}-n_{2})}{n_{1}m_{1}-n_{2}m_{2}}. \end{aligned}$$

(6.1)

This dispersion equation is similar to the one obtained earlier by Chandrasekharaiah [16] for the corresponding problem.

6.2 Magneto-elastic solid

Here, we shall ignore the presence of voids from the considered half-space so that the problem reduces to the problem of propagation of Rayleigh-type surface wave in an elastic half-space under magnetic interactions. For this purpose, we shall set the relevant void parameter a equal to zero, then from (3.14) and (4.8), the quantity $n_{1}=0.$ Substituting these values in (4.9), one can obtain

$$\begin{aligned} \left( 2-\frac{c_{R}^2}{c_{t}^2}\right) ^2=4m_{1}m_{3}+(1+m_{3}^2)\ell _{1}. \end{aligned}$$

(6.2)

This is the dispersion equation of Rayleigh-type waves in the magneto-elastic solid half-space.

6.3 Classical elastic solid

If we ignore the presence of both magnetic field and voids from the considered half-space, then the current problem reduces to the classical problem of Rayleigh waves. For this purpose, we shall set the electro-magnetic parameters to zero, that is, $H=d=0,$ so that $R_{H}=0,$ and consequently, $\ell _{1}=0.$ On substituting these values in the dispersion relation (6.2), we obtain

$$\begin{aligned} \left( 2-\frac{c_{R}^2}{c_{t}^2}\right) ^2=4m_{1}m_{3}. \end{aligned}$$

(6.3)

which is a well-known secular equation of Rayleigh wave propagation in Cauchy elastic solid half-space obtained by Rayleigh [1]. Note that (6.3) shall yield the necessary roots provided $m_{1}>0$ and $m_{3}>0.$

7 Computational results and discussions

To discuss the propagation characteristics of Rayleigh-type surface waves, numerical computations have been carried out for a specific model. The numerical values of relevant parameters have been borrowed from Puri and Cowin [12] as

$$\begin{aligned} \begin{aligned}&\lambda = 1.5\times 10^{10} N/m^2, \quad \mu = 7.5\times 10^9 N/m^2, \quad \zeta = 1.2\times 10^{10} N/m^2, \quad \kappa = 0.16 m^2\\&a= 10^{10} N/m^2, \quad \alpha = 8\times 10^9 N, \quad \rho = 2\times 10^3 kg/m^3, \quad d^2= 0.5\times 10^9 N. \end{aligned} \end{aligned}$$

The medium is under the influence of magnetic field; therefore, we shall consider the half-space having varying conducting property. The numerical computations are performed separately for the half-space having high and low electric conductivity.

Fig. 1

Variation in phase speeds $V_{i}$ (ms$^{-1}$) versus frequency f (Hz)

Firstly, we shall consider when the material of the half-space has high electric conductivity. The dispersion equation (4.11) is solved to compute the velocity of Rayleigh-type surface waves for given values of frequency. Here the values of magnetic permeability $\mu _m$ and magnetic field H are taken as 0.5 and 5000 N$^{1/2}$m$^{-1}$, respectively. It is found that there exists only one root satisfying the original frequency equation (4.9). Since $z=c^2_R,$ which is found to be complex valued, therefore for propagating surface waves, we picked up only that value of $c_R$ whose real part is positive. Then, the phase speed $V_R$ of the Rayleigh-type surface wave is computed using the formula given in (4.10).

Figure 1 depicts the phase speeds of all the three body waves $V_i, (i=1,2,3)$ and that of the Rayleigh-type surface waves $V_R$ with frequency parameter f ranging between 0 and $10^3$ KHz on logarithmic scale. It can be noticed from this figure that $V_R < \{V_1,V_2,V_3\},$ indicating that Rayleigh-type wave travels slower than the body waves. Further, the body wave propagating with phase speed $V_1$ is the fastest among all, but exits only after a certain frequency, while all other waves exist for all non-negative values of frequency.

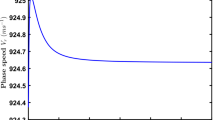
Figure 2 depicts the phase speed $V_{R},$ of Rayleigh-type wave mode, the real parts of $\gamma _{1},$ $\gamma _{2}$ and $\gamma _{3}$ remain positive throughout the frequency.

Fig. 2

Variation in real part of $\gamma _{i}'$s $(i=1,2,3)$ versus frequency f (Hz)

Figure 3 illustrates the comparison of dispersive behavior of Rayleigh-type surface waves in four different models, namely magneto-elastic solid with voids (MESV), elastic solid with voids (ESV), magneto-elastic solid (MES) and elastic solid (ES). One can notice that in the ES and MES models, the surface wave exhibits non-dispersive behavior, whereas in ESV and MESV models, the surface wave exhibits dispersive behavior in low frequency range only and becomes non-dispersive for high frequency range on logarithmic scale. This dispersive nature arises due to the presence of voids in the model. Further, in the high-frequency region, we observe that the surface wave is non-dispersive in all the four models. Also note that, the phase speed of surface wave in MES (MESV) model in the low frequency range on logarithmic scale is much slower than those in ES (ESV) models.

Fig. 3

Variation in phase speed $V_{R}$ (ms$^{-1}$) versus frequency f (Hz)

Figure 4a depicts the variation in phase speed $V_{R}$ with magnetic field H ranging between $10^3$ and $10^5$ N$^{1/2}$m$^{-1}$ on logarithmic scale at constant frequency $f=20$ KHz. One can observe that the phase speed $V_{R}$ decreases significantly with increase in magnetic field. We may conclude that the magnetic field induces hindrance to the motion of Rayleigh-type surface wave.

Figure 4b illustrates the variation in phase speed $V_{R}$ with magnetic permeability $\mu _{m}$ running between 0.001 and 1 on logarithmic scale at constant frequency and constant magnetic field $H=5000$ N$^{1/2}$m$^{-1}.$ Clearly, one can notice that the magnitude of the phase speed of surface wave increases monotonically with magnetic permeability.

Fig. 4

Variation in phase speed $V_{R}$ with a magnetic field H (N$^{1/2}$m$^{-1}$); b magnetic permeability $\mu _m$ at frequency $f=20$ KHz

Next, we shall discuss the behavior of displacement components and various stress components near the interface and in the half-space. For this, we will observe the changes in these components with depth coordinate z at $f=2$ KHz and $f=20$ KHz.

In Figs. 5a, b, the absolute values of displacement components u and w on logarithmic scale are plotted against the depth coordinate z. It can be noticed that the displacement curves of |u| and (|w|) are large near the boundary surface of the half-space, that is, the displacements are maximum near the boundary of the half-space. However, the horizontal displacement component |u| oscillates in comparison to the transverse displacement component |w|. Also, at each frequency, the displacement components |u| and |w| decrease continuously with depth parameter and wipe out finally at larger depth.

Fig. 5

Variation in a longitudinal displacement |u|;  b transverse displacement |w| versus depth coordinate z (m)

Figure 6a reveals the variation in void volume fraction $|\nu |$ with depth coordinate z. Here, it can be noticed that, just like the displacement components, the void volume fraction attains the maximum value near the boundary surface $z=0.$ Moreover, at each frequency, the curve of $|\nu |$ takes a nonzero value up to certain finite depth; thereafter, the curve dies out continuously with increase in depth parameter.

Fig. 6

Comparison of a void volume fraction $|\nu |;$ b tangential stress component $|t_{zx}|;$ (c) normal stress component $|t_{zz}|;$ (d) equilibrated stress vector component $|S_{z}|$ with depth coordinate z

Figure 6b depicts the variation in tangential component $|t_{zx}|$ of stress tensor with the depth coordinate z. It is found that the intensity of stress is maximum near the boundary surface $z=0.$ Further, at high frequency, that is, at $f=20$ KHz, the curves have maximum value which decreases steeply with depth and wipes out ultimately, whereas, at low frequency, that is, at $f=2$ KHz, the curve is almost flat and decline gradually with depth parameter. The pattern of normal component $|t_{zz}|$ of mechanical stress tensor and normal component $|S_{z}|$ of equilibrated stress vector as shown in Fig. 6c and d, respectively, is found to be similar with the depth coordinate z. However, the magnitudes of these stress components may vary from model to model.

In the case when the material is supposed to have low electric conductivity, the phase speed of Rayleigh-type waves $V_{R}$ and that of the body waves $V_{i}, (i=1,2,3)$ exhibits similar behavior against frequency (with di-electric susceptibility $\chi ^E=1.25$ and coupling coefficient $d^2=0.5\times 10^9$), as illustrated in Fig. 1.

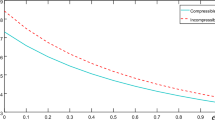
Figure 7 depicts the variation in phase speed $V_{R}$ with dielectric susceptibility $\chi ^E$ running over the range of 0 to 1,  for three different values of frequency. It is evident from this figure that the phase speed increases gradually for each frequency, except at $f=20$ KHz, where the phase speed is nearly constant. Further, it can be observed that the waves travel more slowly at low frequencies than that at high frequencies.

Fig. 7

Variation in phase speed $V_{R}$ (ms$^{-1}$) with di-electric susceptibility $\chi ^E$

8 Conclusions

In the present study, the propagation of Rayleigh-type surface waves in magneto-elastic material containing voids is investigated. Secular equation for Rayleigh-type wave is developed under suitable boundary conditions. Since the medium is kept under primary magnetic field, therefore, we have separately discussed wave propagation characteristics for materials possessing high and low electric conductivity. From the graphical and numerical computations, we may conclude that

• 1. There exist only one Rayleigh-type wave mode propagating with real speed. The wave, in general, is found to be influenced by the presence of voids, elastic and electro-magnetic parameters.

• 2. The Rayleigh-type surface wave exhibits dispersive behavior in low frequency domain. This behavior mainly appears due to the presence of voids in the half-space. However, in high frequency domain, the wave mode exhibits non-dispersive behavior.

• 3. Rayleigh-type wave mode travels slower than the body waves, viz, coupled dilatational waves and a lone shear wave.

• 4. It is found that when the medium with high conductivity is exposed to strong magnetic field, the magnitude of Rayleigh-type surface wave drops down significantly as compared to the classical Rayleigh wave. However, the phase speed increases monotonically with magnetic permeability.

• 5. In a low electric conductive material, it can be noticed that the phase speed of surface wave increases monotonically with di-electric susceptibility in low frequency domain, while, in high frequency domain, the wave travels with a constant speed.

• 6. The particles near the boundary surface describe an elliptical path during the propagation of Rayleigh-type surface wave. Moreover, the orientation of elliptical path is prograde if the phase difference $\eta \in (0,\pi )$ and retrograde if $\eta \in (\pi ,2\pi ).$

Appendix-1

The coefficients of dispersion equation (4.11) are given by

$$\begin{aligned} \begin{aligned}&a_{0}=\epsilon _{5}, \qquad a_{1}=\epsilon _{6}-\Gamma _{1}', \qquad a_{2}=\epsilon _{7}+\Gamma _{1}-\Gamma _{2}', \qquad a_{3}=\epsilon _{8}+\Gamma _{2}-\Gamma _{3}'\\&a_{4}=\epsilon _{9}+\Gamma _{3}-\Gamma _{4}', \qquad a_{5}=\epsilon _{10}+\Gamma _{4}-\Gamma _{5}', \qquad a_{6}=\epsilon _{11}+\Gamma _{5}-\Gamma _{6}',\\&a_{7}=\epsilon _{12}+\Gamma _{6}-\Gamma _{7}', \qquad a_{8}=\epsilon _{13}+1-\Gamma _{8}', \qquad a_{9}=\epsilon _{14}-\Gamma _{9}',\qquad a_{10}=\epsilon _{15},\\&\epsilon _{5}=\frac{\epsilon _{1}^2}{V_{3}^8}, \qquad \epsilon _{6}=\frac{2\epsilon _{1}}{V_{3}^8}\left( \epsilon _{2}-4\epsilon _{1}V_{3}^2\right) , \qquad \epsilon _{7}=\frac{1}{V_{3}^8}\left[ 2\epsilon _{1}\left( \epsilon _{3}-8\epsilon _{2}V_{3}^2+12\epsilon _{1}V_{3}^4\right) +\epsilon _{2}^2\right] ,\\&\epsilon _{8}=\frac{2\epsilon _{1}}{V_{3}^8}\left[ \epsilon _{4}-4(\epsilon _{1}+2\epsilon _{3})V_{3}^2+24\epsilon _{2}V_{3}^4-16\epsilon _{1}V_{3}^6\right] ,\\ \end{aligned} \\ \begin{aligned}&\epsilon _{9}=\frac{1}{V_{3}^8}\left[ \epsilon _{3}\left( \epsilon _{3}-16\epsilon _{2}V_{3}^2+24\epsilon _{1}V_{3}^4\right) +2\epsilon _{4}\left( \epsilon _{2}-8\epsilon _{1}V_{3}^2\right) +16\epsilon _{1}V_{3}^6\left( \epsilon _{1}V_{3}^2-4\epsilon _{2}\right) +24\epsilon _{2}^2V_{3}^4\right] ,\\&\epsilon _{10}=\frac{2}{V_{3}^8}\left[ \epsilon _{4}\left( \epsilon _{3}-8\epsilon _{2}V_{3}^2+24\epsilon _{1}V_{3}^4\right) -4\epsilon _{3}V_{3}^2\left( \epsilon _{3}-6\epsilon _{2}V_{2}^2+8\epsilon _{1}V_{3}^4\right) +16\epsilon _{1}\epsilon _{2}V_{3}^8\right] ,\\&\epsilon _{11}=\frac{1}{V_{3}^8}\left[ \epsilon _{4}\left( \epsilon _{4}-16\epsilon _{3}V_{3}^2+48\epsilon _{2}V_{3}^4-64\epsilon _{1}V_{3}^6\right) +8\epsilon _{3}V_{3}^4\left( 3\epsilon _{3}-8\epsilon _{2}V_{3}^2+4\epsilon _{1}V_{3}^4\right) +16\epsilon _{2}^2V_{3}^8\right] ,\\&\epsilon _{12}=\frac{8}{V_{3}^6}\left[ \epsilon _{4}\left( -\epsilon _{4}+6\epsilon _{3}V_{3}^2-8\epsilon _{2}V_{3}^4+4\epsilon _{1}V_{3}^6\right) -4\epsilon _{3}V_{3}^4\left( \epsilon _{3}-\epsilon _{2}V_{3}^2\right) \right] ,\\&\epsilon _{13}=\frac{2}{V_{3}^4}\left[ \epsilon _{4}\left( 12\epsilon _{4}-32\epsilon _{3}V_{3}^2+\epsilon _{2}V_{3}^4\right) +8\epsilon _{3}^2V_{3}^4\right] , \quad \epsilon _{14}=\frac{32}{V_{3}^2}\epsilon _{4}\left( \epsilon _{3}V_{3}^2-\epsilon _{4}\right) , \quad \epsilon _{15}=16\epsilon _{4}^2,\\&\Gamma =256\left( \frac{V_{1}^2-V_{2}^2}{V_{1}^2V_{2}^2}\right) ^4, \qquad \Gamma _{1}=\frac{\Gamma }{(V_{1}V_{2}V_{3})^4}, \qquad \Gamma _{2}=-2\Gamma _{1}\left( V_{1}^2+V_{2}^2+V_{3}^2\right) ,\\ {}&\Gamma _{3}=\Gamma _{1}\left[ (V_{1}^2+V_{2}^2+V_{3}^2)^2+2(V_{1}^2V_{2}^2+V_{2}^2V_{3}^2+V_{1}^2V_{3}^2)\right] , \qquad \Gamma _{4}=\Gamma _{1}(V_{1}V_{2}V_{3})^2-\frac{\Gamma _{2}}{2},\\&\Gamma _{5}=\left[ \frac{\Gamma _{3}}{2}-\frac{\Gamma _{2}^2}{8\Gamma _{1}}\right] ^2-\frac{\Gamma _{2}}{\Gamma _{1}}\left[ \Gamma _{4}+\frac{\Gamma _{2}}{2}\right] , \qquad \Gamma _{6}=\left[ \frac{\Gamma _{3}}{2\Gamma _{1}}-\frac{\Gamma _{2}^2}{8\Gamma _{1}^2}\right] \left[ \Gamma _{4}+\frac{\Gamma _{2}}{2}\right] ,\\&\Gamma _{1}'=-\frac{2\epsilon _{1}'\sqrt{\Gamma _{1}}}{V_{3}^4}, \qquad \Gamma _{2}'=-\frac{\sqrt{\Gamma _{1}}}{V_{3}^4}\left[ 2\epsilon _{2}'-8\epsilon _{1}'V_{3}^2+\frac{\epsilon _{1}'\Gamma _{2}}{\Gamma _{1}}\right] ,\\ {}&\Gamma _{3}'=-\frac{\sqrt{\Gamma _{1}}}{V_{3}^4}\left[ 2\epsilon _{3}'-8\epsilon _{2}'V_{3}^2+8\epsilon _{1}'V_{3}^4+2\epsilon _{1}'\left( \frac{\Gamma _{3}}{2}-\frac{\Gamma _{2}^2}{8\Gamma _{1}}\right) +(\epsilon _{2}'-4\epsilon _{1}'V_{3}^2)\frac{\Gamma _{2}}{\Gamma _{1}}\right] ,\\&\Gamma _{4}'=-\frac{\sqrt{\Gamma _{1}}}{V_{3}^4}\left[ 2\epsilon _{4}'-8\epsilon _{3}'V_{3}^2+8\epsilon _{2}'V_{3}^4+(2\epsilon _{2}'-8\epsilon _{1}'V_{3}^2)\left( \frac{\Gamma _{3}}{2}-\frac{\Gamma _{2}^2}{8\Gamma _{1}}\right) \right. \\ {}&\left. +(\epsilon _{3}'-4\epsilon _{2}'V_{3}^2+4\epsilon _{1}'V_{3}^4)\frac{\Gamma _{2}}{\Gamma _{1}}-2\epsilon _{1}'\right] ,\\&\Gamma _{5}'=-\frac{\sqrt{\Gamma _{1}}}{V_{3}^4}\left[ 8(\epsilon _{3}'V_{3}^4-\epsilon _{4}'V_{3}^2)+(\epsilon _{4}'-4\epsilon _{3}'V_{3}^2+4\epsilon _{2}'V_{3}^4)\frac{\Gamma _{2}}{\Gamma _{1}}\right] \\&\qquad -\frac{\sqrt{\Gamma _{1}}}{V_{3}^4}\left[ (\epsilon _{3}'-4\epsilon _{2}'V_{3}^2+4\epsilon _{1}'V_{3}^4)\left( \Gamma _{3}-\frac{\Gamma _{2}^2}{4\Gamma _{1}}\right) -\frac{2}{\Gamma _{1}}(\epsilon _{2}'-4\epsilon _{1}')\left( \Gamma _{4}+\frac{\Gamma _{2}}{2}\right) \right] ,\\&\Gamma _{6}'=-\frac{\sqrt{\Gamma _{1}}}{V_{3}^4}\left[ 8\epsilon _{4}'V_{3}^4+4V_{3}^2(\epsilon _{3}'V_{3}^2-\epsilon _{4}')\frac{\Gamma _{2}}{\Gamma _{1}}+2(\epsilon _{4}'-4\epsilon _{3}'V_{3}^2+\epsilon _{2}'V_{3}^4)\left( \Gamma _{3}-\frac{\Gamma _{2}^2}{4\Gamma _{1}}\right) \right] \\&\qquad \frac{2}{\sqrt{\Gamma _{1}}V_{3}^4}\left[ (\epsilon _{3}'-4\epsilon _{2}'V_{3}^2+4\epsilon _{1}'V_{3}^4)\left( \Gamma _{4}+\frac{\Gamma _{2}}{2}\right) \right] ,\\&\Gamma _{7}'=-\frac{\sqrt{\Gamma _{1}}}{V_{3}^4}\left[ 4\epsilon _{4}'\frac{\Gamma _{2}}{\Gamma _{1}}+8V_{3}^2(\epsilon _{3}'V_{3}^2-\epsilon _{4}')\left( \Gamma _{3}-\frac{\Gamma _{2}^2}{4\Gamma _{1}}\right) +\frac{2}{\Gamma _{1}}(\epsilon _{4}'-4\epsilon _{3}'V_{3}^2+\epsilon _{2}'V_{3}^4)\left( \Gamma _{4}+\frac{\Gamma _{2}}{2}\right) \right] ,\\&\Gamma _{8}'=\frac{4\sqrt{\Gamma }}{V_{3}^2}\left[ \epsilon _{4}'V_{3}^2\left( \Gamma _{3}-\frac{\Gamma _{2}^2}{4\Gamma _{1}}\right) -2\epsilon _{4}'+2\epsilon _{3}'V_{3}^2\right] , \qquad \Gamma _{9}'=128\epsilon _{4}', \qquad \epsilon _{1}=\frac{\delta _{1}^2\Omega _{2}}{V_{2}^2}-\frac{\delta _{2}^2\Omega _{1}}{V_{1}^2},\\&\epsilon _{2}=\delta _{2}^4\Omega _{1}-\delta _{1}^4\Omega _{2}-4\epsilon _{1}, \qquad \epsilon _{3}=4\left[ \left( \frac{\Omega _{2}}{V_{2}^2}-\frac{\Omega _{1}}{V_{1}^2}\right) +(\delta _{1}^2\Omega _{2}-\delta _{2}^2\Omega _{1})\right] , \qquad \epsilon _{4}=4(\Omega _{1}-\Omega _{2}),\\ \end{aligned} \\ \begin{aligned}&\epsilon _{1}'=-\left( \frac{\delta _{1}^2\Omega _{2}}{V_{2}^2}+\frac{\delta _{2}^2\Omega _{1}}{V_{1}^2}\right) , \qquad \epsilon _{2}'=\delta _{2}^4\Omega _{1}+\delta _{1}^4\Omega _{2}-4\epsilon _{1}', \qquad \epsilon _{4}'=4(\Omega _{1}+\Omega _{2}), \\ {}&\epsilon _{3}'=-4\left[ \left( \frac{\Omega _{2}}{V_{2}^2}+\frac{\Omega _{1}}{V_{1}^2}\right) +(\delta _{1}^2\Omega _{2}+\delta _{2}^2\Omega _{1})\right] ,\qquad \Omega _{1}^2=\frac{1}{c_{\ell \ell }^2}-\frac{1}{V_{1}^2},\qquad \Omega _{2}^2=\frac{1}{c_{\ell \ell }^2}-\frac{1}{V_{2}^2},\\&\delta _{1}^2=\frac{1}{V_{3}^2}\left( 1+\frac{L_{H}}{V_{1}^2}\right) , \qquad \delta _{2}^2=\frac{1}{V_{3}^2}\left( 1+\frac{L_{H}}{V_{2}^2}\right) , \qquad L_{H}=\alpha _{H}^2\left[ 1-\frac{1+\mu _{m}^2}{\mu _{m}}\right] . \end{aligned} \end{aligned}$$